Partition Bounded Sets Into Sets Having Smaller Diameters

Abstract

For each positive integer m and each real finite dimensional Banach space X, we set $\beta (X,m)$ to be the infimum of $\delta \in (0,1]$ such that each set $A\subset X$ having diameter 1 can be represented as the union of m subsets of A whose diameters are at most $\delta$. Elementary properties of $\beta (X,m)$, including its stability with respect to X in the sense of Banach-Mazur metric, are presented. Two methods for estimating $\beta (X,m)$ are introduced. The first one estimates $\beta (X,m)$ using the knowledge of $\beta (Y,m)$, where Y is a Banach space sufficiently close to X. The second estimation uses the information about $\beta _X(K,m)$, the infimum of $\delta \in (0,1]$ such that $K\subset X$ is the union of m subsets having diameters not greater than $\delta$ times the diameter of K, for certain classes of convex bodies K in X. In particular, we show that $\beta (l_p^3,8)\le 0.925$ holds for each $p\in [1,+\infty ]$ by applying the first method, and we proved that $\beta (X,8)<1$ whenever X is a three-dimensional Banach space satisfying $\beta _X(B_X,8)<\frac{221}{328}$, where $B_X$ is the unit ball of X, by applying the second method. These results and methods are closely related to the extension of Borsuk’s problem in finite dimensional Banach spaces and to C. Zong’s computer program for Borsuk’s conjecture.

1 Introduction

Let $X=({\mathbb {R}}^n,\left\| \cdot \right\| )$ be an n-dimensional Banach space with unit ball $B_X$. For each $A\subset X$, we denote by ${{\,\mathrm{int}\,}}{A}$ and ${{\,\mathrm{bd}\,}}{A}$ the interior and the boundary of A, respectively. When A is nonempty and bounded, we denote by $\delta \left( A\right)$ the diameter of A. I.e., . A compact convex subset of X having interior points is called a convex body. Since any two norms on ${\mathbb {R}}^n$ induce the same topology, K is a convex body (is bounded, resp.) in X if and only if it is a convex body (is bounded, resp.) in ${\mathbb {E}}^n=({\mathbb {R}}^n,\left\| \cdot \right\| _E)$, where $\left\| \cdot \right\| _E$ is the Euclidean norm. Let ${\mathcal {K}}^n$ be the set of all convex bodies in ${\mathbb {E}}^n$. A bounded subset A of X is said to be complete if . It is clear that each complete set is closed and convex. For each bounded subset A of X, there always exists a complete set $A^c$ (cf. the begining of Section 2 in [24] for the existence in the finite-dimensional situation), called a completion of A, with diameter $\delta \left( A\right)$ containing A. Note that A may have different completions. Put

In 1933, Borsuk [5] posed the following:

Problem 1

(Borsuk’s Problem). Is it possible to partition every bounded subset of ${\mathbb {E}}^n$ into $n+1$ sets of smaller diameter?

The answer is affirmative when $n\le 3$ (cf. [10, 14, 17], or [16]), is negative for all $n\ge 64$ (cf. [4] and Theorem 1 in [19]).

Progess has been made by providing upper bounds for , where b(A), called the Borsuk number of A, is the minimal positive integer m such that A is the union of m subsets having smaller diameter. For example, L. Danzer (cf. [9]), M. Lassak (cf. [21]), and O. Schramm (cf. [26] and [6]) showed that

respectively.

One can also study Problem 1 via estimating , where m is a positive integer and, for each $A\in {\mathcal {B}}^n$,

Here we used the shorthand notation .

In 2020, C. Zong (cf. [32]) proved that $\beta (A,m)$ is uniformly continuous on the space ${\mathcal {K}}^n$ endowed with the Hausdorff metric, and reformulated Problem 1 as the following:

Problem 2

Does there exists a positive number $\alpha _n<1$ such that

$$\begin{aligned} \beta (K,n+1)\le \alpha _n,~\forall K\in {\mathcal {D}}^n, \end{aligned}$$

where

Some known estimations of $\beta (n,m)$ are listed in Table 1 below (cf., [12, 14, 20], and [13]).

Table 1 Known estimations on $\beta (n,m)$

Grünbaum extended Borsuk’s problem to the case of Banach spaces and asked the following (cf. [15]):

Problem 3

Let $A\subset X=({\mathbb {R}}^n,\left\| \cdot \right\| )$ be bounded. What is the smallest positive integer m, denoted by $b_X(A)$, such that A can be represented as the union of m sets having smaller diameter.

Put

It is clear that

$$\begin{aligned} b_X(K)\le c(K),~\forall K\in {\mathcal {K}}^n, \end{aligned}$$

(1)

where c(K) is the least number of smaller homothetic copies of K needed to cover K. Indeed, if is a collection of smaller homothetic copies of K that can cover K, then we have

Since Hadwiger’s covering conjecture (see, e.g., [1, 3, 8, 23, 31]) asserts that $c(K)\le 2^n,~\forall K\in {\mathcal {K}}^n$, it is reasonable to make the following conjecture (cf. [2, p. 75]):

Conjecture 1

For each integer $n\ge 3$, $B(n)=2^n$.

When X is two-dimensional and $A\in {\mathcal {B}}^2$, (cf. [3, §33]). Therefore, $B(2)=4$. Let , where

L. Yu and C. Zong [30] proved that

$$\begin{aligned} b(l_p^3)\le 8,~\forall p\in [1,+\infty ]. \end{aligned}$$

(2)

By the main result of [18] and (1), there exist universal constants $c_1$ and $c_2 > 0$ such that $B(n)\le c_1 4^n e^{-c_2\sqrt{n}},~\forall n\ge 2$. Despite this progress, Conjecture 1 is still open when $n\ge 3$.

In this paper, we study Conjecture 1 by estimating

for $A\in {\mathcal {B}}^n$, and

We focus mainly, but not only, on the case $n=3$.

In Sect. 2, we present elementary properties of $\beta (X,m)$, including its stability with respect to X in the sense of Banach-Mazur metric. In Sect. 3, we provide an estimation of $\beta (X,8)$ for three-dimensional Banach spaces X such that $\beta _X(B_X,8)$ is sufficiently small. In Sect. 4, we show that

$$\begin{aligned} \beta (l_p^3,8)\le 0.925,~\forall p\in [1,+\infty ], \end{aligned}$$

which can be viewed as a quantitative version of Yu and Zong’s result (2).

2 Elementary properties of $\beta (X,m)$

Proposition 1

For each finite dimensional Banach space $X=({\mathbb {R}}^n,\left\| \cdot \right\| )$ and each positive integer m, we have

Proof

Put . We only need to show that $\beta (X,m)\le \beta$. Let A be an arbitrary set in ${\mathcal {B}}^n$, and $A^c$ be a completion of A. For each $\varepsilon >0$, there exists a collection of subsets of $A^c$ such that

It follows that

Thus

which implies that $\beta _X(A,m)\le \beta _X(A^c,m)$. Thus $\beta (X,m)\le \beta$ as claimed. $\square$

Let ${\mathcal {T}}^n$ be the set of all non-singular linear transformations on ${\mathbb {R}}^n$. The (multiplicative) Banach-Mazur metric $d_{BM}^M:~{\mathcal {K}}^n \times {\mathcal {K}}^n \mapsto {\mathbb {R}}$ is defined by

The infimum is clearly attained. When both $K_1$ and $K_2$ are symmetric with respect to $o$, we have

In this situation, $d_{BM}^M(K_1, K_2)$ equals to the Banach-Mazur distance between the Banach spaces X and Y having $K_1$ and $K_2$ as unit balls, respectively. I.e.,

We have the following result showing the stability of $\beta (X,m)$ with respect to X in the sense of Banach-Mazur metric.

Theorem 2

If $X=({\mathbb {R}}^n,\left\| \cdot \right\| _X)$ and $Y=({\mathbb {R}}^n,\left\| \cdot \right\| _Y)$ are two Banach spaces satisfying $d_{BM}^M(X,Y)\le \gamma$ for some $\gamma \ge 1$, then

$$\begin{aligned} \beta (X,m)\le \gamma \beta (Y,m),~\forall m\in {\mathbb {Z}}^{+}. \end{aligned}$$

Proof

By applying a suitable linear transformation if necessary, we may assume that

$$\begin{aligned} B_Y\subseteq B_X\subseteq \gamma B_Y. \end{aligned}$$

In this situation we have, for each $x\in {\mathbb {R}}^n$,

Hence,

$$\begin{aligned} \left\| x\right\| _X\le \left\| x\right\| _Y\le \gamma \left\| x\right\| _X. \end{aligned}$$

(3)

In the rest of this proof, we denote by $\delta _X(A)$ and $\delta _Y(A)$ the diameter of a bounded subset A of ${\mathbb {R}}^n$ with respect to $\left\| \cdot \right\| _X$ and $\left\| \cdot \right\| _Y$, respectively. By (3), we have

$$\begin{aligned} \delta _X(A)\le \delta _Y(A)\le \gamma \delta _X(A),~\forall A\in {\mathcal {B}}^n. \end{aligned}$$

(4)

Let A be a bounded subset of X. Then A is also bounded in Y. Let $A^c$ be a completion of A in Y. For any $\varepsilon >0$, there exists a collection of subsets of $A^c$ such that $A^c$ is the union of this collection and that

Then

$$\begin{aligned} A=A\cap A^c=\bigcup \limits _{i\in [m]}(B_i\cap A), \end{aligned}$$

and, by (4),

Therefore, $\beta _X(A,m)\le \gamma \beta _Y(A^c,m)$. It follows that $\beta (X,m)\le \gamma \beta (Y,m)$. $\square$

Corollary 3

If $X=({\mathbb {R}}^n,\left\| \cdot \right\| _X)$ and $Y=({\mathbb {R}}^n,\left\| \cdot \right\| _Y)$ are isometric, then $\beta (X,m)=\beta (Y,m)$.

Proposition 4

Let $l_\infty ^n=({\mathbb {R}}^n,\left\| \cdot \right\| _\infty )$. Then $\beta (l_\infty ^n,2^n)=\frac{1}{2}$.

Proof

Put $X=l_\infty ^n$. Then every complete set in X is a homothetic copy of $B_X$, see [11] and [27]. Therefore,

$$\begin{aligned} \beta _X(A,2^n)=\beta _X(B_X,2^n),~\forall A\in {\mathcal {C}}_X. \end{aligned}$$

Thus it sufficies to show $\beta _X(B_X,2^n)=\frac{1}{2}$.

On the one hand, $B_X=\frac{1}{2}B_X+\frac{1}{2}V$, where V is the set of vertices of $B_X$. Since the cardinality of V is $2^n$, we have $\beta _X(B_X,2^n)\le \frac{1}{2}$.

On the other hand, suppose that $B_X$ is the union of $2^n$ of its subsets $B_1,\ldots ,B_{2^n}$. For each $i\in [2^n]$, let $B_i^c$ be a completion of $B_i$. Then

$$\begin{aligned} B_X\subseteq \bigcup \limits _{i\in [2^n]}B_i^c. \end{aligned}$$

It follows that

which implies that . Thus $\beta _X(B_X,2^n)\ge \frac{1}{2}$, which completes the proof. $\square$

Corollary 5

Let $X=({\mathbb {R}}^n,\left\| \cdot \right\| )$. If $d_{BM}^M(X,l_\infty ^n)<2$, then $\beta (X,2^n)<1$.

We end this section with the following result.

Proposition 6

.

Proof

Put . Let $K\subset {\mathbb {R}}^2$ be a planar convex body. By the main result in [22], K can be covered by four translates of $\frac{\sqrt{2}}{2}K$. It follows that $\beta _X(K,4)\le \frac{\sqrt{2}}{2}$ holds for each two-dimensional Banach space X. Thus, $\eta \le \frac{\sqrt{2}}{2}$.

Let $X=l_2^2$ and $B_X$ be the unit disk of $l_2^2$. To show that $\eta \ge \frac{\sqrt{2}}{2}$, we only need to prove $\beta _X(B_X,4)\ge \frac{\sqrt{2}}{2}$. Suppose the contrary that $B_X$ is the union of $A_1, A_2, A_3, A_4$, where

Let $v_1$, $v_2$, $v_3$, and $v_4$ be the vertices of a square inscribed in the unit circle $S_X$ of X. Then for any

$$\begin{aligned} \left\| v_i-v_j\right\| \ge \sqrt{2}. \end{aligned}$$

Assume without loss of generality that $v_1\in A_1$ and $v_2\in A_2,$ then

$$\begin{aligned} \frac{v_1+v_2}{\left\| v_1+v_2\right\| }\notin A_1\cup A_2. \end{aligned}$$

Assume that $\frac{v_1+v_2}{\left\| v_1+v_2\right\| }\in A_3$. Then $v_3, v_4\notin A_1\cup A_2\cup A_3$, and $A_4$ cannot contain both $v_3$ and $v_4$, a contradiction. Thus, $\beta _X(B_X,4)\ge \frac{\sqrt{2}}{2}$ as claimed. $\square$

3 Estimating $\beta (X,m)$ via $\beta _X(B_X,m)$

Let S be an n-dimensional simplex in $X=({\mathbb {R}}^n,\left\| \cdot \right\| )$. If the distance between each pair of vertices of S all equals to $\delta \left( S\right)$, then we say that S is equilateral.

Proposition 7

Let T be a triangle in ${\mathbb {R}}^2$ and $X=({\mathbb {R}}^2,\left\| \cdot \right\| )$. Then $\beta _X(T,4)\le \frac{1}{2}$. If T is equilateral in X, then $\beta _X(T,4)=\frac{1}{2}$.

Proof

We only need to consider the case when T is equilateral. Assume without loss of generality that $\delta \left( T\right) =1$. It is clear that $\beta _X(T,4)\le \frac{1}{2}$. Denote by the set of vertices of T, and by the set of midpoints of three sides of T. Then $\left\| p-q\right\| =\left\| p-r\right\| =\left\| q-r\right\| =\frac{1}{2}$.

Suppose the contrary that $\beta _X(T,4)<\frac{1}{2}$. Then there exist four subsets $T_1,T_2,T_3,T_4$ of T such that $T=\bigcup _{i\in [4]}T_i$ and that . We may assume that $a\in T_1$, $b\in T_2$, and $c\in T_3$. Since , we have , which is impossible. Thus $\beta _X(T,4)=\frac{1}{2}$ as claimed. $\square$

Proposition 8

Let T be a 3-dimensional simplex in $X=({\mathbb {R}}^3,\left\| \cdot \right\| )$. Then

$$\begin{aligned} \beta _X(T,8)\le \frac{9}{16}. \end{aligned}$$

Proof

Denote by the set of vertices of T. Without loss of generality we may assume that $o=\frac{1}{4}\sum _{i\in [4]}v_i$. For each $i\in [4]$, put $T_i=\frac{7}{16}v_i+\frac{9}{16}T$. Then the portion of T not covered by $\bigcup _{i\in [4]}T_i$ is

Suppose that $\sum _{i\in [4]}\lambda _iv_i\in T_5$. Then

It follows that $\sum _{i\in [4]}\lambda _iv_i\in -\frac{3}{4}T$. Thus $T_5\subset -\frac{3}{4}T$. It is not difficult to verify that T can be covered by 4 translates of $\frac{3}{4}T$, which implies that $T_5$ can be covered by 4 translates of $-\frac{9}{16}T$. Therefore, $\beta _X(T,8)\le \frac{9}{16}$. $\square$

Proposition 9

Let T be a 3-dimensional simplex in $X=({\mathbb {R}}^3,\left\| \cdot \right\| )$. Then

$$\begin{aligned} \beta _X(T,9)\le \frac{9}{17}. \end{aligned}$$

Proof

We use the idea in the proof of Proposition 8. For each $i\in [4]$, put $T_i=\frac{8}{17}v_i+\frac{9}{17}T$. Then the portion of T not covered by $\bigcup _{i\in [4]}T_i$ is

As in the proof of Proposition 8, $T_5\subset -\frac{15}{17}T$. By using the idea in the proof of Proposition 8 again, one can show that $\beta _X(T,5)\le \frac{3}{5}$. Therefore, $T_5$ is the union of 5 subsets of $T_5$ whose diameters are not larger than $\frac{9}{17}\delta \left( T\right)$. It follows that $\beta _X(T,9)\le \frac{9}{17}$. $\square$

Remark 10

The estimations in Proposition 8 and Proposition  9 are independent of the choice of norm on ${\mathbb {R}}^3$.

For a convex body K, the Minkowski measure of symmetry, denoted by s(K), is defined as

It is known that

$$\begin{aligned} 1\le s(K) \le n,~\forall K\in {\mathcal {K}}^{n}; \end{aligned}$$

the equality on the left holds if and only if K is centrally symmetric, and the equality on the right holds if and only if K is an n-dimensional simplex (cf. [29]).

The following lemma shows the stability of $\beta _X(K,m)$ with respect to K.

Lemma 11

Let $X=({\mathbb {R}}^n,\left\| \cdot \right\| )$, and K and L be two convex bodies in X. If there exist a number $\gamma \ge 1$ and a point $c\in {\mathbb {R}}^n$ such that

$$\begin{aligned} K\subseteq L\subseteq \gamma K+c, \end{aligned}$$

then, for each $m\in {\mathbb {Z}}^{+}$, we have

$$\begin{aligned} \beta _X(L,m)\le \gamma \beta _X(K,m). \end{aligned}$$

Proof

For each $\varepsilon >0$, there exists a collection of subsets of $\gamma K+c$ such that

$$\begin{aligned} \gamma K+c=\bigcup _{i\in [m]}K_i \end{aligned}$$

and

$$\begin{aligned} \delta \left( K_i\right) \le \gamma \delta \left( K\right) \beta _X(K,m)+\varepsilon \le \gamma \delta \left( L\right) \beta _X(K,m)+\varepsilon ,~\forall i\in [m]. \end{aligned}$$

Since

we have

$$\begin{aligned} \beta _X(L,m)\le \gamma \beta _X(K,m)+\frac{\varepsilon }{\delta \left( L\right) }. \end{aligned}$$

Since $\varepsilon$ is arbitrary, $\beta _X(L,m)\le \gamma \beta _X(K,m)$ as claimed. $\square$

Theorem 12

Let $X=({\mathbb {R}}^3,\left\| \cdot \right\| )$, $m\in {\mathbb {Z}}^{+}$, and

We have

Proof

Let K be a complete set in X, $\varepsilon$ be a number in . We distinguish two cases.

Case 1. The Banach-Mazur distance from K to three-dimensional simplices is bounded from the above by

$$\begin{aligned} 1+\frac{4\varepsilon }{1-3\varepsilon }. \end{aligned}$$

Then there exist a tetrahedron T and a point $c\in {\mathbb {R}}^3$ such that

By Lemma 11, we have

Case 2. The Banach-Mazur distance from K to three-dimensional simplex is at least

$$\begin{aligned} 1+\frac{4\varepsilon }{1-3\varepsilon }. \end{aligned}$$

From Theorem 2.1 in [25], it follows that

$$\begin{aligned} s(K)\le 3-\varepsilon . \end{aligned}$$

Denote by R(K) the circumradius of K. Theorem 1.1 in [7] shows that

$$\begin{aligned} s(K)=\frac{R(K)/\delta \left( K\right) }{1-R(K)/\delta \left( K\right) }. \end{aligned}$$

It follows that

$$\begin{aligned} \frac{R(K)}{\delta \left( K\right) }\le \frac{3-\varepsilon }{4-\varepsilon }. \end{aligned}$$

By a suitable translation if necessary, we may assume that

$$\begin{aligned} K\subseteq \frac{3-\varepsilon }{4-\varepsilon }\delta \left( K\right) B_X. \end{aligned}$$

For each $\gamma >0$, there exists a collection such that

$$\begin{aligned} B_X=\bigcup _{i\in [8]}B_i\quad \text {and}\quad \delta \left( B_i\right) \le 2\beta _X(B_X,m)+\gamma ,~\forall i\in [m]. \end{aligned}$$

It follows that

$$\begin{aligned} \beta _X(K,m)\le \frac{2(3-\varepsilon )}{4-\varepsilon }\beta _X(B_X,m)+\frac{3-\varepsilon }{4-\varepsilon }\gamma . \end{aligned}$$

Hence

$$\begin{aligned} \beta _X(K,m)\le \frac{2(3-\varepsilon )}{4-\varepsilon }\beta _X(B_X,m). \end{aligned}$$

This completes the proof. $\square$

Corollary 13

Let $X=({\mathbb {R}}^3,\left\| \cdot \right\| )$. If $\beta _X(B_X,8)<\frac{221}{328}$, then $\beta (X,8)<1$.

Proof

Since $\frac{2(3-\frac{7}{57})}{4-\frac{7}{57}}\frac{221}{328}=1$ and

$$\begin{aligned} \frac{2(3-\varepsilon )}{4-\varepsilon }=2-\frac{2}{4-\varepsilon } \end{aligned}$$

is continuous with respect to $\varepsilon$ on $(0,\frac{1}{3})$, there exists a number $\varepsilon _0<\frac{7}{57}$ such that

$$\begin{aligned} \frac{2(3-\varepsilon _0)}{4-\varepsilon _0}\beta _X(B_X,8)<1 \end{aligned}$$

It follows that

$\square$

In particular, Corollary 13 shows that $\beta (l_1^3,8)<1$ since the unit ball of $l_1^3$ can be covered by 8 balls having radius $\frac{2}{3}<\frac{221}{328}$. By solving the optimization problem

one can show that $\beta (l_1^3,8)\le 0.989\ldots$. This estimation can be improved, see the next section.

4 An estimation of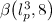

Lemma 14

For each $p\in [1,2]$, .

Proof

Put $c_1=(3,3,-2)$, $c_2=(-2,3,3)$, $c_3=(3,-2,3)$. Denote by Q the parallelipiped having

as the set of vertices. We have

It follows that

$$\begin{aligned} \frac{1}{2\left\| (1,1,4)\right\| _p}Q\subset B_p^3, \end{aligned}$$

where $B_p^3$ is the unit ball of $l_p^3$. Let q be the number satisfying

$$\begin{aligned} \frac{1}{p}+\frac{1}{q}=1, \end{aligned}$$

and let $f_1$, $f_2$, $f_3$ be linear functionals defined on $l_p^3$ such that, for any $(\alpha ,\beta ,\gamma )\in {\mathbb {R}}^3$,

Then

Thus the distances from the origin $o$ to the facets of Q all equals to

$$\begin{aligned} \frac{100}{\left\| (15,-5,15)\right\| _q}. \end{aligned}$$

It follows that

$$\begin{aligned} \frac{1}{2\left\| (1,1,4)\right\| _p}Q\subset B_p^3\subset \frac{\left\| (15,-5,15)\right\| _q}{100}Q=\frac{\left\| (1,1,4)\right\| _p\left\| (3,1,3)\right\| _q}{10}\frac{1}{2\left\| (1,1,4)\right\| _p}Q, \end{aligned}$$

which implies that

$$\begin{aligned} d_{BM}^M(l_p^3,l_\infty ^3)\le \frac{\left\| (1,1,4)\right\| _p\left\| (3,1,3)\right\| _q}{10}\le \frac{\left\| (1,1,4)\right\| _2\left\| (3,1,3)\right\| _2}{10}=\frac{\sqrt{18\cdot 19}}{10}. \end{aligned}$$

$\square$

Remark 15

The last inequality in Lemma 14 can be verified in the following way. Put

Numerical results show that $f'(p)=0$ has a unique solution $p_0\approx 1.320$ in [1, 2], and

$$\begin{aligned} f(p_0)\approx 17.550<f(2). \end{aligned}$$

Moreover, $f(1)<f(2)$. Thus f(p) is maximized at $p=2$.

Numerical results show that when $p\in [1,1.736)$,

$$\begin{aligned} \frac{\left\| (1,1,4)\right\| _p\left\| (3,1,3)\right\| _q}{10}\le \frac{9}{5}. \end{aligned}$$

The estimation in Lemma 14 could be improved by choosing points $c_1$, $c_2$, $c_3$ more carefully for different $p\in [1,2]$.

Theorem 16

We have the following estimation:

Proof

First we consider the case when $p\in [2,+\infty ]$. By Proposition 37.6 in [28], $d_{BM}^M(l_p^3,l_\infty ^3)=3^{1/p}$, this together with Theorem 2, implies that $\beta (l_p^3,8)\le \frac{3^{1/p}}{2}\le \frac{\sqrt{3}}{2}$.

The case when $p\in [1,2]$ follows directly from Lemma 14 and Theorem 2. $\square$