1 Introduction

1.1 Rationale

In the past decade, two major tsunamis, the 2004 Indian Ocean (IO) tsunami (Grilli et al. 2007; Ioualalen et al. 2007) and the 2011 Tohoku tsunami (Grilli et al. 2013), caused tens of thousands of fatalities and enormous destruction in Indonesia, and six other countries in the IO basin, and in Japan. These two extreme events, which were triggered by the 3rd and 5th largest earthquakes ever recorded, of moment magnitude \(M_w = 9.3\) and 9.05, respectively, reminded us that tsunamis are among the most devastating natural disasters that can impact our increasingly populated coastal areas. Where they cause significant onshore inundation, tsunamis have enormous destructive power as a result of the combination of high flow velocity \(U_t\) with total flow depth d (or momentum flux \(\rho dU_t^2\), with \(\rho \) the fluid density). Moreover, the hazard posed by large tsunamis can be reinforced when their source is close to the nearest coastal areas, and thus both their energy spreading is low and their propagation time is short. In the latter case, warning times will also be short, particularly when using traditional means of detection such as seafloor pressure sensors or buoys, and thus there will be little time for completely evacuating coastal populations.

Standard point data measurements of incoming tsunami waves (i.e., pressure gages or buoys) are local and, hence, may not record the incoming tsunami waves if they are also localized, and are often destroyed by the earthquake or the tsunami in the most impacted areas. A short tsunami propagation time was one of the reasons for the high casualties in Banda Aceh, Indonesia, during the 2004 IO tsunami: the city was impacted by large waves and inundation only 15–20 min after the earthquake was triggered in the nearby Sumatra-Andaman subduction zone. Likewise, during the 2011 Tohoku tsunami, large waves and inundation arrived in northern Honshu only 20–25 min after the earthquake triggering in the nearby Japan Trench (JT), causing the nearly complete destruction of some coastal cities and killing entire populations who had been unable to evacuate, despite the increasingly dire warnings, they eventually received, that the earthquake and generated tsunami had been much larger than initially estimated.

While such extreme seismic events are fortunately quite rare, with return periods of 100–1000 years, in many coastal regions of the world with moderate seismicity, the greatest tsunami risk from near-field sources may result, not from co-seismic tsunamis, but from tsunamis induced by submarine mass failures (SMFs) or from meteo-tsunamis. SMFs can be triggered on or near the continental shelf break or slope, by earthquakes as low as \(M_w= 7\) (e.g., Tappin et al. 2008; Fine et al. 2005), that are much more frequent than megathrust earthquakes; given enough sediment accumulation, huge volumes of sediment can be mobilized over significant vertical drops and generate very large “landslide” tsunamis (Grilli and Watts 1999, 2005; Ward 2001; Grilli et al. 2002; Watts et al. 2005; Tappin et al. 2008). Kawamura et al. (2014) recently reviewed potential tsunamigenic submarine landslides in active margins and showed their widespread occurrence historically, as well as a variety of trigger mechanisms besides seismicity. Meteo-tsunamis are tsunami-like long waves generated by unusual weather systems, causing fast moving squalls with low atmospheric pressure. If these systems move at or close to the long wave celerity on the shelf, much of their energy can be transferred to waves by way of resonance (Rabinovich and Stephenson 2004; Monserrat et al. 2006). On June 13, 2013, a meteo-tsunami was triggered along the US upper east coast, which caused significant resonant oscillations in many harbors in the region, in particular in Rhode Island (ten Brink et al. 2014); this meteo-tsunami was recorded as far as Puerto Rico.

Although few confirmed landslide tsunamis have been identified in recent history, they have been devastating. The 1998 Papua New Guinea tsunami is one such case, where a \(M_w = 7.1\) earthquake only caused a moderate tsunami, but then triggered, with some delay, a large and deep underwater slump (i.e., a nearly rigid rotational SMF), which generated much more devastating waves that killed over 2000 people on the nearby the Sissano spit (Tappin et al. 2008). Large SMFs can also be associated with large earthquakes. After observing, through careful modeling of the seismic source and resulting co-seismic tsunami, that they could not reproduce the up to 40 m inundation and runup that destroyed the Sanriku area during the 2011 Tohoku tsunami, many scientists concluded that there should have been some other source or mechanism at play to explain the tsunami generation, such as splay faults or SMFs (Grilli et al. 2013). Based on analyses of wave and seafloor data, Tappin et al. (2014) identified and parameterized a large post-earthquake SMF with an estimated 500 km\(^3\) volume, deep near the JT, north of the main rupture, whose motion could generate additional higher-frequency waves similar to those observed at a several buoys. A detailed modeling of wave generation and propagation from the dual seismic-SMF source closely reproduced all of the observations made at nearshore and deep water buoys, and runup and inundation measured onshore.

Because they need large sediment accumulation to occur, SMFs are triggered more often on continental slopes, in underwater canyons offshore of large estuaries, or on the steeper parts of accretionary prisms onshore of major subduction zones. Potentially large landslide tsunamis can be generated from such near-field sources, for which there will be short propagation and warning times. To assess SMF tsunami hazard along the upper US East Coast, Grilli et al. (2009) conducted a probabilistic analysis based on Monte Carlo simulations (MCS) of slope stability and tsunami generation. MCS results reproduced well the statistical distributions of areas, volumes, and types (slide or slump) of SMFs found in marine geology surveys, and identified regions of elevated SMF tsunami hazard, in terms of 100 and 500 years return period runup. These were mostly located north of the Carolinas with, as expected, elevated risk off of some major estuaries such as the Hudson River and Chesapeake Bay. The largest known historical SMF in the region, the Currituck slide complex, which is over 25,000 years old and 165 km\(^3\) in volume, is in fact located offshore of the latter (Geist et al. 2009). Tsunami generation and coastal impact from this large SMF was modeled by Grilli et al. (2015), who showed that if it occurred nowadays, the tsunami would flood heavily populated coastal areas of Virginia, Maryland, New Jersey and the Chesapeake Bay, with up to 5 m inundation, after 1–2 h of propagation, depending on distance to the source (travel time in this particular case is not that short, due to the very wide shelf in the area). The latter work was conducted as part of the development of comprehensive tsunami inundation maps, under the auspice of NOAA’s National Tsunami Hazard Mitigation Program (NTHMP). Based on the simulation of the historical Currituck event, four separate Currituck proxy SMF sources were sited off of the upper US East Coast, where both the MCS analysis indicated elevated hazard and the seafloor was deemed to have sufficient sediment accumulation to allow for such a large SMF to occur. Tsunami generation and propagation was simulated for these four sources, in a series of nested model grids, which confirmed that significant landslide tsunamis would be generated, that would arrive after fairly short propagation times and cause large inundation in many areas along the coast (see Grilli et al. 2015 for detail).

1.2 Realtime Tsunami Warning and Sensing Systems

Tsunami warning centers have been in operation in the US for over 40 years, essentially to cover sources in the Pacific Ocean [http://ptwc.weather.gov; in Hawaii (PTWC) and Alaska (NTWC)]. Over the years, these centers have served their purpose very well, issuing rapid and reliable warnings, together with specific tsunami runup/inundation forecasts for many far-field locations, whenever a significant earthquake occurred in their geographic area. Regarding landslide tsunamis, however, the centers have so far only been issuing warnings when some seismic threshold is reached in previously identified regions, that near-field landslide tsunamis are possible; no forecast is issued for meteo-tsunamis. To issue forecasts for seismic events, the warning centers have relied on pre-calculated tsunami scenarios which, once the earthquake parameters are estimated based on seismic network data, are “weighed” to fit each specific event (Gica et al. 2008). Additionally, since 2001, the warning centers have increasingly relied on realtime tsunami measurements from “Deep-ocean Assessment and Reporting of Tsunamis” (DART) buoys (Gonzalez et al. 1998), a network of deep water pressure gages, acoustically linked to companion buoys, themselves communicating with Iridium satellites. As of 2008, 39 DART buoys had been deployed by the US, the majority in the Pacific Ocean, but 7 of those being located in the Gulf of Mexico and the Atlantic Ocean. More recently, over 20 additional similar buoys have been put in operation by other countries, in the Indian and Pacific Oceans (see http://www.ndbc.noaa.gov/dart.shtml). In some areas, other instruments or platforms have been used to make realtime tsunami measurements, such as a variety of nearshore bottom pressure sensors and sturdy GPS buoys (e.g., off Japan).

Once a NOAA center issues a tsunami warning, together with a first set of near- and far-field impact forecasts, if a tsunami is actually observed at instruments that are part of its realtime sensing system (e.g., at DART buoys), the center will refine its initial forecast by using realtime data to revise the working tsunami scenario and better match observations; such a revision then periodically takes place as more data become available, on both the source (e.g., earthquake parameters obtained from seismic networks) and the generated tsunami, and new warnings and forecast are issued. For this procedure to reliably work, however, the tsunami needs to first propagate to and be measured at the location of deployed instruments; hence, this process of iterative revision takes time to be initiated; for instance, during the Tohoku 2011 event, it took 30 min for the tsunami to be recorded at the nearest DART buoy (Grilli et al. 2013; Tappin et al. 2014). Thus, in situations such as described above, with nearshore seismic or SMF sources, there may not be enough time with current realtime sensing systems to issue a second warning that is based on actual tsunami data, besides indicating that an earthquake has occurred and, based on its magnitude and depth, a tsunami was possibly generated. For non-seismically induced nearshore SMF tsunamis or for meteo-tsunami events, there may not event be enough time to issue a first warning once a tsunami has been detected nearshore. Hence, new sensing technologies such as shore-based HF radars could help fill in this detection time gap and issue an early warning for near-field tsunami sources.

2 Principles of Tsunami Detection Based on HF Radar Remote Sensing

2.1 Background

As discussed above, new sensing technologies should be developed and implemented to provide early warning and allow for realtime coastal hazard assessment of tsunamis generated from sources in the near-field, such as SMF- and meteo-tsunamis. Due to the nature of these sources, such technologies should also have both a denser and broader spatial coverage than the point measurement buoys and similar sensing systems currently used. Here, we propose to achieve these goals by way of high-frequency (HF) radar remote sensing.

In recent years, Surface Wave High-Frequency Radars (SWHFR) radar remote sensing of coastal currents has been operational, in particular in US coastal waters, based on the CODAR SeaSonde®system (http://www.codar.com/). With this technology, currents are detected by measuring the Doppler shift they induce on the radar signal. Barrick (1979) initially proposed using HF radars for tsunami detection and, more recently, his ideas were validated by the numerical simulations of Lipa et al. (2006), who demonstrated that the 2004 IO tsunami could have been detected at some distance offshore if this technology had been installed in Indonesia. Other numerical studies, based on the WERA HF radar system characteristics (http://www.helzel.com/de/6035-wera-remote-ocean-sensing) reached similar conclusions (Heron et al. 2008; Dzvonkovskaya et al. 2009a; Gurgel et al. 2011). During the 2011 Tohoku tsunami, shore-based HF radars made direct observations of the incoming tsunami current, in the near-field in Japan (Hinata et al. 2011; Lipa et al. 2011, 2012a) and, in the far-field, in Hawaii (Benjamin et al. 2015) and in Chili (Dzvonkovskaya et al. 2011; Dzvonkovskaya 2012). No realtime tsunami detection algorithm was in place, but the a posteriori analysis of radar data obtained during the event allowed identifying the tsunami current in the measurements. In some of these studies, simple tsunami detection and warning algorithms were proposed, based on the magnitude of the current inferred from the radar Doppler spectrum. A more advanced algorithm was proposed by Lipa et al. (2012a), based on detecting elevated correlations of inferred currents in neighboring radar cells, and validated using field data for the Tohoku tsunami. The same approach was later successfully applied to a posteriori detect velocities caused by the weak 2012 Indonesian tsunami in the near-field, using data from radars deployed on the coasts of Sumatra and the Andaman Islands (Lipa et al. 2012b), and the June 2013 US meteo-tsunami, using data from radars deployed along the US East Coast (Lipa et al. 2014).

As we shall see, however, for these approaches based on detecting tsunami currents inverted from the radar Doppler spectrum to work, the current must be sufficiently strong to rise above background noise and current, which limits this type of tsunami detection to fairly shallow water, where tsunami currents become stronger due to shoaling, and thus to nearshore locations, unless there is a wide shelf. This will be detailed later.

Fig. 1
figure 1

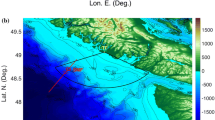
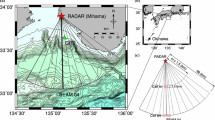
Site of Stradivarius radar bistatic deployment in the Gulf of Lion, Mediterranean sea: solid brown area of coverage, blue symbol transmitter location, red symbol receiver antennas location, and dashed lines equivalent monostatic distance from radar in km. Labels mean: FR France; SP Spain; IT Italy; CR Corsica

Full size image
Fig. 2
figure 2

Numerical modeling of the propagation of a landslide tsunami generated by a SMF in West Corsica (SE corner area), to the Gulf of Lion (NW area). Color scale is surface elevation and black contours are bathymetry in meter. Panels show snapshots of simulations with the long-wave propagation model FUNWAVE-TVD after: a 10\(^\prime \); b 20\(^\prime \); c 30\(^\prime \); d 40\(^\prime \); e 50\(^\prime \); f 1 h; g 1 h10\(^\prime \); h 1 h20\(^\prime \); i 1 h30\(^\prime \); and j 1 h40\(^\prime \) of propagation, initialized at 425 s with results of the tsunami generation model NHWAVE. The x-axis is longitude east, and y-axis is latitude north

Full size image
Fig. 3
figure 3

Same case as Fig. 2. Color scale is horizontal velocity module in m/s computed with the long-wave propagation model FUNWAVE-TVD for the same times as in Fig. 2

Full size image

In this study, we develop and validate a new tsunami detection algorithm, well-suited to HF radar data, that does not have this limitation to strong currents and could thus detect tsunamis in deeper water, further offshore, and provide an earlier warning, particularly for coasts that face narrow shelves. Since actual radar data with tsunami effects were not available during our study, we developed and validated this new algorithm by way of numerical simulations of both tsunami and radar signal. Applications aimed at demonstrating the relevance of the method are presented in this paper for idealized tsunamis and bathymetry, but in follow-up work, we will apply the algorithm to realistic tsunami case studies performed using state-of-the-art propagation models. We give an example of such simulations, for the purpose of illustrating tsunami propagation features, for the Western Mediterranean Basin area where a new type of HF radar, referred to as Stradivarius (developed by Diginext Ltd.) was deployed in late 2014, to cover the Gulf of Lion along and off the southern French Mediterranean coast (Fig. 1). In the radar signal simulations, for sake of illustration, we also use the characteristics of Stradivarius. This HF radar has a lower carrier electromagnetic wave (EMW) frequency (\(f_{\rm{EM}} = 4.5\) MHz) than other radars currently deployed for measuring coastal currents (e.g., CODAR or WERA systems) and has an EMW propagation mode within the atmosphere–ocean interface that allows making measurements significantly beyond the horizon. In a bistatic configuration and using efficient antennas and wave forms, Stradivarius has been shown in field experiments to measure surface currents up to 200–300 km distances, depending on the radar power and environmental noise (Fig. 1).

Because the main goal of this initial study is to demonstrate the validity of the new detection algorithm, we use an idealized framework in simulations, in which the radar is assumed to work in a monostatic configuration (which is the limiting case of Stradivarius’ actual bistatic configuration for long range), with a direction of observation nearly perpendicular to shore. However, to simulate realistic environmental noise levels, which is important for the validation of the algorithm, the actual attenuation of the Stadivarius radar signal measured in field tests is used in the modeling. Both the bathymetry and tsunami wave trains are assumed here to be invariant along the coast, so that tsunami wave crests are approaching the coast perpendicularly to the radar line-of-view. This is in fact a fairly good approximation in many cases of actual tsunami propagation over a wide shelf, with long stretches of nearly straight coastline and shore-parallel bathymetry.

The proposed method, however, is not limited to simple cases of nearly shore-parallel tsunami crests and shore-normal currents, but is applicable to arbitrary bathymetry and incident tsunami trains. For illustration, Figs. 2 and 3 show such an example of surface elevations and current magnitude simulated in the Western Mediterranean Sea, for a landslide tsunami generated by an SMF on the west shore of Corsica, using the Boussinesq long wave model FUNWAVE-TVD (Shi et al. 2012; Grilli et al. 2013). Landslide tsunami generation is simulated using the three-dimensional model NHWAVE (Ma et al. 2012). The SMF has a 2.7 km\(^3\) volume and is located west of Calvi, Corsica, at 42\(^\circ \)34N; 8\(^\circ \)33E on the continental shelf break; it is 12 km long down-slope, 3 km wide cross-slope, has a maximum thickness 0.25 km in depth 776 m, and is assumed to be a rigid slump moving in a direction 280\(^\circ \) from North, over an average 13\(^\circ \) slope. The modeling of the SMF geometry and kinematics follows the method outlined in Grilli et al. (2015) and is not detailed here as it is beyond the scope of this paper. In Fig. 2, we see that after about 50 min the landslide tsunami is propagating onto the Gulf of Lion shelf as a series of long-crested tsunami waves, towards the actual location of Stradivarius’ receiver antennas in Camargue (Fig. 1). Due to refraction, wave crests and troughs have become nearly parallel to the nearshore bathymetry and shoreline over the shelf, despite their initial westward propagation, towards Spain, near the SMF source (see for instance Fig. 2e–j, after waves have propagated over the 100 m isobath). As waves approach shore, due to shoaling, the crests and trough amplitudes increase as well as the horizontal current magnitude, essentially as a function of the reduction in depth, except for a few areas with submarine ridges and canyons, where waves focus or defocus. Figure 3 shows snapshots of the horizontal velocity module computed for this case; as expected, velocities are on the order of a few cm/s in deep water, but become greater than 0.1 m/s after tsunami waves have crossed the 1000 m isobath (see Fig. 3d). Over the shelf, in shallower water, particularly in wave focusing areas, velocities become larger than 0.15 m/s, the approximate threshold for an accurate direct detection by HF radar, based on the radar signal Doppler spectrum.

Other examples of landslide and co-seismic tsunami propagation over the US east coast shelf can be found in Grilli et al. (2010, 2015) and Tehranirad et al. (2015). The application of the HF radar detection algorithm to such more realistic tsunami case studies will be presented in a follow-up paper.

2.2 Principles of Detection by HF Radar

The analysis of EMW interactions with ocean surface waves allows to infer various oceanographic parameters from the SWHFR backscattered signal, with the most frequently analyzed one being the near-surface ocean current (see, e.g., the review papers of Barrick 1978; Shearman 1986; Wyatt et al. 2013). Although most of the material in this section is standard and can be found in various references, for sake of completeness and clarity of the notations and definitions, a brief summary is presented hereafter. It has been known since Crombie (1955) that the dominant contribution to the sea echo is produced by the so-called resonant Bragg wave, whose wavelength \(L_B\) is half the radar wavelength \(\lambda _{\rm{EM}}\). Assuming deep water ocean waves, we find from the linear dispersion relationship,

$$\begin{aligned} L_B = \frac{\lambda _{\rm{EM}}}{2}=\frac{gT_B^2}{2\pi }\quad { \text{ with } }\quad \lambda _{\rm{EM}} = \frac{c_{\rm{EM}}}{f_{EM}}, \end{aligned}$$
(1)

where \(\lambda _{\rm{EM}}\) denotes the EMW wavelength, \(c_{\rm{EM}} = 299{,}700\) km/s is the speed of light in the air, and \(g=9.81\) m/s\(^2\) is the gravitational acceleration. For Stradivarius, we find \(L_B\simeq 33.3\) m and \(T_B = 4.62\) s. Wind waves of this period are present in the ocean for wind speeds exceeding about 6 m/s. The lower radar frequency of Stradivarius, therefore, prevents it from measuring currents in very calm sea conditions; however, with its large range, the radar is likely to find many regions of the sea with proper wind wave coverage.

It follows that the Doppler spectrum of the backscattered radar signal is mainly composed of two peaks at the so-called Bragg frequencies \(\pm f_B\), with from Eq. 1,

$$\begin{aligned} f_B=\sqrt{\frac{g\, f_{\rm{EM}}}{\pi \, c_{\rm{EM}}}} \end{aligned}$$
(2)

For Stradivarius, for instance, we find, \(f_B = 0.217\) Hz.

The presence of an ocean current, with radial velocity \(\pm U_r\) in the direction of the radar, induces a Doppler shift that displaces the Bragg frequencies in the radar Doppler spectrum by a value,

$$\begin{aligned} \Delta f_B=\pm \frac{2U_r}{\lambda _{\rm{EM}}}=\pm \frac{U_r}{L_{B}}. \end{aligned}$$
(3)

When measuring this shift in the radar Doppler spectrum computed over a specified ocean area: a so-called “radar cell”, Eq. 3 allows estimating the radial component of the surface current, averaged over the radar cell.

More specifically, Stewart and Joy (1974) showed that the surface current actually measured by the radar corresponds to an average over the radar cell of the current in the near sub-surface region, to a depth on the order \(L_B/25\) (that is on the order of 1.3 m for the radar frequency considered here).

This approach can in principle be applied to the detection of the radial component of a tsunami-induced current \(\pm U_{tr}\). Thus, from the frequency shift obtained by processing radar data in a given radar cell centered at \({\varvec{x}}=(x,y)\), we find the current magnitude \(\tilde{\overline{U_{tr}}}({\varvec{x}},t)\), averaged over:

  • (overbar) a radar cell of dimension \(\Delta r\) in the radial direction and aperture \(\Delta \phi _r\) in the azimuthal direction (for a monostatic configuration),

  • and (tilde) a measuring (or integration) time interval \(T_i\) (for the Doppler spectrum).

The area of each radar cell must be sufficiently large to include a statistically meaningful sample of wind waves of various wavelengths (i.e., \(\Delta r\) is a few kilometers). The frequency resolution of the Doppler spectrum near its peak is, \(\Delta f_D = 1/T_i\), which implies that the inverted radial current has a resolution, \(\Delta U_r = L_B/T_i\). Hence, to accurately infer weak surface currents based on a Doppler shift, the measuring time interval must be sufficiently long, typically at least 2 min for a 12 MHz (\(\Delta U_r=10\) cm/s), but as much as 5–10 min for a 4.5 MHz (\(\Delta U_r=10-5\) cm/s), radar frequency. For instance, in their recent work, Benjamin et al. (2015) reported a resolution \(\Delta U_r =0.074\) m/s for currents computed from the Doppler spectra measured near Honolulu, HI, with a 16 MHz WERA HF radar, which limited the ability of the radar to detect currents caused by the Tohoku 2011 tsunami in the deeper water areas of their nearshore radar ranges, where they were smaller than this threshold; or in other words to achieve an accurate inversion, currents had to be at least 0.12–0.15 m/s. However, the oscillatory nature, in space and time, of an incoming tsunami wave train (and of the surface current it induces) means that the larger \(T_i\) the lower the maximum value of the estimated current over a given radar cell, due to time averaging of the tsunami signal. Hence, these conflicting requirements must be carefully weighted when selecting parameters of the radar signal processing algorithm. In particular, in view of the long-crestedness of incident tsunami waves, one can reduce \(T_i\) and compensate for the loss of resolution this causes by applying a cell-averaging in the radar azimuthal direction, on either side of a given radar cell.

In the most advanced study of tsunami detection by HF radar to date, Lipa et al. (2012a) analyzed measurements made during the Tohoku 2011 event, at 14 radar sites in Japan and in the US, and proposed a new detection algorithm based on a spatial pattern recognition of the inverted tsunami current. They noted that current velocities of an incoming tsunami, inferred from the radar Doppler spectrum in neighboring radar cells, will be both strongly correlated and exhibit oscillations (associated with successive crests and troughs in the tsunami wave train) that are becoming increasingly significant above background current values, as depth decreases. On this basis, they proposed a multiple-step tsunami detection algorithm based on correlations of average current velocities inverted in neighboring radar bands. The main limitation of this method, however, is that the tsunami current must be detectable over background current values, which depending on the area could be as high as 0.10 m/s; hence, with the expected resolution of the inverted radial current, the tsunami current must be at least \(U_t \sim \) 0.10–0.15 m/s for this method to reliably work (this will be illustrated later in the paper). As shown in Fig. 3, tsunami current velocities are typically very small in deep water, less than 0.05 m/s and below the radar detection resolution, even for extreme tsunamis, and only start increasing when the tsunami propagates into fairly shallow water over the continental shelf. Hence, this direct tsunami detection approach, based on currents inverted from radar Doppler spectra, is limited to shallower water areas (Lipa et al.’s group, for instance, indicate that water depth must be less than 200 m for their method to work) and thus nearshore areas where warning times will be small, unless there is a very wide shelf; but the latter would also require a radar with a large enough measuring range to detect the tsunami early enough on the shelf.

2.3 Basic Tsunami Wave Physics

Although this is standard wave mechanics material as well, in the following, we summarize the salient tsunami wave physics and related equations in the context of HF radar detection.

Except for very close to shore, where nonlinearity becomes large, tsunami wave trains can be accurately represented by linear long wave theory (Dean and Dalrymple 1984), since their characteristic wavelength is typically large compared to depth and verifies \(L_t\ge 20\, h\), with h(x, y) the local depth, and they have a very small steepness \(\eta _t/L_t\ll 1\), with \(\eta _t\) the tsunami surface elevation. This also means that the tsunami-induced horizontal current, \({\varvec{U_{t}}}\), can be assumed to be nearly uniform over depth and thus only function of the horizontal location (x, y) and time t. Additionally, while phase speed is very large in deep water, \(c_t=\sqrt{gh}\), the induced current is small and given by,

$$\begin{aligned} {\varvec{U_{t}}} = \eta _t\, \sqrt{\frac{g}{h}} \frac{{\varvec{k_t}}}{k_t} \end{aligned}$$
(4)

(where \(\eta _t\ll h(x,y)\) in deep water), with \(k_t(x,y,t) = \mid {\varvec{k_t}}\mid =2\pi /L_t\) the tsunami wavenumber, and \({\varvec{k_t}}=k_t\,(\cos {\phi _t}, \sin {\phi _t})\) the wavenumber vector, with \(\phi _t\) the local angle of the tsunami wave ray with respect to the x-axis (here typically orientated shoreward). [The unit vector at the end of Eq. 4 thus points in the local direction of tsunami propagation, \(\phi _t(x,y)\), i.e., the local wave ray.] For linear long waves propagating over a typical ocean bathymetry, the local tsunami elevation \(\eta _t\) can be predicted based on the initial deep water tsunami elevation \(\eta _{t0}\) using Green’s law,

$$\begin{aligned} \eta _t(x,y) = \eta _{t0} \left\{ \frac{c_{t0}(h_0)}{c_t(h)} \right\} ^\frac{1}{2} = \eta _{t0} \left\{ \frac{h_0}{h(x,y)} \right\} ^\frac{1}{4}, \end{aligned}$$
(5)

where \(c_{t0}=\sqrt{gh_0}\) is the tsunami phase speed in reference depth \(h_0\).

Long waves refract as a function of depth even in very deep water, based on changes in phase speed \(c_t(h(x,y))\). Under the geometric optics approximation and for a simple (nearly shore parallel) bathymetry variation (e.g., as on the continental shelf of the Gulf of Lion in Fig. 2), the tsunami direction of propagation can be estimated based on Snell’s law as,

$$\begin{aligned} \phi _t(x,y) = {\text {sin}}^{-1}\left\{ \sin {\phi _{t0}} \left\{ \frac{c_t(x,y)}{c_{t0}}\right\} \right\} = {\text {sin}}^{-1}\left\{ \sin {\phi _{t0}} \left\{ \frac{h(x,y)}{h_{0}}\right\} ^{\frac{1}{2}}\right\} , \end{aligned}$$
(6)

from an initial direction \(\phi _{t0}\) in deep water. Since phase speed gradually decreases \(\propto \sqrt{h(x,y)}\), Eq. 6 eventually yields, in all cases: \(\phi _t \ll \phi _{t0}\), and Eq. 5, \(\eta _t \gg \eta _{t0}\), when the tsunami approaches the shore. Hence, according to these simplified equations and set-up, tsunami wave crests will gradually grow in elevation and rotate to be orientated nearly parallel to the local bathymetric contours, while their horizontal current will increase in the direction normal to those contours; this was the behavior observed in Figs. 2 and 3, based on a complete numerical modeling of tsunami propagation. A consequence of this is that an incoming tsunami, whatever its initial source location and direction of propagation in a given ocean basin, will eventually arrive in a direction nearly normal to shore and thus propagate essentially straight towards a shore-based radar, with a current magnitude gradually increasing, as predicted by Eqs. 4–6, as \(\mid {\varvec{U_{t}}}\mid =U_t \propto h^{-3/4}\). In their recent study, Tehranirad et al. (2015) confirmed this property, for tsunamis propagating towards the US East Coast in the Atlantic Ocean basin, by computing tsunami wave rays based on the eikonal equation. Additionally, they showed that results of the geometric ray approximation were in very good agreement with results of tsunami simulations using the long wave propagation model FUNWAVE-TVD; besides providing an accurate travel path for tsunami waves, they found that the density of wave rays intersecting the coast, a measure of energy flux concentration, could be used as a good predictor of the coastal inundation predicted by FUNWAVE-TVD.

One should note, however, that for an arbitrary bathymetry, one must solve as a minimum the “eikonal” equation to compute wave rays (Dean and Dalrymple 1984); this will be detailed later. It should also be noted that neither Green’s nor Snell’s law (or their more elaborate form with the eikonal equation) depend on bottom slope, which has been shown to be accurate within the mild slope approximation (Booij (1983) showed that the bottom slope could be up to a 1:3 for this approximation to hold, which is much more than any oceanic slope).

According to these fundamental physical properties of long wave propagation and induced currents, a tsunami detection algorithm based on directly “inverting” Doppler spectral shifts, such as proposed by Lipa et al. (2012a), would only be applicable where tsunami currents are sufficiently larger than background currents (also accounting for the inverted current resolution), which typically means nearshore, over the continental shelf; hence, warning times would depend on shelf width and thus could be quite small in some locations. Here, assuming an SWHFR HF radar such as Stradivarius is used, which can sense ocean properties as far as 200–300 km from shore, we are proposing and validating a new type of tsunami detection algorithm that is not based on inverted currents, but instead on directly processing the radar signal. We will show that this algorithm does not require tsunami currents to reach large enough values (e.g., >0.10–0.15 m/s), and rise above background currents, to be detectable. With the new method, an incoming tsunami with currents as low as 0.05 m/s can be detected, even in the presence of larger background currents, and thus tsunami detection can occur in deeper water, beyond the continental shelf, which will increase warning times. This would be particularly important where there is a narrow shelf.

Another advantage of the HF radar over standard instruments, besides making it possible to detect an incoming tsunami at a distance from shore large enough to afford a reasonable warning time, is that it provides a spatially dense set of measurements over a broad oceanic area (Fig. 1), at a resolution commensurate with radar cell scales (i.e., a few km by a few km). For a monostatic radar configuration, for which the radar transmitter and receiver antennas are collocated, measurements are made in radial directions from the radar location, while for a bistatic configuration, where the transmitter and receiver antennas are separated by a large distance (e.g., tens of km; Fig. 1), measurements are made in directions normal to the local ellipse whose focal points are the antenna locations (Grosdidier et al. 2014); more details are provided in a following section.

Because of this property of radar remote sensing, one can thus only estimate the projection of local tsunami currents on specific radar ray directions and, unless at least two radars are used, it is necessary to have a priori knowledge of tsunami propagation patterns, and hence local wave ray directions \(\mid {\varvec{k_t}} \mid \) over the detection area, in order to infer the full current magnitude and estimate local tsunami elevations \(\eta _t\) in each radar cell, based on these using Eq. 5, provided currents are strong enough to be reliably inverted. As will be detailed later, this local knowledge can be obtained by way of numerical simulations of long wave propagation, given the local bathymetry h(x, y) and the most probable tsunami initial directions \(\phi _{t0}\) (which can be obtained from local knowledge of the most probable tsunami sources in the considered ocean basin).

In the following, in Sect. 3, we develop a complete second-order model of both ocean waves, in the presence of a varying surface current, and HF radar scattering. In Sect. 4, we present two tsunami detection algorithms, the first one is standard and based on a direct detection by way of the current inferred from the radar Doppler spectrum, similar to earlier work discussed before, and the second one is a newly proposed algorithm that alleviates the limitation to a large enough current and/or shallow water of the earlier approaches. In Sect. 5, we apply both algorithms to cases with idealized tsunami waves and bathymetry and identify in which situation each one performs best. Based on these results, we discuss what would entail applying the detection algorithms to more realistic cases (such as shown in Figs. 2, 3). Finally, we offer some conclusions and perspective for future work.

3 HF Radar Scattering Model

To simulate tsunami detection by HF radar, we implement numerical models of both ocean wave propagation and radar backscattering by these, in the presence of a surface current. Upon interacting with a rough, wave-covered, ocean surface of elevation \(\eta ({\varvec{r}},t)\) (with respect to a position vector \({\varvec{r}}(x,y)\) defined based on the radar location), EMWs diffract, and a fraction of those propagates back to the radar receiving antennas, to be measured as the backscattered radar signal \({\text {S}}(t)\). In this process, because the celerity of ocean waves is much less than that of EMWs (\(c_B = L_B/T_B \ll c_{\rm{EM}}\)), the ocean surface can be assumed to be stationary. To the first-order, the two-sided power density spectrum of the radar signal, referred to here as “Doppler spectrum”, exhibits two maxima at the Bragg frequencies \(\pm f_B\) defined earlier; each of those corresponding to waves propagating toward or away from the radar, respectively. Higher-order effects, however, cause secondary, lower-energy, peaks to appear in the Doppler spectrum, at frequencies both lower and higher than the Bragg frequency.

Here, we detail the equations and implementation of the two models used for simulating ocean waves and radar scattering, up to second-order. In the models, the total surface current is assumed to be the sum of a: (1) spatially variable, but nearly stationary at the time scale of radar data acquisition (\({>}\mathcal{O}(T_i)\)), background oceanic current, \({\varvec{U_{b}}}({\varvec{r}})\); and (2) spatially and temporally varying current, \({\varvec{U_{t}}}({\varvec{r}},t)\) induced by the tsunami wave train (see, e.g., Eq. 4); hence,

$$\begin{aligned} {\varvec{U}}({\varvec{r}},t)={\varvec{U_{b}}}({\varvec{r}}) + {\varvec{U_{t}}}({\varvec{r}},t). \end{aligned}$$
(7)

The background current, also known as mesoscale current, is spatially variable in a way that depends on local and synoptic environmental ocean conditions. During a tsunami event lasting on the order of 1 h, however, this current can be assumed to be randomly fluctuating around stationary values, during the entire duration of data acquisition by the radar. In a specific case, the background current could be obtained from an operational regional ocean model but, as we shall see, this is not necessary to apply the newly proposed tsunami detection algorithm.

3.1 Ocean Surface Model

Assuming a small steepness, the surface elevation of random ocean waves is represented by a classical second-order perturbation expansion, \(\eta ({\varvec{r}}, t)=\eta _1({\varvec{r}}, t)+\eta _2({\varvec{r}}, t)\), which is sufficient to accurately simulate both the waves’ energy density and resulting backscattered HF radar Doppler spectra (Longuet-Higgins 1963; Weber and Barrick 1977). For first-order waves, the classical expression is adapted to include effects of a surface current,

$$\begin{aligned} \eta _1({\varvec{r}}, t)=\sum _{\epsilon =\pm 1}\int a^\epsilon ({\varvec{K}})\, e^{{i}({\varvec{K}}.{\varvec{r}}-\epsilon \Omega ({\varvec{K}},{\varvec{r}},t) t)}\,{\text {d}}{\varvec{K}}, \end{aligned}$$
(8)

where the integration is carried out over the wavenumber vectors, \({\varvec{K}}=(K_x,K_y)= K(\cos {\theta }, \sin {\theta })\), and wave harmonic amplitudes are given by,

$$\begin{aligned} a^\epsilon ({\varvec{K}})=\frac{1}{\sqrt{2}} \sqrt{\Psi (\epsilon {\varvec{K}})} Z^\epsilon ({\varvec{K}}), \end{aligned}$$
(9)

with \(\Psi \) the directional wave energy density spectrum and \(Z^\epsilon ({\varvec{K}})\) a standard complex normal variable (with unit variance and zero mean), independently for each wave harmonic.

The angular frequency of each wave component, \(\Omega ({\varvec{K}},{\varvec{r}},t)\), is modulated by the surface current \({\varvec{U}}({\varvec{r}},t)\) resulting from both the tsunami wave train and the background current. Assuming that the tsunami current is slowly varying in time at the scale of ocean waves, i.e., the tsunami characteristic period, \(T_t \gg T_p\), the peak spectral wave period, and that waves are in the deep water regime, we have,

$$\begin{aligned} \Omega ({{\varvec{K}},{\varvec{r}}},t) \,t = (\Omega _g+{{\varvec{K}}.{\varvec{U_b}}({\varvec{r}})})\,t\,+\int _0^t{{\varvec{K}}.{\varvec{U_{t}}}({\varvec{r}}},\tau ) {\text {d}}\tau , \end{aligned}$$
(10)

where the integral is a memory term representing the cumulative effects of the tsunami current on the instantaneous wave angular frequency, and,

$$\begin{aligned} \Omega _g=\sqrt{gK} \end{aligned}$$
(11)

is the standard angular frequency of linear gravity waves in deep water (Dean and Dalrymple 1984).

Second-order waves are similarly expressed as,

$$\begin{aligned} \eta _2({\varvec{r}}, t)=\sum _{\epsilon _1,\epsilon _2=\pm 1}\int \Gamma ^{\epsilon _1,\epsilon _2}\,a^{\epsilon _1}({\varvec{ K_1}})\,a^{\epsilon _2}({\varvec{ K_2}})\, e^{{i}({\varvec{K_1}}+{\varvec{K_2}}).{\varvec{r}}}e^{-{i}(\Omega _1+\Omega _2)t}\,{\text {d}}{\varvec{K_1}}\,{\text {d}}{\varvec{K_2}}, \end{aligned}$$
(12)

where \(\Omega _j=\epsilon _j\Omega ({\varvec{K}}_j,{\varvec{r}},t),\ j=1,2,\) and \(\Gamma ^{\epsilon _1,\epsilon _2}\) is a kernel whose expression is given in Appendix 2.

Note that assuming deep water ocean waves implies that the dominant wavelength of ocean wind waves is small with respect to depth. If not, modified expressions of both the wave dispersion relationship and the second-order kernels can be used to account for limited water depth effects (see, e.g., Lipa and Barrick 1986).

In the applications presented hereafter, sea state is assumed to be fully developed and represented by a Pierson–Moskowitz (PM) directional wave energy density spectrum \(\Psi (K_x,K_y)\), parametrized as a function of \(V_{10}\), the wind speed at a 10 m elevation, and with a standard angular spreading function, which includes the power s of a cosine function of direction with respect to the dominant direction of wind waves \(\theta _p\). This function is asymmetric, to model a fraction \(\xi \) of the spectral wave energy associated with waves propagating in the direction opposite to the dominant wind direction; see Appendix 1 for details. For instance, for \(V_{10}=10\) m/s, \(s=5\), and \(\xi =0.1\), we find a sea state with significant wave height, \(H_s = 1.71\) m, peak spectral wavelength \(L_p = 127.4\) m and, assuming deep water, peak period \(T_p = 9.04\) s.

3.2 Definition of Doppler Spectra

The Doppler spectrum \(\sigma (\omega )\) is defined as the radar cross section per unit area and bandwidth. Following Rice’s perturbation theory for shallow rough surfaces, Barrick first established the classical first- (Barrick 1972a) and second-order (Barrick 1972b) theory of HF radar Doppler spectra at near-grazing incidence, in the absence of a background current and for infinite water depth. To the first-order in vertical polarization, the Doppler spectrum is expressed byFootnote 1,

$$\begin{aligned} \sigma _{1}(\omega )=2^6\pi K_0^4\sum _{\epsilon = \pm 1}\Psi (\epsilon {\varvec{K}}_B)\delta (\omega -\epsilon \Omega _B), \end{aligned}$$
(13)

where \(K_0=2\pi /\lambda _{\rm{EM}}\) is the electromagnetic wave number, and the second-order expression is given by,

$$\begin{aligned} \sigma _{2}(\omega )&=2^6\pi K_0^4 \sum _{\epsilon _1,\epsilon _2=\pm 1}\int \left| \Gamma {{(\varvec{K})}} \right| ^{2}\Psi (\epsilon _1{\varvec{K}})\Psi (\epsilon _2{\varvec{K}'}) \nonumber \\&\quad \times \,\delta (\omega -\epsilon _1\sqrt{gK}-\epsilon _2\sqrt{gK'})\, {\rm{d}}{\varvec{K}}, \end{aligned}$$
(14)

where \({\varvec{K}'}={\varvec{K}}_B-{\varvec{K}}\), and the kernel \(\Gamma \) is detailed in Appendix 2.

Barrick’s original theory was more recently extended to include a bistatic configuration and finite radar cells, based on a rigorous electromagnetic theory using pulsed dipole sources at finite distance (Gill and Walsh 2000, 2001; Gill et al. 2006). In the present analysis, we will discard cell truncation effects, due to the choice of a particular incident waveform, and work with a plane wave formalism, which is valid to the limit of large radar cells.

3.3 Simulating Time Series of Radar Signal

The backscattered electric field (a.k.a., radar signal) is denoted by \({\text {S}}(t)={\text {S}}^1(t)+{\text {S}}^2(t)\), and estimated up to second-order and normalized in such a way that the Doppler spectrum can be expressed as,

$$\begin{aligned} \sigma (\omega )= \frac{1}{T} \left\langle \,\left| \int _{-T/2}^{+T/2}\ {\text{S}}(t)\,e^{{i}\omega t}\,{\rm{d}}t \right| ^{2}\right\rangle ,\quad T\rightarrow +\infty \end{aligned}$$
(15)

According to Rice’s perturbation theory, the first- and second-order backscattered fields are proportional to the spatial Fourier transform at the Bragg vector \({\varvec{K}}_B\), of the first- and second-order ocean surfaces defined by Eqs. 8 and 12, respectively, that is,

$$\begin{aligned} {\text {S}}^1(t)&=\sqrt{2}K_B^2\, \sum _{\epsilon =\pm 1}\sqrt{\Psi (\epsilon {\varvec{K}}_B)}e^{-{i}\epsilon \Omega _B t}\, Z^\epsilon ({{\varvec{K}}_B}) \nonumber \\ {\text {S}}^2(t)&= \sqrt{2}K_B^2\, \sum _{\epsilon _1,\epsilon _2=\pm 1}\int \Gamma ({\varvec{K}})\sqrt{\Psi (\epsilon _1 {\varvec{K}})\Psi (\epsilon _2{\varvec{K}'})} \nonumber \\&\quad \times \,e^{-{i}(\epsilon _1\Omega +\epsilon _2\Omega ')t}Z^{\epsilon _1}({\varvec{K}})Z^{\epsilon _2}({\varvec{K}'})\,{\rm{d}}{\varvec{K}}, \end{aligned}$$
(16)

where \(Z^\epsilon \) again denotes a standard complex normal variable (with unit variance and zero mean), \({\varvec{K}'}={\varvec{K}}_B-{\varvec{K}}\), and the factor \(\sqrt{2}K_B^2\) ensures consistency with Eq. 15. The circular frequencies \(\Omega \) and \(\Omega '\) are obtained from the wave dispersion relationship in the presence of a current, Eqs. 10 and 11, applied to \({\varvec{K}}\) and \({\varvec{K}'}\), respectively.

Given a directional wave energy density spectrum \(\Psi ({\varvec{K}})\) and a set of random functions \(Z^\epsilon ({\varvec{K}})\) (representing random phases), Eq. 16 allows simulating time series of backscattered radar signal, up to second-order, in a given radar cell located at distance \({\varvec{r}}(x,y)\) from the radar, for specified radar characteristics (e.g., \(K_B\)) and location, in the presence of a surface current \({\varvec{U}}({\varvec{r}},t)\) in the cell, including a tsunami current \({\varvec{U_{t}}}({\varvec{r}},t)\). Note that this formulation does not yet include effects of the signal attenuation with range and environmental noise, which are discussed in the next section.

3.4 Attenuation Model and Environmental Noise

With the exception of a constant coefficient depending on the radar antenna system and the emitted power, the normalized electric signal received by the radar, from each radar cell, is expressed as

$$\begin{aligned} {\text{V}}(t) &= \mathcal{A}\, {\text {S}}(t) + \mathcal{N}(t)\quad { \text{ with } }\hfill \\ \quad \mathcal{A}(r)&=\left| {\text {F}}(r) \right| ^{2} r^{-2} \sqrt{\Delta {\mathbb {S}}},\hfill \\ \end{aligned}$$
(17)

a geometric attenuation factor function of range r, in which \(\Delta \mathbb {S}=r\,\Delta r\,\Delta \phi _r\), with \(\Delta r\) and \(\Delta \phi _r\) the cells’ radial and azimuthal resolutions, respectively; \(\mathcal{N}\) is environmental noise, detailed below, and \({\text {F}}\) represents the EMW attenuation by the ocean surface, which is computed here using the GRwave model (Grosdidier et al. 2014).

For an integration time \(T_i\), the (non-normalized) radar Doppler spectrum is calculated at time \(t_s\) by applying Eq. 15 over a finite time window \([t_s-T_i/2,t_s+T_i/2]\), to the received radar signal V(t) defined above, that is,

$$\begin{aligned} {\text {I}}(f_D,t_s)= \frac{1}{T_i}\,\left| \int _{t_s-\frac{T_i}{2}}^ {t_s+\frac{T_i}{2}}{\text{V}}(\tau )\,{\text {e}}^{2 i \pi f_D\tau }{\text {d}}\tau\right| ^2, \end{aligned}$$
(18)

with \(f_D\) denoting a set of discrete Doppler frequencies (with \(\omega _D=2\pi f_D\)). If the received radar signal is simulated/(recorded) at a constant temporal sampling rate \(\Delta t=T_i/N\), Eq. 18 can be easily computed as a summation from \(-N/2\) to N / 2.

When the Doppler spectrum is used to reconstruct (invert) the ocean surface current in the cell, \({\varvec{U}}({\varvec{r}},t_s)\), to achieve a sufficient resolution in time, the spectrum must be computed at a time interval, \(\Delta t_s \ll T_t\), the characteristic period of current variation; this also means in general that we need, \(\Delta t_s \le T_i\). To meet these requirements, in practice, one assumes some overlap between time series of radar signal, based on which each Doppler spectrum is computed. This is detailed later.

In the ocean, the backscattered radar signal is affected by thermal noise and various other environmental sources of noise. Since noise is statistically homogeneous and independent of range, the radar signal attenuation with range makes the signal-to-noise ratio (SNR) decrease, which limits the effective measuring range of HF radar systems. To simulate environmental noise, besides range attenuation and the resulting varying SNR with distance, which is already included in the simulated radar signal Eq. 17, in each radar cell, we specify an independent Gaussian distributed noise, with constant standard deviation \(\sigma _N\),

$$\begin{aligned} \mathcal{N}(t)= \sigma _N\,\{\mathcal{G}_{t}^{R}(0,1) + i\,\mathcal{G}_{t}^{I}(0,1)\}, \end{aligned}$$
(19)

which, similar to the signal, is a complex number. The subscript t indicates that different Gaussian random values \([\mathcal{G}_{t}^{R}(0,1), \mathcal{G}_{t}^{I}(0,1)]\), with unit standard deviation and zero mean, are being generated for each time level t.

Diginext Ltd. field tested the Stradivarius radar system in the Gulf of Lion area (Fig. 1) and measured the main Bragg lines’ SNR (according to the noise floor) at 200 km, during a typical day with wind speed \(V_{10} = 10\) m/s and near surface temperature 17 \(^\circ \)C. They found an average SNR of 30 dB, using an integration time of 10 min. In the applications presented hereafter, we use a value of \(\sigma _N\) (in dB) that reproduces the same SNR at the same distance as measured in the field for Stradivarius, when working with a normalized amplitude V(t); other \(\sigma _N\) values applicable to other radar systems, however, could be easily used in our model. This leads to the parameterization of the noise standard deviation as,

$$\begin{aligned} \sigma _N = \sqrt{\frac{K_{BZ}}{2\pi }\,T\,10^{(f_a/10)}} \end{aligned}$$
(20)

with \(K_{BZ}=1.38\,10^{-23}\) K\(^{-1}\) the Boltzmann constant, \(T=290\) K the absolute temperature, and \(f_a\) a parameter allowing to adjust the noise level, and found to be 130 based on field experiments with Stradivarius, yielding, \(\sigma _N =8.0\,10^{-5}\). This value of \(f_a\) will be used in the applications of the tsunami Detection Algorithms presented below, unless specifically noted.

With this constant level of noise in the simulated data, and in view of the attenuation of the radar signal at large range, the simulated SNR decreases with range in a realistic way, which makes the surface current gradually less detectable by the HF radar as distance increases, in a realistic manner.

4 Algorithms for Tsunami Detection by HF Radar

As detailed above, the ocean surface current caused by an incoming tsunami (see Eqs. 4, 5) can be reconstructed based on the shift it causes to the Bragg frequencies of the HF radar signal Doppler spectrum. The current can be computed at regular time intervals in a series of radar cells, in directions either radial to the radar for a monostatic deployment or normal to the local radar ellipse for a bistatic deployment. Several studies have already demonstrated the relevance of this approach for detecting tsunamis propagating in fairly shallow water, over the continental shelf, either by numerical modeling, or by a posteriori analyzing data from HF radars deployed in near- and far-field areas impacted by the Tohoku 2011 tsunami, the 2012 Indonesian tsunami, and the 2013 meteo-tsunami that impacted the US East Coast (Lipa et al. 2006, 2011, 2012a, b, 2014; Dzvonkovskaya et al. 2009a, b, 2011; Gurgel et al. 2011; Hinata et al. 2011; Dzvonkovskaya 2012). Note that all of these studies were based on HF radars with frequency 3–4 times larger than that of Stradivarius, which hence had detection ranges proportionally shorter (i.e., 50–70 km).

In practice, however, such a direct reconstruction of tsunami current can only be achieved when both the radar signals rises sufficiently above environmental noise, i.e., within the practical detection range of the considered radar, and the tsunami current magnitude is sufficiently larger than that of the background current (also accounting for the typical resolution of inverted currents, \(\Delta U = \) 5–10 cm; see Eq. 7). Simulations of radar backscattering for synthetic tsunamis presented later will show that the tsunami current magnitude should be above 0.10–0.15 m/s for a direct reconstruction to be meaningful, which is consistent with the magnitude of tsunami currents reliably detected with this method in existing field studies. Using Eq. 4 and assuming an incoming tsunami amplitude \(\mid \eta _t\mid = \mathcal{O}(1)\) m, which is quite extreme away from nearshore areas, and a current magnitude \(\mid \varvec{U}_t\mid = \mathcal{O}(0.2)\) m/s, we find that the depth range for detection is \(h\le 245\) m (a value close to the \(h\le 200\) m mentioned by Lipa et al. for a reliable detection); under the same conditions, a 0.5 m tsunami would only be detectable for \(h\le 61\) m. Hence, the direct reconstruction method, which linearly relates the current to the HF radar Doppler spectrum shift, can only detect tsunamis that have already propagated over the continental shelf. Nevertheless, this method can achieve an early detection of an incoming tsunami when there is a wide shelf, over which tsunami propagation to shore may still take on the order of 1 h.

In this study, to achieve an early tsunami detection in the absence of a wide shelf, we propose a complementary approach aimed at exploiting the capability of lower frequency HF radars (such as Stradivarius), of measuring ocean properties up to a 200–300 km, which clearly reaches beyond the continental shelf, in deeper water areas where tsunami currents may typically be a few cm/s (Figs. 1, 2, 3). The new approach does not rely on inverted currents, but instead detects the effects of currents as low as 0.05 m/s on the radar signal V(t), even in the presence of much larger background currents, which would otherwise not be reliably inverted from the radar Doppler spectrum. For the two examples given above, the detection depths of a 0.05 m/s tsunami current would become \(h\le 3,924\) and 981 m, respectively. As discussed in the Sect. 1, there are many locations where such a detection ability would be desirable, or even required, in order to develop a tsunami early warning system.

As pointed out by Lipa et al. (2012a), when a tsunami wave train propagates over a typical shelf bathymetry, the current it induces is oscillatory in time and space and tsunami wave crests, due to refraction, become increasingly parallel to the local isobaths and the shore. Hence, the current reconstructed from the Doppler spectrum in a given radar cell should be highly correlated with that inferred in other radar cells. Lipa et al. (2012a) exploited this property to develop a detection algorithm based on spatial correlations of the reconstructed current between neighboring radar cells (in the crown/angular direction) reaching a specific threshold. However, as discussed above, for this method to work, the tsunami current magnitude must sufficiently rise over that of the background current and thus, in practice, the method is limited to shallower water over the shelf (Lipa et al., indicate the need for \(h \le 200\) m).

As will be detailed below, in the newly proposed approach we also exploit this property of high spatial correlation of tsunami currents, but in the range direction. Additionally, we use long wave physics and the fact that tsunami wave crests (and corresponding induced currents) propagate at the local phase speed along a wave ray. Therefore, correlations of time series of radar signal (modulated by the tsunami current), between two distant radar cells located along the same way ray, one closer and one further away from the radar, should be high when shifting one of the two time series by the tsunami propagation time between the two cells; an elevated correlation will thus signify that a tsunami is propagating towards the radar.

In the following, we present the principles for two tsunami detection algorithms and explain how each algorithm can be entirely simulated numerically, based both on computed time series of radar signal in a series of radar cells, from a representation of the ocean surface including effects of a surface current, as discussed above, and results of tsunami simulations using a wave propagation model, that provide synthetic tsunami currents in the radar cells, in lieu of actual field measurements. We first briefly present Tsunami Detection Algorithm 1 (TDA1), which is a standard algorithm based on a direct reconstruction of surface currents from HF radar measurements, by inverting the radar Doppler spectrum; as discussed, this algorithm requires currents to be large enough, and thus TDA1 will work well for detection over the continental shelf, whatever the actual radar range. Then, we present Tsunami Detection Algorithm 2 (TDA2), which is based on the newly proposed approach of time-shifted correlations of the radar signal; we will show that this algorithm is able to detect the presence of weak tsunami currents, even in the presence of much larger background current, and hence TDA2 can achieve tsunami detection in deeper water, beyond the continental shelf. In a practical situation, both algorithms could be simultaneously run on the same radar data, and would thus be complementary, with their ability to cover both shorter and larger ranges.

In a simulation mode, for each tsunami detection algorithm, we implement and run the radar scattering model detailed above to simulate the HF radar signal V(t). A series of radar cells are defined over the ocean area covered by the radar EMWs, of radial resolution \(\Delta r\) and azimuthal resolution \(\Delta \phi _r\), each centered at \({\varvec{r}}_{mn}\) from the radar (where n denotes the radial range and m the azimuthal range). In each cell, sea state is specified by its energy density spectrum \(\Psi ({\varvec{K}})\) as well as a surface current \({\varvec{U}}({\varvec{r}}_{mn} + {\varvec{x}}_{mn},t)\) [where \({\varvec{x}}_{mn}\) are coordinates defined at the center of cell (m, n)]. This current may include a background current plus a simulated tsunami current, obtained from separate numerical simulations. On this basis, random surface elevations \(\eta ({\varvec{r}}_{mn} + {\varvec{x}}_{mn}, t)\) are generated in each cell using Eqs. 8–12 and the corresponding radar signal \({\text{V}}_{mn}(t)\) is calculated using Eqs. 16–19. Both algorithms can only be applied where the radar signal is sufficiently above environmental noise (i.e., the SNR is sufficiently large) and, hence, there is a range limitation for practical detection, which is site specific, as a function of radar characteristics and atmospheric and stratospheric conditions. As detailed before, both environmental noise and range effects are included in the simulations of the radar signal in a realistic manner.

Details of both algorithms are presented in the following sections.

4.1 TDA1: Tsunami Detection Algorithm 1: Doppler Spectrum “Inversion”

In each radar cell (m, n), the radar signal Doppler spectrum \({\text {I}}_{mn}(f_D,t_s)\) is calculated, at regular time intervals \(\Delta t_s\), using Eq. 18 (for an integration time \(T_i\)). The primary peaks of the Doppler spectrum, located at frequencies \(\pm f^{\rm{max}}_{{D}_{mn}}(t_s)\), will be shifted according to Eq. 3 with respect to the Bragg frequency \(f_B\) proportionally to the radial component of the surface current in the cell. Based on this property, the time- and cell-averaged surface current can be reconstructed along the local radial direction \({\varvec{r}}_{mn}\), as

$$\begin{aligned} \tilde{\overline{U}}_{r_{mn}}(t_s) = L_B\, (f^{\rm{max}}_{{D}_{mn}}(t_s) \mp f_B), \end{aligned}$$
(21)

within a resolution \(\Delta U_r = L_B/T_i\) since, as mentioned before, the Doppler spectrum frequency resolution is \(\Delta f=1/T_i\); thus, \(T_i\) should be sufficiently large to provide a good resolution of the inverted current. In direct conflict with this requirement, however, the reconstructed current based on Eq. 21 is time-averaged over \(T_i\) and, hence, \(T_i\) should also be much less than the tsunami characteristic period \(T_t\). Otherwise, the reconstructed currents could be significantly underestimated, due to smoothing out by averaging positive and negative values in the tsunami wave train, and become undetectable with this algorithm. A practical solution to this problem, assuming long-crested tsunami wave trains in the azimuthal direction (e.g., Figs. 2, 3), is to reduce \(T_i\) and compensate this by averaging the Doppler spectra computed in a few cells in the azimuthal direction; details will be provided in applications. It should be stressed, because the reconstructed current \(\tilde{\overline{U}}_{r_{mn}}(t_s)\) also includes the background current, that this algorithm will provide good results only when the tsunami current is significantly above background.

Finally, if the local direction of propagation of the tsunami \({\varvec{k_t}}_{mn}\) is known based on pre-existing tsunami modeling (e.g., using Snell’s law in the simplest case), the tsunami elevation can also be estimated from the reconstructed current using Eq. 4, by performing a simple projection, as,

$$\begin{aligned} \eta _t({\varvec{r}}_{mn},t_s) =\frac{ \tilde{\overline{U}}_{r_{mn}}(t_s)}{\frac{{\varvec{r}}_{mn}}{r_{mn}} \cdot \frac{{\varvec{k_t}}_{mn}}{k_{t_{mn}}} } \sqrt{\frac{h({\varvec{r}}_{mn})}{g}}, \end{aligned}$$
(22)

where \(h({\varvec{r}}_{mn})\) is the depth at the cell center.

4.2 TDA2: Tsunami Detection Algorithm 2: Shifted Signal Correlations

TDA2 directly processes the radar signal V(t) to detect an approaching tsunami and thus overcomes the limitations of TDA1 to short range and/or shallow water, where tsunami currents are sufficiently large to rise above the background. It is based on the fundamental property that, to the first-order, any tsunami propagates at the long wave celerity \(c_t\), which is entirely fixed by the local depth, along site-specific wave rays that can be pre-computed based on the bathymetry h(x, y) in a given area. Hence, radar signals measured in two radar cells located on the same wave ray will be highly correlated when shifted in time by the tsunami propagation time between the cells.

Let us first consider the simple case of a shelf and nearshore area that have no longshore variation, i.e., with a depth given by h(x), where x is the cross-shore coordinate (e.g., Fig. 4), and that there is no background current (the effect of a background current will be evaluated last). In this case, the bathymetric contours are parallel to the straight shoreline and any tsunami wave train, incident with an angle \(\phi _{t0}\) in deeper water of depth \(h_0\), refracts in a way that, for this simple case, is analytically predicted by Snell’s law (Eq. 6); additionally, wave shoaling is also accurately predicted by Green’s law (Eq. 5), corrected by a refraction coefficient also obtained from Snell’s law (Dean and Dalrymple 1984). Furthermore, in the simplest possible case of a normally incident tsunami on this bathymetry (\(\phi _{t0}=0\)), all the wave rays are straight and shore normal, and the refraction coefficient is 1. In this idealized situation and assuming linear long wave theory, the propagation time of an incoming tsunami between two radar cells, say p and q, whose centers are located at \(r_p\) in deeper depth \(h(r_p)\) and \(r_q\) in shallower depth \(h(r_q)\), respectively, along the radar ray that is also normally incident to the bathymetry, is given by,

$$\begin{aligned} \Delta t_{pq} = t(r_q) -t(r_p) = \int _{r_{p}}^{r_q} \frac{{\text {d}}r}{\sqrt{gh(r)}} {\text{, } \text{ or } } \oint _{s({\varvec{r}}_{p})}^{s({\varvec{r}}_{q})} \frac{{\text {d}}s}{\sqrt{gh(s({\varvec{r}}))}} \end{aligned}$$
(23)

for an arbitrary wave ray in a more general case, where \(s({\varvec{r}}(x,y))\) denotes the curvilinear abscissa along the ray, with \({\text {d}}s={\text {d}}x\, \cos {\phi _t} + {\text {d}}y\, \sin {\phi _t}\).

Now, for an approaching tsunami wave train, as already pointed out in earlier work, the current generated in cells p and q should be highly correlated in time, but for two distant cells even more so when shifted by this expected propagation time. Therefore,

$$ \begin{gathered} {\text{corr}}\{ \bar{U}_{{tq}} (\tau - \Delta \tau - \Delta t_{{pq}} ),\bar{U}_{{tp}} (t)\} \hfill \\ \quad = \frac{1}{{T_{c} }}\int_{{t - \frac{{T_{c} }}{2}}}^{{t + \frac{{T_{c} }}{2}}} {\bar{U}_{{tq}} } (\tau - \Delta \tau - \Delta t_{{pq}} )\bar{U}_{{tp}} (\tau ){\text{d}}\tau \hfill \\ \end{gathered} $$
(24)

is maximum when time lag \(\Delta \tau =0\), for a correlation time \(T_c\).

According to this property of long wave propagation, the principle of TDA2 is that the angular frequency changes (i.e., Doppler shifts) induced by the tsunami current on the independent random surface waves occurring in each radar cell, that cause modulations of the radar signal V(t), should also be highly correlated when shifted by the tsunami propagation time between the cells. Hence, correlations of the radar signals measured/simulated in two radar cells p and q, \({\text{V}}_{p}\) and \({\text{V}}_{q}\),

$$ \begin{gathered} {\text{corr}}\{ {\text{V}}_{q} (\tau - \Delta \tau - \Delta t_{{pq}} ),{\text{V}}_{p} (t)\} \hfill \\ \quad = \left| {\frac{1}{{T_{c} }}{\mkern 1mu} \int_{{t - \frac{{T_{c} }}{2}}}^{{t + \frac{{T_{c} }}{2}}} {{\text{V}}_{q} } (\tau - \Delta \tau - \Delta t_{{pq}} ){\mkern 1mu} {\text{V}}_{p}^{*} (\tau ){\text{d}}\tau } \right| \hfill \\ \end{gathered} $$
(25)

should be maximum when time lag \(\Delta \tau =0\), with the star indicating the complex conjugate.

Note that, to prevent border effects in the computation of correlations with Eqs. 24 and 25, which would produce an artificial decay of the correlation function when dealing with finite-duration signals, the correlation function is normalized by a triangular function that compensates for the lack of coefficients at large time lags in the numerical summation. This normalization ensures that a flat correlation is obtained as a function of time lag, for a constant signal with only random variations, as it should be in the absence of a tsunami current, but does not affect the shape of an actual correlation peak close to its maximum near zero time lag, caused by a tsunami current. Correlations of the radar signals between two cells, computed using Eq. 25, will increase with time \(T_c\). Unlike with TDA1, where increasing \(T_i\) improves the resolution of the Doppler spectrum, but also reduces the time-averaged tsunami current and hence smoothes it out, here, one can select a longer correlation time, up to or even larger than the characteristic tsunami period \(T_t\), without causing any ill effect, because time series of radar signal are shifted in time to compute the correlation.

Let us now consider the effects on the signal correlations of a background current, resulting from a spatially varying (but nearly stationary at the considered time scales) mesoscale current, plus local effects of random environmental conditions (e.g., wind). Because of its random fluctuations, there should not be any significant correlation of such a current between two arbitrarily selected cells, whether shifted in time or not, and hence no influence on Eq. 24. Likewise, the random or spatially incoherent changes in the angular frequency of surface waves caused by the background current, even if significantly influencing the radar signal in each cell, are uncorrelated and should thus not affect the correlation of the radar signal computed with Eq. 25. Therefore, only the spatially coherent surface current caused by the tsunami, that propagates deterministically along the selected wave ray, will affect the correlations of the radar signals. This property will be verified in numerical simulations and is the main reason why TDA2 is able to detect effects on the radar signal of a much weaker, but spatially coherent, tsunami current than TDA1, even in the presence of a background current of similar or even larger magnitude, without need for doing any actual estimate of the current itself.

In the absence of the spatially coherent current of an incoming tsunami, numerical simulations will show that correlations of radar signal between pairs of cells, computed using Eq. 25, become independent of time lag \(\Delta \tau \) (i.e., they are flat), whereas in the presence of a tsunami current, these correlations exhibit a strong maximum near the zero time lag (representing the theoretical propagation time between each pair of cell). This difference in correlation pattern with \(\Delta \tau \), around the expected propagation time between two cells, can be exploited to develop a tsunami detection threshold for the algorithm. Thus, using TDA2 in a tsunami detection mode (rather than simulation mode), for which the radar signal is continuously measured in a large number of radar cells, a peaked correlation suddenly appearing near zero time lag, between the radar signals in two cells located along the same wave ray, will indicate that a tsunami is approaching the radar. At the considered time scales, there is indeed no other geophysical phenomenon that can create long wave trains that are spatially coherent, with a current magnitude sufficient to cause measurable Doppler shifts in the radar signal. By computing correlations between signals in all the relevant pairs of radar cells along a given wave ray, and for multiple rays, one would be able to track an incoming tsunami in time from the displacement of peaked correlation patterns from cell to cell.

For more realistic cases, with complex but specified bathymetry h(x, y), tsunami wave rays can still be pre-calculated for a series of incidence angles \(\phi _{t0}\) in deep water, e.g., corresponding to known tsunami source directions in the far- and near-field. To do so, one can of course run a long wave model, such as FUNWAVE-TVD (see Figs. 2, 3), but many studies show that the less computationally demanding solution of the complete equation of geometric optics, the “eikonal” equation (of which Snell’s law is a particular solution), can accurately predict tsunami wave rays on the typical bathymetry of an ocean margin and continental shelf (see, e.g., Tehranirad et al. 2015). The eikonal equation,

$$\begin{aligned} \frac{\partial \phi _t}{\partial x} + f_1(x,y) \tan {\phi _t} \frac{\partial \phi _t}{\partial y} = f_2(x,y) \end{aligned}$$
(26)

is solved for \(\phi _t(x,y)\), with

$$\begin{aligned} f_1 = 1+ N \frac{1}{h} \frac{\partial h}{\partial x}\quad { \text{ and } }\quad f_2 = N \frac{1}{h} \frac{\partial h}{\partial y} \end{aligned}$$
(27)

and

$$\begin{aligned} N = \frac{c_t}{2c_{tg}} - 1 = -\frac{1}{2} \end{aligned}$$
(28)

since for long waves, \(c_t=c_{tg}= \sqrt{gh}\) (with \(c_{tg}\) the group velocity).

The pre-computed wave rays will allow identifying radar cells that are located along specific rays and the expected tsunami propagation time between each pair of such cells (p, q) will be calculated using the second Eq. 23. Except for this more complicated way of computing theoretical time lags between cells, TDA2 can be used unchanged for complex bathymetry cases.

Along a specific wave ray, an overall measure of tsunami detection with TDA2 can be obtained by averaging the correlations given by Eq. 25 for \(n_{p,q}\) pairs of cell from p to q, when applying the appropriate \(\Delta t_{pq}\) value of the time shift. This yields a detection function,

$$\begin{aligned} D_p(\Delta \tau )=\frac{1}{n_{p,q}}\sum _{q}{\text {corr}}\{{\text{V}}_{q}(t-\Delta \tau -\Delta t_{pq}),{\text{V}}_{p}(t)\}, \end{aligned}$$
(29)

which is expected to be maximum for \(\Delta \tau = 0\). Additionally, the maximum of \(D_p(\Delta \tau )\) on a given wave ray should become an increasingly narrow peak near the zero time lag, as both \(n_{p,q}\) increases and p corresponds to a cell closer to the radar, indicating that a tsunami is propagating gradually closer to the HF radar; by contrast, in the absence of a tsunami current, \(D_p(\Delta \tau )\) will remain flat as a function of time lag, whatever the \(n_{p,q}\) or p values; this will be illustrated in applications. In a specific geographic area, an appropriate threshold for the detection of a peaked maximum of \(D_p(\Delta \tau )\) near the zero time lag, beyond which a warning should be issued, could be defined by performing numerical simulations of tsunami case studies. Such more realistic applications will be left out for a future paper.

5 Validation of the Algorithms for Idealized Tsunami and Bathymetry

In the following, we test and validate the two proposed algorithms, TDA1 and TDA2, by applying them to cases with an idealized tsunami wave train propagating over a one-dimensional (1D) bathymetry h(x), representing parallel bottom contours and a straight coastline; it should be noted, in these numerical simulations, the HF radar simulator is based on the complete 2D model detailed above. In the idealized 1D tsunami simulations, the cross-shore seafloor depth varies between a deeper water depth \(h_0\) and a shallow water depth \(h_1\) on the shelf, and is modeled as a hyperbolic tangent (Fig. 4). The tsunami wave train is represented by a so-called “Envelope-Soliton” (ES), which is defined as a 1D group of long periodic waves whose amplitude envelope has a solitary wave shape (Fig. 4).

In the following sub-sections, we give equations for the bathymetry and initial ES shape and kinematics, together with a simple analytical model that can be used to simulate tsunami propagation and transformation by shoaling over the specified bathymetry. The latter is validated based on results of a numerical model solving full potential flow theory by a boundary integral equation method. We then apply the two detection algorithms by HF radar to the idealized tsunami case studies and assess effects of various parameters such as tsunami amplitude, wind speed/sea state, environmental noise, and background current on their detection ability.

In a follow-up paper, we will apply the algorithms to simulations of more realistic tsunami case studies, such as shown in Figs. 2 and 3, obtained using state-of-the-art tsunami generation and propagation models.

5.1 Equations of ES Tsunami

The ES tsunami is made of 1D waves that are normally incident to shore in deep water and long-crested in the along-shore direction (Fig. 4). Because of the idealized bathymetry, the ES will be propagating along wave rays that are normally incident to shore. At time \(t=0\), the ES middle location is at \(x_t(0)=x_{t0}\), in depth \(h_{t0}=h(x_{t0})\); the wave train is made of a series of sinusoidal long waves of initial maximum amplitude \(A_{t0}\), period \(T_t\), and wavelength \(L_{t0}=T_t \, c_{t0}\), whose amplitude (i.e., envelope) is modulated as a solitary wave. Assuming linear long wave theory, the initial celerity of the wave train at the ES center is, \(c_{t0}=\sqrt{gh_{t0}}\).

At time \(t=0\), the ES wave train elevation is analytically defined as,

$$\begin{aligned} \eta _t(x,0)= & {} A_t(x,0) \cos {\{ k_t(x - x_{t0})\}} \nonumber \\ A_t(x,0)= & {} \frac{A_{t0}}{1-\varepsilon _z}\, \left\{ {\text {sech}}^2 \left\{ \frac{\kappa }{h_{t0}}(x - x_{t0})\right\} - \varepsilon _z\right\}, \end{aligned}$$
(30)

where \(k_t = 2\pi /L_t\) and the ES peakedness parameter is the standard value for a solitary wave,

$$\begin{aligned} \kappa = \sqrt{\frac{3A_{t0}}{4\, h_{t0}}}, \end{aligned}$$
(31)

which is a function of the maximum amplitude \(A_{t0}\) and depth \(h_{t0}\) at the middle of the ES. The equivalent initial wavelength \(L_{s}(0)\) of the ES is controlled by the truncation parameter, \(\varepsilon _{z} \ll 1\), such that,

$$\begin{aligned} \left|\eta _t\left( \pm \frac{L_{s}}{2},0\right) \right| = 0. \end{aligned}$$
(32)

Based on Eq. 30, this requirement yields,

$$\begin{aligned} L_{s}(0) = \frac{2h_{t0}}{\kappa } C_z\quad { \text{ with } }\quad C_z = {\text {acosh}}{\sqrt{{\varepsilon _z}^{-1}}}. \end{aligned}$$
(33)

Finally, applying Eq. 4, the initial tsunami current is found as,

$$\begin{aligned} U_{t}(x,0) = \eta _t(x,0)\, \sqrt{\frac{g}{h(x)}}. \end{aligned}$$
(34)

For later times, when the ES wave train propagates over a decreasing depth, its instantaneous dominant wavelength decreases as,

$$\begin{aligned} L_{t}(t) = T_t c_t\quad { \text{ with } } c_t =\sqrt{gh_t} \end{aligned}$$
(35)

while the maximum wave amplitude in the ES increases according to Green’s law (Eq. 5) as,

$$\begin{aligned} A_{tt} = A_{t0}\, \left\{ \frac{h_0}{h_t}\right\} ^{\frac{1}{4}}. \end{aligned}$$
(36)

As these transformations take place, the instantaneous ES equivalent wavelength decreases as,

$$\begin{aligned} L_{s}(t) = L_{s}(0) \frac{L_t}{L_{t0}} = L_{s}(0) \sqrt{\frac{h_t}{h_{0}}}. \end{aligned}$$
(37)

The instantaneous position of the ES wave train middle location can be computed from its initial position \(x_{t0}\) as,

$$\begin{aligned} x_t(t) = x_{t0} + \int _0^t c_{t_i}\{h(x_t(\tau ))\} {\text {d}}\tau \end{aligned}$$
(38)

which can be computed as a function of a specified bathymetry.

With these properties of the ES, and assuming the seafloor has a mild slope (thus reflection is negligible), we define a set of simplified first-order analytical equations to iteratively propagate the ES wave train over a given bathymetry, from time t to \(t+\Delta t\) (with \(\Delta t\) small time step). In this analytical model, the ES is initially defined by a set of points \(x_i(0)\) (\(i=1,\ldots \)), spaced out by \(\Delta x\) over the free surface; these are propagated as follows,

$$\begin{aligned} x'_i(t+\Delta t) = x_i(t) + c_{t_i} \, \Delta t\quad { \text{ with } }\quad c_{t_i} = \sqrt{g h(x_i(t))} \end{aligned}$$
(39)
$$\begin{aligned} \eta '_{t_i}(x'_i(t+\Delta t)) = \eta _{t_i}(x_i(t))\, \left\{ \frac{h(x_i(t))}{h(x'_i(t+\Delta t))}\right\} ^{\frac{1}{4}}. \end{aligned}$$
(40)

At a given time step, once the ES has propagated to locations \(x'_i\) with elevations \(\eta '_{t_i}(x'_i)\), these values are reinterpolated over the initial grid points and the ES wave train is truncated by applying Eq. 32. At each time step, the tsunami horizontal current velocity is finally computed as,

$$\begin{aligned} U_t(x_i(t+\Delta t)) = \eta _{t_i}(x_i(t+\Delta t))\, \sqrt{\frac{g}{h(x_i)}}. \end{aligned}$$
(41)

This process is repeated for the next time step, and so forth.

Fig. 4
figure 4

Example of idealized ES tsunami wave train propagating over a “tanh” bottom topography, for \(A_{t0}=1\) m, \(h_0=2000\) m, \(h_1 = 20\) m, \(T_t = 300\) s, and \(\varepsilon _{z} = 0.05\), based on the analytical model Eqs. 39–41, at times \(t=\) a 0, b 1895, and c 5670 s. The horizontal axis is x (m) in the three panels and the vertical axis represents variables defined in a’s legend: \(\eta \) and h (m), and \(U_t\) (m/s) (note, surface elevations are magnified 100 times and horizontal velocities 500 times)

Full size image

5.2 Numerical Validation of Simplified ES Tsunami Propagation Model

Before applying the tsunami detection algorithms by HF radar to the simulated ES wave trains, we assess the relevance of the simplified propagation model based on linearized analytical Eqs. 39–41, for modeling tsunami propagation and transformation, by comparing its predictions to those of a numerical solution of fully nonlinear potential flow theory. The latter is performed using the higher-order Boundary Element Method (BEM) of Grilli et al. (1989), which was implemented as a two-dimensional (2D) Numerical Wave Tank (NWT), in the vertical plane (x, z), by Grilli and Subramanya (1996) and Grilli and Horrillo (1997) (note that a nonlinear model was not strictly necessary for the tested waves, that all have a small wave steepness, but this was the model that we had available).

The initial geometry of the NWT is that shown in Fig. 4. Boundary conditions on both the bottom and lateral boundaries are no-flow conditions,

$$\begin{aligned} u\,n_x + w\,n_z = \frac{\partial \varphi }{\partial n} = 0, \end{aligned}$$
(42)

where \(\varphi \) is the velocity potential, such that \({\varvec{u}}=(u,w)=\nabla \varphi \), and \({\varvec{n}}=(n_x,n_z)\) is the outward unit vector to the boundary. In the NWT, the required initial conditions are the wave elevation and the value of the potential on the free surface, as a function of the curvilinear abscissa s. Based on the known velocity field of the ES, the latter is obtained as

$$ \begin{aligned} \varphi (s) & = \int_{0}^{s} {\frac{{\partial \varphi }}{{\partial \chi }}} {\text{d}}\chi \quad {\text{ with }} \\ \frac{{\partial \varphi }}{{\partial \chi }} & = u(\chi ){\mkern 1mu} n_{z} (\chi ) - w(\chi ){\mkern 1mu} n_{x} (\chi ), \\ \end{aligned} $$
(43)

where \(u = U_t\), is the initial horizontal particle velocity induced by the ES, given by Eq. 34. Based on linear long wave theory (Dean and Dalrymple 1984), the initial vertical particle velocity on the free surface \((z=0)\) is found as

$$\begin{aligned} w = W_t = A_t(x,0) \,k_t\,c_{t}\,\sin {\{ k_t(x - x_{t0})\}} \end{aligned}$$
(44)

(note, if \(h=h_0\) under the entire initial ES, then we have \(c_t=c_{t0}\) in this equation). Moreover, based on the ES initial elevation (Eq. 30) the surface slope is found as

$$\begin{aligned} \frac{{\text {d}} \eta }{{\text {d}} x} = \frac{{\text {d}} A_t}{{\text {d}} x}\, \cos {\{ k_t(x - x_{t0})\}} - k_t \,A_t \sin {\{ k_t(x - x_{t0})\}} \end{aligned}$$
(45)

with \({\text {d}} \eta /{\text {d}} x = \tan {\alpha }\), \(n_x = -\sin {\alpha }\), \(n_y=\cos {\alpha }\), and

$$\begin{aligned} \frac{{\text {d}} A_t}{{\text {d}} x} = -2A_{t0} \frac{\kappa }{h_{t0}}\,\frac{\sinh {\{ \frac{\kappa }{h_{t0}}(x - x_{t0})\}}}{\cosh ^3{\{ \frac{\kappa }{h_{t0}}(x - x_{t0})\}}}. \end{aligned}$$
(46)

The numerical validation is performed for the ES tsunami case shown in Fig. 4, which has a maximum initial amplitude \(A_{t0}=1\) m and a dominant period of the wave train, \(T_t = 300\) s. The bottom bathymetry is idealized with a hyperbolic tangent shape, varying between \(h_0=2000\) m and \(h_1=20\) m on the continental shelf. The ES is initially truncated using \(\varepsilon _{z} = 0.05\) and specified as far left as possible in the NWT domain. Based on the specified bottom topography, we find the initial location of the ES maximum at, \(x_{t0} = L_{s}(0)/2=197.93\) km in depth \(h_{t0} = 1829\) m (\(\kappa = 0.0202\)), with a maximum current \(U_{t}^{\rm{max}}(x_{t0},0) =0.07\) m/s, as shown in Fig. 4a.

The computational domain, for both the analytical and numerical models varies between \(x=0\) and \(x=600\) km. Whereas a fine spatial mesh with \(\Delta x = 30\) m is used throughout in the analytical solution, with a constant time step \(\Delta t = 5\) s, to reduce the computational effort, the NWT domain is discretized only using 1212 nodes and 1004 BEM elements. On the free surface these are cubic sliding elements (Grilli and Subramanya 1996), with nodes initially spaced out by \(\Delta x = 750\) m; on the bottom, these are 3-node, quadratic isoparametric elements, with nodes spaced out by \(\Delta x = 1500\) m. The time step in the numerical solution is \(\Delta t \simeq 2.4\) s, but is dynamically adjusted based on a mesh Courant number of 0.5 and thus gradually decreases with depth; also, as depth decreases on the shallower part of the domain representing the continental shelf, adaptive integrations are used in the BEM to provide sufficient accuracy, which significantly increases computational time (Grilli and Svendsen 1990).

Both the initial elevation and horizontal current of this idealized ES tsunami are shown in Fig. 4a. The analytical model is applied first, to propagate the ES tsunami until its front reaches \(x=600\) km, which occurs at \(t=10{,}800\) s (3 h). Instantaneous values of free surface elevation and current are shown in Fig. 4b, c, at \(t = 1895\) and 5670 s, respectively. At these times, the ES maximum is at \(x_t = 377.6\) and 493.7 km, in depth \(h_t = 302.48\) and 40.73 m, with a maximum amplitude \(A_t = 1.57\) and 2.49 m, and a maximum current \(U_t^{\rm{max}} = 0.28\) and 1.22 m/s, respectively. As expected, as depth decreases, we observe a gradual increase (accelerated on the shelf) of both the ES tsunami elevation and current, while the tsunami dominant wavelength \(L_t\) decreases, as a result of the decreasing phase velocity \(c_t\); hence, the ES tsunami wave train becomes gradually shorter. The key parameters of the ES are plotted as a function of time in Fig. 5a.

To limit the computational effort in the NWT, the validation was limited to \(t=2234\) s, which corresponds to the ES maximum arriving at \(x_t = 408\) km in depth \(h_t=170.4\) m over the shelf. Figure 5b shows the comparison of the ES tsunami horizontal current \(U_t(x,t)\) computed with the analytical model and in the NWT (on the free surface). The agreement between both methods is found to be reasonable, with only a slightly larger value of the dominant wavelength and slightly lower value of the current in the NWT solution. This can be explained by mild nonlinear amplitude dispersion effects in the BEM solution, which attenuate the decrease of tsunami phase speed with depth. In very shallow water, one would expect the same nonlinear effects to gradually affect wave shoaling and current magnitude, more significantly.

Nevertheless, it can be concluded from this comparison, that the analytical model is sufficiently accurate to simulate the key physical features of the ES tsunami propagation and transformations over the specified bathymetry, for the purpose of validating the tsunami detection algorithms by HF radar. In the latter, the simplified analytical model will allow to rapidly compute simulated data sets of tsunami elevation and current, to be used to simulate Doppler effects on shorter wind waves, in a series of radar cells with their center located at \(\mid {\varvec{r}}_{m}\mid =x_m\) (\(m=1,\ldots ,M\)). In particular, in the analytical model, we will compute as a function of time the spatially averaged surface current in each cell \(\overline{U}_{tm}(t)\), as well as the current memory term required in the wave angular frequency Eq. 10.

Fig. 5
figure 5

Case of Fig. 4. a Values of ES tsunami key parameters calculated with the analytical model, as a function of time. b Comparison of linearized analytical solution (solid), with numerical BEM solution of potential flow theory (dash), for the horizontal current value \(U_t(x,t)\) (m/s) computed at \(t= 2234\) s (on the free surface in the NWT)

Full size image

5.3 Numerical Validation of the HF Radar Tsunami Detection Algorithms Based on Idealized Case Studies

The numerical implementation and application of the 2D radar scattering model equations presented earlier (Eqs. 16–19) to a random sea state modulated by a surface current (Eqs. 7–12), provides a simulator of the backscattered HF radar signal, whose results can be used in lieu of actual field data, as a data base of radar data to test and validate the two proposed tsunami detection algorithms.

In the simulator, for illustration, we use the characteristics of the 4.5 MHz Stradivarius radar system (see parameters in Sect. 1) in a monostatic configuration (or in a bistatic configuration where remote sensing takes place far enough from the radar for the signal to become nearly monostatic); other types of radars could be easily substituted and simulated. We apply the simulator to cases for which the tsunami-induced current is that of the 1D idealized ES tsunami wave train introduced before, which is long-crested in the y direction and shoals up in the x direction, normally incident to shore (\(\phi _{t0} = 0\)) over a simple bathymetry (cylindrical beach), with parallel bottom contours in the y direction (Fig. 4). Although this might seem very idealized, as seen in tsunami case studies in the Gulf of Lion, off of Camargue, in the Mediterranean Basin (Figs. 2, 3), this is in fact quite a realistic hypothesis in many locations, and thus relevant for the purpose of validating the algorithms, pending their application to more complete and realistic tsunami case studies, simulated or from actual field data. Note that with minor changes to the approach presented below, one could also consider tsunamis that are approaching from an arbitrary direction \(\phi _{t0}\) over the same idealized bathymetry, by applying Snell’s law (Eq. 6); this will be left out for future work.

For a monostatic radar configuration, the signal is simulated in a series of cells, whose centers are located at radial directions \({\varvec{r}}_{mn}\) from the radar location, with azimuth \(\phi _{r_n}\) measured from x (\(m=1,\ldots ,M\); \(n=1,\ldots ,N\)), for a radar located at (0,0) (e.g., Fig. 1). The radar signal will be modulated by the approaching tsunami, based on the magnitude of its current projected on these radial directions (assuming to start with that there is no background current, \({\varvec{U}}_b=0\); see Eq. 7),

$$\begin{aligned} U_{tr}(t,{\varvec{r}}_{mn})= {\varvec{U_{t}}}(t,x_{mn},y_{mn}) \cdot {\varvec{r}}_{mn} \end{aligned}$$
(47)

with \({\varvec{r}}_{mn}=x_{mn}{\varvec{e}}_x+y_{mn}{\varvec{e}}_y\), \(\mid {\varvec{r}}_{mn} \mid = r_{mn}\) and (\({\varvec{e}}_x, {\varvec{e}}_y\)) being unit vectors in the x- and y-directions.

We will first present results obtained for both first-order waves \(\eta _1\) and radar signal \({\text{V}}^{1}(t)\), and then show how these are modified when including the second-order contributions, \(\eta _2\) and \({\text{V}}^{2}(t)\). In the HF radar simulator, the effects of environmental noise and range decay on the radar signal are simulated by adding \(\mathcal{N}_{mn}(t)\) to the signal \({\text{V}}_{mn}(t)\) computed in each cell (Eqs. 17, 19).

Although the 2D radar simulator provides results for any azimuth, for clarity, all results resented here will only be shown for a single azimuth of direction, \(\phi _{r_1} = 180^\circ \) (\(n=1\)), i.e, looking directly away and normally to shore, with an angular spacing \(\Delta \phi _{r} = 6^\circ \); hence, \(U_{tr}(t,{{\varvec{r}}_{m1}})= -U_{t}(t,x_m)\). For these simulations, we will use radar cells spaced out by \(\Delta r = 3\) km, at a distance, \(r_{m1} = -x_m = 80\)–230  km from the radar.

To compute the radar signal within each cell, the random sea state is spatially discretized over a \(\Delta x=\Delta y = 3\) m resolution grid, when only considering linear waves, and a 0.5 × 0.5 m resolution grid when including second-order wave effects (this is because the Bragg wavelength is \(L_B=33.3\) (\(k_B = 0.119\) m\(^{-1}\)) and requires 10–12 points to be finely enough discretized, which yields a 3 m spacing; by contrast, second-order waves, which are much shorter, require a minimum spatial spacing of order 0.5 m). Based on this discretization, the wind waves wavenumber vectors, \({\varvec{K}}=(K_x,K_y)\), are defined with a module varying in between \([-K_{\rm{max}},K_{\rm{max}}]\) by steps \(\Delta K = 2\pi /1000\), with \(K_{\rm{max}} = 2\pi /(2 \Delta x)\). Therefore, for linear simulations, waves are discretized in each radar cell by 333 \(\times \) 333 wavenumbers, and 2000 \(\times \) 2000 wavenumbers for nonlinear simulations.

In each radar cell, wind waves are generated based on a directional PM energy spectrum \(\Psi _{PM}\) (Eqs. 48–52), assuming to start with \(V_{10}=10\) m/s and \(\theta _p = 0^\circ \) (i.e., the radar looks in a cross-wind direction); the spectrum obtained in this case is shown in Fig. 24 and corresponds to, \(H_s = 1.71\) m, \(k_p=0.0493\) m\(^{-1}\), \(L_p = 127.4\) m, and \(T_p = 9.04\) s in deep water. The environmental noise is computed in each cell based on Eqs. 19 and 20, with the standard noise coefficient, \(f_a=130\). Waves in each cell are modulated by the current induced by the ES tsunami, which propagates over the bathymetry shown in Fig. 4, varying as a “tanh” between \(h_0=2000\) m and \(h_1 = 20\) m, as detailed in the previous section. We specify an ES with amplitude \(A_{t0}=1\) m and periodicity \(T_t = 300\) s (with \(\varepsilon _{z} = 0.05\)) and, as indicated, we initially assume that there is no background current (\({\varvec{U}}_b=0\)).

We first apply tsunami detection algorithm TDA1 to the simulated HF radar signal, by computing the Doppler spectra over a frequency range \([-f_{D{\rm{max}}},f_{D{\rm{max}}}]\), with \(f_{D{\rm{max}}} = 2.3 f_B=0.5\) Hz. This is done by applying Eq. 18 over the integration interval \([t_s-0.67T_i, t_s+0.33T_i]\), using an integration time, \(T_i = 120\) s (\(<T_t/2\)); new spectra are thus computed at a \(\Delta t_s = 0.33T_i= 40\) s time interval. We then apply the second algorithm TDA2 and compute correlations of the simulated radar signal between two cells, shifted in time, using Eq. 25; here, we use a correlation time, \(T_{c}=300\) s.

5.3.1 Test of Tsunami Detection Algorithm 1 (TDA1)

In a first validation test, the HF radar simulator is used to compute the linear signal \({\text{V}}^{1}(t)\) during 7200 s, in 51 cells located at distances \(r_{m1} = 80\)–230 km from the radar, corresponding to depths varying between 30.5 and 348.5 m.

Doppler spectra computed to apply TDA1 are plotted in Fig. 6, as a function of the distance to the radar (range) \(r_m\), after 30, 60, 90 et 120 min of propagation and shoaling of the ES tsunami. Because of the asymmetric and directional PM spectrum used to generate wind waves in each cell, Doppler spectra have two maxima near the theoretical Bragg frequencies \(f_B=\pm 0.217\) Hz. Outside of the neighborhood of these frequencies, the spectral intensity rapidly decreases to the level of the environmental noise. The effect of the ES tsunami current on the Doppler spectra is to cause an oscillatory shift of the spectral maxima around the Bragg frequencies. More specifically, in the time sequence of spectra in Fig. 6, we see that the propagation of the ES tsunami gradually displaces the oscillations from large ranges (depth) towards shorter ranges and shallower depth, in the radar direction. Also, as this occurs, as a result of the increasing tsunami current magnitude in shallower water, the amplitude of these oscillatory shifts increases and, due to the decreasing tsunami phase speed with depth, the wavelength of the oscillations also decreases.

Fig. 6
figure 6

Test of tsunami detection algorithm 1 (TDA1) based on data from the linear HF radar simulator for ES tsunami (Fig. 4) with \(A_{t0}=1\) m, \(T_t = 300\) s, and \(\varepsilon _{z} = 0.05\), using 51 cells located at \(r_{m1} = 80\)–230 km from the radar (with \(\phi _{r_1} =180^\circ \)). Doppler spectra (color scale in dB) computed with \(T_{i} = 120\) s after: a 30, b 60, c 90, et d 120 min of tsunami propagation

Full size image
Fig. 7
figure 7

Test of tsunami detection algorithm 1 (TDA1) based on data from the linear HF radar simulator, for the cases and Doppler spectra of Fig. 6: blue inverted mean currents in each radar cell; green cell-averaged ES tsunami current; and red ES tsunami current, after: a 30, b 60, c 90, and d 120 min of ES tsunami propagation (Fig. 4)

Full size image

This is confirmed in Fig. 7, which plots the inverted tsunami current as a function of range, obtained by applying Eq. 21 to the most intense maximum in each Doppler spectrum of Fig. 6, and compares it to the known instantaneous ES tsunami current and its space- and time-average in each radar cell (over time \(T_i\)). Despite the coarse 3 km discretization size of the radar cells, overall, one recovers well both the expected cell-averaged current magnitude and its variability, consistent with the observed patterns in Doppler spectra. Note, however, that the cell-averaged current magnitude is significantly smaller than the actual current, since the integration time \(T_{i} = 120\) s is a significant fraction of the tsunami current periodicity, \(T_t = 300\) s. As the ES tsunami propagates towards shallower depth, the current magnitude (both actual and cell-averaged) increases and the ES dominant wavelength decreases, as a result of shoaling. Despite the environmental noise and the fairly large depth in the most distant cells (while still being on or very near the shelf), the figure shows that the current is accurately inverted by this method, for the considered ES tsunami case (also compare Figs. 5b and 7b).

The same case is recomputed using the nonlinear HF radar simulator, that includes both second-order waves and radar signal. Since this computation takes much longer, for sake of efficiency, it is limited to cells located within the range \(r_{m1} = 120 \)–200 km from the radar (i.e., 27 radar cells) and an ES current duration of 6300 s. Figure 8 shows the Doppler spectra computed at 30, 60 and 90 min of propagation of the ES tsunami and Fig. 9 shows the corresponding inverted currents, both as a function of range. Up to a range of 180 km, results appear to be fairly similar with those of the linear simulator in Figs. 6 and 7, for both the computed Doppler spectra and the inverted currents. Beyond that range, however, some artifacts start appearing in the inverted currents, that would indicate that second-order effects make it more difficult estimating the shift of the Doppler frequencies (and hence the currents) in some stages of the ES tsunami shoaling when the average current is weaker. In the present case, a 180 km range corresponds to a depth of 136 m, where maximum tsunami currents still reach 0.52 m/s (see Eqs. 4, 5), but spatially and temporally averaged tsunami currents in the tail of the ES tsunami have a smaller magnitude of \(\sim \)0.2 m/s or less.

Fig. 8
figure 8

Test of tsunami detection algorithm 1 (TDA1) based on data from the nonlinear HF radar simulator, for ES tsunami (Fig. 4) with \(A_{t0}=1\) m, \(T_t = 300\) s, and \(\varepsilon _{z} = 0.05\), using 27 cells located at \(r_{m1} = 120\)–200 km from the radar (with \(\phi _{r_1} =180^\circ \)). Doppler spectra (color scale in dB) computed with \(T_{i} = 120\) s after: a 30, b 60 and c 90 min of tsunami propagation

Full size image
Fig. 9
figure 9

Test of tsunami detection algorithm 1 (TDA1) based on data from the nonlinear HF radar simulator. Inverted mean currents for the case and Doppler spectra of Fig. 8 computed after: a 30, b 60, and c 90 min of ES tsunami propagation (Fig. 4)

Full size image
Fig. 10
figure 10

Test of tsunami detection algorithm 2 (TDA2) for ES tsunami (Fig. 4) with \(A_{t0}=1\) m, \(T_t = 300\) s, and \(\varepsilon _{z} = 0.05\): a space-averaged ES tsunami current \(\overline{U}_{qt}(t)\) in radar cells \(q=1,\ldots , 51\), shifted in time by tsunami travel time to cell 1, \(\Delta t_{1q}=\) 176–5337 s; b correlation of shifted tsunami currents between cells 1 and \(q=2,\ldots 51\), as a function of an additional time lag, with \(T_{c} = 300\) s

Full size image
Fig. 11
figure 11

Test of tsunami detection algorithm 2 (TDA2), based on data from the HF radar simulator, for ES case of Figs. 4 and 10 (wind speed \(V_{10} = 10\) m/s, deep water tsunami amplitude \(A_{t0}=1.0\) m, and noise coefficient \(f_a=130\)): a Linear signal correlation (color scale) between cells 1 and \(q=2,\ldots 51\) (Eq. 25), shifted by tsunami travel time to cell 1, \(\Delta t_{1q}=\) 176–5337 s, as a function of an additional time lag, with \(T_{c} = 300\) s; b same as a for the nonlinear signal (27 cells)

Full size image
Fig. 12
figure 12

Test of tsunami detection algorithm 2 (TDA2) for cases of Fig. 11. Mean over 50 pairs of cells \((1,q=2,\ldots ,51)\), \(D_1(\Delta \tau )\), of signal correlations calculated with: a linear signal correlations of Fig. 11a, with tsunami current; b nonlinear signal correlations of Fig. 11b (27 cells); c same as a, linear signal in the absence of a surface current caused by the tsunami

Full size image
Fig. 13
figure 13

Test of tsunami detection algorithm 2 (TDA2): a same case as Fig. 11a for the linear analytical signal; b same as Fig. 12a for the linear analytical signal

Full size image

5.3.2 Test of Tsunami Detection Algorithm 2 (TDA2)

We apply TDA2 to the same case as above, assuming both linear wind waves and simulated HF radar signal \({\text{V}}^{1}(t)\). Figure 10a shows the space-averaged current \(\overline{U}_{qt}(t)\), computed in radar cells \(q=2,\ldots , 51\) for the incoming ES tsunami, shifted in time by the theoretical tsunami travel time to cell \(p=1\), computed with Eq. 23, \(\Delta t_{1q}=\) 176–5337 s. For these currents, Fig. 10b shows that, as expected, the correlation, \({\text {corr}}\{\overline{U}_{tq}(t-\Delta \tau -\Delta t_{1q}),\overline{U}_{t1}(t)\}\), computed with Eq. 24 (for \(T_{c} = 300\) s), between cell 1 and \(q=2,\ldots 51\), as a function of an additional time lag \(\Delta \tau \), is close to one near the zero time lag for all the radar cells, even the most distant ones. Similar results would be obtained along wave rays of more complex geometry (this will be shown in a follow-up paper).

Figure 11a then shows the time-shifted correlations of the simulated radar signal, \({\text {corr}}\{{\text{V}}^1_{q}(t-\Delta \tau -\Delta t_{1q}),{\text{V}}^1_{1}(t)\}\), computed with Eq. 25 (for \(T_{c} = 300\) s), as a function of an additional time lag \(\Delta \tau \), for the same cells. Despite some high-frequency oscillations in the results, correlations are high for lag times [\(-\)50, 50] s, up to a 160 km range and for [\(-\)50, 150] s beyond that. Outside of these intervals, correlations quickly become negligible. Figure 12a shows the mean correlation \(D_1(\Delta \tau )\) computed with Eq. 29 over \(n_{1,51}=50\) pairs of cells. We see a strong peak of the mean correlation near zero time lag and, in the absence of a surface current, Fig. 12c shows that there is no trend of the mean correlation with time lag. As indicated before, such a significant change in correlation pattern with and in the absence of a tsunami current could be used as a threshold for tsunami detection. These results confirm the relevance of the proposed detection algorithm.

Second-order effects. To further confirm the above results, which were obtained using the linear 2D HF radar simulator, the same computations are repeated using the nonlinear 2D simulator. As for the earlier application of the nonlinear simulator in Figs. 8 and 9, to reduce the computational effort, the range is limited to cells located \(r_{m1} = 120 \)–200 km from the radar (i.e., 27 radar cells). Figure 11b shows the radar signal correlations, \({\text {corr}}\{{\text{V}}_{q}(t-\Delta \tau -\Delta t_{1q}),{\text{V}}_{1}(t)\}\), computed between cells as a function of range, and Fig. 12b shows the mean correlation. Overall, we see a very good agreement with the first-order results shown in Figs. 11a and 12a, which implies that one can continue validating TDA2 using the less computationally demanding linear 2D HF radar simulator.

Analytical signal. High-frequency oscillations were observed in both the linear and nonlinear correlations of Fig. 11, calculated as a function of range, and the mean of these plotted in Fig. 12a, c. It can be shown theoretically that, for a simplified radar signal with a single harmonic with \(K=K_B\), the backscattered signal can be represented by the sum of two contributions, \({\text {S}}(t)= {\text {S}}_B(t)+{\text {S}}_{B'}(t)\), where: (1) \({\text {S}}_B(t) \sim \exp {(-{i}\omega _B\,t)}\), oscillates at the Bragg frequency; and (2) \({\text {S}}_{B'}(t)\), has a spatial modulation with periodicity \(2K_B\) and is proportional to \(\exp {({i}\omega _B\,t)}\). We show that the latter contribution is responsible for the observed oscillations of signal correlations, by eliminating negative frequencies from the Fourier transform of the total signal \(\hat{{\text {S}}}(\omega )\), and then applying an inverse Fourier transform to reconstruct the signal in the time domain; this operation consists in computing the so-called analytical signal.

Figure 13a shows the correlations recomputed as a function of range, between pairs of cells, based on the linear analytical signal \({\text{V}}^1(t)\), with environmental noise and range attenuation, in the presence of the ES tsunami current. Comparing these results to Fig. 11a, while we see overall a similar pattern of the correlations as a function of range and time lag, high-frequency oscillations have clearly been eliminated when using the analytical signal, and the peak in correlation is now narrower for lag times [\(-\)20, 20] s, up to a 160 km range and for [\(-\)20, 50] s beyond that. Moreover, looking more closely we see that the magnitude of correlations has been increased by 0.1–0.25, and is close to one near the zero time lag. The same observation can be made for the mean correlation \(D_1(\Delta \tau )\) computed based on the linear analytical signal, which is shown in Fig. 13b: the high-frequency oscillations have been eliminated and the maximum of the curve is close to one near the zero lag time. Hence, with the analytical signal, the time-shifted correlations are both higher and more monotonous than when using the raw signal. Since it is easy to compute the analytical signal for an actual backscattered HF radar signal (either based on numerically applying an FFT/IFFT operator to the digitized radar signal or by modifying the raw signal with an analog circuit), from now on, we will use the analytical signal in the following applications and validation of the detection algorithms.

Fig. 14
figure 14

Test of tsunami detection algorithm 2 (TDA2). Same case as Fig. 11a, for the analytical linear signal, but for an ES tsunami with reduced maximum amplitude in deep water to, \(A_{t0}=0.5\) m (\(T_{t} = 300\) s, \(\varepsilon _z = 0.1\)) (\(V_{10} = 10\) m/s and noise coefficient \(f_a=130\)): a correlation between cells 1 and \(q=2,\ldots 51\) (\(T_{c} = 300\) s), shifted by tsunami travel time to cell 1, as a function of an additional time lag; b mean of signal correlations over 50 pairs of cells, \(D_1(\Delta \tau )\)

Full size image
Fig. 15
figure 15

Test of tsunami detection algorithm 2 (TDA2). Same case as Fig. 11a, for the analytical linear signal, but with a reduced wind speed to \(V_{10} = 5\) m/s (\(A_{t0}=1.0\) m and noise coefficient \(f_a=130\)): a correlation between cells 1 and \(q=2,\ldots 51\) (\(T_{c} = 300\) s), shifted by tsunami travel time to cell 1, as a function of an additional time lag; b mean of signal correlations over 50 pairs of cells, \(D_1(\Delta \tau )\)

Full size image
Fig. 16
figure 16

Test of tsunami detection algorithm 2 (TDA2). Same case as Fig. 11a, for the analytical linear signal, but with increased environmental noise by a 3.2 factor, using a noise coefficient \(f_a=140\) (\(V_{10} = 10\) m/s and \(A_{t0}=1.0\) m): a correlation between cells 1 and \(q=2,\ldots 51\) (\(T_{c} = 300\) s), shifted by tsunami travel time to cell 1, as a function of an additional time lag; b mean of signal correlations over 50 pairs of cells, \(D_1(\Delta \tau )\)

Full size image
Fig. 17
figure 17

Test of tsunami detection algorithm 2 (TDA2). Same case as Fig. 11a, for the analytical linear signal, but with increased environmental noise by a 3.2 factor, using a noise coefficient \(f_a=140\), reduced wind speed to \(V_{10} = 5\) m/s, and smaller maximum tsunami amplitude in deep water \(A_{t0}=0.5\) m: a signal correlation between cells 1 and \(q=2,\ldots 51\) (\(T_{c} = 300\) s), shifted by tsunami travel time to cell 1, as a function of an additional time lag; b mean of signal correlations over 50 pairs of cells, \(D_1(\Delta \tau )\); c same as b but in the absence of a surface current caused by the tsunami

Full size image

Sensitivity to a weakened radar signal/SNR. Here, we perform a sensitivity analysis of the above results and application of TDA2 to the case of Fig. 11a, for the ES tsunami of deep water maximum amplitude \(A_{t0}=1.0\) m, in the presence of wind waves based on a \(V_{10} = 10\) m/s wind speed, and with the standard environmental noise of Stradivarius, with a noise coefficient \(f_a=130\). The latter parameters were first modified one at a time, in a manner that weakens the radar signal (or decreases its SNR), i.e., by assuming:

  1. 1.

    A deep water tsunami amplitude reduced to \(A_{t0}=0.5\) m, with \(\varepsilon _z = 0.1\), which proportionally decreases the current magnitude to about half the earlier values and thus the radar signal modulation and Doppler shift (Fig. 14).

  2. 2.

    A wind speed decreased to \(V_{10} = 5\) m/s, which decreases the sea state’s significant wave height to \(H_s = 0.42\) m (with a spectral peak wavelength \(\lambda _p = 31.9\) m and deep water period \(T_p = 4.52\) s) and thus the backscattered signal strength and Doppler spectrum level (Fig. 15).

  3. 3.

    An environmental noise increased by a factor of 3.2, with a noise coefficient \(f_a=140\) (which decreases the SNR in all radar cells; Fig. 16).

  4. 4.

    A similar case where all three above effects of SNR reduction are included at once and combined to very much reduce the SNR in all the radar cells.

These results are discussed below.

First, in Fig. 14, we see that reducing the tsunami elevation and current by a factor of two does not significantly affect results of applying TDA2; the maximum average signal correlation near the zero time lag is still nearly 1 and represents a strong peak as compared to values obtained at larger time lags. This is expected since currents are still strong, with maxima of 0.2–0.3 m/s in each time snapshot similar to those in Fig. 7. In fact, one could show that for this case, in which the SNR is still large, currents at those locations could still be accurately inverted from the Doppler spectra by applying TDA1.

Second, in Fig. 15 we see that, although the effect of reducing wind speed is more significant on correlations, particularly for large ranges, beyond 180 km, the average correlation still has a strong peak around 0.9 near the zero time lag and hence the ability of the TDA2 to detect currents is not significantly affected by this factor alone.

Third, in Fig. 16 we similarly see that, although the effect of increasing environmental noise is quite significant on correlations, particularly for large ranges, beyond 160 km, the average correlation still has a strong peak around 0.9 near the zero time lag and hence, once again, the ability of TDA2 to detect currents is not significantly affected by this factor alone.

Finally, in Fig. 17a, when all three sources of SNR weakening are simultaneously included in the simulations, we see that increased signal correlations only occur up to about a 170 km range, in the time lag interval [\(-\)50, +50] s. In Fig. 17b, the average correlation for those still shows a peak, but only about 0.6 near the zero time lag, as compared 0.3–0.35 on either side of it, while in the absence of a tsunami surface current, the mean correlation in Fig. 17c again does not show any trend as a function of time lag. Hence, although less discriminant than when the SNR is higher, the ability of TDA2 to detect currents based on a change in pattern of mean correlations is still intact. In the present situation, TDA1 would of course be unable to invert any current on the basis of such a noisy signal and weak SNR (this will be further illustrated in the last application). Note, however, that assuming a factor 3 increase in environmental noise is both extreme and unlikely, since the simulator already uses a \(f_a\) value based on field data that is realistic for the Stradivarius system in the environment it is deployed. Hence, in the last application in the next section, we no longer vary the noise factor and use \(f_a = 130\), and only consider changes in tsunami amplitude and sea state height, together with the presence of a background current.

Fig. 18
figure 18

Test of tsunami detection algorithm 2 (TDA2) in the presence of a background current. Same case as Fig. 10 with \(\sigma _{U_b}=0.15\) m/s: a space-averaged total current \(\overline{U}_{qt}(t)\) in radar cells \(q=1,\ldots , 51\), shifted in time by tsunami travel time to cell 1, \(\Delta t_{1q}=\) 176–5337 s; b correlation of time-shifted currents between cells 1 and \(q=2,\ldots 51\), as a function of an additional time lag, with \(T_{c} = 300\) s

Full size image
Fig. 19
figure 19

Test of tsunami detection algorithm 2 (TDA2) in the presence of a background current. Same case as Fig. 13 with \(\sigma _{U_b}=0.15\) m/s: a signal correlation between cells 1 and \(q=2,\ldots 51\) (\(T_{c} = 300\) s), shifted by tsunami travel time to cell 1, as a function of an additional time lag; b mean of signal correlations over 50 pairs of cells, \(D_1(\Delta \tau )\); c same as b but in the absence of surface current caused by the tsunami

Full size image
Fig. 20
figure 20

Test of tsunami detection algorithm 2 (TDA2) in the presence of a background current. Same case as Fig. 10 but with a tsunami amplitude reduced to \(A_{t0} = 0.5\) m and \(\sigma _{U_b}=0.15\) m/s: a space-averaged ES tsunami current \(\overline{U}_{qt}(t)\) in radar cells \(q=1,\ldots , 51\), shifted in time by tsunami travel time to cell 1; b same as a for the total current \(\overline{U}_{q}(t)\); c correlation of time-shifted total currents of b, between cells 1 and \(q=2,\ldots 51\), as a function of an additional time lag, with \(T_{c} = 300\) s

Full size image
Fig. 21
figure 21

Test of tsunami detection algorithm 1 (TDA1), in the presence of a background current, based on data from the linear HF radar simulator, for 51 cells located at \(r_{m1} = 80\)–230 km from the radar (with \(\phi _{r_1} =180^\circ \)). Doppler spectra (color scale in dB) using \(T_{i} = 120\) s, for ES tsunami propagation (Fig. 4), but computed for a tsunami amplitude reduced to \(A_{t0} = 0.5\) m, wind reduced to \(V_{10}=5\) m/s, and with \(\sigma _{U_b}=0.15\) m/s, after propagation of: a 45 and b 90 min

Full size image
Fig. 22
figure 22

Test of tsunami detection algorithm 1 (TDA1), in the presence of a background current, based on data from the linear HF radar simulator. Inverted mean currents in each radar cell, for the cases and Doppler spectra of Fig. 21, after: a 45, b 60, c 75, and d 90 min of ES tsunami propagation (Fig. 4)

Full size image
Fig. 23
figure 23

Test of tsunami detection algorithm 2 (TDA2) for a tsunami amplitude reduced to \(A_{t0} = 0.5\) m and wind reduced to \(V_{10}=5\) m/s, in the presence of a background current with \(\sigma _{U_b}=0.15\) m/s. Same case as Figs. 20, 21, 22: a signal correlation between cells 1 and \(q=2,\ldots 51\) (\(T_{c} = 300\) s), shifted by tsunami travel time to cell 1, as a function of an additional time lag; b mean of signal correlations over 50 pairs of cells, \(D_1(\Delta \tau )\); c same as b but in the absence of a tsunami current

Full size image

5.3.3 Test of Tsunami Detection Algorithms 1 and 2 with a Background Current

The previous sensitivity study established that TDA2 can still perform well in the presence of a weaker tsunami and lower wind speed, i.e., sea state. A very large increase in environmental noise has more effect, although the algorithm still performs adequately, but is deemed unrealistic. On this basis, here, we further assess the performance of the TDA1 and TDA2 algorithms in the presence of a random background current, which so far has been neglected, but would of course occur in an oceanic environment. We expect a strong effect of such a current on the direct inversion done with TDA1, in areas where the tsunami current is too weak to rise above background current. However, because of the nature of TDA2, we expect the background current to only have marginal effect on signal correlations and thus on the detection ability of this algorithm, even in areas where the tsunami current is on the same order of magnitude or even less than the background current.

These predictions will be verified in a last set of applications of the simulator, which are detailed below. In each case, we will assume the presence of a normally distributed background current of zero mean and standard deviation \(\sigma _{U_b}\). Note that uncorrelated realizations of this current are generated in the model, for each time level and in each radar cell. In all cases shown here, we use a large value of \(\sigma _{U_b}\) equal to 0.15 m/s; with this value, the instantaneous current has a 95 % chance to vary within the interval [\(-\)0.3, +0.3] m/s, with larger values occasionally occurring.

Thus, in Fig. 18, for the ES tsunami case considered so far, with \(A_{t0} = 1.0\) m and wind speed \(V_{10}=10\) m/s, we first see the effect this background current has on the spatially averaged current \(\overline{U}_{pt}(t)\) in each radar cell, shifted by the tsunami travel time to cell 1, \(\Delta t_{1q}=\) 176–5337 s. Figure 18a corresponds to the same tsunami current as in Fig. 10a, but we see now that the presence of a strong background current makes it impossible to visually observe any pattern in currents. Nevertheless, although smaller, Fig. 18b still shows elevated values of current correlations near the zero time lag. Figure 19 shows results of applying TDA2 to this case, and we still see: in panel (a) the same high correlation of the signal around the zero time lag, even at a range as large as 230 km; and in panel (b) a mean correlation near 1 at zero time lag, with much lower values on either sides, similar to results obtained without a background current. In Fig. 19c, we see again in the absence of the tsunami current, but in the presence of the background current, that there is no pattern in the mean correlation as a function of time lag. Hence, results of applying TDA2 are still as expected and the detection ability of the algorithm is intact in the presence of a background current, with the caveat that both a strong tsunami and sea state were used here.

Therefore, to fully confirm this conclusion, we repeated simulations in the presence of the same background current, but with a reduced tsunami (and current) deep water amplitude to \(A_{t0} = 0.5\) m and wind speed reduced to \(V_{10}=5\) m/s, and tested both TDA1 and TDA2. The time-shifted space-averaged tsunami currents for this case are shown in Fig. 20a, and vary from \(-\)0.1 to 0.065 m/s, while those combined to the background current are shown in Fig. 20b, and vary between \(-\)0.4 and 0.4 m/s; clearly, the tsunami current is much weaker than the background current. The correlations of the time-shifted currents are shown in Fig. 20c for this case; these are even lower than those in Fig. 18b, but still show elevated values near the zero time lag.

Next, Fig. 21 shows two Doppler spectra computed for this case, after 45 and 90 min of tsunami propagation, which clearly have a lower level than before and exhibit oscillations around the theoretical Bragg frequencies that no longer have the clean pattern of the ES tsunami. This is confirmed in Fig. 22, which shows the inverted currents using TDA1 for those two and two additional Doppler spectra, after 60 and 75 min of propagation time. Now, beyond a 120 km range, TDA1 can no longer properly invert currents and, even at shorter ranges, the pattern is no longer fully similar to that of the ES tsunami. By contrast and to conclude, in Fig. 23a we see that TDA2 is still performing well, even at large range where we have very elevated correlations of the time-shifted signal near and around the zero time lag. In Fig. 23b, c, the mean signal correlations with and without tsunami current, but in the presence of the background current in both cases, still show the familiar pattern; hence, the detection ability of TDA2 is unaffected by the background current, even when the radar SNR is weaker.

6 Conclusions

In geographic areas where near-field tsunami sources, such as submarine mass failures (SMFs) or meteo-tsunamis, may occur, tsunami propagation times may be too small to ensure a timely detection based on deep or shallow water buoys. To offer sufficient warning time, it has been proposed to implement early warning systems relying on high-frequency (HF) radar remote sensing, that can provide a dense spatial coverage, as far offshore as 200–300 km (e.g., for Diginext Ltd.’s Stradivarius radar). However, long wave physics is such that tsunami currents will only rise above noise and background currents (i.e., be at least 10–15 cm/s), and become detectable, in fairly shallow water, which would limit the direct detection of tsunami currents by HF radar to nearshore areas, unless there is a very wide shallow shelf.

In this work, we used numerical simulations of both HF radar remote sensing and (idealized) tsunami propagation to develop and validate a new algorithm that is able to detect an approaching tsunami in the presence of environmental noise and a strong background current, in deeper water (i.e., for weaker tsunami currents) than when using a more standard algorithm based on directly inverting tsunami currents from the radar signal Doppler spectrum.

To simulate the radar backscattered signal, we developed a numerical model including second-order effects in both wind waves and radar signal, with the wave angular frequency being modulated by a time-varying surface current, combining tsunami and background currents. In the presented developments and validations, we only considered idealized tsunami wave trains and bathymetry, but verified that such idealized case studies captured well the salient tsunami wave physics. In future work, the same methodology will be applied to actual tsunami case studies, such as was briefly presented here in the Mediterranean Basin. In those case studies, a state-of-the-art tsunami propagation model (such as FUNWAVE-TVD) will be used to create a data base of time series of synthetic tsunami elevation and current, over a computational grid, using the geography and bathymetry of a selected site.

The principle of the new algorithm is to compute correlations of HF radar signals measured/simulated in many pairs of distant radar cells located along the same tsunami wave ray, shifted in time by the tsunami propagation time between these cell locations. Both rays and travel times can easily be computed as a function of long wave phase speed and local bathymetry (e.g., using the long wave model or, more easily, by solving the geometric optic eikonal equation or one of its simplified formulations). In a series of applications, some including a strong background current and a weaker radar signal, we showed that, in the presence of a tsunami current, the time-shifted correlations of the radar signal, computed as a function of range and an additional time lag, exhibit a narrow elevated peak near the zero time lag; whereas, no pattern in correlation is observed in the absence of a tsunami current. This is because both surface waves and background current are uncorrelated between pair of cells, and even more so when time-shifted by the long-wave propagation time. For smaller tsunami amplitude, smaller wind and larger environmental noise, although the maximum range for detection was slightly decreased, we showed that a peak of correlation still occurred in a detectable manner near the zero time lag. Hence this algorithm is robust.

In applications having either a weaker radar SNR or a strong background current, we showed that a standard algorithm based on currents directly inverted from the signal Doppler spectra fails to properly detect tsunami arrival, except at short range where the tsunami current is large. In the best case scenarios, with stronger tsunamis and surface waves (and hence, SNRs), such an algorithm still can only detect the tsunami once it has propagated in sufficiently shallow water for its current to rise above background (i.e., \(>\)0.10–0.15 m/s). By contrast, the new algorithm was shown to have the potential to detect tsunami arrival in areas where its current is as low as 0.05 m/s, in the presence of much stronger background currents; this implies that tsunami detection and warning could take place in deeper water, further away from the shorelines where the HF radar is deployed. Because the standard detection of tsunami currents works well at short range, we envision that both algorithms, referred to as TDA1 and TDA2 here, could be simultaneously run in a field situation, with TDA2 being able to first detect an approaching tsunami, at larger range and in greater depth, and issue a warning without being able to estimate the tsunami magnitude, and TDA1 taking over at shorter range, confirming the warning and providing an additional estimate of tsunami currents and elevations. Hence, both algorithms would be complementary.

Based on results reported here, it appears that in practice, detection of tsunami arrival with TDA2 would be based on the change in correlation pattern of the mean correlation between pairs of radar cells located along site-specific precalculated wave rays. Unlike the simple illustrations presented here, where only the mean correlation \(D_1(\Delta \tau )\) of signals in pairs of cells between cell 1 and other cells was used, a fully operational algorithm would compute the mean \(D_p\) for all pairs of cells, with p varying from distant to nearshore cells along many wave rays. This way, once the detection threshold in mean correlation is met, one could warn of tsunami arrival further offshore, over the broad geographic area of radar coverage (see, e.g., Fig. 1).

In future work, we will generalize the algorithm to arbitrary bathymetry and tsunami wave trains, and perform more realistic case studies of tsunami detection using state-of-the-art tsunami generation and propagation models (see, e.g., Figs. 2, 3).