Expansion and Collapse of Spherically Symmetric Isotropic Elastic Bodies Surrounded by Vacuum

Abstract

A class of isotropic and scale-invariant strain energy functions is given for which the corresponding spherically symmetric elastic motion includes bodies whose diameter becomes infinite with time or collapses to zero in finite time, depending on the sign of the residual pressure. The bodies are surrounded by vacuum so that the boundary surface forces vanish, while the density remains strictly positive. The body is subject only to internal elastic stress.

1 Introduction

We shall be concerned with $C^2$ spherically symmetric and separable motions of a three-dimensional hyperelastic material based on a class of isotropic and scale-invariant strain energy functions. The solid elastic body is surrounded by vacuum so that the boundary surface force vanishes, while the boundary density remains strictly positive. The body is subject only to internal elastic stress. Depending on the sign of the residual pressure, we shall show that the diameter of a spherical body can expand to infinity with time or it can collapse to zero in finite time.

In addition to the assumptions of objectivity and isotropy, we shall impose the more severe restriction of scale invariance on the strain energy function W. That is, W is a homogeneous function of degree in the deformation gradient F. In the next section, we will show that these basic assumptions imply that W has the form:

for all $F\in \textrm{GL}_+(3,\mathbb {R})$, in which

$$\begin{aligned} \Sigma (F)=(\det F)^{-1/3}(FF^\top )^{1/2}, \end{aligned}$$

is the shear strain tensor, see [26]. The factor accounts for compressibility, and the quantity is the bulk modulus at $F=I$. It is physically natural and mathematically advantageous to assume that , and so, we take . The function $\Phi$ measures the resistance of the material to shear. The special case of a polytropic fluid arises when $\Phi$ is constant and , where $\gamma >1$ is the adiabatic index. Here, however, we shall focus on the case where $\Phi$ is far from a constant. This will be measured by the size of a parameter $\beta$ which is proportional to the shear modulus. For example, an admissible choice would be

$$\begin{aligned} W(\Sigma (F))= 1 + c_1\left( \tfrac{1}{3}{{\,\textrm{tr}\,}}\Sigma (F)-1\right) +c_2\left( \tfrac{1}{3}{{\,\textrm{tr}\,}}{{\,\textrm{cof}\,}}\Sigma (F)-1\right) , \end{aligned}$$

(1.1)

with $c_1$, $c_2>0$. This function satisfies

$$\begin{aligned} W(\Sigma (F))-1\sim \beta |\Sigma (F)-I|^2, \quad \beta \equiv c_1+c_2>0, \end{aligned}$$

in a neighborhood of $\Sigma (F)=I$. More generally, higher-order terms of the form $\mathcal O\left( \beta |\Sigma (F)-I|^3\right)$ may be included. We will return to this example in Sect. 11.

Little is known about the long-time behavior of solutions to the initial free boundary value problem in elastodynamics. In order to gain some insight into the possible behavior, we shall investigate the restricted class of separable motions, the existence of which is dependent upon the scale invariance hypothesis mentioned above. We shall call a motion separable if its material description has the form:

$$\begin{aligned} x(t,y)=a(t)\varphi (y), \end{aligned}$$

in which $a:[0,\tau )\rightarrow \mathbb {R}_+$ is a scalar function and $\varphi :\mathcal B\rightarrow \mathbb {R}^3$ is a time-independent deformation of the reference domain $\mathcal B\subset \mathbb {R}^3$. Separable motions are self-similar in spatial coordinates. In order to have nonconstant shear $\Phi$, the function $a(t)$ must be a scalar. This contrasts with the case of polytropic fluids where there exist affine motions with $a(t)$ taking values in $\textrm{GL}_+(3,\mathbb {R})$.

Under the separability assumption, the spatial configuration of the body evolves by simple dilation, whereby the scalar a(t) controls the diameter. The equations of motion split into an ordinary differential equation for the scalar a(t) and an eigenvalue problem for a nonlinear partial differential equation involving the deformation $\varphi (y)$. The evolution of a(t) depends on the sign of the residual pressure, which turns out to be . When , the body continuously expands for all time with $a(t)\sim t$, as $t\rightarrow \infty$. On the other hand, when , we have $a(t)\rightarrow 0$, as $t\rightarrow \tau <\infty$, so that the body collapses to a point in finite time.

The main effort, then, will be devoted to solving the nonlinear eigenvalue problem for the deformation $\varphi$ in $C^2$. This will be carried out under the assumption of spherical symmetry, consistent with the objectivity and isotropy of W, whence the PDE for $\varphi$ reduces to an ODE. For spherically symmetric bodies, the boundary surface force is a pressure, and the nonlinear vacuum (traction) boundary condition requires that the pressure vanishes on $\partial \mathcal B$. The vacuum boundary condition shall be fulfilled with the material in a nongaseous phase, i.e. with strictly positive density on $\partial \mathcal B$. This also contrasts with the results on affine compressible fluid motion where the vacuum boundary condition holds in a gaseous phase, i.e., both pressure and density vanish on the boundary.

The existence of a family of spherically symmetric eigenfunctions $\{\varphi ^\mu \}$ close to the identity deformation with eigenvalue $|\mu |\ll 1$ will be established in Sect. 9 by a perturbative fixed point argument, for every value of the elastic moduli and $\beta >0$. The behavior of $W(\Sigma (F))$ restricted to the set of spherically symmetric deformation gradients plays a decisive role, see Sect. 8. If $\beta$ is sufficiently large, then there exists an eigenvalue for which the eigenfunction satisfies the nongaseous vacuum boundary condition. The positivity of the shear parameter $\beta$ rules out the hydrodynamical case. A detailed statement of the existence results for expanding and collapsing spherically symmetric separable motion follows in Sect. 10.

In the final section, we aim to persuade the reader that the assumptions imposed on the strain energy function are physically plausible. We show that any self-consistent choice for the values of $W(\Sigma (F))$, restricted to the spherically symmetric deformation gradients, can be extended to all deformation gradients, and we also show that the assumptions are consistent with the Baker–Ericksen condition [2].

1.1 Related Literature

The equations of motion for nonlinear elastodynamics with a vacuum boundary condition are locally well-posed in Sobolev spaces under appropriate coercivity conditions, see for example [16, 21, 22, 25]. Local well-posedness for compressible fluids was examined with a liquid boundary condition in [6, 17] and with a vacuum boundary condition in [7, 15], respectively. Affine motion for compressible hydrodynamical models has been studied extensively, see, for example, [1, 9, 14, 20], but without explicit discussion of boundary conditions. Global in time expanding affine motions for compressible ideal fluids satisfying the gaseous vacuum boundary conditions were constructed and analyzed in [24].

For self-gravitating polytropic fluids in the mass critical case, $\gamma =4/3$ (i.e., ), spherically symmetric self-similar collapsing solutions satisfying the gaseous vacuum boundary condition were first studied numerically in [11] and later constructed rigorously in [8, 10, 18]. In the mass supercritical case, $1<\gamma <4/3$, the existence of spherically symmetric collapsing solutions with continuous mass absorption at the origin was established in [12].

An interesting recent article [4] considers the separable (the term homologous is used instead) motion of self-gravitating elastic balls in the mass critical case . Expanding solutions are constructed with a solid vacuum boundary condition, and collapsing solutions with a gaseous vacuum boundary condition are predicted on the basis of numerical simulations.

We emphasize that the present work neglects self-gravitation and external forces. The sign of the residual pressure alone determines whether the body collapses or expands.

2 Notation and Basic Assumptions

We denote by $\mathbb {M}^3$ the set of $3\times 3$ matrices over $\mathbb {R}$ with the Euclidean inner product

$$\begin{aligned} \langle {A},{B}\rangle ={{\,\textrm{tr}\,}}AB^\top . \end{aligned}$$

We define the groups

$$\begin{aligned}&\textrm{GL}_+(3,\mathbb {R})=\{F\in \mathbb {M}^3:\det F>0\}\\&{\textrm{SL}(3,\mathbb {R})}=\{V\in \textrm{GL}_+(3,\mathbb {R}):\det V=1\}\\&\textrm{SO}(3,\mathbb {R})=\{U\in {\textrm{SL}(3,\mathbb {R})}:U^{-1}=U^\top \}. \end{aligned}$$

Let

$$\begin{aligned} W:\textrm{GL}_+(3,\mathbb {R})\rightarrow [0,\infty ) \end{aligned}$$

(2.1a)

be a smooth strain energy function. We shall assume that W is objective:

$$\begin{aligned} W(F)=W(UF),\quad \text {for all}\quad F\in \textrm{GL}_+(3,\mathbb {R}),\;U\in \textrm{SO}(3,\mathbb {R}), \end{aligned}$$

(2.1b)

and isotropic:

$$\begin{aligned} W(F)=W(FU),\quad \text {for all}\quad F\in \textrm{GL}_+(3,\mathbb {R}),\;U\in \textrm{SO}(3,\mathbb {R}). \end{aligned}$$

(2.1c)

Conditions (2.1a), (2.1b), (2.1c) allow for spherically symmetric motion. Finally, we assume that W is scale-invariant, that is, it is homogeneous¹ of degree in F for some :

(2.1d)

Homogeneity of W in F is necessary in order to obtain separable motions. Since , and since we expect on physical grounds that $W(\sigma I)>0$, for $\sigma \ne 1$, we assume that $W(I)=1$.

Using the polar decomposition, it follows from objectivity (2.1b) that

$$\begin{aligned} W(F)=W\left( (F F^\top )^{1/2}\right) ,\quad F\in \textrm{GL}_+(3,\mathbb {R}). \end{aligned}$$

The positive-definite symmetric matrix $A(F)=(F F^\top )^{1/2}$ is called the left stretch tensor, and its eigenvalues are the principal stretches.

With the additional assumption of homogeneity (2.1d), we have

(2.2)

where

$$\begin{aligned} \Sigma (F)=(\det F)^{-1/3}(FF^\top )^{1/2}=\det A(F)^{-1/3}A(F) \end{aligned}$$

is called the shear strain tensor. Note that $\Sigma (F)\in {\textrm{SL}(3,\mathbb {R})}$. The term $W(\Sigma (F))$ measures the response of the material to shear.

If W is isotropic (2.1c), then $W(\Sigma (F))$ must be a function of the principal invariants of $\Sigma (F)$ (see for example [19, Section 4.3.4]). Since $\Sigma (F)\in {\textrm{SL}(3,\mathbb {R})}$, the nontrivial invariants are

$$\begin{aligned} \begin{aligned}&H_1(\Sigma (F))=\tfrac{1}{3}{{\,\textrm{tr}\,}}\Sigma (F)\\&H_2(\Sigma (F))=\tfrac{1}{3}{{\,\textrm{tr}\,}}{{\,\textrm{cof}\,}}\Sigma (F), \end{aligned} \end{aligned}$$

(2.3a)

with the normalizing factor of 1/3 included so that $H_i(I)=1$, $i=1,2$. Thus, under assumptions (2.1a), (2.1b), (2.1c), (2.1d), the strain energy function takes the form:

(2.3b)

for some function

$$\begin{aligned} \Phi :\mathbb {R}^2_+\rightarrow [0,\infty ),\quad \text {with}\quad \Phi (1,1)=W(I)=1. \end{aligned}$$

(2.3c)

Note that $\det F$ and the invariants of $\Sigma (F)$ depend smoothly on F (see [13], Section 3). Therefore, if $\Phi$ is $C^k$, then (2.3a), (2.3b), (2.3c) defines a $C^k$ function W(F) satisfying (2.1a), (2.1b), (2.1c), (2.1d).

Associated with W, we define its (first) Piola–Kirchhoff stress

$$\begin{aligned} S:\textrm{GL}_+(3,\mathbb {R})\rightarrow \mathbb {M}^3,\quad S(F)=\frac{\partial W}{\partial F}(F) \end{aligned}$$

(2.4a)

and Cauchy stress

$$\begin{aligned} T:\textrm{GL}_+(3,\mathbb {R})\rightarrow \mathbb {M}^3,\quad T(F)=(\det F)^{-1}S(F)F^\top . \end{aligned}$$

(2.4b)

If W satisfies (2.1d), then by differentiation with respect to F we find

(2.4c)

3 Equations of Motion for Separable Solutions

We shall be concerned with the problem of constructing certain smooth motions of an elastic body whose reference configuration $\mathcal B$ is the unit sphere

$$\begin{aligned} \mathcal B=\{y\in \mathbb {R}^3:|y|<1\}. \end{aligned}$$

A motion is a time-dependent family of orientation-preserving deformations x(t, y)

$$\begin{aligned} x:[0,\tau )\times \overline{\mathcal B}\rightarrow \mathbb {R}^3, \end{aligned}$$

with

$$\begin{aligned} D_yx:[0,\tau )\times \overline{\mathcal B}\rightarrow \textrm{GL}_+(3,\mathbb {R}). \end{aligned}$$

The image, $\Omega _t$, of $\mathcal B$ under the deformation $x(t,\cdot )$ represents the spatial configuration of an elastic body at time t. The spatial description of the body can be given in terms of the velocity vector ${{\textbf{u}}}(t,x)=D_tx(t,y(t,x))$ and density $\varrho (t,x)=\bar{\varrho }/\det D_yx(t,y(t,x))$ where $y(t,\cdot )=x^{-1}(t,\cdot )$ is the reference map taking the spatial domain $\Omega _t$ back to the material domain $\mathcal B$ and $\bar{\varrho }>0$ is the constant reference density.

The governing equations of elastodynamics, in the absence of external forces, can be written in the form:

$$\begin{aligned} \bar{\varrho }D_t^2x-D_y\cdot S(D_yx)=0,\quad \text {in}\quad [0,\tau )\times \mathcal B, \end{aligned}$$

(3.1a)

subject to the nonlinear vacuum boundary condition

$$\begin{aligned} S(D_yx(t,y))\; \omega =0,\quad \text {on}\quad [0,\tau )\times \partial \mathcal B, \end{aligned}$$

(3.1b)

where $\omega =y/|y|$ is the normal at $y\in \partial \mathcal B$. The initial conditions

$$\begin{aligned} x(0,y),\quad D_tx(0,y),\quad y\in \overline{\mathcal B}\end{aligned}$$

are also prescribed. Local well-posedness for this system was studied in [16, 21, 22, 25].

Remark

In the case of polytropic fluids,

the Cauchy stress is

$$\begin{aligned} T(F)=-(\det F)^{-\gamma }I. \end{aligned}$$

The vacuum boundary condition can only be fulfilled with vanishing density, i.e., $(\det F)^{-1}=0$ on $\partial \mathcal B$. In the sequel, we shall solely consider the case of nonvanishing density on $\partial \mathcal B$, in order that $F\in \textrm{GL}_+(3,\mathbb {R})$ on $\overline{\mathcal B}$.

We shall now impose the major restriction of separability, namely that the motion can be written in the form

$$\begin{aligned} x(t,y)=a(t)\varphi (y), \end{aligned}$$

(3.2)

for some scalar function

$$\begin{aligned} a:[0,\tau )\rightarrow \mathbb {R}_+ \end{aligned}$$

and a time-independent orientation-preserving deformation

$$\begin{aligned} \varphi :\overline{\mathcal B}\rightarrow \mathbb {R}^3\quad \text {with}\quad D_y\varphi :\overline{\mathcal B}\rightarrow \textrm{GL}_+(3,\mathbb {R}). \end{aligned}$$

Thus, the spatial configuration of an elastic body under a separable motion evolves by dilation, $\Omega _t=\{x=a(t)y:y\in \overline{\mathcal B}\}$.

In spatial coordinates, the reference map, velocity, and density of a separable motion are self-similar:

$$\begin{aligned} \begin{aligned} y(t,x)&=\varphi ^{-1}\left( a(t)^{-1}x\right) ,\\ {{\textbf{u}}}(t,x)&=\dot{a}(t)\varphi (y(t,x))={\dot{a}(t)}{a(t)^{-1}}x,\\ \varrho (t,x)&=\bar{\varrho }/\det [a(t) D_y\varphi (y(t,x))]\\&=a(t)^{-3}\bar{\varrho }\det D_x\varphi ^{-1}\left( a(t)^{-1}x\right) , \end{aligned} \end{aligned}$$

for $x\in \Omega _t$. We shall, however, continue to work in material coordinates.

Henceforth, we take $\bar{\varrho }=1$.

Lemma 3.1

Let . Assume that W satisfies (2.1a), (2.1d), and let S be defined by (2.4a).

Suppose that $a\in C^2\left( [0,\tau )\right)$ is a positive solution of:

(3.3)

Suppose that $\varphi \in C^2(\mathcal B,\mathbb {R}^3)\cap C^1(\overline{\mathcal B},\mathbb {R}^3)$ is an orientation-preserving deformation which solves

$$\begin{aligned} D_y\cdot S(D_y\varphi (y))=\mu \varphi (y),\quad \text {in}\quad \mathcal B\end{aligned}$$

(3.4a)

and satisfies the boundary condition

$$\begin{aligned} S(D_y\varphi (y)) \omega =0,\quad \text {on}\quad \partial \mathcal B. \end{aligned}$$

(3.4b)

Then,

$$\begin{aligned} x(t,y)=a(t)\varphi (y),\quad (t,y)\in [0,\tau )\times \overline{\mathcal B}\end{aligned}$$

is a motion satisfying the elasticity system (3.1a), (3.1b), with $\bar{\varrho }=1$.

In addition, $\varphi$ satisfies

and .

Proof

Since $a$ is assumed to be positive and $\varphi$ is assumed to be a deformation, x(t, y), as defined, is a motion.

By (2.4c), (3.3), (3.4a), the motion x satisfies the system (3.1a):

The boundary condition (3.1b) is similarly verified using (3.4b) and the homogeneity of S in F:

Finally, by (2.1d),

for all $F\in \textrm{GL}_+(3,\mathbb {R})$. So, any solution of (3.4a), (3.4b) with $D\varphi \in \textrm{GL}_+(3,\mathbb {R})$ satisfies

$\square$

Remark

The PDE (3.4a) is the Euler–Lagrange equation associated with the action

$$\begin{aligned} \int _\mathcal B\left( W(D_y\varphi )+\tfrac{\mu }{2}|\varphi |^2\right) dy. \end{aligned}$$

(3.5)

We shall consider the initial value problem for (3.3) in the next section. Sections 5–9 will be devoted to the solution of eigenvalue problem (3.4a), (3.4b).

4 Dynamical Behavior

Lemma 4.1

If $a(t)$ is a $C^2$ positive solution of (3.3) with , then the quantity

(4.1)

is conserved.

If and $\mu >0$, then for every $(a(0),\dot{a}(0))\in \mathbb {R}_+\times \mathbb {R}$, the initial value problem for (3.3) has a positive solution $a\in C^2\left( [0,\infty )\right)$ with $0< (2E(0))^{1/2}-a(t)/t\rightarrow 0$, as $t\rightarrow \infty$.

If ./ and $\mu <0$, then for every $(a(0),\dot{a}(0))\in \mathbb {R}_+\times \mathbb {R}$, the initial value problem for (3.3) has a positive solution $a\in C^2\left( [0,\tau )\right)$, with $\tau <\infty$ and $a(t)\rightarrow 0$, as $t\rightarrow \tau$.

Proof

If $(a(0),\dot{a}(0))\in \mathbb {R}_+\times \mathbb {R}$, then the initial value problem for (3.3) has a $C^2$ positive solution on a maximal interval $[0,\tau )$. If $\tau <\infty$, then either $a(t)\rightarrow 0$ or $a(t)\rightarrow \infty$, as $t\rightarrow \tau$.

Conservation of E(t) on the interval $[0,\tau )$ follows directly from (3.3).

Assume that and $\mu >0$. Then by (4.1), $a(t)^{-1}$ and $|\dot{a}(t)|$ are bounded above by some constant $C_0$ on $[0,\tau )$. This implies that $C_0^{-1}\le a(t)\le a(0)+C_0t$, on $[0,\tau )$. It follows that $\tau =+\infty$.

Let $X(t)={\tfrac{1}{2}}a(t)^2$. Then

From (4.1), we obtain

$$\begin{aligned} m E(0)\le \ddot{X}(t)\le M E(0), \end{aligned}$$

(4.2a)

in which

This leads to the bounds

$$\begin{aligned} m E(0)t\le \dot{X}(t)-\dot{X}(0)\le ME(0)t \end{aligned}$$

(4.2b)

and

$$\begin{aligned} m E(0)t^2\le X(t)-\dot{X}(0)t-X(0)\le ME(0)t^2. \end{aligned}$$

(4.2c)

By (4.2b), we see that

$$\begin{aligned} \dot{a}(t)=\dot{X}(t)/a(t)>0,\quad \text {for}\quad t>-\dot{X}(0)/(mE(0)), \end{aligned}$$

and by (4.2c), we deduce that

$$\begin{aligned} a(t)=(2X(t))^{1/2}\sim t, \quad \text {as}\quad t\rightarrow \infty . \end{aligned}$$

With these facts, $E(t)=E(0)$ implies that

$$\begin{aligned} 0< (2E(0))^{1/2}-\dot{a}(t)\rightarrow 0, \quad \text {as}\quad t\rightarrow \infty , \end{aligned}$$

from which follows the asymptotic statement.

Now assume that and $\mu <0$. Let . Since $\mu <0$, (3.3) implies that

and so we obtain

(4.3)

for all $0\le t_0\le t<\tau$. If , then, since $\mu <0$, it follows from (4.3) that $\tau <\infty$. On the other hand, if , then since $a(0)>0$, there exists a $t_0\in [0,\tau )$ such that $\dot{a}(t_0)<0$, whence from (4.3) again there holds $\tau <\infty$. $\square$

Remark

When and $\mu <0$, the time of collapse is given by

Remark

In Lemma 4.1, we have only discussed the qualitative behavior of solutions to equation (3.3) for the parameter range from Lemma 3.1 in which we can construct separable solutions to (3.1a), (3.1b).

5 Spherically Symmetric Deformations

Lemma 5.1

If

$$\begin{aligned} \phi \in C^2\left( [0,1]\right) , \quad \phi (0)=\phi ''(0)=0, \quad \text {and}\quad \phi '>0 \quad \text {on}\quad [0,1], \end{aligned}$$

(5.1)

then

$$\begin{aligned} \varphi (y)=\phi (r)\omega ,\quad r=|y|,\quad \omega =y/|y| \end{aligned}$$

defines an orientation-preserving deformation $\varphi \in C^2(\overline{\mathcal B},\mathbb {R}^3)$.

The function

$$\begin{aligned} \lambda (r)=(\lambda _1(r),\lambda _2(r))=(\phi '(r),\phi (r)/r) \end{aligned}$$

belongs to $C^1([0,1],\mathbb {R}_+^2)$, positivity holds: $\lambda _1(r),\lambda _2(r)>0$ on [0, 1], and $\lambda (0)=(\phi '(0),\phi '(0))$.

The deformation gradient of $\varphi$, $D_y\varphi :\overline{\mathcal B}\rightarrow \textrm{GL}_+(3,\mathbb {R})$, is given by:

$$\begin{aligned} D_y\varphi (y) =F(\lambda (r),\omega ),\quad r=|y|,\quad \omega =y/|y|, \end{aligned}$$

(5.2a)

with

$$\begin{aligned} F(\lambda ,\omega )=\lambda _1P_1(\omega )+\lambda _2P_2(\omega ),\quad \lambda \in \mathbb {R}_+^2,\quad \omega \in \ S^2, \end{aligned}$$

(5.2b)

and

$$\begin{aligned} P_1(\omega )=\omega \otimes \omega ,\quad P_2(\omega )=I-P_1(\omega ). \end{aligned}$$

(5.2c)

Proof

By writing

$$\begin{aligned} \phi (r)=\int _0^1D_s\left( \phi (sr)\right) ds=r\int _0^1\phi '(sr)ds, \end{aligned}$$

we see that the function

$$\begin{aligned} \lambda _2(r)=\phi (r)/r=\int _0^1\phi '(sr)ds \end{aligned}$$

is strictly positive and $C^1$ on (0, 1] with

$$\begin{aligned} \lambda _2(r)\rightarrow \phi '(0)>0,\quad \lambda _2'(r)=\int _0^1s\phi ''(sr)ds\rightarrow {\tfrac{1}{2}}\phi ''(0)=0,\quad \text {as}\quad r\rightarrow 0. \end{aligned}$$

Thus, $\lambda _2(r)$ extends to a strictly positive function in $C^1([0,1])$. It follows that the function

$$\begin{aligned} \chi (r)=\phi '(r)-\phi (r)/r=\lambda _1(r)-\lambda _2(r) \end{aligned}$$

belongs to $C^1([0,1])$, and $\chi (0)=\chi '(0)=0$.

Clearly, $\varphi \in C^2(\overline{\mathcal B}\setminus \{0\})$, so to prove that $\varphi \in C^2(\overline{\mathcal B})$, we need only show that the derivatives up to second order extend continuously to the origin.

The formula (5.2a) for $D_y\varphi (y)$ is easily verified for $y\ne 0$, and it is equivalent to

$$\begin{aligned} D_y\varphi (y) =\chi (r)P_1(\omega )+\lambda _2(r)I. \end{aligned}$$

(5.3a)

This implies that

$$\begin{aligned} D_y\varphi (y)\rightarrow \phi '(0)I,\quad \text {as}\quad y\rightarrow 0, \end{aligned}$$

and so $\varphi \in C^1(\overline{\mathcal B})$.

From the formula (5.2a), we also see that $D_y\varphi (y)$ has the eigenspaces ${{\,\textrm{span}\,}}\{\omega \}$ and ${{\,\textrm{span}\,}}\{\omega \}^\perp$, with strictly positive eigenvalues $\lambda _1(r)$, $\lambda _2(r)$, $\lambda _2(r)$. Thus,

$$\begin{aligned} \det D_y\varphi (y)=\lambda _1(r)\lambda _2(r)^2, \quad \text {for all}\quad y\in \overline{\mathcal B}, \end{aligned}$$

which shows that $D_y\varphi :\overline{\mathcal B}\rightarrow \textrm{GL}_+(3,\mathbb {R})$. Since $\phi '>0$, we see that $\varphi$ is a bijection of $\overline{\mathcal B}$ onto its range. So we conclude that $\varphi$ is a $C^1$ orientation-preserving deformation on $\overline{\mathcal B}$.

It remains to show that $D_y\varphi \in C^1(\overline{\mathcal B})$. For $y\ne 0$, we find from (5.3a) that

$$\begin{aligned} D_jD_k\varphi _i(y)= & {} (\chi '(r)-2\chi (r)/r)\omega _i\omega _j\omega _k\nonumber \\{} & {} +(\chi (r)/r)\left( \delta _{ij}\omega _k+\delta _{ik}\omega _j+\delta _{jk}\omega _i\right) . \end{aligned}$$

(5.3b)

Since $\chi (0)=\chi '(0)=0$, we have that $\chi '(r), \;\chi (r)/r\rightarrow \chi '(0)=0$, as $r\rightarrow 0$. Thus, we see that the second derivatives of $\varphi$ extend to continuous functions on $\overline{\mathcal B}$ which vanish at the origin. $\square$

A deformation of the form $\varphi (y)=\phi (r)\omega$ is said to be spherically symmetric. From now on, we focus exclusively upon $C^2$ spherically symmetric orientation-preserving deformations of the reference domain $\overline{\mathcal B}$ where $\phi$ satisfies (5.1).

Remark

The spatial configuration of a body at time t under a spherically symmetric separable motion $x(t,y)=a(t)\phi (r)\omega$, defined on $[0,\tau )\times \overline{\mathcal B}$, is a sphere of radius $a(t)\phi (1)$.

The next result summarizes the properties of the gradient of a spherically symmetric deformation.

Lemma 5.2

The matrix $F(\lambda ,\omega )$ defined in (5.2b), (5.2c) satisfies

• the eigenspaces of $F(\lambda ,\omega )$ are ${{\,\textrm{span}\,}}\{\omega \}$ and ${{\,\textrm{span}\,}}\{\omega \}^\perp$,s

• the eigenvalues of $F(\lambda ,\omega )$ are $\lambda _1,\lambda _2,\lambda _2$,

• $\det F(\lambda ,\omega )=\lambda _1\lambda _2^2$,

• $F:\mathbb {R}_+^2\times S^2\rightarrow \textrm{GL}_+(3,\mathbb {R})$,

• $F(\lambda ,\omega )$ is positive-definite symmetric, and

• $F(\lambda ,\omega )=\left( F(\lambda ,\omega )F(\lambda ,\omega )^\top \right) ^{1/2}=A(F(\lambda ,\omega ))$.

6 Spherically Symmetric Strain Energy and Stress

Lemma 6.1

Let W be a strain energy function satisfying (2.1a), (2.1b), (2.1c). If $F(\lambda ,\omega )$ is given by (5.2b), (5.2c), then $W\circ F(\lambda ,\omega )$ is independent of $\omega$.

Proof

Fix a vector $\omega _0\in S^2$. For an arbitrary vector $\omega \in S^2$, choose $U\in \textrm{SO}(3,\mathbb {R})$ such that $\omega =U\omega _0$. Then

$$\begin{aligned} F(\lambda ,\omega )=F(\lambda ,U\omega _0 )=\lambda _1 P_1(U\omega _0 ) +\lambda _2P_2(U\omega _0 )=UF(\lambda , \omega _0 )U^\top . \end{aligned}$$

From (2.1b) and (2.1c), we obtain

$$\begin{aligned} W\circ F(\lambda ,\omega )=W\circ F(\lambda ,\omega _0 ), \end{aligned}$$

which is independent of $\omega$. $\square$

Using the result of Lemma 6.1, we may define a $C^2$ function $\mathcal L$ by

$$\begin{aligned} \mathcal L:\mathbb {R}_+^2\rightarrow [0,\infty ),\quad \mathcal L(\lambda )=W\circ F(\lambda ,\omega ). \end{aligned}$$

(6.1a)

In other words, $\mathcal L$ is the restriction of W to the set of spherically symmetric deformation gradients. By (5.2b), (2.1d), $\mathcal L$ scales like W:

(6.1b)

We now obtain expressions for the stresses restricted to the set of spherically symmetric deformation gradients.

Lemma 6.2

If W satisfies (2.1a), (2.1b), (2.1c), and $\mathcal L$ is defined by (6.1a), then the Piola–Kirchhoff stress defined in (2.4a) satisfies

$$\begin{aligned} S\circ F(\lambda ,\omega )=\mathcal L_{,1}(\lambda )P_1(\omega )+{\tfrac{1}{2}}\mathcal L_{,2}(\lambda )P_2(\omega ), \end{aligned}$$

(6.2a)

and the Cauchy stress defined in (2.4b) satisfies

$$\begin{aligned} T\circ F(\lambda ,\omega )=(\lambda _1\lambda _2^2)^{-1}\left[ \lambda _1\mathcal L_{,1}(\lambda )P_1(\omega ) +{\tfrac{1}{2}}\lambda _2\mathcal L_{,2}(\lambda )P_2(\omega )\right] . \end{aligned}$$

(6.2b)

Proof

Differentiation of (6.1a) with respect to $\lambda$ yields

$$\begin{aligned} \begin{aligned}&\mathcal L_{,1}(\lambda )=\langle {S\circ F(\lambda ,\omega )},{P_1(\omega )}\rangle \\&\mathcal L_{,2}(\lambda )=\langle {S\circ F(\lambda ,\omega )},{P_2(\omega )}\rangle , \end{aligned} \end{aligned}$$

(6.3)

where $\langle \cdot ,\cdot \rangle$ is the Euclidean product on $\mathbb {M}^3$.

It is a standard fact [19, Theorem 4.2.5] that the Cauchy stress T(F) associated with an objective and isotropic strain energy function satisfies

$$\begin{aligned} T(F)\in {{\,\textrm{span}\,}}\{I,A(F),A(F)^2\}. \end{aligned}$$

By Lemma 5.2, we have

$$\begin{aligned} A(F(\lambda ,\omega )) =F(\lambda ,\omega ). \end{aligned}$$

Since

$$\begin{aligned} F(\lambda _1,\lambda _2,\omega )^k=F(\lambda _1^k,\lambda _2^k,\omega ) \in {{\,\textrm{span}\,}}\{P_1(\omega ),P_2(\omega )\},\quad k\in \mathbb Z, \end{aligned}$$

we obtain

$$\begin{aligned} T\circ F(\lambda ,\omega )\in {{\,\textrm{span}\,}}\{P_1(\omega ),P_2(\omega )\}. \end{aligned}$$

By (2.4b), there also holds

$$\begin{aligned} S\circ F(\lambda ,\omega )\in {{\,\textrm{span}\,}}\{P_1(\omega ),P_2(\omega )\}. \end{aligned}$$

Hence, we may write

$$\begin{aligned} S\circ F(\lambda ,\omega )=c_1(\lambda ,\omega )P_1(\omega )+c_2(\lambda ,\omega )P_2(\omega ). \end{aligned}$$

Taking the $\mathbb {M}^3$-inner product with $P_1(\omega )$ and $P_2(\omega )$, we have from (6.3)

$$\begin{aligned} \mathcal L_{,1}(\lambda )=c_1(\lambda ,\omega )\quad \text {and}\quad \mathcal L_{,2}(\lambda )=2c_2(\lambda ,\omega ). \end{aligned}$$

This proves (6.2a), and (6.2b) now follows from (2.4b) and Lemma 5.2. $\square$

Corollary 6.3

Under the assumptions of Lemma 6.2, there holds

$$\begin{aligned} \mathcal L_{,1}(\alpha ,\alpha )={\tfrac{1}{2}}\mathcal L_{,2}(\alpha ,\alpha ), \quad \text {for all}\quad \alpha >0. \end{aligned}$$

(6.4)

Proof

For any $\alpha >0$, the map $\varphi (y)=\alpha y=\alpha r\omega$ is a smooth spherically symmetric deformation, and $D_y\varphi (y)=\alpha I$. Since $S:\textrm{GL}_+(3,\mathbb {R})\rightarrow \mathbb {M}^3$ is $C^1$, the map $S(\alpha I)$ is $C^1$ in $\alpha$. By (6.2a), we have

$$\begin{aligned} S(\alpha I)&=\mathcal L_{,1}(\alpha ,\alpha )P_1(\omega )+{\tfrac{1}{2}}\mathcal L_{,2}(\alpha ,\alpha )P_2(\omega )\\&=\left( \mathcal L_{,1}(\alpha ,\alpha )-{\tfrac{1}{2}}\mathcal L_{,2}(\alpha ,\alpha )\right) P_1(\omega )+ {\tfrac{1}{2}}\mathcal L_{,2}(\alpha ,\alpha )I \end{aligned}$$

Now $P_1(\omega )$ is bounded and discontinuous at the origin, so (6.4) must hold. $\square$

Corollary 6.4

Under the assumptions of Lemma 6.2, there holds

$$\begin{aligned} T(\alpha I)=\alpha ^{-2}\mathcal L_{,1}(\alpha ,\alpha )I\equiv -\mathcal P(\alpha ) I. \end{aligned}$$

Proof

This follows directly from Lemma 6.2 and Corollary 6.4. $\square$

We define the residual stress to be $S(I)=T(I)=-\mathcal P(1)I$. We shall refer to $\mathcal P(1)$ as the residual pressure.

Corollary 6.5

Under the assumptions and notation of Lemmas 5.1 and 6.2, we have for any spherically symmetric orientation-preserving deformation $\varphi$

$$\begin{aligned} S(D_y\varphi (y))=\mathcal L_{,1}(\lambda (r))P_1(\omega )+{\tfrac{1}{2}}\mathcal L_{,2}(\lambda (r))P_2(\omega ) \end{aligned}$$

(6.5)

and

$$\begin{aligned} T(D_y\varphi (y))= & {} \left( \lambda _1(r)\lambda _2(r)^2\right) ^{-1}\\{} & {} \quad \times \left( \lambda _1(r) \mathcal L_{,1}(\lambda (r))P_1(\omega )\right. \\{} & {} \left. +{\tfrac{1}{2}}\lambda _2(r) \mathcal L_{,2}(\lambda (r))P_2(\omega )\right) . \end{aligned}$$

7 The Nonlinear Eigenvalue Problem

Lemma 7.1

Suppose that W satisfies (2.1a), (2.1b), (2.1c) and that $\mathcal L$ is defined by (6.1a).

Let $\mu \in \mathbb {R}$. If $\phi$ satisfies (5.1) and

$$\begin{aligned}{} & {} D_r[\mathcal L_{,1}(\phi '(r),\phi (r)/r)]\nonumber \\{} & {} \quad +\tfrac{2}{r}[\mathcal L_{,1}(\phi '(r),\phi (r)/r)-{\tfrac{1}{2}}\mathcal L_{,2}(\phi '(r),\phi (r)/r)]\nonumber \\{} & {} =\mu \phi (r), \quad r\in [0,1) \end{aligned}$$

(7.1a)

then $\varphi (y)=\phi (r)\omega$ is a $C^2$ spherically symmetric orientation-preserving deformation on $\overline{\mathcal B}$ which solves (3.4a).

If

$$\begin{aligned} \left. \mathcal L_{,1}(\phi '(r),\phi (r)/r)\right| _{r=1}=0, \end{aligned}$$

(7.1b)

then $\varphi$ satisfies the boundary condition (3.4b).

Proof

Set

$$\begin{aligned} \Lambda _k(r)=\mathcal L_{,k}(\phi '(r),\phi (r)/r),\quad k=1,2, \end{aligned}$$

so that by (6.5),

$$\begin{aligned} S(D_y\varphi (y)) =\left( \Lambda _1(r)-{\tfrac{1}{2}}\Lambda _2(r)\right) P_1(\omega )+{\tfrac{1}{2}}\Lambda _2(r)I. \end{aligned}$$

Then, using the facts $D_r=\omega _jD_j$, $D_j\omega _j=2/r$, and $D_jr=\omega _j$, we have

$$\begin{aligned}{}[D_y\cdot&S(D_y\varphi (y))]_i\\&=\left[ D_y\cdot \left( \left( \Lambda _1(r)-{\tfrac{1}{2}}\Lambda _2(r)\right) P_1(\omega )+{\tfrac{1}{2}}\Lambda _2(r)I\right) \right] _i\\&=D_j\Big (\left( \Lambda _1(r)-{\tfrac{1}{2}}\Lambda _2(r)\right) \omega _i\omega _j+{\tfrac{1}{2}}\Lambda _2(r)\delta _{ij}\Big )\\&=D_r\left( \Lambda _1(r)-{\tfrac{1}{2}}\Lambda _2(r)\right) \omega _i +\left( \Lambda _1(r)-{\tfrac{1}{2}}\Lambda _2(r)\right) \omega _iD_j\omega _j+{\tfrac{1}{2}}D_i\Lambda _2(r)\\&=\Big ( \Lambda _1'(r)+\tfrac{2}{r}( \Lambda _1(r)-{\tfrac{1}{2}}\Lambda _2(r))\Big )\omega _i. \end{aligned}$$

Thus, (7.1a) implies that (3.4a) holds.

If $y\in \partial \mathcal B$, then $r=1$, so we have from (6.2a)

$$\begin{aligned} \left. S(D_y\varphi (y))\;\omega \right| _{y\in \partial \mathcal B}=\Lambda _1(1)\omega . \end{aligned}$$

So (7.1b) implies (3.4b). $\square$

Remark

The ODE (7.1a) is the Euler–Lagrange equation associated with the action

$$\begin{aligned} 4\pi \int _0^1\left[ \mathcal L\left( \phi '(r),\phi (r)/r\right) +\tfrac{\mu }{2}\phi (r)^2\right] r^2dr, \end{aligned}$$

which is the action (3.5) restricted to the set of spherically symmetric deformations.

Remark

If $\mathcal L^0:\mathbb {R}_+^2\rightarrow [0,\infty )$ is $C^2$ and

$$\begin{aligned} \mathcal L^0_{,11}(\lambda )=0,\quad (\lambda _1-\lambda _2)\mathcal L^0_{,12}(\lambda ) +2\mathcal L^0_{,1}(\lambda )-\mathcal L^0_{,2}(\lambda )=0,\quad \lambda \in \mathbb {R}_+^2, \end{aligned}$$

(7.2)

then (7.1a) is unchanged by replacing $\mathcal L$ with $\mathcal L+\mathcal L^0$. Condition (7.2) holds provided there exists a pair of $C^2$ functions , $i=0,1$, such that

and

for all $\lambda \in \mathbb {R}_+^2$. If $W^0$ satisfies (2.1a), (2.1b), (2.1c) and if $W^0$ is a null Lagrangian, see [3], then $\mathcal L^0=W^0\circ F(\lambda ,\omega )$ satisfies (7.2). Thus, we can think of solutions of (7.2) as being spherically symmetric null Lagrangians.

8 Strain Energy with Scaling Invariance

It is convenient to define the quantities

$$\begin{aligned} v=\det F(\lambda ,\omega )=\lambda _1\lambda _2^2, \quad u=\lambda _1/\lambda _2,\quad \lambda \in \mathbb {R}_+^2, \end{aligned}$$

(8.1a)

so that

$$\begin{aligned} \lambda _1=v^{1/3}u^{2/3},\quad \lambda _2=v^{1/3}u^{-1/3}, \quad (u,v)\in \mathbb {R}_+^2. \end{aligned}$$

(8.1b)

Note that $u=1$ if and only if $\lambda _1=\lambda _2$ if and only if $F(\lambda ,\omega )$ is a multiple of the identity if and only if $\Sigma (F(\lambda ,\omega ))=I$.

Lemma 8.1

If W is a $C^k$ strain energy function satisfying (2.1a), (2.1b), (2.1c), (2.1d), and $\mathcal L$ is defined by (6.1a), then there exists a $C^k$ function

$$\begin{aligned} f:\mathbb {R}_+\rightarrow [0,\infty ), \quad \text {with}\quad f'(1)=0, \end{aligned}$$

such that

(8.2)

Proof

Define

$$\begin{aligned} f(u)=\mathcal L(u^{2/3},u^{-1/3}),\quad u\in \mathbb {R}_+. \end{aligned}$$

Then f is $C^k$ and nonnegative, by (6.1a). It follows from Corollary 6.4 that

$$\begin{aligned} f'(1)=\tfrac{2}{3}\mathcal L_{,1}(1,1)-\tfrac{1}{3}\mathcal L_{,2}(1,1)=0. \end{aligned}$$

By (8.1b) and (6.1b), we have

so that (8.2) holds. $\square$

A partial converse to Lemma 8.1 will be given in Theorem 11.1. We shall also show, in Proposition 11.2, that condition (8.2) is physically plausible, insofar as it is consistent with the Baker–Ericksen inequality, when f is convex.

Remark

We have by (2.2)

(8.3)

That is, f is the restriction of $W(\Sigma (F))$ to the spherically symmetric deformation gradients.

Remark

In the polytropic fluid case, $W(F)=(\det F)^{-(\gamma -1)}$, we see that $f(u)=1$.

Next, we explore the implications of (8.2) for the equation (7.1a).

Lemma 8.2

Suppose that W is a $C^3$ strain energy function which satisfies (2.1a), (2.1b), (2.1c), (2.1d) and that $\mathcal L$ is defined by (6.1a). By Lemma 8.1, there is a $C^3$ function

$$\begin{aligned} f:\mathbb {R}_+\rightarrow [0,\infty ), \quad \text {with}\quad f'(1)=0, \end{aligned}$$

such that

Define the $C^1$ functions

(8.4a)

in which

(8.4b)

Suppose that $\phi$ satisfies (5.1) and define the positive functions

$$\begin{aligned} \lambda (r)=(\lambda _1(r),\lambda _2(r))=(\phi '(r),\phi (r)/r), \end{aligned}$$

(8.4c)

and

$$\begin{aligned} v(r)=\lambda _1(r)\lambda _2(r)^2,\quad u(r)=\lambda _1(r)/\lambda _2(r). \end{aligned}$$

(8.4d)

If $\phi$ solves the equation

(8.5a)

and the boundary condition

(8.5b)

then it also solves (7.1a), (7.1b) and $\varphi (y)=\phi (r)\omega$ is a $C^2$ spherically symmetric orientation-preserving deformation which solves (3.4a), (3.4b).

Proof

Carrying out the differentiation in (7.1a), we may write

$$\begin{aligned} \mathcal L_{,11}(\lambda (r))\;\phi ''(r)+\mathcal L_{,12}(\lambda (r))\; \tfrac{1}{r}\left( \phi '(r)-\phi (r)/r\right) \\ +\tfrac{2}{r}[\mathcal L_{,1}(\lambda (r))-{\tfrac{1}{2}}\mathcal L_{,2}(\lambda (r))]=\mu \phi (r). \end{aligned}$$

Since

$$\begin{aligned} \phi (r)=rv(r)^{1/3}u(r)^{-1/3}\quad \text {and}\quad \phi '(r)-\phi (r)/r=v(r)^{1/3}u(r)^{-1/3}(u(r)-1), \end{aligned}$$

this is equivalent to

$$\begin{aligned}{} & {} \mathcal L_{,11}(\lambda (r))\;\phi ''(r)+\mathcal L_{,12} (\lambda (r))\;\tfrac{1}{r}\left( \phi '(r)-\phi (r)/r\right) \nonumber \\{} & {} \qquad + v(r)^{-1/3}u(r)^{1/3}\left[ \frac{2\mathcal L_{,1} (\lambda (r))-\mathcal L_{,2}(\lambda (r))}{u(r)-1}\right] \tfrac{1}{r}\left( \phi '(r)-\phi (r)/r\right) \nonumber \\{} & {} \quad =\mu \; r \;v(r)^{1/3}u(r)^{-1/3}. \end{aligned}$$

(8.6)

From (8.1a), we derive

$$\begin{aligned}&\partial _{\lambda _1}=v_{,1}\partial _v+u_{,1}\partial _u =v^{-1/3}u^{-2/3}(v\partial _v+u\partial _u)\\&\partial _{\lambda _2}=v_{,2}\partial _v+u_{,2}\partial _u =v^{-1/3}u^{1/3}(2v\partial _v-u\partial _u). \end{aligned}$$

Direct computation from (8.2) yields

(8.7)

Upon substitution of (8.7) relations into (8.6), we obtain (8.5a) after a bit of simplification.

By (8.7), the boundary condition (7.1b) is equivalent to

which reduces to (8.5b).

This shows that the problems (8.5a), (8.5b) and (7.1a), (7.1b) are equivalent. By Lemma 7.1, $\varphi (y)=\phi (r)\omega$ is a $C^2$ spherically symmetric orientation-preserving deformation which solves (3.4a), (3.4b). $\square$

Remark

The quantity defined in (8.4b) corresponds to the bulk modulus, as we shall explain in Lemma 11.3. Materials with a negative bulk modulus are uncommon, and therefore, it is reasonable physically to assume . In the next lemma, we will also see that positivity of relates to the coercivity of the differential operator in (8.5a), and hence, the hyperbolicity of the equations of motion.

Remark

When (8.2) holds, we have

(8.8)

by Corollary 6.4 and (8.7).

Remark

We shall continue to use the notation (8.4c), (8.4d) below.

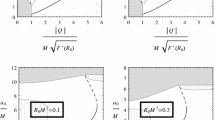
We now introduce the class to which function f in (8.2) will belong. For $a>0$, let us denote

$$\begin{aligned} \mathcal U(a)=\{|u-1|\le a\}. \end{aligned}$$

Given $M\ge 0$, define

$$\begin{aligned} \mathcal C( M)= & {} \{f\in C^3(\mathcal U(1/8)): f(1)=1,\;f'(1)=0,\;f''(1)>0,\\{} & {} \quad \Vert f'''\Vert _\infty \le M f''(1)\}. \end{aligned}$$

The important parameter $f''(1)$ will appear frequently, and for convenience we shall label it as $\beta (f)=f''(1)$. We shall see in Lemma 11.3 that this parameter is proportional to the shear modulus. The family $\{\mathcal C(M)\}_{M\ge 0}$ is increasing with respect to M. Note that for every $B>0$, there exists $f_B\in \mathcal C(M)$ with $\beta (f_B)=B$, as illustrated by the functions

$$\begin{aligned} f_B(u)=1+{\tfrac{1}{2}}B(u-1)^2, \quad B>0. \end{aligned}$$

We have discussed the assumption that $f(1) = W(I)=1$ in Sect. 2. We have also seen in Lemma 8.1 that the condition $f'(1)=0$ is necessary. Along with , the positivity of $\beta (f)$ relates to the coercivity condition for (8.5a). The restriction on the third derivative will enable us to establish estimates for the coefficients in (8.4a) uniform with respect to $\beta (f)$ for any $f\in \mathcal C(M)$ in the following lemma, and this, in turn, will prove essential in establishing existence of solutions.

Lemma 8.3

Fix with , $M\ge 0$, and let $f\in \mathcal C(M)$. Define

(8.9)

Let the functions $U_i(u)$, $i=1,2$, be defined according to (8.4a). Then,

(8.10a)

are well-defined $C^1$ functions on $\mathcal U(\delta )$ such that

$$\begin{aligned} V_1(1)=0,\quad V_2(1)=1, \quad V_2(u)>0,\quad u\in \mathcal U( \delta ), \end{aligned}$$

(8.10b)

and

$$\begin{aligned} |V_i^{(j)}(u)|<C_0,\quad u\in \mathcal U( \delta ),\quad i,j=1,2, \end{aligned}$$

(8.10c)

for some constant $C_0$ depending only on and M.

Suppose that $\phi$ satisfies (5.1) and $u(r)=\lambda _1(r)/\lambda _2(r)=r\phi '(r)/\phi (r)$ satisfies

$$\begin{aligned} u(r)\in \mathcal U(\delta ),\quad r\in [0,1]. \end{aligned}$$

(8.11a)

Then, Eq. (8.5a) is equivalent to

(8.11b)

If , then the function g(u) defined in (8.5b) has a unique zero and . If $u(1)=u_0$, then the boundary condition (8.5b) is satisfied.

Proof

Fix with and $M\ge 0$. Let $f\in \mathcal C(M)$, and recall the notation $\beta (f)=f''(1)$. It follows from Taylor’s theorem and the definition of $\mathcal C(M)$ that

$$\begin{aligned} \begin{aligned}&|f(u)-1-{\tfrac{1}{2}}\beta (f)(u-1)^2|\le \tfrac{1}{6}M\beta (f)|u-1|^3,\\&|f'(u)-\beta (f)(u-1)|\le {\tfrac{1}{2}}M\beta (f)|u-1|^2,\\&|f''(u)-\beta (f)|\le M\beta (f)|u-1|,\\&|f'''(u)|\le M\beta (f), \end{aligned} \end{aligned}$$

(8.12a)

for $u\in \mathcal U(1/8)$.

Define the continuous function

Note that

is also continuous, and thus, is $C^1$ on the interval $\mathcal U(1/8)$. Moreover, by (8.12a), we have the inequalities

(8.12b)

on $\mathcal U(1/8)$.

We now restrict our attention to the interval $\mathcal U(\delta )\subset \mathcal U(1/8)$. From (8.12a), (8.12b), and (8.9), we obtain the estimates

(8.12c)

on the interval $\mathcal U(\delta )$.

From (8.12c), we obtain the coercivity estimate

(8.13a)

on $\mathcal U(\delta )$.

It follows that the functions $V_i(u)$, $i=1,2$ in (8.10a) are well-defined and $C^1$ on $\mathcal U(\delta )$. Therefore, the ODEs (8.5a) and (8.11a), (8.11b) are equivalent. By inspection, (8.10b) holds.

Using (8.12a), (8.12b), (8.12c), it is straightforward to verify that the functions $U_i(u)$, $i=1,2$, defined in (8.4a) satisfy the bounds

$$\begin{aligned} |U_i^{(j)}(u)|\le C(1+\beta (f)),\quad u\in \mathcal U(\delta ), \quad i,j=1,2. \end{aligned}$$

(8.13b)

The constant depends on and M, but not $\beta (f)$.

With the aid of (8.13a), (8.13b), we can now verify that the estimates (8.10c) also hold.

Finally, we prove to the statement concerning the function g defined in (8.5b). Returning to (8.12c), we have

Application of Taylor’s theorem yields

on $\mathcal U(\delta )$, and

on $\mathcal U(\delta )$.

From the first of these inequalities, it follows that if , then

Thus, g has a zero . It follows from the second inequality, that g is strictly increasing on $\mathcal U(\delta )$ and since , that . $\square$

Remark

The homogeneous solutions of (7.2) are given by:

for any . Thus, spherically symmetric null Lagrangians may be homogeneous of any degree in F. Null Lagrangians are necessarily homogeneous of degree , 2, or 3 in F, see [3]. For example, the classical null Lagrangian $W^0(F)=\det F$ has and $\mathcal L^0(\lambda )=\det F(\lambda ,\omega )= \lambda _1\lambda _2^2=v$.

9 Existence of Eigenfunctions

We shall now address the question of existence of solutions to the problem (8.11b), (8.5b).

Theorem 9.1

Fix with , $M\ge 0$, and let $f\in \mathcal C(M)$. There exists a small constant $R>0$ depending only on and M such that if

then Eq. (8.11b) has a solution $\phi ^\mu \in C^2([0,1])$ satisfying

$$\begin{aligned} \phi ^\mu (0)=D^2_r\phi ^\mu (0)=0,\quad D_r\phi ^\mu (0)=1, \end{aligned}$$

(9.1a)

as well as the estimates

$$\begin{aligned} |\phi ^\mu (r)/r-1|,\;|D_r\phi ^\mu (r)-1|,\;|u^\mu (r)-1| \le Rr^2, \end{aligned}$$

(9.1b)

and

$$\begin{aligned} |D_r^2\phi ^\mu (r)|\le Rr, \end{aligned}$$

(9.1c)

for $r\in [0,1]$.

The map from to C([0, 1]) given by

$$\begin{aligned} \mu \mapsto \phi ^\mu \end{aligned}$$

is continuous.

If $\mu >0$, then

$$\begin{aligned} \lambda _1^\mu (r)=D_r\phi ^\mu (r)>\lambda _2^\mu (r)=\phi ^\mu (r)/r>1,\quad r\in (0,1], \end{aligned}$$

(9.2a)

and if $\mu <0$, then

$$\begin{aligned} \lambda _1^\mu (r)<\lambda _2^\mu (r)<1,\quad r\in (0,1]. \end{aligned}$$

(9.2b)

If $\beta (f)$ is sufficiently large, then there exists an eigenvalue $\mu \ne 0$ with such that the solution $\phi ^\mu$ satisfies the boundary condition (8.5b).

Remark

The assumption that $D_r\phi ^\mu (0)=1$ in (9.1a) does not restrict the possible initial data of the motion in (3.2).

Proof of Theorem 9.1

In order to handle the apparent singularity at $r=0$, it is convenient to make the ansatz

$$\begin{aligned} \phi (r)=r+K\zeta (r)\equiv r+\int _0^r(r-\rho )\rho \zeta (\rho )d\rho ,\quad \text {with}\quad \zeta \in C([0,1]). \end{aligned}$$

(9.3)

Notice that K is a bounded linear operator from C([0, 1]) into $C^2([0,1])$. In fact, it follows from (9.3) that

$$\begin{aligned} \begin{aligned}&\phi '(r)=\lambda _1(r)=1+\int _0^r\rho \zeta (\rho )d\rho \\&\phi (r)/r=\lambda _2(r)=1+\frac{1}{r}\int _0^r(r-\rho )\rho \zeta (\rho )d\rho \\&\phi '(r)-\phi (r)/r=\lambda _1(r)-\lambda _2(r) =\frac{1}{r}\int _0^r\rho ^2\zeta (\rho )d\rho \\&\phi ''(r)=r\zeta (r). \end{aligned} \end{aligned}$$

(9.4a)

In particular, $\phi (r)=r+K\zeta (r)$ satisfies the conditions (9.1a).

Assume now that (9.3) holds with

$$\begin{aligned} \zeta \in N_R=\{\zeta \in C([0,1]):\Vert \zeta \Vert _\infty <R\},\quad R\le \delta , \end{aligned}$$

where was previously defined in (8.9).

Straightforward pointwise estimates for $r\in [0,1]$ yield

$$\begin{aligned} \begin{aligned}&|\phi (r)-r|\le \tfrac{1}{6}\Vert \zeta \Vert _\infty r^3\le \tfrac{1}{6} Rr^3\\&|\phi '(r)-1|=|\lambda _1(r)-1|<{\tfrac{1}{2}}\Vert \zeta \Vert _\infty r^2\le {\tfrac{1}{2}}Rr^2\\&|\phi (r)/r-1|=|\lambda _2(r)-1|\le \tfrac{1}{6}\Vert \zeta \Vert _\infty r^2\le \tfrac{1}{6} Rr^2\\&|\lambda _1(r)-\lambda _2(r)|\le \tfrac{1}{3}\Vert \zeta \Vert _\infty r^2\le \tfrac{1}{3}Rr^2\\&\lambda _2(r)\ge 1-|\lambda _2(r)-1|\ge 1-\tfrac{1}{6}Rr^2\ge 2/3\\&|u(r)-1|=\left| \lambda _2(r)^{-1}(\lambda _1(r) -\lambda _2(r))\right| \le \tfrac{1}{2}\Vert \zeta \Vert _\infty r^2\le {\tfrac{1}{2}}Rr^2\\&|v(r)-1|=\left| \lambda _1(r)\lambda _2(r)^2 -1\right| \le 2\Vert \zeta \Vert _\infty r^2\le 2Rr^2. \end{aligned} \end{aligned}$$

(9.4b)

By (9.4b), it follows that (9.1b), (9.1c) hold, and as a consequence (5.1), (8.11a) also are valid.

Since $\zeta \in N_R$ is small, we regard $\phi (r)=r+K\zeta (r)$ as a perturbation of the identity map. Explicitly, $\zeta (s)\equiv 0$ implies that

$$\begin{aligned} \phi (r)=r\quad \text {and}\quad \lambda _1(r)=\lambda _2(r)=u(r)=v(r)=1. \end{aligned}$$

Note that $\phi (r)=r$ solves (8.11b) with $\mu =0$.

Making the substitution (9.3) in equation (8.11b) and using (9.4a), we find that

$$\begin{aligned} L\zeta (r)=\mathcal F(\zeta ,\mu )(r), \end{aligned}$$

(9.5)

with

$$\begin{aligned} L\zeta (r)= \zeta (r)+\frac{2}{r^3}\int _0^r\rho ^2\zeta (\rho )d\rho \end{aligned}$$

and

Recall that the functions $V_i(u)$ depend on $f\in \mathcal C(M)$ and satisfy the conditions (8.10b), (8.10c).

The operator L is an isomorphism on C([0, 1]) with bounded inverse

$$\begin{aligned} L^{-1}\eta (r)=\eta (r)-\frac{2}{r^5}\int _0^r\rho ^4\eta (\rho )d\rho . \end{aligned}$$

From (9.5), we arrive at the reformulation

$$\begin{aligned} \zeta (r)=L^{-1}\mathcal F(\zeta ,\mu )(r). \end{aligned}$$

(9.6)

In order to solve (8.11b), (9.1a), it is sufficient to find a solution $\zeta$ of (9.6) in $N_R$, with $R\le \delta$.

Let us define

since this expression appears repeatedly.

The claim is that for $|\varepsilon |\le R\ll 1$ the map

$$\begin{aligned} \zeta \mapsto L^{-1}\mathcal F(\zeta ,\mu )\end{aligned}$$

is a uniform contraction on $N_R$ taking $N_R$ into itself.

Assume that

$$\begin{aligned} |\varepsilon |\le R\le \delta . \end{aligned}$$

(9.7)

As a consequence of (8.10b), (8.10c), (9.4b), there exists a constant $C_1$, independent of R and $\beta (f)$, such that

$$\begin{aligned}{} & {} \Vert \mathcal F(\zeta _1,\mu )-\mathcal F(\zeta _2,\mu )\Vert _\infty \nonumber \\{} & {} \quad \le C_1 \left( R+\varepsilon \right) \Vert \zeta _1-\zeta _2\Vert _\infty \le 2C_1 R\Vert \zeta _1-\zeta _2\Vert _\infty , \end{aligned}$$

(9.8a)

for all $\zeta _1,\zeta _2\in N_R$. By (8.10b), we have $\mathcal F(0,\mu )(r)=\varepsilon$. It follows from (9.8a) that

$$\begin{aligned} \Vert \mathcal F(\zeta ,\mu )-\varepsilon \Vert _\infty \le 2C_1R^2, \end{aligned}$$

(9.8b)

for all $\zeta \in N_R$.

For the contraction estimate, we have from (9.8a)

$$\begin{aligned}{} & {} \Vert L^{-1}\mathcal F(\zeta _1,\mu )-L^{-1}\mathcal F(\zeta _2,\mu )\Vert _\infty \nonumber \\{} & {} \quad \le \Vert L^{-1}\Vert \;2C_1R\;\Vert \zeta _1-\zeta _2\Vert _\infty \le (1/10)\Vert \zeta _1-\zeta _2\Vert _\infty , \end{aligned}$$

(9.9a)

for all $\zeta _1,\zeta _2\in N_R$, provided $\Vert L^{-1}\Vert 2C_1R\le 1/10$.

Since $L^{-1}\varepsilon =3\varepsilon /5$ for any constant function $\varepsilon$, by (9.8b), (9.7), there holds

$$\begin{aligned} \Vert L^{-1}\mathcal F(\zeta ,\mu )\Vert _\infty= & {} \Vert L^{-1}(\mathcal F(\zeta ,\mu )-\varepsilon )+3\varepsilon /5\Vert _\infty \nonumber \\ {}\le & {} \Vert L^{-1}\Vert 2C_1R^2+3\varepsilon /5\le R/10+3R/5 < R,\nonumber \\ \end{aligned}$$

(9.9b)

for all $\zeta \in N_R$, provided $\Vert L^{-1}\Vert 2C_1R\le 1/10$. This shows that the map leaves $N_R$ invariant.

This establishes the claim under the restrictions

$$\begin{aligned} R\le \delta \quad \text {and}\quad 2C_1\Vert L^{-1}\Vert R\le 1/10. \end{aligned}$$

(9.10)

We emphasize that these restrictions on R do not depend on the value of $\beta (f)$, and therefore, the estimates (9.9a), (9.9b) hold for all $f\in \mathcal C(M)$.

By the uniform contraction principle (see [5] Section 2.2, or [23] Section 5.3), the equation (9.6) has a unique solution $\zeta ^\mu \in N_R\subset C([0,1])$, for each such that $|\varepsilon |\le R$. Moreover, the map $\mu \mapsto \zeta ^\mu$, from $\{\mu :|\varepsilon |<R\}$ to C([0, 1]), is continuous. In particular, $\zeta ^0(r)\equiv 0$, by uniqueness.

For each such $\zeta ^\mu$, we obtain a $C^2$ solution

of (8.11b) which satisfies (9.1a), (9.1b), (9.1c) and depends continuously on the parameter $\mu$.²

Since, by definition (8.4c),

$$\begin{aligned} D_r\lambda _2^\mu (r)=\frac{1}{r}\left( \lambda _1^\mu (r)-\lambda _2^\mu (r)\right) , \end{aligned}$$

(9.11)

it follows from (8.11b) that

This, in turn, may be expressed in the form

$$\begin{aligned} D_r\mathcal X^\mu (r)=\mathcal Y^\mu (r)\mathcal X^\mu (r)+\mu \mathcal Z^\mu (r), \end{aligned}$$

where

Note that, by (8.10b), (9.4b), the coefficients $\mathcal Y^\mu$, $\mathcal Z^\mu$ are continuous on [0, 1] and $\mathcal Z^\mu$ is strictly positive on (0, 1], by (8.10b). So we can write

$$\begin{aligned} \mathcal X^\mu (r)=\mu \int _0^r\left( \exp \int _0^\rho \mathcal Y^\mu (s)ds\right) \mathcal Z^\mu (\rho )d\rho . \end{aligned}$$

We conclude that if $\mu >0$, then $\mathcal X^\mu$ is strictly positive on (0, 1], and then from (9.11), that $D_r\lambda _2^\mu (r)$ is strictly positive on (0, 1]. Thus, from (9.1a), we have

$$\begin{aligned} \lambda _1^\mu (r)>\lambda _2^\mu (r)>\lambda _2^\mu (0)=D_r\phi ^\mu (0)=1, \quad r\in (0,1]. \end{aligned}$$

This proves (9.2a), and (9.2b) follows analogously.

For future reference, we also record the fact that

$$\begin{aligned} {{\,\textrm{sgn}\,}}(u^\mu (1)-1)={{\,\textrm{sgn}\,}}\mathcal X^\mu (1)={{\,\textrm{sgn}\,}}\mu . \end{aligned}$$

(9.12)

We shall now show that for all with and $\beta (f)$ sufficiently large, the eigenvalue $\mu$ may be chosen so that the boundary condition (8.5b) is fulfilled.

We continue to assume that R satisfies the conditions (9.10). Define

and consider the solution family

$$\begin{aligned} \{\phi ^{\mu (\varepsilon )}(r)=r+K\zeta ^{\mu (\varepsilon )}(r):{|\varepsilon |\le R}\}. \end{aligned}$$

The first step will be to establish lower bounds for $|u^{\mu (\pm R)}(1)-1|$. Since $\zeta ^{\mu (\varepsilon )}$ solves (9.6), we have from (9.8b), (9.10),

$$\begin{aligned} \Vert \zeta ^{\mu (\varepsilon )}-3\varepsilon /5\Vert _\infty= & {} \Vert L^{-1}(\mathcal F(\zeta ^{\mu (\varepsilon )},\mu (\varepsilon ))-\varepsilon )\Vert _\infty \\\le & {} \Vert L^{-1}\Vert 2C_1R^2\le R/10. \end{aligned}$$

Letting $\varepsilon =\pm R$, this implies that

$$\begin{aligned} \zeta ^{\mu (R)}(r)\ge R/2\quad \text {and}\quad \zeta ^{\mu (-R)}(r)\le -R/2,\quad \text {for}\quad r\in [0,1]. \end{aligned}$$

(9.13)

From (9.4a), (9.4b), (9.13), we obtain

$$\begin{aligned} \begin{aligned}&\lambda _1^{\mu (R)}(1)-\lambda _2^{\mu (R)}(1) =\int _0^1\rho ^2\zeta ^{\mu (R)}(\rho )d\rho \ge (R/2)(1/3)=R/6\\&\lambda _1^{\mu (-R)}(1)-\lambda _2^{\mu (-R)}(1) =\int _0^1\rho ^2\zeta ^{\mu (-R)}(\rho )d\rho \le -R/6\\&1<\lambda _2^{\mu (R)}(1)=1+\int _0^1(1-\rho )\rho \zeta ^{\mu (R)}(\rho )d\rho \le 1+R/6<7/6\\&1>\lambda _2^{\mu (-R)}(1)=1+\int _0^1(1-\rho )\rho \zeta ^{\mu (-R)}(\rho )d\rho \ge 1-R/6>5/6. \end{aligned} \end{aligned}$$

These estimates combine to show that

$$\begin{aligned} \begin{aligned}&u^{\mu (R)}(1)-1 =\frac{\lambda _1^{\mu (R)}(1)-\lambda _2^{\mu (R)}(1)}{\lambda _2^{\mu (R)}(1)} \ge \frac{R/6}{7/6}=R/7\\&u^{\mu (-R)}(1)-1 =\frac{\lambda _1^{\mu (-R)}(1)-\lambda _2^{\mu (-R)}(1)}{\lambda _2^{\mu (-R)}(1)} \le \frac{-R/6}{5/6}<-R/7. \end{aligned} \end{aligned}$$

(9.14)

Suppose now that $f\in \mathcal C(M)$ with $\beta (f)$ sufficiently large:

(9.15)

Then

so that by Lemma 8.3, g has a unique zero . By continuous dependence upon parameters, the function

$$\begin{aligned} z(\varepsilon )=u^{\mu (\varepsilon )}(1)-1 \end{aligned}$$

is continuous for $|\varepsilon |\le R$. Using (9.14), (9.15), we find that

So there exists $|\varepsilon _0|<R$ such that $z(\varepsilon _0)=u_0-1$, and thus,

$$\begin{aligned} g(u^{\mu (\varepsilon _0)}(1))=g(u_0)=0. \end{aligned}$$

By Lemma 8.3 and (9.12), we also have that

Therefore, we have shown that if the eigenvalue is taken to be , then $\phi ^{\mu (\varepsilon _0)}$ satisfies the boundary condition (8.5b) and . $\square$

Remark

The boundary condition $u^{\mu (\varepsilon _0)}(1)=u_0$ is equivalent to the linear and homogeneous Robin boundary condition

$$\begin{aligned} D_r\phi ^{\mu (\varepsilon _0)}(1)=u_0\phi ^{\mu (\varepsilon _0)}(1). \end{aligned}$$

Corollary 9.2

Fix with and $M\ge 0$. Suppose that W satisfies (2.1a), (2.1b), (2.1c), (2.1d), and using Lemma 8.1,

for all $\lambda \in \mathbb {R}_+^2$ and $\omega \in S^2$. Let S be defined by (2.4a).

If $\beta (f)$ is sufficiently large, then there exists a $C^2$ spherically symmetric orientation-preserving deformation $\varphi :\overline{\mathcal B}\rightarrow \mathbb {R}^3$ and an eigenvalue $\mu$ with satisfying (3.4a), (3.4b).

If , then $\varphi (\overline{\mathcal B})\supset \overline{\mathcal B}$ and the principal stretches satisfy $\lambda _1(r)>\lambda _2(r)>1$, $r\in (0,1]$, while when , the inclusion and inequalities are reversed.

Proof

If $\beta (f)$ is sufficiently large, Theorem 9.1 ensures the existence of an eigenvalue $\mu \in \mathbb {R}$, with , and an eigenfunction function $\phi =\phi ^\mu \in C^2([0,1])$ satisfying the hypotheses of Lemma 8.3, the differential equation (8.11b), and the boundary condition (8.5b). Therefore, $\phi$ also solves the differential equation (8.5a).

By assumption, f(u) is the restriction of an appropriate strain energy function to the spherically symmetric deformation gradients. Therefore, Lemma 8.2 yields the desired deformation $\varphi (y)=\phi (r)\omega$.

Since $\varphi (\overline{\mathcal B})$ is a sphere of radius $\phi (1)=\lambda _2(1)$, the final statements follow from (9.2a), (9.2b). $\square$

Remark

Since we have assumed that the reference density is $\bar{\varrho }=1$, the density of the deformed configuration in material coordinates is $\varrho \circ \varphi (y)=v(r)^{-1}=\left( \lambda _1(r)\lambda _2(r)^2\right) ^{-1}$. If , we have $\varrho \circ \varphi (y)<1$, for $r\in (0,1]$, and if , we have $\varrho \circ \varphi (y)>1$, for $r\in (0,1]$.

10 Existence of Expanding and Collapsing Bodies

Putting together the results of Lemmas 3.1 and 4.1 with Corollary 9.2 yields our main result.

Theorem 10.1

Under the assumptions of Corollary 9.2, let $\varphi :\overline{\mathcal B}\rightarrow \mathbb {R}^3$ be the resulting $C^2$ spherically symmetric orientation-preserving deformation solving (3.4a), (3.4b) with corresponding eigenvalue $\mu$, such that .

Given the eigenvalue $\mu$, let $a:[0,\tau )\rightarrow \mathbb {R}_+$ be the $C^2$ solution of the initial value problem for (3.3) with initial data $(a(0),\dot{a}(0))\in \mathbb {R}_+\times \mathbb {R}$, from Lemma 4.1.

Then by Lemma 3.1, $x(t,y)=a(t)\varphi (y)$ is a motion in $C^2([0,\tau )\times \overline{\mathcal B})$ satisfying (3.1a), (3.1b). Under this motion, the spatial configuration of the elastic body at time t is a sphere $\Omega _t$ of radius $a(t)\phi (1)$.

If , then the lifespan of the solution satisfies $\tau =+\infty$ and $0<(2E(0))^{1/2}-a(t)/t\rightarrow 0$, as $t\rightarrow \infty$, where .

If , then $\tau <\infty$ and $a(t)\rightarrow 0$, as $t\rightarrow \tau$.

Remark

By (8.8), the sign of the residual pressure determines whether the body expands or collapses.

11 Constitutive Theory

The next result is a partial converse to Lemma 8.1.

Theorem 11.1

If $f:\mathbb {R}_+\rightarrow \mathbb {R}_+$ is smooth, with $f'(1)=0$, then there exists a $C^2$ strain energy function W satisfying (2.1a), (2.1b), (2.1c), (2.1d), such that (8.2) holds.

Remark

Note that f is required to be strictly positive and sufficiently differentiable.

Proof of Theorem 11.1

The construction is motivated by (2.3b), (2.3c).

Recall from Lemma 5.2 that $F(\lambda ,\omega )=A(F(\lambda ,\omega ))$ is positive definite and symmetric with eigenvalues $\lambda _1,\lambda _2,\lambda _2$. So from (2.3a), (8.1b), we have

$$\begin{aligned} \det (F(\lambda ,\omega ))=\lambda _1\lambda _2^2=v, \end{aligned}$$

(11.1a)

$$\begin{aligned} \begin{aligned} H_1(\Sigma (F(\lambda ,\omega )))&= \tfrac{1}{3}{{\,\textrm{tr}\,}}\Sigma (F(\lambda ,\omega ))\\&=\tfrac{1}{3}\det (F(\lambda ,\omega ))^{-1/3}{{\,\textrm{tr}\,}}F(\lambda ,\omega )\\&=\tfrac{1}{3}(\lambda _1\lambda _2^2)^{-1/3}(\lambda _1+2\lambda _2)\\&=\tfrac{1}{3}(u^{2/3}+2u^{-1/3})\\&\equiv h_1(u), \end{aligned} \end{aligned}$$

(11.1b)

and since $\Sigma (F(\lambda ,\omega ))\in {\textrm{SL}(3,\mathbb {R})}$,

$$\begin{aligned} \begin{aligned} H_2(\Sigma (F(\lambda ,\omega )))&=\tfrac{1}{3}{{\,\textrm{tr}\,}}{{\,\textrm{cof}\,}}\Sigma (F(\lambda ,\omega ))\\&=\tfrac{1}{3}{{\,\textrm{tr}\,}}\Sigma (F(\lambda ,\omega ))^{-1}\\&=\tfrac{1}{3}\det (F(\lambda ,\omega ))^{1/3}{{\,\textrm{tr}\,}}F(\lambda ,\omega )^{-1}\\&=\tfrac{1}{3}(\lambda _1\lambda _2^2)^{1/3}(\lambda _1^{-1}+2\lambda _2^{-1})\\&=\tfrac{1}{3}(u^{-2/3}+2u^{1/3})\\&\equiv h_2(u). \end{aligned} \end{aligned}$$

(11.1c)

It is enough to find a $C^2$ function $\Phi :\mathbb {R}_+^2\rightarrow \mathbb {R}_+$ such that

$$\begin{aligned} \Phi (h_1(u),h_2(u))=f(u), \quad u\in \mathbb {R}_+, \end{aligned}$$

(11.2)

for then, by (11.1a), (11.1b), (11.1c), the function

automatically satisfies the requirements (2.1a), (2.1b), (2.1c), (2.1d), (8.2). The construction of $\Phi$ is not entirely routine because the curve

$$\begin{aligned} \mathcal H=\{\left( h_1(u),h_2(u)\right) ):u\in \mathbb {R}_+\} \end{aligned}$$

(11.3)

has a cusp at $u=1$, as shown in Fig. 1.

Equivalently, (11.2) will be proven if we can find a $C^2$ function $\widetilde{\Phi }:\mathbb {R}_+^2\rightarrow \mathbb {R}_+$ such that

$$\begin{aligned} \widetilde{\Phi }(\ell _1(u),\ell _2(u))=f(u),\quad u\in \mathbb {R}_+, \end{aligned}$$

where

$$\begin{aligned} \ell _1(u)=h_1(u)-1, \quad \ell _2(u)=h_1(u)-h_2(u), \end{aligned}$$

because we can then simply take

$$\begin{aligned} \Phi (x_1,x_2)=\widetilde{\Phi }\left( x_1-1, x_1-x_2\right) , \quad x\in \mathbb {R}^2. \end{aligned}$$

Observe that $\ell _1,\ell _2\in C^\infty (\mathbb {R}_+)$ and

$$\begin{aligned} \begin{aligned}&\ell _1(1)=\ell _1'(1)=0,&\ell _1''(1)>0,\\&\ell _2(1)=\ell _2'(1)=\ell _2''(1)=0,&\ell _2'''(1)>0, \end{aligned} \end{aligned}$$

(11.4a)

so that

$$\begin{aligned}&|\ell _2^{(k)}(u)|\sim |u-1|^{3-k},\quad k=0,1,2,\quad |u-1|\ll 1. \end{aligned}$$

(11.4b)

The function $\ell _2:\mathbb {R}_+\rightarrow \mathbb {R}$ is a homeomorphism, and it can be written as:

$$\begin{aligned} \ell _2(u)=\hat{\ell }_2(u)(u-1)^3, \end{aligned}$$

(11.4c)

where $\hat{\ell }_2$ is a smooth positive function.

Let $\xi =\ell _2^{-1}$. Then by (11.4b),

$$\begin{aligned} |w|=|\ell _2\circ \xi (w)|\sim |\xi (w)-1|^3,\quad |w|\ll 1, \end{aligned}$$

and so

$$\begin{aligned} |\xi (w)-1|\sim |w|^{1/3},\quad |w|\ll 1. \end{aligned}$$

(11.5a)

Now $\xi \in C^2(\mathbb {R}\setminus \{0\})$, and for $w\ne 0$, we have

$$\begin{aligned} \xi '(w)=1/\ell _2'\circ \xi (w),\quad \xi ''(w)=-\ell _2''\circ \xi (w)/\left( \ell _2'\circ \xi (w)\right) ^3. \end{aligned}$$

Thus, for $0<|w|\ll 1$, we obtain from (11.4b), (11.5a),

$$\begin{aligned} \begin{aligned}&|\xi '(w)|\sim |\xi (w)-1|^{-2}\sim |w|^{-2/3},\\&|\xi ''(w)|\sim |\xi (w)-1|^{-5}\sim |w|^{-5/3}. \end{aligned} \end{aligned}$$

(11.5b)

For $u\in \mathbb {R}_+$, define the smooth function

$$\begin{aligned} g(u)=f(u)-f(1)-g_1 \ell _1(u)-g_2 \ell _2(u)-g_3\ell _1(u)^2-g_4\ell _1(u)\ell _2(u), \end{aligned}$$

with $\{g_k\}_{k=1}^4$ to be determined. Using the hypothesis $f'(1)=0$ and (11.4a), we derive

$$\begin{aligned} g(1)&=0\\ g'(1)&=0\\g^{(2)}(1)&=f^{(2)}(1)-g_1\ell _1^{(2)}(1)\\g^{(3)}(1)&=f^{(3)}(1)-g_1\ell _1^{(3)}(1)-g_2\ell _2^{(3)}(1)\\g^{(4)}(1)&=f^{(4)}(1)-g_1\ell _1^{(4)}(1)-g_2\ell _2^{(4)}(1)-6g_3\ell _1^{(2)}(1)^2\\ g^{(5)}(1)&=f^{(5)}(1)-g_1\ell _1^{(5)}(1)-g_2\ell _2^{(5)}(1) -20g_3\ell _1^{(2)}(1)\ell _1^{(3)}(1)\\ {}&\quad -10g_4 \ell _1^{(2)}(1)\ell _2^{(3)}(1). \end{aligned}$$

The system $g^{(k)}(1)=0$, $k=2,\ldots ,5$ is diagonal, and since $\ell _1^{(2)}(1),\ell _2^{(3)}(1)\ne 0$, there exist unique values $\{g_k\}_{k=1}^4$ such that

$$\begin{aligned} g^{(k)}(1)=0,\quad k=0,\ldots ,5. \end{aligned}$$

Now g is smooth, so there exists $G\in C^2(\mathbb {R}_+)$ such that

$$\begin{aligned} g(u)=(u-1)^6G(u). \end{aligned}$$

By (11.4c), we may write

$$\begin{aligned} g(u) =\ell _2(u)^2\hat{\ell }_2(u)^{-2} G(u) \equiv \ell _2(u)^2{\widehat{G}}(u), \end{aligned}$$

with ${\widehat{G}}=(\hat{\ell }_2)^{-2}\cdot G\in C^2(\mathbb {R}_+)$. This, in turn, may be expressed as:

$$\begin{aligned} g(u)={\widetilde{G}}\circ \ell _2(u),\quad \text {with}\quad {\widetilde{G}}(w)=w^2 {\widehat{G}}\circ \xi (w),\quad w\in \mathbb {R}. \end{aligned}$$

Although $\xi$ is not differentiable at $w=0$, it follows from (11.5a), (11.5b) that ${\widetilde{G}}\in C^2(\mathbb {R})$.

For $x\in \mathbb {R}^2$, define

$$\begin{aligned} \widetilde{\Phi }(x)=f(1)+g_1x_1+g_2x_2+g_3 x_1^2+g_4x_1x_2+{\widetilde{G}}(x_2). \end{aligned}$$

Then $\widetilde{\Phi }$ is in $C^2$ and $\widetilde{\Phi }(\ell _1(u),\ell _2(u))=f(u)$, as desired.

Since $f>0$, by assumption, the resulting function $\Phi$ is positive in a neighborhood of the curve $\mathcal H$, and it can modified away from $\mathcal H$, if necessary, to ensure positivity on its entire domain without changing its values along the curve $\mathcal H$. $\square$

11.1 Example

Going back to the example (1.1) given in the Introduction, we have using (2.3a) that $W(\Sigma (F))=\Phi (H_1(\Sigma (F)),H_2(\Sigma (F))),$ with

$$\begin{aligned} \Phi (x_1,x_2)&=1+c_1(x_1-1)+c_2(x_2-1)\\&=1+(c_1+c_2)(x_1-1)-c_2(x_1-x_2),\quad c_1,\;c_2>0. \end{aligned}$$

Thus, using (8.3) and the notation of the previous proof, we find

$$\begin{aligned} f(u)&=\Phi (H_1(\Sigma (F)),H_2(\Sigma (F)))\Big |_{F=F(\lambda ,\omega )}\\&=1+(c_1+c_2)(h_1(u)-1)-c_2(h_1(u)-h_2(u))\\&=1+(c_1+c_2)\ell _1(u)-c_2 \ell _2(u). \end{aligned}$$

By (11.4a), we have $\beta (f)=(c_1+c_2)\ell _1''(1)>0$, and $f\in \mathcal C(M)$, for all $c_1$, $c_2>0$, with $M=\ell _1''(1)^{-1}(\Vert \ell _1'''\Vert _\infty +\Vert \ell _2'''\Vert _\infty )$. It follows that example (1.1) satisfies the hypotheses of Theorem 10.1 for all $c_1, c_2>0$, with $c_1+c_2$ sufficiently large.

For positive-definite and symmetric matrices $\Sigma \in {\textrm{SL}(3,\mathbb {R})}$, we find by the consideration of eigenvalues that

$$\begin{aligned} H_1(\Sigma )-1\sim |\Sigma -I|^2\quad \text {and}\quad |H_1(\Sigma )-H_2(\Sigma )|\le C|\Sigma -I|^3, \end{aligned}$$

in a neighborhood of $\Sigma =1$. Thus, $W(\Sigma (F))-1$ has a relative minimum when $\Sigma (F)=I$, i.e. when $F=\sigma U$ for some $\sigma >0$ and $U\in \textrm{SO}(3,\mathbb {R})$.

More generally, we could take

$$\begin{aligned} \Phi (x_1,x_2)=1+(c_1+c_2)(x_1-1)-c_2(x_1-x_2)G(x_1,x_2), \quad c_1, c_2>0. \end{aligned}$$

If $G:\mathbb {R}_+^2\rightarrow \mathbb {R}$ is any smooth function with $\Vert G(\ell _1,\ell _2)\Vert _{C^3}$ uniformly bounded independent of $c_1,c_2$, then there exists an $M>0$, such that $f(u)\in \mathcal C(M)$, for all $c_1,c_2>0$.

Remark

The range of the map $F\mapsto \left( H_1(\Sigma (F)),H_2(\Sigma (F))\right)$ from the domain $\textrm{GL}_+(3,\mathbb {R})$ into $\mathbb {R}_+^2$ is given by:

$$\begin{aligned} \mathcal R=\{(x_1,x_2)\in \mathbb {R}_+^2: \Delta (x)\equiv 3x_1^2x_2^2-4x_1^3-4x_2^3+6x_1x_2-1\ge 0\}. \end{aligned}$$

The boundary of this region corresponds to positive-definite symmetric matrices $\Sigma (F)=(\det A(F))^{-1/3}A(F)$ with a repeated eigenvalue, and it is given by the curve $\mathcal H$ defined in (11.3). See Fig. 1. This is because if A(F) has eigenvalues $\{\lambda _i\}_{i=1}^3$ and

$$\begin{aligned} (x_1,x_2)=\left( H_1(\Sigma (F)),H_2(\Sigma (F)\right) , \end{aligned}$$

then

$$\begin{aligned} \Delta (x)=\tfrac{1}{27}(\lambda _1-\lambda _2)^2(\lambda _2-\lambda _3) ^2(\lambda _3-\lambda _1)^2/(\lambda _1\lambda _2\lambda _3)^2. \end{aligned}$$

This expression is nonnegative and vanishes if and only if A(F) has a repeated eigenvalue.³ By the spectral theorem, a matrix A is positive-definite, symmetric, with a repeated eigenvalue if and only if $A=F(\lambda ,\omega )$, for some $\lambda \in \mathbb {R}^2_+$, $\omega \in S^2$, so $\partial \mathcal R=\mathcal H$, by (11.1b), (11.1c).

Fig. 1

The region $\mathcal R$ and its boundary $\mathcal H$

Proposition 11.2

Any $C^2$ strain energy function W satisfying (2.1a), (2.1b), (2.1c), (2.1d) is consistent with the Baker–Ericksen condition [2] along $\mathcal H$, provided (8.2) holds with

$$\begin{aligned} f'(1)=0 \quad \text {and}\quad f''(u)\ge 0,\quad u\in \mathbb {R}_+. \end{aligned}$$

Proof

As noted in Lemma 5.2, the eigenvalues of $F(\lambda ,\omega )$ are $\lambda _1$, $\lambda _2$ with corresponding eigenspaces ${{\,\textrm{span}\,}}\{\omega \}$, ${{\,\textrm{span}\,}}\{\omega \}^\perp$. By (6.2b), the Cauchy stress $T\circ F(\lambda ,\omega )$ shares these eigenspaces, with corresponding eigenvalues

$$\begin{aligned} t_1(\lambda )=\left( \lambda _1\lambda _2^2\right) ^{-1}\lambda _1\mathcal L_{,1}(\lambda ),\quad t_2(\lambda )=\left( \lambda _1\lambda _2^2\right) ^{-1}{\tfrac{1}{2}}\lambda _2\mathcal L_{,2}(\lambda ). \end{aligned}$$

Since the eigenvalue $\lambda _2$ is repeated, the Baker–Ericksen inequality reads:

$$\begin{aligned} \frac{t_1(\lambda )-t_2(\lambda )}{\lambda _1-\lambda _2}\ge 0, \end{aligned}$$

for all $\lambda =(\lambda _1,\lambda _2)\in \mathbb {R}_+^2$ with $\lambda _1\ne \lambda _2$. This is equivalent to the statement

$$\begin{aligned} \frac{\lambda _1\mathcal L_{,1}(\lambda )-{\tfrac{1}{2}}\lambda _2\mathcal L_{,2}(\lambda )}{\lambda _1-\lambda _2}\ge 0, \end{aligned}$$

for all $\lambda =(\lambda _1,\lambda _2)\in \mathbb {R}_+^2$ with $\lambda _1\ne \lambda _2$.

By (8.1a), (8.7), we have

for all $\lambda _1,\lambda _2\in \mathbb {R}_+$ with $\lambda _1\ne \lambda _2$. This is nonnegative since $f'(1)=0$ and $f''\ge 0$, by assumption. (Note that if $f''>0$, then the inequality is strict.) $\square$

Remark

Any function $f\in \mathcal C(M)$ satisfies the hypotheses of Theorem 11.2 with strict inequality in the neighborhood $\mathcal U(\delta )$.

As a final result, we discuss the physical significance of the parameters and $\beta (f)$.

Lemma 11.3

Let and $M\ge 0$. Suppose that W satisfies (2.1a), (2.1b), (2.1c), (2.1d), and for some $f\in \mathcal C(M)$

Then, the bulk and shear moduli of W at $F=I$ are

respectively.

Proof

The bulk modulus at $F=I$ is defined as the change in $-\mathcal P(\alpha )$ with respect to the fractional change in volume at $\alpha =1$. Thus, from (8.8), we find that

For isotropic materials, the linearization of the operator

$$\begin{aligned} D\cdot S(D_y\varphi ) \end{aligned}$$

at $\varphi (y)=y$ is

(11.6)

where is the shear modulus. In the case of spherically symmetric deformations, we have from (5.3b) that

$$\begin{aligned} \Delta \varphi (y)=\nabla (\nabla \cdot \varphi (y))=\left( \phi ''(r)+\tfrac{2}{r}\phi '(r) -\tfrac{2}{r^2}\phi (r)\right) \omega , \end{aligned}$$

and so (11.6) reduces to

Comparing this with (8.5a), we obtain

which implies that . $\square$