Escape Rate and Conditional Escape Rate From a Probabilistic Point of View

Abstract

We prove that for a sequence of nested sets $\{U_n\}$ with $\Lambda = \cap _n U_n$ a measure zero set, the localized escape rate converges to the extremal index of $\Lambda$, provided that the dynamical system is $\phi$-mixing at polynomial speed. We also establish the general equivalence between the local escape rate for entry times and the local escape rate for returns. Examples include a dichotomy for periodic and non-periodic points, Cantor sets on the interval, and submanifolds of Anosov diffeomorphisms on surfaces.

1 Introduction

In recent years, there has been an increasing interest in open dynamical systems, which are dynamical systems with an invariant measure where one places a trap or hole in the phase space, and looks at the decay rate of the measure of points that are not caught by the trap up to some time (the survival set). This rate is known to be related to the rate of the correlations decay for the system (see [16]). When the correlations decay exponentially fast, the decay rate for the measure of the survival set is typically exponential and depends on the location and size of the trap. We invite the readers to the review article [5] for a general overview on this topic.

When the decay rate for the measure of the survival set is normalized by the measure of the trap, one obtains the localized escape rate as the measure of the trap goes to zero. Such problems are loosely related to the entry times and return times distribution but this similarity does not allow to deduce limiting statistics from each other since the limits are taken in different ways, and the rate of convergence for the entry times to its limiting distribution is usually insufficient for the study of escape rates.¹

In the past, local escape rates have been associated with either metric holes centered at a point whose radius decreased to zero or, in the presence of partitions, with cylinder sets which decrease to a single point. In this case, a dichotomy has been established for many systems which shows the local escape rate to be equal to one at non-periodic points and equal to the extremal index at periodic points. See the classical work [8] for conformal attractors, [2, 4] for the transfer operator approach for interval maps, and [14] for a probabilistic approach which applies to systems in higher dimension. This mirrors the behavior of the limiting return times distributions that are Poisson at non-periodic points, and Pólya–Aeppli compound Poisson at periodic points in which case the compounded geometric distribution has the weights given by the extremal index $\theta \in (0,1)$. See [10, 12].

In this paper, we will generalize the concept of localized escape rates to the cases when the limiting set of the shrinking neighborhoods are not any longer points, periodic or non-periodic, but instead are allowed to be any null sets.² One of the key motivations is when the holes are opened around some lower dimensional submanifold in the phase space. We will use the recent progress developed in [13] which shows that the limiting return times distribution at null sets is compound Poisson in a more general sense where the associated parameters form a spectrum that is determined by the limiting cluster size distribution (for this see below the coefficients $\alpha _k$). Unlike the singleton case, however, the general relation between local escape rate and extremal index for null sets has not been discussed before.

We would like to point out that the conventional transfer operator method studied in [2] following the general setup in [16] (see also the book [19] and the references therein) heavily relies on the conformal structure and the fact that in dimension one, the indicator functions of the geometric balls $B_r(x)$ have bounded BV norm³, uniform in r. This makes it difficult to generalize the results in [2] to the case where the limiting set $\Lambda$ is a non-trivial null set, or to higher dimensional systems (especially those that are invertible, where the Banach space that the transfer operator acts are quite complicated). Our approach in this paper uses $\phi$-mixing to avoid those problems. In addition, we only assume the system to be $\phi$-mixing at polynomial speed (surprisingly, this is enough to deduce that the escape rate is exponential!) as opposed to [2, 16] where the unperturbed transfer operator needs to have a spectral gap⁴. This assumption may still not be optimal. However, we believe that the same results does not hold for $\alpha$-mixing systems in general. See the counter examples in [2] for systems modeled by Young towers with first return map and polynomial tail, and note that such systems are $\alpha$-mixing at the same rate.

2 Statement of Results

Throughout this paper, we will assume that $(\mathbf{{M}}, T, {{\mathcal {B}}}, \mu )$ is a measure preserving system on some compact metric space $\mathbf{{M}}$, with ${{\mathcal {B}}}$ the Borel $\sigma$-algebra. Unless otherwise specified, T is assumed to be non-invertible, although our result also holds in the invertible case, see Remark 2.5 and Theorems 4.12, 5.2 below. Let ${\mathcal {A}}$ be a measurable partition of $\mathbf{{M}}$ (finite or countable). Denote, by ${\mathcal {A}}^n=\bigvee _{j=0}^{n-1}T^{-j}{\mathcal {A}},$ its nth join (in the invertible case, see Remark 2.5). Then ${\mathcal {A}}^n$ is a partition of $\mathbf{{M}}$ and its elements are called n-cylinders. We assume that ${\mathcal {A}}$ is generating, that is $\bigcap _nA_n(x)$ consists of the singletons $\{x\}$.

Definition 2.1

• (i) The measure $\mu$ is left $\phi$-mixing with respect to ${\mathcal {A}}$ if

  $$\begin{aligned} |\mu (A \cap T^{-n-k} B) - \mu (A)\mu (B)| \le \phi _L(k)\mu (A) \end{aligned}$$

  for all $A \in \sigma ({\mathcal {A}}^n)$, $n\in {\mathbb {N}}$ and $B \in \sigma (\bigcup _{j\ge 1} {\mathcal {A}}^j )$, where $\phi (k)$ is a decreasing function which converges to zero as $k\rightarrow \infty$. Here $\sigma ({\mathcal {A}}^n)$ is the $\sigma$-algebra generated by n-cylinders.

• (ii) The measure $\mu$ is right $\phi$-mixing w.r.t. ${\mathcal {A}}$ if

  $$\begin{aligned} |\mu (A \cap T^{-n-k} B) - \mu (A)\mu (B)| \le \phi _R(k)\mu (B) \end{aligned}$$

  for all $A \in \sigma ({\mathcal {A}}^n)$, $n\in {\mathbb {N}}$ and $B \in \sigma (\bigcup _j {\mathcal {A}}^j )$, where $\phi (k)\searrow 0$.

• (iii) The measure $\mu$ is $\psi$-mixing w.r.t. ${\mathcal {A}}$ if

  $$\begin{aligned} |\mu (A \cap T^{-n-k} B) - \mu (A)\mu (B)| \le \psi (k)\mu (A)\mu (B) \end{aligned}$$

  for all $A \in \sigma ({\mathcal {A}}^n)$, $n\in {\mathbb {N}}$ and $B \in \sigma (\bigcup _j {\mathcal {A}}^j )$, where $\psi (k)\searrow 0$. Clearly $\psi$-mixing implies both left and right $\phi$-mixing with $\phi (k) = \psi (k)$.

Remark 2.2

If it is clear from context which type of mixing we are referring to (as is always the case in this paper), then we will suppress the subscripts R, L.

We write, for any subset $U\subset \mathbf{{M}}$,

$$\begin{aligned} \tau _U(x)=\min \{j\ge 1: T^j(x)\in U\} \end{aligned}$$

the first entry time to the set U. Then $\tau _U|_U$ is the first return time for points in U. We can now define the escape rate into U by

$$\begin{aligned} \rho (U)=\lim _{t\rightarrow \infty }\frac{1}{t}|\log {\mathbb {P}}(\tau _U>t)| \end{aligned}$$

whenever the limit exists. It captures the exponential decay rate for the set of points whose orbits have not visited U before time t. Observe that if $U\subset U'$ then ${\mathbb {P}}(\tau _{U'}>t)\le {\mathbb {P}}(\tau _{U}>t)$ and consequently $\rho (U)\le \rho (U')$. We define the conditional escape rate as

$$\begin{aligned} \rho _U(U)=\lim _{t\rightarrow \infty }\frac{1}{t}|\log {\mathbb {P}}_U(\tau _U>t)|, \end{aligned}$$

where ${\mathbb {P}}_U$ is the conditioned measure on U.

We are particularly interested in the asymptotic behavior of $\rho (U)$ along a sequence of positive measure sets $\{U_n\}$ whose measure goes zero. For this purpose, we call $\{U_n\}$ a nested sequence of sets if $U_{n+1}\subset U_n$, and if $\lim _n\mu (U_n) = 0$. For the measure zero set $\Lambda = \cap _n U_n$, we define the localized escape rate at $\Lambda$ as:

$$\begin{aligned} \rho (\Lambda , \{U_n\})=\lim _{n\rightarrow \infty }\frac{\rho (U_n)}{\mu (U_n)}. \end{aligned}$$

(1)

provided that the limit exists. We will show that under certain conditions, the localized escape rate of $\Lambda$ exists and does not depend on the choice of $U_n$.

2.1 Local Escape Rate for Unions of Cylinders

First, we consider with the case where each $U_n$ is a union of $\kappa _n$-cylinders, for some non-decreasing sequence of integers $\{\kappa _n\}$.

We make some assumptions on the sizes of the nested sequence $\{U_n\}$. For each n and $j\ge 1$, we define ${{\mathcal {C}}}_j(U_n) =\{A\in {{\mathcal {A}}}^j,A\cap U_n\ne \emptyset \}$ the collection of all j-cylinders that have non-empty intersection with $U_n$. Then, we write

$$\begin{aligned} U_n^j = \bigcup _{A\in {{\mathcal {C}}}_j(U_n)} A \end{aligned}$$

for the approximation of $U_n$ by j-cylinders from outside. For each fixed j, $\{U_n^j\}_n$ is also nested, that is, $U_{n+1}^j\subset U_n^j$. Obviously, we have $U_n\subset U_n^j$ for all j, and $U_n=U_n^j$ if $j\ge \kappa _n$.

Definition 2.3

A nested sequence $\{U_n\in {{\mathcal {A}}}^{\kappa _n}\}$ is called a good neighborhood system, if:

• (1) $\kappa _n\nearrow \infty$ and $\kappa _n\mu (U_n)^\varepsilon \rightarrow 0$ for some $\varepsilon \in (0,1)$;

• (2) there exists $C>0$ and $p'>1$ such that $\mu (U^j_n)\le \mu (U_n) + Cj^{-p'}$ for all $j<\kappa _n$.

2.1.1 Local Escape Rate and the Extremal Index

We make the following definitions, following [13]

For a positive measure set $U\subset \mathbf{{M}}$, we define the higher-order entry times recursively:

$$\begin{aligned} \tau ^1_U=\tau _U, \hbox { and }\tau ^j_U(x) = \tau ^{j-1}_U(x) + \tau _U(T^{\tau ^{j-1}_U}(x)). \end{aligned}$$

For simplicity, we write $\tau ^0_U = 0$ on U.

For a nested sequence $\{U_n\}$, define

$$\begin{aligned} {\hat{\alpha }}_\ell (K,U_n)=\mu _{U_n}(\tau ^{\ell -1}_{U_n}\le K), \end{aligned}$$

(2)

i.e., ${\hat{\alpha }}_\ell (K,U_n)$ is the conditional probability of having at least $(\ell -1)$ returns to $U_n$ before time K. We shall assume that the limit ${\hat{\alpha }}_\ell (K)=\lim _{n\rightarrow \infty }{\hat{\alpha }}_\ell (K,U_n)$ exists for for $K\in {{\mathbb {N}}}$ large enough and every $\ell \ge 1$. By monotonicity the limits

$$\begin{aligned} {\hat{\alpha }}_\ell =\lim _{K\rightarrow \infty }{\hat{\alpha }}_\ell (K) \end{aligned}$$

(3)

exist as ${\hat{\alpha }}_\ell (K)\le {\hat{\alpha }}_\ell (K')\le 1$ for all $K\le K'$. Since we put $\tau ^0_U = 0$, it follows that $\hat{\alpha }_1 = 1$. We will see later that the existence of the limits defining ${\hat{\alpha }}_{\ell }$ implies the existence of the following limits:

$$\begin{aligned} \alpha _1 = \lim _{K\rightarrow \infty }\lim _{n\rightarrow \infty }\mu _{U_n}(\tau _{U_n}>K) = 1-{\hat{\alpha }}_2. \end{aligned}$$

(4)

$\alpha _1\in [0,1]$ is generally known as the extremal index (EI). See the discussion in Freitas et al. [9].

The next theorem shows that the escape rate is indeed given by the extremal index.

Theorem A

Assume that $T:\mathbf{{M}}\rightarrow \mathbf{{M}}$ preserves a probability measure $\mu$ that is right $\phi$-mixing with $\phi (k)\le Ck^{-p}$ for some $C>0$ and $p>1$, and $\{U_n\}$ is a good neighborhood system such that $\{\hat{\alpha }_{\ell }\}$ defined in (3) exists, and satisfies $\sum _{\ell }\ell {\hat{\alpha }}_{\ell }<\infty$.

Then $\alpha _1$ defined by (4) exists, and the localized escape rate at $\Lambda$ exists and satisfies

$$\begin{aligned} \rho (\Lambda , \{U_n\}) = \alpha _1. \end{aligned}$$

Remark 2.4

Theorem A has a similar formulation for left $\phi$-mixing systems. See Remark 4.7 and Theorems 4.12, 5.2 for more detail.

For Gibbs–Markov systems (for the precise definition, see Sect. 3) the same result is true:

Theorem B

Assume that $T:\mathbf{{M}}\rightarrow \mathbf{{M}}$ is a Gibbs–Markov system with respect to the partition ${{\mathcal {A}}}$. Let $\{U_n\}$ be a good neighborhood system such that $\{\hat{\alpha }_{\ell }\}$ defined in (3) exists, and satisfies $\sum _{\ell }\ell {\hat{\alpha }}_{\ell }<\infty$.

Then $\alpha _1$ defined by (4) exists. Furthermore, the localized escape rate at $\Lambda$ exists and satisfies

$$\begin{aligned} \rho (\Lambda , \{U_n\}) = \alpha _1. \end{aligned}$$

Remark 2.5

If T is invertible, then one has to define the n-join by

$$\begin{aligned} {\mathcal {A}}^n=\bigvee _{j=-n}^{n}T^{-j}{\mathcal {A}}. \end{aligned}$$

In this case it is useful to write, for $m,n\in {{\mathbb {Z}}}$, ${{\mathcal {A}}}^n_m: = \bigvee _{j=m}^{n}T^{-j}{\mathcal {A}}$. In particular we have ${{\mathcal {A}}}^n = {{\mathcal {A}}}_{-n}^n$. The $\phi$ and $\psi$-mixing properties are defined by the same formulas. For integers $m,m',n,n'>0$, if $U\in {{\mathcal {A}}}^n_{-m}, V \in {{\mathcal {A}}}^{n'}_{-m'}$ then for $k>n+m'$, we have $\mu (U\cap T^{-k} V) = \mu (T^{-m}U \cap T^{-k-m} V)$ where $T^{-m}U\in {{\mathcal {A}}}_0^{m+n}$, $T^{-k-m}V \in {{\mathcal {A}}}_{k+m-m'}^{k+m+n'}$. Note that $k+m-m'>n+m > 0$, so the estimate can be treated in the same way as the non-invertible case with only minor adjustments. However, the approximation $U^j_n$ need to be handled with care. See Remark 4.8 for a potential problem and the treatment.

2.1.2 In the Absence of Short Returns

We will see below that when points in $\{U_n\}$ do not return to $U_n$ “too soon”, then $\alpha _1 = 1$. To formulate this, we define the period of U as:

$$\begin{aligned} \pi (U) = \min \{k>0: T^{-k}U\cap U\ne \emptyset \}, \end{aligned}$$

and the essential period of U by:

$$\begin{aligned} \pi _{{\text {ess}}}(U) = \min \{k>0: \mu (T^{-k}U\cap U)>0\}. \end{aligned}$$

$\pi$ and $\pi _{{\text {ess}}}$ mark the shortest return of points in U. Note that $\pi (U)\le \pi _{{\text {ess}}}(U)$ for all measurable $U\in \mathbf{{M}}$, and equality holds if T is continuous, U is open and $\mu$ has full support.

Corollary C

Let $(\mathbf{{M}}, T, {{\mathcal {B}}}, \mu )$ be a measure preserving system. Assume that $\{U_n\}$ is a good neighborhood system with $\pi _{{\text {ess}}}(U_n) \rightarrow \infty$, and $(T,\mu ,{{\mathcal {A}}})$ satisfies one of the following two assumptions:

• (1) either $\mu$ is right $\phi$-mixing with $\phi (k)\le Ck^{-p}$ for some $p>1$;

• (2) or T is Gibbs–Markov;

then the localized escape rate at $\Lambda$ exists and satisfies

$$\begin{aligned} \rho (\Lambda , \{U_n\}) = 1. \end{aligned}$$

Combining Corollary C with [21, Proposition 6.3], we have:

Corollary D

The conclusion of Corollary C holds if the assumption “$\pi _{{\text {ess}}}(U_n)\rightarrow \infty$” is replaced by the following assumptions:

• (1) T is continuous, $\Lambda = \cap _nU_n = \cap _n {\overline{U}}_n$;

• (2) $\Lambda$ intersects every forward orbit at most once, that is, for every $x\in \Lambda$ we have $\Lambda \cap \{T^k(x) : k\ge 1\}=\emptyset$.

The proof of both corollaries can be found at the end of Sect. 4.2.

2.2 From Cylinders to Open Sets: Exceedance Rate for the Extreme Value Process

Next, we deal with the case where $\{U_n\}$ consists of open sets. For this purpose, we consider a observable

$$\begin{aligned} {\varphi }:\mathbf{{M}}\rightarrow {{\mathbb {R}}}\cup \{+\infty \} \end{aligned}$$

which is continuous except when ${\varphi }(x)=+\infty$, such that the maximal value of ${\varphi }$, which could be positive infinite, is achieved on a $\mu$ measure zero closed set $\Lambda$. Then we consider the process generated by the dynamics of T and the observable $\varphi :$

$$\begin{aligned} X_0=\varphi ,\,X_1=\varphi \circ T,\,\ldots , X_k = \varphi \circ T^k ,\ldots . \end{aligned}$$

Let $\{u_n\}$ be a non-decreasing sequence of real numbers. We will think of $u_n$ as a sequence of thresholds, and the event $\{X_k>u_n\}$ marks an exceedance above the threshold $u_n$. Also denote by $U_n$ the open set

$$\begin{aligned} U_n: = \{X_0>u_n\}. \end{aligned}$$

(5)

It is clear that $\{U_n\}$ is a nested sequence of sets.

We are interested in the set of points where $X_k(x)$ remains under the threshold $u_n$ before time t. For this purpose, we put

$$\begin{aligned} M_n = \max \{X_k: k=0,\ldots , n-1\}, \end{aligned}$$

and

$$\begin{aligned} \zeta (u_n) = \lim _{t\rightarrow \infty }\frac{1}{t} |\log {{\mathbb {P}}}(M_t<u_n)|. \end{aligned}$$

Finally, define the exceedance rate of ${\varphi }$ along the thresholds $\{u_n\}$ as:

$$\begin{aligned} \zeta ({\varphi }, \{u_n\})=\lim _{n\rightarrow \infty }\frac{\zeta (u_n)}{\mu (U_n)}. \end{aligned}$$

We will make the following assumption on the shape of $U_n$. For each $r_n>0$, we approximate $U_n$ by two open sets (‘o’ and ‘i’ stand for ‘outer’ and ‘inner’):

$$\begin{aligned} U^o_n =B_{r_n}(U_n) = \bigcup _{x\in U_n} B_{r_n}(x), \hbox { and } U^i_n =U_n\setminus \overline{B_{r_n}(U_n)} = U_n\setminus \left( \bigcup _{x\in \partial U_n}\overline{B_{r_n}(x)}\right) . \end{aligned}$$

It is easy to see that

$$\begin{aligned} \overline{U^i_n}\subset U_n\hbox { and } \overline{U_n}\subset U^o_n, \end{aligned}$$

The following assumption requires $U_n$ to be well approximable by $U^{i/o}_n$.

Assumption 1

There exists a positive, decreasing sequence of real numbers $\{r_n\}$ with $r_n\rightarrow 0$, such that

$$\begin{aligned} \mu \left( U^o_n\setminus U^i_n\right) = o(1)\mu (U_n). \end{aligned}$$

(6)

Here o(1) means the term goes to zero under the limit $n\rightarrow \infty$.

Theorem E

Assume that

• (1) either $\mu$ is right $\phi$-mixing with $\phi (k)\le Ck^{-p}$, $p>1$;

• (2) or $(T,\mu ,{{\mathcal {A}}})$ is a Gibbs–Markov system.

Let ${\varphi }:\mathbf{{M}}\rightarrow {{\mathbb {R}}}\cup \{+\infty \}$ be a continuous function achieving its maximum on a measure zero set $\Lambda$. Let $\{u_n\}$ be a non-decreasing sequence of real numbers with $u_n\nearrow \sup {\varphi }$, such that the open sets $U_n$ defined by (5) satisfy Assumption 1 for a sequence $r_n$ that decreases to 0. Assume $\{\hat{\alpha }_{\ell }\}$, defined by (3), exist and satisfy $\sum _{\ell }\ell \hat{\alpha }_{\ell }<\infty$. Let $\kappa _n$ be the smallest positive integer for which ${\text {diam}}{{\mathcal {A}}}^{\kappa _n}\le r_n$ and assume:

• (a) $\kappa _n\mu (U_n)^\varepsilon \rightarrow 0$ for some $\varepsilon \in (0,1)$;

• (b) $U_n$ has small boundary: there exist $C>0$ and $p'>1$, such that $\mu \left( \bigcup _{A\in {{\mathcal {A}}}^j, A\cap B_{r_n}(\partial U_n) \ne \emptyset }A\right) \le C j^{-p'}$ for all n and $j\le \kappa _n$.

Then the exceedance rate of ${\varphi }$ along $\{u_n\}$ exists and satisfies

$$\begin{aligned} \zeta ({\varphi },\{u_n\}) = \alpha _1. \end{aligned}$$

2.3 Conditional Escape Rate: A General Theorem

Our next theorem deals with the relation between the escape rate and the conditioned escape rate.

Theorem F

For any measure preserving ergodic system $(\mathbf{{M}}, T, {{\mathcal {B}}}, \mu )$ and any positive measure set $U\in \mathbf{{M}}$, we have

$$\begin{aligned} \rho (U) = \rho _U(U), \end{aligned}$$

assuming one of them exists and is positive.

Note that this theorem does not rely on the mixing assumption nor any information on the geometry of U. In particular, if one defines the localized conditional escape rate at $\Lambda$ as

$$\begin{aligned} \rho _\Lambda (\Lambda , \{U_n\}) = \lim _{n\rightarrow \infty }\frac{\rho _{U_n}(U_n)}{\mu (U_n)}, \end{aligned}$$

then we immediately have $\rho (\Lambda , \{U_n\}) = \rho _{\Lambda }(\Lambda , \{U_n\})-\alpha _1$ under the assumptions of Theorem A or B.

2.4 Escape Rate on Young Towers With First Return Map and Exponential Tail

Young towers, also known as the Gibbs–Markov–Young structure, is first introduced by Young in [22, 23]. Young tower can be viewed as a discrete time suspension $(\Omega , T,\mu )$ over a Gibbs–Markov system $({\tilde{\Omega } }, {\tilde{T} }, {\tilde{\mu } })$, such that the roof function R (in this case, it is usually call the return time function) is integrable with respect to the measure ${\tilde{\mu } }$. A dynamical system $(\mathbf{{M}},T)$ is modeled by a Young tower, if there exists a semi-conjugacy $\Pi :\Omega \rightarrow \mathbf{{M}}$ that is one-to-one on the base of the tower ${\tilde{\Omega } }$. In this case, we say that the tower is defined using the first return map, if $R(x) = \tau _{\Pi ({\tilde{\Omega } })}(\Pi (x))$ is indeed the first return map on $\Pi ({\tilde{\Omega } })$.

To simply notation, we will use the notation $\lesssim$ which means that the inequality holds up to some constant $C>0$, uniform in n.

Theorem G

Assume that T is a $C^{2}$ map modeled by Young tower defined using the first return map, such that the return time function R has exponential tail: There exists $\lambda \in (0,1)$ such that

$$\begin{aligned} {\tilde{\mu } }(R>n) \lesssim \lambda ^n. \end{aligned}$$

Let $\{U_n\subset {\tilde{\Omega } }\}$ be a nested sequence of sets for which the base system $({\tilde{\Omega } }, {\tilde{T} }, {\tilde{\mu } })$ satisfies the assumptions of Theorem B in the cylinder case, or Theorem E in the open set case. Then the localized escape rate at $\Lambda =\cap _n U_n$ exists and satisfies

$$\begin{aligned} \rho (\Lambda ,\{U_n\}) =\alpha _1. \end{aligned}$$

We would like to remark that similar results for escape rate under suspension have been obtained in [2] and [19] under slightly different settings.

2.5 Organization of the Paper

This paper is organized in the following way. In Sect. 3, we then state some properties that surround the parameters of very short returns whose presence is unaffected by the Kac timescale. In Sect. 4,, we then prove the main results for cylinder approximations of the zero measure target set $\Lambda$. One crucial result here is Lemma 4.6 which yields the extremal index for the near zero time limiting distribution for entry times (as opposed to return times). Those results are then used in Sect. 5 to extend them to the case when the approximating sets are metric neighborhoods. In Sect. 6, we then provide a general argument which shows that the local escape rate for entry times is the same as the local escape rate for returns. In Sect. 7, we then show that the local escape rate persists for the induced map. Section 8 is dedicated to examples.

3 Preliminaries

3.1 Return and Entry Times Along a Nested Sequence of Sets

In this section, we recall the general results in [13] on the number of entries to an arbitrary null set $\Lambda$ within a cluster.

Given a sequence of nested sets $U_n,n=1,2,\ldots$ with $U_{n+1}\subset U_n$, $\cap _n U_n=\Lambda$ and $\mu (U_n)\rightarrow 0$, we will fix a large integer $K>0$ (which will be sent to infinity later) and assume that the limit

$$\begin{aligned} {\hat{\alpha }}_\ell (K) = \lim _{n\rightarrow \infty }\mu _{U_n}(\tau ^{\ell -1}_{U_n}\le K) \end{aligned}$$

exists for K sufficiently large and for every $\ell \in {{\mathbb {N}}}$. By definition ${\hat{\alpha }}_\ell (K)\ge {\hat{\alpha }}_{\ell +1}(K)$ for all $\ell$, and ${\hat{\alpha }}_1(K)=1$ due to our choice of $\tau ^0 = 0$ on U. Also note that ${\hat{\alpha }}_\ell (K)$ is non-decreasing in K for every $\ell$. As a result, we have for every $\ell \ge 1$:

$$\begin{aligned} {\hat{\alpha }}_\ell = \lim _{K\rightarrow \infty }{\hat{\alpha }}_\ell (K) \hbox { exists for every }\ell , \hbox { and } {\hat{\alpha }}_1=1,{\hat{\alpha }}_\ell \ge {\hat{\alpha }}_{\ell +1}. \end{aligned}$$

(7)

Note that in the definition of $\hat{\alpha }$, the cut-off for the short return time K does not depend on the set $U_n$. Another way to study the short return properties for the nested sequence $U_n$ is to look at

$$\begin{aligned} {\hat{\beta }}_\ell = \lim _{n\rightarrow \infty }\mu _{U_n}(\tau _{U_n}^{\ell -1}\le s_n) \end{aligned}$$

(8)

for some increasing sequence of integers $\{s_n\}$, with $s_n\mu (U_n)\rightarrow 0$ as $n\rightarrow \infty$. This is the approach taken by Freitas et al in [11]. It is proven that for many systems (including Gibbs–Markov systems and Young towers with polynomial tails), we have ${\hat{\beta }}_\ell =\hat{\alpha }_{\ell }$. See [21, Proposition 5.4 and 6.2]

To demonstrate the power of desynchronizing K from n, recall that for any set U, the essential period of U is given by:

$$\begin{aligned} \pi _{{\text {ess}}}(U) = \min \{k>0: \mu (T^{-k}U\cap U)>0\}. \end{aligned}$$

Then the following lemma can be easily verified using the definition of $\hat{\alpha }$:

Lemma 3.1

Let $\{U_n\}$ be a sequence of nested sets. Assume that $\pi _{{\text {ess}}}(U_n)\rightarrow \infty$ as $n\rightarrow \infty$, then $\hat{\alpha }_\ell$ exists and equals zero for all $\ell \ge 2$.

Proof

For each K, one can take $n_0$ large enough such that $\pi _{{\text {ess}}}(U_n)> K$ for all $n > n_0$. Then for $\ell \ge 2$,

$$\begin{aligned} \mu _{U_n}(\tau ^{\ell -1}_{U_n}\le K) \le \mu _{U_n} \left( \bigcup _{k=0}^K T^{-k}U_n\cap U_n\right) = 0 \end{aligned}$$

since all the intersections have zero measure. $\square$

Note that ${\hat{\alpha }}_\ell (K)$ is the conditional probability to have at least $\ell -1$ returns in a cluster with length K. If we consider the level set:

$$\begin{aligned} \alpha _\ell (K, U_n) = \mu _{U_n}(\tau ^{\ell -1}_{U_n}\le K<\tau ^\ell _{U_n}), \end{aligned}$$

(9)

and its limit

$$\begin{aligned} \alpha _\ell (K)= & {} \lim _{n\rightarrow \infty }\alpha _\ell (K, U_n),\nonumber \\ \alpha _\ell= & {} \lim _{K\rightarrow \infty }\alpha _\ell (K), \end{aligned}$$

(10)

then it is easy to see that

$$\begin{aligned} \alpha _\ell = {\hat{\alpha }}_\ell - {\hat{\alpha }}_{\ell +1},\hbox { and so }\hat{\alpha }_\ell = \sum _{j\ge \ell }\alpha _j \end{aligned}$$

which, in particular, implies the existence of $\alpha _\ell$.

Next, following [13] we put for every integer $\ell >0$ and $K>0$,

$$\begin{aligned} \lambda _\ell (K,U_n) = \frac{{{\mathbb {P}}}(\sum _{i=1}^{K}{{\mathbb {I}}}_{U_n}\circ f^i=\ell )}{{{\mathbb {P}}}(\sum _{i=1}^{K}{{\mathbb {I}}}_{U_n}\circ f^i\ge 1)}. \end{aligned}$$

(11)

In other words, $\lambda _\ell (K,U_n)$ is, conditioned on having an entry to the set $U_n$, the probability to have precisely $\ell$ entries in a cluster with length K. The next theorem provides the relation between ${\hat{\alpha }}_\ell$ and $\lambda _\ell$:

Theorem 3.2

[13, Theorem 2] Assume that $U_n$ is a sequence of nested sets with $\mu (U_n)\rightarrow 0$. Assume that the limits in (7) exist for K large enough and every $\ell \ge 1$. Also assume that $\sum _{\ell =1}^{\infty }\ell {\hat{\alpha }}_\ell <\infty$.

Then

$$\begin{aligned} \lambda _\ell =\frac{\alpha _\ell - \alpha _{\ell +1}}{\alpha _1}, \end{aligned}$$

where $\alpha _\ell = {\hat{\alpha }}_\ell -{\hat{\alpha }}_{\ell +1}$. In particular, the limit defining $\lambda _\ell$ exists. Moreover, the average length of the cluster of entries satisfies

$$\begin{aligned} \sum _{\ell =1}^{\infty }\ell \lambda _\ell = \frac{1}{\alpha _1}. \end{aligned}$$

For more properties on $\{\hat{\alpha }_\ell \}$, $\{\alpha _{\ell }\}$ and $\{\lambda _\ell \}$, we direct the readers to [13] and [21, Section 3].

3.2 Gibbs–Markov Systems

A map $T:\mathbf{{M}}\rightarrow \mathbf{{M}}$ is called Markov if there is a countable measurable partition ${{\mathcal {A}}}$ on $\mathbf{{M}}$ with $\mu (A)>0$ for all $A\in {{\mathcal {A}}}$, such that for all $A\in {{\mathcal {A}}}$, T(A) is injective and can be written as a union of elements in ${{\mathcal {A}}}$. Write ${{\mathcal {A}}}^n=\bigvee _{j=0}^{n-1}T^{-j}{{\mathcal {A}}}$ as before, it is also assumed that ${{\mathcal {A}}}$ is (one-sided) generating.

Fix any $\lambda \in (0,1)$ and define the metric $d_\lambda$ on $\mathbf{{M}}$ by $d_\lambda (x,y) = \lambda ^{s(x,y)}$, where s(x, y) is the largest positive integer n such that x, y lie in the same n-cylinder. Define the Jacobian $g=JT^{-1}=\frac{d\mu }{d\mu \circ T}$ and $g_k = g\cdot g\circ T \cdots g\circ T^{k-1}$.

The map T is called Gibbs–Markov if it preserves the measure $\mu$, and also satisfies the following two assumptions:

• (i) The big image property: there exists $C>0$ such that $\mu (T(A))>C$ for all $A\in {{\mathcal {A}}}$.

• (ii) Distortion: $\log g|_A$ is Lipschitz for all $A\in {{\mathcal {A}}}$.

In view of (i) and (ii), there exists a constant $D>1$ such that for all x, y in the same n-cylinder, we have the following distortion bound:

$$\begin{aligned} \left| \frac{g_n(x)}{g_n(y)}-1\right| \le D d_\lambda (T^nx,T^ny), \end{aligned}$$

and the Gibbs property:

$$\begin{aligned} D^{-1}\le \frac{\mu (A_n(x))}{g_n(x)}\le D. \end{aligned}$$

It is well known (see, for example, Lemma 2.4(b) in [18]) that Gibbs–Markov systems are exponentially $\phi$-mixing, that is, $\phi (k)\lesssim \eta ^k$ for some $\eta \in (0,1)$.

4 Escape Rate for Unions of Cylinders

This section contains the Proof of Theorem A,  B and Corollary C, D. We will suppress the dependence of $\rho$ on $\{U_n\}$ and simply write $\rho (\Lambda )$ for the local escape rate at $\Lambda$.

4.1 The Block Argument

In this section, we will provide a general framework on the escape rate for polynomially $\phi$-mixing systems. The main lemma, which is Lemma 4.3, allows us to reduce the escape rate (which is on the points that do not enter U in a large time-scale) to the probability of having short entries.

First we introduce the following standard result for systems that are either left or right $\phi$-mixing. The proof can be found in [1, 14].

Lemma 4.1

[14, Lemma 4] Assume that $\mu$ is either left or right $\phi$-mixing for the partition ${{\mathcal {A}}}$. For $U\in \sigma ({{\mathcal {A}}}^{\kappa _n})$, let $s,t>0$ and $\Delta <\frac{s}{2}$ then we have

$$\begin{aligned} |{{\mathbb {P}}}(\tau _U>s+t)-{{\mathbb {P}}}(\tau _U>s){{\mathbb {P}}}(\tau _U>t)| \le 2(\Delta \mu (U)+\phi (\Delta -\kappa _n)){{\mathbb {P}}}(\tau _U>t-\Delta ). \end{aligned}$$

Iterating the previous lemma, we obtain:

Lemma 4.2

Assume that $\mu$ is either left or right $\phi$-mixing for the partition ${{\mathcal {A}}}$. Let $s>0$ and $\Delta <\frac{s}{2}$. Define $q=\left\lfloor \, \frac{s}{\Delta } \, \right\rfloor$, $\eta =\frac{q}{q+1}$, and $\delta =2(\Delta \mu (U)+\phi (\Delta -\kappa _n)).$ Assume that $\delta ^\eta < {{\mathbb {P}}}(\tau _U>s)$, then there exists $a(q)>0$ such that for every $k\ge 2-q^{-1}$ that is an integer multiple of $q^{-1},$ we have

$$\begin{aligned} ({{\mathbb {P}}}(\tau _U>s)-\delta ^\eta )^{k+a(q)}\le {{\mathbb {P}}}(\tau _U>ks)\le ({{\mathbb {P}}}(\tau _U>s)+\delta ^\eta )^{k-2}. \end{aligned}$$

(12)

Proof

We follow the proof of Theorem 1 in [14] and use induction. We first take $a(q)>0$ large enough such that

$$\begin{aligned} ({{\mathbb {P}}}(\tau _U>s)-\delta ^\eta )^{2-q^{-1}+a(q)}\le {{\mathbb {P}}}(\tau _U>3s). \end{aligned}$$

Also note that for $k \le k'$ we have ${{\mathbb {P}}}(\tau _u> k's) \le {{\mathbb {P}}}(\tau _u > ks).$ Then for $k\in [2-q^{-1}, 3]$ that is an integer multiple of $q^{-1}$, we have

$$\begin{aligned} ({{\mathbb {P}}}(\tau _U>s)-\delta ^\eta )^{k+a(q)} \le&({{\mathbb {P}}}(\tau _U>s)-\delta ^\eta )^{2-q^{-1}+a(q)}\nonumber \\ \le&{{\mathbb {P}}}(\tau _U>3s)\nonumber \\ \le&{{\mathbb {P}}}(\tau _U>ks). \end{aligned}$$

(13)

On the other hand, we have, for $k\le 3$,

$$\begin{aligned} {{\mathbb {P}}}(\tau _U>ks) \le {{\mathbb {P}}}(\tau _U>s) \le {{\mathbb {P}}}(\tau _U>s)+\delta ^\eta \le ({{\mathbb {P}}}(\tau _U>s)+\delta ^\eta )^{k-2}. \end{aligned}$$

Combining with (13), this shows that (12) holds for $k\in [2-q^{-1}, 3]$ that is an integer multiple of $q^{-1}$.

For $k>3$, we use induction on $m=k\cdot q\in {{\mathbb {N}}}$:

$$\begin{aligned}&{{\mathbb {P}}}(\tau _U>ks)\\&\le {{\mathbb {P}}}(\tau _U>s){{\mathbb {P}}}(\tau _U>(k-1)s)+\delta {{\mathbb {P}}}(\tau _U>(k-1-q^{-1})s)\\&\le {{\mathbb {P}}}(\tau _U>s)({{\mathbb {P}}}(\tau _U>s)+\delta ^\eta )^{k-3}+\delta ({{\mathbb {P}}}(\tau _U>s) +\delta ^\eta )^{k-3-q^{-1}}\\&=({{\mathbb {P}}}(\tau _U>s)+\delta ^\eta )^{k-3-q^{-1}}[{{\mathbb {P}}}(\tau _U>s)({{\mathbb {P}}}(\tau _U>s) +\delta )^{q^{-1}}+\delta ]\\&\le ({{\mathbb {P}}}(\tau _U>s)+\delta ^\eta )^{k-2}. \end{aligned}$$

The second inequality follows from the induction assumption. We justify the last inequality as follows. By definition of $\eta ,$ we have $\delta =\delta ^\eta \delta ^{\frac{\eta }{q}}\le \delta ^\eta ({{\mathbb {P}}}(\tau _U>s) +\delta ^\eta )^{q^{-1}}.$ Consider the bracketed term in the forth line:

$$\begin{aligned}&{{\mathbb {P}}}(\tau _U>s)({{\mathbb {P}}}(\tau _U>s)+\delta )^{q^{-1}}+\delta \\ =&{{\mathbb {P}}}(\tau _U>s)({{\mathbb {P}}}(\tau _U>s)+\delta )^{q^{-1}}+\delta ^\eta ({{\mathbb {P}}}(\tau _U>s) +\delta ^\eta )^{q^{-1}}\\ =&({{\mathbb {P}}}(\tau _U>s)+\delta ^\eta )^{1+q^{-1}}. \end{aligned}$$

By induction this completes the proof of the right-hand-side of (12). The proof of the left-hand-side is largely analogous (with $\delta$ replaced by $-\delta$ and the direction of the inequality reversed) and thus omitted. $\square$

The next lemma establishes the relation between the escape rate and the probability of short entries:

Lemma 4.3

Assume that $\mu$ is either left or right $\phi$-mixing for the partition ${{\mathcal {A}}}$, with $\phi (k)\le Ck^{-p}$ for some $p>0$. Let $\{U_n\in \sigma ({{\mathcal {A}}}^{\kappa _n})\}$ be a nested sequence of sets for some $\kappa _n\nearrow \infty$. Furthermore, assume that there exists $\varepsilon \in (0,1)$, such that $\kappa _n\mu (U_n)^\varepsilon \rightarrow 0$.

Then we have

$$\begin{aligned} \rho (\Lambda ) = \lim _{n\rightarrow \infty }\frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)}, \end{aligned}$$

(14)

where $s_n= \left\lfloor \, \mu (U_n)^{-(1-a)} \, \right\rfloor$ for any fixed $a>0$ small enough.

Remark 4.4

At first glance, the RHS of (14) is similar to the definition of the local escape rate in (1). However, since $s_n \ll \mu (U_n)^{-1}$ (where the latter is the average return time given by Kac’s formula), ${{\mathbb {P}}}(\tau _{U_n}\le s_n)$ concerns the probability of short entries to U. A similar observation was made in [2].

Proof

Let $\{s_n\}, \{\Delta _n\}$ be increasing sequences of positive integers with $\Delta _n<s_n/2$, whose choice will be specified later. Write $q_n = \left\lfloor \, s_n/\Delta _n \, \right\rfloor$, $\eta _n = \frac{q_n}{q_n+1}$ and $\delta _n = 2(\Delta _n\mu (U_n) + \phi (\Delta _n-\kappa _n))$ as before. Our choice of $s_n$ and $\Delta _n$ below will guarantee that $\delta _n^{\eta _n} = o(s_n\mu (U_n))$, which also implies that $\delta _n^{\eta _n}< {{\mathbb {P}}}(\tau _{U_n} > s_n)$.

We again follow largely the Proof of Theorem 1 in [14] and get by Lemma 4.2

$$\begin{aligned} \frac{k+a(q_n)}{ks_n}\log \left( {{\mathbb {P}}}(\tau _{U_n}>s_n) -\delta _n^{\eta _n}\right)&\le \frac{1}{ks_n} \log {{\mathbb {P}}}(\tau _{U_n}>ks_n)\\&\le \frac{k-2}{ks_n}\log \left( {{\mathbb {P}}}(\tau _{U_n}>s_n)+\delta _n^{\eta _n}\right) . \end{aligned}$$

Taking limit as $k\rightarrow \infty$ (with n fixed) and note that ${{\mathbb {P}}}(\tau _{U_n}>s_n) = 1-{{\mathbb {P}}}(\tau _{U_n}\le s_n)$, we obtain

$$\begin{aligned} \rho (U_n) =&\lim _{k\rightarrow \infty }\frac{1}{ks_n} |\log {{\mathbb {P}}}(\tau _{U_n}>ks_n)|\nonumber \\ =&\frac{1}{s_n}\big ({{\mathbb {P}}}(\tau _{U_n}\le s_n)+o(s_n\mu (U_n))+{\mathcal {O}}(\delta _n^{\eta _n})\big ). \end{aligned}$$

(15)

Here we used the trivial estimate

$$\begin{aligned} {{\mathbb {P}}}(\tau _{U_n}\le s_n) \le {{\mathbb {P}}}\!\left( \bigcup _{1\le k\le s_n}T^{-k}(U_n)\right) \le s_n\mu (U_n). \end{aligned}$$

(16)

Divide (15) by $\mu (U_n)$ and let $n\rightarrow \infty$, we obtain

$$\begin{aligned} \rho (\Lambda ) = \lim _{n\rightarrow \infty }\left( \frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)} + \frac{\delta _n^{\eta _n}}{s_n\mu (U_n)}\right) . \end{aligned}$$

(17)

It remains to show that the second term converges to zero for some proper choice of $\{s_n\}$ and $\Delta _n$. For this purpose, we fix some $a\in (0,1), b\in (\varepsilon ,1)$ and choose $s_n= \left\lfloor \, \mu (U_n)^{-(1-a)} \, \right\rfloor$, and $\Delta _n = \left\lfloor \, \mu (U_n)^{-b} \, \right\rfloor \gg \kappa _n = o(\mu (U_n)^{-\varepsilon })$. Then we have:

$$\begin{aligned} \frac{\delta _n^{\eta _n}}{s_n\mu (U_n)}\lesssim&\frac{\Delta _n^{\eta _n} \mu (U_n)^{\eta _n}}{s_n\mu (U_n)} + \frac{\phi (\Delta _n-\kappa _n)^{\eta _n}}{s_n\mu (U_n)}\\ \le&\Delta _n\mu (U_n)^{\eta _n-a} + \Delta _n^{-p\eta _n}\mu (U_n)^{-a}\\ \le&\mu (U_n)^{\eta _n-a-b} + \mu (U_n)^{bp\eta _n-a}. \end{aligned}$$

In order for both terms to go to zero, we need:

• (1) $1-a>b$, which guarantees that $s_n\gg \Delta _n$, so $q_n\rightarrow \infty$ and consequently $\eta _n\nearrow 1$; then the first term will go to zero;

• (2) $bp>a$, so that the second term goes to zero.

Both requirements are satisfied if we take any $b\in (\varepsilon ,1)$, then choose $0<a<\min \{1-b,bp\}$. Combining this with (17), we conclude that

$$\begin{aligned} \rho (\Lambda ) = \lim _{n\rightarrow \infty }\frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)}, \end{aligned}$$

as desired. $\square$

In the remaining part of this section, we will prove that the RHS of (14) coincides with the extreme index defined by (4). But before we move on, let us state a direct corollary of the previous lemma, which is interesting in its own right.

Proposition 4.5

Assume that $\mu$ is either left or right $\phi$-mixing for the partition ${{\mathcal {A}}}$, with $\phi (k)\le Ck^{-p}$ for some $p>0$. Let $\{U_n\in \sigma ({{\mathcal {A}}}^{\kappa _n})\}$ be a nested sequence of sets for some $\kappa _n\nearrow \infty$. Furthermore, assume that there exists $\varepsilon \in (0,1)$, such that $\kappa _n\mu (U_n)^\varepsilon \rightarrow 0$.

Then we have

$$\begin{aligned} \rho (\Lambda ) \in [0,1], \end{aligned}$$

(18)

provided that the local escape rate at $\Lambda$ exists.

Proof

The lower bound is clear. For the upper bound, the trivial estimate (16) yields

$$\begin{aligned} \frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)} \le \frac{s_n\mu (U_n)}{s_n\mu (U_n)}=1. \end{aligned}$$

$\square$

4.2 Proof of Theorem A and B

First we prove Theorem A using the following lemma, which is stated for right $\phi$-mixing systems. The proof can be adapted for left $\phi$-mixing systems as well, with certain modification on the assumptions of $U_n$ (in particular, on how $U_n$ can be approximated by shorter cylinders). See Remark 4.7 below and the discussion in Sect. 4.3.

Lemma 4.6

Let $\mu$ be right $\phi$-mixing for the partition ${{\mathcal {A}}}$, with $\phi (k) \le Ck^{-p}$ for some $p>1$. Assume that $\{U_n\}$ is a good neighborhood system, such that ${\hat{\alpha }}_\ell (K)$ exists for K large enough, and $\sum _{\ell }\hat{\alpha }_\ell <\infty$. Then we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)}=\alpha _1 \end{aligned}$$

for any increasing sequence $\{s_n\}$ for which $s_n\mu (U_n)\rightarrow 0$ as $n\rightarrow \infty$.

Proof

For an given integer s, write $Z_n^{s} = \sum _{j=1}^s{\mathbb {I}}_{U_n}\circ T^j$ which counts the number of entries to $U_n$ before time s. Let K be a large integer, then by [13] Lemma 3 for every $\varepsilon >0$ one has ${\mathbb {P}}(\tau _{U_n}\le K)=\alpha _1K\mu (U_n)(1+{\mathcal {O}}^*(\varepsilon ))$ for all n large enough, where the notation ${\mathcal {O}}^*$ means that the implied constant is one (i.e., $x={\mathcal {O}}^*(\varepsilon )$ if $|x|< \varepsilon$). For simplicity, assume $r=s_n/K$ is an integer and put

$$\begin{aligned} V_q=\{Z_n^K\circ T^{qK}\ge 1\}, \end{aligned}$$

$q=0,1,\dots ,r-1$, and

$$\begin{aligned} D_q=\{V_q,Z_n^{(r-q-1)K}\circ T^{(q+1)K}=0\}. \end{aligned}$$

Then

$$\begin{aligned} \{Z_n^{s_n}\ge 1\}=\bigcup _{q=0}^{r-1}D_q \end{aligned}$$

is a disjoint union. Let us now estimate

$$\begin{aligned}&{\mathbb {P}}(Z_n^{(r-q-1)K}\circ T^{(q+1)K}\ge 1, V_q)\nonumber \\&\quad \le {\mathbb {P}}(Z_n^{(r-q-1)K-2\sqrt{K}}\circ T^{(q+1)K+2\sqrt{K}}\ge 1, V_q)+2\sqrt{K}\mu (U_n)\nonumber \\&\quad \le 2\sqrt{K}\mu (U_n)+\mu (V_q, Z_n^{s_n - (q+1)K - 2\kappa _n}\circ T^{(q+1)K+2\kappa _n} \ge 1)x\nonumber \\&\quad +\sum _{j=qK}^{(q+1)K-1}\sum _{i=(q+1)K+2\sqrt{K}}^{(q+1)K +2\kappa _n}\mu (T^{-j}U_n\cap T^{-i}U_n)\nonumber \\&\quad =: \mathrm{I}+\mathrm{II}+\mathrm{III}. \end{aligned}$$

(19)

To bound $\mathrm{II}$, note that $\{Z_n^{s_n - (q+1)K - 2\kappa _n}\circ T^{(q+1)K+2\kappa _n}\ge 1\}$ is the event of having a hit between $[(q+1)K+2\kappa _n, s_n]$. We cut this interval into $t_n = \left\lfloor \, \frac{s_n - (q+1)K - 2\kappa _n}{K} \, \right\rfloor \ge 0$ (II is void when $t_n$ is negative) many blocks with length K. This allow us to estimate:

$$\begin{aligned} \mathrm{II}\le&\sum _{j=0}^{t_n+1} \mu (Z_n^K\circ T^{qK}\ge 1, Z_n^K\circ T^{(q+1+j)K+2\kappa _n}\ge 1) \\ =&\sum _{j=0}^{t_n+1}\sum _{k = 1}^K \mu (T^{-qK-k}U_n, Z_n^K\circ T^{(q+1+j)K+2\kappa _n}\ge 1) \\ \le&\sum _{j=0}^{t_n+1}\sum _{k = 1}^K\mu (Z_n^K\ge 1)(\mu (U_n) + \phi ((j+1)K+\kappa _n -k ))\\ \le&\sum _{i=\kappa _n}^{s_n+K} \mu (V_q)(\mu (U_n) + \phi (i)), \end{aligned}$$

where we used $(t_n +1)$ many blocks instead of $t_n$ to cover the remaining $\le K$ many hits at the end. The third inequality follows from right $\phi$-mixing, and the last line is due to $\mu (Z_n^K\ge 1) = \mu (V_q)$.

For the third term in (19), we use right $\phi$-mixing again to get (and recall that $U_n^j$ is the outer approximation of $U_n$ by j-cylinders):

$$\begin{aligned} \mathrm{III}\le&\sum _{j=qK}^{(q+1)K-1}\sum _{i=(p+1)K+2\sqrt{K}}^{(q+1)K +2\kappa _n}\mu (U_n\cap T^{-(i-j)}U_n)\\ \le&K\sum _{j=2\sqrt{K}}^{2\kappa _n}\mu (U_n^{j/2}\cap T^{-j}U_n)\\ \le&K\sum _{j=2\sqrt{K}}^{2\kappa _n} \mu (U_n)(\mu (U_n^{j/2}) + \phi (j/2))\\ =&{{\mathcal {O}}}(1)\mu (V_q)\sum _{j=2\sqrt{K}}^{2\kappa _n} (\mu (U_n^{j/2}) + \phi (j/2)), \end{aligned}$$

where the last equality follows from

$$\begin{aligned} \mu (V_q) = {{\mathbb {P}}}(\tau _{U_n}\le K) = \alpha _1K\mu (U_n)(1+{{\mathcal {O}}}^*(\varepsilon )). \end{aligned}$$

Combining the previous estimates, we get

$$\begin{aligned}&{\mathbb {P}}(Z_n^{(r-q-1)K}\circ T^{(q+1)K}\ge 1, V_q)\\&\quad \le {\mathbb {P}}(Z_n^{(r-q-1)K-2\sqrt{K}}\circ T^{(q+1)K+2\sqrt{K}}\ge 1, V_q)+2\sqrt{K}\mu (U_n)\\&\quad \le 2\sqrt{K}\mu (U_n) +\mu (V_q)\sum _{i=\kappa _n}^{s_n+K}(\mu (U_n)+\phi (i))\\&\quad +\mu (V_q){{\mathcal {O}}}(1)\sum _{j=\sqrt{K}}^{\kappa _n}(\mu (U_n^{j})+\phi (j))\\&\quad \le \mu (V_q)F, \end{aligned}$$

where

$$\begin{aligned} F=\frac{2}{\sqrt{K}}+(s_n+K)\mu (U_n)+{{\mathcal {O}}}(1)(\phi ^1(\sqrt{K}) +\sum _{j=\sqrt{K}}^{\kappa _n}\mu (U_n^{i})) \end{aligned}$$

and $\phi ^1(u)=\sum _{i=u}^\infty \phi (i)$ is the tail-sum of $\phi$ which by assumption goes to zero as u goes to infinity.

If n is large enough so that $\max \{s_n\mu (U_n), \kappa _n\mu (U_n), \phi ^1(\kappa _n)\}<\varepsilon$, then

$$\begin{aligned} F&\le 2\varepsilon +\frac{2}{\sqrt{K}}+{{\mathcal {O}}}(1)\left( \phi ^1(\sqrt{K}) +\kappa _n\mu (U_n)+\sum _{i=\sqrt{K}}^{\kappa _n}i^{-p'}\right) \\&\lesssim \varepsilon +\frac{1}{\sqrt{K}}+\phi ^1(\sqrt{K}) +K^{-\frac{p'-1}{2}}, \end{aligned}$$

where we used the assumption that $\mu (U_n^{i})\le \mu (U_n)+ Ci^{-p'}$ for some $p'>1$. Consequently

$$\begin{aligned} \mu (D_q)=\mu (V_q)-{\mathbb {P}}(V_q,Z_n^{(r-q-1)K}\circ T^{(q+1)K}\ge 1) =\mu (V_q)(1+{\mathcal {O}}^*(F)), \end{aligned}$$

and since $\{Z_n^{qK}\ge 1,V_q\}=V_q$ and $\mu (V_q)=\mu (V_0)$ we get

$$\begin{aligned} {\mathbb {P}}(Z_n^{s_n}\ge 1) =\sum _{q=0}^{r-1}{\mathbb {P}}(D_q) =r\mu (V_0)(1+{\mathcal {O}}^*(F)). \end{aligned}$$

Since by [13] Lemma 3 $\mu (V_0)=\alpha _1K\mu (U_n)(1+{\mathcal {O}}^*(\varepsilon ))$, we obtain

$$\begin{aligned} {\mathbb {P}}(\tau _{U_n}\le s_n) =r\mu (V_0)(1+{\mathcal {O}}^*(F)) =\alpha _1s_n\mu (U_n)(1+{\mathcal {O}}^*(\varepsilon +F)). \end{aligned}$$

The statement of the lemma now follows if we let $\varepsilon \rightarrow 0$ and then $K\rightarrow \infty$.

$\square$

Remark 4.7

Similar to the previous lemmas which hold for both left and right $\phi$-mixing measures, Lemma 4.6 has a similar formulation in the left $\phi$-mixing case. The estimate of II in (19) is mostly the same (see the proof of Lemma 4.9 below for more detail). However, this would require us to modify the definition of the approximated sets $U^i_n$ as

$$\begin{aligned} \tilde{U}_n^i=T^{-(n-i)}A_i(T^{n-i}U_n), \end{aligned}$$

with the assumption that the measure of $\tilde{U}^i_n$ is small (preferably summable in i, similar to (2) in Definition 2.3). This is indeed the treatment in [14, Lemma 3] when $\Lambda = \{x\}$. However, such an assumption may not hold when $\Lambda$ is a non-singleton null set. The right $\phi$-mixing property avoids this problem.

Remark 4.8

So far we have assumed that T is non-invertible. This is because in the invertible case, the approximation $U^j_n$ and ${\tilde{U}}^j_n$ may become the entire space. As an example, take $\mathbf{{M}}=\Omega$ to be a full, two-sided shift space and $T=\sigma$ the left-shift. Let the sets $U_n$ be n-approximation of an unstable leaf $\Gamma$ through a non-periodic point $x\in \Omega$, e.g., $\Gamma =\{y\in \Omega : y_i=x_i\;\forall \;i\le 0\}$. Obviously $\Gamma$ is a null set but in this case we get that $\tilde{U}^j=\Omega$ the entire space whenever $i<n/2$. For a geometric example,let T be an Anosov diffeomorphisms on ${{\mathbb {T}}}^n$ with minimal unstable foliations and $\Lambda$ be the local unstable manifold at some $x\in \mathbf{{M}}$. Then $T^j \Lambda$ eventually becomes $\varepsilon$-dense in $\mathbf{{M}}$, and the approximation $\tilde{U}^i_n$ (with respect to a Markov partition ${{\mathcal {A}}}$) is the entire space for i small. By symmetry and Remark 4.8, we see that if $\Lambda$ is chosen to be a local stable manifold then $U^j_n = \mathbf{{M}}$ for j small.

On the other hand, in the proof of Lemma 4.6, the approximation $U^j_n$ is only used to control III of (19). Later this observation will allow us to obtain a result for invertible systems where this term does not appear. See Theorem 4.12 and 5.2 below.

Below we state an alternate version of Lemma 4.6 where the right $\phi$-mixing assumption is replaced by the Gibbs–Markov property. This allows us to bypass the issue stated in Remark 4.7 and keep the choice of $U_n^i$.

Lemma 4.9

Let $(T,\mu ,{{\mathcal {A}}})$ be a Gibbs–Markov system. Assume that $\{U_n\}$ is a good neighborhood system, such that ${\hat{\alpha }}_\ell (K)$ exists for K large enough, and $\sum _{\ell }\hat{\alpha }_\ell <\infty$. Then we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)}=\alpha _1 \end{aligned}$$

for any increasing sequence $\{s_n\}$ for which $s_n\mu (U_n)\rightarrow 0$ as $n\rightarrow \infty$.

Proof

Recall that Gibbs–Markov systems are left $\phi$-mixing with exponential rate. The proof follows the lines of Lemma 4.6 up to Eq. (19), which is now estimated using the left $\phi$-mixing as:

$$\begin{aligned} {\mathrm{II}} =&\ \mu (V_q, Z_n^{s_n - (q+1)K - 2\kappa _n}\circ T^{(q+1)K+2\kappa _n} \ge 1)\\ \le&\sum _{i=(q+1)K+2\kappa _n}^{s_n}\mu (V_q \cap T^{-i}U_n)\\ \le&\sum _{i=\kappa _n}^{s_n}\mu (V_q)(\mu (U_n) + \phi (i)). \end{aligned}$$

Note that the proof in this case is much short and the bound is almost the same as before.

For III, we first split the term into the summation over the intersections of $U_n$ with $T^iU_n$:

$$\begin{aligned} {\mathrm{III}}\le&\sum _{j=qK}^{(q+1)K-1}\sum _{i=(p+1)K+2\sqrt{K}}^{(q+1)K+2\kappa _n} \mu (U_n\cap T^{-(i-j)}U_n)\\ \le&\ K\sum _{j=2\sqrt{K}}^{2\kappa _n}\mu (U_n\cap T^{-j}U_n). \end{aligned}$$

Each term in the summation can be bounded by:

$$\begin{aligned} \mu (U_n\cap T^{-j}U_n)\le&\sum _{A\in {{\mathcal {C}}}_j(U_n)}\mu (T^{-j}U_n\cap A)\\ =&\sum _{A\in {{\mathcal {C}}}_j(U_n)}\frac{\mu (T^{-j}U_n\cap A)}{\mu (A)}\mu (A)\\ \lesssim&\sum _{A\in {{\mathcal {C}}}_j(U_n)}\frac{\mu (T^j(T^{-j}U_n\cap A))}{\mu (T^jA)}\mu (A)\\ \lesssim&\sum _{A\in {{\mathcal {C}}}_j(U_n)}\mu (U_n)\mu (A)\\ =&\mu (U_n)\mu \left( \bigcup _{A\in {{\mathcal {C}}}_j(U_n)}A\right) =\mu (U_n)\mu (U_n^j), \end{aligned}$$

where the third and forth inequality follow from the distortion and the big image property of Gibbs–Markov systems. See [21, Theorem D].

Then

$$\begin{aligned} {{\mathrm{III}}} \le c_1K\mu (U_n)\sum _{j= 2\sqrt{K}}^{\kappa _n} \mu (U_n^j) = {{\mathcal {O}}}(1)\mu (V_p)\sum _{j= 2\sqrt{K}}^{2\kappa _n} \mu (U_n^j), \end{aligned}$$

for some $c_1$ and the rest of the proof is identical to Lemma 4.6. $\square$

Now Theorem A and B are immediate consequences of Lemmas 4.3, 4.6 and 4.9 .

Proof of Corollary C

This corollary directly follows from Lemma 3.1. $\square$

Proof of Corollary D

We need the following proposition from [21]:

Proposition 4.10

[21, Proposition 6.3] Let T be a continuous map on the compact metric space $\mathbf{{M}}$, and $\{U_n\}$ a nested sequence of sets such that $\cap _nU_n = \cap _n {\overline{U}}_n$. Then $\pi (U_n) \rightarrow \infty$ if and only if $\Lambda =\cap _nU_n$ intersects every forward orbit at most once.

Since $\pi _{{\text {ess}}}(U)\ge \pi (U)$, we have $\pi _{{\text {ess}}}(U_n)\rightarrow \infty$. Combined with Corollary C, we obtain Corollary D. $\square$

4.3 Some Remarks on the Extremal Index

In the classic literature (for example, [7, 9, 11]), the extremal index is defined as

$$\begin{aligned} \theta = \lim _{n\rightarrow \infty }\mu _{U_n}(\tau _{U_n}>K_n), \end{aligned}$$

(20)

where $K_n\rightarrow \infty$ is some increasing sequence of integers. It is shown in [21, Proposition 5.4] that under the assumption of Theorem B we have

$$\begin{aligned} \alpha _1 = \theta . \end{aligned}$$

It is also straight forward to check that the Proof of Lemmas 4.6 and 4.9 remain true with $\alpha _1$ replaced by $\theta$. We state this as the following proposition:

Proposition 4.11

Assume that one of the following assumptions holds:

• (1) either $\mu$ is right $\phi$-mixing with $\phi (k)\lesssim k^{-p}$, $p>1$;

• (2) or $(T,\mu ,{{\mathcal {A}}})$ is a Gibbs–Markov system.

Let $\theta$ be the extremal index defined by (20) for some sequence $\{K_n\}$. Then for any good neighborhood system $\{U_n\}$ and any increasing sequence $\{s_n\}$ with $s_n\mu (U_n)\rightarrow 0$ and $s_n/K_n\rightarrow \infty$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{{{\mathbb {P}}}(\tau _{U_n}\le s_n)}{s_n\mu (U_n)}=\theta . \end{aligned}$$

Furthermore, the local escape rate at $\Lambda = \bigcap _n U_n$ exists and satisfies

$$\begin{aligned} \rho (\Lambda ) = \theta . \end{aligned}$$

Note that in the Proof of Lemma 4.6, the bound on II of (19) holds for both left and right $\phi$-mixing systems, as already demonstrated in Lemma 4.9. On the other hand, for $\theta$ defined by (20), III of (19) does not exist when $K_n > \kappa _n^2$. By Remarks 4.7 and 4.8 , we can drop the right $\phi$-mixing and the Gibbs–Markov assumption, obtaining the following theorem for left $\phi$-mixing systems that is either invertible or non-invertible:

Theorem 4.12

Assume that $T:\mathbf{{M}}\rightarrow \mathbf{{M}}$ is a dynamical system, either invertible or non-invertible, and preserves a measure $\mu$ that is left $\phi$-mixing with $\phi (k)\le Ck^{p}$ for some $C>0$ and $p>1$. Let $\{U_n\in {{\mathcal {A}}}^{\kappa _n}\}$ be a nested sequence of sets with $\kappa _n \mu (U_n)^\varepsilon \rightarrow 0$ for some $\varepsilon \in (0,1)$.

Assume that $\theta$ defined by (20) exists for some sequence $\{K_n\}$ with $K_n > \kappa _n^2$. Then the localized escape rate at $\Lambda$ exists and satisfies

$$\begin{aligned} \rho (\Lambda ) = \theta . \end{aligned}$$

5 Escape Rate for Open Sets: An Approximation Argument

First, observe that

$$\begin{aligned} \{M_t<u_n\} = \{\tau _{U_n} > t\}. \end{aligned}$$

As a result, we have

$$\begin{aligned} \zeta (u_n) = \lim _{t\rightarrow \infty }\frac{1}{t} |\log {{\mathbb {P}}}(M_t < u_n)| = \lim _{t\rightarrow \infty }\frac{1}{t}|\log {{\mathbb {P}}}(\tau _{U_n} > t)| = \rho (U_n), \end{aligned}$$

therefore we have

$$\begin{aligned} \zeta (\varphi , \{u_n\}) = \rho (\Lambda , \{U_n\}). \end{aligned}$$

The following proposition allows us to replace $\{U_n\}$ by its cylinder-approximation.

Proposition 5.1

Let $\{U_n\}$, $\{V_n\}$ and $\{W_n\}$ be sequences of nested sets with $V_n\subset U_n\subset W_n$ for each n, and $\Lambda = \bigcap _n U_n = \bigcap _n V_n = \cap _n W_n$. Assume that

$$\begin{aligned} \mu (W_n\setminus V_n) = o(1)\mu (V_n), \end{aligned}$$

(21)

and $\rho (\Lambda , \{W_n\})=\rho (\Lambda , \{V_n\}) = \alpha$.

Then

$$\begin{aligned} \rho (\Lambda , \{U_n\}) =\alpha . \end{aligned}$$

Proof

$V_n\subset U_n\subset W_n$ implies that $\tau _{W_n}\ge \tau _{V_n} \ge \tau _{U_n}$ and therefore

$$\begin{aligned} \rho (W_n)\ge \rho (U_n) \ge \rho (V_n). \end{aligned}$$

On the other hand, (21) means that $\mu (W_n)/\mu (V_n)\rightarrow 1$. We thus obtain

$$\begin{aligned} \rho (\Lambda , \{W_n\})\ge \rho (\Lambda , \{U_n\}) \ge \rho (\Lambda , \{V_n\}), \end{aligned}$$

and the proposition follows from the squeeze theorem. $\square$

Proof of Theorem E

For the sequence $\{r_n\}$ given in Assumption 1, we write $\kappa _n$ for the smallest integer such that ${\text {diam}}{{\mathcal {A}}}^{\kappa _n} \le r_n$. Then consider

$$\begin{aligned} V_n = \cup _{A\in {{\mathcal {A}}}^{\kappa _n}, A\subset U_n} A, \quad W_n = \cup _{A\in {{\mathcal {A}}}^{\kappa _n}, A\cap U_n\ne \emptyset } A. \end{aligned}$$

Clearly we have $V_n\subset U_n\subset W_n$ for each n. Moreover, the choice of $\kappa _n$ gives

$$\begin{aligned} U^i_n\subset V_n, W_n\subset U^o_n. \end{aligned}$$

Combine this with (6), we have $\mu (W_n\setminus V_n) = o(1)\mu (V_n).$

Let us write ${\hat{\alpha }}_\ell ^*$, $* = U,V,W$ for ${\hat{\alpha }}_\ell$ defined using $\{U_n\},\{V_n\},\{W_n\}$, respectively. Then it is proven in [21, Lemma 5.6] that

$$\begin{aligned} {\hat{\alpha }}_\ell ^V = {\hat{\alpha }}_\ell ^U ={\hat{\alpha }}_\ell ^W. \end{aligned}$$

In particular, $\sum _\ell \ell {\hat{\alpha }}_\ell ^U<\infty$ implies that the same holds for ${\hat{\alpha }}_\ell ^*$, $* = V, W$, and the value of $\alpha _1$ defined by $\{V_n\}, \{U_n\}, \{W_n\}$ are equal.

It remains to show that $\{V_n\}$ and $\{W_n\}$ are good neighborhood systems. (1) of Definition 2.3 holds due to (a) in Theorem E. For (2) of Definition 2.3, observe that

$$\begin{aligned} \mu (V_n^j) = \mu \left( \bigcup _{A\in {{\mathcal {C}}}_j(V_n)} A\right) \le \mu (V_n) + \mu \left( \bigcup _{A\in {{\mathcal {A}}}^j, A\cap B_{r_n}(\partial U_n)\ne \emptyset } A\right) \le \mu (V_n) + Cj^{-p'}, \end{aligned}$$

thanks to (b) in Theorem E. A similar argument shows that $\{W_n\}$ is also a good neighborhood system.

Now we can apply Theorem A or B on $\{V_n\}$ and $\{W_n\}$ to obtain

$$\begin{aligned} \rho (\Lambda , \{W_n\})=\rho (\Lambda , \{V_n\}) = \alpha _1. \end{aligned}$$

It then follows from Proposition 5.1 that $\rho (\Lambda , \{U_n\}) = \alpha _1$. This concludes the Proof of Theorem E. $\square$

Similar to Theorem 4.12, when the extremal index $\theta$ is defined as

$$\begin{aligned} \theta = \lim _{n\rightarrow \infty }\mu _{U_n}(\tau _{U_n}>K_n) \end{aligned}$$

for some sequence $K_n > \kappa _n^2$, the conditions on the right $\phi$-mixing and $V_n^j$ can be dropped. We thus obtain the following version of Theorem 4.12 for open sets $\{U_n\}$:

Theorem 5.2

Assume that $T:\mathbf{{M}}\rightarrow \mathbf{{M}}$ is a dynamical system, either invertible or non-invertible, and preserves a measure $\mu$ that is left $\phi$-mixing with $\phi (k)\le Ck^{p}$ for some $C>0$ and $p>1$.

Let ${\varphi }:\mathbf{{M}}\rightarrow {{\mathbb {R}}}\cup \{+\infty \}$ be a continuous function achieving its maximum on a measure zero set $\Lambda$. Let $\{u_n\}$ be a non-decreasing sequence of real numbers with $u_n\nearrow \sup {\varphi }$, such that the open sets $U_n$ defined by (5) satisfy Assumption 1 for a sequence $r_n$ that decreases to 0 as $n\rightarrow \infty$. Let $\kappa _n$ be the smallest positive integer for which ${\text {diam}}{{\mathcal {A}}}^{\kappa _n}\le r_n$ and assume that:

• (i) $\kappa _n\mu (U_n)^\varepsilon \rightarrow 0$ for some $\varepsilon \in (0,1)$;

• (ii) $U_n$ has small boundary: there exist $C>0$ and $p'>1$, such that $\mu \left( \bigcup _{A\in {{\mathcal {A}}}^j, A\cap B_{r_n}(\partial U_n) \ne \emptyset }A\right) \le C j^{-p'}$ for all n and $j\le \kappa _n$;

• (iii) the extremal index $\theta$ defined by (20) exists for some sequence $K_n > \kappa _n^2$.

Then the exceedance rate of ${\varphi }$ along $\{u_n\}$ exists and satisfies

$$\begin{aligned} \zeta ({\varphi },\{u_n\}) = \rho (\Lambda , \{U_n\}) = \theta . \end{aligned}$$

6 The Conditional Escape Rate

In this section, we will prove Theorem F.

First we establish the following relation between the hitting times and return times.

Lemma 6.1

For any set $U\subset M$ with $\mu (U)>0,$ let $A_k:=\{x\in \mathbf{{M}}|\tau _U\ge k\},$ and $B_k:=\{x\in U|\tau _U\ge k\}=A_k\cap U.$ Then we have

$$\begin{aligned} \mu _U(A_k)\mu (U) =\mu (B_k)=\mu (A_k)-\mu (A_{k+1}) \end{aligned}$$

(22)

Proof

By definition we have $A_{k+1}\subset A_k.$ Thus, we compute

$$\begin{aligned} \mu (A_{k+1})&=\mu (\cap _{j=1}^k T^{-j}U^c)\\&=\mu (T^{-1}(\cap _{j=0}^{k-1} T^{-j}U^c))\\&=\mu (U^c\cap _{j=1}^{k-1}T^{-j}U^c)\\&=\mu (U^c\cap A_k)\\&=\mu (A_k)-\mu (U\cap A_k)\\&=\mu (A_k)-\mu (B_k), \end{aligned}$$

where the third equality follows from the invariance of $\mu .$ $\square$

Next, we need the following arithmetic lemma on the exponential decay rate for a sequence of real numbers $\{a_n\}$ and its difference sequence $\{b_n = a_n - a_{n+1}\}$.

Lemma 6.2

Suppose that $\{a_n\}$ is a decreasing sequence of positive real numbers with $a_n\searrow 0$. Let $b_n=a_n-a_{n+1}.$ Suppose, also, that $b_n$ is non-increasing. Then the following statements are equivalent:

• (1) $\lim _{n\rightarrow \infty }-\frac{\log a_n}{n}=\vartheta$ for some $\vartheta >0$;

• (2) $\lim _{n\rightarrow \infty }-\frac{\log b_n}{n}=\vartheta$ for some $\vartheta >0$.

Remark 6.3

Note that there are counter-examples for which the statement of the lemma fails without the monotonicity assumption on the sequence $\{b_n\}$.

Proof

First note that since $a_n\searrow 0$ we have $a_n = \sum _{k\ge n} b_k$; therefore (2) $\implies$ (1) is obvious. It thus remains to show that (1) $\implies$ (2). Let $\gamma >1$ be fixed. Since by assumption the limit $\lim _{n\rightarrow \infty }\frac{1}{n}|\log a_n|=\vartheta$ exists and $\vartheta >0$, there is an N so that

$$\begin{aligned} \left| \frac{\log a_n}{n}+\vartheta \right| <\varepsilon \;\;\; \forall n\ge N, \end{aligned}$$

for some positive $\varepsilon <(\gamma -1)\vartheta /4$. Hence

$$\begin{aligned} \left| \frac{\log a_n}{n}-\frac{\log a_{\gamma n}}{\gamma n}\right| <2\varepsilon \;\;\; \forall n\ge N \end{aligned}$$

which implies

$$\begin{aligned} a_{\gamma n}<\left( a_ne^{2\varepsilon n}\right) ^\gamma <\frac{1}{2}a_n \end{aligned}$$

for all n large enough (assuming $\varepsilon <\frac{\vartheta }{2}$). Since

$$\begin{aligned} a_n-a_{\gamma n}=\sum _{j=n}^{\gamma n-1}b_j \end{aligned}$$

we get by monotonicity of the sequence $b_j$

$$\begin{aligned} b_{\gamma n}(\gamma -1)n\le a_n-a_{\gamma n}\le b_n(\gamma -1)n \end{aligned}$$

and consequently $a_n\le 2b_n(\gamma -1)n$. Hence

$$\begin{aligned} \frac{\log b_{\gamma n}}{n} +\frac{\log (\gamma -1)n}{n} \le \frac{\log a_n}{n} \le \frac{\log b_n}{n}+\frac{\log 2(\gamma -1)n}{n} \end{aligned}$$

which in the limit $n\rightarrow \infty$ yields

$$\begin{aligned} \limsup _{n\rightarrow \infty }\frac{\log b_n}{n}\le -\frac{\vartheta }{\gamma }\end{aligned}$$

and

$$\begin{aligned} -\vartheta \le \liminf _{n\rightarrow \infty }\frac{\log b_n}{n}. \end{aligned}$$

Since this applies to every $\gamma >1$ we obtain that $\lim _{n\rightarrow \infty }\frac{1}{n}\log b_n=-\vartheta$. $\square$

Proof of Theorem F

Let $a_k=\mu (A_k) = {{\mathbb {P}}}(\tau _U\ge k)$ and $b_k=\mu (U)\mu (B_k) = \mu (U){{\mathbb {P}}}_U(\tau _U\ge k).$ Since $\mu$ is assumed to be ergodic one has $a_k\searrow 0$. Also note that $b_k$ is non-increasing. Now the theorem follows from Lemma 6.2,

$\square$

7 Escape Rate Under Inducing

In this section, we will state a general theorem for the local escape rate under inducing. For this purpose, we consider a measure preserving dynamical system $({\tilde{\Omega } }, {\tilde{T} },{\tilde{\mu } })$ with ${\tilde{\mu } }$ being a probability measure. Given a measurable function $R: {\tilde{\Omega } }\rightarrow {{\mathbb {Z}}}^+$ consider the space $\Omega = {\tilde{\Omega } }\times {{\mathbb {Z}}}^+ /\sim$ with the equivalence relation $\sim$ given by

$$\begin{aligned} (x,R(x))\sim ({\tilde{T} }(x), 0). \end{aligned}$$

Define the (discrete-time) suspension map over ${\tilde{\Omega } }$ with roof function R as the measurable map T on the space $\Omega$ acting by

$$\begin{aligned} T(x,j)=\left\{ \begin{array}{ll}(x,j+1) &{}\hbox {if } j<R(x)-1,\\ (\hat{T}x,0)&{}\hbox {if } j=R(x)-1.\end{array}\right. \end{aligned}$$

We will call $\Omega$ a tower over ${\tilde{\Omega } }$ and refer to the set $\Omega _k:=\{(x,k): x\in {\tilde{\Omega } }, k<R(x)\}$ as the kth floor where ${\tilde{\Omega } }$ can be naturally identified with the 0th floor called the base of the tower.

For $0\le k < i$, set $\Omega _{k,i} = \{(x,k): R(x) = i\}$. The map

$$\begin{aligned} \Pi : (x,k)\mapsto x \end{aligned}$$

is naturally viewed as a projection from the tower $\Omega$ to the base ${\tilde{\Omega } }$ and for any given set $U\subset \Omega$ we will write

$$\begin{aligned} {\tilde{U} }= \Pi (U). \end{aligned}$$

The measure ${\tilde{\mu } }$ can be lifted to a measure ${\hat{\mu }}$ on $\Omega$ by

$$\begin{aligned} {\hat{\mu }}(A) = \sum _{i=1}^{\infty }\sum _{k=0}^{i-1} {\tilde{\mu } }(\Pi (A\cap \Omega _{k,i})). \end{aligned}$$

It is easy to verify that ${\hat{\mu }}$ is T-invariant and if ${\tilde{\mu } }(R) = \int R\, d{\tilde{\mu } }<\infty$ then ${\hat{\mu }}$ is a finite measure. In this case, the measure

$$\begin{aligned} \mu = \frac{{\hat{\mu }}}{{\tilde{\mu } }(R)} \end{aligned}$$

is a T-invariant probability measure on $\Omega$.

We write ${\tilde{U}} = \Pi (U)\subset {\tilde{\Omega } }$, ${\tilde{\Lambda }} = \cap _n{\tilde{U}}_n$ and define ${\tilde{\rho }}({\tilde{\Lambda }}, \{{\tilde{U}}_n\})$ to be the localized escape rate at ${\tilde{\Lambda }}$ for the system $({\tilde{\Omega } }, {\tilde{T} },{\tilde{\mu } })$. The following theorem relates the escape rate of the base system with that of the suspension. A similar result is obtained for continuous suspensions under the assumption that R is bounded, see [6].

Theorem 7.1

Let $(\Omega , T, \mu )$ be a discrete-time suspension over an ergodic measure preserving system $({\tilde{\Omega } }, {\tilde{T} }, {\tilde{\mu } })$ with a roof function R satisfying the following assumptions:

• (1) R has exponential tail: there exists $C, c>0$ such that ${\tilde{\mu } }(R>n) \le Ce^{-cn}$;

• (2) exponential large deviation estimate: for every $\varepsilon >0$ small, there exists $C_\varepsilon , c_\varepsilon >0$ such that the set

  $$\begin{aligned} B_{\varepsilon , k} = \left\{ y\in {\tilde{\Omega } }: \left| \frac{1}{n}\sum _{j=0}^{n-1}R(\tilde{T}^jy_0) - \frac{1}{\mu (\Omega _0)} \right| >\varepsilon \hbox { for some } n\ge k\right\} , \end{aligned}$$

  satisfies ${\tilde{\mu }}(B_{\varepsilon ,k}) \le C_\varepsilon e^{-c_\varepsilon k}$.

Then for every nested sequence $\{U_n\}$, we have

$$\begin{aligned} \rho (\Lambda , \{U_n\}) = {\tilde{\rho }}({\tilde{\Lambda }}, \{{\tilde{U}}_n\}). \end{aligned}$$

Proof

The result of this theorem is in fact hidden in the proof of Theorem 4 of [14] and Theorem 3.2 (1) in [2]. We include the proof here for completeness.

For every $y= (x,m)\in \Omega$, we take $y_0 = x\in {\tilde{\Omega } }$. Then we have

$$\begin{aligned} \tau _{U_n}(y) =-m+\sum _{j=0}^{{\tilde{\tau }}_{{\tilde{U}}_n}(y_0)-1} R(\tilde{T}^j(y_0)), \end{aligned}$$

(23)

where ${\tilde{\tau }}$ is the return times defined for the system $({\tilde{\Omega } }, {\tilde{T} },{\tilde{\mu } })$. By the Birkhoff ergodic theorem on $({\tilde{\Omega } },\tilde{T},{\tilde{\mu }})$, we see that

$$\begin{aligned} \frac{1}{n}\sum _{j=0}^{n-1}R(\tilde{T}^jy_0)\rightarrow \int _{{\tilde{\Omega } }} R(y)\,d{\tilde{\mu }}(y) = \frac{1}{\mu (\Omega _0)}, \end{aligned}$$

where we apply the Kac’s formula on the last equality and use the fact that $\mu$ is the lift of ${\tilde{\mu }}$.

On the other hand, since the return time function R has exponential tail, we get, for each $\varepsilon >0$ and t large enough,

$$\begin{aligned} \mu ((x,m):m>\varepsilon t)\lesssim e^{-c\varepsilon t}. \end{aligned}$$

To simplify notation, we introduce the set (n is fixed)

$$\begin{aligned} A_t=\left\{ y = (x,m):m<\varepsilon t,\sum _{j=0}^{{\tilde{\tau }}_{{\tilde{U}}_n}(y_0)-1} R(\tilde{T}^j(y_0))>(1+\varepsilon )t\right\} \cap B^c_{\varepsilon ,k}. \end{aligned}$$

Combine (23) with the previous estimates on $B_{\varepsilon ,k}$, for $k=t(1+\varepsilon )$ we get

$$\begin{aligned} \left| \mu (\tau _{{\tilde{U}}_n}>t) - \mu (A_t)\right| \lesssim e^{-c\varepsilon t}+e^{-c_\varepsilon (1+\varepsilon ) t}. \end{aligned}$$

(24)

Note that $A_t$ contains the set

$$\begin{aligned} A_t^- = \left\{ y:m<\varepsilon t, {\tilde{\tau }}_{{\tilde{U}}_n}(y_0)>\frac{(1+\varepsilon )t}{\mu ^{-1}(\Omega _0)-\varepsilon }\right\} , \end{aligned}$$

and is contained in

$$\begin{aligned} A_t^+ = \left\{ y:m<\varepsilon t, {\tilde{\tau }}_{{\tilde{U}}_n}(y_0)>\frac{(1+\varepsilon )t}{\mu ^{-1}(\Omega _0)+\varepsilon }\right\} . \end{aligned}$$

Now we are left to estimate $\mu (A_t^\pm )$. Since $\mu$ is the lift of ${\tilde{\mu }}$, we have

$$\begin{aligned} \mu (A^\pm _t) =&\frac{1}{{\tilde{\mu }}(R)}\sum _{j=0}^{\infty }\sum _{i=0}^{\min (\varepsilon t, R_j)}{\tilde{\mu }}(T^{-i}A^\pm _t\cap \Omega _{0,i})\nonumber \\ =&\mu (\Omega _0)(1+{\mathcal {O}}(\varepsilon t)){\tilde{\mu }}(\tilde{A}^\pm _t), \end{aligned}$$

(25)

where

$$\begin{aligned} \tilde{A}^\pm _t = \left\{ y_0\in \Omega _0: {\tilde{\tau }}_{{\tilde{U}}_n}(y_0)>\frac{(1+\varepsilon )t}{\mu ^{-1}(\Omega _0)\pm \varepsilon }\right\} . \end{aligned}$$

Let $\alpha = {\tilde{\rho }}({\tilde{\Lambda }}, \{{\tilde{U}}_n\})$. Then we have (recall that ${\tilde{\mu }}({\tilde{U}}_n) \mu (\Omega _0)=\mu (U_n)$)

$$\begin{aligned} \lim _{n\rightarrow \infty }\lim _{t\rightarrow \infty }\frac{1}{t\mu (U_n)}|\log {\tilde{\mu }} (\tilde{A}^\pm _t)| =\alpha \frac{(1+\varepsilon )}{1\pm \varepsilon \mu (\Omega _0)}. \end{aligned}$$

By (25), we get that

$$\begin{aligned} \lim _{n\rightarrow \infty }\lim _{t\rightarrow \infty }\frac{1}{t\mu (U_n)}|\log \mu (\tilde{A}^\pm _t)| = \alpha \frac{(1+\varepsilon )}{1\pm \varepsilon \mu (\Omega _0)}. \end{aligned}$$

For each $\varepsilon >0$ we can take $n_0$ large enough, such that for $n>n_0:$

$$\begin{aligned} \alpha \frac{1+\varepsilon }{1\pm \varepsilon \mu (\Omega _0)}\mu (U_n) < \min \{c\varepsilon ,c_\varepsilon (1+\varepsilon )\}. \end{aligned}$$

It then follows that the right-hand-side of (24) is of order $o(\mu (A^\pm _t)).$ We thus obtain

$$\begin{aligned} \rho (\Lambda ,\{U_n\})=\lim _{n\rightarrow \infty }\lim _{t\rightarrow \infty }\frac{1}{t\mu (U_n)}|\log \mu (\tau _{U_n}>t)| \in \left( \alpha \frac{(1+\varepsilon )}{1+\varepsilon \mu (\Omega _0)},\alpha \frac{(1+\varepsilon )}{1-\varepsilon \mu (\Omega _0)}\right) \end{aligned}$$

for every $\varepsilon >0$. This shows that $\rho (\Lambda , \{U_n\})=\alpha = {\tilde{\rho }}({\tilde{\Lambda }}, \{{\tilde{U}}_n\})$. $\square$

Proof of Theorem G

Young towers can be seen as discrete-time suspension over Gibbs–Markov maps. Moreover, the exponential tail of $\mu (R>n)$ implies the exponential large deviation estimate (see for example [2] Appendix B). Therefore, Theorem G immediately follows from Theorems B, E and 7.1. $\square$

8 Examples

8.1 Periodic and Non-periodic Points Dichotomy

First we consider the case where $\Lambda = \{x\}$ is a singleton, and $U_n = B_{\delta _n}(x)$ is a sequence of balls shrinking to x. Alternatively one could take $\varphi (y) = g(d(y,x))$ for some function $g(x): {{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\cup \{+\infty \}$ achieving its maximum at 0 (for example, $g(y) = -\log y$) and let $u_n\nearrow \infty$ be a sequence of threshold tending to infinity. Then $U_n = \{y:\varphi (y) > u_n\}$ is a sequence of balls with diameter shrinking to zero.

This situation has been dealt with in [2] for certain interval maps, and in [14] for maps that are polynomially $\phi$-mixing. A dichotomy is obtained: when x is non-periodic the local escape rate is 1; when x is periodic then $\rho (x) = 1-\theta$ where

$$\begin{aligned} \theta = \theta (x) = \lim _{n\rightarrow \infty } \frac{\mu (U_n\cap T^{-m}U_n)}{\mu (U_n)}, \end{aligned}$$

(26)

where m is the period of x. When $\mu$ is an equilibrium state for some potential function h(x) with zero pressure, one has $\theta = e^{S_mh(x)}$ where $S_m$ is the Birkhoff sum. See [2].

Note that if x is non-periodic then one naturally deduces that $\pi (U_n)\nearrow \infty$ (see for example [14, Lemma 1]). When x is periodic, in [13, Section 8.3] it is shown that ${\hat{\alpha }}_\ell = \theta ^{l-1}$ is a geometric distribution. In particular, one has $\sum _\ell \ell {\hat{\alpha }}_\ell <\infty$ and $\alpha _1 = 1-\theta .$ This leads to the following theorem:

Theorem 8.1

Assume that

• (1) either $\mu$ is right $\phi$-mixing with $\phi (k)\le Ck^{-p}$, $p>1$;

• (2) or $(T,\mu ,{{\mathcal {A}}})$ is a Gibbs–Markov system.

Assume that $0<r_n<\delta _n$ satisfies

$$\begin{aligned} \mu (B_{\delta _n + r_n}(x)\setminus B_{\delta _n - r_n}(x)) = o(1) \mu (B_{\delta _n}(x)). \end{aligned}$$

Write $\kappa _n$ for the smallest positive integer with ${\text {diam}}{{\mathcal {A}}}^{\kappa _n}\le r_n$. We assume that:

• (a) $\kappa _n\mu (U_n)^\varepsilon \rightarrow 0$ for some $\varepsilon \in (0,1)$;

• (b) $U_n$ has small boundary: there exists $C>0$ and $p'>1$, such that $\mu \left( \bigcup _{A\in {{\mathcal {A}}}^j, A\cap B_{r_n}(\partial U_n) \ne \emptyset }A\right) \le C j^{-p'}$ for all n and $j\le \kappa _n$.

• (c) when x is periodic with period m, $\theta$ defined by (26) exists.

Then we have

$$\begin{aligned} \rho (\{x\},\{B_{\delta _n}(x)\}) = \alpha _1 = {\left\{ \begin{array}{ll} 1&{}\hbox {if }x \hbox { is non-periodic}\\ 1-\theta &{}\hbox {if }x \hbox { is periodic}\end{array}\right. }. \end{aligned}$$

This theorem improves [14, Theorem 2] by dropping the assumption $\theta < 1/2$. Also note that such results can be generalized to interval maps which can be modeled by Young towers using Theorem G.

8.2 Cantor Sets for Interval Expanding Maps

For simplicity, below we will only consider the Cantor ternary set. However, the argument below can be adapted to a large family of dynamically defined Cantor set discussed in [11] with only minor modification.

Consider the uniformly expanding map $T(x) = 3x \mod 1$ defined on the unit interval [0, 1]. We take $\Lambda$ to be the ternary Cantor set on [0, 1], and define recursively: $U_0 = [0,1];$ $U_{n+1}$ is obtained by removing the middle third of each connected component of $U_{n}$. Then we have $\cap _n U_n = \Lambda$.

Theorem 8.2

For the uniformly expanding map $T(x) = 3x\mod 1$ on [0, 1], the Cantor ternary set $\Lambda$ and the nested sets $\{U_n\}$, we have

$$\begin{aligned} \rho (\Lambda , \{U_n\}) = \frac{1}{3}. \end{aligned}$$

Proof

Let ${{\mathcal {A}}}= \{[0,1/3), [1/3, 2/3), [2/3, 1]\}$ be a Markov partition of T, with respect to which the Lebesgue measure $\mu$ is exponentially $\psi$-mixing. Below we will verify the assumptions of Proposition 4.11.

It is easy to see that $U_n \in {{\mathcal {A}}}^n$, i.e., $\kappa _n = n$. On the other hand, $\mu (U_n) = 2^n/3^n$ which shows that item (1) of Definition 2.3 is satisfied for any $\varepsilon \in (0,1)$. For item (2), note that $U_n^j = U_j$ which implies that

$$\begin{aligned} \mu (U_n^j) \le \mu (U_n) + \mu (U_j) = \mu (U_n) + \left( \frac{2}{3}\right) ^j. \end{aligned}$$

We conclude that $\{U_n\}$ is a good neighborhood system.

The extremal index can be found as follows. Let us write $U_n=\bigcup _{|\alpha |=n} J_\alpha$ where the disjoint union is over all n-words $\alpha =\alpha _1\alpha _2\dots \alpha _n\in \{0,2\}^n$ and

$$\begin{aligned} J_\alpha =\sum _{j=1}^n\frac{\alpha _j}{3^j}+3^{-n}I, \end{aligned}$$

where $I=[0,1]$ is the unit interval. The length $|J_\alpha |$ is equal to $3^{-n}$. For $j<n$

$$\begin{aligned} T^{-j}J_\alpha =\bigcup _{\beta \in \{0,1,2\}^j} J_{\beta \alpha } \end{aligned}$$

(disjoint union), thus

$$\begin{aligned} U_n\cap T^{-j}U_n =\bigcup _{\alpha \in \{0,2\}^n}\bigcup _{\beta \in \{0,2\}^j}J_{\beta \alpha } \end{aligned}$$

and therefore $U_n\cap T^{-j}U_n=U_{n+j}$. Consequently,

$$\begin{aligned} \{\tau _{U_n}\le K\}\cap U_n =U_n\cap \bigcup _{j=1}^KT^{-j}U_n=U_{n+1}. \end{aligned}$$

Since $\mu (U_{n+j})=\!\left( \frac{2}{3}\right) ^j\mu (U_n)$ this implies that ${\hat{\alpha }}_2(K,U_n)=\frac{\mu (U_{n+1})}{\mu (U_n)}=\frac{2}{3}$ and therefore $\alpha _1=\frac{1}{3}$.

This result was recently shown in [11, Theorem 3.3] in more generality. By Proposition 4.11, we conclude that $\rho (\Lambda , \{U_n\})$ = 1/3. $\square$

8.3 Submanifolds of Anosov Maps

In this section, we consider the case where $\Lambda$ is a submanifold for some Anosov map T. More importantly, we will show how our results can be applied to those cases where the extremal index $\theta$ is defined using time cut-off $K_n$ that depends on $U_n$ [see (20)].

Let $T = \begin{pmatrix} 2 &{} 1\\ 1 &{} 1 \end{pmatrix}$ be an Anosov system on ${{\mathbb {T}}}^2$ and $\mu$ be the Lebesgue measure. It is well known that $\mu$ is exponentially $\psi$-mixing with respect to its Markov partition ${{\mathcal {A}}}$. Also denote by $\lambda >1$ the eigenvalue of T. Following [3] we take $\Lambda$ to be a line segment with finite length $l(\Lambda )$. We will lift $\Lambda$ to ${\hat{\Lambda }}\subset {{\mathbb {R}}}^2$ and parametrize ${\hat{\Lambda }}$ by $p_1 + t v$ for some $p_1\in {{\mathbb {R}}}^2$ and $t\in [0, l(\Lambda )]$. Write $p_2$ for the other end point of ${\hat{\Lambda }}$, that is, $p_2 = p_1 + l(\Lambda ) v$.

Consider the function $\varphi _\Lambda (y) = -\log d(x, \Lambda )$ which achieves its maximum ($+\infty$) on $\Lambda$. Write $v^{*}, * = s, u$ for the unit vector along the stable and unstable direction, respectively. Then we have:

Theorem 8.3

For the sequence $\{u_n = \log n\}$,

• (1) if $\Lambda$ is not aligned with the stable direction $v^s$ or the unstable direction $v^u$ then $\zeta (\varphi _\Lambda , \{u_n\}) = 1$;

• (2) if $\Lambda$ is aligned with the unstable direction but $\{p_1 + tv^u, t\in {{\mathbb {R}}}\}$ has no periodic point, then $\zeta (\varphi _\Lambda , \{u_n\}) = 1$;

• (3) if $\Lambda$ is aligned with the stable direction but $\{p_1 + tv^s, t\in {{\mathbb {R}}}\}$ has no periodic point, then $\zeta (\varphi _\Lambda , \{u_n\}) = 1$;

• (4) $\Lambda$ is aligned with $v^{*}, *=s,u$ and L contains a periodic point with prime period q, then $\zeta (\varphi _\Lambda , \{u_n\}) = 1 - \lambda ^{-q}$;

• (5) $\Lambda$ is aligned with the unstable direction $v^u$, $\Lambda$ has no periodic points but $\{p_1+tv^u, t\in {{\mathbb {R}}}\}$ contains a periodic point of prime period q; if $\Lambda \cap T^{-q}\Lambda = \emptyset$ then $\zeta (\varphi _\Lambda , \{u_n\}) = 1$; if $\Lambda \cap T^{-q} \Lambda \ne \emptyset$ then $\zeta (\varphi _\Lambda , \{u_n\}) = (1 - \lambda ^{-q})\frac{|p_2|}{l(\Lambda )}$;

• (6) $\Lambda$ is aligned with the stable direction $v^u$, $\Lambda$ has no periodic points but $\{p_1+tv^u, t\in {{\mathbb {R}}}\}$ contains a periodic point of prime period q; if $\Lambda \cap T^{-q}\Lambda = \emptyset$ then $\zeta (\varphi _\Lambda , \{u_n\}) = 1$; if $\Lambda \cap T^{-q} \Lambda \ne \emptyset$ then $\zeta (\varphi _\Lambda , \{u_n\}) = (1 - \lambda ^{-q})\frac{|p_2|}{l(\Lambda )}$;

Proof

We will only prove case (1), in which we will need the result of [3, Theorem 2.1 (1)]. The other cases use similar arguments and correspond to case (2) to (6) of [3, Theorem 2.1].

Below we verify the assumptions of Theorem 5.2.

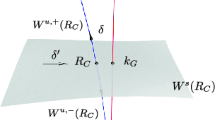
Put $\delta _n = e^{-u_n}$. Then we see that $U_n = \{y: \varphi _\Lambda (y) > u_n\} = B_{\delta _n}(\Lambda )$. Since $\mu$ is the Lebesgue measure, it is straightforward to verify that Assumption 1 is satisfied with $r_n = \delta _n^2 = e^{-2 u_n}$. See [3, Figure 1].

By the hyperbolicity of T, there exists $C>0$ such that ${\text {diam}}{{\mathcal {A}}}^n < C\lambda ^{-n}$. This invites us to take

$$\begin{aligned} \kappa _n = \left\lfloor \, \frac{{\text {ln}}C + 2u_n}{{\text {ln}}\lambda } \, \right\rfloor +1 = {{\mathcal {O}}}(\log n) \end{aligned}$$

which guarantees that ${\text {diam}}{{\mathcal {A}}}^{\kappa _n} < r_n$. On the other hand, $\mu (U_n)\lesssim e^{-u_n}l(\Lambda ) = {{\mathcal {O}}}(1/n)$, so item (i) of Theorem 5.2 is satisfied for any $\varepsilon \in (0,1)$.

To prove (ii), we write $\epsilon _j = {\text {diam}}{{\mathcal {A}}}^j$, and note that if $A\in {{\mathcal {A}}}^j$ has non-empty intersection with $B_{r_n}(\partial U_n)$, then $A\subset B_{r_n+\epsilon _j}(\partial U_n)$. In particular,

$$\begin{aligned}&\mu \left( \bigcup _{A\in {{\mathcal {A}}}^j, A\cap B_{r_n}(\partial U_n) \ne \emptyset }A\right) \le \mu (B_{r_n+\epsilon _j}(\partial U_n))\\ =&{\mathcal {O}}(r_n+\epsilon _j)={\mathcal {O}}(e^{-2u_n})+{\mathcal {O}} (\lambda ^{-j}). \end{aligned}$$

Recall that $j\le \kappa _n = {\mathcal {O}}(u_n)$, we see that the right-hand side is exponentially small in j.

We are left with the extremal index $\theta$ defined by (20). For this purpose, we choose $K_n = (\log n)^5 \gg \kappa _n^2$. Now we estimate:

$$\begin{aligned} \mu _{U_n}(\tau _{U_n} \le K_n)\le&\frac{1}{\mu (U_n)} \sum _{j=1}^{(\log n)^5} \mu (U_n\cap T^{-j} U_n )\\ \lesssim&\, n\sum _{j=1}^{(\log n)^5} \mu (U_n\cap T^{-j} U_n )\\ =&\, o(1) \end{aligned}$$

where the last inequality follows from [3, Section 3.3, page 16]. This shows that

$$\begin{aligned} \theta = \lim _n\mu _{U_n}(\tau _{U_n} > K_n) = 1- \lim _n\mu _{U_n}(\tau _{U_n} \le K_n) = 1, \end{aligned}$$

finishing the proof of (iii) of Theorem 5.2. We conclude that

$$\begin{aligned} \zeta (\varphi , \{\log n\}) = \theta = 1. \end{aligned}$$

$\square$