General Toeplitz Matrices Subject to Gaussian Perturbations

Abstract

We study the spectra of general $N\times N$ Toeplitz matrices given by symbols in the Wiener Algebra perturbed by small complex Gaussian random matrices, in the regime $N\gg 1$. We prove an asymptotic formula for the number of eigenvalues of the perturbed matrix in smooth domains. We show that these eigenvalues follow a Weyl law with probability sub-exponentially close to 1, as $N\gg 1$, in particular that most eigenvalues of the perturbed Toeplitz matrix are close to the curve in the complex plane given by the symbol of the unperturbed Toeplitz matrix.

1 Introduction and main result

Let $a_{\nu }\in \mathbf{C}$, for $\nu \in \mathbf{Z}$ and assume that

$$\begin{aligned} |a_\nu |\le {{\mathcal {O}}}(1)m(\nu ), \end{aligned}$$

(1.1)

where $m:\mathbf{Z}\rightarrow ]0,+\infty [$ satisfies

$$\begin{aligned} (1+|\nu |)m(\nu )\in \ell ^1, \end{aligned}$$

(1.2)

and

$$\begin{aligned} m(-\nu )=m(\nu ),\ \forall \nu \in \mathbb {Z}. \end{aligned}$$

(1.3)

Let

$$\begin{aligned} p(\tau )=\sum _{-\infty }^{+\infty }a_\nu \tau ^\nu , \end{aligned}$$

(1.4)

act on complex valued functions on $\mathbf{Z}$. Here $\tau$ denotes translation by 1 unit to the right: $\tau u(j)=u(j-1)$, $j\in \mathbf{Z}$. By (1.2) we know that $p(\tau )={{\mathcal {O}}}(1):\ell ^2(\mathbf{Z})\rightarrow \ell ^2(\mathbf{Z})$. Indeed, for the corresponding operator norm, we have

$$\begin{aligned} \Vert p(\tau )\Vert \le \sum |a_j|\Vert \tau ^j\Vert =\Vert a\Vert _{\ell ^1}\le {{\mathcal {O}}}(1)\Vert m\Vert _{\ell ^1}. \end{aligned}$$

(1.5)

From the identity, $\tau (e^{ik\xi })=e^{-i\xi }e^{ik\xi }$, we define the symbol of $p(\tau )$ by

$$\begin{aligned} p(e^{-i\xi })=\sum _{-\infty }^\infty a_\nu e^{-i\nu \xi }. \end{aligned}$$

(1.6)

It is an element of the Wiener algebra [4] and by (1.2) in $C^1(S^1)$.

We are interested in the Toeplitz matrix

$$\begin{aligned} P_N {\mathop {=}\limits ^{\mathrm {def}}}1_{[0,N[}p(\tau )1_{[0,N[}, \end{aligned}$$

(1.7)

acting on ${\mathbf {C}}^N \simeq \ell ^2([0,N[)$, for $1\ll N<\infty$. Furthermore, we frequently identify $\ell ^2([0,N[)$ with the space $\ell ^2_{[0,N[}(\mathbf{Z})$ of functions $u\in \ell ^2(\mathbf{Z})$ with support in [0, N[.

The spectra of such Toeplitz matrices have been studied thoroughly, see [4] for an overview. Let $P_\infty$ denote $p(\tau )$ as an operator $\ell ^2(\mathbf{Z})\rightarrow \ell ^2(\mathbf{Z})$. It is a normal operator and by Fourier series expansions, we see that the spectrum of $P_\infty$ is given by

$$\begin{aligned} \sigma (P_\infty )=p(S^1). \end{aligned}$$

(1.8)

The restriction $P_{{\mathbf {N}}}=P_{\infty }|_{\ell ^2({\mathbf {N}})}$ of $P_{\infty }$ to $\ell ^2({\mathbf {N}})$ is in general no longer normal, except for specific choices of the coefficients $a_\nu$. The essential spectrum of the Toeplitz operator $P_{{\mathbf {N}}}$ is given by $p(S^1)$ and we have pointspectrum in all loops of $p(S^1)$ with nonzero winding number, i.e.,

$$\begin{aligned} \sigma (P_{{\mathbf {N}}}) = p(S^1) \cup \{ z\in {\mathbf {C}}; \mathrm {ind}_{p(S^1)}(z)\ne 0 \}. \end{aligned}$$

(1.9)

By a result of Krein [4, Theorem 1.15], the winding number of $p(S^1)$ around the point $z\not \in p(S^1)$ is related to the Fredholm index of $P_{{\mathbf {N}}}-z$: $\mathrm {Ind}(P_{{\mathbf {N}}}-z) = - \mathrm {ind}_{p(S^1)}(z)$.

The spectrum of the Toeplitz matrix $P_N$ is contained in a small neighborhood of the spectrum of $P_{{\mathbf {N}}}$. More precisely, for every $\epsilon >0$,

$$\begin{aligned} \sigma (P_{N}) \subset \sigma (P_{{\mathbf {N}}})+D(0,\epsilon ) \end{aligned}$$

(1.10)

for $N>0$ sufficiently large, where D(z, r) denotes the open disc of radius r, centered at z. Moreover, the limit of $\sigma (P_{N})$ as $N\rightarrow \infty$ is contained in a union of analytic arcs inside $\sigma (P_{{\mathbf {N}}})$, see [4, Theorem 5.28].

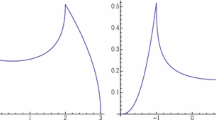
We show in Theorem 1.1 that after adding a small random perturbation to $P_N$, most of its eigenvalues will be close to the curve $p(S^1)$ with probability very close to 1. See Fig. 1 for a numerical illustration.

1.1 Small Gaussian perturbation

Consider the random matrix

$$\begin{aligned} Q_{\omega }{\mathop {=}\limits ^{\mathrm {def}}}Q_{\omega }(N) {\mathop {=}\limits ^{\mathrm {def}}}(q_{j,k}(\omega ))_{1\le j,k\le N} \end{aligned}$$

(1.11)

with complex Gaussian law

$$\begin{aligned} (Q_{\omega })_*(d\mathbb {P}) = \pi ^{-N^2} \mathrm {e}^{-\Vert Q\Vert _{\mathrm {HS}}^2} L(dQ), \end{aligned}$$

where L denotes the Lebesgue measure on ${\mathbf {C}}^{N\times N}$. The entries $q_{j,k}$ of $Q_{\omega }$ are independent and identically distributed complex Gaussian random variables with expectation 0, and variance 1, i.e., $q_{j,k\sim {\mathcal {N}}_{{\mathbf {C}}}(0,1)}$.

We recall that the probability distribution of a complex Gaussian random variable $\alpha \sim {\mathcal {N}}_{{\mathbf {C}}}(0,1)$ is given by

$$\begin{aligned} \alpha _*(d\mathbb {P}) = \pi ^{-1} \mathrm {e}^{-|\alpha |^2} L(d\alpha ), \end{aligned}$$

where $L(d\alpha )$ denotes the Lebesgue measure on ${\mathbf {C}}$. If $\mathbb {E}$ denotes the expectation with respect to the probability measure $\mathbb {P}$, then

$$\begin{aligned} \mathbb {E}[\alpha ] = 0, \quad \mathbb {E}[|\alpha |^2] = 1. \end{aligned}$$

We are interested in studying the spectrum of the random perturbations of the matrix $P_N^0=P_N$:

$$\begin{aligned} P_N^{\delta } {\mathop {=}\limits ^{\mathrm {def}}}P_N^0 + \delta Q_{\omega }, \quad 0 \le \delta \ll 1. \end{aligned}$$

(1.12)

1.2 Eigenvalue asymptotics in smooth domains

Let $\Omega \Subset {\mathbf {C}}$ be an open simply connected set with smooth boundary $\partial \Omega$, which is independent of N, satisfying

• (1) $\partial \Omega$ intersects $p(S^1)$ in at most finitely many points;

• (2) $p(S^1)$ does not self-intersect at these points of intersection;

• (3) these points of intersection are non-critical, i.e.,

  $$\begin{aligned} d p \ne 0 \hbox { on } p^{-1}(\partial \Omega \cap p(S^1) ); \end{aligned}$$

• (4) $\partial \Omega$ and $p(S^1)$ are transversal at every point of the intersection.

Theorem 1.1

Let p be as in (1.6) and let $P_N^{\delta }$ be as in (1.12). Let $\Omega$ be as above, satisfying conditions (1)–(4), pick a $\delta _0\in ]0,1[$ and let $\delta _1 >3$. If

$$\begin{aligned} \mathrm {e}^{- N^{\delta _0} } \le \delta \ll N^{-\delta _1}, \end{aligned}$$

(1.13)

then there exists $\varepsilon _N = o(1)$, as $N\rightarrow \infty$, such that

$$\begin{aligned} \left| \#(\sigma (P^{\delta }_N)\cap \Omega ) - \frac{N}{2\pi } \int _{S^1\cap \, p^{-1}(\Omega )}L_{S^1}(d\theta )\right| \le \varepsilon _N N, \end{aligned}$$

(1.14)

with probability

$$\begin{aligned} \ge 1 - \mathrm {e}^{-N^{\delta _0}}. \end{aligned}$$

(1.15)

In (1.14), we view p as a map from $S^1$ to ${\mathbf {C}}$. Theorem 1.1 shows that most eigenvalues of $P_N^{\delta }$ can be found close to the curve $p(S^1)$ with probability subexponentially close to 1. This is illustrated in Fig. 1 for two different symbols. The left-hand side of Fig. 1 shows the spectrum of a perturbed Toeplitz matrix with $N=2000$ and $\delta =10^{-14}$, given by the symbol $p = p_0 + p_1$ where

$$\begin{aligned} p_0(1/\zeta ) = -\zeta ^{-4} -(3+2i)\zeta ^{-3} +i\zeta ^{-2}+\zeta ^{-1} +10\zeta +(3+i)\zeta ^2+4\zeta ^3+i\zeta ^4 \end{aligned}$$

(1.16)

and

$$\begin{aligned} p_1(1/\zeta ) = \sum _{\nu \in {\mathbf {Z}}} a_{\nu } \zeta ^{\nu }, \quad a_{0}=0, ~ a_{-\nu } = 0.7|\nu |^{-5}+i|\nu |^{-9} ,~ a_\nu = -2i\nu ^{-5}+0.5\nu ^{-9}~~ \nu \in {\mathbf {N}}. \end{aligned}$$

(1.17)

The red line shows the curve $p(S^1)$. The right-hand side of Fig. 1 similarly shows the spectrum of the perturbed Toeplitz matrix given by $p= p_0 + p_1$ where $p_1$ is as above and

$$\begin{aligned} p_0(1/\zeta ) = -4\zeta ^{1} -2i \zeta ^{2}+ 2i\zeta ^{-1}-\zeta ^{-2}+2\zeta ^{-3}. \end{aligned}$$

(1.18)

In our previous work [15], we studied Toeplitz matrices with a finite number of bands, given by symbols of the form

$$\begin{aligned} p(\tau ) = \sum _{j=-N_-}^{N_+} a_j \tau ^j, \quad a_{-N_-}, a_{-N_-+1},\dots , a_{N_+} \in {\mathbf {C}},\ a_{\pm N_\pm }\ne 0. \end{aligned}$$

(1.19)

In this case, the symbols are analytic functions on $S^1$ and we are able to provide in [15, Theorem 2.1] a version of Theorem 1.1 with a much sharper remainder estimate. See also [13, 14], concerning the special cases of large Jordan block matrices $p(\tau ) = \tau ^{-1}$ and large bi-diagonal matrices $p(\tau ) = a\tau + b\tau ^{-1}$, $a,b\in {\mathbf {C}}$. However, Fig. 1 suggests that one could hope for a better remainder estimate in Theorem 1.1 as well.

Fig. 1

The left-hand side shows the spectrum of the perturbed Toeplitz matrix with symbol defined in (1.16), (1.17) and the right-hand side shows the spectrum of the perturbed Toeplitz matrix with symbol defined in (1.18), (1.17). The red line shows the symbol curve $p(S^1)$

Theorems 1.1 and 1.2 can be extended to allow for coupling constants with $\delta _1 >1/2$. Furthermore, one can allow for much more general perturbations, for example perturbations given by random matrices whose entries are iid copies of a centered random variables with bounded fourth moment. However, both extensions require some extra work which we will present in a follow-up paper.

1.3 Convergence of the empirical measure and related results

An alternative way to study the limiting distribution of the eigenvalues of $P_N^{\delta }$, up to errors of o(N), is to study the empirical measure of eigenvalues, defined by

$$\begin{aligned} \xi _N {\mathop {=}\limits ^{\mathrm {def}}}\frac{1}{N}\sum _{\lambda \in \mathrm {Spec}( P_N^{\delta })} \delta _{\lambda } \end{aligned}$$

(1.20)

where the eigenvalues are counted including multiplicity and $\delta _{\lambda }$ denotes the Dirac measure at $\lambda \in {\mathbf {C}}$. For any positive monotonically increasing function $\phi$ on the positive reals and random variable X, Markov’s inequality states that $\mathbb {P} [ |X| \ge \varepsilon ] \le \phi (\varepsilon )^{-1} \mathbb {E}[ \phi (|X|)]$, assuming that the last quantity is finite. Using $\phi (x) = \mathrm {e}^{x/C}$, $x\ge 0$, with a sufficiently large $C>0$, yields that for $C_1>0$ large enough

$$\begin{aligned} { \mathbb {P} [ \Vert Q_{\omega }\Vert _{\mathrm {HS}} \le C_1 N ] \ge 1 - \mathrm {e}^{-N^2}.} \end{aligned}$$

(1.21)

If $\delta \le N^{-1}$, then (1.5) and the Borel–Cantelli Theorem shows that, almost surely, $\xi _N$ has compact support for $N>0$ sufficiently large.

We will show that, almost surely, $\xi _N$ converges weakly to the push-forward of the uniform measure on $S^1$ by the symbol p.

Theorem 1.2

Let $\delta _0\in ]0,1[$, let $\delta _1 >3$ and let p be as in (1.4). If (1.13) holds, i.e.,

$$\begin{aligned} \mathrm {e}^{- N^{\delta _0} } \le \delta \ll N^{-\delta _1} \end{aligned}$$

then, almost surely,

$$\begin{aligned} \xi _N \rightharpoonup p_*\left( \frac{1}{2\pi } L_{S^1}\right) , \quad N\rightarrow \infty , \end{aligned}$$

(1.22)

weakly, where $L_{S^1}$ denotes the Lebesgue measure on $S^1$.

This result generalizes [15, Corollary 2.2] from the case of Toeplitz matrices with a finite number of bands to the general case (1.4).

Similar results to Theorem 1.2 have been proven in various settings. In [2, 3], the authors consider the special case of band Toeplitz matrices, i.e. $P_N$ with p as in (1.19). In this case, they show that the convergence (1.22) holds weakly in probability for a coupling constant $\delta = N^{-\gamma }$, with $\gamma >1/2$. Furthermore, they prove a version of this theorem for Toeplitz matrices with non-constant coefficients in the bands, see [2, Theorem 1.3, Theorem 4.1]. They follow a different approach than we do: They compute directly the $\log |\det {\mathcal {M}}_N -z|$ by relating it to $\log |\det M_N(z)|$, where $M_N(z)$ is a truncation of $M_N -z$, where the smallest singular values of $M_N-z$ have been excluded. The level of truncation, however, depends on the strength of the coupling constant and it necessitates a very detailed analysis of the small singular values of $M_N -z$.

In the earlier work [9], the authors prove that the convergence (1.22) holds weakly in probability for the Jordan bloc matrix $P_N$ with $p(\tau ) = \tau ^{-1}$ (1.4) and a perturbation given by a complex Gaussian random matrix whose entries are independent complex Gaussian random variables whose variances vanish (not necessarily at the same speed) polynomially fast, with minimal decay of order $N^{-1/2+}$. See also [6] for a related result.

In [20], using a replacement principle developed in [18], it was shown that the result of [9] holds for perturbations given by complex random matrices whose entries are independent and identically distributed random complex random variables with expectation 0 and variance 1 and a coupling constant $\delta = N^{-\gamma }$, with $\gamma >2$.

1.4 Notation

We will frequently use the following notation: When we write $a \ll b$, we mean that $Ca \le b$ for some sufficiently large constant $C>0$. The notation $f = {\mathcal {O}}(N)$ means that there exists a constant $C>0$ (independent of N) such that $|f| \le C N$. When we want to emphasize that the constant $C>0$ depends on some parameter k, then we write $C_k$, or with the above notation ${\mathcal {O}}_k(N)$.

2 The unperturbed operator

We are interested in the Toeplitz matrix

$$\begin{aligned} P_N=1_{[0,N[}p(\tau )1_{[0,N[}: \ell ^2([0,N[)\rightarrow \ell ^2([0,N[) \end{aligned}$$

(2.1)

for $1\ll N<\infty$, see also (1.7). Here we identify $\ell ^2([0,N[)$ with the space $\ell ^2_{[0,N[}(\mathbf{Z})$ of functions $u\in \ell ^2(\mathbf{Z})$ with support in [0, N[. Sometimes we write $P_N=P_{[0,N[}$ and identify $P_N$ with $P_{I}=1_Ip(\tau )1_I$ where $I=I_N$ is any interval in $\mathbf{Z}$ of “length” $|I|=\# I=N$.

Let $P_\mathbf{N}=P_{[0,+\infty [}$ and let $P_{\mathbf{Z}/{\widetilde{N}}{} \mathbf{Z}}$ denote $P=p(\tau )$, acting on $\ell ^2(\mathbf{Z}/{\widetilde{N}}{} \mathbf{Z})$ which we identify with the space of ${\widetilde{N}}$-periodic functions on $\mathbf{Z}$. Here ${\widetilde{N}}\ge 1$. Using the discrete Fourier transform, we see that

$$\begin{aligned} \sigma (P_{\mathbf{Z}/{\widetilde{N}}{} \mathbf{Z}})=p(S_{{\widetilde{N}}}), \end{aligned}$$

(2.2)

where $S_{{\widetilde{N}}}$ is the dual of $\mathbf{Z}/{\widetilde{N}}{\mathbf {Z}}$ and given by

$$\begin{aligned} S_{{\widetilde{N}}}=\{ e^{ik2\pi /{\widetilde{N}}};\, 0\le k<{\widetilde{N}} \}. \end{aligned}$$

Let

$$\begin{aligned} p_N(\tau )=\sum _{|\nu |\le N}a_\nu \tau ^\nu =\sum _{\nu \in \mathbf{Z}}a_\nu ^N \tau ^\nu ,\ \ a_\nu ^N=1_{[-N,N]}(\nu )a_\nu . \end{aligned}$$

(2.3)

and notice that

$$\begin{aligned} P_N=1_{[0,N[}\, p_N(\tau )1_{[0,N[}. \end{aligned}$$

(2.4)

We now consider [0, N[ as an interval $I_N$ in $\mathbf{Z}/{\widetilde{N}}{} \mathbf{Z}$, ${\widetilde{N}}=N+M$, where $M\in \{1,2,.. \}$ will be fixed and independent of N. The matrix of $P_N$, indexed over $I_N\times I_N$ is then given by

$$\begin{aligned} P_N(j,k)=a^N_{{\widetilde{j}}-{\widetilde{k}}},\ j,k\in I_N\subset \mathbf{Z}/{\widetilde{N}}Z, \end{aligned}$$

(2.5)

where ${\widetilde{j}},{\widetilde{k}}\in \mathbf{Z}$ are the preimages of j, k under the projection $\mathbf{Z}\rightarrow \mathbf{Z} /{\widetilde{N}}\mathbf{Z}$ that belong to the interval $[0,N[\subset \mathbf{Z}$.

Let ${\widetilde{P}}_N$ be given by the formula (2.4), with the difference that we now view $\tau$ as a translation on $\ell ^2(\mathbf{Z}/{\widetilde{N}}{} \mathbf{Z})$:

$$\begin{aligned} {\widetilde{P}}_N=1_{I_N}p_N(\tau )1_{I_N}. \end{aligned}$$

(2.6)

The matrix of ${\widetilde{P}}_N$ is given by

$$\begin{aligned} {\widetilde{P}}_N(j,k)=\sum _{\nu \in \mathbf{Z},\atop \nu \equiv j-k\, \mathrm {mod}\,{\widetilde{N}}{} \mathbf{Z}}a_\nu ^N,\quad j,k\in I_N. \end{aligned}$$

(2.7)

Alternatively, if we let ${\widetilde{j}},{\widetilde{k}}$ be the preimages in [0, N[ of $j,k\in I_N$, then

$$\begin{aligned} {\widetilde{P}}_N(j,k)=\sum _{{\widehat{j}}\in \mathbf{Z};\ {\widehat{j}}\equiv {\widetilde{j}}\,\mathrm {mod}\,{\widetilde{N}}\mathbf{Z}}a^N_{{\widehat{j}}-{\widetilde{k}}}. \end{aligned}$$

(2.8)

Recall that the terms in (2.7), (2.8) with $|\nu |>N$ or $|{\widehat{j}}-{\widetilde{k}}|>N$ do vanish. This implies that with ${\widetilde{j}}$, ${\widetilde{k}}$ as in (2.8),

$$\begin{aligned} {\widetilde{P}}_N(j,k)-P_N(j,k)=a^N_{{\widetilde{j}}-{\widetilde{N}}-{\widetilde{k}}}+a^N_{{\widetilde{j}}+{\widetilde{N}}-{\widetilde{k}}}. \end{aligned}$$

(2.9)

Here

$$\begin{aligned} \begin{aligned}&{\widetilde{j}}-{\widetilde{N}}\in [0,N[-{\widetilde{N}}=[-{\widetilde{N}},N-{\widetilde{N}}[=[-N-M,-M[,\\&{\widetilde{j}}+{\widetilde{N}}\in [0,N[+{\widetilde{N}}=[{\widetilde{N}},N+{\widetilde{N}}[=[N+M,2N+M[. \end{aligned} \end{aligned}$$

Since ${\widetilde{k}}\in [0,N[$, we have for the first term in (2.9) that $|{\widetilde{j}}-{\widetilde{N}}-{\widetilde{k}}|={\widetilde{k}}+M+(N-{\widetilde{j}})$ with nonnegative terms in the last sum. Similarly for the second term in (2.9), we have $|{\widetilde{j}}+{\widetilde{N}}-{\widetilde{k}}|={\widetilde{j}}+M+(N-{\widetilde{k}})$ where the terms in the last sum are all $\ge 0$.

It follows that the trace class norm of $P_N-{\widetilde{P}}_N$ is bounded from above by

$$\begin{aligned} \begin{aligned}&\sum _{j<-M,\ k\ge 0}|a_{j-k}| +\sum _{j\ge N+M,\ k<N }|a_{j-k}| \\&\quad =\sum _{k\ge 0,\ j\le -M}|a_{j-k}|+\sum _{k\le 0,\ j\ge M}|a_{j-k}|\\&\quad \le 2C\sum _{k=0}^\infty \sum _{j=0}^\infty m(M+k+j) =2C \sum _{k=0}^\infty (k+1)m(M+k)\\&\quad =2C\sum _{k=M}^\infty (k+1-M)m(k). \end{aligned} \end{aligned}$$

By (1.2), it follows that

$$\begin{aligned} \Vert P_N-{\widetilde{P}}_N\Vert _{\mathrm {tr}}\le 2C\sum _{k=M}^{+\infty }(k+1-M)m(k)\rightarrow 0,\ M\rightarrow \infty , \end{aligned}$$

(2.10)

uniformly with respect to N. Here $\Vert A\Vert _{\mathrm {tr}} = \mathrm {tr} (A^*A)^{1/2}$ denotes the Schatten 1-norm for a trace class operator A.

Remark 2.1

To illustrate the difference between $P_N$ and ${\widetilde{P}}_N$ let $N\gg 1$, $M>0$ and consider the example of $p(\tau ) = \tau ^{n}$, so $a_{n} =1$, for some fixed $n\in {\mathbf {N}}$, and $a_{\nu }=0$ for $\nu \ne n$. Since $P_N(j,k) = a^N_{{\widetilde{j}}-{\widetilde{k}}}$, we see that

$$\begin{aligned} P_N(j,k) = {\left\{ \begin{array}{ll} 1, ~ {\widetilde{j}}=n+{\widetilde{k}}\\ 0, ~\text {else}. \end{array}\right. } \end{aligned}$$

In other words $P_N = (J^*)^n$ where J denotes the $N\times N$ Jordan block matrix. The matrix elements of ${\widetilde{P}}_N$ on the other hand are given by ${\widetilde{P}}_N(j,k) = a^N_{{\widetilde{j}}-{\widetilde{N}}-{\widetilde{k}}} + a^N_{{\widetilde{j}}-{\widetilde{k}}} +a^N_{{\widetilde{j}}+{\widetilde{N}}-{\widetilde{k}}}$, so

$$\begin{aligned} {\widetilde{P}}_N(j,k) = {\left\{ \begin{array}{ll} 1, ~ {\widetilde{j}}=n+{\widetilde{k}} \\ 1, ~ {\widetilde{j}} = n + {\widetilde{k}} - (N+M) \\ 0, ~\text {else}. \end{array}\right. } \end{aligned}$$

So ${\widetilde{P}}_N = P_N + J^{(N+M-n)}$, when $n\ge M$, otherwise ${\widetilde{P}}_N = P_N$.

3 A Grushin problem for $P_N-z$

Let $K\Subset {\mathbf {C}}$ be an open relatively compact set and let $z\in K$. Consider

$$\begin{aligned} J=[-M,0[,\ I_N=[0,N[ \end{aligned}$$

(3.1)

as subsets of $\mathbf{Z}/(N+M)\mathbf{Z}$ so that

$$\begin{aligned} J \cup I_N=\mathbf{Z}/(N+M)\mathbf{Z}=:\mathbf{Z}_{N+M} \end{aligned}$$

is a partition. Recall (2.3), (2.6) and consider

$$\begin{aligned} p_N(\tau )-z:\ell ^2(\mathbf{Z}_{N+M})\rightarrow \ell ^2(\mathbf{Z}_{N+M}) \end{aligned}$$

and write this operator as a $2\times 2$ matrix

$$\begin{aligned} p_N-z=\begin{pmatrix} {\widetilde{P}}_N-z &{}R_-\\ R_+&{} R_{+-}(z)\end{pmatrix}, \end{aligned}$$

(3.2)

induced by the orthogonal decomposition

$$\begin{aligned} \ell ^2(\mathbf{Z}_{N+M})=\ell ^2(I_N)\oplus \ell ^2(J). \end{aligned}$$

(3.3)

The operator $p_N(\tau )$ is normal and we know by (2.2) that its spectrum is

$$\begin{aligned} \sigma (p_N(\tau ))=p_N(S_{N+M}). \end{aligned}$$

(3.4)

Replacing ${\widetilde{P}}_N$ in (3.2) by $P_N$ (2.4), we put

$$\begin{aligned} {{\mathcal {P}}}_N(z)=\begin{pmatrix}P_N-z &{} R_- \\ R_+ &{}R_{+-}(z)\end{pmatrix}. \end{aligned}$$

(3.5)

Then, by (2.10),

$$\begin{aligned} \Vert {{\mathcal {P}}}_N(z)-(p_N-z)\Vert _{\mathrm {tr}}\le 2C\sum _{k=M}^{+\infty }(k+1-M)m(k)=:\epsilon (M) . \end{aligned}$$

(3.6)

If $\epsilon (M)<\mathrm {dist}\,(z,p_N(S_{N+M}))=:d_N(z)$, then ${{\mathcal {P}} }_N(z)$ is bijective and

$$\begin{aligned} \Vert {{\mathcal {P}}}_N(z)^{-1}\Vert \le \frac{1}{d_N(z)-\epsilon (M)}. \end{aligned}$$

(3.7)

Write,

$$\begin{aligned} \begin{aligned} {{\mathcal {P}}}_N(z)&=p_N(\tau )-z+{{\mathcal {P}}}_N(z)-(p_N(\tau )-z)\\&=(p_N(\tau )-z)\left( 1+(p_N(\tau )-z)^{-1}({{\mathcal {P}}}_N(z)-(p_N(\tau ) -z)) \right) . \end{aligned} \end{aligned}$$

Here,

$$\begin{aligned} \begin{aligned} \big | \det \big (1+(p_N(\tau )-z)^{-1}&({{\mathcal {P}}}_N(z)-(p_N(\tau )-z))\big ) \big |\\&\le \exp \Vert (p_N(\tau )-z)^{-1}({{\mathcal {P}}}_N(z)-(p_N(\tau )-z))\Vert _{\mathrm {tr}}\\&\le \exp (\epsilon (M)/d_N(z)), \end{aligned} \end{aligned}$$

so

$$\begin{aligned} |\det {{\mathcal {P}}}_N(z)|\le | \det (p_N(\tau )-z) |\, e^{\epsilon (M)/d_N(z)}. \end{aligned}$$

(3.8)

Similarly from

$$\begin{aligned} \begin{aligned} p_N(\tau )-z&={{\mathcal {P}}}_N(z)+p_N(\tau )-z-{{\mathcal {P}}}_N(z)\\&={{\mathcal {P}}}_N(z)\left( 1+{{\mathcal {P}}}_N(z)^{-1}(p_N(\tau )-z-{{\mathcal {P}}}_N(z) \right) , \end{aligned} \end{aligned}$$

we get

$$\begin{aligned} |\det (p_N(\tau )-z)|\le |\det {{\mathcal {P}}}_N(z)| e^{\frac{\epsilon (M)}{d_N(z)-\epsilon (M)}}. \end{aligned}$$

(3.9)

In analogy with (3.5), we write

$$\begin{aligned} {{\mathcal {P}}}_N(z)^{-1}={{\mathcal {E}}}_N(z)=\begin{pmatrix}E^N &{}E_+^N\\ E_-^N &{}E_{-+}^N \end{pmatrix} :\ \ell ^2(I_N)\oplus \ell ^2(J)\rightarrow \ell ^2(I_N)\oplus \ell ^2(J), \end{aligned}$$

(3.10)

where J, $I_N$ were defined in (3.1), still viewed as intervals in $\mathbf{Z}_{N+M}$. From (3.7), we get for the respective operator norms:

$$\begin{aligned} \Vert E^N\Vert , \Vert E^N_+\Vert , \Vert E^N_-\Vert , \Vert E^N_{-+}\Vert \le (d_N(z)-\epsilon (M))^{-1}. \end{aligned}$$

(3.11)

4 Second Grushin problem

We begin with a result, which is a generalization of [16, Proposition 3.4] to the case where $R_{+-}\ne 0$.

Proposition 4.1

Let ${{\mathcal {H}}}_1, {{\mathcal {H}}}_2, {{\mathcal {H}}}_{\pm }, {{\mathcal {S}}}_{\pm }$ be Banach spaces. If

$$\begin{aligned} {{\mathcal {P}}}=\begin{pmatrix}P &{}R_-\\ R_+ &{}R_{+-}\end{pmatrix}: {{\mathcal {H}}}_1\times {{\mathcal {H}}}_-\rightarrow {{\mathcal {H}}}_2\times {{\mathcal {H}}}_+ \end{aligned}$$

(4.1)

is bijective with bounded inverse

$$\begin{aligned} {{\mathcal {E}}}=\begin{pmatrix}E &{}E_+\\ E_- &{}E_{-+}\end{pmatrix}: {{\mathcal {H}}}_2\times {{\mathcal {H}}}_+\rightarrow {{\mathcal {H}}}_1\times {{\mathcal {H}}}_-, \end{aligned}$$

and if

$$\begin{aligned} {{\mathcal {S}}}=\begin{pmatrix}E_{-+} &{}S_-\\ S_+ &{} 0\end{pmatrix}: {{\mathcal {H}}}_+\times {{\mathcal {S}}}_-\rightarrow {{\mathcal {H}}}_-\times {{\mathcal {S}}}_+ \end{aligned}$$

(4.2)

is bijective with bounded inverse

$$\begin{aligned} {{\mathcal {F}}}=\begin{pmatrix}F &{}F_+\\ F_- &{}F_{-+}\end{pmatrix}: {{\mathcal {H}}}_-\times {{\mathcal {S}}}_+\rightarrow {{\mathcal {H}}}_+\times {{\mathcal {S}}}_-, \end{aligned}$$

then

$$\begin{aligned} {{\mathcal {T}}}=\begin{pmatrix} P &{}R_-S_-\\ S_+R_+ &{}S_+R_{+-}S_- \end{pmatrix}=: \begin{pmatrix}P &{}T_-\\ T_+ &{}T_{+-}\end{pmatrix} : {{\mathcal {H}}}_1\times {{\mathcal {S}}}_-\rightarrow {{\mathcal {H}}}_2\times {{\mathcal {S}}}_+ \end{aligned}$$

(4.3)

is bijective with bounded inverse

$$\begin{aligned} {{\mathcal {G}}}=\begin{pmatrix}G &{}G_+\\ G_- &{}G_{-+}\end{pmatrix}= \begin{pmatrix}E-E_+FE_- &{}E_+F_+\\ F_-E_- &{}-F_{-+}\end{pmatrix} :{{\mathcal {H}}}_2\times {{\mathcal {S}}}_+ \rightarrow {{\mathcal {H}}}_1\times {{\mathcal {S}}}_-. \end{aligned}$$

(4.4)

Proof

We can essentially follow the proof of [16, Proposition 3.4]. We need to solve

$$\begin{aligned} {\left\{ \begin{array}{ll} Pu+R_-S_-u_- = v \\ S_+R_+u + S_+R_{+-}S_-u_-=v_+. \end{array}\right. } \end{aligned}$$

(4.5)

Putting ${\widetilde{v}}_+=R_+u+R_{+-}S_-u_-$, the first equation is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} Pu+R_-S_-u_- = v \\ R_+u+R_{+-}S_-u_-={\widetilde{v}}_+, \end{array}\right. } \quad \text {i.e.} \quad {\mathcal {P}} \begin{pmatrix} u \\ S_-u_- \\ \end{pmatrix} = \begin{pmatrix} v \\ {\widetilde{v}}_+\\ \end{pmatrix}, \end{aligned}$$

and hence to

$$\begin{aligned} {\left\{ \begin{array}{ll} u = Ev+E_+{\widetilde{v}}_+ \\ S_-u_-=E_-v + E_{-+}{\widetilde{v}}_+. \end{array}\right. } \end{aligned}$$

(4.6)

Therefore, we can replace u by ${\widetilde{v}}_+$ and (4.5) is equivalent to

$$\begin{aligned} \begin{pmatrix} E_{-+} &{} S_- \\ S_+ &{} 0 \\ \end{pmatrix} \begin{pmatrix} {\widetilde{v}}_+ \\ -u_- \\ \end{pmatrix} = \begin{pmatrix} -E_-v \\ v_+ \\ \end{pmatrix} \end{aligned}$$

(4.7)

which can be solved by ${\mathcal {F}}$. Hence, (4.7) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} {\widetilde{v}}_+ = - FE_-v + F_+v_+ \\ -u_-= - F_-E_-v+F_{-+}v_+, \end{array}\right. } \end{aligned}$$

and (4.6) gives the unique solution of (4.5)

$$\begin{aligned} {\left\{ \begin{array}{ll} u = (E - E_+FE_-)v + E_+F_+v_+ \\ u_- = F_-E_-v - F_{-+}v_+. \end{array}\right. } \end{aligned}$$

$\square$

4.1 Grushin problem for $E_{-+}(z)$

We want to apply Proposition 4.1 to ${{\mathcal {P}}}={{\mathcal {P}}}(z)={{\mathcal {P}}}_N(z)$ in (3.5) with the inverse ${{\mathcal {E}}}={{\mathcal {E}}}_N(z)$ in (3.10), where we sometimes drop the index N. We begin by constructing an invertible Grushin problem for $E_{-+}$:

Let $0\le t_1 \le \dots \le t_M$ denote the singular values of $E_{-+}(z)$. Let $e_1, \dots , e_M$ denote an orthonormal basis of eigenvectors of $E_{-+}^*E_{-+}$ associated to the eigenvalues $t_1^2 \le \dots \le t_M^2$. Since $E_{-+}$ is a square matrix, we have that $\dim {\mathcal {N}}(E_{-+}(z)) = \dim {\mathcal {N}}(E_{-+}^*(z))$¹. Using the spectral decomposition $\ell ^2(J) = {\mathcal {N}}(E_{-+}^*E_{-+}) \oplus _{\perp } {\mathcal {R}}(E_{-+}^*E_{-+})$ together with the fact that ${\mathcal {N}}(E_{-+}^*E_{-+}) = {\mathcal {N}}(E_{-+})$ and ${\mathcal {R}}(E_{-+}^*) = {\mathcal {N}}(E_{-+})^{\perp }$, it follows that ${\mathcal {R}}(E_{-+}^*) = {\mathcal {R}}(E_{-+}^*E_{-+})$. Similarly, we get that ${\mathcal {R}}(E_{-+}) = {\mathcal {R}}(E_{-+}E_{-+}^*)$. One then easily checks that $E_{-+}: {\mathcal {R}}(E_{-+}^*E_{-+}) \rightarrow {\mathcal {R}}(E_{-+}E_{-+}^*)$ is a bijection. Similarly, $E_{-+}^*: {\mathcal {R}}(E_{-+}E_{-+}^*) \rightarrow {\mathcal {R}}(E_{-+}^*E_{-+})$ is a bijection. Let $f_1,\dots ,f_{M_0}$ denote an orthonormal basis of ${\mathcal {N}}(E_{-+}^*(z))$ and set

$$\begin{aligned} f_j = t_j^{-1} E_{-+} e_j , \quad j=M_0+1, \dots , M. \end{aligned}$$

Then, $f_1,\dots ,f_M$ is an orthonormal basis of $\ell ^2(J)$ comprised of eigenfunctions of $E_{-+}E_{-+}^*$ associated with the eigenvalues $t_1^2 \le \dots \le t_M^2$. In particular, $\sigma (E_{-+}E_{-+}^*) = \sigma (E_{-+}^*E_{-+})$ and

$$\begin{aligned} E_{-+} e_j = t_j f_j, \quad E_{-+}^* f_j = t_je_j, \quad j=1, \dots , M. \end{aligned}$$

(4.8)

Let $0\le t_1\le ...\le t_k$ be the singular values of $E_{-+}(z)$ in the interval $[0,\tau ]$ for $\tau >0$ small. Let ${{\mathcal {S}}}_+,\, {{\mathcal {S}}}_-\subset \ell ^2(J)$ be the corresponding (sums of) spectral subspaces for $E_{-+}^*E_{-+}$ and $E_{-+}E_{-+}^*$, respectively, corresponding to the eigenvalues $t_1^2\le t_2^2\le ... \le t_k^2$ in $[0,\tau ^2]$. Using (4.8), we see that the restrictions (denoted by the same symbols)

$$\begin{aligned} E_{-+}:{{\mathcal {S}}}_+\rightarrow {{\mathcal {S}}}_-,\ E_{-+}^*:{{\mathcal {S}}}_-\rightarrow {{\mathcal {S}}}_+, \end{aligned}$$

have norms $\le \tau$. Also,

$$\begin{aligned} E_{-+}:{{\mathcal {S}}}_+^\perp \rightarrow {{\mathcal {S}}}_-^\perp ,\ E_{-+}^*: {{\mathcal {S}} }_-^\perp \rightarrow {{\mathcal {S}}}_+^\perp \end{aligned}$$

(4.9)

are bijective with inverses of norm $\le 1/\tau$.

Let $S_+$ be the orthogonal projection onto ${{\mathcal {S}}}_+$, viewed as an operator $\ell ^2(J)\rightarrow {{\mathcal {S}}}_+$, whose adjoint is the inclusion map ${{\mathcal {S}}}_+\rightarrow \ell ^2(J)$. Let $S_-:{{\mathcal {S}} }_-\rightarrow \ell ^2(J)$ be the inclusion map. Let ${{\mathcal {S}}}$ be the operator in (4.2) with ${{\mathcal {H}}}_\pm =\ell ^2(J)$, corresponding to the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} E_{-+}g+S_-g_-=h\in \ell ^2(J),\\ S_+g=h_+\in {{\mathcal {S}}}_+, \end{array}\right. } \end{aligned}$$

(4.10)

for the unknowns $g\in \ell ^2(J)$, $g_-\in {{\mathcal {S}}}_-$. Using the orthogonal decompositions,

$$\begin{aligned} \ell ^2(J)={{\mathcal {S}}}_+^\perp \oplus {{\mathcal {S}}}_+,\ \ell ^2(J)={{\mathcal {S}} }_-^\perp \oplus {{\mathcal {S}}}_-, \end{aligned}$$

we write $g=\sum _1^kg_je_j + g^{\perp }$ and $h=\sum _1^kh_jf_j + h^{\perp }$. Then, (4.10) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} g^{\perp }=(E_{-+})^{-1}h^{\perp }\\ \begin{pmatrix}g_j\\ g_-^j\end{pmatrix} = \begin{pmatrix}0 &{}1\\ 1 &{} - t_j\end{pmatrix} \begin{pmatrix}h_j \\ h_+^j\end{pmatrix}, ~~ j=1,\dots ,M, \end{array}\right. } \end{aligned}$$

where we also used that $g_-=\sum _1^kg_-^jf_j$ and $h_+=\sum _1^kh_+^je_j$. It follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} g = (E_{-+})^{-1}h^{\perp } + \sum _1^k h_+^je_j \\ g_- = \sum _1^k h^j f_j - \sum _1^k t_j h_+^jf_j. \end{array}\right. } \end{aligned}$$

(4.11)

Hence, the unique solution to (4.10) is given by

$$\begin{aligned} \begin{pmatrix}g\\ g_-\end{pmatrix}={{\mathcal {F}}}\begin{pmatrix}h\\ h_+\end{pmatrix} = \begin{pmatrix}F &{}F_+\\ F_- &{}F_{-+}\end{pmatrix} \begin{pmatrix}h \\ h_+\end{pmatrix}, \end{aligned}$$

(4.12)

where

$$\begin{aligned} \begin{aligned} F&=E_{-+}^{-1}\Pi _{{{\mathcal {S}}}_-^\perp },\ \ F_+=S_+^*,\\ F_-&=S_-^*,\ \ F_{-+}=-{{E_{-+}}_\vert }_{{{\mathcal {S}}}_+}:\, {{\mathcal {S}}}_+\rightarrow {{\mathcal {S}}}_- . \end{aligned} \end{aligned}$$

(4.13)

Here $\Pi _{B}$ denotes the orthogonal projection onto the subspace B of A, viewed as a self-adjoint operator $A\rightarrow A$. Notice that $F = \Pi _{{\mathcal {S}}_+^{\perp }} F$ and that

$$\begin{aligned} F_{-+} = - \sum _1^k t_j f_j \circ e_j^*, \quad \hbox {i.e. }F_{-+}u=-\sum _1^k t_j(u|e_j)f_j. \end{aligned}$$

(4.14)

Using as well (4.9), we have

$$\begin{aligned} \Vert F\Vert \le 1/\tau ,\ \Vert F_+\Vert , \Vert F_-\Vert \le 1, \Vert F_{-+}\Vert \le \tau . \end{aligned}$$

(4.15)

4.2 Composing the Grushin problems

From now on we assume that

$$\begin{aligned} 0<\alpha \ll 1,\ \ \epsilon (M)\le \alpha /2, \end{aligned}$$

(4.16)

and the estimates below will be uniformly valid for $z\in K\setminus \gamma _\alpha$, $N\gg 1$, where K is some fixed relatively compact open set in $\mathbf{C}$ and

$$\begin{aligned} \gamma _\alpha =\{ z\in \mathbf{C};\, \mathrm {dist}\,(z,\gamma )\le \alpha \},\ \ \gamma =p(S^1). \end{aligned}$$

(4.17)

We apply Proposition 4.1 to ${{\mathcal {P}}_N}$ in (3.5) with the inverse ${\mathcal {E}}_N$ in (3.10), and to ${\mathcal {S}}$ defined in (4.10) with inverse in ${\mathcal {F}}$ in (4.12). Let $z\in K\backslash \gamma _\alpha$, then

$$\begin{aligned} {{\mathcal {T}}_N}=\begin{pmatrix} P_N-z &{}R_-S_-\\ S_+R_+ &{}S_+R_{+-}S_- \end{pmatrix} = \begin{pmatrix}P_N-z &{}T_-\\ T_+ &{}T_{+-}\end{pmatrix} : L^2(I_N)\times {{\mathcal {S}}}_-\rightarrow L^2(I_N)\times {{\mathcal {S}}}_+, \end{aligned}$$

(4.18)

defined as in (4.3), is bijective with the bounded inverse

$$\begin{aligned} {{\mathcal {G}}_N}=\begin{pmatrix}G^N &{}G_+^N\\ G_-^N &{}G_{-+}^N\end{pmatrix}= \begin{pmatrix}E^N-E_+^NFE_-^N &{}E_+^NF_+\\ F_-E_-^N &{}-F_{-+}\end{pmatrix}. \end{aligned}$$

(4.19)

Since $S_\pm$ have norms $\le 1$, we get

$$\begin{aligned} \Vert T_\pm \Vert \le \Vert R_\pm \Vert = {\mathcal {O}}(1), \end{aligned}$$

(4.20)

uniformly in N, $\alpha$ and $z\in K$. Also, since the norms of $E^N,E_+^N, E_-^N$ are $\le 2/\alpha$ (uniformly as $N\rightarrow \infty$) by (3.11), we get from (4.4), (4.15), that

$$\begin{aligned} \Vert G^N\Vert \le \frac{2}{\alpha }+\frac{4}{\tau \alpha ^2},\ \Vert G^N_{-+}\Vert \le \tau ,\ \Vert G^N_\pm \Vert \le \frac{2}{\alpha }. \end{aligned}$$

(4.21)

Proposition 4.2

Let $K\Subset {\mathbf {C}}$ be an open relatively compact set, let $z\in K\backslash \gamma _\alpha$, and let $\tau >0$ be as in the definition of the Grushin problem (4.10). Then, for $\tau >0$ small enough, depending only on K, we have that $G_+^N$ is injective and $G_-^N$ is surjective. Moreover, there exists a constant $C>0$, depending only on K, such that for all $z\in K\backslash \gamma _{\alpha }$ the singular values $s_j^+$ of $G_+^N$, and $s_j^-$ of $(G_-^N)^*$ satisfy

$$\begin{aligned} \frac{1}{C}\le s_j^\pm \le \frac{2}{\alpha }, \quad 1 \le j \le k(z) =\mathrm {rank}(G^N_\pm ). \end{aligned}$$

(4.22)

Proof

To ease the notation we will omit the sub/superscript N. We begin with the injectivity of $G_+$. From

$$\begin{aligned} \begin{pmatrix}P-z &{}T_-\\ T_+ &{}T_{+-}\end{pmatrix} \begin{pmatrix}G &{}G_+\\ G_- &{}G_{-+}\end{pmatrix}=1, \end{aligned}$$

(4.23)

we have $T_+G_++T_{+-}G_{-+}=1$ which we write $T_+G_+=1-T_{+-}G_{-+}$. Here

$$\begin{aligned} \Vert T_{+-}G_{-+}\Vert \le \Vert R_{+-}\Vert \tau ={{\mathcal {O}}}(\tau ), \end{aligned}$$

where we used that $\Vert R_{+-} \Vert \le \Vert p(\tau )-z\Vert = {\mathcal {O}}(1)\Vert m\Vert _{\ell ^1}$, thus the error term above only depends on K. Choosing $\tau >0$ small enough, depending on K but not on N, we get that $\Vert T_{+-}G_{+-}\Vert \le 1/2$. Then, $1-T_{+-}G_{-+}$ is bijective with $\Vert (1-T_{+-}G_{-+})^{-1}\Vert \le 2$ and $G_+$ has the left inverse

$$\begin{aligned} (1-T_{+-}G_{-+})^{-1}T_+ \end{aligned}$$

(4.24)

of norm $\le 2\Vert R_+\Vert ={{\mathcal {O}}}(1)$, depending only on K.

Now we turn to the surjectivity of $G_-$. From

$$\begin{aligned} \begin{pmatrix}G &{} G_+\\ G_-&{} G_{-+}\end{pmatrix} \begin{pmatrix}P-z &{}T_-\\ T_+ &{}T_{+-}\end{pmatrix}= 1, \end{aligned}$$

we get

$$\begin{aligned} \begin{pmatrix}(P-z)^* &{}T_+^*\\ T_-^* &{}T_{+-}^*\end{pmatrix} \begin{pmatrix}G^* &{} G_-^*\\ G_+^*&{} G_{-+}^*\end{pmatrix} = 1, \end{aligned}$$

and as above we then see that $G_-^*$ has the left inverse $(1-T_{+-}^*G_{-+}^*)^{-1}T_-^*$. Hence, $G_-$ has the right inverse

$$\begin{aligned} T_-(1-G_{-+}T_{+-})^{-1}, \end{aligned}$$

(4.25)

of norm $\le 2\Vert R_-\Vert = {\mathcal {O}}(1)$, depending only on K.

The lower bound on the singular values follows from the estimates on the left inverses of $G_+$ and $G_-^*$, and the upper bound follows from (4.21). $\square$

5 Determinants

We continue working under the assumptions (4.16), (4.17). Additionally, we fix $\tau >0$ sufficiently small (depending only on the fixed relatively compact set $K\Subset {\mathbf {C}}$) so that $\Vert T_{+-}G_{-+}\Vert$, $\Vert G_{-+}T_{+-}\Vert$ (both $={{\mathcal {O}}}(\tau )$) are $\le 1/2$, which implies that $G_+$ is injective and $G_+$ is surjective, see Proposition 4.2. Here, we sometimes drop the sub-/superscript N.

From now on, we will work with $z\in K\backslash \gamma _{\alpha }$. The constructions and estimates in Sect. 3 are then uniform in z for $N\gg 1$ and the same holds for those in Sect. 4.

Remark 5.1

To get the o(N) error term in Theorem 1.1, we will take $\alpha >0$ arbitrarily small, and $M>1$ large enough (but fixed) so that $\varepsilon (M) \le \alpha /2$, see (2.10) as well as $N>1$ sufficiently large. In the following, the error terms will typically depend on $\alpha$, although we will not always denote this explicitly, however, they will be uniform in $N>1$ and in $z\in K\backslash \gamma _{\alpha }$.

5.1 The unperturbed operator

For $z\in K\setminus \gamma _\alpha$, we have $d_N(z)\ge \alpha$ and (3.8), (3.9) give

$$\begin{aligned} | \det {{\mathcal {P}}}_N(z)|\le & {} e^{\epsilon (M)/\alpha }|\det (p_N(\tau )-z)| , \end{aligned}$$

(5.1)

$$\begin{aligned} |\det (p_N(\tau )-z)|\le & {} e^{2\epsilon (M)/\alpha } | \det {{\mathcal {P}}}_N(z)|, \end{aligned}$$

(5.2)

where we also used that

$$\begin{aligned} \frac{\epsilon (M)}{d_N(z)-\epsilon (M)}\le \frac{\epsilon (M)}{\alpha -\epsilon (M)}\le \frac{2\epsilon (M)}{\alpha }, \end{aligned}$$

by the second inequality in (4.16). Recall here that $p_N(\tau )$ acts on $\ell ^2(\mathbf{Z}/{\widetilde{N}}{} \mathbf{Z})$, ${\widetilde{N}}=N+M$.

By the Schur complement formula, we have

$$\begin{aligned} \begin{aligned} \det (P_N-z)&= \det {{\mathcal {P}}}_N(z)\, \det E_{-+}(z),\\ \det (P_N-z)&= \det {{\mathcal {T}}}_N(z)\, \det G_{-+}(z), \end{aligned} \end{aligned}$$

(5.3)

so

$$\begin{aligned} \frac{\det {{\mathcal {T}}_N}}{\det {{\mathcal {P}}_N}}=\frac{\det E_{-+}}{\det G_{-+}}. \end{aligned}$$

(5.4)

Recall from Sect. 4.1 that the singular values of $E_{-+}$ are denoted by $0\le t_1\le t_2\le \dots \le t_M$ and that those of $G_{-+}$ are $t_1,...,t_k$, where $k=k(z,N)$ is determined by the condition $t_k\le \tau <t_{k+1}$. Thus

$$\begin{aligned} \left| \frac{\det E_{-+}}{\det G_{-+}} \right| =\prod _{k+1}^M t_j \end{aligned}$$

and we get (since $\tau \ll 1$)

$$\begin{aligned} \tau ^M\le \left| \frac{\det E_{-+}}{\det G_{-+}} \right| \le \left( \frac{2}{\alpha } \right) ^M. \end{aligned}$$

Since $\tau >0$ is small, but fixed depending only on K, we have uniformly for $z\in K\setminus \gamma _\alpha$, $N\gg 1$:

$$\begin{aligned} \left| \ln |\det E_{-+}|-\ln |\det G_{-+}|\right| \le {\mathcal {O}}(1) \end{aligned}$$

(5.5)

and by (5.4)

$$\begin{aligned} \left| \ln |\det {{\mathcal {T}}_N}|-\ln |\det {{\mathcal {P}}_N}|\right| \le {\mathcal {O}}(1). \end{aligned}$$

(5.6)

From (5.1), (5.2), we get

$$\begin{aligned} \left| \ln |\det {{\mathcal {P}}_N}|-\ln |\det (p_N(\tau )-z)|\right| \le {\mathcal {O}}(1), \end{aligned}$$

(5.7)

hence

$$\begin{aligned} \left| \ln |\det {{\mathcal {T}}_N}|-\ln |\det (p_N(\tau )-z)|\right| \le {\mathcal {O}}(1). \end{aligned}$$

(5.8)

5.2 The perturbed operator

We next extend the estimates to the case of a perturbed operator

$$\begin{aligned} P_N^\delta =P_N+\delta Q, \end{aligned}$$

(5.9)

where $Q:\ell ^2(I_N)\rightarrow \ell ^2(I_N)$ satisfies

$$\begin{aligned} \delta \Vert Q\Vert \ll 1. \end{aligned}$$

(5.10)

Proposition 5.2

Let $K\Subset {\mathbf {C}}$ be an open relatively compact set and suppose that (4.16) hold. Recall (4.17) and (3.5), if $\delta \Vert Q\Vert \alpha ^{-1} \ll 1$, then for all $z\in K\backslash \gamma _{\alpha }$

$$\begin{aligned} {\mathcal {P}}_N^\delta =\begin{pmatrix}P_N^\delta -z &{}R_-\\ R_+ &{}R_{+-}(z)\end{pmatrix} ={{\mathcal {P}}}+\begin{pmatrix}\delta Q &{}0\\ 0 &{}0\end{pmatrix}, \end{aligned}$$

(5.11)

is bijective with bounded inverse

$$\begin{aligned} {\mathcal {E}}_N^\delta =\begin{pmatrix}E^\delta &{}E^\delta _+\\ E^\delta _- &{}E^\delta _{+-}\end{pmatrix}. \end{aligned}$$

(5.12)

Recall (4.18), if $\delta \Vert Q\Vert \alpha ^{-2} \ll 1$, then for all $z\in K\backslash \gamma _{\alpha }$

$$\begin{aligned} {\mathcal {T}}_N^\delta =\begin{pmatrix}P_N^\delta -z &{}T_-\\ T_+ &{}T_{+-}\end{pmatrix} ={{\mathcal {T}}_N}+\begin{pmatrix}\delta Q &{}0\\ 0 &{}0\end{pmatrix}. \end{aligned}$$

(5.13)

is bijective with bounded inverse

$$\begin{aligned} {\mathcal {G}}_N^\delta =\begin{pmatrix}G^\delta &{}G^\delta _+\\ G^\delta _- &{}G^\delta _{+-}\end{pmatrix}, \end{aligned}$$

(5.14)

with

$$\begin{aligned} G_{-+}^\delta (z)=G_{-+}-G_-\delta Q(1+G\delta Q)^{-1}G_+. \end{aligned}$$

(5.15)

Moreover, $\Vert {\mathcal {E}}_N^\delta \Vert \le 4/\alpha$, $\Vert {\mathcal {G}}_N^\delta \Vert \le {\mathcal {O}}(\alpha ^{-2})$, uniformly in $z\in K\backslash \gamma _{\alpha }$ and $N>1$.

Proof

We sometimes drop the subscript N. By (3.10),

$$\begin{aligned} {\mathcal {P}}^\delta {\mathcal {E}} = 1 + \begin{pmatrix}\delta Q E&{}\delta Q E_+\\ 0 &{}0\end{pmatrix}. \end{aligned}$$

By (3.11), it follows that $\Vert E\Vert \le 2/\alpha$, so if $\delta \Vert Q\Vert \alpha ^{-1} \ll 1$, then by Neumann series argument, the above is invertible and

$$\begin{aligned} {\mathcal {E}} \left( 1 + \begin{pmatrix}\delta Q E&{}\delta Q E_+\\ 0 &{}0\end{pmatrix} \right) ^{-1} \end{aligned}$$

(5.16)

is a right inverse of ${\mathcal {P}}^\delta$, of norm $\le 2 \Vert {\mathcal {E}} \Vert \le 4/\alpha$. Since ${\mathcal {P}}^\delta$ is Fredholm of index 0, this is also a left inverse.

The proof for ${\mathcal {T}}_N^\delta$ is similar, using that $\Vert G\Vert ={\mathcal {O}}(\alpha ^{-2})$ by (4.21), since $\tau >0$ is fixed. Finally, the expression (5.15) follows easily from expanding (5.16). $\square$

We drop the subscript N until further notice. By (5.13), we have

$$\begin{aligned} \Vert {{\mathcal {T}}}-{{\mathcal {T}}}^\delta \Vert _{\mathrm {tr}}\le \delta \Vert Q\Vert _{\mathrm {tr}}. \end{aligned}$$

(5.17)

Recall from the text after (2.10) the definition of the Schatten norm $\Vert \cdot \Vert _{\mathrm {tr}}$. Write,

$$\begin{aligned} {{\mathcal {T}}}^\delta ={{\mathcal {T}}}(1-{{\mathcal {T}}}^{-1}({{\mathcal {T}}}-{{\mathcal {T}}}^\delta )), \end{aligned}$$

where

$$\begin{aligned} \Vert {{\mathcal {T}}}^{-1}({{\mathcal {T}}}-{{\mathcal {T}}}^\delta )\Vert _{\mathrm {tr}}\le {{\mathcal {O}} }(\delta )\Vert Q\Vert _{\mathrm {tr}}. \end{aligned}$$

(5.18)

Here, we used that $\Vert {{\mathcal {T}}}^{-1}\Vert = \Vert {\mathcal {G}} \Vert = {\mathcal {O}}(1)$, by (4.21) and the fact that $\tau >0$ is fixed. We recall that the estimates here depend on $\alpha$, yet are uniform in $z\in K\backslash \gamma _{\alpha }$ and $N>1$. It follows that

$$\begin{aligned} | \det (1-{{\mathcal {T}}}^{-1}({{\mathcal {T}}}-{{\mathcal {T}}}^\delta ))|\le \exp \Vert {{\mathcal {T}} }^{-1}({{\mathcal {T}}}-{{\mathcal {T}}}^\delta )\Vert _{\mathrm {tr}}\le \exp ({{\mathcal {O}} }(\delta )\Vert Q\Vert _{\mathrm {tr}}), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} |\det {{\mathcal {T}}}_\delta |&=|\det {{\mathcal {T}}}| |\det (1-{{\mathcal {T}} }^{-1}({{\mathcal {T}}}- {{\mathcal {T}}}^\delta ))|\\&\le \exp ({{\mathcal {O}}}(\delta )\Vert Q\Vert _{\mathrm {tr}})|\det {{\mathcal {T}}}|. \end{aligned} \end{aligned}$$

(5.19)

Similarly from the identity

$$\begin{aligned} {{\mathcal {T}}} ={{\mathcal {T}}}^\delta (1-{{\mathcal {T}}}_\delta ^{-1}({{\mathcal {T}}}^\delta -{{\mathcal {T}}} )), \end{aligned}$$

(putting $\delta$ as a subscript whenever convenient), we get

$$\begin{aligned} |\det {{\mathcal {T}}} |\le \exp ({{\mathcal {O}}}(\delta )\Vert Q\Vert _{\mathrm {tr}})|\det {{\mathcal {T}}}^\delta |, \end{aligned}$$

(5.20)

thus

$$\begin{aligned} \left| \ln |\det {{\mathcal {T}}}_\delta |-\ln |{{\mathcal {T}}}| \right| \le {{\mathcal {O}} }(\delta )\Vert Q\Vert _{\mathrm {tr}}. \end{aligned}$$

(5.21)

Assume that (uniformly in $N>1$ and independently of $\alpha$)

$$\begin{aligned} \delta \Vert Q\Vert _{\mathrm {tr}}\le {{\mathcal {O}}}(1) \end{aligned}$$

(5.22)

and recall (5.8). Then,

$$\begin{aligned} \left| \ln |\det {{\mathcal {T}}}_\delta |-\ln |\det (p_N(\tau )-z)|\right| \le {{\mathcal {O}}}(1). \end{aligned}$$

(5.23)

Notice that the error term depends on $\alpha$. Using also the general identity (cf. (5.3)),

$$\begin{aligned} \begin{aligned} \det (P_N^\delta -z) = \det {{\mathcal {T}}}^\delta (z)\, \det G^\delta _{-+}(z), \end{aligned} \end{aligned}$$

(5.24)

we get

$$\begin{aligned} \ln |\det (P_N^\delta -z)|= \ln |\det (p_N(\tau )-z)|+\ln |\det G_{-+}^\delta |+{{\mathcal {O}}}(1), \end{aligned}$$

(5.25)

uniformly for $z\in K\setminus \gamma _\alpha$, $N\gg 1$.

6 Lower bounds with probability close to 1

We now adapt the discussion in [15, Section 5] to ${{\mathcal {T}} }^\delta$. Let

$$\begin{aligned} P_N^\delta =P_N+\delta Q_\omega ,\ \ Q_\omega =(q_{j,k}(\omega ))_{1\le j,k\le N}, \end{aligned}$$

(6.1)

where $0\le \delta \ll 1$ and $q_{j,k}(\omega )\sim {{\mathcal {N}}}(0,1)$ are independent normalized complex Gaussian random variables. Recall from (1.21) that

$$\begin{aligned} \mathbf{P}[\Vert Q_\omega \Vert _{\mathrm {HS}}\le C_1N ]\ge 1-e^{-N^2}, \end{aligned}$$

(6.2)

for some universal constant $C_1>0$. In the following, we restrict the attention to the case when

$$\begin{aligned} \Vert Q_\omega \Vert _{\mathrm {HS}}\le C_1N , \end{aligned}$$

(6.3)

and (as before) $z\in K\setminus \gamma _\alpha$, $N\gg 1$. We assume that

$$\begin{aligned} \delta \ll N^{-3/2}. \end{aligned}$$

(6.4)

Then,

$$\begin{aligned} \delta \Vert Q\Vert _{\mathrm {tr}}\le \delta N^{1/2}\Vert Q\Vert _{\mathrm {HS}}\le \delta C_1N^{3/2} \ll 1, \end{aligned}$$

and the estimates of the previous sections apply.

Let ${{\mathcal {Q}}}_{C_1N}$ be the set of matrices satisfying (6.3). As in [15, Section 5.3], we study the map (5.15), i.e.,

$$\begin{aligned} \begin{aligned} {{\mathcal {Q}}}_{C_1N}\ni Q\mapsto G_{-+}^\delta (z)&=G_{-+}-G_-\delta Q(1+G\delta Q)^{-1}G_+\\&=G_{-+}-\delta G_-(Q+T(z,Q))G_+, \end{aligned} \end{aligned}$$

(6.5)

where

$$\begin{aligned} T(z,Q)=\sum _1^\infty (-\delta )^nQ(GQ)^n, \end{aligned}$$

(6.6)

and notice first that by (4.21)

$$\begin{aligned} \Vert T\Vert _{\mathrm {HS}}\le {{\mathcal {O}}}(\delta \alpha ^{-2}N^2 ). \end{aligned}$$

(6.7)

We strengthen the assumption (6.4) to

$$\begin{aligned} \delta \ll N^{-2}\alpha ^2. \end{aligned}$$

(6.8)

At the end of Sect. 4, we have established the uniform injectivity and surjectivity respectively for $G_+$ and $G_-$. This means that the singular values $s_j^\pm$ of $G_\pm$ for $1\le j\le k(z)=\mathrm {rank}\,(G_-)=\mathrm {rank}\,(G_+)$ satisfy

$$\begin{aligned} \frac{1}{C}\le s_j^\pm \le \frac{2}{\alpha } \end{aligned}$$

(6.9)

This corresponds to [15, (5.27)] and the subsequent discussion there carries over to the present situation with the obvious modifications. Similarly to [15, (5.42)], we strengthen the assumption on $\delta$ to

$$\begin{aligned} \delta \ll N^{-3}\alpha ^2 \end{aligned}$$

(6.10)

Notice that assumption (6.10) is stronger than the assumptions on $\delta$ in Proposition 5.2. The same reasoning as in [15, Section 5.3] leads to the following adaptation of Proposition 5.3 in [15]:

Proposition 6.1

Let $K\subset \mathbf{C}$ be compact, $0<\alpha \ll 1$ and choose M so that $\epsilon (M)\le \alpha /2$. Let $\delta$ satisfy (6.10). Then, the second Grushin problem with matrix ${{\mathcal {T}} }^\delta$ is well posed with a bounded inverse ${{\mathcal {G}}}^\delta$ introduced in Proposition 5.2. The following holds uniformly for $z\in K\setminus \gamma _\alpha$, $N\gg 1$:

There exist positive constants $C_0$, $C_2$ such that

$$\begin{aligned} \mathbf{P}\left( \ln |\det G_{-+}^\delta (z)|^2\ge -t\hbox { and }\Vert Q\Vert _{\mathrm {HS}}\le C_1 N\right) \ge 1-e^{-N^2}-C_2\delta ^{-M}e^{-t/2}, \end{aligned}$$

when

$$\begin{aligned} t\ge C_0-2M \ln \delta ,\ \ 0<\delta \ll N^{-3}\alpha ^2. \end{aligned}$$

7 Counting eigenvalues in smooth domains

In this section, we will prove Theorem 1.1. We will begin with a brief outline of the key steps:

We wish to count the zeros of the holomorphic function $u(z) = \det (P_N^{\delta }-z)$, which depends on the large parameter $N>0$, in smooth domains $\Omega \Subset {\mathbf {C}}$ as in Theorem 1.1.

1. We work in some sufficiently large but fixed compact set $K\Subset {\mathbf {C}}$ containing $\Omega$. In Sect. 7.1, we begin by showing that u(z) satisfies with probability close to 1 an upper bound of the form

$$\begin{aligned} \ln |u(z) | \le N(\phi (z) + \varepsilon ), \end{aligned}$$

(7.1)

for $z\in K$. Here, $0< \varepsilon \ll 1$ and $\phi (z)$ is some suitable continuous subharmonic function. Next, we will show that u(z) satisfies for any fixed point $z_0$ in $K\backslash \Gamma _{\alpha }$ a lower bound of the form

$$\begin{aligned} \ln |u(z_0) | \ge N(\phi (z_0) - \varepsilon ) \end{aligned}$$

(7.2)

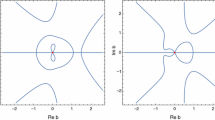
with probability close to 1. Here, $\Gamma _{\alpha }$ denotes the set $\gamma _{\alpha }$ suitably enlarged to be a compact set with smooth boundary, see Fig. 2 for an illustration. The function $\phi$ will be constructed in the following way : Outside $\Gamma _{\alpha }$ we set $\phi (z)$ to be $\ln |\det (p_N(\tau )-z)|$, which in view of (5.25) and Proposition 6.1 yields the estimates (7.1), (7.2) outside $\Gamma _{\alpha }$. Inside $\Gamma _{\alpha }$, we set $\phi$ to be the solution to the Dirichlet problem for the Laplace operator on $\Gamma _{\alpha }$ with boundary conditions $\phi \!\upharpoonright _{\partial \Gamma _{\alpha }} = \ln |\det (p_N(\tau )-z)|\!\upharpoonright _{\partial \Gamma _{\alpha }}$. Since $\ln |u(z)|$ is subharmonic we have that the bound (7.1) holds in all of K.

2. In Sect. 7.2, we will use (7.1), (7.2) and [12, Theorem 1.1] (see also [13, Chapter 12]) to estimate the number of zeros of u in $\Omega$ and thus the number of eigenvalues of $P_N^{\delta }$ in $\Omega$, i.e.,

$$\begin{aligned} \# (\sigma (P_N^{\delta }) \cap \Omega ) = \# (u^{-1}(0)\cap \Omega ) \sim \frac{N}{2\pi }\int _{\Omega }\Delta \phi L(dz), \end{aligned}$$

(7.3)

see (7.22).

3. In Sect. 7.3, we study the measure $\Delta \phi$ by analyzing the Poisson and Green kernel of $\Gamma _{\alpha }$. We will use this analysis to give precise error estimates on the asymptotics (7.3) and we will show that $\frac{N}{2\pi } \Delta \phi$ integrated over $\Omega$ is, up to a small error, given by the number of eigenvalues $\lambda _j$ of $p_N(\tau )$ (3.4) in $\Omega$, i.e.,

$$\begin{aligned} \frac{N}{2\pi }\int _{\Omega }\Delta \phi L(dz)= \#\{ \lambda _j\in \Omega \}+{\mathcal {O}}(\alpha N), \end{aligned}$$

see (7.53). This, in combination with (7.3), see (7.22), will let us conclude Theorem 1.1.

7.1 Estimates on the log-determinant

We work under the assumptions of Proposition 6.1 and from now on we assume that $\delta$ satisfies (1.13), i.e.,

$$\begin{aligned} \mathrm {e}^{- N^{\delta _0} } \le \delta \ll N^{-\delta _1}, \end{aligned}$$

(7.4)

for some fixed $\delta _0 \in ]0,1[$ and $\delta _1 >3$. Notice that (6.10) holds for $N>1$ sufficiently large (depending on $\alpha$). Then with probability $\ge 1-e^{-N^2}$, we have $G_{-+}^\delta (z)={{\mathcal {O}}}(1)$ for every $z\in K\setminus \gamma _\alpha$, hence by (5.25)

$$\begin{aligned} \ln |\det (P_N^\delta -z)|\le \ln |\det (p_N(\tau )-z)|+{{\mathcal {O}}}(1). \end{aligned}$$

(7.5)

On the other hand, by (5.25) and Proposition 6.1, we have for every $z\in K\setminus \gamma _\alpha$ that

$$\begin{aligned} \ln |\det (P_N^\delta -z)|\ge \ln |\det (p_N(\tau )-z)|-\frac{t}{2}-{{\mathcal {O}}}(1) \end{aligned}$$

(7.6)

with probability

$$\begin{aligned} \ge 1-e^{-N^2}-C_2\delta ^{-M}e^{-t/2}, \end{aligned}$$

(7.7)

when

$$\begin{aligned} t\ge C_0-2M\ln \delta . \end{aligned}$$

(7.8)

Next we enlarge $\gamma _{\alpha }$ to $\Gamma _{\alpha }$, away from a neighborhood of the region $\partial \Omega \cap \gamma$, so that $\Gamma _{\alpha }$ has a smooth boundary. More precisely, let $g \in C^\infty ({\mathbf {C}};{\mathbf {R}})$ be a boundary defining function of $\Omega$, so that $g(z)<0$ for $z\in \Omega$ and $dg \ne 0$ on $\partial \Omega$. Then, for $C>0$ sufficiently large and $\alpha >0$ sufficiently small, we define

$$\begin{aligned} \Gamma ^0_{\alpha } {\mathop {=}\limits ^{\mathrm {def}}}\gamma _{\alpha } \cup \{ z\in {\mathbf {C}}; g(z) < - 1/C \} \cup \{z\in {\mathbf {C}}; g(z)>1/C \text { and } |z|\le C\}, \end{aligned}$$

(7.9)

Notice that due to the assumption that the intersection of $\partial \Omega$ with $\gamma$ is transversal, the boundary of $\Gamma ^0_{\alpha }$ may be only Lipschitz near the intersection points

$$\begin{aligned} \{ z_0, \dots , z_q\} =\partial \gamma _{\alpha } \cap \partial G, \quad \text {where } G {\mathop {=}\limits ^{\mathrm {def}}}\{ z\in {\mathbf {C}}; |g(z)| \le 1/C \}. \end{aligned}$$

By the assumptions on $\Omega$, we have that $q < \infty$. Away from these points, we have that $\partial \Gamma ^0_{\alpha }$ is smooth. To remedy this lack of regularity, we will slightly deform $\Gamma ^0_{\alpha }$ in an $\alpha$-neighborhood of these points.

Pick $z_0\in \partial \gamma _{\alpha }\cap \partial G$. Since $\partial \gamma _{\alpha }\cap D(z_0,\alpha )$ and $\partial G\cap D(z_0,\alpha )$ are transversal to each other, it follows that there exists new affine coordinates ${\widetilde{z}} = U(z-z_0)$, ${\mathbf {R}}^2\simeq {\mathbf {C}}\ni z=(z^1,z^2)$ being the old coordinates, where U is orthogonal, and smooth functions $f_1,f_2$ independent of $\alpha$, such that $\gamma _{\alpha }\cap D(z_0,\alpha )$ takes the form

$$\begin{aligned} A= \{ z\in D(z_0,\alpha ); {\widetilde{z}}^2 \le f_2({\widetilde{z}}^1), ~ |{\widetilde{z}}^1|< \alpha , ~\Vert {\widetilde{z}}\Vert < \alpha \}, \end{aligned}$$

and that $({\mathbf {C}}\backslash \mathring{G})\cap D(z_0,\alpha )$ takes the form

$$\begin{aligned} B= \{ z\in D(z_0,\alpha ); {\widetilde{z}}^2 \le f_1({\widetilde{z}}^1), ~ |{\widetilde{z}}^1|< \alpha , ~\Vert {\widetilde{z}}\Vert < \alpha \}. \end{aligned}$$

Here, $f_1$, respectively $f_2$, is (after translation and rotation) a smooth local parametrization of $\partial G$, resp. $\partial \gamma _{\alpha }$, near $z_0$. Moreover, $f_2(0) = f_1(0)$ and the transversality assumption yields that ${\widetilde{z}}^1=0$ is the only point in the interval $]-\alpha ,\alpha [$ where $f_2({\widetilde{z}}^1) = f_1({\widetilde{z}}^1)$.

Then, $\Gamma ^0_{\alpha }\cap D(z_0,\alpha )$ takes the form

$$\begin{aligned} A\cup B = \{ z\in D(z_0,\alpha ); {\widetilde{z}}^2 \le \max \{f_1({\widetilde{z}}^1),f_2({\widetilde{z}}^1)\}, ~ |{\widetilde{z}}^1|< \alpha , ~\Vert {\widetilde{z}}\Vert < \alpha \}. \end{aligned}$$

Continuing, let $\chi \in C_c^{\infty }({\mathbf {R}};[0,1])$ so that $\chi =1$ on $[-1/4,1/4]$ and $\chi =0$ outside $]-1/2,1/2[$, and let $C>0$ be sufficiently large. Set

$$\begin{aligned} f (t ) = \left( 1 - \chi \!\left( \frac{t}{\alpha }\right) \right) \max \{f_1(t),f_2(t)\} + \chi \!\left( \frac{t}{\alpha }\right) \frac{\alpha }{C}, \quad t \in ]-\alpha ,\alpha [, \end{aligned}$$

which is a smooth function. Then, let $\Gamma _{\alpha }^1$ be equal to $\Gamma ^0_{\alpha }$ outside $D(z_0,\alpha )$, and equal to

$$\begin{aligned} \{ z\in D(z_0,\alpha ); {\widetilde{z}}^2 \le f({\widetilde{z}}^1), ~ |{\widetilde{z}}^1|< \alpha , ~\Vert {\widetilde{z}}\Vert < \alpha \}, \end{aligned}$$

inside $D(z_0,\alpha )$. Summing up, we have that the boundary of $\Gamma _{\alpha }^1$ is smooth at $z_0$ and $\Gamma _{\alpha }^0 \subset \Gamma _{\alpha }^1$.

Next, we perform the same procedure for $\Gamma _{\alpha }^1$ at the point $z_1$ and obtain $\Gamma _{\alpha }^2$ whose boundary is smooth at $z_0$ and $z_1$ and which contains $\Gamma _{\alpha }^1$. Continuing in this way until $z_q$, and defining

$$\begin{aligned} \Gamma _{\alpha } {\mathop {=}\limits ^{\mathrm {def}}}\Gamma ^q_{\alpha }, \end{aligned}$$

(7.10)

we have that $\Gamma _{\alpha }$ has a smooth boundary and it contains $\Gamma ^0_{\alpha }$ (7.9), and thus $\gamma _{\alpha }$. Figure 2 presents an illustration of this “fattening” of $\gamma _{\alpha }$.

Remark 7.1

Notice that the deformation of the boundary of $\Gamma _{\alpha }^0$ (7.9) has been done in such a way that the rescaled domain $\frac{1}{\alpha } \Gamma _{\alpha }$ has a smooth boundary which can be locally parametrized by a smooth function f with $\partial ^{\beta } f = {\mathcal {O}}(1)$, $\beta \in {\mathbf {N}}$, uniformly in $\alpha$.

Fig. 2

Left-hand side shows the curve $\gamma$ surrounded by the tube $\gamma _{\alpha }$ and the domain $\Omega$ (dashed line) where we are counting the eigenvalues of $P_N^{\delta }$. The right-hand side shows the same picture with $\gamma _{\alpha }$ enlarged to $\Gamma _{\alpha }=\Gamma _{\alpha }^{ext}\cup \Gamma _{\alpha }^{int}\cup \Gamma _{1,\alpha }\cup \Gamma _{2,\alpha }$, i.e., the whole gray area. The decomposition into an “exterior” part, an “interior” part and into the thin tubes $\Gamma _{j,\alpha }$ connecting exterior and interior will play a role in the proof of Lemma 7.3

Continuing, we define $\phi (z)=\phi _N(z)$ by requiring that

$$\begin{aligned} N\phi (z)=\ln |\det (p_N(\tau )-z)| \hbox { on } K\setminus {\Gamma _\alpha } , \end{aligned}$$

(7.11)

and

$$\begin{aligned} \phi (z)\hbox { is continuous in }K\hbox { and harmonic in }{{\mathop {\Gamma }\limits ^{\circ }} _\alpha } \end{aligned}$$

(7.12)

Here we assume that K is large enough to contain a neighborhood of $\Gamma _\alpha$. Choose

$$\begin{aligned} t=N^{\epsilon _0}, \end{aligned}$$

(7.13)

for some fixed $\epsilon _0\in ]0,1[$ with $\delta _0< \varepsilon _0$, see (7.4), (1.13). Then,

$$\begin{aligned} C_2\delta ^{-M}e^{-t/2}=\exp \left( \ln C_2 -M\ln \delta -N^{\epsilon _0}/2\right) , \end{aligned}$$

and we require from $\delta$ that

$$\begin{aligned} \ln C_2 -M\ln \delta -N^{\epsilon _0}/2\le -N^{\epsilon _0}/4, \end{aligned}$$

i.e.,

$$\begin{aligned} \ln \delta \ge \frac{\ln C_2 }{M} -\frac{N^{\epsilon _0}}{4M}. \end{aligned}$$

This is fulfilled if $N\gg 1$ and

$$\begin{aligned} \ln \delta \ge -\frac{N^{\epsilon _0}}{5M}, \end{aligned}$$

i.e.,

$$\begin{aligned} \delta \ge \exp \left( -\frac{1}{5M} N^{\epsilon _0} \right) \end{aligned}$$

(7.14)

and (7.13), (7.14) imply (7.8) when $N\gg 1$. Notice that (7.4) implies (7.14) for $N\gg 1$.

Combining (7.6), (7.11), (7.13) and (7.14), we get for each $z\in K\setminus { \Gamma _\alpha }$ that

$$\begin{aligned} \ln |\det (P_N^\delta -z)|\ge N(\phi (z)-\epsilon _1), \end{aligned}$$

(7.15)

with probability

$$\begin{aligned} \ge 1-e^{-N^2}-e^{-N^{\epsilon _0}/4} \end{aligned}$$

(7.16)

where

$$\begin{aligned} \epsilon _1=N^{\epsilon _0-1}. \end{aligned}$$

(7.17)

Here and in the following, we assume that $N\ge N(\alpha ,K)$ sufficiently large.

On the other hand, with probability $\ge 1-e^{-N^2}$, we have by (7.5)

$$\begin{aligned} \ln |\det (P_N^\delta -z)|\le N(\phi (z)+\epsilon _1) \end{aligned}$$

(7.18)

for all $z\in K\setminus \Gamma _\alpha$. Then, since the left- hand side in (7.18) is subharmonic and the right-hand side is harmonic in $\Gamma _\alpha$, we see that (7.18) remains valid also in $\Gamma _\alpha$ and hence in all of K.

7.2 Counting zeros of holomorphic functions with exponential growth

Let $\Omega \Subset \mathbf{C}$ be as in Theorem 1.1, so that $\partial \Omega$ intersects $\gamma$ at finitely many points ${\widetilde{z}}_1,...,{\widetilde{z}}_{k_0}$ which are not critical values of p and where the intersection is transversal. Choose $z_1,...,z_L\in \partial \Omega \setminus \Gamma _\alpha$ such that with $r_0=C_0\alpha$, $C_0\gg 1$, we have

$$\begin{aligned} \frac{r_0}{4}\le |z_{j+1}-z_j|\le \frac{r_0}{2} \end{aligned}$$

(7.19)

where the $z_j$ are distributed along the boundary in the positively oriented sense and with the cyclic convention that $z_{L+1}=z_{1}$. Notice that $L={{\mathcal {O}}}(1/\alpha )$. Then,

$$\begin{aligned}\partial \Omega \subset \bigcup _{1}^L D(z_j,r_0/2)\end{aligned}$$

and we can arrange so that $z_j\not \in \Gamma _\alpha$ and even so that

$$\begin{aligned} \mathrm {dist}\,(z_j,\Gamma _\alpha )\ge \alpha , \end{aligned}$$

(7.20)

for $\alpha >0$ sufficiently small.

Choose K above so that ${\overline{\Omega }}\Subset K$. Combining (7.18) and (7.15), we have that $\det (P_N^\delta -z)$ satisfies the upper bound (7.18) for all $z\in K$ and the lower bound (7.15) for $z = z_1,\dots , z_L$ with probability

$$\begin{aligned} \ge 1-{\mathcal {O}}(\alpha ^{-1})(e^{-N^2}+e^{-N^{\epsilon _0}/4}). \end{aligned}$$

(7.21)

Since $\phi$ is continuous and subharmonic, we can apply [12, Theorem 1.1] (see also [13, Chapter 12]) to the holomorphic function $\det (P_N^\delta -z)$ and get

$$\begin{aligned}&\left| \# (\sigma (P_N^\delta )\cap \Omega )-\frac{N}{2\pi }\int _{\Omega }\Delta \phi L(dz) \right| \le {{\mathcal {O}}}(N)\nonumber \\&\quad \times \left( L\epsilon _1 +\int _{\partial \Omega +D(0,r_0 )}\Delta \phi L(dz)+\sum _1^L \int _{D(z_j,r_0)} \Delta \phi (z) \left| \ln \frac{|z-z_j|}{r_0} \right| L(dz) \right) \nonumber \\ \end{aligned}$$

(7.22)

with probability (7.21).

Recall that $L={{\mathcal {O}}}(1/\alpha )$ (hence ${{\mathcal {O}}}(1)$ for every fixed $\alpha$). $\Delta \phi$ is supported in $\Gamma _\alpha$ and the number of discs $D(z_j,r_0)$ that intersect $\Gamma _\alpha$ is $\le {{\mathcal {O}}}(1)$ uniformly with respect to $\alpha$. Also $\ln (|z-z_j|/r_0)={{\mathcal {O}} }(1)$ on the intersection of each such disc with $\Gamma _\alpha$. Since $\epsilon _1=N^{\epsilon _0-1}$, we get from (7.22):

$$\begin{aligned}&\left| \# (\sigma (P_N^\delta )\cap \Omega )-\frac{N}{2\pi }\int _{\Omega }\Delta \phi L(dz) \right| \nonumber \\&\quad \le {{\mathcal {O}}}(N)\left( {{\mathcal {O}}}_\alpha (N^{\epsilon _0-1})+\int _{(\gamma \cap \partial \Omega )+D(0,2r_0)} \Delta \phi (z) L(dz) \right) . \end{aligned}$$

(7.23)

7.3 Analysis of the measure $\Delta \phi$

By (3.4), we have that

$$\begin{aligned} \ln |\det (p_N(\tau )-z)|=\sum _1^{N+M}\ln |z-\lambda _j|, \end{aligned}$$

(7.24)

where

$$\begin{aligned} \lambda _j=p\left( \exp \frac{2\pi ij}{N+M} \right) ,\ 1\le j\le N+M, \end{aligned}$$

and this expression is equal to $N\phi (z)$ in $K\setminus \Gamma _\alpha$.

Define

$$\begin{aligned} \psi (z)=\phi (z)-\frac{1}{N}\sum _1^{N+M}\ln |z-\lambda _j|, \end{aligned}$$

(7.25)

so that $\psi$ is continuous away from the $\lambda _j\in \gamma$,

$$\begin{aligned} \psi (z)= & {} 0\hbox { in }{} \mathbf{C}\setminus \Gamma _\alpha , \end{aligned}$$

(7.26)

$$\begin{aligned} {\psi }\!\upharpoonright _{\partial \Gamma _\alpha }= & {} 0, \end{aligned}$$

(7.27)

$$\begin{aligned} \Delta \psi= & {} -\frac{2\pi }{N}\sum _1^{N+M}\delta _{\lambda _j}\hbox { in }{\mathop {\Gamma }\limits ^{\circ }}_\alpha . \end{aligned}$$

(7.28)

It follows that in $\Gamma _\alpha$:

$$\begin{aligned} \psi (z)=-\frac{2\pi }{N}\sum _1^{N+M} G_{\Gamma _\alpha }(z,\lambda _j), \end{aligned}$$

(7.29)

where $G_{\Gamma _\alpha }$ is the Green kernel for $\Gamma _\alpha$.

$\phi$ is harmonic away from $\partial \Gamma _\alpha$, so for $\phi$ as a distribution on $\mathbf{C}$, we have $\mathrm {supp}\,\Delta \phi \subset \partial \Gamma _\alpha$. Now $\psi -\phi$ is harmonic near $\partial \Gamma _\alpha$, so $\Delta \psi =\Delta \phi$ near $\partial \Gamma _\alpha$. In the interior of $\Gamma _\alpha$ we have (7.28) and in order to compute $\Delta \psi$ globally, we let $v\in C_0^\infty (\mathbf{C})$ and apply Green’s formula to get

$$\begin{aligned} \langle \Delta \psi ,v\rangle= & {} \langle \psi ,\Delta v\rangle =\int _{\Gamma _\alpha }\psi \Delta v L(dz)\\= & {} \int _{\Gamma _\alpha }\Delta \psi v L(dz)+\int _{\partial \Gamma _\alpha }\psi \partial _{\nu }v |dz|-\int _{\partial \Gamma _\alpha }\partial _\nu \psi v |dz|. \end{aligned}$$

Here $\nu$ is the exterior unit normal and in the last term, it is understood that we apply $\partial _\nu$ to the restriction of $\psi$ to ${\mathop {\Gamma }\limits ^{\circ }}_\alpha$ then take the boundary limit. (7.27), (7.28) and (7.29) imply that in the sense of distributions on $\mathbf{C}$,

$$\begin{aligned} \Delta \psi =- \frac{2\pi }{N}\sum _1^{N+M}\delta _{\lambda _j} +\frac{2\pi }{N}\partial _\nu \left( \sum _1^{N+M}G_{\Gamma _\alpha }(\cdot ,\lambda _j) \right) L_{\partial \Gamma _\alpha }(dz) \end{aligned}$$

(7.30)

where $L_{\partial \Gamma _\alpha }$ denotes the (Lebesgue) arc length measure supported on $\partial \Gamma _\alpha$.

By the preceding discussion, we conclude that

$$\begin{aligned} \Delta \phi =\frac{2\pi }{N} \left( \sum _1^{N+M}\partial _\nu G_{\gamma _\alpha }(\cdot ,\lambda _j) L_{\partial \Gamma _\alpha }(dz) \right) . \end{aligned}$$

(7.31)

Each term in the sum is a nonnegative measure of mass 1:

$$\begin{aligned} \int \partial _\nu G(z ,\lambda _j)L_{\partial \Gamma _\alpha }(dz)=1. \end{aligned}$$

(7.32)

Before continuing, we will present two technical lemmas.

Lemma 7.2

Let $X \Subset {\mathbf {C}}$ be an open relatively compact, simply connected domain with smooth boundary. Let $u\in C^{\infty }({\overline{X}})$ with $u\!\upharpoonright _{\partial X} =0$. Let $z_0\in \partial X$ and let ${\widetilde{W}} \Subset W\Subset {\mathbf {C}}$ be two open relatively compact small complex neighborhoods of $z_0$, so that the closure of ${\widetilde{W}}$ is contained in W. If u is harmonic in $X\cap W$, then for any $s\in {\mathbf {N}}$

$$\begin{aligned} \Vert u \Vert _{H^s(X\cap {\widetilde{W}})} \le {\mathcal {O}}_{s, {\widetilde{W}}}(1) \Vert u \Vert _{H^0(X\cap W)}. \end{aligned}$$

(7.33)

Here $H^s$ are the standard Sobolev spaces.

Proof

The proof is standard, and we present it here for the reader’s convenience.

1. Let $W_1 \Subset W\Subset {\mathbf {C}}$ be two open relatively compact small complex neighborhoods of $z_0$, so that the closure of $W_1$ is contained in W. Let $\chi \in C^{\infty }_c({\mathbf {C}};[0,1])$ be so that $\chi =1$ on $W_1$ and $\mathrm{supp}\chi \subset W$. Integration by parts then yields that

$$\begin{aligned} \begin{aligned} \int _{X\cap W} |\chi \nabla u|^2 dx&= \int _{X\cap W} \chi \nabla u \cdot ( \nabla (\chi {\overline{u}} )- {\overline{u}} \,\nabla \chi )dx \\&= - \int _{X\cap W} \chi {\overline{u}}\, \nabla (\chi \nabla u) + \chi {\overline{u}}\, \nabla u \cdot \nabla \chi ) dx \\&= -2 \int _{X\cap W} \chi {\overline{u}}\, \nabla u \cdot \nabla \chi dx. \end{aligned} \end{aligned}$$

In the last equality, we used as well that u is harmonic in $X\cap W$. By the Cauchy–Schwarz inequality

$$\begin{aligned} \Vert \chi \nabla u \Vert ^2_{L^2(X\cap W)} \le {\mathcal {O}}(1) \Vert \chi \nabla u \Vert _{L^2(X\cap W)} \Vert u \Vert _{L^2(X\cap W)}, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert \chi \nabla u \Vert _{L^2(X\cap W)} \le {\mathcal {O}}(1) \Vert u \Vert _{L^2(X\cap W)}. \end{aligned}$$

Hence,

$$\begin{aligned} \Vert u \Vert _{H^1(X\cap W_1)} \le {\mathcal {O}}(1) \Vert u \Vert _{L^2(X\cap W)}. \end{aligned}$$

(7.34)

2. Since W is small, we may pass to new local coordinates y, and we can suppose that $z_0 =0$ and that locally $\partial X = \{y_2 = 0\}$. If $\phi$ is a local diffeomorphism realizing this change of variables, then the Laplacian can be formally written in the new coordinates as

$$\begin{aligned} L{\mathop {=}\limits ^{\mathrm {def}}}\, ^t( (\phi ')^{-1}\nabla _y)\cdot ((\phi ')^{-1}\nabla _y), \quad \text {with } \Delta _x = (\phi ^{-1})^* \circ \Delta \circ \phi ^*. \end{aligned}$$

(7.35)

Here, L is an elliptic second-order differential operator, and $\phi '$ is the Jacobian map associated with the diffeomorphism $\phi$.

Working from now on in these new coordinates, we proceed by an induction argument: suppose that

$$\begin{aligned} \Vert u \Vert _{H^{s+1}(X\cap W_1 )} \le {\mathcal {O}}(1) \Vert u \Vert _{H^{s}X \cap W)}. \end{aligned}$$

(7.36)

holds for some $s\in {\mathbf {N}}$. Here we write as well $W,W_1$ for the respective sets in the new coordinates to ease notation. We want to show that we then also have

$$\begin{aligned} \Vert u \Vert _{H^{s+2}(X\cap W_2 )} \le {\mathcal {O}}(1) \Vert u \Vert _{H^{s+1}X \cap W_1)}. \end{aligned}$$

(7.37)

where $W_2\Subset W_1$ is a slightly smaller neighborhood of $z_0=0$, whose closure is contained inside $W_1$.

Let $\chi \in C^{\infty }_c({\mathbf {C}};[0,1])$ be so that $\chi =1$ on $W_2$ and $\mathrm{supp}\chi \subset W_1$. Let $\partial _{t,j}u(y): = t^{-1}(u(y+te_j) - u(y)$, where $x\in {\mathbf {C}}\simeq {\mathbf {R}}^2$ and $e_1, e_2$ is the standard orthonormal basis of ${\mathbf {R}}^2$. Then, by the hypothesis (7.36) applied to $\partial _{t,j}\chi u$, for $|t| \ll 1$, we get

$$\begin{aligned} \begin{aligned} \Vert \partial _{t,1}\chi u \Vert _{H^{s+1}(X\cap W_1 )}&\le {\mathcal {O}}(1) \Vert \partial _{t,1}\chi u \Vert _{H^s(X \cap W)} \\&\le {\mathcal {O}}(1) \Vert \chi \partial _{t,1} u \Vert _{H^s(X \cap W)} + {\mathcal {O}}(1) \Vert [\partial _{t,1},\chi ] u \Vert _{H^s(X \cap W)} \\&\le {\mathcal {O}}(1) \Vert u \Vert _{H^{s+1}(X \cap W_1)} + {\mathcal {O}}(1) \Vert u \Vert _{H^s(X \cap W_1)}, \end{aligned} \end{aligned}$$

uniformly in $|t|\ll 1$. In the last inequality, we used as well that $\chi \partial _{t,1} u$ and $[\partial _{t,1},\chi ] u = (\partial _{t,1}\chi ) u(\cdot + te_1)$ are supported in $W_1$ for $|t|\ll 1$. Performing the limit $t\rightarrow 0$, we get

$$\begin{aligned} \Vert \partial _{y_1}\chi u \Vert _{H^{s+1}(X\cap W_1 )} \le {\mathcal {O}}(1) \Vert u \Vert _{H^{s+1}X \cap W_1)}. \end{aligned}$$

(7.38)

Thus, for $j=1,2$, we have that

$$\begin{aligned} \Vert \partial _{y_1}\partial _{y_j}\chi u \Vert _{H^{s}(X\cap W_1 )} \le {\mathcal {O}}(1) \Vert \partial _{y_1} u \Vert _{H^{s+1}(X \cap W_1)} \le {\mathcal {O}}(1) \Vert u \Vert _{H^{s+1}(X \cap W_1)}. \end{aligned}$$

(7.39)

By (7.35), it follows that there exists some smooth function $a\ne 0$, such that

$$\begin{aligned} \partial _{y_2}^2 \chi u = \frac{1}{a} L\chi u - {\widetilde{L}} \chi u, \end{aligned}$$

(7.40)

where ${\widetilde{L}}$ is a second-order differential operator with smooth coefficients and which does not contain the derivative $\partial _{y_2}^2$. Since u is harmonic in $X\cap W$, it follows that $L\chi u = [L,\chi ] u$. Since $[L,\chi ]$ is a differential operator of order 1, it follows from (7.40) and (7.39) that

$$\begin{aligned} \Vert \partial _{y_2}\chi u \Vert _{H^{s+1}(X\cap W_1 )} \le {\mathcal {O}}(1) \sum _1^2 \Vert \partial _{y_j}\partial _{y_2}\chi u \Vert _{H^{s}(X\cap W_1 )} \le {\mathcal {O}}(1) \Vert u \Vert _{H^{s+1}(X \cap W_1)}. \end{aligned}$$

(7.41)

In combination with (7.38), this yields

$$\begin{aligned} \Vert u \Vert _{H^{s+2}(X\cap W_2 )} \le \Vert \chi u \Vert _{H^{s+2}(X\cap W_1 )} \le {\mathcal {O}}(1) \Vert u \Vert _{H^{s+1}X \cap W_1)}. \end{aligned}$$

(7.42)

Thus, by choosing a decreasing sequence of nested compact neighborhoods of $z_0$, say ${\widetilde{W}} = W_{s+1} \Subset W_{s} \dots \Subset W_0 = W$, we may iterate the estimate (7.36), which then in combination with (7.34) yields (7.33). $\square$

Lemma 7.3

There exists a $C>0$ independent of $\alpha >0$, such that for any $1 \le j \le N+M$

$$\begin{aligned} \left| \partial _\nu G_{\Gamma _\alpha }(z ,\lambda _j) \right| \le \frac{1}{\alpha }e^{-\frac{|z-\lambda _j|}{C\alpha }}, \end{aligned}$$

(7.43)

for $z\in \partial \Gamma _\alpha \cap \mathrm {neigh}\,(\gamma \cap \partial \Omega )$, $\lambda _j\in \Gamma _\alpha$, $|z-\lambda _j|\ge \alpha /C$. (7.43) also holds when $z\in \partial \Gamma _\alpha ,$ $\lambda _j\in \Gamma _\alpha$, $|z-\lambda _j|\ge \alpha /C$ and $(z,\lambda _j)\in (\Omega \times (\mathbf{C}\setminus \Omega ))\cup ((\mathbf{C}\setminus \Omega )\times \Omega )$.

Proof

1. By scaling of the harmonic function $G_{\Gamma _\alpha }(\cdot ,\lambda _j)$ by a factor $1/\alpha$, it suffices to show that

$$\begin{aligned} \left| G_{\Gamma _\alpha }(z ,\lambda _j) \right| \le e^{-\frac{|z-\lambda _j|}{C\alpha }}, \end{aligned}$$

(7.44)

for $(z,\lambda _j)$ as after (7.43) with the difference that z now varies in $\Gamma _{\alpha }$ instead of $\partial \Gamma _{\alpha }$.

To see this, recall from the construction of $\Gamma _{\alpha }$ after (7.8) that $\mathrm {dist}(\partial \Gamma _{\alpha },\lambda _j) \ge \alpha$ and fix a point $z_0 \in \partial \Gamma _{\alpha }$, let $C_1>0$ be sufficiently large so that for any $z\in D( z_0, \alpha /C_1)\cap \Gamma _{\alpha }$ we have that $(z,\lambda _j)$ satisfies the conditions after (7.43) with z varying in $D( z_0, \alpha /C_1)\cap \Gamma _{\alpha }$ instead of $\partial \Gamma _{\alpha }$.

Let $u(z) := G_{\gamma _\alpha }(\alpha z,\lambda _j)$, $z\in \frac{1}{\alpha } \Gamma _{\alpha }$, be the scaled function, and recall Remark 7.1. Let $\chi \in C^{\infty }_c({\mathbf {C}};[0,1])$ be so that $\chi =1$ on $D( z_0/\alpha , 1/(4C_1))$, $\mathrm{supp}\chi \subset D( z_0/\alpha , 1/2C_1)=:W'$ and $\partial ^{\beta } = {\mathcal {O}}(1)$, uniformly in $\alpha$ for any $\beta \in {\mathbf {N}}^2$. Moreover, put $W=D( z_0/\alpha , 1/C_1)$.

Then, $\chi u \in H^s(\Gamma _{\alpha }\cap W')$ for any $s>0$. We can find an extension $v\in H^s({\mathbf {R}}^2)$ of $\chi u$ so that $\Vert v\Vert _{H^s} \le {\mathcal {O}}(1) \Vert \chi u\Vert _{H^s(\Gamma _{\alpha }\cap W')}$. Using the Fourier transform, we see that for $s>2$ and for $z\in D( z_0/\alpha , 1/(4C_1))$

$$\begin{aligned} | \nabla v(z) | \le {\mathcal {O}}(1) \Vert |\xi | {\widehat{v}}\Vert _{L^2} \le {\mathcal {O}}(1) \Vert |\xi | \langle \xi \rangle ^{-s}\Vert _{L^2} \Vert v\Vert _{H^{s}} \le {\mathcal {O}}(1) \Vert \chi u\Vert _{H^s(\Gamma _{\alpha }\cap W')}. \end{aligned}$$

(7.45)

By Lemma 7.2 and (7.44), we see that

$$\begin{aligned} | \partial _{\nu } v(z) | \le {\mathcal {O}}(1) \Vert u\Vert _{L^{\infty }(\Gamma _{\alpha }\cap W)} \le {\mathcal {O}}(1) \,e^{-\frac{|z-\lambda _j/\alpha |}{C }}, \end{aligned}$$

(7.46)

and

$$\begin{aligned} | \alpha ( \partial _{\nu } G_{\Gamma _\alpha })(\alpha z,\lambda _j) | \le {\mathcal {O}}(1) \,e^{-\frac{|z-\lambda _j/\alpha |}{C }}, \end{aligned}$$

(7.47)

which implies (7.44) after rescaling and potentially slightly increasing the constant $C>0$.

2. We decompose $\Gamma _\alpha$ as $\Gamma ^{int}\cup \Gamma ^{ext}\cup \Gamma _{1,\alpha }\cup ...\cup \Gamma _{T,\alpha }$, where $\Gamma ^{int}$ and $\Gamma ^{ext}$ are the enlarged parts of $\Gamma _\alpha$ with $\Gamma ^{int}\subset \Omega$, $\Gamma ^{ext}\subset \mathbf{C}\setminus \Omega$ and $\Gamma _{1,\alpha },...,\Gamma _{T,\alpha }$ are the regular parts of width $2\alpha$, corresponding to the segments of $\gamma$, that intersect $\partial \Omega$ transversally, see Fig. 2 for an illustration. Here, T is the number of intersections of $\gamma$ with $\partial \Omega$, notice that T is finite and independent of $N,\alpha$.

For simplicity, we assume that $\Gamma ^{int}$ and $\Gamma ^{ext}$ are connected and that each segment $\Gamma _{k,\alpha }$ links $\Gamma ^{int}$ to $\Gamma ^{ext}$ and crosses $\partial \Omega$ once. We may think of $\Gamma _{\alpha }$ as a graph with the vertices $\Gamma ^{int}$, $\Gamma ^{ext}$ and with $\Gamma _{k,\alpha }$ as the edges.

Let first $\lambda _j$ belong to $\Gamma ^{int}$. We apply the first estimate in Proposition 2.2 in [12] or equivalently Proposition 12.2.2 in [13] and see that $-G_{\Gamma _\alpha }(z,\lambda _j)\le {{\mathcal {O}}}(1)$ for $z\in \Gamma _\alpha$, $|z-\lambda _j|\ge 1/{{\mathcal {O}}}(1)$. Here and in the following the constants ${\mathcal {O}}(1)$ are independent of j and $\alpha$. Furthermore, the notation $1/{{\mathcal {O}}}(1)$ means 1/C for some sufficiently large constant $C>0$.

Possibly, after cutting away a piece of $\Gamma _{k,\alpha }$ and adding it to $\Gamma ^{int}$, we may assume that $-G_{\Gamma _\alpha }(z,\lambda _j)\le {{\mathcal {O}}}(1)$ in $\Gamma _{k,\alpha }$. Consider one of the $\Gamma _{k,\alpha }$ as a finite band with the two ends given by the closure of the set of $z\in \partial \Gamma _{k,\alpha }$ with $\mathrm {dist}\,(z,\partial \Gamma _\alpha )<\alpha$. Let $G_{\Gamma _{k,\alpha }}$ denote the Green kernel of $\Gamma _{k,\alpha }$. Then, the second estimate in the quoted proposition applies and we find

$$\begin{aligned} -G_{\Gamma _{k,\alpha }}(x,y)\le {{\mathcal {O}}}(1)e^{-|x-y|/(\alpha \, {{\mathcal {O}}}(1 )) }, \hbox { when } x,y\in \Gamma _{k,\alpha },\ |x-y|\ge \alpha /{{\mathcal {O}}}(1). \end{aligned}$$

Let

$$\begin{aligned} u=\chi {G_{\Gamma _\alpha }(\cdot ,\lambda _j)}\!\upharpoonright _{\Gamma _{k,\alpha }}, \end{aligned}$$

where $\chi \in C^\infty (\Gamma _{k,\alpha };[0,1])$ vanishes near the ends of $\Gamma _{k,\alpha }$, is equal to 1 away from an $\alpha$-neighborhood of these end points and with the property that $\nabla \chi ={{\mathcal {O}}}(1/\alpha )$, $\nabla ^2\chi ={{\mathcal {O}}}(1/\alpha ^2)$. Then, ${{u}_\vert }_{\partial \Gamma _{k,\alpha }}=0$ and $\Delta u={{\mathcal {O}}}(\alpha ^{-2})$ is supported in an $\alpha$-neighborhood of the union of the two ends and hence of uniformly bounded $L^1$-norm. Now we apply the second estimate in the quoted proposition to $u=\int G_{\Gamma _{k,\alpha }}(\cdot ,y)\Delta u(y)L(dy)$ and we see that

$$\begin{aligned} G_{\Gamma _\alpha }(\cdot ,\lambda _j)={{\mathcal {O}}}(e^{-1/(\alpha \,{{\mathcal {O}}}(1 )) }). \end{aligned}$$

(7.48)

in $\{ x\in \Gamma _{k,\alpha };\,\mathrm {dist}\,(x,\partial \Omega \cap \Gamma _{k,\alpha })\le 1/{{\mathcal {O}}}(1) \}$. Here, we also recall that $\lambda _j \in \gamma \Subset \mathring{\Gamma }_{\alpha }$. Varying k, we get (7.48) in $\{ x\in \Gamma _\alpha ;\, \mathrm {dist}\,(x,\partial \Omega \cap \Gamma )\le 1/{{\mathcal {O}}}(1) \}$. Applying the maximum principle to the harmonic function ${G_{\Gamma _\alpha }(\cdot ,\lambda _j)}\!\upharpoonright _{(\mathbf{C}\setminus \Omega )\cap \Gamma _\alpha }$, we see that (7.48) holds uniformly in $(\mathbf{C}\setminus \Omega )\cap \Gamma _\alpha$.

Similarly, we have (7.48) uniformly in

$$\begin{aligned} \{x\in \Gamma _\alpha ;\, \mathrm {dist}\,(x,\partial \Omega \cap \gamma )\le 1/{{\mathcal {O}}}(1) \}\cup (\Omega \cap \Gamma _\alpha ), \end{aligned}$$

when $\lambda _j\in \Gamma ^{ext}$ and we have shown (7.44), (7.43) when $\lambda _j\in \Gamma ^{int}\cup \Gamma ^{ext}$. Similarly, we have (7.43) when $\lambda _j\in \gamma _{k,\alpha }$ is close to one of the ends.

It remains to treat the case when $\lambda _j\in \gamma _{k,\alpha }$ is at distance $\ge 1/{{\mathcal {O}}}(1)$ from the ends of $\gamma _{k,\alpha }$. Defining $u=\chi {G_{\Gamma _\alpha }(\cdot ,\lambda _j)}\!\upharpoonright _{\gamma _{k,\alpha }}$ as before we now have

$$\begin{aligned} \Delta u=[\Delta ,\chi ]G_{\Gamma _\alpha (\cdot ,\lambda _j)}+\delta _{\lambda _j}, \end{aligned}$$

where the first term in the right-hand side has its support in an $\alpha$-neighborhood of the union of the ends and is ${{\mathcal {O}}}(1)$ in $L^1$. By the second part of the quoted proposition, we have

$$\begin{aligned} u(x)={{\mathcal {O}}}(1)\exp \left( -\frac{1}{{{\mathcal {O}}}(1 )\alpha }\min \left( \mathrm {dist}\, (x,\mathrm {ends}\,(\gamma _{k,\alpha })),|x-\lambda _j| \right) \right) , \end{aligned}$$

(7.49)

away from an $\alpha$-neighborhood of $\mathrm {ends}\,(\gamma _{k,\alpha })\cup \{\lambda _j\}$. Here $\mathrm {ends}\,(\gamma _{k,\alpha })$ denotes the union of the two ends of $\gamma _{k,\alpha }$. Since u is harmonic away from $\lambda _j$ and from $\alpha$-neighborhoods of the ends, we get from (7.49) that

$$\begin{aligned} \nabla u(x)={{\mathcal {O}}}\left( \frac{1}{\alpha } \right) \exp \left( -\frac{1}{{{\mathcal {O}}}(1 )\alpha }\min \left( \mathrm {dist}\, (x,\mathrm {ends}\,(\gamma _{k,\alpha })),|x-\lambda _j| \right) \right) , \end{aligned}$$

(7.50)

which gives (7.43) near $\partial \Omega \cap \gamma$. By using the maximum principle as before, we can extend the validity of (7.43) to all of $\partial \Gamma _\alpha \setminus D(\lambda _j,\alpha /{{\mathcal {O}}}(1))$. $\square$

Continuing, notice that by (3.4), (7.24)

$$\begin{aligned} \#\{ \sigma (P_{S_{{\widetilde{N}}}}) \cap \eta \} = \#\{{\widehat{S}}_{{\widetilde{N}}} \cap p_N^{-1}(\eta ) \}, \quad {\widetilde{N}} = N + M, \end{aligned}$$

(7.51)

for $\eta \subset \gamma$. Since two consecutive points of ${\widehat{S}}_{{\widetilde{N}}}$ differ by an angle of $2\pi /{\widetilde{N}}$ and by the assumptions (1)-(4) prior to Theorem 1.1, we get that

$$\begin{aligned} \# \{ \lambda _j;\, \mathrm {dist}\,(\lambda _j,\partial \Omega \cap \gamma )<4r_0 \} ={\mathcal {O}}(\alpha N) \end{aligned}$$

and also

$$\begin{aligned} \# \{ \lambda _j;\, \mathrm {dist}\,(\lambda _j,\partial \Omega \cap \gamma )\in [2^kr_0,2^{k+1}r_0[ \} ={\mathcal {O}}(\alpha 2^k N),\ k=2,3,... \end{aligned}$$

From (7.43) and (7.31), we get

$$\begin{aligned} \begin{aligned} \frac{N}{2\pi }\int _{(\partial \Omega \cap \gamma )+D(0,2r_0)}\Delta \phi L(dz)&=\sum _j \int _{((\partial \Omega \cap \gamma )+D(0,2r_0))\cap \partial \Gamma _\alpha }\partial _\nu G_{\Gamma _\alpha }(z,\lambda _j) L(dz)\\&={\mathcal {O}}(\alpha N)+\sum _{k=2}^\infty \sum _{\lambda _j;\atop \mathrm {dist}\,(\lambda _j,\partial \Omega \cap \gamma )\in [2^kr_0,2^{k+1}r_0[}e^{-2^k/{\mathcal {O}}(1)}\\&={\mathcal {O}}(1)\left( \alpha N+\sum _{k=2}^\infty e^{-2^k/{\mathcal {O}}(1)} \alpha 2^kN\right) \\&={\mathcal {O}}(\alpha N)+{\mathcal {O}}(1)N\alpha \int _0^\infty e^{-t/{{\mathcal {O}}}(1)}dt \\&={\mathcal {O}}(\alpha N). \end{aligned} \end{aligned}$$

(7.52)

Combining (7.32) and (7.43), we get when $\mathrm {dist}\,(\lambda _j,\partial \Omega \cap \gamma )\ge 2r_0$:

$$\begin{aligned} \int _{\partial \Gamma _\alpha \cap \Omega }\partial _\nu G_{\gamma _\alpha }(z,\lambda _j)L_{\partial \Gamma _\alpha }(dz) ={\left\{ \begin{array}{ll} 1+{\mathcal {O}}(1)e^{-\mathrm {dist}\,(\lambda _j,\partial \Omega \cap \gamma )/{\mathcal {O}}(\alpha )},&{}\hbox {when }\lambda _j\in \Omega ,\\ {\mathcal {O}}(1)e^{-\mathrm {dist}\,(\lambda _j,\partial \Omega \cap \gamma )/{\mathcal {O}}(\alpha )},&{}\hbox {when }\lambda _j\not \in \Omega . \end{array}\right. } \end{aligned}$$

We now get

$$\begin{aligned} \begin{aligned} \frac{N}{2\pi }\int _{\Omega }\Delta \phi L(dz)=&\sum _{j;\, \mathrm {dist}\,(\lambda _j,\gamma \cap \partial \Omega )\le 4r_0} \int _{\partial \Gamma _\alpha \cap \Omega }\partial _\nu G_{\Gamma _\alpha }(z,\lambda _j)L_{\partial \Gamma _\alpha }(dz)\\&+\sum _{k=2}^\infty \sum _{\lambda _j\in \Omega , \atop \mathrm {dist}\,(\lambda _j,\gamma \cap \partial \Omega )\in [2^kr_0,2^{k+1}r_0[}\int _{\partial \Gamma _\alpha \cap \Omega }\partial _\nu G_{\Gamma _\alpha }(z,\lambda _j)L_{\partial \gamma _\alpha }(dz) \\&+\sum _{k=2}^\infty \sum _{\lambda _j\in \mathbf{C}\setminus \Omega , \atop \mathrm {dist}\,(\lambda _j,\gamma \cap \partial \Omega )\in [2^kr_0,2^{k+1}r_0[}\int _{\partial \Gamma _\alpha \cap \Omega }\partial _\nu G_{\Gamma _\alpha }(z,\lambda _j)L_{\partial \gamma _\alpha }(dz)\\ =&{\mathcal {O}}(\alpha N)+ \sum _{k=2}^\infty \sum _{\lambda _j\in \Omega , \atop \mathrm {dist}\,(\lambda _j,\gamma \cap \partial \Omega )\in [2^kr_0,2^{k+1}r_0[} (1+{\mathcal {O}}(1)e^{-2^k/{\mathcal {O}}(1)}) \\&+\sum _{k=2}^\infty \sum _{\lambda _j\in \mathbf{C}\setminus \Omega , \atop \mathrm {dist}\,(\lambda _j,\gamma \cap \partial \Omega )\in [2^kr_0,2^{k+1}r_0[}{\mathcal {O}}(1)e^{-2^k/{\mathcal {O}}(1)}\\&=\#\{ \lambda _j\in \Omega \}+{\mathcal {O}}(\alpha N). \end{aligned} \end{aligned}$$

(7.53)

Thus, (7.23) gives

$$\begin{aligned} \begin{aligned} \# (\sigma (P_N^\delta )\cap \Omega )&=\# (\{\lambda _j \}\cap \Omega )+{{\mathcal {O}}}(\alpha N)+{{\mathcal {O}}}_\alpha (N^{\epsilon _0})\\&=\frac{N}{2\pi }\left( \int _{S^1\cap p^{-1}(\Omega )}L_{S^1}(d\theta ) \right) +{{\mathcal {O}}}(\alpha N )+{{\mathcal {O}}}_\alpha (N^{\epsilon _0})+o(N), \end{aligned} \end{aligned}$$

(7.54)

with a probability as in (7.21) which is bounded from below by the probability (1.15) for $N>1$ sufficiently large. Here and in the next formula, we view $p_N$ and p as maps from $S^1$ to ${\mathbf {C}}$. In the second equality, we used that by (7.51)

$$\begin{aligned} \begin{aligned} \# (\{\lambda _j \}\cap \Omega )&=\frac{{\widetilde{N}}}{2\pi } \int _{S^1\cap p_N^{-1}(\Omega )}L_{S^1}(d\theta ) +{\mathcal {O}}(1) \\&=\frac{N}{2\pi } \int _{S^1\cap p_N^{-1}(\Omega )}L_{S^1}(d\theta ) +{\mathcal {O}}(M) \\&=\frac{N}{2\pi } \int _{S^1\cap p^{-1}(\Omega )}L_{S^1}(d\theta ) +o(N), \end{aligned} \end{aligned}$$

(7.55)

where we used that $p_N \rightarrow p$ uniformly on $S^1$ and where the measure $L_{S^1}(d\theta )$ in the integral denotes the Lebesgue measure on $S^{1}$.

Theorem 1.1 follows by taking $\alpha >0$ in (7.54) arbitrarily small and $N>1$ sufficiently large.

8 Convergence of the empirical measure

In this section, we present a proof of Theorem 1.2 following the strategy of [15, Section 7.3]. An alternative, and perhaps more direct way, to conclude the weak convergence of the empirical measure from a counting theorem as Theorem 1.2, is presented in [15, Section 7.1].

Recall the definition of the empirical measure $\xi _N$ (1.20). By (1.21), (1.5) combined with a Borel Cantelli argument, it follows that almost surely

$$\begin{aligned} \mathrm{supp}\xi _N \subset \overline{D(0,\Vert p \Vert _{L^{\infty }(S^1)}+1)} {\mathop {=}\limits ^{\mathrm {def}}}K\subset D(0,\Vert p \Vert _{L^{\infty }(S^1)}+2){\mathop {=}\limits ^{\mathrm {def}}}K' \end{aligned}$$

(8.1)

for N sufficiently large. For p as in (1.4), put

$$\begin{aligned} \xi =p_*\left( \frac{1}{2\pi } L_{S^1}\right) \end{aligned}$$

(8.2)

which has compact support,

$$\begin{aligned} \mathrm{supp}\xi = p(S^1) \subset K. \end{aligned}$$

(8.3)

Here, $\frac{1}{2\pi } L_{S^1}$ denotes the normalized Lebesgue measure on $S^1$.

We recall [15, Theorem 7.1]:

Theorem 8.1

Let $K,K'\Subset {\mathbf {C}}$ be open relatively compact sets with ${\overline{K}}\subset K'$, and let $\{\mu _n\}_{n\in {\mathbf {N}}} \in {\mathcal {P}}({\mathbf {C}})$ be as sequence of random measures so that almost surely

$$\begin{aligned} \mathrm{supp}\mu _n \subset K \hbox { for } n \hbox { sufficiently large}. \end{aligned}$$

Suppose that for a.e. $z\in K'$ almost surely

$$\begin{aligned} U_{\mu _n}(z)\rightarrow U_{\mu }(z), \quad n \rightarrow \infty , \end{aligned}$$

where $\mu \in {\mathcal {P}}({\mathbf {C}})$ is some probability measure with $\mathrm{supp}\mu \subset K$. Then, almost surely,

$$\begin{aligned} \mu _n\rightharpoonup \mu , \quad n \rightarrow \infty , \quad \hbox {weakly.} \end{aligned}$$

This theorem is a modification of a classical result which allows to deduce the weak convergence of measures from the point-wise convergence of the associated Logarithmic potentials, see for instance [17, Theorem 2.8.3] or [1].

In view of Theorem 8.1, it remains to show that for almost every $z\in K'$ we have that $U_{\xi _N}(z) \rightarrow U_{\xi }(z)$ almost surely, where

$$\begin{aligned} U_{\xi _N}(z) = - \int \log | z- x | \xi _N(dx), \quad U_{\xi }(z) = - \int \log | z- x | \xi (dx). \end{aligned}$$

For $z\notin \sigma ( P_N^{\delta })$

$$\begin{aligned} U_{\xi _N}(z) = -\frac{1}{N} \log | \det (P_N^{\delta } -z)|. \end{aligned}$$

(8.4)

For any $z\in {\mathbf {C}}$ the set $\Sigma _z = \{ Q \in {\mathbf {C}}^{N\times N}; \det (P_N +\delta Q -z) =0\}$ has Lebesgue measure 0, since ${\mathbf {C}}^{N\times N} \ni Q \mapsto \det (P_N^{\delta } -z)$ is analytic and not constantly 0. Thus, $\mu _N(\Sigma _z)=0$, where $\mu _N$ is the Gaussian measure given in after (1.11), and for every $z\in {\mathbf {C}}$ (8.4) holds almost surely.

Let $\delta$ satisfy (1.13) for some fixed $\delta _0\in ]0,1[$ and $\delta _1>3$. Pick a $\varepsilon _0 \in ]\delta _0,1[$. Let $z\in K'\backslash p(S^1)$. Recall (4.17). For $\alpha >0$ sufficiently small, we have that $z\in K'\backslash \gamma _{\alpha }$.

Put $t=N^{\varepsilon _0}$ as in (7.13), which together with (7.14) implies (7.8) when $N\gg 1$. Since (1.13) implies (7.14), it follows by combining (7.14), (7.5), (7.6) and (7.7) that

$$\begin{aligned} \left| \frac{1}{N} \log | \det (P_N^{\delta } -z)| - \phi (z) \right| \le {\mathcal {O}}(N^{\varepsilon _0 -1}). \end{aligned}$$

(8.5)

with probability $\ge 1 - \mathrm {e}^{-N^2}- \mathrm {e}^{-N^{\varepsilon _0/4}}$. Here, $\phi (z) := N^{-1}\ln |\det (p_N(\tau )-z)|$, since $z\notin \gamma _\alpha$.

Using a Riemann sum argument and the fact that $p_N \rightarrow p$ uniformly on $S^1$, we have that

$$\begin{aligned} \left| \phi (z) + U_{\xi }(z) \right| \longrightarrow 0, \quad \hbox {as } N\rightarrow \infty . \end{aligned}$$

(8.6)

Thus, by (8.5), (8.6), we have for any $z\in K'\backslash p(S^1)$ that

$$\begin{aligned} \left| U_{\xi _N}(z) - U_{\xi }(z) \right| = o(1) \end{aligned}$$

(8.7)

with probability $\ge 1 - \mathrm {e}^{-N^2}- \mathrm {e}^{-N^{\varepsilon _0/4}}$. By the Borel–Cantelli theorem, if follows that for every $z\in K'\backslash p(S^1)$

$$\begin{aligned} U_{\xi _N}(z) \longrightarrow U_{\xi }(z), \quad \hbox {as } N\rightarrow \infty , \hbox { almost surely}, \end{aligned}$$

(8.8)

which by Theorem 8.1 concludes the proof of Theorem 1.2.