In loose language, a deltoid is a closed curve in the shape of the capital Greek letter delta, the symbol of a triangle. The classical deltoid was introduced by Jacob Steiner in 1856; it is the locus of a marked point on a circle rolling inside a fixed circle that is three times larger, or a tri-hypocycloid; see [52] or [71]. A second deltoid was introduced in 1972 by J. E. Dunn and J. E. Pretty in [26]— see Fig. 1 (Left), as the envelope of all area-bisecting lines of a triangle. It is a triangle whose sides are outwardly-looking arcs of hyperbolas. This was named as the area-bisecting deltoid in [8] along with the perimeter-bisecting deltoid, a third deltoid introduced and studied in that paper—see Fig. 1 (right). The perimeter-bisecting deltoid is the envelope of the perimeter-bisecting lines of a triangle; it is a triangle whose sides are outwardly-looking arcs of parabolas that are smoothly extended with up to two line segments.

Fig. 1
figure 1

(left) The area-bisecting deltoid of a triangle; (right) the perimeter-bisecting deltoid

Full size image
Fig. 2
figure 2

(left): Fermat–Torricelli point of a triangle; (right): Fermat–Ceder point of a generalized deltoid

Full size image

This article introduces the generalized deltoid as a triangle whose sides are outwardly-looking arcs of convex curves—see Fig. 2 (right), which we believe to be the appropriate triangle for convex geometry, in spite of its not being a convex curve. In addition to numerous basic properties of this most general triangle/deltoid, we have one main result, the Fermat–Torricelli theorem in convex geometry, and an application of it to affine diameters and area or perimeter-bisecting deltoids.

Before proceeding with the statements of these two theorems, we provide a few basic definitions, examples and some background. At the end of the Introduction, we look at our results in historical perspective and explore venues for future research.

1 Background

Two major areas in convex geometry that reflected all of its more than a century long history are the theory of equipartitions and the one of affine diameters. An equipartition is roughly the problem of dividing a convex set into parts of equal area or perimeter. One of the earliest results on equipartitions is due to Zindler in [73,74,75] (1920), proving that each convex set is partitioned into four pieces of equal area by two perpendicular chords. Buck and Buck’s result in [18] (1949), that every bounded convex planar set can be divided into six parts of equal area by three concurrent lines, marked the beginning of the chapter on sixpartite problems. Neumann in [60] (1945) introduced measure theory into the subject by allowing the area or perimeter to have non-constant mass distribution; see also Eggleston [28,29,30] or Grünbaum [35]. The subject has grown over the last seven decades, and is still popular today. It now includes ideas from geometry, measure theory, analysis, topology and combinatorics; see [2, 4, 6, 11, 38, 64]. For more on the earlier developments in convex geometry, see the expository book [70] by Yaglom and Boltyanskii.

Fig. 3
figure 3

Affine diameters: (left) of a triangle; (right) of a quadrilateral

Full size image

1.1 Affine diameters

An affine diameter of a convex set is a chord whose endpoints belong to two parallel lines that support the set. For example, the affine diameters of a triangle are all its cevians, including sides—see Fig. 3 (left), and the affine diameters of a quadrilateral with no parallel sides are extensions of the affine diameters of a triangle determined by three of its vertices—see Fig. 3 (right). Affine diameters were introduced by Blaschke in [12] (1917), and developed into a major area of convex geometry in the 1950’s through the work of Hammer [41,42,43] and Grünbaum [36] on measures of symmetry of convex bodies, and Klee [47], Neumann [59] and Süss [65] on the critical set of a convex body. For recent developments, see [3, 67, 68], the expository article [62] by Soltan and the books [61] by Schneider and [69] by Toth.

1.1.1 Continuous families of lines

The direction of a line in the plane is the trigonometric angle between the positive part of the x-axis and a parallel to the line that passes through the origin. It is a real number \(\alpha \) modulo \(\pi \) or 180\(^{\circ }\), depending on whether \(\alpha \) is measured in radians or degrees. Refining the definition of a family of lines in the plane that admit a continuous selection, given by J. G. Ceder in [19], we say that a family \({\mathcal {M}}\) of lines in the plane is a continuous family of lines if (1) for each direction \(\alpha \) there is exactly one line \(M_{\alpha }\) of \({\mathcal {M}}\) in the direction of \(\alpha \); and (2) if \(\alpha _n\rightarrow \alpha \), then \(M_{\alpha _n}\rightarrow M_{\alpha }\) (pointwise). For example, all area-bisecting lines and all perimeter-bisecting lines of a convex set, and all affine diameters of a convex set whose perimeter does not contain parallel segments are three continuous families of lines in the plane. For more on continuous families of lines, see Chapter 5 of the book [53] by Martini, Montejano and Oliveros.

1.1.2 The Fermat–Ceder point of a family of lines

Ceder’s main result in [19] says that if \({\mathcal {M}}\) is a continuous family of lines in the plane, then for each triplet \(\alpha _1,\alpha _2,\alpha _3\) of positive real numbers such that \(\alpha _1+\alpha _2+\alpha _3=180^{\circ } \), there exist three concurrent lines of \({\mathcal {M}}\) subtending angles of \(\alpha _1\), \(\alpha _2\), \(\alpha _3\), \(\alpha _1\), \(\alpha _2\), and \(\alpha _3\) respectively. In particular, by taking \(\alpha _i=60^{\circ }\), for \(i=1,2,3\), any continuous family of lines admits an equiangular sixpartite point. We call this a Fermat–Ceder point of the family. This implies that each convex set has three concurrent equiangular area-bisecting lines, three concurrent equiangular perimeter-bisecting lines, and three concurrent equiangular affine diameters. We call the respective intersection points an area Fermat–Ceder point, a perimeter Fermat–Ceder point, and an (affine) Fermat–Ceder point of the convex set.

A tangent to a generalized deltoid is either a line through a point of an open side that supports the side, or a line through a vertex that separates the adjacent sides. As all tangents to a generalized deltoid form a continuous family of lines, a Fermat–Ceder point of a generalized deltoid is one through which pass three equiangular tangents. In this way, the area and perimeter Fermat–Ceder points of a triangle are respectively the same as the Fermat–Ceder points for the triangle’s area or perimeter-bisecting deltoids. Finally, observe that an interior Fermat–Ceder point of a deltoid is also defined by the property that it sees the visible part of each side at a 120\(^{\circ }\) angle—see Fig. 2 (right).

2 Results

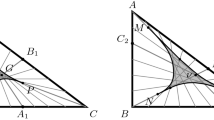
The classical Fermat–Torricelli theorem says that each triangle admits a unique point that minimizes the sum of distances to the vertices. In addition, if all angles are \(<120^{\circ }\), then the Fermat–Torricelli point is an interior point. Otherwise, it coincides with the obtuse angle vertex. Torricelli’s proof of the theorem is based on the construction in Fig. 2 (left), which highlights the Fermat–Torricelli point as being the same as the (affine) Fermat–Ceder point of the triangle. In this way, the classical Fermat–Torricelli theorem can be restated in the following convex, equiangular form:

Each triangle has a unique Fermat–Ceder point. Moreover, (i) if one angle is \(\ge 120^{\circ }\), then the Fermat–Ceder point is that angle’s vertex; (ii) otherwise, the Fermat–Ceder point is an interior point of the triangle.

Our main result generalizes this version of the Fermat–Torricelli theorem for a triangle to a Fermat–Torricelli theorem for a generalized deltoid. The theorem is stated as follows:

Theorem 1

(The Fermat–Torricelli theorem in convex geometry). Each generalized deltoid has a unique Fermat–Ceder point. This falls in one of the following disjoint cases:

  1. (i)

    if the deltoid has a vertex angle \(\ge 120^{\circ }\), then the Fermat–Ceder point is that vertex;

  2. (ii)

    same conclusion, if there is an angular point on a side whose angle is \(\ge 300^{\circ }\);

  3. (iii)

    if the deltoid has an angular point on a side whose angle is in the interval \([240^{\circ },300^{\circ })\), then either the same conclusion holds true or, otherwise,

  4. (iv)

    in all other cases, the Fermat–Ceder point is an interior point of the deltoid.

Fig. 4
figure 4

The three types of border Fermat–Ceder points in Theorem 1: (i) Type 1 (left); (ii) Type 2 (center); and (iii) Type 3 (right). The points are shown together with a triplet of equiangular tangents through them, and the range of directions for all tangents at them

Full size image

Cases (i)–(iii) are visualized in Fig. 4; Case (iv) in Fig. 2 (right). The theorem shows that the Fermat–Ceder point of a generalized deltoid comes with additional features when compared with the Fermat–Ceder point of a triangle. One of these is that, unlike the case of a triangle, the condition that all angles of the deltoid are \(<120^{\circ }\) is neither necessary nor sufficient for the Fermat–Ceder point to be an interior point of the deltoid. The existence of the Fermat–Ceder point of a generalized deltoid follows from a sixpartite result of Ceder in [19]; we prove its uniqueness.

The proof of the generalized Fermat–Torricelli theorem is given in Sect. 2. It uses properties of the generalized deltoid outlined Sect. 1. Of these, a crucial property is that the generalized deltoid admits an inscribed curve as in Fig. 5 (right) with three loops and the Fermat–Ceder point is the unique self-intersection point of this curve.

Our second result, which we state next, is an application of Theorem 1 to continuous families of affine diameters and area or perimeter-bisecting lines of convex polygons.

Theorem 2

(Application of the Fermat–Torricelli theorem in convex geometry). 

  1. (i)

    The affine, area and perimeter Fermat–Ceder points are unique for every triangle and not unique for every pentagon.

  2. (ii)

    The affine Fermat–Ceder points are unique for all quadrilaterals, except for trapezoids; the area Fermat–Ceder points are unique for all quadrilaterals; the uniqueness of the perimeter Fermat–Ceder points holds for elliptic quadrilaterals (including parallelograms), and is unresolved for the rest.

The proof of Theorem 2 is given in Sect. 3. All uniqueness cases are argued by use of Theorem 1 and showing that the affine diameters, area-bisecting lines, or perimeter-bisecting lines of the polygon are families of tangents to certain generalized deltoids. The non-uniqueness proofs are not based on Theorem 1. Both theorems highlight the subject of area and perimeter-bisecting deltoids, introduced in [8, 10, 26], as a concrete deformation of Euclidean geometry in convex geometry, and the subject of generalized deltoids that we begin in this paper as a general deformation of Euclidean geometry in convex geometry. We believe this new chapter on the geometry of generalized deltoids might be the missing link between convex geometry and the classical Euclidean geometry. Other unique and non-unique sixpartite points of convex sets are featured in [7] and [9].

Generalizing the Fermat–Torricelli theorem: our results in historical perspective. The Fermat–Torricelli problem is one of the richest problems in Euclidean geometry and optimization theory. It captured the attention of numerous famous mathematicians, such as Descartes, Fermat, Torricelli, Viviani, Cavalieri, Gauss, Simpson, Steiner, Lindelöf, Sturm, and many others. Roughly speaking, some of these mathematicians generalized the Fermat–Torricelli problem by replacing the three fixed points in the plane with n non-collinear points in a d-dimensional normed or non-Euclidean space; others replaced the fixed points with k-dimensional affine flats, such as lines, planes, and so on (Steiner-Weber problem). For an accurate history of the problem and an account of the specific work of each individual mathematician, see the expository article [50] by Kupitz and Martini, and the book [13] by Boltyanski, Martini and Soltan. More expository presentations of the Fermat–Torricelli theorem can be found in the books [24] by Courant and Robbins, and [46] by Honsberger. Galois theory showed that the Fermat–Torricelli point is non-constructible when \(n\ge 5\), and that is why numerical and nonlinear programming methods are important in approximating the point; see [1, 23, 48, 57]. The Fermat–Torricelli problem is connected to other topics in geometry, such as the Napoleon problem [39, 40, 56], the theory of multifocal ellipses [31, 34], or the one of Steiner minimal trees [21, 33]. For more on the geometric or optimizational aspects of the Fermat–Torricelli or Steiner-Weber problems, see [5, 22, 25, 27, 49, 51, 55, 58, 66].

Our approach to generalizing the Fermat–Torricelli theorem is different from any of these ideas. We transform the optimization problem for the sum of distances to three fixed points in the plane (Fermat–Torricelli point) into an equivalent equiangular visibility problem relative to the sides of the triangle determined by the three points (Fermat–Ceder point). We then deform the sides of the triangle in the most general way possible so that the new equiangular visibility problem has a unique solution. Our final product – the generalized deltoid – does not only satisfy a natural generalization of the Fermat–Torricelli theorem, but is opening up a new, geometric chapter in convex geometry, one where more classical theorems in the Euclidean geometry of the triangle will find their natural generalizations in the convex geometry of the generalized deltoid. The concept of visibility in convex geometry was pioneered by N. M. Stavrakas [63], K. J. Falconer [32] and M. Breen [14,15,16,17]. It has become a major subject through the subsequent work of Marilyn Breen on star-shaped and other variants of convex sets.

A particular case of the generalized deltoid is when its sides are given by explicit equations. This is the case of the area and perimeter-bisecting deltoids of [8, 10, 26]. The algebraic computation of the Fermat–Ceder or other sixpartite points in some of these cases have led to non-constructibility [7]. Based on this evidence, our generalization of the Fermat–Torricelli theorem or its application have the potential of opening up a new chapter in optimization theory, one where many of the above classical and more recent ideas from the Fermat–Torricelli optimization problem will find their way into the Fermat–Ceder visibility problem.

3 Properties of generalized deltoids

This section outlines a baker’s dozen properties of a generalized deltoid, some of which will be used in the proof of Theorem 1, given in Sect. 2. These properties are divided in two categories.

3.1 Basic properties of the deltoid

The first category has seven easy-to-imagine properties, primarily dealing with angles and tangents. These are listed as (D1)–(D7).

3.1.1 (D1)

The sum of the angles of a generalized deltoid is a number between 0\(^{\circ }\) and 180\(^{\circ }\), with the sum is zero when the deltoid has cusps at all vertices, and the sum is 180\(^{\circ }\) when the deltoid is a triangle.

3.1.2 (D2)

In each direction there is a unique tangent to the deltoid. The tangency point of a variable tangent, whose directional angle runs continuously counterclockwise from \(0^{\circ }\) to \(180^{\circ }\), moves continuously clockwise around the entire perimeter. This means that all tangents to a generalized deltoid form a continuous family of lines.

3.1.3 (D3)

Any two tangents to the deltoid intersect at a point that is either interior or on the deltoid.

3.1.4 (D4)

From each exterior point of the deltoid one can draw exactly one tangent; from each interior point one can draw exactly three tangents. From each point on the boundary without vertices one can draw at least one tangent to the current side and exactly one tangent to the union of the remaining two sides. All tangents at a vertex are tangent to both of the adjacent sides. Infinitely many tangents at a point of the deltoid make the point an angular point of the deltoid. The first part of this property implies that there is only one tangent line that passes through each point outside the circumscribed circle of the triangle determined by the vertices of the deltoid. This makes the family of all tangents to the deltoid an outwardly simple line family. Outwardly simple line families were introduced by Hammer and Sobczyk in [44] and further studied in [45] and [20]. Both the continuous families of lines and the outwardly simple line families were extended to the larger class of continuous families of curves by Grünbaum in [37]; see also Zamfirescu [72].

3.1.5 (D5)

None of the three tangent rays from an interior point to the deltoid is contained in the proper angle determined by the other two.

3.1.6 (D6)

The part of the perimeter of the deltoid that is visible from an interior point is the union of three subarcs, one on each side. The dividers are the three tangents from the point to the deltoid—see Fig. 2 (right).

3.1.7 (D7)

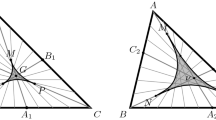
A variable point on a side of a generalized deltoid, moving from an endpoint to the other, sees the incoming side at an increasing angle. Equivalently, it sees the outgoing side at a decreasing angle—see Fig. 5 (left). In particular, by allowing each angular point on a side to see another side at the range of angles between the tangent from the point and the range of tangents at the point, with the notation in Fig. 5 (left), a variable point P, moving on AB from A to B, sees BC at a continuously increasing (shaded) angle, from \(\angle A\) to \(180^{\circ }-\angle B\), while P sees AC at a continuously decreasing angle, from \(180^{\circ }-\angle A\) to \(\angle B\).

3.2 Curves and arcs capable of given angles subtended by sides

The second category of properties of a generalized deltoid, listed as (D8)–(D13), refer to an interesting curve associated with any generalized deltoid, whose self-intersection point is the Fermat–Ceder point of the deltoid. We provide proofs to most of these properties. Unless otherwise stated, the properties are illustrated in Fig. 5 (right).

Fig. 5
figure 5

(left) Property (D7); (right) Properties (D8)–(D13): The curve \({\mathcal {C}}(\theta )=DEFGHI\) capable of angle \(\theta \) relative to the sides of a generalized deltoid ABC, drawn for \(\theta =120^{\circ }\). Solid line arcs are those capable of angle \(\theta \). The sides of the highlighted angle \(\theta \) are \(Q(\alpha )B=t(\alpha )\) and \(Q(\alpha )C=t(\alpha +\theta )\)

Full size image

3.2.1 (D8)

For each angle \(\theta \) between the smallest angle of the deltoid and its supplement, the set of points of the deltoid that see a side either at angle \(\theta \) or \(180^{\circ }-\theta \) is a closed curve \({\mathcal {C}}(\theta )={\mathcal {C}}(180^{\circ }-\theta )\), the curve capable of angle \(\theta \) (or \(180^{\circ }-\theta \)) relative to the sides of the deltoid. To prove this, observe that the locus \({\mathcal {C}}(\theta )\) of points that see either side at angles \(\theta \) or \(180^{\circ }-\theta \) is generated by the intersection point \(Q(\alpha )\) between the tangents \(t(\alpha )\) and \(t(\alpha +\theta )\) that have directional angles \(\alpha \) and \(\alpha +\theta \), for a real number \(\alpha \) modulo \(180^{\circ }\). Since the map \(\alpha \mapsto t(\alpha )\) is continuous, so is \(\alpha \mapsto Q(\alpha )\), making \({\mathcal {C}}(\theta )\) a closed curve.

3.2.2 (D9)

The curve \({\mathcal {C}}(\theta )\) meets the perimeter of its deltoid ABC at six points, labeled in order as D, E, F, G, H, I, so that D, G are the points on side AB that see side BC at angles \(\theta \) and \(180^{\circ }-\theta \), F, I on BC see AC at \(\theta \) and \(180^{\circ }-\theta \), and H, E on AC see AB at \(\theta \) and \(180^{\circ }-\theta \). By (D7), the point D exists only for \(\angle A\le \theta \le 180^{\circ }-\angle B\), with \(D=A\) precisely when \(\theta =\angle A\), and \(D=B\) precisely when \(\theta =180^{\circ }-\angle B\). For simplicity, we allow D to exist for all \(\theta \in [0,180^{\circ }]\), by taking \(D=A\) when \(\theta <\angle A\) and \(D=B\) when \(\theta >180^{\circ }-\angle B\). A similar extension is given for the remaining points E – I.

3.2.3 (D10)

Each of the six arcs determined by the points \(D-I\) on the curve \({\mathcal {C}}(\theta )\) in (D9) is either the locus of all points on the deltoid that see a side at angle \(\theta \), the arc capable of angle \(\theta \) relative to that side, or the locus of all points on the deltoid that see a side at angle \(180^{\circ }-\theta \), the arc capable of \(180^{\circ }-\theta \) relative to the side. In this way, arc DE is capable of angle \(\theta \) relative to side BC, EF is capable of \(180^{\circ }-\theta \) relative to AB, FG is capable of \(\theta \) relative to AC, and so on. To prove the property, with the setting in the proof of (D8), on each of the six arcs, the map \(\alpha \mapsto (\gamma ,\Gamma )\), where \(\gamma \in \{ \theta ,180^{\circ }-\theta \}\), \(\Gamma \) is one of the sides, and \(Q(\alpha )\) sees \(\Gamma \) at angle \(\gamma \), is locally constant, hence constant. The rest is easy, by looking at the figure. Non-degenerate arcs capable of obtuse angles in a generalized deltoid occur more often than non-degenerate arcs capable of their supplements. For example, the curve \({\mathcal {C}}={\mathcal {C}}(120^{\circ })\) for the triangle in Fig. 2 (left) has three (proper) arcs capable of 120\(^{\circ }\) and only one arc capable of 60\(^{\circ }\) relative to the sides—see Fig. 6 (left).

Fig. 6
figure 6

(left): the curve \({\mathcal {C}}(120^{\circ })\) for the triangle in Fig. 2 (left); (right): property (D12). Here \(QB=t(\alpha )\), \(QN=t(\alpha +\theta )\), \(QA=t(\alpha +\theta +\eta )\)

Full size image

3.2.4 (D11)

Each interior point of a generalized deltoid sees each side at an angle strictly larger than the vertex angle opposite to the side. Indeed, let \(\theta _A\) be the angle an interior point P sees the side BC of a generalized deltoid ABC. Then P belongs to the proper arc DE capable of angle \(\theta _A \) relative to BC. By (D9), we must have \(\theta _A>\angle A\). Similarly, \(\theta _B>\angle B\) and \(\theta _C>\angle C\).

3.2.5 (D12)

A point moving from one endpoint to the other on an arc capable of an angle relative to a side of a generalized deltoid, sees the incoming side at a strictly increasing angle and the outgoing side at a strictly decreasing angle—see Fig. 6 (right). To prove this, note that a variable point Q on arc DE capable of angle \(\theta \) relative to side BC sees AC at angle \(\eta \), a continuous function of Q, whose monotonicity is equivalent to injectivity. Suppose two points \(Q_1\) and \(Q_2\) on DE, with \(Q_1<Q_2\) in the sense that \(Q_1\) is closer to D and \(Q_2\) is closer to E, see AC at the same angle \(\eta \), and argue by contradiction. With the notation in the proof of (D8), for \(i=1,2\), \(Q_i\) is the intersection of tangents \(t(\alpha _i)\) and \(t(\alpha _i+\theta )\), for a directional angle \(\alpha _i\). Since the tangent \(t(\alpha )\) at a variable point on the path DBCE sweeps DE from E to D for increasing \(\alpha \), the assumption \(Q_1<Q_2\) translates into \(\alpha _1>\alpha _2\). Then the third tangent from \(Q_i\) to the deltoid has direction \(\beta _i=\alpha _i+\theta +\eta \), with \(\beta _1>\beta _2\). As the tangent \(t(\beta )\) at a variable point on the path DAE sweeps arc DE from D to E for increasing \(\beta \), we must have \(Q_1>Q_2\), a contradiction.

3.2.6 (D13)

A generalized deltoid admits an interior Fermat–Ceder point if and only if the three arcs capable of \(120^{\circ }\) angles relative to the sides meet at an interior point.

4 Proof of Theorem 1

Recall that the existence of Fermat–Ceder points in a generalized deltoid, or, more precisely, the existence of Fermat–Ceder points for the continuous family of tangents to a generalized deltoid, is assured by a result of Ceder from the 1960s, and that we are only proving uniqueness. The proof of Theorem 1 is divided into four easy-to-follow steps.

Step 1: Uniqueness of interior Fermat–Ceder points. Suppose \(\Phi _1\) and \(\Phi _2\) are two interior Fermat–Ceder points of the generalized deltoid ABC. Then \(\Phi _1\) and \(\Phi _2\) belong to arc DE capable of 120\(^{\circ }\) angle relative to side BC. Since they both see side AC at a 120\(^{\circ }\) angle, by continuity and (D12), they must coincide.

Step 2: Three types of border Fermat–Ceder points. By property (D3), the three equiangular tangents to the deltoid at a border Fermat–Ceder point can either be all tangent at the point, or two tangents at the point and one tangent from the point. The range of directions for tangents at a border point is a connected set. In the first case, this is a closed interval of directions at least 120\(^{\circ }\) wide; and in the second case, the interval is at least 60\(^{\circ }\) wide. The first case splits into two subcases: when the angle at the point is proper \(\ge 120^{\circ }\), hence the point is a vertex; and when the angle at the point is improper \(\ge 300^{\circ }\). In the second case, the proper angle subcase is impossible, leading to the only possibility of an improper angle \(\ge 240^{\circ }\). Summarizing, a border Fermat–Ceder point of a generalized deltoid falls in one of the following three types:

Type 1::

A vertex whose angle is \(\ge 120^{\circ }\).

Type 2::

An angular point (on an open side) whose angle is \(\ge 300^{\circ }\).

Type 3::

An angular point whose angle belongs to the interval \([240^{\circ },300^{\circ })\).

These three types of border Fermat–Ceder points of a generalized deltoid respectively correspond to Cases (i)-(iii) in Theorem 1. They are illustrated in Fig. 4.

Note that a Type 1 or 2 angular point must be a Fermat–Ceder point, while a Type 3 may not. For example, the deltoid in Fig. 6 (right) has a 240\(^{\circ }\) angular point at K that is not a Fermat–Ceder point.

Step 3: Uniqueness of border Fermat–Ceder points. The next lemma is useful in proving uniqueness for border Fermat–Ceder points. It says that, by smoothening Types 2 or 3 border Fermat–Ceder points, these will turn into nearby interior Fermat–Ceder points.

Lemma 3

Let V be a Type 2 or 3 Fermat–Ceder point of a generalized deltoid \({\triangle }\). Then for each \(\varepsilon >0\), there exists a generalized deltoid \({\triangle }(\varepsilon )\) such that:

  1. (i)

    \({\triangle }(\varepsilon )={\triangle }\) outside the ball \({\mathcal {B}}\) centered at V and with radius \(\varepsilon \).

  2. (ii)

    \({\triangle }(\varepsilon )\cap {\mathcal {B}}\) is smooth;

  3. (iii)

    \({\triangle }(\varepsilon )\) admits an interior Fermat–Ceder point contained inside \({\mathcal {B}}\).

Proof

Let V be a Type 3 Fermat–Ceder point, and let VXYZ be a tripod made with three equiangular tangents to \({\triangle }\) that pass through V—see Fig. 7. Type 3 means that one of the tangents, say VZ, is a tangent from V, and the remaining two, VX and VY, are tangents at V and the 240\(^{\circ }\) angle \(\angle XVY\) is contained in the angle \(\angle V\) of \({\triangle }\). We translate the tripod VXYZ to \(VX'Y'Z'\) by a vector \(-\varepsilon \overrightarrow{VZ}\), for some small \(\varepsilon >0\), such that \(V'X'\cap {\triangle }=\{ \mu \}\) and \(V'Y'\cap {\triangle }=\{ \nu \}\). We smoothen the angular points \(V',\mu ,\nu \) so that \(V'X'\) and \(V'Y'\) remain tangent to the new curve. For small \(\varepsilon \), all changes made to \({\triangle }\) will fit inside \({\mathcal {B}}\). The new deltoid \({\triangle }(\varepsilon )\) satisfies (i) and (ii), and has \(V'\) as an interior Fermat–Ceder point that belongs to \({\mathcal {B}}\). Type 2 is similar. \(\square \)

Fig. 7
figure 7

Proof of Lemma 3. The old deltoid \({\triangle }\) is marked by dotted lines. The new deltoid \({\triangle }(\varepsilon )\) is obtained from \({\triangle }\) by having the solid line curve replace the two dotted segments from its endpoints to V

Full size image

By the uniqueness in Step 1 and Lemma 3, each generalized deltoid has up to one Type 2 or 3 border Fermat–Ceder point. Suppose now that there are two border Fermat–Ceder points. Then one of the points must be Type 1, and has a range of directions for the tangents at it an interval length \(\ge 120^{\circ }\). The second point is of either type, and has a range of directions an interval length \(\ge 60^{\circ }\)—see Fig. 4. Since the union of the two ranges is a set of measure \(\le 180^{\circ }\), by inclusion-exclusion, the common range falls in one of two cases. First, if the intersection of ranges (intervals) has positive measure, then there are two distinct common directions for tangents at each of the two points. Then the two (unique, by (D2)) tangents to the deltoid in these directions pass through both points, making them coincide with the intersection point of the two tangents. Second, if the intersection of the ranges is measure zero, then the two closed interval ranges concatenate to cover the whole spectrum of directions, and there will be no direction left for tangents at other points on the deltoid, a contradiction. This finishes the proof of Step 3.

Step 4: Uniqueness of all Fermat–Ceder points. To finish the proof of Theorem 1, we need to show that each of the three types of border Fermat–Ceder points is mutually exclusive with an interior Fermat–Ceder point. If there is a Type 1 Fermat–Ceder point then, by (D11), each interior point of the deltoid sees the side opposite the Fermat–Ceder point at \(>120^{\circ }\), so the deltoid has no interior Fermat–Ceder points. Let now P be a Type 2 or 3 Fermat–Ceder point, and let T be the tangency point of the (unique, by (D2)) tangent from P to the deltoid—see Fig. 8. The direction of this tangent does not belong to the range of directions for all tangents at P. In either type, segment PT divides the deltoid into two deltoids for which P is an angular vertex with angle \(\ge 120^{\circ }\). By (D11), the interior points of the smaller deltoids, as well as those on the open segment PT, will see their sides opposite to P at angles \(>120^{\circ }\). Since each such side is a portion of a side in the larger deltoid, each interior point of the larger deltoid sees a side at an angle \(>120^{\circ }\). Thus there are no interior Fermat–Ceder points in these two types as well.

This completes the proof of Theorem 1. Note that although the Fermat–Ceder point of a generalized deltoid is unique, the three equiangular tangents through it might not be unique. For example, a slight rotation of the three equiangular tangents through the border Fermat–Ceder point P in Fig. 8 (left) leads to another triplet of equiangular tangents through P. In general, the three equiangular tangents through a Fermat–Ceder point of a generalized deltoid are not unique if and only if the Fermat–Ceder point is a border point, either Type 1 with \(>120^{\circ }\) angle or Type 2 with \(>300^{\circ }\) angle.

Fig. 8
figure 8

Proof of Step 4: Type 2 (left); and Type 3 (right)

Full size image

5 Proof of Theorem 2

The proof is organized in three parts: (1) the case of a triangle, where the uniqueness follows easily from Theorem 1; (2) the case of a quadrilateral, which comes in subcases with different uniqueness outcomes; and (3) the case of a pentagon, where we prove non-uniqueness for the Fermat–Ceder points.

5.1 Fermat–Ceder points of a triangle

As we have seen in the Introduction, examples of generalized deltoids include all triangles, their area-bisecting deltoids, and their perimeter-bisecting deltoids.

5.1.1 Affine Fermat–Ceder point

When a generalized deltoid is a triangle, all tangents to it are its affine diameters, and the affine Fermat–Ceder point is the Fermat–Torricelli point, whose uniqueness comes from Theorem 1, which in this case is the same as the classical Fermat–Torricelli theorem.

5.1.2 Area Fermat–Ceder point

The area-bisecting deltoid of a triangle, or the envelope of all its area-bisecting lines, see Fig. 1 (left), was studied in [26]. It is a tri-cusped generalized deltoid whose sides are arcs of hyperbolas. By Theorem 1, this admits a unique interior Fermat–Ceder point, which is the triangle’s area Fermat–Ceder point.

5.1.3 Perimeter Fermat–Ceder point

The perimeter-bisecting deltoid of a triangle, shown in Fig. 1 (right), was studied in [8]. It is a tri-cusped generalized deltoid whose each side is an arc of a parabola that is smoothly connected with up to one line segment at either end. By Theorem 1, the perimeter-bisecting deltoid also admits a unique interior Fermat–Ceder point, the perimeter Fermat–Ceder point of the triangle.

By the last observation in Sect. 2, each triangle admits three unique equiangular area-bisecting lines and three unique equiangular perimeter-bisecting lines; it admits three unique equiangular affine diameters precisely when the largest angle is \(\le 120^{\circ }\).

5.2 Fermat–Ceder points of a quadrilateral

The notions of affine Fermat–Ceder points (resp. area Fermat–Ceder points, or perimeter Fermat–Ceder points) extend from triangles to polygons as the points through which pass three equiangular affine diameters (resp. area-bisecting lines, or perimeter-bisecting lines).

5.2.1 Affine Fermat–Ceder point

All quadrilaterals fall in three classes relative to their affine Fermat–Ceder points: parallelograms, trapezoids and neither. The affine Fermat–Ceder point of a parallelogram is its center. Suppose a convex quadrilateral ABCD has no parallel sides, and assume without loss of generality that the points of intersection of opposite sides are positioned on the sides, as shown in Fig. 3 (right). Then the affine diameters of the quadrilateral are extensions of the affine diameters of triangle BCD. In particular, the quadrilateral has a unique affine Fermat–Ceder point, the Fermat–Ceder point of triangle BCD. The Fermat–Torricelli point of a quadrilateral, or the point that minimizes the sum of the distances to the vertices, is the intersection of the diagonals. Unlike the case of a triangle, the affine Fermat–Ceder point of a quadrilateral is in general different from the Fermat–Torricelli point. Since all its affine diameters do not form a continuous family of lines, the trapezoid may be exempted from the study of affine Fermat–Ceder points of quadrilaterals. On the other hand, the affine diameters of a trapezoid satisfy the weaker property of a family with a continuous selection, given in [19], which means that it contains a continuous family. For example, if ABCD is a trapezoid labeled as in Fig. 9 (left), with small base AB, O is the intersection of diagonals, and P is any point on the closed triangle OAB, then, as the figure shows, the affine diameters of triangle PCD extend to a continuous family of affine diameters of the trapezoid. By the case of a triangle, this particular family has a unique affine Fermat–Ceder point, and by varying P, the trapezoid has infinitely many affine Fermat–Ceder points. As a parenthesis, we observe that the property of the triangle that through each interior point pass the same number of affine diameters does not carry over to quadrilaterals. In fact, the triangle is the only convex polygon in the plane that enjoys this property. More generally, the d-dimensional simplex is the only d-dimensional convex polytope whose each interior point belongs to the same maximal number \(\gamma =2^d-1\) of affine diameters [54].

5.2.2 Area Fermat–Ceder point

All quadrilaterals have been classified in [10] according to the shape of their area-bisecting deltoids. The deltoid of a parallelogram is reduced to a point, its center; the one for a trapezoid is a two-cusps/one-angle generalized deltoid—see Fig. 9 (Right); and the area-bisecting deltoid for the remaining quadrilaterals is a three-cusped generalized deltoid. By Theorem 1, each quadrilateral admits a unique area Fermat–Ceder point, the Fermat–Ceder point of its area-bisecting deltoid. This is an interior point of the deltoid in all cases, except for the trapezoid whose area-bisecting deltoid has an angle \(\ge 120^{\circ }\), that is, a trapezoid whose area-bisecting lines through the endpoints of the smaller base make \(\ge 120^{\circ }\) vertical angles looking at the bases. This is the angle \(\angle AMB\) in Fig. 9 (right), shown acute. The area Fermat–Ceder point of such trapezoid is the angular vertex M of its area-bisecting deltoid.

Fig. 9
figure 9

(left): a trapezoid with a continuous family of affine diameters. (right): the area-bisecting deltoid of a trapezoid. Its vertices are the midpoints of the area-bisecting lines through A, B, C, D

Full size image

5.2.3 Perimeter Fermat–Ceder point

All quadrilaterals are classified in [10] according to the shape of their perimeter-bisecting deltoids. The deltoid of a parallelogram is reduced to a point, its center; the one for the elliptic quadrilateral – the quadrilateral whose one diagonal bisects the perimeter – is a tri-cusped generalized deltoid; and the perimeter-bisecting deltoid for each of the remaining quadrilaterals is not a generalized deltoid. By Theorem 1, each elliptic quadrilateral admits a unique perimeter Fermat–Ceder point, the Fermat–Ceder point of its perimeter-bisecting deltoid, which is an interior point of the deltoid. The parallelogram has the center as its perimeter Fermat–Ceder point. For the remaining quadrilaterals, by Ceder’s result, perimeter Fermat–Ceder points exist, but we cannot use Theorem 1 directly to prove their uniqueness, due to the perimeter-bisecting deltoid not being a generalized deltoid. Nevertheless, Theorem 1 can be adapted to work in that case as well. We leave this as exercise to the interested reader.

5.3 Non-uniqueness of Fermat–Ceder points

An area or perimeter sixpartite point of a convex set is the point of intersection of three concurrent lines that divide the area or the perimeter of the set in six equal parts. It was shown in [7] that the area and perimeter sixpartite points are unique for triangles, and in [9] that they are not unique for general polygons. The counterexample in [9] is constructed in two steps: first, construct a dodecagon \(A_1B_1A_2B_2\ldots A_6B_6\) such that the hexagons \(A_1A_2\ldots A_6\) and \(B_1B_2\ldots B_6\) are regular and have distinct centers P and Q; and second, double up the number of sides of the dodecagon by bordering it with isosceles triangles so that the main diagonals of the two hexagons above bisect the area (perimeter) of the 24-gon. Since the three main diagonals in each of the two hexagons are equiangular and bisect the area (perimeter) of the 24-gon, the points P and Q are distinct area (perimeter) Fermat–Ceder points of the 24-gon. The same construction can be modified slightly so that the 24-gon has no parallel sides and the main diagonals in the two hexagons are affine diameters of the 24-gon. This will make P and Q distinct affine Fermat–Ceder points of the new 24-gon. We conclude that the area, perimeter and affine Fermat–Ceder points are not unique for general polygons, hence for general convex sets. The above proof shows that if \(n_1,n_2,n_3\) denote the smallest number of sides that a convex polygon may have such that respectively its affine, area, or perimeter Fermat–Ceder point is not unique, then \(n_1,n_2,n_3\le 24\). The next example shows that the exact values of these numbers are \(n_1=n_2=n_3=5\), with \(n_1=4\) if we include all quadrilaterals whose all affine diameters do not form a continuous family of lines (all trapezoids), and \(n_3=4\) if we include all quadrilaterals whose perimeter-bisecting deltoid is not a generalized deltoid and, additionally, the extension to them of Theorem 1, which we left as an exercise, will turn false for at least one such quadrilateral.

For a regular pentagon, an affine diameter passes through its center if and only if it is an angle bisector. By analyzing the area or perimeter-bisecting deltoid, described in [9] and the first of which is shown in Fig. 10 (left), the same is true about an area or perimeter bisector. The angle bisectors corresponding to consecutive vertices of a regular pentagon meet at 72\(^{\circ }\) angles. They are at the same time affine diameters, area bisectors, perimeter bisectors and symmetry axes for the pentagon. The acute angles determined by any two diagonals are either 36\(^{\circ }\) or 72\(^{\circ }\). Let \(AA_1\) be an angle bisector of the regular pentagon ABCDE. Then the two affine diameters (resp. area or perimeter bisectors) that make 60\(^{\circ }\) angles with it are symmetric, hence all three intersect at an affine Fermat–Ceder point (resp. area Fermat–Ceder point, or perimeter Fermat–Ceder point), which is not the center of the pentagon—see Fig. 10 (right). Its orbit under the action of the dihedral group consists of five affine Fermat–Ceder (resp. area Fermat–Ceder, or perimeter Fermat–Ceder) points. Thus neither of these three kinds of Fermat–Ceder points is unique for the pentagon. This finishes the proof of Theorem 2.

Fig. 10
figure 10

(Left): area-bisecting deltoid of a regular pentagon. Its vertices are the midpoints of the angle bisectors of the much larger, not shown pentagon (dashed lines); its sides are arcs of hyperbolas. The tangent at each non-cuspidal point X separates the adjacent side and the center. (Right): a regular pentagon with its affine diameters and five affine Fermat–Ceder points, one of which is the intersection of equiangular affine diameters \(AA_1\), BF and EG

Full size image