On a Stokes System Arising in a Free Surface Viscous Flow of a Horizontally Periodic Fluid with Fractional Boundary Operators

Abstract

In this note we investigate the initial-boundary value problem for a Stokes system arising in a free surface viscous flow of a horizontally periodic fluid with fractional boundary operators. We derive an integral representation of solutions by making use of the multiple Fourier series. Moreover, we demonstrate a unique solvability in the framework of the Sobolev space of $L^2$-type.

1 Introduction

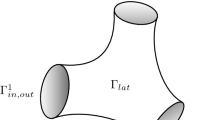
In this note we investigate a Stokes system on the horizontally periodic domain of the mean depth $\frac{\pi }{2}$:

$$\begin{aligned} \begin{aligned} \Omega := \left\{ x=(x_1,x') \in \mathbb {R}^3: 0< x_1 < \frac{\pi }{2}, ~x':=(x_2,x_3) \in \mathbb {T}^2 \right\} , \end{aligned} \end{aligned}$$

where $x_1$ is the vertical coordinate and $x'=(x_2,x_3)$ is the horizontal coordinates in the 2-dimensional torus $\mathbb {T}^2=(-\pi ,\pi ]^2 \cong \mathbb {R}^2/(2\pi \mathbb {Z})^2$. The upper and lower boundaries are denoted by

$$\begin{aligned} \begin{aligned} S_F&= \left\{ (\frac{\pi }{2}, x') : x' \in \mathbb {T}^2 \right\} \equiv \left\{ x_1 = \frac{\pi }{2} \right\} , \\ S_B&=\{(0, x') : x' \in \mathbb {T}^2\} \equiv \{x_1=0\}. \end{aligned} \end{aligned}$$

Our target system is the governing equations:

$$\begin{aligned} \frac{\partial \eta }{\partial t} -u_1&=0 \qquad \text {on } S_F \times (0,\infty ), \end{aligned}$$

(1.1)

$$\begin{aligned} \frac{\partial u}{\partial t} - \nu \Delta u + \nabla p&=0 \qquad \text {in } \Omega \times (0,\infty ), \end{aligned}$$

(1.2)

$$\begin{aligned} \nabla \cdot u&=0 \qquad \text {in } \Omega \times (0,\infty ) \end{aligned}$$

(1.3)

subject to the boundary conditions:

$$\begin{aligned} p- 2\nu \frac{\partial u_1}{\partial x_1} - g \left( \eta -\frac{\pi }{2}\right) - \sigma (-\Delta ')^\alpha \eta&=0 \qquad \text {on } S_F \times (0,\infty ), \end{aligned}$$

(1.4)

$$\begin{aligned} \frac{\partial u_i}{\partial x_1} + \frac{\partial u_1}{\partial x_i}&=0 \quad (i=2,3) \quad \text {on } S_F \times (0,\infty ), \end{aligned}$$

(1.5)

$$\begin{aligned} u&=0 \qquad \text {on } S_B \times (0,\infty ) \end{aligned}$$

(1.6)

with $\Delta ':=\frac{\partial ^2}{\partial x_2^2} + \frac{\partial ^2}{\partial x_3^2}$ and the initial conditions: for $x=(x_1, x') \in \Omega$,

$$\begin{aligned} (\eta , u)|_{t=0}&= (\eta _0, a) =(\eta _0(x'), a_1(x),a_2(x),a_3(x)) \end{aligned}$$

(1.7)

satisfying certain compatibility conditions. Here $\eta =\eta (x',t)$ is an unknown graph of the free surface on $S_F$ and $u=(u_i(x,t))_{1 \le i \le 3}$ is an unknown velocity field of the fluid with a pressure function $p= p(x,t)$. Furthermore, $\nu >0$ is a constant coefficient of the viscosity of the fluid, $\sigma >0$ is the surface tension coefficient, and $g \ge 0$ is a constant describing the effect of gravitational acceleration on the fluid. For simplicity, we assume that only gravity acts on the fluid as an external force.

The motion of a viscous incompressible fluid bounded above by an atmospheric pressure on an upper free surface and below by a rigid bottom is modelled by the Navier–Stokes equations with appropriate boundary conditions (cf. [10]), where the effect of the surface tension is taken into account by using the mean curvature of the free interface $x_1= \eta (x',t)$:

$$\begin{aligned} \sigma \mathcal {H}[\eta ] = \sigma \nabla ' \cdot \left( \frac{\nabla ' \eta }{\sqrt{1+ |\nabla ' \eta |^2}} \right) , \qquad \nabla ':= (\partial _2,\partial _3). \end{aligned}$$

(1.8)

In [2], J. T. Beale studied the initial-boundary value problem of an infinite layer of a viscous fluid having a non-compact upper free surface $\{x_1=\eta (x',t)\}$ and a rigid bottom surface $\{x_1=-b(x)\}$ under the effect of surface tension at free surface, where he showed by using the contraction mapping principle that there exists a unique global solution to the free surface Navier-Stokes problem for a sufficiently small initial data with certain compatibility conditions. For this task, he transformed the Navier-Stokes system to a linearized system on the infinite layer $(-b(x), 0) \times \mathbb {R}^2$ by stretching/compressing on vertical line segments instead of using the Lagrangian formulation (cf. [2, (2.1)–(2.6) in Sect. 2]).

In [6], Nishida–Teramoto–Yoshihara studied the motion of horizontally periodic Navier–Stokes fluid with surface tension. Then they showed such a global-in-time existence for small initial data and the exponential-in-time decay of energy via the linearized problem with $\alpha =1$ at the equilibrium domain $(-b,0) \times \mathbb {T}^2$ (cf. [6, (2.4)–(2.9) in Sect. 2]).

In [9], Tice and Zbarsky introduced the generalized boundary condition of fractional Laplacian type (1.4) in the Stokes system and then studied the decay rate of energy when $0 < \alpha \le 1$ in both cases of the infinite layer $(0,b) \times \mathbb {R}^{d-1}$ and the horizontally periodic domain $(0,b) \times \mathbb {T}^{d-1}$ for arbitrary dimension $d \ge 3$.

In this note, we are concerned with construction of solution operator for the initial-boundary value problem (1.1)–(1.7) constituted of the horizontally periodic Stokes system with fractional boundary operators. Indeed, we show that the problem possesses an integral representation of solutions by making use of the multiple Fourier series (cf. Theorem 3.1). From the alternative formulation, we demonstrate the unique solvability, provided that $0< \alpha < 3/2$ (cf. Theorem 4.1).

This note is organized as follows. In Sect. 2, as a preliminary, we review the almost-everywhere convergence results of the multiple Fourier series in the Sobolev spaces and also introduce the Sobolev–Slobodeckij spaces of $L^2$-type. In Sect. 3, we derive a Fourier representation of solutions to the IBVP (1.1)–(1.7). In Sect. 4, we establish the unique solvablity of the IBVP (1.1)–(1.7).

2 Preliminaries

Let $\partial _i = \partial /\partial x_i$ for $i=1,\dots ,d$. We use the standard multi-index notation for the spatial differential operator: $\partial ^\beta = \partial _1^{\beta _1} \dots \partial _d^{\beta _d}$ with the order $|\beta |=\beta _1 + \dots + \beta _d$ for $\beta =(\beta _1,\dots ,\beta _d) \in \mathbb {N}_0^d$, and $\partial ^0 = Id$.

We denote by $\mathbb {T}^d$ the d-dimensional torus $(-\pi , \pi ]^d \cong \mathbb {R}^d/(2\pi \mathbb {Z})^d$, and specially, $\mathbb {T}:= \mathbb {T}^1$.

Let $\{\mathcal {F} [f](n)\}_{n \in \mathbb {Z}^d}$ denote the Fourier coefficients of an absolutely integral function $f(x)=f(x_1,\dots ,x_d)$ on $\mathbb {T}^d$:

$$\begin{aligned} \mathcal {F}[f](n):= \frac{1}{(2\pi )^d} \int _{\mathbb {T}^d} e^{-\sqrt{-1}n \cdot x} f(x) dx, \end{aligned}$$

(2.1)

where $n \cdot x = n_1 x_1+ \dots + n_d x_d$ and $dx = dx_1 \dots dx_d$. The multiple Fourier series is formally defined by the series

$$\begin{aligned} \mathcal {F}^*[\mathcal {F}[f]](x):=\sum _{n \in \mathbb {Z}^d} \mathcal {F}[f](n) e^{\sqrt{-1}n \cdot x}. \end{aligned}$$

(2.2)

Here we recall the celebrated almost-everywhere convergence result of the multiple Fourier series on $\mathbb {T}^d$ (cf. [3, 4, 7, 8]). If $f=f(x)$ lies in the Lebesgue space $L^p(\mathbb {T}^d)$ with $p >1$, the rectangular partial sum

$$\begin{aligned} S^\square _N[f](x) = \sum _{|n_1|,\dots ,|n_d| \le N} \mathcal {F}[f](n) e^{\sqrt{-1}n \cdot x} \end{aligned}$$

converges to f(x) for almost every $x \in \mathbb {T}^d$ as $N \rightarrow \infty$. Recently, for the Sobolev (or Bessel potential) space $H^{r,p}(\mathbb {T}^d)$ with the norm

$$\begin{aligned} \Vert f\Vert _{H^{r,p}(\mathbb {T}^d)} = \Biggl \Vert \sum _{n \in \mathbb {Z}^d} (1+|n|^2)^{\frac{r}{2}} \mathcal {F}[f](n) e^{\sqrt{-1}n \cdot x} \Biggr \Vert _{L^p(\mathbb {T}^d)}, \end{aligned}$$

Ashurov [1] proved that the spherical partial sum

$$\begin{aligned} S_N[f](x) = \sum _{|n|^2=n_1^2+ \dots +n_d^2 \le N} \mathcal {F}[f](n) e^{\sqrt{-1}n \cdot x} \end{aligned}$$

converges to f(x) in $H^{r,p}(\mathbb {T}^d)$ for almost every $x \in \mathbb {T}^d$ as $N \rightarrow \infty$, provided that $1 < p \le 2$ and $r > (d-1)(\frac{1}{p}-\frac{1}{2})$. Therefore, when $p=2$, if $f \in H^{r,2}(\mathbb {T}^d)$ for $r \ge 0$, then we obtain the inversion formula $f(x)= \mathcal {F}^*[\mathcal {F}[f]](x)$ for a.e. $x \in \mathbb {T}^d$, where the Fourier series $\mathcal {F}^*[\,\cdot \,](x)$ corresponds to the pointwise limit of the spherical (resp. rectangular) partial sum when $r>0$ (resp. $r=0$). Hence, from the Parseval formula

$$\begin{aligned} \Vert f\Vert _{H^{r,2}(\mathbb {T}^d)}^2 = \frac{1}{(2\pi )^d} \sum _{n \in \mathbb {Z}^d} (1+|n|^2)^r \left| \mathcal {F}[f](n) \right| ^2, \end{aligned}$$

we get the characterization of $H^{r,2}(\mathbb {T}^d) = \{ f \in L^2(\mathbb {T}^d): \Vert f\Vert _{H^{r,2}(\mathbb {T}^d)} < \infty \}$. From now on, we shall use the shorthand notation $H^r(\mathbb {T}^d):= H^{r,2}(\mathbb {T}^d)$.

For $m \in \mathbb {N}_0$, we set the Slobodeckij space of $L^2$-type on $D= \mathbb {T}^d$ or $\Omega$:

$$\begin{aligned} W^m(D):= \left\{ f \in L^2(D):\Vert f\Vert _{W^{m}(D)}:= \sum _{|\beta |=0}^m \Vert \partial ^\beta f\Vert _{L^2(D)} < \infty \right\} . \end{aligned}$$

In particular, $W^m(\mathbb {T}^d)$ (resp. $W^0(D)$) coincides with $H^m(\mathbb {T}^d)$ (resp. $L^2(D)$). We also define the space of the $\frac{1}{2}$-fractional type on $\mathbb {T}^d$:

$$\begin{aligned} W^{m+\frac{1}{2}}(\mathbb {T}^d):= \left\{ f \in W^{m}(\mathbb {T}^d): \frac{|f(x)-f(y)|}{|x-y|^{\frac{d+1}{2}}} \in L^2(\mathbb {T}^d \times \mathbb {T}^d) \right\} \end{aligned}$$

with the norm

$$\begin{aligned} \Vert f\Vert _{W^{m+\frac{1}{2}}(\mathbb {T}^d)}:= \Vert f\Vert _{W^{m}(\mathbb {T}^d)} + \left( \int _{\mathbb {T}^d}\int _{\mathbb {T}^d} \frac{|f(x)-f(y)|^2}{|x-y|^{d+1}} dxdy \right) ^\frac{1}{2}. \end{aligned}$$

We should notice that there exists a trace operator $\gamma : W^m (\Omega ) \rightarrow W^{m-\frac{1}{2}}(S_B \cup S_F)$ such that $\gamma f = f|_{S_B \cup S_F}$ for $m \in \mathbb {N}$ (cf. [5]).

Let us introduce the subspace of $W^m(\mathbb {T}^3)$ (resp. $H^r(\mathbb {T}^3)$) consisting of functions with the sine-like symmetry in $x_1 \in \mathbb {T}$:

$$\begin{aligned} \begin{aligned} W_{s_1}^m(\mathbb {T}^3)&:= \bigl \{ f \in W^m(\mathbb {T}^3) : f(-x_1,x') = -f(x), ~f(\pi -x_1,x') =f(x) ~\text{ for } x \in \mathbb {T}^3 \bigr \} \\ \bigl ( \text{ resp. } H_{s_1}^r(\mathbb {T}^3)&:= \bigl \{ f \in H^r(\mathbb {T}^3) : f(-x_1,x') = -f(x), ~f(\pi -x_1,x') =f(x) ~\text{ for } x \in \mathbb {T}^3 \bigr \} \bigr ). \end{aligned} \end{aligned}$$

The space restricted to $\Omega$ is denoted by

$$\begin{aligned} W_{s_1}^m(\Omega ):= \bigl \{ f=f^\star |_{\{0< x_1 < \frac{\pi }{2}\}}: f^\star \in W_{s_1}^m(\mathbb {T}^3) \bigr \} \end{aligned}$$

(2.3)

with the norm

$$\begin{aligned} \Vert f\Vert _{W_{s_1}^m(\Omega )} = \Vert f^\star \Vert _{W^m(\mathbb {T}^d)}. \end{aligned}$$

(2.4)

In particular, when $m = 2$ (resp. $m = 3$), $f \in W_{s_1}^m(\mathbb {T}^3)$ satisfies $f=0$ on $S_B$ (resp. $f=0$ on $S_B$ and $\partial _1 f=0$ on $S_F$), since $W^2(\mathbb {T}^3) \subset C(\mathbb {T}^3)$ (resp. $W^3(\mathbb {T}^3) \subset C^1(\mathbb {T}^3)$) by the embedding theorem.

For a function $f(x)=f(x_1,x_2,x_3)=f(x_1, x'): \mathbb {T}^3 \rightarrow \mathbb {R}$, we denote the tangential Fourier coefficients by

$$\begin{aligned} \mathcal {F}'[f](x_1, n') \equiv \hat{f}(x_1, n'):= \frac{1}{(2\pi )^2} \int _{\mathbb {T}^2} e^{-\sqrt{-1}n' \cdot x' } f(x) dx' \end{aligned}$$

(2.5)

for $(x_1, n') \in \mathbb {T}\times \mathbb {Z}^2$, where $n'=(n_2, n_3)$, $n' \cdot x' = n_2x_2+ n_3 x_3$ and $dx' = dx_2dx_3$. The Fourier series of a given function $\hat{f}(x_1, n'): \mathbb {T}\times \mathbb {Z}^2 \rightarrow \mathbb {C}$ is denoted by

$$\begin{aligned} \mathcal {F}'^*[\hat{f}](x):= \sum _{n' \in \mathbb {Z}^2} \hat{f}(x_1,n') e^{\sqrt{-1}n' \cdot x'}. \end{aligned}$$

(2.6)

We define the $x_1$-tangential fractional Laplacian acting on $f(x): \Omega \rightarrow \mathbb {R}$ by

$$\begin{aligned} \mathcal {F}'[(-\Delta ')^\alpha f](x_1,n'):= |n'|^{2\alpha } \hat{f}(x_1,n') \qquad (\alpha >0) \end{aligned}$$

(2.7)

with $|n'|^2 = n_2^2+n_3^2$ and $\hat{f}(x_1,n')=\mathcal {F}'[f](x_1,n')$.

For a function $g(x_1): (0, \frac{\pi }{2}) \rightarrow \mathbb {R}$, we set the sine-type (resp. cosine-type) Fourier coefficients

$$\begin{aligned} \mathcal {S}_1[g](n_1):=&\frac{4}{\pi } \int _0^\frac{\pi }{2} \sin ((2n_1 -1) x_1) g(x_1) dx_1 \nonumber \\ \biggl ( \mathcal {C}_1[g](n_1):=&\frac{4}{\pi } \int _0^\frac{\pi }{2} \cos ((2n_1 -1) x_1) g(x_1) dx_1 \biggr ) \end{aligned}$$

(2.8)

for $n_1 \in \mathbb {N}$ and the associated Fourier series

$$\begin{aligned} \mathcal {S}_1^*[\mathcal {S}_1[g]](x_1):=&\sum _{n \in \mathbb {N}} \mathcal {S}_1[g](n_1) \sin ((2n_1 -1) x_1) \nonumber \\ \biggl ( \mathcal {C}_1^*[\mathcal {C}_1[g]](x_1):=&\sum _{n \in \mathbb {N}} \mathcal {C}_1[g](n_1) \cos ((2n_1 -1) x_1) \biggr ) \end{aligned}$$

(2.9)

for $x_1 \in \mathbb {T}$.

For a function $f(x): \Omega \rightarrow \mathbb {R}$, we define the coefficients of the hybrid $x_1$-sine-type Fourier series by

$$\begin{aligned} \mathcal {F}_{s_1}[f](n):= \mathcal {S}_1[\mathcal {F}'[f]](n) = \frac{1}{\pi ^3} \int _\Omega \sin ((2n_1 -1) x_1) e^{-\sqrt{-1}n' \cdot x'} f(x) dx \end{aligned}$$

(2.10)

for $n=(n_1,n') \in \mathbb {N}\times \mathbb {Z}^2$ and the associated series of $\mathcal {F}_{s_1}[f]: \mathbb {N}\times \mathbb {Z}^2 \rightarrow \mathbb {C}$ by

$$\begin{aligned} \mathcal {F}^*_{s_1}[\mathcal {F}_{s_1}[f]](x):=\sum _{n \in \mathbb {N}\times \mathbb {Z}^2} \mathcal {F}_{s_1}[f](n) \sin ((2n_1 -1) x_1) e^{\sqrt{-1}n' \cdot x'}. \end{aligned}$$

(2.11)

Here we note that for $f(x):\mathbb {T}^3 \rightarrow \mathbb {R}$ and $l_1 \in \mathbb {Z}$,

$$\begin{aligned} \mathcal {F} [f](l_1,n')&= \frac{1}{2\pi } \int _{\mathbb {T}} e^{-\sqrt{-1} l_1 x_1} \mathcal {F}'[f](x_1,n') dx_1 \\&= \frac{1}{\pi } \int _0^\pi \sin (l_1 x_1) \mathcal {F}'[f](x_1,n') dx_1 \\&= {\left\{ \begin{array}{ll} 0 &{} (\text {for } |l_1| =2n_1), \\ \displaystyle \frac{1}{2} \mathcal {F}_{s_1}[f](n_1,n') &{} (\text {for } |l_1|=2n_1-1) \end{array}\right. } \end{aligned}$$

for $n_1 \in \mathbb {N}_0$, and thus, $\mathcal {F}^*[\mathcal {F} [f]] = \mathcal {F}^*_{s_1}[\mathcal {F}_{s_1}[f]]$. On the other hand, thanks to the convergence results as mentioned above, the inversion formula $\mathcal {F}_{s_1}^*[\mathcal {F}_{s_1}[f]] =f$ holds on $W_{s_1}^m(\Omega )= H_{s_1}^m(\mathbb {T}^3)$ for $m \in \mathbb {N}_0$ under the suitable limit operation. Therefore, we may redefine

$$\begin{aligned} \Vert f\Vert _{W_{s_1}^m(\Omega )}&:= \left( \sum _{n \in \mathbb {N}\times \mathbb {Z}^2} ((2n_1-1)^2+|n'|^2)^\frac{m}{2} \left| \mathcal {F}_{s_1}[f](n) \right| ^2 \right) ^\frac{1}{2} \nonumber \\&=\bigl \Vert ((2n_1-1)^2+|n'|^2)^\frac{m}{2} \mathcal {F}_{s_1}[f](n) \bigr \Vert _{l^2(\mathbb {N}\times \mathbb {Z}^2)}. \end{aligned}$$

(2.12)

For $\rho ,r >0$, we define the fractional differential operator $|\partial _1|^\rho |\nabla '|^r$ acting on $f \in W_{s_1}^0(\Omega ) \cong L^2(\Omega )$ by

$$\begin{aligned} \mathcal {F}_{s_1} [|\partial _1|^\rho |\nabla '|^r f](n):= (2n_1-1)^\rho |n'|^r \mathcal {F}_{s_1} [f](n) \end{aligned}$$

(2.13)

for $n=(n_1,n') \in \mathbb {N}\times \mathbb {Z}^2$.

We finish this section to provide basic properties regarding the heat semigroups.

Proposition 2.1

For $f: \mathbb {T}^d \rightarrow \mathbb {R}$, let

$$\begin{aligned} \begin{aligned} e^{\nu t \Delta } f:= \mathcal {F}^*[e^{-\nu |n|^2 t} \mathcal {F}[f]] \qquad (t\ge 0). \end{aligned} \end{aligned}$$

(2.14)

Then $\{ e^{\nu t \Delta } \}_{t \ge 0}$ is a strongly continuous semigroup on $H^r(\mathbb {T}^d)$.

Moreover, for every $m \in \mathbb {N}$, there exists a constant $C=C(m) >0$ such that

$$\begin{aligned} \sup _{t > 0} t^\frac{m}{2} \sup _{|\beta | = m} \Vert \partial ^\beta e^{\nu t \Delta } f \Vert _{L^2(\mathbb {T}^d)} \le C \Vert f \Vert _{L^2(\mathbb {T}^d)}, \end{aligned}$$

and $v:= e^{\nu t \Delta }f$ is a smooth solution to the heat equation $\partial _t v= \nu \Delta v$ on $\mathbb {T}^d \times (0,\infty )$, where $\Delta = \partial _1^2 + \dots +\partial _d^2$.

In addition, $\Vert e^{\nu t \Delta } f\Vert _{H^r(\mathbb {T}^2)} \le \Vert f\Vert _{H^r(\mathbb {T}^2)}$ for $t \ge 0$.

Proof

We can verify the main statement by using the inversion formula and the Parseval formula. We omit the detail of the proof. $\square$

Proposition 2.2

Let $m \in \mathbb {N}_0$ be arbitrary. For $f: \Omega \rightarrow \mathbb {R}$, let

$$\begin{aligned} e^{\nu t \Delta _{s_1}} f:= \mathcal {F}_{s_1}^*[e^{-\nu ((2n_1-1)^2+ |n'|^2) t} \mathcal {F}_{s_1}[f]] \qquad (t \ge 0). \end{aligned}$$

(2.15)

Then $\{ e^{\nu t \Delta _{s_1}} \}_{t \ge 0}$ is a strongly continuous semigroup on $W_{s_1}^m(\Omega )$ such that $v:= e^{\nu t \Delta _{s_1}} f$ is a smooth solution to the heat equation $\partial _t v = \nu \Delta v$ in $\Omega \times (0,\infty )$. Moreover, the solution $v=v(t)$ satisfies $\partial _1^{2k} v=0$ on $S_B$ and $\partial _1^{2k+1} v=0$ on $S_F$ for all $t>0$ and every $k \in \mathbb {N}_0$.

Proof

For $f \in W_{s_1}^m (\Omega )$, let $f^\star \in W_{s_1}^m (\mathbb {T}^d)$ with $f^\star |_{\{0< x_1 < \frac{\pi }{2}\}} =f$. Let $v:=e^{\nu t \Delta } f^\star$. Since $v= e^{\nu t \Delta _{s_1}} f$, the main assertion follows from Proposition 2.1. Furthermore, it is easily verified that $\partial _1^{2k} v|_{x_1=0}=\partial _1^{2k+1} v|_{x_1=\frac{\pi }{2}}=0$. $\square$

3 Fourier Representation of Solutions

In this section, we present a Fourier representation of solutions to the IBVP (1.1)–(1.7).

For a function $z=z(x_2,x_3)=z(x'): \mathbb {T}^2 \rightarrow \mathbb {R}$, we set the heat semigroups:

$$\begin{aligned} e^{\nu t \Delta '} z:= \mathcal {F}'^*[e^{-\nu |n'|^2 t} \mathcal {F}'[z]], \qquad |n'|^2 = n_2^2 + n_3^2, \end{aligned}$$

(3.1)

and

$$\begin{aligned} e^{\nu t \Delta _{s_1}} (x_1 z):= \mathcal {F}_{s_1}^* \left[ \frac{4}{\pi } \frac{(-1)^{n_1-1}}{(2n_1-1)^2} e^{-\nu \kappa (n) t} \mathcal {F}'[z] \right] , \end{aligned}$$

(3.2)

which is consistent with the semigroup (2.15) when $f= x_1z(x_2,x_3)$.

For a set of functions $\{ \eta (x',t),\eta _0(x'), u(x,t), a(x), p(x,t)\}$ in (1.1)–(1.7), we set

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{\eta }=\hat{\eta }(n',t):= \mathcal {F}'[\eta ], \\ \hat{\eta }_0=\hat{\eta }_0(n',t):= \mathcal {F}'[\eta _0], \\ \hat{u}=(\hat{u}_i(x_1,n',t))_{1 \le i \le 3}:= \mathcal {F}'[u]= (\mathcal {F}'[u_i])_{1 \le i \le 3}, \\ \hat{a}=(\hat{a}_i(x_1,n',t))_{1 \le i \le 3}:= \mathcal {F}'[a] = (\mathcal {F}'[a_i])_{1 \le i \le 3}, \\ \hat{p}=\hat{p}(x_1,n',t):= \mathcal {F}'[p]. \end{array}\right. } \end{aligned}$$

(3.3)

Theorem 3.1

Consider the initial-boundary value problem (1.1)–(1.7) with the additional boundary condition:

$$\begin{aligned} \partial _1^2 u =0 \quad \text {on } S_B, \qquad \partial _1^3 u =0 \quad \text {on } S_F. \end{aligned}$$

(3.4)

Let

$$\begin{aligned} \kappa (n):= (2n_1-1)^2 + |n'|^2, \qquad \lambda ^\alpha (n'):= g + \sigma |n'|^{2\alpha }, \end{aligned}$$

(3.5)

and let

$$\begin{aligned} h(x',t):= \eta (x',t) - \frac{\pi }{2}, \qquad \hat{h}(n',t):= \mathcal {F}'[h](n') = \hat{\eta }(n',t) - \frac{\pi }{2}. \end{aligned}$$

(3.6)

We set the auxiliary functions:

$$\begin{aligned} \begin{aligned}&z_0(x', t) = e^{\nu t \Delta '} a_1(\frac{\pi }{2}, x') - \int _0^t e^{\nu (t-s) \Delta '} \mathcal {F}'^* \biggl [ |n'| \tanh \frac{\pi }{2} |n'| \bigl ( 2\nu \hat{z}_1(n',s) + \lambda ^\alpha (n') \hat{h}(n',s) \bigr ) \biggr ] ds, \end{aligned} \end{aligned}$$

(3.7)

$$\begin{aligned} \begin{aligned}&\quad z_1(x', t) = e^{3\nu t \Delta '} \partial _1 a_1(\frac{\pi }{2}, x') + \bigl (g+(-\Delta ')^\alpha \bigr ) \Delta ' \int _0^t e^{3\nu (t-s) \Delta '} h(s) ds, \end{aligned} \end{aligned}$$

(3.8)

and

$$\begin{aligned} Q_1(x,t)&:= \mathcal {F}_{s_1}^* \left[ \frac{4}{\pi } \frac{ (-1)^{n_1-1} |n'|^4 }{(2n_1-1)^2 \kappa (n)} \int _0^t e^{-\nu \kappa (n) (t-s)} \bigl ( 2\nu \hat{z}_1(n',s) + \lambda ^\alpha (n') \hat{h}(n',s) \bigr ) ds \right] , \end{aligned}$$

(3.9)

$$\begin{aligned} Q_i(x,t)&:= \mathcal {F}_{s_1}^* \biggl [ \frac{4}{\pi } \sqrt{-1} n_i |n'| \frac{ (-1)^{n_1-1} (2(2n_1-1)^2 + |n'|^2) }{(2n_1-1) \kappa (n)} \tanh \frac{\pi }{2} |n'| \nonumber \\&\qquad \times \int _0^t e^{-\nu \kappa (n) (t-s)} \bigl ( 2\nu \hat{z}_1(n',s) + \lambda ^\alpha (n') \hat{h}(n',s) \bigr ) ds \biggr ] \end{aligned}$$

(3.10)

for $i=2,3$. Then the solution $(\eta , u)$ satisfies the equations

$$\begin{aligned} \eta (x',t) = \eta _0(x') + \int _0^t z_0(x',s) ds \end{aligned}$$

(3.11)

and

$$\begin{aligned} \begin{aligned} u_1(x,t)&= x_1 z_1(t) - e^{\nu t \Delta _{s_1}} \left( x_1 \partial _1a_1 (\frac{\pi }{2}, x') \right) + e^{\nu t \Delta _{s_1}} a_1 + Q_1(x,t), \end{aligned} \end{aligned}$$

(3.12)

$$\begin{aligned} \begin{aligned} u_i(x,t)&= -x_1 \partial _i z_0(t)+ e^{\nu t \Delta _{s_1}} \left( x_1 \partial _i a_1 (\frac{\pi }{2}, x' ) \right) + e^{\nu t \Delta _{s_1}} a_i + Q_i(x,t) \end{aligned} \end{aligned}$$

(3.13)

for $i=2,3$.

Proof

We have that the initial datum $a=u|_{t=0}$ satisfies the conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla \cdot a =0, \quad a|_{x_1=0}=0, \quad \partial _1^2 a|_{x_1=0}=0, \quad \partial _1^3 a|_{x_1=\frac{\pi }{2}} =0, \\ \partial _1 a_i|_{x_1=\frac{\pi }{2}} =- \partial _i a_1|_{x_1=\frac{\pi }{2}} \quad (i=2,3). \end{array}\right. } \end{aligned}$$

(3.14)

Set

$$\begin{aligned} {\left\{ \begin{array}{ll} v= (v_i(x,t))_{1\le i \le 3}:=(\partial _1 u_i)_{1 \le i \le 3}, \\ \hat{v}=(\hat{v}_i(x_1,n',t))_{1 \le i \le 3}:= \mathcal {F}'[v]= (\partial _1 \hat{u}_i)_{1 \le i \le 3}, \\ z_1= z_1(x',t):= v_1 |_{x_1=\frac{\pi }{2}}= \partial _1 u_1 |_{x_1=\frac{\pi }{2}}, \\ \hat{z}_1=\hat{z}_1(n',t):=\mathcal {F}'[z_1]= \hat{v}_1 |_{x_1=\frac{\pi }{2}}= \partial _1 \hat{u}_1 |_{x_1=\frac{\pi }{2}}, \\ z_0= z_0(x',t):= u_1 |_{x_1=\frac{\pi }{2}}, \\ \hat{z}_0=\hat{z}_0(n',t):= \mathcal {F}'[z_0]= \hat{u}_1|_{x_1=\frac{\pi }{2}}. \end{array}\right. } \end{aligned}$$

(3.15)

The boundary condition (1.4) can be rewritten as

$$\begin{aligned} p|_{x_1=\frac{\pi }{2}} = 2 \nu z_1 + g h + \sigma (-\Delta ')^\alpha h, \end{aligned}$$

(3.16)

which gives

$$\begin{aligned} \begin{aligned} \hat{p}(\frac{\pi }{2},n',t) =2\nu \hat{z}_1(n',t) + \lambda ^\alpha (n') \hat{h}(n',t). \end{aligned} \end{aligned}$$

Applying the divergence operator $\nabla \cdot$ to the second equation (1.2), we obtain that $\Delta p =0$, i.e., $(\partial _1^2 -|n'|^2) \hat{p}=0$. Therefore, $\hat{p}=C_1(n',t) e^{x_1|n'|}+ C_2(n',t) e^{-x_1|n'|}$. Here we impose the boundary condition on $S_B$: $\partial _1 p|_{x_1=0} = 0$, that is, $\partial _1 \hat{p}|_{x_1=0} = 0$. We thus deduce from the two boundary data that

$$\begin{aligned} \hat{p}(x_1, n',t) = \frac{\cosh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} \, \bigl ( 2\nu \hat{z}_1(n',t) + \lambda ^\alpha (n') \hat{h}(n',t) \bigr ). \end{aligned}$$

(3.17)

Since the second equation (1.2) yields

$$\begin{aligned} \partial _t v_i - \nu \Delta v_i + \partial _i \partial _1 p =0 \qquad (i=1,2,3), \end{aligned}$$

(3.18)

we deduce from the additional boundary condition $\partial _1^3 u |_{x_1=\frac{\pi }{2}} =0$ in (3.4) that the function $z_1(x',t)=v_1(\frac{\pi }{2}, x', t)$ satisfies

$$\begin{aligned} \partial _t z_1 - \nu \Delta ' z_1 + \partial _1^2 p |_{x_1=\frac{\pi }{2}}=0, \qquad \Delta '= \partial _2^2+\partial _3^2. \end{aligned}$$

(3.19)

On the other hand, we can see from (3.18) with the pressure (3.17) that $\hat{v}_1(x_1,n',t)$ is a solution to the IBVP of the 1-D heat equation:

$$\begin{aligned} \partial _t \hat{v}_1 - \nu \partial _1^2 \hat{v}_1 + \nu |n'|^2 \hat{v}_1 + |n'|^2 \hat{p} =0 \end{aligned}$$

(3.20)

for $(x_1,n',t) \in [0,\hbox { }\ \frac{\pi }{2}] \times \mathbb {Z}^2 \times [0,\infty )$ subject to the boundary conditions

$$\begin{aligned} \hat{v}_1|_{x_1=\frac{\pi }{2}} = \hat{z}_1, \qquad \partial _1 \hat{v}_1|_{x_1=0} =0, \qquad \partial _1^2 \hat{v}_1|_{x_1=\frac{\pi }{2}} =0 \end{aligned}$$

(3.21)

and the initial condition $\hat{v}_1|_{t=0} = \partial _1 \hat{a}_1$. In particular, it follows from (3.19) with the pressure (3.17) that

$$\begin{aligned} \frac{d \hat{z}_1}{dt} + \nu |n'|^2 \hat{z}_1 + |n'|^2 (2\nu \hat{z}_1 + \lambda ^\alpha \hat{h}) = 0, \qquad \hat{z}_1|_{t=0} = \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}} \end{aligned}$$

(3.22)

for $(n',t) \in \mathbb {Z}^2 \times [0,\infty )$, which yields

$$\begin{aligned} \hat{z}_1(n', t) = e^{-3\nu |n'|^2t} \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}} - \lambda ^\alpha (n') |n'|^2 \int _0^t e^{-3\nu |n'|^2(t-s)} \hat{h}(n', s)ds. \end{aligned}$$

(3.23)

Therefore, we obtain (3.8).

Set $\hat{w}_1:= \hat{v}_1 -\hat{z}_1$. We deduce from (3.20)–(3.22) with (3.17) that

$$\begin{aligned} \partial _t \hat{w}_1 - \nu \partial _1^2 \hat{w}_1 + \nu |n'|^2 \hat{w}_1 + |n'|^2 \left( \frac{\cosh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} -1 \right) (2\nu \hat{z}_1 + \lambda ^\alpha \hat{h}) =0 \end{aligned}$$

(3.24)

subject to the boundary conditions

$$\begin{aligned} \hat{w}_1|_{x_1=\frac{\pi }{2}}=0, \qquad \partial _1 \hat{w}_1|_{x_1=0}=0, \qquad \partial _1^2 \hat{w}_1|_{x_1=\frac{\pi }{2}}=0 \end{aligned}$$

(3.25)

and the initial condition $\hat{w}_1|_{t=0} = \partial _1 \hat{a}_1 - \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}}$. By using the Fourier method and the Duhamel formula, we get

$$\begin{aligned}&\hat{w}_1(x_1, n',t) \\&\quad = \mathcal {C}_1^* \bigl [e^{-\nu \kappa (n) t} \mathcal {C}_1[ \partial _1 \hat{a}_1 - \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}}] \bigr ] \\&\qquad - |n'|^2 \mathcal {C}_1^* \left[ \mathcal {C}_1 \biggl [ \frac{\cosh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} -1 \biggr ] \int _0^t e^{-\nu \kappa (n) (t-s)} (2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s)) ds \right] \\&\quad = \mathcal {C}_1^* \bigl [(2n_1-1) e^{-\nu \kappa (n) t} \mathcal {F}_{s_1}[a_1]\bigr ] - \mathcal {C}_1^* \left[ \frac{4}{\pi } \frac{(-1)^{n_1-1}}{2n_1-1} e^{-\nu \kappa (n) t} \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}} \right] \\&\qquad - \mathcal {C}_1^* \left[ \frac{4}{\pi } (-1)^{n_1-1} |n'|^2 \biggl ( \frac{2n_1-1}{(2n_1-1)^2+ |n'|^2} - \frac{1}{2n_1-1} \biggr ) \int _0^t e^{-\nu \kappa (n) (t-s)} (2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s)) ds \right] \\&\quad = \mathcal {C}_1^* \bigl [(2n_1-1) e^{-\nu \kappa (n) t} \mathcal {F}_{s_1}[a_1]\bigr ] - \frac{4}{\pi } \mathcal {C}_1^* \left[ \frac{(-1)^{n_1-1}}{2n_1-1} e^{-\nu \kappa (n) t} \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}} \right] \\&\qquad + \mathcal {C}_1^* \left[ \frac{4}{\pi } \frac{ (-1)^{n_1-1} |n'|^4 }{(2n_1-1) \kappa (n)} \int _0^t e^{-\nu \kappa (n) (t-s)} (2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s)) ds \right] , \end{aligned}$$

since

$$\begin{aligned} \mathcal {C}_1[\partial _1 \hat{a}_1] = (2n_1-1) \mathcal {F}_{s_1}[a_1], \qquad \mathcal {C}_1[1] = \frac{4}{\pi } \, \frac{(-1)^{n_1-1}}{2n_1-1}, \end{aligned}$$

and

$$\begin{aligned} \mathcal {C}_1 \bigl [ \cosh x_1|n'| \bigr ] = \frac{4}{\pi } \, \frac{(-1)^{n_1-1}(2n_1-1)}{(2n_1-1)^2+ |n'|^2} \cosh \frac{\pi }{2} |n'|. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \hat{u}_1(t) = \int _0^{x_1} \hat{v}_1(y_1,n',t)dy_1 = x_1 \hat{z}_1(t) + \int _0^{x_1} \hat{w}_1(y_1,n',t)dy_1, \end{aligned}$$

(3.26)

since $\partial _1 \hat{u}_1=\hat{v}_1=\hat{z}_1 + \hat{w}_1$ and $\hat{u}_1|_{x_1=0} =0$. We compute

$$\begin{aligned} \int _0^{x_1} \hat{w}_1(y_1,n',t)dy_1&= \mathcal {S}_1^* \bigl [ e^{-\nu \kappa (n) t} \mathcal {F}_{s_1}[a_1]\bigr ] - \mathcal {S}_1^* \left[ \frac{4}{\pi } \frac{(-1)^{n_1-1}}{(2n_1-1)^2} e^{-\nu \kappa (n) t} \partial _1 \hat{a}_1|_{x_1=\frac{\pi }{2}} \right] \\&\quad + \mathcal {S}_1^* \left[ \frac{4}{\pi } \frac{ (-1)^{n_1-1} |n'|^4 }{(2n_1-1)^2 \kappa (n)} \int _0^t e^{-\nu \kappa (n) (t-s)} \bigl ( 2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s) \bigr ) ds \right] . \end{aligned}$$

We apply $\mathcal {F}'^*[\, \cdot \,]$ to the both sides in (3.26) to obtain (3.12).

We deduce from the first component in equation (1.2) with the pressure (3.17) that

$$\begin{aligned} \partial _t \hat{u}_1 - \nu \partial _1^2 \hat{u}_1 + \nu |n'|^2 \hat{u}_1 + |n'| \frac{\sinh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} \, ( 2\nu \hat{z}_1 + \lambda ^\alpha \hat{h}) =0. \end{aligned}$$

Thus $\hat{z}_0(n',t)=\hat{u}_1(\frac{\pi }{2},n',t)$ is governed by

$$\begin{aligned} \frac{d \hat{z}_0}{dt} + \nu |n'|^2 \hat{z}_0 + |n'| \tanh \frac{\pi }{2} |n'| ( 2\nu \hat{z}_1 + \lambda ^\alpha \hat{h} )=0, \qquad \hat{z}_0|_{t=0}= \hat{a}_1|_{x_1=\frac{\pi }{2}}. \end{aligned}$$

(3.27)

since $\partial _1^2 \hat{u}_1|_{x_1=\frac{\pi }{2}}=0$ (cf. (3.4)). That is,

$$\begin{aligned} \hat{z}_0(t) = e^{- \nu |n'|^2 t} \hat{a}_1|_{x_1=\frac{\pi }{2}} - |n'| \tanh \frac{\pi }{2} |n'| \int _0^t e^{- \nu |n'|^2 (t-s)} \bigl (2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s) \bigr ) ds, \end{aligned}$$

(3.28)

and we get Eq. (3.7). Furthermore, Eq. (3.11) follows from the first equation (1.1).

Let us derive integral representations of $\hat{u}_i=\hat{u}_i(t)$ for $i=2,3$ similarly as above. For $\hat{v}_i$ for each $i=2,3$, we deduce from (3.18) with the pressure (3.17) the governing equation

$$\begin{aligned} \partial _t \hat{v}_i - \nu \partial _1^2 \hat{v}_i + \nu |n'|^2 \hat{v}_i + \sqrt{-1} n_i |n'| \frac{\sinh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} (2\nu \hat{z}_1 + \lambda ^\alpha \hat{h}) =0 \end{aligned}$$

(3.29)

for all $(x_1,n',t) \in [0,\frac{\pi }{2}] \times \mathbb {Z}^2 \times [0,\infty )$ and from (1.5) and (3.4) the boundary conditions

$$\begin{aligned} \hat{v}_i|_{x_1=\frac{\pi }{2}} = -\sqrt{-1} n_i \hat{u}_1|_{x_1=\frac{\pi }{2}}, \qquad \partial _1 \hat{v}_i|_{x_1=0} =0, \qquad \partial _1^2 \hat{v}_i |_{x_1=\frac{\pi }{2}} =0 \end{aligned}$$

(3.30)

and from (1.7) the initial condition

$$\begin{aligned} \hat{v}_i|_{t=0} = \partial _1 \hat{a}_i. \end{aligned}$$

(3.31)

Set

$$\begin{aligned} \hat{w}_i:= \hat{v}_i + \sqrt{-1} n_i \hat{z}_0 \qquad (i=2,3). \end{aligned}$$

From (3.27)–(3.31), we have the IBVP of the 1–D heat equation on $[0,\hbox { }\ \frac{\pi }{2}]$: for $i=2,3$,

$$\begin{aligned} \partial _t \hat{w}_i - \nu \partial _1^2 \hat{w}_i + \nu |n'|^2 \hat{w}_i + \sqrt{-1} n_i |n'| \left( \frac{\sinh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} + \tanh \frac{\pi }{2} |n'| \right) (2\nu \hat{z}_1 + \lambda ^\alpha \hat{h}) =0 \end{aligned}$$

subject to the boundary conditions

$$\begin{aligned} \hat{w}_i|_{x_1=\frac{\pi }{2}}=0, \qquad \partial _1 \hat{w}_i|_{x_1=0}=0, \qquad \partial _1^2 \hat{w}_i|_{x_1=\frac{\pi }{2}}=0 \end{aligned}$$

and the initial condition

$$\begin{aligned} \hat{w}_i|_{t=0} = \partial _1 \hat{a}_i + \sqrt{-1} n_i \hat{a}_1|_{x_1=\frac{\pi }{2}}. \end{aligned}$$

Again, by using the Fourier method and the Duhamel formula, we get

$$\begin{aligned} \begin{aligned}&\hat{w}_i(x_1, n',t) \\ {}&\quad = \mathcal {C}_1^* \bigl [e^{-\nu \kappa (n) t} \mathcal {C}_1[ \partial _1 \hat{a}_i + \sqrt{-1} n_i \hat{a}_1|_{x_1=\frac{\pi }{2}}] \bigr ] \\ {}&\qquad \quad - \mathcal {C}_1^* \left[ \mathcal {C}_1 \biggl [ \frac{\sinh x_1|n'|}{\cosh \frac{\pi }{2} |n'|} + \tanh \frac{\pi }{2} |n'| \biggr ] \sqrt{-1} n_i |n'| \int _0^t e^{-\nu \kappa (n) (t-s)} (2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s)) ds \right] \\ {}&\quad = \mathcal {C}_1^* \bigl [(2n_1-1) e^{-\nu \kappa (n) t} \mathcal {F}_{s_1}[a_i]\bigr ] + \mathcal {C}_1^* \left[ \frac{4}{\pi } \frac{(-1)^{n_1-1}}{2n_1-1} e^{-\nu \kappa (n) t} \mathcal {F}' [\partial _i a_1](\frac{\pi }{2},n') \right] \\ {}&\qquad \quad - \mathcal {C}_1^* \biggl [ \frac{4}{\pi } \sqrt{-1} n_i |n'| \left( \frac{(-1)^{n_1-1} (2n_1-1)}{(2n_1-1)^2 + |n'|^2} + \frac{(-1)^{n_1-1}}{2n_1-1} \right) \tanh \frac{\pi }{2} |n'| \\ {}&\qquad \qquad \times \int _0^t e^{-\nu \kappa (n) (t-s)} (2\nu \hat{z}_1(s)+ \lambda ^\alpha \hat{h}(s))ds \biggr ], \end{aligned} \end{aligned}$$

since

$$\begin{aligned} \mathcal {C}_1 \bigl [ \sinh x_1|n'| \bigr ] = \frac{4}{\pi } \, \frac{(-1)^{n_1-1}(2n_1-1)}{(2n_1-1)^2+ |n'|^2} \sinh \frac{\pi }{2} |n'|. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \hat{u}_i(t) = \int _0^{x_1} \hat{v}_i(y_1,n',t)dy_1 = - x_1 \sqrt{-1} n_i \hat{z}_0(t) + \int _0^{x_1} \hat{w}_i(y_1,n',t)dy_1, \end{aligned}$$

(3.32)

since $\partial _1 \hat{u}_i=\hat{v}_i= -\sqrt{-1} n_i \hat{z}_0 + \hat{w}_i$ and $\hat{u}_i|_{x_1=0} =0$. We compute

$$\begin{aligned} \begin{aligned}&\int _0^{x_1} \hat{w}_1(y_1,n',t)dy_1 \\ {}&\quad = \mathcal {S}_1^* \bigl [ e^{-\nu \kappa (n) t} \mathcal {F}_{s_1}[a_1]\bigr ] + \mathcal {S}_1^* \left[ \frac{4}{\pi } \frac{(-1)^{n_1-1}}{(2n_1-1)^2} e^{-\nu \kappa (n) t} \mathcal {F}' [\partial _i a_1](\frac{\pi }{2},n') \right] \\ {}&\qquad - \mathcal {S}_1^* \biggl [ \frac{4}{\pi } \sqrt{-1} n_i |n'| \frac{ (-1)^{n_1-1} (2(2n_1-1)^2 + |n'|^2) }{(2n_1-1) \kappa (n)} \tanh \frac{\pi }{2} |n'| \\ {}&\qquad \quad \times \int _0^t e^{-\nu \kappa (n) (t-s)} \bigl ( 2\nu \hat{z}_1(s) + \lambda ^\alpha \hat{h}(s) \bigr ) ds \biggr ]. \end{aligned} \end{aligned}$$

Therefore, (3.13) is obtained by applying $\mathcal {F}'^*$ to the both sides in (3.32). $\square$

4 Unique Solvability

In this section, we establish the unique solvability of the IBVP (1.1)–(1.7) under the condition $0< \alpha <3/2$.

Theorem 4.1

Assume $0< \alpha < 3/2$. Let an integer $m \ge 2$ and $T>0$ be arbitrary. Suppose that $\eta _0 \in H^{m+1} (\mathbb {T}^2)$ and that $a=(a_i)_{1 \le i \le 3}$, $a_i \in W_{s_1}^m(\Omega )$ satisfies the compatibility conditions:

$$\begin{aligned} \nabla \cdot a =0 \quad \text {in } \Omega , \qquad \partial _1 a_i + \partial _i a_1 =0 \quad (i=2,3) \quad \text {on } S_F. \end{aligned}$$

(4.1)

Then there exist unique functions $h, z_0,z_1$ and $Q=(Q_i)_{1 \le i \le 3}$ in (3.6)–(3.10) such that

$$\begin{aligned}&h \in L^\infty ([0,T), H^{m+1} (\mathbb {T}^2)), \quad h|_{t=0}= \eta _0 - \frac{\pi }{2}, \end{aligned}$$

(4.2)

$$\begin{aligned}&z_0 \in C([0,T), H^{m-1} (\mathbb {T}^2)), \quad z_0|_{t=0}= a_1|_{S_F}, \end{aligned}$$

(4.3)

$$\begin{aligned}&z_1 \in C([0,T), H^{m-2} (\mathbb {T}^2)), \quad z_1|_{t=0}= \partial _1 a_1|_{S_F}, \end{aligned}$$

(4.4)

$$\begin{aligned}&|\partial _1|^\rho |\nabla '|^{m-2} Q_1 \in L^\infty ([0,T), L^2 (\mathbb {T}^3)) \quad (\forall \rho < 3/2), \quad Q_1|_{t=0} =0, \end{aligned}$$

(4.5)

$$\begin{aligned}&|\partial _1|^{\rho '} |\nabla '|^{m-2} Q_i \in L^\infty ([0,T), L^2 (\mathbb {T}^3)) \quad (\forall \rho ' < 1/2), \quad Q_i|_{t=0} =0 \end{aligned}$$

(4.6)

for $i=2,3$, and the velocity field $u=(u_i(x,t))_{1\le i \le 3}$ given by

$$\begin{aligned} u_1(x,t)&= x_1 z_1 + e^{\nu t \Delta _{s_1}} a_1 + Q_1(x,t), \end{aligned}$$

(4.7)

$$\begin{aligned} u_i(x,t)&= -x_1 \partial _i z_0 + e^{\nu t \Delta _{s_1}} \bigl (x_1 \partial _i a_1|_{S_F} \bigr ) + e^{\nu t \Delta _{s_1}} a_i + Q_i(x,t) \quad (i=2,3) \end{aligned}$$

(4.8)

is a solution with $\eta (x',t)= h(x',t) + \frac{\pi }{2}$ to the problem (1.1)–(1.7).

Proof

Let us redefine the $H^r$-norm of a function $z(x')=z(x_2,x_3):\mathbb {T}^2 \rightarrow \mathbb {R}$ for $r \ge 0$ by

$$\begin{aligned} \Vert z\Vert _{H^r(\mathbb {T}^2)}&:= |\mathcal {F}'[z](0)| + \left( \sum _{n' \in \mathbb {Z}^2 \backslash \{0\}} |n'|^r \left| \mathcal {F}'[z](n') \right| ^2 \right) ^\frac{1}{2} \nonumber \\&\equiv |\mathcal {F}'[z](0)| + \bigl \Vert |n'|^r \mathcal {F}'[z](n') \bigr \Vert _{l^2(\mathbb {Z}^2)}. \end{aligned}$$

(4.9)

We have from Eq. (1.1) that $\{ \hat{h}(n',t)\}_{n' \in \mathbb {Z}^2, t>0}$ is governed by

$$\begin{aligned} \hat{h}(n', t) = \hat{h}_0(n') + \int _0^t \hat{z}_0(n',t), \qquad \hat{h}_0(n'):= \hat{\eta }_0(n') - \frac{\pi }{2}, \end{aligned}$$

(4.10)

where

$$\begin{aligned} \begin{aligned} \hat{z}_0(n', t) = e^{- \nu |n'|^2 t} \hat{a}_1( \frac{\pi }{2},n') - |n'| \tanh \frac{\pi }{2} |n'| \int _0^t e^{- \nu |n'|^2 (t-s)} \bigl (2\nu \hat{z}_1(n',s) + \lambda ^{\alpha }(n') \hat{h}(n',s) \bigr ) ds\\ \end{aligned} \end{aligned}$$

(4.11)

associated with

$$\begin{aligned} \begin{aligned} \hat{z}_1(n', t) = e^{-\nu |n'|^2 t} \partial _1 \hat{a}_1 ( \frac{\pi }{2}, n') - \lambda ^{\alpha }(n') |n'|^2 \int _0^t e^{-3\nu |n'|^2(t-s)} \hat{h}(n', s)ds, \end{aligned} \end{aligned}$$

(4.12)

corresponding to equations (3.28) and (3.23) respectively.

For $n'=0$, we deduce from (4.10) with (4.11) that

$$\begin{aligned} \begin{aligned} \hat{h}(0,t) = \hat{h}_0(0) + t \hat{a}_1( \frac{\pi }{2}, 0) = \hat{\eta }_0(0) - \frac{\pi }{2}+ t \hat{a}_1( \frac{\pi }{2}, 0). \end{aligned} \end{aligned}$$

(4.13)

For every $n' \ne 0$, by substituting (4.11) into (4.10) and integrating by parts, we obtain that

$$\begin{aligned} \begin{aligned} \hat{h}(n', t)&= \hat{h}_0(n') + \frac{1-e^{- \nu |n'|^2 t}}{\nu |n'|^2} \hat{a}_1 ( \frac{\pi }{2},n' ) - 2 \frac{\tanh \frac{\pi }{2} |n'|}{|n'|} \int _0^t \bigl (1-e^{- \nu |n'|^2(t-s)} \bigr ) \hat{z}_1(n',s) ds \\ {}&\qquad - \frac{\lambda ^{\alpha }(n')}{\nu |n'|^2} \tanh \frac{\pi }{2} |n'| \int _0^t \bigl (1-e^{- \nu |n'|^2(t-s)} \bigr ) \hat{h}(n',s) ds. \end{aligned} \end{aligned}$$

Substituting (4.12) into the above equation, we get

$$\begin{aligned} \begin{aligned} \hat{h}(n', t)&= I_0(n',t) + 2 \lambda ^\alpha (n') |n'| \tanh \frac{\pi }{2} |n'| \biggl ( \int _0^t e^{- 3\nu |n'|^2s} \int _0^s e^{3\nu |n'|^2 \sigma } \hat{h}(n',\sigma ) d\sigma \\ {}&\qquad \quad - e^{- \nu |n'|^2t} \int _0^t e^{- 2\nu |n'|^2s} \int _0^s e^{3\nu |n'|^2 \sigma } \hat{h}(n',\sigma ) d\sigma \biggr ) \\ {}&\qquad - \frac{\lambda ^{\alpha }(n')}{\nu |n'|^2} \tanh \frac{\pi }{2} |n'|\int _0^t \bigl (1-e^{- \nu |n'|^2(t-s)} \bigr ) \hat{h}(n',s) ds \\ {}&= I_0(n',t) + 2 \lambda ^\alpha (n') |n'| \tanh \frac{\pi }{2} |n'| \biggl ( \frac{1}{3 \nu |n'|^2} \int _0^t \bigl ( 1 - e^{- 3\nu |n'|^2(t-s)} \bigr ) \hat{h}(n',s) ds \\ {}&\qquad \quad - \frac{1}{2 \nu |n'|^2} \int _0^t \bigl ( e^{- \nu |n'|^2(t-s)} -e^{- 3\nu |n'|^2(t-s)} \bigr ) \hat{h}(n',s) ds \biggr ) \\ {}&\qquad - \frac{\lambda ^{\alpha }(n')}{\nu |n'|^2} \tanh \frac{\pi }{2} |n'| \int _0^t \bigl (1-e^{- \nu |n'|^2(t-s)} \bigr ) \hat{h}(n',s) ds \\ {}&= I_0(n',t) - \frac{\lambda ^\alpha (n')}{3\nu |n'|} \tanh \frac{\pi }{2} |n'| \int _0^t \bigl (1-e^{- 3\nu |n'|^2(t-s)} \bigr ) \hat{h}(n',s) ds, \end{aligned} \end{aligned}$$

(4.14)

where

$$\begin{aligned} \begin{aligned} I_0(n',t)&:= \hat{h}_0(n') + \frac{1-e^{- \nu |n'|^2 t}}{\nu |n'|^2} \hat{a}_1( \frac{\pi }{2},n') - \frac{2}{\nu } \frac{\tanh \frac{\pi }{2} |n'| }{|n'|^3} \bigl (1-e^{- \nu |n'|^2 t} \bigr ) \partial _1 \hat{a}_1( \frac{\pi }{2},n') \\ {}&\qquad + \frac{2 \tanh \frac{\pi }{2} |n'|}{|n'|} te^{- \nu |n'|^2 t} \partial _1 \hat{a}_1 ( \frac{\pi }{2},n' ) . \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} \mu ^\alpha (n'):= \lambda ^\alpha (n') |n'| \tanh \frac{\pi }{2} |n'| = \left( g|n'| + \sigma |n'|^{2\alpha +1} \right) \tanh \frac{\pi }{2} |n'|. \end{aligned}$$

Differentiating the Eq. (4.14), we obtain that $\hat{h}=\hat{h}(n',t)$ satisfies

$$\begin{aligned} D_t \hat{h}(n',t)&= D_t \hat{I}_0(n',t) - \mu ^\alpha (n') e^{- 3\nu |n'|^2t} \int _0^t e^{3\nu |n'|^2s} \hat{h}(n',s) ds \nonumber \end{aligned}$$

with $D_t= d/dt$. Multiplying the above equation by $e^{3 \nu |n'|t}$, we get by differentiation,

$$\begin{aligned} D_t \bigl ( e^{3 \nu |n'|^2 t} D_t \hat{h} \bigr ) = D_t \bigl ( e^{3 \nu |n'|^2 t} D_t \hat{I}_0 \bigr ) - \mu ^\alpha (n') e^{3\nu |n'|^2t} \hat{h}. \end{aligned}$$

Thus we obtain the governing ODE of $\{\hat{h}(n',t)\}_{n' \ne 0, t>0}$:

$$\begin{aligned} \bigl (D_t^2 + 3\nu |n'|^2 D_t + \mu ^\alpha (n') \bigr ) \hat{h} = D_t ( D_t + 3\nu |n'|^2) I_0=:D_tJ_0(n',t) \end{aligned}$$

(4.15)

with the initial conditions

$$\begin{aligned} \begin{aligned} \hat{h}(n',0)=\hat{h}_0(n'), \qquad D_t \hat{h }(n',0)= \hat{z}_0(n',0) =\hat{a}_1 ( \frac{\pi }{2},n' ) , \end{aligned} \end{aligned}$$

(4.16)

where

$$\begin{aligned} \begin{aligned} J_0(n',t)&:= \bigl ( D_t +3\nu |n'|^2 \bigr ) I_0(n',t) \\ {}&= 3 \nu |n'|^2 \hat{h}_0(n') + (3 - 2 e^{- \nu |n'|^2 t}) \hat{a}_1 ( \frac{\pi }{2},n' ) \\ {}&\qquad + \frac{2\tanh \frac{\pi }{2} |n'|}{|n'|} \bigl (e^{- \nu |n'|^2 t} + 2 \nu |n'|^2 t e^{- \nu |n'|^2 t} -3 \bigr ) \partial _1 \hat{a}_1 ( \frac{\pi }{2},n' ) . \end{aligned} \end{aligned}$$

Since the characteristic equation $\xi ^2 + 3\nu |n'|^2\xi + \mu ^\alpha (n')=0$, we set

$$\begin{aligned} \omega _1(n')&:= \frac{3}{2} \nu |n'|^2 \bigl ( 1 - \sqrt{R^\alpha (n')} \bigr ), \\ \omega _2(n')&:= \frac{3}{2} \nu |n'|^2 \bigl ( 1 + \sqrt{R^\alpha (n')} \bigr ) \end{aligned}$$

with

$$\begin{aligned} R^\alpha (n') = 1 - \frac{4 \mu ^\alpha (n')}{9\nu ^2 |n'|^4} = 1 - \frac{4\tanh \frac{\pi }{2}|n'|}{9\nu ^2} \left( \frac{g}{|n'|^3} + \frac{\sigma }{|n'|^{3-2\alpha }} \right) . \end{aligned}$$

Then we can find a number $N_0 \in \mathbb {N}$, a sum of two squares such that

$$\begin{aligned} \begin{aligned} \mathrm {(i)} ~~R^\alpha (n') > 0 \quad \text{ for } |n'| \ge \sqrt{N_0} \qquad \quad \mathrm {(ii)} ~~R^\alpha (n') \le 0 \quad \text{ for } |n'| \le \sqrt{N_0-1}, \end{aligned} \end{aligned}$$

(4.17)

since $\tanh \frac{\pi }{2} |n'|/|n'|^{3-2\alpha }$ is a decreasing function in terms of $|n'|$ for every $\alpha < 3/2$. Furthermore, thanks to the discreteness of $n'$, there exists a constant $\varepsilon _0 = \varepsilon _0(\nu ,g,\sigma ,\alpha ) \in (0,1)$ independent of $n'$ such that

$$\begin{aligned} R^\alpha (n') \ge \varepsilon _0 >0 \quad \text {for } |n'| \ge \sqrt{N_0}. \end{aligned}$$

In the case (i), we set

$$\begin{aligned} g_1(n', t):= e^{-\omega _1(n') t}, \qquad g_2(n', t):= e^{-\omega _2(n') t} \end{aligned}$$

with the Wronskian

$$\begin{aligned} W(n',t)&:= g_1(n', t) D_t g_2(n', t) - D_t g_1(n', t) g_2(n', t) \nonumber \\&= -3\nu |n'|^2 \sqrt{R^\alpha (n')} e^{-3\nu |n'|^2 t}. \end{aligned}$$

(4.18)

By the solution formula for the 2nd order linear ODE:

$$\begin{aligned} \begin{aligned} \hat{h}(n',t)&= \left( C_1 - \int D_t J_0(n',t) \frac{g_2(n',t)}{W(n',t)} dt \right) g_1(n',t) \\ {}&\quad + \left( C_2 + \int D_t J_0(n',t) \frac{g_1(n',t)}{W(n',t)} dt \right) g_2(n',t) \\ {}&= \left( C_1 + \int J_0(n',t) D_t \left( \frac{g_2(n',t)}{W(n',t)} \right) dt \right) g_1(n',t) \\ {}&\quad + \left( C_2 - \int J_0(n',t) D_t \left( \frac{g_1(n',t)}{W(n',t)} \right) dt \right) g_2(n',t), \end{aligned} \end{aligned}$$

(4.19)

we obtain the general solution to (4.15) given by

$$\begin{aligned} \hat{h}(n',t)&= \left( C_1(n') - \frac{\omega _1(n')}{3 \nu |n'|^2 \sqrt{R^\alpha (n')}} \int _0^t e^{\omega _1(n')s} J_0(n',s) ds \right) e^{-\omega _1(n')t} \nonumber \\&\quad + \left( C_2(n') + \frac{\omega _2(n') }{3 \nu |n'|^2 \sqrt{R^\alpha (n')}} \int _0^t e^{\omega _2(n')s} J_0(n',s) ds \right) e^{-\omega _2(n')t}. \end{aligned}$$

We also have that the initial conditions of $\hat{h}(n',t)$ imply $C_1+C_2 =\hat{h}_0(n')$ and $-\omega _1(n')C_1 -\omega _2(n')C_2 + J_0(n',0)= \hat{a}_1(\hbox { }\ \frac{\pi }{2},n')$, that is,

$$\begin{aligned} \left( \!\! \begin{array}{r} C_1 \\ C_2 \end{array} \!\!\right)&= \frac{1}{\omega _2 - \omega _1} \left( \!\! \begin{array}{rr} \omega _2 &{} -1 \\ -\omega _1 &{} 1 \end{array} \!\!\right) \left( \!\! \begin{array}{c} \hat{h}_0(n') \\ J_0(n',0) - \hat{a}_1(\frac{\pi }{2},n') \end{array} \!\!\right) \\&= \frac{\hat{h}_0(n')}{2} \left( \!\! \begin{array}{c} 1+ 1/\sqrt{R^\alpha (n')} \\ 1 - 1/\sqrt{R^\alpha (n')} \end{array} \!\!\right) + \frac{\hat{a}_1(\frac{\pi }{2},n') - J_0(n',0)}{3 \nu |n'|^2 \sqrt{R^\alpha (n')}} \left( \!\! \begin{array}{c} 1 \\ -1 \end{array} \!\!\right) . \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} |J_0(n',t)| \le 3 \nu |n'|^2 |\hat{h}_0(n')| + 3|\hat{a}_1(\frac{\pi }{2},n')| + \frac{6}{|n'|}|\partial _1 \hat{a}_1( \frac{\pi }{2},n')| \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} |C_1(n')| + |C_2(n')|&\le \left( 1+ \frac{1}{\sqrt{\varepsilon _0}} \right) |\hat{h}_0(n')| + \frac{2}{ 3\nu |n'|^2 \sqrt{\varepsilon _0}} |\hat{a}_1(\frac{\pi }{2},n') -J_0(n',0)| \\ {}&\le \left( 1+ \frac{3}{\sqrt{\varepsilon _0}} \right) |\hat{h}_0(n')| + \frac{3}{\nu |n'|^3 \sqrt{\varepsilon _0}} |\partial _1 \hat{a}_1(\frac{\pi }{2},n')|, \end{aligned} \end{aligned}$$

we deduce from (4.19) that

$$\begin{aligned} |\hat{h}(n',t)|&\le |C_1(n')| + |C_2(n')| + \frac{2 - e^{\omega _1(n')t} - e^{\omega _2(n')t}}{3\nu |n'|^2 \sqrt{\varepsilon _0}} \sup _{0< s < t} |J_0(n',s)|\nonumber \\&\le \left( 1+ \frac{3}{\sqrt{\varepsilon _0}} \right) |\hat{h}_0(n')| + \frac{1}{\nu \sqrt{\varepsilon _0}} \left( 2 \frac{|\hat{a}_1(\frac{\pi }{2},n')|}{|n'|^2} + 7\frac{|\partial _1 \hat{a}_1(\frac{\pi }{2},n')|}{|n'|^3} \right) \end{aligned}$$

(4.20)

for all $|n'| \ge \sqrt{N_0}$. Therefore, it follows from the above estimate that

$$\begin{aligned} \begin{aligned}&\bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\{|n'| \ge \sqrt{N_0}\})} \\ {}&\quad \le C_3 \Bigl ( \bigl \Vert |n'|^{m+1} |\hat{h}_0(n')| \bigr \Vert _{l^2(\{|n'| \ge \sqrt{N_0}\})} + \bigl \Vert |n'|^{m-1} |\hat{a}_1(n')| \bigr \Vert _{l^2(\{|n'| \ge \sqrt{N_0}\})} \\ {}&\qquad \quad + \bigl \Vert |n'|^{m-2} |\partial _1 \hat{a}_1(n')| \bigr \Vert _{l^2(\{|n'| \ge \sqrt{N_0}\})} \Bigr ) \end{aligned} \end{aligned}$$

(4.21)

with a constant $C_3=C_3(\nu ,g,\sigma ,\alpha )>0$. If $N_0=1$, then we have

$$\begin{aligned} \Vert h(t) \Vert _{H^{m+1}(\mathbb {T}^2)} \le C_3 (1+T) \bigl ( 1+ \Vert \eta _0 \Vert _{H^{m+1}(\mathbb {T}^2)} + \Vert a_1\Vert _{W_{s_1}^m(\Omega )} \bigr ), \end{aligned}$$

(4.22)

since (4.13). On the other hand, if $N_0 > 1$, we must divide the case (ii) in (4.17) into the two cases separately:

$$\begin{aligned} \begin{aligned} \mathrm {(a)} ~~R^\alpha (n') < 0 \quad \text{ for } |n'| \le \sqrt{N_0-1} \qquad \quad \mathrm {(b)} ~~R^\alpha (n') = 0 \quad \text{ for } |n'| = \sqrt{N_0-1}. \end{aligned} \end{aligned}$$

In the case (a), a set of solutions $\{\hat{h}(n',t)\}_{1 \le |n'| \le \sqrt{N_0-1},t>0}$ is obtained by the solution formula (4.19) with

$$\begin{aligned} g_1(n', t)&:= e^{-\frac{3}{2} \nu |n'|^2 t} \cos \left( \frac{3}{2} \nu \sqrt{-R^\alpha (n')} |n'|^2t \right) , \\ g_2(n', t)&:= e^{-\frac{3}{2} \nu |n'|^2 t} \sin \left( \frac{3}{2} \nu \sqrt{-R^\alpha (n')} |n'|^2t \right) , \end{aligned}$$

associated with the Wronskian $W(n',t)$. Similarly as above, since there exists a constant $\varepsilon _1=\varepsilon _1(\nu ,g,\sigma ,\alpha )>0$ independent of $n'$ such that

$$\begin{aligned} -R^\alpha (n') \ge \varepsilon _1 >0 \quad \text {for } |n'| \le \sqrt{N_0-1}, \end{aligned}$$

we can find a constant $C_4=C_4(\nu , g, \sigma , \alpha )>0$ such that

$$\begin{aligned} \begin{aligned}&\bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\{|n'| \le \sqrt{N_0-1}\})} \\ {}&\quad \le C_4 e^{-\frac{3}{2} \nu |n'|^2 t} \Bigl ( \bigl \Vert |n'|^{m+1} |\hat{h}_0(n')| \bigr \Vert _{l^2(\{|n'| \le \sqrt{N_0-1}\})} + \bigl \Vert |n'|^{m-1} |\hat{a}_1(n')| \bigr \Vert _{l^2(\{|n'| \le \sqrt{N_0-1}\})} \\ {}&\qquad \qquad + \bigl \Vert |n'|^{m-2} |\partial _1 \hat{a}_1(n')| \bigr \Vert _{l^2(\{|n'| \le \sqrt{N_0-1}\})} \Bigr ). \end{aligned} \end{aligned}$$

(4.23)

In the case (b), a set of solutions $\{\hat{h}(n',t)\}_{|n'| = \sqrt{N_0-1}, t>0}$ is obtained by the solution formula (4.19) with $g_1(n', t):= e^{-\frac{3}{2} \nu |n'|^2 t}$ and $g_2(n', t):= te^{-\frac{3}{2} \nu |n'|^2 t}$. We also have

$$\begin{aligned} \begin{aligned}&\bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\{|n'| = \sqrt{N_0-1}\})} \\ {}&\quad \le C_5 (1+t) e^{-\frac{3}{2} \nu |n'|^2 t} \Bigl ( \bigl \Vert |n'|^{m+1} |\hat{h}_0(n')| \bigr \Vert _{l^2(\{|n'| = \sqrt{N_0-1}\})} + \bigl \Vert |n'|^{m-1} |\hat{a}_1(n')| \bigr \Vert _{l^2(\{|n'| = \sqrt{N_0-1}\})} \\ {}&\qquad \qquad + \bigl \Vert |n'|^{m-2} |\partial _1 \hat{a}_1(n')| \bigr \Vert _{l^2(\{|n'| = \sqrt{N_0-1}\})} \Bigr ) \end{aligned} \end{aligned}$$

(4.24)

with a constant $C_5=C_5(\nu , g, \sigma , \alpha )>0$. Therefore, we get

$$\begin{aligned} \begin{aligned} \bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\mathbb {Z}^2)}&=\bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\{|n'| < \sqrt{N_0-1}\})} + \bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\{|n'| = \sqrt{N_0-1}\})} \\ {}&\qquad + \bigl \Vert |n'|^{m+1} |\hat{h}(n',t)| \bigr \Vert _{l^2(\{|n'| \ge \sqrt{N_0}\})} \\ {}&\le C_6 (1+ T) \bigl ( \bigl \Vert |n'|^{m+1} |\hat{h}_0(n')| \bigr \Vert _{l^2(\mathbb {Z}^2)} + \bigl \Vert |n'|^{m-1} |\hat{a}_1(\frac{\pi }{2},n')| \bigr \Vert _{l^2(\mathbb {Z}^2)} \\ {}&\qquad + \bigl \Vert |n'|^{m-2} | \partial _1 \hat{a}_1(\frac{\pi }{2},n')| \bigr \Vert _{l^2(\mathbb {Z}^2)} \bigr ) \end{aligned} \end{aligned}$$

with $C_6=C_6(\nu , g, \sigma , \alpha ):= \max \{C_3, C_4,C_5\}$. Hence, it follows that

$$\begin{aligned} \Vert h(t)\Vert _{H^{m+1} (\mathbb {T}^2)} \le C_6 (1+T) \bigl ( 1+ \Vert \eta _0 \Vert _{H^{m+1} (\mathbb {T}^2)} + \Vert a_1 \Vert _{W_{s_1}^m(\Omega )} \bigr ) \end{aligned}$$

(4.25)

for all $0< t < T$.

For the Eq. (4.12), we have

$$\begin{aligned} \begin{aligned} |\hat{z}_1(n', t)| \le |\partial _1 \hat{a}_1(\frac{\pi }{2}, n')| + (g+\sigma ) |n'|^{2\alpha -1} \int _0^t e^{-3\nu |n'|^2(t-s)} ds \sup _{0< s < t} (|n'|^3 |\hat{h}(n', s)|), \end{aligned} \end{aligned}$$

which yields that for all $0< t < T$,

$$\begin{aligned} \begin{aligned} \bigl \Vert |n'|^{m-2} |\hat{z}_1(n',t)| \bigr \Vert _{l^2(\mathbb {Z}^2)}&\le \bigl \Vert |n'|^{m-2} | \partial _1 \hat{a}_1(\frac{\pi }{2},n')| \bigr \Vert _{l^2(\mathbb {Z}^2)} \\ {}&\qquad + \frac{g+\sigma }{(3\nu )^{\alpha -\frac{1}{2}}} \int _0^1 \frac{d \tau }{(1-\tau )^{\alpha -\frac{1}{2}}} \, t^{\frac{3}{2} -\alpha } \sup _{0< t < T} \bigl \Vert |n'|^{m+1} |\hat{h}(n', t)| \bigr \Vert _{l^2(\mathbb {Z}^2)}. \end{aligned} \end{aligned}$$

Therefore, we deduce from (4.25) with $\hat{z}_1(0,t)= \partial _1 \hat{a}_1(\frac{\pi }{2},0)$ that

$$\begin{aligned} \Vert z_1(t) \Vert _{H^{m-2}(\mathbb {T}^2)} \le C_7(1+T^{\frac{5}{2} -\alpha } ) \bigl (1 + \Vert \eta _0 \Vert _{H^{m+1} (\mathbb {T}^2)} + \Vert a_1 \Vert _{W_{s_1}^m(\Omega )} \bigr ) \end{aligned}$$

(4.26)

for all $0<t <T$ with a constant $C_7 =C_7(\nu ,g,\sigma ,\alpha )>0$. Furthermore, one can see that such a solution $z_1$ lies in $C([0,T), H^{m-2}(\mathbb {T}^2))$.

Substituting (4.12) into (4.11), we have that for every $n' \ne 0$,

$$\begin{aligned} \begin{aligned} \hat{z}_0(n', t)&= e^{- \nu |n'|^2 t} \hat{a}_1(\frac{\pi }{2},n') - 2 \nu |n'| \tanh \frac{\pi }{2} |n'| \, t e^{- \nu |n'|^2 t} \partial _1 \hat{a}_1( \frac{\pi }{2},n') \\ {}&\qquad - \mu ^\alpha (n') \int _0^t e^{- 3\nu |n'|^2 (t-s)} \hat{h}(n',s) ds, \end{aligned} \end{aligned}$$

(4.27)

which implies

$$\begin{aligned} \begin{aligned} |\hat{z}_0(n', t)| \le |\hat{a}_1(\frac{\pi }{2},n')| + \frac{2|\partial _1 \hat{a}_1( \frac{\pi }{2},n')|}{|n'|} + (g+\sigma )|n'|^{2\alpha -1} \int _0^t e^{- 3\nu |n'|^2 (t-s)} ds \sup _{0<s <t} ( |n'|^2 |\hat{h}(n', s)|) \end{aligned} \end{aligned}$$

for all $0<t <T$. Thus,

$$\begin{aligned} \begin{aligned} \bigl \Vert |n'|^{m-1} \hat{z}_0(n',t) \bigr \Vert _{l^2(\mathbb {Z}^2)}&\le \bigl \Vert |n'|^{m-1} \hat{a}_1(\frac{\pi }{2},n') \bigr \Vert _{l^2(\mathbb {Z}^2)} + 2 \bigl \Vert |n'|^{m-2} \partial _1 \hat{a}_1(n',s) \bigr \Vert _{l^2(\mathbb {Z}^2)} \\ {}&\qquad + \frac{g+ \sigma }{(3\nu )^{\alpha -\frac{1}{2}}} \int _0^1 \frac{d \tau }{(1-\tau )^{\alpha -\frac{1}{2}}} \, t^{\frac{3}{2} -\alpha } \sup _{0<s <t} \bigl \Vert |n'|^{m+1} \hat{h}(n',s) \bigr \Vert _{l^2(\mathbb {Z}^2)}. \end{aligned} \end{aligned}$$

Therefore, we have that for all $0< t < T$,

$$\begin{aligned} \begin{aligned} \Vert z_0(t) \Vert _{H^{m-2}(\mathbb {T}^2)} \le C_8 \bigl (1+T^{\frac{5}{2} -\alpha } \bigr ) \bigl ( 1+ \Vert \eta _0 \Vert _{H^{m+1} (\mathbb {T}^2)} + \Vert a_1 \Vert _{W_{s_1}^m(\Omega )} \bigr ) \end{aligned} \end{aligned}$$

(4.28)

with a constant $C_8=C_8(\nu , g, \sigma , \alpha )>0$, since $\hat{z}_0(0,t) = \hat{a}_1(\frac{\pi }{2},0)$. Furthermore, one can verify that $z_0$ belongs to $C([0,T), H^{m-1}(\mathbb {T}^2))$.

As for $Q_1$ in (3.9), we estimate for any $\rho < 3/2$,

$$\begin{aligned} \begin{aligned}&\bigl \Vert |\partial _1|^\rho |\nabla '|^{m-2} Q_1(t) \bigr \Vert _{L^2(\mathbb {T}^3)} \\ {}&\qquad = \bigl \Vert (2n_1-1)^\rho |n'|^{m-2} \mathcal {F}_{s_1} [Q_1](n,t) \bigr \Vert _{l^2(\mathbb {N}\times \mathbb {Z}^2)} \\ {}&\quad \le \frac{8}{\pi } \left( \sum _{n_1 \in \mathbb {N}} \frac{1}{(2n_1-1)^{2(2-\rho )}} \left\| \frac{|n'|^{m+2}}{\kappa (n)^2} (1 -e^{-\nu \kappa (n)t}) \sup _{0< s< t} |z_1(n',s)| \right\| _{l^2(n' \in \mathbb {Z}^2)}^2 \right) ^\frac{1}{2} \\ {}&\qquad + \frac{8}{\pi } \frac{g+\sigma }{\nu }\left( \sum _{n_1 \in \mathbb {N}} \frac{1}{(2n_1-1)^{2(2-\rho )}} \left\| \frac{|n'|^{m+2+2\alpha }}{\kappa (n)^2} (1 -e^{-\nu \kappa (n)t}) \sup _{0< s< t} |h(n',s)| \right\| _{l^2(n' \in \mathbb {Z}^2)}^2 \right) ^\frac{1}{2} \\ {}&\quad \le C_\rho \left( 1+ \frac{g+\sigma }{\nu } \right) \Bigl ( \sup _{0<s<t} \bigl \Vert |n'|^{m-2} \hat{z}_1(n',s) \bigr \Vert _{l^2(\mathbb {Z}^2)} + \sup _{0<s<t} \bigl \Vert |n'|^{m+1} \hat{h}(n',s) \bigr \Vert _{l^2(\mathbb {Z}^2)} \Bigr ) \\ {}&\quad \le C_\rho \left( 1+ \frac{g+\sigma }{\nu } \right) \Bigl ( \sup _{0<t<T} \Vert z_1(n',t)\Vert _{H^{m-2}(\mathbb {T}^2)} + \sup _{0<t <T} \Vert h(n',t)\Vert _{H^{m+1}(\mathbb {T}^2)} \Bigr ) \\ {}&\quad \le C'_\rho \left( 1+ \frac{g+\sigma }{\nu } \right) \bigl (1+T^{\frac{5}{2} -\alpha }\bigr ) \bigl (1+ \Vert \eta _0 \Vert _{H^{m+1} (\mathbb {T}^2)} + \Vert a_1 \Vert _{W_{s_1}^m(\Omega )} \bigr ) \end{aligned}\end{aligned}$$

for all $0< t < T$, where $C_\rho , C'_\rho$ are positive constants depending only on $\rho ,\nu , g, \sigma , \alpha$. Similarly, we can see that that for any $\rho ' <1/2$, $Q_i$ for $i=2,3$ satisfies

$$\begin{aligned} \begin{aligned}&\bigl \Vert |\partial _1|^{\rho '} |\nabla '|^{m-2} Q_i(t) \bigr \Vert _{L^2(\mathbb {T}^3)} \\ {}&\quad \le C_{\rho '} \left( 1+ \frac{g+\sigma }{\nu } \right) \Bigl ( \sup _{0<t<T} \Vert z_1(n',t)\Vert _{H^{m-2}(\mathbb {T}^2)} + \sup _{0<t <T} \Vert h(n',t)\Vert _{H^{m+1}(\mathbb {T}^2)} \Bigr ) \\ {}&\quad \le C'_{\rho '} \left( 1+ \frac{g+\sigma }{\nu } \right) \bigl (1+T^{\frac{5}{2} -\alpha }\bigr ) \bigl (1+ \Vert \eta _0 \Vert _{H^{m+1} (\mathbb {T}^2)} + \Vert a_1 \Vert _{W_{s_1}^m(\Omega )} \bigr ) \end{aligned} \end{aligned}$$

for all $0< t < T$, where $C_{\rho '}, C'_{\rho '}$ are positive constants depending only on $\rho ', \nu , g, \sigma , \alpha$. Hence, we complete the proof of Theorem 4.1. $\square$