Theoretical and Numerical Analysis of a Simple Model Derived from Compressible Turbulence

Abstract

Turbulent compressible flows are encountered in many industrial applications, for instance when dealing with combustion or aerodynamics. This paper is dedicated to the study of a simple turbulent model for compressible flows. It is based on the Euler system with an energy equation and turbulence is accounted for with the help of an algebraic closure that impacts the thermodynamical behavior. Thereby, no additional PDE is introduced in the Euler system. First, a detailed study of the model is proposed: hyperbolicity, structure of the waves, nature of the fields, existence and uniqueness of the Riemann problem. Then, numerical simulations are proposed on the basis of existing finite-volume schemes. These simulations allow to perform verification test cases and more realistic explosion-like test cases with regards to the turbulence level.

1 Introduction

The modeling of compressible turbulent flows has actually been widely investigated for many years. It is basically grounded on compressible Navier-Stokes equations, with an unsteady setting (see for instance [1, 2, 4,5,6,7, 9, 10, 18, 19, 21]).

Compressible turbulent models are used in many applications, for instance in the framework of combustion and aerodynamics. They always involve three conservation laws that govern the evolution of mass, momentum and total energy of the fluid. Using classical Reynolds averaging and denoting $\overline{\overline{\phi }}$ the mean value of quantity $\phi$, we recall that the Favre average ${\tilde{\psi }}$ of any variable $\psi$ is defined as [5,6,7]:

$$\begin{aligned} {\tilde{\psi }} = \frac{\overline{\overline{\rho \psi } }}{\overline{\overline{ \rho }}}. \end{aligned}$$

Hence, in the sequel, $\overline{\overline{\rho }}$, $\overline{{\overline{P}}}$ will represent the mean density and the mean pressure respectively, while ${\tilde{u}}$ and ${\tilde{e}}$ will stand for the Favre average of velocity and internal energy. Exact balance laws thus read:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}(\overline{\overline{\rho }}) + \nabla .(\overline{\overline{\rho }} {\tilde{u}}) =0 \\&\partial _{t}(\overline{\overline{\rho }} {\tilde{u}}) + \nabla .\left( \overline{\overline{\rho }} {\tilde{u}} \otimes {\tilde{u}} + \left( \overline{{\overline{P}}} +\frac{2K}{3}\right) .{\mathcal {I}} \right) =\epsilon _{0} \nabla .(\Sigma ^{tot}(\nabla ^{s} {\tilde{u}})) \\&\partial _{t}(\overline{\overline{\rho }} E) +\nabla .\left( {\tilde{u}} \left( \overline{\overline{\rho }} E + \overline{{\overline{P}}} +\frac{2K}{3} \right) \right) =\epsilon _{0} \nabla .(\Sigma ^{tot}(\nabla ^{s} {\tilde{u}}){\tilde{u}}) \end{aligned} \right. \end{aligned}$$

(1)

where ${\mathcal {I}}$ is the identity matrix.

The second order tensor $\Sigma ^{tot}(\nabla ^{s} {\tilde{u}})$ cumulates laminar and turbulent viscous contributions, $\epsilon _{0}$ is a positive parameter in [0,1] and K denotes the turbulent kinetic energy. The total energy is:

$$\begin{aligned}\overline{\overline{\rho }} E =\overline{\overline{\rho }} (\frac{{{\tilde{u}}}^{2}}{2} +{\tilde{e}}) + K, \end{aligned}$$

and ${\tilde{e}}$ is a function that is expected to be given through an equation of state (EOS), for instance, for a perfect gas EOS:

$$\begin{aligned} {\tilde{e}} (\overline{{\overline{P}}},\overline{\overline{\rho }}) = \frac{\overline{{\overline{P}}}}{(\gamma -1) \overline{\overline{\rho }}}, \end{aligned}$$

with $\gamma > 1$. Obviously, $\epsilon _0 = 0$ corresponds to the limit case of vanishing viscosity. Actually, the three-equation model (1) involves four main unknowns $\overline{\overline{\rho }}$, $\overline{{\overline{P}}}$, ${\tilde{u}}$ and K. Thus one closure law is required for the latter turbulent kinetic energy K, and several strategies have been proposed in the past for that purpose, that we briefly summarize below.

The most widespread approach consists in deriving the governing equation for K, starting from Euler or Navier-Stokes equations, and focusing on smooth solutions. Setting W the state variable, this leads to the following PDE for K:

$$\begin{aligned} \partial _{t}(K) + \nabla .(K {\tilde{u}}) + \frac{2K}{3} \nabla .({\tilde{u}}) =rhs_K(W,\nabla W), \end{aligned}$$

(2)

where the right-handside term $rhs_K(W,\nabla W)$ does not include any convective (first-order differential) term. Thus, by introducing a change of variable:

$$\begin{aligned} \xi = K\ (\overline{\overline{\rho }})^{-5/3}, \end{aligned}$$

where $\xi$ is sometimes refered to as the turbulent entropy, Eq. (2) may be rewritten as:

$$\begin{aligned} \partial _{t}(\xi ) + {\tilde{u}} \nabla .(\xi ) =(\overline{\overline{\rho }})^{-5/3} rhs_K(W,\nabla W), \end{aligned}$$

or alternatively using the mass balance equation:

$$\begin{aligned} \partial _{t}(\overline{\overline{\rho }} \xi ) + \nabla .(\overline{\overline{\rho }} \xi {\tilde{u}} ) =(\overline{\overline{\rho }})^{-2/3} rhs_K(W,\nabla W). \end{aligned}$$

Obviously, this only makes sense when restricting to smooth solutions. Some possible closure laws for $rhs_K(W,\nabla W)$ can be found in [18, 21] for instance. However, as emphasized in [1, 2, 8, 10], in the non viscous case, it remains to define jump conditions, and this is not straightforward, due to the occurence of non-conservative products $(2K/3\ \nabla . {\tilde{u}})$ in (2), which are active in genuinely non-linear fields associated with eigenvalues ${\tilde{u}} \pm$c$_t$, noting:

$$\begin{aligned} ({ c_t} )^2 = c^2 + \frac{10 K}{9 \overline{\overline{\rho }}}, \end{aligned}$$

where c stands for the speed of acoustic waves in laminar flows.

Among other possibilities, we recall that the strategy proposed in [8] is only valid for weak enough shock waves; besides, the approach suggested in [1, 2] is expected to be meaningful for stronger shocks. The reader is refered to [10] for a brief review. In the present paper, focus will be given on a simple turbulent model obtained while neglecting $rhs_K(W,\nabla W)$; thus, using the mass balance equation, an obvious solution is:

$$\begin{aligned} \xi = \xi _0. \end{aligned}$$

This implies:

$$\begin{aligned} K = K(\overline{\overline{\rho }}) = \xi _0(\overline{\overline{\rho }})^{5/3}. \end{aligned}$$

(3)

The resulting three-equation model [14] (whose counterpart is [15] in the two-phase framework) has thus three main unknowns $\overline{\overline{\rho }}, \overline{{\overline{P}}}, {\tilde{u}}$, that are governed by the closed system (1).

We will assume the following numerical strategy, which consists in computing approximate solutions of (1), using an explicit scheme for convective terms, and an implicit formulation for viscous terms, thus using the following time scheme:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\overline{\overline{\rho }}^{n+1} - \overline{\overline{\rho }}^{n}}{\Delta t}= -\left\{ \nabla .(\overline{\overline{\rho }}{\tilde{u}})) \right\} ^{n} \\&\frac{(\overline{\overline{\rho }} \tilde{u})^{n+1} - (\overline{\overline{\rho }} \tilde{u})^{n}}{\Delta t} - \epsilon _{0} \left\{ \nabla .(\Sigma ^{tot}(\nabla ^{s} {\tilde{u}}))\right\} ^{n+1}= - \left\{ \nabla .\left( \overline{\overline{\rho }} {\tilde{u}} \otimes {\tilde{u}} + \left( \overline{{\overline{P}}}+\frac{2K}{3}\right) .{\mathcal {I}} \right) \right\} ^{n}\\&\frac{(\overline{\overline{\rho }} E)^{n+1} - (\overline{\overline{\rho }} E)^{n}}{\Delta t} - \epsilon _{0} \left\{ \nabla .(\Sigma ^{tot}(\nabla ^{s} {\tilde{u}})\tilde{u})\right\} ^{n+1}= -\left\{ \nabla .\left( {\tilde{u}} \left( \overline{\overline{\rho }} E + \overline{{\overline{P}}} +\frac{2K}{3} \right) \right) \right\} ^{n} \end{aligned} \right. \end{aligned}$$

The present paper only focuses on the convective part of the system, second order tensors are not considered here and it investigates the main properties of the convective system associated with:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}(\overline{\overline{\rho }}) + \nabla .(\overline{\overline{\rho }} {\tilde{u}}) = 0 \\&\partial _{t}(\overline{\overline{\rho }} {\tilde{u}}) + \nabla .\left( \overline{\overline{\rho }} {\tilde{u}} \otimes {\tilde{u}} + \left( \overline{{\overline{P}}} +\frac{2K}{3}\right) .{\mathcal {I}} \right) = 0 \\&\partial _{t}(\overline{\overline{\rho }} E) +\nabla .\left( {\tilde{u}} \left( \overline{\overline{\rho }} E + \overline{{\overline{P}}} +\frac{2K}{3} \right) \right) = 0 \end{aligned} \right. \end{aligned}$$

(4)

which are detailed in Sect. 1. In particular, we will derive an entropy inequality which will enable to select admissible solutions when investigating the one-dimensional Riemann problem, and we will find the Riemann invariants associated with the LD (Linearly degenerate) and GNL (Genuinely non linear) fields and characterize the conditions of the jump associated with system (4) in Sect. 2. In the case of a perfect gas EOS, the existence and uniqueness of the solution of the Riemann problem of system (4) will be proved in Sect. 3 (with “Appendix A”). In Sect. 4, we will introduce a simple approximate Riemann solver in order to compute approximate solutions of the system introduced in Sect. 1. Some test cases for verification including shock structures will be carried out in Section 5, where it will be checked that this scheme enables to retrieve numerical convergence towards the exact solution even when shock waves occur, with the expected convergence rate. Section 6 will be devoted to the presentation of some two-dimensional computation The last section will be a conclusion of the work done in this paper.

Throughout the paper, standard $\tilde{a}$ and $\overline{{\overline{b}}}$ notations will be skipped.

2 Turbulent Compressible Flow Model

As recalled before, the model [14] has been obtained by a statistical averaging of the Euler / Navier-Stokes equations, and thus the following system of partial differential equations is considered:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}(\rho ) + \partial _{x}(\rho u) =0 \\&\partial _{t}(\rho u) + \partial _{x}\left( \rho u^{2} + P +\frac{2K}{3} \right) =0 \\&\partial _{t}(\rho E) +\partial _{x}\left( u\left( \rho E + P +\frac{2K}{3}\right) \right) =0 \end{aligned} \right. \end{aligned}$$

(5)

It governs the mean evolution of mass, momentum and energy. The quantities $\rho$, u, P, K, and E respectively represent the mean density, the mean velocity, the mean pressure, the turbulent kinetic energy and the mean total energy. The latter quantity is given by:

$$\begin{aligned} \begin{aligned} \rho E = \rho e(P,\rho ) + \frac{\rho u^{2}}{2} + K \end{aligned}, \end{aligned}$$

(6)

where e=e(P,$\rho$) is the mean specific internal energy, and the turbulent kinetic energy follows the law:

$$\begin{aligned} \begin{aligned} K=\xi _0 \rho ^{5/3}, \end{aligned} \end{aligned}$$

(7)

with $\xi _0$ a positive constant.

We introduce the celerity of density waves c(P,$\rho$) and the temperature T, such that:

$$\begin{aligned} c^{2}(P,\rho )= & {} \left( \frac{P}{\rho ^{2}} -\partial _{\rho }e(P,\rho )\right) /\partial _{P}e(P,\rho ) , \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{T}= & {} (\partial _{P}e)^{-1} (\partial _{P} s), \end{aligned}$$

(9)

where s=$s(P,\rho )$ is the specific entropy complying with the constraint:

$$\begin{aligned} \begin{aligned} c^{2}(P,\rho )(\partial _{p} s ) +(\partial _{\rho } s) =0. \end{aligned} \end{aligned}$$

(10)

We will also define the modified pressure $P^{*}$:

$$\begin{aligned} \begin{aligned} P^{*} = P +\frac{2}{3}K. \end{aligned} \end{aligned}$$

(11)

3 Main Properties of the Flow Model

In this section, we give some properties of system (5) in a general framework with respect to the EOS.

3.1 Entropy Inequality

In order to introduce an entropy inequality, we consider a viscous perturbation of system (5), which is chosen as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}(\rho ) + \partial _{x}(\rho u) =0 \\&\partial _{t}(\rho u) + \partial _{x}\left( \rho u^{2} + P +\frac{2K}{3} \right) =\epsilon _{0}\partial _{x}\left( \frac{2}{3} \mu \partial _{x} u \right) \\&\partial _{t}(\rho E) +\partial _{x}\left( u\left( \rho E + P +\frac{2K}{3}\right) \right) =\epsilon _{0}\partial _{x}\left( \frac{2}{3} \mu u \partial _{x} u\right) \end{aligned} \right. \end{aligned}$$

(12)

Here $\mu$ represents the total viscosity and $\epsilon _{0}$ is a constant in ]0, 1]. In the following we consider the conservative state variable:

$$\begin{aligned} w=(\rho ,\rho u, \rho E), \end{aligned}$$

and the flux:

$$\begin{aligned} F(w)=(\rho u, \rho u^{2} +P^{*}, u(\rho E +P^{*})). \end{aligned}$$

We introduce the entropy–entropy flux pair $(\eta ,f_{\eta })$ with:

$$\begin{aligned} \begin{aligned} \eta (w)= -\rho ln(s),\quad \text {and} \quad f_{\eta }(w)=u\eta . \end{aligned} \end{aligned}$$

(13)

Proposition 1

Then the following inequality holds for smooth solutions of (12):

$$\begin{aligned} \begin{aligned} \partial _{t} \eta + \partial _{x} f_{\eta } \le 0. \end{aligned} \end{aligned}$$

(14)

Proof

In the case of the viscous perturbed system (12), simple computations lead to the entropy inequality:

$$\begin{aligned} \partial _{t} \eta + \partial _{x} f_{\eta } = - \frac{1}{s} \frac{\partial s}{\partial P} \left( \frac{\partial e}{\partial P} \right) ^{-1} \frac{2}{3} \epsilon _{0} \mu (\partial _{x} u )^{2} = - \frac{2}{3T} \epsilon _{0} \mu (\partial _{x} u )^{2}\le 0 . \end{aligned}$$

$\square$

Remark 1

In the non viscous case, for a discontinuity travelling at speed $\sigma$, we will thus assume that the following inequality holds true:

$$\begin{aligned} -\sigma [\eta ] +[f_{\eta }] \le 0. \end{aligned}$$

(15)

This will enable us to select the admissible solution of the Riemann problem associated with the conservative system (5).

3.2 Hyperbolicity

The system is written in the form:

$$\begin{aligned} \partial _{t} W + A(W) \partial _{x} W = 0, \end{aligned}$$

(16)

where the primitive variable W reads:

$$\begin{aligned} W=(\rho , u, P)^{t}. \end{aligned}$$

The jacobian matrix A(W) is:

$$\begin{aligned} A(W)=\begin{pmatrix} u&{}\rho &{}0\\ \frac{10K}{9\rho ^{2}}&{}u&{}\tau \\ 0&{}\rho c^{2}&{}u \end{pmatrix}, \end{aligned}$$

where $\tau =1/\rho$ denotes the specific volume.

Proposition 2

We define c$_t$ such that:

$$\begin{aligned} {c_t^{2}}=c^{2} +\frac{10K}{9\rho }. \end{aligned}$$

System (16) is strictly hyperbolic, it admits three real eigenvalues:

$$\begin{aligned} \lambda _{1}(W)= u -{c_t}, \lambda _{2}(W)=u , \lambda _{3}(W)= u + {c_t}, \end{aligned}$$

(17)

and the associated eigenvectors $r_{k}$(W) span the whole space ${\mathbb {R}}^{3}$ provided that ${c_t}\ne 0$:

$$\begin{aligned} r_{1}(W)=\left( \rho ,-{c_t},\rho c^{2} \right) ^{T}, r_{2}(W)=\left( \rho ,0,-\frac{10K}{9}\right) ^{T}, r_{3}(W)=\left( \rho ,{c_t},\rho c^{2}\right) ^{T}. \end{aligned}$$

(18)

Fields associated with $\lambda _{1}(W)~ and~ \lambda _{3}(W)$ are genuinely non linear (GNL), and field associated with $\lambda _{2}(W)$ is linearly degenerate (LD).

Proof

The proof is simple when using the system written in the non conservative variable $(s,u,P^*)$, see system (22), and it is thus left to the reader. Moreover, it should also be noted that examining the nature (GNL or LD) of the waves is more simple when using this set of variables, see the following section. $\square$

3.3 Riemann Invariants

Proposition 3

The two Riemann invariants associated with the LD field ($\lambda _{2}=u$) are the following whatever the EOS is:

$$\begin{aligned} I^{2}_{1}(W)=u , I^{2}_{2}(W)=P^{*}(P,\rho ). \end{aligned}$$

(19)

The Riemann invariants associated with the two GNL waves read:

$$\begin{aligned}&1-rarefaction~wave: I^{1}_{1}(W)= s(P,\rho ) , I^{1}_{2}(W)=u +\displaystyle \int _{0}^{\rho } \frac{{c_t}(I^{1}_{1}(W),\rho \prime )}{\rho \prime } \,\mathrm {d}\rho \prime . \end{aligned}$$

(20)

$$\begin{aligned}&3-rarefaction~wave: I^{3}_{1}(W)= s(P,\rho ) , I^{3}_{2}(W)=u -\displaystyle \int _{0}^{\rho } \frac{{c_t}(I^{3}_{1}(W),\rho \prime )}{\rho \prime } \,\mathrm {d}\rho \prime . \end{aligned}$$

(21)

Proof

$I_{k}^{i}$ represents the k-th Riemann invariants for the i-th wave (1-rarefraction, 2-contact, 3-rarefraction ). A Riemann invariant is a function that remains constant along the pathes defined by the corresponding eigenvectors, it thus complies with:

$$\begin{aligned} dI_{k}^{i}(W).r_{i}(W) = 0. \end{aligned}$$

It is straightforward to check that functions given by (19)–(20)–(21) comply with the condition above. We also note that we can express Riemann invariants with the variable:

$$\begin{aligned} Y =(s,u,P^{*}). \end{aligned}$$

Actually, it may be checked that smooth solutions of (16) comply with:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t} s + u\partial _{x} s =0 \\&\partial _{t} u + u\partial _{x}u + \tau \partial _{x} P^{*}=0 \\&\partial _{t} P^{*} +\rho {{c_t^{2}}} \partial _{x} u + u\partial _{x} P^{*}=0 \end{aligned} \right. \end{aligned}$$

(22)

If $\bar{\tilde{ r}}_{i}(Y)$ denote the eigenvectors associated with system (22) written in terms of variable Y, it may be checked that functions $\bar{\tilde{I}}_{k}^{i}$(Y) satisfying:

$$\begin{aligned} d\bar{\tilde{I}}_{k}^{i}(Y). \bar{\tilde{ r}}_{i}(Y) = 0, \end{aligned}$$

are as follows:

$$\begin{aligned} \begin{array}{ll} 1-rarefaction~wave: &{} \bar{\tilde{I}}^{1}_{1}(Y)= s, \bar{\tilde{I}}^{1}_{2}(Y)=u +\displaystyle \int _{0}^{P^{*}} \frac{1}{\rho (s,P^{*\prime }){c_t}(s,P^{*\prime })} \,\mathrm {d}P^{*\prime }. \\ 2-contact~wave:&{} \bar{\tilde{I}}^{2}_{1}(Y)=u, \bar{\tilde{I}}^{2}_{2}(Y)=P^{*}.\\ 3-rarefaction~ wave: &{} \bar{\tilde{I}}^{3}_{1}(Y)= s, \bar{\tilde{I}}^{3}_{2}(Y)=u -\displaystyle \int _{0}^{P^{*}} \frac{1}{\rho (s,P^{*\prime }){c_t}(s,P^{*\prime })} \,\mathrm {d}P^{*\prime }. \end{array} \end{aligned}$$

Then, the same Riemann invariants $I^{i}_{k}(W)$ and $\bar{\tilde{I}}^{i}_{k}(Y)$ are retrieved up to the variable change $W\mapsto Y$.

$\square$

3.4 Jump Conditions

We are now interested in discontinous solutions for sytem (5) whatever the EOS is. We denote

$$[f]=f_{R} - f_{L},$$

the jump between the left and right states on each side of a discontinuity travelling at speed $\sigma$.

Proposition 4

Jump conditions associated with system (5) may be written:

$$\begin{aligned} \left\{ \begin{aligned}&-\sigma [\rho ] + [\rho u] =0, \\&-\sigma [\rho u] + \left[ \rho u^{2} + P +\frac{2K}{3} \right] =0, \\&-\sigma [\rho E] +\left[ u \left( \rho E + P +\frac{2K}{3}\right) \right] =0. \end{aligned} \right. \end{aligned}$$

(23)

Those jump conditions may be rewritten as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\sigma = [\rho u]/[\rho ], \\&\rho _{R} \rho _{L}[u]^{2}=\left[ P+\frac{2}{3}K\right] [\rho ], \\&\rho (u-\sigma ) \left( \left[ e +\frac{K}{\rho }\right] +\overline{P^{*}}\left[ \frac{1}{\rho }\right] \right) =0. \end{aligned} \right. \end{aligned}$$

(24)

with ${\bar{\phi }}= \frac{\phi _{L}+\phi _{R}}{2}$.

Remark 2

When dealing with the LD field associated with $\lambda _{2}$=u the solution of the above jump conditions is equivalent to the Riemann invariants (19), i.e. [$I^{2}_{k}]$= 0.

Proof

By applying the Rankine-Hugoniot relation to the conservative system (5):

$$\begin{aligned} -\sigma [w] +[F(w)]=0, \end{aligned}$$

system (23) is straightforwardly obtained. For the first two equations of system (24), we can find it thanks to simple calculations. We now detail the calculations necessary to find the third equation for system (24).

We first note:

$$\begin{aligned} v=u - \sigma . \end{aligned}$$

(25)

From the first two relations of system (23), taking into account (25), we have:

$$\begin{aligned} -\sigma [\rho ] + [\rho u] = [\rho v] =0, \end{aligned}$$

(26)

$$\begin{aligned} -\sigma [\rho u] + \left[ \rho u^{2} + P +\frac{2K}{3} \right] = [\rho v u] + [P^{*}] = 0. \end{aligned}$$

(27)

We deduce from (26) that $\rho v$ is a constant across the discontinuity. By introducing v into the third equation of system (23) and by using (26), we get the following form:

$$\begin{aligned} \rho v[ e] +\rho v\left[ \frac{u^{2}}{2}\right] + \rho v[ K \tau ] + \bar{P^{*}}[u] + {\bar{u}}[P^{*}]=0. \end{aligned}$$

(28)

Then, by multiplying (27) by ${\bar{u}}$, we have:

$$\begin{aligned} \rho v\left[ \frac{u^{2}}{2}\right] = - {\bar{u}}[P^{*}]. \end{aligned}$$

(29)

Third equation of (24) is finally obtained by introducing (29) into (28):

$$\begin{aligned} \rho v [e+ K\tau ] + \bar{P^{*}} [u]= \rho v [e+ K\tau ] + \bar{P^{*}} [\rho v \tau ]=\rho v ([e+ K\tau ] + \bar{P^{*}} [\tau ])=0, \end{aligned}$$

(30)

this completes the proof. $\square$

Remark 3

In the case of a turbulent perfect gas EOS:

$$\begin{aligned} P=(\gamma -1)\rho e, \end{aligned}$$

jump conditions (23) provide bounds for the density ratio whereas the pressure ratio has no bounds, i.e. a shock wave separating two states $Y_{R}$ and $Y_{L}$ is such that:

$$\begin{aligned} \beta ^{-1} \le \frac{\rho _{r}}{\rho _{l}} \le \beta , \end{aligned}$$

with $\beta =\frac{\gamma +1}{\gamma -1}$.

Proof

For the Euler equations (i.e. without turbulent contribution) with the instantaneous perfect gas EOS:

$$\begin{aligned} P^{\prime }=(\gamma -1)\rho ^{\prime }e^{\prime }, \end{aligned}$$

we know that (see [17] ) the value of the ratio $\frac{max(\rho _{r}^{\prime },\rho _{l}^{\prime })}{min(\rho _{r}^{\prime },\rho _{l}^{\prime })}$ across a shock wave is bounded by:

$$\begin{aligned} \beta =\frac{\gamma +1}{\gamma -1}. \end{aligned}$$

This means that in the non turbulent case:

$$\begin{aligned} \beta ^{-1} \rho _{l}^{\prime }< \rho _{r}^{\prime } < \beta \rho _{l}^{\prime }. \end{aligned}$$

(31)

Since $\beta$ is a constant for the perfect gas EOS, a straightforward averaging of (31) provides:

$$\begin{aligned} \beta ^{-1} \rho _{l}< \rho _{r} < \beta \rho _{l}. \end{aligned}$$

(32)

We thus may wonder whether the solution of (5) also satisfies (32). Actually, formulae (53) in “Appendix A.1” for the 1-shock wave provide:

$$\begin{aligned} \frac{P_{r}}{P_{l}}= \frac{\beta z_{1} -1 +g_{1}(z_{1})}{\beta -z_{1}},\qquad \text {and} \qquad g_{1}(z_{1})> 0,\qquad \text {with} \qquad z_{1}=\frac{\rho _{r}}{\rho _{l}} > 1. \end{aligned}$$

Thus, it is staightforward to see that pressure ratio has no bound. Moreover, positive values of $P_{r} ~,~P_{l}$ imply $z_{1} < \beta$, which means that:

$$\begin{aligned} \rho _{r}=max(\rho _{r},\rho _{l}) < \beta \rho _{l} = \beta ~min(\rho _{r},\rho _{l}), \end{aligned}$$

which completes the proof, since a similar result holds using formulae (55) in “Appendix A.1” for the 3-shock wave. $\square$

4 Solution of the Riemann Problem

In this section, we are interested in finding the solution of the Riemann problem associated with (5) in the case of a perfect gas EOS:

$$\begin{aligned} P=(\gamma -1)\rho e. \end{aligned}$$

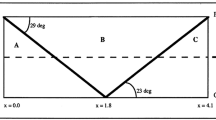
First we have to start connecting $W_{L}$ to $W_{R}$ through the intermediate states $W_{1}$ and $W_{2}$, where the subscripts L and R denote respectively the left and the right states of the initial discontinuity, and the subscript 1 (respectively 2) represents the intermediate state of the solution of the Riemann problem between waves $\lambda _{1}$ and $\lambda _{2}$ (respectively between $\lambda _{2}$ and $\lambda _{3}$), see Fig. 1.

Fig. 1

Solution of the Riemann problem which consists in four constant states $W_L$, $W_1$, $W_2$ and $W_R$ separated by the waves $\lambda _i$, $i=\{1,2,3\}$

4.1 Waves Connection

We must first distinguish 4 cases for the solution of the Riemann problem, depending on the nature of the two GNL waves associated with $\lambda _1$ and $\lambda _3$:

• case 1: 1-shock / 2-contact / 3-shock

• case 2: 1-rarefaction / 2-contact / 3-rarefaction

• case 3: 1-shock / 2-contact / 3-rarefaction

• case 4: 1-rarefaction / 2-contact / 3-shock

Proposition 5

We first set:

$$\begin{aligned} z_{1}=\frac{\rho _{1}}{\rho _{L}} \quad \text {and} \quad z_{2}=\frac{\rho _{2}}{\rho _{R}}. \end{aligned}$$

The solution of the Riemann problem associated with (5) is as follows:

case 1. We have for $z_{1}> 1$ and $z_{2} > 1$:

$$\begin{aligned} u_{R} - u_{L} +c_{L}f_{1}(z_{1},K_{L}/P_{L}) +c_{R}f_{2}(z_{2},K_{R}/P_{R})=0, \end{aligned}$$

and:

$$\begin{aligned} P_{L}h_{1}(z_{1},K_{L}/P_{L}) +\frac{2K_{L}}{3} z_{1}^{5/3} = P_{R}h_{2}(z_{2},K_{R}/P_{R}) +\frac{2K_{R}}{3} z_{2}^{5/3}, \end{aligned}$$

with the following definitions:

$$\begin{aligned} f_{1}(z_{1},K_{L}/P_{L})= & {} \sqrt{\left( \frac{z_{1}-1}{\gamma z_{1}} \right) \left( -1 +\frac{2}{3} \frac{K_{L}}{P_{L}}(z_{1}^{5/3}-1) +h_{1}(z_{1},K_{L}/P_{L})\right) },\\ h_{1}(z_{1},K_{L}/P_{L})= & {} \displaystyle \frac{\beta z_{1} -1 + g_{1}(z_{1},K_{L}/P_{L})}{\beta -z_{1}},\\ g_{1}(z_{1},K_{L}/P_{L})= & {} \displaystyle \frac{2K_{L}}{3P_{L}}\left( z_{1}^{8/3} -4z_{1}^{5/3} +4z_{1}-1 \right) , \end{aligned}$$

and:

$$\begin{aligned} f_{2}(z_{2},K_{R}/P_{R})= & {} \sqrt{\left( \frac{z_{2}-1}{\gamma z_{2}}\right) \left( -1 +\frac{2}{3} \frac{K_{R}}{P_{R}}(z_{2}^{5/3}-1) +h_{2}(z_{2},K_{R}/P_{R})\right) },\\ h_{2}(z_{2},K_{R}/P_{R})= & {} \displaystyle \frac{\beta z_{2} -1 + g_{2}(z_{2},K_{R}/P_{R})}{\beta -z_{2}},\\ g_{2}(z_{2},K_{R}/P_{R})= & {} \displaystyle \frac{2K_{R}}{3P_{R}}\left( z_{2}^{8/3} -4z_{2}^{5/3} +4z_{2}-1\right) , \end{aligned}$$

and $K_{L,R}= \xi _0 \rho _{L,R}^{5/3}.$

case 2. We have for $z_{1} \le 1$ and $z_{2} \le 1$:

$$\begin{aligned} u_{R} - u_{L} +c_L {B_{1}}(z_{1},K_{L}/P_{L}) +c_R {B_{2}}(z_{2},K_{R}/P_{R}) =0, \end{aligned}$$

and:

$$\begin{aligned} P_{L}Q_{1}(z_{1}) +\frac{2K_{L}}{3} z_{1}^{5/3} = P_{R}Q_{2}(z_{2}) +\frac{2K_{R}}{3} z_{2}^{5/3}, \end{aligned}$$

with the following definitions:

$$\begin{aligned} {B_{1}}(z_{1},K_{L}/P_{L})= & {} \displaystyle \int _{1}^{z_{1}} {\left( z^{\gamma -3} +\frac{10 K_L}{9 \gamma P_{L}} z^{-4/3}\right) }^{1/2} \,\mathrm {d}z,\\ Q_{1}(z_{1})= & {} z_{1}^{\gamma },\\ {B_{2}}(z_{2},K_{R}/P_{R})= & {} \displaystyle \int _{1}^{z_{2}} {\left( z^{\gamma -3} +\frac{10 K_R}{9 \gamma P_{R}} z^{-4/3}\right) }^{1/2} \,\mathrm {d}z,\\ Q_{2}(z_{2})= & {} z_{2}^{\gamma }. \end{aligned}$$

case 3. We have for $z_{1} > 1$ and $z_{2} \le 1$:

$$\begin{aligned} u_{R} - u_{L} +c_R {B_{2}}(z_{2},K_{R}/P_{R}) +c_{L}f_{1}(z_{1},K_{L}/P_{L}) = 0, \end{aligned}$$

and

$$\begin{aligned} P_{L}h_{1}(z_{1},K_{L}/P_{L}) +\frac{2K_{L}}{3} z_{1}^{5/3} = P_{R}Q_{2}(z_{2}) +\frac{2K_{R}}{3} z_{2}^{5/3}. \end{aligned}$$

case 4. We have for $z_{1} \le 1$ and $z_{2} > 1$:

$$\begin{aligned}&u_{R} - u_{L} + c_L {B_{1}}(z_{1},K_{L}/P_{L}) +c_{R}f_{2}(z_{2},K_{R}/P_{R}) = 0, \\&\quad P_{L}Q_{1}(z_{1}) +\frac{2K_{L}}{3} z_{1}^{5/3} = P_{R}h_{2}(z_{2},K_{R}/P_{R}) +\frac{2K_{R}}{3} z_{2}^{5/3}. \end{aligned}$$

The reader is referred to Appendices A.1 and A.2 for a proof.

4.2 Existence and Uniqueness of the Solution

Proposition 6

The Riemann problem associated with (5) and initial states:

$$\begin{aligned} W(x<0,t=0)= & {} W_{L}, \\ W(x>0,t=0)= & {} W_{R}, \end{aligned}$$

admits a unique self-similar solution:

$$\begin{aligned} W(x,t)=\omega (x/t), \end{aligned}$$

with no vacuum occurrence, provided that initial left and right states, $W_L$ and $W_R$, are such that:

$$\begin{aligned} u_{R} - u_{L} < X_{L} + X_{R}, \end{aligned}$$

(33)

with $X_{i}=\displaystyle \int ^{\rho _{i}}_0 \frac{{c_t}(s,\rho ')}{\rho '} \,\mathrm {d}\rho '$.

The reader is referred to “Appendix A” for a proof which is based on the proof proposed in [17].

Remark 4

For $\xi _0=0$, we have ${c_t}=c$ and condition (33) is equivalent to the condition of no vacuum occurrence for Euler with a perfect gas EOS.

5 An Approximate Numerical Riemann Solver

Approximate Riemann solvers are commonly used in order to compute approximate solutions of hyperbolic problems, where contact waves, rarefactions and shock waves co-exist (see among others the original paper [12] and the books [11, 20]).

We consider a classical finite volume formulation. The segment [a, b] is divided into cells $I_{i}$, where $x_{i+\frac{1}{2}}$ represents the cell interface between cells $I_i$ and $I_{i+1}$, and $x_{i}$ represents the cell center. We define $\Delta t^{n}$ the time step at time $t^{n}$ and $\Delta x_{i}$ the length of $I_{i}$: $t^{n+1}= t^{n} + \Delta t^{n}$ and $\Delta x_{i}= x_{i+\frac{1}{2}} - x_{i-\frac{1}{2}}$.

5.1 VFRoe-ncv Scheme

In this section, we recall an extension of the VFRoe scheme [16] called VFRoe-ncv which was proposed in order to deal with hyperbolic systems in [3]. The VFRoe-ncv scheme is an approximate Godunov scheme where the approximate value at the interface between two cells is computed as detailed below.

First, system (5) may be rewritten as follows:

$$\begin{aligned} \partial _{t} Z + B(Z) \partial _{x} Z=0, \end{aligned}$$

(34)

where:

$$\begin{aligned} Z=(\rho , u, P^{*})^{t}, \end{aligned}$$

and

$$\begin{aligned} B(Z)=\begin{pmatrix} u&{}\rho &{}0\\ 0&{}u&{}\tau \\ 0&{}\rho {c_t}^{2}&{}u \end{pmatrix}, \end{aligned}$$

and also:

$$\begin{aligned} P^{*}=P+ \frac{2K}{3}, \tau =\frac{1}{\rho }. \end{aligned}$$

We then consider the Riemann problem associated with system (34) and initial conditions:

$$\begin{aligned} Z(x<0,t=0)=Z_{L}, \qquad Z(x>0,t=0)=Z_{R}. \end{aligned}$$

(35)

At each interface between two cells, we solve the following linearized Riemann problem:

$$\begin{aligned} \partial _{t} Z + B({\bar{Z}}) \partial _{x} Z=0, \end{aligned}$$

(36)

where ${\bar{Z}} = (Z_{L} + Z_{R})/2$. System (36) contains 3 linearly degenerate fields, thus the solution of the one-dimensional Riemann problem is simple. Indeed, it only requires computing three real coefficients noted $\alpha _{i}$ (for i=1 to 3) and such that:

$$\begin{aligned} Z_{R} - Z_{L} = \sum _{i=1}^{3} \alpha _{i} \widehat{r_{i}}, \end{aligned}$$

where $\widehat{r_{i}}$ represents the basis of right eigenvectors of the matrix B(${\bar{Z}}$):

$$\begin{aligned} \widehat{r_{1}}=(1,-\hat{{c_t}}{\bar{\tau }},\hat{{c_t}}^{2})^{T}, \widehat{r_{2}}=(1,0,0)^{T}, \widehat{r_{3}}=(1,\hat{{c_t}}{\bar{\tau }},\hat{{c_t}}^{2})^{T}. \end{aligned}$$

More details concerning the explicit computation of the intermediate states $Z_{1}$ and $Z_{2}$ can be found in “Appendix B”. Hence the exact solution $Z^{*}(Z_L,Z_R)$ at the initial discontinuity location, i.e. at $x/t=0$, of the linearized Riemann problem associated with system (36) and initial conditions (35) is given by:

$$\begin{aligned} Z^{*}(Z_L,Z_R)= \left\{ \begin{array}{l} Z_{L} ~~\text {if} ~~\bar{\lambda _{1}}\ge 0;\\ Z_{1} ~~\text {if} ~~\bar{\lambda _{1}}<0~ \text {and} ~\bar{\lambda _{2}} \ge 0;\\ Z_{2}~~ \text {if}~~ \bar{\lambda _{2}}<0~ \text {and} ~\bar{\lambda _{3}}\ge 0;\\ Z_{R}~~ \text {if}~~ \bar{\lambda _{3}}<0; \end{array} \right. \end{aligned}$$

(37)

where:

$$\begin{aligned} \lambda _{1}={\bar{u}} -\widehat{{c_t}}, \lambda _{2}={\bar{u}}, \lambda _{3}={\bar{u}} +\widehat{ {c_t}}, \end{aligned}$$

and also:

$$\begin{aligned} \widehat{ {c_t}}(\rho ,P)= {c_t}({\bar{\rho }},{\bar{P}})=\sqrt{\frac{\gamma P(\bar{P^{*}},{\bar{\rho }})}{{\bar{\rho }}} +\frac{10}{9}\frac{K({\bar{\rho }})}{{\bar{\rho }}}}. \end{aligned}$$

(38)

Finally the numerical scheme reads:

$$\begin{aligned} \Delta x_{i}( w_{i}^{n+1} - w_{i}^{n} ) + \Delta t( {\mathcal {F}}_{i+\frac{1}{2}}^{n} -{\mathcal {F}}_{i-\frac{1}{2}}^{n} ) = 0, \end{aligned}$$

(39)

where the numerical flux is computed thanks to the exact solution (37) of the linearized problem (36)–(35) with $Z_L=Z_i^n$ and $Z_R=Z_{i+1}^n$:

$$\begin{aligned} {\mathcal {F}}_{i+\frac{1}{2}}^{n}=F(w(Z^*(Z_i^n,Z_{i+1}^n))). \end{aligned}$$

In the definition of the numerical flux above, it should be noted that we have $w=(\rho ,\rho u, \rho E)$ and that $w\mapsto F(w)$ corresponds to the analytical flux of system (5) as defined in Sect. 2.1. Moreover, we apply the Courant–Friedrichs–Lewy (CFL) condition:

$$\begin{aligned} \frac{\Delta t^{n}}{\Delta x_{j}} max(|\lambda _{i}|) < 1, \end{aligned}$$

in scheme (39).

Remark 5

An entropy correction is required (see [13]) to compute shock tube problems when one sonic point is present in the rarefaction wave.

Remark 6

The alternative choice of the non-conservative variable $(s, u, P^*)$ has not been retained here because it requires a non-explicit change of variable. The latter thus increases the computational cost of the scheme. This variable change corresponds to finding $\rho$ such that:

$$\begin{aligned} P(\rho ,s_{L,R} ) + \frac{2}{3}\xi _0 \rho ^{\frac{5}{3}}=P^{*}_{L,R}, \end{aligned}$$

for given $s_{L,R}$ and $P^{*}_{L,R}$. Thus it will not be considered in the sequel.

6 Numerical Results

We present now some numerical results obtained for the model and scheme detailed in the previous sections. We focus here on two test cases that involve shock waves: the double-shock test case (i.e. case 1 in Sect. 3.1) and a “strong shock wave” test case. The former allows to compute accurately the solution of the Riemann problem, and it is thus useful for convergence study. Indeed, the computation of an exact solution of a Riemann problem involving a rarefaction wave requires a numerical integration of the rarefaction fan. These are thus less accurately computed. The second test case corresponds to a situation where initial states present a great ratio of pressure and density. It is representative of situations involving explosion or detonation waves. It should be noted that qualitative results for a test case involving two symmetric rarefaction waves have been added in “Appendix C”.

Numerical convergence curves, at a given time, are represented by the logarithm of the relative $L^{1}$-error as a function of the logarithm of the mesh size. The relative $L^{1}$-error is computed at time $t^{n}$ on the whole regular mesh as:

$$\begin{aligned} \frac{\sum _{i} |\phi _{i}^{approx,n} - \phi ^{exact}(x_{i},t^{n})|\Delta x_{i}}{\sum _{i}|\phi ^{exact}(x_{i},t^{n})|\Delta x_{i}}. \end{aligned}$$

(40)

Obviously, when $\sum _{i}|\phi ^{exact}(x_{i},t^{n})|=0$ , this definition is meaningless and we change it into:

$$\begin{aligned} \sum _{i} |\phi _{i}^{approx,n} - \phi ^{exact}(x_{i},t^{n})|. \end{aligned}$$

The first test case provides a comparison between the exact solution and the approximate solution and it enables to obtain a numerical convergence curve on the basis of the error (40). For the other test cases, only qualitative plots of the approximate solutions are presented at a given final time for the density, the velocity, the pressure P and the modified pressure $P^{*}$.

All the computations are performed for a given value of $CFL=0.5$, and for different values of the parameter $\xi _0$. It should be recalled that when $\xi _0=0$, the modified pressure $P^{*}$ is equal to the thermodynamical pressure P. Moreover, in all the tests below, we have considered the perfect gas EOS:

$$\begin{aligned} P=(\gamma -1)\rho e, \end{aligned}$$

where the constant $\gamma$ is equal to $\frac{7}{5}$. The computational domain is [0, 1] and the initial discontinuity separating states $W_{L}$ and $W_{R}$ is located at x$=0.5$. The domain [0, 1] is discretized using uniform cells, $\Delta x_{i} = \Delta x$, and the number of cells varies from 200 up to 1$\times$ $10^{5}$ cells.

6.1 Test 1: Double Shock Wave

In this test case, we compare the exact solution of the one-dimensional Riemann problem with the approximate solution. Three different values of $\xi _0$ are used $\xi _0=\{ 0; 10{,}000; 50{,}000\}$. Each value of $\xi _0$ leads to a different Riemann problem whose initial conditions are given below:

• For $\xi _0$=0:

  $$\begin{aligned} (\rho _{L},u_{L},P_{L})=(1,550,10^{6}) \end{aligned}$$
  $$\begin{aligned} (\rho _{R},u_{R},P_{R})=(1,-618.107550,103990.112994) \end{aligned}$$

• For $\xi _0$=10,000:

  $$\begin{aligned} (\rho _{L},u_{L},P_{L})=(1,650,10^{6}) \end{aligned}$$
  $$\begin{aligned} (\rho _{R},u_{R},P_{R})=(1,-687.545913,98007.273140) \end{aligned}$$

• For $\xi _0$=50,000:

  $$\begin{aligned} (\rho _{L},u_{L},P_{L})=(1,750,10^{6}) \end{aligned}$$
  $$\begin{aligned} (\rho _{R},u_{R},P_{R})=(1,-750.364690,94038.441853 ) \end{aligned}$$

Figures 2, 4 and 6 show qualitative comparisons between the exact solutions and the approximate solutions for a mesh that contains 500 cells and for respectively $\xi _0=\{0;10{,}000;50{,}000\}$. Figures 3, 5 and 7 show the convergence curves for the set of variables $\{\rho , u, P, P^{*}\}$ and for the three different values of $\xi _0$.

First of all we notice that $\frac{\max (\rho _{l},\rho _{r})}{\min (\rho _{l},\rho _{r})}\approx 4.25$, which is less than $\beta$ (for $\gamma =1.4$ we get $\beta = 6$). This is in agreement with the theory as mentioned in Remark 3. The approximated shock wave profile is monotonic; there are no spurious oscillations in the vicinity of the shock. The error varies as $\approx$ $h^{1}$ for variables u and $P^*$ on fine meshes, and as $\approx$ $h^{1/2}$ for $\rho$ and P on fine meshes (owing to the occurrence of the contact discontinuity), see Fig. 3. This behavior is due to the VFRoe-ncv scheme using the variable $(u,P^*)$ and the perfect gas EOS. Indeed, thanks to the latter, profiles for the velocity and the modified pressure are almost uniform around the contact location. On fine meshes, the error on the approximated velocity and modified pressure are thus not influenced by the larger error on the contact wave. This is not the case for the density and the pressure P, which therefore have an effective convergence rate of 1/2. For $\xi _0=0$, the system corresponds to the classical Euler system and $P=P^*$. Then the effective convergence rate reported in [3] is recovered for P (Fig. 3).

Fig. 2

Double-shock wave test case. Density (top left), velocity (top right) and pressure (bottom). Comparison between the exact solution (green) and the approximate solution (purple) at $t=3\ 10^{-2}$ s, $CFL=0.5$, 500 cells, $\xi _0=0$ (Color figure online)

Fig. 3

Double-shock wave test case. Convergence curves: logarithm of the relative L1-error versus the logarithm of the mesh size with uniform meshes containing from 200 to 55,000 cells. The error is plotted for variables, $\rho$, u and $P^{*}$, $\xi _0=0$ (recall that here $P^{*}=P)$

Fig. 4

Double-shock wave test case. Density (top left), velocity (top right), pressure (bottom left) and $P^{*}$ (bottom right). Comparison between the exact solution (green) and the approximate solution (purple) at $t=3\ 10^{-2}$ s, $CFL=0.5$, 500 cells, $\xi _0=10{,}000$ (Color figure online)

Fig. 5

Double-shock wave test case. Convergence curves: logarithm of the relative L1-error versus the logarithm of the mesh size with uniform meshes containing from 200 to 55,000 cells. The error is plotted for variables, $\rho$, u, P and $P^{*}$, $\xi _0=10{,}000$

Fig. 6

Double-shock wave test case. Density (top left), velocity (top right), pressure (bottom left) and $P^{*}$ (bottom right). Comparison between the exact solution (green) and the approximate solution (purple) at $t=3\ 10^{-2}$ s, $CFL=0.5$, 500 cells, $\xi _0=50{,}000$ (Color figure online)

Fig. 7

Double-shock wave test case. Convergence curves: logarithm of the relative L1-error versus the logarithm of the mesh size with uniform meshes containing from 200 to 55,000 cells. The error is plotted for variables, $\rho$, u, P and $P^{*}$, $\xi _0=50{,}000$

6.2 Test 2: Strong Shock Wave

The propagation of strong shock waves, generated by a strong explosion is of great interest from a physical point of view due to its numerous applications in various fields. In order to mimic such situations, we consider here a Riemann problem for which the left state corresponds to a gas at very high pressure with respect to the right state, the latter representing the ambient conditions. The high pressurized gas then expands rapidly and generates strong waves. When the pressure ratios between left and right states are high enough, a supersonic rarefaction wave is observed. For the latter the two extremities of the fan of the rarefaction wave travel in opposite directions (see Fig. 8). In these situations, an entropy correction is mandatory for the VFRoe-ncv scheme, as the one proposed in [13] and implemented here. Without the latter, computations fail because of the occurrence of a discontinuous - and non physical - pattern in the rarefaction fan (in fact at the location of the initial discontinuity). Thus this test is of interest and it shows what happens for the flows during strong variations in density, which originate from strong variations in pressure and temperature.

We propose here to examine the approximate solution for a Riemann problem with a pressure and density ratio equal to 1000. More precisely, we choose the left and right states such that:

$$\begin{aligned} (\rho , u, P)_{L}= (1000\times \rho _{0}, 0, 1000 \times P_{0}), \qquad \text {and} \qquad (\rho , u, P)_{R}= (\rho _{0}, 0, P_{0}), \end{aligned}$$

and where the right state corresponds to ambient gas at rest: ($\rho _{0}$, P$_{0}$)= (1, 10$^{5}$). Figures 9, 10, 11 and 12 show the behavior of the density, velocity, pressure and modified pressure at a given time $T_f=1.25\ 10^{-4}\ s$, on different meshes with 500 cells, 5000 cells and 50,000 cells. Moreover, we set $\xi _0=10{,}000$ which corresponds to a high level of turbulence.

It should be noted that in this test case, the contact wave and the shock wave travel to the right with a high velocity: respectively $\sim 2168\ m/s$ (see Fig. 10) and $\sim 2680\ m/s$. Moreover, the fan of the rarefaction wave expands to the left with a velocity of $-1152\ m/s$ and to the right with a velocity of $1791\ m/s$. Hence, both the shock wave and the rarefaction wave remain very close to the contact wave (see on the density variable in Fig. 9 or on the pressure P on Fig. 11). In particular, when focusing on the present final time $T_f=1.25\ 10^{-4}\ s$: the rarefaction fan corresponds to the interval [0.356, 0.724], the contact wave is located around $x=0.771$ and the shock wave is located around $x=0.835$ (see Fig. 8). The distance between the two GNL waves and the contact wave is thus small. Since the numerical scheme is not very accurate on the contact wave, the approximated values for the intermediate states 1 and 2 (see Fig. 8) are not very accurate on coarse meshes. Indeed, the results of Fig. 11 clearly show that at least 5000 cells are needed in order to get a correct approximation of the intermediate state 2; whereas it is not yet sufficient for intermediate state 1. As a consequence, fine meshes have to be used in order to get a correct accuracy of the location of the approximate contact wave and of the pressure level of $P^*$ between the rarefaction wave and the shock wave. Obviously, an other solution could be to use a second order extension of the scheme based for instance on a MUSCL reconstruction with a slope limiter and a second order Runge–Kutta time-scheme, see [11] or [20] among others. This is an important point because the increase of $P^*$ across the front of the shock will determine the importance of the impact of the shock on the surroundings. Moreover, an accurate location of the front of the shock enables to get the correct time at which the surroundings would be impacted.

Due to the entropy correction implemented in the numerical scheme, the approximate profiles in the rarefaction fan remain “regular” and monotonic, even if very small perturbations may be observed on very coarse meshes around $x=0.5$. We also notice that in the vicinity of the shock wave, we have $\frac{\rho _{2}}{\rho _{L}} \approx \frac{5.35}{1}=5.35$. This is still less than the theoretical limit $\beta =6$ (see Fig. 9) as pointed out by remark  3. At last, the VFRoe-ncv scheme using the variable $(\rho ,u,P^*)$ enables to maintain uniform profiles for the modified pressure $P^*$ and the velocity u around the contact wave, see Figs. 10 and 12 .

Fig. 8

Sketch of the waves in the (x, t)-plane for the strong shock test case at time $T_f=1.25\ 10^{-4}\ s$

Fig. 9

Strong shock wave test case. Density for $\xi _0=10{,}000$ and for meshes with 500, 5000 and 50,000 cells

Fig. 10

Strong shock wave test case. Velocity for $\xi _0=10{,}000$ and for meshes with 500, 5000 and 50,000 cells

Fig. 11

Strong shock wave test case. Pressure P for $\xi _0=10{,}000$ and for meshes with 500, 5000 and 50,000 cells

Fig. 12

Strong shock wave test case. Modified pressure $P^*$ for $\xi _0=10{,}000$ and for meshes with 500, 5000 and 50,000 cells

7 2D Numerical Results

In the two-dimensional case, the numerical scheme reads:

$$\begin{aligned} vol( \Omega _i)(w_i^{n+1} - w_i^{n}) +\Delta t^n \sum _{j \in {\mathcal {V}}(i)} F(w(Z^*_{ij}),n_{ij})\Gamma _{ij} =0, \end{aligned}$$

(41)

where ${\mathcal {V}}(i)$ refers to the neighboring cells of $\Omega _i$, $\Gamma _{ij}$ is the length of the interface between cells $\Omega _i$ and $\Omega _j$, and vol($\Omega _i$) is the area of $\Omega _i$. The quantity $F(w(Z^*_{ij}),n_{ij})$ denotes the numerical flux at the interface between cells $\Omega _i$ and $\Omega _j$, $n_{ij}$ stands for the unit normal vector directed from $\Omega _i$ to $\Omega _j$ and $Z^*_{ij}$ is the solution of the linearized Riemann problem at the face between cells $\Omega _i$ and $\Omega _j$ along the $n_{ij}$-direction. The flux for model (4) in 2D is given in the $n_{ij}$-direction by:

$$\begin{aligned} F(w,n_{i,j})=\begin{pmatrix} (\rho U.n)_{ij}\\ ( \rho (U.n)U +P^*n)_{ij}\\ ( (U.n)(\rho E + P^*) )_{ij} \end{pmatrix}, \end{aligned}$$

(42)

where $w=(\rho ,\rho U,\rho E)$, and where the velocity vector U gathers the two components of the velocity along the axis x and y: $U=(u_x,u_y)$. The solution $Z^*_{ij}$ of the linearized Riemann problem is computed thanks to shceme used for 1D simulations by using $\Omega _i$ and $\Omega _j$ as L and R states, see also appendix B .Indeed, it should be noted that for the 2D flux (42), the velocity component wich is orthogonal to $n_{ij}$ is simply advected with velocity $U.n_{ij}$ [3].

In order to compute the numerical fluxes at the rigid wall boundaries, we use the classical “mirror state” technique. For the numerical treatment of inlet and outlet boundary conditions the reader may also refer to [3] for more details. Moreover, we apply the Courant–Friedrichs–Lewy (CFL) condition:

$$\begin{aligned} \frac{\Delta t^{n}}{vol(\Omega _i)} max(|\lambda _{i}|)= \frac{1}{2}, \end{aligned}$$

in scheme (41).

We present here a numerical simulation obtained in a two-dimensional domain for model (4). The parameters of the EOS are the same than those chosen for the 1D results of the previous sections. Let us consider the domain $(x,y) \in [-1,1]\times [0,1]$. A small rectangular obstacle with a length $L_b= 0.05\,\hbox {m}$ and a height $H_b= 0.1\,\hbox {m}$ is placed at $x=0.15\,\hbox {m}$. The obstacle and the boundary $y=0$ (i.e. the ground) are considered as rigid walls. Outlet conditions are imposed for the other boundaries. The complete setting is depicted in Fig. 13. The initial conditions of the test case carried out in this section are representative of an explosion involving hydrogen. At ambiant temperature and pressure, the AICC¹ pressure of stoechiometric mixture of air and hydrogen is close to $10\ \hbox {bars}$. We choose here to set a high pressure zone inside a half-circle, whose centre is (0, 0) and whose radius is $0.05\,\hbox {m}$. In the rest of the domain, ambiant conditions are set. The initial flow is assumed to be at rest everywhere in the domain. In the whole computational domain, we set $\xi _0=10^5$, and the perfect gas EOS:

$$\begin{aligned} P=(\gamma -1)\rho e, \end{aligned}$$

with the constant $\gamma =\frac{7}{5}$ is still considered. Thus, according to the EOS parameters, the initial conditions read:

$$\begin{aligned} (\rho ,u,v,P)= \left\{ \begin{array}{l} (1.2\ \hbox {kg/m}^3,0\ \hbox {m/s},0\ \hbox {m/s},10^6\ \hbox {Pa}) ~~\text {if} ~~x^2 +y^2\le (0.05)^2;\\ (0.8\ \hbox {kg/m}^3,0\ \hbox {m/s},0\ \hbox {m/s},10^5\ \hbox {Pa}) ~~\text {if} ~~ x^2 +y^2>(0.05)^2. \end{array} \right. \end{aligned}$$

(43)

In order to highlight the influence of the turbulence for this test case, the current results (for $\xi _0=10^5$) are compared with the same case without turbulence ($\xi _0$=0). Three probes are chosen at elevation $y=0.1$ and for different x:

• probe 1 is centered, $x=0$,

• probe 2 is set on the left part of the domain $\hbox {x}=-0.15$,

• and probe 3 is set on the right part, just above the rectangular obstacle, at $x=0.15$ (see also Fig. 13).

The following results have been obtained for an unstructured mesh composed of 67,300 triangular cells, see in Figs. 14 and 15 for a view of the mesh. In Figs. 16 and 17 , the turbulent kinetic energy, the modified pressure and the velocity field have been plotted. The influence of the obstacle can clearly be observed. The effects of turbulence can be observed in Figs. 18 and 19 when comparing the laminar and the turbulent cases. With $\xi _0=10^5$ the turbulent energy reaches an important level. In particular, the influence on the pressure P is clear: the traveling velocity of the waves is slightly different, while the amplitude of the pressure waves are noticeably modified. Most of the turbulent kinetic energy is located at the shock front, which seems quite natural owing to the model.

Fig. 13

Sketch of the domain for the 2D simulation. The half-circle delimited by a dashed line corresponds to the initial high pressure domain. The rectangular domain delimited by a doted line corresponds to the part of the domain where the mesh is refined. The black dots correspond to the three probes

Fig. 14

Overview of the whole mesh for the 2D computational domain

Fig. 15

Zoom of the 2D mesh around the high pressure zone (in red) and the obstacle (Color figure online)

Fig. 16

Distributions of the turbulent kinetic energy K (top) and modified pressure $P^*$ (bottom)

Fig. 17

Distributions of the norm of the velocity field (top) and velocity field (bottom)

Fig. 18

Comparison between the pressure values in the turbulent ($\xi _0=10^5$) and laminar ($\xi _0=0$) cases at the three probes versus time

Fig. 19

Plot of the turbulent energy at the 3 probes versus time for $\xi _0=10^5$

8 Conclusion

The main aim of the paper is to study a simple compressible turbulent model, with a specific behaviour in shocks waves (turbulent entropy is constant across shock waves).

From a mathematical modeling point of view, an analysis of the conservative system (5) shows the hyperbolicity and the wave structure associated with LD and GNL (Riemann invariants) fields. In order to characterize shock waves, exact jump conditions can be defined. This analysis with a turbulent perfect gas EOS shows that the Riemann problem associated with system (5) admits a unique self-similar solution with no vaccum occurence. This result is the straightforward counterpart of the well-known result of existence and uniqueness in the Euler framework, while focusing on perfect gas equation of state (see for instance [11, 17]).

An approximate Godunov solver has been implemented and some verification test cases including shock structures have been computed. A 2D hydrogen explosion test case has been computed and shown in Sect. 6.

Ongoing work concerns a more complex model [10], which would allow variations of the turbulent entropy $\xi$ through the shock waves. This one reads:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}(\overline{\overline{\rho }}) + \nabla .(\overline{\overline{\rho }} {\tilde{u}}) =0 \\&\partial _{t}(\overline{\overline{\rho }} {\tilde{u}}) + \nabla .\left( \overline{\overline{\rho }}{\tilde{u}} \otimes {\tilde{u}} + \left( \overline{{\overline{P}}} +\frac{2K}{3}\right) .{\mathcal {I}} \right) =\epsilon _{0} \nabla .(\Sigma ^{tot}(\nabla ^{s} {\tilde{u}})) \\&\partial _{t}(\overline{\overline{\rho }} E) +\nabla .\left( {\tilde{u}} \left( \overline{\overline{\rho }} E + \overline{{\overline{P}}} +\frac{2K}{3} \right) \right) =\epsilon _{0} \nabla .(\Sigma ^{tot}(\nabla ^{s} {\tilde{u}}){\tilde{u}})\\&\partial _{t}(\overline{\overline{\rho }} \xi ) + \nabla .(\overline{\overline{\rho }} \xi {\tilde{u}} ) =(\overline{\overline{\rho }})^{-2/3} rhs_K(W,\nabla W) + RHS^{SW} \end{aligned} \right. \end{aligned}$$

(44)

The first term on the right-hand side of the last equation in (44) takes classical source terms into account (see introduction), while $RHS^{SW}$ enables to account for turbulent entropy local variations through shock waves [10].

Appendices

Solution of the Riemann Problem

In this section, the notations depicted by Fig. 1 are used. We recall that the subscript L, 1, 2 and R respectively denote: the left state, the intermediate states between 1- and 2-wave, the intermediate states between 2- and 3-wave and the right state. The left and right states correspond to the initial states of the Riemann problem. We also recall that v stands for the velocity in the shock referential: $v=u-\sigma$, where $\sigma$ is the shock speed.

The proof of existence and uniqueness of a solution of the Riemann problem associated with system (5) is built here following [17]. In reference [17], the proof of the existence and uniqueness of a solution of the Riemann problem is built for the Euler system with a perfect gas EOS, but it may be extended to some suitable EOS. System of Eqs. (5) corresponds in fact to the Euler system of equations with a pressure law $P^*$ that is a correction of the perfect gas pressure law $P^{pg}$. We have the pressure law $P^*(\rho ,e)=P^{pg}(\rho ,e)+2K(\rho )/3$ and the modified internal energy $e^*(\rho ,e)=e+K(\rho )/\rho$. Actually, we show below that the proof proposed in [17] can also be extended to our system of equations.

As in [17], the outline of the proof in this appendix is the following. First, the paths across each wave are defined using the Riemann invariants or the Rankine-Hugoniot relations established in Sects. 2.3 and 2.4 . These paths are defined through two parameters which are the density ratios: $z_1=\rho _1/\rho _2$ and $z_2=\rho _2/\rho _R$. Then, the connection between the different waves is performed. Afterwards, it can be proved that solving the Riemann problem is equivalent to finding a root in $]0,\beta [$ of a function $z_2\mapsto {\mathcal {H}}(z_2)$ which is continuous and increasing, with $\beta =(\gamma +1)/(\gamma -1)$. It should be noted that, since $\gamma >1$, we have $\beta >1$. Moreover, under the assumption that void does not occur, it can be shown that this function ${\mathcal {H}}$ is such that:

$$\begin{aligned} \underset{z_2\rightarrow 0^+}{lim} {\mathcal {H}}(z_2) \times \underset{z_2\rightarrow \beta ^-}{lim} {\mathcal {H}}(z_2)<0. \end{aligned}$$

At least, this allows to conclude the proof of existence and uniqueness of a solution of the Riemann problem thanks to the theorem of the intermediate values.

1.1 Paths Across the Waves of the System

According to section (2.2), the waves associated with the eigenvalues $\lambda _1$ and $\lambda _3$ are GNL waves. They can be either shock waves or rarefaction waves. For the former the path across the wave is defined thanks to the Rankine-Hugoniot relations, whereas for the latter the Riemann invariants are used. The field associated with the eigenvalue $\lambda _2$ is linearly degenerated so that it can be described by both the Rankine-Hugoniot relations or the Riemann Invariants.

Definition of shock waves.

Let us first start by the case of the shock waves. The jump conditions for system (5) are given in Sect. 2.4 by relations (24) and are recalled below:

$$\begin{aligned} \left\{ \begin{aligned}&~[\rho v] = 0, \\&[\rho v^2 + P^*]=0, \\&\rho v \left( \left[ e +\frac{K}{\rho }\right] +\overline{P^{*}}\left[ \frac{1}{\rho }\right] \right) =0. \end{aligned} \right. \end{aligned}$$

(45)

These relations involve the square of the jump of the velocity: $[u]^2$. Hence the velocity jump is not uniquely defined and an additional information must be added to relations (24) in order to get a unique definition of the velocity jump across the shock. We use here the entropy inequality for that purpose. We recall the entropy inequality associated with (45), and given by (15):

$$\begin{aligned} {\mathcal {B}}= -\sigma [\eta ]^R_L + [u\eta ]^R_L <0, \end{aligned}$$

(46)

with $\eta = -\rho ln(s)$.

Since $[\rho v]^R_L$ =0, we can rewrite ${\mathcal {B}}$ in the following form:

$$\begin{aligned} {\mathcal {B}}=-[\rho v ln(s)]^R_L= -\rho v \frac{[ln(s)]^R_L}{[s]^R_L}[s]^R_L <0, \end{aligned}$$

so that we get:

$$\begin{aligned} {\mathcal {A}}= \rho v[s]^R_L= [\rho vs]^R_L >0. \end{aligned}$$

By using the first jump relation equation of (45):

$$\begin{aligned} {[}\rho v]^R_L= {\bar{\rho }}[v]^R_L + {\bar{v}}[\rho ]^R_L=0, \end{aligned}$$

${\mathcal {A}}$ can be rewritten :

$$\begin{aligned} {\mathcal {A}}= \vartheta [v]^R_L, \end{aligned}$$

(47)

with:

$$\vartheta = \bar{\rho s} - {\bar{\rho }}\frac{[\rho s]^R_L}{[\rho ]^R_L}.$$

In the case of a perfect gas EOS, we have $\rho s= P\tau ^{\gamma -1}$. Let us define:

$$\begin{aligned} a=\frac{\tau _R}{\tau _L},\quad R_p= \frac{P_R}{P_L}, \end{aligned}$$

so that $\vartheta$ reads:

$$\begin{aligned} \vartheta = \frac{(P\tau ^{\gamma -1})_L}{1-a} (1 - R_p a^{\gamma }). \end{aligned}$$

(48)

In the following the sign of $\vartheta$ is studied, so that the sign of $[v]^R_L$ and then $[u]^R_L$ can be exhibited. By using the third jump relation equation of (45):

$$\begin{aligned}{}[e+ K\tau ]^R_L + \bar{P^*}[\tau ]^R_L=0, \end{aligned}$$

we get:

$$\begin{aligned} \gamma {\bar{P}}[\tau ]^R_L + {\bar{\tau }} [P]^R_L +(\gamma -1){\bar{\tau }}[K]^R_L +\frac{5}{3}(\gamma -1) {\bar{K}}[\tau ]^R_L =0. \end{aligned}$$

Thus, we have:

$$\begin{aligned} R_p(\beta a -1)= \beta -a + \frac{K_L}{P_L}\left( (a+1)(1-a^{-5/3}) +5/3(1-a)(1+a^{-5/3})\right) . \end{aligned}$$

(49)

By replacing the formula of $R_p$ (49) into that of $\vartheta$ (48), we get:

$$\begin{aligned} \frac{\vartheta }{(P\tau ^{\gamma -1})_L}= (1-a)^{-1} (\beta a -1)^{-1}g^L(a) + \frac{2K_L}{3P_L}a^{\gamma -5/3}(1-a)^{-1} (\beta a -1)^{-1}g^T(a), \end{aligned}$$

where:

$$\begin{aligned} \left\{ \begin{array}{l} g^L(a)= \beta a -1 - a^{\gamma }(\beta -a),\\ g^T(a)= a^{8/3} - 1 - 4a^{5/3} + 4a. \end{array} \right. \end{aligned}$$

(50)

Figure 20 gives the sign and variations of these 2 functions on the interval $[\frac{1}{\beta }, \beta ]$.

Fig. 20

Variation table for $g^L$ and $g^T$ functions

We can deduce from Fig. 20 that:

$$\begin{aligned} \frac{\vartheta }{(P\tau ^{\gamma -1})_L} \le 0 \quad \forall a \in ]\frac{1}{\beta },\beta [. \end{aligned}$$

Since ${\mathcal {A}}$ > 0, we deduce from (47) that $[v]^R_L <0$ and thus that $[u]^R_L<0$ .

Hence, for system (5) the relation $[u]<0$ holds across a shock wave, and thus the entropy inequality (10) allows to define shocks in a unique manner through:

$$\begin{aligned} {[}u]^2+[\tau ][P]=0 \quad \text {and} \quad [u]<0 \Longleftrightarrow [u]=-\sqrt{-[\tau ][P]}. \end{aligned}$$

Furthermore, when void does not occur, ${\tilde{c}}_i >0$ for $i\in \{L,1,2,R\}$, we always get the same order for the eigenvalues: $\lambda _1<\lambda _2<\lambda _3$, so that we also have the relation:

$$\begin{aligned} u_1=\lambda _2(W_1)>\sigma _1 \Longrightarrow v_1= u_1 - \sigma _1 >0 \end{aligned}$$

(51)

and

$$\begin{aligned} u_2=\lambda _2(W_2)<\sigma _2 \Longrightarrow v_2= u_2 - \sigma _2 <0 \end{aligned}$$

(52)

Since $[u]=[v]=[\rho \tau v]=\rho v [\tau ]$, and $[u]<0$ in shocks, we have $v [\tau ]<0$ in shocks. Thus, thanks to the signs of $v_1$ and $v_2$:

$$\begin{aligned} \tau _1<\tau _L \quad \Longrightarrow \quad z_1>1, \end{aligned}$$

in the 1-shock, and:

$$\begin{aligned} \tau _R>\tau _2 \quad \Longrightarrow \quad z_2>1, \end{aligned}$$

in the 3-shock. It should be noted that the jump relations (24) also leads to the relation:

$$\begin{aligned} (\rho v)^2 [\tau ]+[P^*]=0. \end{aligned}$$

Therefore, using the results above on $[\tau ]$, we get that $P_1^*>P_L^*$ in a 1-shock and $P_R^*<P_2^*$ in a 3-shock

Path across a 1-shock wave.

The path across a 1-shock wave is obtained through the parameter $z_1$ thanks to the Rankine-Hugoniot relations (24) and to the Lax criterion. After some calculus, it yields that a 1-shock is defined for $z_1>1$ by the relations:

$$\begin{aligned} \left\{ \begin{array}{l} u_{1}=u_{L} -c_{L}f_{1}(z_{1},K_{L}/P_{L}),\\ P_{1}=P_{L}h_{1}(z_{1},K_{L}/P_{L}), \end{array} \right. \end{aligned}$$

(53)

with the functions:

$$\begin{aligned} f_{1}(z_{1},K_{L}/P_{L})= & {} \sqrt{\left( \frac{z_{1}-1}{\gamma z_{1}} \right) \left( -1 +\frac{2}{3} \frac{K_{L}}{P_{L}}(z_{1}^{5/3}-1) +h_{1}(z_{1},K_{L}/P_{L})\right) },\nonumber \\ h_{1}(z_{1},K_{L}/P_{L})= & {} \displaystyle \frac{\beta z_{1} -1 + g_{1}(z_{1},K_{L}/P_{L})}{\beta -z_{1}},\nonumber \\ g_{1}(z_{1},K_{L}/P_{L})= & {} \displaystyle \frac{2K_{L}}{3P_{L}}\left( z_{1}^{8/3} -4z_{1}^{5/3} +4z_{1}-1 \right) , \end{aligned}$$

(54)

and $K_{L}= \xi _0 \rho _{L}^{5/3}$.

Path across a 3-shock wave.

For a 3-shock, the path depends on $z_2>1$ and by using the Rankine-Hugoniot relations (24) and the Lax criterion we get:

$$\begin{aligned} \left\{ \begin{array}{l} u_{2}=u_{R} +c_{R}f_{2}(z_{2},K_{R}/P_{R}),\\ P_{2}=P_{R} h_{2}(z_{2},K_{R}/P_{R}), \end{array} \right. \end{aligned}$$

(55)

with the functions:

$$\begin{aligned} f_{2}(z_{2},K_{R}/P_{R})= & {} \sqrt{\left( \frac{z_{2}-1}{\gamma z_{2}}\right) \left( -1 +\frac{2}{3} \frac{K_{R}}{P_{R}}(z_{2}^{5/3}-1) +h_{2}(z_{2},K_{R}/P_{R})\right) },\nonumber \\ h_{2}(z_{2},K_{R}/P_{R})= & {} \displaystyle \frac{\beta z_{2} -1 + g_{2}(z_{2},K_{R}/P_{R})}{\beta -z_{2}},\nonumber \\ g_{2}(z_{2},K_{R}/P_{R})= & {} \displaystyle \frac{2K_{R}}{3P_{R}}\left( z_{2}^{8/3} -4z_{2}^{5/3} +4z_{2}-1\right) , \end{aligned}$$

(56)

and $K_{R}= \xi _0 \rho _{R}^{5/3}$.

Path across a 1-rarefaction wave.

In a 1-rarefaction wave the Riemann Invariants $\tilde{{\bar{I}}}_1^1$ and $\tilde{{\bar{I}}}_2^1$ exhibited in Sect. 2.3 remain constant. Hence, we get the following relations in a 1-rarefaction wave for $z_1<1$:

$$\begin{aligned} s_{L}=s_{1}, \end{aligned}$$

(57)

and

$$\begin{aligned} u_{L} +\displaystyle \int _{0}^{\rho _{L}} \frac{{c_t}(s,\rho \prime )}{\rho \prime } \,\mathrm {d}\rho \prime =u_{1} +\displaystyle \int _{0}^{\rho _{1}} \frac{{c_t}(s,\rho \prime )}{\rho \prime } \,\mathrm {d}\rho \prime . \end{aligned}$$

(58)

Then, using the thermodynamical closures chosen for the model, (57) and (58) can be rewritten in the form:

$$\begin{aligned} \left\{ \begin{array}{l} u_{1} - u_{L} + c_L {B_{1}}(z_{1},K_{L}/P_{L})=0,\\ P_{1}=P_{L}Q_{1}(z_{1}), \end{array} \right. \end{aligned}$$

(59)

with the following definitions:

$$\begin{aligned} \begin{array}{l} {B_{1}}(z_{1},K_{L}/P_{L}) = \displaystyle \int _{1}^{z_{1}} {\left( z^{\gamma -3} +\frac{10 K_L}{9 \gamma P_{L}} z^{-4/3}\right) }^{1/2} \,\mathrm {d}z,\\ Q_{1}(z_{1})=z_{1}^{\gamma }.\\ \end{array} \end{aligned}$$

(60)

Path across a 3-rarefaction wave.

With the same arguments, using the Riemann Invariants $\tilde{{\bar{I}}}_1^3$ and $\tilde{{\bar{I}}}_2^3$, one can write for a 3-rarefaction wave for $z_2<1$:

$$\begin{aligned} \left\{ \begin{array}{l} u_{2} - u_{R} - c_R {B_{2}}(z_{2},K_{R}/P_{R})=0,\\ P_{2}=P_{R}Q_{2}(z_{2}), \end{array} \right. \end{aligned}$$

(61)

with the following definitions:

$$\begin{aligned} \begin{array}{l} {B_{2}}(z_{2},K_{R}/P_{R}) = \displaystyle \int _{1}^{z_{2}} {\left( z^{\gamma -3} +\frac{10 K_R}{9 \gamma P_{R}} z^{-4/3}\right) }^{1/2} \,\mathrm {d}z,\\ Q_{2}(z_{2})=z_{2}^{\gamma }. \end{array} \end{aligned}$$

(62)

Path across the 2-contact wave.

In the 2-wave, the 2-Riemann invariants u and $P^{*}$ are constant. Hence, the following relations arise:

$$\begin{aligned} P^{*}_{1}=P^{*}_{2}, \end{aligned}$$

(63)

and

$$\begin{aligned} u_{1}=u_{2}. \end{aligned}$$

(64)

Remark 7

Functions ${B_{1}}$ and ${B_{2}}$ are defined on the basis of an integral of the form:

$$\begin{aligned} I(z)=\int _{z}^{1} {\left( x^{\gamma -3} +a_0 x^{-4/3}\right) }^{1/2} \,\mathrm {d}x, \end{aligned}$$

for $z\in [0,1]$, with $a_0\ge 0$, $\gamma >1$ and $\beta =(\gamma +1)/(\gamma -1)>1$. Oviously, we have $I(z)\ge 0$. For $\gamma \in ]1,5/3]$ and $\gamma \ge 5/3$, the integral I(z) can be respectively bounded by:

$$\begin{aligned} I(z)\le \frac{2 \sqrt{1+a_0}}{\gamma -1}(1-z^{(\gamma -1)/2}), \end{aligned}$$

and

$$\begin{aligned} I(z)\le 3 \sqrt{1+a_0}(1-z^{1/3}). \end{aligned}$$

Hence, the integral I(z), and thus functions ${B_{1}}$ and ${B_{2}}$, are defined for z in [0, 1]. Moreover, it should be noticed that:

$$\begin{aligned} I(z)=3 \sqrt{1+a_0}(1-z^{1/3}), \end{aligned}$$

for $\gamma =5/3$.

1.2 Connection Between the Different Waves

Thanks to the relations of the previous section, the left state $W_L$ and the intermediate state $W_1$ are related through the 1-wave thanks to

$$\begin{aligned} \left\{ \begin{aligned} u_{1}= u_{L} - c_L {\mathcal {G}}_{L}(z_{1}),\\ P_{1}= P_{L}{\mathcal {F}}_{L}(z_{1}), \end{aligned} \right. \end{aligned}$$

(65)

where the functions ${\mathcal {F}}_{L}$ and ${\mathcal {G}}_{L}$ are respectively defined piecewise through the relations obtained either for a rarefaction wave, $z_{1}\le 1$, or for a shock wave, $z_{1}$ > 1, using respectively (53)–(54) and (59)–(60). So we obtain the definitions:

$$\begin{aligned} {\mathcal {F}}_{L}(z_{1})= \left\{ \begin{aligned} h_{1}(z_{1},K_{L}/P_{L})~~ \text {if}~~ z_{1}>1, \\ Q_{1}(z_{1}) ~~\text {if} ~~z_{1}\le 1, \end{aligned} \right. \end{aligned}$$

(66)

and

$$\begin{aligned} {\mathcal {G}}_{L}(z_{1})= \left\{ \begin{aligned} f_{1}(z_{1},K_{L}/P_{L})~~ \text {if}~~ z_{1}>1, \\ {B_{1}}(z_{1},K_{L}/P_{L}) ~~\text {if} ~~z_{1}\le 1. \end{aligned} \right. \end{aligned}$$

(67)

In the same way, for the 3-wave, the following relations hold between $W_{R}$ and $W_{2}$:

$$\begin{aligned} \left\{ \begin{aligned}&u_{2}= u_{R} + c_R {\mathcal {G}}_{R}(z_{2}),\\&P_{2}= P_{R}{\mathcal {F}}_{R}(z_{2}), \end{aligned} \right. \end{aligned}$$

(68)

where according to (55)–(56) and (61)–(62), we have:

$$\begin{aligned} {\mathcal {F}}_{R}(z_{2})= \left\{ \begin{aligned} h_{2}(z_{2},K_{R}/P_{R})~~ \text {if}~~ z_{2}>1, \\ Q_{2}(z_{2}) ~~\text {if} ~~z_{2}\le 1, \end{aligned} \right. \end{aligned}$$

(69)

and

$$\begin{aligned} {\mathcal {G}}_{R}(z_{2})= \left\{ \begin{aligned}&f_{2}(z_{2},K_{R}/P_{R})~~ \text {if}~~ z_{2}>1, \\&{B_{2}}(z_{2},K_{R}/P_{R}) ~~\text {if} ~~z_{2}\le 1. \end{aligned} \right. \end{aligned}$$

(70)

Due to the order of the different waves for system (5) which is always such that $\lambda _1<\lambda _2<\lambda _3$, the connection of the two GNL waves is easily performed through the contact wave using relations (63) and (64). Indeed, the modified pressure reads: $P^*=P+ 2K/3$. Hence by combining Eq. (63) with first equation of (65) and first equation of (68), we obtain:

$$\begin{aligned} P_{L}{\mathcal {F}}_{L}(z_{1}) + \frac{2}{3}K_{L}z_{1}^{5/3}= P_{R}{\mathcal {F}}_{R}(z_{2}) + \frac{2}{3}K_{R}z_{2}^{5/3}, \end{aligned}$$

(71)

The velocity equality (64) combined with second equation of (65) and second equation of (68) yields:

$$\begin{aligned} u_{R} + c_R {\mathcal {G}}_{R}(z_{2}) - u_{L} + c_L {\mathcal {G}}_{L}(z_{1})=0. \end{aligned}$$

(72)

System (71)–(72) is a $2\times 2$ non-linear system for the unknowns $(z_1,z_2)\in ]0,\beta [^2$. Let us now study this system.

1.3 Existence and Uniqueness of a Solution for the Riemann Problem

It can been proved that ${\mathcal {F}}_{L}$ and ${\mathcal {G}}_{L}$ (respectively ${\mathcal {F}}_{R}$ and ${\mathcal {G}}_{R}$) are differentiable functions of $z_1\in ]0,\beta [$ (respectively of $z_2\in ]0,\beta [$). By differentiating Eq. (71) with respect to $z_1$ and $z_2$, it can be shown that $dz_1/dz_2>0$. Then, thanks to (71) one can implicitly define a variable change $z_2 \mapsto {\mathcal {Z}}_1(z_2)$ which gives $z_1$ as a function of $z_2$:

$$\begin{aligned} z_1={\mathcal {Z}}_1(z_2). \end{aligned}$$

Relation (72) can thus be expressed as a function of the sole variable $z_2$, and finding a solution of system (71)–(72) is equivalent to finding a root of the function $z_{2}\mapsto {\mathcal {H}}(z_{2})$ defined on $]0,\beta [$ as:

$$\begin{aligned} {\mathcal {H}}(z_{2})= u_{R} + c_R {\mathcal {G}}_{R}(z_{2}) - u_{L} + c_L {\mathcal {G}}_{L}({\mathcal {Z}}_{1}(z_{2})). \end{aligned}$$

(73)

When differentiating ${\mathcal {H}}$ with respect to $z_2$, we find that:

$$\begin{aligned} {\mathcal {H}}^{\prime }(z_{2})= c_R {\mathcal {G}}^{\prime }_{R}(z_{2})+c_L \frac{d {\mathcal {Z}}_{1}(z_{2})}{d z_{2}}{\mathcal {G}}^{\prime }_{L}({\mathcal {Z}}_{1}(z_{2})). \end{aligned}$$

(74)

It can be shown that ${\mathcal {G}}^{\prime }_{L}$ and ${\mathcal {G}}^{\prime }_{R}$ are positive functions, so that $z_{2}\mapsto {\mathcal {H}}(z_{2})$ is a continuous and increasing function on $]0,\beta [$.

By studying the definition of ${\mathcal {G}}_{L}$ and ${\mathcal {G}}_{R}$, the following limits can be found:

$$\begin{aligned} \underset{z_2\rightarrow 0^+}{\lim }\left( c_L {\mathcal {G}}_{L}({\mathcal {Z}}_{1}(z_{2}))+ c_R {\mathcal {G}}_{R}(z_{2}) \right) = c_L {B_{1}}(0,K_L/P_L) + c_R {B_{2}}(0,K_R/P_R). \end{aligned}$$

and

$$\begin{aligned} \underset{z_2\rightarrow \beta ^-}{\lim }\left( c_L {\mathcal {G}}_{L}({\mathcal {Z}}_{1}(z_{2}))+ c_R {\mathcal {G}}_{R}(z_{2}) \right) =+\infty \end{aligned}$$

The variable change ${\mathcal {Z}}_1$ is an increasing function of $z_2$. Hence, when $z_2$ tends to zero, $z_1$ also tends to zero. This means that the first limit above is reached in the cases where both 1- and 3- waves are rarefaction waves. On the contrary, the second limit is reached in the cases where both 1- and 3- waves are shock waves (we recall that $\gamma>1\Rightarrow \beta >1$). These two limits then give the following limits for ${\mathcal {H}}$:

$$\begin{aligned} \underset{z_{2} \rightarrow 0^+ }{\lim } {\mathcal {H}}(z_{2})= u_{R}- u_{L} +c_L {B_{1}}(0,K_L/P_L) + c_R {B_{2}}(0,K_R/P_R), \end{aligned}$$

and

$$\begin{aligned} \underset{z_{2} \rightarrow \beta ^- }{\lim } {\mathcal {H}}(z_{2}) = +\infty . \end{aligned}$$

Since the function $z_2\mapsto {\mathcal {H}}(z_{2})$ is increasing and continuous on $]0,\beta [$, the intermediate value theorem can be applied in order to conclude that ${\mathcal {H}}$ admits a unique root provided that the following condition holds:

$$\begin{aligned} u_{R}- u_{L} +c_L {B_{1}}(0,K_L/P_L) + c_R {B_{2}}(0,K_R/P_R) < 0 \end{aligned}$$

(75)

As a consequence, the Riemann problem associated with system (5) possesses a unique solution if and only if condition (75) holds.

Fig. 21

Double rarefaction test case. Density (top left), velocity (top right) and pressure (bottom). Approximate solution at time $t_{f}=3\ 10^{-4}$s, $CFL=0.5$, for 500 cells and $\xi _0=0$

Fig. 22

Double rarefaction test case. Density (top left), velocity (top right), pressure P (bottom left) and modified pressure $P^{*}$ (bottom right). Approximate solution at time $t_{f}=3\ 10^{-4}$s, $CFL=0.5$, for 500 cells and $\xi _0=5000$

Fig. 23

Double rarefaction test case. Density (top left), velocity (top right), pressure P (bottom left) and modified pressure $P^{*}$ (bottom right). Approximate solution at time $t_{f}=3\ 10^{-4}$s, $CFL=0.5$, for 500 cells and $\xi _0=10{,}000$

Building the Intermediate States for VFRoe-ncv

As depicted in Sect. 4, the VFRoe-ncv scheme is based on the computation of the exact solution of a linearized version of the Riemann problem at the interface between two cells. It thus relies on finding the two intermediate states $Z_1$ and $Z_2$: the state $Z_1$ (resp. $Z_2$) is between the linearized waves ${{\bar{\lambda }}}_1$ and ${{\bar{\lambda }}}_2$ (resp. ${{\bar{\lambda }}}_2$ and ${{\bar{\lambda }}}_3$). We have:

$$\begin{aligned} Z_{1}&= Z_{L} +\alpha _{1}\widehat{r_{1}}, \end{aligned}$$

(76)

$$\begin{aligned} Z_{2}&= Z_{1} +\alpha _{2}\widehat{r_{2}}, \end{aligned}$$

(77)

$$\begin{aligned} Z_{R}&= Z_{2} +\alpha _{3}\widehat{r_{3}}, \end{aligned}$$

(78)

where the linearized right eigenvectors are:

$$\begin{aligned} \widehat{r_{1}}=(1,-\widehat{{c_t}} {\bar{\tau }},\widehat{{c_t}}^{2})^{T}, \widehat{r_{2}}=(1,0,0)^{T}, \widehat{r_{3}}=(1,\widehat{{c_t}}{\bar{\tau }},\widehat{{c_t}}^{2})^{T}, \end{aligned}$$

and where the coefficients $\alpha _{1}$ and $\alpha _{3}$ associated with the eigenvalues ${{\bar{\lambda }}}_1$ and ${{\bar{\lambda }}}_3$ read:

$$\begin{aligned} \alpha _{1}= & {} \frac{1}{2}\frac{[P^{*}]^{R}_{L}}{\widehat{{c_t}}^{2}} - \frac{1}{2}\frac{[u]^{R}_{L}{\bar{\rho }}}{\widehat{{c_t}}},\\ \alpha _{3}= & {} \frac{1}{2}\frac{[P^{*}]^{R}_{L}}{\widehat{{c_t}}^{2}} + \frac{1}{2}\frac{[u]^{R}_{L}{\bar{\rho }}}{\widehat{{c_t}}}. \end{aligned}$$

The linearized sound speed $\widehat{{c_t}}$ is defined by Eq. (38). It should be noted that thanks to (77), we have:

$$\begin{aligned} u_{1} = u_{2}, \quad \text {and} \quad P^{*}_{1} = P^{*}_{2}. \end{aligned}$$

After simple calculus on Eqs. (76) and (78), the following intermediate values can be found:

$$\begin{aligned} u_{1}= & {} u_{2}={\bar{u}} - \frac{1}{2 {\bar{\rho }} \widehat{{c_t}}} [P^{*}]^{R}_{L}, \\ P^{*}_{1}= & {} P^{*}_{2}=\bar{P^*} - \frac{{\bar{\rho }}\widehat{{c_t}}}{2} [u]^{R}_{L}, \\ \rho _{1}= & {} \rho _{L} + \frac{[P^{*}]^{R}_{L}}{2\widehat{{c_t}}^2} - \frac{{\bar{\rho }}}{2\widehat{{c_t}}} [u]^{R}_{L}, \rho _{2}= \rho _{R} - \frac{[P^{*}]^{R}_{L}}{2\widehat{{c_t}}^2} - \frac{{\bar{\rho }}}{2\widehat{{c_t}}} [u]^{R}_{L}. \end{aligned}$$

Additional Numerical Results: A Symmetric Double Rarefaction Wave

This test case is representative of what happens close to a wall when the fluid flows outward or in a bluff-body. In these situations, the pressure decreases at the wall generating a rarefaction wave that propagates outwards from the wall. We reproduce such a configuration here with a symmetric double rarefaction wave test case for which the initial condition of the Riemann problem uses the “mirror state” strategy:

$$\begin{aligned} (\rho ,u,P)_{L}=(\rho _{0},-u_{0},P_{0}), \qquad \text {and} \qquad (\rho ,u,P)_{R}=(\rho _{0},u_{0},P_{0}), \end{aligned}$$

with a negative normal velocity $u_{0}$ and $(\rho _{0}, u_{0}, P_{0})=(1, 370, 10^{5})$. The first test case ($\xi _0=0$) is inspired from [3].

Profiles of the approximate solutions along the x-domain are given in Figs. 21, 22 and 23 for a mesh with 500 cells and using three values of $\xi _0=\{ 0, 5000, 10{,}000\}$. They involve a low-density state in the center of the domain, between the two rarefaction waves. This feature makes this problem a test for assessing the performance of numerical methods for low-density flows. Indeed, this test case allows to examine the stability of the scheme together with the preservation of positivity of the approximate density around $x=0.5$ (which corresponds to the fictive wall location). The classical drawback of Godunov-type schemes on the density variable near the position of initial discontinuity $x=0.5$ can be observed: an undershoot of the density profile which tends to vanish when the mesh is refined.