Rotation Problem for a Two-Phase Drop

Abstract

The paper deals with the stability of a uniformly rotating finite mass consisting of two immiscible viscous incompressible fluids with unknown interface and exterior free boundary. Capillary forces act on both surfaces. The proof of stability is based on the analysis of an evolutionary problem for small perturbations of the equilibrium state of a rotating two-phase fluid. It is proved that for small initial data and small angular velocity, as well as the positivity of the second variation of energy functional, the perturbation of the axisymmetric equilibrium figure exponentially tends to zero as $t\rightarrow \infty$, the motion of the drop going over to the rotation of the liquid mass as a rigid body.

1 Introduction

The problem on an isolated liquid mass rotating about a fixed axis as a rigid body was treated by many outstanding mathematicians such as Newton, Maclaurin, Jacobi, Kovalevskaya, Lyapunov [1, 2], Poincarè [3] and others. Most of them considered self-gravitating rotating fluids but without surface tension.

The famous Plateau experiment raises an interesting mathematical problem of equilibrium figures of a rotating fluid subjected to the capillary forces. In this experiment, one can observe the deformation of a liquid sphere, consisting of oil and rotating in a fluid of the same density, into a torus as the angular velocity increases. The attraction can be completely neglected in this case and the form is determined solely by the rotation and the surface tension of the liquid. Mathematical treatment of this problem was carried out by Globa-Mikhailenko [4], Boussinesq and especially by Charrueau [5, 6]. The latter gave a detailed analysis of the problem, calculated the form of equilibrium figures including the toroidal case and considered some stability aspects. These results were presented in the book of Appell [7]. There one can find reasoning about the dominant effect and calculations of the sizes of rotating liquid masses which are affected by both self-gravity and capillarity. The potential of attraction forces increases in proportion to the square of the dimensions, while the surface tension changes in inverse proportion to the radius of curvature, which, for figures similar to each other, is proportional to the linear dimensions. Therefore, with big masses, the attraction dominates, and the effect of surface tension is negligible. For small masses, on the contrary, the attraction is negligible, and only the surface tension is significant; it is this that restricts the amount of deformation caused by the centrifugal force and determines its limits.

The stability of equilibrium figures is one of the most important their characteristics. The first who used analytical methods for studying the stability and instability of the forms of a rotating fluid mass was Lyapunov [1, 8]. He analyzed the second variation of energy functional with respect to small perturbations of figure boundary. The positivity of this variation guarantees the stability of the system because the energy has a minimum at this state. The Lyapunov method was developed for the case of a rotating capillary fluid by means of an analysis of the corresponding evolutionary free boundary problem in [9, 10].

In the present paper, we extend the above technique to the case of a finite mass of two immiscible liquids and treat stability problem for two rotating incompressible capillary fluids separated by an unknown interface close to the boundary of an equilibrium figure. In addition, we rely on the previously obtained results, in particular, we employ the existence of equilibrium figures for a two-phase liquid [11] and adapt the proof of the global-in-time solvability for a nonlinear two-fluid problem with small data without rotation to our case [12,13,14]. One of the main points is global solvability of a linear problem which is based on the construction of a generalized energy function and a priori exponential energy inequality for a solution. The idea of constructing such a function was formulated and used in the works of M. Padula and one of the authors of the paper [15, 16].

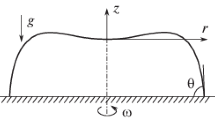
Let two viscous incompressible immiscible fluids of densities $\rho ^\pm$ and viscosities $\mu ^\pm$ be contained in a domain $\Omega _t\subset {\mathbb {R}}^3$ bounded by the free surface $\Gamma ^-_{t}$ and separated by the variable interface $\Gamma _{t}^+$. It is assumed that $\Gamma _{t}^+$ is the boundary of the domain $\Omega _{t}^+$ filled with a fluid of the density $\rho ^+$ which is surrounded by another fluid of the density $\rho ^-$ occupying the domain $\Omega ^-_{t} =\Omega _t\setminus \overline{\Omega _{t}^+}$. This two-phase drop rotates about the vertical axis $x_3$ (see Fig. 1). At the initial instant $t=0$, the surfaces $\Gamma _{0}^-$, $\Gamma _{0}^+$ are given. It is necessary to find $\Gamma ^-_{t}$, $\Gamma _{t}^+$, as well as velocity vector field ${\varvec{v}} (x,t)$ and pressure function p(x, t) satisfying the interface problem for the Navier–Stokes system

$$\begin{aligned}&\rho ^\pm \big ({\mathcal {D}}_t{{\varvec{v}}}+({{\varvec{v}}}\cdot \nabla ){{\varvec{v}}}\big )-\mu ^\pm \nabla ^{2}{{\varvec{v}}}+ \nabla p=0, \nonumber \\&\nabla \cdot {{\varvec{v}}}=0 \quad \text {in} \,\, \cup \Omega ^\pm _t=\Omega ^+_{t}\cup \Omega ^-_{t},\;\;t>0, \nonumber \\&{\varvec{v}}(x,0)={\varvec{v}}_0(x) \,\,\,\text {in} \,\,\,\cup \Omega ^\pm _0,\nonumber \\&{\mathbb {T}}({{\varvec{v}}},p){{\varvec{n}}}\big |_{\Gamma ^-_{t}}= \sigma ^- H^- {{\varvec{n}}} \quad \text {on } \Gamma ^-_{t},\nonumber \\&[{\varvec{v}}]\big |_{\Gamma ^+_{t}}\equiv \lim _{\begin{array}{c} x\rightarrow x_0 \in \Gamma _{t}^+,\\ x\in \Omega _{t}^+ \end{array}}{\varvec{v}}(x,t) -\lim _{\begin{array}{c} x\rightarrow x_0\in \Gamma _{t}^+,\\ x\in \Omega _{t}^- \end{array}}{\varvec{v}}(x,t)=0, \nonumber \\&[{\mathbb {T}}({{\varvec{v}}},p){{\varvec{n}}}]\big |_{\Gamma _{t}^+}=\sigma ^+ H^+ {{\varvec{n}}}\quad \text {on } \Gamma _{t}^+,\nonumber \\&V_{{\varvec{n}}}={{\varvec{v}}}\cdot {{\varvec{n}}}\quad \text {on } \Gamma _t=\Gamma ^+_{t}\cup \Gamma _{t}^-, \end{aligned}$$

(1.1)

where ${\mathcal {D}}_t=\partial /\partial t$, $\nabla =(\partial /\partial x_1, \partial /\partial x_2,\partial /\partial x_3)$, ${{\varvec{v}}}_0$ is initial velocity distribution, ${\mathbb {T}} ({\varvec{v}},p )=-p +\mu ^\pm {\mathbb {S}}({\varvec{v}} )$ is stress tensor, ${\mathbb {S}}({\varvec{v}})=(\nabla {\varvec{v}})+(\nabla {\varvec{v}})^T$ is doubled rate-of-strain tensor, the superscript T denotes the transposition, $\rho ^\pm , \mu ^\pm >0$ are the step-functions of density and dynamical viscosity equal to $\rho ^-, \ \mu ^-$ in $\Omega ^-_{t}$ and $\rho ^+, \ \mu ^+$ in $\Omega _{t}^+$; $H^-$, $H^+$ are twice the mean curvatures of the surfaces $\Gamma ^-_{t}$, $\Gamma _{t}^+$ $(H^+<0$ at the points where $\Gamma _{t}^+$ is convex toward $\Omega _{t}^-$); $\sigma ^-,\sigma ^+>0$ are the coefficients of the surface tension on $\Gamma ^-_{t}$, $\Gamma _{t}^+$, respectively; ${\varvec{n}}(x,t)$ is the outward normal to $\Gamma ^-_{t}$ and $\Gamma _{t}^+$, $V_{{\varvec{n}}}$ is the velocity of evolution of the surfaces $\Gamma ^-_{t}$ and $\Gamma _{t}^+$ in the direction of ${\varvec{n}}$. We suppose that a Cartesian coordinate system $\{x\}$ is introduced in ${\mathbb {R}}^3$. The centered dot means the Cartesian scalar product.

The summation is implied over the repeated indices from 1 to 3 if they are denoted by Latin letters. We mark the vectors and the vector spaces by boldface letters.

We assume that the domains $\Omega _0^+$, $\Omega _0$ differ little from equilibrium figures ${\mathcal {F}}^+$ and ${\mathcal {F}}$ such that

$$\begin{aligned} |\Omega _0^+|=|{\mathcal {F}}^+|,\quad |\Omega _0|=|{\mathcal {F}}|. \end{aligned}$$

(1.2)

We denote ${\mathcal {F}}^-={\mathcal {F}}\setminus \overline{{\mathcal {F}}^+ }$. Due to the incompressibility of the liquids, equalities (1.2) hold for any $t>0$:

$$\begin{aligned} |\Omega _t^+|=|{\mathcal {F}}^+|,\quad |\Omega _t|=|{\mathcal {F}}|. \end{aligned}$$

(1.3)

It implies the conservation of mass because of constant densities of the fluids. A solution of problem (1.1) also satisfies the other conservation laws for $t>0$:

$$\begin{aligned}&\int _{\Omega _t}\rho ^\pm x_j\,\mathrm {d}x=\int _{\Omega _0}\rho ^\pm x_j \,\mathrm {d}x\equiv 0,\quad j=1,2,3,\;\text{(barycenter } \text{ conservation) },\nonumber \\ {}&\int _{\Omega _t}\rho ^\pm {{\varvec{v}}}(x,t)\,\mathrm {d}x=\int _{\Omega _0}\rho ^\pm {{\varvec{v}}}_0(x)\,\mathrm {d}x\equiv 0\quad \text{(momentum } \text{ conservation) },\nonumber \\ {}&\int _{\Omega _t}\rho ^\pm {{\varvec{v}}}(x,t)\cdot {{\varvec{\eta }}}_i(x)\,\mathrm {d}x =\int _{\Omega _0}\rho ^\pm {{\varvec{v}}}_0(x)\cdot {{\varvec{\eta }}}_i(x)\,\mathrm {d}x \equiv \omega \int _{\mathcal {F}}\bar{\rho }{{\varvec{\eta }}}_3(x) \cdot {{\varvec{\eta }}}_i(x)\,\mathrm {d}x\\ {}&\qquad \qquad \qquad \qquad \qquad =\beta \delta _{i}^3\nonumber \quad \text{(angular } \text{ momentum } \text{ conservation), } \end{aligned}$$

(1.4)

where ${\varvec{\eta }}_i(x)={\varvec{e}}_i\times {\varvec{x}},$ $i=1,2,3$, $\bar{\rho }$ is the step-function of density equal to $\rho ^-$ in ${\mathcal {F}}^-$ and $\rho ^+$ in ${\mathcal {F}}^+$, $\delta ^k_i$ is the Kronecker delta; $\omega$ is the angular velocity of the rotation,

$$\begin{aligned} \beta =\omega \int _{\mathcal {F}}\bar{\rho }(x)|x'|^2\,\mathrm{d}x\equiv \omega {\mathcal {I}}\end{aligned}$$

is the angular momentum of the rotating liquids, and $|x'|^2=x_1^2+x_2^2$. One can prove that (1.4) holds for all $t>0$ if it is satisfied for $t=0$ (see [11]).

We introduce ${\mathcal {G}}^+ =\partial {\mathcal {F}}^+$ and ${\mathcal {G}}^- =\partial {\mathcal {F}}$ (see Fig. 1).

Fig. 1

Two-phase drop

Two-phase liquid mass uniformly rotating about the $x_3$-axis with constant angular velocity $\omega =\beta /I_0$ has velocity vector field

$$\begin{aligned} {{\varvec{{\mathcal {V}}}}}(x)=\omega {{\varvec{e}}}_3\times {{\varvec{x}}}\equiv \omega {\varvec{\eta }}_3. \end{aligned}$$

and pressure function

$$\begin{aligned} {\mathcal {P}}(x)=\bar{\rho }\frac{\omega ^2}{2}|x'|^2+p_0^\pm , \end{aligned}$$

where $\bar{\rho }$, $p_0^\pm$ are step-functions in ${\mathcal {F}}^\pm$. This motion is governed by the homogeneous steady Navier–Stokes equations

$$\begin{aligned} \bar{\rho } ({{\varvec{{\mathcal {V}}}}}\cdot \nabla ){{\varvec{{\mathcal {V}}}}} -\bar{\mu } \nabla ^{2}{{\varvec{{\mathcal {V}}}}}+ \nabla {\mathcal {P}}=0, \qquad \nabla \cdot {{\varvec{{\mathcal {V}}}}}=0 \quad \text {in}\,\, {\mathcal {F}} =\cup {\mathcal {F}}^\pm \end{aligned}$$

with the step-function $\bar{\mu }\equiv \mu ^+$ in ${\mathcal {F}}^+$ and $\bar{\mu }\equiv \mu ^-$ in ${\mathcal {F}}^-$. If one substitutes ${{\varvec{{\mathcal {V}}}}}, {\mathcal {P}}$ into the boundary conditions in (1.1), one obtains the equations for the surface ${\mathcal {G}}^-$ of the domain ${\mathcal {F}}$ and for the interface ${\mathcal {G}}^+$ between the fluids

$$\begin{aligned}&\sigma ^-{\mathcal {H}}^-(x)+\rho ^-\frac{\omega ^2}{2}|x'|^2+p_{0}^-=0, \quad x\in {\mathcal {G}}^-,\nonumber \\&\sigma ^+{\mathcal {H}}^+(x)+(\rho ^+-\rho ^-)\frac{\omega ^2}{2}|x'|^2 +p_{0}^+-p_{0}^-=0,\quad x\in {\mathcal {G}}^+, \end{aligned}$$

(1.5)

where ${\mathcal {H}}^-$, ${\mathcal {H}}^+$ are twice the mean curvatures of ${\mathcal {G}} ^-$, ${\mathcal {G}}^+$. In [11] it was proved the existence of the surfaces ${\mathcal {G}}^-$, ${\mathcal {G}}^+$ satisfying equations (1.5).

We assume the axial symmetry of ${\mathcal {F}}^\pm$ and the symmetry of them about the plane $x_3=0$; it implies that

$$\begin{aligned}&\int _{\mathcal {F}}\bar{\rho }(x)x_idx=0,\quad i=1,2.\nonumber \\&\int _{\mathcal {F}}\bar{\rho } x_3dx=0,\quad \int _{\mathcal {F}} \bar{\rho } x_3x_jdx=0,\quad j=1,2. \end{aligned}$$

(1.6)

Condition (1.6) corresponds to the first relation in (1.4) which means that the barycenter of the liquids coincides with the origin all the time. The other conditions in (1.4), the conservation of momentum and angular one, take the form

$$\begin{aligned}&\int _{\Omega _t}\rho ^\pm {{\varvec{v}}}(x,t)dx =\int _{\mathcal {F}}\bar{\rho } {{\varvec{{\mathcal {V}}}}}(x)dx=0,\nonumber \\&\int _{\Omega _t}\rho ^\pm {{\varvec{v}}}(x,t)\cdot {{\varvec{\eta }}}_i(x)dx = \int _{\mathcal {F}}\bar{\rho } {{\varvec{{\mathcal {V}}}}}(x)\cdot {{\varvec{\eta }}}_i(x)dx =\delta _{i}^3\beta ,\quad i=1,2,3. \end{aligned}$$

(1.7)

It is reasonable to work with the problem for the perturbations of the velocity and pressure

$$\begin{aligned} {{\varvec{v}}}_r(x,t)={{\varvec{v}}}(x,t)-{{\varvec{{\mathcal {V}}}}}(x),\quad p_r(x,t)=p(x,t)-{\mathcal {P}}(x) \end{aligned}$$

written in the coordinate system rotating about the $x_3$-axis with the angular velocity $\omega$.

We introduce the new coordinates $\{y_i\}$ and the new unknown functions ($\tilde{{\varvec{v}}}$, $\tilde{p}$) by the formulas

$$\begin{aligned}&x={\mathcal {Z}}(\omega t)y, \\&{\tilde{{\varvec{v}}}}(y,t)={\mathcal {Z}}^{-1}(\omega t){{\varvec{v}}}_r ({\mathcal {Z}}(\omega t)y,t),\quad \tilde{p}(y,t) =p_r({\mathcal {Z}}(\omega t)y,t), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {Z}}(\theta )= \left( \begin{array}{ccc} \cos \theta &{} -\sin \theta &{} 0 \\ \sin \theta &{} \cos \theta &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) . \end{aligned}$$

We note that

$$\begin{aligned}&{\mathcal {Z}}^{-1}(\omega t)({\varvec{{\mathcal {V}}}}\cdot \nabla _x){\varvec{v}}_r =\omega \big ({\varvec{\eta }}_3(x)\cdot \nabla _x\big )\tilde{{\varvec{v}}}(y,t) =\omega \big ({\mathcal {Z}}^{-1}{\varvec{\eta }}_3(y)\cdot \nabla _y\big )\tilde{{\varvec{v}}}\\&\quad =\omega \big ({\varvec{\eta }}_3(y)\cdot \nabla _y\big )\tilde{{\varvec{v}}}(y,t) =\omega \big (y_2\frac{\partial \tilde{{\varvec{v}}}}{\partial y_1}-y_1 \frac{\partial \tilde{{\varvec{v}}}}{\partial y_2}\big ) \end{aligned}$$

and ${\mathcal {D}}_t{\varvec{v}}_{r}|_{x={\mathcal {Z}}y}={\mathcal {D}}_{t}{\varvec{v}}_r({\mathcal {Z}}y,t) -({\varvec{{\mathcal {V}}}}\cdot \nabla ){\varvec{v}}_r.$ Substituting this in (1.1) and acting by ${\mathcal {Z}}^{-1}$, we arrive at the free boundary problem for the perturbations of the velocity $\tilde{{\varvec{v}}}$ and pressure $\tilde{p}$:

$$\begin{aligned}&\rho ^\pm \big ({\mathcal {D}}_t{\tilde{{\varvec{v}}}}+({\tilde{{\varvec{v}}}}\cdot \nabla ) {\tilde{{\varvec{v}}}}+2\omega (e_3\times {\tilde{{\varvec{v}}}})\big ) -\mu ^\pm \nabla ^2{\tilde{{\varvec{v}}}}+\nabla \tilde{p}=0,\nonumber \\&\nabla \cdot {\tilde{{\varvec{v}}}}=0 \qquad \text {in }\cup \tilde{\Omega }_t^\pm \equiv \tilde{\Omega }_{t}^-\cup \tilde{\Omega }_{t}^+,\qquad t>0,\nonumber \\&{\tilde{{\varvec{v}}}}(y,0)={\varvec{v}}_0(y)-{\varvec{{\mathcal {V}}}}(y) \equiv {\tilde{{\varvec{v}}}}_0(y), \quad y\in \cup \tilde{\Omega }_0^\pm \equiv \tilde{\Omega }_{0}^-\cup \tilde{\Omega }_{0}^+, \nonumber \\&{\mathbb {T}}({\tilde{{\varvec{v}}}},\tilde{p}) \tilde{{\varvec{n}}}\big |_{\tilde{\Gamma }_{t}^-} =\big (\sigma ^- H^-(y)+\rho ^-\frac{\omega ^2}{2}|y'|^2 +p_{0}^-\big )\tilde{{\varvec{n}}}, \quad y\in \tilde{\Gamma }_{t}^-,\nonumber \\&[{\tilde{{\varvec{v}}}}]\big |_{\tilde{\Gamma }_{t}^+}=0, \nonumber \\&[{\mathbb {T}}({\tilde{{\varvec{v}}}},\tilde{p})\tilde{{\varvec{n}}}] \big |_{\tilde{\Gamma }_{t}^+}=\big (\sigma ^+ H^+(y)+[\rho ^\pm ]|_{\tilde{\Gamma }_{t}^+}\frac{\omega ^2}{2}|y'|^2 +p_{0}^+-p_{0}^-\big )\tilde{{\varvec{n}}}, \quad y\in \tilde{\Gamma }_{t}^+,\nonumber \\&\tilde{V}_{\tilde{{\varvec{n}}}}={\tilde{{\varvec{v}}}} \cdot \tilde{{\varvec{n}}} \quad \text {on } \tilde{\Gamma }_t \equiv \tilde{\Gamma }_{t}^-\cup \tilde{\Gamma }_{t}^+, \end{aligned}$$

(1.8)

where $\tilde{\Omega }_t^\pm ={\mathcal {Z}}^{-1}(\omega t)\Omega _t^\pm ,$ $\tilde{\Gamma }_{t}^\pm ={\mathcal {Z}}^{-1}(\omega t)\Gamma _{t}^\pm$, $\tilde{{\varvec{n}}}$ is the outward normal to $\tilde{\Gamma }_{t}$, ${\varvec{n}}= {\mathcal {Z}}\tilde{{\varvec{n}}}$, $y'=(y_1,y_2,0)$, $p_{0}^-$, $p_{0}^+$ are constants on $\tilde{\Gamma }_{t}^-$ and $\tilde{\Gamma }_{t}^+$, respectively.

The kinematic boundary condition in (1.1)

$$\begin{aligned} V_{{\varvec{n}}}={\varvec{v}}\cdot {\varvec{n}}, \end{aligned}$$

where $V_{{\varvec{n}}}$ is the normal velocity of $\Gamma _t$, is invariant with respect to our transformation. Indeed, let x(t) be a point of $\Gamma _t$. We have $V_{{\varvec{n}}}={\mathcal {D}}_t {\varvec{x}}\cdot {\varvec{n}}$, and since ${\mathcal {D}}_t {\varvec{x}} =\omega {\mathcal {D}}_\theta \big |_{\theta =\omega t}{\mathcal {Z}} {\varvec{y}}+{\mathcal {Z}}{\mathcal {D}}_t{\varvec{y}}$, ${\mathcal {Z}}^T={\mathcal {Z}}^{-1}$, then ${\mathcal {D}}_t {\varvec{x}}\cdot {\varvec{n}}=\omega ({\varvec{e}}_3 \times {\varvec{y}})\cdot \tilde{{\varvec{n}}}+{\mathcal {D}}_t {\varvec{y}}\cdot \tilde{{\varvec{n}}}$. On the other hand, ${\varvec{v}}\cdot {\varvec{n}}=\tilde{{\varvec{v}}}\cdot \tilde{{\varvec{n}}}+\omega ({\varvec{e}}_3\times {\varvec{y}})\cdot \tilde{{\varvec{n}}}$. Hence, ${\mathcal {D}}_t {\varvec{y}}\cdot \tilde{{\varvec{n}}}= \tilde{{\varvec{v}}}\cdot \tilde{{\varvec{n}}}$ which means $\tilde{V}_{\tilde{{\varvec{n}}}}=\tilde{{\varvec{v}}}\cdot \tilde{{\varvec{n}}}$.

Relations (1.3), (1.4), (1.7) go over into

$$\begin{aligned}&|\tilde{\Omega }_t^+|=|{\mathcal {F}}^+|,\quad |\tilde{\Omega }_t| =|{\mathcal {F}}|, \end{aligned}$$

(1.9)

$$\begin{aligned}&\int _{\tilde{\Omega }_t}\rho ^\pm y_j\,\mathrm{d}y=0,\quad j=1,2,3, \quad \text {(barycenter conservation)}\nonumber \\&\int _{\tilde{\Omega }_t}\rho ^\pm {\tilde{{\varvec{v}}}}(y,t) \,\mathrm{d}y=0,\quad \text {(momentum conservation)}\nonumber \\&\int _{\tilde{\Omega }_t}\rho ^\pm {\tilde{{\varvec{v}}}}(y,t) \cdot {{\varvec{\eta }}}_i(y)\,\mathrm{d}y +\omega \int _{\tilde{\Omega }_t} \rho ^\pm {{\varvec{\eta }}}_3\cdot {{\varvec{\eta }}}_i(y)\,\mathrm{d}y = \omega \int _{\mathcal {F}}\bar{\rho }{{\varvec{\eta }}}_3 \cdot {{\varvec{\eta }}}_i(y)\,\mathrm{d}y =\beta \delta _{i}^3, \end{aligned}$$

(1.10)

where ${\varvec{\eta }}_i(y)={\varvec{e}}_i\times {\varvec{y}}$, $i=1,2,3$.

Let us suppose that the surfaces $\tilde{\Gamma }_{t}^\pm$ can be given by the relations

$$\begin{aligned} \tilde{\Gamma }_{t}^\pm =\{y=z+{\varvec{N}}(z)r(z,t), \quad z\in {\mathcal {G}}^\pm \}, \end{aligned}$$

and we map $\tilde{\Omega }_{t}^\pm$ on ${\mathcal {F}}^\pm$ by the transformation the inverse of which is

$$\begin{aligned} y=z+{\varvec{N}}^*(z)r^*(z,t)\equiv e_r(z,t), \end{aligned}$$

(1.11)

where ${\varvec{N}}^*$ and $r^*$ are extensions of ${\varvec{N}}$ and r into ${\mathcal {F}}$, respectively.

Due to (1.5), the boundary conditions

$$\begin{aligned}&{\mathbb {T}}({\tilde{{\varvec{v}}}},\tilde{p})\tilde{{\varvec{n}}} \big |_{\tilde{\Gamma }_{t}^-}=\big (\sigma ^- H^-(y) +\rho ^-\frac{\omega ^2}{2}|y'|^2 +p_{0}^-\big )\tilde{{\varvec{n}}},\quad y\in \tilde{\Gamma }_{t}^-,\\&[{\mathbb {T}}({\tilde{{\varvec{v}}}},\tilde{p}) \tilde{{\varvec{n}}}]|_{\tilde{\Gamma }_{t}^+}=\big (\sigma ^+ H^+(y) +[\rho ^\pm ]|_{\tilde{\Gamma }_{t}^+}\frac{\omega ^2}{2}| y'|^2 +p_{0}^+-p_{0}^-\big )\tilde{{\varvec{n}}}, \quad y\in \tilde{\Gamma }_{t}^+, \end{aligned}$$

in (1.8) are equivalent to ones

$$\begin{aligned} -\tilde{p}\tilde{\mathbf{{n}}}+\mu ^- {\mathbb {S}}(\tilde{\mathbf{{v}}}) \tilde{\mathbf{{n}}}\big |_{\tilde{\Gamma }_{t}^-}&=\Big \{\sigma ^- \big (H^-(y)-{\mathcal {H}}^-(z)\big )\nonumber \\ {}&\qquad \qquad +\rho ^-\frac{\omega ^2}{2}\big (|y'|^2- |z'|^2\big )\Big \} \tilde{\mathbf{{n}}},\quad y\in \tilde{\Gamma }_{t}^-,\; z\in {\mathcal {G}}^-,\nonumber \\ {[}-\tilde{p}\tilde{\mathbf{{n}}}+ \mu ^\pm {\mathbb {S}}({\tilde{\mathbf{{v}}}}) \tilde{\mathbf{{n}}}]|_{\tilde{\Gamma }_{t}^+}&=\Big \{\sigma ^+\big (H^+(y)-{\mathcal {H}}^+(z)\big )\nonumber \\ {}&\qquad \qquad +[\rho ^\pm ]|_{\Gamma _{t}^+}\frac{ \omega ^2 }{2} \big (|y'|^2- |z'|^2\big )\Big \}\tilde{\mathbf{{n}}}, \quad y\in \tilde{\Gamma }_{t}^+,\; z\in {\mathcal {G}}^+. \end{aligned}$$

(1.12)

Our next goal is to linearize problem (1.8). To this end, we need to compute the first variation with respect to r of the expressions $H(y)-{\mathcal {H}}(z)$, $|y'|^2-|z'|^2$, where y is connected with z by the relation (1.11).

We compute the first and second variations of a functional R[r] with respect to r by the formulas

$$\begin{aligned} \delta _0 R[r]=\frac{\,\mathrm{d}}{\,\mathrm{d}s}R[sr]\big |_{s=0},\qquad \delta ^2_0 R[r]=\frac{\,\mathrm{d}^2}{\,\mathrm{d}s^2}R[sr]\big |_{s=0}. \end{aligned}$$

(1.13)

It is clear that

$$\begin{aligned} \delta _0\big (|y'|^2-|z'|^2\big )= \frac{\,\mathrm{d}}{\,\mathrm{d}s} \big (|{\varvec{z}}'+{\varvec{N}}' s r |^2-|{\varvec{z}}'|^2\big ) \big |_{s=0}=2{\varvec{z}}'\cdot {\varvec{N}}' r,\qquad {\varvec{N}}'=(N_1,N_2,0), \end{aligned}$$

and, according to [17],

$$\begin{aligned} \delta _0\big (H^\pm (y)-{\mathcal {H}}^\pm (z)\big ) =\Delta ^\pm r +\big ({\mathcal {H}}^{\pm ^2}(z) -2{\mathcal {K}}^\pm (z)\big )r, \end{aligned}$$

where $\Delta ^\pm$ are the Laplace – Beltrami operators on ${\mathcal {G}} ^\pm$, respectively.

Applying (1.11) and using the above relations, we arrive at the linear problem corresponding to (1.8), (1.12)

$$\begin{aligned}&\rho ^\pm \big ({\mathcal {D}}_t{{\varvec{w}}} +2\omega (e_3\times {{\varvec{w}}})\big ) -\mu ^\pm \nabla ^2{{\varvec{w}}}+\nabla p=0,\nonumber \\&\nabla \cdot {{\varvec{w}}}=0 \qquad \text {in}\,\, {{\mathcal {F}}} \equiv {\mathcal {F}}^-\cup {\mathcal {F}}^+,\qquad t>0,\nonumber \\&{{\varvec{w}}}(z,0)={\varvec{v}}_0(z)-{\varvec{{\mathcal {V}}}}(z)\equiv {{\varvec{w}}}_0(z), \quad z\in {\mathcal {F}},\nonumber \\&{\mathbb {T}}({{\varvec{w}}},p) {\varvec{N}}+{\varvec{N}}{\mathcal {B}}_0^-r =0 \quad \;\text {on}\,\, {{\mathcal {G}}}^-,\nonumber \\&[{{\varvec{w}}}]\big |_{{{\mathcal {G}}}^+}=0, \quad [{\mathbb {T}}({{\varvec{w}}},p) {\varvec{N}}]\big |_{{\mathcal {G}}^+} +{\varvec{N}}{\mathcal {B}}_0^+r =0\quad \;\text {on}\,\,{\mathcal {G}}^+,\nonumber \\&{\mathcal {D}}_tr={{\varvec{w}}}\cdot {{\varvec{N}}} \quad \text {on } {{\mathcal {G}}} \equiv {{\mathcal {G}}} ^-\cup {{\mathcal {G}}} ^+,\qquad r\big |_{t=0}=r_0 \quad \text {on } {{\mathcal {G}}}, \end{aligned}$$

(1.14)

where

$$\begin{aligned}&{\mathcal {B}}^-_0r=-\sigma ^-\Delta ^- r-b^-(z)r, \quad z\in {\mathcal {G}}^-,\nonumber \\&{\mathcal {B}}^+_0r=-\sigma ^+\Delta ^+ r-b^+(z)r, \quad z\in {\mathcal {G}}^+ \end{aligned}$$

(1.15)

with $b^-(z)=\sigma ^-({{\mathcal {H}}^-}^2-2{\mathcal {K}}^-) +\rho ^-\omega ^2{\varvec{N}}\cdot {\varvec{z}}'$, $b^+(z)=\sigma ^+ ({{\mathcal {H}}^+}^2-2{\mathcal {K}}^+)+[\bar{\rho }] \big |_{{\mathcal {G}}^+}\omega ^2{\varvec{N}}\cdot {\varvec{z}}',$ ${\varvec{z}}'=(z_1,z_2,0)$, ${\mathcal {K}}^\pm$ are the Gaussian curvatures of ${\mathcal {G}} ^\pm$.

We recall the definition of the Sobolev–Slobodetskiǐ spaces which we use in the present paper. The isotropic space $W_2^l(\Omega )$, $\Omega \subset {\mathbb {R}}^n$, is the space with the norm

$$\begin{aligned} \Vert u\Vert ^2_{W_2^l(\Omega )}=\sum _{0\leqslant |{\varvec{j}}|\leqslant l} \Vert {\mathcal {D}}_x^{{\varvec{j}}}u\Vert ^2_\Omega \equiv \sum _{0\leqslant |{\varvec{j}}|\leqslant l} \int _\Omega |{\mathcal {D}}_x^{{\varvec{j}}} u(x)|^2\,\mathrm{d}x \end{aligned}$$

if $l=[l]$, i. e., l is an integral number, and

$$\begin{aligned} \Vert u\Vert ^2_{W_2^l(\Omega )}=\Vert u\Vert ^2_{W_2^{[l]}(\Omega )} +\sum _{|{\varvec{j}}|=[l]}\int _\Omega \int _\Omega |{\mathcal {D}}_x^{{\varvec{j}}} u(x) -{\mathcal {D}}_y^{{\varvec{j}}} u(y)|^2 \frac{\,\mathrm{d}x \,\mathrm{d}y }{|x-y|^{n+2\lambda }} \end{aligned}$$

if $l=[l]+\lambda$, $\lambda \in (0,1)$. As usual, ${\mathcal {D}}_x^{{\varvec{j}}} u$ denotes a (generalized) partial derivative $\frac{\partial ^{|{\varvec{j}}|}u}{\partial x_1^{j_1}\ldots \partial x_n^{j_n}}$, where ${\varvec{j}}=(j_1,j_2,\ldots j_n)$ and $|{\varvec{j}}|=j_1+\cdots +j_n$.

We introduce the anisotropic spaces

$$\begin{aligned} W_2^{l,0}(Q_T)=L_2\big ((0,T), W_2^l(\Omega )\big ), \quad W_2^{0,l/2}(Q_T)=W_2^{l/2}\big ((0,T), L_2(\Omega )\big ); \end{aligned}$$

$Q_T=\Omega \times (0,T)$, the squares of norms in these spaces coincide, respectively, with

$$\begin{aligned} \Vert u\Vert ^2_{W_2^{l,0}(Q_T)}=\int _0^T\Vert u(\cdot ,t)\Vert ^2_{W_2^l(\Omega )} \,\mathrm{d}t,\qquad \Vert u\Vert ^2_{W_2^{0,l/2}(Q_T)}=\int _{\Omega }\Vert u(x,\cdot ) \Vert ^2_{W_2^{l/2}(0,T)}\,\mathrm{d}x. \end{aligned}$$

The space $W_2^{l,l/2}(Q_T)\equiv W_2^{l,0}(Q_T)\cap W_2^{0, l/2}(Q_T)$ can be supplied with the norm

$$\begin{aligned} \Vert u\Vert _{W_2^{l,l/2}(Q_T)}\equiv \Vert u\Vert _{W_2^{l,0}(Q_T)} +\Vert u\Vert _{W_2^{0, l/2}(Q_T)}. \end{aligned}$$

We will use another equivalent norm in $W_2^{l,l/2}(Q_T)$ below.

The Sobolev–Slobodetskiǐ spaces of functions given on smooth surfaces, in particular, on ${\mathcal {G}}^\pm$ and on $G_T^\pm ={\mathcal {G}}^\pm \times (0,T)$, $T\leqslant \infty$, are introduced in the standard way, with the help of local maps and partition of unity.

Moreover, we introduce also the norm

$$\begin{aligned} \pmb |u \pmb |^{(s+l,l/2)}_{G_{T}^\pm }=\Vert u\Vert _{W_2^{s+l,0}(G_{T}^\pm )} +\Vert u\Vert _{W_2^{l/2}\big (0,T;W_2^s({\mathcal {G}}^\pm )\big )},\quad s>0. \end{aligned}$$

Finally, we set

$$\begin{aligned} \Vert u\Vert ^2_{W_2^l(\cup {\mathcal {F}}^\pm )} \equiv \Vert u\Vert ^2_{W_2^l({\mathcal {F}}^+)} +\Vert u\Vert ^2_{W_2^l({\mathcal {F}}^-)}, \quad \Vert u\Vert _{ \Omega }\equiv \Vert u\Vert _{L_2(\Omega )}. \end{aligned}$$

2 Linear Problem

An analysis of nonstationary problem with free boundaries for the Navier – Stokes equations (1.8) with initial data close to the regime of rotation of a two-layer fluid as a solid (see Fig. 2) is based on linearisation (1.14).

Fig. 2

Two-phase equilibrium figure

We study the following two initial–boundary value problems for the Stokes equations in a given two-phase domain separated by an axisymmetric surface of revolution ${\mathcal {G}}^+$ and bounded by an axisymmetric surface ${\mathcal {G}}^-$ with respect to the unknown velocity vector field ${\varvec{w}}$ and pressure function p:

$$\begin{aligned}&\bar{\rho }\big ({\mathcal {D}}_t{{\varvec{w}}} +2\omega ({\varvec{e}}_3\times {\varvec{w}})\big ) -\bar{\mu }\nabla ^2{\varvec{w}}+\nabla p=\bar{\rho }{\varvec{f}},\nonumber \\&\nabla \cdot {{\varvec{w}}}=f \equiv \nabla \cdot {\varvec{F}} \quad \text {in }{\mathcal {F}}\equiv {\mathcal {F}}^- \cup {\mathcal {F}}^+,\,\,\,t>0,\nonumber \\&{\varvec{w}}\big |_{t=0} ={\varvec{w}}_0 \quad \text {in }{\mathcal {F}}, \nonumber \\&{\mathbb {T}}({\varvec{w}},p){\varvec{N}}\big |_{{\mathcal {G}}^-} +{\varvec{N}} {\mathcal {B}}^-_0 r ={\varvec{d}} \quad \text {on }{\mathcal {G}}^-,\nonumber \\&[{\varvec{w}}]\big |_{{\mathcal {G}}^+}=0,\quad [{\mathbb {T}}({\varvec{w}},p){\varvec{N}}] \big |_{{\mathcal {G}}^+} +{\varvec{N}} {\mathcal {B}}^+_0r ={\varvec{d}} \quad \text {on }{\mathcal {G}}^+,\nonumber \\&{\mathcal {D}}_tr -{\varvec{w}}\cdot {\varvec{N}} =g \quad \text {on } \;{\mathcal {G}}\equiv {\mathcal {G}}^-\cup {\mathcal {G}}^+, \qquad r\big |_{t=0}=r_0 \quad \text {on }{\mathcal {G}}, \end{aligned}$$

(2.1)

and

$$\begin{aligned}&\bar{\rho }({\mathcal {D}}_t{{\varvec{w}}} +2\omega ({\varvec{e}}_3\times {\varvec{w}})) -\bar{\mu }\nabla ^2{\varvec{w}}+\nabla p=0,\qquad \nabla \cdot {{\varvec{w}}}=0 \quad \text {in }{\mathcal {F}},\,\,\,t>0, \nonumber \\&{\varvec{w}}\big |_{t=0}={\varvec{w}}_0 \quad \text {in }{\mathcal {F}},\nonumber \\&{\mathbb {T}}({\varvec{w}},p){\varvec{N}}\big |_{{\mathcal {G}}^-} +{\varvec{N}} {\mathcal {B}}^-_0 r =0 \quad \text {on }{\mathcal {G}}^-,\nonumber \\&[{\varvec{w}}]\big |_{{\mathcal {G}}^+}=0,\quad [{\mathbb {T}}({\varvec{w}},p){\varvec{N}}] \big |_{{\mathcal {G}}^+}+{\varvec{N}}{\mathcal {B}}^+_0r=0 \quad \text {on }{\mathcal {G}}^+,\nonumber \\&{\mathcal {D}}_tr-{\varvec{w}}\cdot {\varvec{N}}=0 \quad \text {on }{\mathcal {G}}, \qquad r\big |_{t=0}=r_0 \quad \text {on }{\mathcal {G}}, \end{aligned}$$

(2.2)

where $\omega$ is the angular velocity of the rotation, r(x, t) is an unknown function defining the surfaces $\Gamma ^\pm _ {t}$; ${\varvec{N}}$ is the outward unit normal to ${\mathcal {G}} ^- \cup {\mathcal {G}} ^+$; ${\varvec{f}}, f, {\varvec{d}}, g,$ ${\varvec{w}}_0, r_0$ are given functions; the expressions ${\mathcal {B}}^\pm _{0}r$ are defined by (1.15).

We assume that the domains ${\mathcal {F}}^\pm$ are symmetric with respect to $x_1,x_2,x_3$, as well as the initial data satisfy, in accordance with the linearization of assumptions (1.9), (1.10), orthogonality conditions

$$\begin{aligned}&\int _{{\mathcal {G}}^\pm }r_0(x)\,\mathrm{d}{\mathcal {G}}=0,\nonumber \\&\rho ^-\int _{{\mathcal {G}}^-} r_0(x)x_j\,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} r_0(x)x_j\,\mathrm{d}{\mathcal {G}}=0,\quad j=1,2,3, \end{aligned}$$

(2.3)

$$\begin{aligned}&\int _{\mathcal {F}}\bar{\rho } \mathbf{{w}}_0(x)\,\mathrm {d}x=0,\nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho } \mathbf{{w}}_0(x)\cdot \mathbf{{\eta }}_j(x)\,\mathrm {d}x +\omega \Big (\rho ^-\int _{{\mathcal {G}}^-} r_0(x)\mathbf{{\eta }}_3(x)\cdot \mathbf{{\eta }}_j(x)\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \qquad \qquad +[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} r_0(x)\mathbf{{\eta }}_3(x)\cdot \mathbf{{\eta }}_j(x)\,\mathrm {d}{\mathcal {G}}\Big )=0. \end{aligned}$$

(2.4)

We introduce the notation $Q_T^\pm ={\mathcal {F}}^\pm \times (0,T)$, $G_T^\pm ={\mathcal {G}}^\pm \times (0,T)$, $D_T= Q_T^+\cup Q_T^-$, $Q_T= Q_T^+\cup \overline{Q_T^-}$, $G_T= G_T^+\cup G_T^-$.

First, we study homogeneous problem (2.2).

Proposition 2.1

A solution of problem (2.2)–(2.4) satisfies conditions (2.3), (2.4) for all $t>0$.

Proof

Due to the boundary conditions in (2.2), we have

$$\begin{aligned}&\frac{\,\mathrm{d}}{\,\mathrm{d}t}\int _{{\mathcal {G}}^+}r(x,t)\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {G}}^+}{\varvec{w}}\cdot {\varvec{N}}\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {F}}^+}\nabla \cdot {\varvec{w}} \,\mathrm{d}x=0, \\&\frac{\,\mathrm{d}}{\,\mathrm{d}t}\int _{{\mathcal {G}}^-}r(x,t)\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {G}}^-}{\varvec{w}}\cdot {\varvec{N}}\,\mathrm{d}{\mathcal {G}}=0 \end{aligned}$$

which implies

$$\begin{aligned} \int _{{\mathcal {G}}^+}r\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {G}}^+}r_0 \,\mathrm{d}{\mathcal {G}}=0,\quad \int _{{\mathcal {G}}^-}r\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {G}}^-} r_0\,\mathrm{d}{\mathcal {G}}=0. \end{aligned}$$

(2.5)

Now we integrate the first equation in (2.2) over ${\mathcal {F}}^-\cup \overline{{\mathcal {F}}^+}={\mathcal {F}}$. In view of (2.8), we obtain

$$\begin{aligned}&\frac{\,\mathrm {d}}{\,\mathrm {d}t}\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t)\,\mathrm {d}x +2\omega \Big (\mathbf{{e}}_3\times \int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}\,\mathrm {d}x\Big ) +\int _{{\mathcal {G}}^-}{\mathcal {B}}^-_0(r)\mathbf{{N}}\,\mathrm {d}{\mathcal {G}}+\int _{{\mathcal {G}}^+}{\mathcal {B}}^+_0(r)\mathbf{{N}}\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \equiv \frac{\,\mathrm {d}}{\,\mathrm {d}t}\int _{\mathcal {F}}\bar{\rho } \mathbf{{w}}(x,t)\,\mathrm {d}x+2\omega \Big (\mathbf{{e}}_3\times \int _{\mathcal {F}} \bar{\rho }{} \mathbf{{w}}\,\mathrm {d}x\Big )+\int _{{\mathcal {G}}^-} r{\mathcal {B}}^-_0(N_i)\mathbf{{e}}_i\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \qquad \qquad +\int _{{\mathcal {G}}^+}r{\mathcal {B}}^+_0 (N_i)\mathbf{{e}}_i\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \equiv \frac{\,\mathrm {d}}{\,\mathrm {d}t}\int _{\mathcal {F}} \bar{\rho }{} \mathbf{{w}}\,\mathrm {d}x+2\omega \Big (\mathbf{{e}}_3 \times \int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}\,\mathrm {d}x\Big )\nonumber \\ {}&\qquad \qquad \qquad -\omega ^2\Big (\rho ^-\int _{{\mathcal {G}}^-}r \mathbf{{x}}'\,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} r\mathbf{{x}}'\,\mathrm {d}{\mathcal {G}}\Big )=0. \end{aligned}$$

(2.6)

Since

$$\begin{aligned} \frac{\,\mathrm{d}}{\,\mathrm{d}t}\big (\rho ^-\int _{{\mathcal {G}}^-}r{\varvec{x}} \,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}r{\varvec{x}} \,\mathrm{d}{\mathcal {G}}\big )=\int _{\mathcal {F}}\bar{\rho } {\varvec{w}} (x,t)\,\mathrm{d}x, \end{aligned}$$

equation (2.6) together with initial conditions (2.3), (2.4) can be regarded as a homogeneous Cauchy problem for

$$\begin{aligned} y_\alpha (t)=\rho ^-\int _{{\mathcal {G}}^-}r(x,t) x_\alpha \,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}r(x,t) x_\alpha \,\mathrm{d}{\mathcal {G}},\quad \alpha =1,2, \end{aligned}$$

and for $\int _{\mathcal {F}}\bar{\rho } w_3\,\mathrm{d}x$. From the uniqueness of a trivial solution, it follows that $y_\alpha (t)=0,$ $\int _{\mathcal {F}}\bar{\rho } w_3(x,t)\,\mathrm{d}x=0,$ which implies $\int _{\mathcal {F}}\bar{\rho } w_\alpha \,\mathrm{d}x=y'_\alpha (t)=0,$ $\int _{\mathcal {F}}\bar{\rho } w_3\,\mathrm{d}x=y_3'(t)=0,$ and $y_3(t)=y_3(0)=0$.

When we multiply the first equation in (2.2) by ${\varvec{\eta }}_j(x)$ and integrate, we get

$$\begin{aligned}&\frac{\,\mathrm {d}}{\,\mathrm {d}t}\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t) \cdot \mathbf{{\eta }}_3(x)\,\mathrm {d}x+2\omega \int _{\mathcal {F}}\bar{\rho } \mathbf{{w}}\cdot \mathbf{{x}}'\,\mathrm {d}x\\ {}&\quad \equiv \frac{\,\mathrm {d}}{\,\mathrm {d}t}\Big (\int _{\mathcal {F}} \bar{\rho }{} \mathbf{{w}}\cdot \mathbf{{\eta }}_3(x)\,\mathrm {d}x+\omega \big (\rho ^-\int _{{\mathcal {G}}^-} r|\mathbf{{\eta }}_3(x)|^2\,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}r| \mathbf{{\eta }}_3|^2\,\mathrm {d}{\mathcal {G}}\big )\Big )\\ {}&\quad =0,\\ {}&\frac{\,\mathrm {d}}{\,\mathrm {d}t}\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t) \cdot \mathbf{{\eta }}_\alpha (x)\,\mathrm {d}x- 2\omega \int _{\mathcal {F}} \bar{\rho } w_\alpha (x,t)x_3\,\mathrm {d}x-\omega ^2 \big (\rho ^- \int _{{\mathcal {G}}^-}{} \mathbf{{\eta }}_\alpha (x) \cdot \mathbf{{x}}'\,\mathrm {d}{\mathcal {G}}\\ {}&\qquad +[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} \mathbf{{\eta }}_\alpha \cdot \mathbf{{x}}'\,\mathrm {d}{\mathcal {G}}\big )=0,\qquad \alpha =1,2, \end{aligned}$$

which can be written as follows

$$\begin{aligned}&\frac{\,\mathrm {d}}{\,\mathrm {d}t}\Big (\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t) \cdot \mathbf{{\eta }}_1(x)\,\mathrm {d}x +\omega \big (\rho ^-\int _{{\mathcal {G}}^-} r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_1(x)\,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_1\,\mathrm {d}{\mathcal {G}}\big )\Big )\\ {}&\quad -\omega \int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t)\cdot \mathbf{{\eta }}_2(x)\,\mathrm {d}x +\omega \big (\rho _1\int _{{\mathcal {G}}^-}r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_2(x) \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}r \mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_2\,\mathrm {d}{\mathcal {G}}\big )\\ {}&\quad =0,\\ {}&\frac{\,\mathrm {d}}{\,\mathrm {d}t}\Big (\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t) \cdot \mathbf{{\eta }}_2(x)\,\mathrm {d}x +\omega \big (\rho ^-\int _{{\mathcal {G}}^-} r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_2(x)\,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_2\,\mathrm {d}{\mathcal {G}}\big )\Big )\\ {}&\quad +\omega \int _{\mathcal {F}}\bar{\rho }{} \mathbf{{w}}(x,t)\cdot \mathbf{{\eta }}_1(x)\,\mathrm {d}x +\omega \big (\rho _1\int _{{\mathcal {G}}^-}r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_1(x) \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}r \mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_1\,\mathrm {d}{\mathcal {G}}\big )\\ {}&\quad =0. \end{aligned}$$

Hence relations (2.4) are valid for all positive t, and the proposition is proved. $\square$

Due to momentum conservation law, it is valid the following statement.

Corollary 2.1

There holds the following decomposition

$$\begin{aligned} {\varvec{w}}={\varvec{w}}^\perp +\sum _{i=1}^3d_i(r){\varvec{\eta }}_i, \end{aligned}$$

where ${\varvec{w}}^\perp$ is a vector field orthogonal to all the vectors of rigid motion ${\varvec{\eta }}$, i. e.,

$$\begin{aligned} \int _{\mathcal {F}}\bar{\rho }{\varvec{w}}^\perp \cdot {\varvec{\eta }}\,\mathrm{d}x=0, \qquad {\varvec{\eta }}(x)={\varvec{e}}_i \quad \text {or}\quad {\varvec{\eta }}(x)={\varvec{\eta }}_i(x),\quad i=1,2,3, \end{aligned}$$

and

$$\begin{aligned} d_i(r)=-\frac{\omega }{S_i}\big (\rho ^-\int _{{\mathcal {G}}^-}r {\varvec{\eta }}_3\cdot {\varvec{\eta }}_i\,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}r{\varvec{\eta }}_3\cdot {\varvec{\eta }}_i \,\mathrm{d}{\mathcal {G}}\big ), \quad S_i=\int _{\mathcal {F}}\bar{\rho }|{\varvec{\eta }}_i|^2\,\mathrm{d}x. \end{aligned}$$

(2.7)

Proposition 2.2

The following relations hold:

$$\begin{aligned}&{\mathcal {B}}^-_0({\varvec{\eta }} \cdot {\varvec{N}} )=-\omega ^2 \rho ^-{\varvec{\eta }} \cdot {\varvec{x}}',\quad x\in {\mathcal {G}}^-,\nonumber \\&{\mathcal {B}}^+_0({\varvec{\eta }} \cdot {\varvec{N}} ) =-\omega ^2 [\bar{\rho }]|_{{\mathcal {G}}_{t}^+}{\varvec{\eta }} \cdot {\varvec{x}}',\quad x\in {\mathcal {G}}^+, \end{aligned}$$

(2.8)

where ${\varvec{\eta }}$ is an arbitrary vector of rigid motion.

Proof

Let $\Omega _\varepsilon$ be a bounded domain with the boundary $\Gamma _\varepsilon$, and ${\varvec{n}}_\varepsilon$ be the external normal to $\Gamma _\varepsilon$. The equality

$$\begin{aligned} \int _{\Gamma _\varepsilon }\Big (\sigma H_\varepsilon (x)+\rho \frac{\omega ^2}{2}|x'|^2+p_0\Big )\mathbf{{n}}_\varepsilon (x) \cdot \mathbf{{\eta }}_i(x)\,\mathrm {d}\Gamma _\varepsilon&=\rho \omega ^2 \int _{\Omega _\varepsilon }{} \mathbf{{\eta }}_i(x)\cdot \mathbf{{x}}'\,\mathrm {d}\Gamma _\varepsilon ,\nonumber \\&\qquad \qquad i=1,2,3, \end{aligned}$$

(2.9)

follows from

$$\begin{aligned} \int _{\Gamma _\varepsilon } H_\varepsilon (x){\varvec{n}}_\varepsilon \cdot {\varvec{\eta }}_i\,\mathrm{d}\Gamma _\varepsilon = \int _{\Gamma _\varepsilon } \Delta _{\Gamma _\varepsilon }{\varvec{x}}\cdot {\varvec{\eta }}_i\,\mathrm{d}\Gamma _\varepsilon =0, \end{aligned}$$

which is a consequence of the well-known Weierstrass formula

$$\begin{aligned} H_\varepsilon (x){\varvec{n}}_\varepsilon =\Delta _{\Gamma _\varepsilon }{\varvec{x}}, \end{aligned}$$

and from

$$\begin{aligned}&\int _{\Gamma _\varepsilon }|x'|^2{\varvec{n}}_\varepsilon \cdot {\varvec{\eta }}_i(x) \,\mathrm{d}\Gamma _\varepsilon = \int _{\Omega _\varepsilon }\nabla \cdot |x'|^2 {\varvec{\eta }}_i\,\mathrm{d}x=2\int _{\Omega _\varepsilon }{\varvec{\eta }}_i(x) \cdot {\varvec{x}}'\,\mathrm{d}x, \\&\int _{\Gamma _\varepsilon }{\varvec{n}}_\varepsilon \cdot {\varvec{\eta }}_i\,\mathrm{d}\Gamma _\varepsilon =\int _{\Omega _\varepsilon }\nabla \cdot {\varvec{\eta }}_i(x) \,\mathrm{d}x=0. \end{aligned}$$

Next, by $\Gamma _{\varepsilon }^\pm$ we denote the surfaces given by $x=y+\varepsilon {\varvec{N}} r$, $y \in {\mathcal {G}}^\pm$, and $\Omega ^+_{\varepsilon }$, $\Omega _{\varepsilon }^-$ mean the domains bounded by the surfaces $\Gamma ^+_\varepsilon$, $\Gamma ^+_\varepsilon \cup \Gamma _\varepsilon ^-$ and close to ${\mathcal {F}} ^\pm$, respectively; $\Omega _\varepsilon =\overline{\Omega ^+_\varepsilon } \cup \Omega _\varepsilon ^-$. Finally, let ${\varvec{N}}^*$ and $r^*$ be the extensions of ${\varvec{N}}^\pm$ and r into ${\mathcal {F}}$.

We generalize (2.9) on the surfaces $\Gamma ^\pm _\varepsilon$:

$$\begin{aligned}&\int _{\Gamma ^-_\varepsilon }\Big (\sigma ^-H^-_\varepsilon (x) +\rho ^-\frac{\omega ^2}{2}|x'|^2+ p_0^-\Big ){\varvec{n}}^-_\varepsilon (x) \cdot {\varvec{\eta }}_i(x)\,\mathrm{d}\Gamma _\varepsilon \\&\qquad +\int _{\Gamma ^+_\varepsilon }\Big (\sigma ^+H^+_\varepsilon (x) +[\rho ^\pm ]\big |_{\Gamma ^+_\varepsilon }\frac{\omega ^2}{2}|x'|^2 + p_0^+-p_0^-\Big ){\varvec{n}}^+_\varepsilon (x)\cdot {\varvec{\eta }}_i(x) \,\mathrm{d}\Gamma _\varepsilon \\&\quad =\omega ^2\Big (\int _{\Omega _\varepsilon }\rho ^-{\varvec{\eta }}_i(x) \cdot {\varvec{x}}'\,\mathrm{d}x+\int _{\Omega ^+_\varepsilon }[\rho ^\pm ] \big |_{\Gamma ^+_\varepsilon }{\varvec{\eta }}_i(x)\cdot {\varvec{x}}'\,\mathrm{d}x\Big )\\&\quad =\omega ^2\Big (\int _{\Omega ^-_\varepsilon }\rho ^- {\varvec{\eta }}_i\cdot {\varvec{x}}'\,\mathrm{d}x+\int _{\Omega ^+_\varepsilon }\rho ^+ {\varvec{\eta }}_i\cdot {\varvec{x}}'\,\mathrm{d}x\Big )= \omega ^2\int _{\Omega _\varepsilon } \rho ^\pm {\varvec{\eta }}_i\cdot {\varvec{x}}'\,\mathrm{d}x. \end{aligned}$$

By using equations (1.5) for ${\mathcal {G}}^\pm$, we obtain

$$\begin{aligned}&\varepsilon ^{-1}\Big \{\int _{{\mathcal {G}}^-}\Big (\sigma ^- \big (H^-_\varepsilon (x)-{\mathcal {H}}^-(y)\big )\nonumber \\&\qquad +\rho ^-\frac{\omega ^2}{2}(|x'|^2-|y'|^2) \Big ) {\varvec{n}} _\varepsilon (x)\cdot {\varvec{\eta }}_i(x)\big |_{x=y+\varepsilon {\varvec{ N}} r}|\widehat{{\mathbb {L}}} _\varepsilon ^T(y){\varvec{N}}(y)|\,\mathrm{d}{\mathcal {G}}\nonumber \\&\qquad +\int _{{\mathcal {G}}^+}\Big (\sigma ^+\big (H^+_\varepsilon (x) -{\mathcal {H}}^+(y)\big )\nonumber \\&\qquad +[\rho ]\big |_{\Gamma ^+_\varepsilon }\frac{\omega ^2}{2} (|x'|^2-|y'|^2)\Big ){\varvec{n}}_\varepsilon (x)\cdot {\varvec{\eta }}_i(x) \big |_{x=y+\varepsilon {\varvec{N}} r}|\widehat{{\mathbb {L}}}_\varepsilon ^T (y){\varvec{N}}(y)|\,\mathrm{d}{\mathcal {G}}\Big \}\nonumber \\&\quad =\varepsilon ^{-1}\omega ^2\Big \{\rho ^- \Big (\int \limits _{\Omega ^-_\varepsilon }{\varvec{\eta }}_i(x) \cdot {\varvec{x}}'\,\mathrm{d}x-\int \limits _{{\mathcal {F}}^-} {\varvec{\eta }}_i(y) \cdot {\varvec{y}}'\,\mathrm{d}y\Big )+\rho ^+\Big (\int \limits _{\Omega ^+_\varepsilon } {\varvec{\eta }}_i\cdot {\varvec{x}}'\,\mathrm{d}x -\int \limits _{{\mathcal {F}}^+} {\varvec{\eta }}_i(y)\cdot {\varvec{y}}'\,\mathrm{d}y\Big )\Big \}, \end{aligned}$$

(2.10)

where ${\mathbb {L}}_\varepsilon$ is the Jacobi matrix of the (invertible) transformation

$$\begin{aligned} x=y+\varepsilon {\varvec{N}}^*r^*: \quad {\mathcal {F}}\; \rightarrow \; \Omega _\varepsilon , \end{aligned}$$

$\widehat{{\mathbb {L}}}_\varepsilon$ is its co-factor matrix.

The first variation of (2.10) leads to

$$\begin{aligned}&\int _{{\mathcal {G}}^-}{\mathcal {B}}^-_0(r){\varvec{N}}\cdot {\varvec{\eta }}_i(y) \,\mathrm{d}{\mathcal {G}}+\int _{{\mathcal {G}}^+}{\mathcal {B}}^+_0(r){\varvec{N}} \cdot {\varvec{\eta }}_i(y)\,\mathrm{d}{\mathcal {G}}\\&\quad =-\lim _{\varepsilon \rightarrow 0}\varepsilon ^{-1}\omega ^2\rho ^- \Big (\int _{\Omega ^-_\varepsilon } {\varvec{\eta }}_i(x)\cdot {\varvec{x}}'\,\mathrm{d}x -\int _{{\mathcal {F}}^-}{\varvec{\eta }}_i(y)\cdot {\varvec{y}}'\,\mathrm{d}y\Big )\\&\qquad -\lim _{\varepsilon \rightarrow 0}\varepsilon ^{-1}\omega ^2\rho ^+ \Big (\int _{\Omega ^+_\varepsilon } {\varvec{\eta }}_i(x)\cdot {\varvec{x}}'\,\mathrm{d}x-\int _{{\mathcal {F}}^+}{\varvec{\eta }}_i(y)\cdot {\varvec{y}}'\,\mathrm{d}y\Big )\\&\quad =-\omega ^2\rho ^-\Big (\int _{{\mathcal {G}}^-}{\varvec{\eta }}_i(y) \cdot {\varvec{y}}'r\,\mathrm{d}S-\int _{{\mathcal {G}}^+}{\varvec{\eta }}_i(y) \cdot {\varvec{y}}'r\,\mathrm{d}{\mathcal {G}}\Big )-\omega ^2\rho ^+\int _{{\mathcal {G}}^+} {\varvec{\eta }}_i(y)\cdot {\varvec{y}}'r\,\mathrm{d}{\mathcal {G}}\\&\quad =-\omega ^2\rho ^-\int _{{\mathcal {G}}^-}{\varvec{\eta }}_i(y) \cdot {\varvec{y}}'r\,\mathrm{d}{\mathcal {G}}-\omega ^2[\bar{\rho }]\big |_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}{\varvec{\eta }}_i(y)\cdot {\varvec{y}}'r\,\mathrm{d}{\mathcal {G}}\end{aligned}$$

which implies

$$\begin{aligned} \int _{{\mathcal {G}}^-} {\mathcal {B}}^-_0(r){\varvec{N}}\cdot {\varvec{\eta }}_i (y)\,\mathrm{d}{\mathcal {G}}=-\omega ^2\rho ^-\int _{{\mathcal {G}}^-}{\varvec{\eta }}_i(y) \cdot {\varvec{y}}'r\,\mathrm{d}{\mathcal {G}}\end{aligned}$$

and

$$\begin{aligned} \int _{{\mathcal {G}}^+} {\mathcal {B}}^+_0(r){\varvec{N}} \cdot {\varvec{\eta }}_i(y)\,\mathrm{d}{\mathcal {G}}=-\omega ^2[\bar{\rho }] \big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}{\varvec{\eta }}_i(y) \cdot {\varvec{y}}'r\,\mathrm{d}{\mathcal {G}}. \end{aligned}$$

It is true the same for ${\varvec{N}}\cdot {\varvec{e}}_i$ instead of ${\varvec{N}}\cdot {\varvec{\eta }}_i$. In view of the arbitrariness of r, Proposition 2.2 is proved. $\square$

Theorem 2.1

(Local Solvability of the Linear Problem). Let ${\mathcal {G}}\in W_2^{3/2+l}$ and $r_0 \in W_2^{2+l} ({\mathcal {G}})$ with $l\in (1/2,1).$ For arbitrary ${\varvec{f}} \in {\varvec{W}}_2^{l,l/2}(D_T)$, $f \in W_2^{1+l,0}(D_T)$, $f=\nabla \cdot {\varvec{F}}$, ${\varvec{F}}\in {\varvec{W}}_2^{0, 1+\frac{l}{2}}(D_T)$, $[{\varvec{F}}\cdot {{\varvec{N}}}]|_{{\mathcal {G}}}=0$, ${\varvec{w}}_0 \in W_2^{1+l}({\mathcal {F}})$, ${\varvec{d}}= {\varvec{d}}_\tau +d{\varvec{N}}$, ${\varvec{d}}_\tau \in {\varvec{W}}_2^{ l+\frac{1}{2} ,\frac{l}{2}+\frac{1}{4}}(G_T)$, ${\varvec{N}}\cdot {\varvec{d}}_\tau =0$, $d\in W_2^{ l+\frac{1}{2},0}(G_T)\cap W_2^{l/2}\big (0,T;W_2^{1/2}({\mathcal {G}})\big )$, $g\in W_2^{3/2+l ,3/4+l/2}(G_T)$, $T<\infty$, satisfying compatibility conditions

$$\begin{aligned}&\nabla \cdot {\varvec{w}}_0=f|_{t=0},\\&[{\varvec{w}}_0]|_{{\mathcal {G}}^+}=0,\quad [\mu ^\pm \Pi _{{\mathcal {G}}}{\mathbb {S}}({{\varvec{w}}_0}){{\varvec{N}}}]|_{{\mathcal {G}}^+} ={\varvec{d}}_\tau |_{t=0},\quad \mu ^-\Pi _{{\mathcal {G}}}{\mathbb {S}} ({{\varvec{w}}_0}){{\varvec{N}}}|_{{\mathcal {G}}^-}={\varvec{d}}_\tau |_{t=0}, \end{aligned}$$

where $\Pi _{{\mathcal {G}}}{\varvec{b}}={\varvec{b}}-({\varvec{N}}\cdot {\varvec{b}}){\varvec{N}}$, problem (2.1) has a unique solution $({\varvec{w}},p, r)$ such that ${\varvec{w}}\in {\varvec{W}}_2^{2+l,1+\frac{l}{2}}(D_T)$, $p\in {\varvec{W}}_2^{l,\frac{l}{2}}(D_T),$ $\nabla p\in {\varvec{W}}_2^{l,\frac{l}{2}}(D_T),$ $r(\cdot ,t)\in W_2^{2+l}({{\mathcal {G}}})$ for any $t\in (0,T)$ and

$$\begin{aligned}&\Vert \mathbf{{w}}\Vert _{\mathbf{{W}}_2^{2+l,1+l/2}(D_T)}+\Vert \nabla p\Vert _{{bf{W}}_2^{l,l/2}(D_T)}+ \Vert p\Vert _{W_2^{l,l/2}(D_T)} +{\Vert r\Vert _{W_2^{5/2+l,5/4+l/2}(G_T)}} \nonumber \\ {}&\quad +\Vert {\mathcal {D}}_t r\Vert _{W_2^{3/2+l,3/4+l/2}(G_T)} \leqslant c(T)\Big \{\Vert {bf{f}}\Vert _{{bf{W}}_2^{l,l/2}(D_T)} +\Vert f\Vert _{W_2^{1+l,0}(D_T)}\nonumber \\ {}&\qquad \qquad \quad +\Vert {bf{F}}\Vert _{W_2^{0,1+l/2}(D_T)}+\Vert {bf{d}}_\tau \Vert _{{bf{W}}_2^{ l+1/2,l/2+1/4}(G_T)} +\sigma { \pmb |d \pmb |^{(l+1/2,l/2)}_{G_T}} \nonumber \\ {}&\qquad \qquad \quad +\Vert g\Vert _{W_2^{3/2+l,3/4+l/2}(G_T)}+\Vert \mathbf{{w}}_0 \Vert _{{bf{W}}_2^{1+l}({\mathcal {F}})}+\Vert r_0\Vert _{W_2^{2+l} ({\mathcal {G}})}\Big \}. \end{aligned}$$

(2.11)

Remark 2.1

From trace theorem for $\rho \in W_2^{1,1}(G_T),$ it follows that

$$\begin{aligned} \Vert \rho (\cdot ,t)\Vert _{W_2^{1/2}({\mathcal {G}})}\leqslant c \Big \{\Vert \rho \Vert _{W_2^{1,0}(G_T)} +\Vert {\mathcal {D}}_t \rho \Vert _{G_T}\Big \},\ t\in [0,T], \end{aligned}$$

which implies the inequality

$$\begin{aligned} \Vert r(\cdot ,t)\Vert _{W_2^{2+l}({\mathcal {G}})}\leqslant c \Big \{\Vert r\Vert _{W_2^{5/2+l,0}(G_T)} +\Vert {\mathcal {D}}_t r\Vert _{W_2^{3/2+l,0}(G_T)}\Big \}. \end{aligned}$$

This means that $\Gamma _t^\pm \in W_2^{2+l}$ for all $t\in [0,T]$.

Proof

Let $r_1$ be a function satisfying the conditions

$$\begin{aligned}&r_1(y,0)=r_0(y),\\&{\mathcal {D}}_t r_1(y,0)=g(y,0)+ {\varvec{w}}_0(y)\cdot {\varvec{N}}(y)\equiv r_0'(y) \end{aligned}$$

and the estimates

$$\begin{aligned} {\pmb |r_1\pmb |^{(\frac{5}{2}+l,\frac{l}{2})}_{G_T}}+\Vert {\mathcal {D}}_t r_1\Vert _{W_2^{\frac{3}{2} +l,\frac{3}{4}+\frac{l}{2}}(G_T)}&\leqslant c\big \{\Vert r_1\Vert _{W_2^{\frac{5}{2}+l,\frac{5}{4} +\frac{l}{2}}(G_T)} +\Vert {\mathcal {D}}_t r_1\Vert _{W_2^{\frac{3}{2}+l, \frac{3}{4}+\frac{l}{2}}(G_T)}\big \}\nonumber \\&\leqslant c\big \{\Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}})} +\Vert r'_0\Vert _{W_2^{ l+1/2 }({\mathcal {G}})}\big \}. \end{aligned}$$

(2.12)

Such $r_1$ exists due to Proposition 4.1 in [20] and equivalent normalizations of the Sobolev – Slobodetskiǐ spaces.

We can write

$$\begin{aligned} {\mathcal {B}}^\pm _0 r(y,t)&={\mathcal {B}}^\pm _0 r_1(y,t) +\int _0^t{\mathcal {B}}^\pm _0 {\mathcal {D}}_t\big (r(y,\tau ) -r_1(y,\tau )\big ) \,\mathrm{d}\tau \\&={\mathcal {B}}^\pm _0 r_1(y,t)+\int _0^t{\mathcal {B}}^\pm _0 \Big (g(y,\tau )+{\varvec{w}}(y,\tau )\cdot {\varvec{N}}(y) -{\mathcal {D}}_t r_1(y,\tau )\Big ) \,\mathrm{d}\tau . \end{aligned}$$

Consequently, system (2.1) can be transformed to the form:

$$\begin{aligned}&\bar{\rho }\big ({\mathcal {D}}_t{\mathbf{{w}}} +2\omega (\mathbf{{e}}_3\times \mathbf{{w}})\big ) -\bar{\mu }\nabla ^2\mathbf{{w}}+\nabla p=\bar{\rho }{} \mathbf{{f}}, \nonumber \\ {}&\qquad \qquad \nabla \cdot {\mathbf{{w}}}=f\,\,\,\quad \text{ in }\,\,\,{\mathcal {F}},\;\;t>0, \nonumber \\ {}&\mathbf{{w}}(y,0)=\mathbf{{w}}_0(y)\,\,\,\quad \text{ in } \,\,\,{\mathcal {F}},\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}({\mathbf{{w}}}){\mathbf{{N}}} \big |_{{\mathcal {G}}^-}=\mathbf{{d}}_\tau ,\quad [\mathbf{{w}}]|_{{\mathcal {G}}^+}=0, \quad [\mu ^\pm \Pi _{\mathcal {G}}{\mathbb {S}}({\mathbf{{w}}}){\mathbf{{N}}}] \big |_{{\mathcal {G}}^+}=\mathbf{{d}}_\tau , \nonumber \\ {}&\mathbf{{N}}\cdot {\mathbb {T}}(\mathbf{{w}},p)\mathbf{{N}}\big |_{{\mathcal {G}}^-} -\sigma ^-\mathbf{{N}}\!\cdot \! \Delta ^-\!\int \limits _0^t\!\mathbf{{w}}|_{{\mathcal {G}}^-}\,\mathrm {d}\tau =d' +\sigma ^-\!\int \limits _0^t\!B'\,\mathrm {d}\tau +\sigma ^-\nabla _{\mathcal {G}}{\mathcal {H}}\cdot \!\int \limits _0^t \!\mathbf{{w}}\,\mathrm {d}\tau \nonumber \\ {}&\qquad -\sigma ^-\omega ^2\rho ^-\mathbf{{N}}\!\cdot \!\mathbf{{y}}' \!\int \limits _0^t\! \mathbf{{w}}\cdot \mathbf{{N}}\,\mathrm {d}\tau +2\sigma ^-\!\int \limits _0^t\!\nabla _{\mathcal {G}}{} \mathbf{{w}}:\nabla _{\mathcal {G}} \mathbf{{N}}\, \mathrm {d}\tau \qquad \text{ on }\;\, {\mathcal {G}}^-,\nonumber \\ {}&[\mathbf{{N}}\cdot {\mathbb {T}}(\mathbf{{w}},p)\mathbf{{N}}]\big |_{{\mathcal {G}}^+}\! -\sigma ^+\mathbf{{N}}\cdot \Delta ^+\!\! \int \limits _0^t\!\mathbf{{w}}|_{{\mathcal {G}}^+}\,\mathrm {d}\tau =d' +\sigma ^+\!\int \limits _0^t\!B'\,\mathrm {d}\tau +\sigma ^+\nabla _{\mathcal {G}}{\mathcal {H}}\!\cdot \! \!\int \limits _0^t\!\mathbf{{w}}\ \mathrm {d}\tau \nonumber \\ {}&\qquad -\sigma ^+\omega ^2[\bar{\rho }]|_{{\mathcal {G}}^+} \mathbf{{N}}\cdot \mathbf{{y}}'\int \limits _0^t \mathbf{{w}}\cdot \mathbf{{N}}\,\mathrm {d}\tau +2\sigma ^+\int \limits _0^t\nabla _{\mathcal {G}}{} \mathbf{{w}}: \nabla _{\mathcal {G}} \mathbf{{N}}\,\mathrm {d}\tau \,\,\quad \text{ on } \,\,\,{\mathcal {G}}^+, \end{aligned}$$

(2.13)

where $d'=d-\sigma {\mathcal {B}}^\pm _0r_1$, $B'={\mathcal {B}}^\pm _0({\mathcal {D}}_t r_1-g)$, $\nabla _{\mathcal {G}}$ is the surface gradient on ${\mathcal {G}}^+$; ${\mathbb {S}}{:}{\mathbb {T}}\equiv S_{ij}T_{ij}$. In (2.13), we have used that

$$\begin{aligned} \Delta ^{\pm }{\varvec{N}}=\nabla _{\mathcal {G}}{\mathcal {H}}^\pm -({\mathcal {H}}^{\pm ^2}-2{\mathcal {K}}^\pm ){\varvec{N}} \end{aligned}$$

(Lemma 10.7 in [18]). Such problems were investigated in [14, 21, 22], where, in particular, the solvability of (2.13) without the terms $2\omega ({\varvec{e}}_3\times {\varvec{w}})$ and

$$\begin{aligned} \sigma ^\pm \nabla _{\mathcal {G}}{\mathcal {H}}\cdot \int _0^t\mathbf{{w}} \,\mathrm {d}\tau&-\sigma ^\pm \omega ^2 [\bar{\rho }]|_{{\mathcal {G}}^\pm } \mathbf{{N}}\cdot \mathbf{{y}}'\int _0^t \mathbf{{w}}\cdot \mathbf{{N}}|_{{\mathcal {G}}^\pm }\,\mathrm {d}\tau \\ {}&+2\sigma ^\pm \int _0^t\nabla _{\mathcal {G}} \mathbf{{w}}(y,t): \nabla _{\mathcal {G}}{} \mathbf{{N}}(y)|_{{\mathcal {G}}^\pm }\,\mathrm {d}\tau \end{aligned}$$

and the estimate of its solution

$$\begin{aligned}&\Vert \mathbf{{w}}\Vert _{W_2^{2+l,1+l/2 }(D_T)}+\Vert \nabla p\Vert _{\mathbf{{W}}_2^{l,l/2}(D_T)} +\Vert p\Vert _{W_2^{0,l/2}(D_T)} \leqslant c(T) \Big \{\Vert \mathbf{{f}}\Vert _{\mathbf{{W}}_2^{l,l/2}(D_T)}\nonumber \\ {}&\qquad \qquad \quad +\Vert f\Vert _{W_2^{1+l,0}(D_T)}+\Vert \mathbf{{F}}\Vert _{\mathbf{{W}}_2^{0, 1+l/2 } (D_T)}+\Vert \mathbf{{d}}_\tau \Vert _{\mathbf{{W}}_2^{ l+1/2,l/2+1/4}(G_T)}\nonumber \\ {}&\qquad \qquad \quad + \pmb |d' \pmb |^{(l+1/2,l/2)}_{G_T} +\Vert B'\Vert _{W_2^{l-1/2,l/2-1/4}(G_T)}+\Vert \mathbf{{w}}_0 \Vert _{\mathbf{{W}}_2^{1+l}({\mathcal {F}})}\Big \} \end{aligned}$$

(2.14)

were established. Inequality (2.14) together with (2.12) implies estimate (2.11) because the additional terms are of lower order and have no essential influence on the final result. In addition, in [21, 22], we considered the whole space with a closed interface. We note that the results for bounded domains are similar [14]. Near the outer boundary, one should apply the estimates obtained in [23] for a single liquid of finite volume. $\square$

Now we consider homogeneous problem (2.2) with ${\varvec{w}}_0$ and $r_0$ satisfying orthogonality conditions (2.3), (2.4). At first, exponentially weighted $L_2$-estimates of ${\varvec{w}}$ and r will be obtained.

Proposition 2.3

Assume that the form

$$\begin{aligned} R_0(r)= \int _{{\mathcal {G}}}r{\mathcal {B}}_0^\pm r \,\mathrm{d}{\mathcal {G}}\end{aligned}$$

(2.15)

is positive definite, i. e.,

$$\begin{aligned} c^{-1} \Vert r\Vert ^2_{W_2^1({\mathcal {G}})}\leqslant R_0(r)\leqslant c \Vert r\Vert ^2_{W_2^1({\mathcal {G}})} \end{aligned}$$

(2.16)

for arbitrary r(x) satisfying (2.3). Then a solution of (2.2)–(2.4) satisfies the inequality

$$\begin{aligned} \Vert e^{\beta _1 t}{\varvec{w}}(\cdot ,t)\Vert ^2_{{\mathcal {F}}}+\Vert e^{\beta _1 t}r(\cdot ,t)\Vert ^2_{W_2^1({\mathcal {G}})}\leqslant c\big \{\Vert {\varvec{w}}_0 \Vert ^2_{{\mathcal {F}}}+\Vert r_0\Vert ^2_{W_2^1({\mathcal {G}})}\big \},\quad t>0, \end{aligned}$$

(2.17)

where $\beta _1,$ $c>0$ are independent of t.

Proof

In order to prove (2.17), we multiply the first equation in problem (2.2) by ${\varvec{w}}$ and integrate by parts. As a result, using the boundary conditions and the self-adjointness of the operators ${\mathcal {B}}_0^\pm (r)$, we have energy relations

$$\begin{aligned} 0&=\int _{\mathcal {F}}\big (\overline{\rho }{\mathcal {D}}_t\mathbf{{w}}\cdot \mathbf{{w}}-\nabla \cdot {\mathbb {T}}(\mathbf{{w}},q)\cdot \mathbf{{w}}\big )\,\mathrm {d}x=\frac{1}{2}\frac{\,\mathrm {d}}{\,\mathrm {d}t}\int _{\mathcal {F}}\overline{\rho }|\mathbf{{w}}|^2\,\mathrm {d}x +\int _{\mathcal {F}}\bar{\mu }|{\mathbb {S}}(\mathbf{{w}})|^2\,\mathrm {d}x\nonumber \\ {}&\qquad -\int _{{\mathcal {G}}^-}{\mathbb {T}}(\mathbf{{w}},p)\mathbf{{N}}\cdot \mathbf{{w}}\,\mathrm {d}{\mathcal {G}}-\int _{{\mathcal {G}}^+}[{\mathbb {T}}(\mathbf{{w}},p)\mathbf{{N}}]\big |_{{\mathcal {G}}^+}\cdot \mathbf{{w}}\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&=\frac{1}{2}\frac{\,\mathrm {d}}{\,\mathrm {d}t}\!\int \limits _{\mathcal {F}}\!\overline{\rho }|\mathbf{{w}}|^2\,\mathrm {d}x +\!\int \limits _{\mathcal {F}}\!\bar{\mu }|{\mathbb {S}}(\mathbf{{w}})|^2\,\mathrm {d}x +\!\int \limits _{{\mathcal {G}}^+}\!\mathbf{{w}}\cdot \mathbf{{N}}{\mathcal {B}}^+_0(r)\,\mathrm {d}{\mathcal {G}}+\!\int \limits _{{\mathcal {G}}^-}\!\mathbf{{w}}\cdot \mathbf{{N}}{\mathcal {B}}^-_0(r)\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&=\frac{1}{2}\frac{\,\mathrm {d}}{\,\mathrm {d}t}\Big (\int \limits _{\mathcal {F}}\overline{\rho }|\mathbf{{w}}|^2\,\mathrm {d}x+\int \limits _{{\mathcal {G}}^+}r {\mathcal {B}}^+_0(r)\,\mathrm {d}{\mathcal {G}}+\int \limits _{{\mathcal {G}}^-}r{\mathcal {B}}^-_0(r)\,\mathrm {d}{\mathcal {G}}\Big )+\int \limits _{\mathcal {F}}\mu |{\mathbb {S}}(\mathbf{{w}})|^2\,\mathrm {d}x. \end{aligned}$$

(2.18)

Making the same but with ${\varvec{W}}\in W_2^1({\mathcal {F}})$ such that

$$\begin{aligned}&\nabla \cdot {\varvec{W}}=0\quad \text {in}\quad {\mathcal {F}},\quad {\varvec{W}} \cdot {\varvec{N}}|_{{\mathcal {G}}^\pm }=r,\\&\Vert {\varvec{W}}\Vert _{W_2^1({\mathcal {F}})} \leqslant c\Vert r\Vert _{W_2^{1/2}({\mathcal {G}})},\\&\Vert {\mathcal {D}}_t{\varvec{W}}\Vert _{{\mathcal {F}}}\leqslant c \Vert {\mathcal {D}}_tr\Vert _{{\mathcal {G}}}\leqslant c \Vert {\varvec{w}} \cdot {\varvec{N}}\Vert _{{\mathcal {G}}}, \end{aligned}$$

we obtain

$$\begin{aligned} 0&=\frac{\,\mathrm{d}}{\,\mathrm{d}t}\int _{\mathcal {F}}\overline{\rho }{\varvec{w}} \cdot {\varvec{W}}\,\mathrm{d}x-\int _{\mathcal {F}}\overline{\rho } {\varvec{w}}\cdot {\mathcal {D}}_t{\varvec{W}}\,\mathrm{d}x+2\omega \int _{\mathcal {F}}({\varvec{e}}_3 \times {\varvec{w}})\cdot {\varvec{W}}\,\mathrm{d}x\nonumber \\&\quad +\int _{{\mathcal {G}}^-} {\varvec{W}}\cdot {\varvec{N}} {\mathcal {B}}^-_0(r)\,\mathrm{d}{\mathcal {G}}+\int _{{\mathcal {G}}^+}{\varvec{W}} \cdot {\varvec{N}}{\mathcal {B}}^+_0(r)\,\mathrm{d}{\mathcal {G}}+\int _{\mathcal {F}} \bar{\mu }{\mathbb {S}}({\varvec{w}}):{\mathbb {S}}({\varvec{W}})\,\mathrm{d}x\nonumber \\&=\frac{\,\mathrm{d}}{\,\mathrm{d}t}\int _{\mathcal {F}}\overline{\rho }{\varvec{w}} \cdot {\varvec{W}}\,\mathrm{d}x-\int _{\mathcal {F}}\overline{\rho } {\varvec{w}} \cdot {\mathcal {D}}_t{\varvec{W}}\,\mathrm{d}x+2\omega \int _{\mathcal {F}} ({\varvec{e}}_3\times {\varvec{w}})\cdot {\varvec{W}}\,\mathrm{d}x \nonumber \\&\quad + \int _{\mathcal {F}}\bar{\mu }{\mathbb {S}} ({\varvec{w}}):{\mathbb {S}}({\varvec{W}})\,\mathrm{d}x +\int _{{\mathcal {G}}^-}r {\mathcal {B}}^-_0(r)\,\mathrm{d}{\mathcal {G}}+\int _{{\mathcal {G}}^+}r {\mathcal {B}}^+_0(r)\,\mathrm{d}{\mathcal {G}}. \end{aligned}$$

(2.19)

Since due to (2.5) $\int _{{\mathcal {G}}^\pm }r \,\mathrm{d}{\mathcal {G}}=0,$ such ${\varvec{W}}$ exists.

Now we estimate the generalized energy. We multiply (2.19) by small $\gamma >0$ and add to (2.18), which gives

$$\begin{aligned} \frac{\,\mathrm{d}}{\,\mathrm{d}t}{\mathcal {E}}(t)+{\mathcal {E}}_1(t)=0, \end{aligned}$$

where

$$\begin{aligned}&{\mathcal {E}}=\frac{1}{2}\Big (\int _{\mathcal {F}}\bar{\rho }| {\varvec{w}}|^2\,\mathrm{d}x+\int _{{\mathcal {G}}^+}r {\mathcal {B}}^+_0(r) \,\mathrm{d}{\mathcal {G}}+\int _{{\mathcal {G}}^-}r{\mathcal {B}}^-_0(r)\,\mathrm{d}{\mathcal {G}}+\gamma \int _{\mathcal {F}}\bar{\rho }{\varvec{w}}\cdot {\varvec{W}}\,\mathrm{d}x\Big ), \\&{\mathcal {E}}_1=\int _{\mathcal {F}}\bar{\mu }|{\mathbb {S}}({\varvec{w}})|^2\,\mathrm{d}x +\gamma \Big (2\omega \int _{\mathcal {F}}({\varvec{e}}_3\times {\varvec{w}})\cdot {\varvec{W}}\,\mathrm{d}x -\int _{\mathcal {F}}\bar{\rho } {\varvec{w}}\cdot {\mathcal {D}}_t{\varvec{W}}\,\mathrm{d}x\\&\qquad +\int _{\mathcal {F}}\bar{\mu }{\mathbb {S}}({\varvec{w}}): {\mathbb {S}}({\varvec{W}})\,\mathrm{d}x +\int _{{\mathcal {G}}^-}r {\mathcal {B}}^-_0 (r)\,\mathrm{d}{\mathcal {G}}+\int _{{\mathcal {G}}^+}r {\mathcal {B}}^+_0(r)\,\mathrm{d}{\mathcal {G}}\Big ). \end{aligned}$$

By virtue (2.16), we have

$$\begin{aligned} c_3\big \{\Vert {\varvec{w}}\Vert ^2_{{\mathcal {F}}}+\Vert r\Vert ^2_{W_2^1 ({\mathcal {G}})}\big \}\leqslant {\mathcal {E}}\leqslant c_4 \big \{\Vert {\varvec{w}}\Vert ^2_{{\mathcal {F}}}+\Vert r\Vert ^2_{W_2^1({\mathcal {G}})}\big \}. \end{aligned}$$

In view of Corollary 2.1, ${\varvec{w}}={\varvec{w}}^\perp +\sum _{i=1}^3d_i(r){\varvec{\eta }}_i(x)\equiv {\varvec{w}}^\perp +{\varvec{w}}'$ and, hence,

$$\begin{aligned} \Vert \sqrt{\bar{\rho }}{\varvec{w}}\Vert ^2_{\mathcal {F}}=\Vert \sqrt{\bar{\rho }}{\varvec{w}}^\perp \Vert ^2_{\mathcal {F}} +\Vert \sqrt{\bar{\rho }}{\varvec{w}}'\Vert ^2_{\mathcal {F}}, \end{aligned}$$

where $\Vert \sqrt{\bar{\rho }}{\varvec{w}}'\Vert ^2_{{\mathcal {F}}} =\sum _{k,j=1}^3d_kd_jS_{kj}=\sum _{j=1}^3 S_{j}d_j^2$, $S_{kj}=\int _{\mathcal {F}}\bar{\rho } {\varvec{\eta }}_k\cdot {\varvec{\eta }}_j\,\mathrm{d}x$, $S_j\equiv S_{jj}$, and $d_j$, $j=1,2,3,$ are defined by (2.7). It is easily seen that $\Vert \sqrt{\rho }{\varvec{w}}'\Vert ^2_{{\mathcal {F}}}$ is a positive quadratic form with respect to r. Consequently,

$$\begin{aligned} c_5\big \{\Vert {\varvec{w}}^\perp \Vert ^2_{{\mathcal {F}}} +\Vert r\Vert ^2_{W_2^1({\mathcal {G}})}\big \}\leqslant {\mathcal {E}} \leqslant c_6\big \{\Vert {\varvec{w}}^\perp \Vert ^2_{{\mathcal {F}}} +\Vert r\Vert ^2_{W_2^1({\mathcal {G}})}\big \}. \end{aligned}$$

Next, we apply the Korn inequality, valid for the functions orthogonal to all rigid displacement vectors [24],

$$\begin{aligned} c_7 \Vert \nabla {\varvec{w}}^\perp \Vert ^2_{{\mathcal {F}}} \leqslant c_8 \Vert \sqrt{\bar{\mu }}{\mathbb {S}}({\varvec{w}}^\perp )\Vert ^2_{{\mathcal {F}}} =c_8 \Vert \sqrt{\bar{\mu }}{\mathbb {S}}({\varvec{w}})\Vert ^2_{{\mathcal {F}}}. \end{aligned}$$

Then we can use the Poincaré inequality

$$\begin{aligned} c_9 \Vert {\varvec{w}}^\perp \Vert ^2_{{\mathcal {F}}} \leqslant c_{10} \Vert \bar{\rho }{\varvec{w}}^\perp \Vert ^2_{{\mathcal {F}}} \leqslant c_{11} \Vert \bar{\rho }\nabla {\varvec{w}}^\perp \Vert ^2_{{\mathcal {F}}} \end{aligned}$$

since

$$\begin{aligned} 0=\int _{\mathcal {F}}\bar{\rho }{\varvec{w}}\,\mathrm{d}x =\int _{\mathcal {F}}\bar{\rho }{\varvec{w}}^\perp \,\mathrm{d}x \end{aligned}$$

due to (2.4) and (1.6).

Hence, by the Hölder inequality, for small enough $\gamma$, we have

$$\begin{aligned} {\mathcal {E}}_1\geqslant 2\beta _1{\mathcal {E}} \end{aligned}$$

with some $\beta _1>0$. Consequently,

$$\begin{aligned} \frac{\,\mathrm{d}}{\,\mathrm{d}t}{\mathcal {E}}(t)+2\beta _1{\mathcal {E}}(t)\leqslant 0 \end{aligned}$$

which implies

$$\begin{aligned} {\mathcal {E}}\leqslant e^{-2\beta _1t}{\mathcal {E}}(0) \end{aligned}$$

and inequality (2.17). $\square$

Remark 2.2

We observe that condition (2.16) coincides with the positiveness of the second variation of the potential energy

$$\begin{aligned} G(r)=\sigma ^+|\Gamma ^+_t|+\sigma ^-|\Gamma ^-_t|- \frac{\omega ^2}{2} \int _{\Omega _t} \rho ^\pm |x'|^2\,\mathrm{d}x-p_0^+|\Omega ^+_t|-p_0^-|\Omega ^-_t| \end{aligned}$$

for given volumes of $\Omega ^\pm _t$. One can calculate it by (1.13):

$$\begin{aligned} \delta _0^2G(r)&=\int _{{\mathcal {G}}^-} \Big \{\sigma ^-(|\nabla _ {\mathcal {G}}r|^2 +2{\mathcal {K}} r^2)-\rho ^-\frac{\omega ^2}{2} \Big (\frac{\partial }{\partial {\varvec{N}}}|x'|^2-|x'|^2{\mathcal {H}}\Big )r^2 +p_0^-{\mathcal {H}}r^2\Big \}\,\mathrm{d}{\mathcal {G}}\\&\quad +\int _{{\mathcal {G}}^+}\Big \{\sigma ^+ (|\nabla _ {\mathcal {G}}r|^2 +2{\mathcal {K}} r^2) -[\bar{\rho }]\big |_{{\mathcal {G}}^+}\frac{\omega ^2}{2} \Big (\frac{\partial }{\partial {\varvec{N}}}|x'|^2-|x'|^2{\mathcal {H}}\Big )r^2 +(p_0^+-p_0^-){\mathcal {H}}r^2\Big \}\,\mathrm{d}{\mathcal {G}}\end{aligned}$$

(see [9, 11]). Due to equations (1.5), this yields

$$\begin{aligned} \delta _0^2G(r)&=\int _{{\mathcal {G}}^-}\Big \{\sigma ^- |\nabla _ {\mathcal {G}}r|^2 +\Big (\sigma ^-(2{\mathcal {K}}-{\mathcal {H}}^2) -\rho ^- \omega ^2 {\varvec{N}}\cdot {\varvec{x}}' \Big )r^2 \Big \}\,\mathrm{d}{\mathcal {G}}\\&\quad +\int _{{\mathcal {G}}^+}\Big \{\sigma ^+|\nabla _ {\mathcal {G}}r|^2 +\Big (\sigma ^+(2{\mathcal {K}}-{\mathcal {H}}^2) -[\bar{\rho }]\big |_{{\mathcal {G}}^+} \omega ^2 {\varvec{N}}\cdot {\varvec{x}}' \Big ) r^2\Big \}\,\mathrm{d}{\mathcal {G}}. \end{aligned}$$

The nonnegativity of the second variation of the potential G(r) on the subspace of r satisfying orthogonality conditions (2.3) guarantees weak lower semicontinuity of it whence together with the coerciveness of the potential it follows the existence of a minimum. It is clear that the minimum realizes at $r=0$ which implies the stability of equilibrium figures ${\mathcal {F}}$ and ${\mathcal {F}}^+$ given by (1.5) that are the Euler equations for the potential G(r) .

This approach corresponds to the variational setting for stability problem of the boundaries ${\mathcal {G}}^\pm$.

Theorem 2.2

(Global Solvability of the Linear Homogeneous Problem). If estimate (2.16) is valid for the functional $R_0(r)$ defined by (2.15) then problem (2.2) with ${\varvec{w}}_0 \in W_2^{1+l}({\mathcal {F}})$, $r_0 \in W_2^{2+l}({\mathcal {G}})$, $l\in (1/2,1)$, satisfying compatibility conditions

$$\begin{aligned} \nabla \cdot {\varvec{w}}_0=0, \quad [{\varvec{w}}_0]|_{{\mathcal {G}}^+}=0, \quad [\mu ^\pm \Pi _{{\mathcal {G}}}{\mathbb {S}}({{\varvec{w}}_0}) {{\varvec{N}}}]|_{{\mathcal {G}}^+}=0,\quad \mu ^-\Pi _{{\mathcal {G}}} {\mathbb {S}}({{\varvec{w}}_0}){{\varvec{N}}}|_{{\mathcal {G}}^-}=0, \end{aligned}$$

(2.20)

and orthogonality conditions (2.3), (2.4), has a unique solution $({\varvec{w}}, p, r)$ such that ${\varvec{w}}\in {\varvec{W}}_2^{2+l,1+l/2}(D_\infty )$, $p\in {\varvec{W}}_2^{l,l/2}(D_\infty )$, $\nabla p\in {\varvec{W}}_2^{l,l/2}(D_\infty )$, $r(\cdot ,t)\in W_2^{2+l}({\mathcal {G}})$ for any $t\in (0,\infty )$. This solution is subjected to the inequality

$$\begin{aligned}&\Vert \mathrm{e}^{\beta t}{\varvec{w}}\Vert _{{\varvec{W}}_2^{2+l,1+\frac{l}{2}} (D_\infty )}+\Vert \mathrm{e}^{\beta t}\nabla p\Vert _{{\varvec{W}}_2^{l,\frac{l}{2}} (D_\infty )}+\Vert \mathrm{e}^{\beta t}p\Vert _{W_2^{l,\frac{l}{2}}(D_\infty )} +\Vert \mathrm{e}^{\beta t} r\Vert ^2_{W_2^{\frac{5}{2}+l,\frac{5}{4} +\frac{l}{2}}(G_\infty )}\nonumber \\&\qquad \quad +\Vert \mathrm{e}^{\beta t}{\mathcal {D}}_t r\Vert _{W_2^{\frac{3}{2}+l,\frac{3}{4}+\frac{l}{2}}(G_\infty )} \leqslant c\big \{\Vert {\varvec{w}}_0\Vert _{{\varvec{W}}_2^{1+l}({\mathcal {F}})} +\Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}})}\big \} \end{aligned}$$

(2.21)

with certain $\beta >0$ and the constant c independent of T.

For obtaining bounds for higher order norms of the solution similar to (2.17), we invoke a local-in-time estimate of the solution.

Proposition 2.4

Let $T>2$. The solution of problem (2.2), (2.3), (2.4) is subject to the inequality

$$\begin{aligned}&\Vert \mathbf{{w}}\Vert _{\mathbf{{W}}_2^{2+l,1+\frac{l}{2}}(D_{t_0-1,t_0})} +\Vert \nabla p\Vert _{\mathbf{{W}}_2^{l,\frac{l}{2}}(D_{t_0-1,t_0})} +\Vert p\Vert _{W_2^{l,\frac{l}{2}}(D_{t_0-1,t_0})} \nonumber \\ {}&\qquad + \Vert r\Vert _{W_2^{\frac{5}{2}+l,\frac{5}{4} +\frac{l}{2}}(G_{t_0-1,t_0})}+ \Vert {\mathcal {D}}_t r\Vert _{W_2^{\frac{3}{2}+l,\frac{3}{4}+\frac{l}{2}} (G_{t_0-1,t_0})} \nonumber \\ {}&\qquad \qquad \qquad \qquad \quad \leqslant c\big \{\Vert \mathbf{{w}}\Vert _{Q_{t_0-2,t_0}} +\Vert r\Vert _{G_{t_0-2,t_0}}\big \}, \end{aligned}$$

(2.22)

where $2<t_0\leqslant T$, $D _{t_1,t_2}={\mathcal {F}} \times (t_1,t_2)$, $Q_{t_1,t_2}=\Omega \times (t_1,t_2)$, $\Omega =\overline{{\mathcal {F}}^+}\cup {\mathcal {F}}^-$, $G_{t_1,t_2}= {\mathcal {G}}\times (t_1,t_2)$.

Proof

We fix $t_0\in (2,T)$ and multiply (2.2) by the cutoff function $\zeta _\lambda (t)$, smooth, monotone, equal to zero for $t\leqslant t_0-2+\lambda /2$ and to one for $t\geqslant t_0-2+\lambda$, where $\lambda \in (0,1]$, and such that for $\dot{\zeta }_\lambda (t) \equiv \frac{\mathrm{d}\zeta _\lambda (t)}{\mathrm{d}t}$ and $\ddot{\zeta }_\lambda (t)$, the inequalities

$$\begin{aligned} \sup _{t\in {\mathbb {R}}}\big | \dot{\zeta }_\lambda (t) \big |\leqslant c\lambda ^{-1}, \quad \sup _{t\in {\mathbb {R}}} {|\ddot{\zeta }_\lambda (t)|} \leqslant c\lambda ^{-2} \end{aligned}$$

hold.

Then for ${\varvec{w}}_\lambda ={\varvec{w}}\zeta _\lambda$, $p_\lambda =p\zeta _\lambda$, $r_\lambda =r\zeta _\lambda ,$ we obtain

$$\begin{aligned}&\rho ^\pm \big ({\mathcal {D}}_t{\mathbf{{w}}_\lambda } +2\omega \nabla \cdot (\mathbf{{e}}_3\times \mathbf{{w}}_\lambda )\big ) -\mu ^\pm \nabla ^{2}{\mathbf{{w}}_\lambda }+ \nabla p_\lambda =\rho ^\pm \mathbf{{w}}\dot{\zeta }_\lambda ,\nonumber \\ {}&\qquad \qquad \qquad \nabla \cdot {\mathbf{{w}}_\lambda }=0\,\,\, \text{ in } \,\,\,{\mathcal {F}}^\pm ,\;\;t>0, \nonumber \\ {}&\mathbf{{w}}_\lambda (y,0)=0\,\,\, \text{ in }\,\,\,{\mathcal {F}}, \quad r_\lambda (y,0)=0\,\,\, \text{ on }\,\,\,{\mathcal {G}},\nonumber \\ {}&[\mathbf{{w}}_\lambda ]|_{{\mathcal {G}}^+}=0,\quad [\mu ^\pm \Pi _{\mathcal {G}}{\mathbb {S}}({\mathbf{{w}}_\lambda }){\mathbf{{N}}}] \big |_{{\mathcal {G}}^+}=0,\nonumber \\ {}&[\mathbf{{N}}\cdot {\mathbb {T}}(\mathbf{{w}}_\lambda ,p_\lambda )\mathbf{{N}}] \big |_{{\mathcal {G}}^+}+\sigma ^+{{\mathcal {B}}}_0 r_\lambda |_{{\mathcal {G}}^+}=0,\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}({\mathbf{{w}}_\lambda }){\mathbf{{N}}} \big |_{{\mathcal {G}}^-}=0,\qquad \mathbf{{N}}\cdot {\mathbb {T}} (\mathbf{{w}}_\lambda ,p_\lambda )\mathbf{{N}} \big |_{{\mathcal {G}}^-} +\sigma ^-{{\mathcal {B}}}_0r_\lambda |_{{\mathcal {G}}^-}=0,\nonumber \\ {}&{\mathcal {D}}_t r_\lambda - \mathbf{{w}}_\lambda \cdot \mathbf{{N}}=r\dot{\zeta }_\lambda (t) \,\,\, \text{ on }\,\,\,{\mathcal {G}}. \end{aligned}$$

(2.23)

By Theorem 2.1 applied to system (2.23), (2.3), (2.4), estimate (2.11) for ${\varvec{w}}_{\lambda },$ $p_{\lambda }$, $r_{\lambda }$ is valid whence it follows that

$$\begin{aligned} \Psi (\lambda )&\equiv \Vert {\varvec{w}}\Vert _{{\varvec{W}}_2^{2+l,1+l/2} (D_{t_1+\lambda ,t_0})}+\Vert \nabla p\Vert _{{\varvec{W}}_2^{l,l/2}(D_{t_1+\lambda ,t_0})} +\Vert p \Vert _{W_2^{l,l/2}(D_{t_1+\lambda ,t_0})}\nonumber \\&\quad + \Vert r \Vert _{W_2^{5/2+l,5/4+l/2}(G_{t_1+\lambda ,t_0})} +\Vert {\mathcal {D}}_t r \Vert _{W_2^{3/2+l,3/4+l/2}(G_{t_1+\lambda ,t_0})}\nonumber \\&\leqslant c\lambda ^{-2}\Big \{\Vert {\varvec{w}}\Vert _{{\varvec{W}}_2^{l,l/2} (D_{t_1+\lambda /2,t_0})}+\Vert r\Vert _{W_2^{3/2+l,3/4+l/2} (G_{t_1+\lambda /2,t_0})}\Big \}, \end{aligned}$$

(2.24)

where $t_1=t_0-2$.

Now, we apply interpolation inequalities

$$\begin{aligned}&\Vert {\varvec{w}}\Vert _{{\varvec{W}}_2^{l,l/2}(D_{t_1+\lambda /2,t_0})} \leqslant \varkappa ^2\Vert {\varvec{w}}\Vert _{{\varvec{W}}_2^{2+l,1+l/2} (D_{t_1+\lambda /2,t_0})}+c\varkappa ^{-l}\Vert {\varvec{w}} \Vert _{Q_{t_1+\lambda /2,t_0}},\\&\Vert r\Vert _{W_2^{3/2+l,0}(G_{t_1+\lambda /2})} \leqslant \varkappa ^2\Vert r\Vert _{W_2^{5/2+l,0}(G_{t_1+\lambda /2,t_0})} +c\varkappa ^{-3-2l}\Vert r\Vert _{G_{t_1+\lambda /2,t_0}},\\&\Vert r\Vert _{W_2^{0,3/4+l/2}(G_{t_1+\lambda /2})}\leqslant \varkappa ^2\Vert {\mathcal {D}}_t r\Vert _{W_2^{0,3/4+l/2}(G_{t_1+\lambda /2,t_0})} +c\varkappa ^{-3/2-l}\Vert r\Vert _{G_{t_1+\lambda /2,t_0}} \end{aligned}$$

with $\varkappa >0$ which leads to

$$\begin{aligned} \Psi (\lambda )\leqslant c_1\varkappa ^2\lambda ^{-2}\Psi (\lambda /2) +c_2\varkappa ^{-m}\lambda ^{-2}K. \end{aligned}$$

Here $\Psi (\lambda )$ denotes the left-hand side in (2.24), $K=\Vert {\varvec{w}}\Vert _{Q_{t_1,t_0}}+\Vert r\Vert _{G_{t_1,t_0}}$, $m=3+2l$. Setting $\varkappa =\delta \lambda \leqslant 1$, we obtain

$$\begin{aligned} \lambda ^{m+2}\Psi (\lambda )\leqslant c_1\delta ^2 2^{m+2}(\lambda /2)^{m+2} \Psi (\lambda /2)+c_2\delta ^{-m}K. \end{aligned}$$

This implies

$$\begin{aligned} \Psi (\lambda )\leqslant c_3(\delta )\lambda ^{-m-2}(K+2^{-1} K+2^{-2} K+\cdots ) \leqslant \frac{ c_3\lambda ^{-m-2}}{1-1/2}K\leqslant 2c_3\lambda ^{-m-2}K \end{aligned}$$

if $c_1\delta ^22^{m+2}<1/2.$ For $\lambda =1$ this inequality is equivalent to (2.22). $\square$

Proof of Theorem 2.2

By Theorem 2.1 and Proposition 2.4, one has

$$\begin{aligned}&e^{2\beta (T-j)}\Big \{ \Vert {\varvec{w}}\Vert ^2_{{\varvec{W}}_2^{2+l,1+l/2} (D_{T-j-1,T-j})}+\Vert \nabla p\Vert ^2_{{\varvec{W}}_2^{l,l/2}(D_{T-j-1,T-j})} \nonumber \\&\qquad +\Vert p\Vert ^2_{W_2^{l,l/2}(D_{T-j-1,T-j})} + \Vert r\Vert ^2_{W_2^{5/2+l,5/4+l/2} (G_{T-j-1,T-j} )} \nonumber \\&\qquad +\Vert {\mathcal {D}}_t r\Vert ^2_{W_2^{3/2+l,3/4+l/2} (G_{T-j-1,T-j} )}\Big \}\nonumber \\&\quad \leqslant ce^{2\beta (T-j)} \Big \{\Vert {\varvec{w}}\Vert ^2_{Q_{T-j-2,T-j}}+\Vert r\Vert ^2_{G_{T-j-2,T-j}}\Big \}, \quad j=0,1,\ldots ,[T]-2. \end{aligned}$$

(2.25)

Taking the sum of (2.25) from $j=0$ to $j=[T]-2$, we obtain the inequality which implies

$$\begin{aligned} Y^2_{T-[T]+1,T}(e^{\beta t}{\varvec{w}},e^{\beta t}p,e^{\beta t}r) \leqslant c\int _{T-[T]}^Te^{2\beta t}\Big (\Vert {\varvec{w}}(\cdot ,t)\Vert ^2_\Omega +\Vert r(\cdot ,t)\Vert ^2_{{\mathcal {G}}}\Big )\,\mathrm{d}t, \end{aligned}$$

(2.26)

where

$$\begin{aligned} Y_{t_1,t_2}({\varvec{u}},q,\rho )&=\Vert {\varvec{u}}\Vert _{{\varvec{W}}_2^{2+l,1+l/2} (D_{t_1,t_2})}+\Vert \nabla q\Vert _{{\varvec{W}}_2^{l,l/2}(D_{t_1,t_2})} +\Vert q\Vert _{W_2^{l,l/2}(D_{t_1,t_2})}\nonumber \\&\quad +\Vert \rho \Vert _{W_2^{5/2+l,5/4+l/2}(G_{t_1,t_2})}+\Vert {\mathcal {D}}_t \rho \Vert _{W_2^{3/2+l,3/4+l/2}(G_{t_1,t_2})}. \end{aligned}$$

By adding the estimate

$$\begin{aligned} Y^2_{0,2}({\varvec{w}},p,r)\leqslant c\Big \{\Vert {\varvec{w}}_0\Vert ^2_{{\varvec{W}}_2^{1+l} ({\mathcal {F}})}+ \Vert r_0\Vert ^2_{W_2^{2+l}({\mathcal {G}})}\Big \} \end{aligned}$$

to (2.26), choosing $\beta <\beta _1$ and making use of (2.17), we arrive at an inequality equivalent to (2.21). $\square$

3 The Nonlinear Problem

After transformation (1.11), problem (1.8), (1.12) can be written in the form [13]:

$$\begin{aligned}&\bar{\rho }\big ({\mathcal {D}}_t\mathbf{{u}}+2\omega (\mathbf{{e}}_3\times \mathbf{{u}})\big ) -\bar{\mu }\nabla ^2\mathbf{{u}} +\nabla q=\mathbf{{l}}_1(\mathbf{{u}},q,r),\nonumber \\ {}&\qquad \qquad \qquad \nabla \cdot \mathbf{{u}}=l_2(\mathbf{{u}},r)\equiv \nabla \cdot \mathbf{{L}} (\mathbf{{u}},r) \quad \quad \text{ in } {\mathcal {F}},\,\,\,t>0,\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}})\mathbf{{N}}=\mathbf{{l}}_3^-(\mathbf{{u}},r) \quad \text{ on } {\mathcal {G}}^-,\nonumber \\ {}&[\bar{\mu } \Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}})\mathbf{{N}}] \big |_{{\mathcal {G}}^+}=\mathbf{{l}}_3^+(\mathbf{{u}},r)\quad \text{ on } {\mathcal {G}}^+,\nonumber \\ {}&-q+\mu ^-\mathbf{{N}}\cdot {\mathbb {S}}(\mathbf{{u}})\mathbf{{N}}+{\mathcal {B}}^-_0 r =l_4^-(\mathbf{{u}},r) +l_5^-(r)\quad \text{ on } {\mathcal {G}}^-,\nonumber \\ {}&[\mathbf{{u}}]\big |_{{\mathcal {G}}^+}=0,\quad [-q+\bar{\mu }{} \mathbf{{N}} \cdot {\mathbb {S}}(\mathbf{{u}})\mathbf{{N}}]\big |_{{\mathcal {G}}^+} +{\mathcal {B}}^+_0r =l_4^+(\mathbf{{u}},r) +l_5^+(r)\quad \text{ on } {\mathcal {G}}^+,\nonumber \\ {}&{\mathcal {D}}_tr-\mathbf{{u}}\cdot \mathbf{{N}}=l_6(\mathbf{{u}},r) \quad \text{ on } {\mathcal {G}},\nonumber \\ {}&\mathbf{{u}}\big |_{t=0}=\mathbf{{u}}_0 \quad \text{ in } {\mathcal {F}}, \quad r\big |_{t=0}=r_0\quad \text{ on } {\mathcal {G}}, \end{aligned}$$

(3.1)

where ${\varvec{u}}(z,t)=\tilde{{\varvec{v}}}\big (e_r(z,t),t\big )$, ${\varvec{u}}_0(z)=\tilde{{\varvec{v}}}\big ( e_{r_0}(z,0),0\big )$, $q(z,t)=\tilde{p}\big (e_r(z,t),t\big )$,

$$\begin{aligned} \mathbf{{l}}_1(\mathbf{{u}},q,r)&=\bar{\mu }(\tilde{\nabla }^2-\nabla ^2) \mathbf{{u}}+(\nabla -\tilde{\nabla })q+\bar{\rho } {\mathcal {D}}_tr^* ({\mathcal {L}}^{-1}{} \mathbf{{N}}^*\cdot \nabla )\mathbf{{u}}\nonumber \\ {}&\qquad \qquad -\bar{\rho } ({\mathcal {L}}^{-1}{} \mathbf{{u}}\cdot \nabla )\mathbf{{u}},\nonumber \\l_2(\mathbf{{u}},r)&=({\mathcal {I}}-\widehat{\mathcal {L}}^T)\nabla \cdot \mathbf{{u}} =\nabla \cdot \mathbf{{L}}(\mathbf{{u}},r),\quad \mathbf{{L}}(\mathbf{{u}},r) =({\mathcal {I}}-\widehat{\mathcal {L}})\mathbf{{u}},\nonumber \\\mathbf{{l}}_3^-(\mathbf{{u}},r)&=\mu ^-\Pi _{\mathcal {G}}\big (\Pi _{\mathcal {G}} {\mathbb {S}}(\mathbf{{u}})\mathbf{{N}}-\tilde{\Pi }\widetilde{{\mathbb {S}}} (\mathbf{{u}})\tilde{\mathbf{{n}}}(e_r)\big ),\nonumber \\\mathbf{{l}}_3^+(\mathbf{{u}},r)&=\big [\bar{\mu }\Pi _{\mathcal {G}} \big (\Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}})\mathbf{{N}} -\tilde{\Pi }\widetilde{{\mathbb {S}}}(\mathbf{{u}}) \tilde{\mathbf{{n}}}(e_r)\big )\big ]\big |_{{\mathcal {G}}^+},\nonumber \\l_4^-(\mathbf{{u}},r)&=\mu ^-\big (\mathbf{{N}}\cdot {\mathbb {S}} (\mathbf{{u}})\mathbf{{N}}-\tilde{\mathbf{{n}}}(e_r)\cdot \widetilde{{\mathbb {S}}} (\mathbf{{u}})\tilde{\mathbf{{n}}}(e_r)\big ),\nonumber \\l_4^+(\mathbf{{u}},r)&=\big [\bar{\mu }\big (\mathbf{{N}} \cdot {\mathbb {S}}(\mathbf{{u}})\mathbf{{N}}-\tilde{\mathbf{{n}}}(e_r) \cdot \widetilde{{\mathbb {S}}}(\mathbf{{u}})\tilde{\mathbf{{n}}}(e_r)\big )\big ] \big |_{{\mathcal {G}}^+},\nonumber \\l_5^-(r)&= \sigma ^-\int _0^1(1-s)\frac{\,\mathrm {d}^2}{\,\mathrm {d}s^2} \Big ({\mathcal {L}}^{-T}(z,sr )\nabla _{\mathcal {G}} \cdot \frac{\widehat{\mathcal {L}}^T(z,sr)\mathbf{{N}}}{|\widehat{\mathcal {L}}^T(z,sr)\mathbf{{N}}|}\Big )\,\mathrm {d}s +\frac{\omega ^2}{2}\rho ^-| \mathbf{{N}}'|^2 r^2,\nonumber \\l_5^+(r)&= \sigma ^+\int _0^1(1-s)\frac{\,\mathrm {d}^2}{\,\mathrm {d}s^2} \Big ({\mathcal {L}}^{-T}(z,sr)\nabla _{\mathcal {G}} \cdot \frac{\widehat{\mathcal {L}}^T(z,sr)\mathbf{{N}}}{|\widehat{\mathcal {L}}^T(z,sr)\mathbf{{N}}|}\Big )\,\mathrm {d}s \nonumber \\ {}&\qquad \qquad +\frac{\omega ^2}{2}[\bar{\rho }]\big |_{{\mathcal {G}}^+}| \mathbf{{N}}'|^2 r^2,\nonumber \\l_6(\mathbf{{u}},r)&=\Big (\frac{\widehat{\mathcal {L}}^T\mathbf{{N}}}{\mathbf{{N}} \cdot \widehat{\mathcal {L}}^T\mathbf{{N}}}-\mathbf{{N}}\Big )\cdot \mathbf{{u}}, \end{aligned}$$

(3.2)

${\mathcal {I}}$ is the identity matrix, ${{\mathcal {L}}}$ is the Jacobi matrix of transformation (1.11):

$$\begin{aligned} {\mathcal {L}}(z,r)&=\Big \{ \delta ^i_{j}+\frac{\partial \big (r(z,t)N_i(z)\big )}{\partial z_j}\Big \}^3_{i,j=1}, \; L\equiv \text{ det }{\mathcal {L}},\quad \widehat{{\mathcal {L}}}\equiv L{\mathcal {L}}^{-1}; \\ \tilde{\mathbf{{n}}}&= \frac{\widehat{\mathcal {L}}^T(z,r) \mathbf{{N}}}{|\widehat{\mathcal {L}}^T(z,r)\mathbf{{N}}|}, \end{aligned}$$

$\tilde{\nabla }={\mathcal {L}}^{-T}\nabla$ is the transformed gradient $\nabla _x$ (“T” means transposition),

$\widetilde{{\mathbb {S}}}(\mathbf{{u}})=\tilde{\nabla }{} \mathbf{{u}} +(\tilde{\nabla }{} \mathbf{{u}})^T$ is the transformed doubled rate-of-strain tensor;

$\tilde{\Pi }{\varvec{b}}={\varvec{b}}-\tilde{{\varvec{n}}} \cdot {\varvec{b}}\tilde{{\varvec{n}}}$ is the projection of a vector ${\varvec{b}}$ on the tangent plane to $\tilde{\Gamma }_t$, $\nabla _{\mathcal {G}}=\Pi _{\mathcal {G}}\nabla$.

The conditions (1.9), (1.10) can be expressed in terms of r as follows (see [16])

$$\begin{aligned}&\int _{{\mathcal {G}}^\pm }\varphi ^\pm (z,r)\,\mathrm{d}{\mathcal {G}}=0, \qquad \rho ^-\int _{{\mathcal {G}}^-}{\varvec{\psi }} ^-(z,r)\,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} {\varvec{\psi }} ^+(z,r)\,\mathrm{d}{\mathcal {G}}=0, \nonumber \\&\int _{\mathcal {F}}\bar{\rho }{\varvec{u}}(z,t)L(z,r)\,\mathrm{d}z=0,\nonumber \\&\int _{\mathcal {F}}\bar{\rho }{\varvec{u}}(z,t)\cdot {\varvec{\eta }}_j(e_r)L(z,r)\,\mathrm{d}z + \omega \int _{\mathcal {F}}\bar{\rho }{\varvec{\eta }}_3(e_r)\cdot {\varvec{\eta }}_j (e_r)L(z,r)\,\mathrm{d}z\nonumber \\&\qquad =\int _{\mathcal {F}}\bar{\rho }{\varvec{\eta }}_3(z)\cdot {\varvec{\eta }}_j (z)\,\mathrm{d}z,\quad j=1,2,3, \end{aligned}$$

(3.3)

where

$$\begin{aligned} \varphi ^\pm (z,r)&=r-\frac{r^2}{2}{\mathcal {H}}^\pm (z) +\frac{r^3}{3}{\mathcal {K}}^\pm (z),\\ {\varvec{\psi }}^\pm (z,r)&=\varphi ^\pm (z,r){\varvec{z}} +{\varvec{N}}(z)\Big (\frac{r^2}{2} -\frac{r^3}{3}{\mathcal {H}}^\pm (z)+\frac{r^4}{4}{\mathcal {K}}^\pm (z)\Big ). \end{aligned}$$

Proposition 3.1

For arbitrary numbers $l^\pm$, vectors ${{\varvec{l}}},{{\varvec{m}}},{{\varvec{M}}}=(M_1,M_2,M_3)$, a function $f_0\in W_2^{l}({\mathcal {F}})$ and a vector field ${{\varvec{b}}}_0\in W_2^{l+1/2}({ {\mathcal {G}}})$, there exist $r\in W_2^{2+l}({ {\mathcal {G}}})$ and ${{\varvec{u}}}\in {\varvec{W}}_2^{1+l}({\mathcal {F}})$ satisfying the conditions

$$\begin{aligned}&\int _{{\mathcal {G}}^-}r(z)\,\mathrm {d}{\mathcal {G}}=l^-,\quad \int _{{\mathcal {G}}^+}r(z)\,\mathrm {d}{\mathcal {G}}=l^+,\nonumber \\ {}&\rho ^-\int _{{\mathcal {G}}^-}r(z)\mathbf{{z}} \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} r(z)\mathbf{{z}} \,\mathrm {d}{\mathcal {G}}=\mathbf{{l}},\nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho }{\mathbf{{u}}}(z)\,\mathrm {d}z={\mathbf{{m}}},\nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho }{\mathbf{{u}}}(z)\cdot {\mathbf{{\eta }}}_j(z)\,\mathrm {d}z +\omega \Big (\rho ^-\int _{{\mathcal {G}}^-}r(z){\mathbf{{\eta }}}_3(z) \cdot {\mathbf{{\eta }}}_j(z)\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \qquad \qquad +[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}r(z)\mathbf{{\eta }}_3(z) \cdot \mathbf{{\eta }}_j(z)\,\mathrm {d}{\mathcal {G}}\Big )=M_j,\quad j=1,2,3,\nonumber \\ {}&\nabla \cdot {\mathbf{{u}}}=f_0 \quad \text{ in } {\mathcal {F}}, \quad \mathbf{{b}}_0\cdot \mathbf{{n}}_0=0\quad \text{ on } \,\,{\mathcal {G}}^\pm ,\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}({\mathbf{{u}}}){\mathbf{{N}}} ={\mathbf{{b}}}_0 \quad \text{ on } {\mathcal {G}}^-,\quad [\mathbf{{u}}]|_{{\mathcal {G}}^+}=0, \quad [\bar{\mu }\Pi _{\mathcal {G}}{\mathbb {S}} ({\mathbf{{u}}})\mathbf{{N}}]|_{{\mathcal {G}}^+}=\mathbf{{b}}_0 \quad \text{ on } {\mathcal {G}}^+, \end{aligned}$$

(3.4)

and the inequality

$$\begin{aligned}&\Vert r\Vert _{W_2^{2+l}({\mathcal {G}})}+ \Vert {{\varvec{u}}} \Vert _{W_2^{1+l}({\mathcal {F}})} \\&\quad \leqslant c\Big ( |l^+|+ |l^-|+|{\varvec{l}}|+ |{{\varvec{m}}}|+|{{\varvec{M}}}| +\Vert f_0\Vert _{W_2^{l}( {\mathcal {F}} )}+ \Vert {\varvec{b}}_0 \Vert _{W_2^{l+1/2}({\mathcal {G}})} \Big ). \end{aligned}$$

Proof

We set

$$\begin{aligned}&r(z)=\frac{l^-{\varvec{N}}(z)\cdot {\varvec{z}}}{3|{\mathcal {F}}|} +\frac{C^-}{|{\mathcal {F}}|}{\varvec{l}}\cdot {\varvec{N}}(z), \quad z\in {\mathcal {G}}^-,\nonumber \\&r(z)=\frac{l^+{\varvec{N}}(z)\cdot {\varvec{z}}}{3|{\mathcal {F}}^+|} +\frac{C^+}{|{\mathcal {F}}^+|}{\varvec{l}}\cdot {\varvec{N}}(z), \quad z\in {\mathcal {G}}^+. \end{aligned}$$

(3.5)

For these functions, relations (3.4) hold if $\rho ^- C^-+[\bar{\rho }]|_{{\mathcal {G}}^+}C^+=1;$ we put

$$\begin{aligned} C^-=\frac{\rho ^-}{{\rho ^-}^2+[\bar{\rho }]|_{{\mathcal {G}}^+}^2}, \quad C^+=\frac{[\bar{\rho }]|_{{\mathcal {G}}^+}}{{\rho ^-}^2 +[\bar{\rho }]|_{{\mathcal {G}}^+}^2}. \end{aligned}$$

Next, we construct ${\varvec{u}}_1$ satisfying the equations

$$\begin{aligned}&\nabla \cdot {\varvec{u}}_1=f_0 \quad \text {in } {\mathcal {F}},\nonumber \\&[{\varvec{u}}_1]|_{{\mathcal {G}}^+}=0, \qquad {\varvec{u}}_1\cdot {\varvec{N}} =f_1\quad \text {on }{\mathcal {G}}, \end{aligned}$$

(3.6)

where

$$\begin{aligned}&f_1(z)=\frac{{\varvec{N}}(z)\cdot {\varvec{z}} }{3|{\mathcal {F}}|} \int _{\mathcal {F}}f_0(z)\,\mathrm{d}z+\frac{1}{|{\mathcal {F}}|} {\varvec{K}}^-\cdot {\varvec{N}}(z),\quad z\in {\mathcal {G}}^-,\\&f_1(z)=\frac{{\varvec{N}}(z)\cdot {\varvec{z}}}{3|{\mathcal {F}}^+|} \int _{{\mathcal {F}}^+}f_0(z)\,\mathrm{d}z+\frac{1}{|{\mathcal {F}}^+|} {\varvec{K}}^+\cdot {\varvec{N}}(z),\quad z\in {\mathcal {G}}^+ \end{aligned}$$

with some vectors ${\varvec{K}}^\pm$ defined below. Since

$$\begin{aligned} \int _{{\mathcal {G}}^-}f_1(z)\,\mathrm{d}{\mathcal {G}}=\int _{\mathcal {F}} f_0(z)\,\mathrm{d}z,\quad \int _{{\mathcal {G}}^+}f_1(z)\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {F}}^+}f_0(z)\,\mathrm{d}z, \end{aligned}$$

the necessary compatibility conditions

$$\begin{aligned} \int _{{\mathcal {F}}^-}f_0(z)\,\mathrm {d}z=\int _{{\mathcal {G}}^-} f_1(z)\,\mathrm {d}{\mathcal {G}}-\int _{{\mathcal {G}}^+}f_1(z)\,\mathrm {d}{\mathcal {G}},\quad \quad \int _{{\mathcal {G}}^+}f_1(z)\,\mathrm {d}{\mathcal {G}}=\int _{{\mathcal {F}}^+}f_0(z)\,\mathrm {d}z \end{aligned}$$

hold and there exists ${\varvec{u}}_1$ satisfying (3.6) and the inequality

$$\begin{aligned} \Vert {\varvec{u}}_1\Vert _{W_2^{1+l}({\mathcal {F}})} \leqslant c \big (\Vert f_0\Vert _{W_2^l({\mathcal {F}})}+\Vert f_1\Vert _{W_2^{l+1/2} ({\mathcal {G}})}\big ). \end{aligned}$$

From the relations

$$\begin{aligned}&\int _{\mathcal {F}}\bar{\rho }(\nabla \cdot \mathbf{{u}}_1) \mathbf{{z}} \,\mathrm {d}z=-\!\int _{\mathcal {F}}\!\bar{\rho } \mathbf{{u}}_{1}\,\mathrm {d}z+\rho ^-\! \int _{{\mathcal {G}}^-}\!(\mathbf{{u}}_1\cdot \mathbf{{N}})\mathbf{{z}}\,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\!\int _{{\mathcal {G}}^+}\! (\mathbf{{u}}_1\cdot \mathbf{{N}} )\mathbf{{z}} \,\mathrm {d}{\mathcal {G}},\\ {}&\int _{{\mathcal {G}}^-}f_1 \mathbf{{z}} \,\mathrm {d}{\mathcal {G}}=\mathbf{{K}}^-, \quad \int _{{\mathcal {G}}^+}f_1 \mathbf{{z}} \,\mathrm {d}{\mathcal {G}}=\mathbf{{K}}^+, \end{aligned}$$

we can conclude that

$$\begin{aligned} \int _{\mathcal {F}}\bar{\rho } {\varvec{u}}_1 \,\mathrm{d}z =-\int _{\mathcal {F}}\bar{\rho } f_0 {\varvec{z}} \,\mathrm{d}z +\rho ^-{\varvec{K}}^- +[\bar{\rho }]|_{{\mathcal {G}}^+}{\varvec{K}}^+={\varvec{m}} \end{aligned}$$

if

$$\begin{aligned} \mathbf{{K}}^-&=\frac{\rho ^-}{{\rho ^-}^2+[\bar{\rho }]|_{{\mathcal {G}}^+}^2} \big (\mathbf{{m}} +\int _{\mathcal {F}}\bar{\rho } f_0 \mathbf{{z}} \,\mathrm {d}z\big ), \\ \mathbf{{K}}^+&=\frac{[\bar{\rho }]|_{{\mathcal {G}}^+}}{{\rho ^-}^2 +[\bar{\rho }]|_{{\mathcal {G}}^+}^2}\big (\mathbf{{m}} +\int _{\mathcal {F}} \bar{\rho } f_0 \mathbf{{z}} \,\mathrm {d}z\big ); \end{aligned}$$

hence,

$$\begin{aligned} \Vert {\varvec{u}}_1\Vert _{W_2^{1+l}({\mathcal {F}})}\leqslant c \big (\Vert f_0\Vert _{W_2^l({\mathcal {F}})}+|{\varvec{m}}|\big ). \end{aligned}$$

Now we find a vector field ${\varvec{u}}_2$ satisfying the relations

$$\begin{aligned}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}({\varvec{u}}_2){\varvec{N}}={\varvec{b}}_0(z) -\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}({\varvec{u}}_1){\varvec{N}}\equiv {\varvec{b}}'(z), \quad z\in {\mathcal {G}}^-,\\&[\bar{\mu } \Pi _{\mathcal {G}}{\mathbb {S}}({\varvec{u}}_2) {\varvec{N}}]|_{{\mathcal {G}}^+}={\varvec{b}}_0(z)-[\bar{\mu } \Pi _{\mathcal {G}}{\mathbb {S}}({\varvec{u}}_1){\varvec{N}}]|_{{\mathcal {G}}^+} \equiv {\varvec{b}}'(z),\quad z\in {\mathcal {G}}^+, \end{aligned}$$

Following [13], we set ${\varvec{u}}_2=$rot$\mathbf{{\Phi }}(z)$, where ${\varvec{\Phi }}\in W_2^{2+l}({\mathcal {F}} )$,

$$\begin{aligned}&{\varvec{\Phi }}(z)=\frac{\partial {\varvec{\Phi }}(z)}{\partial {\varvec{N}}}=0, \quad \frac{\partial ^2{\varvec{\Phi }}(z)}{\partial {\varvec{N}}^2}={\varvec{b}}'(z) \times {\varvec{N}},\quad z\in {\mathcal {G}}^-,\\&{\varvec{\Phi }}(z)=\frac{\partial {\varvec{\Phi }}(z)}{\partial {\varvec{N}}}=0, \quad \Big [\bar{\mu } \frac{\partial ^2{\varvec{\Phi }}(z)}{\partial {\varvec{N}}^2}\Big ] \Big |_{{\mathcal {G}}^+}={\varvec{b}}'(z)\times {\varvec{N}}, \quad z\in {\mathcal {G}}^+, \end{aligned}$$

and we require that

$$\begin{aligned} \Vert {\varvec{\Phi }}\Vert _{W_2^{2+l}({\mathcal {F}}^\pm )} \leqslant c \Vert {\varvec{b}}'\Vert _{W_2^{l+1/2}({\mathcal {G}}^\pm )}. \end{aligned}$$

Finally, we define

$$\begin{aligned} {\varvec{u}}_3(z)=\sum _{k=1}^3\widehat{M}_k\mathrm{rot}{\varvec{e}}_iA(z), \end{aligned}$$

where $A\in C_0^\infty ({\mathcal {F}}^-)$, $\rho ^-\int _{{\mathcal {F}}^-}A(z)\,\mathrm{d}z=\frac{1}{2}$ and

$$\begin{aligned} \widehat{M}_k&=M_k-\int _{\mathcal {F}}\bar{\rho }({\varvec{u}}_1(z)+{\varvec{u}}_2(z)) \cdot {\varvec{\eta }}_k(z)\,\mathrm{d}z \\&\quad -\omega \Big (\rho ^-\int _{{\mathcal {G}}^-}r {\varvec{\eta }}_3\cdot {\varvec{\eta }}_k \,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^-}r {\varvec{\eta }}_3\cdot {\varvec{\eta }}_k \,\mathrm{d}{\mathcal {G}}\Big ). \end{aligned}$$

We have $\int _{\mathcal {F}}\bar{\rho }{\varvec{u}}_3(z) \cdot {\varvec{\eta }}_j(z)\,\mathrm{d}z=\widehat{M}_j$ and

$$\begin{aligned} \Vert {\varvec{u}}_3\Vert _{W_2^{1+l}({\mathcal {F}})}\leqslant c|\widehat{{\varvec{M}}}|. \end{aligned}$$

It is easily seen that the function r defined in (3.5) and the vector ${\varvec{u}}={\varvec{u}}_1+{\varvec{u}}_2+{\varvec{u}}_3$ satisfy all the necessary requirements. The proposition is proved. $\square$

The main result of the paper is as follows.

Theorem 3.1

(Global Solvability of the Nonlinear Problem). Let ${\varvec{u}}_0 \in W_2^{1+l}({\mathcal {F}})$, $r_0\in W_2^{2+l}( {\mathcal {G}})$, $l\in (1/2,1)$. We assume that smallness and compatibility conditions

$$\begin{aligned}&\qquad \Vert \mathbf{{u}}_0\Vert _{W_2^{1+l}({\mathcal {F}})}+\Vert r_0\Vert _{W_2^{2+l} ({\mathcal {G}})} \leqslant \varepsilon \ll 1,\\&\nabla \cdot \mathbf{{u}}_0=l_2(\mathbf{{u}}_0,r_0) \quad \text{ in } {\mathcal {F}},\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}}_0)\mathbf{{N}} =\mathbf{{l}}_3^-(\mathbf{{u}}_0,r_0) \quad \text{ on } {\mathcal {G}}^-,\nonumber \\ {}&[\mathbf{{u}}_0]\big |_{{\mathcal {G}}^+}=0,\quad [\bar{\mu } \Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}}_0)\mathbf{{N}}] \big |_{{\mathcal {G}}^+}=\mathbf{{l}}_3^+(\mathbf{{u}}_0,r_0) \quad \text{ on } {\mathcal {G}}^+ \nonumber \end{aligned}$$

(3.7)

are satisfied, as well as restrictions (3.3) at $t=0$ and inequality (2.16) hold.

Then problem (3.1) has a unique solution defined in the infinite time interval $t>0$ and

$$\begin{aligned}&\Vert \mathrm {e}^{\alpha t}{} \mathbf{{u}}\Vert _{W_2^{2+l,1+l/2}(D_\infty )} +\Vert \mathrm {e}^{\alpha t}\nabla q\Vert _{W_2^{l,l/2}(D_\infty )} +\Vert \mathrm {e}^{\alpha t}q\Vert _{W_2^{l/2}\big (0,\infty ;W_2^{1/2} ({\mathcal {G}})\big )}\nonumber \\ {}&+\Vert \mathrm {e}^{\alpha t}q\Vert _{W_2^{l,l/2}(D_\infty )} +\Vert \mathrm {e}^{\alpha t}r\Vert _{W_2^{5/2+l,5/4+l/2}(G_\infty )} +\Vert \mathrm {e}^{\alpha t}{\mathcal {D}}_tr\Vert ^2_{W_2^{3/2+l,3/4+l/2}(G_\infty )} \nonumber \\ {}&\qquad \qquad \qquad \leqslant c \Big (\Vert \mathbf{{u}}_0\Vert _{W_2^{1+l}({\mathcal {F}})} +\Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}})}\Big ) \end{aligned}$$

(3.8)

with certain $\alpha >0$.

Proof

We outline the main ideas of the proof.

A solution to (3.1) is sought in the form of the sum

$$\begin{aligned} {\varvec{u}}={\varvec{u}}'+{\varvec{u}}'',\quad q=q'+q'',\quad r=r'+r''. \end{aligned}$$

We write conditions (3.3) in the form

$$\begin{aligned}&\int _{{\mathcal {G}}^\pm }r \,\mathrm {d}{\mathcal {G}}=\int _{{\mathcal {G}}^\pm } \big (r-\varphi ^\pm (z,r )\big )\,\mathrm {d}{\mathcal {G}}, \; \text{ on } {\mathcal {G}}^\pm ,\nonumber \\ {}&\rho ^-\int _{{\mathcal {G}}^-}r\mathbf{{z}} \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}r\mathbf{{z}} \,\mathrm {d}{\mathcal {G}}= \rho ^-\int _{{\mathcal {G}}^-}\big (r\mathbf{{z}} -\mathbf{{\psi }} ^-(z,r)\big )\,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad +[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} \big (r\mathbf{{z}} -\mathbf{{\psi }} ^+(z,r)\big )\,\mathrm {d}{\mathcal {G}},\nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}\,\mathrm {d}z =\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}\big (1-L(z,r)\big )\,\mathrm {d}z,\nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}\cdot \mathbf{{\eta }}_j(z)\,\mathrm {d}z +\omega \Big (\rho ^-\int _{{\mathcal {G}}_i}r\mathbf{{\eta }}_3 \cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}_i} r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}\Big )\nonumber \\ {}&\quad =\omega \Big (\rho ^- \int _{{\mathcal {G}}_i}r\mathbf{{\eta }}_3 \cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}_i} r\mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}-\int _{\widetilde{\Omega }_t}\rho ^\pm \mathbf{{\eta }}_3(y) \cdot \mathbf{{\eta }}_j(y)\,\mathrm {d}y\Big )\nonumber \\ {}&\qquad +\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}\cdot \mathbf{{\eta }}_j(z) \big (1-L(z,r)\big )\,\mathrm {d}z +\int _{\mathcal {F}}\bar{\rho } \mathbf{{\eta }}_3(z)\cdot \mathbf{{\eta }}_j(z)\,\mathrm {d}z,\quad j=1,2,3, \end{aligned}$$

(3.9)

and construct the functions ${\varvec{u}}''_0, r''_0$ satisfying the relations (see Proposition 3.1)

$$\begin{aligned}&\int _{{\mathcal {G}}^\pm }r''_{0}\,\mathrm {d}{\mathcal {G}}=\int _{{\mathcal {G}}^\pm }\big (r_{0}-\varphi ^\pm (z,r_{0})\big ) \,\mathrm {d}{\mathcal {G}}, \nonumber \\ {}&\rho ^-\int _{{\mathcal {G}}^-}r_0\mathbf{{z}} \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+}{r_0}{} \mathbf{{z}} \,\mathrm {d}{\mathcal {G}}= \rho ^-\int _{{\mathcal {G}}^-}\big (r_{0}{} \mathbf{{z}} -\mathbf{{\psi }} ^-(z,r_0)\big ) \,\mathrm {d}{\mathcal {G}}\nonumber \\ {}&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} \big (r_{0}{} \mathbf{{z}} -\mathbf{{\psi }} ^+(z,r_0)\big )\,\mathrm {d}{\mathcal {G}}, \nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}''_0\,\mathrm {d}z= \int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}_0\big (1-L(z,r_0)\big )\,\mathrm {d}z,\nonumber \\ {}&\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}''_0\cdot \mathbf{{\eta }}_j(z)\,\mathrm {d}z +\omega \Big (\rho ^- \int _{{\mathcal {G}}^-}r_0''{} \mathbf{{\eta }}_3 \cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }]\big |_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+} r_0''{} \mathbf{{\eta }}_3 \cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}\Big )\nonumber \\ {}&\quad =\omega \Big (\rho ^- \int _{{\mathcal {G}}^-}r_0 \mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}+[\bar{\rho }] \big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}_i} r_0 \mathbf{{\eta }}_3\cdot \mathbf{{\eta }}_j \,\mathrm {d}{\mathcal {G}}-\int _{\widetilde{\Omega }_0} \rho ^\pm \mathbf{{\eta }}_3(y)\cdot \mathbf{{\eta }}_j(y)\,\mathrm {d}y\Big )\nonumber \\ {}&\qquad +\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{u}}_0\cdot \mathbf{{\eta }}_j(z) \big (1-L(z,r)\big )\,\mathrm {d}z+\int _{\mathcal {F}}\bar{\rho }{} \mathbf{{\eta }}_3(z) \cdot \mathbf{{\eta }}_j(z)\,\mathrm {d}z,\quad j=1,2,3,\nonumber \\ {}&\nabla \cdot \mathbf{{u}}''_0=l_2(\mathbf{{u}}_0,r_0) \quad \text{ in } {\mathcal {F}},\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}}''_0) \mathbf{{N}}\big |_{{\mathcal {G}}^-}=\mathbf{{l}}_{3}^-(\mathbf{{u}}_0,r_0), \quad [\mathbf{{u}}''_0]\big |_{{\mathcal {G}}^+}=0, \quad [\bar{\mu }\Pi _{\mathcal {G}}{\mathbb {S}} (\mathbf{{u}}_0'')\mathbf{{N}}]\big |_{{\mathcal {G}}^+} =\mathbf{{l}}_{3}^+(\mathbf{{u}}_0,r_0). \end{aligned}$$

(3.10)

Then we set ${\varvec{u}}'_0={\varvec{u}}_0-{\varvec{u}}''_0$, $r'_0=r_0-r_0''$ and define $({\varvec{u}}',q',r')$ as a solution to the problem

$$\begin{aligned}&\bar{\rho }\big ({\mathcal {D}}_t{\varvec{u}}'(z,t)+2\omega ({\varvec{e}}_3\times {\varvec{u}}')\big ) -\bar{\mu }\nabla ^2{\varvec{u}}' +\nabla q'=0, \qquad \nabla \cdot {\varvec{u}}'=0\quad \text {in }{\mathcal {F}},\nonumber \\&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}({\varvec{u}}'){\varvec{N}} \big |_{{\mathcal {G}}^-}=0,\quad -q'+\mu ^-{\varvec{N}} \cdot {\mathbb {S}}({\varvec{u}}'){\varvec{N}}+{\mathcal {B}}^-_{0}r'=0 \quad \text {on }{\mathcal {G}}^-,\nonumber \\&[{\varvec{u}}']\big |_{{\mathcal {G}}^+}=0, \quad \big [\bar{\mu } \Pi _{\mathcal {G}}{\mathbb {S}} ({\varvec{u}}'){\varvec{N}}(z)\big ]\big |_{{\mathcal {G}}^+}=0,\nonumber \\&\big [-q'+\mu ^-{\varvec{N}}\cdot {\mathbb {S}}({\varvec{u}}'){\varvec{N}}\big ] \big |_{{\mathcal {G}}^+}+{\mathcal {B}}^+_{0}r'=0 \quad \text {on }{\mathcal {G}}^+,\nonumber \\&{\mathcal {D}}_t r'-{\varvec{u}}'\cdot {\varvec{N}} =0 \quad \text {on }{\mathcal {G}},\nonumber \\&{\varvec{u}}'(z,0)={\varvec{u}}'_0(z),\quad z\in {\mathcal {F}}, \quad r'(z,0)=r'_0(z),\quad z\in {\mathcal {G}}. \end{aligned}$$

(3.11)

We note that the initial data ${\varvec{u}}'_0,\,r'_0$ satisfy (2.3), (2.4) and homogeneous compatibility conditions (2.20).

Finally, we find $({\varvec{u}}'', q'', r'')$ as a solution to the system

$$\begin{aligned}&\bar{\rho }\big ({\mathcal {D}}_t\mathbf{{u}}''+2\omega (\mathbf{{e}}_3\times \mathbf{{u}}'')\big ) -\bar{\mu }\nabla ^2\mathbf{{u}}'' +\nabla q''=\mathbf{{l}}_1(\mathbf{{u}}'+\mathbf{{u}}'',q' +q'',r'+r''),\nonumber \\ {}&\qquad \qquad \qquad \qquad \qquad \nabla \cdot \mathbf{{u}}''=l_2(\mathbf{{u}}'+\mathbf{{u}}'',r'+r'') \quad \text{ in } {\mathcal {F}},\,\,\,t>0,\nonumber \\ {}&\mu ^-\Pi _{\mathcal {G}}{\mathbb {S}}(\mathbf{{u}}'')\mathbf{{N}} =\mathbf{{l}}_3^-(\mathbf{{u}}'+\mathbf{{u}}'',r'+r'') \quad \text{ on } {\mathcal {G}}^-,\nonumber \\ {}&[\mathbf{{u}}'']\big |_{{\mathcal {G}}^+}=0, \quad \big [\bar{\mu } \Pi _{\mathcal {G}}{\mathbb {S}} (\mathbf{{u}}'')\mathbf{{N}}\big ]\big |_{{\mathcal {G}}^+}=\mathbf{{l}}_3^+ (\mathbf{{u}}'+\mathbf{{u}}'',r'+r'') \quad \text{ on } {\mathcal {G}}^+,\nonumber \\ {}&-q''+\mu ^-\mathbf{{N}}\cdot {\mathbb {S}}(\mathbf{{u}}'')\mathbf{{N}} +{\mathcal {B}}^-_0r'' =l_4^-(\mathbf{{u}}'+\mathbf{{u}}'',r'+r'') +l_5^-(r'+r'') \quad \text{ on } {\mathcal {G}}^-,\nonumber \\ {}&[-q''+\bar{\mu } \mathbf{{N}}\cdot {\mathbb {S}}(\mathbf{{u}}'')\mathbf{{N}} ] |_{{\mathcal {G}}^+}+{\mathcal {B}}^+_0r'' =l_4^+(\mathbf{{u}}'+\mathbf{{u}}'',r'+r'') +l_5^+(r'+r'') \;\, \text{ on } {\mathcal {G}}^+,\nonumber \\ {}&{\mathcal {D}}_tr''-\mathbf{{u}}''\cdot \mathbf{{N}}=l_6(\mathbf{{u}}'+\mathbf{{u}}'',r'+r'') \quad \text{ on } {\mathcal {G}},\nonumber \\ {}&\mathbf{{u}}''\big |_{t=0}=\mathbf{{u}}_0''\quad \text{ in } {\mathcal {F}}, \qquad r''\big |_{t=0}=r_0'' \quad \text{ on } {\mathcal {G}}. \end{aligned}$$

(3.12)

We consider restrictions (3.10). If (3.7) holds, then the expressions

$$\begin{aligned}&l^\pm = \int _{{\mathcal {G}}^\pm }\big (r_{0} -\varphi (z,r_{0})\big )\,\mathrm{d}{\mathcal {G}}, \\&{\varvec{l}} =\rho ^-\int _{{\mathcal {G}}^-} \big (r_{0}{\varvec{z}} -{\varvec{\psi }} ^-(z,r_0)\big ) \,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}(r_{0}{\varvec{z}} -{\varvec{\psi }} ^+(z,r_0))\,\mathrm{d}{\mathcal {G}},\\&{\varvec{m}}=\int _{\mathcal {F}}\rho {\varvec{u}}_0\big (1-L(z,r_0)\big )\,\mathrm{d}z,\\&M_j=\int _{\mathcal {F}}\rho {\varvec{u}}_0\cdot {\varvec{\eta }}_j \big (1-L(z,r_0)\big )\,\mathrm{d}z,\quad j=1,2,3, \end{aligned}$$

and the functions $f_0=l_2({\varvec{u}}_0,r_0)$, ${\varvec{b}}_0(z)={\varvec{l}}^\pm _{3}({\varvec{u}}_0,r_0)$, $z\in {\mathcal {G}}^\pm$, satisfy the inequality

$$\begin{aligned}&|l^+|+|l^-|+|{\varvec{l}}|+ |{{\varvec{m}}}|+|{{\varvec{M}}}|+ \Vert f_0\Vert _{W_2^{l} (\cup {\mathcal {F}}^\pm )}+ \Vert {\varvec{b}}_0\Vert _{W_2^{l+1/2}({\mathcal {G}})}\\&\quad \leqslant c \varepsilon \big (\Vert {\varvec{u}}_0\Vert _{W_2^{1+l}({\mathcal {F}})} +\Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}})}\big ). \end{aligned}$$

Hence,

$$\begin{aligned}&\Vert {\varvec{u}} _0''\Vert _{W_2^{1+l}({\mathcal {F}})} + \Vert r''_0\Vert _{W_2^{2+l}({\mathcal {G}} )} \leqslant c\varepsilon \big (\Vert {\varvec{u}}_0\Vert _{W_2^{1+l}({\mathcal {F}})} + \Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}} )}\big ),\\&\Vert {\varvec{u}}'_0\Vert _{W_2^{1+l}({\mathcal {F}})} +\Vert r'_0\Vert _{W_2^{2+l}({\mathcal {G}} )} \leqslant c \big (\Vert {\varvec{u}}_0\Vert _{W_2^{1+l}({\mathcal {F}} )} +\Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}} )}\big ). \end{aligned}$$

Moreover, in view of (3.9), (3.10), ${\varvec{u}}'_0, r' _0$ is subject to the necessary conditions

$$\begin{aligned}&\int _{{\mathcal {G}}^\pm }r_0^{'\pm }\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {G}}^\pm }(r_0-r_0^{''\pm })\,\mathrm{d}{\mathcal {G}}=\int _{{\mathcal {G}}^\pm }\varphi (z,r_0)\,\mathrm{d}S=0, \\&\rho ^-\int _{{\mathcal {G}}^-}r_0^{'-}z_j\,\mathrm{d}{\mathcal {G}}+[\bar{\rho }]\big |_{{\mathcal {G}}^+}\int _{{\mathcal {G}}^+} r_0^{'+}z_j\,\mathrm{d}{\mathcal {G}}=\rho ^-\int _{{\mathcal {G}}^-}\psi ^-_j(z,r_0)\,\mathrm{d}{\mathcal {G}}+ [\bar{\rho }]\big |_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+} \psi ^{'+}_j\,\mathrm{d}{\mathcal {G}}=0,\\&\int _{\mathcal {F}}\bar{\rho }{\varvec{u}}'_0\,\mathrm{d}{\mathcal {G}}=0, \\&\int _{\mathcal {F}}\bar{\rho }{\varvec{u}}'_0\cdot {\varvec{\eta }}_j(z)\,\mathrm{d}z+\omega \Big (\rho ^-\int _{{\mathcal {G}}^-}r_0^{'-}{\varvec{\eta }}_3 \cdot {\varvec{\eta }}_j\,\mathrm{d}{\mathcal {G}}+ [\bar{\rho }]|_{{\mathcal {G}}^+} \int _{{\mathcal {G}}^+}r_0^{'+}{\varvec{\eta }}_3 \cdot {\varvec{\eta }}_j\,\mathrm{d}S\Big )=0. \end{aligned}$$

By Theorem 2.2, the solution $({\varvec{u}}',q',r')$ of problem (3.11) satisfies the inequality

$$\begin{aligned} N_T({\varvec{u}}',r')&\equiv \Vert {\varvec{u}}'(\cdot ,T)\Vert _{W_2^{1+l}({\mathcal {F}})} + \Vert r'(\cdot ,T)\Vert _{W_2^{2+l}({\mathcal {G}} )}\\&\leqslant c_1\mathrm{e}^{-\beta T} \big \{\Vert {\varvec{u}}_0\Vert _{W_2^{1+l} ({\mathcal {F}})}+ \Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}} )}\big \}. \end{aligned}$$

We fix $T=T_0$ so large that

$$\begin{aligned} c_1e^{-\beta T_0}\leqslant \theta /2\ll 1/2, \qquad \beta >0. \end{aligned}$$

As for the problem (3.12), it is solved by iterations, as in [13], on the basis of inequality (2.11) and the estimate of nonlinear terms (3.2)

$$\begin{aligned} Z_T({\varvec{u}},q,r)\leqslant cY_T^2({\varvec{u}},q,r), \end{aligned}$$

(see also [19]), where

$$\begin{aligned} Y_T(\mathbf{{u}},q,r)&=\Vert \mathbf{{u}}\Vert _{W_2^{2+l,1+l/2} (D_T )}+ \Vert \nabla q\Vert _{W_2^{l,l/2}( D_T )} +\Vert q\Vert _{W_2^{l,l/2}( D_T )}\\ {}&\quad +\Vert r\Vert _{W_2^{5/2+l,5/4+l/2}( G_T )}+ \Vert {\mathcal {D}}_t r\Vert _{W_2^{3/2+l,3/4+l/2}( G_T )},\\ Z_T(u,q,r)&= \Vert \mathbf{{l}}_1(u,q,r)\Vert _{W_2^{l,l/2} (D_T )}+\Vert l_2(u,r)\Vert _{W_2^{1+l,0}( D_T)} +\Vert \mathbf {L}(\mathbf{{u}},r)\Vert _{W_2^{0,1+l/2}(D_T)}\\ {}&\quad +\Vert \mathbf{{l}}_3(\mathbf{{u}},r)\Vert _{W_2^{{l+1/2},l/2+1/4}(G_T)} +\Vert l_4(\mathbf{{u}},r)\Vert _{W_2^{{l+1/2},l/2+1/4}( G_T)} +\pmb |l_5(r)\pmb |^{(l+1/2,l/2)}_{ G_T}\\ {}&\quad +\Vert \mathbf{{l}}_6(\mathbf{{u}},r)\Vert _{W_2^{3/2+l,3/4+l/2}( G_T)}. \end{aligned}$$

Thus, if $\varepsilon$ is small enough, we obtain

$$\begin{aligned} Y_{T_0}({\varvec{u}}'', q'',r'')\leqslant c_2\varepsilon \big (\Vert {\varvec{u}}_0\Vert _{W_2^{1+l}( {\mathcal {F}})} + \Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}} )}\big ). \end{aligned}$$

It follows that

$$\begin{aligned} N_{T_0}({\varvec{u}}, r)&\leqslant N_{T_0}({\varvec{u}}', r') + N_{T_0}({\varvec{u}}'', r'')\\&\leqslant (\theta /2+c_2\varepsilon )\big (\Vert {\varvec{u}}_0 \Vert _{W_2^{1+l}( {\mathcal {F}} )}+ \Vert r_0\Vert _{W_2^{2+l} ({\mathcal {G}} )}\big ). \end{aligned}$$

In the case of $c_2\varepsilon <\theta /2$, due to (3.7), this implies

$$\begin{aligned} Y_{T_0}({\varvec{u}},q,r)&\leqslant c \Big (\Vert {\varvec{u}}_0 \Vert _{W_2^{1+l}( {\mathcal {F}} )}+ \Vert r_0\Vert _{W_2^{2+l} ({\mathcal {G}} )}\big )\leqslant c\varepsilon ,\nonumber \\&\quad \Vert {\varvec{u}}(\cdot ,{T_0})\Vert _{W_2^{1+l}( {\mathcal {F}} )} + \Vert r(\cdot ,{T_0})\Vert _{W_2^{2+l}({\mathcal {G}} )} \leqslant \theta \big (\Vert {\varvec{u}}_0\Vert _{W_2^{1+l}({\mathcal {F}})} + \Vert r_0\Vert _{W_2^{2+l}({\mathcal {G}} )}\big )\leqslant \varepsilon . \end{aligned}$$

(3.13)

Inequalities (3.13) allow us to extend the solution $({\varvec{u}},q,r)$ to the intervals $(T_0,2T_0), \ldots , (kT_0,(k+1)T_0),\ldots$ up to the infinite interval $t>0$ by the repeated applications of the obtained local result and to complete the proof of Theorem 3.1, as in [13].

Let us consider the case $k=1$. Estimate (3.13) means

$$\begin{aligned} N_1\equiv N_{T_0}({\varvec{u}}_1,r_1)\leqslant \varepsilon , \end{aligned}$$

with ${\varvec{u}}_k={\varvec{u}}(\cdot ,k{T_0})$, $r_k=r(\cdot ,k{T_0})$. So the problem is solvable in the time interval $(T_0,2T_0)$ and

$$\begin{aligned}&Y_1({\varvec{u}},q,r)\leqslant c N_1, \\&N_2\leqslant \theta N_1\leqslant \varepsilon , \end{aligned}$$

where $N_k=N_{kT_0}({\varvec{u}}_k,r_k)$, $Y_k=Y_{kT_0,(k+1)T_0}$. If the solution is found for $t<(k+1)T_0$ and the inequalities

$$\begin{aligned}&N_{j}^2\leqslant \theta ^2N_{j-1}^2,\quad \theta <1,\nonumber \\&Y_{j}^2\leqslant c N_{j}^2,\quad j=1,\ldots ,k, \end{aligned}$$

(3.14)

are proved, then

$$\begin{aligned} N_j^2 \leqslant \cdots \leqslant \theta ^{2j}N_0^2\leqslant \theta ^{2j}\varepsilon ^2. \end{aligned}$$

(3.15)

Let $\theta _1>\theta$ ($\theta _1=\mathrm{e}^{-\alpha T_0}$, $0<\alpha <\beta$). We take the sum of (3.14), (3.15) multiplied by $\theta _1^{-2j}$. This leads to

$$\begin{aligned} \sum _{j=0}^k\theta _1^{-2j} N_j^2&\leqslant N_0^2+N_0^2 \sum _{j=1}^k\frac{\theta ^{2j}}{\theta _1^{2j}} \leqslant \frac{\theta _1^2}{\theta _1^2-\theta ^2}N_0^2, \\ \sum _{j=0}^k\theta _1^{-2j}Y^2_j({\varvec{u}},q,r)&\leqslant c \frac{\theta _1^2}{\theta _1^2-\theta ^2}N_0^2 \leqslant c N_0^2. \end{aligned}$$

And, finally, by passing to the limit as $k\rightarrow \infty$ in the last estimate, we arrive at an inequality equivalent to (3.8). $\square$