Abstract
We consider a viscous incompressible fluid governed by the Navier–Stokes system written in a domain where a part of the boundary can deform. We assume that the corresponding displacement follows a damped beam equation. Our main results are the existence and uniqueness of strong solutions for the corresponding fluid-structure interaction system in an \(L^p\)-\(L^q\) setting for small times or for small data. An important ingredient of the proof consists in the study of a linear parabolic system coupling the non stationary Stokes system and a damped plate equation. We show that this linear system possesses the maximal regularity property by proving the \({\mathcal {R}}\)-sectoriality of the corresponding operator. The proof of the main results is then obtained by an appropriate change of variables to handle the free boundary and a fixed point argument to treat the nonlinearities of this system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
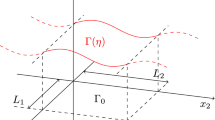
In this work, we study the interaction between a viscous incompressible fluid and a deformable structure located on a part of the fluid domain boundary. More precisely, we denote by \({\mathcal {F}}\) the reference domain for the fluid. We assume that it is a smooth bounded domain of \({\mathbb {R}}^3\) such that its boundary \(\partial {\mathcal {F}}\) contains a flat part \(\Gamma _{S}\) corresponding to the reference domain of the plate. We assume \(\Gamma _{S} = {\mathcal {S}} \times \{0\}\), where \({\mathcal {S}}\) is a smooth domain of \({\mathbb {R}}^2\) and we set \(\Gamma _{0} : = \partial {\mathcal {F}} {\setminus } \overline{\Gamma _{S}}.\) The set \(\Gamma _0\) is rigid and remains unchanged whereas the plate domain \(\Gamma _{S}\) can deform through exterior forces and in particular the force coming from the fluid and if we denote by \(\eta \) its displacement, then the plate domain changes from \(\Gamma _{S}\) to
In our study, we consider only displacements \(\eta \) regular enough and satisfying the boundary conditions (the plate is clamped):
and a condition insuring that the deformed plate does not have any contact with the other part of the boundary of the fluid domain:
We have denoted by \(n_{\mathcal {S}}\) the unitary exterior normal to \(\partial {\mathcal {S}}\) and in the whole article we add the index s in the gradient and in the Laplace operators if they apply to functions defined on \({\mathcal {S}}\subset {\mathbb {R}}^2\) (and we keep the usual notation for functions defined on a domain of \({\mathbb {R}}^3\)).
With the above notations and hypotheses, \(\Gamma _{0} \cup \overline{\Gamma _{S}(\eta )}\) corresponds to a closed simple and regular surface which interior is the fluid domain \({\mathcal {F}}(\eta )\). In what follows, we consider that \(\eta \) is also a function of time and its evolution is governed by a plate equation. If \(\eta (t,\cdot )\) satisfies the above conditions, we can define the fluid domain \({\mathcal {F}}(\eta (t))\) and we then denote by \((\widetilde{v}, \widetilde{\pi })\) the Eulerian velocity and the pressure of the fluid and we assume that they satisfy the incompressible Navier-Stokes system in \({\mathcal {F}}(\eta (t))\). Then the corresponding system we analyze reads as follows:
where \((e_1,e_3,e_{3})\) is the canonical basis of \({\mathbb {R}}^3\). The fluid stress tensor \({\mathbb {T}}(\widetilde{v},\widetilde{\pi })\) is given by
The function \({\mathbb {H}}\) corresponds to the force of the fluid acting on the plate and can be expressed as follows:
where
is the unit normal to \(\Gamma _{S}(\eta (t))\) outward \({\mathcal {F}}(\eta (t)).\) The above system is completed by the following initial data

System (1.3) is a simplified model for blood flow in arteries (see, for instance the survey article [38]) and \(\alpha ,\beta ,\gamma \) are non negative constants that corresponds to the physical properties of the wall tissue. Our analysis will be done in the case \(\alpha >0\), \(\beta \geqslant 0\) and \(\gamma >0\) and to simplify, we consider in what follows the case
and the other cases can be done in the same way. Let us remark that the term \(- \gamma \Delta _{s} \partial _{t}\eta \) corresponds to the damping in the plate equation. The other positive constant, appearing in (1.4) is the viscosity \(\nu \).
An important remark in the study of (1.3)–(1.6) is that a solution \((\widetilde{v}, \widetilde{\pi }, \eta )\) satisfies
Assuming that \(\eta _1^0\) has a zero mean, we deduce that this property is preserved for \(\eta \) all along. This leads us to consider the space
and the orthogonal projection \(P_{m} : L^{q}({\mathcal {S}}) \rightarrow L^{q}_{m}({\mathcal {S}})\), that is
Taking the projection of the plate equation in (1.3) onto \(L^{q}_{m}({\mathcal {S}})\) and onto \(L^{q}_{m}({\mathcal {S}})^\perp \) yields the following two equations:
and
This means that, in contrast to the Navier–Stokes system without structure, the pressure is not determined up to a constant. In what follows, we only keep (1.9) and solve the corresponding system up to constant for the pressure, and Eq. (1.10) is used at the end to fix the constant for the pressure. We thus consider the following system
To state our main result, we introduce some notations for our functional spaces. Firstly \(W^{s,q}(\Omega )\), with \(s\geqslant 0\) and \(q\geqslant 1\), denotes the usual Sobolev space. Let \(k,k' \in {\mathbb {N}}\), \(k<k'\). For \(1\leqslant p < \infty \), \(1\leqslant q < \infty \), we consider the standard definition of the Besov spaces by real interpolation of Sobolev spaces
We refer to [1] and [44] for a detailed presentation of the Besov spaces. We also introduce functional spaces for the fluid velocity and pressure for a spatial domain depending on the displacement \(\eta \) of the structure. Let \(1< p, q < \infty \) and \(\eta \in L^{p}(0,\infty ;W^{4,q}({\mathcal {S}})) \cap W^{2,p}(0,\infty ;L^{q}({\mathcal {S}}))\) satisfying (1.1) and (1.2). We show in Sect. 2 that there exists a mapping \(X=X_\eta \) such that \(X(t,\cdot )\) is a \(C^{1}\)-diffeomorphism from \({\mathcal {F}}\) onto \({\mathcal {F}}(\eta (t))\) and such that \(X\in L^{p}(0,\infty ;W^{2,q}({\mathcal {F}})) \cap W^{2,p}(0,\infty ;L^{q}({\mathcal {F}}))\). Then for \(T \in (0, \infty ]\), we define
where we have set \((v\circ X^{-1})(t,x):=v(t,(X(t,\cdot ))^{-1}(x))\) for simplicity.
Finally, let us give the conditions we need on the initial conditions for the system (1.11): we assume
with the compatibility conditions
and
Here \(\widetilde{n}^0\) is the unit exterior normal to \(\Gamma _{S}(\eta _1^0)\) outward \({\mathcal {F}}(\eta _1^0).\)
We are now in a position to state our main results. The first one is the local in time existence and uniqueness of strong solutions for (1.11).
Theorem 1.1
Let \(p,q\in (1,\infty )\) such that
Let us assume that \(\eta _{1}^{0} = 0\) and \((\eta _2^0,\widetilde{v}^0)\) satisfies (1.12), (1.13), (1.14). Then there exists \(T > 0,\) depending only on \((\eta _2^0,\widetilde{v}^0),\) such that the system (1.11) admits a unique strong solution \((\widetilde{v}, \widetilde{\pi }, \eta )\) in the class of functions satisfying
Moreover, \(\Gamma _{0} \cap \Gamma _{S}(\eta (t)) = \emptyset \) for all \(t \in [0,T].\)
Our second main result asserts the global existence and uniqueness of strong solution for (1.11) under a smallness condition on the initial data.
Theorem 1.2
Let \(p,q\in (1,\infty )\) satisfying the conditions (1.15). Then there exists \(\beta _{0} > 0\) such that, for all \(\beta \in [0,\beta _{0}]\) there exists \(\varepsilon _{0}\) such that for any \((\eta _1^0,\eta _2^0,\widetilde{v}^0)\) satisfying (1.12), (1.13), (1.14) and
the system (1.11) admits a unique strong solution \((\widetilde{v}, \widetilde{\pi }, \eta )\) in the class of functions satisfying
Moreover, \(\Gamma _{0} \cap \Gamma _{S}(\eta (t)) = \emptyset \) for all \(t \in [0,\infty ).\)
In the above statement, we have used a similar notation as in (1.7):
We also set
We denote by \(W^{s,q}_0({\mathcal {S}})\) the closure of \(C^{\infty }_c({\mathcal {S}})\) in \(W^{s,q}({\mathcal {S}})\) and we set
We define similarly \(W^{s,q}_0({\mathcal {F}})\), \(W^{s,q}_{0,m}({\mathcal {F}})\).
Finally, we also need the following notation in what follows: for \(T\in (0,\infty ]\),
We have the following embeddings (see, for instance, [2, Theorem 4.10.2, p.180]),
where \(C^k_b\) is the set of continuous and bounded functions with derivatives continuous and bounded up to the order k. In particular, in what follows, we use the following norm for \(W^{1,2}_{p,q}((0,T); {\mathcal {F}})\):
and we proceed similarly for the two other spaces.
For \(\beta \geqslant 0\), \(p\in [1,\infty ]\) and for \({\mathbb {X}}\) a Banach space, we also introduce the notation
and a similar notation for \(W^{1,2}_{p,q,\beta }((0,\infty ) ; {\mathcal {F}})\), \(W^{2,4}_{p,q,\beta }((0,\infty ) ; {\mathcal {S}})\), etc.
Let us give some remarks on Theorems 1.1 and 1.2. First let us point out that the system (1.11) has already been studied by several authors: existence of weak solutions ([9, 26, 37]), uniqueness of weak solutions ([25]), existence of strong solutions ([7, 32, 34]), feedback stabilization ([5, 40]), global existence of strong solutions and study of the contacts ([22]). Some works consider also the case of a beam/plate without damping (that is without the term \( - \Delta _{s} \partial _{t}\eta \)): [6, 21, 23]. We refer, for instance, to [24] and references therein for a concise description of recent progress in this field. It is important to notice that all the above works correspond to a “Hilbert” framework whereas our results are done in a “\(L^{p}\)-\(L^{q}\)” framework. Working in such a framework allows us to extend the result obtained in the “Hilbert” framework, but it should be noticed that several questions on fluid-structure interaction systems, in the “Hilbert” framework, have been handled by considering a “\(L^{p}\)-\(L^{q}\)” framework: for instance, the uniqueness of weak solutions (see [8, 20]), the asymptotic behavior for large time (see [16]), the asymptotic behavior for small structures (see [31]), etc.
For this approach, several recent results have been obtained for fluid systems, with or without structure. For instance, one can quote [19] (viscous incompressible fluid), [15], (viscous compressible fluid), [27, 28] (viscous compressible fluid with rigid bodies), [18, 35] (incompressible viscous fluid and rigid bodies). Here we consider an incompressible viscous fluid coupled with a structure satisfying an infinite-dimensional system and we thus need to go beyond the theory developed for instance in [35].
Our approach to prove Theorems 1.1 and 1.2 is quite classical. Since the fluid domain \({\mathcal {F}}(\eta (t))\) depends on the structure displacement \(\eta ,\) we first reformulate the problem in a fixed domain. This is achieved by “geometric” change of variables. Next we associate the original nonlinear problem to a linear one. The linear system preserves the fluid-structure coupling. A crucial step here is to establish the \(L^{p}\)-\(L^{q}\) regularity property in the infinite time horizon. This is done by showing that the associate linear operator is \({\mathcal {R}}\)-sectorial and generates an exponentially stable semigroup. We then use the Banach fixed point theorem to prove existence and uniqueness results. Note that for Theorem 1.2, we assume the same conditions on (p, q) than for Theorem 1.1 but the result should be also true for \(\frac{1}{p}+\frac{3}{2q}=\frac{3}{2}.\) However to deal with this case one needs some precise results on the interpolation of Besov spaces (see for instance Lemma 2.1).
Let us also remark that this work could also be done in the corresponding 2D/1D model, that is \({\mathcal {F}}\) a regular bounded domain in \({\mathbb {R}}^2\) such that \(\partial {\mathcal {F}}\) contains a flat part \(\Gamma _S={\mathcal {S}}\times \{0\}\), where \({\mathcal {S}}\) is an open bounded interval of \({\mathbb {R}}\). In that case, we would obtain the same result as in Theorem 1.1 and in Theorem 1.2 but with the following condition on p, q:
The plan of the paper is as follows. In the next section, we use a change of variables to rewrite the governing equations in a cylindrical domain and we also restate our result after change of variables. Then, in Sect. 3, we recall several important results about maximal \(L^{p}\) regularity for Cauchy problems and in particular how to use the \({\mathcal {R}}\)-sectoriality property. We use these results to study in Sect. 4 the linearized system. Finally in Sect. 5 and in Sect. 6, we estimate the nonlinear terms which allows us to prove the main results with a fixed point argument.
2 Change of Variables
In order to prove Theorem 1.2, we first rewrite the system (1.11) in the cylindrical domain \((0,\infty ) \times {\mathcal {F}}\) by constructing an invertible mapping \(X(t,\cdot )\) from the reference configuration \({\mathcal {F}}\) onto \({\mathcal {F}}(\eta (t)).\) More generally, for any \(\eta \in C^{1}(\overline{{\mathcal {S}}})\) satisfying (1.1) and a smallness condition
that ensures in particular (1.2), we can construct a diffeomorphism \(X_\eta : {\mathcal {F}}\rightarrow {\mathcal {F}}(\eta ).\) To do this, we follow the approach of [5]: there exists \(\alpha >0\) such that
Notice that, \(\partial {\mathcal {V}}_{\alpha } \cap \partial {\mathcal {F}}= \Gamma _{S}.\) We consider \(\psi \in C_{c}^{\infty }({\mathbb {R}})\) such that
Let us extend \(\eta \) by 0 in \({\mathbb {R}}^2\setminus {\mathcal {S}}\) so that \(\eta \in C^{1}_c({\mathbb {R}}^2)\) and let us define \(X_\eta \) by
If we choose \(c_0\) in (2.1) as
then \(X_\eta \) is a \(C^{1}\)-diffeomorphism from \({\mathcal {F}}\) onto \({\mathcal {F}}(\eta )\) with \(X_\eta (\Gamma _{S}) = \Gamma _{S}(\eta )\). Note that (2.1) and (2.5) yield that \(|\eta |\leqslant {\alpha }/{2}\) in \({\mathcal {S}}\).
Let us assume now that \(\eta \) depends also on time and satisfies for all t relation (2.1) with \(c_0\) given by (2.5). We can define
In particular, \(X(t,\cdot )\) is a \(C^{1}\)-diffeomorphism from \({\mathcal {F}}\) onto \({\mathcal {F}}(\eta (t)).\) For each \(t \geqslant 0,\) we denote by \(Y(t,\cdot ) = X(t,\cdot )^{-1},\) the inverse of \(X(t,\cdot ).\) We have \(X \in C_{b}^0([0,\infty ); C^{1}(\overline{{\mathcal {F}}}))\) and for all \(t \in (0,\infty )\), \(y=[y_1 \ y_2 \ y_3]^{\top } \in {\mathcal {S}}\times (-\alpha /2,\alpha /2),\)
We consider the following change of unknowns
The system (1.11) can be rewritten in the form
where
Let us write
so that
After some standard calculation, we find that in (2.9), the expressions of \(F=\left( F_\alpha \right) _{\alpha =1,2,3}\) and H are
We prove the following result
Lemma 2.1
Let \(1< p, q < \infty \) such that
and \((\eta _{1}^{0}, \widetilde{v}^{0})\) satisfies (1.12). Then \(v^{0}\) defined by (2.10) satisfies \(v^{0} \in B^{2(1-1/p)}_{q,p}({\mathcal {F}}).\)
Proof
By using (2.15), we deduce that \(\eta _1^0\in C^1(\overline{{\mathcal {S}}})\). In particular, the map
is linear and continuous from \(L^q({\mathcal {F}}(\eta _1^0))\) into \(L^q({\mathcal {F}})\). Let us show that it is also continuous from \(W^{2,q}({\mathcal {F}}(\eta _1^0))\) into \(W^{2,q}({\mathcal {F}})\): Some computation yields
Using that \(\eta _1^0\in C^1(\overline{{\mathcal {S}}})\), we deduce that the first term in the right-hand side of the above relation belongs to \(L^{q}({\mathcal {F}}).\) For the second term, we first note that \(\displaystyle \frac{\partial \widetilde{v}^{0}}{\partial x_{k}}(X(\cdot )) \in W^{1,q}({\mathcal {F}})\) and \(\displaystyle \frac{\partial ^{2} X_{\eta _{1}^{0},k}}{\partial y_{i} \partial y_{j}} \in B^{2(1-1/p)}_{q,p}({\mathcal {F}}).\) Therefore by [44, Theorem(i), page 196], \(\displaystyle \frac{\partial ^{2} X_{\eta _{1}^{0},k}}{\partial y_{i} \partial y_{j}} \in W^{s_{1},q}({\mathcal {F}})\) for any \(s_{1} < 2(1-1/p).\) Applying standard result on the product of Sobolev spaces we conclude that the second term in (2.17) also belongs to \(L^{q}({\mathcal {F}}).\)
Then by interpolation, we deduce that the map (2.16) is linear continuous from \(B^{2(1-1/p)}_{q,p}({\mathcal {F}}(\eta _1^0))\) into \(B^{2(1-1/p)}_{q,p}({\mathcal {F}})\). Therefore, if \(v^0\in B^{2(1-1/p)}_{q,p}({\mathcal {F}}(\eta _1^0))\), we have
and we deduce that the product \(v^0\in B^{2(1-1/p)}_{q,p}({\mathcal {F}})\) by using [41, Theorem 2, pp.191-192, relation (17)]. \(\square \)
Using the above lemma and the definition of X defined in (2.6), the hypotheses (1.12), (1.13), (1.14) on the initial conditions are transformed into the following conditions:
Here n is the unit normal to \(\partial {\mathcal {F}}\) outward \({\mathcal {F}}\) and in particular on \(\Gamma _S\), \(n=e_3\).
Using the above change of variables Theorem 1.1 and Theorem 1.2 can be rephrased as
Theorem 2.2
Let \(p,q\in (1,\infty )\) satisfying the condition (1.15). Let us assume that \(\eta _{1}^{0} = 0\) and \((\eta _2^0,v^0)\) satisfies (2.18), (2.19), (2.20). Then there exists \(T > 0,\) depending only on \((\eta _2^0,v^0),\) such that the system (2.9) admits a unique strong solution \((v, \pi , \eta )\) in the class of functions satisfying
Moreover, \(\eta \) satisfies (2.1) and \(X(t,\cdot ) : {\mathcal {F}}\rightarrow {\mathcal {F}}(\eta (t))\) is a \(C^{1}\)-diffeomorphism for all \(t \in [0,T].\)
Theorem 2.3
Let \(p,q\in (1,\infty )\) satisfying the condition (1.15). Then there exists \(\beta _{0} > 0\) such that, for all \(\beta \in [0,\beta _{0}],\) there exist \(\varepsilon _{0}\) and \(C > 0,\) such that for any \((\eta _1^0,\eta _2^0,{v}^0)\) satisfying (2.18), (2.19), (2.20) and
the system (2.9) admits a unique strong solution \((v, \pi , \eta )\) in the class of functions satisfying
Moreover, \(\eta \) satisfies (2.1) and \(X(t,\cdot ) : {\mathcal {F}}\rightarrow {\mathcal {F}}(\eta (t))\) is a \(C^{1}\)-diffeomorphism for all \(t \in [0,\infty )\).
3 Some Background on \({\mathcal {R}}\)-sectorial Operators
In this section, we recall some important facts on \({\mathcal {R}}\)-sectorial operators. This notion is associated with the property of \({\mathcal {R}}\)-boundedness (\({\mathcal {R}}\) for Randomized) for a family of operators that we recall here (see, for instance, [10, 11, 30, 45]):
Definition 3.1
Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be Banach spaces. A family of operators \({\mathcal {E}} \subset {\mathcal {L}}({\mathcal {X}},{\mathcal {Y}})\) is called \({\mathcal {R}}-\)bounded if there exist \(p\in [1,\infty )\) and a constant \(C>0\), such that for any integer \(N \geqslant 1\), any \(T_1, \ldots T_N \in {\mathcal {E}}\), any independent Rademacher random variables \(r_1, \ldots , r_N\), and any \(x_1, \ldots , x_N \in {\mathcal {X}}\),
The smallest constant C in the above inequality is called the \({\mathcal {R}}_p\)-bound of \({\mathcal {E}}\) on \({\mathcal {L}}({\mathcal {X}},{\mathcal {Y}})\) and is denoted by \({\mathcal {R}}_p({\mathcal {E}})\).
In the above definition, we denote by \({\mathbb {E}}\) the expectation and a Rademacher random variable is a symmetric random variables with value in \(\{-1,1\}\). It is proved in [11, p.26] that this definition is independent of \(p\in [1,\infty )\).
We have the following useful properties (see Proposition 3.4 in [11]):
For any \(\beta \in (0,\pi )\), we write
We recall the following definition:
Definition 3.2
(sectorial and \({\mathcal {R}}\)-sectorial operators). Let A be a densely defined closed linear operator on a Banach space \({\mathcal {X}}\) with domain \({\mathcal {D}}(A)\). We say that A is a (\({\mathcal {R}}\))-sectorial operator of angle \(\beta \in (0, \pi )\) if
and if the set
is (\({\mathcal {R}}\))-bounded in \({\mathcal {L}}({\mathcal {X}})\).
We denote by \(M_\beta (A)\) (respectively \({\mathcal {R}}_{\beta }(A)\)) the bound (respectively the \({\mathcal {R}}\)-bound) of \(R_\beta \). One can replace in the above definitions \(R_\beta \) by the set
In that case, we denote the uniform bound and the \({\mathcal {R}}\)-bound by \(\widetilde{M}_\beta (A)\) and \(\widetilde{{\mathcal {R}}_{\beta }}(A)\).
This notion of \({\mathcal {R}}\)-sectorial operators is related to the maximal regularity of type \(L^p\) by the following result due to [45] (see also [11, p.45]).
Theorem 3.3
Let \({\mathcal {X}}\) be a UMD Banach space and A a densely defined, closed linear operator on \({\mathcal {X}}\). Then the following assertions are equivalent:
-
1.
For any \(T\in (0,\infty ]\) and for any \(f\in L^p(0,T;{\mathcal {X}})\), the Cauchy problem
$$\begin{aligned} u' = A u + f \quad \text {in} \quad (0,T), \quad u(0) = 0 \end{aligned}$$(3.2)admits a unique solution u with \(u', Au\in L^{p}(0,T;{\mathcal {X}})\) and there exists a constant \(C>0\) such that
$$\begin{aligned} \Vert u'\Vert _{L^{p}(0,T;{\mathcal {X}})}+\Vert Au\Vert _{L^{p}(0,T;{\mathcal {X}})}\leqslant C\Vert f\Vert _{L^{p}(0,T;{\mathcal {X}})}. \end{aligned}$$ -
2.
A is \({\mathcal {R}}\)-sectorial of angle \(> \frac{\pi }{2}\).
We recall that \({\mathcal {X}}\) is a UMD Banach space if the Hilbert transform is bounded in \(L^p({\mathbb {R}};{\mathcal {X}})\) for \(p\in (1,\infty )\). In particular, the closed subspaces of \(L^q(\Omega )\) for \(q\in (1,\infty )\) are UMD Banach spaces. We refer the reader to [2, pp.141–147] for more information on UMD spaces.
Combining the above theorem with [13, Theorem 2.4] and [43, Theorem 1.8.2], we can deduce the following result on the system
Corollary 3.4
Let \({\mathcal {X}}\) be a UMD Banach space, \(1< p < \infty \) and let A be a closed, densely defined operator in \({\mathcal {X}}\) with domain \({\mathcal {D}}(A).\) Let us assume that A is a \({\mathcal {R}}\)-sectorial operator of angle \( > \frac{\pi }{2}\) and that the semigroup generated by A has negative exponential type. Then for every \(u_{0} \in ({\mathcal {X}}, {\mathcal {D}}(A))_{1-1/p,p}\) and for every \(f \in L^{p}(0,\infty ;{\mathcal {X}}),\) the system (3.3) admits a unique solution in \(L^{p}(0,\infty ;{\mathcal {D}}(A)) \cap W^{1,p}(0,\infty ;{\mathcal {X}}).\)
Let us also mention, the following useful result on the perturbation theory of \({\mathcal {R}}\)-sectoriality, obtained in [29, Corollary 2].
Proposition 3.5
Let A be a \({\mathcal {R}}\)-sectorial operator of angle \(\beta \) on a Banach space \({\mathcal {X}}\). Let \(B : {\mathcal {D}}(B) \rightarrow {\mathcal {X}}\) be a linear operator such that \({\mathcal {D}}(A) \subset {\mathcal {D}}(B)\) and such that there exist \(a,b\geqslant 0\) satisfying
If
then \(A+B -\lambda \) is \({\mathcal {R}}\)-sectorial of angle \(\beta \).
4 Linearized System
In order to study the system (2.9), we linearized it and use the theory of the previous section. To this aim, we introduce the operator \({\mathcal {T}} : L^2({\mathcal {S}}) \rightarrow {L}^2(\partial {\mathcal {F}})\) defined by
We consider the following linear system
One can simplify the system (4.2): using that \(\mathrm{div}\,v = 0\) in \({\mathcal {F}}\) and \(v_{1}=v_2 = 0\) on \(\Gamma _{S}\) we deduce that \((Dv)|_{\Gamma _S}e_3\cdot e_3 = 0\). Thus
where \(\gamma _m\) is the following modified trace operator:
This cancelation plays no role in our result and is only used to simplify the calculation.
4.1 The Fluid Operator
Here we recall some results on the Stokes operator in the \(L^q\) framework. Let us introduce the Banach space
equipped with the norm
We recall (see, for instance, [17, Lemma 1]) that the normal trace can be extended as a continuous and surjective map
In particular, we can define
We have the following Helmholtz-Weyl decomposition (see, for instance Section 3 and Theorem 2 of [17]):
The corresponding projection operator \({\mathcal {P}}\) from \({ L}^q({\mathcal {F}})\) onto \(L^{q}_{\sigma }({\mathcal {F}})\) can be obtained as
where \(\varphi \in W^{1,q}({\mathcal {F}})\) is a solution of the following Neumann problem
that is a solution of
where \(q'\) is the conjugate exponent of q.
Let us denote by \(A_{F} = {\mathcal {P}} \Delta ,\) the Stokes operator in \(L^{q}_{\sigma }({\mathcal {F}})\) with domain
Theorem 4.1
Assume \(1< q< \infty .\) Then the Stokes operator \(A_{F}\) generates a \(C^{0}\)-semigroup of negative type. Moreover \(A_{F}\) is an \({\mathcal {R}}\)-sectorial operator in \(L^{q}_{\sigma }({\mathcal {F}})\) of angle \(\beta \) for any \(\beta \in (0,\pi )\).
For the proof, we refer to Corollary 1.2 and Theorem 1.4 in [19].
4.2 The Structure Operator
Let us set
and let us consider the operator \(A_{S} : {\mathcal {D}}(A_{S}) \rightarrow {\mathcal {X}}_{S}\) defined by
where \(P_m\) is defined by (1.8).
Theorem 4.2
Let us assume that \(1< q< \infty .\) Then there exists \(\gamma _{1} > 0\) such that \(A_{S} - \gamma _{1}\) is an \({\mathcal {R}}\)-sectorial operator on \({\mathcal {X}}_{S}\) of angle \(\beta _{1} > \pi /2.\)
Proof
We first consider
and the operator \(A_{S}^{0}\) defined by
Applying Theorem 5.1 in [12], we have that \(A_{S}^0\) is \({\mathcal {R}}\)-sectorial in \({\mathcal {X}}_{S}^{0}\) of angle \(\beta _{0} > \pi /2.\)
Now we can extend \(A_S\) on \({\mathcal {D}}(A_{S}^{0})\) by \(\widetilde{A}_S = A_{S}^{0}+B_{S}\) where
Using standard result on the trace operator, we see that \(B_S\) satisfies the hypotheses of Proposition 3.5 and in particular for any \(a>0\) there exists \(b>0\) such that (3.4) holds. Therefore, there exists \(\gamma _{1} > 0\) such that \(\widetilde{A}_{S} - \gamma _{1}\) is an \({\mathcal {R}}\)-sectorial operator on \({\mathcal {X}}_{S}^{0}\) of angle \(\beta _0.\)
Let \(\lambda \ne 0\), \((g_{1}, g_{2}) \in {\mathcal {X}}_{S}\) and \((\eta _1,\eta _2)\in {\mathcal {D}}(A_{S}^{0})\) such that
We can write this equation as
Integrating the first two equations over \({\mathcal {S}}\) we find that \((\eta _1,\eta _2)\in {\mathcal {D}}(A_{S})\). Thus
Using basic properties on \({\mathcal {R}}\)-boundedness, we deduce the result. \(\square \)
4.3 The Fluid-Structure Operator
In this subsection we rewrite (4.2) in a suitable operator form. The idea is to eliminate the pressure from both the fluid and the structure equations. To eliminate the pressure from the fluid equation we use the Leray projector \({\mathcal {P}}\) defined in Eq. (4.4). Following [39], we first decompose the fluid velocity into two parts \({\mathcal {P}}v\) and \((\mathrm{Id}-{\mathcal {P}})v.\) Next, we split the pressure into two parts, one which depends on \({\mathcal {P}} v\) and another part which depends on \(\eta _{2}.\) This will lead us to an equation of evolution for \(({\mathcal {P}} v, \eta _{1}, \eta _{2})\) and an algebraic equation for \((\mathrm{Id}- {\mathcal {P}})v.\)
The advantage of this formulation is that the \({\mathcal {R}}\)-boundedness of the fluid-structure operator can be obtained just by using the fact that the operators \(A_{F}\) and \(A_{S}\) are \({\mathcal {R}}\)-sectorial and a perturbation argument. This idea has been used in several fluid-solid interaction problems in the Hilbert space setting as well as in \(L^{q}\)-setting (see, for instance, [27, 34, 36, 40] and the references therein).
Let us consider the following problem :
From [42, Proposition 2.3, p. 35], we have the following result:
Lemma 4.3
Assume \(1< q < \infty \). For any \(f \in L^{q}({\mathcal {F}})\) and \(g \in W^{2,q}_{0,m}({\mathcal {S}})\), the system (4.6) admits a unique solution \((w,\psi )\in W^{2,q}({\mathcal {F}}) \times W_{m}^{1,q}({\mathcal {F}}).\)
This allows us to introduce the following operators: we consider
defined by
where \((w,\psi )\) is the solution to the problem (4.6) associated with g and in the case \(f = 0.\)
Second, we consider the Neumann problem
Let us denote by N the operator defined by
Using classical results (see for instance Theorem 4.2 and Theorem 4.3 of [33]), we have the following properties of N:
for any \(\varepsilon > 0.\) We recall that \(W^{-1/q,q}_{m}(\partial {\mathcal {F}})\) is defined as follows:
where \(q'\) the conjugate exponent of q.
We also define
From the above properties of N, we deduce that
for any \(\varepsilon > 0.\)
Finally, we introduce the operator \(N_{HW} \in {\mathcal {L}}(L^{q}({\mathcal {F}}), W^{1,q}_{m}({\mathcal {F}}))\) defined by
where \(\varphi \) solves (4.5).
Using the above operators, we can obtain the following proposition. The proof is similar to the proof of [36, Proposition 3.7]. For the sake of completeness, we provide a short proof here.
Proposition 4.4
Let \(1<p,q<\infty .\) Assume
Then \((v,\pi , \eta _{1}, \eta _{2})\) is a solution of (4.2) if and only if
Proof
Considering the equation satisfied by \((v - D_{\mathrm{v}} g,\pi - D_{\mathrm{p}} g)\), we obtain (4.16)\(_{1}\) and (4.16)\(_{5}.\) Using (4.4) and (4.5), it follows that \(\Delta (\mathrm{Id}- {\mathcal {P}} ) v = 0\) in \({\mathcal {F}}.\) Thus applying the divergence and normal trace operators to (4.6), we infer that
Note that \(\mathrm{div}\,\Delta {\mathcal {P}} v = 0\) and therefore \(\Delta {\mathcal {P}} v \cdot n\) belongs to \(W^{-1/q,q}_{m}(\partial {\mathcal {F}}).\) The expression of \(\psi \) then follows from the definition of the operators N, \(N_S\) and \(N_{HW}\) defined in (4.10), (4.13) and (4.15) respectively. Finally, using the expression of the pressure \(\pi \) we can rewrite the equation satisfied by \(\eta _{2}\) as in (4.16)\(_{3}.\) \(\square \)
In the literature, the operator
is known as the added mass operator. We are going to show that it is invertible.
Lemma 4.5
The operator \(M_{S} = \mathrm{Id}+ \gamma _{m} N_{S} \in {\mathcal {L}}(L^{q}_{m}({\mathcal {S}}))\) is an automorphism in \(W^{s,q}_{m}({\mathcal {S}})\) for any \(s \in [0,1).\) Moreover, \(M_{S}^{-1} - \mathrm{Id}\in {\mathcal {L}}(L^{q}_{m}({\mathcal {S}}), W^{s,q}_{m}({\mathcal {S}})),\) for any \(s \in [0,1).\) In particular, \(M_{S}^{-1} - \mathrm{Id}\) is a compact operator on \(L^{q}_{m}({\mathcal {S}}).\)
Proof
At first, we show that \(M_{S}\) is an invertible operator on \(L^{q}_{m}({\mathcal {S}}).\) Since
for any \(\varepsilon \in (0,1]\), it is sufficient to show that the kernel of \(M_S\) is reduced to \(\{0\}\): assume
Then \(f\in W^{1-\varepsilon ,q}_{m}({\mathcal {S}})\subset L^{2}_{m}({\mathcal {S}})\) for \(\varepsilon \) small enough. In particular (see (4.13)), \(\vartheta = N_{S} f \in H^1({\mathcal {F}})\) is the weak solution of
Multiplying (4.18) by f and using the above system, we deduce after integration by parts,
Thus \(f = 0\) and \(M_{S}\) is an invertible operator on \(L^{q}_{m}({\mathcal {S}}).\) Let \(s\in [0,1)\) and \(f_{0} \in W^{s,q}_{m}({\mathcal {S}}).\) By the above argument, there exists a unique \(f \in L^{q}_{m}({\mathcal {S}})\) such that
As \(\gamma _{m}N_{S} f\in W^{s.q}_{m}({\mathcal {S}})\) we conclude that \(f \in W^{s,q}_{m}({\mathcal {S}}).\) Thus \(M_{S}\) is an invertible operator on \(W^{s,q}_{m}({\mathcal {S}}).\) Finally, the compactness of the operator \(M_{S}^{-1} - \mathrm{Id}\) follows from the following identity
\(\square \)
We are now in a position to rewrite the system (4.2) in a suitable operator form. Let us set
and consider the operator \({\mathcal {A}}_{FS} : {\mathcal {D}}({\mathcal {A}}_{FS}) \rightarrow {\mathcal {X}}\) defined by
and
with
and
Combining Proposition 4.4 and Lemma 4.5, we can rewrite the system (4.2) as
where
4.4 \({\mathcal {R}}\)-Sectoriality of the Operator \({\mathcal {A}}_{FS}\)
In this subsection we prove the following theorem
Theorem 4.6
Let \(1< q < \infty .\) There exists \(\gamma _{2} > 0\) such that \({\mathcal {A}}_{FS} - \gamma _{2}\) is an \({\mathcal {R}}\)-sectorial operator in \({\mathcal {X}}\) of angle \(>\pi /2.\) Moreover the operator \({\mathcal {A}}_{FS}\) generates an exponentially stable semigroup on \({\mathcal {X}}:\) there exist constants \(C> 0\) and \(\beta _{0} > 0\) such that
Proof
Observe that
where \(\widetilde{D}_{\mathrm{v}} \left[ f_{1}, f_{2} \right] ^{\top } =D_{\mathrm{v}} {f}_{2}.\) Using a standard transposition method and Lemma 4.3, we see that
Therefore by Theorems 4.1 and 4.2, there exists \(\gamma > 0\) such that \({\mathcal {A}}_{FS}^{0}-\gamma \) is \({\mathcal {R}}\)-sectorial operator in \({\mathcal {X}}\) of angle \(> \pi /2.\)
Next, we want to show \({\mathcal {B}}_{FS} \in {\mathcal {L}}({\mathcal {D}}({\mathcal {A}}_{FS}), {\mathcal {X}})\) is a compact operator. Assume \([v,\eta _1,\eta _2]^{\top }\in {\mathcal {D}}({\mathcal {A}}_{FS})\). Then \(\Delta v\in L^{q}({\mathcal {F}})\) and \(\mathrm{div}\,\Delta v= 0\) and thus from the trace result recalled in Sect. 4.1,
This yields \(N((\Delta v) \cdot n) \in W^{1,q}_{m}({\mathcal {F}})\), \(\gamma _m N((\Delta v) \cdot n) \in W_m^{1-1/q,q}({\mathcal {S}})\) and, using Lemma 4.5,
On the other hand, using again Lemma 4.5, we deduce
for any \(\varepsilon >0\). Therefore, \({\mathcal {B}}_{FS} \in {\mathcal {L}}({\mathcal {D}}({\mathcal {A}}_{FS}), {\mathcal {X}})\) is a compact operator and by [14, Chapter III, Lemma 2.16], \({\mathcal {B}}_{FS}\) is a \({\mathcal {A}}_{FS}^0\)-bounded operator with relative bound 0. Finally, using Proposition 3.5 we conclude the first part of the theorem. In particular \({\mathcal {A}}_{FS}\) generates an analytic semigroup and to show the second part of the theorem, it is sufficient to show that
Moreover, using that \({\mathcal {A}}_{FS}\) has a compact resolvent and the Fredholm alternative theorem, we can show the above relation by proving that \(\ker (\lambda - {\mathcal {A}}_{FS})=\{0\}\) for \(\lambda \in {\mathbb {C}}^{+}\). Assume \(\lambda \in {\mathbb {C}}^{+}\) and
satisfy
First we notice that
If \(q \geqslant 2\) then it is a consequence of Hölder’s inequality. Let us assume that \(1< q< 2\) and let us take \(\lambda _0 \in \rho ({\mathcal {A}}_{FS})\) (see Theorem 4.6). We have
By following the calculation done in Sect. 4.3, we see that the system (4.28) can be written as
Since \(W^{2,q}({\mathcal {F}}) \subset L^{2}({\mathcal {F}}),\) \(W^{2,q}({\mathcal {S}}) \subset L^{2}({\mathcal {S}})\) and \((\lambda _0 - {\mathcal {A}}_{FS})\) is invertible, we deduce (4.29).
Using (4.29), we can multiply (4.28)\(_{1}\) by \(\overline{v}\) and (4.28)\(_{5}\) by \(\overline{\eta _{2}},\) and we obtain after integration by parts:
Since \(\mathrm {Re} \lambda \geqslant 0,\) from the above equality and using the boundary conditions we obtain that \(v = \pi = \eta _{1} =\eta _{2} = 0.\) This completes the proof of the theorem. \(\square \)
In order to obtain a result of well-posedness on the system (4.2), we need to impose some compatibility conditions on the data:
and
We deduce from Theorem 4.6 the following result
Corollary 4.7
Let \(p,q\in (1,\infty )\) with \(\displaystyle \frac{1}{p} + \frac{1}{2q} \ne \frac{1}{2},\) \(\displaystyle \frac{1}{p} + \frac{1}{2q} \ne 1\) and let \(\beta \in [0,\beta _{0}],\) where \(\beta _{0}\) is the constant in Theorem 4.6. Assume
satisfy the compatibility conditions (4.30) and (4.31). Then the system (4.2) admits a unique strong solution
Moreover, there exists a constant \(C_{L}\) depending on p, q and the geometry such that
Proof
Let us first consider the case \(\beta =0.\) Using (4.25), (4.15) and Lemma 4.5 we can also verify that \(\overline{h} \in L^{p}(0,\infty ;L^{q}_{m}({\mathcal {S}})).\)
The compatibility conditions (4.30), (4.31) and the interpolation results [3, Theorem 3.4] and [4, Theorem 4.9.1 and Example 4.9.3]) yield
and
From Theorem 4.6, we know that \({\mathcal {A}}_{FS}\) generates an analytic exponentially stable semigroup on \({\mathcal {X}}\) and is a \({\mathcal {R}}\)-sectorial operator on \({\mathcal {X}}.\) Therefore by Corollary 3.4
We deduce from (4.23), (4.7) and (4.27) that \(v \in W^{1,2}_{p,q}((0,\infty ) ; {\mathcal {F}})\) and next using relations (4.11), (4.14) and (4.15), we obtain \(\pi \in L^{p}(0,\infty ;W^{1,q}_{m}({\mathcal {F}})).\)
The case \(\beta > 0\) can be reduced to the previous case by multiplying all the functions by \(e^{\beta t}\) and using the fact that \({\mathcal {A}}_{FS} + \beta \) is a \({\mathcal {R}}\)-sectorial operator and generates an exponentially stable semigroup. \(\square \)
5 Local in Time Existence
The aim of this section is to prove Theorems 1.1 and 2.2. Throughout this section we assume the following
Assumption 5.1
\(\eta _{1}^{0} = 0\), \((p,q) \in (1,\infty )\) satisfies (1.15) and \((\eta _2^0,v^0)\) satisfies (2.18), (2.19), (2.20).
For \(T>0\) and \(R>0\), we define \({\mathbb {S}}_{T,R}\) as follows
In order to prove Theorem 2.2, we show that for R fixed and for T small, we can define the map
where \((v, \pi , \eta )\) is the solution to the system (4.2) in \((0,T) \times {\mathcal {F}}\) (see Corollary 4.7) and where F and H are given by (2.13)–(2.14). Then we show that for T small enough and R fixed \({\mathcal {N}}_{T,R}({\mathbb {S}}_{T,R}) \subset {\mathbb {S}}_{T,R}\) (see Proposition 5.2 below) and that, \({\mathcal {N}}_{T,R}|_{{\mathbb {S}}_{T,R}}\) is a strict contraction (see Proposition 5.3 below). This shows that \({\mathcal {N}}_{T,R}\) admits a unique fixed point and allows us to deduce Theorem 2.2.
First, we deduce from Corollary 4.7 that
We take in what follows
and the constants below may depend on R, but not on T. In order to simplify the computation, we also assume that \(T\in (0,1)\).
With these conventions, by using [44, (7), p.196], we have that for any \(s_{1}\in (0,2(1-1/p))\), with \(s_{1}\) not an integer,
Since \(\eta (0,\cdot ) = 0,\) we have
Thus, by interpolation between (5.4) and (5.5) ([43, Theorem 2, p. 317]), we deduce that for any \(s_{1}\in (0,2(1-1/p))\), there exists \(\varepsilon =\varepsilon (s_1)>0\) such that
From (1.15), there exists \(s_{1}\in (0,2(1-1/p))\), such that \(s_1+1>3/q\) and thus with the Sobolev embeddings, we deduce that
Therefore, for T small enough, \(\eta (t,\cdot )\) satisfies (2.1) for all \(t\in [0,T]\) where \(c_{0}\) is defined in (2.5). We can thus construct X by (2.6) so that \(X(t,\cdot )\) is a \(C^{1}\)-diffeomorphism from \({\mathcal {F}}\) onto \({\mathcal {F}}(\eta (t)).\) We can also consider \(F(v, \pi , \eta )\) and \(H(v, \pi , \eta ))\) given by (2.13)–(2.14). In order to estimate these expressions, we also note that by (real or complex) interpolation ([43, Theorem 2, p. 317]) for \(\theta \in (0,1)\),
if \(s_2\) is not an integer. We can find \(\theta \in (0,1/3)\) and \(s_{1}\in (0,2(1-1/p))\) such that \(s_2 \geqslant 2/q\) so that by Sobolev embeddings,
and similarly,
We are now in position to prove the following result:
Proposition 5.2
With the above assumptions (in particular Assumption 5.1), there exists \(T>0\) small enough such that the map \({\mathcal {N}}_{T,R}\) (see (5.2)) is well-defined and satisfies \({\mathcal {N}}_{T,R}({\mathbb {S}}_{T,R}) \subset {\mathbb {S}}_{T,R}\).
Proof
From (2.4) and (5.7), we deduce that for \(T>0\) small enough
We recall that a and b are defined by (2.11).
By using standard properties of linear algebra, we have that
and thus for all i, j, k,
We also have
Combining the above estimates with (5.8), (5.9) and (5.10), we deduce that F defined by (2.13) satisfies
Using trace theorems, we deduce from (5.3) and from (5.10) that
From this relation, the above estimates and (5.9), (5.10), we deduce that H defined by (2.14) satisfies
Relations (5.20) and (5.21) yield that \({\mathcal {N}}({\mathcal {B}}_{T,R}) \subset {\mathcal {B}}_{T,R}\) for T small enough. \(\square \)
Proposition 5.3
With the above assumptions (in particular Assumption 5.1), there exists \(T>0\) small enough such that the map \({\mathcal {N}}_{T,R}\) (see (5.2)) is a strict contraction on \({\mathbb {S}}_{T,R}\).
Proof
The proof is similar to the proof of Proposition 5.2, we only give the main ideas and omit the details. We consider \((f^{(i)}, h^{(i)})\), \(i=1,2\). We have
where \((v^{(i)}, \pi ^{(i)}, \eta ^{(i)})\) is the solution to the system (4.2) in \((0,T) \times {\mathcal {F}}\) (see Corollary 4.7) associated with \((f^{(i)}, h^{(i)})\), \(i=1,2\) and where F and H are given by (2.13)-(2.14). By taking T as Proposition 5.2, we have for each i that \((v^{(i)}, \pi ^{(i)}, \eta ^{(i)})\) satisfies the same property obtained in the proof of Proposition 5.2 and in particular, \(X^{(i)}\), \(Y^{(i)}\), \(a^{(i)}\), \(b^{(i)}\) defined by (2.6) and (2.11) satisfy also the same properties obtained in the proof of Proposition 5.2.
We write
Applying Corollary 4.7, we first obtain
As in the proof of Proposition 5.2, the constants below may depend on R, but not on T and we assume \(T\in (0,1)\) to simplify. Following the proof of (5.7), we can obtain
and following the proof of (5.8), (5.9) and (5.10), we deduce
and
Using trace theorems, we deduce from the above estimates that
We also deduce from the above estimate and from (2.6) that
From (5.14) and from the above estimates, we obtain for all i, j, k,
Combining the above estimates with (5.11)–(5.19), with (5.8)–(5.10) and with (5.25)–(5.26), we deduce that
Thus for T small enough, we deduce the result. \(\square \)
6 Global in Time Existence
The aim of this section is to prove Theorem 1.2 and Theorem 2.3. The proof is similar to the proof of Theorem 1.1 and Theorem 2.2 given in Sect. 5. Throughout this section we assume the following
Assumption 6.1
\((p,q) \in (1,\infty )\) satisfies (1.15) and \((\eta _1^0,\eta _2^0,v^0)\) satisfies (2.18), (2.19), (2.20).
Let us fix \(\beta \in [0, \beta _{0}],\) where \(\beta _{0}\) is introduced in Corollary 4.7 and for \(R>0\), we define \({\mathbb {S}}_{R}\) as follows
We take in what follows
and to simplify the computation, we assume that \(R\in (0,1)\).
In order to prove Theorem 2.3, we show that for R small, we can define the map
where \((v, \pi , \eta )\) is the solution to the system (4.2) in \((0,\infty ) \times {\mathcal {F}}\) (see Corollary 4.7) and where F and H are given by (2.13)–(2.14). Then we show that for R small enough \({\mathcal {N}}_R({\mathbb {S}}_{R}) \subset {\mathbb {S}}_{R}\) (see Proposition 6.2 below) and that, \({\mathcal {N}}_R|_{{\mathbb {S}}_{R}}\) is a strict contraction (see Proposition 6.3 below). This shows that \({\mathcal {N}}_{R}\) admits a unique fixed point and allows us to deduce Theorem 2.3.
First, we deduce from Corollary 4.7 that
By using [44, (7), p.196] and the Sobolev embeddings, we deduce from the above estimate
Therefore, for R small enough, \(\eta (t,\cdot )\) satisfies (2.1) for all \(t\in [0,\infty )\) where \(c_{0}\) is defined in (2.5). We can thus construct X by (2.6) so that \(X(t,\cdot )\) is a \(C^{1}\)-diffeomorphism from \({\mathcal {F}}\) onto \({\mathcal {F}}(\eta (t)).\) We can also consider \(F(v, \pi , \eta )\) and \(H(v, \pi , \eta ))\) given by (2.13)–(2.14).
As in the previous section, we use (real or complex) interpolation results ([43, Theorem 2, p. 317]) to deduce that
for any \(s_2<2(1+s_1)/3\). Using (1.15), there exists \(s_{1}\in (0,2(1-1/p))\) such that \(s_2 \geqslant 2/q\) so that by Sobolev embeddings,
and similarly,
and
Using trace theorems, we deduce from (6.3) and from (6.7) that
We are now in position to prove the following result:
Proposition 6.2
With the above assumptions (in particular Assumption 6.1), there exists \(R>0\) small enough such that the map \({\mathcal {N}}_{R}\) (see (6.2)) is well-defined and satisfies \({\mathcal {N}}_{R}({\mathbb {S}}_{R}) \subset {\mathbb {S}}_{R}\).
Proof
From (2.4) and (6.4), we deduce that for \(T>0\) small enough
We recall that a and b are defined by (2.11).
Using the above estimates, relations (5.15)–(5.19), (6.3), (6.5), (6.6), (6.7) and (6.8) we deduce that F and H defined by (2.13), (2.14) satisfy
which yields that \({\mathcal {N}}_R({\mathbb {S}}_{R}) \subset {\mathcal {S}}_{R}\) for R small enough. \(\square \)
We can also prove the following result by following the method used to prove Proposition 5.3 (we omit the proof).
Proposition 6.3
With the above assumptions (in particular Assumption 6.1), there exists \(R>0\) small enough such that the map \({\mathcal {N}}_{R}\) (see (6.2)) is a strict contraction on \({\mathbb {S}}_{R}\).
By combining Propositions 6.2 and 6.3, we deduce Theorem 2.3.
References
Adams, R.A., Fournier, J.J.F.: Sobolev spaces, vol. 140 of Pure and Applied Mathematics (Amsterdam), 2nd ed. Elsevier/Academic Press, Amsterdam (2003)
Amann, H.: Linear and quasilinear parabolic problems. Vol. I, vol. 89 of Monographs in Mathematics, Birkhäuser Boston, Inc., Boston, MA, (1995). Abstract linear theory
Amann, H.: On the strong solvability of the Navier–Stokes equations. J. Math. Fluid Mech. 2, 16–98 (2000)
Amann, H.: Anisotropic function spaces and maximal regularity for parabolic problems. Part 1, vol. 6 of Jindřich Nečas Center for Mathematical Modeling Lecture Notes, Matfyzpress, Prague, (2009). Function spaces
Badra, M., Takahashi, T.: Feedback boundary stabilization of 2D fluid-structure interaction systems. Discrete Contin. Dyn. Syst. 37, 2315–2373 (2017)
Badra, M., Takahashi, T.: Gevrey regularity for a system coupling the Navier–Stokes system with a beam equation. SIAM J. Math. Anal. 51, 4776–4814 (2019)
Beirão da Veiga, H.: On the existence of strong solutions to a coupled fluid-structure evolution problem. J. Math. Fluid Mech. 6, 21–52 (2004)
Bravin, M.: Energy equality and uniqueness of weak solutions of a viscous incompressible fluid + rigid body system with Navier slip-with-friction conditions in a 2D bounded domain. J. Math. Fluid Mech. 21, 31 (2019)
Chambolle, A., Desjardins, B., Esteban, M.J., Grandmont, C.: Existence of weak solutions for the unsteady interaction of a viscous fluid with an elastic plate. J. Math. Fluid Mech. 7, 368–404 (2005)
Clément, P., Prüss, J.: An operator-valued transference principle and maximal regularity on vector-valued \(L_p\)-spaces, In: Evolution equations and their applications in physical and life sciences (Bad Herrenalb, 1998), vol. 215 of Lecture Notes in Pure and Appl. Math., Dekker, New York, (2001), pp. 67–87
Denk, R., Hieber, M., Prüss, J.: \({\mathscr {R}}\)-boundedness, Fourier multipliers and problems of elliptic and parabolic type. Mem. Am. Math. Soc. 166, viii+114 (2003)
Denk, R., Schnaubelt, R.: A structurally damped plate equation with Dirichlet-Neumann boundary conditions. J. Differ. Equ. 259, 1323–1353 (2015)
Dore, G.: \(L^p\) regularity for abstract differential equations, In: Functional analysis and related topics, 1991 (Kyoto), vol. 1540 of Lecture Notes in Math. Springer, Berlin, (1993), pp. 25–38
Engel, K.-J., Nagel, R.: One-parameter semigroups for linear evolution equations, vol. 194 of Graduate Texts in Mathematics, Springer-Verlag, New York, (2000). With contributions by S. Brendle, M. Campiti, T. Hahn, G. Metafune, G. Nickel, D. Pallara, C. Perazzoli, A. Rhandi, S. Romanelli and R. Schnaubelt
Enomoto, Y., Shibata, Y.: On the \({\mathscr {R}}\)-sectoriality and the initial boundary value problem for the viscous compressible fluid flow. Funkcial. Ekvac. 56, 441–505 (2013)
Ervedoza, S., Hillairet, M., Lacave, C.: Long-time behavior for the two-dimensional motion of a disk in a viscous fluid. Commun. Math. Phys. 329, 325–382 (2014)
Fujiwara, D., Morimoto, H.: An \(L_{r}\)-theorem of the Helmholtz decomposition of vector fields. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24, 685–700 (1977)
Geissert, M., Götze, K., Hieber, M.: \(L^p\)-theory for strong solutions to fluid-rigid body interaction in Newtonian and generalized Newtonian fluids. Trans. Am. Math. Soc. 365, 1393–1439 (2013)
Geissert, M., Hess, M., Hieber, M., Schwarz, C., Stavrakidis, K.: Maximal \(L^p\)-\(L^q\)-estimates for the Stokes equation: a short proof of Solonnikovs theorem. J. Math. Fluid Mech. 12, 47–60 (2010)
Glass, O., Sueur, F.: Uniqueness results for weak solutions of two-dimensional fluid-solid systems. Arch. Ration. Mech. Anal. 218, 907–944 (2015)
Grandmont, C.: Existence of weak solutions for the unsteady interaction of a viscous fluid with an elastic plate. SIAM J. Math. Anal. 40, 716–737 (2008)
Grandmont, C., Hillairet, M.: Existence of global strong solutions to a beam-fluid interaction system. Arch. Ration. Mech. Anal. 220, 1283–1333 (2016)
Grandmont, C., Hillairet, M., Lequeurre, J.: Existence of local strong solutions to fluid-beam and fluid-rod interaction systems. Ann. de lInstitut Henri Poincaré C Anal. Non Linéaire 36, 1105–1149 (2019)
Grandmont, C., Lukáčová-Medvid’ová, M., Nečasová, V.: Mathematical and numerical analysis of some FSI problems. In: Fluid-structure interaction and biomedical applications. Adv. Math. Fluid Mech., Birkhäuser/Springer, Basel, pp. 1–77 (2014)
Guidoboni, G., Guidorzi, M., Padula, M.: Continuous dependence on initial data in fluid-structure motions. J. Math. Fluid Mech. 14, 1–32 (2012)
Guidorzi, M., Padula, M., Plotnikov, P.I.: Hopf solutions to a fluid-elastic interaction model. Math. Models Methods Appl. Sci. 18, 215–269 (2008)
Haak, B.H., Maity, D., Takahashi, T., Tucsnak, M.: Mathematical analysis of the motion of a rigid body in a compressible Navier–Stokes–Fourier fluid. Math. Nachr. 292, 1972–2017 (2019)
Hieber, M., Murata, M.: The \(L^p\)-approach to the fluid-rigid body interaction problem for compressible fluids. Evol. Equ. Control Theory 4, 69–87 (2015)
Kunstmann, P.C., Weis, L.: Perturbation theorems for maximal \(L_{p}\)-regularity. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 30(4), 415–435 (2001)
Kunstmann, P.C., Weis, L.: Maximal \(L_{p}\)-regularity for parabolic equations, Fourier multiplier theorems and \(H^{\infty }\)-functional calculus. In: Functional analytic methods for evolution equations, vol. 1855 of Lecture Notes in Math. Springer, Berlin, pp. 65–311 (2004)
Lacave, C., Takahashi, T.: Small moving rigid body into a viscous incompressible fluid. Arch. Ration. Mech. Anal. 223, 1307–1335 (2017)
Lequeurre, J.: Existence of strong solutions to a fluid-structure system. SIAM J. Math. Anal. 43, 389–410 (2011)
Lions, J.-L., Magenes, E.: Problemi ai limiti non omogenei. V, Ann. Scuola Norm Sup. Pisa 16(3), 1–44 (1962)
Maity, D., Raymond, J.-P., Roy, A.: Maximal-in-time existence and uniqueness of strong solution of a 3D fluid-structure interaction model. SIAM J. Math. Anal. 52, 6338–6378 (2020)
Maity, D., Tucsnak, M.: A maximal regularity approach to the analysis of some particulate flows, In: Particles in flows. Adv. Math. Fluid Mech., Birkhäuser/Springer, Cham, pp. 1–75 (2017)
Maity, D., Tucsnak, M.: \(L^p\)-\(L^q\) maximal regularity for some operators associated with linearized incompressible fluid-rigid body problems Selected Recent Results. In: Mathematical analysis in fluid mechanics selected recent results, vol. 710 of Contemp. Math. Amer. Math. Soc., Providence, RI, pp. 175–201 (2018)
Muha, B., Canić, S.: Existence of a weak solution to a nonlinear fluid-structure interaction problem modeling the flow of an incompressible, viscous fluid in a cylinder with deformable walls. Arch. Ration. Mech. Anal. 207, 919–968 (2013)
Quarteroni, A., Tuveri, M., Veneziani, A.: Computational vascular fluid dynamics: problems, models and methods. Comput. Vis. Sci. 2, 163–197 (2000)
Raymond, J.-P.: Stokes and Navier–Stokes equations with nonhomogeneous boundary conditions. Ann. Inst. H. Poincaré Anal. Non Linéaire 24, 921–951 (2007)
Raymond, J.-P.: Feedback stabilization of a fluid-structure model. SIAM J. Control Optim. 48, 5398–5443 (2010)
Runst, T., Sickel, W.: Sobolev spaces of fractional order, Nemytskij operators, and nonlinear partial differential equations. vol. 3 of De Gruyter Series in Nonlinear Analysis and Applications, Walter de Gruyter & Co., Berlin (1996)
Temam, R.: Navier-Stokes equations, vol. 2 of Studies in Mathematics and its Applications, North-Holland Publishing Co., Amsterdam-New York, revised ed., (1979). Theory and numerical analysis, With an appendix by F. Thomasset
Triebel, H.: Interpolation Theory, Function Spaces, Differential Operators, 2nd edn. Johann Ambrosius Barth, Heidelberg (1995)
Triebel, H.: Theory of function spaces, Modern Birkhäuser Classics, Birkhäuser/Springer Basel AG, Basel, (2010). Reprint of 1983 edition [MR0730762], Also published in 1983 by Birkhäuser Verlag [MR0781540]
Weis, L.: Operator-valued Fourier multiplier theorems and maximal \(L_p\)-regularity. Math. Ann. 319, 735–758 (2001)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by C. Grandmont.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Debayan Maity was partially supported by INSPIRE faculty fellowship (IFA18-MA128) and by Department of Atomic Energy, Government of India, under Project No. 12-R & D-TFR-5.01-0520.
Rights and permissions
About this article
Cite this article
Maity, D., Takahashi, T. \(L^{p}\) Theory for the Interaction Between the Incompressible Navier–Stokes System and a Damped Plate. J. Math. Fluid Mech. 23, 103 (2021). https://doi.org/10.1007/s00021-021-00628-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s00021-021-00628-5
Keywords
- Incompressible Navier–Stokes system
- Fluid-structure interaction
- Strong solutions
- Maximal \(L^{p}\) regularity