Semi-classical 2-dimensional Minkowski planes

Abstract

Semi-classical geometries have been investigated in the context of 2-dimensional affine planes, projective planes, Möbius planes and Laguerre planes. Here we deal with the case of 2-dimensional Minkowski planes. Semi-classical 2-dimensional Minkowski planes are obtained by pasting together two halves of the classical real Minkowski plane along two circles or parallel classes. By solving some functional equations for the functions that describe the pasting we determine all semi-classical 2-dimensional Minkowski planes. In contrast to the rich variety of other semi-classical planes there are only very few models of such Minkowski planes.

1 Introduction

The classical real Minkowski plane can be described as the geometry of the graphs of fractional linear transformations of the 1-sphere $\mathbb {S}^1$. Equivalently, it is obtained as the geometry of plane sections of a non-degenerate ruled quadric in a 3-dimensional projective space over the field $\mathbb {R}$ of real numbers. The point space is homeomorphic to a torus $\mathbb {S}^1 \times \mathbb {S}^1$. Close relatives of the classical real Minkowski plane are the so-called 2-dimensional Minkowski planes where the fractional linear transformations are replaced by a suitable collection of homeomorphisms of $\mathbb {S}^1$, see Sect. 2 for a more explicit definition. There are various ways to characterize the classical real Minkowski plane among all 2-dimensional Minkowski planes, see [6, Theorem 4.6.13]. In particular, it is the only locally classical 2-dimensional Minkowski plane where each point has a neighbourhood such that the induced geometry on it is isomorphic to a subgeometry of the classical real Minkowski plane.

In this paper we investigate a different kind of 2-dimensional Minkowski plane that is almost locally classical. These are the semi-classical 2-dimensional Minkowski planes. They can be imagined as two halves of the classical real Minkowski plane being pasted together along some circles and/or parallel classes, see Definition 2.1 for a more precise definition. Clearly, almost all points have classical neighbourhoods except those points on circles or parallel classes along which we paste.

Similar notions of semi-classical planes have been used in (topological, locally compact) 2-dimensional affine planes, projective planes, Möbius planes and Laguerre planes, see [6, 2.7.2, 3.3.3 and 5.3.2]. Many different models were obtained for each of these semi-classical planes.

Although there are many combinations of circles and parallel classes possible whose removal will disconnect the point space of the classical real Minkowski plane, there are only a few proper (non-classical) semi-classical 2-dimensional Minkowski planes. These are obtained by removing a set consisting of two parallel classes of the same type. We show that there is only one one-parameter family of semi-classical 2-dimensional Minkowski planes.

MainTheorem

A 2-dimensional Minkowski plane is semi-classical if and only if it is isomorphic to a Minkowski plane $\mathcal {M}(f_k,\textrm{id})$ where $f_k:\mathbb {R}\cup \{\infty \} \rightarrow \mathbb {R}\cup \{\infty \}$, $k>0$, is given by

$$\begin{aligned} f_k(x) = {\left\{ \begin{array}{ll} x, &{}\text{ if } x\ge 0,\\ kx, &{}\text{ if } x<0,\\ \infty , &{}\text{ if } x=\infty , \end{array}\right. } \end{aligned}$$

see Remark 2.4 for a description of the Minkowski planes $\mathcal {M}(f,\textrm{id})$. Furthermore, the planes $\mathcal {M}(f_k,\textrm{id})$, $0<k\le 1$, are pairwise non-isomorphic.

In Sect. 2 we give a summary of some basic geometric and topological properties of 2-dimensional Minkowski planes and introduce semi-classical 2-dimensional Minkowski planes. Furthermore, the first, and as it turns out only, examples of proper (non-classical) semi-classical 2-dimensional Minkowski planes are described. The following Sect. 3 deals with semi-classical 2-dimensional Minkowski planes obtained by pasting along two disjoint parallel classes and completely classifies those planes. In the last Sect. 4 semi-classical 2-dimensional Minkowski planes obtained by pasting along two circles are investigated. The cases where the circles intersect in two points, are tangent or are disjoint are treated separately. In each case it is shown that only the classical real Minkowski plane can arise.

2 Two-dimensional Minkowski planes

A Minkowski plane $\mathcal {M}=(P,\mathcal {C},\{||_+,||_-\})$ is an incidence structure consisting of a point set P, a circle set $\mathcal {C}$, elements of which are nonempty subsets of P, and two equivalence relations $||_+$ and $||_-$ (parallelisms) defined on the point set such that three mutually non-parallel points can be joined by a unique circle, such that the circles which touch a fixed circle K at $p \in K$ partition $P \setminus [p]$ where [p] denotes the set of all points parallel to p, such that each parallel class meets each circle in a unique point (parallel projection), such that each (+)-parallel class and each (–)-parallel class intersect in a unique point, and such that there is a circle that contains at least three points (richness); compare [2, III.4], [7, 4] or [3]. It readily follows that for each point p of $\mathcal {M}$ the incidence structure $\mathcal {A}_p=(A_p,\mathcal {L}_p)$ whose point set $A_p$ consists of all points of $\mathcal {M}$ that are not parallel to p and whose line set $\mathcal {L}_p$ consists of all restrictions to $A_p$ of circles of $\mathcal {M}$ passing through p and of all parallel classes not passing through p is an affine plane, called the derived affine plane at p.

In this paper we are only concerned with 2-dimensional Minkowski planes whose common point set is the torus $\mathbb {S}^1 \times \mathbb {S}^1$ (where $\mathbb {S}^1$ usually is represented as $\mathbb {R}\cup \{\infty \}$), whose circles are graphs of homeomorphisms of $\mathbb {S}^1$ and whose parallel classes of points are the horizontals $\mathbb {S}^1\times \{v\}$ and verticals $\{u\}\times \mathbb {S}^1$ on the torus where $u,v\in \mathbb {S}^1$. We say that $\mathcal {M}$ is in standard representation if parallel classes and circles are represented as above. In this case we will omit the two equivalence relations and simply write $\mathcal {M}=(\mathbb {S}^1 \times \mathbb {S}^1, \mathcal {C})$. Parallel classes are often called generators in the literature.

In 2-dimensional Minkowski planes the geometric operations of joining three mutually non-parallel points by a circle, intersecting of two circles, and touching become continuous when the circle set is suitably topologised. Furthermore, 2-dimensional Minkowski planes are coherent, see [7, Satz 3.17]. In particular, touching is the limit of proper intersection. For more information on 2-dimensional Minkowski planes we refer to [7] and [6, Chapter 4].

In the following sections we represent, for easier visualization, the torus $\mathbb {S}^1\times \mathbb {S}^1$ on the square $Q=[-1,1] \times [-1,1]$ where for each $x\in [-1,1]$ the point $(x,-1)$ is identified with (x, 1) and similarly, for each $y\in [-1,1]$ the point $(-1,y)$ is identified with (1, y). No other points are identified. This is a well-known representation of the torus on the square, see for example [1, §3.3]. The left edge of Q is identified with the right edge, and the top edge of Q is identified with the bottom edge. This identification is indicated by the single and double arrows, which also indicate the orientation of identification, see Fig. 1. (For example, reversing one of the single arrows results in a Klein bottle as identification space.)

Fig. 1

The torus as an identification space

If $h:\mathbb {R}\rightarrow (-1,1)$ is the homeomorphism $h(x)=\frac{x}{1+|x|}$, then $h\times h: \mathbb {R}^2 \rightarrow (-1,1) \times (-1,1), (x,y)\mapsto (h(x),h(y))$ also is a homeomorphism from $\mathbb {R}^2$ to the open square $(-1,1) \times (-1,1)$, and we can transfer circles and parallel classes of the affine part (that is, on $A_{(\infty ,\infty )}$) of a 2-dimensional Minkowski plane onto the open square. With the above identification this yields a representation of the entire 2-dimensional Minkowski plane on Q. Clearly, parallel classes become horizontal and vertical line segments in Q, and the diagonal in $\mathbb {S}^1 \times \mathbb {S}^1$ becomes the diagonal in Q. We will use this representation on Q in the following diagrams. Note that the four vertices of the boundary of Q represent the same point (in the above description the point $(\infty ,\infty )$).

We are interested in collections of parallel classes and circles that separate the torus, that is, their complement in the point set $\mathbb {S}^1\times \mathbb {S}^1$ is disconnected. One readily sees that a single parallel class G or a single circle C or one parallel class and one circle do not separate the torus, see Fig. 2 where a deleted parallel class or circle is indicated by a dashed line segment.

Fig. 2

The torus minus one parallel class, one circle, or one parallel class and one circle

Semi-classical 2-dimensional Minkowski planes can be imagined as two halves of the classical real Minkowski plane being pasted together along some circles and/or parallel classes. By the above we need at least two circles or at least two parallel classes. More formally, we have the following definition.

Definition 2.1

We say that a 2-dimensional Minkowski plane is semi-classical if there are two parallel classes or two circles that separate the torus into two connected components $P_1$ and $P_2$ such that the geometry induced on the closure on each of the connected components is the same as the one induced by the classical real Minkowski plane $\mathcal {M}_\textrm{cl}$.

Remark 2.2

One can more broadly define semi-classical 2-dimensional Minkowski planes by allowing a minimal set of finitely many parallel classes/circles along which the closures of the connected components in the complement are glued together or allowing more than two connected components in their complement. Here minimal means that removal of any one member in the set results in a connected complement. In Fig. 3 the possible extra cases that arise under this broader definition of semi-classical are illustrated.

Fig. 3

Three parallel classes/circles or three connected components

There is a different way to cut-and-paste via separating sets in the circle set. One example is as follows. Let $\mathcal {M}=(\mathbb {S}^1 \times \mathbb {S}^1,\mathcal {C})$ be a 2-dimensional Minkowski plane in standard representation. Let $\mathcal {C}^+$ and $\mathcal {C}^-$ be the sets of all circles in $\mathcal {C}$ that are graphs of orientation-preserving and orientation-reversing homeomorphisms $\mathbb {S}^1\rightarrow \mathbb {S}^1$, respectively. Clearly, $\mathcal {C}=\mathcal {C}^+ \cup \mathcal {C}^-$. We call $\mathcal {C}^+$ the positive half and and $\mathcal {C}^-$ the negative half of $\mathcal {M}$. These two halves are completely independent of each other, that is, we can combine these parts from different 2-dimensional Minkowski planes and obtain another 2-dimensional Minkowski plane; see [5, Proposition 3] or [6, Theorem 4.3.1].

Theorem 2.3

Let $\mathcal {M}_i =(\mathbb {S}^1 \times \mathbb {S}^1,\mathcal {C}_i)$, $i=1,2$ be two 2-dimensional Minkowski planes. Then the geometry $\mathcal {M}=(\mathbb {S}^1 \times \mathbb {S}^1,\mathcal {C}_1^+\cup \mathcal {C}_2^-)$ is a 2-dimensional Minkowski plane.

Remark 2.4

In other words, the above Theorem says that we can exchange one half of the circle set of one 2-dimensional Minkowski plane by the corresponding half from another 2-dimensional Minkowski plane and obtain again 2-dimensional Minkowski plane. This method has been used to construct a variety of Minkowski planes from two different models of the classical real Minkowski plane $\mathcal {M}_\textrm{cl}$, see [6, 4.3.1] or [10]. Circles of $\mathcal {M}_\textrm{cl}$ are the graphs of transformations in $\textrm{PGL}(2,\mathbb {R})$, the projective linear group of all fractional linear transformations of $\mathbb {S}^1$. Furthermore, the positive and negative halves of $\mathcal {M}_\textrm{cl}$ consist of all graphs of transformations in $\textrm{PGL}^+(2,\mathbb {R}) = \textrm{PSL}(2,\mathbb {R})$ and $\textrm{PGL}^-(2,\mathbb {R}) = \textrm{PGL}(2,\mathbb {R}) \setminus \textrm{PSL}(2,\mathbb {R})$, respectively, where $\textrm{PSL}(2,\mathbb {R})$ is the unique normal subgroup of index 2 in $\textrm{PGL}(2,\mathbb {R})$.

Let f and g be two orientation-preserving homeomorphisms of $\mathbb {S}^1$. Then $(x,y)\mapsto (f(x),g(y))$ is an isomorphism from $\mathcal {M}_\textrm{cl}$ to another copy of $\mathcal {M}_\textrm{cl}$. We now swap the negative halves of these two planes. More precisely, we replace all graphs of transformations in $\textrm{PGL}^-(2,\mathbb {R})$ by graphs of transformations in $g^{-1}\textrm{PGL}^-(2,\mathbb {R}) f$. The 2-dimensional Minkowski plane one obtains according to Theorem 2.3 is denoted by $\mathcal {M}(f,g)$. Note that each 2-dimensional Minkowski plane $\mathcal {M}(f,g)$ is isomorphic to one where both describing homeomorphisms f and g fix $\infty$, 1 and 0 and that the homeomorphism $(x,y) \mapsto (y,x)$ of $\mathbb {S}^1\times \mathbb {S}^1$ to itself defines an isomorphism from $\mathcal {M}(f,g)$ to $\mathcal {M}(g,f)$.

By construction $\mathcal {M}(f_k,\textrm{id})$ is a 2-dimensional Minkowski plane. Since the restriction of $f_k$ on the interval $(-\infty ,0)$ is linear and its restriction on $(0,\infty )$ is the identity, one readily obtains the following.

Theorem 2.5

The planes $\mathcal {M}(f_k,\textrm{id})$ where $f_k$, $k>0$, is as in the Main Theorem are semi-classical 2-dimensional Minkowski planes.

We will show that a semi-classical 2-dimensional Minkowski plane is isomorphic to a plane $\mathcal {M}(f_k, \textrm{id})$ from Theorem 2.5 with $0<k\ge 1$. Note that $\mathcal {M}(f_1, \textrm{id})$ is the classical real Minkowksi plane.

An automorphism of a Minkowski plane is a permutation of the point set such that parallel classes are mapped to parallel classes and circles are mapped to circles. Every automorphism of the classical real Minkowski plane is of the form $(x,y)\mapsto (\gamma (x),\delta (y))$ or $(x,y)\mapsto (\delta (y), \gamma (x))$ where $\gamma , \delta \in \textrm{PGL}(2,\mathbb {R})$. By [8] each classical subgeometry of a semi-classical 2-dimensional Minkowski plane can be uniquely embedded into the classical real Minkowski plane $\mathcal {M}_\textrm{cl}$, up to automorphisms of $\mathcal {M}_\textrm{cl}$. As a consequence automorphisms of semi-classical 2-dimensional Minkowski planes can be explicitly determined and a complete classification of all semi-classical 2-dimensional Minkowski planes carried out.

We end this section with some notation for circles which will be used in the remainder of this paper. Since $\mathbb {S}^1$ is often represented as $\mathbb {R}\cup \{\infty \}$, it is usual to distinguish circles according to whether or not they pass through the point $(\infty ,\infty )$. If a circle in $\mathcal {M}_\textrm{cl}$ passes through this point we have an extended Euclidean (straight) line

$$\begin{aligned} E_{m,t}=\{(x,y)\in \mathbb {R}^2 \mid y=mx+t\} \cup \{(\infty ,\infty )\} \end{aligned}$$

where $m,t\in \mathbb {R}$, $m\ne 0$. A circle not passing through $(\infty ,\infty )$ is an extended Euclidean hyperbola with horizontal and vertical asymptotes

$$\begin{aligned} H_{a,b,c} = \left\{ (x,y)\in \mathbb {R}^2 \mid x\ne b, y=\frac{a}{x-b}+c \right\} \cup \{(\infty ,c),(b,\infty )\} \end{aligned}$$

where $a,b,c\in \mathbb {R}$, $a\ne 0$. With this notation circles of a semi-classical 2-dimensional Minkowski plane are of the form

$$\begin{aligned} L_{m,t}&= (E_{m,t} \cap P_1) \cup \psi (E_{m',t'} \cap P_2), \\ C_{a,b,c}&= (H_{a,b,c} \cap P_1) \cup \psi (H_{a',b',c'} \cap P_2) \end{aligned}$$

where $\psi :P_2\rightarrow P_2$ is an isomorphism from $\mathcal {M}_\textrm{cl}$ on $P_2$ to $\mathcal {M}$ on $P_2$ and where $m',t'$ depend on m and t, and similarly $a',b',c'$ depend on a, b and c. We call a line or circle of a semi-clasical 2-dimensional Minkowski plane straight if $L_{m,t}=E_{m,t}$ and $C_{a,b,c} =H_{a,b,c}$, respectively, that is, this line or circle is as in the classical real Minkowski plane.

3 Pasting along two disjoint parallel classes

In this section we consider a set consisting of two parallel classes $G_1$ and $G_2$ of the same type so that these parallel classes are disjoint. $G_1\cup G_2$ separates the torus into two open connected subsets $P_1$ and $P_2$ that are both homeomorphic to the cylinder, see Fig. 4 where the top and bottom edge of the square are still identified.

Fig. 4

The two connected components $P_1$ and $P_2$ determined by $G_1$ and $G_2$

Since we are making multiple use of derived affine planes at points on $G_1\cup G_2$ and these planes are ‘semi-classical’, we give a brief description of the planes from [9], see also [6, 2.7.2].

Proposition 3.1

Let $\varphi$ and $\psi$ be increasing homeomorphisms of $\mathbb {R}$ that fix 0 and 1. Define

$$\begin{aligned} L_{m,t} = \{(x,mx+t) \in \mathbb {R}^2 \mid x\ge 0\} \cup \{(x,\psi ^{-1}(\varphi (m) x+\psi (t))) \in \mathbb {R}^2 \mid x\le 0\} \end{aligned}$$

where $m,t\in \mathbb {R}$. Then $\{L_{m,t} \mid m,t\in \mathbb {R}\}$ is the set of non-vertical lines of a (topological, locally compact) 2-dimensional affine plane $\mathcal {A}_{\varphi ,\psi }$ such that the induced geometries on the right half $H_+=[0,\infty ) \times \mathbb {R}$ and left half $H_+=(-\infty ,0] \times \mathbb {R}$ are desarguesian.

Conversely, a 2-dimensional affine plane that is composed of two desarguesian half-planes is isomorphic to a plane $\mathcal {A}_{\varphi ,\psi }$ for some increasing homeomorphisms $\varphi$ and $\psi$ of $\mathbb {R}$ that fix 0 and 1.

Theorem 3.2

Let $\mathcal {M}$ be a 2-dimensional Minkowski plane obtained by pasting two classical halves along two disjoint parallel classes. Then $\mathcal {M}$ is isomorphic to exactly one Minkowski plane of the form $\mathcal {M}(f_k,id)$ where $0<k\le 1$ and $f_k:\mathbb {R}\cup {\infty } \rightarrow \mathbb {R}\cup {\infty }$ is given by

$$\begin{aligned} f_k(x) = {\left\{ \begin{array}{ll} x, &{}\text{ if } x\ge 0,\\ kx, &{}\text{ if } x<0,\\ \infty , &{}\text{ if } x=\infty . \end{array}\right. } \end{aligned}$$

Proof

Since the automorphism group of the classical real Minkowski plane is 2-transitive on the set of $(+)$- or $(-)$-parallel classes, we may assume w.l.o.g. that the two parallel classes along which the two classical halves are pasted together are $G_1=\{\infty \}\times \mathbb {S}^1$ and $G_2=\{0\}\times \mathbb {S}^1$.

Let $P_1$ and $P_2$ be the closures of the connected components of $(\mathbb {S}^1 \times \mathbb {S}^1)\setminus (G_1\cup G_2)$. We assume that the induced geometry on each $P_i$ is isomorphic to the geometry of the classical real Minkowski induced on the corresponding half of the torus. Via these isomorphisms we may w.l.o.g. assume that on $P_1$ we have the geometry of the classical real Minkowski plane. Since parallel classes are taken to parallel classes under an isomorphism, we may further assume that the isomorphism from $P_2$ to the classical real Minkowski plane is of the form $(x,y)\mapsto (x,f(y))$ for some homeomorphism f of $\mathbb {S}^1$. Using the group $\textrm{PGL}(2,\mathbb {R})$ we may additionally assume that f fixes $\infty$, 0 and 1. This means that we may introduce coordinates on each of the two halves $P_1$ and $P_2$ such that $(+)$-parallel classes are $\{u\}\times \mathbb {S}^1$, $u\in \mathbb {S}^1$, the $(-)$-parallel classes are $(\mathbb {S}^1\times \{v\})\cap P_i$, $v\in \mathbb {S}^1$, and circles are of the form

$$\begin{aligned} \left\{ \left. \left( x,\frac{ax+b}{cx+d}\right) \right| x\ge 0\right\}&\quad \text{ on } P_1 \text{ and } \\ \left\{ \left. \left( x,f^{-1}\left( \frac{a^*x+b^*}{c^*x+d^*}\right) \right) \right| x\le 0\right\}&\quad \text{ on } P_2 \end{aligned}$$

where $a^*,b^*,c^*,d^*$ are continuous functions of a, b, c, d and $ad-bc, a^*d^*-b^*c^* \ne 0$.

If a circle passes through $(\infty ,\infty )$ we describe it as

$$\begin{aligned}L_{m,t}=\{(x,mx+t) \mid x\ge 0\} \cup \{(x,f^{-1}(m'x+t')) \mid x\le 0\} \cup \{(\infty ,\infty )\}\end{aligned}$$

where $m,t\in \mathbb {R}$, $m\ne 0$, and $m',t'$ are continuous functions of m and t such that $m'\ne 0$. If the circle does not pass through $(\infty ,\infty )$, then we use

$$\begin{aligned} C_{a,b,c}&= \left\{ \left. \left( x,\frac{a}{x-b}+c\right) \right| {\tilde{b}} \ne x\ge 0\right\} \cup \left\{ \left. \left( x,f^{-1}\left( \frac{a'}{x-b'}+c'\right) \right) \right| {\tilde{b}} \ne x\le 0\right\} \\ {}&\qquad \cup \{(\tilde{b},\infty ),(\infty ,c) \} \end{aligned}$$

where $a,b,c\in \mathbb {R}$, $a\ne 0$, and ${\tilde{b}}=b$ if $b\ge 0$ and $\tilde{b}=b'$ in case $b<0$, and where again $a',b',c'$ are continuous functions of a, b, c such that $a'\ne 0$. Since the definition of these circles must agree on $G_1$, one immediately obtains that

$$\begin{aligned} c'=f(c). \end{aligned}$$

(1)

Considering points on $G_2$ one similarly finds that $c'-\frac{a'}{b'} = f\left( c-\frac{a}{b}\right)$ so that

$$\begin{aligned} f\left( c-\frac{a}{b}\right) = f(c) -\frac{a'}{b'} \end{aligned}$$

(2)

for all $a,b,c\in \mathbb {R}$, $a,b\ne 0$.

By assumption the derived affine plane $\mathcal {A}_p$ at every point $p\in G_1 \cup G_2$ is a topological affine plane which is composed of two desarguesian half-planes. Hence it has to be isomorphic to one of the planes from Proposition 3.1. In particular, the non-horizontal and non-vertical lines of the derived affine plane at $(\infty ,\infty )$ are the circles $L_{m,t}$ minus the point $(\infty ,\infty )$. From Proposition 3.1 it follows that $t'=f(t)$ and that there is a homeomorphism g of $\mathbb {S}^1$, which also fixes $\infty$, 0 and 1, such that $m'=g(m)$. Note that $m'$ is independent of t.

We now consider the derived affine plane at a point $(\infty ,c)$, $c\in \mathbb {R}$. After the coordinate transformation

$$\begin{aligned}(x,y) \mapsto {\left\{ \begin{array}{ll} \left( x,\frac{1}{y-c}\right) , &{} \text{ if } x\ge 0, \\ \left( x,f^{-1}\left( \frac{1}{f(y)-f(c)}\right) \right) , &{} \text{ if } x\le 0, \end{array}\right. } \end{aligned}$$

the affine parts of circles $C_{a,b,c}$ become

$$\begin{aligned} \left\{ \left. \left( x,\frac{x-b}{a}\right) \right| x\ge 0\right\} \cup \left\{ \left. \left( x,f^{-1}\left( \frac{x-b'}{a'}\right) \right) \right| x\le 0\right\} .\end{aligned}$$

As noted before, it follows that the ‘slope’ $\frac{1}{a'}$ only depends on $\frac{1}{a}$, that is, $a'=a'(a,b,c)$ as a function of a, b, c does not depend on b. When $x=0$ we obtain that $-\frac{b'}{a'} = f\left( \frac{-b}{a}\right)$. With this identity (2) becomes

$$\begin{aligned} f\left( c-\frac{a}{b}\right) = f(c)+ f\left( -\frac{a}{b}\right) .\end{aligned}$$

It follows that f is additive. Since $f(1)=1$, we thus obtain that $f=\textrm{id}$.

We next consider the derived affine plane at the point $(0,\infty )$. After the coordinate transformation

$$\begin{aligned}(x,y) \mapsto \left( \frac{1}{x},y\right) \end{aligned}$$

the affine parts of circles $C_{a,0,c}$ become

$$\begin{aligned} \{ (u,au +c) \mid u\ge 0 \} \cup \{ (u,a'u+c) \mid u< 0 \}.\end{aligned}$$

Again as before, $a'$ does not depend on c. From these two cases we infer that $a'$ only depends on a, that is, there is a homeomorphism h of $\mathbb {S}^1$ that fixes $\infty$ and 0 such that $a'=h(a)$.

In summary, we have established so far that

$$\begin{aligned} f=\textrm{id} \end{aligned}$$

and for the circles $C_{a,b,c}$ we have

$$\begin{aligned} a'=h(a), \quad b'=b\frac{h(a)}{a} \quad \text{ and } \quad c'=c \end{aligned}$$

for all $a,b,c\in \mathbb {R}$, $a\ne 0$. For the circles $L_{m,t}$ we have

$$\begin{aligned} m'=g(m) \quad \text{ and } \quad t'=t\end{aligned}$$

for all $m,t\in \mathbb {R}$, $m\ne 0$. Here g and h are homeomorphisms of $\mathbb {S}^1$ that fix $\infty$ and 0, and $g(1)=1$.

The coherence of $\mathcal {M}$ implies that the circle through $(\infty ,\infty )$ that is tangent to $C_{a,b,c}$ at each of its points is of the form $L_{m,t}$ where m is the derivative of $y=\frac{a}{x-b}+c$ at $x\ne 0$; at $x=0$ we use the left-sided and right-sided derivative. In this way we obtain that $m =-\frac{a}{b^2}$ (from the right) and $m' =-\frac{a'}{(b')^2}$ (from the left). Hence

$$\begin{aligned} -\frac{a'}{(b')^2} = m' = g(m) = g\left( -\frac{a}{b^2}\right) . \end{aligned}$$

(3)

Since $\frac{a'}{b'} = \frac{a}{b}$, multiplication by $a'=h(a)$ in (3) yields

$$\begin{aligned} -\frac{a^2}{b^2} = h(a) g\left( -\frac{a}{b^2}\right) .\end{aligned}$$

When $a=-1$, this gives us $g(x)= rx$ for all $x\ge 0$ where $r= -\frac{1}{h(-1)} > 0$. But $g(1)=1$ so that $r=1$ and $h(-1)=-1$. When $a=1$, we obtain $g(x) = kx$ for all $x\le 0$ where $k=\frac{1}{h(1)} > 0$. Hence $g=f_k$. Finally, when $b=1$ we find that $h(a)= - \frac{a^2}{g(-a)}$. It now follows that $h(x)=\frac{x}{k}$ for all $x\ge 0$ and $h(x)= x$ for all $x\le 0$. Hence

$$\begin{aligned} g=f_k \quad \text{ and } \quad h=\frac{1}{k} f_k.\end{aligned}$$

This shows that g and h are uniquely determined by the positive number k. With these formulas we have

$$\begin{aligned}\frac{a'}{x-b'}+c' = \frac{a'}{x-b\frac{a'}{a}}+c = \frac{a}{\frac{a}{a'}x-b}+c \end{aligned}$$

where $x\le 0$. When $a<0$, then $\frac{a}{a'} = \frac{a}{h(a)} = 1$ and $b'=b$ so that

$$\begin{aligned} C_{a,b,c} = \left\{ \left. \left( x,\frac{a}{x-b}+c\right) \right| x\ne b\right\} \cup \{(b,\infty ),(\infty ,c) \} \end{aligned}$$

is as in the classical real Minkowski plane. Similarly, when $m>0>x$, then $m'x+t'= g(m)x+t=mx+t$ and $L_{m,t}$ is as in the classical real Minkowski plane. Since the circles $C_{a,b,c}$, $a<0$, and $L_{m,t}$, $m>0$, comprise all circles in the positive half $\mathcal {C}^+$ of $\mathcal {M}$, this shows that circles in $\mathcal {C}^+$ are straight, that is, are as in the classical real Minkowski plane.

If $m,x<0$, then

$$\begin{aligned} m'x+t'= g(m)x+t=kmx+t =m(kx)+t =mf_k(x) +t\end{aligned}$$

and

$$\begin{aligned}L_{m,t}=\{(x,mf_k(x)+t) \mid x\in \mathbb {R}\}\cup \{(\infty ,\infty )\}\end{aligned}$$

for all $m< 0$. Similarly, in case $a>0>x$ we find that

$$\begin{aligned}\frac{a}{a'}x = \frac{a}{h(a)}x = kx = f_k(x).\end{aligned}$$

Thus

$$\begin{aligned} C_{a,b,c} = \left\{ \left. \left( x,\frac{a}{f_k(x)-b}+c\right) \right| x\ne f_k^{-1}(b)\right\} \cup \{(f_k^{-1}(b),\infty ),(\infty ,c) \} \end{aligned}$$

for all $a,b,c\in \mathbb {R}$, $a>0$. Since the circles $C_{a,b,c}$, $a>0$, and $L_{m,t}$, $m<0$, comprise all circles in the negative half $\mathcal {C}^-$ of $\mathcal {M}$, this shows that circles in $\mathcal {C}^-$ are precisely the graphs of homeomorphisms in $\textrm{PGL}^-(2,\mathbb {R}) f_k$. Hence, put together, we have obtained $\mathcal {M}(f_k,id)$.

Let $\sigma \in \textrm{PGL}(2,\mathbb {R})$ be given by $\sigma (x)=\frac{1}{x}$. Direct calculation shows that $\sigma f_k \sigma = f_{\frac{1}{k}}$. It then readily follows that $(x,y)\mapsto (\sigma (x),\sigma (y))$ is an isomorphism from $\mathcal {M}(f_k,id)$ to $\mathcal {M}(f_{1/k},id)$; see also [10, Theorem 3.14]. Applying the above isomorphism, if necessary, we find that $\mathcal {M}$ is isomorphic to a Minkowski plane $\mathcal {M}(f_k,id)$ where $k\le 1$. Furthermore, no two distinct ones of these planes are isomorphic, see [10, Example 3.15]. $\square$

4 Pasting along two circles

4.1 The general set-up

Let $C_1$ and $C_2$ be two circles, and let $P_1$ and $P_2$ be the closures of the two connected components of $(\mathbb {S}^1 \times \mathbb {S}^1){\setminus } (C_1\cup C_2)$. We assume that the induced geometry on each $P_i$ is isomorphic to the classical real Minkowski geometry induced on the corresponding half of the torus. Via these isomorphisms we may introduce coordinates on each of the two halves $P_1$ and $P_2$ such that $(+)$-parallel classes are $(\{u\}\times \mathbb {S}^1) \cap P_i$, $u\in \mathbb {S}^1$, the $(-)$-parallel classes are $(\mathbb {S}^1\times \{v\}) \cap P_i$, $v\in \mathbb {S}^1$, and circles are formed from non-vertical and non-horizontal lines or hyperbolas with vertical and horizontal asymptotes.

Since the automorphism group of the classical real Minkowski plane is transitive on $\mathcal {C}$, we may assume w.l.o.g. that one of the two circles along which the two classical halves are pasted together is $C_1=\{(x,x) \mid x\in \mathbb {S}^1\}$. Then $C_2=\{(x,\gamma (x)) \mid x\in \mathbb {S}^1\}$ for some $\gamma \in \textrm{PGL}(2,\mathbb {R})$.

We may further assume that on $P_1$ the geometry of the classical real Minkowski plane is induced. On $P_2$ we may only have the geometry of the classical real Minkowski plane up to an isomorphism. W.l.o.g. this isomorphism has the form $(x,y) \mapsto (f(x),g(y))$ for suitable homeomorphisms f and g of $\mathbb {S}^1$. Since we are gluing the two halves along $C_1$, this circle has to be preserved by this isomorphism so that $g=f$. We call f the pasting function. Since the stabilizer of $C_1$ is transitive on $C_1$ we may further assume that f fixes $\infty$.

Similarly, a point $(x,\gamma (x))\in C_2\subset P_1$ is identified with a point $(f(x),g(\gamma (x))) = (f(x),f(\gamma (x)))\in C_2\subset P_2$. Hence,

$$\begin{aligned} \gamma (f(x)) =f(\gamma (x)) \qquad \text{ for } \text{ all } x\in \mathbb {S}^1. \end{aligned}$$

(4)

Recall that circles that pass through $(\infty ,\infty )$ are described as

$$\begin{aligned} L_{m,t} = (E_{m,t} \cap P_1) \cup \psi (E_{m',t'} \cap P_2) \end{aligned}$$

where $\psi$ is an isomorphism from $P_2$ in the classical real Minkowski plane $\mathcal {M}_\textrm{cl}$ to $P_2$ in $\mathcal {M}$ and where $m,m',t,t'\in \mathbb {R}$, $m,m'\ne 0$, and $m'$ and $t'$ are continuous functions of m and t. One calculates that

$$\begin{aligned} E_{m,t} \cap L_{1,0}=\left( \frac{t}{1-m}, \frac{t}{1-m}\right) \end{aligned}$$

(5)

where $m\ne 0,1$.

Those circles that do not pass through $(\infty ,\infty )$ are of the form

$$\begin{aligned} C_{a,b,c} = (H_{a,b,c} \cap P_1) \cup \psi (H_{a',b',c'} \cap P_2). \end{aligned}$$

where $a,a',b,b',c,c'\in \mathbb {R}$, $a,a'\ne 0$, and each of $a'$, $b'$ and $c'$ is a continuous function of a, b and c. One calculates that

$$\begin{aligned} H_{a,b,c} \cap L_{1,0}= \left( \frac{1}{2}\left( c+b \pm \sqrt{(c-b)^2+4a}\right) , \frac{1}{2}\left( c+b \pm \sqrt{(c-b)^2+4a}\right) \right) \end{aligned}$$

(6)

if $(c-b)^2+4a>0$.

When pasting the two classical halves together the above formulas show that

$$\begin{aligned} \frac{t'}{1-m'} =f\left( \frac{t}{1-m}\right) . \end{aligned}$$

Similarly,

$$\begin{aligned} \frac{1}{2}\left( c'+b' \pm \sqrt{(c'-b')^2+4a'}\right) = f\left( \frac{1}{2}\left( c+b \pm \sqrt{(c-b)^2+4a}\right) \right) , \end{aligned}$$

so that

$$\begin{aligned} c'+b'&= f\left( \frac{1}{2}\left( c+b + \sqrt{(c-b)^2+4a}\right) \right) \nonumber \\&\qquad + f\left( \frac{1}{2}\left( c+b - \sqrt{(c-b)^2+4a}\right) \right) , \end{aligned}$$

(7)

$$\begin{aligned} \sqrt{(c'-b')^2+4a'}&= f\left( \frac{1}{2}\left( c+b + \sqrt{(c-b)^2+4a}\right) \right) \nonumber \\&\qquad - f\left( \frac{1}{2}\left( c+b - \sqrt{(c-b)^2+4a}\right) \right) . \end{aligned}$$

(8)

The general strategy is to use circles that meet $C_1\cup C_2$ in four points. Since there is a unique circle through three pairwise non-parallel points, the fourth point of intersection results in a condition on the pasting function f. We will find that the resulting functional equations for f force f to be the identity. In a second step circles that do not meet $C_1\cup C_2$ in four points are determined.

4.2 Two circles meeting in two points

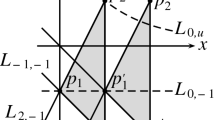
Let $C_1$ and $C_2$ be two circles in the same component of $\mathcal {C}$ that intersect in two points. In this case $(\mathbb {S}^1\times \mathbb {S}^1)\setminus (C_1\cup C_2)$ has three connected components, compare the right diagram in Fig. 3. Since this does not agree with our definition of a semi-classical real Minkowski geometry, we do assume from now on that $C_1$ and $C_2$ are in different connected components of $\mathcal {C}$ (Fig. 5).

Fig. 5

The connected components $P_1$, $P_2$ w.r.t. $C_1$, $C_2$

Let $C_1$ and $C_2$ be two circles, one in each of the two connected components of $\mathcal {C}$. Then $|C_1\cap C_2|=2$. As in Sect. 4.1 we assume $C_1=E_{1,0}$. Since the stabilizer of $C_1$ is 2-transitive on it, we may assume w.l.o.g. that $C_1\cap C_2=\{(\infty ,\infty ),(0,0)\}$. Then $C_2=\{(x,sx) \mid x\in \mathbb {S}^1\}$ for some $s\in \mathbb {R}$, $s<0$. From Eq. (4) we find that

$$\begin{aligned} f(sx)=sf(x) \qquad \text{ for } \text{ all } x\in \mathbb {R}. \end{aligned}$$

(9)

Lemma 4.1

In the case of two circles in different components the pasting function f is the identity.

Proof

As in Sect. 4.1 one calculates that

$$\begin{aligned} C_{a,b,c} \cap L_{s,0} =\left( \frac{1}{2s}\left( c+sb \pm \sqrt{(c-sb)^2+4sa}\right) , \frac{1}{2}\left( c+sb \pm \sqrt{(c-sb)^2+4sa}\right) \right) \end{aligned}$$

if $(c-sb)^2+4sa>0$ so that

$$\begin{aligned} \frac{1}{2}\left( c'+sb' \pm \sqrt{(c'-sb')^2+4sa'}\right)&= f\left( \frac{1}{2}\left( c+sb \pm \sqrt{(c-sb)^2+4sa}\right) \right) . \end{aligned}$$

Thus,

$$\begin{aligned} c'+sb'&= f\left( \frac{1}{2}\left( c+sb + \sqrt{(c-sb)^2+4sa}\right) \right) \nonumber \\&\qquad + f\left( \frac{1}{2}\left( c+sb - \sqrt{(c-sb)^2+4sa}\right) \right) , \end{aligned}$$

(10)

$$\begin{aligned} \sqrt{(c'-sb')^2+4sa'}&= f\left( \frac{1}{2}\left( c+sb + \sqrt{(c-sb)^2+4sa}\right) \right) \nonumber \\&\qquad - f\left( \frac{1}{2}\left( c+sb - \sqrt{(c-sb)^2+4sa}\right) \right) . \end{aligned}$$

(11)

We write the expressions under the square roots as $(c-b)^2+4a=(c+b)^2-4(bc-a)$ and $(c-sb)^2+4sa=(c+sb)^2-4\,s(bc-a)$, and similarly for the formulas involving $a',b',c'$. Let $d=bc-a$ and $d'=b'c'-a'$ and let

$$\begin{aligned} u&= \frac{1}{2}\left( c+b + \sqrt{(c+b)^2-4d}\right) , \\ {\bar{u}}&= \frac{1}{2}\left( c+b - \sqrt{(c+b)^2+-d}\right) , \\ v&= \frac{1}{2}\left( c+sb + \sqrt{(c+sb)^2-4sd}\right) , \\ {\bar{v}}&= \frac{1}{2}\left( c+sb - \sqrt{(c+sb)^2-4sd}\right) . \end{aligned}$$

Then Eqs. (7), (8) and the above two equations become

$$\begin{aligned} c'+b'&= f(u) + f({\bar{u}}), \\ \sqrt{(c'+b')^2-4d'}&= f(u) - f({\bar{u}}), \\ c'+sb'&= f(v) + f({\bar{v}}), \\ \sqrt{(c'+sb')^2-4sd'}&= f(v) - f({\bar{v}}). \end{aligned}$$

The first two identities yield

$$\begin{aligned} d'= f(u)f({\bar{u}}), \end{aligned}$$

and the last two give us

$$\begin{aligned} sd'=f(v) f({\bar{v}}). \end{aligned}$$

Then

$$\begin{aligned} f(v)f({\bar{v}})=sd'=sf(u)f({\bar{u}}). \end{aligned}$$

(12)

One calculates $u{\bar{u}}= d$ and $v{\bar{v}}=sd$. Furthermore, $u > \bar{u}$ and $v > {\bar{v}}$, and when $u,v\ne 0$, one obtains

$$\begin{aligned} c+b&= u +{\bar{u}} = u+ \frac{d}{u},\\ c+sb&= v +{\bar{v}} = v+ \frac{sd}{v}. \end{aligned}$$

Hence

$$\begin{aligned} b&= \frac{1}{1-s} \left( u+ \frac{d}{u} - v- \frac{sd}{v}\right) ,\\ c&= \frac{1}{1-s} \left( v+ \frac{sd}{v} - su- \frac{sd}{u}\right) ,\\ a = bc -d&= -\frac{1}{(1-s)^2 v^2}(v-u)(v-su)\left( v-\frac{d}{u}\right) \left( v-\frac{sd}{u}\right) . \end{aligned}$$

This shows that a, b, c are functions of d, u, v. One thus has a one-to-one correspondence between triples (a, b, c) for which $C_{a,b,c}$ intersects $L_{1,0} \cup L_{s,0}$ in four distinct points and triples (d, u, v) such that

$$\begin{aligned} d,u,v\ne 0, \quad v\ne u, su, \frac{d}{u}, \frac{sd}{u}, \quad u>\frac{d}{u}, \quad v> \frac{sd}{v}. \end{aligned}$$

(13)

(Given a, b, c as functions of d, u, v as above, one calculates, for example, $\sqrt{(c+b)^2-4d} = \sqrt{\left( u+\frac{d}{u}\right) ^2-4d} = \sqrt{\left( u-\frac{d}{u}\right) ^2} = u-\frac{d}{u}$ so that u is obtained back.) It follows from (12) that $f(v)f\left( \frac{sd}{v}\right) =sf(u)f\left( \frac{d}{u}\right)$ and thus

$$\begin{aligned} f(v)f\left( \frac{d}{v}\right) =f(u)f\left( \frac{d}{u}\right) \end{aligned}$$

(14)

for all $d,u,v\in \mathbb {R}$ satisfying (13). This identity trivially remains true when $v =u, su, \frac{d}{u}, \frac{sd}{u}$, that is, (14) holds for all $d,u,v\ne 0$, $u>\frac{d}{u}$, $v> \frac{sd}{v}$.

When $d>\frac{1}{s}$ put $v=1$ to obtain $f(d)=f(u)f\left( \frac{d}{u}\right)$ or

$$\begin{aligned} f\left( u\cdot \frac{d}{u}\right) =f(u)f\left( \frac{d}{u}\right) . \end{aligned}$$

(15)

for all $d,u\in \mathbb {R}$, $d,u\ne 0$, $d>\frac{1}{s}$, $u>\frac{d}{u}$. This identity remains valid when $u<\frac{d}{u}$ because $u=\frac{d}{d/u}$. When $d<\frac{1}{s}$, put $v=sd$ to again obtain $f(d)=f(u)f\left( \frac{d}{u}\right)$.

Let $w=\frac{d}{u}$. Then (15) becomes

$$\begin{aligned} f(u)f(w)=f(uw) \end{aligned}$$

for all $u,w\ne 0$, $u\ne w$, $uw\ne \frac{1}{s}$. But this identity remains trivially true if $u=0$ or $w=0$ or $u=w$. By (9) and the continuity of f also the case $uw=\frac{1}{s}$ follows. This shows that f is multiplicative. Hence $f(x)=x|x|^{k-1}$ for some $k\in \mathbb {R}$, $k>0$. However, $sf(x)=f(sx)=f(s)f(x)$ implies that $f(s)=s$ so that $|s|^{k-1}=1$.

If $-1\ne s<0$, we obtain $k=1$ and thus $f=\text{ id }$.

It remains to deal with the special case $s=-1$. Then f is an odd function by (9). The formulas from above for $C_{a^2,b,b}$ where $0<a<b$ become

$$\begin{aligned} c'+b'&= f(b +a) +f(b-a), \\ \sqrt{(c'-b')^2+4a'}&= f(b + a) - f(b-a),\\ c' -b'&= f\left( \sqrt{b^2 -a^2}\right) + f\left( -\sqrt{b^2 -a^2}\right) = 0\\ \sqrt{(c' +b')^2 -4(a')^2}&= f\left( \sqrt{b^2 -a^2}\right) - f\left( -\sqrt{b^2 -a^2}\right) = 2 f\left( \sqrt{b^2 -a^2}\right) \end{aligned}$$

It follows that

$$\begin{aligned} c'=b'&=\frac{1}{2} ( f(b +a) +f(b-a)), \nonumber \\ a'&= \frac{1}{2} ( f(b +a) -f(b-a)) \qquad \text{ and }\nonumber \\ \sqrt{(b')^2 -(a')^2}&= f\left( \sqrt{b^2 -a^2}\right) . \end{aligned}$$

(16)

Using lines one calculates

$$\begin{aligned} L_{m,t} \cap L_{-1,0}=\left( -\frac{t}{1+m}, \frac{t}{1+m}\right) \end{aligned}$$

where $m\ne 0,=1$. Hence, and because f is odd,

$$\begin{aligned} \frac{t'}{1+m'} =f\left( \frac{t}{1+m}\right) . \end{aligned}$$

Together with Eq. (5) we obtain that

$$\begin{aligned} m' = \frac{f\left( \frac{t}{1-m}\right) -f\left( \frac{t}{1+m}\right) }{f\left( \frac{t}{1-m}\right) + f\left( \frac{t}{1+m}\right) } \qquad \text{ and }\qquad t' = \frac{-2f\left( \frac{t}{1-m}\right) f\left( \frac{t}{1+m}\right) }{f\left( \frac{t}{1-m}\right) +f\left( \frac{t}{1+m}\right) }. \end{aligned}$$

Since f is multiplicative, the formula for $m'$ now becomes

$$\begin{aligned} m' = \frac{f\left( \frac{m+1}{m-1}\right) + 1}{f\left( \frac{m+1}{m-1}\right) -1}. \end{aligned}$$

Direct calculation shows that

$$\begin{aligned} \frac{m'+1}{m'-1} = f\left( \frac{m+1}{m-1}\right) . \end{aligned}$$

We now consider the tangent lines to $C_{a^2,b,,b}$ at the points of intersection with $L_{-1,0}$. The slopes of these lines are found as $-\frac{a^2}{(x-b)^2}$ which gives us

$$\begin{aligned} m = -\frac{a^2}{(x-b)^2} = - \frac{a^2}{(\pm \sqrt{b^2-a^2}-b)^2}. \end{aligned}$$

Thus

$$\begin{aligned} \frac{m+1}{m-1} = \frac{2b^2-2a^2 \mp 2b\sqrt{b^2-a^2}}{-2b^2 \pm 2b\sqrt{b^2-a^2}} = \frac{\sqrt{b^2-a^2}(\sqrt{b^2-a^2} \mp b)}{\pm b(\mp b + \sqrt{b^2-a^2})} = \pm \frac{\sqrt{b^2-a^2}}{b}. \end{aligned}$$

Since $c'=b'$ we similarly find

$$\begin{aligned} f\left( \pm \frac{\sqrt{b^2-a^2}}{b}\right) = \frac{m'+1}{m'-1} = \pm \frac{\sqrt{(b')^2-(a')^2}}{b'} = \pm \frac{f(\sqrt{b^2-a^2})}{b'}. \end{aligned}$$

Hence $b'=f(b)$. Equation (16) then yields $2f(b)=f(b+a) + f(b-a)$ for all $0<a<b$. Since f is continuous, this identity remains valid as $a\rightarrow b$. Thus $2f(b)=f(2b)$. In particular, $2=2f(1)=f(2)=2^k$ so that $k=1$. Hence $f=\textrm{id}$. $\square$

We finally show that $f=\textrm{id}$ implies that only the classical real Minkowski plane can be obtained.

Theorem 4.2

A semi-classical Minkowski plane obtained by pasting along two circles in different components of $\mathcal {C}$ is classical.

Proof

$f=\textrm{id}$ shows that circles $C_{a,b,c}$ are straight (that is, are as in the classical real Minkowski plane) if they meet $C_1 \cup C_2$ in at least three points. In particular, every line $L_{m,t}$ is straight. This follows as above in case $m\ne \pm 1$. When $m=\pm 1$, these lines can be obtained as a limit of straight lines with slopes $\ne \pm 1$ by coherence of 2-dimensional Minkowski planes. Hence these lines are straight as well. Since every circle $\ne C_1,C_2$ meets $C_1$ or $C_2$ in two points, it remains to determine those circles that intersect $C_1 \cup C_2$ in two points. Suppose that $C_{a,b,c} \in \mathcal {C}^-$ so that it meets $C_1$ in two points. Note that $a>0$. These points of intersection are $p_\pm =(x_\pm , x_\pm )$ where $x_\pm =\frac{1}{2}\left( c+b \pm \sqrt{(c-b)^2+4a}\right)$. We consider the tangent line $L_{m,t}$ to $C_{a,b,c}$ at $p_+$. As noticed above this line is straight. But then $C_{a,b,c}$ is described as the tangent circle to $L_{m,t}$ at $p_+$ and passing through $p_-$. In each half $P_i$ this uniquely determines $C_{a,b,c}$, and because $L_{m,t}$ is straight, so is $C_{a,b,c}$.

The case when $C_{a,b,c} \in \mathcal {C}^+$ is dealt with in a similar fashion by looking at points of intersection with $C_2$. This shows that only the classical real Minkowski plane can be obtained. $\square$

4.3 Two tangent circles

Let $C_1$ and $C_2$ be two circles that touch at a point p. Using the automorphism group of the classical real Minkowski plane, we may assume w.l.o.g. that $C_2$ touches $C_1=\{(x,x) \mid x\in \mathbb {S}^1\}$ at $(\infty ,\infty )$, and that $C_2=\{(x,x+1) \mid x\in \mathbb {S}^1\}$ (Fig. 6).

Fig. 6

The connected components $P_1$, $P_2$ w.r.t. touching circles $C_1$, $C_2$

From Eq. (4) we know that for the pasting function f we have

$$\begin{aligned} f(x+1)=f(x)+1 \qquad \text{ for } \text{ all } x\in \mathbb {R}. \end{aligned}$$

We may further assume that $f(0)=0$. But then $f(1)=1$ too.

Lemma 4.3

In the case of two tangent circles the pasting function f is the identity.

Proof

One calculates

$$\begin{aligned} C_{a,b,c} \cap L_{1,1}= & {} \left( \frac{1}{2}\left( c+b-1 \pm \sqrt{(c-b-1)^2+4a}\right) ,\right. \\{} & {} \quad \left. \frac{1}{2}\left( c+sb \pm \sqrt{(c-sb)^2+4sa}\right) \right) \end{aligned}$$

where we assume that $(c-b)^2+4a,(c-b-1)^2+4a>0$. Let $u=\frac{1}{2}(c+b)$ and $v=\frac{1}{2}(c-b)$, and similarly $u'=\frac{1}{2}(c'+b')$ and $v'=\frac{1}{2}(c'-b')$. When pasting the two classical halves together the above formula and (6) show that

$$\begin{aligned} u' \pm \sqrt{(v')^2+a'}&= f\left( u \pm \sqrt{v^2+a}\right) \\ u' - \frac{1}{2} \pm \sqrt{\left( v'- \frac{1}{2} \right) ^2+a'}&= f\left( u - \frac{1}{2} \pm \sqrt{\left( v- \frac{1}{2}\right) ^2+a}\right) . \end{aligned}$$

so that

$$\begin{aligned} 2u'&= f\left( u + \sqrt{v^2+a}\right) + f\left( u - \sqrt{v^2+a}\right) \\ 2u' -1&= f\left( u - \frac{1}{2} + \sqrt{\left( v- \frac{1}{2}\right) ^2+a}\right) + f\left( u - \frac{1}{2} - \sqrt{\left( v- \frac{1}{2}\right) ^2+a}\right) \end{aligned}$$

Hence,

$$\begin{aligned}&f(u + \sqrt{v^2+a}) + f(u - \sqrt{v^2+a}) \nonumber \\&\qquad = f\left( u -\frac{1}{2} + \sqrt{\left( v- \frac{1}{2}\right) ^2+a}\right) + f\left( u -\frac{1}{2} - \sqrt{\left( v- \frac{1}{2}\right) ^2+a}\right) +1 \end{aligned}$$

(17)

for all $a,u,v\in \mathbb {R}$ $a\ge 0$. By the continuity of f this identity remains valid when $a=0$. For each $w\ge \frac{1}{2}$ there is a unique $n\in \mathbb {Z}$, $n\ge 1$, such that $w-\frac{1}{2} < n \le w+\frac{1}{2}$. Now let $v=w^2- n^2 +\frac{1}{4}$. One calculates

$$\begin{aligned} w^2-v^2&= (w-v)(w+v) =\left( w-w^2+ n^2 -\frac{1}{4}\right) \left( w+w^2- n^2 +\frac{1}{4}\right) \\&= \left( n^2 -\left( w -\frac{1}{2}\right) ^2\right) \left( \left( w+\frac{1}{2}\right) ^2 - n^2\right) \\&= \left( n -w +\frac{1}{2}\right) \left( n +w -\frac{1}{2}\right) \left( w+\frac{1}{2} - n\right) \left( w+\frac{1}{2} + n\right) \\&\ge 0. \end{aligned}$$

Thus, if we define $a= w^2 -v^2$, then $a\ge 0$ and

$$\begin{aligned} \sqrt{v^2+a}&=w \\ \sqrt{\left( v- \frac{1}{2}\right) ^2+a}&= \sqrt{v^2+a-v +\frac{1}{4}} = n. \end{aligned}$$

Hence (17) becomes

$$\begin{aligned} f(u+w) + f(u-w)&= f\left( u -\frac{1}{2} + n\right) + f\left( u -\frac{1}{2} - n\right) +1 \nonumber \\&= f\left( u +\frac{1}{2} \right) + f\left( u -\frac{1}{2} \right) . \end{aligned}$$

(18)

This identity is valid for all $u,w\in \mathbb {R}$, $w\ge \frac{1}{2}$. But $f(u+w) + f(u-w) = f(u+w+m) + f(u-w-m)$ for each $m\in \mathbb {Z}$. This shows that (18) remains valid for all $u,w\in \mathbb {R}$. When $w=0$, we obtain that $f\left( u +\frac{1}{2} \right) + f\left( u- \frac{1}{2} \right) =2f(u)$. Thus

$$\begin{aligned} f(u+w)+f(u-w)=2f(u) \end{aligned}$$

for all $u\in \mathbb {R}$. Now $w=u$ yields $f(2u)=2f(u)$ and so $f(u+w)+f(u-w)=f(2u)$. Finally, let $x=u+w$ and $y=u-w$. Then

$$\begin{aligned} f(x)+f(y)=f(x+y) \end{aligned}$$

for all $c,y\in \mathbb {R}$. This shows that f is additive. Hence $f=\textrm{id}$ because $f(1)=1$. $\square$

Theorem 4.4

A semi-classical Minkowski plane obtained by pasting along two tangent circles is classical.

Proof

The pasting function f is the identity by Lemma 4.3.

Let C be a circle that intersects each of $C_1$ and $C_2$ in two points. If $C=C_{a,b,c}$, the formulas above show that $b'+c'=b+c$, $\sqrt{(c'-b')^2+4a'} = \sqrt{(c-b)^2+4a}$, $\sqrt{(c'-b'-1)^2+4a'} = \sqrt{(c-b-1)^2+4a}$. Squaring the last two equations and subtracting yields $c'-b'=c-b$. Hence $b'=b$, $c'=c$, and $a'=a$ follows, that is, the circle $C_{a,b,c}$ is straight.

As in the previous case, the continuity of the geometric operations and coherence of 2-dimensional Minkowski planes implies that circles through $(\infty ,\infty )$ are also straight. For the same reason circles that are tangent to one of $C_1$ or $C_2$ and meet the other circle in two points are straight as well.

If a circle C meets neither $C_1$ nor $C_2$, it is entirely contained in one of the connected components of $(\mathbb {S}^1\times \mathbb {S}^1){\setminus }(C_1 \cup C_2)$. Hence, such a circle is straight by definition of a semi-classical Minkowski plane. Similarly, if C is tangent to one of $C_1$ or $C_2$ and does not meet the other circle or if C is tangent to both of $C_1$ and $C_2$, it is entirely contained in the closure of one of the connected components of $(\mathbb {S}^1\times \mathbb {S}^1)\setminus (C_1 \cup C_2)$ and thus is straight.

This leaves us with the case where C intersects one of $C_1$ or $C_2$ in two points and is disjoint to the other circle.

We consider the tangent line $L_{m,t}$ to C at one of the points $p_+$ of intersection with $C_i$. This line is straight. But then C is described as the tangent circle to $L_{m,t}$ at $p_+$ and passing through the other point $p_-$ of intersection with $C_i$. In each half $P_i$ this uniquely determines C, and because $L_{m,t}$ is straight, so is C.

$\square$

4.4 Two disjoint circles

Let $C_1$ and $C_2$ be two disjoint circles and let $P_1$ and $P_2$ be the closures of the connected components of $(\mathbb {S}^1\times \mathbb {S}^1) {\setminus } (C_1\cup C_2)$. We assume that the induced geometry on each $P_i$ is isomorphic the classical real Minkowski geometry induced on the corresponding half of the torus. As before, via these isomorphisms we introduce coordinates on each of the two halves $P_1$ and $P_2$ such that $(+)$-parallel classes are $(\{u\}\times \mathbb {S}^1) \cap P_i$, $u\in \mathbb {S}^1$, the $(-)$-parallel classes are $(\mathbb {S}^1\times \{v\}) \cap P_i$, $v\in \mathbb {S}^1$, and circles are formed from non-vertical and non-horizontal lines or hyperbolas with vertical and horizontal asymptotes.

As in Sect. 4.1 we assume that $C_1=L_{1,0}$. Using the stabilizer of $C_1$ in the automorphism group of the classical real Minkowski plane, we see that we may further assume that

$$\begin{aligned} C_2=H_{-1-s^2,s,-s}=\left\{ \left. \left( x,-\frac{1+s^2}{x-s}-s\right) \right| x\in \mathbb {R}\setminus \{s\}\right\} \cup \{(\infty ,-s),(s,\infty )\} \end{aligned}$$

where $s\in \mathbb {R}$, see Fig. 7. (First move the centre of $C_2$ onto the line $E_{-1,0}$ by a translation $(x,y) \mapsto (x+t,y+t)$, and then use a homothety $(x,y) \mapsto (rx,ry)$.)

Fig. 7

The connected components $P_1$, $P_2$ w.r.t. $C_1$, $C_2$

From Eq. (4) we obtain

$$\begin{aligned} f\left( -\frac{1+s^2}{x-s}-s\right) =-\frac{1+s^2}{f(x)-s}-s \qquad \text{ for } \text{ all } x\in \mathbb {R}\setminus \{s\} \end{aligned}$$

for the pasting function f. It directly follows that $f(-s)=-s$ and $f(s)=s$.

Lemma 4.5

In the case of two disjoint circles the pasting function f is the identity.

Proof

We consider the hyperbola $H_{a,b,-s}$ where $(b+s)^2 +4a >0$, $b\ne s$. It meets $C_2$ in the points $(\infty ,-s)$ and $\left( \frac{as+(1+s^2)b}{a+1+s^2}, \frac{a+1+bs}{s-b} \right)$. Thus, the other half of the circle $C_{a,b,-s}$ must be induced by $H_{a',b',-s}$ for some $a',b'$, and so (from the second coordinate)

$$\begin{aligned} \frac{a'+1+b's}{s-b'} = f\left( \frac{a+1+bs}{s-b} \right) . \end{aligned}$$

The intersection of $H_{a,b,-s}$ and $C_1$ consists of the points

$$\begin{aligned} \left( \frac{1}{2} \left( b-s \pm \sqrt{(b+s)^2+4a}\right) , \frac{1}{2} \left( b-s \pm \sqrt{(b+s)^2+4a}\right) \right) . \end{aligned}$$

Let

$$\begin{aligned} u&=\frac{1}{2} \left( b-s +\sqrt{(b+s)^2+4a}\right) \qquad \text{ and }\\ v&= \frac{1}{2} \left( b-s -\sqrt{(b+s)^2+4a}\right) \end{aligned}$$

so that

$$\begin{aligned} b=s+u+v\qquad \text{ and } \qquad a= -(u+s)(v+s). \end{aligned}$$

Then $u>v$, $u+v \ne 0$, $u,v \ne -s$ and

$$\begin{aligned} a'&= -(f(u)+s)(f(v)+s), \\ b'&= s +f(u) + f(v). \end{aligned}$$

One calculates

$$\begin{aligned} \frac{a+1+bs}{s-b} = \frac{uv-1}{u+v} \qquad \text{ and } \qquad \frac{a'+1+b's}{s-b'} = \frac{f(u)f(v)-1}{f(u)+f(v)}. \end{aligned}$$

Hence

$$\begin{aligned} \frac{f(u)f(v)-1}{f(u)+f(v)} = f\left( \frac{uv-1}{u+v} \right) \end{aligned}$$

for all $u,v\in \mathbb {R}$, $u>v$, $u,v \ne -s$. However, this equation is symmetric in u and v, and by continuity it must be valid for all $u,v\in \mathbb {R}$.

Write $u=\cot \alpha$, $v=\cot \beta$ for some $\alpha , \beta \in (0,\pi )$. Then $\frac{uv-1}{u+v}=\cot (\alpha +\beta )$ by the addition theorem for the $\cot$ function. We now write $f \circ \,\cot = \cot \circ \,\varphi$ for some increasing homeomorphism $\varphi :(0,\pi ) \rightarrow (0,\pi )$ so that $f(u)=\cot (\varphi (\alpha ))$, $f(v)=\cot (\varphi (\beta ))$. Then

$$\begin{aligned} \cot \varphi (\alpha +\beta )= & {} f(\cot ( \alpha +\beta )) =f\left( \frac{uv-1}{u+v} \right) = \frac{f(u)f(v)-1}{f(u)+f(v)}\\= & {} \cot (\varphi (\alpha ) + \varphi (\beta )). \end{aligned}$$

It follows that $\varphi (\alpha +\beta ) = \varphi (\alpha ) + \varphi (\beta ) \pmod {\pi }$ for all $\alpha , \beta \in (0,\pi )$. One can extend $\varphi$ to an increasing homeomorphism ${\tilde{\varphi }}:\mathbb {R}\rightarrow \mathbb {R}$ by ${\tilde{\varphi }}(k\pi )=k\pi$ for each $k\in \mathbb {Z}$ and ${\tilde{\varphi }}(x)=\varphi (\overline{x})+n\pi$ where $n=\lfloor \frac{x}{\pi }\rfloor$, the largest integer $\le \frac{x}{\pi }$, and $\overline{x} =x-n\pi \in (0,\pi )$ where $x\notin \pi \mathbb {Z}$. It readily follows that ${\tilde{\varphi }}$ is additive. Note that $\varphi (\theta )=\theta$ where $\theta =\cot ^{-1}(s)$ because $f(s)=s$. By the continuity of ${\tilde{\varphi }}$ it then follows that ${\tilde{\varphi }}=\textrm{id}$ and so $\varphi =\textrm{id}$. Hence $f=\textrm{id}$. $\square$

Remark 4.6

Let $\theta =\cot ^{-1}(s) \in (0,\pi )$. Then

$$\begin{aligned} \gamma (x)=-\frac{1+s^2}{x-s}-s = \frac{-sx -1}{x-s} = \frac{x\cos \theta -\sin \theta }{x\sin \theta + \cos \theta } \end{aligned}$$

comes from a rotation through the angle $\theta$. If $\theta$ is an irrational multiple of $\pi$, then the subgroup $\Gamma =\langle \gamma \rangle =\{\gamma ^m\mid m\in \mathbb {Z}\}\le \textrm{SO}(2,\mathbb {R})$ generated by $\gamma$ is dense in $\textrm{SO}(2,\mathbb {R})$; compare Dirichlet’s approximation theorem or Weyl’s equidistribution theorem. Since f commutes with $\gamma$ by Eq. (4), one sees that f commutes with every member in $\textrm{SO}(2,\mathbb {R})$, that is,

$$\begin{aligned} f\left( \frac{x\cos t -\sin t}{x\sin t + \cos t}\right) = \frac{f(x)\cos t -\sin t}{f(x)\sin t + \cos t} \end{aligned}$$

for all $t\in \mathbb {R}$, $x\in \mathbb {R}\cup \{\infty \}$. When $x=\infty$ one finds $f(\cot t)=\cot t$. Hence $f=\textrm{id}$.

Theorem 4.7

A semi-classical Minkowski plane obtained by pasting along two disjoint circles is classical.

Proof

By Lemma 4.5 the pasting function f is the identity. Hence a circle that meets $C_1\cup C_2$ in at least three points is straight.

As in the previous cases, the continuity of the geometric operations and coherence of 2-dimensional Minkowski planes implies that circles that are tangent to each of $C_1$ and $C_2$ are straight as well.

If a circle C meets neither $C_1$ nor $C_2$, it is entirely contained in one of the connected components of $(\mathbb {S}^1\times \mathbb {S}^1)\setminus (C_1 \cup C_2)$. Hence, such a circle is straight by definition of a semi-classical Minkowski plane. Similarly, if C is tangent to one of $C_1$ or $C_2$ and does not meet the other circle or if C is tangent to both of $C_1$ and $C_2$, it is entirely contained in the closure of one of the connected components of $(\mathbb {S}^1\times \mathbb {S}^1)\setminus (C_1 \cup C_2)$ and thus is straight.

Hence, all circles are straight, and the plane is classical. $\square$

The Main Theorem now follows from Theorems 2.5, 3.2, 4.2, 4.4 and 4.7.