Graphs in which all maximal bipartite subgraphs have the same order

Abstract

Motivated by the concept of well-covered graphs, we define a graph to be well-bicovered if every vertex-maximal bipartite subgraph has the same order (which we call the bipartite number). We first give examples of them, compare them with well-covered graphs, and characterize those with small or large bipartite number. We then consider graph operations including the union, join, and lexicographic and cartesian products. Thereafter we consider simplicial vertices and 3-colored graphs where every vertex is in triangle, and conclude by characterizing the maximal outerplanar graphs that are well-bicovered.

1 Introduction

Plummer [4] defined a graph to be well-covered if every maximal independent set is also maximum. That is, a graph is well-covered if every maximal independent set has the same cardinality, namely the independence number $\mathop {\alpha }(G)$. Much has been written about these graphs. For example, Ravindra [6] characterized well-covered bipartite graphs, Campbell, Ellingham, and Royle [1] characterized well-covered cubic graphs, and Finbow, Hartnell, and Nowakowski [2] characterized well-covered graphs of girth 5 or more.

Motivated by this idea, we define a graph to be well-bicovered if every vertex-maximal bipartite subgraph has the same order. Equivalently, one can define the bipartite number of a graph G, denoted b(G), as the maximum cardinality of a bipartite induced subgraph in G. (We will henceforth just assume that subgraph means induced subgraph.) Then, being well-bicovered means all maximal bipartite subgraphs have cardinality b(G). The problem of finding a maximum bipartite subgraph is well-studied. For instance, Zhu [8] showed that any triangle-free subcubic graph G with order n has $b(G) \ge \frac{5}{7}n$, and the Four Color Theorem shows that $b(G)\ge n/2$ for any planar graph G.

In this paper, we introduce and study well-bicovered graphs. We give examples and compare well-bicovered graphs with well-covered graphs, and characterize well-bicovered graphs with small or large bipartite numbers. We then consider their relationship to graph operations including the union, join, and lexicographic and cartesian products. Thereafter we consider 3-colorable graphs and simplicial vertices, and conclude by characterizing the maximal outerplanar graphs that are well-bicovered.

1.1 Definitions and terminology

Let $G = (V(G), E(G))$ be a simple, finite graph of order $n(G)=|V(G)|$. The open neighborhood of a vertex $v \in V(G)$ is $N(v) = \{ \, x \in V(G) : xv \in E(G) \,\}$. The degree of $v \in V(G)$ is $\deg (v) = |N(v)|$, and the maximum degree of G is denoted $\Delta (G)$. Given a set $X \subseteq V(G)$, we let G[X] represent the subgraph induced by X. If $\deg _G(x) = 1$, we refer to x as a leaf in G, and the edge incident with x as a pendant edge. In general, a bridge is an edge whose removal increases the number of components.

2 Examples of well-bicovered graphs

In this section, we construct examples of well-bicovered graphs and study well-bicovered graphs whose maximal bipartite subgraphs have a given cardinality.

Trivially, every bipartite graph is well-bicovered. So are the complete graphs and the cycles. Further, bridges are irrelevant, as adding or removing a bridge does not alter the property. In particular, note for example that adding a pendant edge to any well-bicovered graph results in a well-bicovered graph.

2.1 The relationship to well-covered graphs

While the concept of being well-bicovered was motivated by the concept of being well-covered, the two properties are distinct. In particular, neither property implies the other. For example, the path $P_3$ is well-bicovered but not well-covered. On the other hand, the graph F, obtained from $K_4 - e$ and adding a pendant edge to a vertex of degree 2, is well-covered but not well-bicovered. The house graph H ($C_5$ plus a chord) is both. See Fig. 1.

Fig. 1

Two well-covered graphs

The house graph and complete graph have the property that their bipartite number is twice their independence number. But there are also examples where this is not the case. Two such graphs are shown in Fig. 2.

Fig. 2

Two well-covered and well-bicovered graphs G with $b(G) < 2\mathop {\alpha }(G)$

Though not equivalent to being well-bicovered, there is another “bipartite subgraph” property that is more closely related to being well-covered, that we mention in passing. Let us define the “weight” of a subgraph as the sum of twice the number of isolated vertices and the number of nonisolated vertices. Then being well-covered implies that every maximal bipartite subgraph has the same weight:

Lemma 1

If a graph G is well-covered, then the weight of every maximal bipartite subgraph is the same.

Proof

Consider a maximal bipartite subgraph B. Let X denote the isolates of B and let $(Y_1,Y_2)$ denote the bipartition of $V(B)-X$. The maximality condition means that adding to B any other vertex v produces an odd cycle. This requires that vertex v be adjacent to both a vertex of $Y_1$ and $Y_2$. Further, every vertex of $Y_1$ has a neighbor in $Y_2$ and vice versa, by the definition of Y. Thus, both $X \cup Y_1$ and $X\cup Y_2$ are maximal independent sets in G: that is $2|X|+|V(B)-X| = 2 \mathop {\alpha }(G)$. $\square$

2.2 Classifying graphs based on their bipartite number

First, we classify well-bicovered graphs with small bipartite number.

Lemma 2

A connected graph G is well-bicovered with bipartite number 2 if and only if $G=K_n$ for $n \ge 2$.

Proof

It is clear that if $G= K_n$ for $n \ge 2$, then G is well-bicovered with bipartite number 2. On the other hand, if G is connected and not complete, then it contains an induced $P_3$, and so $b(G)\ge 3$. $\square$

Lemma 3

A connected graph G is well-bicovered with bipartite number 3 if and only if G is obtained by taking a nontrivial complete graph $K_n$ and attaching a pendant edge to one vertex of $K_n$.

Proof

First, note that if G is obtained by taking a nontrivial complete graph $K_n$ and attaching a pendant edge to one vertex of $K_n$, then G is well-bipartite with bipartite number 3. Conversely, suppose G is well-bicovered with bipartite number 3. If G has order 3, then $G = P_3$ and we are done. So we may assume that G has order at least 4.

Since G is connected and not complete, there exists an induced $P_3$ with central vertex v; this must be a maximal bipartite subgraph in G. Thus, every vertex of G is adjacent to v. Suppose there exists an induced $P_3$ in $G-v$ with central vertex w. As before, this implies that every vertex of G is adjacent to w. However, $G[\{v, w\}]$ is then a maximal bipartite subgraph of G, which is a contradiction. It follows that $G-v$ is a disjoint union of cliques and we may write $G-v = K_{n_1} \cup \cdots \cup K_{n_j}$. We can create a maximal bipartite subgraph H of G by choosing one vertex from each $K_{n_i} = K_1$ and two vertices from each $K_{n_i}$ where $n_i \ge 2$. Since H has order 3, it follows that $G - v = K_1 \cup K_n$ where $n \ge 2$. $\square$

Next, we consider the other end of the spectrum and classify well-bicovered graphs G with bipartite number $n(G) - 1$.

Lemma 4

A graph G is well-bicovered with bipartite number $n(G)-1$ if and only if there exists an odd cycle C in G such that every odd cycle of G contains every vertex on C.

Proof

Suppose first that G is well-bicovered of bipartite number $n(G) - 1$. Thus, G is not bipartite. Let C be a shortest odd cycle in G, and let v be any vertex on C. Note that there exists a maximal bipartite subgraph H of G that contains v. If v is not on every odd cycle in G, then the cardinality of H is at most $n(G) - 2$. Thus, v must lie on every odd cycle in G.

Conversely, suppose that G contains an odd cycle C in G such that every odd cycle of G contains every vertex on C. (Necessarily C is chordless.) Let H be a maximal bipartite subgraph of G. We know that H must contain some vertex v on C. Since $G - v$ is bipartite, it follows that $n(H) = n(G) - 1$. $\square$

3 Graph operations

In this section we consider how the property of being well-bicovered relates to several graph operations including disjoint union (and related “gluing” operations), join, lexicographic product, and cartesian product.

3.1 Union

The question for disjoint union of graphs is trivial. The disjoint union is well-bicovered if and only if each component is well-bicovered. Indeed, we observed earlier that bridges are irrelevant, and so one can take the disjoint union and add a bridge.

But consider instead taking two disjoint well-bicovered graphs G and H and identifying a vertex g of G with a vertex h of H to form vertex v. The result need not be well-bicovered: consider for example $G=H=K_3$. Indeed, the result is guaranteed to be not well-bicovered unless for at least one of the graphs, the identified vertex is in every maximal bipartite subgraph. This holds, for example, when one of G or H is bipartite. This idea is generalized slightly in the following operation:

Lemma 5

Let G be a well-bicovered graph with adjacent vertices u and v and let H be a bipartite graph with adjacent vertices $u'$ and $v'$. Let F be the graph formed from their disjoint union by identifying u with $u'$ and v with $v'$. Then F is well-bicovered.

Proof

Any chordless odd cycle of F has all its vertices in G (since if it uses new vertices in H then uv is a chord). Thus any maximal bipartite subgraph of G can be extended to one of F by adding all vertices of $H-\{u',v'\}$. Conversely, any maximal bipartite subgraph of F contains all of $H-\{u',v'\}$, and removal thereof yields a maximal bipartite subgraph of G. $\square$

A simple example of the above is the case that H is an even cycle. One can also glue on odd cycles and general well-bicovered graphs under some circumstances.

Lemma 6

Let G be a well-covered graph with clique C and let H be a well-bicovered graph with clique D, where $|C|=|D|=k$. Then the graph F formed from their disjoint union by adding k disjoint paths between C and D such that all the added paths have the same parity, is well-bicovered.

Proof

Any chordless cycle of F containing a vertex of both G and H necessarily consists of two of the added paths and the edges joining their end points, and thus has even length. It follows that every chordless odd cycle is contained entirely within either G or H. Thus, every maximal bipartite subgraph of F consists of a maximal bipartite subgraph of G, a maximal bipartite subgraph of H, and all the interior vertices of the added paths. $\square$

We consider for a moment girth. Finbow et al. [2] classified all connected well-covered graphs of girth at least 5. But there does not appear an easy characterization of well-bicovered graphs of large girth. For example, all cycles are well-bicovered and both the above lemmas can be used to grow a well-bicovered graph while preserving the girth. One can even grow the girth under some circumstances using the following lemma:

Lemma 7

Let G be a well-bicovered graph with edge e incident with a vertex y of degree 2. Then the graph $G'$ obtained from G by replacing the edge e by a path of length 3 is well-bicovered.

Proof

Say the added path has interior vertices u and v. Every maximal bipartite subgraph B of G can be augmented with u and v to be a maximal bipartite subgraph of $G'$. Conversely, if $B'$ is a maximal bipartite subgraph of $G'$, then it must contains at least two of u, v, y; form B by removing u, v if it contains both, or the two of the triple it does contain. The resultant B is a maximal bipartite subgraph of G. $\square$

Of course, one can replace three by any odd number in the above lemma, or equivalently, iterate use of the lemma.

3.2 Join

We consider the join next.

Theorem 1

Let G and H be graphs both with at least one edge. Then, the join of G and H is well-bicovered if and only if each is both well-covered and well-bicovered, and $b(G) = b(H) = 2\mathop {\alpha }(G) = 2\mathop {\alpha }(H)$.

Proof

Let B be any maximal bipartite subgraph of the join. If B contains vertices from both G and H, then it must consist of an independent set from each graph. Indeed, its vertex set must be the union of a maximal independent set from each graph. Since this cardinality is constant, we need both G and H to be well-covered.

On the other hand, if B contains vertices only from G, then for its cardinality to be constant, it must be that G is well-bicovered. (And note that since G has at least one edge, there do exist such B.) We get a similar result if B contains only vertices from H. Thus it is necessary that $b(G) = b(H) = \mathop {\alpha }(G) + \mathop {\alpha }(H)$. But since $b(G)\le 2\mathop {\alpha }(G)$, this forces $\mathop {\alpha }(G)=\mathop {\alpha }(H)$, and thus the above conditions are necessary.

Finally, it easy to see that the conditions imply that all bipartite subgraphs of the join have the same cardinality. $\square$

For the case that one of the graphs is edgeless, one gets a similar result with a similar proof:

Theorem 2

The join of $rK_1$ and H is well-bicovered if and only if H is both well-covered and well-bicovered, and $b(H) = r + \mathop {\alpha }(H)$.

3.3 Well-bicovered graphs with large cliques

We next ask what operations can be applied to a complete graph to create other well-bicovered graphs.

Lemma 8

Let G be the graph obtained by taking a nontrivial complete graph $K_n$ and, for each edge $e \in E(K_n)$, adding a vertex $v_e$ that is adjacent to both vertices incident to e. Then G is well-bicovered.

Proof

Let B be a maximal bipartite subgraph of G. Note that $|V(B) \cap V(K_n)| \le 2$. If B contains no vertices of the clique $K_n$, then $V(B) = \{v_e: e \in E(K_n)\}$. However, this is not maximal, as the graph induced by $\{v_e: e \in E(K_n)\} \cup \{v\}$ for any $v \in V(K_n)$ is also bipartite in G. If B contains only one vertex from $K_n$, say w, then $V(B) = \{w\} \cup \{v_e: e \in E(K_n)\}$. If B contains two vertices from $K_n$, say u and w, then $V(B) = \{u, w\} \cup \{v_e: e \in E(K_n) - \{uw\}\}$. In every case, $|V(B)| = n+1$. $\square$

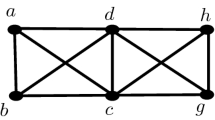
As an example of Lemma 8, if we start with $K_3$ then we get the Hajós graph or 3-sun, shown in Fig. 3.

Fig. 3

A well-bicovered graph

Lemma 9

Let G be the graph obtained by taking a disjoint union of nontrivial complete graphs $K_{n_1} \cup \cdots \cup K_{n_{\ell }}$ and adding edges between the cliques so that the added edges form a matching. Then G is well-bicovered.

Proof

Let M represent the matching added and let S be a subset of V(G) formed by taking two vertices from $K_{n_i}$ for each $1 \le i \le \ell$. Then in G[S] the edges not in M form a matching. This means that every cycle in G[S] alternates between M and non-M edges and so has even length. It follows that G[S] is bipartite. On the other hand, no bipartite subgraph can have three vertices from any of the cliques. It follows that every maximal bipartite subgraph has exactly two vertices from each clique. The result follows. $\square$

3.4 Lexicographic product

Recall that the lexicographic product (or composition) of graphs G and H, denoted $G\circ H$, is the graph with $V(G\circ H)= V(G) \times V(H)$ whereby (u, v) and (x, y) are adjacent if $ux \in E(G)$, or $u=x$ and $vy \in E(H)$.

Topp and Volkmann [7] proved that the lexicographic product $G\circ H$ of two graphs G and H both containing edges is well-covered if and only if G and H are well-covered graphs. We now determine when the lexicographic product $G\circ H$ is well-bicovered. If H is edgeless, the result is immediate:

Lemma 10

$G\circ mK_1$ is well-bicovered if and only if G is well-bicovered.

Now we consider the case when both G and H contain edges. In the following, given a vertex $x \in V(G)$, we refer to the subgraph of $G\circ H$ induced by $\{(x, v):v \in V(H)\}$ as the $H^x$-fiber.

Theorem 3

Let G and H be graphs both containing at least one edge. Then $G\circ H$ is well-bicovered if and only if

• (i) G is well-covered; and

• (ii) H is both well-covered and well-bicovered, and also $b(H)=2 \mathop {\alpha }(H)$.

Proof

Assume first that $G\circ H$ is well-bicovered. Define a good pair (X, Y) as disjoint subsets X and Y of V(G) such that X is independent, there is no edge between X and Y, and Y induces a bipartite subgraph without isolates. We say that a good pair is maximal if there is no other good pair $(X',Y')$ such that $X\subseteq X'$ and $Y\subseteq Y'$. Note that a maximal good pair has the following property: If z is any vertex of $V(G)-(X\cup Y)$, and z is not in N(X), then since z cannot be added to X it must have a neighbor in Y, and since z cannot be added to Y, it must create an odd cycle with Y. By definition, any good pair can be extended to a maximal good pair.

Now, given a maximal good pair $P=(X,Y)$, one can construct a subset $B_P$ of $V(G\circ H)$ as follows. For every $H^x$-fiber where $x \in X$, take a maximal bipartite subgraph of H. For every $H^y$-fiber where $y \in Y$, take a maximal independent set of H. The resultant set $B_P$ is clearly bipartite. Further:

Claim 1

The subgraph induced by the set $B_P$ is maximal bipartite.

Proof

Consider adding another vertex v to $B_P$; say from the $H^w$-fiber. If $w \in X$, then vertex v creates an odd cycle with $B_P$, since we already took a maximal bipartite subgraph of such $H^w$. If $w \in N(X)$, say adjacent to $x\in X$, then vertex v creates a triangle with the vertices of $B_P$ in $H^x$, since any maximal bipartite subgraph of $H^x$ has at least one edge. If $w\in Y$, say adjacent to $y\in Y$, then vertex v creates a triangle with a vertex of $B_P$ in $H^w$ and in $H^{y}$. Finally, by the maximality of the good pair, if $w\in V(G)-N[X]-Y$, then vertex v creates an odd cycle with $B_P$, since w creates an odd cycle with Y. $\square$

Consider a good pair $P_1$ with X a maximal independent set of G and Y empty; necessarily $P_1$ is a maximal good pair. Since all resultant sets $B_{P_1}$ must have the same size, it follows that H must be well-bicovered, and G must be well-covered. Further, every maximal bipartite subgraph of $G\circ H$ must have size

$$\begin{aligned} |B_{P_1}| = \mathop {\alpha }(G)\, b(H) . \end{aligned}$$

Consider a maximal good pair $P_2$ where Y is nonempty and $X\cup Y$ is maximal bipartite. (This exists since G has at least one edge: start with such an edge, extend to a maximal bipartite subgraph, and then partition into isolates and nonisolates.) Since every resultant set $B_{P_2}$ must have the same size, it follows that H must be well-covered. Further, the resultant $B_{P_2}$ must have size

$$\begin{aligned} |B_{P_2}| = |X| b(H) + |Y| \mathop {\alpha }(H) . \end{aligned}$$

By Lemma 1, it holds that $2|X|+ |Y| = 2 \mathop {\alpha }(G)$. Thus the condition $|B_{P_1}|=|B_{P_2}|$ is equivalent to $|Y|\mathop {\alpha }(H) = 2 |Y| b(H)$. Since $|Y|\ne 0$, it follows that (it is necessary and sufficient that) $\mathop {\alpha }(H) = 2 b(H)$. That is, we have shown that conditions (i) and (ii) are necessary.

Conversely, assume conditions (i) and (ii) hold. Let $B'$ be a maximal bipartite subgraph in the composition. Let P be the subset of V(G) in the projection of $B'$ onto G. Say X is the isolated vertices in the subgraph induced by P, and Y the non-isolates. By the maximality of $B'$, for every $H^x$-fiber where $x \in X$, the set $B'$ must contain a maximal bipartite subgraph of H, and for every $H^y$-fiber where $y \in Y$, it must contain a maximal independent set of H. It follows that

$$\begin{aligned} |B'| = |X| b(H) + |Y| \mathop {\alpha }(H) . \end{aligned}$$

Furthermore, the maximality of $B'$ means that (X, Y) is a maximal good pair and as above, by Lemma 1 we get that $|Y| = 2(\mathop {\alpha }(G) - |X|)$. It follows that $B'$ has size $\mathop {\alpha }(G) b(H)$. Since this is true for all maximal bipartite subgraphs of $G\circ H$, we have that $G\circ H$ is well-bipartite. $\square$

3.5 Cartesian product

Recall that the Cartesian product of graphs G and H, denoted $G \, \Box \,H$, is the graph with $V(G \, \Box \,H) = \{(u,v): u \in V(G) \text { and } v \in V(H)\}$ and $(u,v)(x,y) \in E(G \, \Box \,H)$ if either $u = x$ and $vy \in E(H)$ or $ux \in E(G)$ and $v = y$. An obvious guess is that the product of two well-bicovered graphs is well-bicovered. However, this is far from true. Indeed, it does not hold even if one graph is $K_2$. For example, the house graph H has bipartite number 4, and so $b(K_2 \, \Box \,H) = 8$. But in the prism shown in Fig. 4, the dark vertices represent a maximal bipartite subgraph of order 7.

Fig. 4

A Cartesian product that is not well-bicovered

One can at least observe that if H is bipartite, then a necessary condition for $G \, \Box \,H$ to be well-bicovered is that G is well-bicovered. For, one can build a maximal bipartite subgraph of the product by starting with any maximal bipartite subgraph B of G and taking these vertices in all copies of G. In order for the result to always be the same size, it is necessary that all the B have the same cardinality.

In [3], Hartnell and Rall showed that if $G \, \Box \,H$ is well-covered, then one of G or H must be well-covered. We do not know the answer to the analogous question: namely, if $G \, \Box \,H$ is well-bicovered, then must one of G or H be well-bicovered?

4 3-Colorable graphs

As we mentioned earlier, Ravindra [6] characterized the well-covered bipartite graphs. So one might hope to classify well-bicovered 3-colorable graphs, but this seems challenging. We note that in the case of well-covered bipartite graphs, one can trivially assume that every vertex is in a $K_2$. So perhaps one can characterize well-bicovered 3-colorable graphs where every vertex is in a triangle. We present here some partial results. We then use these to characterize well-bicovered maximal outerplanar graphs.

4.1 Triangles and simplicial vertices

Lemma 11

Let G be a 3-colorable well-bicovered graph such that every vertex is in a triangle. Then each color class $V_i$ in every proper 3-coloring of G has size b(G)/2. Further, if every edge of G is in a triangle, then each subgraph $G-V_i$ is well-covered.

Proof

Let $T_i = G- V_i$ for each $1\le i \le 3$. Because the subgraph $T_i$ is induced by two color classes, it is bipartite. If w is any other vertex, then it has color i; by construction $T_i$ contains all the neighbors of w and so adding w to $T_i$ would create a triangle with $T_i$. That is, $T_i$ is a maximal bipartite subgraph. Therefore, $|T_1|=|T_2|=|T_3|$. It follows that $|V_1|=|V_2|=|V_3|$; and indeed, each is b(G)/2.

Now, suppose every edge is in a triangle. We can build a bipartite subgraph B of G by starting with the color class $V_i$ and then adding a maximal independent set S of $T_i$. Consider some other vertex x of $T_i$. Then x has a neighbor y in S; further, the edge xy is in a triangle, say with vertex z, where z is in $V_i$. That is, if we add x to B we complete a triangle. It follows that B is maximal bipartite. Since all such B must have the same cardinality, we get that $T_i$ is well-covered. $\square$

Recall that a simplicial vertex is one whose neighborhood is complete. Prisner, Topp, and Vestergaard [5] considered simplicial vertices in well-covered graphs. In particular, they defined a simplex as a maximal clique containing a simplicial vertex, and showed that if a graph is well-covered then the simplices are vertex-disjoint, and if every vertex belongs to exactly one simplex then the graph is well-covered.

It is unclear what the exact analogue of their results should be. For example, Lemma 8 showed the well-bicovered graphs can have overlapping simplices. But here are two results in that spirit.

Lemma 12

Suppose graph G has vertices u and v that are nonadjacent simplicial vertices with $N(u)\cap N(v)$ nonempty, and there exist distinct vertices $x\in N(u)$ and $y\in N(v)$ that are nonadjacent. Then G is not well-bicovered.

Proof

Let $c\in N(u) \cap N(v)$. Note that the condition implies that $x\notin N(v)$ and $y\notin N(u)$. Take the set $\{c,x,y\}$ and extend to a maximal bipartite set B. Necessarily, the set B cannot contain u or v nor any other vertex of $N(u) \cup N(v)$. Now, let $B'$ be the set $(B\cup \{u,v\})-\{c\}$. Then this set is bipartite and bigger than B, a contradiction. $\square$

Define a bisimplex S as a maximal clique that contains a simplicial vertex s (implying it has no neighbor outside S) and a second vertex t that has at most one neighbor outside S.

Lemma 13

If the vertex set of graph G has a partition into bisimplices, then G is well-bicovered.

Proof

Let the partition of V(G) into bisimplices be $S_1, \ldots , S_m$, with $s_i$ the simplicial vertex of $S_i$ and $t_i$ the other relevant vertex of $S_i$. Let B be the subgraph induced by all the $s_i$ and $t_i$. Then B is bipartite: indeed, every component in B is a path either of length 1 (of the form $s_it_i$) or of length 3 (of the form $s_it_it_js_j$). Since one cannot take more than two vertices from each bisimplex, it follows that $b(G) = 2m$.

Now consider any maximal bipartite subgraph $B'$ of G. Suppose $B'$ contains no vertex from some bisimplex $S_i$. Then one can add the vertex $s_i$ to $B'$ and preserve bipartiteness. Suppose $B'$ contains only one vertex from $S_i$. If that vertex is not $s_i$, then one can just add it. If that vertex is $s_i$, then one can add $t_i$, as it is adjacent to at most one other vertex in $B'$. In either case this contradicts the claimed maximality of $B'$. It follows that $B'$ contains two vertices from each bisimplex, and so has cardinality 2m. $\square$

4.2 Maximal outerplanar graphs

Recall that graph G is outerplanar if G has a planar drawing for which all vertices belong to the outer face of the drawing. We say that G is maximal outerplanar, or a MOP, if G is outerplanar and the addition of any edge results in a graph that is not outerplanar. Since every MOP is a 2-tree and every 2-tree is chordal, we point out that Prisner, Topp, and Vestergaard [5] classified well-covered chordal graphs. In this section, we classify all well-bicovered MOPs.

We construct a class of graphs W referred to as whirlygigs as follows. Take a MOP M with $m\ge 3$ vertices and let C represent the outside cycle of M. For each edge $u_iu_{i+1}$ on C, add a new vertex $t_i$ adjacent only to $u_{i}$ and $u_{i+1}$, and then add another vertex $s_i$ that is adjacent to only $t_i$ and $u_i$. Figure 5 shows the whirlygig of order 15 (there is only one MOP of order 5). We can extend this definition to $m=2$ by considering the MOP $K_2$ to be a cycle with two edges; the resultant whirlygig is $P^2_6$, the square of the path.

Fig. 5

The unique whirlygigs of orders 6 and 15

Lemma 14

If $G \in W$, then G is well-bicovered.

Proof

This follows from Lemma 13. Each $\{s_i,t_i,u_i\}$ is a bisimplex, and these partition the vertex set of G. $\square$

Theorem 4

A MOP G is well-bicovered if and only if G is $K_3$, the Hajós graph, or a whirlygig.

Proof

Let G be a well-bicovered MOP. It is well-known that outerplanar graphs are 3-colorable. Let $V_1, V_2$, and $V_3$ be the color classes of G. Let $T_i = G- V_i$ for each $1\le i \le 3$. Note that $T_i$ is a tree. (This follows for example from the fact that G is chordal and therefore the subgraph induced by the vertices of a cycle cannot be 2-colored.) By Lemma 11, we know that the cardinality of $V_1, V_2$, and $V_3$ must be equal; say $|V_i| = m$ for $1\le i \le 3$. Moreover, each $T_i$ is well-covered. By the characterization of Ravindra [6], it follows that each $T_i$ is a corona of a tree.

We partition V(G) into three sets. Let LL represent the vertices in G that are a leaf with respect to $T_i$ and $T_j$ for some $1 \le i < j \le 3$. Let LN represent the vertices that are a leaf with respect to $T_i$ and a non-leaf with respect to $T_j$, and let NN represent the vertices that are a non-leaf with respect to $T_i$ and $T_j$ for some $1 \le i < j \le 3$. We know that the only MOP of order 3 is $K_3$. So we may assume that $n(G) \ge 6$.

Case 1 Suppose first that G contains a vertex $v_1$ in LN. Without loss of generality, we may assume $v_1$ has color 1, is a leaf in $T_2$ and is a non-leaf in $T_3$. Thus, $v_1$ has exactly one neighbor of color 3, say $x_1$, and at least two neighbors of color 2, say $w_1$ and $x_2$.

Since in a MOP the open neighborhood of a vertex induces a path, any vertex must have almost equal representation of the other two colors in its neighborhood. It follows that $v_1$ has exactly two neighbors of color 2, and in particular, its open neighborhood induces the path $w_1x_1x_2$. Further, one of $w_1$ and $x_2$ is a leaf in $T_3$, say $w_1$. Since $w_1$ has only one neighbor of color 1, it must be that the edge $w_1x_1$ is an exterior edge. Since $v_1$ has only one neighbor of color 3, the edge $v_1w_1$ is also an exterior edge. In particular, $w_1$ has degree 2 in G.

Note that the above argument holds for any vertex that is in LN. We refer to $v_1w_1x_1$ as a leafy triangle as all three vertices are leaves in their respective coronas. Note too that any vertex in G is incident with exactly one pendant edge from two different coronas $T_i$ and $T_j$. In particular, $x_1$ is not contained in another leafy triangle of G.

Next, consider vertex $x_2$. Since $w_1$ is a leaf in both $T_1$ and $T_3$, it follows that $x_2$ must be a non-leaf in both $T_1$ and $T_3$. Therefore, $x_2$ has a leaf-neighbor in $T_1$ and a leaf-neighbor in $T_3$. We claim that one of these leaf-neighbors, call it $v_2$, must be in LN. Indeed, if both leaf-neighbors were in LL, then they would each have degree 2 in G making $x_2$ a cut-vertex, which cannot happen.

Applying the above argument where $v_2$ plays the role of $v_1$, it follows that $v_2$ has exactly two neighbors other than $x_2$, say $w_2$ and $x_3$, where $x_2w_2v_2x_3$ is a path on the exterior of G and $x_2$, $w_2$, and $v_2$ induce a leafy triangle. Continuing this same line of reasoning, we establish the exterior path $P = x_1w_1v_1x_2w_2v_2\dots x_kw_kv_k$ where each $x_i$ is in NN, each $w_i$ is in LL, and each $v_i$ is in LN. Furthermore, from above we know that $v_k$ has degree 3 in G and is adjacent to $x_k$ and $w_k$.

Let k be the first index where the third neighbor of $v_k$ is z which is already on P. Since each $w_i$ has degree 2 in G, and each $v_i$ is only adjacent to $w_i$, $x_i$, and $x_{i+1}$, it must be that $z = x_i$ for some $1\le i \le k$. If $k=2$, then G is the graph depicted $P^2_6$. So we may assume that $k\ge 3$. If $i \ne 1$, then $x_i$ is a cut-vertex as the exterior edges of G contain the cycle $x_iw_iv_i\dots x_kw_kv_kx_i$. It follows that all vertices of NN are on the cycle $x_1x_2\dots x_kx_1$. Moreover, the vertices in NN must induce a MOP, and thus G is in fact a whirlygig.

Case 2 Next, suppose LN $= \emptyset$. Let v be a vertex in LL with color 1. Thus, v has degree 2 in G. Let u be the neighbor of v with color 2 and let w be the neighbor of v with color 3. It follows that u and w are adjacent in G. Since w is not a leaf in $T_1$, w has a neighbor, call it x, in LL that has degree 2 and color 2. Let z be the other neighbor of x which is necessarily in NN, has color 1 and is also adjacent to w. Continuing this same line of reasoning, we deduce that the exterior edges of G can be expressed as $v_1w_1v_2w_2\cdots v_kw_kv_1$ where each $v_i$ is in LL and each $w_i$ is in NN. Further, G contains the cycle $C= w_1w_2\cdots w_kw_1$ as each $v_i$ has degree 2 in G. Without loss of generality, we may assume $v_1$ has color 1 and $w_1$ has color 2. From the above argument, it follows that $v_2$ has color 3, $w_2$ has color 1 and so forth. This implies that on C, the order of the colors starting with the color of $w_1$ is $2, 1, 3, 2, 1, 3, \dots , 2, 1, 3$.

Let H be the MOP induced by the vertices of NN. We claim that based on the pattern of colors on C, each vertex of degree 3 or more in H is adjacent to a vertex of degree 2 in H. Indeed, let uvw be on C where u has color 2, v has color 1 and w has color 3. We shall assume that v has degree at least 3 in H and that v is adjacent to a vertex $z \ne u$ with color 2. Thus, on C vertex z is followed by a vertex t with color 1. However, either uz or vt must be an edge in H, which is a contradiction based on their color assignment. Thus, either u has degree 2, or the only neighbor of v with color 2 is u. However, assuming that u is adjacent to a vertex $p\ne w$ with color 3, the same argument implies that w has degree 2 in H.

Next, we claim that the subgraph J of G containing all vertices of degree 2 in H along with all vertices in LL in G is maximal bipartite. Indeed, for $v \in V(G) - V(J)$, v is in NN and therefore contained in a triangle vxw where x has degree 2 in H and w is in LL. Thus, $|V(J)| = \frac{2}{3}n = |\text {LL}| + x = \frac{n}{2} + x$ where x represents the number of vertices in H of degree 2. It follows that $x = \frac{n}{6}$ and every third vertex on C is a vertex of degree 2 in H. Recoloring if necessary, we may assume every vertex of degree 2 in H has color 1 and each vertex of H with color 2 or 3 has degree at least 3 in H. If $|V(H)| = 3$, then G is the Hajós graph. However, if $|V(H)| \ge 6$, then H does not induce a MOP as each vertex of color 2 is adjacent to exactly one vertex of color 1 and therefore only two vertices of color 3, and so that case is impossible. $\square$

5 Further thoughts

Apart from the questions mentioned in the text, there are several natural questions yet to be resolved. For example, it would be nice to characterize well-bicovered planar or outerplanar graphs of given girth, or well-bicovered triangulations. Another obvious direction is to establish the complexity of recognizing well-bicovered graphs.