Generating the Mapping Class Group by Two Torsion Elements

Abstract

We prove that the mapping class group of a closed connected orientable surface of genus $g\ge 6$ is generated by two elements of order g. Moreover, for $g\ge 7$, we obtain a generating set of two elements, of order g and $g'$, where $g'$ is the least divisor of g greater than 2. We also prove that the mapping class group is generated by two elements of order $g/\gcd (g,k)$ for $g\ge 3k^2+4k+1$ and any positive integer k.

1 Introduction

The mapping class group $\mathrm{Mod}(\Sigma _g)$ of a closed, connected orientable surface $\Sigma _g$ is the group of orientation-preserving diffeomorphisms of $\Sigma _g\rightarrow \Sigma _g$ up to isotopy. Dehn [3] showed that $\mathrm{Mod}(\Sigma _g)$ is generated by $2g(g-1)$ many Dehn twists. Afterwards, Lickorish [12] decreased this number to $3g-1$. Humphries [6] introduced a generating set consisting of $2g+1$ many Dehn twists and proved that this is the least such number.

Note that, the above-generating sets contain only elements of infinite order. Maclachlan [15] proved that $\mathrm{Mod}(\Sigma _g)$ can also be generated by only using torsions. Wajnryb [20] proved that $\mathrm{Mod}(\Sigma _g)$ can be generated by two elements; one of order $4g+2$ and the other a product of opposite Dehn twists. In this paper, we study the problem of generating $\mathrm{Mod}(\Sigma _g)$ by two torsion elements of small orders. Korkmaz [8] found a generating set for $\mathrm{Mod}(\Sigma _g)$ consisting of two torsion elements of order $4g+2$. He also posed the following problem [10]: for which $k<4g+2$, $\mathrm{Mod}(\Sigma _g)$ can be generated by two elements of order k (A similar question is also asked by Margalit [16])? In particular, what is the smallest such k?

We first prove that $\mathrm{Mod}(\Sigma _g)$ is generated by two elements of order g if $g \ge 6$.

Theorem 1

The mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by two elements of order g for $g \ge 6$.

We also obtain generating sets consisting of the elements of smaller orders.

Theorem 2

For $g\ge 7$ the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by two elements of order g and order $g'$ where $g'$ is the least divisor of g such that $g'>2$.

Theorem 3

For $g\ge 3k^2+4k+1$ and any positive integer k, the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by two elements of order $g/\gcd (g,k)$.

Since there is a surjective homomorphism from $\mathrm{Mod}(\Sigma _g)$ onto the symplectic group $\mathrm{Sp}(2g,{{\mathbb {Z}}})$, we have the following immediate result:

Corollary 4

The symplectic group $\mathrm{Sp}(2g,{{\mathbb {Z}}})$ is generated by two elements of order g for $g\ge 6$.

See [2, 7, 15, 17] or [14] for generating sets consisting of involutions, [11, 13, 18] or [4] for generating sets consisting of torsions and [19] or [1] for other generating sets for the mapping class groups.

2 Preliminaries

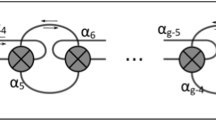
Throughout the paper, we always consider $\Sigma _g$, where all genera are depicted as in Fig. 1. Note that the rotation by $2\pi /g$ degrees about z-axis, denoted by R, is a well-defined self-diffeomorphism of $\Sigma _g$. Following the notation in [21], we denote simple closed curves by lowercase letters $a_i$, $b_i$, $c_i$ and corresponding positive Dehn twists by uppercase letters $A_i$, $B_i$, $C_i$ or with the usual notation $t_{a_i}$,$t_{b_i}$,$t_{c_i}$, respectively. All indices should be considered modulo g. For the composition of diffeomorphisms, $f_1f_2$ means that $f_2$ is first and then $f_1$ comes second as usual.

Commutativity, braid relation and the following basic facts on the mapping class group are used throughout the paper for many times: For any simple closed curves $c_1$ and $c_2$ on $\Sigma _g$ and diffeomorphism $f:\Sigma _g \rightarrow \Sigma _g$, $ft_{c_1}f^{-1}=t_{f(c_1)}$; $c_1$ is isotopic to $c_2$ if and only if $t_{c_1}=t_{c_2}$ in $\mathrm{Mod}(\Sigma _g)$; and if $c_1$ and $c_2$ are disjoint, then $t_{c_1}(c_2)=c_2$. We always refer to [5] for all the remaining properties of the mapping class groups.

Now, let us present Humphries minimal generating set for $\mathrm{Mod}(\Sigma _g)$:

Theorem 5

(Dehn–Lickorish–Humphries) The mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the set $\{ A_1,A_2,B_1,B_2,\ldots ,B_g,C_1,C_2,\ldots ,C_{g-1}\}.$

It is easy to see that the rotation R satisfies that $R(a_k)=a_{k+1}$, $R(b_k)=b_{k+1}$ and $R(c_k)=c_{k+1}$. Deducing from Theorem 5, Korkmaz [9] showed that the mapping class group is generated by four elements. Note that his first element is the rotation R and others are products of one positive and one negative Dehn twists.

Theorem 6

If $g\ge 3$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the four elements $R, A_1A_2^{-1},B_1B_2^{-1}, C_1C_2^{-1}.$

The next result easily follows from Theorem 6.

Corollary 7

If $g\ge 3$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the four elements $R, A_1B_1^{-1}, B_1C_1^{-1}, C_1B_2^{-1}.$

Proof

Let H be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set

$\{ R, A_1B_1^{-1}, B_1C_1^{-1}, C_1B_2^{-1}\}$.

It is enough to show that H contains the elements $A_1A_2^{-1}$, $B_1B_2^{-1}$ and $C_1C_2^{-1}$ by Theorem 6.

It is easy to see that $B_2A_2^{-1} \in H$ since $B_2A_2^{-1} = R(B_1A_1^{-1})R^{-1} \in H$ and $B_2C_2^{-1} = R(B_1C_1^{-1})R^{-1}\in H$.

One can also show that $B_1B_2^{-1}=(B_1C_1^{-1})(C_1B_2^{-1}) \in H$. Similarly, we have that $C_1C_2^{-1}=(C_1B_2^{-1})(B_2C_2^{-1}) \in H$ and we also have that

$A_1A_2^{-1}=(A_1B_1^{-1})(B_1B_2^{-1})(B_2A_2^{-1}) \in H$.

It follows from Theorem 6 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the corollary. $\square$

Fig. 1

The curves $a_i,b_i,c_i$ and the rotation R on the surface $\Sigma _g$

3 Twelve New Generating Sets for $\mathrm{Mod}(\Sigma _g)$

In this section, we introduce twelve new generating sets consisting of two elements of small orders for the mapping class group. Following the ideas in [9], we construct generating sets consisting of R, an element of order g, and another element which can be expressed as a product of Dehn twists.

The corollaries in this section are mainly the corollaries of Theorem 6. We use the first four corollaries to create generating sets of elements of order g. We use Corollaries  12, 13, 14,  15, 16 and 20 to create generating sets of elements of order g and $g'$, where $g'$ is the least divisor of g greater than 2. In the following, we give four new generating sets to prove Theorem 1.

Corollary 8

If $g=6$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $C_1B_4A_6A_1^{-1}B_5^{-1}C_2^{-1}$.

Proof

Let $F_1=C_1B_4A_6A_1^{-1}B_5^{-1}C_2^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _6)$ generated by the set $\{ R, F_1\}$.

If H contains the elements $A_1A_2^{-1}$, $B_1B_2^{-1}$ and $C_1C_2^{-1}$, then we are done by Theorem 6 (Fig. 2).

Let

$$\begin{aligned} F_2= & {} RF_1R^{-1} \\= & {} R(C_1B_4A_6A_1^{-1}B_5^{-1}C_2^{-1})R^{-1}\\= & {} RC_1R^{-1}RB_4R^{-1}RA_6R^{-1}RA_1^{-1}R^{-1}RB_5^{-1}R^{-1}RC_2^{-1}R^{-1}\\= & {} Rt_{c_1}R^{-1}Rt_{b_4}R^{-1}Rt_{a_6}R^{-1}Rt_{a_1}^{-1}R^{-1}Rt_{b_5}^{-1}R^{-1}Rt_{c_2}^{-1}R^{-1}\\= & {} t_{R(c_1)}t_{R(b_4)}t_{R(a_6)}t_{R(a_1)}^{-1}t_{R(b_5)}^{-1}t_{R(c_2)}^{-1}\\= & {} t_{c_2}t_{b_5}t_{a_1}t_{a_2}^{-1}t_{b_6}^{-1}t_{c_3}^{-1}\\= & {} C_2B_5A_1A_2^{-1}B_6^{-1}C_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = C_3B_6A_2A_1^{-1}B_5^{-1}C_2^{-1}. \end{aligned}$$

Fig. 2

Proof of Corollary 8

We have $F_3F_1(c_3,b_6,a_2,a_1,b_5,c_2)=(b_4,a_6,a_2,a_1,b_5,c_2)$ so that

$F_4=B_4A_6A_2A_1^{-1}B_5^{-1}C_2^{-1}\in H$. Note that $F_3F_1(c_3) = b_4$ since

$$\begin{aligned} t_{F_3F_1(c_3)}= & {} (F_3F_1)t_{c_3}(F_3F_1)^{-1}\\= & {} F_3F_1C_3F_1^{-1}F_3^{-1}\\= & {} C_3B_4C_3B_4^{-1}C_3^{-1}\\= & {} (t_{c_3}t_{b_4})t_{c_3}(t_{c_3}t_{b_4})^{-1}\\= & {} t_{t_{c_3}t_{b_4}(c_3)}\\= & {} t_{b_4}. \end{aligned}$$

We get $F_1F_4^{-1}=C_1A_2^{-1} \in H$. Hence, by conjugating $C_1A_2^{-1}$ with R iteratively, we get $C_iA_{i+1}^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5= & {} F_4(C_2A_3^{-1}) = B_4A_6A_2A_1^{-1}B_5^{-1}A_3^{-1}, \\ F_6= & {} RF_5R^{-1} = B_5A_1A_3A_2^{-1}B_6^{-1}A_4^{-1} \end{aligned}$$

and

$$\begin{aligned} F_7 = F_5F_6 = B_4A_6B_6^{-1}A_4^{-1}. \end{aligned}$$

Hence, $(C_4A_5^{-1})F_7(c_4,a_5)=(b_4,a_5)$ so that $B_4A_5^{-1} \in H$. We then get $B_iA_{i+1}^{-1} \in H$ for all i and $B_iC_i^{-1}=(B_iA_{i+1}^{-1})(A_{i+1}C_i^{-1}) \in H$ for all i.

Similarly, we see that $(A_4B_3^{-1})F_7(a_4,b_3)=(b_4,b_3)$ so that $B_4B_3^{-1} \in H$ implying that $B_{i+1}B_i^{-1} \in H$ for all i. In particular, we get $B_1B_2^{-1} \in H$.

Finally, we have $C_1C_2^{-1}=(C_1B_1^{-1})(B_1B_2^{-1})(B_2C_2^{-1}) \in H$ and

$A_1A_2^{-1}=(A_1B_6^{-1})(B_6B_1^{-1})(B_1A_2^{-1}) \in H$.

It follows from Theorem 6 that $H=\mathrm{Mod}(\Sigma _6)$, completing the proof of the corollary. $\square$

Corollary 9

If $g=7$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $C_1B_4A_6A_7^{-1}B_5^{-1}C_2^{-1}$ Fig. 3.

Fig. 3

Proof of Corollary 9

Proof

Let $F_1=C_1B_4A_6A_7^{-1}B_5^{-1}C_2^{-1}$. Let H denote the subgroup of $\mathrm{Mod}(\Sigma _7)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = C_2B_5A_7A_1^{-1}B_6^{-1}C_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = C_3B_6A_1A_7^{-1}B_5^{-1}C_2^{-1}. \end{aligned}$$

We have $F_3F_1(c_3,b_6,a_1,a_7,b_5,c_2)=(b_4,a_6,a_1,a_7,b_5,c_2)$ so that

$F_4=B_4A_6A_1A_7^{-1}B_5^{-1}C_2^{-1}\in H$.

Let

$$\begin{aligned} F_5 = RF_4R^{-1} = B_5A_7A_2A_1^{-1}B_6^{-1}C_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_6 = F_5^{-1} = C_3B_6A_1A_2^{-1}A_7^{-1}B_5^{-1}. \end{aligned}$$

We get $F_6F_4(c_3,b_6,a_1,a_2,a_7,b_5)=(b_4,a_6,a_1,a_2,a_7,b_5)$ so that

$F_7=B_4A_6A_1A_2^{-1}A_7^{-1}B_5^{-1} \in H$.

Let

$$\begin{aligned} F_8 = RF_7R^{-1} = B_5A_7A_2A_3^{-1}A_1^{-1}B_6^{-1} \end{aligned}$$

and

$$\begin{aligned} F_9 = F_8^{-1} = B_6A_1A_3A_2^{-1}A_7^{-1}B_5^{-1}. \end{aligned}$$

Hence, we have $F_9F_7(b_6,a_1,a_3,a_2,a_7,b_5)=(a_6,a_1,a_3,a_2,a_7,b_5)$ so

that $F_{10}=A_6A_1A_3A_2^{-1}A_7^{-1}B_5^{-1} \in H$.

We then see that $F_{10}F_8=A_6B_6^{-1} \in H$ and by conjugating $A_6B_6^{-1}$ with R iteratively, we get $A_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{11} = (B_6A_6^{-1})F_4 = B_4B_6A_1A_7^{-1}B_5^{-1}C_2^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{12} = R^{-1}F_{11}R = B_3B_5A_7A_6^{-1}B_4^{-1}C_1^{-1}. \end{aligned}$$

We also have $F_{12}F_1=B_3C_2^{-1} \in H$ and then $B_{i+1}C_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{13} = (B_6A_6^{-1})F_1(A_7B_7^{-1}) = C_1B_4B_6B_7^{-1}B_5^{-1}C_2^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{14} = RF_{13}R^{-1} = C_2B_5B_7B_1^{-1}B_6^{-1}C_3^{-1}. \end{aligned}$$

Finally, $F_{13}F_{14}(C_3B_4^{-1})=C_1B_1^{-1} \in H$ which gives $C_iB_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _7)$, which finishes the proof.

$\square$

Corollary 10

If $g=8$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $B_1C_4A_7A_8^{-1}C_5^{-1}B_2^{-1}$ Fig. 4.

Fig. 4

Proof of Corollary 10

Proof

Let $F_1=B_1C_4A_7A_8^{-1}C_5^{-1}B_2^{-1}$ and let H be the subgroup of $\mathrm{Mod}(\Sigma _8)$ generated by the set $\{ R, F_1\}$.

Let us consider the elements

$$\begin{aligned} F_2 = RF_1R^{-1} = B_2C_5A_8A_1^{-1}C_6^{-1}B_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = B_3C_6A_1A_8^{-1}C_5^{-1}B_2^{-1}. \end{aligned}$$

We have $F_3F_1(b_3,c_6,a_1,a_8,c_5,b_2)=(b_3,c_6,b_1,a_8,c_5,b_2)$ so that

$F_4=B_3C_6B_1A_8^{-1}C_5^{-1}B_2^{-1}\in H$.

We get that $F_4F_3^{-1}=B_1A_1^{-1} \in H$ and then by conjugating $B_1A_1^{-1}$ with R iteratively, we get $B_iA_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5= & {} R^2F_1R^{-2} = B_3C_6A_1A_2^{-1}C_7^{-1}B_4^{-1}, \\ F_6= & {} F_5^{-1} = B_4C_7A_2A_1^{-1}C_6^{-1}B_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_7 = (B_2A_2^{-1})F_6(A_1B_1^{-1}) = B_4C_7B_2B_1^{-1}C_6^{-1}B_3^{-1}. \end{aligned}$$

We also have $F_7F_1(b_4,c_7,b_2,b_1,c_6,b_3)=(c_4,c_7,b_2,b_1,c_6,b_3)$ so that

$F_8=C_4C_7B_2B_1^{-1}C_6^{-1}B_3^{-1} \in H$. It is easy to check that $F_8F_7^{-1}=C_4B_4^{-1} \in H$ and then we get $C_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_9 = RF_7R^{-1} = B_5C_8B_3B_2^{-1}C_7^{-1}B_4^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{10} = (C_4B_4^{-1})F_9^{-1}(B_5C_5^{-1}) = C_4C_7B_2B_3^{-1}C_8^{-1}C_5^{-1}. \end{aligned}$$

Similarly, we see that $F_{10}F_8(c_4,c_7,b_2,b_3,c_8,c_5)=(c_4,c_7,b_2,b_3,b_1,c_5)$ so that $F_{11}=C_4C_7B_2B_3^{-1}B_1^{-1}C_5^{-1} \in H$. Thus, $F_{10}^{-1}F_{11}=C_8B_1^{-1} \in H$ and then we get $C_iB_{i+1}^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _8)$, completing the proof of the corollary. $\square$

Corollary 11

If $g\ge 9$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $C_1B_4A_7A_8^{-1}B_5^{-1}C_2^{-1}$ (Fig. 5).

Fig. 5

Proof of Corollary 11

Proof

Let $F_1=C_1B_4A_7A_8^{-1}B_5^{-1}C_2^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = C_2B_5A_8A_9^{-1}B_6^{-1}C_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = C_3B_6A_9A_8^{-1}B_5^{-1}C_2^{-1}. \end{aligned}$$

We have $F_3F_1(c_3,b_6,a_9,a_8,b_5,c_2)=(b_4,b_6,a_9,a_8,b_5,c_2)$ so that

$F_4=B_4B_6A_9A_8^{-1}B_5^{-1}C_2^{-1}\in H$.

Hence, we see that $F_4F_3^{-1}=B_4C_3^{-1} \in H$ and then by conjugating $B_4C_3^{-1}$ with R iteratively, we get $B_{i+1}C_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5= & {} F_4(C_2B_3^{-1}) = B_4B_6A_9A_8^{-1}B_5^{-1}B_3^{-1}, \\ F_6= & {} R^{-2}F_5R^2 = B_2B_4A_7A_6^{-1}B_3^{-1}B_1^{-1} \end{aligned}$$

and

$$\begin{aligned} F_7 = F_6^{-1} = B_1B_3A_6A_7^{-1}B_4^{-1}B_2^{-1}. \end{aligned}$$

We get $F_7F_5(b_1,b_3,a_6,a_7,b_4,b_2)=(b_1,b_3,b_6,a_7,b_4,b_2)$ so that

$F_8=B_1B_3B_6A_7^{-1}B_4^{-1}B_2^{-1} \in H$.

We also have $F_8F_7^{-1}= B_6A_6^{-1} \in H$ and then $B_iA_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_9= & {} F_5(A_8B_8^{-1})(B_8C_7^{-1}) = B_4B_6A_9C_7^{-1}B_5^{-1}B_3^{-1}, \\ F_{10}= & {} R^{-1}F_9R = B_3B_5A_8C_6^{-1}B_4^{-1}B_2^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{11} = F_{10}^{-1} = B_2B_4C_6A_8^{-1}B_5^{-1}B_3^{-1}. \end{aligned}$$

Hence, we have $F_{11}F_9(b_2,b_4,c_6,a_8,b_5,b_3)=(b_2,b_4,b_6,a_8,b_5,b_3)$ so that $F_{12}=B_2B_4B_6A_8^{-1}B_5^{-1}B_3^{-1} \in H$.

Finally, we see that $F_{12}F_{11}^{-1}\!=\! B_6C_6^{-1}\! \in \! H$ and then $B_iC_i^{-1}\! \in \! H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the corollary. $\square$

We introduce six new generating sets in Corollaries  12, 13, 14,  15, 16 and 20 to prove Theorem 2.

Corollary 12

If $g=8$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $B_1A_5C_5C_7^{-1}A_7^{-1}B_3^{-1}$.

Proof

Let $F_1=B_1A_5C_5C_7^{-1}A_7^{-1}B_3^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = B_2A_6C_6C_8^{-1}A_8^{-1}B_4^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = B_4A_8C_8C_6^{-1}A_6^{-1}B_2^{-1}. \end{aligned}$$

We have $F_3F_1(b_4,a_8,c_8,c_6,a_6,b_2)=(b_4,a_8,b_1,c_6,a_6,b_2)$ so that

$F_4=B_4A_8B_1C_6^{-1}A_6^{-1}B_2^{-1}\in H$.

We get $F_4F_3^{-1}=B_1C_8^{-1} \in H$ and then by conjugating $B_1C_8^{-1}$ with R iteratively, we get $B_{i+1}C_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5 = RF_4R^{-1} = B_5A_1B_2C_7^{-1}A_7^{-1}B_3^{-1}. \end{aligned}$$

We also have $F_5F_4(b_5,a_1,b_2,c_7,a_7,b_3)=(b_5,b_1,b_2,c_7,a_7,b_3)$ so that

$F_6=B_5B_1B_2C_7^{-1}A_7^{-1}B_3^{-1} \in H$.

Hence, we get $F_6F_5^{-1}= B_1A_1^{-1} \in H$ and then $B_iA_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_7= & {} (C_4B_5^{-1})F_6(C_7B_8^{-1})(A_7B_7^{-1}) = C_4B_1B_2B_3^{-1}B_8^{-1}B_7^{-1},\\ F_8= & {} RF_7R^{-1} = C_5B_2B_3B_4^{-1}B_1^{-1}B_8^{-1} \end{aligned}$$

and

$$\begin{aligned} F_9 = F_8^{-1} = B_8B_1B_4B_3^{-1}B_2^{-1}C_5^{-1}. \end{aligned}$$

Similarly, check that $F_9F_7(b_8,b_1,b_4,b_3,b_2,c_5)=(b_8,b_1,c_4,b_3,b_2,c_5)$ so that $F_{10}=B_8B_1C_4B_3^{-1}B_2^{-1}C_5^{-1} \in H$.

Finally, we see that $F_{10}F_9^{-1}\!=\! C_4B_4^{-1} \in H$ and then $C_iB_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _8)$, completing the proof of the corollary. $\square$

Corollary 13

If $g=9$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $B_1A_3C_5C_8^{-1}A_6^{-1}B_4^{-1}$.

Proof

Let $F_1=B_1A_3C_5C_8^{-1}A_6^{-1}B_4^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _9)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = B_2A_4C_6C_9^{-1}A_7^{-1}B_5^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = B_5A_7C_9C_6^{-1}A_4^{-1}B_2^{-1}. \end{aligned}$$

We have that $F_3F_1(b_5,a_7,c_9,c_6,a_4,b_2)=(c_5,a_7,b_1,c_6,b_4,b_2)$ so that $F_4=C_5A_7B_1C_6^{-1}B_4^{-1}B_2^{-1}\in H$.

Let

$$\begin{aligned} F_5 = RF_4R^{-1} = C_6A_8B_2C_7^{-1}B_5^{-1}B_3^{-1} \end{aligned}$$

and

$$\begin{aligned} F_6 = F_5^{-1} = B_3B_5C_7B_2^{-1}A_8^{-1}C_6^{-1}. \end{aligned}$$

We get $F_6F_4(b_3,b_5,c_7,b_2,a_8,c_6)=(b_3,c_5,c_7,b_2,a_8,c_6)$ so that

$F_7=B_3C_5C_7B_2^{-1}A_8^{-1}C_6^{-1}\in H$.

We see that $F_7F_6^{-1}=C_5B_5^{-1} \in H$ and then by conjugating $C_5B_5^{-1}$ with R iteratively, we get $C_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_8= & {} (B_7C_7^{-1})F_6(C_6B_6^{-1}) = B_3B_5B_7B_2^{-1}A_8^{-1}B_6^{-1}, \\ F_9= & {} RF_8R^{-1} = B_4B_6B_8B_3^{-1}A_9^{-1}B_7^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{10} = F_9^{-1} = B_7A_9B_3B_8^{-1}B_6^{-1}B_4^{-1}. \end{aligned}$$

We also have $F_{10}F_8(b_7,a_9,b_3,b_8,b_6,b_4)=(b_7,a_9,b_3,a_8,b_6,b_4)$ so that

$F_{11}=B_7A_9B_3A_8^{-1}B_6^{-1}B_4^{-1} \in H$.

Finally, we have $F_{11}^{-1}F_{10}= A_8B_8^{-1} \in H$ and then $A_iB_i^{-1} \in H$ for all i.

Check $F_4(B_4A_4^{-1})F_2(B_5C_5^{-1})= B_1C_9^{-1} \in H$ and then $B_{i+1}C_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _9)$, completing the proof of the corollary. $\square$

Corollary 14

If $g=10$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $A_1C_1B_3B_7^{-1}C_5^{-1}A_5^{-1}$.

Proof

Let $F_1=A_1C_1B_3B_7^{-1}C_5^{-1}A_5^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _{10})$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = A_2C_2B_4B_8^{-1}C_6^{-1}A_6^{-1}. \end{aligned}$$

We have $F_2F_1(a_2,c_2,b_4,b_8,c_6,a_6)=(a_2,b_3,b_4,b_8,b_7,a_6)$ so that

$F_3=A_2B_3B_4B_8^{-1}B_7^{-1}A_6^{-1}\in H$.

Let

$$\begin{aligned} F_4 = R^4F_3R^{-4} = A_6B_7B_8B_2^{-1}B_1^{-1}A_{10}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_5 = F_4^{-1} = A_{10}B_1B_2B_8^{-1}B_7^{-1}A_6^{-1}. \end{aligned}$$

We get $F_5F_3(a_{10},b_1,b_2,b_8,b_7,a_6)=(a_{10},b_1,a_2,b_8,b_7,a_6)$ so that

$F_6=A_{10}B_1A_2B_8^{-1}B_7^{-1}A_6^{-1} \in H$.

We see that $F_6F_5^{-1}=A_2B_2^{-1} \in H$ and then by conjugating $A_2B_2^{-1}$ with R iteratively, we get $A_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_7= & {} (B_2A_2^{-1})(A_3B_3^{-1})F_3(B_7A_7^{-1})(A_6B_6^{-1}) = B_2A_3B_4B_8^{-1}A_7^{-1}B_6^{-1}, \\ F_8= & {} RF_2F_3^{-1}R^{-1}F_7 = B_2A_3C_3C_7^{-1}A_7^{-1}B_6^{-1}, \\ F_9= & {} F_8^{-1} = B_6A_7C_7C_3^{-1}A_3^{-1}B_2^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{10} = R^4F_9R^{-4} = B_{10}A_1C_1C_7^{-1}A_7^{-1}B_6^{-1}. \end{aligned}$$

We also have $F_{10}F_8(b_{10},a_1,c_1,c_7,a_7,b_6)=(b_{10},a_1,b_2,c_7,a_7,b_6)$ so that $F_{11}=B_{10}A_1B_2C_7^{-1}A_7^{-1}B_6^{-1} \in H$.

We then get $F_{11}F_{10}^{-1}= B_2C_1^{-1} \in H$ and then $B_{i+1}C_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{12}= & {} (B_2A_2^{-1})F_3(A_6B_6^{-1})(B_6C_5^{-1})(B_7A_7^{-1})(B_8A_8^{-1})= B_2B_3B_4A_8^{-1}A_7^{-1}C_5^{-1}, \\ F_{13}= & {} F_{12}^{-1} = C_5A_7A_8B_4^{-1}B_3^{-1}B_2^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{14} = RF_{13}R^{-1} = C_6A_8A_9B_5^{-1}B_4^{-1}B_3^{-1}. \end{aligned}$$

Hence, we have $F_{14}F_{12}(c_6,a_8,a_9,b_5,b_4,b_3)=(c_6,a_8,a_9,c_5,b_4,b_3)$ so that $F_{15}=C_6A_8A_9C_5^{-1}B_4^{-1}B_3^{-1} \in H$.

Finally, we see that $F_{15}^{-1}F_{14}\!=\! C_5B_5^{-1} \!\in \! H$ and then $C_iB_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _{10})$, completing the proof of the corollary. $\square$

Corollary 15

If $g \ge 13$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $A_1B_4C_8C_{10}^{-1}B_6^{-1}A_3^{-1}$.

Proof

Let $F_1=A_1B_4C_8C_{10}^{-1}B_6^{-1}A_3^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = A_2B_5C_9C_{11}^{-1}B_7^{-1}A_4^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = A_4B_7C_{11}C_9^{-1}B_5^{-1}A_2^{-1}. \end{aligned}$$

We have $F_3F_1(a_4,b_7,c_{11},c_9,b_5,a_2)=(b_4,b_7,c_{11},c_9,b_5,a_2)$ so that

$F_4=B_4B_7C_{11}C_9^{-1}B_5^{-1}A_2^{-1}\in H$.

We see that $F_4F_3^{-1}=B_4A_4^{-1} \in H$ and then by conjugating $B_4A_4^{-1}$ with R iteratively, we get $B_iA_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5 = R^2F_1R^{-2} = A_3B_6C_{10}C_{12}^{-1}B_8^{-1}A_5^{-1} \end{aligned}$$

and

$$\begin{aligned} F_6 = F_5^{-1} = A_5B_8C_{12}C_{10}^{-1}B_6^{-1}A_3^{-1}. \end{aligned}$$

We also have $F_6F_1(a_5,b_8,c_{12},c_{10},b_6,a_3)=(a_5,c_8,c_{12},c_{10},b_6,a_3)$ so that $F_7=A_5C_8C_{12}C_{10}^{-1}B_6^{-1}A_3^{-1} \in H$.

We get $F_7F_6^{-1}= C_8B_8^{-1} \in H$ and then $C_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_8= & {} (A_4B_4^{-1})F_1(A_3B_3^{-1}) = A_1A_4C_8C_{10}^{-1}B_6^{-1}B_3^{-1}, \\ F_9= & {} R^3F_8R^{-3} = A_4A_7C_{11}C_{13}^{-1}B_9^{-1}B_6^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{10} = F_9^{-1} = B_6B_9C_{13}C_{11}^{-1}A_7^{-1}A_4^{-1}. \end{aligned}$$

Hence, check that $F_{10}F_8(b_6,b_9,c_{13},c_{11},a_7,a_4)=(b_6,c_8,c_{13},c_{11},a_7,a_4)$ so that $F_{11}=B_6C_8C_{13}C_{11}^{-1}A_7^{-1}A_4^{-1} \in H$.

Finally, we have $F_{11}F_{10}^{-1}= C_8B_9^{-1} \in H$ and then $C_iB_{i+1}^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the corollary. $\square$

Corollary 16

If $g \ge 12$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $B_1A_3C_6C_{10}^{-1}A_7^{-1}B_5^{-1}$.

Proof

Let $F_1=B_1A_3C_6C_{10}^{-1}A_7^{-1}B_5^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = B_2A_4C_7C_{11}^{-1}A_8^{-1}B_6^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = B_6A_8C_{11}C_7^{-1}A_4^{-1}B_2^{-1}. \end{aligned}$$

We have $F_3F_1(b_6,a_8,c_{11},c_7,a_4,b_2)=(c_6,a_8,c_{11},c_7,a_4,b_2)$ so that

$F_4=C_6A_8C_{11}C_7^{-1}A_4^{-1}B_2^{-1}\in H$.

We get $F_4F_3^{-1}=C_6B_6^{-1} \in H$ and then by conjugating $C_6B_6^{-1}$ with R iteratively, we get $C_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5 = F_1(C_{10}B_{10}^{-1})(B_5C_5^{-1}) = B_1A_3C_6B_{10}^{-1}A_7^{-1}C_5^{-1} \end{aligned}$$

and

$$\begin{aligned} F_6 = R^2F_5R^{-2} = B_3A_5C_8B_{12}^{-1}A_9^{-1}C_7^{-1}. \end{aligned}$$

We also have $F_6F_5(b_3,a_5,c_8,b_{12},a_9,c_7)=(a_3,a_5,c_8,b_{12},a_9,c_7)$ so that

$F_7=A_3A_5C_8B_{12}^{-1}A_9^{-1}C_7^{-1} \in H$.

We get $F_7F_6^{-1}= A_3B_3^{-1} \in H$ and then $A_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_8 = (C_1B_1^{-1})(B_3A_3^{-1})F_1(B_5C_5^{-1}) = C_1B_3C_6C_{10}^{-1}A_7^{-1}C_5^{-1} \end{aligned}$$

and

$$\begin{aligned} F_9 = RF_8R^{-1} = C_2B_4C_7C_{11}^{-1}A_8^{-1}C_6^{-1}. \end{aligned}$$

Then check that $F_9F_8(c_2,b_4,c_7,c_{11},a_8,c_6)=(b_3,b_4,c_7,c_{11},a_8,c_6)$ so that $F_{10}=B_3B_4C_7C_{11}^{-1}A_8^{-1}C_6^{-1} \in H$.

Finally, we have $F_{10}F_9^{-1}= B_3C_2^{-1} \in H$ and then $B_{i+1}C_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the corollary. $\square$

Lemma 17

If $g \ge 11$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $A_1B_2C_4C_{g-1}^{-1}B_{g-3}^{-1}A_{g-4}^{-1}$.

Proof

Let $F_1=A_1B_2C_4C_{g-1}^{-1}B_{g-3}^{-1}A_{g-4}^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = A_2B_3C_5C_g^{-1}B_{g-2}^{-1}A_{g-3}^{-1}. \end{aligned}$$

We have $F_2F_1(a_2,b_3,c_5,c_g,b_{g-2},a_{g-3})=(b_2,b_3,c_5,c_g,b_{g-2},b_{g-3})$ so that $F_3=B_2B_3C_5C_g^{-1}B_{g-2}^{-1}B_{g-3}^{-1}\in H$.

Let

$$\begin{aligned} F_4 = R^{-1}F_3R = B_1B_2C_4C_{g-1}^{-1}B_{g-3}^{-1}B_{g-4}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_5 = F_3^{-1} = B_{g-3}B_{g-2}C_gC_5^{-1}B_3^{-1}B_2^{-1}. \end{aligned}$$

We also have $F_5F_4(b_{g-3},b_{g-2},c_g,c_5,b_3,b_2)=(b_{g-3},b_{g-2},b_1,c_5,b_3,b_2)$ so that $F_6=B_{g-3}B_{g-2}B_1C_5^{-1}B_3^{-1}B_2^{-1} \in H$.

We see that $F_6F_5^{-1}=B_1C_g^{-1} \in H$ and then by conjugating $B_1C_g^{-1}$ with R iteratively, we get $B_{i+1}C_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_7 = (C_{g-3}B_{g-2}^{-1})(C_{g-4}B_{g-3}^{-1})F_6 = C_{g-3}C_{g-4}B_1C_5^{-1}B_3^{-1}B_2^{-1} \end{aligned}$$

and

$$\begin{aligned} F_8 = R^2F_7R^{-2} = C_{g-1}C_{g-2}B_3C_7^{-1}B_5^{-1}B_4^{-1}. \end{aligned}$$

We have $F_8F_7(c_{g-1},c_{g-2},b_3,c_7,b_5,b_4)=(c_{g-1},c_{g-2},b_3,c_7,c_5,b_4)$ so that $F_9=C_{g-1}C_{g-2}B_3C_7^{-1}C_5^{-1}B_4^{-1} \in H$.

We then get $F_9F_8^{-1}= C_5B_5^{-1} \in H$ and then $C_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{10} = F_1(B_{g-3}C_{g-3}^{-1}) = A_1B_2C_4C_{g-1}^{-1}C_{g-3}^{-1}A_{g-4}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{11} = RF_{10}R^{-1} = A_2B_3C_5C_g^{-1}C_{g-2}^{-1}A_{g-3}^{-1}. \end{aligned}$$

Hence, we see $F_{11}F_{10}(a_2,b_3,c_5,c_g,c_{g-2},a_{g-3})=(b_2,b_3,c_5,c_g,c_{g-2},a_{g-3})$

so that $F_{12}=B_2B_3C_5C_g^{-1}C_{g-2}^{-1}A_{g-3}^{-1} \in H$.

Finally, we have $F_{12}F_{11}^{-1}= B_2A_2^{-1} \in H$ and then $B_iA_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the lemma. $\square$

Lemma 18

If $g \ge 13$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the two elements R and $A_1B_2C_4C_{g-2}^{-1}B_{g-4}^{-1}A_{g-5}^{-1}$.

Proof

Let $F_1=A_1B_2C_4C_{g-2}^{-1}B_{g-4}^{-1}A_{g-5}^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = RF_1R^{-1} = A_2B_3C_5C_{g-1}^{-1}B_{g-3}^{-1}A_{g-4}^{-1}. \end{aligned}$$

We have $F_2F_1(a_2,b_3,c_5,c_{g-1},b_{g-3},a_{g-4})=(b_2,b_3,c_5,c_{g-1},b_{g-3},b_{g-4})$ so that $F_3=B_2B_3C_5C_{g-1}^{-1}B_{g-3}^{-1}B_{g-4}^{-1}\in H$.

Let

$$\begin{aligned} F_4 = F_2F_3^{-1}= & {} A_2B_2^{-1}A_{g-4}^{-1}B_{g-4} , \\ F_5= & {} RF_4R^{-1} = A_3B_3^{-1}A_{g-3}^{-1}B_{g-3} , \\ F_6= & {} F_5F_3 = B_2A_3C_5C_{g-1}^{-1}A_{g-3}^{-1}B_{g-4}^{-1} , \\ F_7= & {} R^{-2}F_6R^2 = B_gA_1C_3C_{g-3}^{-1}A_{g-5}^{-1}B_{g-6}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_8 = F_7^{-1} = B_{g-6}A_{g-5}C_{g-3}C_3^{-1}A_1^{-1}B_g^{-1}. \end{aligned}$$

We get $F_8F_6(b_{g-6},a_{g-5},c_{g-3},c_3,a_1,b_g)=(b_{g-6},a_{g-5},c_{g-3},c_3,a_1,c_{g-1})$ so that $F_9=B_{g-6}A_{g-5}C_{g-3}C_3^{-1}A_1^{-1}C_{g-1}^{-1} \in H$.

We see that $F_9F_8^{-1}=C_{g-1}B_g^{-1} \in H$ and then by conjugating $C_{g-1}B_g^{-1}$ with R iteratively, we get $C_iB_{i+1}^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{10} = F_3(C_{g-1}B_g^{-1}) = B_2B_3C_5B_g^{-1}B_{g-3}^{-1}B_{g-4}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{11} = R^2F_{10}R^{-2} = B_4B_5C_7B_2^{-1}B_{g-1}^{-1}B_{g-2}^{-1}. \end{aligned}$$

We also have $F_{11}F_{10}(b_4,b_5,c_7,b_2,b_{g-1},b_{g-2})=(b_4,c_5,c_7,b_2,b_{g-1},b_{g-2})$

so that $F_{12}=B_4C_5C_7B_2^{-1}B_{g-1}^{-1}B_{g-2}^{-1} \in H$.

We then get $F_{12}F_{11}^{-1}= C_5B_5^{-1} \in H$ and then $C_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{13} = F_1(B_{g-4}C_{g-4}^{-1}) = A_1B_2C_4C_{g-2}^{-1}C_{g-4}^{-1}A_{g-5}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_{14} = RF_{13}R^{-1} = A_2B_3C_5C_{g-1}^{-1}C_{g-3}^{-1}A_{g-4}^{-1}. \end{aligned}$$

Hence, $F_{14}F_{13}(a_2,b_3,c_5,c_{g-1},c_{g-3},a_{g-4})=(b_2,b_3,c_5,c_{g-1},c_{g-3},a_{g-4})$ so that $F_{15}=B_2B_3C_5C_{g-1}^{-1}C_{g-3}^{-1}A_{g-4}^{-1} \in H$.

Finally, we have $F_{15}F_{14}^{-1}= B_2A_2^{-1} \in H$ and then $B_iA_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the corollary. $\square$

Lemma 19

If $k \ge 7$ and $g \ge 2k+1$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by elements R and $A_1B_2C_4C_{g-k+4}^{-1}B_{g-k+2}^{-1}A_{g-k+1}^{-1}$.

Proof

Let $F_1=A_1B_2C_4C_{g-k+4}^{-1}B_{g-k+2}^{-1}A_{g-k+1}^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, F_1\}$.

Let

$$\begin{aligned} F_2 = R^{k-3}F_1R^{3-k} = A_{k-2}B_{k-1}C_{k+1}C_1^{-1}B_{g-1}^{-1}A_{g-2}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = A_{g-2}B_{g-1}C_1C_{k+1}^{-1}B_{k-1}^{-1}A_{k-2}^{-1}. \end{aligned}$$

$F_3F_1(a_{g-2},b_{g-1},c_1,c_{k+1},b_{k-1},a_{k-2})=(a_{g-2},b_{g-1},b_2,c_{k+1},b_{k-1},a_{k-2})$ so that $F_4=A_{g-2}B_{g-1}B_2C_{k+1}^{-1}B_{k-1}^{-1}A_{k-2}^{-1}\in H$.

We get $F_4F_3^{-1}=B_2C_1^{-1} \in H$ and then by conjugating $B_2C_1^{-1}$ with R iteratively, we get $B_{i+1}C_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5 = F_1(B_{g-k+2}C_{g-k+1}^{-1}) = A_1B_2C_4C_{g-k+4}^{-1}C_{g-k+1}^{-1}A_{g-k+1}^{-1} \end{aligned}$$

and

$$\begin{aligned} F_6 = RF_5R^{-1} = A_2B_3C_5C_{g-k+5}^{-1}C_{g-k+2}^{-1}A_{g-k+2}^{-1}. \end{aligned}$$

$F_6F_5(a_2,b_3,c_5,c_{g-k+5},c_{g-k+2},a_{g-k+2})=(b_2,b_3,c_5,c_{g-k+5},c_{g-k+2},a_{g-k+2})$

so that $F_7=B_2B_3C_5C_{g-k+5}^{-1}C_{g-k+2}^{-1}A_{g-k+2}^{-1} \in H$.

We then get $F_7F_6^{-1}= B_2A_2^{-1} \in H$ and then $B_iA_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_8 = R^{k-2}F_6R^{2-k} = A_kB_{k+1}C_{k+3}C_3^{-1}Cg^{-1}A_g^{-1} \end{aligned}$$

and

$$\begin{aligned} F_9 = F_8^{-1} = A_gC_gC_3C_{k-3}^{-1}B_{k+1}^{-1}A_k^{-1}. \end{aligned}$$

We have $F_9F_6(a_g,c_g,c_3,c_{k+3},b_{k+1},a_k)=(a_g,c_g,b_3,c_{k+3},b_{k+1},a_k)$

so that $F_{10}=A_gC_gB_3C_{k-3}^{-1}B_{k+1}^{-1}A_k^{-1} \in H$.

Finally, we see that $F_{10}F_9^{-1}= B_3C_3^{-1} \in H$ and then $B_iC_i^{-1} \in H$ for all i.

It follows from Corollary 7 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the lemma. $\square$

Corollary 20

If $k \ge 5$ and $g \ge 2k+1$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by elements R and $A_1B_2C_4C_{g-k+4}^{-1}B_{g-k+2}^{-1}A_{g-k+1}^{-1}$.

Proof

It directly follows from Lemmas 17,  18 and  19. $\square$

4 Main Results

In this section, we prove the main results of this paper. The following Lemma is useful to decide the order of an element.

Lemma 21

If R is an element of order k in a group G and if x and y are elements in G satisfying $RxR^{-1}=y$, then the order of $Rxy^{-1}$ is also k.

Proof

$(Rxy^{-1})^{k}=(yRy^{-1})^{k}=yR^ky^{-1}=1$.

On the other hand, if $(Rxy^{-1})^{l}=1$ then $(Rxy^{-1})^{l}=(yRy^{-1})^{l}=yR^ly^{-1}=1$ i.e. $R^l=1$ and hence $k \mid l$. $\square$

Now, we are ready to prove Theorem 2.

Proof

For $g=10$, we let $H_{10}$ be the subgroup of $\mathrm{Mod}(\Sigma _{10})$ generated by the set $\{ R, R^4A_1C_1B_3B_7^{-1}C_5^{-1}A_5^{-1}\}$. We get $H_{10} =$ $\mathrm{Mod}(\Sigma _{10})$ by Corollary 14. Then we are done by Lemma 21 since $R^4(A_1C_1B_3)R^{-4}=A_5C_5B_7$. Note that, order of $R^4$ is clearly 5 and hence order of the element $R^4(A_1C_1B_3)(A_5C_5B_7)^{-1}$ is also 5 by Lemma  21 since $R^4(a_1)=a_5$, $R^4(c_1)=c_5$ and $R^4(b_3)=b_7$ implies $R^4(A_1C_1B_3)R^{-4} = A_5C_5B_7$.

For $g=9$, we let $H_9$ be the subgroup of $\mathrm{Mod}(\Sigma _9)$ generated by the set $\{ R, R^3B_1A_3C_5C_8^{-1}A_6^{-1}B_4^{-1}\}$. We have $H_9 =$ $\mathrm{Mod}(\Sigma _9)$ by Corollary 13. Then we are done by Lemma 21 since $R^3(B_1A_3C_5)R^{-3}=B_4A_6C_8$.

For $g=8$, we let $H_8$ be the subgroup of $\mathrm{Mod}(\Sigma _8)$ generated by the set $\{ R, R^2B_1A_5C_5C_7^{-1}A_7^{-1}B_3^{-1}\}$. Hence, $H_8 =$ $\mathrm{Mod}(\Sigma _8)$ by Corollary 12. Then we are done by Lemma 21 since $R^2(B_1A_5C_5)R^{-2}=B_3A_7C_7$.

For $g=7$, we let $H_7$ be the subgroup of $\mathrm{Mod}(\Sigma _7)$ generated by the set $\{ R, RC_1B_4A_6A_7^{-1}B_5^{-1}C_2^{-1}\}$. We have $H_7 =$ $\mathrm{Mod}(\Sigma _7)$ by Corollary 9. Then we are done by Lemma 21 since $R(C_1B_4A_6)R^{-1}=C_2B_5A_7$.

The remaining part of the proof is the case of $g\ge 11$. Let $k=g/g'$ so that k is the greatest divisor of g such that k is strictly less than g/2. Clearly, the number k can be any positive integer but three.

If $k=2$, let $K_2$ be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, R^2A_1B_4C_8C_{10}^{-1}B_6^{-1}A_3^{-1}\}$. We get $K_2 =$ $\mathrm{Mod}(\Sigma _g)$ by Corollary 15. Then we are done by Lemma 21 since $R^2(A_1B_4C_8)R^{-2}=A_3B_6C_{10}$.

If $k=4$, let $K_4$ be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, R^4B_1A_3C_6C_{10}^{-1}A_7^{-1}B_5^{-1}\}$. We get $K_4 =$ $\mathrm{Mod}(\Sigma _g)$ by Corollary 16. Then we are done by Lemma 21 since $R^4(B_1A_3C_6)R^{-4}=B_5A_7C_{10}$.

If $k=1$ or $k=5$, let $K_5$ be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{R, R^{-5}A_1B_2C_4C_{g-1}^{-1}B_{g-3}^{-1}A_{g-4}^{-1}\}$. We get $K_5 =$ $\mathrm{Mod}(\Sigma _g)$ by Corollary 20. Then we are done by Lemma 21 since $R^{-5}(A_1B_2C_4)R^5=A_{g-4}B_{g-3}C_{g-1}$.

If $k=6$, let $K_6$ be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, R^{-6}A_1B_2C_4C_{g-2}^{-1}B_{g-4}^{-1}A_{g-5}^{-1}\}$. We get $K_6 =$ $\mathrm{Mod}(\Sigma _g)$ by Corollary 20. Then we are done by Lemma 21 since $R^{-6}(A_1B_2C_4)R^6=A_{g-5}B_{g-4}C_{g-2}$.

If $k\ge 7$, let K be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, R^{-k}A_1B_2C_4C_{g-k+4}^{-1}B_{g-k+2}^{-1}A_{g-k+1}^{-1}\}$. We get $K =$ $\mathrm{Mod}(\Sigma _g)$ by Corollary 20. Then we are done by Lemma 21 since $R^{-k}(A_1B_2C_4)R^k = A_{g-k+1}B_{g-k+2}C_{g-k+4}$. $\square$

Finally, we prove Theorem 1.

Proof

If $g=6$, let $H_6$ be the subgroup of $\mathrm{Mod}(\Sigma _6)$ generated by the set $\{ R, RC_1B_4A_6A_1^{-1}B_5^{-1}C_2^{-1}\}$. We get $H_6 =$ $\mathrm{Mod}(\Sigma _6)$ by Corollary 8. Then we are done by Lemma 21 since $R(C_1B_4A_6)R^{-1}=C_2B_5A_1$. Note that, since $R(c_1)=c_2$, $R(b_4)=b_5$ and $R(a_6)=a_1$, we have $R(C_1B_4A_6)R^{-1} = C_2B_5A_1$ which implies order of the element $R(C_1B_4A_6)(C_2B_5A_1)^{-1}$ is g.

If $g=7$, let $H_7$ be the subgroup of $\mathrm{Mod}(\Sigma _7)$ generated by the set $\{ R, RC_1B_4A_6A_7^{-1}B_5^{-1}C_2^{-1}\}$. We get $H_7 =$ $\mathrm{Mod}(\Sigma _7)$ by Corollary 9. Then we are done by Lemma 21 since $R(C_1B_4A_6)R^{-1}=C_2B_5A_7$.

If $g=8$, let $H_8$ be the subgroup of $\mathrm{Mod}(\Sigma _8)$ generated by the set $\{ R, RB_1C_4A_7A_8^{-1}C_5^{-1}B_2^{-1}\}$. We get $H_8 =$ $\mathrm{Mod}(\Sigma _8)$ by Corollary 10. Then we are done by Lemma 21 since $R(B_1C_4A_7)R^{-1}=B_2C_5A_8$.

If $g\ge 9$, let $H_9$ be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R, RC_1B_4A_7A_8^{-1}B_5^{-1}C_2^{-1}\}$. We get $H_9 =$ $\mathrm{Mod}(\Sigma _g)$ by Corollary 11. Then we are done by Lemma 21 since $R(C_1B_4A_7)R^{-1}=C_2B_5A_8$. $\square$

5 Further Results

In this section, we prove Theorem 3 which states as: for $g\ge 3k^2+4k+1$ and any positive integer k, the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by two elements of order $g/\gcd (g,k)$.

Korkmaz showed the following result in the proof of Theorem  6.

Theorem 22

If $g\ge 3$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the elements $A_iA_j^{-1},B_iB_j^{-1}, C_iC_j^{-1}$ for all i, j.

Sketch of the proof is as follows: $A_1A_2^{-1}B_1B_2^{-1}(a_1,a_3) = (b_1,a_3)$. $B_1A_3^{-1}C_1C_2^{-1}(b_1,a_3) = (c_1,a_3)$. Korkmaz then showed that $A_3$ can be generated by these elements using lantern relation. Hence, $A_i = (A_iA_3^{-1})A_3$, $B_i = (B_iB_1^{-1})(B_1A_3^{-1})A_3$ and $C_i = (C_iC_1^{-1})(C_1A_3^{-1})A_3$ are generated by given elements. This finishes the proof.

Now, we prove the next statement as a corollary to Theorem  22.

Corollary 23

If $g\ge 3$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the elements $A_iB_i^{-1},C_iB_i^{-1}, C_iB_{i+1}^{-1}$ for all i.

Proof

Let us denote by H the subgroup generated by the elements $A_iB_i^{-1},C_iB_i^{-1}, C_iB_{i+1}^{-1}$ for all i.

We have $B_iB_j^{-1}=(B_iC_i^{-1})(C_iB_{i+1}^{-1})\cdots (B_{j-1}C_{j-1}^{-1})(C_{j-1}B_j^{-1}) \in H$ for all i, j, we also have $C_iC_j^{-1}=(C_iB_i^{-1})(B_iB_j^{-1})(B_jC_j^{-1}) \in H$ for all i, j and $A_iA_j^{-1}=(A_iB_i^{-1})(B_iB_j^{-1})(B_jA_j^{-1}) \in H$ for all i, j.

It follows from Theorem 22 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the lemma. $\square$

Theorem 24

If $g\ge 21$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the elements $R^2,B_1B_2A_5A_8C_{11}C_{14}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}.$

Proof

Let $F_1=B_1B_2A_5A_8C_{11}C_{14}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R^2, F_1\}$.

Let

$$\begin{aligned} F_2 = R^2F_1R^{-2} = B_3B_4A_7A_{10}C_{13}C_{16}C_{18}^{-1}C_{15}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}B_5^{-1} \end{aligned}$$

and

$$\begin{aligned} F_3 = F_2^{-1} = B_5B_6A_9A_{12}C_{15}C_{18}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}. \end{aligned}$$

We have $F_3F_1(b_5,b_6, \ldots ,b_3)=(a_5,b_6, \ldots ,b_3)$ so that

$F_4=A_5B_6A_9A_{12}C_{15}C_{18}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}\in H$.

Note that $\ldots$ refers to the elements remaining fixed under the given maps.

We also have $F_4F_3^{-1}=A_5B_5^{-1} \in H$ and then by conjugating $A_5B_5^{-1}$ with $R^2$ iteratively, we get $A_{2i+1}B_{2i+1}^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_5 = R^4F_1R^{-4} = B_5B_6A_9A_{12}C_{15}C_{18}C_{20}^{-1}C_{17}^{-1}A_{14}^{-1}A_{11}^{-1}B_8^{-1}B_7^{-1} \end{aligned}$$

and

$$\begin{aligned} F_6= & {} (A_7B_7^{-1})F_5^{-1}(B_5A_5^{-1})\\= & {} A_7B_8A_{11}A_{14}C_{17}C_{20}C_{18}^{-1}C_{15}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}A_5^{-1}. \end{aligned}$$

We then have $F_6F_1(a_7,b_8,a_{11}, \ldots ,b_6,a_5)=(a_7,a_8,a_{11}, \ldots ,b_6,a_5)$ so that $F_7=A_7A_8A_{11}A_{14}C_{17}C_{20}C_{18}^{-1}C_{15}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}A_5^{-1}\in H$.

$F_7F_6^{-1}=A_8B_8^{-1} \in H$ and then by conjugating $A_8B_8^{-1}$ with $R^2$ iteratively, we get $A_{2i}B_{2i}^{-1} \in H$ for all i.

Hence, we get $A_iB_i^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_8 = (B_{12}A_{12}^{-1})F_4 = A_5B_6A_9B_{12}C_{15}C_{18}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}. \end{aligned}$$

We then get $F_8F_1( \ldots ,b_{12}, \ldots )=( \ldots ,c_{11}, \ldots )$ so that

$F_9=A_5B_6A_9C_{11}C_{15}C_{18}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}\in H$.

We have $F_9F_8^{-1}=C_{11}B_{12}^{-1} \in H$ and then by conjugating $C_{11}B_{12}^{-1}$ with $R^2$ iteratively, we get $C_{2i+1}B_{2i+2}^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{10} = (B_{11}A_{11}^{-1})F_7 = A_7A_8B_{11}A_{14}C_{17}C_{20}C_{18}^{-1}C_{15}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}A_5^{-1}. \end{aligned}$$

Similarly, we have $F_{10}F_1( \ldots ,b_{11}, \ldots )=( \ldots ,c_{11}, \ldots )$ so that

$F_{11}=A_7A_8C_{11}A_{14}C_{17}C_{20}C_{18}^{-1}C_{15}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}A_5^{-1} \in H$.

Hence, we get $F_{11}F_{10}^{-1}= C_{11}B_{11}^{-1} \in H$ and we get $C_{2i+1}B_{2i+1}^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{12} = (B_{15}C_{15}^{-1})F_4 = A_5B_6A_9A_{12}B_{15}C_{18}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}. \end{aligned}$$

We also have $F_{12}F_1( \ldots ,b_{15}, \ldots )=( \ldots ,c_{14}, \ldots )$ so that

$F_{13}=A_5B_6A_9A_{12}C_{14}C_{18}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1} \in H$.

Check that $F_{13}F_{12}^{-1}= C_{14}B_{15}^{-1} \in H$ and then we get $C_{2i}B_{2i+1}^{-1} \in H$ for all i. Hence, we have $C_iB_{i+1}^{-1} \in H$ for all i.

Let

$$\begin{aligned} F_{14} = F_7(C_{15}B_{16}^{-1}) = A_7A_8A_{11}A_{14}C_{17}C_{20}C_{18}^{-1}B_{16}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}A_5^{-1}. \end{aligned}$$

We then get $F_{14}F_1(\ldots ,b_{16}, \ldots )=( \ldots ,c_{16}, \ldots )$ so that

$F_{15}=A_7A_8A_{11}A_{14}C_{17}C_{20}C_{18}^{-1}C_{16}^{-1}A_{12}^{-1}A_9^{-1}B_6^{-1}A_5^{-1} \in H$.

Hence, we see that $F_{15}^{-1}F_{14}= C_{16}B_{16}^{-1} \in H$ and then we get $C_{2i}B_{2i}^{-1} \in H$ for all i. Finally, we have $C_iB_i^{-1} \in H$ for all i.

It follows from Corollary 23 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the theorem. $\square$

Corollary 25

If g is even and $g\ge 22$, then the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by two elements of order g/2.

Proof

Let H be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set

$\{ R^2, R^2B_1B_2A_5A_8C_{11}C_{14}C_{16}^{-1}C_{13}^{-1}A_{10}^{-1}A_7^{-1}B_4^{-1}B_3^{-1}\}$.

We get $H=$ $\mathrm{Mod}(\Sigma _g)$ by Theorem 24. Then we are done by Lemma 21 since $R^2(B_1B_2A_5A_8C_{11}C_{14})R^{-2}=B_3B_4A_7A_{10}C_{13}C_{16}$. $\square$

Generalization of Theorem 24 and Corollary 25 is as follows:

Theorem 26

For $k\ge 2$ and $g\ge 3k^2+4k+1$, the mapping class group $\mathrm{Mod}(\Sigma _g)$ is generated by the elements $R^k,R^kF(R^kF^{-1}R^{-k})$ where $F=B_1B_2\ldots B_kA_{2k+1}A_{3k+2}\cdots A_{k^2+2k}C_{k^2+3k+1}C_{k^2+4k+2}\ldots C_{2k^2+3k}$ Fig. 6.

Fig. 6

Generator for Theorem 3

Proof

We define an algorithm to prove the desired result.

Let $F=B_1B_2\cdots B_kA_{2k+1}A_{3k+2}\cdots A_{k^2+2k}C_{k^2+3k+1}C_{k^2+4k+2}\cdots C_{2k^2+3k}$ and $F_1=F(R^kF^{-1}R^{-k})$. Let us denote by H the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{ R^k, F_1\}$.

A) Use conjugation of $F_1$ with $R^k, R^{2k} , \ldots , R^{k^2}$ with proper multiplications to get $A_{k+1}B_{k+1}^{-1} \in H$, $A_{k+2}B_{k+2}^{-1} \in H$, $\ldots$ , $A_{2k-1}B_{2k-1}^{-1} \in H$, $A_{2k}B_{2k}^{-1} \in H$, respectively. Hence, we have $A_iB_i^{-1} \in H$ for all i.

B) Follow the next k steps.

1) Use conjugation of $F_1$ with $R^{kl}$ for some positive integers l’s with proper multiplications to get $C_{ik+1}B_{ik+1}^{-1} \in H$ and $C_{ik+1}B_{ik+2}^{-1} \in H$ for all i.

2) Use conjugation of $F_1$ with $R^{kl}$ for some positive integers l’s with proper multiplications to get $C_{ik+2}B_{ik+2}^{-1} \in H$ and $C_{ik+2}B_{ik+3}^{-1} \in H$ for all i.

$\ldots$

k) Use conjugation of $F_1$ with $R^{kl}$ for some positive integers l’s with proper multiplications to get $C_{ik}B_{ik}^{-1} \in H$ and $C_{ik}B_{ik+1}^{-1} \in H$ for all i.

Hence, $C_iB_i^{-1} \in H$ and $C_iB_{i+1}^{-1} \in H$ for all i.

It follows from Corollary 23 that $H=\mathrm{Mod}(\Sigma _g)$, completing the proof of the theorem.

See Theorem 24 for an example application of the algorithm. $\square$

Now, we prove Theorem 3.

Proof

For $k\ge 2$ and $g\ge 3k^2+4k+1$, let H be the subgroup of $\mathrm{Mod}(\Sigma _g)$ generated by the set $\{R^k, R^kF(R^kF^{-1}R^{-k})\}$. Then $H =$ $\mathrm{Mod}(\Sigma _g)$ by Theorem  26. Hence, we are done by Lemma 21 since the orders of $R^k$ and $R^kF(R^kF^{-1}R^{-k})$ are g/d where d is the greatest common divisor of g and k. If $k=1$, we are done by Theorem 1. $\square$