Genericity of Nondegenerate Free Boundary CMC Embeddings

Abstract

Let $\Sigma ^n$ and $M^{n+1}$ be smooth manifolds with smooth boundary. In this paper, following the techniques developed by White (Indiana Univ Math J 40:161–200, 1991) and Biliotti–Javaloyes–Piccione (Indiana Univ Math J, 1797–1830, 2009), we prove that, given a compact manifold with boundary $\Sigma ^n$ and a manifold with boundary $M^{n+1}$, for a generic set of Riemannian metrics on M every free boundary CMC embedding $\phi :\Sigma \rightarrow M$ is non-degenerate.

1 Introduction

In calculus of variations, there is a class of problems called isoperimetric; the classical isoperimetric problem consists in finding the minimum area among all hypersurfaces of a Riemannian manifold enclosing a region with prescribed volume. We know that solutions to this problem are hypersurfaces with constant mean curvature (in short CMC). More precisely, if $\varphi :\Sigma \rightarrow M$ is an immersion of an orientable n-dimensional compact manifold $\Sigma$ into the $(n+1)$-dimensional Riemannian manifold M, the condition that $\varphi$ has constant mean curvature $H_0$ is equivalent to the fact that $\varphi$ is a critical point of the area functional defined in the space of embeddings of $\Sigma$ in M that bound a region of fixed volume (see, for instance, [5]). The solutions of the isoperimetric problem correspond to minima of the constrained variational problem, however, it is interesting to study all critical points of the problem. One of the interesting questions concerning general CMC hypersurfaces is establishing the non-degeneracy as constrained critical points, and this paper deals with aspects of this question.

If $\varphi _t$ is a smooth variation of $\varphi$, $t\in (-\epsilon , \epsilon )$, $\varphi _0=\varphi$, such that $V_t=V_0$, for all $t\in (-\epsilon , \epsilon )$, where $V_t$ is the volume of the region bounded by $\varphi _t(\Sigma )$, a standard approach to find the solution of such a isoperimetric problem is to look the critical points of functional $\mathfrak {f}(t)=A_t+\lambda V_t$, $A_t$ the area of $\varphi _t$, $\lambda =\text {const.}$, which is the classical method of Lagrange multipliers. When $\lambda =nH_0$ we have the aforementioned equivalence.

In the case where M is a manifolds with boundary $\partial M$ and $\Sigma$ is also a manifold with boundary, the isoperimetric problem can be described as follows. One wants to minimize the area among all compact hypersurfaces diffeomorphic to $\Sigma$ in M with boundary contained in $\partial M$ and whose interior lies in the interior of M, and which divide M in two regions such that the closure of one of them is compact and with prescribed volume. The solutions of this problem, called free boundary CMC hypersurfaces, are the so-called normal CMC hypersurfaces. Let $H_0$ be denote the value (constant) of the mean curvature of one such hypersurface. If $H_0=0$ then we say that $\varphi (\Sigma )$ is a orthogonal free boundary minimal hypersurface. A. Ros and E. Vergasta obtain results on the stability of solutions of this isoperimetric problem in the case where M is compact and convex, see [15].

In this context, we prove the genericity of Riemannian metrics $\gamma$ of M for which every free boundary orthogonal minimal immersion $\varphi :\Sigma ^n \rightarrow M^{n+1}$ is non-degenerate. In analogy with the classical result for nondegenerate closed geodesics, we will call such metrics $(M,\Sigma )$-bumpy metrics. This result is analogous to a similar result for closed geodesics, obtained by Abraham [1] and Anosov [4] which are related to properties of geodesic flows for generic Riemannian metrics on a closed smooth manifold. We will see that this result is valid also in the case non-zero constant mean curvature. Genericity of the nondegeneracy assumption are very important in many situations, like for instance in Morse Theory, see for instance [10, 11] for applications in General Relativity, and [9] for applications in the theory of semi-Riemannian geodesics.

To give a formal statement of the result, let us recall that the group of diffeomorphisms of $\Sigma$ acts freely on the set of embeddings of $\Sigma$ into M by composition on the right. Given an embedding $\varphi :\Sigma \rightarrow M$, we denote by $[\varphi ]$ its equivalence class with respect to this action, and by $\mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M)$ the set of $[\varphi ]$ such that $\varphi (\Sigma )\cap \partial M = \varphi ( \partial \Sigma )$ and $\varphi$ is a $\gamma$-orthogonal embedding with CMC. So, our main result (see Theorem 4.1) is stated as follows:

Theorem

Let $M^{n+1}$ be a differential manifold with smooth boundary $\partial M \ne \emptyset ,$ and $\Sigma ^n$ a compact differential manifold with smooth boundary $\partial \Sigma \ne \emptyset$. $Met^k(M)$ the set of all $C^k$ Riemannian metric tensors in M, $k\ge 2$, and let $\Gamma \subset Met^k(M)$ be a subset with a structure of separable Banach space¹. We define the following set:

$$\begin{aligned} \mathcal {M}=\{ (\gamma , [\varphi ])\in \Gamma \times \mathcal {E}_{\partial }(\Sigma ,M) : [\varphi ]\in \mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M), \varphi \ \text {is}\ \gamma \text {-minimal} \}. \end{aligned}$$

Then,

• 1. $\mathcal {M}$ is a separable Banach manifold modelled on $\Gamma$.

• 2. $\Pi :\mathcal {M}\rightarrow \Gamma$, defined by $\Pi (\gamma ,[\varphi ])=\gamma$, is a Fredholm map with index 0.

• 3. $\gamma _0$ is critical value of $\Pi$ if and only if there is a $\gamma _0$-minimal embedding $\varphi _0:\Sigma \rightarrow M$ which is degenerate.

For the proof of (2), we will show that $\Pi$ satisfies the conditions of the Sard–Smale theorem (see [17]); the proof of the genericity of regular points of $\Pi$ will also follow from this result. Let us observe that, when M is noncompact, $\mathrm {Met}^k(M)$ has no natural Banach manifold structure; so, we have to choose a suitable subset $\Gamma \subset \mathrm {Met}^k(M)$, where a Banach structure can be found. Typically, $\Gamma$ consist of metrics satisfying some growth control at infinity (see Definition 3.3). This theorem is the version in Riemannian manifolds for minimal hypersurfaces with free boundary analogous to results of White [18], and Biliotti–Javaloyes–Piccione [8]. White proves that, given a compact manifold S and a complete Riemannian manifold $(N, \gamma )$, with $\dim (S ) < \dim (N )$, then the Riemannian metrics $\gamma$ on N such that every minimal embedding $\varphi : S \rightarrow (N, \gamma )$ is nondegenerate, form a generic set. When S is a circle, then such result gives a somewhat weaker² result than the classing bumpy metric theorem for closed geodesics, see [1, 4, 8].

Sard–Smale theorem for infinite dimensions is the main tool when it comes to solving problems of genericity of non-degenerate critical points for classes of maps between Banach manifolds. One of the central assumptions of Sard’s theory in infinite dimension is the Fredholmness of the maps considered in the theory. To guarantee Fredholmness, we must require a condition of regularity type Hölder, $C^{j,\alpha }$, for our embeddings. The space of the Hölder functions defined in $\Sigma$ that satisfies the so-called linearized free boundary condition is defined as

$$\begin{aligned} C^{j,\alpha }_\partial (\Sigma ):=\big \{ f \in C^{j,\alpha }(\Sigma )\ :\ \gamma \big (\nabla f,\mathbf {n}_{\partial M}\big )+\mathrm {I\!I}^{\partial M}\big (\mathbf {n}_{\Sigma },\mathbf {n}_{\Sigma }\big ) f=0 \big \}, \end{aligned}$$

where $\nabla$ is the gradient operator, $\mathbf {n}_{\partial M}$ is the outer unit normal field in $\partial M$, $\mathrm {I\!I}^{\partial M}$ is the second fundamental form in $\partial M$ and $\mathbf {n}_{\Sigma }$ is a unit normal field along $\Sigma$. Let $\{\varphi _t\}_{t\in (-\epsilon , \epsilon )}$ be a smooth variation of $\varphi$, with $\varphi _0=\varphi$, $\Sigma _0=\varphi _0(\Sigma )$. There is a bijection between a neighborhood V of $[\varphi _0] \in \mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M)$ and a sufficiently small neighborhood U of $0\in C^{j,\alpha }_\partial (\Sigma _0)$, determined by

$$\begin{aligned} \varphi _f(p):=\exp _{\varphi _0(p)}(f(p)\mathbf {n}_0(p)), \end{aligned}$$

where $\exp$ is the exponential map in M defined by $\gamma$ and $\mathbf {n}_0$ is a unit normal field in $\Sigma _0$ (see [7, Proposition 4.1]). In the proof of Fredholm condition for the map $\Pi$, we used one of the most important objects in the study of our theory, the Jacobi Operator, which appears in the formula of the second variation of the area functional. For $\varphi _0$ the Jacobi operator is defined by

$$\begin{aligned} J_{\varphi _0}(f)=\Delta _{\Sigma _0} f - \big (||\mathrm {I\!I}^{\Sigma _0} ||_{HS}^2+\mathrm {Ric}_g(\eta _{\Sigma _0},\eta _{\Sigma _0})\big ) f, \end{aligned}$$

where $\Delta _{\Sigma _0}$ is the nonnegative Laplacian of $(\Sigma _0, \varphi _0^*(g))$. $J_{\varphi _0}$ restricted to space $C_{\partial }^{j,\alpha }(\Sigma )$, is a Fredholm operator of zero index. We give a characterization of free boundary CMC hypersurfaces non-degenerate in terms of the kernel of the Jacobi operator.

Finally, it may be interesting to observe that we deal here with a family of constrained variational problems, parameterized by the family $\Gamma$ of metrics on M, where the constraint (the volume) depends in fact on the particular metric. This entails that our main functional framework does not possess a product structure, but rather a fiber bundle structure over $\Gamma$. To deal with this situation, we formulate an abstract Fredholmness and transversality result that applies in particular to the case of CMC embeddings, see Theorem 3.1. This result has an interest on its own, and it is one of the central technical result of the present paper.

It is natural to ask whether similar genericity results hold also in the case when the ambient space is a semi-Riemannian manifold. We will address this question in a forthcoming paper.

2 Preliminaries

Throughout this paper we will consider M as a $(n+1)$-dimensional differential manifold with smooth boundary $\partial M\ne \emptyset$ and $\Sigma$ as n-dimensional differential manifold with smooth boundary $\partial \Sigma \ne \emptyset$. In this section, we introduce the concepts of admissibility and orthogonality of hypersurfaces with boundary in a manifold with smooth boundary, we will give the definition of mean curvature and free boundary CMC (Constant Mean Curvature) hypersurface. Also, we give the meaning of nondegeneracy of CMC hypersurfaces, under the Hölder condition of regularity $C^{j,\alpha }$, through Jacobi operator restricted to the Banach space of the Hölder functions defined on a manifold with boundary that fulfill the linearized free boundary condition.

2.1 Orthogonal Submanifolds and Mean Curvature

Definition 2.1

Let $\varphi :\Sigma \rightarrow M$ be an embedding. We identify $\varphi$ with its image $\varphi (\Sigma )\subset M$. $\mathbf {\eta }_{\partial M}$ is the outer unit normal field along the boundary of M. We call $\varphi$ admissible if it satisfies (a) and (b), and normal (orthogonal) if it also satisfies (c):

• (a) $\varphi (\Sigma )\cap \partial M =\varphi (\partial \Sigma )$,

• (b) the normal bundle $T(\varphi (\Sigma ))^\bot$ is orientable,

• (c) and for each point $p\in \varphi (\partial \Sigma )$, $\mathbf {\eta }_{\partial M}(p)\in T_p\varphi (\Sigma )$.

The admissible hypersurface $\varphi (\Sigma )$ is said to bound a finite volume if

• (d) $M{\setminus } \varphi (\Sigma )=\Omega _1\cup \Omega _2$, with $\overline{\Omega }_1$ compact and $\Omega _1\cap \Omega _2=\emptyset$.

If $\varphi :\Sigma \rightarrow M$ is an orthogonal admissible embedding, then $\varphi (\Sigma )$ it is compact and $\varphi (\Sigma )$ and $\partial M$ are transverse submanifolds. We say that $\varphi (\Sigma )$ is a orthogonal submanifold of M (see Fig. 1).

Fig. 1

Orthogonal admissible embedding

Let g be a Riemannian metric on M and $\varphi _0:\Sigma \rightarrow M$ an orthogonal immersion. And write $\Sigma _0:=\varphi _0(\Sigma )$. We define the second fundamental form on $\Sigma _0$ as

$$\begin{aligned} \mathrm {I\!I}^{\Sigma _0}(X,Y):=g(\nabla _XY,\mathbf {\eta }_{\Sigma _0}), \end{aligned}$$

(2.1)

where $\mathbf {\eta }_{\Sigma _0}$ is the unit normal vector field to $\Sigma _0$ in the orientable normal bundle, $\nabla$ is the Levi–Civita connection in M, and X, Y are vector fields in $T\Sigma _0$.

The mean curvature function $H_{\Sigma _0}:\Sigma _0 \rightarrow \mathbb {R}$ is defined as trace of the second fundamental form $\mathrm {I\!I}^{\Sigma _0}$. The mean curvature vector of $\Sigma _0$ is defined as $\mathbf {H}_{\Sigma _0}=H_{\Sigma _0}\mathbf {\eta }_{\Sigma _0}$. If $H_{\Sigma _0}$ is constant, $\Sigma _0$ is called a constant mean curvature hypersurface (or CMC hypersurface), and if $H_{\Sigma _0}=0$, $\Sigma _0$ is a minimal hypersurface.

2.2 Variational Problem

In the theory of variational problems is known that the hypersurfaces with CMC of M minimize the area among all hypersurfaces enclosing a fixed volume. In the case where $\partial \Sigma$ is allowed to move freely along $\partial M$ the variational problem is called free boundary CMC problem. The solutions of this problem are orthogonal hypersurfaces with CMC which are called free boundary CMC hypersurfaces. We introduce the following notation:

• $\mathrm {Emb}_\partial (\Sigma ,M)$ be the space of admissible embeddings of $\Sigma$ in M,

• $\mathrm {Emb}_{\partial \bot }(\Sigma ,M)\subset \mathrm {Emb}_\partial (\Sigma ,M)$ the subspace of normal admissible embeddings and bounding a finite volume.

We have (see Barbosa-do Carmo [5]) that $\varphi _0\in \mathrm {Emb}_{\partial \bot }(\Sigma ,M)$ have CMC H if only if is a critical point of functional $\mathfrak {f}_H:\mathrm {Emb}_{\partial \bot }(\Sigma ,M)\rightarrow \mathbb {R}$, defined by

$$\begin{aligned} \mathfrak {f}_H(\varphi )=\int _\Sigma vol_{\varphi ^*(g)}-H\int _{\Omega _1}vol_g. \end{aligned}$$

(2.2)

Note that if $H=0$ then $\varphi _0(\Sigma )$ has the minimal volume over all hypersurfaces $\varphi (\Sigma )$, $\varphi \in \mathrm {Emb}_\partial (\Sigma ,M)$. In this case, $\varphi _0$ is said to be a free boundary minimal hypersurface.

We say that $\varphi _0:\Sigma \rightarrow M$ is non-degenerate if $\varphi _0$ is a non-degenerate critical point of $\mathfrak {f}_H$.

Definition 2.2

yA metric g on M is called “$(\Sigma , M)$-Bumpy”, if all $\varphi \in \mathrm {Emb}_{\partial \bot }(\Sigma ,M)$, with CMC in the metric g, is non-degenerate.

We discuss below some other characterizations of non-degenerate hypersurfaces.

2.3 Jacobi Operator

Let $\Sigma _0=\varphi _0(\Sigma )$ be a orthogonal CMC hypersurface, $\varphi _0\in \mathrm {Emb}_{\partial \bot }(\Sigma ,M)$. $C^j(\Sigma _0)$ is the set of functions $f:\Sigma _0\rightarrow \mathbb {R}$ with continuous derivatives to j order, j could be infinite. The second-order linear differential operator $J_{\varphi _0}:C^j(\Sigma _0)\rightarrow C^{j-2}(\Sigma _0)$, $j\ge 2$, defined by

$$\begin{aligned} J_{\varphi _0}(f):=\Delta _{\Sigma _0} f - \big (||\mathrm {I\!I}^{\Sigma _0} ||_{HS}^2+\mathrm {Ric}_g(\eta _{\Sigma _0},\eta _{\Sigma _0})\big ) f \end{aligned}$$

(2.3)

is called Jacobi operator, where $\Delta _{\Sigma _0}$ is the (nonnegative) Laplacian of $(\Sigma _0,\gamma )$ and $||\mathrm {I\!I}^{\Sigma _0} ||_{HS}^2$ is the square of Hilbert–Schmidt norm of the second fundamental form of $\varphi _0$. A Jacobi scalar field along of $\varphi _0$ is a smooth function $f \in C^{j}(\Sigma _0)$ such that $J_{\varphi _0}(f)=0$.

We consider a smooth variation of $\varphi _0$ as follows:

$$\begin{aligned} \Phi :\Sigma \times (-\epsilon ,\epsilon )\rightarrow M ,\ \ \epsilon >0, \end{aligned}$$

(2.4)

such that $\Phi (\Sigma ,s)=\varphi _s(\Sigma )=\Sigma _s\subset M$, $\varphi _s \in \mathrm {Emb}_\partial (\Sigma ,M)$ with CMC $H_s$. Let $V=\frac{\partial }{\partial s}\big |_{s=0}\Phi$ be the corresponding variational vector field. Then $\xi _0=g(V,\mathbf {\eta }_{\Sigma _0})$ satisfies

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}H_s = \Delta _{\Sigma _0} \xi _0 - \big (||\mathrm {I\!I}^{\Sigma _0} ||_{HS}^2+\mathrm {Ric}_g(\eta _{\Sigma _0},\eta _{\Sigma _0})\big ) \xi _0 = J_{\varphi _0}(\xi _0), \end{aligned}$$

(2.5)

Then $J_{\varphi _0}$ represents the second variation $d^2\mathfrak {f}_H(\varphi _0)$ of $\mathfrak {f}_H$ at the critical point $\varphi _0$, with respect to $L^2$ inner product.

Remark 2.1

Note that $\xi _0$ is a Jacobi field exactly when $\frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}H_s =0$.

Lemma 2.2

If each $\varphi _s$ is normal, that is $\varphi _s\in \mathrm {Emb}_{\partial \bot }(\Sigma ,M)$, with CMC, then $\xi _0$ satisfies the so-called linearized free boundary condition

$$\begin{aligned} g(\nabla \xi _0, \mathbf {\eta }_{\partial M}) + \mathrm {I\!I}^{\partial M}(\mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\Sigma _0}) \xi _0=0, \end{aligned}$$

(2.6)

where $\nabla \xi _0$ is the g-gradient of $\xi _0$ in $\Sigma _0$.

Proof

We can decompose V in its tangent and normal components

$$\begin{aligned} V=V^T+ \xi _0 \mathbf {\eta }_{\Sigma _0}, \end{aligned}$$

and

$$\begin{aligned} \nabla _V \mathbf {\eta }_{\Sigma _0}=\nabla _{V^T} \mathbf {\eta }_{\Sigma _0}-\nabla \xi _0, \end{aligned}$$

(see Proposition 15 of Ambrozio, [3]). So, if $V^T = 0$ then

$$\begin{aligned} Vg(\mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\partial M}) =&\, g(\nabla _{V} \mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\partial M}) + g(\mathbf {\eta }_{\Sigma _0},\nabla _{V}\mathbf {\eta }_{\partial M})\\ =&\, g(\nabla _{V^T} \mathbf {\eta }_{\Sigma _0} - \nabla \xi _0,\mathbf {\eta }_{\partial M}) + g(\mathbf {\eta }_{\Sigma _0},\nabla _{V}\mathbf {\eta }_{\partial M})\\ =&\, -g(\nabla \xi _0,\mathbf {\eta }_{\partial M}) + g(\mathbf {\eta }_{\Sigma _0},\nabla _{\xi _0 \mathbf {\eta }_{\Sigma _0}}\mathbf {\eta }_{\partial M})\\ =&\, -\frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}} + g(\mathbf {\eta }_{\Sigma _0},\nabla _{\mathbf {\eta }_{\Sigma _0}}\mathbf {\eta }_{\partial M})\xi _0. \end{aligned}$$

Thus,

$$\begin{aligned} \frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}}=g(\mathbf {\eta }_{\Sigma _0},\nabla _{\mathbf {\eta }_{\Sigma _0}}\mathbf {\eta }_{\partial M}) \xi _0 - Vg(\mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\partial M}). \end{aligned}$$

Therefore, if each $\varphi _s$ is a free boundary CMC hypersurface

$$\begin{aligned} \frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}}=g(\mathbf {\eta }_{\Sigma _0},\nabla _{\mathbf {\eta }_{\Sigma _0}}\mathbf {\eta }_{\partial M}) \xi _0. \end{aligned}$$

Then

$$\begin{aligned} g(\nabla \xi _0,\mathbf {\eta }_{\partial M})+ \mathrm {I\!I}^{\partial M}(\mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\Sigma _0}) \xi _0&= \frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}} + g(\nabla _{\mathbf {\eta }_{\Sigma _0}}\mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\partial M}) \xi _0\\&= \frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}} - g(\mathbf {\eta }_{\Sigma _0},\nabla _{\mathbf {\eta }_{\Sigma _0}}\mathbf {\eta }_{\partial M}) \xi _0\\&= \frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}} - \frac{\partial \xi _0}{\partial \mathbf {\eta }_{\partial M}}\\&=0. \end{aligned}$$

$\square$

2.4 Regularity

Sard’s theorem or Sard–Smale theorem in the case of infinite dimensions (see [17]) is the main tool when it comes to solving problems of genericity of regular points for a certain map between Banach manifolds. Said map needs the condition of being Fredholm with a certain index. To obtain this condition it is necessary to establish a regularity condition type Hölder, $C^{j,\alpha }$, for our embeddings. We can endow space of functions defined from $\Sigma$ to $\mathbb {R}$, $C^{j,\alpha }(\Sigma )$, with regularity $C^{j,\alpha }$, with the following norm:

$$\begin{aligned} \Vert f\Vert _{C^{j, \alpha }} = \Vert f\Vert _{C^j}+\max _{|\beta | = j} \left| D^\beta f \right| _{C^{0,\alpha }}{,} \end{aligned}$$

(2.7)

where $\beta$ ranges over multi-indices and

$$\begin{aligned} \Vert f\Vert _{C^j} = \max _{| \beta | \le j} \sup _{x\in \Sigma } \left| D^\beta f (x) \right| , \ \ \ |Df |_{C^{0,\alpha }}= \sup _{x\ne y\in T\Sigma }\frac{|Df(x)-Df(y)|}{||x-y||^{\alpha }}. \end{aligned}$$

It is well known that $C^{j,\alpha }(\Sigma )$ endowed with this norm is a (nonseparable) Banach space.

Remark 2.3

When the operator $\mathfrak {f}_H$ defined in (2.2) is considered on the space of $C^{j,\alpha }$-embeddings, the Jacobi operator acts on the corresponding tangent space at $\varphi _0$, which can be identified with $C^{j,\alpha }_{\partial }(\Sigma _0)$ (see Proposition 3.2).

We define the following space:

$$\begin{aligned} C^{j,\alpha }_\partial (\Sigma _0){:=}\{ f \in C^{j,\alpha }(\Sigma _0)\ :\ g\big (\nabla f,\eta _{\partial M}\big ){+}\mathrm {I\!I}^{\partial M}\big (\mathbf {n}_{\Sigma _0},\mathbf {n}_{\Sigma _0}\big ) f=0 \}. \end{aligned}$$

(2.8)

The restriction of $J_{\varphi _0}$ $J_{\varphi _0}:C^{j,\alpha }_\partial (\Sigma )\rightarrow C^{j-2}(\Sigma )$ is a Fredholm operator of index zero (see [14, section 2]).

Since $J_{\varphi _0}$ is the representation of the second variation of the area functional, we can define the following.

Definition 2.3

The embedding $\varphi _0\in \mathrm {Emb}_{\partial \bot }(\Sigma ,M)$ with g-CMC is called non-degenerate if $J_{\varphi _0}\big |_{C^{j,\alpha }_\partial (\Sigma )}$ is an isomorphism of Banach spaces, i.e. $\mathrm {ker}\ J_{\varphi _0}\cap C^{j,\alpha }_\partial (\Sigma )=\emptyset$.

3 Genericity of Regular Points and the Smooth Structure of the Set of Orthogonal embeddings

In this section, we will prove an important theorem (Theorem 3.1) in general terms that will be a key tool in the proof of the main theorem in our work. Is a result given in general terms over Banach spaces $\Gamma$, X and Y, where it is proved that the kernel of a certain application $H:\Gamma \times X \rightarrow Y$, defined from a functional $A:\Gamma \times X \rightarrow \mathbb {R}$, is a Banach manifold and the first projection $\Pi$, defined on that manifold is a Fredholm operator of zero index, whose critical points $(\gamma _0, u_0)$ are elements such that $u_0$ is a degenerate critical point of $A(\gamma _0,\cdot )$. We also define a Whitney space of tensor fields and we will see that the set of unparameterized embeddings has a Banach manifold structure.

Definition 3.1

A subset of metrical space is said to be generic if it is the countable intersection of dense open subsets. By Baires’s theorem, a generic set is dense.

3.1 An Abstract Fredholmness and Transversality Result

We will present here an important abstract result for smooth maps on a locally fibrated manifold, see Theorem 3.1 below. The result shows the genericity of the regular points for maps between Banach spaces in an abstract formulation, and will be used in the proof of the main theorem of this Chapter. It will be supposed that $A:\Gamma \times X\rightarrow \mathbb {R}$ is a map of class $C^j$, with $j\ge 2$, where $\Gamma$ and X are Banach spaces; we also assume that X has an inner product. We require a condition of transversality (see Definition 6.2) between the function $\frac{\partial }{\partial x}A:\Gamma \times X\rightarrow TX^*$ and the zero section of $TX^*$, this is equivalent to saying that $\forall (\gamma _0,x_0)$, $\frac{\partial A}{\partial x}(\gamma _0,x_0)$ and $w\ne 0$, $w\in \text {ker}(\frac{\partial ^2 A}{\partial x^2})$, $\exists v\in T_{\gamma _0}\Gamma$ such that $\frac{\partial ^2 A}{\partial \gamma \partial x}(\gamma _0,x_0)(w,v)\ne 0$ (see [8, Proposition 3.1]).

It is necessary to give the following definition of locally fibered submanifold that is imposed as a condition in the Theorem 3.1

Definition 3.2

Let $\Gamma$ and X be Banach spaces and $\Pi :\Gamma \times X\rightarrow \Gamma$ the first projection. Let $\mathfrak {X}\subset \Gamma \times X$ be a submanifold. We say that $\mathfrak {X}$ is a locally fibered if it meets the following condition: for each $(u_0,v_0)\in \mathfrak {X}$, there is an open $U\subset \Gamma$ and a closed subspace $W\subset X$, with $u_0\in U$ and $v_0\in W$, and a diffeomorphism $\varphi :U\times W\rightarrow \Pi ^{-1}(U)$, such that the following diagram is commutative:

i.e., for all $(u,w)\in U\times W$, $\Pi \circ \varphi (u,w)=u$.

The following theorem is a version analogous to theorem of B. White (see [18, Theorem 1.1]).

Theorem 3.1

Let $\Gamma$, X and Y be Banach spaces, $\mathcal {H}$ a Hilbert space with inner product $\langle \cdot ,\cdot \rangle$, and $X\subset Y \subset \mathcal {H}$. Let

$$\begin{aligned} A:\Gamma \times X \rightarrow \mathbb {R} \end{aligned}$$

(3.1)

be a $C^j$ function, $j\ge 2$. Suppose that there exists a map $H:\Gamma \times X \rightarrow Y$ such that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}A(\gamma ,u+tv)=\langle H(\gamma ,u),v\rangle , \end{aligned}$$

(3.2)

for all $\gamma \in \Gamma$ and $u,v \in X$.

Let $\mathfrak {X}\subset \Gamma \times X$ be a locally fibrated submanifold such that for all $(\gamma _0,u_0)\in \mathfrak {X}$ the operator

$$\begin{aligned} \frac{\partial H}{\partial u}(\gamma _0, u_0)\Big |_{T_{u_0}X}:{T_{u_0}X}\rightarrow Y \end{aligned}$$

(3.3)

is a Fredholm with index zero (${T_{u_0}X}\cong X$).

Furthermore, suppose that for all $k\in \text { Ker}\frac{\partial H}{\partial u}(\gamma _0, u_0)\cap T_{u_0}X$, $k\ne 0$, there exists a family $(\gamma (s),u(t))\in \mathfrak {X}$, such that $\gamma (0)=\gamma _0$, $u(0)=u_0$, $u'(0)=k$ and

$$\begin{aligned} \frac{\partial ^2}{\partial s \partial t}\big |_{s=t=0}A(\gamma (s),u(t))\ne 0. \end{aligned}$$

(3.4)

Then

• 1. $H\big |_{\mathfrak {X}}:\mathfrak {X}\rightarrow Y$ is a submersion near $(\gamma _0,u_0)$, so there exists a neighborhood $W\subset \mathfrak {X}$, $(\gamma _0,u_0)\in W$, such that

  $$\begin{aligned}\mathcal {M}=\{(\gamma ,u)\in W : H(\gamma ,u)=0\}\end{aligned}$$

  is a submanifold of $\mathfrak {X}$, and

  $$\begin{aligned}T_{(\gamma ,u)}\mathcal {M}=\text { Ker}\left( dH(\gamma ,u)\Big |_{T_{(\gamma ,u)}\mathfrak {X}}\right) .\end{aligned}$$

• 2. The projection

  $$\begin{aligned}\Pi :\mathcal {M}\rightarrow \Gamma ,\ \ \ \ \Pi (\gamma ,u)=\gamma \end{aligned}$$

  is an Fredholm operator with index zero.

• 3. The critical points of $\Pi \big |_{\mathcal {M}}$ are elements $(\gamma _0, u_0)\in \mathcal {M}$ such that $u_0$ is a degenerate critical point of the functional $A(\gamma _0,\cdot )$.

Proof

• 1. To simplify the notation we write $J=\frac{\partial H}{\partial u}(\gamma _0, u_0)\big |_{T_{u_0}\mathfrak {X}_{\gamma _0}}$. We show that J is symmetric with respect to the product in $\mathcal {H}$. Indeed,

  $$\begin{aligned} \frac{\partial ^2}{\partial s \partial t}\Big |_{s=t=0}A(\gamma _0,u_0+sv+tw)=&\,\frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}\left( \frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}A\big (\gamma _0,u_0+sv+tw\big )\right) \\ =&\,\frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}\langle H(\gamma _0,u_0+sv),w\rangle \\ =&\, \langle Jv,w\rangle . \end{aligned}$$

  On the other hand

  $$\begin{aligned} \frac{\partial ^2}{\partial t \partial s}\Big |_{s=t=0}A(\gamma _0,u_0+sv+tw)=\langle Jw,v\rangle . \end{aligned}$$

  Now, for all $u\in \text {ker}J$ and $v\in \mathfrak {X}_{\gamma _0}$, we have $\langle Ju,v\rangle =\langle u,Jv\rangle =0$. Thus, $\text {im}(J)\subset (\text {ker}J)^\bot$. Since J is Fredholm with index 0, we obtain

  $$\begin{aligned} \text {im}(J) = (\text {ker}J)^\bot . \end{aligned}$$

  (3.5)

  To prove that $H:\mathfrak {X}\rightarrow Y$ is a submersion we have to prove that $dH(\gamma _0,u_0)\Big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}$ is surjective and its kernel is complemented. First, we prove surjectivity. Let $(\gamma (s),u(t))$ be a family compatible with $\mathfrak {X}$, such that $\gamma (0)=\gamma _0$, $u(0)=u_0$, $u'(0)=k\ne 0$, $k\in \text {Ker} J$ (for example, take $u(t)=u_0+tk$). Note that $\gamma _0'=\frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}\gamma (s)$, $\mathbb {R}\cdot \gamma _0'\subset T_{\gamma _0}\Gamma$ and $(\mathbb {R}\cdot \gamma _0') \times \{0\}\subset T_{(\gamma _0,u_0)}\mathfrak {X}$. So,

  $$\begin{aligned} 0 \ne&\, \frac{\partial ^2}{\partial s \partial t}A(\gamma (s),u(t)) \\ =&\, \frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}A(\gamma (s),u(t))\\ =&\,\frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}\langle H(\gamma (s), u_0) , k\rangle \\ =&\, \left\langle \frac{\partial H}{\partial \gamma }(\gamma _0,u_0)\gamma _0' , k\right\rangle . \end{aligned}$$

  Since $\frac{\partial H}{\partial \gamma }(\gamma _0,u_0)\gamma _0'\in \text {Im}(dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}})$, we use Lemma 7.2, with $V=Y$, $W=\text {Ker} J$ and $Z=\text {Im}(dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}})$, which shows that $dH(\gamma _0,u_0)$ restricted to $T_{(\gamma _0,u_0)}\mathfrak {X}$ is surjective. Now, we have

  $$\begin{aligned} \text {ker}\left( dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}\right) \subset \text {ker}J, \end{aligned}$$

  and from the fact that J is Fredholm we infer that

  $$\begin{aligned} \text {Dim}\left( \text {ker}\left( dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}\right) \right) \le \text {Dim}(\text {ker}J)<\infty . \end{aligned}$$

  Therefore, $\text {ker}(dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}))$ is complemented in $T_{(\gamma _0,u_0)}\mathfrak {X}$. Thus $H:\mathfrak {X}\rightarrow Y$ is a submersion. Whence there is a neighborhood U of $(\gamma _0,u_0)$ such that

  $$\begin{aligned} \mathcal {M}=H^{-1}(0)\cap U \end{aligned}$$

  is a submanifold and

  $$\begin{aligned} T_{(\gamma _0,u_0)}\mathcal {M}=\text {ker}\left( dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}\right) . \end{aligned}$$

• 2. Let

  $$\begin{aligned} \Pi :\Gamma \times X&\longrightarrow \Gamma \\ (\gamma ,u)&\longmapsto \gamma \end{aligned}$$

  be the projection on the first factor. Take the restriction of $\Pi$ to $\mathcal {M}$, $\Pi \big |_{\mathcal {M}}$. We have to prove that $\text {Dim}(\text {ker}(\mathrm{d}\Pi \big |_{T_{(\gamma _0,u_0)}\mathcal {M}}))<\infty$ and $\text {im}(\mathrm{d}\Pi \big |_{T_{(\gamma _0,u_0)}\mathcal {M}}))$ is closed and has finite co-dimension. We have that

  $$\begin{aligned} \text {ker}\left( \mathrm{d}\Pi \big |_{T_{(\gamma _0,u_0)}\mathcal {M}}\right) =&\,\text {ker}\Pi \cap T_{(\gamma _0,u_0)}\mathcal {M}\\ =&\,(\{0\}\times X) \cap \text {ker}\left( dH(\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}\right) \\ =&\, \{0\} \times \text {ker}J, \end{aligned}$$

  which is of finite dimension. Now, by hypothesis about $\mathfrak {X}$, there is a neighborhood $U\subset \Gamma$, $\gamma \in U$, and a diffeomorphism $\varphi :U\times W\rightarrow \Pi ^{-1}(U)$, $W\subset X$ a closed subspace, such that the following diagram is commutative:

  

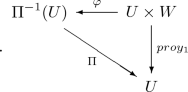
  So, locally $\Pi$ is as a projection from a product space. In particular for $\gamma _0$ fixed, we can take $\varphi$ such that $\varphi (\gamma _0,u)=(\gamma _0,u)$, for all $u\in W$. Set

  $$\begin{aligned}\overline{H}:=H\circ \varphi :U\times W\longrightarrow Y.\end{aligned}$$

  Then

  $$\begin{aligned} \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)&=\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}\overline{H}(\gamma _0,u_0 + tv)\\&=\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}H(\varphi (\gamma _0,u_0 + tv))\\&=\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}H(\gamma _0,u_0 + tv)\\&=\frac{\partial H}{\partial u}(\gamma _0,u_0). \end{aligned}$$

  And we have

  $$\begin{aligned} \text {ker}(\mathrm{d}\overline{H}(\gamma _0,u_0))=\left\{ (\xi ,\omega ) : \frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)\xi + \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0) \omega = 0\right\} \end{aligned}$$

  and $\xi \in [\frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)]^{-1}(\text {im} J)$. We prove that $\text {im}(\mathrm{d}\Pi \big |_{T_{(\gamma _0,u_0)}\mathcal {M}})$ has finite co-dimension.

  $$\begin{aligned} \text {im}(\mathrm{d}\Pi \big |_{T_{(\gamma _0,u_0)}\mathcal {M}})= & {} \Pi (T_{(\gamma _0,u_0)}\mathcal {M})\nonumber \\= & {} \Pi (\text {ker}(\mathrm{d}\overline{H}(\gamma _0,u_0))) \nonumber \\= & {} \left[ \frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)\right] ^{-1}\left( \text {im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) \right) \nonumber \\= & {} \left[ \frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)\right] ^{-1}(\text {im} J). \end{aligned}$$

  (3.6)

  The Fredholmness of J implies that its image is closed and finite co-dimensional. Thus, we use Lemma 7.3 with $U=T_{\gamma _0}\Gamma$, $V=Y$, $S=\text {im} \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)$ and $L=\frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)$. Now, we have

  $$\begin{aligned} \text {im}\frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)+\text {im}\frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)&= \text {im}(\mathrm{d}\overline{H}(\gamma _0,u_0))\\&=\text {im}(dH(\gamma _0,u_0))\Big |_{T_{(\gamma _0.u_0)}\mathfrak {X}}, \end{aligned}$$

  but $dH(\gamma _0,u_0))\Big |_{T_{(\gamma _0.u_0)}\mathfrak {X}}$ is surjective, so

  $$\begin{aligned} \text {Codim}_Y\left( \text {im}\frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)+\text {im}\frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) =0 \end{aligned}$$

  and

  $$\begin{aligned} \text {Codim}_Y\text {im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) =\text {Codim}_{T_{\gamma _0}\Gamma }\left( \left[ \frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)\right] ^{-1}(\text {im} J)\right) . \end{aligned}$$

  On the other hand,

  $$\begin{aligned} \text {Codim}_Y\text {im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) =\text {Dim}(\text {im}J)^\bot = \text {ker}(J) \end{aligned}$$

  Thus, $\Pi$ is Fredholm with index 0.

• 3. Recall that $(\gamma _0,u_0)$ is a regular point of $\Pi \big |_{\mathcal {M}}$ if

  $$\begin{aligned} \mathrm{d}\Pi (\gamma _0,u_0)\big |_{T_{(\gamma _0,u_0)}\mathcal {M}} \end{aligned}$$

  is surjective, and also remember that

  $$\begin{aligned} \text {im}(\mathrm{d}\Pi \big |_{T_{(\gamma _0,u_0)}\mathcal {M}})= \left[ \frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)\right] ^{-1}\left( \text {Im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) \right) , \end{aligned}$$

  as we see in 3.6. Then $(\gamma _0,u_0)$ is a regular point of $\Pi \big |_{\mathcal {M}}$ if and only if

  $$\begin{aligned} \text {im} (\frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)) \subset \text {im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) , \end{aligned}$$

  but

  $$\begin{aligned} \text {im}(\mathrm{d}\overline{H}(\gamma _0,u_0)) {=} \text {im} \left( \frac{\partial \overline{H}}{\partial \gamma }(\gamma _0,u_0)\right) +\text {im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) {=} \text {im} \left( \frac{\partial \overline{H}}{\partial u}(\gamma _0,u_0)\right) {=} \text {im}J. \end{aligned}$$

  Now

  $$\begin{aligned} \text {im}(\mathrm{d}\overline{H}(\gamma _0,u_0))=\text {im}\left( dH(\gamma _0,u_0)\Big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}\right) \end{aligned}$$

  and $dH(\gamma _0,u_0)\Big |_{T_{(\gamma _0,u_0)}\mathfrak {X}}$ is surjective. Hence, $\text {ker}J=\{0\}$, since J is Fredholm of index 0. Therefore, $(\gamma _0,u_0)\in \mathcal {M}$ is a regular point to $\Pi \big |_{\mathcal {M}}$ if and only if $\text {ker}J=\{0\}$. Whence $\gamma _0$ is a critical valor of $\Pi \big |_{\mathcal {M}}$ if and only if there exists $u_0$ which is a degenerate critical point of $A(\gamma _0,\cdot )$.

$\square$

3.2 $C^k$-Whitney Type Banach Space of Tensor Fields

The definitions of this section are taken from [6, 8]. We denote by $\mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ the vector space of all sections $\sigma$ of class $C^k$, $k\ge 2$, of the vector bundle $TM^*\otimes TM^*$ such that $\sigma _p:T_pM\times T_pM \rightarrow \mathbb {R}$ is symmetric for all p. Let $Met^k(M)\subset \mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ be the set of all metric tensors g on M of class $C^k$. The set $\mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ does not have necessarily a canonical Banach space structure, for example if M is noncompact. To give a structure of Banach space to this space of tensors, we introduce the following definition (see [8, section 4.1]).

Definition 3.3

A vector subspace $\mathcal {W}\subset \mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ will be called $C^k$-Whitney type Banach space of tensor fields over M if complies the following conditions:

• 1. $\mathcal {W}$ contains all tensor fields in $\mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ having compact support;

• 2. $\mathcal {W}$ has a Banach space norm $||\cdot ||_\mathcal {E}$ with the property that $||\cdot ||_\mathcal {E}$-convergence of a sequence implies convergence in the weak Whitney $C^k$-topology.³

The second condition means that given any sequence $(b_n)_{n\in \mathbb {N}}$ and $b_\infty \in \mathcal {W}$ such that $\lim _{n\rightarrow \infty }||b_n-b_\infty ||_\mathcal {W}=0$, then for each compact set $K\subset M$, the restriction $b_n|_K$ converges to $b_\infty |_K$ in the $C^k$-topology as $n\rightarrow \infty$.

We can construct a $C^k$-Whitney type Banach space of tensors on M using an auxiliary Riemannian metric $g_R$ on M as follows (see [8, Example 1]). The Levi-Civita connection $\nabla ^R$ of $g_R$ induces a connection on all vector bundles over M obtained with functorial constructions from the tangent bundle TM. Also for each $r,s\in \mathbb {N}$, $g_R$ induces canonical Hilbert space norms on each tensor bundle $TM^{*(r)}\otimes TM^{(s)}$, which will be denoted $||\cdot ||_R$. Now, we define $\mathcal {G}^k_{sym}(TM^*\otimes TM^*;g_R)$ as the subset of $\mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ consisting of all sections $\sigma$ such that

$$\begin{aligned} ||\sigma ||_k=\max _{i=0,\ldots ,k}\left[ \sup _{x\in M}\Vert (\nabla ^R)^i\sigma (x)\Vert _R\right] <+\infty . \end{aligned}$$

(3.7)

The norm $||\cdot ||_k$ in (3.7) turns $\mathcal {G}^k_{sym}(TM^*\otimes TM^*;g_R)$ into a separable normed space (see [16]), which is complete if the Riemannian metric $g_R$ is complete. Thus, we have that $\mathcal {G}^k_{sym}(TM^*\otimes TM^*;g_R)$ is a $C^k$-Whitney type Banach space of tensors.

When M is compact, $\mathcal {G}^k_{sym}(TM^*\otimes TM^*;g_R)=\mathcal {G}^k_{sym}(TM^*\otimes TM^*)$, and $Met^k(M)$ is an open subset.

3.3 The Smooth Structure of the Set of Orthogonal Embeddings

The appropriate setup for studying the set of submanifolds of a diffeomorphism type is obtained by considering the notion of unparameterized embeddings. Unparameterized embeddings are the elements of the quotient space generated from the free action to right of the diffeomorphisms group on the space of embeddings of $\Sigma$ into M. The area and volume functional are invariant by this action.

Definition 3.4

Two embeddings $\varphi _1$ and $\varphi _2$ from $\Sigma$ in M will be equivalent if there exists a diffeomorphism $\phi :\Sigma \rightarrow \Sigma$ such that $\varphi _2 = \varphi _1\circ \phi$, i.e., if they are different parametrizations of the same submanifold of M diffeomorphic to $\Sigma$. For $\varphi \in \mathrm {Emb}(\Sigma ,M)$, we denote by $[\varphi ]$ the class of all embedding that are equivalent to $\varphi$. We say that $[\varphi ]$ is a unparametrized embedding of $\Sigma$ in M.

Definition 3.5

We define the following sets:

• $\mathcal {E}(\Sigma , M):=\{[\varphi ] : \varphi \ \text {is a embedding of order}\ C^{j,\alpha }\}$,

• $\mathcal {E}_{\partial }(\Sigma ,M):=\{ [\varphi ]\in \mathcal {E}(\Sigma , M) : \varphi (\Sigma )\cap \partial M = \varphi ( \partial \Sigma ) \},$

• Let $\gamma \in Met(M)$,

  $$\begin{aligned} \mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M):=\{[\varphi ]\in \mathcal {E}_{\partial }(\Sigma ,M) : \varphi \ \text {is}\ \gamma \text {-orthogonal}\}. \end{aligned}$$

There is a smooth Banach manifold structure, of infinite dimension, for a sufficiently small neighborhood of $[\varphi _0]\in \mathcal {E}_{\partial \gamma }^\bot (\Sigma ,M)$ in some suitable topology.

Proposition 3.2

[7, Proposition 4.1]. Let $\Sigma$ be a compact manifold with boundary and $\varphi _0\in \mathrm {Emb}_\partial (\Sigma ,M)$. Let $\mathcal {U}\subset \mathcal {E}_{\partial \gamma }^\bot (\Sigma ,M)$ be a sufficiently small neighborhood of $[\varphi _0]$, then $\mathcal {U}$ can be identified with an infinite-dimensional smooth submanifold $\mathcal {N}$ of Banach space $C^{j,\alpha }(\Sigma )$, with $0\in \mathcal {N}$ corresponding to $[\varphi _0]$, such that $T_0\mathcal {N}=C^{j,\alpha }_{\partial }(\Sigma )$ (see 2.8). $\square$

4 Genericity of Bumpy Metrics

Here we prove the principal theorem (Theorem 4.1). Then, for the spaces $\Gamma = \mathcal {W} \cap Met^k (M)$, ($\mathcal {W}$ is a Banach subspace of type $C^k$-Whitney of the symmetric tensor fields on M, defined in the Sect. 3.2), $X = C^{j,\alpha }(\Sigma )$ and $Y = C^{j-2,\alpha }(\Sigma )$, the functional area $A:\Gamma \times X\rightarrow \mathbb {R}$ and the mean curvature of the operator $H:\Gamma \times X\rightarrow Y$, the conditions of Theorem 3.1 are fulfilled. Thus, as an immediate consequence of the Theorem 4.1 and the Sard–Smale Theorem, we obtained the genericity of non-degenerate free boundary CMC embeddings, Corollary 4.6. In other words, we prove that the set of Bumpy metrics in M is generic in the space of all Riemannian metrics of M.

Theorem 4.1

Let M be a $(n+1)$-dimensional differential manifold with smooth boundary $\partial M \ne \emptyset ,$ and $\Sigma$ a n-dimensional compact differential manifold with smooth boundary $\partial \Sigma \ne \emptyset$. Let $\mathcal {W}\subset \mathcal {G}^k_{sym}(TM^*\otimes TM^*)$ be a $C^k$-Whitney type Banach subspace of the symmetrical tensor fields over M, with $k > j \ge 2$, let $\Gamma \subset \mathcal {W}\cap Met^k(M)$ be an open subset of $\mathcal {W}$. Let $\mathcal {M}$ be the set defined as

$$\begin{aligned} \mathcal {M}=\{ (\gamma , [\varphi ])\in \Gamma \times \mathcal {E}_{\partial }(\Sigma ,M) : [\varphi ]\in \mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M), \varphi \ \text {is}\ \gamma \text {-minimal} \}. \end{aligned}$$

Then

• 1. $\mathcal {M}$ is a separable Banach manifold modelled on $\Gamma$.

• 2. $\Pi :\mathcal {M}\rightarrow \Gamma$, defined by $\Pi (\gamma ,[\varphi ])=\gamma$, is a Fredholm map with index 0.

• 3. $\gamma _0$ is critical value of $\Pi$ if and only if there is a $\gamma _0$-minimal embedding $\varphi _0:\Sigma \rightarrow M$ which is degenerate.

4.1 Analytic Preliminaries

We begin by proving some lemmas to clarify the ideas in the proof of Theorem 4.1.

Lemma 4.2

Let $\Sigma _0=\varphi _0(\Sigma )$ be a free boundary minimal surface and $\bar{f}:\Sigma _0 \rightarrow \mathbb {R}$ satisfying the linearized free boundary condition

$$\begin{aligned} \gamma _0(\nabla \bar{f}, \mathbf {\eta }_{\partial M}) + \mathrm {I\!I}^{\partial M}(\mathbf {\eta }_{\Sigma _0},\mathbf {\eta }_{\Sigma _0})\bar{f}=0. \end{aligned}$$

Then there is a map

$$\begin{aligned} o:(-\epsilon ,\epsilon )\rightarrow C^{j,\alpha }(\Sigma _0), \end{aligned}$$

with $\frac{o(t)}{t}\rightarrow 0$ if $t\rightarrow 0$, such that $\varphi _t:\Sigma _0\rightarrow M$ defined by

$$\begin{aligned} \varphi _t(p):=\exp _{\varphi _0(p)}\Big ([t\bar{f}(p)+o(t)(p)]\mathbf {n}_{\Sigma _0}(p)\Big ) \end{aligned}$$

is orthogonal (orthogonal in the sense of Definition 2.1 (c))

Proof

By Proposition 3.2 there is a bijective correspondence between a neighborhood $\mathcal {U}\subset \mathcal {E}_\partial ^\bot (\Sigma ,M)$ of $[\varphi _0]$ and a infinite-dimensional smooth submanifold $\mathcal {N}$ of the Banach space $C^{j,\alpha }(\Sigma )$, with $0\in \mathcal {N}$ corresponding to $[\varphi _0]$ and $T_0\mathcal {N}=C^{j,\alpha }_{\partial }(\Sigma )$. So, there is a diffeomorphism, given by the inverse mapping theorem (see 6.1), between $\mathcal {U}$ and a neighborhood $V\subset T_0\mathcal {N}$ of 0, such that $\varphi _t\mapsto t \bar{f}$. On the other hand, $exp_{\varphi _0}$ also generates a diffeomorphism between $\mathcal {U}$ and some neighborhood $V'\subset T_0\mathcal {N}$, such that $\varphi _t\mapsto t \bar{g}_t$, with $g_0=0$ and $g'_0=\bar{f}$. Since V and $V'$ are diffeomorphic we have $g_t=t\bar{f} + o(t)$, where o(t) is differentiable and $\frac{o(t)}{t}\rightarrow 0$ if $t\rightarrow 0$. $\square$

Lemma 4.3

Let $\Sigma$ be a n-dimensional compact submanifold embedded in M, $f:\Sigma \rightarrow \mathbb {R}$ function, $f\in C^j$, $f\ne 0$ and $n_{\Sigma }$ the unit normal vector field to $\Sigma$. Then there is a map $\psi :M\rightarrow \mathbb {R}$ such that

• (i) $\psi (p) = 0$, for all $p\in \Sigma$,

• (ii) $\int _{\Sigma }\mathrm{d}\psi (n_{\Sigma })\cdot f(p)\mathrm{d}\Sigma \ne 0$.

Proof

Let $p_0\in \Sigma$ be such that $f(p_0)>0$. There is a local coordinate chart around of $p_0$, $(U, x=(x_1,\ldots ,x_{n+1}))$, such that

• 1. $x(U)=B_1(0)\subset \mathbb {R}^{n+1}$,

• 2. $x\big |_{U\cap \Sigma }=(x_1,\ldots ,x_{n},0)$ and

• 3. $f(p)>0$ for all $p\in U\cap \Sigma$.

We have

$$\begin{aligned} \mathrm{d}x_p(\mathbf {n}_p)=\mathbf {v}_{x(p)}, \end{aligned}$$

where $v_{x(p)}=(v_1,\ldots ,v_{n+1})$ with $v_{n+1}\ne 0$. We may assume that $v_{n+1}> 0$.

Set

$$\begin{aligned} h:\ \ \ B_1(0)\ \ \&\longrightarrow \mathbb {R}\\ (x_1,\ldots ,x_{n+1})&\longmapsto l(x_{n+1}), \end{aligned}$$

where $l:\mathbb {R}\rightarrow \mathbb {R}$ is a smooth function such that

• (i) $Supp(l)\subset [-1,1]$,

• (ii) $l(0)=0$ and

• (iii) $l'(0)>0$.

For example l can be taken as follows (see Fig. 2):

$$\begin{aligned}l(t)= {\left\{ \begin{array}{ll} -[2(2(-t-1))^3+3(2(-t-1))^2], &{}\text {if}\ -1<t\le -1/2\\ \sin (\pi t), &{}\text {if}\ -1/2<t<1/2\\ 2(2(t-1))^3+3(2(t-1))^2, &{}\text {if}\ 1/2\le t < -1/2\\ 0 &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

Fig. 2

Graph of l(t)

Under these conditions we have

$$\begin{aligned}&h(B_1(0)\cap \mathbb {R}^n) = 0\\&\nabla h_p = (0,\ldots ,0,l'(0)) \ \ \text {for all}\ \ p\in B_1(0)\cap \mathbb {R}^n). \end{aligned}$$

So, we define $\psi :M\rightarrow \mathbb {R}$ as

$$\begin{aligned} \psi (p)= {\left\{ \begin{array}{ll} h\circ x (p) &{}\text {if}\ p\in U \\ 0 &{} \text {if}\ p\in M{\setminus } U. \end{array}\right. } \end{aligned}$$

Therefore, $\psi$ fulfills statement i).

Now, for all $p\in U\cap \Sigma$, we have

$$\begin{aligned} \mathrm{d}\psi _p(\mathbf {n}_p)=&\,\nabla h_{x(p)}\cdot \mathrm{d}x_p(\mathbf {n}_p) \\ =&\,\nabla h_{x(p)}\cdot \mathbf {v}_{x(p)} \\ =&\,l'(0)\cdot v_{n+1}>0 \end{aligned}$$

and

$$\begin{aligned} \mathrm{d}\psi _p(\mathbf {n}_p)=0\ \ \text {for} \ \ p\in \Sigma {\setminus } U. \end{aligned}$$

Then

$$\begin{aligned} \int _{\Sigma }\mathrm{d}\psi _p(\mathbf {n}_p)\cdot f(p)\mathrm{d}\Sigma =\int _{\Sigma \cap U}\mathrm{d}\psi _p(\mathbf {n}_p)\cdot f(p)\mathrm{d}\Sigma > 0. \end{aligned}$$

$\square$

Lemma 4.4

Let (X, d) be a non-separable metric space and let $(Y,\tau _s)$ be a separable topological space, with $\emptyset \ne Y\subset X$. Assume that $\tau _d|_Y\subset \tau _s$, where $\tau _d$ is the topology generated by d. Then the closure of Y in $\tau _d$ is separable.

Proof

Let $\overline{Y}$ be the closure of Y in $\tau _d$, and $y\in \overline{Y}$. Let $B_r(y)$ be a d-ball with center y and radio r, thus $B_r(y)\cap Y\in \tau _s$. If D is a dense subset of Y then there is $x\in D\cap [B_r(y)\cap Y]$, so $x\in B_r(y)$. Therefore, $\overline{Y}$ is separable in $\tau _d$. $\square$

4.2 Proof of the Genericity Theorem of Metrics Bumpy

Now we will prove Theorem 4.1. Under suitable constraints on the set of metrics in M and the space of embeddings of $\Sigma$ in M, the its proof follows from Theorem 3.1.

Parts (2) and (3) are immediate consequence of Theorem 3.1.

To prove (1), let g be a metric in M, g of class $C^{\infty }$, such that $\partial M$ is g-totally geodesic. Take $(\gamma _0,[\varphi _0])\in \mathcal {M}$. Let $\mathbf {n}_0$ be the unit normal vector field along of $\varphi _0(\Sigma )$. For each $f:\Sigma \rightarrow \mathbb {R}$ of class $C^{k,\alpha }$ sufficiently small, we associate the embedding $\varphi _f:\Sigma \rightarrow M$ defined by

$$\begin{aligned} \varphi _f(p):=\exp _{\varphi _0(p)}(f(p)\mathbf {n}_0(p)), \end{aligned}$$

where $\exp$ is the exponential map in M defined by g. We set $\mathbf {n}_0(p):=\mathbf {n}_{0_{\varphi _0(p)}}$. Since $\varphi _0$ is orthogonal then $\mathbf {n}_0(p)\in T_{\varphi _0(p)}(\partial M)$, for all $p\in \varphi _0^{-1}(\varphi _0(\Sigma )\cap \partial M)$. Hence $\varphi _f(\partial \Sigma )\subset \partial M$ since $\partial M$ is totally geodesic. Note that if $f\equiv 0$ then $\varphi _f=\varphi _0$.

Now, let $U\subset C^{j,\alpha }(\Sigma )$ be a sufficiently small neighborhood of 0 such that $\exp$ is a diffeomorphism in a neighborhood V generated by U,

$$\begin{aligned}\exp _{\varphi _0(p)}:C^{j,\alpha }&(\Sigma )\longrightarrow M \\&f\longmapsto \exp (f.\mathbf {n}_0)=:\varphi _f(p). \end{aligned}$$

Note that the map $f\mapsto [\varphi _f]$ is a diffeomorphism between U and a neighborhood $\tilde{U}$ of $[\varphi _0]\in \mathcal {E}_{\partial }(\Sigma ,M)$.

Defined the following spaces:

$$\begin{aligned} X=&\,C^{j,\alpha }(\Sigma )\\ Y=&\,C^{j-2,\alpha }(\Sigma )\\ \mathcal {H}=&\,L^2(\Sigma ), \end{aligned}$$

and the set

$$\begin{aligned} \mathfrak {X}=\{ (\gamma ,f) : f\in U, \varphi _f\ \text {is}\ \gamma \text {-orthogonal to }\ \partial M \}. \end{aligned}$$

Let us see that $\mathfrak {X}\subset \Gamma \times X$ is a locally fiber sub-bundle.

Proposition 4.5

$\mathfrak {X}$ is a locally fibered submanifold over $\Gamma$

Proof

Let us denote $X=C^{j,\alpha }(\Sigma )$ to simplify writing. We define the following map, clearly differentiable,

$$\begin{aligned} \phi : \Gamma \times X&\longrightarrow C^{j-1,\alpha }(\partial \Sigma )\\ (\gamma ,f)&\longmapsto \gamma (\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M}), \end{aligned}$$

where $\mathbf {n}_{\varphi _f}$ is a unitary normal field to $\varphi _f(\Sigma )$ and $\mathbf {n}_{\partial M}$ is a unitary normal field to $\partial M$. So $\mathfrak {X}=\phi ^{-1}(0)$. Therefore, if $\phi$ is a submersion for all $(\gamma , f)\in \mathfrak {X}$, then $\mathfrak {X}$ is a submanifold.

Let $(\gamma _0, f_0)\in \mathfrak {X}$, we have to $T_{\gamma _0}\Gamma \times \{0\} \subset T_{(\gamma _0, f_0)}\mathfrak {X}\subset T_{\gamma _0}\Gamma \times T_{f_0}X.$

Now,

$$\begin{aligned} \mathrm{d}\phi (\gamma ,f):T_{\gamma }\Gamma \times T_{f}X\longrightarrow T_{\phi (\gamma ,f)}C^{j-1,\alpha }(\partial \Sigma ), \end{aligned}$$

then, we must prove that $\mathrm{d}\phi (\gamma ,f)$ is surjective and Ker($\mathrm{d}\phi (\gamma ,f)$) is complemented.

We have that

$$\begin{aligned} \mathrm{d}\phi (\gamma ,f)(\tilde{\gamma },\tilde{f})=&\,\frac{\partial \phi }{\partial \gamma }\tilde{\gamma } + \frac{\partial \phi }{\partial f}\tilde{f}\\ =&\,\tilde{\gamma }(\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M}) + \frac{\partial \tilde{f}}{\partial \mathbf {n}_{\partial M}} + \gamma (\nabla _{\mathbf {n}_{\varphi _f}}\mathbf {n}_{\varphi _f},\mathbf {n}_{\partial M})\tilde{f}\\ =&\,\tilde{\gamma }(\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M}) + \frac{\partial \tilde{f}}{\partial \mathbf {n}_{\partial M}} + \mathrm {I\!I}^{\partial M}(\mathbf {n}_{\varphi _f},\mathbf {n}_{\varphi _f})\tilde{f}. \end{aligned}$$

To prove that $\mathrm{d}\phi (\gamma ,f)$ is surjective we observe that $\tilde{\gamma }\in T_{\gamma }\Gamma$ is a symmetric bilinear form, then for any $h\in T_{\phi (\gamma ,f)}C^{j-1,\alpha }(\partial \Sigma )$, we choose $\tilde{\gamma }$ such that

$$\begin{aligned} \tilde{\gamma }(\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M})=h-\left( \frac{\partial \tilde{f}}{\partial \mathbf {n}_{\partial M}} + \mathrm {I\!I}^{\partial M}(\mathbf {n}_{\varphi _f},\mathbf {n}_{\varphi _f})\tilde{f}\right) . \end{aligned}$$

Now, to see that $\mathrm{d}\phi (\gamma ,f)$ is complemented, notice that the projection in the second factor,

$$\begin{aligned} P_2:\text {Ker}(\mathrm{d}\phi (\gamma ,f))\longrightarrow T_fX, \end{aligned}$$

is surjective. Indeed, if $\tilde{f}\in T_fX$, we can take $\tilde{\gamma }$ such that $\tilde{\gamma }(\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M})=-\Big (\frac{\partial \tilde{f}}{\partial \mathbf {n}_{\partial M}} + \mathrm {I\!I}^{\partial M}(\mathbf {n}_{\varphi _f},\mathbf {n}_{\varphi _f})\tilde{f}\Big )$.

For fixed $\tilde{f}\in T_fX$, we define the following space.

$$\begin{aligned} \{ \tilde{\gamma } : (\tilde{\gamma },\tilde{f})\in \text {Ker}(\mathrm{d}\phi (\gamma ,f)) \}=\tilde{\gamma }_{\tilde{f}}+\{ \tilde{\gamma } : \tilde{\gamma }(\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M})=0 \}, \end{aligned}$$

where $\tilde{\gamma }_{\tilde{f}}=-\Big (\frac{\partial \tilde{f}}{\partial \mathbf {n}_{\partial M}} + \mathrm {I\!I}^{\partial M}(\mathbf {n}_{\varphi _f},\mathbf {n}_{\varphi _f})\tilde{f}\Big )$.

Let us see that

$$\begin{aligned} \Gamma _0=\{ \tilde{\gamma } : \tilde{\gamma }(\mathbf {n}_{\varphi _f}, \mathbf {n}_{\partial M})=0 \} \end{aligned}$$

is complemented. In general, if $N_1$ and $N_2$ are differentiable fields in M, such that $N_1\big |_{\partial M}=\mathbf {n}_{\partial M}$, $N_2\big |_{\varphi _f}=\mathbf {n}_{\varphi _f}$ and let $\eta _0 \in \Gamma ^{0,2}_{Sym}(M)$ be such that, in a neighborhood of $\partial M \cup \Sigma _f$,

$$\begin{aligned} \eta _0(N_1,N_2)=1. \end{aligned}$$

Then for all $\eta \in \Gamma ^{0,2}_{Sym}(M)$

$$\begin{aligned} \eta =\eta _1 + \eta _2, \end{aligned}$$

where $\eta _1=-\eta (N_1,N_2)\cdot \eta _0$ and $\eta _2=\eta -\eta (N_1,N_2)\cdot \eta _0$. So, $\eta _1$ is in the generated by $\eta _0$, $\eta _2(N_1,N_2)=0$, then $\eta _2 \in \Gamma _0$. Therefore, $\Gamma _0$ is complemented.

Thus, the complement of $\text {Ker}(\mathrm{d}\phi (\gamma ,f))$ is the set

$$\begin{aligned} \{ (\tilde{f}, \Gamma _0-\tilde{\gamma }_{\tilde{f}}) : \tilde{f} \in T_fX \}. \end{aligned}$$

Now, by the local form of the submersions (see statement in 6.3), we get that $\mathfrak {X}$ is locally fibered. $\square$

Now, we define the function

$$\begin{aligned} A=\Gamma \times X&\longrightarrow \mathbb {R}\\ (\gamma , f)&\longmapsto A(\gamma , f):= \gamma \text {-area of}\ \varphi _f(\Sigma ), \end{aligned}$$

and the operator

$$\begin{aligned} H=\ \ \mathfrak {X}\ \&\longrightarrow Y\\ (\gamma , f)&\longmapsto H(\gamma , f):= \gamma \text {-mean curvature of}\ \varphi _f(\Sigma ). \end{aligned}$$

We have, therefore, that

$$\begin{aligned} \frac{\partial H}{\partial f}(\gamma _0,0)=J_{(\gamma _0,\varphi _0),} \end{aligned}$$

where $J_{(\gamma _0,\varphi _0)}$ is the Jacobi operator $J_{\varphi _0}$ defined in the metric $\gamma _0$ (see Sect. 2.3), which restricted to $C_{\partial }^{j,\alpha }(\Sigma )$ is Fredholm with index 0.

Also, we have that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}A(\gamma ,f+tl)=&\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}\int _{\Sigma }Vol_{\varphi ^*_{(f+tl)}(\gamma )}\\ =&\int _{\Sigma }H(\gamma ,f)\cdot l\\ =&\langle H(\gamma ,f),l \rangle _\mathcal {H} \end{aligned}$$

It remains to show that the condition of transversality defined by equation 3.4 is fulfilled, to verify the hypotheses of Theorem 3.1.

Let $\bar{f}\in \text {ker}(\frac{\partial H}{\partial f}(\gamma _0,0))=\text {ker}(J_{\varphi _0})$ be non-zero. As $J_{\varphi _0}$ is restricted to $C_{\partial }^{j,\alpha }(\Sigma )$, then $\bar{f}$ satisfied the linearized free boundary condition. Take a smooth variation of $\varphi _0$, $\varphi _t:=\varphi _{f_t}$, $-\epsilon<t<\epsilon$, such that

$$\begin{aligned} \varphi _t(p)=\mathrm{Exp}_{\varphi _0(p)}\big ( [t\bar{f}(p)+o(t)]\mathbf {n}_0(p) \big ), \end{aligned}$$

(4.1)

where $o(t):(-\epsilon ,\epsilon )\rightarrow C^{k,\alpha }(\Sigma _0)$ is a differential application with $\frac{o(t)}{t}\rightarrow 0$ if $t\rightarrow 0$. By Lemma 4.2$\varphi _t$ is orthogonal to $\partial M$.

Now, take a variation $\gamma _s$, $-\delta<s<\delta$, of $\gamma _0$ by conformal metrics as follows:

$$\begin{aligned} \gamma _s(q)=\big (1+s\psi (q) \big )\gamma _0(q), \end{aligned}$$

(4.2)

where $\psi :M\rightarrow \mathbb {R}$ is a smooth function such that $\psi (q)=0$ for all $q\in \varphi _0(\Sigma )$, this is, if $q=\varphi _0(p)$, $\psi (\mathrm{Exp}_q(0))=\psi (q)=0$.

Let $\{ \Omega , (x_1,\ldots ,x_n)\}$ be a local coordinate chart of $\Sigma$, $p\in \Omega$. The volume form associated to the metric $\gamma _s$ is given by

$$\begin{aligned} vol_{\varphi _f^*(\gamma _s)}\big |_p=&\,\sqrt{\text {Det}\left[ \varphi _f^*(\gamma _s)\right] }\mathrm{d}x^1\wedge \cdots \wedge \mathrm{d}x^n\big |_p\\ =&\,\sqrt{\text {Det}\left[ \gamma _s\left( \mathrm{d}\varphi _f\left( \frac{\partial }{\partial x_i}\right) ,\mathrm{d}\varphi _f\left( \frac{\partial }{\partial x_j}\right) \right) \right] }\mathrm{d}x^1\wedge \cdots \wedge \mathrm{d}x^n\big |_p\\ =&\,\sqrt{\text {Det}\left[ \Big (1+s\psi \big (\mathrm{Exp}_{\varphi _0(p)}(f(p)\mathbf {n}_0(p))\big )\Big )\gamma _0\left( \mathrm{d}\varphi _f\left( \frac{\partial }{\partial x_i}\right) ,\mathrm{d}\varphi _f\left( \frac{\partial }{\partial x_j}\right) \right) \right] } \nonumber \\& \mathrm{d}x^1\wedge \cdots \wedge \mathrm{d}x^n\\ =&\,\Big (1+s\psi \big (\mathrm{Exp}_{\varphi _0(p)}(f(p)\mathbf {n}_0(p))\big )\Big )^{n/2}\sqrt{\text {Det}\left[ \gamma _0\left( \mathrm{d}\varphi _f\left( \frac{\partial }{\partial x_i}\right) ,\mathrm{d}\varphi _f\left( \frac{\partial }{\partial x_j}\right) \right) \right] } \nonumber \\& \mathrm{d}x^1\wedge \cdots \wedge \mathrm{d}x^n\\ =&\,\Big (1+s\psi \big (\mathrm{Exp}_{\varphi _0(p)}(f(p)\mathbf {n}_0(p))\big )\Big )^{n/2}vol_{\varphi _f^*(\gamma _0)}. \end{aligned}$$

To simplify the notation we write

$$\begin{aligned} f_t=t\bar{f} + o(t) \end{aligned}$$

and

$$\begin{aligned} v_t=f_t\mathbf {n}_0. \end{aligned}$$

Note that $f_0\equiv 0$, so $v_0=\mathbf {0}$. Also take $q=\varphi _0(p)$ and $\varphi _t=\varphi _{f_t}$. Hence, the area function over the variations of $\varphi _0$ and $\gamma _0$ given by Eqs. 4.1 and 4.2 has the following form:

$$\begin{aligned} A(\gamma _s,f_t)=&\int _{\Sigma }vol_{\varphi _t^*(\gamma _s)}\\ =&\int _{\Sigma }\Big (1+s\psi \big (\mathrm{Exp}_q(v_t(p))\big )\Big )^{n/2}vol_{\varphi _t^*(\gamma _0).} \end{aligned}$$

On the other hand,

$$\begin{aligned}&\frac{\partial ^2}{\partial t \partial s}A(\gamma _s,f_t)\Big |_{s=t=0}\\&\quad =\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}\frac{\mathrm{d}}{\mathrm{d}s}\Big |_{s=0}\int _{\Sigma }\Big (1+s\psi \big (\mathrm{Exp}_q(v_t)\big )\Big )^{n/2}vol_{\varphi ^*_t(\gamma _0)}\\&\quad =\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}\int _{\Sigma }\frac{n}{2}\Big (1+s\psi \big (\mathrm{Exp}_q(v_t)\big )\Big )^{n/2-1}\Big |_{s=0}\Big (\psi \big (\mathrm{Exp}_q(v_t)\big )\Big )vol_{\varphi ^*_t(\gamma _0)}\\&\quad =\frac{\mathrm{d}}{\mathrm{d}t}\Big |_{t=0}\int _{\Sigma }\frac{n}{2}\psi \big (\mathrm{Exp}_q(v_t)\big )vol_{\varphi ^*_t(\gamma _0)}\\&\quad =\int _{\Sigma }\frac{n}{2}\Big [\frac{\mathrm{d}}{\mathrm{d}t}\Big (\psi \big (\mathrm{Exp}_q(v_t)\big )\Big )vol_{\varphi ^*_t(\gamma _0)}+\psi \big (\mathrm{Exp}_q(v_t)\big )\frac{\mathrm{d}}{\mathrm{d}t}vol_{\varphi ^*_t(\gamma _0)}\Big ]_{t=0}\\&\quad =\int _{\Sigma }\frac{n}{2}\Big [d \psi (\mathrm{Exp}_q(v_t))\cdot \mathrm{d}\mathrm{Exp}_q(v_t)(\frac{\mathrm{d}}{\mathrm{d}t}v_t)vol_{\varphi ^*_t(\gamma _0)}\Big ]_{t=0} + 0,\\&\mathrm{but}\;\frac{\mathrm{d}}{\mathrm{d}t}(v_t)=\frac{\mathrm{d}}{\mathrm{d}t}\big ( (t\bar{f} + O(t))\mathbf {n}_0 \big )=(\bar{f} + O'(t))\mathbf {n}_0, \mathrm{then}\\&\quad =\int _{\Sigma }\frac{n}{2}\Big [d \psi \big (\mathrm{Exp}_q(0)\big )\cdot \mathrm{d}\mathrm{Exp}_q(0)(\bar{f}(p) \mathbf {n}_0(p))\Big ]vol_{\varphi ^*_0(\gamma _0)}\\&\quad =\int _{\Sigma }\frac{n}{2}\Big [d \psi \big (\varphi _0(p)\big )\cdot \bar{f}(p) \mathbf {n}_0(p)\Big ]vol_{\varphi ^*_0(\gamma _0)}\\&\quad =\int _{\Sigma }\frac{n}{2}\bar{f}(p)\Big [d \psi \big (\varphi _0(p)\big )( \mathbf {n}_0(p))\Big ]vol_{\varphi ^*_0(\gamma _0)} \end{aligned}$$

so, by Lemma 4.3, we can to choose $\psi$ such that the last integral be nonvanishing.

Therefore, by Theorem 3.1, there is a neighborhood W of $(\gamma _0,0)$ such that

$$\begin{aligned} \widetilde{\mathcal {M}}=\{(\gamma ,f)\in W : H(\gamma ,f)=0\} \end{aligned}$$

is a Banach submanifold of $\Gamma \times X$. Now, since $h(\gamma ,f)=(\gamma ,[\varphi _f])$ is a diffeomorphism between $\widetilde{\mathcal {M}}$ and an open subset of $\mathcal {M}$, we conclude that $\mathcal {M}$ is a Banach submanifold of $\Gamma \times \mathcal {E}_{\partial }(\Sigma ,M)$.

It remains to show the separability of $\mathcal {M}$. For a coordinate system $(x_1,\ldots ,x_n)$ in $\varphi _f(\Sigma )=\Sigma _f$, the $\gamma$-mean curvature of $\Sigma _f$ is

$$\begin{aligned} H(\gamma ,f)=\gamma ^{ij}\gamma (\nabla _{\frac{\partial \varphi _f}{\partial x_{i}}}\frac{\partial \varphi _f}{\partial x_{j}}, \mathbf {\eta }_{\Sigma _f}), \end{aligned}$$

where $\gamma _{ij}=\gamma (\frac{\partial }{\partial x_i},\frac{\partial }{\partial x_j})$ and $\gamma ^{il}\gamma _{lj}=\delta _{ij}$. If $H(\gamma _0,0)=0$, then $\varphi _0$ is solution of a linear elliptic partial differential equation. So by the Schauder theory for elliptic equations we have that $\varphi _0$ is $C^k$ (see [2, Sec. 10]). Let S be the set of $\gamma$-orthogonal minimal embeddings of $\Sigma$ in M. $S\subset C^k(\Sigma ,M)$. Since $C^k(\Sigma ,M)$ is a separable space and $C^k(\Sigma ,M)\subset C^{j,\alpha }(\Sigma ,M)$, Lemma 4.4 implies that the closure of S in the topology $C^{j,\alpha }$ is also separable.

Now we state Smale’s theorem which is a generalization of Sard’s theorem for infinite-dimensional spaces. For a proof, see [17]. We will say almost all instead of “except for a set of first category”.

Sard–Smale Theorem  Let V and W be two differentiable Banach manifolds, connected and second-countable. Let $\phi :V\rightarrow W$ be a $C^k$ Fredholm map with $k>$max$\{index\ \phi ,0\}$. Then, the set of regular values of $\phi$ is generic in W. $\square$

Whence, as a consequence of Theorem 4.1 and the Sard–Smale theorem, we infer the following result.

Corollary 4.6

Under hypotheses of Theorem 4.1, the set of $(M,\Sigma )$-Bumpy metrics is generic in $\Gamma$. $\square$

5 Nonzero Constant Mean Curvature

Let us see now that the main result is valid also when the mean curvature is a constant different from zero.

Let $\gamma \in \text {Met}(M)$, recall the following notation (see 3.5):

$$\begin{aligned} \text {Emb}_{\partial \perp }^\gamma (\Sigma , M)&:= \{ \varphi : \varphi :\Sigma \rightarrow M \ \text {is}\ \gamma \text {-orthogonal admissible}\\&\qquad \text {embedding and bounding a finite volume}\} \end{aligned}$$

$\varphi \in \text {Emb}_{\partial \perp }^\gamma (\Sigma , M)$ has CMC, $H\ne 0$, if and only if it is a critical point for the functional

$$\begin{aligned}\mathfrak {f}_H(\varphi )=\int _{\Sigma }vol_{\varphi ^*(\gamma )}-H\int _{\Omega _\varphi }vol_{\gamma },\end{aligned}$$

where $\Omega _\varphi$ is the finite volume that bounded $\varphi$.

If in the statement of the main theorem we modify the condition of zero mean curvature by the condition of constant mean curvature $\mathfrak {h} \ne 0$ in the definition of $\mathcal {M}$, that is,

$$\begin{aligned}\mathcal {M}=\{ (\gamma , [\varphi ])\in \Gamma \times \mathcal {E}_{\partial }(\Sigma ,M) : [\varphi ]\in \mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M), \varphi \ \text {with}\ \gamma -\text {CMC},\ H\ne 0 \},\end{aligned}$$

the proof of the theorem is not modified, except for transversality. More explicitly, we must verify that, given $(\gamma _0,[\varphi _0]) \in M$, for all $\bar{f} \in \text {Ker}(\frac{\partial H}{\partial f}(\gamma _0,0))$, $\bar{f} \ne 0$, there exists a family $(\gamma _s,f_t) \in \mathfrak {X}$, $s,t\in (-\epsilon ,\epsilon )$,

$$\begin{aligned}\mathfrak {X}=\{(\gamma , f)\in \Gamma \times C^{j,\alpha }: f\in U,\varphi _f \in Emb_{\partial \perp }^\gamma (\Sigma , M)\},\end{aligned}$$

with $f'(0)=\bar{f}$, such that

$$\begin{aligned}\frac{\partial ^2}{\partial s \partial t}\Big |_{s=t=0}\bar{A}(\gamma _s,f_t)\ne 0,\end{aligned}$$

where

$$\begin{aligned}\bar{A}(\gamma _s,f_t)=\int _{\Sigma }vol_{\varphi _t^*(\gamma _s)}-H\int _{\Omega _{\varphi _t}}vol_{\gamma _s}.\end{aligned}$$

As before, we take a family of conformal metrics of the form $\gamma _s=(1+s\psi )\gamma _0$, with $\psi :M\rightarrow \mathbb {R}$ a smooth function such that $\phi (p)=0$ for all $p\in \Sigma _0=\varphi _0(\Sigma )$, where

$$\begin{aligned}\frac{\partial ^2}{\partial s \partial t}\Big |_{s=t=0}\int _{\Sigma }vol_{\varphi _t^*(\gamma _s)}\ne 0,\end{aligned}$$

it is sufficient to prove that

$$\begin{aligned}\frac{\partial ^2}{\partial s \partial t}\Big |_{s=t=0}\int _{\Omega _{\varphi _t}}vol_{\gamma _s}=0.\end{aligned}$$

Now,

$$\begin{aligned} \frac{\partial }{\partial t}\Big |_{t=0}\int _{\Omega _{\varphi _t}}vol_{\gamma _s}&= \int _{\Sigma _0}\gamma _s\left( \frac{\partial \varphi _t}{\partial t}\Big |_{t=0},\mathbf {n}_{\Sigma _0}\right) vol_{\varphi _0^*(\gamma _s)}\\&= \int _{\Sigma _0}\gamma _0\left( \frac{\partial \varphi _t}{\partial t}\Big |_{t=0},\mathbf {n}_{\Sigma _0}\right) vol_{\varphi _0^*(\gamma _0)}. \end{aligned}$$

The last integral does not depend on s.

So, if we replaces the hypothesis that $\varphi$ is $\gamma$-minimal by $\varphi$ has nonzero CMC in Theorem 4.1, the set of $(M,\Sigma )$-Bumpy metrics is generic in $\Gamma$. We can write the following corollary.

Corollary 5.1

Using the same notations as in Theorem 4.1, let $\mathcal {M}$ be the set defined as

$$\begin{aligned}\mathcal {M}=\{ (\gamma , [\varphi ])\in \Gamma \times \mathcal {E}_{\partial }(\Sigma ,M) : [\varphi ]\in \mathcal {E}_{\partial ,\gamma }^\bot (\Sigma ,M), \varphi \ \text {is}\ \gamma \text {-CMC} \}.\end{aligned}$$

Then

• 1. $\mathcal {M}$ is a separable Banach manifold modelled on $\Gamma$.

• 2. $\Pi :\mathcal {M}\rightarrow \Gamma$, defined by $\Pi (\gamma ,[\varphi ])=\gamma$, is a Fredholm map with index 0.

• 3. $\gamma _0$ is critical value of $\Pi$ if and only if there is a $\gamma _0$-CMC embedding $\varphi _0:\Sigma \rightarrow M$ which is degenerate.

Appendices

Appendix A

In this appendix, we will give some definitions and important results of functional analysis, which were necessary during the development of the whole paper.

Definition 6.1

If $f:N\rightarrow M$ is a smooth map and $S\subset M$ is an embedded submanifold, we say that f is transverse to S if, for every $p\in f^{-1}(S)$, $T_{f(p)}M=T_{f(p)}S+df_p(T_pN)$.

Definition 6.2

The definition of transversality between a map $F:\mathcal {X}\rightarrow \mathcal {Y}$ and $\mathcal {Z} \subset \mathcal {Y}$ a smooth submanifold, where $\mathcal {X}$ and $\mathcal {Y}$ are Banach manifolds, is that presented in the Definition 6.1 but with the additional assumption that $dF_{\mathfrak {x}_0}^{-1}(T_{F(\mathfrak {x}_0)}\mathcal {Z})$ is a complemented subspace of $T_{\mathfrak {x}_0}\mathcal {X}$, i.e., there is a subspace $\mathcal {V}\subset T_{\mathfrak {x}_0}\mathcal {X}$ such that $T_{\mathfrak {x}_0}\mathcal {X}=dF_{\mathfrak {x}_0}^{-1}(T_{F(\mathfrak {x}_0)}\mathcal {Z})\oplus \mathcal {V}$.

Definition 6.3

If A is a bounded operator in a Hilbert space H and $\{e_i:i\in I\}$ is a orthonormal bases for H, is defined the Hilbert–Schmidt norm as $||A||_{HS}^2=Tr(A^*A)=\sum _{i\in I}||Ae_i||_H^2$, where $||\cdot ||_H$ is the norm of H.

Definition 6.4

The Hölder space $C^{j,\alpha }(\Omega )$, where $\Omega$ is an open subset of some Euclidean space and $j\ge 0$ an integer, consists of those functions on $\Omega$ having continuous derivatives up to order j and such that the jth partial derivatives are Hölder continuous with exponent $\alpha$, where $0<\alpha \le 1$. A real-valued function f on n-dimensional Euclidean space is Hölder continuous, when there are nonnegative real constants c, such that

$$\begin{aligned}|f(x)-f(y)|\le c||x-y||^{\alpha }\end{aligned}$$

Definition 6.5

A linear continuous operator $T:E\rightarrow F$ between normed spaces is Fredholm if $\mathrm {Ker}\ T$ is finite dimensional and $\mathrm {Im}\ T$ is close and finite codimensional, the index of T is $\mathrm {ind}\ T=\mathrm {dim}\ \mathrm {Ker}\ T - \mathrm {dim}\ \mathrm {coker}\ T$. A Fredholm map is a $C^1$ map $f: M \rightarrow N$, M and N being differentiable Banach manifolds, such that for each $x\in M$, the derivative $df_x: T_x(M) \rightarrow T_{f(x)}(N)$ is a Fredholm operator. The index of f is defined to be the index of $df_x$ for some x. The definition does not depend on x, see [12].

Theorem 6.1

[13, The Inverse Mapping Theorem, 5.2] Let E, F Banach spaces, U an open subset of E, and Let $f:U\rightarrow F$ a $C^p$-morphism with $p\ge 1$. Assume that for some point $x_0\in U$ The derivative $f'(x_0):E \rightarrow F$ is a toplinear isomorphism. Them f is a local $C^p$-isomorphism at $x_0$.

Theorem 6.2

[13, The Implicit Mapping Theorem, 5.9] Let U, V be open sets in Banach Spaces E, F respectively, and set $f:U\times V\rightarrow G$ be a $C^p$ mapping. Let $(a,b)\in U\times V$, and assume that $D_2f(a,b):\mathbf{F}\rightarrow G$ is a isomorphism. Let $f(a,b)=0$. Then there exist a continuous map $g:U_0\rightarrow V$ defined on an open neighborhood $U_0$ of a such that $g(a)=0$ and such that $f(x,g(x))=0$ for all $x\in U_0$. If $U_0$ is taken to be a sufficiently small ball, then g is uniquely determined, and is also of class $C^p$.

Theorem 6.3

(Local Form of the Submersions) Let X and Y be Banach spaces and let $f:X\rightarrow Y$ be a submersion in $x_0$, e.i, $df(x_0):T_{x_0}\rightarrow T_{f(x_0)}Y$ is surjective and $\text {Ker}(df(x_0))$ is complemented. Then, there are open sets $U\subset X$ and $V\subset \text {Ker}(df(x_0))$, with $x_0\in U$ and $0\in V$, and a diffeomorphism $\varphi : V\times W \rightarrow U$, $W\subset Y$ closed subspace, such that $f\circ \varphi (x,w)=w$, for all $(x,w)\in V\times W$

Appendix B

In this appendix, we prove some lemmas of linear algebra in spaces of infinite dimension that are necessary in the proof of the genericity of the Bumpy Metrics in Sect. 3

Lemma 7.1

Let V be a infinite dimensional vector space with inner product $\langle , \rangle$ and $W\subset V$ an finite dimensional subspace. Let us suppose that $V=W\oplus W^\bot$. Let $Z\subset V$ be a subspace, $Z\supset W^\bot$. Then

• 1. $(W^\bot )^\bot =W$.

• 2. $V=Z\oplus Z^\bot$

Proof

• 1. Clearly $W\subset (W^\bot )^\bot$. Now, if $w\in (W^\bot )^\bot$, we can write $w=w_1+w_2$, with $w_1\in W$ and $w_2\in W^\bot$. From the fact $W\subset (W^\bot )^\bot$, we have $w_1\in (W^\bot )^\bot$. Thus $w_2=w+w_1 \in (W^\bot )^\bot$ (recall that $(W^\bot )^\bot$ is a closed subspace of V). Whence $w_2\in W^\bot \cap (W^\bot )^\bot =\{0\}$, that is, $w=w_1\in W$. So, we conclude that $(W^\bot )^\bot \subset W$.

• 2. Note that the quotient spaces $Z/W^\bot$ and $V/W^\bot$ are both finite dimensional and $Z/W^\bot \subset V/W^\bot$. Given $v\in V$, there are unique $v_1\in W$ and $v_2\in W^\bot$ such that $v=v_1+v_2$. Therefore, the map $\pi _1:V/W^\bot \rightarrow W$, $\pi _1(v+W^\bot )=v_1$, is an isomorphism. Let $i:Z/W^\bot \hookrightarrow V/W^\bot$ be the inclusion map. Consider $L=\pi _1\circ i:Z/W^\bot \rightarrow W$ and let $\widetilde{Z}=\text {Im}L\subset W$. Thus, $\widetilde{Z}=\{ z-z_2 : z\in Z, z=z_1+z_2, z_1\in W,z_2\in W^\bot \}\subset Z$ and $W=\widetilde{Z}\oplus \widetilde{Z}^\bot$. Let $\{x_1,\ldots ,x_k \}\subset W$ be a basis for $\widetilde{Z}^\bot$. We claim that $x_1,\ldots ,x_k\in Z^\bot$. Let $z+W^\bot \in Z/W^\bot$, $z=z_1+z_2\in Z$, $z_1\in W$ and $z_2\in W^\bot$. We have

  $$\begin{aligned} \langle z, x_i\rangle&= \langle z, x_i\rangle + \langle W^\bot , x_i\rangle =\langle z+W^\bot , x_i\rangle \\&= \langle z_1+z_2+W^\bot , x_i\rangle = \langle z_1+W^\bot , x_i\rangle \\&= \langle z_1, x_i\rangle + \langle W^\bot , x_i\rangle =0, \end{aligned}$$

  since $z_1\in \widetilde{Z}$, $x_i\in \widetilde{Z}^\bot \subset W$, $i=1,\ldots ,k$.

Now we prove that $\text {Span}\{Z,x_1,\ldots ,x_k\}=V$. Let $v=v_1+v_2\in V$ be given, with $v_1\in W$ and $v_2\in W^\bot \subset Z$. There holds that $v_1= \widetilde{z}_1 + \sum _{i=1}^k a_ix_i$, $\widetilde{z}_1\in \widetilde{Z}$, where $a_i$, $i=1,\ldots ,k$, are scalars. Whence $v=(\widetilde{z}+v_2)+\sum _{i=1}^k a_ix_i$.

It remains to show that $\text {Span}\{x_1,\ldots ,x_k\}=Z^\bot$. In fact, it suffices to show that $\text {Span}\{x_1,\ldots ,x_k\}\supset Z^\bot$. Let

$$\begin{aligned}i:Z^\bot \hookrightarrow V=Z\oplus \text {Span}\{x_1,\ldots ,x_k\}\end{aligned}$$

be the inclusion map, and

$$\begin{aligned}\pi _2:Z\oplus \text {Span}\{x_1,\ldots ,x_k\}\rightarrow \text {Span}\{x_1,\ldots ,x_k\}\end{aligned}$$

the natural projection. We have that $\text {Ker}(\pi _2\circ i)=\{0\}$, so $\pi _2\circ i$ is injective, thus $\text {Dim}(Z^\bot )\le k$. $\square$

Lemma 7.2

Let V be a infinite-dimensional vector space with inner product $\langle , \rangle$ and $W\subset V$ an finite dimensional subspace. Suppose that $V=W\oplus W^\bot$. Let $Z\subset V$ be a subspace, $Z\supset W^\bot$, such that for all $w\in W{\setminus }\{0\}$, there exist $z\in Z$ with $\langle z,w\rangle \ne 0$. Then $Z=V$

Proof

We show that

$$\begin{aligned} (\forall w\in W{\setminus }\{0\})(\exists z\in Z)(\langle z,w\rangle \ne 0) \Leftrightarrow W\cap Z^\bot =\{0\}). \end{aligned}$$

(7.1)

First suppose that ($\forall w\in W{\setminus }\{0\})(\exists z\in Z)(\langle z,w\rangle \ne 0$. Let $w\in W\cap Z^\bot$ be given, then $\forall z \in Z$, $\langle z,w\rangle = 0$, so $w=0$, that is, $W\cap Z^\bot =\{0\}$.

Now suppose that $W\cap Z^\bot =\{0\}$ and let $w\in W{\setminus } \{0\}$, then $w\notin Z^\bot$, so there is $z\in Z$ such that $\langle z,w\rangle \ne 0$.

Since $Z\supset W^\bot$, by 1) of Lemma 7.1 we have $Z^\bot \subset (W^\bot )^\bot = W$. From the fact $W\cap Z^\bot =\{0\}$, we deduce that $Z^\bot =\{0\}$. Also by 2) of Lemma 7.1 we have $V=Z\oplus Z^\bot$. So, $V=Z$. $\square$

Next lemma were taken from [8, Lemma 2.2].

Lemma 7.3

Let $L : U \rightarrow V$ be a linear map between vector spaces, and let $S\subset V$ be a subspace of finite codimension. Then $L^{-1}(S)$ is finite co-dimensional in U, and

$$\begin{aligned} \text {Codim}_U (L^{-1}(S))=\text {Codim}_V (S)-\text {Codim}_V (\text {Im}(L)+S)\end{aligned}$$

.