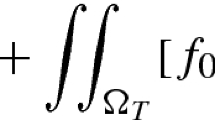Existence Results to a Class of Nonlinear Parabolic Systems Involving Potential and Gradient Terms

Abstract

In this paper, we investigate the existence of solutions to a nonlinear parabolic system, which couples a non-homogeneous reaction-diffusion-type equation and a non-homogeneous viscous Hamilton–Jacobi one. The initial data and right-hand sides satisfy suitable integrability conditions and non-negative. To simplify the presentation of our results, we will consider separately two simplified models : first, vanishing initial data, and then, vanishing right-hand sides.

1 Introduction

The main goal of this paper is to study the existence of solutions to the following non-linear system:

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t -\Delta u &{}=&{} v^q+f &{}{} \text{ in } &{}{} \Omega _T=\Omega \times (0,T), \\ v_ t-\Delta v &{}=&{} |\nabla u|^{p}+g &{}{} \text{ in } &{}{}\Omega _T=\Omega \times (0,T), \\ u=v&{}=&{} 0 &{}{} \text{ on } &{}{}\Gamma _T=\partial \Omega \times (0,T),\\ u(x,0)&{}= &{} u_0(x)\, &{}{} \text{ in } &{}{}\Omega , \\ v(x,0) &{}= &{} v_0(x) &{}{} \text{ in } &{}{}\Omega , \\ u,v &{}\ge &{} 0 &{}{} \text{ in } &{}{}\Omega \times (0,T), \end{array} \right. . \end{aligned}$$

(1.1)

where $\Omega$ is a bounded domain of $\mathbb {R}^N$, $N\ge 1$ and $p, q\ge 1$. Here (f, g) and $(u_0,v_0)$ are non-negative data and satisfy some suitable integrability conditions that we will specify later. Our objective is to find “natural” relation between p, q and the regularity of the data to get the existence of a solution to system (1.1).

Systems with gradient term appear for instance when considering electrochemical models in engineering and some other models in fluid dynamics. We refer to [23] and [28] for more details and more applications of this class of systems.

Before stating our main results, let us begin by recalling some previous results related to our system.

Stationary case Concerning existence of solutions, it is well known in some particular cases. For this, we refer to [8, 19, 20] and [1] where some general existence results were established.

Parabolic case In the case of a single equation and under the presence of gradient term, many results of global existence are known. We refer to [2, 18] and the references therein. On the other hand, there is an extensive literature devoted to the study and solvability and properties of solutions to the so-called viscous Hamilton–Jacobi equation (HJ).

More precisely, let us consider the following Dirichlet and Cauchy problems:

$$\begin{aligned} (HJD)\left\{ \begin{array}{lllcc} u_t-\Delta u &{} =&{} a|\nabla u|^{p} +h(x,t) &{}{}\quad \text{ in } &{}{} \Omega _T , \\ u(x,t) &{} = &{} 0 &{}{}\quad \text{ on } &{}{}\Gamma _T, \\ u(x,0)&{} = &{} u_0(x) &{}{}\quad \text{ in } &{}{}\Omega \; ;\\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} (HJC)\left\{ \begin{array}{llll} u_t-\Delta u &{}=&{} a|\nabla u|^{p} +h(x,t) &{}{}\quad \text{ in } \mathbb {R}^N\times (0,T) , \\ u(x,0) &{}= &{} u_0(x) &{}{} \quad \text{ in } \mathbb {R}^N,\\ \end{array} \right. \end{aligned}$$

where $a\in \mathbb {R}^*$, $p\ge 0$.

First case If $h\equiv 0$. In bounded domains, existence and uniqueness results of (HJD) may be found for example in [4, 10, 24, 47, 48] and the references therein. A considerable literature has also been devoted to the analogous whole-space Cauchy problem (HJC) ; we refer to [7, 12,13,14, 35, 49] and the references therein.

Needless to say, the references mentioned above do not exhaust the rich literature on the subject.

Second case If $h\not \equiv 0$. As far as we know, Problems (HJD) and (HJC) have been considered in [50, 51]. We recall also the result of [2] where, in the case $p=2$, sharp regularity results are proved for positive solution to problem (HJD) and, as a consequence, a complete classification of the set of nonnegative solutions is obtained in relation with the classical parabolic capacity.

In the case of parabolic systems, we refer to [36, 37, 29, 32, 40, 44] and the references therein. Let us briefly recall some related results. The case where the gradient term appears as an absorption term was treated in [40]. A particular case with natural growth in the gradient was considered in [29]. We also mention the paper [16] where applications of a such parabolic systems are given in the context of stochastic differential games.

Systems with potential nonlinearities was studied in depth in [32], where the authors proved the existence of a Fujita-type exponents. An interesting contribution for this class of systems was recently made in [44, section 32].

Our main contribution in this work is to get the existence of solution to (1.1) for all $p,q \ge 1$ under “natural” conditions on the data $(u_0, v_0)$ and (f, g). By solution, we mean either energy solution or entropy solution (for more specifics, see Definition 2.2 and Definition 2.5).

To simplify the presentation, we will mostly discuss two simplified models (we refer to the proof of Theorem 3.3 for the relation between the two cases).

• (1) The first one is obtained by taking $(u_0,v_0)=(0,0)$ in (1.1), namely

  $$\begin{aligned} \left\{ \begin{array}{lllll} u_t &{}=&{} \Delta u+ v^q+f &{}{}\quad \text{ in } &{}{} \Omega _T, \\ v_ t &{}=&{} \Delta v + |\nabla u|^{p}+g &{}{}\quad \text{ in } &{}{} \Omega _T, \\ u=v&{}=&{} 0 &{}{}\quad \text{ on } &{}{} \Gamma _T,\\ u(x,0)&{}=&{} 0 &{}{}\quad \text{ in } &{}{} \Omega , \\ v(x,0) &{}=&{} 0 &{}{}\quad \text{ in } &{}{} \Omega , \\ u,v &{}\ge &{} 0 &{}{} \quad \text{ in } &{}{} \Omega _T. \end{array} \right. \end{aligned}$$

  (1.2)

  Using regularity arguments and a suitable fixed-point Theorem, we get the existence of a solution to (1.2) in a suitable parabolic-Sobolev space.

• (2) The second simplified model corresponds to $(f,g)=(0,0)$, i.e:

  $$\begin{aligned} \left\{ \begin{array}{lllll} u_t &{}=&{} \Delta u+ v^q &{}\quad \text { in } &{} \Omega _T, \\ v_ t &{}=&{} \Delta v + |\nabla u|^{p} &{}\quad \text { in } &{}\Omega _T, \\ u=v&{}=&{} 0 &{}\quad \text { on } &{} \Gamma _T,\\ u(x,0) &{}=&{}u_0(x) &{}\quad \text { in } &{} \Omega , \\ v(x,0)&{}=&{}v_0(x) &{}\quad \text { in } &{} \Omega , \\ u,v &{}\ge &{} 0 &{} \quad \text { in } &{} \Omega _T. \end{array} \right. \end{aligned}$$

  (1.3)

  Taking advantage from the study of the first model, and using a change of function, we will prove that system (1.3) has a solution under suitable hypotheses on initial data $(u_0,v_0)$.

In a forthcoming work, we shall investigate questions of global existence and Fujita-type blow-up for the whole-space Cauchy problem.

The paper is composed of four sections. In Sect. 2, we give some useful tools like the notion of parabolic-Sobolev spaces and some of their properties. We also specify the sense in which solutions are considered, as well as some optimal regularity results. The first part of Sect. 3 is devoted to get existence results, and is split into two parts: Sect. 3.1 is devoted to the first simplified model (1.2) and Sect. 3.2 for the second one (1.3). In Sect. 3.3, we analyze the question of blow-up in finite time, in a suitable norm of the solution and under additional condition on p, q. The last section is devoted to treating variants of the previous model, where the gradient term appears in both evolution equations.

2 Preliminary Results and Functional Setting

In this section, we give some useful tools that will be used many times in this paper.

2.1 Functional Setting

Let $r\ge 1$. In the sequel, we denote by $L^{r}(0,T; W^{1,r}_0(\Omega ))$ the set of functions u such that $u\in L^r(\Omega _T)$ and $u(.,t)\in W^{1,r}_0(\Omega )$. The space $L^{r}(0,T; W^{1,r}_0(\Omega ))$ is equipped with the norm

$$\begin{aligned} ||u||_{L^{r}(0,T; W^{1,r}_0(\Omega ))} := \left( \int _0^T\int _{\Omega }|\nabla u(x,t)|^r\,\text {d}x\,\text {d}t\right) ^{\frac{1}{r}} \end{aligned}$$

is a Banach space. We shall often refer to this space by the shorthand $E_r(\Omega _T) := L^r(0,T;W^{1,r}_0(\Omega ))$.

For $s, r\ge 1$, the space $V^{s,r}_0(\Omega _T) : = L^{\infty }(0,T;L^s(\Omega ))\cap E_r(\Omega _T)$ endowed with the norm

$$\begin{aligned} ||\varphi ||_{V^{s,r}_0(\Omega _T)}: = \text {ess}\sup \limits _{0\le t\le T}||\varphi (.,t)||_{L^s(\Omega )}+||\varphi ||_{E_r(\Omega _T) } \end{aligned}$$

is also a Banach space. If $s=1$, we have,

$$\begin{aligned} V_0^{1,r}(\Omega _T)=L^{\infty }(0,T;L^1(\Omega ))\cap E_r(\Omega _T). \end{aligned}$$

The next proposition will be useful to show a priori estimates, and it will be used throughout this work. We refer to [31, Proposition 3.1] for more details.

Proposition 2.1

Let $s, r\ge 1$ and $\nu =r\dfrac{N+s}{N}$, then there exists a positive constant C depending only on $N, \nu , s$ such that for all $v\in V^{s,r}_0(\Omega _T)$,

$$\begin{aligned}&\displaystyle \int \int _{\Omega _T} |v(x,t)|^{\nu } \mathrm{d}x\,\mathrm{d}t \le C^\nu \Big (\displaystyle \int \int _{\Omega _T} |\nabla v(x,t)|^r \mathrm{d}x\,\mathrm{d}t\Big )\nonumber \\&\quad \times \Big ( \mathrm{ess}\sup \limits _{0\le t\le T}\displaystyle \int _{\Omega }|v(x,t)|^s \mathrm{d}x\,\mathrm{d}t\Big )^{\frac{r}{N}}; \end{aligned}$$

(2.1)

moreover,

$$\begin{aligned} ||v||_{L^\nu (\Omega _T)}\le C||v||_{V^{s,r}_0(\Omega _T)}. \end{aligned}$$

(2.2)

The multiplicative inequality (2.1) and the embedding inequality (2.2) continue to hold for functions $v \in V^{s,r}(\Omega _T)$ such that

$$\begin{aligned} \displaystyle \int _{\Omega } v(x,t) \, \text {d}x=0, \qquad \qquad \text {for all a.e} \quad t\in (0, T). \end{aligned}$$

$\bullet$Notions of solution : Now, we define the two notions of solution that we will systematically use throughout this paper: energy solution and entropy solution.

The starting point is to treat each equation in system (1.1) separately.

To this end, let us consider the problem

$$\begin{aligned} \left\{ \begin{array}{lllll} w_t-\Delta w = h &{}\quad \text{ in } &{}\Omega _T, \\ w = 0 &{}\quad \text{ on } &{} \Gamma _T,\\ w(x,0)=w_0(x) &{}\quad \text{ in } &{}\Omega . \end{array} \right. \end{aligned}$$

(2.3)

Definition 2.2

Assume that $(h,w_0)\in L^{2}(0,T; H^{-1}(\Omega ))\times L^2(\Omega )$. We say that w is an energy solution to problem (2.3) if $w\in L^{2}(0,T; H_0^1(\Omega ))\cap \mathcal {C}(0,T; L^2(\Omega ))$, $w_t\in L^{2}(0,T; H^{-1}(\Omega ))$, $w(x,t)\rightarrow w_0$ strongly in $L^2(\Omega )$ as $t\rightarrow 0$ and for all $v\in L^{2}(0,T; H_0^1(\Omega ))$ we have

$$\begin{aligned} \int _0^T\langle w_t, v\rangle \text {d}t+\iint _{\Omega _T} \nabla w\cdot \nabla v\,\text {d}x\,\text {d}t=\int _0^T\langle h(x,t), v\rangle \,\text {d}t. \end{aligned}$$

Related to nonlinear system (1.1), we have the following definition of energy solution.

Definition 2.3

(Energy solution) Assume that $(f,u_0), (g,v_0)\in L^{2}(0,T; H^{-1}(\Omega ))\times L^2(\Omega )$. Let $(u,v)\in (L^{2}(0,T; H_0^1(\Omega ))\, \cap \, \mathcal {C}(0,T; L^2(\Omega )))^2$ be nonnegative functions such that $(u_t,v_t)\in (L^{2}(0,T; H^{-1}(\Omega )))^2$. Define $F(x,t):= v^q+f, G(x,t):=|\nabla u|^{p}+g$.

We say that (u, v) is an energy solution to the system (1.1) if $F,G\in L^{2}(0,T; H^{-1}(\Omega ))$, $u(\cdot ,t)\rightarrow w_0$, $v(\cdot ,t)\rightarrow v_0$ strongly in $L^2(\Omega )$ as $t\rightarrow 0$ and for all $(\psi , \theta )\in (L^{2}(0,T; H_0^1(\Omega )))^2$, we have

$$\begin{aligned}&\int _0^T\langle u_t, \psi \rangle \text {d}t+\iint _{\Omega _T} \nabla u\cdot \nabla \psi \,\text {d}x\,\text {d}t=\int _0^T\langle F(x,t), \psi \rangle \,\text {d}t, \\&\int _0^T\langle v_t, \theta \rangle \text {d}t+\iint _{\Omega _T} \nabla v\cdot \nabla \theta \,\text {d}x\,\text {d}t=\int _0^T\langle G(x,t), \theta \rangle \,\text {d}t. \end{aligned}$$

In the case of $L^1$ data, we need to use the concept of entropy solution introduced in [42] (which is equivalent, in this case, to the concept of renormalized solution defined in [17]). We note that the concept of entropy solution was introduced for the first time in [15] to treat nonlinear elliptic problem with general data.

Let us first recall the following definition:

Definition 2.4

Let $p\ge 1$ and let w be a measurable function. We say that $w\in {\mathcal {T} }^{1,p}_0(\Omega _T)$ if $T_k(w)\in L^p(0,T;W^{1,p}_0(\Omega ))$ for all $k>0$ where

$$\begin{aligned} T_k(s): =\left\{ \begin{array}{ccc} s\,&{}\hbox { if } &{} |s|\le k\,;\\ k\dfrac{s}{|s|}\,&{}\hbox { if } &{} |s|> k. \end{array}\right. \end{aligned}$$

(2.4)

We begin by stating the defining of the entropy solution in the case of scalar equation.

Definition 2.5

Assume that $(h,w_0)\in L^1(\Omega _T)\times L^1(\Omega )$. We say that $w\in \mathcal {C}(0,T;L^1(\Omega ))$ is an entropy solution to problem (2.3) if $w\in {\mathcal {T} }^{1,2}_0(\Omega _T)$ and for all $v\in L^2(0,T;H_0^1(\Omega ))\cap L^\infty (\Omega _T)\cap \mathcal {C}(0,T;L^1(\Omega ))$ and for all $k>0$,

$$\begin{aligned} \begin{array}{rcll} &{}&{}\displaystyle \int _{\Omega }\Theta _{k}(w-v)(T)\, \text {d}x+\displaystyle \iint _{\Omega _T} v_t T_{k}(w-v)\,\text {d}x\,\text {d}t+ \displaystyle \iint _{\Omega _T} \nabla w \nabla \Theta _{k}(w-v)\,\text {d}x\,\text {d}t\\ &{}&{}\quad =\displaystyle \int _{\Omega }\Theta _{k}(w_0-v(0, .))\, dx+\displaystyle \iint _{\Omega _T} h\, T_{k}(w-v)\, \text {d}x\,\text {d}t, \end{array} \end{aligned}$$

where

$$\begin{aligned} \Theta _k(s):=\displaystyle \int _{0}^s T_k(t)\, \text {d}t. \end{aligned}$$

Notice that,

$$\begin{aligned} \int _{\Omega }w_tT_{k}(w)\, \text {d}x=\frac{d}{\text {d}t}\Big (\int _{\Omega }\Theta _{k}(w)\,\text {d}x\Big ), \end{aligned}$$

where

$$\begin{aligned} \int _{\Omega }\Theta _{k}(w(x,t))\, \text {d}x-\int _{\Omega }\Theta _{k}(w(x,0))\, \text {d}x=\int _0^t\int _{\Omega }w_s\Theta _{k}(w)\,\text {d}x\,\text {d}s. \end{aligned}$$

If w is an entropy solution to problem (2.3), then w is a distributional solution.

In a similar way, we define the entropy solution for system (1.1).

Definition 2.6

(Entropy solution) Assume that $(f,u_0), (g,v_0)\in L^1(\Omega _T)\times L^1(\Omega )$. Let $(u,v)\in (\mathcal {C}(0,T;L^1(\Omega )))^2$ be nonnegative functions. We say that (u, v) is an entropy solution to system (1.1) if $(u,v)\in ({\mathcal {T} }^{1,2}_0(\Omega _T))^2$, $F,G\in L^{1}(\Omega _T)$ (where F, G are defined as in Definition 2.3), and for all $(\psi , \theta )\in (L^2(0,T;H_0^1(\Omega ))\cap L^\infty (\Omega _T)\cap \mathcal {C}(0,T;L^1(\Omega )))^2$ and for all $k>0$,

$$\begin{aligned}&\displaystyle \int _{\Omega }\Theta _{k}(u-\psi )(T)\, \text {d}x+\displaystyle \iint _{\Omega _T} \psi _t T_{k}(u-\psi )\,\text {d}x\,\text {d}t+ \displaystyle \iint _{\Omega _T} \nabla u \nabla \Theta _{k}(u-\psi )\,\text {d}x\,\text {d}t\\&\quad =\displaystyle \int _{\Omega }\Theta _{k}(u_0-\psi (0, .))\, \text {d}x+\displaystyle \iint _{\Omega _T} F\, T_{k}(u-\psi )\, \text {d}x\,\text {d}t,\\&\displaystyle \int _{\Omega }\Theta _{k}(v-\theta )(T)\, \text {d}x+\displaystyle \iint _{\Omega _T} \theta _t T_{k}(v-\theta )\,\text {d}x\,\text {d}t+ \displaystyle \iint _{\Omega _T} \nabla v \nabla \Theta _{k}(u-\theta )\,\text {d}x\,\text {d}t\\&\quad =\displaystyle \int _{\Omega }\Theta _{k}(u_0-\theta (0, .))\, \text {d}x+\displaystyle \iint _{\Omega _T} G\, T_{k}(v-\theta )\, \text {d}x\,\text {d}t. \end{aligned}$$

The next existence and compactness result is proved in [42] and [17].

Theorem 2.7

Let $(h,w_0)\in L^1(\Omega _T)\times L^1(\Omega )$. Then problem (2.3) has a unique entropy solution $w\in \mathcal {C}(0,T;L^1(\Omega ))$ such that $w\in L^s(0,T;W^{1,s}_0(\Omega ))$ for all $s<\frac{N+2}{N+1}$. Moreover, there exists a positive constant $C=C(\Omega , N,s)$ such that

$$\begin{aligned} ||w||_{\mathcal {C}(0,T; L^1(\Omega ))}+||w||_{L^s(0,T;W^{1,s}_0(\Omega ))}\le C(||w_0||_{L^1(\Omega )}+||h||_{L^1(\Omega _T)}).\nonumber \\ \end{aligned}$$

(2.5)

As a consequence of Proposition 2.1, it holds that, for all $\nu <\frac{N+2}{N}$ and for all $r<\frac{N+2}{N+1}$,

$$\begin{aligned}&\displaystyle \int \int _{\Omega _T} |w(x,t)|^{\nu } \text {d}x\,\text {d}t \le C^\nu \Big (\displaystyle \int \int _{\Omega _T} |\nabla w(x,t)|^r \text {d}x\,\text {d}t\Big )\nonumber \\&\quad \times \Big ( \text {ess}\sup \limits _{0\le t\le T}\displaystyle \int _{\Omega }|w(x,t)| \text {d}x\,\text {d}t\Big )^{\frac{r}{N}}. \end{aligned}$$

(2.6)

Furthermore, for $s<\frac{N+2}{N+1}$ fixed, the operator $L : (h,w_0) \mapsto u$ is compact from $L^1(\Omega _T)\times L^1(\Omega )$ to $L^s(0,T;W^{1,s}_0(\Omega ))$.

Now, let us recall some regularity results that will allow us to establish some a priori estimates when dealing with approximating problems. We refer to [14, 18, 44] for a complete proof.

Theorem 2.8

Let w be the unique solution (in sense of Definition 2.5) to problem (2.3) with $(h,w_0)\in L^{\kappa }(\Omega _T)\times L^\tau (\Omega )$. Then we have

The case $w_0\equiv 0$ :

• If $1<\kappa < \frac{N+2}{2}$, then $w\in L^{\delta }(\Omega _T)$ where $\delta =\frac{(N+2)\kappa }{N+2-2\kappa }$, $w\in E_{\overline{\kappa }}(\Omega _T)$ where $\overline{\kappa }=\frac{(N+2)\kappa }{N+2-\kappa }$ and $w\in L^\infty (0,T; L^a(\Omega ))$ where $a=\frac{\kappa N}{N+2-2\kappa }$.

  Moreover, there exists $C= C(\Omega ,N,\kappa )>0$ such that

  $$\begin{aligned} ||w||_{L^\infty (0,T; L^a(\Omega ))}+||w||_{E_{\overline{\kappa }}(\Omega _T)}+ ||w||_{L^\delta (\Omega _T)} \le C||h||_{L^\kappa (\Omega _T)}. \end{aligned}$$

  (2.7)

• If $\kappa =\frac{N+2}{2}$, then there exists $\alpha >0$ depending only on $\Omega$ and N such that $e^{\alpha w}\in L^\infty (0,T; L^2(\Omega ))$ and there exists $C\equiv C(\Omega , N, \kappa )>0$ such that

  $$\begin{aligned} ||e^{\alpha w}||_{L^\infty (0,T;L^2(\Omega ))}\le C||h||_{L^\kappa (\Omega _T)}. \end{aligned}$$

  (2.8)

• If $\kappa >\frac{N+2}{2}$, then $w\in L^\infty (\Omega _T)$ and there exists $C\equiv C(\Omega ,N,\kappa )$ such that

  $$\begin{aligned} ||w||_{L^\infty (\Omega _T)}\le C||h||_{L^\kappa (\Omega _T)}. \end{aligned}$$

  (2.9)

The case $h\equiv 0$:

Let $w_0\in L^\tau (\Omega )$, $\tau \in [1, \infty [$, then there exist $C_1, C_2> 0$ depending only on $\gamma , \tau , s, N, \Omega$ such that

$$\begin{aligned} ||w(.,t)||_{L^\gamma (\Omega )}\le C_1\dfrac{||w_0||_{L^\tau (\Omega )}}{t^{\frac{N}{2}(\frac{1}{\tau }-\frac{1}{\gamma }) }}, \quad \,\,\,\, \, \tau \le \gamma \le +\infty \,, \end{aligned}$$

(2.10)

and

$$\begin{aligned} ||\nabla w(.,t)||_{L^s(\Omega )}\le C_2\dfrac{||w_0||_{L^\tau (\Omega )}}{t^{\frac{N}{2}(\frac{1}{\tau }-\frac{1}{s})+\frac{1}{2} }}, \quad \,\,\,\, \, \tau \le s\le +\infty . \end{aligned}$$

(2.11)

Moreover, $w\in L^\theta (\Omega _T)$ for all $\theta <(\frac{2}{N}+1)\tau$ and $|\nabla w|\in L^s(\Omega _T)$ for all $s<\frac{(N+2)\tau }{N+\tau }.$ Furthermore, we have

$$\begin{aligned} ||w||_{L^\theta (\Omega _T)} +||w||_{E_s(\Omega _T)} \le C(\Omega ,N,\tau )||w_0||_{L^\tau (\Omega )}. \end{aligned}$$

Remark 1

The regularity results of Theorem 2.7 and Theorem 2.8 are sharp, in the sense that if the algebraic conditions are violated, one can construct data h or $w_0$ such that the above estimates are invalidated and no local solution to the associate equation exists.

Finally, let us recall the famous Schauder fixed-point theorem.

Theorem 2.9

(Schauder fixed-point theorem) Assume that E is a closed convex set of a Banach space X. Let L be a continuous and compact mapping from E into itself. Then L has a fixed point in E.

3 Existence Results

As already mentioned in Sect. 1, to simplify the presentation of our results, we will consider separately two cases : the case $(f,g)\ne (0,0)$ with $(u_0,v_0)\equiv (0,0)$ and the case $(u_0,v_0)\ne (0,0)$ with $(f,g)\equiv (0,0)$.

Henceforth, we denote by C any positive constant that depends only on the data of the problem, and can change from one line to next.

3.1 First Case:

$(u_0,v_0)\ne (0,0)$

The main system is:

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t-\Delta u &{} =&{} v^q+f &{} \text { in } &{}\Omega _T, \\ v_t-\Delta v &{}=&{} |\nabla u|^{p}+g &{}\text { in } &{} \Omega _T, \\ u=v&{}=&{} 0 &{} \text { on } &{} \Gamma _T,\\ u(x,0)&{}=&{}v(x,0)=0 &{}\text { in } &{} \Omega , \\ u,v &{}\ge &{} 0 &{} \text { in } &{} \Omega _T, \end{array} \right. \end{aligned}$$

(3.1)

where $\Omega$ is a bounded domain of $\mathbb {R}^N$ and $p, q\ge 1$. Here f and g are nonnegative measurable functions with additional assumptions.

The main existence result in this case is the following:

Theorem 3.1

Let $T>0$ and $p, q\ge 1$ with $pq>1$. Assume that $(f,g) \in L^{m}(\Omega _T)\times L^{\sigma }(\Omega _T)$, where $(m,\sigma )\in [1,+\infty )^2$ satisfies one of the following conditions:

$$\begin{aligned}&m,\sigma \in [1, N+2) \,\text { with } p\sigma< \overline{m}= \dfrac{m (N+2)}{N+2-m}\,\text { and } \,\nonumber \\&qm < \dfrac{(N+1)\overline{\sigma }}{N}=\dfrac{(N+1)(N+2)\sigma }{N(N+2-\sigma )} \,; \end{aligned}$$

(3.2)

$$\begin{aligned}&\text {or},\quad \sigma \le N+2\le m, \text { with } \end{aligned}$$

(3.3)

$$\begin{aligned}&\begin{array}{llll} \quad (a) \text { either } &{} q\le \dfrac{\sigma (N+1)}{N(N+2-\sigma )} &{} \text{ and } &{} p\in [1,+\infty ),\\ \\ \quad (b)\text { or}\,\, &{} \dfrac{\sigma (N+1)}{N(N+2-\sigma )}<q<\dfrac{(N+1)\overline{\sigma }}{N} &{} \text{ and } \nonumber \\ {} &{} p\Big [q-\dfrac{\sigma (N+1)}{N(N+2-\sigma )}\Big ]<\dfrac{N+1}{N}\,;\\ \\ \end{array} \nonumber \\&\text {or},\quad m\le N+2\le \sigma ,\text { with } \end{aligned}$$

(3.4)

$$\begin{aligned}&\begin{array}{llll} \quad (a) \text { either } &{} p\sigma<\overline{m} &{} \text{ and } &{} q\in [1,+\infty ),\\ \\ \quad (b)\text { or}\,\, &{} p\sigma \ge \overline{m}&{} \text{ and } &{} q<\dfrac{(N+1)(N+2)}{N\Big (p[N+2-m]-m\Big )_+}\,; \end{array} \nonumber \\&\text {or},\quad m, \sigma \ge N+2, \text { with } q \in [1,+\infty ) \text { and } p \in [1,+\infty ). \end{aligned}$$

(3.5)

Then there exists $T^*\le T$ such that the system (3.1) has a nonnegative solution (u, v). Moreover, $(u,v)\in V^{1,\alpha }_0(\Omega _{T^*})\times V^{1,\beta }_0(\Omega _{T^*})$ for all $\alpha <\frac{(N+2)m}{(N+2-m)_+}$ and $\beta <\frac{(N+2)\sigma }{(N+2-\sigma )_+}$.

Remark 2

To give some light on the hypotheses (3.2)-(3.5), let us make explicit the size conditions on (p, q) for a given $(m,\sigma )$.

• If $m=\sigma =1$, condition (3.2) holds for all $p<\frac{N+2}{N+1}$ and $q<\frac{N+2}{N}$, which are the maximal regularity results of the potential term and gradient term, respectively, for the solution of parabolic problem with $L^1$ data. (See Remark 4).

• If $m=\sigma =2$, condition (3.2) is satisfied for all $p<\frac{N+2}{N}$ and $q<\frac{(N+1)(N+2)}{N^2}$.

• If $m>N+2, \sigma =N$, condition (3.3) is satisfied for all $p<\infty$ and for all $q<\dfrac{N+1}{2}$.

• If $m=N, \sigma =N+2$, condition (3.4) is satisfied for all $p<\frac{N}{2}$ and $q<\infty$.

• If $m=\sigma \ge N+2$, condition (3.5) holds for all $(p,q)\in [1,+\infty )^2$.

Remark 3

The above restrictions on the parameters are natural to get existence of solution if we consider elliptic or parabolic systems (or equations) with gradient term. As an example, let us consider a single elliptic equation with gradient term:

$$\begin{aligned} -\Delta w=|\nabla w|^p +f \text{ in } \Omega , \, w=0 \text{ on } \partial \Omega , \end{aligned}$$

with $f\in L^m(\Omega )$ and $p>1$. As proved in [38], existence holds under the optimal condition $m>\frac{N}{p'}$ which means that $p<\frac{N}{(N-m)_+}$. In particular, if $m = 2$, the condition $p<\frac{N}{N-2}$ needs to be satisfied. The parabolic case is treated in [27] and [2]. If $p=2$, we can prove that for all $\varepsilon >0$, setting $f(x)=\frac{1}{|x|^{N/2+\varepsilon }}\notin L^{\frac{N}{2}}(B_1(0))$, then the corresponding parabolic problem with quadratic gradient term as non-local solution.

Proof of Theorem 3.1

We will give the proof under condition (3.2) i.e

$$\begin{aligned} m, \sigma \in (1,N),\quad p\sigma<\dfrac{m (N+2)}{N+2-m}\text { and } qm <\dfrac{(N+1)(N+2)\sigma }{N(N+2-\sigma )}. \end{aligned}$$

The other cases follow in a similar way.

The proof will be achieved in several steps. $\square$

$\bullet$ First step : Is A priori estimates and the construction of the main operator

Let $r\ge 1$, recall that $E_1(\Omega _T):= L^1(0,T;W^{1,1}_0(\Omega ))$ and $V_0^{1,r}(\Omega _T)=L^{\infty }(0,T;L^1(\Omega ))\cap E_r(\Omega _T)$ and define the set

$$\begin{aligned} F_r(\Omega _T):=\bigg \{\varphi \in E_1(\Omega _T)\; ;\; \varphi \in E_r(\Omega _T)\cap L^{\infty }(0,T;L^1(\Omega )) \text{ with } ||\varphi ||_{V^{1,r}_0(\Omega _T)}\le M\bigg \}, \end{aligned}$$

where

$$\begin{aligned} ||\varphi ||_{V^{1,r}_0(\Omega _T)}:=\bigg (\int _0^T||\nabla \varphi ||_{L^{r}(\Omega )}^r\text {d}t\bigg )^{\frac{1}{r}}+||\varphi ||_{L^{\infty }(0,T;L^1(\Omega ))}, \end{aligned}$$

and M is a positive constant that will be chosen later. It is clear that $F_r(\Omega _T)$ is a closed convex subset of $E_1(\Omega _T)$.

By taking into consideration that $qm < \dfrac{(N+1)\overline{\sigma }}{N}=\dfrac{(N+1)(N+2)\sigma }{N(N+2-\sigma )}$, we can choose $r>1$ such that

$$\begin{aligned} \frac{qm\,N}{N+1} <r\le \overline{\sigma }. \end{aligned}$$

(3.6)

Now, let $\varphi \in F_r(\Omega _T)$, according to Proposition 2.1, we have $|\varphi |^{r\frac{N+1}{N}}\in L^1(\Omega _T)$. Moreover, $q<r\frac{N+1}{N}$, then $|\varphi |^{q}\in L^1(\Omega _T)$. Thus, we can define u to be the unique weak solution to the problem

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }llll} u_t-\Delta u &{} =&{} (\varphi _+)^q+ f &{}{} \text{ in } &{}{}\Omega _T, \\ u &{} =&{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u(x,0) &{}=&{} 0&{}{} \text{ in } &{}{}\Omega , \end{array} \right. \end{aligned}$$

and $u\in V^{1,s}_0(\Omega _T)$ for all $s<\frac{N+2}{N+1}$.

Furthermore, (3.6) implies that $qm<r\frac{N+1}{N}$. Therefore, $\varphi _+^q\in L^m(\Omega _T)$. Hence, applying the estimate (2.7) (Theorem 2.8) and Proposition 2.1 to obtain

$$\begin{aligned} ||\nabla u||_{L^{\overline{m}}(\Omega _T)}\le C\bigg (||\varphi ||^q_{L^{qm}(\Omega _T)}+||f||_{L^{m}(\Omega _T)}\bigg )\le C\bigg (||\varphi ||^q_{V^{1,r}_0(\Omega _T)}+||f||_{L^{m}(\Omega _T)}\bigg ),\nonumber \\ \end{aligned}$$

(3.7)

with $\overline{m}=\dfrac{(N+2)m}{N+2-m}$.

In addition, $p\le p\sigma <\overline{m}$, then $|\nabla u|^p\in L^\sigma (\Omega _T)\subset L^1(\Omega _T)$. Thus we can define v to be the unique weak solution to the problem

$$\begin{aligned} \left\{ \begin{array}{rclll} v_t-\Delta v &{} = &{} |\nabla u|^{p}+ g &{} \text { in } &{}\Omega _T,\\ v &{}=&{} 0 &{} \text { on } &{}\Gamma _T,\\ v(x,0)&{}=&{} 0&{} \text { in } &{}\Omega , \end{array} \right. \end{aligned}$$

and $v\in V^{1,s}_0(\Omega _T)$ for all $s<\frac{N+2}{N+1}$. Applying again estimate (2.7) (Proposition 2.8) gives

$$\begin{aligned} ||\nabla v||_{L^{\overline{\sigma }}(\Omega _T)}\le C\bigg (||\nabla u||^p_{L^{p\sigma }(\Omega _T)}+||g||_{L^{\sigma }(\Omega _T)}\bigg ), \end{aligned}$$

(3.8)

with $\overline{\sigma }=\frac{(N+2)\sigma }{N+2-\sigma }$. Since $p\sigma <\overline{m}=\dfrac{m(N+2)}{N+2-m}$, using (3.7), we get

$$\begin{aligned} \begin{array}{rcll} ||\nabla v||_{L^{\overline{\sigma }}(\Omega _{T})}\le C\Big [||\varphi ||_{L^{qm}(\Omega _{T})}^{pq} +||f||_{L^{m}(\Omega _{T})}^p+||g||_{L^{\sigma }(\Omega _T)}\Big ]. \end{array} \end{aligned}$$

(3.9)

Now, using the fact that $qm\le r\frac{N+1}{N}$ and $r\le \overline{\sigma }=\frac{\sigma (N+2)}{N+2-\sigma }$, then according to Proposition 2.1, we have

$$\begin{aligned} ||\nabla v||_{L^{r}(\Omega _T)}\le C\Big [||\varphi ||_{V^{1,r}_0(\Omega _T)}^{pq} +||f||_{L^{m}(\Omega _T)}^p+||g||_{L^{\sigma }(\Omega _T)}\Big ]. \end{aligned}$$

We estimate now $||v||_{L^\infty (0,T;L^1(\Omega ))}$. Using the estimate (2.5) (Theorem 2.7), estimate (3.7) and by Hölder’s inequality, we get

$$\begin{aligned} \begin{array}{rcll} ||v||_{L^\infty (0,T;L^1(\Omega ))}&{}\le &{} C\bigg \Vert |\nabla u|^p+ g \bigg \Vert _{L^{1}(\Omega _T)}=C(||\nabla u||_{L^{p}(\Omega _T)}^p+||g ||_{L^{1}(\Omega _T)})\\ \\ &{}\le &{} C\bigg (||\nabla u||_{L^{\overline{m}}(\Omega _T)}^p+||g ||_{L^{\sigma }(\Omega _T)}\bigg )\\ \\ &{}\le &{}C\bigg (||\varphi ||_{L^{qm}(\Omega _T)}^{pq}+||g ||_{L^{\sigma }(\Omega _T)}+||f||_{L^{m}(\Omega _T)}^p\bigg )\\ \\ &{} \le &{} C\Big [||\varphi ||_{V^{1,r}_0(\Omega _T)}^{pq} +||f||_{L^{m}(\Omega _T)}^p+||g||_{L^{\sigma }(\Omega _T)}\Big ]. \end{array} \end{aligned}$$

Thus, combining the above estimates leads to

$$\begin{aligned} ||v||_{V^{1,r}_0(\Omega _T)}\le C\Big [||\varphi ||_{V^{1,r}_0(\Omega _T)}^{pq}+||g ||_{L^{\sigma }(\Omega _T)}+||f||_{L^{m}(\Omega _T)}^p \Big ]. \end{aligned}$$

(3.10)

So, the operator

$$\begin{aligned} \begin{array}{rcll} L: F_r(\Omega _T) &{}\longmapsto &{} E_1(\Omega _T)\\ \varphi &{}\longmapsto &{} L(\varphi )=v, \end{array} \end{aligned}$$

is well defined. In addition, if v is a fixed point of L in $F_r(\Omega _T)$, then (u, v) solves System (3.1). Thus we just have to show that L has a fixed point in $F_r(\Omega _T)$.

$\bullet$ Second step: L is continuous and compact operator.

We begin by proving the continuity of L. Let $\{\varphi _n\}_n\subset F_r(\Omega _T), \varphi \in F_r(\Omega _T)$ such that $\varphi _n \rightarrow \varphi \text { strongly in } E_1(\Omega _T)$. Define $v_n:=L(\varphi _n)$ and $v:=L(\varphi )$. So $(u_n,v_n)$ and (u, v) satisfy

$$\begin{aligned} \left\{ \begin{array}{ccccc} \partial _t u_{n}-\Delta u_n &{}= &{} (\varphi _n^{+})^q +f &{} \text { in } &{}\Omega _T, \\ \partial _t u-\Delta u &{}= &{} (\varphi ^+)^q+ f &{} \text { in } &{}\Omega _T, \\ u_n= u&{}=&{} 0 &{} \text { on } &{}\Gamma _T,\\ \end{array} \right. \end{aligned}$$

(3.11)

and

$$\begin{aligned} \left\{ \begin{array}{ccccc} \partial _tv_{n}-\Delta v_n &{} = &{} |\nabla u_n|^{p}+ g &{} \text { in } &{}\Omega _T,\\ \partial _tv-\Delta v &{} = &{} |\nabla u|^{p}+g &{} \text { in } &{}\Omega _T,\\ v_n = v&{}=&{}0 &{} \text { on }&{}\Gamma _T. \end{array} \right. \end{aligned}$$

(3.12)

Since $\{\varphi _n\}_n\subset F_r(\Omega _T)$, then

$$\begin{aligned} ||\varphi _n||_{E_r(\Omega _T)}+||\varphi _n||_{L^{\infty }(0,T;L^1(\Omega ))}\le M. \end{aligned}$$

Taking into consideration that $\varphi _n \rightarrow \varphi \text { strongly in } E_1(\Omega _T)$, by Proposition 2.1 and using Vitali’s lemma we conclude that $\varphi _n \rightarrow \varphi \text { strongly in } L^\gamma (\Omega _T)$ for all $\gamma <r\frac{N+1}{N}$. Since $qm<r\frac{N+1}{N}$, then $\varphi _n \rightarrow \varphi \text { strongly in } L^{qm}(\Omega _T)$.

Going back to (3.11) and using estimate (2.7) (Theorem 2.8) to obtain for all $\mu \le \overline{m}$

$$\begin{aligned} ||\nabla u_n-\nabla u||_{L^{\mu }(\Omega _T)}\le C||(\varphi _n^+)^q-(\varphi ^+)^q||_{L^{m}(\Omega _T)}\rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

Now, thanks to Theorem 2.7$v_n \rightarrow v\text { strongly in } E_s(\Omega _T)$ for all $s<\dfrac{N+2}{N+1}$ which implies the continuity of L.

It remains to prove that L is compact. Let $\{\varphi _n\}_n\subset F_r(\Omega _T)$ be such that $||\varphi _n||_{V^{1,r}_0(\Omega _T)}\le C$. Define $v_n=L(\varphi _n)$. Since $\{\varphi _n\}_n\subset F_r(\Omega _T)$, it follows that

$$\begin{aligned} ||\varphi _n||_{E_r(\Omega _T)}+||\varphi _n||_{L^{\infty }(0,T;L^1(\Omega ))}\le M. \end{aligned}$$

Therefore, as in the proof of the continuity of L, it holds that the sequence $\{\varphi _n\}_n$ is bounded in $L^{qm+\varepsilon }(\Omega _T)$ for some $\varepsilon >0$. Define $h_n :=(\varphi _{n}^+)^q +f$, then $||h_n||_{L^1(\Omega _T)}\le C$ for all n. Thus, by the compactness result in Theorem 2.7, we obtain that, up to a subsequence, $u_n\rightarrow u$ strongly in $E_s(\Omega _T)$ for all $s<\frac{N+2}{N+1}$. Taking into consideration that $\{u_n\}_n$ is bounded in $E_{\mu }(\Omega _T)$ for all $\mu \le \overline{m}$ and by Vitali’s lemma, we conclude that $v_n \rightarrow v\text { strongly in } E_s(\Omega _T)$ for all $s<\dfrac{N+2}{N+1}$, in particular for $s=1$. Hence the result follows.

$\bullet$Third step : To finish our proof, we will choose M and $T^*$ such that $L(F_r(\Omega _{T^*}))\subset F_r(\Omega _{T^*})$.

For $s\ge 0$, we consider the concave function

$$\begin{aligned} \Upsilon (s):=s^{\frac{1}{pq}} -\widetilde{C}s, \end{aligned}$$

(3.13)

where $\widetilde{C}$ is a universal positive constant (depending only on data) that will specified later.

Using the fact that $pq>1$, then there exists $s_0>0$ such that $\Upsilon (s_0) =0$, $\Upsilon (s) >0$ for all $s\in (0,s_0)$, $\Upsilon (s) <0$ for all $s\in (s_0, +\infty )$. Thus, we get the existence of positive constants $\ell$ and $\Lambda ^*$ such that

$$\begin{aligned} \max _{s\ge 0}\Upsilon (s)=\Upsilon (\ell )=\Lambda ^*. \end{aligned}$$

Moreover,

$$\begin{aligned} \ell ^{\frac{1}{pq}}=\tilde{C}(\ell +\frac{\Lambda ^*}{\tilde{C}}). \end{aligned}$$

(3.14)

Let $\ell >0$ satisfying (3.14), then we can fix $T^*\le T$ such that

$$\begin{aligned} ||f||_{L^{m}(\Omega _{T^*})}^p+||g||_{L^{\sigma }(\Omega _{T^*})}\le \frac{\Lambda ^*}{\tilde{C}}. \end{aligned}$$

(3.15)

Setting $M=\ell ^{\frac{1}{pq}}$, then thanks to (3.14) and (3.15), we have

$$\begin{aligned} \tilde{C}\bigg (M^{pq}+||f||_{L^{m}(\Omega _{T^*})}^p+||g||_{L^{\sigma }(\Omega _{T^*})}\bigg )\le M. \end{aligned}$$

(3.16)

Now, from (3.10), we deduce that

$$\begin{aligned} ||v||_{V^{1,r}_0(\Omega _{T^*})}\le C\Big [M^{pq}+||g ||_{L^{\sigma }(\Omega _{T^*})}+||f||_{L^{m}(\Omega _{T^*})}^p \Big ]\le M. \end{aligned}$$

Hence $L(F_r(\Omega _{T^*}))\subset F_r(\Omega _{T^*})$.

Fourth step : Since L is a continuous compact operator with $L(F_r(\Omega _{T^*}))\subset F_r(\Omega _{T^*})$, using the Schauder fixed-point Theorem we get the existence of $v\in F_r(\Omega _{T^*})$ such that $L(v)=v$. By the maximum principle it holds that $u, v>0$. Thus, (u, v) solves system (3.1). $\square$

Remark 4

Notice that, if $m=\sigma =1$, assumptions $p<\frac{N+2}{N+1}$ and $q<\frac{N+2}{N}$ are optimal in the sense that if $p\ge \frac{N+2}{N+1}$ or $q\ge \frac{N+2}{N}$, we can show the existence of a suitable data $(f,g)\in L^1(\Omega _T)\times L^1(\Omega _T)$ such that system (3.1) has no local solution. Assume for example that $p\ge \frac{N+2}{N+1}$ and suppose by contradiction that system (3.1) has a local solution for all data $(f,g)\in L^1(\Omega _T)\times L^1(\Omega _T)$. It is clear that u is a supersolution to the problem

$$\begin{aligned} \left\{ \begin{array}{ccccc} w_t-\Delta w &{}{} = &{}{}f(x,t) &{}{} \text{ in } &{}{} \Omega _T , \\ w(x,t)&{}{}=&{}{}0 &{}{} \text{ on } &{}{}\Gamma _T,\\ w(x,0)&{}{}=&{}{}u_0(x) &{}{} \text{ in } &{}{}\Omega . \end{array} \right. \end{aligned}$$

(3.17)

Denoting w the unique local entropy solution to problem (3.17), then $w\le u$. Let us fix $f\in L^1(\Omega _T)$ such that if $\nu _0>\frac{N+2}{N}$, then $\int \int _{\Omega _T} w^{\nu _0}(x,t)\text {d}x\,\text {d}t=\infty$. (This follows by taking into consideration the optimality of the regularity result in Theorem 2.7, see also [14, 18, 44]).

Now, as $|\nabla u|^p\in L^1(\Omega _T)$, we deduce from Proposition 2.1 that

$$\begin{aligned} \displaystyle \int \int _{\Omega _T} u^{\nu }(x,t) \text {d}x\,\text {d}t \le C^\nu \Big (\displaystyle \int \int _{\Omega _T} |\nabla u(x,t)|^r \text {d}x\,\text {d}t\Big )\Big ( \text {ess}\sup \limits _{0\le t\le T}\displaystyle \int _{\Omega } u(x,t)\text {d}x\,\text {d}t\Big )^{\frac{r}{N}}<\infty \end{aligned}$$

with $\nu =p\frac{N+1}{N}$. Since $u\ge w$, then $\int \int _{\Omega _T} w^{\nu }(x,t) \text {d}x\,\text {d}t<\infty$. Hence, $\nu \le \nu _0<\frac{N+2}{N}$ and then $p<\frac{N+2}{N+1}$, a contradiction with the hypothesis. Hence we conclude.

In the case where $p=q=1$, we have the next existence result, which improves the existence result obtained in [8] for the elliptic case.

Theorem 3.2

Let $T>0$. Assume that $(f,g)\in L^1(\Omega _T)\times L^1(\Omega _T)$ with $f,g\gneqq 0$ in $\Omega _T$. Then the following system

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t-\Delta u &{}=&{} v+f &{} ~\text {in } &{}\Omega _T, \\ v_t-\Delta v &{}=&{} |\nabla u|+g &{}\text { in } &{} \Omega _T, \\ u=v&{}=&{} 0 &{} \text { on } &{} \Gamma _T,\\ u(x,0)&{}=&{}0 &{}\text { in } &{} \Omega , \\ v(x,0)&{}=&{}0 &{}\text { in } &{} \Omega ,\\ u,v &{}\ge &{} 0 &{} \text { in } &{} \Omega _T \end{array} \right. \end{aligned}$$

(3.18)

has a solution $(u,v)\in (V^{1,\theta }_0(\Omega _T))^2$ for all $\theta <\frac{N+2}{N+1}$.

Proof

Notice that, in this case we lose the concavity of the real function defined in (3.13). Therefore, we proceed by approximation. By [39], we get the existence of a sequence $\{(u_n,v_n)\}_n\subset (V^{1,\theta }_0(\Omega _T))^2$, for all $\theta <\frac{N+2}{N+1}$ such that $(u_n,v_n)$ solves the system

$$\begin{aligned} \left\{ \begin{array}{lllll} \partial _t{u_n}-\Delta u_n &{}=&{} \dfrac{v_n}{1+\frac{1}{n}v_n}+\dfrac{f}{1+\frac{1}{n}f} &{} \text { in } &{}\Omega _T, \\ \partial _t{v_n}-\Delta v_n &{}=&{} \dfrac{|\nabla u_n|}{1+\frac{1}{n} |\nabla u_n|}+\dfrac{g}{1+\frac{1}{n}g} &{}\text { in } &{} \Omega _T, \\ u_n=v_n&{}=&{} 0 &{} \text { on } &{} \Gamma _T,\\ u_n(x,0)&{}=&{}v_n(x,0)=0 &{}\text { in } &{} \Omega , \\ u_n,v_n &{}\ge &{} 0 &{} \text { in } &{} \Omega _T. \end{array} \right. \end{aligned}$$

(3.19)

For $s\ge 0$, we consider the function $k(s)=1-\dfrac{1}{(1+s)^a}$ with $a>0$. Let $\widehat{K}(s)=\displaystyle \int _0^sk(\tau ) d\tau$, then $\widehat{K}(s)\ge C_1 s-C_2$ for all $s\ge 0$.

Using $k(v_n)$ as a test function in the equation of $v_n$, it follows that

$$\begin{aligned} \int \limits _\Omega \widehat{K}(v_n)(x,t) \text{ d }x +a\int _0^{t}\int \limits _\Omega \dfrac{|\nabla v_n|^2}{(1+v_n)^{1+a}}\text{ d }x\,\text{ d }\tau \le \int _0^t\int \limits _\Omega |\nabla u_n|\text{ d }x\, \text{ d }\tau +\int _0^t\int \limits _\Omega g\,\text{ d }x\,\text{ d }\tau .\nonumber \\ \end{aligned}$$

(3.20)

Thanks to Theorem 2.7, we have for all $r<\frac{N+2}{N+1}$ and for all $t\le T$,

$$\begin{aligned} \bigg (\int _0^t\int \limits _\Omega |\nabla u_n|^r \text{ d }x\,\text{ d }\tau \bigg )^{\frac{1}{r}}\le C\bigg (\int _0^t\int \limits _\Omega v_n \text{ d }x\,\text{ d }\tau +\int _0^t\int \limits _\Omega f \text{ d }x\,\text{ d }\tau \bigg ). \end{aligned}$$

Thus, for $r=1$, we get

$$\begin{aligned} \int _0^t\int \limits _\Omega |\nabla u_n| \text {d}x\,\text {d}\tau \le C\bigg (\int _0^t\int \limits _\Omega v_n \,\text {d}x\,\text {d}\tau +||f||_{L^1(\Omega _T)}\bigg ). \end{aligned}$$

Going back to (3.20), we obtain

$$\begin{aligned} \int \limits _\Omega \widehat{K}(v_n)(x,t) \text {d}x\le \bigg (\int _0^t\int \limits _\Omega v_n \text {d}x\,\text {d}\tau +||f||_{L^1(\Omega _T)}+||g||_{L^1(\Omega _T)}\bigg ). \end{aligned}$$

Recall that $\widehat{K}(v_n)\ge C_1 v_n-C_2$, then using Gronwall’s Lemma we conclude that

$$\begin{aligned} ||v_n||_{L^1(\Omega _T)}\le C\equiv C(\Omega _T,||f||_{L^1(\Omega _T)},||g||_{L^1(\Omega _T)}). \end{aligned}$$

Thus, by Theorem 2.7 , we have for all $s_1, s_2<\frac{N+2}{N+1}$,

$$\begin{aligned}&||u_n||_{\mathcal {C}(0,T; L^1(\Omega ))}+||u_n||_{E_{s_1}(\Omega _T)}\le C,\\&||v_n||_{\mathcal {C}(0,T; L^1(\Omega ))}+||v_n||_{E_{s_2}(\Omega _T)}\le C. \end{aligned}$$

Hence the existence result follows using the compactness result in Theorem 2.7. $\square$

3.2 The Case $(f,g)=(0,0)$ and $(u_0,v_0)\ne (0,0)$

In this subsection, we suppose that $f\equiv g\equiv 0$ and $(u_0, v_0)\in L^{m_1}(\Omega )\times L^{\sigma _1}(\Omega )$ where $m_1, \sigma _1\ge 1$. Then, the system (1.1) is reduced to the following one:

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t-\Delta u &{}=&{} v^q &{} \text {in } &{} \Omega _T, \\ v_ t-\Delta v &{}=&{}|\nabla u|^{p} &{}\text {in } &{}\Omega _T, \\ u=v&{}=&{}0 &{} \text {on } &{} \Gamma _T,\\ u(x,0)&{}=&{}u_0(x) &{}\text {in } &{}\Omega , \\ v(x,0)&{}=&{}v_0(x) &{}\text {in } &{}\Omega , \\ u,v &{}\ge &{} 0 &{} \text {in } &{} \Omega _T. \end{array} \right. \end{aligned}$$

(3.21)

The main existence result in this case is the following.

Theorem 3.3

Assume that $(u_0,v_0) \in L^{m_1}(\Omega )\times L^{\sigma _1}(\Omega )$, where $m_1,\sigma _1\ge 1$. Let $p, q> 1$ be such that

$$\begin{aligned} \left\{ \begin{array}{rcll} q &{}<&{}\sigma _1(\dfrac{2}{N}+\dfrac{1}{m_1}), \\ \\ p &{}<&{} \dfrac{m_1(N+\sigma _1+1)}{\sigma _1(N+m_1)}. \end{array} \right. \end{aligned}$$

(3.22)

Then, for all $T>0$, there exists a positive constant $\mathrm {S}$ depending only on T and the data such that if

$$\begin{aligned} ||u_0||_{L^{m_1}(\Omega )}+||v_0||_{L^{\sigma _1}(\Omega )}\le \mathrm {S}, \end{aligned}$$

System (3.21) has a nonnegative solution (u, v) such that $(u,v)\in V^{1,\alpha }_0(\Omega _T)\times V^{1,\beta }_0(\Omega _T)$ for all $\alpha <\dfrac{m_1(N+2)}{N+m_1}$ and for all $\beta <\dfrac{\sigma _1(N+2)}{N+1}$.

Remark 5

The upper bound for q obtained in the previous Theorem is the same as in the case of nonlinear system with potential nonlinearities. We refer to [32] and [44, Theorem 32.1], for more details about this class of systems.

Proof of Theorem 3.3

To prove the main existence result, we will take advantage of the argument used in the proof of Theorem 3.1 obtained in the first part of the paper. Using a suitable change of variable, we will show a relationship between the system (3.21) and the system (3.1) with suitable data $(f_1,g_1)$. $\square$

Let $\psi$ and $\eta$ to be the unique solutions to the following problems:

$$\begin{aligned} \left\{ \begin{array}{lllll} \psi _t - \Delta \psi &{}=&{}0 &{} \text {in } &{} \Omega _T, \\ \psi (x,t) &{}=&{} 0 &{} \text {on } &{} \Gamma _T,\\ \psi (x,0)&{}=&{}u_0(x)&{}\text {in } &{} \Omega , \\ \end{array} \right. \text { and } \left\{ \begin{array}{lllll} \eta _t - \Delta \eta =0 &{} \text {in } &{} \Omega _T, \\ \eta (x,t) = 0 &{} \text {on } &{} \Gamma _T,\\ \eta (x,0)=v_0(x) &{}\text {in } &{} \Omega . \\ \end{array} \right. \end{aligned}$$

Thanks to Theorem 2.8, we have

$$\begin{aligned} \eta \in L^{\gamma }(\Omega _T) \text{ for } \text{ all } \gamma<\bigg (\frac{2}{N}+ 1\bigg )\sigma _1 \text{ and } \;\; |\nabla \psi |\in L^{s}(\Omega _T) \text{ for } \text{ all } s<\frac{(N+2)m_1}{N+m_1}.\nonumber \\ \end{aligned}$$

(3.23)

Notice that, if (u, v) solves System (3.21), then $\psi \le u$ and $\eta \le v$.

We set $u_1= u-\psi$ and $v_1= v-\eta$, then $(u_1,v_1)$ solves

$$\begin{aligned} \left\{ \begin{array}{lllll} \partial _t u_{1}-\Delta u_1 &{}=&{} (v_1+\eta )^q &{}{} \text{ in } &{}{} \Omega _T, \\ \partial _tv_{1}-\Delta v_1 &{}=&{} |\nabla u_1+\nabla \psi |^{p} &{}{}\text{ in } &{}{} \Omega _T, \\ u_1=v_1&{}=&{}0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u_1(x,0)&{}=&{} 0\,\,&{}{} \text{ in } &{}{}\Omega , \\ v_1(x,0)&{}=&{} 0 &{}{} \text{ in } &{}{}\Omega . \end{array} \right. \end{aligned}$$

(3.24)

Hence, to show the main existence result, we have just to show that system (3.24) has a non-negative solution.

As above, we fix $1<r<\frac{(N+2)\sigma _1}{N+\sigma _1}$ very close to $\frac{(N+2)\sigma _1}{N+\sigma _1}$, then we consider the set

$$\begin{aligned} F_r(\Omega _T):=\bigg \{\varphi \in E_1(\Omega _T)\; ;\; \varphi \in E_r(\Omega _T)\cap L^{\infty }(0,T;L^1(\Omega )) \text{ with } ||\varphi ||_{V^{1,r}_0(\Omega _T)}\le \ell ^{\frac{1}{pq}}\bigg \}, \end{aligned}$$

where

$$\begin{aligned} ||\varphi ||_{V^{1,r}_0(\Omega _T)}:=\bigg (\int _0^T||\nabla \varphi ||_{L^{r}(\Omega )}^r\text {d}t\bigg )^{\frac{1}{r}}+||\varphi ||_{L^{\infty }(0,T;L^1(\Omega ))}. \end{aligned}$$

We define now the operator $L: F_r(\Omega _T)\longrightarrow E_1(\Omega _T)$ by setting $L(\varphi )=v_1$, where $v_1$ is the unique solution to problem

$$\begin{aligned} \left\{ \begin{array}{lllll} \partial _tv_{1}-\Delta v_1 = |\nabla u_1+\nabla \psi |^{p} &{} \text { in } &{} \Omega _T,\\ v_1 = 0 &{} \text { on } &{} \Gamma _T,\\ v_1(x,0)= 0&{} \text { in } &{} \Omega \end{array} \right. \end{aligned}$$

with $u_1$ being the unique solution to the problem

$$\begin{aligned} \left\{ \begin{array}{rcll} \partial _tu_{1}-\Delta u_1 &{}= &{} (\eta +\varphi ^+)^q&{} \text { in }\Omega _T, \\ u_1&{}=&{} 0 &{} \text { on }\Gamma _T.\\ u_1(x,0)&{}=&{} 0&{} \text { in }\Omega \end{array} \right. \end{aligned}$$

It is clear that if $v_1$ is a fixed point of L in $F_r(\Omega _T)$, then $(u_1,v_1)$ solves System (3.24).

Notice that, for a universal constant $C>0$, we have

$$\begin{aligned} (\eta +\varphi _+)^q\simeq C (\varphi _+^q+\eta ^q), \end{aligned}$$

and

$$\begin{aligned} |\nabla u_1+\nabla \psi |^{p}\le C(|\nabla u_1|^{p}+|\nabla \psi |^{p}). \end{aligned}$$

We set $f_1=C\eta ^q$ and $g_1= C|\nabla \psi |^{p}$. Then thanks to the regularity of $(u_0,v_0)$ and by (3.23), we conclude that $f_1\in L^{{m}}(\Omega _T)$ for all ${m}<(\frac{2}{N}+ 1)\frac{\sigma _1}{q}$ and $g_1\in L^{{\sigma }}(\Omega _T)$ for all ${\sigma }<\frac{(N+2)m_1}{p(N+m_1)}$.

Since (3.22) holds, then by a direct computations, we verify that $(m,\sigma )$ satisfies condition (3.2).

Thus, Theorem 3.1 implies that system (3.24) has a solution $(u_1,v_1)\in V^{1,\theta _1}_0(\Omega )\times V^{1,\theta _2}_0(\Omega )$ for all $\theta _1<\frac{m(N+2)}{N+2-m}$ and $\theta _2<\frac{(N+2)\sigma }{N+2-\sigma }$.

Recall that $u=u_1+\psi$, thus $|\nabla u|\in L^\theta (\Omega _T)$ with $\theta =\min \{\theta _1, \frac{m_1(N+2)}{N+m_1}\}.$ Since m can be chosen very close to $(\frac{2}{N}+ 1)\frac{\sigma _1}{q}$, it holds that

$$\begin{aligned} \theta _1\simeq \dfrac{m(N+2)}{N+2-m}\simeq \dfrac{\sigma _1(N+2)}{Nq-\sigma _1}, \end{aligned}$$

which means that for all $\varepsilon >0$, we have

$$\begin{aligned} \theta _1<\dfrac{\sigma _1(N+2)}{Nq-\sigma _1}<\theta _1+\varepsilon . \end{aligned}$$

Now using the fact that $q<\sigma _1(\dfrac{2}{N}+\dfrac{1}{m_1})$ to conclude that $\theta _1>\frac{m_1(N+2)}{N+m_1}$. Thus $\theta \simeq \frac{m_1(N+2)}{N+m_1}$.

In the same way, we obtain that $|\nabla v|\in L^r(\Omega _T)$ for all $r\simeq \frac{\sigma _1(N+2)}{N+1}$.

To finish, we have just to show, in this case, that the smallness condition (3.15) can be imposed on $||u_0||_{L^{m_1}(\Omega )}$ and $||v_0||_{L^{\sigma _1}(\Omega )}$. Recall that from (3.15), we need that

$$\begin{aligned} ||f_1||_{L^{m}(\Omega _{T})}^p+||g_1||_{L^{\sigma }(\Omega _{T})}\le \frac{\Lambda ^*}{\tilde{C}}. \end{aligned}$$

(3.25)

Since $f_1=C\eta ^q$ and $g_1= C|\nabla \psi |^{p}$, using estimates (2.10) and (2.11) (Theorem 2.8) yields to

$$\begin{aligned} ||f_1||_{L^{m}(\Omega _{T})}^p=C||\eta ||^{pq}_{L^{qm}(\Omega _{T})}\le \tilde{C}||v_0||^{pq}_{L^{\sigma _1}(\Omega )}\bigg (\int _0^T t^{-qm\frac{N}{2}(\frac{1}{\sigma _1}-\frac{1}{qm})}\text {d}t\bigg )^{\frac{p}{m}}, \end{aligned}$$

where $\tilde{C}$ depends only on $p,q,m_1,\sigma _1$ and $|\Omega |$. Since $qm<\sigma _1(\frac{2}{N}+ 1)$, then $qm\frac{N}{2}(\frac{1}{\sigma _1}-\frac{1}{qm})<1$. Thus,

$$\begin{aligned} ||f_1||_{L^{m}(\Omega _{T})}^p\le \tilde{C}||v_0||^{pq}_{L^{\sigma _1}(\Omega )}T^{\frac{p}{m}(1-qm\frac{N}{2}(\frac{1}{\sigma _1}-\frac{1}{qm}))}. \end{aligned}$$

In the same way, we obtain

$$\begin{aligned} ||g_1||_{L^{\sigma }(\Omega _{T})}=\tilde{C}\bigg (\int _0^T\int \limits _\Omega |\nabla \psi |^{p\sigma } \text {d}x\,\text {d}t\bigg )^{\frac{1}{\sigma }}\le \tilde{C}||u_0||^p_{L^{m_1}(\Omega )}T^{ \frac{1}{\sigma }(1-p\sigma \frac{N}{2}(\frac{1}{m_1}-\frac{1}{p\sigma }))}, \end{aligned}$$

which follows using the fact that ${p\sigma }<\frac{(N+2)m_1}{N+m_1}$. Combining the above estimates, it hods that

$$\begin{aligned}&||f_1||_{L^{m}(\Omega _{T})}^p+||g_1||_{L^{\sigma }(\Omega _{T})}\\&\quad \le \tilde{C}\bigg (||v_0||^{pq}_{L^{\sigma _1}(\Omega )}T^{\frac{p}{m}(1-qm\frac{N}{2}(\frac{1}{\sigma _1}-\frac{1}{qm}))}+ ||u_0||^p_{L^{m_1}(\Omega )}T^{ \frac{1}{\sigma }(1-p\sigma \frac{N}{2}(\frac{1}{m_1}-\frac{1}{p\sigma }))}\bigg ). \end{aligned}$$

Hence, for T fixed, we can choose $\mathrm {S}>0$ such that if

$$\begin{aligned} ||u_0||_{L^{m_1}(\Omega )}+||v_0||_{L^{\sigma _1}(\Omega )}\le \mathrm {S}, \end{aligned}$$

then

$$\begin{aligned} ||f_1||_{L^{m}(\Omega _{T})}^p+||g_1||_{L^{\sigma }(\Omega _{T})}\le \frac{\Lambda ^*}{\tilde{C}}, \end{aligned}$$

given in (3.25). Thus, we conclude. $\square$

Remark 6

As in Remark 4, if $m_1=\sigma _1=1$, we deduce from (3.2) that $p<\frac{N+2}{N+1}$ and $q<\frac{N+2}{N}$, the natural entropy regularity for the potential and the gradient term respectively when dealing with $L^1$ data.

3.3 Blow-Up Result

In this subsection, we analyze the question of blow-up in the time of the solution to system (3.21) in a suitable norm.

In the potential case, the blow up is based on a suitable convexity argument and Jensen inequality. In our case, and to get a control of the gradient term, we need to use a specifically weighted Hardy-type inequality. More precisely we have the next universal inequality proved in [45, Theorem 1.6].

Theorem 3.4

Assume that $\Omega \subset \mathbb {R}^N$, $N \ge 2$, be a bounded regular domain. Let $a>1$ and suppose that $0<\sigma <a-1$. Setting $d(x):=\text {dist}(x,\partial \Omega )$, then there exists a positive constant $C(\Omega ,a,\sigma )$ such that for all $v \in \mathcal {C}^\infty _0(\Omega )$, we have

$$\begin{aligned} \int _{\Omega } d^{\sigma -a}(x)|v(x)|^a \text {d}x \le C \int _{\Omega } d^{\sigma }(x)|\nabla v(x)|^a \text {d}x\,. \end{aligned}$$

(3.26)

Notice that the above result is not valid in general if $\sigma \ge a-1$. As a consequence we get the next blow-up result.

Theorem 3.5

Let $\lambda _1$ the fist eigenvalue of the Laplacian operator with Dirichlet condition and denote $\varphi _1$, the associated positive eigenfunction normalized in $L^1(\Omega )$. Suppose that $q>1$ and $p>2$, then there exists a positive constant $C(p,q,\Omega )$ such that if

$$\begin{aligned} \int \limits _\Omega (u^p_0+v^q_0)\varphi _1 \text {d}x >C(p,q,\Omega ), \end{aligned}$$

then any solution to system (3.1) blow up in a finite time in the sense that, for some $T^*(p,q,\Omega )<\infty$, we have

$$\begin{aligned} \lim \limits _{t\rightarrow T^*}\int \limits _\Omega (u^p(x,t)+v^q(x,t))\varphi _1(x) \text {d}x=\infty . \end{aligned}$$

Proof

Using $\varphi _1$ as a test function in booth equations of u, v, it holds that

$$\begin{aligned} \frac{d}{\text {d}t}\int \limits _\Omega u(x,t)\varphi _1(x) \text {d}x+\lambda _1\int \limits _\Omega u(x,t)\varphi _1(x) \text {d}x\ge \int \limits _\Omega v^q(x,t)\varphi _1(x) \text {d}x,\qquad \end{aligned}$$

(3.27)

and

$$\begin{aligned} \frac{d}{\text {d}t}\int \limits _\Omega v(x,t)\varphi _1(x) \text {d}x+\lambda _1\int \limits _\Omega v(x,t)\varphi _1(x) \text {d}x\ge \int \limits _\Omega |\nabla u(x,t)|^p\varphi _1(x) \text {d}x.\qquad \end{aligned}$$

(3.28)

By Jensen inequality we conclude that

$$\begin{aligned} \frac{d}{\text {d}t}\int \limits _\Omega u(x,t)\varphi _1(x) \text {d}x+\lambda _1\int \limits _\Omega u(x,t)\varphi _1(x) \text {d}x\ge \bigg (\int \limits _\Omega v(x,t)\varphi _1(x) \text {d}x\bigg )^q. \end{aligned}$$

Since $\varphi _1\backsimeq \text {dist}(x,\partial \Omega )$, then

$$\begin{aligned} \int \limits _\Omega |\nabla u(x,t)|^p\varphi _1(x) \text {d}x\ge C\int \limits _\Omega |\nabla u(x,t)|^p\text {dist}(x,\partial \Omega ) \text {d}x. \end{aligned}$$

Recall that $p>2$, using the weighted Hardy inequality in Theorem 3.4 and by Jensen inequality, there results that

$$\begin{aligned} \int \limits _\Omega |\nabla u(x,t)|^p\text {dist}(x,\partial \Omega ) \text {d}x\ge & {} C(\Omega ) \int \limits _\Omega u^p(\text {dist}(x,\partial \Omega ))^{1-p}\text {d}x\ge C \int \limits _\Omega u^p(x,t)\varphi _1(x) \text {d}x\\\ge & {} C\bigg (\int \limits _\Omega u(x,t)\varphi _1(x) \text {d}x\bigg )^p. \end{aligned}$$

Denoting by $Y(t)=\int \limits _\Omega u(x,t)\varphi _1(x) \text {d}x$ and $Z(t)=\int \limits _\Omega v(x,t)\varphi _1(x) \text {d}x$, it holds that

$$\begin{aligned} \left\{ \begin{array}{ccccc} Y'(t)+\lambda _1 Y(t) &{}\ge &{} C Z^q(t),\\ Z'(t)+\lambda _1 Z(t) &{}\ge &{} C Y^p(t). \end{array} \right. \end{aligned}$$

Setting $l=\min \{p,q\}>1$, we get

$$\begin{aligned} (Y+Z)'(t)+\lambda _1(Y+Z)(t)\ge C(Z^q(t)+Y^p(t))\ge C(Y(t)+Z(t))^l-C(Y(t)+Z(t)). \end{aligned}$$

Denoting by $W(t)=Y(t)+Z(t)$, then

$$\begin{aligned} W'(t)+C W(t)\ge W^l(t). \end{aligned}$$

Since $l>1$, then we get the existence of positive constant $C_0$ such that if $W(0)>C_0$, then there exists $T^*>0$, depending only on the data, such that

$$\begin{aligned} \lim \limits _{t\rightarrow T^*}W(t)=\infty . \end{aligned}$$

Hence we conclude. $\square$

Remark 7

• (1) The above argument is based on a suitable Hardy (or Poincaré) type inequality. In the case where $p\in (1,2)$, inequality like (3.26) does not holds in general and another approach is needed to treat this case.

• (2) Notice that from [1], we know that the associate elliptic system has a solution. Hence, we hope that, under suitable conditions of the initial data, existence of a global solution holds. However, the main difficulty is to get a suitable comparison principle (to use monotony arguments). In the case of single equation with gradient term, the comparison principle was proved in [3] under natural condition on the exponent of the gradient and following the ideas of [5]. The argument in [3] does not work for system and it seems to be very interesting to find another way to prove the associate comparison principle.

4 Some Extensions

Following closely the arguments developed in the previous section, we shall also treat the following nonlinear system, where the gradient terms $|\nabla u|^{p}$ and $|\nabla v|^q$ act as a source term.

4.1 First Model

Let us consider the system

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t - \Delta u &{} = &{} |\nabla v|^q+f &{}{} \text{ in } &{}{}\Omega _T, \\ v_ t- \Delta v &{} = &{} |\nabla u|^{p}+g &{}{} \text{ in } &{}{}\Omega _T, \\ u=v &{}=&{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u(x,0)&{}= &{} 0 &{}{} \text{ in } &{}{}\Omega , \\ v(x,0) &{}= &{} 0 &{}{} \text{ in } &{}{}\Omega , \\ u,v &{}\ge &{} 0 &{}{} \text{ in } &{}{}\Omega _T \end{array} \right. \end{aligned}$$

(4.1)

where $(f,g) \in L^{m}(\Omega _T)\times L^{\sigma }(\Omega _T)$.

Notice that the case where $f=g=0$ with non-trivial initial conditions and $p,q\le 2$ was treated in [6]. In that paper, the authors showed the existence of global solutions of the associated Cauchy problem under additional assumptions on $p,\ q$ and the initial data.

Without the condition $p,q\le 2$, and under some natural conditions on f and g, we are able to prove the next existence result.

Theorem 4.1

Suppose that $m, \sigma \in [1, N+2)$ and let p, q be such that

$$\begin{aligned} \left\{ \begin{array}{rcll} p\sigma &{}< &{}\overline{m}=\dfrac{m (N+2)}{N+2-m},\\ \\ qm &{}<&{} \overline{\sigma }=\dfrac{\sigma (N+2)}{N+2-\sigma }. \end{array} \right. \end{aligned}$$

(4.2)

Then there exists $T^*\le T$ such that system (4.1) has a nonnegative solution $(u,v)\in V^{1,\alpha }_0(\Omega _{T^*})\times V^{1,\beta }_0(\Omega _{T^*})$ for all $\alpha <\overline{m}$ and $\beta <\overline{\sigma }$.

Proof

The proof follows closely the arguments of Sect. 3, and uses the same fixed-point arguments. However, for the reader’s convenience we include here some details.

According to (4.2), let us fix $r>1$ such that $\frac{qm\,N}{N+1}<r<\overline{\sigma }$ and define the set

$$\begin{aligned}&F_r(\Omega _T)\\&\quad :=\bigg \{\varphi \in E_1(\Omega _T)\; ;\; \varphi \in E_r(\Omega _T)\cap L^{\infty }(0,T;L^1(\Omega )) \text{ with } ||\varphi ||_{V^{1,r}_0(\Omega _T)}\le \ell ^{\frac{1}{pq}}\bigg \} \end{aligned}$$

Then $F_r(\Omega _T)$ is a closed convex subset of $E_1(\Omega _T)$.

Now, define the operator

$$\begin{aligned} \begin{array}{rcll} L: F_r(\Omega _T) &{}\longmapsto &{} E_1(\Omega _T)\\ \varphi &{}\longmapsto &{} L(\varphi )=v \end{array} \end{aligned}$$

where v is the unique solution to problem

$$\begin{aligned} \left\{ \begin{array}{lllll} v_t-\Delta v &{}=&{} |\nabla u|^{p}+ g &{}{} \text{ in } &{}{}\Omega _T,\\ v &{} = &{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ v(x,0) &{}= &{} 0&{}{} \text{ in } &{}{}\Omega \end{array} \right. \end{aligned}$$

with u being the unique solution of the problem

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t-\Delta u &{} =&{} |\nabla \varphi |^q+ f &{}{} \text{ in } &{}{}\Omega _T, \\ u &{}=&{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u(x,0) &{}=&{} 0&{}{} \text{ in } &{}{}\Omega . \end{array} \right. \end{aligned}$$

It is clear that if v is a fixed point of L in $F_r(\Omega _T)$, then (u, v) solves the system (4.1).

Since $qm<r$, then $|\nabla \varphi |^q\in L^1(\Omega _T)$. Thus u is well defined and $u\in V^{1,\alpha }_0(\Omega _T)$ for all $\alpha <\dfrac{N+2}{N+1}$. By Theorem 2.8, we get

$$\begin{aligned} ||\nabla u||_{L^{\overline{m}}(\Omega _T)}\le C\bigg \Vert |\nabla \varphi |^q+ f \bigg \Vert _{L^{m}(\Omega _T)}\le C\bigg (||\nabla \varphi ||^q_{L^{qm}(\Omega _T)}+||f ||_{L^{m}(\Omega _T)}\bigg ),\nonumber \\ \end{aligned}$$

(4.3)

Now, since $p\le \overline{m}$ then $|\nabla u|^p +g\in L^1(\Omega _T)$. Thus v is well defined and, at least $v\in V^{1,\alpha }_0(\Omega _T)$ for all $\alpha <\dfrac{N+2}{N+1}$. Thus, L is well defined. In the same way, it holds that

$$\begin{aligned} ||\nabla v||_{L^{\overline{\sigma }}(\Omega _T)}\le C\Big [||\nabla u||^p_{L^{p\sigma }(\Omega _T)}+||g||_{L^{\sigma }(\Omega _T)}\Big ], \end{aligned}$$

(4.4)

with $\overline{\sigma }=\dfrac{\sigma (N+2)}{N+2-\sigma }$. Since $p\sigma <\overline{m}$, and using inequality (4.3), we obtain

$$\begin{aligned} \begin{array}{rcll} ||\nabla v||_{L^{\overline{\sigma }}(\Omega _T)}\le & {} C\Big [||\nabla \varphi ||_{L^{qm}(\Omega _T)}^{pq} +||f||_{L^{m}(\Omega _T)}^p+||g||_{L^{\sigma }(\Omega _T)}\Big ]. \end{array} \end{aligned}$$

Since $qm<r<\overline{\sigma }$, using Hölder’s inequality and Proposition 2.1 we obtain

$$\begin{aligned} ||\nabla v||_{L^{r}(\Omega _T)}\le C\Big [||\varphi ||_{V^{1,r}_0(\Omega _T)}^{pq} +||f||_{L^{m}(\Omega _T)}^p+||g||_{L^{\sigma }(\Omega _T)}\Big ]. \end{aligned}$$

Now, by Theorem 2.7, we reach that

$$\begin{aligned} ||v||_{L^\infty (0,T;L^1(\Omega ))}\le C\Big [||\varphi ||_{V^{1,r}_0(\Omega _T)}^{pq}+||g ||_{L^{\sigma }(\Omega _T)}+||f||_{L^{m}(\Omega _T)}^p \Big ]. \end{aligned}$$

Thus,

$$\begin{aligned} ||v||_{V^{1,r}_0(\Omega _T)}\le C\Big [||\varphi ||_{V^{1,r}_0(\Omega _T)}^{pq} +||f||_{L^{m}(\Omega _T)}^p+||g||_{L^{\sigma }(\Omega _T)}\Big ]. \end{aligned}$$

It is clear that the above estimate holds in $\Omega _{T^*}$ for all $T^*\le T$. Hence, by choosing $T^*<T$ such that

$$\begin{aligned} C\Big [\ell +||f||_{L^{m}(\Omega _{T^*})}^p+||g||_{L^{\sigma }(\Omega _{T^*})}\Big ]\le \ell ^{\frac{1}{pq}}, \end{aligned}$$

we have $L(F_r(\Omega _{T^*}))\subset F_r(\Omega _{T^*})$.

Now the continuity and the compactness property of L follow as in the proof of Theorem 3.1. Hence, we conclude. $\square$

4.2 Second Model

We deal now with the system

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t - \Delta u &{}=&{} |\nabla v|^q &{}{} \text{ in } &{}{}\Omega _T, \\ v_ t- \Delta v &{}=&{} |\nabla u|^{p} &{}{} \text{ in } &{}{}\Omega _T, \\ u=v&{}=&{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u(x,0)&{}=&{} u_0(x) &{}{} \text{ in } &{}{}\Omega , \\ v(x,0) &{}= &{} v_0(x) &{}{} \text{ in } &{}{}\Omega , \\ u,v &{}\ge &{} 0 &{}{} \text{ in } &{}{}\Omega _T, \end{array} \right. \end{aligned}$$

(4.5)

where $(u_0,v_0) \in L^{m_1}(\Omega _T)\times L^{\sigma _1}(\Omega _T)$. We have the next existence result.

Theorem 4.2

Assume that $(u_0,v_0) \in L^{m_1}(\Omega )\times L^{\sigma _1}(\Omega )$ where $m_1,\sigma _1\ge 1$. Let $p, q> 1$ be such that

$$\begin{aligned} \left\{ \begin{array}{llll} q<\dfrac{\sigma _1(N+2m_1)}{m_1(N+\sigma _1)}, \\ \\ p < \dfrac{m_1(N+2\sigma _1)}{\sigma _1(N+m_1)}. \end{array} \right. \end{aligned}$$

(4.6)

Then for all $T>0$, there exists a positive constant $\mathrm {S}$ depending on T and the data such that if

$$\begin{aligned} ||u_0||_{L^{m_1}(\Omega )}+||v_0||_{L^{\sigma _1}(\Omega )}\le \mathrm {S}, \end{aligned}$$

System (4.5) has a nonnegative solution (u, v) such that $(u,v)\in V^{1,\alpha }_0(\Omega _T)\times V^{1,\beta }_0(\Omega _T)$ for all $\alpha <\dfrac{m_1(N+2)}{N+m_1}$ and for all $\beta <\dfrac{\sigma _1(N+2)}{N+\sigma _1}$.

Proof

We follow closely the change of variables used in the proof of Theorem 3.3. Let $\psi$ and $\eta$ to be the unique solutions to the following problems:

$$\begin{aligned} \left\{ \begin{array}{lllll} \psi _t - \Delta \psi &{}=&{}0 &{} \text {in } &{} \Omega _T, \\ \psi (x,t) &{}=&{} 0 &{} \text {on } &{} \Gamma _T,\\ \psi (x,0)&{}=&{}u_0(x)&{}\text {in } &{} \Omega , \\ \end{array} \right. \text { and } \left\{ \begin{array}{lllll} \eta _t - \Delta \eta &{}=&{}0 &{} \text {in } &{} \Omega _T, \\ \eta (x,t) &{}=&{} 0 &{} \text {on } &{} \Gamma _T,\\ \eta (x,0)&{}=&{}v_0(x) &{}\text {in } &{} \Omega . \\ \end{array} \right. \end{aligned}$$

Thanks to Theorem 2.8, we have

$$\begin{aligned} |\nabla \eta |\in L^{\gamma }(\Omega _T) \text{ for } \text{ all } \gamma<\frac{(N+2)\sigma _1}{N+\sigma _1} \text{ and } \;\; |\nabla \psi |\in L^{s}(\Omega _T) \text{ for } \text{ all } s<\frac{(N+2)m_1}{N+m_1}.\nonumber \\ \end{aligned}$$

(4.7)

We set $u_1= u-\psi$ and $v_1= v-\eta$, then $(u_1,v_1)$ solves

$$\begin{aligned} \left\{ \begin{array}{lllll} \partial _t u_{1}-\Delta u_1 &{}=&{} |\nabla v_1+\nabla \eta |^q &{} \text {in } &{} \Omega _T, \\ \partial _tv_{1}-\Delta v_1 &{}=&{} |\nabla u_1+\nabla \psi |^{p} &{}\text {in }&{} \Omega _T, \\ u_1=v_1&{}=&{}0 &{} \text {on } &{}\Gamma _T,\\ u_1(x,0)&{}=&{} 0\,\,&{}\text { in } &{}\Omega , \\ v_1(x,0)&{}=&{} 0 &{}\text { in } &{}\Omega . \end{array} \right. \end{aligned}$$

(4.8)

Hence, to show the main existence result, we have just to show that system (4.8) has a non-negative solution.

For r close to $\frac{(N+2)\sigma _1}{N+\sigma _1}$, we consider the set

$$\begin{aligned} F_r(\Omega _T):=\bigg \{\varphi \in E_1(\Omega _T)\; ;\; \varphi \in E_r(\Omega _T)\cap L^{\infty }(0,T;L^1(\Omega )) \text{ with } ||\varphi ||_{V^{1,r}_0(\Omega _T)}\le \ell ^{\frac{1}{pq}}\bigg \}. \end{aligned}$$

We define now the operator $L: F_r(\Omega _T)\longrightarrow E_1(\Omega _T)$ by setting $L(\varphi )=v_1$ where $v_1$ is the unique solution to problem

$$\begin{aligned} \left\{ \begin{array}{lllll} \partial _tv_{1}-\Delta v_1 &{}=&{} |\nabla u_1+\nabla \psi |^{p} &{} \text { in } &{} \Omega _T,\\ v_1&{} =&{} 0 &{} \text { on } &{} \Gamma _T,\\ v_1(x,0)&{}=&{} 0&{} \text { in } &{} \Omega , \end{array} \right. \end{aligned}$$

with $u_1$ being the unique solution to the problem

$$\begin{aligned} \left\{ \begin{array}{llll} \partial _tu_{1}-\Delta u_1 &{}=&{} |\nabla \eta +\nabla \varphi |^q&{} \text { in }\Omega _T, \\ u_1&{}=&{} 0 &{} \text { on }\Gamma _T,\\ u_1(x,0)&{}=&{} 0&{} \text { in }\Omega . \end{array} \right. \end{aligned}$$

It is clear that if $v_1$ is a fixed point of L in $F_r(\Omega _T)$, then $(u_1,v_1)$ solves the system (4.8).

Following the same approach as in the proof of Theorem 3.3, we reach to the desired result. $\square$

4.3 Third Model

Finally, let us analyze the following system:

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t - \Delta u &{}=&{} u|\nabla v|^q+f &{}{} \text{ in } &{}{}\Omega _T, \\ v_ t- \Delta v &{}=&{} v|\nabla u|^{p}+g &{}{} \text{ in } &{}{}\Omega _T, \\ u=v&{}=&{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u(x,0)&{}=&{} 0 &{}{} \text{ in } &{}{}\Omega , \\ v(x,0)&{}=&{} 0&{}{} \text{ in } &{}{}\Omega _T, \\ u,v &{}\ge &{} 0 &{}{} \text{ in } &{}{}\Omega _T, \end{array} \right. \end{aligned}$$

(4.9)

which is more involved due to the presence of an interaction term in both equations (the dependence on u and v appears in the two equations).

Notice that, in the case of one equation and in the particular case $p=2$, the problem

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t - \Delta u &{}=&{} u|\nabla u|^2+f &{}{} \text{ in } &{}{}\Omega _T, \\ u &{}=&{} 0 &{}{} \text{ on } &{}{}\Gamma _T,\\ u(x,0) &{}=&{} 0 &{}{} \text{ in } &{}{}\Omega \\ \end{array} \right. \end{aligned}$$

(4.10)

was studied deeply in [27]. The authors proved the existence of a solution to (4.10) if $f\in L^m(\Omega _T)$ with $m>\frac{N+2}{2}$. See also [26] for some extensions.

In the sprit of the results obtained in [27] and [26] and keeping free the values of $p,q>1$, we have the next existence result for System (4.9).

Theorem 4.3

Suppose that $(f,g)\in L^m(\Omega _T)\times L^\sigma (\Omega _T)$ with $1<m, \sigma <N+2$. Let $p,q>1$ be such that

$$\begin{aligned} \left\{ \begin{array}{llll} p\sigma< \dfrac{m (N+2+N\sigma )}{(N+2-m)(N+1)},\\ \\ qm < \dfrac{\sigma (N+2+N m)}{(N+2-\sigma )(N+1)}. \end{array} \right. \end{aligned}$$

(4.11)

Then System (4.9) has a nonnegative solution $(u,v)\in V^{1,\alpha }_0(\Omega _T)\times V^{1,\beta }_0(\Omega _T)$ for all $\alpha <\dfrac{(N+2)m}{(N+2-m)_+}$ and $\beta <\dfrac{(N+2)\sigma }{(N+2-\sigma )_+}$.

Proof

We follow closely the argument used in the proof of Theorem 4.1. However, taking into consideration the structure of System (4.9), some technical modifications are needed.

Define the function

$$\begin{aligned} \Upsilon _1(s):=s-\widetilde{C}(s^{1+q}+s^{1+p}), \end{aligned}$$

with $\widetilde{C}$ being a universal positive constant depending only on the data. Since $q,p>1$, then we get the existence of a unique value $\ell$ such that

$$\begin{aligned} \max _{s\ge 0}\Upsilon _1(s)=\Upsilon _1(\ell )=\Lambda ^*. \end{aligned}$$

Thus

$$\begin{aligned} \ell =\tilde{C}(\ell ^{1+q}+\ell ^{1+p}+\frac{\Lambda ^*}{\tilde{C}}). \end{aligned}$$

(4.12)

By a continuity argument, we choose $0<T^*<T$ such that

$$\begin{aligned} ||f||_{L^{m}(\Omega _{T^*})}+||g||_{L^{\sigma }(\Omega _{T^*})}\le \frac{\Lambda ^*}{\tilde{C}}; \end{aligned}$$

hence,

$$\begin{aligned} \tilde{C}\bigg (\ell ^{1+q}+\ell ^{1+p}+||f||_{L^{m}(\Omega _{T^*})}+||g||_{L^{\sigma }(\Omega _{T^*})}\bigg )\le \ell . \end{aligned}$$

(4.13)

Now, we define the set

$$\begin{aligned} \begin{array}{lll} &{}F_{r,\theta }(\Omega _{T^*})=\bigg \{(\varphi ,\psi )\in E_1(\Omega _{T^*})\times E_1(\Omega _{T^*}), \\ &{} (\varphi ,\psi )\in V^{1,r}_0(\Omega _{T^*})\times V^{1,\theta }_0(\Omega _{T^*}) \text{ and } ||\varphi ||_{V^{1,r}_0(\Omega _{T^*})}+||\psi ||_{V^{1,\theta }_0(\Omega _{T^*})}\le \ell \bigg \}, \end{array} \end{aligned}$$

where r and $\theta$ are chosen such that

$$\begin{aligned} \left\{ \begin{array}{rcll} \dfrac{p\sigma (N+1)}{\theta (N+1)-N\sigma }<r<\dfrac{m(N+2)}{N+2-m}:=\overline{m},\\ \\ \dfrac{qm (N+1)}{r(N+1)-Nm}<\theta < \dfrac{\sigma (N+2)}{N+2-\sigma }:=\overline{\sigma }. \end{array} \right. \end{aligned}$$

(4.14)

Notice that, under the condition (4.11), we get the existence of $(r,\theta )$ closed to $(\overline{m},\overline{\sigma })$ such that the condition (4.14) holds.

It is clear that $F_{r,\theta }(\Omega _{T^*})$ is a closed convex subset of $E_1(\Omega _{T^*})\times E_1(\Omega _{T^*})$.

Now consider the operator

$$\begin{aligned} \begin{array}{rcll} L: F_{r,\theta }(\Omega _{T^*}) &{}\longmapsto &{} E_1(\Omega _{T^*})\times E_1(\Omega _{T^*})\\ \overline{\varphi }=(\varphi , \psi ) &{}\longmapsto &{} L(\varphi ,\psi )=(u,v) \end{array} \end{aligned}$$

where u and v solve, respectively, the following problems:

$$\begin{aligned} \left\{ \begin{array}{lllll} u_t-\Delta u &{}=&{} \varphi _+|\nabla \psi |^q+ f &{}{} \text{ in } &{}{}\Omega _{T^*},\\ u &{}=&{} 0 &{}{} \text{ on } &{}{} \Gamma _{T^*},\\ u(x,0) &{}=&{} 0&{}{} \text{ in } &{}{} \Omega \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{lllll} v_t-\Delta v &{}=&{} \psi _+|\nabla \varphi |^p+ g &{} \text { in } &{}\Omega _{T^*}, \\ v &{}=&{} 0 &{} \text { on }&{}\Gamma _{T^*},\\ v(x,0)&{}=&{} 0&{} \text { in } &{}\Omega . \end{array} \right. \end{aligned}$$

Of course, if (u, v) is a fixed point of L in $F_{r,\theta }(\Omega _{T^*})$, then (u, v) solves system (4.9).

We claim that if $(\varphi ,\psi )\in F_{r}(\Omega _{T^*})$, then

$$\begin{aligned} \bigg \Vert \varphi _+|\nabla \psi |^q\bigg \Vert _{L^m(\Omega _{T^*})}\le C||\varphi ||_{V^{1,r}_0(\Omega _{T^*})}\times ||\psi ||^q_{V^{1,r}_0(\Omega _{T^*})}. \end{aligned}$$

Indeed, we have

$$\begin{aligned} \bigg \Vert \varphi _+|\nabla \psi |^q\bigg \Vert ^m_{L^m(\Omega _{T^*})}=\iint _{\Omega _{T^*}}\varphi ^m_+|\nabla \psi |^{qm} \text {d}x\,\text {d}t\le \iint _{\Omega _{T^*}}|\varphi |^m|\nabla \psi |^{qm} \text {d}x\,\text {d}t. \end{aligned}$$

Hence, using Hölder’s inequality gives

$$\begin{aligned} \bigg \Vert \varphi _+|\nabla \psi |^q\bigg \Vert ^m_{L^m(\Omega _{T^*})}\le C\bigg (\iint _{\Omega _{T^*}}|\varphi |^\nu dxdt \bigg )^{\frac{m}{\nu }} \bigg (\iint _{\Omega _{T^*}} |\nabla \psi |^{qm\frac{\nu }{\nu -m}} \text {d}x\,\text {d}t\bigg )^{\frac{\nu -m}{\nu }},\nonumber \\ \end{aligned}$$

(4.15)

where $\nu =r\frac{N+1}{N}$. Moreover, $qm\frac{\nu }{\nu -m}=qm\frac{r(N+1)}{r(N+1)-mN}$. Thus, by the definition of r and $\theta$, it holds that $qm\frac{\nu }{\nu -m}<\theta$.

Going back to (4.15) and applying Proposition 2.1 to obtain

$$\begin{aligned}&\bigg \Vert \varphi _+|\nabla \psi |^q\bigg \Vert ^m_{L^m(\Omega _{T^*})}\le C\bigg (\iint _{\Omega _{T^*}}|\varphi |^\nu \text {d}x\text {d}t \bigg )^{\frac{m}{\nu }} \bigg (\iint _{\Omega _{T^*}} |\nabla \psi |^{\theta } \text {d}x\,\text {d}t\bigg )^{\frac{qm}{\theta }}\\&\le C||\varphi ||^m_{V^{1,r}_0(\Omega _{T^*})}\times ||\psi ||^{qm}_{V^{1,\theta }_0(\Omega _{T^*})}, \end{aligned}$$

and hence the claim follows.

In a symmetric way and since $p\sigma \frac{\theta (N+1)}{\theta (N+1)-\sigma N}<r$, we obtain that

$$\begin{aligned} \bigg \Vert \psi _+|\nabla \varphi |^p\bigg \Vert _{L^\sigma (\Omega _{T^*})}\le C||\psi ||_{V^{1,\theta }_0(\Omega _{T^*})}\times ||\varphi ||^p_{V^{1,r}_0(\Omega _{T^*})}. \end{aligned}$$

Thus u, v are well defined and $(u,v)\in E_1(\Omega _{T^*})\times E_1(\Omega _{T^*})$. Now, by Theorem 2.8, we get

$$\begin{aligned}&|| \nabla u||_{L^{\overline{m}}(\Omega _{T^*})}\le C(\Omega _{T^*})\bigg (||\varphi ||_{V^{1,r}_0(\Omega _{T^*})}\times ||\psi ||^q_{V^{1,\theta }_0(\Omega _{T^*})} +||f||_{L^m(\Omega _{T^*})}\bigg ), \\&|| \nabla v||_{L^{\overline{\sigma }}(\Omega _{T^*})}\le C(\Omega _{T^*})\bigg (||\psi ||_{V^{1,\theta }_0(\Omega _{T^*})}\times ||\varphi ||^p_{V^{1,r}_0(\Omega _{T^*})} +||g||_{L^\sigma (\Omega _{T^*})}\bigg ), \end{aligned}$$

where $\overline{m}=\dfrac{m(N+2)}{N+2-m}$ and $\overline{\sigma }=\dfrac{\sigma (N+2)}{N+2-\sigma }$. Since $r<\overline{m}$ and $\theta <\overline{ \sigma }$, then $(u,v)\in V^{1,r}_0(\Omega _{T^*})\times V^{1,\theta }_0(\Omega _{T^*})$ and

$$\begin{aligned} \begin{array}{rcll} &{}&{}||u||_{V^{1,r}_0(\Omega _{T^*})}+||v||_{V^{1,r}_0(\Omega _{T^*})} \le C(\Omega _{T^*})\bigg (||\varphi ||_{V^{1,r}_0(\Omega _{T^*})} ||\psi ||^q_{V^{1,\theta }_0(\Omega _{T^*})}\\ &{}&{}\qquad +||\psi ||_{V^{1,\theta }_0(\Omega _{T^*})} ||\varphi ||^p_{V^{1,r}_0(\Omega _{T^*})} +||f||_{L^m(\Omega _{T^*})}+ ||g||_{L^\sigma (\Omega _{T^*})} \bigg )\\ &{}&{}\quad \le C(\Omega _{T^*})\bigg (\ell ^{1+q}+\ell ^{1+p}+||f||_{L^m(\Omega _{T^*})}+ ||g||_{L^\sigma (\Omega _{T^*})} \bigg )\\ &{}&{}\quad \le \ell . \end{array} \end{aligned}$$

The last estimate follows by (4.13). Therefore, we conclude that $L(F_{r,\theta }(\Omega _{T^*}))\subset F_{r,\theta }(\Omega _{T^*})$.

The rest of the proof is the same as the proof of Theorem 4.1. $\square$

Remark 8

To illustrate our previous result, let us give some examples of $p,\,q, \, m$ and $\sigma$.

• If $m,\sigma >N+2$, the existence result holds for all $p,q>1$.

• If $p=q=1$ and $m=\sigma$, a sufficient condition on m that guarantees the existence of a solution is $m=\sigma >\frac{N(N+2)}{2N+1}$.

• If $p=q=2$ and $m=\sigma$, condition (4.11) implies that $m=\sigma >\frac{(N+2)(2N+1)}{3N+2}$.

• If $m=\sigma =2$, then the condition (4.11) implies that

  $$\begin{aligned} \left\{ \begin{array}{rcll} p &{}< &{}\dfrac{3N+2}{N(N+1)},\\ \\ q &{}<&{} \dfrac{3N+2}{N(N+1)}, \end{array} \right. \end{aligned}$$

  Or $\frac{3N+2}{N(N+1)}>1$ if $N\le 2$. Hence for $N\ge 3$, it seems that the condition $p,q<1$ is necessary as it will be shown in the next proposition.

Proposition 4.4

Assume that $m=\sigma =2$. Then for all $p,q>1$, there exist $f,\ g\in L^2(\Omega _T)$ such that System (4.9) has no solution at least for N large.

Proof

We consider the case where $0\in \Omega$ and $f(x,t)=g(x,t)=\frac{1}{|x|^\alpha }$, where $2<\alpha <\frac{N}{2}$. If (u, v) is a solution to System (4.9), then using a suitable comparison principle it holds that :

$$\begin{aligned} u(x,t), v(x,t)\ge \frac{C}{|x|^{\alpha -2}} \, \text { in } \, B_r(0)\times (t_1,t_2)\subset \subset \Omega _T. \end{aligned}$$

Thus,

$$\begin{aligned} \iint _{\Omega _T}|x|^{-(\alpha -2)}|\nabla u|^p \text {d}x\text {d}t +\iint _{\Omega _T}|x|^{-(\alpha -2)}|\nabla v|^q \text {d}x\text {d}t<\infty . \end{aligned}$$

Hence, applying Caffarelli–Kohn–Nirenberg’s inequality (see [22]) to obtain

$$\begin{aligned} \int _0^T\bigg (\int \limits _\Omega \frac{u^{p^*}}{|x|^{\frac{p^*}{p}(\alpha -2)}}dx\bigg )^{\frac{p}{p^*}}\text {d}t + \int _0^T\bigg (\int \limits _\Omega \frac{v^{q^*}}{|x|^{\frac{q^*}{q}(\alpha -2)}}dx\bigg )^{\frac{q}{q^*}}\text {d}t<\infty . \end{aligned}$$

Now, using the behavior of u, v at the origin, it holds that

$$\begin{aligned} \int _{B_r(0)} \frac{1}{|x|^{p^*(\alpha -2)+\frac{p^*}{p}(\alpha -2)}}\text {d}x+ \int _{B_r(0)}\frac{1}{|x|^{q^*(\alpha -2)+\frac{q^*}{q}(\alpha -2)}}\text {d}x\le C(T,\Omega ). \end{aligned}$$

Thus

$$\begin{aligned} p^*(\alpha -2)+\frac{p^*}{p}(\alpha -2)<N \text{ and } q^*(\alpha -2)+\frac{q^*}{q}(\alpha -2)<N. \end{aligned}$$

Let $p,q>1$ fixed, by choosing $N>\max \{\frac{2p+4}{p-1}, \frac{2q+4}{q-1}\}$, we get the existence of $\alpha <\frac{N}{2}$ such that

$$\begin{aligned} p^*(\alpha -2)+\frac{p^*}{p}(\alpha -2)\ge N \text{ and } q^*(\alpha -2)+\frac{q^*}{q}(\alpha -2)\ge N, \end{aligned}$$

which is a contradiction with the existence result. $\square$

Remark 9

In a forthcoming work we will treat the case of the Cauchy problem, and analyze questions such global existence versus finite-time blow-up. Notice that, for a semi-linear reaction-diffusion system with potential terms, the existence of a Fujita-type exponent has been proved in [32], see also [44, Theorem 32.7] for an alternative proof in the subcritical case.