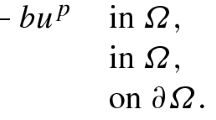1 Introduction

Consider the boundary value problem

$$\begin{aligned} \left\{ \!\begin{aligned}&-\Delta u = \lambda K(|x|)f(u) \quad \text {in}\ \Omega ,\\&\frac{\partial u}{\partial {{{\varvec{n}}}}}+\tilde{c}(u)u=0 \quad \quad \quad \; \text {on}\ |x|=r_0,\\&u(x) \rightarrow 0 \qquad \qquad \qquad \; \text {as}\ |x| \rightarrow \infty ,\\ \end{aligned} \right. \end{aligned}$$

where \(\Omega = \{x \in \mathbb {R}^N : |x|> r_0 > 0\}\), \(N > 2\), \(K : [r_0, \infty ) \rightarrow (0, \infty )\), \(\tilde{c}: [0, \infty )\rightarrow [0, \infty )\) and \(f : (0, \infty ) \rightarrow \mathbb {R}\) are continuous, and \(\lambda \) is a positive parameter. Here, \({{\varvec{n}}}\) denotes the outer unit normal vector on \(\partial \Omega \).

It is well known that a nontrivial radial function u(t),  where \(t = |x|\), is a solution of the above problem if and only if u(t) is a solution of the problem

$$\begin{aligned} \left\{ \!\begin{aligned}&-u''=\lambda f(t, u), \ \ \ \ \ 0<t<1,\\&u(0)=0, \ \ u'(1)+c(u(1))u(1)=0.\\ \end{aligned} \right. \end{aligned}$$
(1.1)

In this paper, we deal with the existence of positive solutions of (1.1). We assume that \(f\in C([0,1]\times \mathbb {R}^+, \mathbb {R})\) and \(c\in C(\mathbb {R}, \mathbb {R})\) satisfy

(f1) \(f(t, 0)<0, \ \ \ t\in [0,1]\);

(c1) \(c:[0, \infty )\rightarrow (0, \infty )\) is nondecreasing, and \(c(0)\le c(s)\le c(\infty )<\infty \) for \(s\in [0, \infty )\).

If \(f(t, 0)\ge 0\), then (1.1) is called a positone problem and has been extensively studied, see the survey papers of Amamm [1] and Loins [17].

On the contrary, we deal here with the so called semi-positone problem, when f satisfies (f1). Existence, uniqueness and multiplicity of positive solutions of semi-positone problems have been studied by several authors, see [2,3,4, 6, 7, 9,10,11,12,13,14] for semi-positone problems with linear boundary conditions, and [8, 15, 16, 21] for semi-positone problems with nonlinear boundary conditions.

With the exception of Ambrosetti et al. [2] that deals with semi-positone problems with linear boundary conditions via bifuraction method, the common feature of the papers mentioned above is that their main results are obtained by fixed point theorems in cone, sub- and super-solutions, time-map estimation in ODE case, and hence they provide no information about the global behavior of the set of positive solutions.

The main purpose of the present paper is to show that bifurcation theory can be easily used to study semi-positone problems with nonlinear boundary conditions. The same abstract setting is employed to handle both superlinear as well as sublinear problems with nonlinear boundary conditions.

After some notation and preliminaries listed in Sect. 2, we deal in Sect. 3 with superlinear problems. A ‘blow-up’ argument jointly with some a priori estimates allows one to show that (1.1) possesses positive solutions for \(0<\lambda <\lambda _*\). Similar arguments can be used in the sublinear case, discussed in Sect. 4, to show that (1.1) has positive solutions, provided \(\lambda \) is large enough.

2 Notation and Preliminaries

Standard notation will be used for Lebesgue and Sobolev spaces. The norm in \(L^r(0,1)\) will be denoted by \(|\cdot |_r\) and the scalar product in \(L^2(0,1)\) by \((\cdot , \cdot )\). We will work in \(X = C[0,1]\) or \(Y = \{u\in C^1[0,1]:\, u(0)=0\} \), the space of continuous, \(C^1\) with continuous first derivative, respectively, functions. The usual norm in such spaces will be denoted by \(||\cdot ||_\infty \) and \(||\cdot ||_{C^1}\); we also set \(B_r = \{u \in X: ||u||<r\}\). The first eigenvalue of the linear problem

$$\begin{aligned} \left\{ \!\begin{aligned}&-u''=\lambda a(t)u, \ \ \ \ \ 0<t<1,\\&u(0)=0, \ \ u'(1)+\beta u(1)=0,\\ \end{aligned} \right. \end{aligned}$$

is denoted by \(\lambda _1[a(\cdot );\beta ]\). We also set \(\mathbb {R}^+ = [0, \infty )\). The Green function of linear problem

$$\begin{aligned} \left\{ \!\begin{aligned}&-u''=e, \ \ \ \ \ 0<t<1,\\&u(0)=0, \ \ u'(1)+\beta u(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(2.1)

(\(e\in X\)), is explicitly given by

$$\begin{aligned} H_\beta (t,s)=\left\{ \!\begin{aligned} \frac{1+\beta -\beta t}{1+\beta }\; s, \ \ \ \ 0\le s\le t\le 1,\\ t\; \frac{1+\beta -\beta s}{1+\beta }, \ \ \ \ 0\le s\le t\le 1.\\ \end{aligned} \right. \end{aligned}$$

Obviously, for given \((t,s)\in [0,1]\times [0,1]\), \(H_\beta (t,s)\) is decreasing in \(\beta \in [0, \infty )\).

Let us define a linear operator \(T_\beta :X\rightarrow X\) by

$$\begin{aligned} u=T_\beta \, e,\ \end{aligned}$$

where u is the unique solution of (2.1).

Lemma 2.1

Let (c1) hold. Then, for every \(e\in X\), the problem

$$\begin{aligned} \left\{ \!\begin{aligned}&-v''(t)=e(t), \ \ \ \ \ 0<t<1,\\&v(0)=0, \ \ v'(1)+c(v(1)) v(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(2.2)

has a unique solution \(v\in C^2[0,1]\).

Proof

We first show that (2.2) has at least one solution.

In fact, (2.1) is equivalent to

$$\begin{aligned} v(t)=\mathcal {A}(v)(t), \end{aligned}$$

where

$$\begin{aligned} \mathcal {A}(v)(t):=\int ^1_0 H_{c(v(1))}(t,s)e(s). \end{aligned}$$

Since

$$\begin{aligned} H_{c(\infty )}(t,s)\le H_{c(v(1))}(t,s)\le H_{c(0)}(t,s) \ \ \ \ (t,s)\in [0,1]\times [0,1], \end{aligned}$$

it is easy to check that \(\mathcal {A}: X\rightarrow X\) is completely continuous and \(\mathcal {A}(X)\subseteq B_\rho \), where

$$\begin{aligned} \rho := \max \{ H_{c(0)}(t,s):(t,s)\in [0,1]\times [0,1]\}\cdot ||e||_\infty . \end{aligned}$$

By Schauder fixed point theorem, \(\mathcal {A}\) has a fixed point in \(B_\rho \), and accordingly, (2.2) has a solution.

Next, we show (2.2) has a unique solution in \(C^2[0,1]\).

Assume on the contrary that u and v are two different solutions of (2.2). Then,

$$\begin{aligned} \left\{ \!\begin{aligned}&-(u-v)''(t)=0, \ \ \ \ \ 0<t<1,\\&(u-v)(0)=0, \ \ (u-v)'(1)+[c(u(1)) u(1)-c(v(1)) v(1)]=0.\\ \end{aligned} \right. \end{aligned}$$

Since

$$\begin{aligned} (c(x)x)'=c'(x)x+c(x)\ge c(0)>0, \end{aligned}$$
(2.3)

and

$$\begin{aligned} c(u(1)) u(1)-c(v(1)) v(1)=[c'(\xi )\xi +c(\xi )](u(1)-v(1)) \end{aligned}$$

for some \(\xi \in \big [\min \{u(1), v(1)\}, \, \max \{u(1), v(1)\}\big ]\). Thus,

$$\begin{aligned} \left\{ \!\begin{aligned}&-(u-v)''(t)=0, \ \ \ \ \ 0<t<1,\\&(u-v)(0)=0, \ \ (u-v)'(1)+[c'(\xi )\xi +c(\xi )] ( u(1)-v(1))=0.\\ \end{aligned} \right. \end{aligned}$$

This together with (2.3) implies that

$$\begin{aligned} u(t)-v(t)\equiv 0,\ \ \ \ \ t\in [0,1]. \end{aligned}$$

\(\square \)

In view of Lemma 2.1, we may define a nonlinear operator \(\mathcal {K}: X\rightarrow C^2[0,1]\) by

$$\begin{aligned} u:=\mathcal {K}e, \end{aligned}$$

where \(u\in C^2[0,1]\) is the unique solution of the problem (2.2). It is easy to check that \(\mathcal {K}:X\rightarrow Y\) is completely continuous.

By a solution of (1.1), we mean a \(u\in C^2[0,1]\), which solves (1.1). With the above notation, problem (1.1) is equivalent to

$$\begin{aligned} u- \mathcal {K}\big (\lambda f(\cdot ,u)\big ) = 0, \quad u \in X. \end{aligned}$$
(2.4)

Hereafter, we will use the same symbol to denote both the function and the associated Nemitski operator.

We say that \(\lambda _\infty \) is a bifurcation from infinity for (2.4) if there exist \(\mu _n\rightarrow \lambda _\infty \) and \(u_n\in X\), such that \(u_n-\mathcal {K}\big (\mu _n f(\cdot ,u_n)\big ) = 0\) and \(||u_n||_\infty \rightarrow \infty \). Extending the preceding definition, we will say that \(\lambda _\infty =\infty \) is a bifurcation from infinity for (2.4) if solutions \((\mu _n, u_n)\) of (2.4) exist with \(\mu _n\rightarrow \infty \) and \(||u_n||_\infty \rightarrow \infty \). This is the case we will meet in Sect. 4.

In some situations, like the specific ones we will discuss later, an appropriate rescaling permits one to find bifurcation from infinity by means of Leray–Schauder topological degree \(\deg (\cdot ,\;\cdot ,\;\cdot )\). Recall that \(\mathcal {K} : X\rightarrow X\) is continuous and compact, and hence it makes sense to consider the topological degree of \(I- \mathcal {K}\big (\lambda f\big )\), I identity map.

3 Superlinear Problems

In this section, we deal with the existence of positive solutions of nonlinear boundary value problems like

$$\begin{aligned} \left\{ \begin{aligned}&-u''=\lambda f(t, u), \quad 0<t<1,\\&u(0)=0, \; u'(1)+c(u(1))u(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(3.1)

when \(f(t, \cdot )\) is superlinear. Precisely, we suppose that \(f\in C([0,1]\times \mathbb {R}^+, \mathbb {R})\) satisfies (f1) and

(f2) there exists \(b\in X\) with \(b(t) > 0\) in [0, 1], such that

$$\begin{aligned} \lim _{u\rightarrow +\infty }\frac{f(t, u)}{u^p } = b \quad \text {uniformly in}\ t\in [0,1] \end{aligned}$$

for some constant \(p>1\).

We will study the existence of positive solutions of problem (3.1). Our main result is

Theorem 3.1

Let (f1), (f2) and (c1) hold. Then, there exists \(\lambda _* > 0\) such that (3.1) has positive solutions for all \(0 < \lambda \le \lambda _*\). More precisely, there exists a connected set of positive solutions of (3.1) bifurcating from infinity at \(\lambda _\infty = 0\).

First of all, we extend \(f(t,\cdot )\) to all of \(\mathbb {R}\) by setting

$$\begin{aligned} F(t, u)=f(t, |u|). \end{aligned}$$
(3.2)

Let

$$\begin{aligned} G(t, u)=F(t, u)-b|u|^p. \end{aligned}$$
(3.3)

For the remainder of the proof, we will omit the dependence with respect to \(t\in [0,1]\). To prove that \(\lambda _\infty = 0\) is a bifurcation from infinity for

$$\begin{aligned} u- \mathcal {K}(\lambda F(u))=0, \end{aligned}$$
(3.4)

we use the rescaling

$$\begin{aligned} w = \gamma u, \quad \lambda =\gamma ^{p-1}, \quad \gamma >0. \end{aligned}$$
(3.5)

A direct calculation shows that \((\lambda , u)\) is a solution of (3.4) if and only if

$$\begin{aligned} w=\mathcal {K}\tilde{F}(\gamma , w), \end{aligned}$$
(3.6)

where

$$\begin{aligned} \tilde{F}(\gamma , w):=b|w|^p+\gamma ^p G(\gamma ^{-1}w),\ \ \ \ \gamma >0. \end{aligned}$$
(3.7)

We can extend \(\tilde{F}\) to \(\gamma = 0\) by setting

$$\begin{aligned} \tilde{F}_0(w)=\tilde{F}(0, w)=b|w|^p \end{aligned}$$
(3.8)

and, by (f2), such an extension is continuous. We set

$$\begin{aligned} S(\gamma , w)=w-\mathcal {K}\tilde{F}(\gamma , w), \ \ \ \ \gamma \in \mathbb {R}^+. \end{aligned}$$
(3.9)

Let us point out explicitly that \(S(\gamma , \cdot )=I-\mathcal {K}\tilde{F}(\gamma , \cdot )\), with \(\mathcal {K}\) compact. For \(\gamma = 0\), solutions of \(S_0(w) := S(0, w) = 0\) are nothing but solutions of

$$\begin{aligned} \left\{ \begin{aligned}&-w''=b|w|^p, \ \ \ \ \ 0<t<1,\\&w(0)=0, \ \ w'(1)+ c(\infty )w(1)=0.\\ \end{aligned} \right. \end{aligned}$$
(3.10)

It follows from [10], Theorem 1(i)] that (3.10) has at least one positive solution w. In the following, we are only interested in the positive solution w of (3.10), although 0 is also a solution of (3.10).

We claim that there exist two constants r, R :  \(R> r > 0\), such that

$$\begin{aligned}&S_0(w)\ne 0, \quad \forall \ \ ||w||_\infty \ge R; \end{aligned}$$
(3.11)
$$\begin{aligned}&S_0(w)\ne 0, \quad \forall \ 0<||w||_\infty \le r; \end{aligned}$$
(3.12)
$$\begin{aligned}&\deg (S_0(\cdot ), B_R{\setminus } \bar{B}_r, 0) = -1. \end{aligned}$$
(3.13)

Assume on the contrary that (3.11) is not true. Then, there exists a sequence \(\{w_n\}\) of solutions of (3.10) satisfying

$$\begin{aligned} ||w_n||_\infty \rightarrow \infty , \quad n\rightarrow \infty . \end{aligned}$$

In fact, we have from (3.10) that

$$\begin{aligned} \left\{ \begin{aligned}&-w_n''=\big (b|w_n|^{p-1}\big ) w_n, \qquad t\in (0, 1), \\&w_n(0)=0, \ \ w_n'(1)+c(\infty ) w_n(1)=0.\\ \end{aligned} \right. \end{aligned}$$

Since \(w_n''(t)<0\) for \(t\in (0,1)\), \(w_n\) is concave down in [0, 1], and subsequently,

$$\begin{aligned} w_n(t)\ge ||w_n||_\infty \min \{t, 1-t\}, \end{aligned}$$

which means that

$$\begin{aligned} w_n(t)\ge \frac{1}{4} ||w_n||_\infty \quad t\in \left[ \frac{1}{4}, \frac{3}{4}\right] . \end{aligned}$$

Thus,

$$\begin{aligned} \lim _{n\rightarrow \infty } b|w_n(t)|^{p-1}=\infty \quad \text {uniformly in}\ t\in \left[ \frac{1}{4}, \frac{3}{4}\right] , \end{aligned}$$

which implies that \(w_n\) must changes its sign in \([\frac{1}{4}, \frac{3}{4}]\). However, this contradicts \(w_n>0\) in (0, 1].

Therefore, (3.11) is valid.

Assume on the contrary that (3.12) is not true. Then, there exists a sequence \(\{w_n\}\) of solutions of (3.10) satisfying

$$\begin{aligned} ||w_n||_\infty \rightarrow 0, \ \ \ \ \ n\rightarrow \infty . \end{aligned}$$
(3.14)

Let \(v_n:=w_n/||w_n||_\infty \). From (3.10), we have

$$\begin{aligned} \left\{ \begin{aligned}&-v_n''=\big (b|w_n|^{p-1}\big ) v_n, \ \ \ \ \ t\in (0, 1), \\&v_n(0)=0, \ \ v_n'(1)+c(\infty ) v_n(1)=0.\\ \end{aligned} \right. \end{aligned}$$
(3.15)

From (3.14), we have that

$$\begin{aligned} \lim _{n\rightarrow \infty }\, b|w_n(t)|^{p-1}=0\quad \text {uniformly in}\ t\in [0,1]. \end{aligned}$$

By the standard argument, after taking a subsequence and relabeling if necessary, it follows that there exists \(v_*\in X\) with \(||v_*||_\infty =1\), such that

$$\begin{aligned} v_n\rightarrow v_*, \ \ \ \ \ n\rightarrow \infty \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{aligned}&-v_*''=0, \quad t\in (0, 1), \\&v_*(0)=0, \ \ v_*'(1)+c(\infty ) v_*(1)=0,\\ \end{aligned} \right. \end{aligned}$$

which implies that \(v_*=0\). However, this is a contradiction. Therefore, (3.12) is valid.

To show (3.13) is valid, let us define a cone

$$\begin{aligned} K=\{u\in X:\, u(t)\ge 0 \ \text {for}\ t\in [0, 1]\}. \end{aligned}$$

Denote

$$\begin{aligned} K_\rho =\{u\in K:\, ||u||_\infty \le \rho \}. \end{aligned}$$

By use [9, Lemma 3.1] and the fact

$$\begin{aligned} H_{c(\infty )}(t,s)\le H_{c(u(1))}(t,s)\le H_{c(0)}(t,s)\ \ \ \ (t,s)\in [0,1]\times [0,1], \end{aligned}$$

and the similar argument to prove [10, Theorem 1(i)], we may deduce the following

$$\begin{aligned} \mathrm{{ind}}(\mathcal {K}\tilde{F}(0, \cdot ), K_r, K)=1, \ \ \ \ \mathrm{{ind}}(\mathcal {K}\tilde{F}(0, \cdot ), K_R, K)=0, \end{aligned}$$

and subsequently

$$\begin{aligned} \mathrm{{ind}}(\mathcal {K}\tilde{F}(0, \cdot ), K_R{\setminus } \overset{\circ }{K}_r, K)=-1. \end{aligned}$$
(3.16)

Combining this together with the fact \(S_0: X\rightarrow K_R{\setminus } \overset{\circ }{K}_r\) and using (3.11) and (3.12), it deduces that

$$\begin{aligned} \deg (S_0(\cdot ), B_{R}{\setminus } \bar{B}_r, 0) = -1. \end{aligned}$$

Lemma 3.1

There exists \(\gamma _0 > 0\) such that

(1)

$$\begin{aligned} \deg (S(\gamma , \cdot ), B_R{\setminus } \bar{B}_r, 0) = -1, \ \ \ \ \gamma \in [0, \gamma _0]. \end{aligned}$$
(3.17)

(2) if \(S(\gamma , w) = 0\), \(\gamma \in [0, \gamma _0]\), \(r\le ||w||_\infty \le R\), then \(w > 0\) in (0, 1].

Proof

Clearly, (i) follows if we show that \(S(\gamma , w) \ne 0\) for all \(||w||_\infty \in \{r, R\}\) and all \(0\le \gamma \le \gamma _0\). Otherwise, there exists a sequence \((\gamma _n, w_n)\) with \(\gamma _n\rightarrow 0\), \(||w_n||_\infty \in \{r, R\}\) and \(w_n = \mathcal {K}\tilde{F}(\gamma _n, w_n)\). Since \(\mathcal {K}\) is compact then, up to a subsequence, \(w_n\rightarrow w\) and \(S_0(w) = 0\), \(||w||_\infty \in \{r, R\}\), a contradiction with (3.11) and (3.12).

To prove (ii), we argue again by contradiction. As in the preceding argument, we find a sequence \(w_n \in X\), with \(\{x \in (0,1) : w_n(x)\le 0\} \ne \emptyset \), such that \(w_n\rightarrow w\), \(||w||_\infty \in [r, R]\) and \(S_0(w) = 0\), namely, w solves (3.10). By the maximum principle \(w > 0\) on (0, 1] and \(w'(0)>0\). Moreover, without relabeling, \(w_n\rightarrow w\) in \(C^1[0,1]\). Therefore, \(w_n > 0\) on (0, 1] for n large, a contradiction. \(\square \)

Proof of Theorem 3.1

By Lemma 3.1, (3.6) has a positive solution \(w_\gamma \) for all \(0\le \gamma \le \gamma _0\). As remarked before, for \(\gamma >0\), the rescaling \(\lambda = \gamma ^{p-1}\), \(u = w/\gamma \) gives a solution \((\lambda ,u_\lambda )\) of (3.4) for all \(0<\lambda <\lambda _*= \gamma _0^{p-1}\). Since \(w_\gamma > 0\), \((\lambda ,u_\lambda )\) is a positive solution of (3.1). Finally, \(||w_\gamma ||_\infty \ge r\) for all \(\gamma \in [0, \gamma _0]\) implies that

$$\begin{aligned} ||u_\lambda ||_\infty = ||w_\gamma ||_\infty /\gamma \rightarrow \infty , \ \ \ \ \text {as}\ \gamma \rightarrow 0. \end{aligned}$$

This completes the proof. \(\square \)

4 Sublinear Problems

In this final section, we deal with sublinear f, namely \(f\in C([0,1]\times \mathbb {R}^+, \mathbb {R})\) that satisfy (f1) and

(f3) there exists \(b\in X\) with \(b(t) > 0\) in [0, 1], such that

$$\begin{aligned} \lim _{u\rightarrow +\infty }\frac{f(t, u)}{u^q} = b\ \ \ \ \text {uniformly in}\ t\in [0,1], \end{aligned}$$

with \(0\le q <1\).

We will show that in this case, positive solutions of (1.1) branch off from \(\infty \) for \(\lambda _\infty =+\infty \). First, some preliminaries are in order. It is convenient to work on Y. Following the same procedure as for the superlinear case, we employ the rescaling \(w = \gamma u\), \(\lambda = \gamma ^{q-1}\) and use the same notation, with q instead of p and Y instead of X. As before, \((\lambda , u)\) solves (3.4) if and only if \((\gamma , w)\) satisfies (3.6). Note that now, since \(0\le q < 1\), one has that

$$\begin{aligned} \lambda \rightarrow +\infty \ \Leftrightarrow \ \gamma \rightarrow 0. \end{aligned}$$
(4.1)

Lemma 4.1

Let \(q\in (0,1)\) and \(\beta \in [0, \infty )\). Then the nonlinear problem

$$\begin{aligned} \left\{ \begin{aligned}&-v''=b(t)v^{q}, \ \ \ \ \ 0<t<1,\\&v(0)=0, \ \ v'(1)+\beta v(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(4.2)

has a unique positive solution.

Proof

Existence of positive solutions of (4.2) is an immediate consequence of [10, Theorem 1 (i)].

Assume that u, v are positive solutions of (4.2), i.e.

$$\begin{aligned} -u''= & {} b(t)u^q, \ \ \ u(0)=0, \ \ u'(1)+\beta u(1)=0,\\ -v''= & {} b(t)v^q, \ \ \ v(0)=0, \ \ v'(1)+\beta v(1)=0. \end{aligned}$$

Then, u and v are concave down in [0, 1].

We will show that \(u\ge v\) and \(v\ge u\).

Suppose on the contrary that \(u\not \ge v\). We consider the elements \(\phi _r(t)\) of the form

$$\begin{aligned} \phi _r(t):=u(t)-rv(t)\ \ \ \ t\in [0,1]. \end{aligned}$$

We denote by \(r_0\) the value of r such that \(\phi _{r_0}\in K\), \(\phi _r\not \in K\) for \(r>r_0\). The number \(r_0\) is positive since \(u\gg 0\), the element \(\phi _r\in K\) for sufficiently small positive r.

From the definition of \(r_0\), it follows that there exists \(\tau _0\in (0,1]\) such that

$$\begin{aligned} \phi _{r_0}(\tau _0)=u(\tau _0)-r_0v(\tau _0)=0. \end{aligned}$$
(4.3)

On the other hand,

$$\begin{aligned} -\phi ''_{r_0}(t)= & {} -(u(t)-r_0v(t))''=b(t)[u^q(t)-r_0 v^q(t)]\\&\quad \ge b(t)[r^q_0 v^q(t)-r_0 v^q(t)] =b(t)[r^q_0 -r_0 ]v^q(t)>0,\\ \phi _{r_0}(0)= & {} 0,\ \ \ \phi '_{r_0}(1)+\beta \phi _{r_0}(1)=0. \end{aligned}$$

Thus,

$$\begin{aligned} \phi _{r_0}(t)>0\ \ \ \ \ t\in (0,1]. \end{aligned}$$

However, this contradicts (4.3).

Therefore, \(u\ge v\) in [0, 1].

By the same method, we may prove that \(u\le v\) in [0, 1]. \(\square \)

From Lemma 4.1, the problem

$$\begin{aligned} \left\{ \begin{aligned}&-w''=bw^q, \ \ \ \ \ 0<t<1,\\&w(0)=0, \ \ w'(1)+c(0)w(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(4.4)

has a unique positive solution \(w_0\). Moreover, letting \(\lambda _1[bw_0^{q-1}; c(0)]\) denote the first eigenvalue of the linearized problem

$$\begin{aligned} \left\{ \begin{aligned}&-v''=\lambda [b|w_0|^{q-1}] v, \ \ \ \ \ 0<t<1,\\&v(0)=0, \ \ v'(1)+c(0)v(1)=0.\\ \end{aligned} \right. \end{aligned}$$
(4.5)

(4.4) implies that \(v = w_0\) is an eigenfunction corresponding to

$$\begin{aligned} \lambda _1[bw_0^{q-1};c(0)]=1. \end{aligned}$$
(4.6)

Concerning (4.5), it is worth pointing out that, although \(0\le q < 1\), the spectral theory can be carried over; see, for example, a similar version of Asakawa [5] by Ma and Chang [18].

We set

$$\begin{aligned} D_\delta =\{w\in Y : ||w- w_0||_{C^1}\le \delta \} \end{aligned}$$

and extend \(\tilde{F}\) to \(\gamma =0\) by

$$\begin{aligned} \tilde{F}_0(w)=\tilde{F}(0, w)=b|w|^q. \end{aligned}$$

Lemma 4.2

There exists \(\delta > 0\) such that \(\mathcal {K} \tilde{F}: [0, \infty ) \times D_\delta \rightarrow Y\) is compact and continuous.

Proof

When \(0< q < 1,\) the same arguments used for \(p > 1\) show that \(\tilde{F}\) is continuous. Let \(q = 0\) and let \(\delta > 0\) be such that \(w > 0\) for all \(w\in D_\delta \). Plainly, it suffices to show that \(\mathcal {K} \tilde{F}(\gamma _n, w_n)\rightarrow \mathcal {K}\tilde{F}_0(w)\) whenever \(\gamma _n\rightarrow 0\) and \(w_n\rightarrow w\) in Y. Since \(w > 0\) then \(\gamma _n^{-1}w_n\rightarrow +\infty \) point wise in [0, 1]. Notice (f3) with \(q=0\) implies \(\lim _{u\rightarrow \infty } f(x, u)=b\), and subsequently

$$\begin{aligned} G(\gamma _n^{-1} w_n)\rightarrow 0 \ \ \ \ \text {in}\ L^r(0,1), \ \ \forall r\ge 1. \end{aligned}$$

Then

$$\begin{aligned} \mathcal {K}\tilde{F}(\gamma _n, w_n)=\mathcal {K}\tilde{F}_0(w_n)+\mathcal {K}G(\gamma _n^{-1} w_n)\rightarrow \mathcal {K} \tilde{F}_0(w) \end{aligned}$$

in the Sobolev space \(H^{2,r}\), \(\forall r\ge 1\), and the result follows in a standard way. \(\square \)

Theorem 4.1

Let (f1), (f3) and (c1) hold. Then, there exists \(\lambda ^* > 0\) such that (1.1) has positive solutions for all \(\lambda \ge \lambda ^*\). More precisely, there exists a connected set of positive solutions of (1.1) bifurcating from infinity at \(\lambda _\infty =+\infty \).

Proof

By Lemma 4.2, degree theoretic arguments apply to \(S(\gamma , w) = w-\mathcal {K}\tilde{F}(\gamma , w)\). Moreover, note that \(S_0(w) = S(0, w) = w- \mathcal {K}\tilde{F}_0(w)\) is \(C^1\) on \(D_\delta \) and its Fréchet derivative \(S_0'(w_0)\) is given by

$$\begin{aligned} S_0'(w_0)v =\left\{ \begin{aligned}&v-\mathcal {K}'[qbw_0^{q-1}]v, \ \ \ \ \text {if}\quad 0<q<1\\&v, \qquad \qquad \qquad \qquad \text {if}\quad q=0.\\ \end{aligned} \right. \end{aligned}$$

To estimate the first eigenvalue of the linear operator \(\mathcal {K}'[qbw_0^{q-1}]\), let us consider the following

$$\begin{aligned} \left\{ \begin{aligned}&-(w_0+v)''=b(w_0+v)^{q},\\&(w_0+v)(0)=0, (w_0+v)'(1)+c((w_0+v)(1))(w_0+v)(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(4.7)

and

$$\begin{aligned} \left\{ \begin{aligned}&-w_0''=bw_0^{q},\\&w_0(0)=0, w_0'(1)+c(w_0(1))w_0(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(4.8)

where \(v\in Y\). Subtracting (4.7) with (4.8), we get

$$\begin{aligned} \left\{ \begin{aligned}&-v''=b(w_0+v)^{q}-b w_0^{q},\\&v(0)=0,\ v'(1)+\big [c((w_0+v)(1))(w_0+v)(1)-c(w_0(1))w_0(1)\big ]=0.\\ \end{aligned} \right. \nonumber \\ \end{aligned}$$
(4.9)

Since

$$\begin{aligned}{}[c(x)x]'=c'(x)x+c(x)\ge c(0), \end{aligned}$$

we deduce that

$$\begin{aligned} c((w_0+v)(1))(w_0+v)(1)-c(w_0(1))w_0(1)=[c'(\xi )\xi +c(\xi )]v(1)\ (\ge c(0)v(1)\;)\nonumber \\ \end{aligned}$$
(4.10)

for some \(\xi \in \big [\min \{w_0(1),(w_0+v)(1)\},\max \{w_0(1),(w_0+v)(1)\}\big ]\). Because

$$\begin{aligned} b(w_0+v)^{q}-b w_0^{q}=bq w_0^{q-1}v+\circ (||v||_\infty ), \ \ \ \text {as}\ ||v||_\infty \rightarrow 0, \end{aligned}$$

it follows that

$$\begin{aligned} \left\{ \begin{aligned}&-v''=bqw_0^{q-1}v,\\&v(0)=0,\ v'(1)+[c'(\xi )\xi +c(\xi )]v(1)=0,\\ \end{aligned} \right. \end{aligned}$$
(4.11)

which is equivalent to the operator equation

$$\begin{aligned} v=\mathcal {K}'[bqw_0^{q-1}]v. \end{aligned}$$
(4.12)

Combining this with the facts that \(H_c(s,t)\) is decreasing in \(c\in [0, \infty )\) for \((t,s)\in (0,1)\times (0,1)\) and \(\lambda _1[bqw_0^{q-1}, \beta ]\) is increasing in \(\beta \), it concludes that

$$\begin{aligned} \mathcal {K}_{c'(\xi )\xi +c(\xi )}'[qbw_0^{q-1}]< \mathcal {K}'_{c(0)}[qbw_0^{q-1}] \end{aligned}$$

and accordingly

$$\begin{aligned} \lambda _1(\mathcal {K}'[qbw_0^{q-1}; c'(\xi )\xi +c(\xi )])> \lambda _1(\mathcal {K}'[bw_0^{q-1}; c(0)])=1. \end{aligned}$$

Therefore, (4.6) implies that all the characteristic values of \(I-S_0'(w_0)\) are greater than 1. Therefore, we infer that

$$\begin{aligned} \deg (S_0, D_\delta , 0)=1, \ \ \ \ q\in [0,1). \end{aligned}$$

By continuation, we deduce that there exists a connected subset \(\Gamma \) of solutions of \(S(\gamma , w) = 0\) (\(\gamma > 0\)), such that \((0, w_0) \in \bar{\Gamma }\). Moreover, there exists \(\gamma _0 > 0\) such that these solutions are positive provided \(0 < \gamma \le \gamma _0\). By the rescaling \(\lambda = \gamma ^{q-1}\), \(u = w/\gamma \), \(\Gamma \) is transformed into a connected subset \(\Sigma _\infty \) of solutions of (1.1). These solutions are indeed positive for all \(\lambda >\lambda ^*:= \gamma _0^{q-1}\), and according to (4.1), \(\Sigma _\infty \) bifurcates from infinity for \(\lambda _\infty = +\infty \). \(\square \)