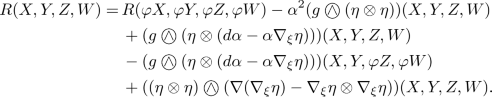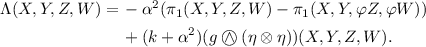Curvature of $C_5\oplus C_{12}$-Manifolds

Abstract

The Chinea–Gonzalez class $C_5\oplus C_{12}$ consists of the almost contact metric manifolds that are locally described as double-twisted product manifolds $I\times _{(\lambda _1,\lambda _2)}{\widehat{M}}$, $I\subset {\mathbb {R}}$ being an open interval, ${\widehat{M}}$ a Kähler manifold and $\lambda _1,\lambda _2$ smooth positive functions. In this article, we investigate the behavior of the curvature of $C_5\oplus C_{12}$-manifolds. Particular attention to the N(k)-nullity condition is given and some local classification theorems in dimension $2n+1\ge 5$ are stated. This allows us to classify $C_5\oplus C_{12}$-manifolds that are generalized Sasakian space forms. In addition, we provide explicit examples of these spaces.

1 Introduction

Double-twisted products play an interesting role in clarifying the interrelation between almost Hermitian (a.H.) and almost contact metric (a.c.m.) manifolds. In fact, the Chinea–Gonzalez class $C_{1-5}\oplus C_{12}={\bigoplus }_{1\le i\le 5}C_i\oplus C_{12}$ consists of the a.c.m. manifolds that are, locally, double-twisted products $]-\epsilon ,\epsilon [\times _{(\lambda _1,\lambda _2)}{\widehat{M}}=(]-\epsilon ,\epsilon [\times {\widehat{M}},\varphi ,\xi ,\eta ,g_{(\lambda _1,\lambda _2)})$, $\epsilon >0$, $({\widehat{M}},{\widehat{J}},{\widehat{g}})$ being an a.H. manifold, $\lambda _1,\lambda _2:]-\epsilon ,\epsilon [\times {\widehat{M}}\rightarrow {\mathbb {R}}$ smooth positive functions and $(\varphi ,\xi ,\eta ,g_{(\lambda _1,\lambda _2)})$ the structure defined in (2.1). The class $C_5\oplus C_{12}$ is the subclass of $C_{1-5}\oplus C_{12}$ consisting of the a.c.m. manifolds that are locally realized as double-twisted products $]-\epsilon ,\epsilon [\times _{(\lambda _1,\lambda _2)}{\widehat{M}}$, where $({\widehat{M}},{\widehat{J}},{\widehat{g}})$ is a Kähler manifold [9]. This points out the interrelation between Kähler and $C_5\oplus C_{12}$-manifolds.

Relevant results involving the behavior of the curvature of Kähler manifolds are well known [13, 17].

In this article, we develop a systematic study of the curvature of $C_5\oplus C_{12}$-manifolds and obtain some classification theorems for those manifolds that satisfy suitable curvature conditions. We also recall that, considering an a.c.m. manifold $(M,\varphi ,\xi ,\eta ,g)$ with fundamental 2-form $\Phi$ and Levi-Civita connection $\nabla$, the $C_5$, $C_{12}$ components of $\nabla \Phi$ are determined by the codifferential $\delta \eta$ and the 1-form $\nabla _{\xi }\eta$, respectively [6]. This allows to specify the defining conditions for the manifolds which fall in the class $C_5\oplus C_{12}$ and in its proper subclasses $C_5$, $C_{12}$.

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold, with $\dim M=2n+1$, and put $\alpha =-\frac{\delta \eta }{2n}$, $V=\nabla _{\xi }\xi$. For any vector fields X, Y, the “cosymplectic defect” $R(X,Y)\circ \varphi -\varphi \circ R(X,Y)$, R denoting the curvature of $\nabla$, depends on $\alpha$, $d\alpha$, V and $\nabla V$. In Sect. 3, we evaluate the cosymplectic defect and derive several consequences, involving the Ricci and the $*$-Ricci tensors, also.

We put our attention to the $(k,\mu )$-condition proving that, in the context of $C_5\oplus C_{12}$-manifolds, it is equivalent to the N(k)-condition. Considering an N(k)-manifold of dimension $2n+1\ge 5$, the function k is expressed as a combination of $\alpha$, $\xi (\alpha )$ and $divV$. Several properties of N(k)-manifolds are derived. In particular, we prove that a manifold with constant sectional curvature k either is a $C_5$-manifold and $k<0$ or it is flat and falls in the class $C_{12}$. Moreover, suitable N(k)-spaces are locally isometric to a warped product $N\times _\lambda N'$, N being a two-dimensional Riemannian manifold of Gaussian curvature k and $N'$ is endowed with an ${\overline{\alpha }}$-Sasakian structure.

Section 6 deals with $C_5\oplus C_{12}$-manifolds that are generalized Sasakian (g.S.) space forms. These spaces are characterized as the N(k)-manifolds with pointwise constant $\varphi$-sectional curvature, say c. Denoting by $M^{2n+1}(c,k)$, $n\ge 2$, a g.S. space form, we prove that the function $c+\alpha ^2$ satisfies a suitable differential equation. This allows us to state a classification theorem. More precisely, if $M^{2n+1}(c,k)$ is a g.S. space form in the class $C_5\oplus C_{12}$ and $\alpha =0$, then either M is cosymplectic or it falls in the class $C_{12}$ and $c=0$. If $\alpha \ne 0$, then either M is locally conformal to $C_{12}$-manifolds that are g.S. space forms with zero $\varphi$-sectional curvature or M is $\alpha$-Kenmotsu and globally conformal to a cosymplectic manifold with constant $\varphi$-sectional curvature.

Finally, in Sect. 7, for any $n\ge 2$, we construct a family of $C_{12}$-manifolds $M^{2n+1}(0,k)$.

Throughout this article, all manifolds are assumed smooth and connected.

2 Preliminaries

Given an almost Hermitian (a.H.) manifold $({\widehat{M}},{\widehat{J}},{\widehat{g}})$, an open interval $I\subset {\mathbb {R}}$ and two smooth positive functions $\lambda _1,\lambda _2:I\times {\widehat{M}}\rightarrow {\mathbb {R}}$, one considers the almost contact metric (a.c.m.) structure $(\varphi ,\xi ,\eta ,g_{(\lambda _1,\lambda _2)})$ on the product manifold $I\times {\widehat{M}}$, acting as

$$\begin{aligned} \begin{aligned}&\varphi \Bigl (a\frac{\partial }{\partial t},X\Bigl )=(0,{\widehat{J}}X), \quad \eta \Bigl (a\frac{\partial }{\partial t},X\Bigl )=a\lambda _1, \\&\xi =\frac{1}{\lambda _1}\Bigl (\frac{\partial }{\partial t},0\Bigl ), \quad g_{(\lambda _1,\lambda _2)}=\lambda _1^2\pi _1^{*}(\mathrm{d}t\otimes \mathrm{d}t)+\lambda _2^2\pi _2^{*}({\widehat{g}}), \end{aligned} \end{aligned}$$

(2.1)

for any $a\in {\mathfrak {F}}(I \times {\widehat{M}}), X\in \Gamma (T{\widehat{M}})$, $\pi _1:I\times {\widehat{M}}\rightarrow I$, $\pi _2:I\times {\widehat{M}}\rightarrow {\widehat{M}}$ denoting the canonical projections. Note that $g_{(\lambda _1,\lambda _2)}$ is the double-twisted product of the Euclidean metric $g_0$ and ${\widehat{g}}$ [16]. The a.c.m. manifold $I \times _{(\lambda _1,\lambda _2)}{\widehat{M}}=(I \times {\widehat{M}},\varphi ,\xi ,\eta ,g_{(\lambda _1,\lambda _2)})$ is named the double-twisted product manifold of $(I,g_0)$ and $({\widehat{M}},{\widehat{J}},{\widehat{g}})$ by $(\lambda _1,\lambda _2)$. If $\lambda _1=1$, $I\times _{(1,\lambda _2)}{\widehat{M}}$ is denoted by $I\times _{\lambda _2}{\widehat{M}}$ and is called the twisted product manifold of $(I,g_0)$ and $({\widehat{M}},{\widehat{J}},{\widehat{g}})$ by $\lambda _2$. If $\lambda _2=1$, the manifold $I\times _{(\lambda _1,1)}{\widehat{M}}$ is denoted by $_{\lambda _1}I\times {\widehat{M}}$. In the case that $\lambda _1$ is independent of the Euclidean coordinate t and $\lambda _2$ only depends on t, $I \times _{(\lambda _1,\lambda _2)}{\widehat{M}}$ is called a double-warped product manifold, the metric $g_{(\lambda _1,\lambda _2)}$ being just the double-warped product metric of $g_0$ and ${\widehat{g}}$ by $(\lambda _1,\lambda _2)$. If $\lambda _2$ only depends on t, $I\times _{\lambda _2}{\widehat{M}}$ is said to be a warped product manifold.

Applying the theory developed in [6, 9], we are able to specify the Chinea–Gonzalez class of the mentioned manifolds. In particular, if $\dim {\widehat{M}}=2$, then $I \times _{(\lambda _1,\lambda _2)}{\widehat{M}}$ belongs to the class $C_5\oplus C_{12}$. In the case that $\dim {\widehat{M}}=2n\ge 4$, $({\widehat{J}},{\widehat{g}})$ is a Kähler structure and the function $\lambda _2$ is constant on ${\widehat{M}}$, then $I \times _{(\lambda _1,\lambda _2)}{\widehat{M}}$ is a $C_5\oplus C_{12}$-manifold. Furthermore, if $\lambda _2=1$, $_{\lambda _1}I\times {\widehat{M}}$ falls in the class $C_{12}$. It is also known that any warped product manifold $I\times _{\lambda _2}{\widehat{M}}$, where $({\widehat{M}},{\widehat{J}},{\widehat{g}})$ is a Kähler manifold, belongs to the class $C_5$ and is called an $\alpha$-Kenmotsu manifold, where $\alpha =\xi (\log \lambda _2)$. More generally, any double-warped product manifold $I\times _{(\lambda _1,\lambda _2)}{\widehat{M}}$, such that $({\widehat{M}},{\widehat{J}},{\widehat{g}})$ is Kähler and both the functions $\lambda _1$, $\lambda _2$ are non constant, is in the class $C_5\oplus C_{12}{\setminus } (C_5\cup C_{12})$. This shows that $C_5$, $C_{12}$ are proper subclasses of $C_5\oplus C_{12}$. Cosymplectic manifolds set up the class $C=C_5\cap C_{12}$.

In Table 1, we list the defining conditions of any a.c.m. manifold $(M,\varphi ,\xi ,\eta ,g)$ which falls in $C_5\oplus C_{12}$ or in its subclasses. These conditions are formulated in terms of the covariant derivatives $\nabla \varphi$, $\nabla \eta$, $\nabla$ denoting the Levi-Civita connection of M. Note that, since $\nabla _{\xi }\xi$ is the vector field g-associated to the 1-form $\nabla _{\xi }\eta$, the vanishing of $\nabla _{\xi }\xi$ is equivalent to the condition that the considered manifold is in the class $C_5$, namely it is an $\alpha$-Kenmotsu manifold. Moreover, it is known that any $C_5\oplus C_{12}$-manifold satisfies

$$\begin{aligned}&\nabla _X\xi =\alpha (X-\eta (X)\xi )+\eta (X)\nabla _{\xi }\xi ,\quad X\in \Gamma (TM) \end{aligned}$$

(2.2)

$$\begin{aligned}&\mathrm{d}\eta =\eta \wedge \nabla _{\xi }\eta ,\quad \mathrm{d}(\nabla _{\xi }\eta )=-(\alpha \nabla _{\xi }\eta +\nabla _{\xi }(\nabla _{\xi }\eta ))\wedge \eta , \end{aligned}$$

(2.3)

where $\dim M=2n+1$ and $\alpha =-\frac{\delta \eta }{2n}$. Furthermore, if $\dim M\ge 5$, the Lee form of M is $\omega =-\alpha \eta$ and it is closed. Applying (2.3), one has

$$\begin{aligned} \mathrm{d}\alpha =\xi (\alpha )\eta +\alpha \nabla _{\xi }\eta . \end{aligned}$$

(2.4)

In the sequel, given a $C_5\oplus C_{12}$-manifold $(M,\varphi ,\xi ,\eta ,g)$ we will denote by D, $D^{\perp }$ the mutually orthogonal distributions associated with the subbundles $\text {Ker}\eta$ and $\text {span}\{\xi \}$ of the tangent bundle TM, respectively. These distributions are both totally umbilical foliations. More precisely, $H=-\alpha \xi _{|_N}$ is the mean curvature vector field of any leaf $(N,g')$ of D, $g'$ being the metric induced by g. Furthermore, $(J=\varphi _{|_{TN}},g')$ is a Kähler structure on N. For the sake of simplicity, we will denote by V the vector field $\nabla _{\xi }\xi$, which represents the mean curvature vector field of any integral curve of $D^{\perp }$.

Table 1 Defining conditions of some Chinea-Gonzalez classes

Applying the main results in [9, 16], one obtains a local description of a $C_5\oplus C_{12}$-manifold $(M,\varphi ,\xi ,\eta ,g)$. More precisely, for any point $x\in M$, there exist an open neighborhood U of x, $\epsilon >0$, a Riemannian manifold $(F,{\widehat{g}})$, two smooth positive functions $\lambda _1, \lambda _2:]-\epsilon ,\epsilon [\times F\rightarrow {\mathbb {R}}$ and an isometry $f:(]-\epsilon ,\epsilon [\times F, g_{(\lambda _1,\lambda _2)})\rightarrow (U,g_{|_{U}})$ such that the canonical foliations of the product manifold correspond to the distributions D, $D^{\perp }$. It follows that $f_{*}(\frac{1}{\lambda _1}\frac{\partial }{\partial t})=\xi _{|_U}$ and, for any $t\in ]-\epsilon ,\epsilon [$, $f_t(F)$ is a leaf of D, where $f_t=f(t,\cdot )$. Note that there exists $t_0\in ]-\epsilon ,\epsilon [$ such that ${\widehat{g}}=f_{t_0}^*(g_{|_{U}})$. Furthermore, considering the Kähler structure $({\widehat{J}}=(f_{*}^{-1}\circ \varphi \circ f_{*})_{|_{TF}},{\widehat{g}})$ on F and the corresponding a.c.m. manifold $]-\epsilon ,\epsilon [\times _{(\lambda _1,\lambda _2)} F$ defined as in (2.1), then the map $f:]-\epsilon ,\epsilon [\times _{(\lambda _1,\lambda _2)} F\rightarrow (U,\varphi _{|_U},\xi _{|_U},\eta _{|_U},g_{|_U})$ is an almost contact isometry.

Finally, if $(M,\varphi ,\xi ,\eta ,g)$ is a $C_{12}$-manifold, then D is a totally geodesic foliation. By [16], it follows that $\lambda _2=1$ so that M is, locally, realized as the a.c.m. manifold $_{\lambda }]-\epsilon ,\epsilon [\times F$, F being a Kähler manifold.

3 Some Curvature Relations

In this section, we focus on the main properties of the curvature R of the Levi-Civita connection $\nabla$ of a $C_5\oplus C_{12}$-manifold $(M,\varphi ,\xi ,\eta ,g)$, $R(X,Y)=[\nabla _X,\nabla _Y]-\nabla _{[X,Y]}$. For the Riemannian curvature, we adopt the convention $R(X,Y,Z,W)=g(R(Z,W,Y),X)=-g(R(X,Y,Z),W)$. This allows us to obtain an explicit expression of the cosymplectic defect, namely the (0, 4)-tensor field $\Lambda$ acting as

$$\begin{aligned} \Lambda (X,Y,Z,W)=R(X,Y,Z,W)-R(X,Y,\varphi Z,\varphi W). \end{aligned}$$

We also state some properties of the Ricci tensor $\rho$ and the $*$-Ricci tensor $\rho ^{*}$ and evaluate the mixed sectional curvature, denoted by $K(X,\xi )$, for any unit vector X orthogonal to $\xi$.

Proposition 3.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold. For any vector fields X, Y, Z on M one has:

$$\begin{aligned} R(X,Y)\varphi Z= & {} \varphi (R(X,Y)Z)+\alpha (\alpha g(\varphi Y,Z)+\eta (Y)g(\varphi V,Z))X\\&-\alpha (\alpha g(\varphi X,Z)+\eta (X)g(\varphi V,Z))Y\\&+(Y(\alpha )\eta (Z)+\alpha ^2g(Y,Z)+\alpha \eta (Y)g(V,Z))\varphi X\\&-(X(\alpha )\eta (Z)+\alpha ^2g(X,Z)+\alpha \eta (X)g(V,Z))\varphi Y\\&+\alpha (\eta (X)g(\varphi Y,Z)-\eta (Y)g(\varphi X,Z))V\\&+(\eta (X)(\alpha g(Y,Z)-\eta (Z)g(V,Y))-\eta (Y)(\alpha g(X,Z)\\&-\eta (Z)g(V,X)))\varphi V\\&+\eta (Z)(\eta (X)\nabla _Y\varphi V-\eta (Y)\nabla _X\varphi V)\\&+(X(\alpha )g(\varphi Y,Z)-Y(\alpha )g(\varphi X,Z)\\&+g(\varphi V,Z)(\eta (X)g(V,Y)-\eta (Y)g(V,X))\\&-\eta (X)g(\nabla _Y\varphi V,Z)+\eta (Y)g(\nabla _X\varphi V,Z))\xi . \end{aligned}$$

Proof

Since M is a $C_5\oplus C_{12}$-manifold, for any $X,Y\in \Gamma (TM)$ one has

$$\begin{aligned} (\nabla _X\varphi )Y=\alpha (g(\varphi X,Y)\xi -\eta (Y)\varphi X)-\eta (X)(g(V,\varphi Y)\xi +\eta (Y)\varphi V).\nonumber \\ \end{aligned}$$

(3.1)

Let X, Y, Z be vector fields on M. By direct calculus, applying (2.2), (3.1), we have

$$\begin{aligned} \begin{aligned} R(X,Y)\varphi Z=\,&\varphi (R(X,Y)Z)+\nabla _X((\nabla _Y\varphi )Z)-\nabla _Y((\nabla _X\varphi )Z)-(\nabla _{[X,Y]}\varphi )Z\\&+(\nabla _X\varphi )(\nabla _YZ)-(\nabla _Y\varphi )(\nabla _XZ)\\ =\,&\varphi (R(X,Y)Z)-2d\eta (X,Y)(\eta (Z)\varphi V-g(\varphi V,Z)\xi )\\&-\alpha \eta (Z)(\nabla _X\varphi Y-\nabla _Y\varphi X-\varphi [X,Y])\\&+X(\alpha )(g(\varphi Y,Z)\xi -\eta (Z)\varphi Y)-Y(\alpha )(g(\varphi X,Z)\xi -\eta (Z)\varphi X)\\&+\alpha ^2(g(\varphi Y,Z)(X-\eta (X)\xi )-g(\varphi X,Z)(Y-\eta (Y)\xi ))\\&+\alpha (\eta (X)g(\varphi Y,Z)-\eta (Y)g(\varphi X,Z))V\\&+\eta (Z)(\eta (X)\nabla _Y\varphi V-\eta (Y)\nabla _X\varphi V)\\&+\alpha g(\varphi V,Z)(\eta (Y)X-\eta (X)Y)\\&-(\nabla _X\eta )Z(\alpha \varphi Y+\eta (Y)\varphi V)+(\nabla _Y\eta )Z(\alpha \varphi X+\eta (X)\varphi V)\\&+(\alpha (g(\nabla _X\varphi Y,Z)-g(\nabla _Y\varphi X,Z)-g(\varphi [X,Y],Z))\\&+\eta (Y)g(\nabla _X\varphi V,Z)-\eta (X)g(\nabla _Y\varphi V,Z))\xi . \end{aligned} \end{aligned}$$

(3.2)

By (3.1) we also have

$$\begin{aligned} \begin{aligned} \nabla _X\varphi Y-\nabla _Y\varphi X=\,&\varphi [X,Y]+(\nabla _X\varphi )Y-(\nabla _Y\varphi )X\\ =\,&\varphi [X,Y]+\alpha (\eta (X)\varphi Y-\eta (Y)\varphi X)\\&+(2\alpha g(\varphi X,Y)+\eta (X)g(\varphi V,Y)-\eta (Y)g(\varphi V,X))\xi . \end{aligned} \end{aligned}$$

Then, substituting into (3.2) and applying (2.2), (2.3), one obtains the statement. $\square$

Corollary 3.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M=2n+1$. The following properties hold:

• (i) For any $X,Y\in \Gamma (TM)$, we have

  $$\begin{aligned} \begin{aligned} R(X,Y)\xi =\,&X(\alpha )(Y-\eta (Y)\xi )-Y(\alpha )(X-\eta (X)\xi )+\alpha ^2(\eta (X)Y-\eta (Y)X)\\&+(\eta (X)g(V,Y)-\eta (Y)g(V,X))(V-\alpha \xi )\\&-\eta (X)\nabla _YV+\eta (Y)\nabla _XV\\ =\,&X(\alpha )(Y-\eta (Y)\xi )-Y(\alpha )(X-\eta (X)\xi )\\&+\eta (X)(R(\xi ,Y)\xi -\xi (\alpha )Y)-\eta (Y)(R(\xi ,X)\xi -\xi (a)X). \end{aligned} \end{aligned}$$

• (ii) For any unit vector X orthogonal to $\xi$, one has

  $$\begin{aligned} K(X,\xi )=-(\xi (\alpha )+\alpha ^2)-g(V,X)^2+g(\nabla _XV,X). \end{aligned}$$

• (iii) The Ricci tensor satisfies

  $$\begin{aligned}&\rho (\xi ,\xi )=-2n(\xi (\alpha )+\alpha ^2)-divV, \\&\rho (X,\xi )=-(2n-1)(X-\eta (X)\xi )(\alpha )+\eta (X)\rho (\xi ,\xi ). \end{aligned}$$

Proof

Let X, Y be vector fields on M. By Proposition 3.1, we get

$$\begin{aligned} R(X,Y)\xi =-\varphi ^2(R(X,Y)\xi )=\,&(Y(\alpha )+\alpha ^2\eta (Y))\varphi ^2X\\&-(X(\alpha )+\alpha ^2\eta (X))\varphi ^2Y\\&-\eta (X)(\alpha \eta (Y)-g(V,Y))V\\&+\eta (Y)(\alpha \eta (X)-g(V,X))V\\&+\eta (X)\varphi (\nabla _Y\varphi V)-\eta (Y)\varphi (\nabla _X\varphi V). \end{aligned}$$

Moreover, using (3.1), we have

$$\begin{aligned} \eta (X)\varphi (\nabla _Y\varphi V)-\eta (Y)\varphi (\nabla _X\varphi V)=\,&-\eta (X)(\nabla _Y\varphi )\varphi V+\eta (Y)(\nabla _X\varphi )\varphi V\\&-\eta (X)\nabla _YV+\eta (Y)\nabla _XV\\ =\,&-\alpha (\eta (X)g(V,Y)-\eta (Y)g(V,X))\xi \\&-\eta (X)\nabla _YV+\eta (Y)\nabla _XV. \end{aligned}$$

Thus, substituting into the previous formula, we obtain the first equality in (i). The second relation follows by a direct calculus.

To prove property (ii) it is enough to apply (i) observing that, for any $X\in TM$, $X\perp \xi$, $||X||=1$, one has $K(\xi ,X)=-g(R(\xi ,X)\xi ,X)$.

Let $\{e_1,\dots ,e_{2n},e_{2n+1}=\xi \}$ be a local orthonormal frame on M. Since V is orthogonal to $\xi$, applying (ii) we have

$$\begin{aligned} \rho (\xi ,\xi )=\sum _{i=1}^{2n}K(\xi ,e_i)=\,&-2n(\xi (\alpha )+\alpha ^2)-||V||^2+\sum _{i=1}^{2n}g(\nabla _{ei}V,e_i)\\ =\,&-2n(\xi (\alpha )+\alpha ^2)+\sum _{i=1}^{2n+1}g(\nabla _{ei}V,e_i). \end{aligned}$$

Thus, the first formula in (iii) is proved. Finally, by (i) we obtain

$$\begin{aligned} \rho (X,\xi )&=\sum _{i=1}^{2n}R(X,e_i,\xi ,e_i)\\&=-2nX(\alpha )+\sum _{i=1}^{2n}e_i(\alpha )g(X-\eta (X)\xi ,e_i)+\eta (X)\rho (\xi ,\xi )+2n\eta (X)\xi (\alpha )\\&=-(2n-1)(X-\eta (X)\xi )(\alpha )+\eta (X)\rho (\xi ,\xi ). \end{aligned}$$

$\square$

We recall that, given two (symmetric) (0, 2)-tensor fields P, Q, the Kulkarni–Nomizu product acts as

(3.3)

In particular, for the sake of simplicity, one puts .

Proposition 3.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M=2n+1$. For any $X,Y,Z,W\in \Gamma (TM)$ one has:

Proof

We only outline the proof, which requires a quite long calculation.

Let X, Y, Z, W be vector fields on M. Starting by the equality

$$\begin{aligned} \Lambda (X,Y,Z,W)=g(R(X,Y)\varphi Z-\varphi (R(X,Y)Z),\varphi W)+g(R(X,Y)\xi ,Z)\eta (W), \end{aligned}$$

one applies Proposition 3.1, Corollary 3.1 and adopts the notation

$$\begin{aligned} \nabla (\nabla _{\xi }\eta )(X,Y)=(\nabla _X(\nabla _{\xi }\eta ))Y=g(\nabla _XV,Y). \end{aligned}$$

Then the statement follows by direct calculation, also applying (3.3). $\square$

Remark 3.1

In [9], the cosymplectic defect of a manifold that belongs to a class containing $C_5\oplus C_{12}$ as a proper subclass was evaluated with respect to the minimal U(n)-connection. Considering a manifold in the class $C_5\oplus C_{12}$, it is easy to verify that the formulas in Proposition 3.2 and in [9] are equivalent.

Corollary 3.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold with $\dim M=2n+1$. The following properties hold:

• (i) For any $X,Y\in \Gamma (D)$, we get

  $$\begin{aligned} \Lambda (X,Y,X,Y)=-\alpha ^2(||X||^2||Y||^2-g(X,Y)^2-g(X,\varphi Y)^2). \end{aligned}$$

• (ii) For any $X,Y\in \Gamma (TM)$, we have

  $$\begin{aligned} (\rho -\rho ^{*})(X,Y)=\,&-((2n-1)\alpha ^2+\xi (\alpha ))g(X,Y)-\alpha ^2\eta (X)\eta (Y)\\&-((2n-1)X(\alpha )+divV\eta (X)-\alpha g(V,X))\eta (Y)\\&-(2(n-1)\alpha \eta (X)+g(V,X))g(V,Y)\\&+g(\nabla _XV-\eta (X)\nabla _{\xi }V,Y). \end{aligned}$$

• (iii) Denoting by $\tau$, $\tau ^{*}$ the scalar and $*$-scalar curvatures, we get

  $$\begin{aligned} \tau -\tau ^{*}=-2(2n^2\alpha ^2+2n\xi (\alpha )+divV). \end{aligned}$$

• (iv) The skew-symmetric component of $\rho ^{*}$ is given by

  $$\begin{aligned} \rho ^{*}(X,Y)-\rho ^{*}(Y,X)=\,&(2n-1)(X(\alpha )\eta (Y)-Y(\alpha )\eta (X))\\&+2(n-1)\alpha (g(V,Y)\eta (X)-g(V,X)\eta (Y)). \end{aligned}$$

Proof

Property (i) is a direct consequence of Proposition 3.2.

Let X, Y be vector fields on M. With respect to a local orthonormal frame $\{e_1,\dots ,e_{2n},\xi \}$, we write $(\rho -\rho ^{*})(X,Y)=\sum _{i=1}^{2n}\Lambda (X,e_i,Y,e_i)-R(X,\xi ,\xi ,Y)$ and apply Proposition 3.2 and Corollary 3.1. So, we obtain (ii) and then (iii). Furthermore, since $\rho$ is symmetric, by (ii) we have

$$\begin{aligned} \rho ^{*}(X,Y)-\rho ^{*}(Y,X)=\,&(2n-1)(X(\alpha )\eta (Y)-Y(\alpha )\eta (X)\\&-\alpha g(V,X)\eta (Y)+\alpha g(V,Y)\eta (X))\\&-g(\nabla _XV-\eta (X)\nabla _{\xi }V,Y)+g(\nabla _YV-\eta (Y)\nabla _{\xi }V,X). \end{aligned}$$

On the other hand, applying (2.3) we get

$$\begin{aligned} 0=\,&g(\nabla _XV,Y)-g(\nabla _YV,X)+(\alpha g(V,X)+g(\nabla _{\xi }V,X))\eta (Y)\\&-(\alpha g(V,Y)+g(\nabla _{\xi }V,Y))\eta (X). \end{aligned}$$

Hence, substituting into the previous formula, we obtain (iv). $\square$

Proposition 3.3

Let $(M,\varphi ,\xi ,\eta ,g)$ be an a.c.m. manifold with $\dim M\ge 5$. If M is $\alpha$-Kenmotsu or a $C_{12}$-manifold, then $\rho ^{*}$ is symmetric.

Proof

Since $\dim M\ge 5$, by (2.4) and Corollary 3.2, for any $X,Y\in \Gamma (TM)$ we have

$$\begin{aligned} \rho ^{*}(X,Y)-\rho ^{*}(Y,X)=\alpha (g(V,X)\eta (Y)-g(V,Y)\eta (X)). \end{aligned}$$

$\square$

Proposition 3.4

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold with $\dim M\ge 5$. The following properties are satisfied:

• (i) For any $X,Y,Z,W\in \Gamma (TM)$, one has

  

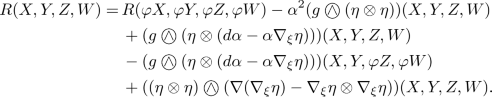
• (ii) For any $X,Y\in \Gamma (TM)$, one has

  $$\begin{aligned} \rho (X,Y)=\,&\rho (\varphi X,\varphi Y)-(2n\alpha ^2+divV)\eta (X)\eta (Y)\\&-(2(n-1)\alpha (\nabla _{\xi }\eta )Y+(\nabla _{\xi }(\nabla _{\xi }\eta ))Y+Y(\alpha ))\eta (X)\\&+(\alpha (\nabla _{\xi }\eta )X-(2n-1)X(\alpha ))\eta (Y)\\&+(\nabla _X(\nabla _{\xi }\eta ))Y-(\nabla _{\xi }\eta )X(\nabla _{\xi }\eta )Y\\&-(\nabla _{\varphi X}(\nabla _{\xi }\eta ))\varphi Y+(\nabla _{\xi }\eta )\varphi X(\nabla _{\xi }\eta )\varphi Y. \end{aligned}$$

Proof

We observe that, for any $X,Y,Z,W\in \Gamma (TM)$, one has

$$\begin{aligned} R(X,Y,Z,W)-R(\varphi X,\varphi Y,\varphi Z,\varphi W)=\Lambda (X,Y,Z,W)+\Lambda (\varphi Z,\varphi W,X,Y). \end{aligned}$$

Thus, property (i) follows by Proposition 3.2.

Considering an adapted local orthonormal frame $\{e_1,\dots ,e_n,e_{n+1}=\varphi e_1,\dots ,e_{2n}=\varphi e_n,\xi \}$ on M, for any $X,Y\in \Gamma (TM)$, we write

$$\begin{aligned} \rho (X,Y)-\rho (\varphi X,\varphi Y)=\,&\sum _{i=1}^{2n}(R(X,e_i,Y,e_i)-R(\varphi X,\varphi e_i,\varphi Y,\varphi e_i))\\&+g(R(X,\xi )\xi ,Y)-g(R(\varphi X,\xi )\xi ,\varphi Y). \end{aligned}$$

Then, applying (i) and Corollary 3.1, one proves (ii). $\square$

Remark 3.2

We point out that, being $\rho$ symmetric, the tensor field considered at the right side of formula (ii) in Proposition 3.4 has to be symmetric. This is equivalent to the condition

$$\begin{aligned} 0=\,&2(n-1)((X(\alpha )-\alpha (\nabla _{\xi }\eta )X)\eta (Y)-(Y(\alpha )-\alpha (\nabla _{\xi }\eta )Y)\eta (X))\\&+Q(X,Y)-Q(Y,X)-Q(\varphi X,\varphi Y)+Q(\varphi Y,\varphi X), \end{aligned}$$

for any $X,Y\in \Gamma (TM)$, where $Q=\nabla (\nabla _{\xi }\eta )+(\nabla _{\xi }(\nabla _{\xi }\eta )+\alpha \nabla _{\xi }\eta )\otimes \eta$. In fact, by (2.3) we know that Q is symmetric. Thus, if $\dim M=3$, the above equality reduces to an identity. If $\dim M\ge 5$, by (2.4) we obtain that $(d\alpha -\alpha \nabla _{\xi }\eta )\otimes \eta$ is symmetric, also.

4 The k-Nullity Condition

In contact geometry, the behavior of the tensor field $h=\frac{1}{2}L_{\xi }\varphi$, $L_{\xi }$ denoting the Lie derivative with respect to $\xi$, plays an important role for the classification of manifolds satisfying suitable curvature conditions [2, 3].

The following result shows that the vector field V of any $C_5\oplus C_{12}$-manifold specifies h.

Lemma 4.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold. For any $X\in \Gamma (TM)$ one has $h(X)=-\frac{1}{2}g(V,\varphi X)\xi$. Therefore, h vanishes if and only if M falls in the class $C_5$.

Proof

By direct calculation, for any $X\in \Gamma (TM)$ one has

$$\begin{aligned} 2h(X)=(\nabla _{\xi }\varphi )X-\nabla _{\varphi X}\xi +\varphi (\nabla _X\xi )=-(\nabla _{\xi }\eta )\varphi X\xi =-g(V,\varphi X)\xi . \end{aligned}$$

Since V is orthogonal to $\xi$, we obtain $h=0$ if and only if $V=0$. $\square$

Lemma 4.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold. Assume the existence of smooth functions $k,\mu$ on M such that

$$\begin{aligned} R(X,Y)\xi =k(\eta (Y)X-\eta (X)Y)+\mu (\eta (Y)h(X)-\eta (X)h(Y)), \end{aligned}$$

(4.1)

for any $X,Y\in \Gamma (TM)$. Then one has $\mu h=0$ and $d\alpha =\xi (\alpha )\eta$.

Proof

By Corollary 3.1 and the hypothesis, for any $X,Y\in \Gamma (D)$, we have

$$\begin{aligned} X(\alpha )Y-Y(\alpha )X=R(X,Y)\xi =0. \end{aligned}$$

It follows that $X(\alpha )=0$ so that $d\alpha =\xi (\alpha )\eta$.

Given X orthogonal to $\xi$, by Corollary 3.1 and Lemma 4.1, we obtain

$$\begin{aligned} -kX+\frac{1}{2}\mu g(V,\varphi X)\xi&=-R(X,\xi )\xi \\&=(\xi (\alpha )+\alpha ^2)X+g(V,X)(V-\alpha \xi )-\nabla _XV. \end{aligned}$$

Taking the inner product by $\xi$, we get $-\alpha g(V,X)-g(\nabla _XV,\xi )=\frac{1}{2}\mu g(V,\varphi X)$. Moreover, applying (2.2) one has $g(\nabla _XV,\xi )=-g(\nabla _X\xi ,V)=-\alpha g(V,X)$. It follows that $\mu g(V,\varphi X)=0$, for any $X\in \Gamma (TM)$. $\square$

Condition (4.1) was first considered in [4] in the context of contact manifolds, $k,\mu$ being suitable real numbers. Contact manifolds satisfying (4.1), also named $(k,\mu )$-manifolds, have been deeply studied ( [3] and References therein). We call N(k)-space an a.c.m. manifold $(M,\varphi ,\xi ,\eta ,g)$ admitting a smooth function k such that

$$\begin{aligned} R(X,Y)\xi =k(\eta (Y)X-\eta (X)Y),\quad X,Y\in \Gamma (TM). \end{aligned}$$

(4.2)

Lemma 4.2 clarifies that conditions (4.1), (4.2) are equivalent in the case of a $C_5\oplus C_{12}$-manifold.

In [15], the authors proved that the curvature of an $\alpha$-Kenmotsu manifold always satisfies (4.2), where $k=-(\xi (\alpha )+\alpha ^2)$. The next results show that this property does not extend to $C_5\oplus C_{12}$-manifolds.

Proposition 4.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M=2n+1\ge 5$. If M is an N(k)-manifold, the following properties hold:

• (i) $d\alpha =\xi (\alpha )\eta$, $\alpha V=0$.

• (ii) $k=-(\xi (\alpha )+\alpha ^2)-\frac{1}{2n}divV$.

• (iii) $\alpha divV=0$.

• (iv) For any $X\in \Gamma (TM)$, one has

  $$\begin{aligned} \nabla _XV=-\frac{1}{2n}divV(X-\eta (X)\xi )+g(V,X)V+\eta (X)\nabla _{\xi }V. \end{aligned}$$

Proof

By Lemma 4.2, we have $d\alpha =\xi (\alpha )\eta$ and comparing with (2.4) we obtain $\alpha V=0$. Then, also applying Corollary 3.1, for any $X\in \Gamma (D)$ one gets

$$\begin{aligned} kX=R(X,\xi )\xi =-(\xi (\alpha )+\alpha ^2)X-g(V,X)V+\nabla _XV. \end{aligned}$$

(4.3)

Let $\{e_1,\dots ,e_{2n},e_{2n+1}=\xi \}$ be a local orthonormal frame on M. By (4.3), we have

$$\begin{aligned} 2nk=\sum _{i=1}^{2n}g(R(e_i,\xi )\xi ,e_i)&=-2n(\xi (\alpha )+\alpha ^2)-||V||^2+\sum _{i=1}^{2n}g(\nabla _{e_i}V,e_i)\\&=-2n(\xi (\alpha )+\alpha ^2)-divV. \end{aligned}$$

Then, (ii) follows. Moreover, since $\alpha V=0$, we get $0=\sum _{i=1}^{2n}g(\nabla _{e_i}(\alpha V),e_i)=d\alpha (V)-\alpha divV=-\alpha divV$. This proves (iii). Finally, using (4.3), for any X orthogonal to $\xi$, we have

$$\begin{aligned} \nabla _XV=\Bigl (-\frac{1}{2n}divV\Bigl ) X+g(V,X)V. \end{aligned}$$

This relation entails (iv). $\square$

We point out that the distribution D on any manifold as in Proposition 4.1 is spherical. In fact, the equation $d\alpha =\xi (\alpha )\eta$ means that the leaves of D are extrinsic spheres.

Proposition 4.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M=2n+1\ge 5$. Assume that M is an N(k)-manifold. Then, for any $U,X\in \Gamma (D)$, one has:

• (i) $R(U,X)V=(U(k)-kg(V,U))X-(X(k)-kg(V,X))U$.

• (ii) $U(k+\frac{1}{2n}divV)=(k+\frac{1}{2n}divV)(\nabla _{\xi }\eta )U$.

Proof

Let U, X, Y be vector fields on M. By direct calculation, applying (2.2) and (4.2), one has

$$\begin{aligned} \begin{aligned} (\nabla _UR)(X,Y)\xi =\,&U(k)(\eta (Y)X-\eta (X)Y)+k\eta (U)(g(V,Y)X-g(V,X)Y)\\&+\alpha k(g(U,Y)X-g(U,X)Y)-\alpha R(X,Y)U-\eta (U)R(X,Y)V. \end{aligned}\nonumber \\ \end{aligned}$$

(4.4)

Now we consider U, X orthogonal to $\xi$ and apply the second Bianchi identity, namely

$$\begin{aligned} (\nabla _UR)(X,\xi )\xi +(\nabla _XR)(\xi ,U)\xi +(\nabla _{\xi }R)(U,X)\xi =0. \end{aligned}$$

By(4.4) we get

$$\begin{aligned} U(k)X-X(k)U+k(g(V,X)U-g(V,U)X)-R(U,X)V=0. \end{aligned}$$

Hence, (i) follows. Furthermore, applying Proposition 4.1, we have

$$\begin{aligned} R(U,X)V&=\nabla _U(\nabla _XV)-\nabla _X(\nabla _UV)-\nabla _{[U,X]}V\\&=-\frac{1}{2n}divV(g(V,X)U-g(V,U)X)\\&\quad -\frac{1}{2n}(U(divV)X-X(divV)U). \end{aligned}$$

Thus, comparing with (i), one has

$$\begin{aligned}&U\Bigl (k+\frac{1}{2n}divV\Bigr )X-X\Bigl (k+\frac{1}{2n}divV\Bigr )U\\&\quad =\Bigl (k+\frac{1}{2n}divV\Bigr )(g(V,U)X-g(V,X)U). \end{aligned}$$

It follows that (ii) holds. $\square$

Remark 4.1

By Proposition 4.1, it is easy to verify that property (ii) of Proposition 4.2 is equivalent to the condition

$$\begin{aligned} U(\xi (\alpha ))=\xi (\alpha )g(V,U),\quad U\in \Gamma (D). \end{aligned}$$

Proposition 4.3

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M=2n+1\ge 5$. Assume that M is an N(k)-manifold. For any $X,Y,Z,W\in \Gamma (TM)$ one has:

• (i) $\begin{aligned} R(X,Y)\varphi Z=\,&\varphi (R(X,Y)Z)+(k+\alpha ^2)\eta (X)(\eta (Z)\varphi Y-g(\varphi Y,Z)\xi ) \\&-(k+\alpha ^2)\eta (Y)(\eta (Z)\varphi X-g(\varphi X,Z)\xi )\\&+\alpha ^2(g(\varphi Y,Z)X-g(\varphi X,Z)Y\\&+g(Y,Z)\varphi X-g(X,Z)\varphi Y). \end{aligned}$

• (ii)

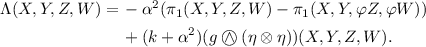
Proof

Let X, Y, Z, W be vector fields on M. By Propositions 3.1, 4.1 we have

$$\begin{aligned} R(X,Y)\varphi Z=\,&\varphi (R(X,Y)Z)+\xi (\alpha )\eta (Z)(\eta (Y)\varphi X-\eta (X)\varphi Y)\\&+\alpha ^2(g(\varphi Y,Z)X-g(\varphi X,Z)Y+g(Y,Z)\varphi X-g(X,Z)\varphi Y)\\&+\eta (Z)(g(V,X)\eta (Y)-g(V,Y)\eta (X))\varphi V\\&+\eta (Z)(\eta (X)\nabla _Y\varphi V-\eta (Y)\nabla _X\varphi V)\\&+(\xi (\alpha )(\eta (X)g(\varphi Y,Z)-\eta (Y)g(\varphi X,Z))\\&+g(\varphi V,Z)(\eta (X)g(V,Y)-\eta (Y)g(V,X))\\&-\eta (X)g(\nabla _Y\varphi V,Z)+\eta (Y)g(\nabla _X\varphi V,Z))\xi . \end{aligned}$$

Moreover, applying (3.1) and Proposition 4.1, we get

$$\begin{aligned} \nabla _X\varphi V=(\nabla _X\varphi )V+\varphi (\nabla _XV)=g(V,X)\varphi V-\Bigl (\frac{1}{2n}divV\Bigl )\varphi X+\eta (X)\varphi (\nabla _{\xi }V). \end{aligned}$$

Substituting into the previous formula and using property (ii) of Proposition 4.1, (i) follows.

Finally, property (ii) is obtained by (i) and the relation

$$\begin{aligned} \Lambda (X,Y,Z,W)= & {} g(R(X,Y)\varphi Z-\varphi (R(X,Y)Z),\varphi W)\\&+k\eta (W)(\eta (Y)g(X,Z)-\eta (X)g(Y,Z)). \end{aligned}$$

$\square$

Theorem 4.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M\ge 5$. Assume that M has constant sectional curvature k. Then either M is an $\alpha$-Kenmotsu manifold and $k=-\alpha ^2$ or M is flat and falls in the class $C_{12}$.

Proof

Let x be a point of M and consider unit vectors $X,Y\in T_xM$ such that $g_x(X,Y)=g_x(X,\varphi Y)=\eta _x(X)=\eta _x(Y)=0$. Since M has constant sectional curvature, we have $R=k\pi _1$, so that

$$\begin{aligned} R_x(X,Y)\varphi _x Y-\varphi _x(R_x(X,Y)Y)=-k\varphi _x X. \end{aligned}$$

On the other hand, by Proposition 4.3, one obtains

$$\begin{aligned} R_x(X,Y)\varphi _x Y-\varphi _x(R_x(X,Y)Y)=\alpha (x)^2\varphi _x X. \end{aligned}$$

It follows $k+\alpha (x)^2=0$. Thus, $\alpha$ is a constant function. Since $\alpha V=0$, one of the following two cases occurs

• (i) $\alpha \ne 0$, $V=0$, $k=-\alpha ^2$,

• (ii) $\alpha =0$, $k=0$.

In case (i), M falls in the class $C_5$, namely it is $\alpha$-Kenmotsu, $\alpha =\text {constant}$ and $k=-\alpha ^2<0$. In case (ii), M is flat and falls in $C_{12}$. $\square$

We remark that, for any $\alpha \in {\mathbb {R}}$, $\alpha \ne 0$, an $\alpha$-Kenmotsu manifold with constant sectional curvature $k=-\alpha ^2$ is locally a warped product $]-\epsilon ,\epsilon [\times _{\lambda } F$, where F is a flat Kähler manifold and $\lambda (t)=a\exp (-|\alpha |t)$, $a=\text {const}>0$. On the other hand, a flat $C_{12}$-manifold is locally realized as a product $_{\lambda }]-\epsilon ,\epsilon [\times F$, F being a flat Kähler manifold and $\lambda :]-\epsilon ,\epsilon [\times F\rightarrow {\mathbb {R}}$ a smooth positive function. The action of $\lambda$ will be specified in Sect. 7.

Proposition 4.4

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold such that $\dim M\ge 5$. If M is an N(k)-manifold, the curvature satisfies the following identities:

$$\begin{aligned} \begin{aligned} R(X,Y,Z,W)=\,&R(X,Y,\varphi Z,\varphi W)+R(\varphi X,Y,Z,\varphi W)\\&+R(X,\varphi Y,Z,\varphi W)\\&+k\eta (W)(\eta (Y)g(X,Z)-\eta (X)g(Y,Z)), \end{aligned} \end{aligned}$$

(4.5)

(4.6)

for any $X,Y,Z,W\in \Gamma (TM)$.

Proof

The statement follows by Proposition 4.3 observing that, for any vector fields X, Y, Z, W on M, one has:

$$\begin{aligned} R(X,Y,Z,W)=\,&R(X,Y,\varphi Z,\varphi W)+R(\varphi X,Y,Z,\varphi W)+R(X,\varphi Y,Z,\varphi W)\\&+\Lambda (X,Y,Z,W)-\Lambda (Z,\varphi W,X,\varphi Y)+\eta (Y)R(Z,\varphi W,\xi ,\varphi X) \end{aligned}$$

and

$$\begin{aligned} R(X,Y,Z,W)=R(\varphi X,\varphi Y,\varphi Z,\varphi W)+\Lambda (X,Y,Z.W)+\Lambda (\varphi Z,\varphi W,X,Y). \end{aligned}$$

$\square$

Remark 4.2

If $k=\text {const}=1$, properties (4.5) and (4.6) correspond to the identities, called $G_2$, $G_3$ identities, introduced and studied in [14]. Obviously, the curvature of any $\alpha$-Kenmotsu manifold satisfies (4.5), (4.6), being $k=-(\xi (\alpha )+\alpha ^2)$.

5 Local Description of N(k)-Manifolds

We are going to provide some local descriptions of a $C_5\oplus C_{12}$-manifold $(M,\varphi ,\xi ,\eta ,g)$ satisfying the N(k)-condition, examining suitable distributions on M. Assuming that V is nowhere zero, we can consider the rank 2 distribution $D_1=\text {span}\{\xi ,V\}$ and its orthogonal complement $D_1^{\perp }=\text {ker}\eta \cap \text {ker}\nabla _{\xi }\eta$. By (2.3), one gets that $D_1^{\perp }$ is integrable. Moreover, Proposition 4.1 entails that M falls in the class $C_{12}$. It follows that, if $D^{\perp }=\text {span}\{\xi \}$ is spherical, equivalently $\nabla _{\xi }V=-||V||^2\xi$, M is, locally, the a.c.m. manifold $_{\lambda }]-\epsilon ,\epsilon [\times F$, F being a Kähler manifold and $\lambda :F\rightarrow {\mathbb {R}}^{*}_{+}$ a smooth function [9].

We recall that a Riemannian submanifold N of an a.c.m. manifold $(M,\varphi ,\xi ,\eta ,g)$ is said to be a semi-invariant $\xi ^{\perp }$-submanifold if the vector field $\xi \in \Gamma (T^{\perp }N)$ and there exist two orthogonal distributions, ${\overline{D}}$ and ${\overline{D}}^{\perp }$, on N such that $TN={\overline{D}}\oplus {\overline{D}}^{\perp }$, $\varphi ({\overline{D}})={\overline{D}}$ and $\varphi {\overline{D}}^{\perp }\subseteq T^{\perp }N$ [5].

In the sequel, for the sake of simplicity, by $V\ne 0$ we mean that V is nowhere zero on M.

Proposition 5.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_{12}$-manifold such that $\dim M=2n+1\ge 5$, $V\ne 0$ and $\nabla _{\xi }V=-||V||^2\xi$. If M is an N(k)-manifold, then the distribution $D_1$ is totally geodesic and $D_1^{\perp }$ is spherical. Furthermore, each leaf of $D_1$ is an anti-invariant submanifold of M with Gaussian curvature k and each leaf of $D_1^{\perp }$ is a semi-invariant $\xi ^{\perp }$-submanifold of M admitting a $C_6$-structure.

Proof

By hypotheses and Proposition 4.1, we have that $k=-\frac{1}{2n}divV$ and

$$\begin{aligned} \nabla _XV=kX+g(V,X)V-\eta (X)(||V||^2+k)\xi , \quad X\in \Gamma (TM). \end{aligned}$$

(5.1)

It follows that

$$\begin{aligned} \mathrm{d}(||V||^2)=2(||V||^2+k)\nabla _{\xi }\eta . \end{aligned}$$

(5.2)

By (2.3) and (5.2), we get $0=d(||V||^2+k)\wedge \nabla _{\xi }\eta -(||V||^2+k)\nabla _{\xi }(\nabla _{\xi }\eta )\wedge \eta$. Since $\nabla _{\xi }V=-||V||^2\xi$, it follows that $\nabla _{\xi }(\nabla _{\xi }\eta )\wedge \eta =0$ and thus

$$\begin{aligned} \mathrm{d}k=\frac{1}{||V||^2}V(k)\nabla _{\xi }\eta . \end{aligned}$$

(5.3)

Applying (2.2) and (5.1), it is easy to verify that the distribution $D_1$ is totally geodesic. Moreover, considering a leaf N of $D_1$, we have $\varphi (TN)\subseteq T^{\perp }N$, namely N is anti-invariant, and the Gauss curvature of N is given by $k(x)=\frac{R_x(\xi ,V,\xi ,V)}{||V||^2}$, $x\in N$.

Let $N'$ be a leaf of $D_1^{\perp }$. For any $X,Y\in \Gamma (TN')$, by (2.2), (5.1), we obtain $g(\nabla _XY,\xi )=0$ and $g(\nabla _XY,V)=-kg(X,Y)$. By the Gauss formula, it follows that $N'$ is totally umbilical with mean curvature vector field $H=-\frac{k}{||V||^2}V$. Moreover, denoting by $\nabla ^{\perp }$ the normal connection of $N'$, we have

$$\begin{aligned} \nabla ^{\perp }_XH=-\Biggl (X\Biggl (\frac{k}{||V||^2}\Biggl )V+\frac{k}{||V||^2}\nabla ^{\perp }_XV\Biggl ), \quad X\in \Gamma (TN'). \end{aligned}$$

On the other hand, by (5.2), (5.3), we get $X(\frac{k}{||V||^2})=0$. Moreover, using (5.1), we have $\nabla _X^{\perp }V=0$. Substituting into the above equation, it follows that $N'$ is an extrinsic sphere.

Now, we consider the distribution $\text {span}\{\varphi V\}$ on $N'$ and denote by ${\overline{D}}$ its orthogonal complement on $N'$. Since $\varphi ^2V=-V\in \Gamma (T^{\perp }N')$, we have $\varphi (\text {span}\{\varphi V\})\subseteq T^{\perp }N'$. Moreover, for any $X\in \Gamma ({\overline{D}})$ one has $g(\varphi X,\varphi V)=0$, namely $\varphi ({\overline{D}})={\overline{D}}$. This means that $N'$ is a semi-invariant $\xi ^{\perp }$-submanifold of M.

Finally, putting $g'=g_{|_{TN'\times TN'}}$, $\xi '=\frac{1}{||V||}\varphi V$, $\eta '={\xi '}^{b}$, we consider the (1,1)-tensor field $\varphi '$on $N'$ such that $\varphi '(\xi ')=0$ and $\varphi '(X)=\varphi X$, for any $X\perp \xi '$. In particular, for any $X\in \Gamma (TN')$ one has

$$\begin{aligned} \varphi '(X)=\varphi X+\frac{1}{||V||^2}g(\varphi V,X)V. \end{aligned}$$

(5.4)

It is easy to check that $(\varphi ',\xi ',\eta ',g')$ is an a.c.m. structure on $N'$. Furthermore, we denote by $\nabla '$ the Levi-Civita connection of $(N',g')$, apply the Gauss formula and obtain

$$\begin{aligned} \nabla _XY=\nabla '_XY-\frac{k}{||V||^2}g(X,Y)V, \quad X,Y\in \Gamma (TN'). \end{aligned}$$

Then, by direct calculation, also applying (5.1), (5.4), one has

$$\begin{aligned} (\nabla '_X\varphi ')Y=-\frac{k}{||V||}(g'(X,Y)\xi '-\eta '(Y)X), \quad X,Y\in \Gamma (TN'). \end{aligned}$$

It follows that $(N',\varphi ',\xi ',\eta ',g')$ is an ${\overline{\alpha }}$-Sasakian manifold, with ${\overline{\alpha }}=-\frac{k}{||V||}$, and it falls in the class $C_6$ [3, 6]. $\square$

Applying Proposition 5.1 and the decomposition theorem of Hiepko, we are able to state the following classification theorem.

Theorem 5.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_{12}$-manifold such that $\dim M=2n+1\ge 5$, $V\ne 0$ and $\nabla _{\xi }V=-||V||^2\xi$. If M is an N(k)-manifold, then (M, g) is locally isometric to a warped product $N\times _{\lambda }N'$, where $\dim N=2$, N has Gaussian curvature k and $N'$ is an ${\overline{\alpha }}$-Sasakian manifold, ${\overline{\alpha }}=-\frac{k}{||V||}$.

Corollary 5.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_{12}$-manifold such that $\dim M=2n+1\ge 5$, $V\ne 0$ and $\nabla _{\xi }V=-||V||^2\xi$. If M is flat, then (M, g) is locally isometric to a Riemannian product $N\times N'$, $\dim N=2$ and N, $N'$ are flat manifolds. Furthermore, $N'$ admits a cosymplectic structure.

Proof

Since M is flat, M is an N(0)-manifold. Hence, using Proposition 5.1, both the distributions $D_1$ and $D_1^{\perp }$ are totally geodesic. In fact, for any $X\in \Gamma (D_1^{\perp })$ one has $\nabla _XV=0=\nabla _X\xi$. By Theorem 5.1, (M, g) is locally isometric to a Riemannian product $N\times N'$, where N is a flat 2-dimensional manifold and $N'$ admits an ${\overline{\alpha }}$-Sasakian structure, with ${\overline{\alpha }}=0$. $\square$

We end this section considering the distribution $D'=\text {span}\{\xi ,V,\varphi V\}$ on M. As in the previous case, we assume $V\ne 0$ and $D^{\perp }$ spherical.

Proposition 5.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_{12}$-manifold such that $\dim M=2n+1\ge 5$, $V\ne 0$ and $\nabla _{\xi }V=-||V||^2\xi$. If M is an N(k)-manifold, the distribution $D'$ is totally geodesic and each leaf of $D'$ is an N(k)-manifold belonging to the class $C_{12}$.

Proof

By Proposition 4.1, we get $k=-\frac{1}{2n}divV$. Moreover, applying (2.2), (5.1) and the defining condition of the class $C_{12}$ (see Table 1), an easy calculus entails

$$\begin{aligned}&\nabla _V\xi =0=\nabla _{\varphi V}\xi =\nabla _{\xi }\varphi V,\\&\nabla _VV=(||V||^2+k)V, \quad \nabla _V\varphi V=(||V||^2+k)\varphi V, \\&\nabla _{\varphi V}V=k\varphi V, \quad \nabla _{\varphi V}\varphi V=-kV. \end{aligned}$$

The above formulas, together with the hypothesis $\nabla _{\xi }V=-||V||^2\xi$, imply that the distribution $D'$ is totally geodesic.

Let $N'$ be a leaf of $D'$. It is easy to verify that $(\varphi '=\varphi _{|_{TN'}},\xi '=\xi _{|_{TN'}},\eta '=\eta _{|_{TN'}},g'=g_{|_{TN'\times TN'}})$ is an a.c.m. structure on $N'$. Since $N'$ is totally geodesic, $(N',\varphi ',\xi ',\eta ',g')$ is an N(k)-manifold and falls in the class $C_{12}$. $\square$

Theorem 5.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_{12}$-manifold such that $\dim M=2n+1\ge 5$, $V\ne 0$ and $\nabla _{\xi }V=-||V||^2\xi$. If M is flat, then (M, g) is locally isometric to a Riemannian product $N'\times N''$, where $N'$ is a three-dimensional $C_{12}$-manifold, $N''$ is a Kähler manifold and $N'$, $N''$ are both flat.

Proof

Since M is flat, M is an N(0)-manifold. Let $D'^{\perp }$ be the orthogonal complement of $D'$. By (2.2), (5.1), for any $X,Y\in \Gamma (D'^{\perp })$ we get $g(\nabla _XY,\xi )=0=g(\nabla _XY,V)=g(\nabla _XY,\varphi V)$. Hence, the distribution $D'^{\perp }$ is totally geodesic and each leaf $N''$ of $D'^{\perp }$ is totally geodesic and flat. Moreover, $(J''=\varphi _{|_{TN''}},g''=g_{|_{TN''\times TN''}})$ is a Kähler structure on $N''$. Then, also applying Proposition 5.2, we get the statement. $\square$

6 The Case of Generalized Sasakian Space Forms

In this section, we consider a $C_5\oplus C_{12}$-manifold $(M,\varphi ,\xi ,\eta ,g)$ which is a generalized Sasakian space form (g.S. space form), namely M admits three smooth functions $f_1$, $f_2$, $f_3$ such that the curvature tensor satisfies

$$\begin{aligned} R=f_1\pi _1+f_2S+f_3T, \end{aligned}$$

(6.1)

where $\pi _1$, S, T are the tensor fields acting as

$$\begin{aligned}&\pi _1(X,Y,Z)=g(Y,Z)X-g(X,Z)Y,\\&S(X,Y,Z)=g(X,\varphi Z)\varphi Y-g(Y,\varphi Z)\varphi X+2g(X,\varphi Y)\varphi Z,\\&T(X,Y,Z)=\eta (X)\eta (Z)Y-\eta (Y)\eta (Z)X+g(X,Z)\eta (Y)\xi -g(Y,Z)\eta (X)\xi . \end{aligned}$$

This class of a.c.m. manifolds was introduced in [1] and subsequently studied by a number of mathematicians from several points of view. In particular, in [8] it was proved that M is a g.S. space form if and only if M is an N(k)-manifold with pointwise constant $\varphi$-sectional curvature c and, for any $X,Y\in \Gamma (D)$, the cosymplectic defect satisfies $\Lambda (X,Y,X,Y)=l(||X||^2||Y||^2-g(X,Y)^2-g(X,\varphi Y)^2)$, l being a smooth function on M.

Now, also applying Corollary 3.2 and Proposition 4.1, it is easy to obtain the following result.

Proposition 6.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold with $\dim M=2n+1\ge 5$. The following conditions are equivalent:

• (i) M is a g.S. space form.

• (ii) M is an N(k)-manifold with pointwise constant $\varphi$-sectional curvature c.

Moreover, if one of the previous conditions holds, one has $k=-(\xi (\alpha )+\alpha ^2)-\frac{1}{2n}divV$, $f_1=\frac{c-3\alpha ^2}{4}$, $f_2=\frac{c+\alpha ^2}{4}$, $f_3=f_1-k=\frac{c+\alpha ^2}{4}+\xi (\alpha )+\frac{1}{2n}divV$.

Taking into account Proposition 6.1, we denote by $M^{2n+1}(c,k)$ a g.S. space form with pointwise constant $\varphi$-sectional curvature c and satisfying the k-nullity condition.

Proposition 6.2

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold. If $M^{2n+1}(c,k)$, $n\ge 2$, is a g.S. space form, the following properties hold:

• (i) For any point $x_0\in M$, the leaf $(N,J,g')$ of D through $x_0$ is a Kähler manifold with constant holomorphic sectional curvature $(c+\alpha ^2)(x_0)$.

• (ii) $dc=\xi (c)\eta$.

• (iii) For any $X\in \Gamma (D)$, one has $X(\xi (c))=\xi (c)g(V,X)$.

• (iv) $cV=0$.

• (v) $dk=\xi (k)\eta +k\nabla _{\xi }\eta$.

Proof

Let $x_0\in M$ and $(N,J=\varphi _{|_{TN}},g'=g_{|_{TN\times TN}})$ be the leaf of the distribution D through $x_0$. Since M is a $C_5\oplus C_{12}$-manifold, we know that $(J,g')$ is a Kähler structure on N and N is totally umbilical with mean curvature vector field $H=-\alpha \xi _{|_N}$. Denoting by $R'$ the Riemannian curvature of N and applying the Gauss equation, for any $x\in N$ and any unit vector $X\in T_xN$, we get

$$\begin{aligned} R'_x(X,J_xX,X,J_xX)=R_x(X,\varphi _x X,X,\varphi _x X)+\alpha (x)^2=(c+\alpha ^2)(x). \end{aligned}$$

Since $\dim N\ge 4$, it follows that N has constant holomorphic sectional curvature $(c+\alpha ^2)_{|_N}$. So, we obtain (i). On the other hand, by Proposition 6.1, M is an N(k)-manifold. Hence, applying Proposition 4.1, $\alpha$ is constant on N. This implies that c is constant on N. It follows that the function c is constant on any leaf of D, that is (ii) holds.

By (ii), we obtain $d(\xi (c)\eta )=0$. So, applying (2.3), one has $(d\xi (c)-\xi (c)\nabla _{\xi }\eta )\wedge \eta =0$ and (iii) follows.

Finally, using the second Bianchi identity, one has $f_2V=0$ and $dk=\xi (k)\eta -f_3\nabla _{\xi }\eta$ (cf. [7], Section 4). Applying Propositions 4.1, 6.1, we easily obtain (iv) and (v). $\square$

Remark 6.1

In the same hypotheses of Proposition 6.2, applying the main results in [9], we have that M is locally almost contact isometric to a double-twisted product manifold $]-\epsilon ,\epsilon [\times _{(\lambda _1,\lambda _2)} F$, where $\epsilon >0$, $(F,{\widehat{J}},{\widehat{g}})$ is a Kähler manifold with constant holomorphic sectional curvature $(c+\alpha ^2)_{|_F}$ and $\lambda _1,\lambda _2: ]-\epsilon ,\epsilon [\times F \rightarrow {\mathbb {R}}$ are smooth positive functions.

Proposition 6.3

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold. If $M^{2n+1}(c,k)$, $n\ge 2$, is a g.S. space form, then the following differential equation holds:

$$\begin{aligned} d(c+\alpha ^2)=-2(c+\alpha ^2)\alpha \eta . \end{aligned}$$

(6.2)

Proof

Let U, X, Y be vector fields on M and $Z\in \Gamma (D)$. By (6.1), we have

$$\begin{aligned} \begin{aligned} (\nabla _UR)(X,Y,Z)=\,&U(f_1)\pi _1(X,Y,Z)+U(f_2)S(X,Y,Z)+U(f_3)T(X,Y,Z)\\&+f_2(\nabla _US)(X,Y,Z)+f_3(\nabla _UT)(X,Y,Z), \end{aligned} \end{aligned}$$

(6.3)

where $f_1$, $f_2$, $f_3$ are related to c, k as in Proposition 6.1. Furthermore, it is easy to verify the following relations:

$$\begin{aligned} \begin{aligned} (\nabla _US)(X,Y,Z)=\,&g(\varphi Y,Z)(\nabla _U\varphi )X-g((\nabla _U\varphi )Z,Y)\varphi X\\&-g(\varphi X,Z)(\nabla _U\varphi )Y+g((\nabla _U\varphi )Z,X)\varphi Y\\&+2g(\varphi Y,X)(\nabla _U\varphi )Z+2g((\nabla _U\varphi )Y,X)\varphi Z, \end{aligned} \\ \begin{aligned} (\nabla _UT)(X,Y,Z)=\,&(\eta (X)Y-\eta (Y)X)(\nabla _U\eta )Z\\&+(g(X,Z)(\nabla _U\eta )Y-g(Y,Z)(\nabla _U\eta )X)\xi \\&+(g(X,Z)\eta (Y)-g(Y,Z)\eta (X))\nabla _U\xi . \end{aligned} \end{aligned}$$

To apply the second Bianchi identity, using the above formulas, Propositions 4.1, 6.1, 6.2 and (2.2), (3.1), a direct calculus entails

$$\begin{aligned}&U(f_1)=\frac{1}{4}\xi (c-3\alpha ^2)\eta (U), \quad U(f_2)=\frac{1}{4}\xi (c+\alpha ^2)\eta (U), \end{aligned}$$

(6.4)

$$\begin{aligned}&f_2\underset{(U,X,Y)}{\sigma }(\nabla _US)(X,Y,Z)=2\alpha f_2\Bigl (\underset{(U,X,Y)}{\sigma }(g(\varphi X,Z)\eta (Y)-g(\varphi Y,Z)\eta (X)) \varphi U\nonumber \\&\qquad \qquad +2\underset{(U,X,Y)}{\sigma }g(\varphi Y,X)\eta (U)\varphi Z\Bigl ), \end{aligned}$$

(6.5)

$$\begin{aligned}&f_3\underset{(U,X,Y)}{\sigma }(\nabla _UT)(X,Y,Z)=f_3\Bigl (2\alpha \underset{(U,X,Y)}{\sigma }(g(X,Z)\eta (Y)-g(Y,Z)\eta (X))U\nonumber \\&\qquad \qquad +\underset{(U,X,Y)}{\sigma }\eta (U)(\eta (X)Y-\eta (Y)X)g(V,Z)\nonumber \\&\qquad \qquad +\underset{(U,X,Y)}{\sigma }(g(X,Z)g(V,Y)-g(Y,Z)g(V,X))\eta (U)\xi \Bigl ), \end{aligned}$$

(6.6)

where $\sigma$ represents the cyclic sum over U, X, Y.

Now, choosing $U=\xi$, $Y=Z$, $X\perp U,Y,\varphi Y$, and substituting into (6.3)–(6.6), the second Bianchi identity gives

$$\begin{aligned} \Bigl (\frac{1}{4}\xi (c-3\alpha ^2)+2\alpha f_3\Bigl )||Z||^2X+(X(f_3)-f_3g(V,X))||Z||^2\xi =0. \end{aligned}$$

This implies $\xi (c-3\alpha ^2)+8\alpha f_3=0$. Using (iii) in Proposition 4.1 and Proposition 6.1, it follows that $0=\xi (c-3\alpha ^2)+2\alpha (c+\alpha ^2)+8\alpha \xi (\alpha )= \xi (c+\alpha ^2)+2\alpha (c+\alpha ^2)$. On the other hand, by Propositions 4.1, 6.2, we know that $d(c+\alpha ^2)=\xi (c+\alpha ^2)\eta$. Hence, the statement holds. $\square$

Now, we are able to classify g.S. space forms belonging to the class $C_5\oplus C_{12}$.

Theorem 6.1

Let $(M,\varphi ,\xi ,\eta ,g)$ be a $C_5\oplus C_{12}$-manifold. If $M^{2n+1}(c,k)$, $n\ge 2$, is a g.S. space form, then exactly one of the following cases occurs:

• (i) M is cosymplectic and c is constant.

• (ii) M falls in the class $C_{12}{\setminus } C$ and $c=0$.

• (iii) $\alpha \ne 0$ and $c+\alpha ^2=0$. Moreover, there exist an open covering $\{U_i\}_{i\in I}$ of M and, for any $i\in I$, a smooth function $\sigma _i:U_i\rightarrow {\mathbb {R}}$ such that $(U_i,\varphi _i=\varphi _{|_{U_i}},\xi _i=\exp (-\sigma _i)\xi _{|_{U_i}},\eta _i=\exp (\sigma _i)\eta _{|_{U_i}},g_i=\exp (2\sigma _i)g_{|_{U_i}})$ is a g.S. space form with zero $\varphi$-sectional curvature, which falls in the class $C_{12}$.

• (iv) M is $\alpha$-Kenmotsu and the function $c+\alpha ^2$, which is nowhere zero, has constant sign. Moreover, M is globally conformal to a cosymplectic manifold with constant $\varphi$-sectional curvature $sign(c+\alpha ^2)$.

Proof

If $\alpha =0$, by Proposition 6.3, we get that c is a constant function. If $c\ne 0$, applying Proposition 6.2, it follows that the vector field V vanishes, so that M is a cosymplectic manifold. If $c=0$, by Proposition 6.1 and (6.1), the curvature tensor of M is given by $R=\Bigl (\frac{1}{2n}divV\Bigl ) T$. In this case, if $divV\ne 0$, then M is a $C_{12}$-manifold but it is not cosymplectic. If $divV=0$, M is flat and either M is cosymplectic or M falls in the class $C_{12}{\setminus } C$. We conclude that, if $\alpha =0$, one of the cases, (i) and (ii), occurs.

Now, we suppose that $\alpha \ne 0$. Since the Lee form $\omega =-\alpha \eta$ is closed, by Proposition 4.4 in [9], M is a locally conformal $C_{12}$-manifold, namely there exist an open covering $\{U_i\}_{i\in I}$ of M and, for any $i\in I$, a smooth function $\sigma _i:U_i\rightarrow {\mathbb {R}}$ such that $U_i$ is endowed with the $C_{12}$-structure $(U_i,\varphi _i=\varphi _{|_{U_i}},\xi _i=\exp (-\sigma _i)\xi _{|_{U_i}},\eta _i=\exp (\sigma _i)\eta _{|_{U_i}},g_i=\exp (2\sigma _i)g_{|_{U_i}})$ and $d\sigma _i=\omega _{|_{U_i}}$.

The Levi-Civita connections of the local metrics $g_i$ fit up to the Weyl connection ${\overline{\nabla }}$ acting as

$$\begin{aligned} {\overline{\nabla }}_XY=\nabla _XY-\alpha \eta (X)Y-\alpha \eta (Y)X+\alpha g(X,Y)\xi , \quad X,Y\in \Gamma (TM). \end{aligned}$$

Furthermore, fixed $i\in I$ and denoting by ${\overline{R}}$ the (0, 4)-curvature tensor of ${\overline{\nabla }}$, it is well known that in $U_i$ one has

(6.7)

where $P=\nabla \omega -\omega \otimes \omega +\frac{1}{2}||\omega ||^2g$. Applying Proposition 4.1 and (2.2), it is easy to verify the following relations

Substituting into (6.7) and applying (6.1), Proposition 6.1, it follows that

$$\begin{aligned} {\overline{R}}=\frac{c+\alpha ^2}{4}(\pi _1+S)+\Bigl (\frac{c+\alpha ^2}{4}+\frac{1}{2n}divV\Bigl )T. \end{aligned}$$

(6.8)

Since $\omega$ is closed, by (6.2) and the connectedness of M, one of the following two cases occurs

• (a) $c+\alpha ^2=0$,

• (b) $c+\alpha ^2\ne 0$ everywhere.

In case (a), Eq. (6.8) reduces to ${\overline{R}}=\Bigl (\frac{1}{2n}divV\Bigl ) T$. To rewrite this equation with respect to the metrics $g_i$, $i\in I$, we put $V_i={\overline{\nabla }}_{\xi _i}\xi _i$ and denote by $T_i$ the tensor field on $U_i$ defined as T. An easy calculation entails

$$\begin{aligned} V_i=\exp (-2\sigma _i)V_{|_{U_i}},\quad divV_i=\exp (-2\sigma _i){divV}_{|_{U_i}}, \quad T_{|_{U_i}}=\exp (-2\sigma _i)T_i. \end{aligned}$$

It follows that

$$\begin{aligned} {\overline{R}}_{|_{U_i}}=\Bigl (\frac{1}{2n}divV_i\Bigl ) T_i, \quad i\in I. \end{aligned}$$

Combining the above formula with Proposition 6.1, we get that the $C_{12}$-manifolds $(U_i,\varphi _i,\xi _i,\eta _i,g_i)$ are g.S. space forms with zero $\varphi$-sectional curvature. Hence, (iii) holds.

Finally, we examine case (b). Since M is connected, the function $c+\alpha ^2$ has constant sign. Moreover, by Propositions 4.1, 6.2, we have $(c+\alpha ^2)V=0$. This implies that $V=0$, namely M is an $\alpha$-Kenmotsu manifold. On the other hand, solving (6.2), we get $\omega =d\log {\sqrt{|c+\alpha ^2|}}$. Since $\omega$ is exact, M is globally conformal to the a.c.m. manifold $(M,\varphi ,\frac{1}{\sqrt{|c+\alpha ^2|}}\xi ,\sqrt{|c+\alpha ^2|}\eta ,|c+\alpha ^2|g)$, which is cosymplectic [15]. Furthermore, with respect to the metric ${\overline{g}}=|c+\alpha ^2|g$, (6.8) becomes

$$\begin{aligned} {\overline{R}}=\frac{1}{4}\frac{c+\alpha ^2}{|c+\alpha ^2|}(\overline{\pi _1}+{\overline{S}}+{\overline{T}})=\frac{1}{4}sign(c+\alpha ^2)(\overline{\pi _1}+{\overline{S}}+{\overline{T}}). \end{aligned}$$

The above equation means that $(M,\varphi ,\frac{1}{\sqrt{|c+\alpha ^2|}}\xi ,\sqrt{|c+\alpha ^2|}\eta ,|c+\alpha ^2|g)$ has constant $\varphi$-sectional curvature $sign(c+\alpha ^2)$. Hence, (iv) occurs. $\square$

Remark 6.2

In [7], the authors gave a local classification of g.S. space forms $M^{2n+1}(f_1,f_2,f_3)$, $n\ge 2$, assuming that for any $i=1,2,3$, if the function $f_i$ does not vanish, then $f_i\ne 0$ everywhere. The authors proved that nine cases can occur and these cases are not mutually exclusive. Obviously, a restriction on the Chinea–Gonzalez class of the g.S. space form entails that some of the mentioned cases have to be excluded. Comparing the result stated in Theorem 6.1 with main Theorem 1.3 in [7], we get that a $C_5\oplus C_{12}$-manifold $M^{2n+1}(c,k)$ has to satisfy one of four cases listed in [7], namely the ones denoted by (a), (e), (f), (g). We also remark that in our context the hypothesis $f_i=0$ or $f_i\ne 0$ everywhere is needless.

7 Examples

In Theorem 4.1, we have shown that a $C_5\oplus C_{12}$-manifold $(M,\varphi ,\xi ,\eta ,g)$ with $\dim M=2n+1\ge 5$ and constant sectional curvature is either an $\alpha$-Kenmotsu manifold or a flat $C_{12}$-manifold. Note that, as remarked in Section 4, in the first case, it is known that M is locally described as a warped product. Furthermore, the hyperbolic space ${\mathbb {H}}^{2n+1}(-\alpha ^2)$ is the local model of space forms carrying a non-cosymplectic $\alpha$-Kenmotsu structure.

More generally, in Theorem 6.1 we have classified g.S. space forms $M^{2n+1}(c,k)$. Taking into account case (ii), we are going to provide a method for constructing a whole family of g.S. space forms $M^{2n+1}(0,k)$ falling in the class $C_{12}{\setminus } C$.

Let $(J_0,g_0)$ be the canonical Kähler structure on ${\mathbb {R}}^{2n}$, $n\ge 2$, $I\subset {\mathbb {R}}$ an open interval and $\lambda :I\times {\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}$ a smooth positive function. We know that the a.c.m. manifold $M=$ $_{\lambda }I\times {\mathbb {R}}^{2n}$, defined as in (2.1), falls in the class $C_{12}{\setminus } C$. According to Proposition 6.1, Theorem 6.1 and formula (6.1), the condition that M is a g.S. space form $M^{2n+1}(0,k)$ is equivalent to require that its curvature tensor satisfies

$$\begin{aligned} R=\Bigl (\frac{1}{2n}divV\Bigl ) T=-kT. \end{aligned}$$

(7.1)

Using the curvature formulas in [16], we have

$$\begin{aligned} R(X,\xi )Z=(g(\nabla _X(\text {grad}\log \lambda ),Z)+X(\log \lambda )Z(\log \lambda ))\xi , \quad X,Z\in \Gamma (D), \end{aligned}$$

where $\nabla$ is the Levi-Civita connection on $(M,g=g_{(\lambda ,1)})$ and $\text {grad}$ is evaluated with respect to g. By an easy calculation, also considering Corollary 3.1 and Proposition 4.1, one can check that (7.1) is equivalent to the condition

$$\begin{aligned} g(\nabla _X(\text {grad}\log \lambda ),Z)+X(\log \lambda )Z(\log \lambda )=-kg(X,Z), \quad X,Z\in \Gamma (D). \end{aligned}$$

Considering the orthonormal frame $\{\frac{\partial }{\partial x^1},\dots ,\frac{\partial }{\partial x^{2n}},\xi \}$ on M, the above equation corresponds to the following PDE’s system:

$$\begin{aligned} \frac{\partial ^2\lambda }{\partial x^i\partial x^j}+k\lambda \delta _{ij}=0, \quad i,j=1,\dots ,2n. \end{aligned}$$

(7.2)

Hence, for any $i\ne j$, one has $\frac{\partial ^2\lambda }{\partial x^i\partial x^j}=0$. It follows that $\lambda (t,x^1,\dots ,x^{2n})=\sum _{k=1}^{2n}a_k(t,x^k)$, where $a_k$ is a function only depending on t and $x^k$. Substituting into (7.2) and assuming $i=j$, we get $\frac{\partial ^2 a_i}{\partial (x^i)^2}=-k\lambda$. This implies that the function $k\lambda$ only depends on t. Putting $-k\lambda =2C(t)$, it follows that $a_i(t,x^i)=C(t)(x^i)^2+B_i(t)x^i+E_i(t)$, for any $i=1,\dots ,2n$. We can conclude that (7.1) is satisfied if and only if

$$\begin{aligned} \lambda (t,x^1,\dots ,x^{2n})=\sum _{i=1}^{2n}(C(t)(x^i)^2+B_i(t)x^i)+E(t), \end{aligned}$$

(7.3)

where $E(t)=\sum _{i=1}^{2n}E_i(t)$ and $C(t)=-\frac{1}{2}k\lambda$.

We observe that for $\lambda$ to be a positive function we have to narrow its domain. Supposing $0\in I$, we can assume $C(0)\ge 0$, $E(0)>0$ and $B_i(0)>0$, $i=1,\dots ,2n$. Thus, there exists an open interval J, $0\in J\subset I$, such that $C(t)\ge 0$, $E(t)>0$ and $B_i(t)>0$, for any $i=1,\dots ,2n$, $t\in J$. Putting $U={\mathbb {R}}_{+}^{*}\times \dots \times {\mathbb {R}}_{+}^{*}$, the function $\lambda :J\times U\rightarrow {\mathbb {R}}$, defined as in (7.3), is smooth and positive.

We conclude that the a.c.m. manifolds $M=$ $_{\lambda }J\times U$ are g.S. space forms $M^{2n+1}(0,k)$ belonging to the class $C_{12}{\setminus } C$.

Remark 7.1

The condition $k=0$ is equivalent to require that the a.c.m. manifolds $M=$ $_{\lambda }J\times U$ are flat and $\lambda (t,x^1,\dots ,x^{2n})=\sum _{i=1}^{2n}B_i(t)x^i+E(t)$. Note that the method above described is similar to the procedure used in Theorem 5.2 in [7]. In our case, the hypothesis that $f_3=-k$ is nowhere zero is needless.

Finally, we provide an explicit example of a $C_{12}$-manifold satisfying the hypotheses of Theorem 5.2.

Example 7.1

Given three non-negative real numbers $B_1, B_{n+1}, E$ such that $(B_1,B_{n+1})\ne (0,0)$, one considers the open set $W=\{(x^1,\dots ,x^{2n})\in {\mathbb {R}}^{2n} | x^1>0, x^{n+1}>0\}$ and the smooth positive function $\lambda :{\mathbb {R}}\times W\rightarrow {\mathbb {R}}$ acting as

$$\begin{aligned} \lambda (t,x^1,\dots ,x^{2n})=B_1x^1+B_{n+1}x^{n+1}+E. \end{aligned}$$

By Remark 7.1, we know that the a.c.m. manifold $M=$ $_{\lambda }{\mathbb {R}}\times W=({\mathbb {R}}\times W,\varphi ,\xi =\frac{1}{\lambda }\frac{\partial }{\partial t},\eta =\lambda \mathrm{d}t,g=\lambda ^2 \mathrm{d}t\otimes \mathrm{d}t+g_0)$ is flat and falls in the class $C_{12}{\setminus } C$. Note that, for any $i=1,\dots ,n$, $\varphi (\frac{\partial }{\partial x^i})=J_0(\frac{\partial }{\partial x^i})=\frac{\partial }{\partial x^{n+i}}$. Using the formulas in [16], it is easy to verify that the tensor field $V=\nabla _{\xi }\xi =-\frac{1}{\lambda }(B_1\frac{\partial }{\partial x^1}+B_{n+1}\frac{\partial }{\partial x^{n+1}})$ satisfies the condition $\nabla _{\xi }V=-||V||^2\xi$. Moreover, considering the distribution $D'=\text {span}\{\xi ,V,\varphi V\}$ on M and putting $U_1=\frac{\partial }{\partial x^1}+\frac{\partial }{\partial x^{n+1}}$, $U_2=\varphi U_1$, we have $D'=\text {span}\{\lambda \xi ,U_1,U_2\}$.

Given the open set $N'=\{(t,y,z)\in {\mathbb {R}}^3 | y>0,-y<z<y\}$, $(t_0,x_0)=(t_0,x_0^1,\dots ,x_0^{2n})\in M$, we define the map $f:N'\rightarrow {\mathbb {R}}\times W$ acting as

$$\begin{aligned} f(t,y,z)=\left( t,\frac{1}{\sqrt{2}}(y-z),x_0^2,\dots ,x_0^n,\frac{1}{\sqrt{2}}(y+z),\dots ,x_0^{2n}\right) . \end{aligned}$$

Putting $\lambda '=\lambda \circ f$ and $g'=\lambda '^2 \mathrm{d}t\otimes \mathrm{d}t+\mathrm{d}y\otimes \mathrm{d}y+\mathrm{d}z\otimes \mathrm{d}z$, it is easy to check that f is an isometric immersion with respect to the metrics $g'$ and g. Note that $(N',g')$ is the leaf of $D'$ through $(t_0,x_0)$ and, applying Proposition 5.2, $(N',\varphi '=-\frac{\partial }{\partial y}\otimes \mathrm{d}z+\frac{\partial }{\partial z}\otimes \mathrm{d}y,\xi =\frac{1}{\lambda '}\frac{\partial }{\partial t},\eta '=\lambda ' \mathrm{d}t,g')$ is a flat $C_{12}$-manifold. Moreover, up to an isometry, the leaf of $D'^{\perp }$ through $(t_0,x_0)$ is ${\mathbb {R}}^{2n-2}$ endowed with its canonical Kähler structure. Thus, applying Theorem 5.2, M is locally isometric to the Riemannian product $N'\times {\mathbb {R}}^{2n-2}$.