Baer–Kaplansky Classes in Grothendieck Categories and Applications

Abstract

We study Baer–Kaplansky classes in Grothendieck categories. We apply our results to functor categories, and discuss the transfer of the Baer–Kaplansky property to finitely accessible additive categories, exactly definable additive categories and categories $\sigma [M]$.

1 Introduction

The classical Baer–Kaplansky theorem states that any two torsion abelian groups having isomorphic endomorphism rings are isomorphic [11, Theorem 108.1]. An interesting topic of research has been to find other classes of abelian groups, and more generally, of modules, for which a Baer–Kaplansky-type theorem is still true. Such classes have been called Baer–Kaplanksy classes by Ivanov and Vámos [17]. For instance, the class of finitely generated abelian groups is Baer–Kaplansky (e.g., see [18, Example 1.3]), but the class of torsion-free abelian groups is not (e.g., see [21, Example 3.8]). There are several Baer–Kaplansky classes of modules over commutative rings, but there have been exhibited relatively few over non-commutative rings. Among them, Morita showed that the class of all modules over a primary artinian uniserial ring is Baer–Kaplansky [24, Lemma 7.4], while Ivanov proved that the class of all modules over a non-singular artinian serial ring is Baer–Kaplansky [16, Theorem 9]. Noticing that every isomorphism between endomorphism rings of torsion abelian groups preserves indecomposables, Ivanov [16] introduced and proposed in the study of Baer–Kaplansky classes of modules the use of the stronger notion of IP-isomorphism (i.e., indecomposable-preserving isomorphism) instead of isomorphism, together with direct sum decompositions into indecomposables. Recently, Keskin Tütüncü and Tribak have also studied Baer–Kaplansky classes of modules [18].

These are the motivating and leading ideas in our investigation of Baer–Kaplansky classes in Grothendieck categories. In particular, they can be used in functor categories. Let $\mathrm{Mod}(R)$ ($\mathrm{mod}(R)$) and $(R)\mathrm{Mod}$ ($(R)\mathrm{mod}$) be the categories of (finitely presented) right R-modules and left R-modules, respectively, for some ring R with identity. It is well known that there is a fully faithful functor $H:\text {Mod(R)}\rightarrow ((\text {mod(R))}^{\mathrm{op}},\mathrm{Ab})$ defined by $H(M)=\mathrm{Hom}_R(-,M)$, which induces an equivalence between $\mathrm{Mod}(R)$ and the full subcategory of flat functors in the category $((\mathrm{mod}(R))^{\mathrm{op}},\mathrm{Ab})$ of contravariant (additive) functors from $\mathrm{mod}(R)$ to the category Ab of abelian groups. In addition, there is a fully faithful functor $T:(R)\mathrm{Mod} \rightarrow (\text {mod(R)},\mathrm{Ab})$ defined by $T(M)=-\otimes _R M$, which induces an equivalence between $(R)\mathrm{Mod}$ and the full subcategory of FP-injective functors in the category $(\text {mod(R)},\mathrm{Ab})$ of covariant (additive) functors from $\mathrm{mod}(R)$ to Ab. These functors have been successfully used by several authors, such as Auslander [1], Gruson and Jensen [13], or Stenström [28] to relate properties of module categories and of the corresponding functor categories. Later on, they were extended from module categories to finitely accessible additive categories [4, 25], exactly definable additive categories [19, 25] and their associated categories.

We use functor categories techniques to relate Baer–Kaplansky classes in Grothendieck categories to Baer–Kaplansky classes in finitely accessible additive categories (in particular, the category of torsion-free abelian groups), exactly definable categories (in particular, the category of divisible abelian groups) and categories $\sigma [M]$ (in particular, the category of comodules over a coalgebra over a field). Even if our results in these categories are somehow similar to each other, we point out that the above three types of categories are independent in general.

In Sect. 2, we study Baer–Kaplansky classes in Grothendieck categories. We recall that fully faithful functors preserve Baer–Kaplansky classes. We show that if M and N are objects of a Grothendieck category ${\mathcal {C}}$, such that M has a direct sum decomposition into indecomposable objects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$, then M is (isomorphic to) a pure subobject of N. If, moreover, $({\mathcal {A}},{\mathcal {B}})$ is a cotorsion pair in ${\mathcal {C}}$, $M\in {\mathcal {B}}$ and $N/M\in {\mathcal {A}}$, then M and N are isomorphic. For a class ${\mathcal {M}}$ of objects of a Grothendieck category ${\mathcal {C}}$ closed under summands, such that every object of ${\mathcal {M}}$ has a direct sum decomposition into indecomposable summands and the finite embedding property, we prove that ${\mathcal {M}}$ is Baer–Kaplansky if and only if the class of indecomposable objects of ${\mathcal {M}}$ is Baer–Kaplansky.

In Sect. 3, we consider finitely accessible additive categories. If X and Y are objects of such a category ${\mathcal {C}}$, such that X has a direct sum decomposition into indecomposable subobjects and either Y / X is pure-projective or X is pure-injective, and such that there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(X)\rightarrow \mathrm{End}_{{\mathcal {C}}}(Y)$, we prove that X and Y are isomorphic. For a Krull–Schmidt finitely accessible (in particular pure semisimple) additive category ${\mathcal {C}}$, we show that the class of finitely presented (indecomposable) objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if so is the class of pure-projective indecomposable objects of ${\mathcal {C}}$. We exhibit an example of a pure semisimple finitely accessible additive category all of whose objects form a Baer–Kaplasky class.

In Sect. 4, we deal with exactly definable additive categories. We give some examples of module categories (which are always finitely accessible and exactly definable), and classes of objects in the associated functor categories which are Baer–Kaplansky. If X and Y are objects of an exactly definable additive category ${\mathcal {C}}$, such that X has a direct sum decomposition into indecomposable subobjects and either Y / X is pure-projective or X is pure-injective, and such that there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(X)\rightarrow \mathrm{End}_{{\mathcal {C}}}(Y)$, we prove that X and Y are isomorphic. For a pure semisimple exactly definable additive category ${\mathcal {C}}$, we show that the class of finitely presented objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if the class of finitely presented indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky.

Finally, in Sect. 5, we give some similar results in categories $\sigma [M]$, which are full subcategories of the category of left R-modules consisting of modules isomorphic to M-generated modules for some left R-module M.

2 Baer–Kaplansky Classes in Grothendieck Categories

Let ${\mathcal {C}}$ be a preadditive category and let ${\mathcal {M}}$ be a class of objects of ${\mathcal {C}}$. Following Ivanov and Vámos [17], ${\mathcal {M}}$ is called a Baer–Kaplansky class if for any two objects M and N of ${\mathcal {M}}$, such that $\mathrm{End}_{{\mathcal {C}}}(M)\cong \mathrm{End}_{{\mathcal {C}}}(N)$ (as rings), one has $M\cong N$.

The following result is also given in [7], but we include it for reader’s convenience. It will be frequently used throughout this paper.

Proposition 2.1

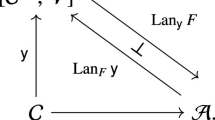
Let $F:{\mathcal {A}}\rightarrow {\mathcal {B}}$ be a fully faithful covariant functor between preadditive categories ${\mathcal {A}}$ and ${\mathcal {B}}$. Then, a class ${\mathcal {M}}$ of objects of ${\mathcal {A}}$ is a Baer–Kaplansky class if and only if so is the class ${\mathcal {N}}=\{F(M) \mid M \in {\mathcal {M}}\}$.

Proof

We first note that since F is fully faithful, we have

$$\begin{aligned} \mathrm{End}_{{\mathcal {A}}}(A) \cong \mathrm{End}_{{\mathcal {B}}}(F(A))\; \mathrm{(as \; rings)} \end{aligned}$$

(*)

for every object A of ${\mathcal {A}}$. Now, let X and Y be objects of ${\mathcal {M}}$, such that $\mathrm{End}_{{\mathcal {A}}}(X)\cong \mathrm{End}_{{\mathcal {A}}}(Y)$ or $\mathrm{End}_{{\mathcal {B}}}(F(X)) \cong \mathrm{End}_{{\mathcal {B}}}(F(Y))$ (as rings). From $(*)$, we obtain

$$\begin{aligned} \mathrm{End}_{{\mathcal {A}}}(X) \cong \mathrm{End}_{{\mathcal {B}}}(F(X)) \cong \mathrm{End}_{{\mathcal {B}}}(F(Y)) \cong \mathrm{End}_{{\mathcal {A}}}(Y) \; \mathrm{(as \; rings)}. \end{aligned}$$

Now, the result follows. $\square$

Let ${\mathcal {C}}$ be an abelian category and let ${\mathcal {M}}$ be a class of objects of ${\mathcal {C}}$. Denote

$$\begin{aligned} {\mathcal {M}}^{\perp }= & {} \{C\in {\mathcal {C}}\mid \mathrm{Ext}^1_{{\mathcal {C}}}(M,C)=0 \text { for every }M\in {\mathcal {M}}\},\\ {}^{\perp }{\mathcal {M}}= & {} \{C\in {\mathcal {C}}\mid \mathrm{Ext}^1_{{\mathcal {C}}}(C,M)=0 \text { for every }M\in {\mathcal {M}}\}. \end{aligned}$$

Recall that a pair $({\mathcal {A}},{\mathcal {B}})$ of classes of objects of ${\mathcal {C}}$ is called a cotorsion pair if ${\mathcal {A}}^{\perp }={\mathcal {B}}$ and ${}^{\perp }{\mathcal {B}}={\mathcal {A}}$.

Recall that a ring isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$ is called an IP-isomorphism if for every primitive idempotent $e\in \mathrm{End}_{{\mathcal {C}}}(M)$, one has $\Phi (e)N\cong eM$ [16].

The following theorem is one of the main results of the paper. It is inspired by [16, Proposition 1], but the hypotheses on modules to be finitely embedded and generated by indecomposable summands, respectively, are replaced by conditions involving a cotorsion pair in a Grothendieck category.

Theorem 2.2

Let M and N be objects of a Grothendieck category ${\mathcal {C}}$, such that M has a direct sum decomposition into indecomposable objects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$. Then

• (1) M is (isomorphic to) a pure subobject of N.

• (2) If $({\mathcal {A}},{\mathcal {B}})$ is a cotorsion pair in ${\mathcal {C}}$, $M\in {\mathcal {B}}$ and $N/M\in {\mathcal {A}}$, then M and N are isomorphic.

Proof

(1) Let $M=\bigoplus _{k\in K}M_k$ be a direct sum decomposition of M into indecomposable subobjects. For every $k\in K$, denote by $p_k:M\rightarrow M_k$ the canonical projection, by $i_k:M_k\rightarrow M$ the inclusion monomorphism and consider the idempotent $e_k=i_kp_k\in \mathrm{End}_{{\mathcal {C}}}(M)$. Since $\Phi$ is an IP-isomorphism, $\Phi (e_k)N\cong e_kM=M_k$ is an indecomposable subobject of N for every $k\in K$. Since ${\mathcal {C}}$ has split idempotents, it follows that $M\cong e_kM\oplus (1-e_k)M$ for every $k\in K$. For every $k\in K$, let $f_k:M_k\rightarrow \Phi (e_k)N$ be an isomorphism. Consider $\Psi '=\bigoplus _{k\in K}f_k:\bigoplus _{k\in K}M_k\rightarrow \bigoplus _{k\in K}\Phi (e_k)N$ and $j:\bigoplus _{k\in K}\Phi (e_k)N\rightarrow N$ the inclusion monomorphism. Since each $\Phi (e_k)N$ is a summand of N, j is a pure monomorphism. Hence, $\Psi =j\Psi ':M\rightarrow N$ is a pure monomorphism and $\mathrm{Im}(\Psi )$ generates a direct sum of indecomposable subobjects of N, say $\mathrm{Im}(\Psi )=\bigoplus _{k\in K}N_k$.

(2) Suppose that $\mathrm{Im}(\Psi )\ne N$. The induced (pure) exact sequence $0\rightarrow M\rightarrow N\rightarrow N/M\rightarrow 0$ splits, because $M\in {\mathcal {B}}$ and $N/M\in {\mathcal {A}}$. Hence, $N=\mathrm{Im}(\Psi )\oplus P$ for some non-zero subobject P of N. Then, there exists an idempotent $f\in \mathrm{End}_{{\mathcal {C}}}(N)$, such that $P=fN$. Then, f is orthogonal to every idempotent $\Phi (e_k)$ of N for $k\in K$, and therefore, $\Phi ^{-1}(f)$ is orthogonal to every idempotent $e_k$ of M for $k\in K$, a contradiction. Hence, $\Psi$ is an isomorphism. $\square$

The first part of the following corollary generalizes [16, Proposition 2].

Corollary 2.3

Let ${\mathcal {C}}$ be a Grothendieck category. Let M and N be objects of ${\mathcal {C}}$ such that M has a direct sum decomposition into indecomposable objects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$. If one of the following conditions holds:

• (1) M is injective;

• (2) N / M is projective;

then M and N are isomorphic.

Proof

(1) Use Theorem 2.2 for the cotorsion pair $({\mathcal {A}},{\mathcal {B}})$, where ${\mathcal {A}}={\mathcal {C}}$ and ${\mathcal {B}}$ is the class of injective objects of ${\mathcal {C}}$.

(2) Use Theorem 2.2 for the cotorsion pair $({\mathcal {A}},{\mathcal {B}})$, where ${\mathcal {A}}$ is the class of projective objects of ${\mathcal {C}}$ and ${\mathcal {B}}={\mathcal {C}}$. $\square$

Let ${\mathcal {C}}$ be a Grothendieck category. Recall that an object M of ${\mathcal {C}}$ is called:

• (i) flat if every epimorphism $C\rightarrow M$ is pure.

• (ii) FP-injective if every monomorphism $M\rightarrow C$ is pure.

• (iii) cotorsion if $\mathrm{Ext}^1_{{\mathcal {C}}}(F,M)=0$ for every flat object F of ${\mathcal {C}}$ [30].

• (iv) FP-projective if $\mathrm{Ext}^1_{{\mathcal {C}}}(M,F)=0$ for every FP-injective object F of ${\mathcal {C}}$ [22].

Corollary 2.4

Let ${\mathcal {C}}$ be a Grothendieck category. Let M and N be objects of ${\mathcal {C}}$, such that M is cotorsion and N is flat. Assume that M has a direct sum decomposition into indecomposable objects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$. Then, M and N are isomorphic.

Proof

Consider the cotorsion pair $({\mathcal {A}},{\mathcal {B}})$, where ${\mathcal {A}}$ is the class of flat objects of ${\mathcal {C}}$ and ${\mathcal {B}}$ is the class of cotorsion objects of ${\mathcal {C}}$ (see [22, Theorem 2.14], whose proof works in our setting). We have seen in the proof of Theorem 2.2 that there is a pure exact sequence $0\rightarrow M\rightarrow N\rightarrow N/M\rightarrow 0$. Since the class of flat objects of ${\mathcal {C}}$ is closed under pure factor objects, we have $N/M\in {\mathcal {A}}$. Now, use Theorem 2.2. $\square$

Corollary 2.5

Let ${\mathcal {C}}$ be a locally coherent Grothendieck category. Let M and N be objects of ${\mathcal {C}}$, such that N is FP-injective and N / M is FP-projective. Assume that M has a direct sum decomposition into indecomposable objects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$. Then, M and N are isomorphic.

Proof

Consider the cotorsion pair $({\mathcal {A}},{\mathcal {B}})$, where ${\mathcal {A}}$ is the class of FP-projective objects of ${\mathcal {C}}$ and ${\mathcal {B}}$ is the class of FP-injective objects of ${\mathcal {C}}$ (see [22, Theorems 2.12 and 2.14], whose proofs work in our setting). We have seen in the proof of Theorem 2.2 that there is a pure exact sequence $0\rightarrow M\rightarrow N\rightarrow N/M\rightarrow 0$. Since the class of FP-injective objects of ${\mathcal {C}}$ is closed under pure subobjects, we have $M\in {\mathcal {B}}$. Now, use Theorem 2.2. $\square$

Next, we recall and generalize to categories some needed terminology from [16]. Let ${\mathcal {C}}$ be a category and let M be an object of ${\mathcal {C}}$. Let $M=\bigoplus _{k\in K}M_k$ be a direct sum decomposition into indecomposable summands. A subobject L of M is called finitely embedded in M with respect to the above direct sum decomposition of M if $L\subseteq \bigoplus _{k\in F}M_k$ for some finite $F\subseteq K$. Then, M has the finite embedding property if every indecomposable summand of M is finitely embedded in M with respect to the above direct sum decomposition. Clearly, every finitely generated subobject is finitely embedded.

Proposition 2.6

Let ${\mathcal {C}}$ be a Grothendieck category. Let M be an object of ${\mathcal {C}}$ having the finite embedding property with respect to a direct sum decomposition into indecomposable summands, and let N be an object of ${\mathcal {C}}$ generated by indecomposable summands. If there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$, then M and N are isomorphic.

Proof

The proof of [16, Proposition 1] immediately generalizes to Grothendieck categories. $\square$

Theorem 2.7

Let ${\mathcal {C}}$ be a Grothendieck category. Let ${\mathcal {M}}$ be a class of objects of ${\mathcal {C}}$ closed under summands such that every object of ${\mathcal {M}}$ has a direct sum decomposition into indecomposable summands and the finite embedding property. Then, ${\mathcal {M}}$ is Baer–Kaplansky if and only if the class of indecomposable objects of ${\mathcal {M}}$ is Baer–Kaplansky.

Proof

Assume that the class of indecomposable objects of ${\mathcal {M}}$ is Baer–Kaplansky. Let M and N be objects of ${\mathcal {M}}$, such that there exists a ring isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(M)\rightarrow \mathrm{End}_{{\mathcal {C}}}(N)$. Let $e\in \mathrm{End}_{{\mathcal {C}}}(M)$ be a primitive idempotent. Then, $\Phi$ restricts to a ring isomorphism between $\mathrm{End}_{{\mathcal {C}}}(eM)$ and $\mathrm{End}_{{\mathcal {C}}}(\Phi (e)N)$. However, eM is an indecomposable summand of M and $\Phi (e)N$ is an indecomposable summand of N. Since $eM,\Phi (e)N\in {\mathcal {M}}$, it follows by hypothesis that eM and $\Phi (e)N$ are isomorphic. This shows that $\Phi$ is an IP-isomorphism. Now, $M\cong N$ by Proposition 2.6. Hence, ${\mathcal {M}}$ is Baer–Kaplansky.

The converse is clear. $\square$

Recall that a module M over a ring (with enough idempotents) is called local if M has a proper submodule which contains all other proper submodules (e.g., see [29, p. 351]).

Corollary 2.8

Let R be a ring with enough idempotents.

• (1) [18, Proposition 2.12] The class of semisimple right R-modules is Baer–Kaplansky if and only if the class of simple right R-modules is Baer–Kaplansky.

• (2) Assume that R is semiperfect. Then the class of finitely generated projective right R-modules is Baer–Kaplansky if and only if the class of projective local right R-modules is Baer–Kaplansky.

• (3) Assume that R is right noetherian. Then the class of finitely generated injective right R-modules is Baer–Kaplansky if and only if the class of finitely generated indecomposable injective right R-modules is Baer–Kaplansky.

Proof

(1) This is clear by Theorem 2.7.

(2) If R is semiperfect, then every finitely generated projective right R-module is a direct sum of local right R-modules [29, 49.10]. In addition, note that every local right R-module is finitely generated (e.g., see [29, 41.4]). Then, use Theorem 2.7.

(3) If R is right noetherian, then it is well known that every finitely generated injective right R-module is a direct sum of finitely generated indecomposable injective right R-modules. Then use Theorem 2.7. $\square$

Remark 2.9

In general, the classes of simple right R-modules and indecomposable projective right R-modules are not Baer–Kaplansky by [18, Example 2.16].

3 Baer–Kaplansky Classes in Finitely Accessible Categories

Following Crawley-Boevey [4] and Prest [25], we recall some terminology on finitely accessible additive categories. An additive category ${\mathcal {C}}$ is called finitely accessible if it has direct limits, the class of finitely presented objects is skeletally small, and every object is a direct limit of finitely presented objects. The category of unitary modules over a ring with enough idempotents, the category of torsion abelian groups [25, Example 10.2] and the category of torsion-free abelian groups [25, Examples 10.5] are typical examples of finitely accessible additive categories.

Finitely accessible additive categories offer a suitable framework for defining purity. Let ${\mathcal {C}}$ be a finitely accessible additive category. By a sequence $0\rightarrow X{\mathop {\rightarrow }\limits ^{f}}Y{\mathop {\rightarrow }\limits ^{g}}Z\rightarrow 0$ in the additive category ${\mathcal {C}}$ we mean a pair of composable morphisms $f:X\rightarrow Y$ and $g:Y\rightarrow Z$ such that $gf=0$. The sequence is called pure exact if it induces an exact sequence of abelian groups $0\rightarrow \mathrm{Hom}_{{\mathcal {C}}}(P,X)\rightarrow \mathrm{Hom}_{{\mathcal {C}}}(P,Y)\rightarrow \mathrm{Hom}_{{\mathcal {C}}}(P,Z)\rightarrow 0$ for every finitely presented object P of ${\mathcal {C}}$. This implies that f and g form a kernel–cokernel pair, that f is a monomorphism and g an epimorphism. In such a pure exact sequence, f is called a pure monomorphism and g a pure epimorphism. An object M of ${\mathcal {C}}$ is called pure-injective if every pure exact sequence in ${\mathcal {C}}$ with the first term M splits, and pure-projective if every pure exact sequence in ${\mathcal {C}}$ with the third term M splits.

Proposition 3.1

([4, Theorem 1.4 and Lemma 3.1], [9, Theorem 1.1], [15, Lemma 3]). Let ${\mathcal {C}}$ be a finitely accessible additive category. Then, there is a Grothendieck category ${\mathcal {A}}({\mathcal {C}})$ (uniquely determined up to equivalence) and a fully faithful functor $H:{\mathcal {C}}\rightarrow {\mathcal {A}}({\mathcal {C}})$ (naturally isomorphic to the inclusion functor), which induces an equivalence between ${\mathcal {C}}$ and the full subcategory of flat objects of ${\mathcal {A}}({\mathcal {C}})$. Moreover, a sequence in ${\mathcal {C}}$ is pure exact if and only if H takes it into an exact sequence in ${\mathcal {A}}({\mathcal {C}})$.

The above equivalence restricts to equivalences between:

• (1) Pure-projective objects of ${\mathcal {C}}$ and projective objects of ${\mathcal {A}}({\mathcal {C}})$.

• (2) Finitely presented objects of ${\mathcal {C}}$ and finitely generated projective objects of ${\mathcal {A}}({\mathcal {C}})$.

• (3) Pure-injective objects of ${\mathcal {C}}$ and flat cotorsion objects of ${\mathcal {A}}({\mathcal {C}})$.

Remark 3.2

Let ${\mathcal {C}}$ be a finitely accessible additive category. Then ${\mathcal {A}}({\mathcal {C}})$ is equivalent to any of the following categories:

• (1) The category $(\mathrm{fp}({\mathcal {C}})^{\mathrm{op}},\mathrm{Ab})$ of all contravariant additive functors from the full subcategory $\mathrm{fp}({\mathcal {C}})$ of finitely presented objects of ${\mathcal {C}}$ to the category $\mathrm{Ab}$ of abelian groups [4, Theorem 1.4].

• (2) The category $\mathrm{Mod}(A)$ of unitary right A-modules, where A is the functor ring (with enough idempotents) of ${\mathcal {C}}$ [9, Theorem 1.1].

• (3) The right Freyd category ${\mathcal {F}}^{\mathrm{pproj}({\mathcal {C}})}$, where $\mathrm{pproj}({\mathcal {C}})$ is the full subcategory of pure-projective objects of ${\mathcal {C}}$ (see [3, Corollary 3.16] and [10, Theorem 1.4]).

Remark 3.3

For ${\mathcal {C}}=\mathrm{Mod}(R)$, there are further restricted equivalences involving flat or FP-injective right R-modules and corresponding objects in the associated functor category [5, 23].

Theorem 3.4

Let ${\mathcal {C}}$ be a finitely accessible additive category. Let X and Y be objects of ${\mathcal {C}}$, such that X has a direct sum decomposition into indecomposable subobjects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(X)\rightarrow \mathrm{End}_{{\mathcal {C}}}(Y)$. If one of the following conditions holds:

• (1) Y / X is pure-projective.

• (2) X is pure-injective.

then X and Y are isomorphic.

Proof

Consider the above functor $H:{\mathcal {C}}\rightarrow {\mathcal {A}}({\mathcal {C}})$.

(1) Since H preserves direct sums and indecomposables, H(X) has a direct sum decomposition into indecomposable subobjects in ${\mathcal {A}}({\mathcal {C}})$. In addition, H(Y / X) is projective in ${\mathcal {A}}({\mathcal {C}})$ by Proposition 3.1. Since H is fully faithful, we have the ring isomorphisms

$$\begin{aligned} \mathrm{End}_{{\mathcal {A}}({\mathcal {C}})}(H(X))\cong \mathrm{End}_{{\mathcal {C}}}(X)\overset{\Phi }{\cong }\mathrm{End}_{{\mathcal {C}}}(Y)\cong \mathrm{End}_{{\mathcal {A}}({\mathcal {C}})}(H(Y)). \end{aligned}$$

Denote by $\Delta :\mathrm{End}_{{\mathcal {A}}({\mathcal {C}})}(H(X))\rightarrow \mathrm{End}_{{\mathcal {A}}({\mathcal {C}})}(H(Y))$ their composition. Since H preserves indecomposables and $\Phi$ is an IP-isomorphism, so is $\Delta$. By Theorem 2.2, there is a pure exact sequence $0\rightarrow H(X)\rightarrow H(Y)\rightarrow N\rightarrow 0$. Since H(Y) is flat, so is N. Write $N\cong H(Z)$ for some object Z of ${\mathcal {C}}$. Then, we have an induced sequence $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ in ${\mathcal {C}}$ with Z pure-projective. It follows that $N\cong H(Y)/H(X)$ is projective in ${\mathcal {A}}({\mathcal {C}})$ by Proposition 3.1. Then, $H(X)\cong H(Y)$ by Corollary 2.3, and so, $X\cong Y$.

(2) As in the proof of (1), there exists an IP-isomorphism

$$\begin{aligned} \Delta :\mathrm{End}_{{\mathcal {A}}({\mathcal {C}})}(H(X))\rightarrow \mathrm{End}_{{\mathcal {A}}({\mathcal {C}})}(H(Y)). \end{aligned}$$

Then, $H(X)\cong H(Y)$ by Corollary 2.4. Since H is fully faithful, we have $X\cong Y$. $\square$

Corollary 3.5

Let ${\mathcal {C}}$ be a finitely accessible additive category. Let X and Y be objects of ${\mathcal {C}}$, such that X is $\Sigma$-pure-injective. If there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(X)\rightarrow \mathrm{End}_{{\mathcal {C}}}(Y)$, then X and Y are isomorphic.

Proof

Consider the above functor $H:{\mathcal {C}}\rightarrow {\mathcal {A}}({\mathcal {C}})$. Then, H(X) and H(Y) are flat objects of ${\mathcal {A}}({\mathcal {C}})$ by Proposition 3.1. Since X is a $\Sigma$-pure-injective object of ${\mathcal {C}}$, H(X) is a flat $\Sigma$-cotorsion object of ${\mathcal {A}}({\mathcal {C}})$. Then, H(X) has an indecomposable decomposition by [14, Proposition 7]. Since H is fully faithful, it follows that X has an indecomposable decomposition in ${\mathcal {C}}$. Hence, $X\cong Y$ by Theorem 3.4. $\square$

Recall that a finitely accessible additive category ${\mathcal {C}}$ is called Krull–Schmidt if every finitely presented object of ${\mathcal {C}}$ has a finite direct sum decomposition into subobjects with local endomorphism rings (e.g., see [2]).

The following result is known for finitely accessible additive categories with products [2, Proposition 4.1.15]. Its proof works in any finitely accessible additive category and we include it for reader’s convenience.

Proposition 3.6

Let ${\mathcal {C}}$ be a finitely accessible additive category. Then ${\mathcal {C}}$ is Krull–Schmidt if and only if ${\mathcal {A}}({\mathcal {C}})$ is semiperfect.

Proof

An object X of ${\mathcal {C}}$ is finitely presented if and only if H(X) is a finitely generated projective object of ${\mathcal {A}}({\mathcal {C}})$ by Proposition 3.1. Then, ${\mathcal {C}}$ is Krull–Schmidt if and only if every finitely generated projective object of ${\mathcal {A}}({\mathcal {C}})$ has a finite direct sum decomposition into finitely generated projective objects of ${\mathcal {A}}({\mathcal {C}})$ with local endomorphism ring, equivalently projective local objects of ${\mathcal {A}}({\mathcal {C}})$ (e.g., see [2, Lema 4.1.13]). But this is equivalent to ${\mathcal {A}}({\mathcal {C}})$ being semiperfect [29, 49.10]. $\square$

Theorem 3.7

Let ${\mathcal {C}}$ be a Krull–Schmidt finitely accessible additive category. The following are equivalent:

• (1) The class of finitely presented objects of ${\mathcal {C}}$ is Baer–Kaplansky.

• (2) The class of pure-projective indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky.

• (3) The class of finitely presented indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky.

Proof

We use Propositions 2.1 and 3.1 repeatedly. The class of finitely presented objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if so is the class of finitely generated projective objects of ${\mathcal {A}}({\mathcal {C}})$. However, ${\mathcal {C}}$ is Krull–Schmidt if and only if ${\mathcal {A}}({\mathcal {C}})$ is semiperfect by Proposition 3.6. Then, the class of finitely generated projective objects of ${\mathcal {A}}({\mathcal {C}})$ is Baer–Kaplansky if and only if so is the class of projective local objects of ${\mathcal {A}}({\mathcal {C}})$ (by Corollary 2.8) if and only if so is the class of projective indecomposable objects of ${\mathcal {A}}({\mathcal {C}})$ (e.g., see [2, Lema 4.1.13]). The class of pure-projective indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if so is the class of projective indecomposable objects of ${\mathcal {A}}({\mathcal {C}})$. The class of finitely presented indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if so is the class of finitely generated projective indecomposable objects of ${\mathcal {A}}({\mathcal {C}})$. Now, the conclusion follows. $\square$

Recall that a finitely accessible additive category ${\mathcal {C}}$ is called pure semisimple if every pure exact sequence in ${\mathcal {C}}$ splits [3]. Note that ${\mathcal {C}}$ is pure semisimple if and only if every object of ${\mathcal {C}}$ is pure-injective if and only if every object of ${\mathcal {C}}$ is pure-projective. In addition, a finitely accessible additive category ${\mathcal {C}}$ with products is pure semisimple if and only if every object of ${\mathcal {C}}$ is isomorphic to a direct sum of indecomposable objects [12, Theorem 3.2].

The following result is known for finitely accessible additive categories with products [2, Proposition 4.1.4]. Its proof works in any finitely accessible additive category and we include it for reader’s convenience. It implies that every pure semisimple finitely accessible category is Krull–Schmidt.

Proposition 3.8

Let ${\mathcal {C}}$ be a finitely accessible additive category. Then, ${\mathcal {C}}$ is pure semisimple if and only if ${\mathcal {A}}({\mathcal {C}})$ is perfect.

Proof

Assume that ${\mathcal {C}}$ is pure semisimple. Let $N\cong H(Z)$ be a flat object of ${\mathcal {A}}({\mathcal {C}})$ for some object Z of ${\mathcal {C}}$. Since Z is pure-projective, N is projective by Proposition 3.1. Hence, ${\mathcal {A}}({\mathcal {C}})$ is perfect.

Conversely, assume that ${\mathcal {A}}({\mathcal {C}})$ is perfect. Let Z be an object of ${\mathcal {C}}$. Then, the flat object H(Z) of ${\mathcal {A}}({\mathcal {C}})$ must be projective. Then, Z is pure-projective by Proposition 3.1. Hence, ${\mathcal {C}}$ is pure semisimple. $\square$

Corollary 3.9

Let ${\mathcal {C}}$ be a pure semisimple finitely accessible additive category. Then, the class of finitely presented objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if the class of (finitely presented) indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky.

Proof

This follows by Propositions 3.6, 3.8 and Theorem 3.7. $\square$

Example 3.10

(1) Let ${\mathcal {C}}$ be a finitely accessible additive category. Assume that the functor ring R of ${\mathcal {C}}$ is local artinian with radical W, such that $W^2=0$, $Q=R/W$ is commutative, $dim(_QW)=1$ and $dim(W_Q)=2$. Consider the functor $H'=FH:{\mathcal {C}}\rightarrow \mathrm{Mod}(R)$, where $H:{\mathcal {C}}\rightarrow {\mathcal {A}}({\mathcal {C}})$ is the above functor and $F:{\mathcal {A}}({\mathcal {C}})\rightarrow \mathrm{Mod}(R)$ is an equivalence of categories. By [18, Example 2.3], the class of projective right R-modules (and the class of injective right R-modules) is Baer–Kaplansky. By Proposition 3.1, an object X of ${\mathcal {C}}$ is pure-projective if and only if $H'(X)$ is projective in $\mathrm{Mod}(R)$. Hence, the class of pure-projective objects of ${\mathcal {C}}$ is Baer–Kaplansky. On the other hand, since R is right perfect, ${\mathcal {C}}$ is pure semisimple by Proposition 3.8. Therefore, every object of ${\mathcal {C}}$ is pure-projective. This shows that the class of all objects of ${\mathcal {C}}$ is Baer–Kaplansky.

(2) Let F be a field and $R=\left[ \begin{array}{r@{\quad }r} F &{} 0 \\ 0&{} F \\ \end{array} \right]$. Consider ${\mathcal {C}}=\mathrm{Mod}(R)$, which is (pure) semisimple. Let $e_1=\left[ \begin{array}{r@{\quad }r} 1 &{} 0 \\ 0&{} 0 \\ \end{array} \right] , e_2=\left[ \begin{array}{r@{\quad }r} 0 &{} 0 \\ 0&{} 1 \\ \end{array} \right] \in R$. Then, $e_1R=\left[ \begin{array}{r@{\quad }r} F &{} 0 \\ 0&{} 0 \\ \end{array} \right]$ and $e_2R=\left[ \begin{array}{r@{\quad }r} 0 &{} 0 \\ 0&{} F \\ \end{array} \right]$ are (finitely presented) indecomposable. By [18, Example 2.16], $e_1R$ and $e_2R$ are not isomorphic, but $\mathrm{End}_R(e_1R)\cong e_1Re_1\cong e_2Re_2\cong \mathrm{End}_R(e_2R)$. Hence, the class of (finitely presented) indecomposable right R-modules is not Baer–Kaplansky.

4 Baer–Kaplansky Classes in Exactly Definable Categories

Following Krause [19] and Prest [25], we recall some terminology on exactly definable additive categories. An additive category ${\mathcal {C}}$ is called exactly definable if it is equivalent to the category $\mathrm{Ex}({\mathcal {A}}^{\mathrm{op}},\mathrm{Ab})$ of exact contravariant additive functors from ${\mathcal {A}}$ to the category Ab of abelian groups for some skeletally small abelian category ${\mathcal {A}}$. Every finitely accessible additive category with products is exactly definable [4, 3.3]. More generally, an additive category is exactly definable if and only if it is a definable subcategory (in the sense that it is closed under products, direct limits and pure subobjects) of a finitely accessible additive category with products [25, Proposition 11.1]. The category of unitary modules over a ring with enough idempotents, the category of torsion abelian groups [25, Example 10.2], and the category of torsion-free abelian groups [25, Examples 10.5] are not only finitely accessible categories, but also exactly definable. Note that a Grothendieck category is exactly definable if and only if it is finitely accessible [26, Theorem 3.6]. In general, exactly definable additive categories need not be finitely accessible. For instance, the category of divisible abelian groups is a definable subcategory of the category of abelian groups; hence, it is exactly definable, but not finitely accessible [25, Example 10.3].

Purity may also be defined in exactly definable additive categories. Let ${\mathcal {C}}$ be an exactly definable additive category. An object M of ${\mathcal {C}}$ is called pure-injective if for every set I the summation morphism $M^{(I)}\rightarrow M$ factors through the canonical morphism $M^{(I)}\rightarrow M^I$ [19]. A sequence $0\rightarrow X{\mathop {\rightarrow }\limits ^{f}}Y{\mathop {\rightarrow }\limits ^{g}}Z\rightarrow 0$ in ${\mathcal {C}}$ is called pure exact if it induces an exact sequence of abelian groups $0\rightarrow \mathrm{Hom}_{{\mathcal {C}}}(Z,Q)\rightarrow \mathrm{Hom}_{{\mathcal {C}}}(Y,Q)\rightarrow \mathrm{Hom}_{{\mathcal {C}}}(X,Q)\rightarrow 0$ for every pure-injective object Q of ${\mathcal {C}}$. This implies that f and g form a kernel–cokernel pair, that f is a monomorphism and g an epimorphism. In such a pure exact sequence, f is called a pure monomorphism and g a pure epimorphism. An object M of ${\mathcal {C}}$ is called pure-projective if every pure exact sequence in ${\mathcal {C}}$ with the third term M splits.

Proposition 4.1

Let ${\mathcal {C}}$ be an exactly definable additive category. Then there is a locally coherent Grothendieck category ${\mathcal {D}}({\mathcal {C}})$ (uniquely determined up to equivalence) and a fully faithful functor $T:{\mathcal {C}}\rightarrow {\mathcal {D}}({\mathcal {C}})$ (naturally isomorphic to the inclusion functor), which induces an equivalence between ${\mathcal {C}}$ and the full subcategory of FP-injective objects of ${\mathcal {D}}({\mathcal {C}})$. Moreover, a sequence in ${\mathcal {C}}$ is pure exact if and only if T takes it into an exact sequence in ${\mathcal {D}}({\mathcal {C}})$.

The above equivalence restricts to equivalences between:

• (1) Pure-injective objects of ${\mathcal {C}}$ and injective objects of ${\mathcal {D}}({\mathcal {C}})$.

• (2) Pure-projective objects of ${\mathcal {C}}$ and FP-projective FP-injective objects of ${\mathcal {D}}({\mathcal {C}})$.

• (3) Finitely presented objects of ${\mathcal {C}}$ and finitely presented FP-injective objects of ${\mathcal {D}}({\mathcal {C}})$.

Proof

The equivalence and (1) follow by [19, Theorem 2.8], while (3) follows by [4, Lemma 3.3] and [2, Proposition 1.6.4].

(2) Let Z be a pure-projective object of ${\mathcal {C}}$. Let K be an FP-injective object of ${\mathcal {D}}({\mathcal {C}})$, and let $0\rightarrow K\rightarrow M\rightarrow T(Z)\rightarrow 0$ be a short exact sequence in ${\mathcal {D}}({\mathcal {C}})$. Since the class of FP-injective objects of ${\mathcal {D}}({\mathcal {C}})$ is closed under extensions, M is also FP-injective. Hence, the short exact sequence becomes $0\rightarrow T(X)\rightarrow T(Y)\rightarrow T(Z)\rightarrow 0$, which yields a pure exact sequence $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ in ${\mathcal {C}}$. But this splits, since Z is pure-projective. Hence, the initial short exact sequence splits, which shows that T(Z) is FP-projective.

Now, let T(Z) be an FP-injective FP-projective object of ${\mathcal {D}}({\mathcal {C}})$ for some object Z of ${\mathcal {C}}$. Let $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ be a pure exact sequence in ${\mathcal {C}}$. This induces a short exact sequence $0\rightarrow T(X)\rightarrow T(Y)\rightarrow T(Z)\rightarrow 0$ in ${\mathcal {D}}({\mathcal {C}})$, which splits, because T(Z) is FP-projective. Then, the initial pure exact sequence $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ splits, which shows that Z is pure-projective. $\square$

Remark 4.2

Let ${\mathcal {C}}$ be an exactly definable additive category. Then ${\mathcal {D}}({\mathcal {C}})$ is equivalent to any of the following categories:

• (1) The category $\mathrm{Lex}({\mathcal {A}}^{\mathrm{op}},\mathrm{Ab})$ of left exact contravariant additive functors from ${\mathcal {A}}$ to the category Ab of abelian groups for some skeletally small abelian category ${\mathcal {A}}$ [19, Lemma 1.1].

• (2) The category $\mathrm{Flat}(\mathrm{Mod}(B))$ of flat unitary right B-modules, where B is a two-sided panoramic ring (with enough idempotents) [6, Proposition 2.1].

• (3) The left Freyd category ${\mathcal {F}}_{\mathrm{pinj}({\mathcal {C}})}$, where $\mathrm{pinj}({\mathcal {C}})$ is the full subcategory of pure-injective objects of ${\mathcal {C}}$ (see [3, Corollary 3.8] and [10, Theorem 1.4]).

Remark 4.3

For ${\mathcal {C}}=\mathrm{Mod}(R^{\mathrm{op}})$, there are further restricted equivalences involving flat or FP-injective left R-modules and corresponding objects in the associated functor category [5, 23].

Example 4.4

(1) Consider ${\mathcal {C}}=\mathrm{Ab}$. The class of finitely generated (equivalently, finitely presented) abelian groups is Baer–Kaplansky [18, Example 1.3 (i)]. Then, the class of finitely generated projective objects of ${\mathcal {A}}({\mathcal {C}})$ is Baer–Kaplansky by Propositions 2.1 and 3.1. In addition, the class of finitely presented FP-injective objects of ${\mathcal {D}}({\mathcal {C}})$ is Baer–Kaplansky by Propositions 2.1 and 4.1.

(2) Consider ${\mathcal {C}}=\mathrm{Mod}(R)$, where R is a primary uniserial artinian ring. The class of all objects of the module category $\mathrm{Mod}(R)$ is Baer–Kaplansky by [24, Lemma 7.4]. Then, the class of flat objects of ${\mathcal {A}}({\mathcal {C}})$ is Baer–Kaplansky by Propositions 2.1 and 3.1. In addition, the class of FP-injective objects of ${\mathcal {D}}({\mathcal {C}})$ is Baer–Kaplansky by Propositions 2.1 and 4.1.

(3) Consider ${\mathcal {C}}=\mathrm{Mod}(R)$, where $R={\mathbb {Z}}/2{\mathbb {Z}}\,\oplus \, {\mathbb {Z}}/3{\mathbb {Z}}$. Then R is semisimple, and so ${\mathcal {A}}({\mathcal {C}})$ and ${\mathcal {D}}({\mathcal {C}})$ are regular (e.g., see [29, 52.8] and [22, p. 1671]). It follows that every object of ${\mathcal {A}}({\mathcal {C}})$ is flat and every object of ${\mathcal {D}}({\mathcal {C}})$ is FP-injective (see [28, Theorem 4] and [29, 37.6]). The class of all objects of the module category $\mathrm{Mod}(R)$ is Baer–Kaplansky by [18, Example 2.15]. Then, the class of all objects of ${\mathcal {A}}({\mathcal {C}})$ is Baer–Kaplansky by Propositions 2.1 and 3.1. In addition, the class of all objects of ${\mathcal {D}}({\mathcal {C}})$ is Baer–Kaplansky by Propositions 2.1 and 4.1.

Theorem 4.5

Let ${\mathcal {C}}$ be an exactly definable additive category. Let X and Y be objects of ${\mathcal {C}}$, such that X has a direct sum decomposition into indecomposable subobjects and there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(X)\rightarrow \mathrm{End}_{{\mathcal {C}}}(Y)$. If one of the following conditions hold:

• (1) X is pure-injective.

• (2) Y / X is pure-projective.

then X and Y are isomorphic.

Proof

Consider the above functor $T:{\mathcal {C}}\rightarrow {\mathcal {D}}({\mathcal {C}})$.

(1) Since T preserves direct sums and indecomposables, T(X) has a direct sum decomposition into indecomposable subobjects in ${\mathcal {D}}({\mathcal {C}})$. In addition, T(X) is injective in ${\mathcal {D}}({\mathcal {C}})$ by Proposition 4.1. Since T is fully faithful, we have the ring isomorphisms

$$\begin{aligned} \mathrm{End}_{{\mathcal {D}}({\mathcal {C}})}(T(X))\cong \mathrm{End}_{{\mathcal {C}}}(X)\overset{\Phi }{\cong }\mathrm{End}_{{\mathcal {C}}}(Y)\cong \mathrm{End}_{{\mathcal {D}}({\mathcal {C}})}(T(Y)). \end{aligned}$$

Denote by $\Delta :\mathrm{End}_{{\mathcal {D}}({\mathcal {C}})}(T(X))\rightarrow \mathrm{End}_{{\mathcal {D}}({\mathcal {C}})}(T(Y))$ their composition. Since T preserves indecomposables and $\Phi$ is an IP-isomorphism, so is $\Delta$. Then, $T(X)\cong T(Y)$ by Corollary 2.3, and so, $X\cong Y$.

(2) As in the proof of (1), there exists an IP-isomorphism

$$\begin{aligned} \Delta :\mathrm{End}_{{\mathcal {D}}({\mathcal {C}})}(T(X))\rightarrow \mathrm{End}_{{\mathcal {D}}({\mathcal {C}})}(T(Y)). \end{aligned}$$

By Theorem 2.2, there is a pure exact sequence $0\rightarrow T(X)\rightarrow T(Y)\rightarrow N\rightarrow 0$. Since T(Y) is FP-injective and ${\mathcal {D}}({\mathcal {C}})$ is locally coherent, N is also FP-injective. Write $N\cong T(Z)$ for some object Z of ${\mathcal {C}}$. Then, we have an induced sequence $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ in ${\mathcal {C}}$ with Z pure-projective. It follows that $N\cong T(Y)/T(X)$ is FP-projective in ${\mathcal {D}}({\mathcal {C}})$ by Proposition 4.1. Then, $T(X)\cong T(Y)$ by Corollary 2.5, and so $X\cong Y$. $\square$

Corollary 4.6

Let ${\mathcal {C}}$ be an exactly definable additive category. Let X and Y be objects of ${\mathcal {C}}$, such that X is $\Sigma$-pure-injective. If there exists an IP-isomorphism $\Phi :\mathrm{End}_{{\mathcal {C}}}(X)\rightarrow \mathrm{End}_{{\mathcal {C}}}(Y)$, then X and Y are isomorphic.

Proof

Consider the above functor $T:{\mathcal {C}}\rightarrow {\mathcal {D}}({\mathcal {C}})$. Then, T(X) and T(Y) are injective objects of ${\mathcal {D}}({\mathcal {C}})$ by Proposition 4.1. Since X is a $\Sigma$-pure-injective object of ${\mathcal {C}}$, T(X) is a $\Sigma$-injective object of ${\mathcal {D}}({\mathcal {C}})$. Then, T(X) has an indecomposable decomposition. Since T is fully faithful, it follows that X has an indecomposable decomposition in ${\mathcal {C}}$. Hence, $X\cong Y$ by Theorem 4.5. $\square$

An exactly definable additive category ${\mathcal {C}}$ is called pure semisimple if every pure exact sequence in ${\mathcal {C}}$ splits. Note that ${\mathcal {C}}$ is pure semisimple if and only if every object of ${\mathcal {C}}$ is pure-injective if and only if every object of ${\mathcal {C}}$ is pure-projective. In addition, the proof of [12, Theorem 3.2] implies that an exactly definable additive category ${\mathcal {C}}$ is pure semisimple if and only if every object of ${\mathcal {C}}$ is isomorphic to a direct sum of indecomposable objects.

Proposition 4.7

Let ${\mathcal {C}}$ be an exactly definable additive category. Then, ${\mathcal {C}}$ is pure semisimple if and only if ${\mathcal {D}}({\mathcal {C}})$ is locally noetherian.

Proof

Assume that ${\mathcal {C}}$ is pure semisimple. Let K be an FP-injective object of ${\mathcal {D}}({\mathcal {C}})$. Then $K\cong T(X)$ for some object X of ${\mathcal {C}}$. Since X is pure-injective, K is injective by Proposition 4.1. Hence, ${\mathcal {D}}({\mathcal {C}})$ is locally noetherian (e.g., see [20, Proposition A.11]).

Conversely, assume that ${\mathcal {D}}({\mathcal {C}})$ is locally noetherian. Let X be an object of ${\mathcal {C}}$. Then, the FP-injective object T(X) of ${\mathcal {D}}({\mathcal {C}})$ must be injective (e.g., see [20, Proposition A.11]). Then, X is pure-injective by Proposition 4.1. Hence, ${\mathcal {C}}$ is pure semisimple. $\square$

Theorem 4.8

Let ${\mathcal {C}}$ be a pure semisimple exactly definable additive category. Then, the class of finitely presented objects of ${\mathcal {C}}$ is Baer–Kaplansky if and only if the class of finitely presented indecomposable objects of ${\mathcal {C}}$ is Baer–Kaplansky.

Proof

Consider the above functor $T:{\mathcal {C}}\rightarrow {\mathcal {D}}({\mathcal {C}})$. By Propositions 4.1 and 4.7, ${\mathcal {C}}$ is equivalent to the full subcategory of injective objects of ${\mathcal {D}}({\mathcal {C}})$. The functor T preserves and reflects finitely presented objects by Proposition 4.1. By Corollary 2.8, the class of finitely generated injective objects of ${\mathcal {D}}({\mathcal {C}})$ is Baer–Kaplansky if and only if the class of finitely generated indecomposable injective objects of ${\mathcal {D}}({\mathcal {C}})$ is Baer–Kaplansky. Now, the conclusion follows by Proposition 2.1. $\square$

5 Baer–Kaplansky Classes in Categories $\sigma [M]$

Let R be a ring with identity and M a left R-module. Then, the category $\sigma [M]$ is the full subcategory of the category of left R-modules consisting of modules isomorphic to M-generated modules [29, Section 15]. It is the smallest Grothendieck category containing M. For instance, when $M=R$, $\sigma [M]$ is the category of left R-modules. In addition, when C is a coalgebra over a field k, C is a left $C^*$-module, where $C^*=\mathrm{Hom}_k(C,k)$, and $\sigma [{}_{C^*}C]$ is the category of right C-comodules [8]. Since it is a Grothendieck category, all properties on Baer–Kaplansky classes in Grothendieck categories established earlier in the paper are valid in $\sigma [M]$. However, let us note that in general $\sigma [M]$ need not be finitely accessible [27, Example 1.7]. In addition, since a Grothendieck category is exactly definable if and only if it is finitely accessible [26, Theorem 3.6], in general, $\sigma [M]$ need not be exactly definable. Hence, one cannot apply to $\sigma [M]$ the results on finitely accessible and exactly definable given earlier in the paper. Nevertheless, we shall see that there are some similar results. Let us note that one may define purity, pure-injectivity and pure-projectivity in categories $\sigma [M]$ in a similar way as for a usual module category [29, Section 34]. If $(U_i)_{i\in I}$ is a representing set of all finitely presented objects of $\sigma [M]$, then one may construct a certain ring with enough idempotents associated to $\sigma [M]$, called the functor ring of $\sigma [M]$ (see [29, Section 52]).

Proposition 5.1

([29, 52.2]). Let R be a ring with identity, M a left R-module and T the functor ring of $\sigma [M]$. Let $(U_i)_{i\in I}$ be a representing set of all finitely presented objects of $\sigma [M]$ and $U=\bigoplus _{i\in I}U_i$. Assume that U is a generator in $\sigma [M]$. Then, there is a fully faithful functor $F:\sigma [M]\rightarrow (T)\mathrm{Mod}$, which induces an equivalence between $\sigma [M]$ and the full subcategory of flat left T-modules. Moreover, a sequence in $\sigma [M]$ is pure exact if and only if F takes it into a (pure) exact sequence in $(T)\mathrm{Mod}$.

The above equivalence restricts to equivalences between:

• (1) Pure-projective objects of $\sigma [M]$ and projective left T-modules.

• (2) Finitely presented objects of $\sigma [M]$ and finitely generated projective left T-modules.

Theorem 5.2

Let R be a ring with identity and let M be a left R-module. Let X and Y be objects of $\sigma [M]$, such that X has a direct sum decomposition into indecomposable subobjects and Y / X is pure-projective. If there exists an IP-isomorphism $\Phi :\mathrm{End}_{R}(X)\rightarrow \mathrm{End}_{R}(Y)$, then X and Y are isomorphic.

Proof

This follows in a similar way as Theorem 3.4, using Proposition 5.1. $\square$

Recall that a left R-module M is called pure semisimple if every pure exact sequence in $\sigma [M]$ splits. Note that M is pure semisimple if and only if every object of $\sigma [M]$ is pure-injective if and only if every object of $\sigma [M]$ is pure-projective. In addition, M is pure semisimple if and only if every object of $\sigma [M]$ is isomorphic to a direct sum of (finitely presented) indecomposable objects [29, 53.4].

Proposition 5.3

( [29, 53.4]). Let R be a ring with identity, M a left R-module and T the functor ring of $\sigma [M]$. Let $(U_i)_{i\in I}$ be a representing set of all finitely presented objects of $\sigma [M]$ and $U=\bigoplus _{i\in I}U_i$. Then, M is pure semisimple if and only if U is a generator in $\sigma [M]$ and T is left perfect if and only if U is a generator in $\sigma [M]$ and every indecomposable object is finitely presented in $\sigma [M]$.

Corollary 5.4

Let R be a ring with identity and let M be a pure semisimple left R-module. Then the class of finitely presented objects of $\sigma [M]$ is Baer–Kaplansky if and only if the class of (finitely presented) indecomposable objects of $\sigma [M]$ is Baer–Kaplansky.

Proof

This follows in a similar way as Theorem 4.8, using Propositions 5.1 and 5.3. $\square$