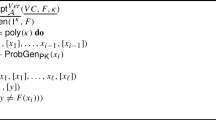Protostar: Generic Efficient Accumulation/Folding for Special-Sound Protocols

Abstract

Accumulation is a simple yet powerful primitive that enables incrementally verifiable computation (IVC) without the need for recursive SNARKs. We provide a generic, efficient accumulation (or folding) scheme for any $(2k-1)$-move special-sound protocol with a verifier that checks $\ell$ degree-d equations. The accumulation verifier only performs $k+2$ elliptic curve multiplications and $k\,+\,d\,+\,O(1)$ field/hash operations. Using the compiler from BCLMS21 (Crypto 21), this enables building efficient IVC schemes where the recursive circuit only depends on the number of rounds and the verifier degree of the underlying special-sound protocol but not the proof size or the verifier time. We use our generic accumulation compiler to build Protostar. Protostar is a non-uniform IVC scheme for Plonk that supports high-degree gates and (vector) lookups. The recursive circuit is dominated by 3 group scalar multiplications and a hash of $d^*$ field elements, where $d^*$ is the degree of the highest gate. The scheme does not require a trusted setup or pairings, and the prover does not need to compute any FFTs. The prover in each accumulation/IVC step is also only logarithmic in the number of supported circuits and independent of the table size in the lookup.

1 Introduction

Incrementally Verifiable Computation [30] is a powerful primitive that enables a possibly infinite computation to be run, such that the correctness of the state of the computation can be verified at any point. IVC, and it’s generalization to DAGs, PCD [12], have many applications, including distributed computation [3, 13], blockchains [5, 18], verifiable delay functions [4], verifiable photo editing [25], and SNARKs for machine-computations [2]. An IVC-based VDF construction is the current candidate VDF for Ethereum [19]. One of the most exciting applications of IVC and PCD is the ZK-EVM. This is an effort to build a proof system that can prove that Ethereum blocks, as they exist today, are valid [10].

Accumulation and Folding. Historically, IVC was built from recursive SNARKs, proving that the previous computation step had a valid SNARK that proves correctness up to that point. Recently, an exciting new approach was initiated by Halo [6] and has led to a series of significant advances [8, 9, 22]. The idea is related to batch verification. Instead of verifying a SNARK at every step of the computation, we can instead accumulate the SNARK verification check with previous checks. We define an accumulator¹ such that we can combine a new SNARK and an old accumulator into a new accumulator. Checking or deciding the new accumulator implies that all previously accumulated SNARKs were valid. Now the recursive statement just needs to ensure the accumulation was performed correctly. Amazingly, this accumulation step can be significantly cheaper than SNARK verification [6, 9]. Even more surprising, this process does not even require a SNARK but instead can be instantiated with a non-succinct NARK [8], as long as there exists an efficient accumulation scheme for that NARK. The most efficient accumulation (aka folding) scheme constructions yield IVC constructions, where the recursive circuit is dominated by as few as 2 elliptic curve scalar multiplications [8, 22]. These constructions only require the discrete logarithm assumption in the random oracle model and, unlike many efficient SNARK-based IVCs, do not require a trusted setup, pairings, or FFTs. These constructions build an accumulation scheme for one fixed (but universal) R1CS language by taking a random linear combination between the accumulator and a new proof. R1CS is a minimal expression of NP, defined by three matrices A, B, C, that close resembles arithmetic circuits with addition and multiplication gates. However, it has limited flexibility, especially as the current constructions require fixing R1CS matrices that are used for all computation steps. These limitations are especially problematic for ZK-EVMs. In a ZK-EVM, each VM instruction (OP-CODE) is encoded in a different circuit. Each circuit uses high-degree gates, instead of just multiplication, and so-called lookup gates [16]. These lookup gates enable looking up that a circuit value is in some table, simplifying range proofs and bit-operations. These R1CS-based accumulation schemes contrast non-IVC SNARK developments, with an increased focus on high-degree gate [11, 16] and lookup support [15]. For lookups, a recent line of work has shown that if the table can be pre-computed, we can perform n lookups in a table of size T in time $O(n\log n)$, independent of T [14, 27, 33, 34].

More Expressive Accumulation. There have been efforts to build accumulation schemes that overcome the limitations of fixed R1CS. SuperNova [21] enables selecting the appropriate R1CS instance at runtime without a recursive circuit that is linear in all R1CS instances. The approach, however, still has limitations. The recursive circuit still requires many (though a constant number of) hashes and a hash-to-group gadget, and additionally, the accumulator, and thus the final proof, is still linear in the total size of all instances.

Sangria [24] describes an accumulation scheme for a Plonk-like [16] constraint system with degree-2 gates. It also proposes a solution for higher-degree gates in the future work section but without security proof. Moreover, as the gate degree d increases, the number of group operations in Sangria grows by a factor of d, which cancels out the advantages of using the more expressive high-degree gates. Origami [35] recently introduced a folding scheme for lookups using a product check and degree 7 polynomials. These accumulation schemes are built from simple underlying protocols performing a linear combination between an accumulator and a proof. However, the constructions seem ad hoc and need individual security proof. This leads us to our main research questions:

• Recipe for accumulation. Is there a general recipe for building accumulation schemes? Can we formalize this recipe, simplifying the task of constructing secure and efficient accumulation schemes?

• Efficient accumulation for ZK-EVM. Can we build an accumulation/folding scheme for a language that combines the benefits of the most advanced proof systems today? Can we support multiple circuits, high-degree, and lookup gates?

We answer both questions positively. Firstly we show a general compiler that takes any $(2k-1)$-move special-sound interactive argument for an NP-complete relation $\mathcal {R}_\textsf{NP}$ with an algebraic degree d verifier and construct an efficient IVC-scheme from it. This is done in 4 simple steps.

• 1. We compress the prover message by committing to them in a homomorphic commitment scheme.

• 2. Then we apply the Fiat-Shamir transform to yield a secure NARK. [1, 31]

• 3. We build a simple and efficient accumulation scheme that samples a random challenge $\alpha$ and takes a linear combination between the current accumulator and the new NARK.

• 4. We apply the compiler by [8] to yield a secure IVC scheme.

The recursive circuit of this transformation is dominated by only $d+k-1$ scalar multiplications in the additive group of the commitment scheme² for a protocol with k prover messages and a degree d verifier. For R1CS, where $k=1$ and $d=2$, this yields the same protocol and efficiency as Nova [22]. We can further reduce the size of the recursive circuit to only $k+2$ group scalar multiplication, by compressing all verification equations using a random linear combination.

Efficient Simple Protocols for $\mathcal {R}_{mplkup}$. Equipped with this compiler, we design $\textsc {Protostar}$, a simple and efficient IVC scheme for a highly expressive language $\mathcal {R}_{\text {mplkup}}$ that supports multiple non-uniform circuits and enables high degree and lookup gates. The schemes can be instantiated from any linearly homomorphic vector commitment, e.g., the discrete logarithm-based Pedersen commitment [26], and do not require a trusted setup or the computation of large FFTs. The protocol has several advantages over prior schemes:

• Non-uniform IVC without overhead. Each iteration has a program counter $\textbf{pc}$ that selects one out of $I$ circuits. Part of the circuit constrains $\textbf{pc}$; e.g., $\textbf{pc}$ could depend on the iteration or indicate which instruction within a VM is executed. The IVC-prover, including the recursive statement, only requires one exponentiation per non-zero bit in the witness. The prover’s computation is independent of $I$.

• Flexible high degree gates. Our protocol supports Plonk-like constraint systems with degree d gates instead of just addition and multiplication. The recursive statement consists of 3 group scalar multiplications and $d+O(1)$ hash and field operations. Unlike in traditional Plonk, there is no additional cost for additional gate types (of degree less than d) and additional selectors. This enables a high level of non-uniformity, even within a circuit.

• Lookups, linear and independent of table size. $\textsc {Protostar}$ supports lookup gates that ensure a value is in some precomputed table T. In each computation step, the prover commits to 2 vectors of length $\ell _{\textsf{lk}}$, where $\ell _{\textsf{lk}}$ is the number of lookups. The prover, in each step, is independent of the table size (assuming free indexing in T). We also support tables that store tuples of size v using 1 additional challenge computations within the recursive circuit.

Table 1. The comparison between IVCs.

Our protocols are built of multiple small building blocks. In the protocol for high-degree gates, the prover simply sends the witness, and the degree d verifier checks the circuit with degree d gates. For lookup, we leverage an insight by Haböck [17] on logarithmic derivates. This yields a protocol where a prover performing $\ell _{\textsf{lk}}$ in a table of size T only needs to commit to two vectors of length $\ell _{\textsf{lk}}$, independent of T. This is the most efficient lookup protocol today. While the verification is linear time, it is low degree (2) and thus compatible with our generic compiler. Combining all these yields $\textsc {Protostar}$, a new IVC-scheme for $\mathcal {R}_{\text {mplkup}}$. We compare $\textsc {Protostar}$, with SuperNova [21] and HyperNova [20], in Table 1 (for more detail see Corollary 1): $\textsf{P}$ native is the running time of the accumulation prover and $\textsf{P}$ recursive refers to the cost of implementing the accumulation verifier as a circuit. In the table, $|\textbf{w}|$ is the number of non-zero entries of the witness for circuit i, and $\ell _{\textsf{lk}}$ is the number of lookups in a table of size $T$. $\mathbb {G}$ is the cost of a group scalar multiplication. $\mathbb {F}$ is the cost of a field multiplication. $d\,\textsf{H}$ denotes the cost of hashing d $\lambda$-bit numbers. We assume that the cost scales linearly with the size of the input and output. In Protostar d field elements are hashed once and in HyperNova d field elements are hashed $\log (n)$ times. $\textsf{H}_\mathbb {G}$ is the cost of a hash-to-group function. ${\textsf{H}_{\textsf{in}}}$ is the cost of hashing the public input and the accumulator instance. Note that the $O(1)\,\textsf{H}$ in SuperNova’s recursive circuit involves constant number of hashes to the input of two accumulator instances and one circuit verification key, by using multiset-based offline memory checking in a circuit [28].

Concurrent Work. In a paper concurrent with this work, Kothapalli and Setty [20] introduce an IVC for high degree relations. They use a generalization of R1CS called customizable constraint systems (CCS) [29] that covers the Plonkish relations. It also enables gates with a high additive fan-in. Protostar also has no restriction to the fan-in an individual gate has, but we subsequently showed that our compiler can also be directly applied to CCS (See full version [7]). HyperNova is based on so-called multi-folding schemes. They also provide a lookup argument suitable for recursive arguments. However, they do not explicitly explain how to integrate lookup to Plonk/CCS in their IVC scheme or provide any explicit constructions for non-uniform computations. Their scheme is built using sumchecks [23] and the resulting IVC recursive circuit is dominated by 1 group scalar multiplication, $d \log {n}\,+\,{\ell _{\textsf{in}}}$ hash operations and $O(d\log {n}+{\ell _{\textsf{in}}})$ field multiplications where d is the custom gate degree, n is the number of gates and ${\ell _{\textsf{in}}}$ is the public input length. In comparison, our IVC recursive circuit, even with lookup and non-uniformity support, is only dominated by 3 group scalar multiplications and $O({\ell _{\textsf{in}}}+d)$ field/hash operations, entirely independent of n. The 2 additional group operations compared to HyperNova are likely offset by the additional lookup support [32] and the significantly fewer hashes and non-native field operations (d vs. $d\log (n)$). A detailed comparison is given in Table 1.

For a lookup relation with table size T and $\ell _{\textsf{lk}}$ lookup gates, their accumulation/folding scheme leads to an accumulation prover whose work is dominated by O(T) field operations and an accumulation verifier whose work is dominated by $O(\ell _{\textsf{lk}}\log {T})$ field operations and $O(\log {T})$ hashes. This is undesirable when the table size $T \gg \ell _{\textsf{lk}}$. In comparison, our scheme has prover complexity $O(\ell _{\textsf{lk}})$ and the verifier is only dominated by 3 group scalar multiplications, 2 hashes and 2 field multiplications. Moreover, the lookup support adds almost no overhead to the IVC scheme for high-degree Plonk relations. In particular, it adds no group scalar multiplications. Lastly, their lookup scheme does not support vector-valued lookups, which is essential for applications like ZK-EVM and encoding bit-wise operations in circuits.

1.1 Technical Overview

Given an NP-complete relation $\mathcal {R}$, we introduce a generic framework for constructing efficient incremental verifiable computation (IVC) schemes with predicates expressed in $\mathcal {R}$. For $\mathcal {R}$ being the non-uniform Plonkup circuit satisfiability relation, we obtain an efficient (non-uniform) IVC scheme for proving correct program executions on stateful machines (e.g., EVM). The framework starts by designing a simple special-sound protocol $\varPi _\textsf{sps}$ for relation $\mathcal {R}$, which is easy to analyze. Next, we use a generic compiler to transform $\varPi _\textsf{sps}$ into a Non-interactive Argument of Knowledge Scheme (NARK) whose verification predicate is easy to accumulate/fold. Finally, we build an efficient accumulation/folding scheme for the NARK verifier, and apply the generic compiler from [8] to obtain the IVC/PCD scheme for relation $\mathcal {R}$. We describe the workflow in Fig. 1.

Fig. 1.

The workflow for building an IVC from a special sound protocol. We start from a special-sound protocol $\varPi _\textsf{sps}$ for an NP-complete relation $\mathcal {R}_\textsf{NP}$, and transform it to $\textsf{CV}[\varPi _\textsf{sps}]$ with a compressed verifier check. $\textsf{CV}[\varPi _\textsf{sps}]$ is converted to a NARK $\textsf{FS}[\textsf{cm}[\textsf{CV}[\varPi _\textsf{sps}]]]$ via commit-and-open and the Fiat-Shamir transform. We then build a generic accumulation scheme for the NARK and apply Theorem 1 from [8] to obtain the IVC scheme. This last connection is dotted as it requires heuristically replacing random oracles with cryptographic hash functions.

The paper begins by describing the compiler from special-sound protocols to NARKs in Sect. 3, and presents an efficient accumulation scheme for the compiled NARK verifier in Sect. 3.2. Next, we describe simple and efficient special-sound protocols for Plonkup circuit-satisfiability relations and extend it to support non-uniform computation in Sect. 5. Similarly, we extend the CCS relation [29] to support non-uniform computation and lookup (see full version [7]). We give an overview of our approach below.

Efficient IVCs from Special-Sound Protocols. Let $\varPi _\textsf{sps}$ be any multi-round special-sound protocol for some relation $\mathcal {R}$, in which the verifier is algebraic, that is, the verifier algorithm only checks algebraic equations over the input and the prover messages. E.g., the following naive protocol for the Hadamard product relation over vectors $\textbf{a}, \textbf{b}, \textbf{c} \in \mathbb {F}^n$ is special-sound and has a degree-2 algebraic verifier: The prover simply sends the vectors $\textbf{a}$, $\textbf{b}$, $\textbf{c}$ to the verifier, and the verifier checks that $a_i \cdot b_i = c_i$ for all $i \in [n]$. However, as shown in the example, the prover message can be large in $\varPi _\textsf{sps}$ and the folding scheme can be expensive if we directly accumulate the verifier predicate. Inspired by the splitting accumulation scheme [8], to enable efficient accumulation/folding, we split each prover message into a short instance and a large opening, where the short instance is built from the homomorphic commitment to the prover message. Next, we use the Fiat-Shamir transform to compile the protocol into a NARK where the verifier challenges are generated from a random oracle.

Now we can view the NARK transcript as an accumulator (or a relaxed NP instance-witness pair in the language of folding schemes), where the accumulator instance consists of the prover message commitments and the verifier challenges; while the accumulator witness consists of the prover messages (i.e., the opening to the commitments). Note we also need to introduce an error vector/commitment into the accumulator witness/instance to absorb the “noise” that arises after each accumulation/folding step.

In the accumulation scheme, given two accumulators (or NARK proofs), the prover folds the witnesses and the instances of both accumulators via a random linear combination and generates a list of d “error-correcting terms” as accumulation proof (d is the degree of the NARK verifier); the verifier only needs to check that the folded accumulator instance is consistent with the accumulation proof and the original instances being folded, both of which are small. After finishing all the accumulation steps, a decider applies a final check to the accumulator, scrutinizing that (i) the accumulator witness is consistent with the commitments in the accumulator instance, and (ii) the “relaxed” NARK verifier check still passes. Here by “relaxed” we mean that the algebraic equation also involves the error vector in the accumulator. If the decider accepts, this implies that all accumulated NARKs were valid and thus that all accumulated statements are in $\mathcal {R}$ (and the prover knows witnesses for these statements).

Finally, given the accumulation scheme, if the relation $\mathcal {R}$ is NP-complete, we can apply the compiler in [8] to obtain an efficient IVC scheme with predicates expressed in $\mathcal {R}$.

In Theorem 3, we show that for any $(2k-1)$-move³ special-sound protocols with degree-d verifiers, the resulting IVC recursive circuit only involves $k+d+O(1)$ hashes, $k+1$ non-native field operations and $k+d-1$ commitment group scalar multiplications. We also introduce a generic approach for further reducing the number of group operations to $k+2$ in Sect. 3.3. This is favorable for $d\ge 3$. The idea is to compress all $\ell$ degree d verification checks into a single verification check using a random linear combination with powers of a challenge $\beta$. This means that error-correcting terms are field elements and, thus, can be sent directly without committing to them. The prover also sends a single commitment to powers of $\beta$ and powers of $\beta ^{\sqrt{\ell }}$. The verification equation uses one power of $\beta$ and one power of $\beta ^{\sqrt{\ell }}$, which increases the degree of the verification check to $d+2$. The verifier also checks the correctness of the powers of $\beta$ using $2\sqrt{\ell }$ degree 2 checks.

Special-Sound Protocols for (Non-uniform) Plonkup Relations. Given the generic compiler above, our ultimate goal of constructing a (non-uniform) IVC scheme for zkEVM becomes much easier. It is now sufficient to design a multi-round special-sound protocol for the (non-uniform) Plonkup relation. We describe the components of the special-sound protocol in Fig. 2. Note we also extend CCS relation [29] to support lookup and non-uniform computation and build a special-sound protocol for it (See Fig. 2). Recall that a Plonkup circuit-satisfiability relation consists of three modular relations, namely, (i) a high-degree gate relation checking that each custom gate is satisfied; (ii) a permutation (wiring-identity) relation checking that different gate values are consistent if the same wire connects them, and (iii) a lookup relation checking that a subset of gate values belongs to a preprocessed table. The special-sound protocols for the permutation and high-degree gate relations are trivial, where the prover directly sends the witness to the verifier, and the verifier checks that the permutation/high-degree gate relation holds. The degree of the permutation check is only 1, and the degree of the gate-check is the highest degree in the custom gate formula.

Fig. 2.

The special-sound protocols for Protostar and $\textsc {Protostar}{}_{\text {ccs}}$. The special-sound protocol $\varPi _{\textrm{mplkup}}$ for the multi-circuit Plonkup relation $\mathcal {R}_{\textrm{mplkup}}$ consists of the sub-protocols for permutation, high-degree custom gate, lookup, and circuit selection relations. The special-sound protocol $\varPi _{\text {mccs+}}$ for the extended CCS relation $\mathcal {R}_{\text {mccs+}}$ consists of the sub-protocols for lookup, circuit selection, as well as the CCS relation [29]. From $\varPi _{\textrm{mplkup}}$ or $\varPi _{\text {mccs+}}$, we can apply the workflow described in Fig. 1 to obtain the IVC schemes Protostar or $\textsc {Protostar}{}_{\text {ccs}}$.

The special-sound protocol for the lookup relation $\mathcal {R}_{\text {LK}}$ is more interesting as the statement of the lookup relation is not algebraic. Inspired by the log-derivative lookup scheme [17], in Sect. 4.3, we design a simple 3-move special-sound protocol $\varPi _\text {LK}$ for $\mathcal {R}_{\text {LK}}$, in which the verifier degree is only 2. A great feature of $\varPi _\text {LK}$ is that the number of non-zero elements in the prover messages is only proportional to the number of lookups, but independent of the table size. Thus the IVC prover complexity for computing the prover message commitments is independent of the table size, which is advantageous when the table size is much larger than the witness size. However, the prover work for computing the error terms is not independent of the table size because the accumulator is not sparse. Fortunately, we observe that the prover can efficiently update the error term commitments without recomputing the error term vectors from scratch, thus preserving the efficiency of the accumulation prover. Moreover, we extend $\varPi _\text {LK}$ in Sect. 4.3 to further support vector-valued lookup, where each table entry is a vector of elements. This feature is useful in applications like zkEVM and for simulating bit operations in circuits.

Given the special-sound protocols for permutation/high-degree gate/lookup relations, the special-sound protocol $\varPi _{\text {plonkup}}$ for Plonkup is just a parallel composition of the three protocols. Furthermore, in Sect. 5, we apply a simple trick to support non-uniform IVC. More precisely, let $\{\mathcal {C}_i\}_{i=1}^{I}$ be $I$ different branch circuits (e.g., the set of supported instructions in EVM), let $\textsf{pi}\mathrel {\mathop :}=(pc, \textsf{pi}')$ be the public input where $pc\in [I]$ is a program counter indicating which instruction/branch circuit is going to be executed in the next IVC step. Our goal is to prove that $(\textsf{pi},\textbf{w})$ is in the relation $\mathcal {R}_{\text {mplkup}}$ in the sense that $\mathcal {C}_{pc}(\textsf{pi}, \textbf{w}) = 0$ for witness $\textbf{w}$. The relation statement can also add additional constraints on pc depending on the applications. The special-sound protocol for $\mathcal {R}_{\text {mplkup}}$ is almost identical to $\varPi _{\text {plonkup}}$ for the Plonkup relation, except that the prover further sends a bool vector $\textbf{b} \in \mathbb {F}^{I}$, and the verifier uses $2I$ degree 2 equations to check that $b_{pc} = 1$ and $b_{i} = 0\forall i \ne pc$. Additionally, each algebraic equation $\mathcal {G}$ checked in $\varPi _{\text {plonkup}}$ is replaced with $\sum _{i=1}^{I} \mathcal {G}_i\cdot b_i$ where $\mathcal {G}_i$ $(1\le i\le I)$ is the corresponding gate in the i-th branch circuit. The resulting special-sound protocol has 3 moves, and the verifier degree is $d+1$, where d is the highest degree of the custom gates. This means that the IVC scheme for the non-uniform Plonkup relation adds negligible overhead to that for the Plonkup relation.

2 Preliminaries

The definitions of special-sound protocols and non-interactive arguments follow from [1]. We defer the definition of Fiat-Shamir transform and commitment schemes to the full version [7].

Lemma 1

(Fiat-Shamir transform of Special-sound Protocols [1]). The Fiat-Shamir transform of a $(\alpha _1,\dots ,\alpha _\mu )$-out-of-N special-sound interactive proof $\varPi$ is knowledge sound with knowledge error

$$\kappa _\textsf{fs}(Q)=(Q+1) \kappa $$

where $\kappa =1-\prod (1-\frac{\alpha _i}{N})$ is the knowledge error of the interactive proof $\varPi$.

2.1 Incremental Verifiable Computation (IVC)

We adapt and simplify the definition from [8, 22].

Definition 1 (IVC)

An incremental verifiable computation (IVC) scheme for function predicates expressed in a circuit-satisfiability relation $\mathcal {R}_{\textsf{NP}}$ is a tuple of algorithms $\textsf{IVC}= (\textsf{P}_\textsf{IVC}, \textsf{V}_\textsf{IVC})$ with the following syntax and properties:

• $\textsf{P}_\textsf{IVC}(m, z_0,z_m,z_{m-1}, \textbf{w}_{\textsf{loc}}, \pi _{m-1}]) \rightarrow \pi _m$. The IVC prover $\textsf{P}_\textsf{IVC}$ takes as input a program output $z_m$ at step m, local data $\textbf{w}_{\textsf{loc}}$, initial input $z_0$, previous program output $z_{m-1}$ and proof $\pi _{m-1}$ and outputs a new IVC proof $\pi _m$.

• $\textsf{V}_\textsf{IVC}(m, z_0, z_m, \pi _m) \rightarrow b$. The IVC verifier $\textsf{V}_\textsf{IVC}$ takes the initial input $z_0$, the output $z_m$ at step m, and an IVC proof $\pi _m$, ‘accepts’ by outputting $b=0$ and ‘rejects’ otherwise.

The scheme $\textsf{IVC}$ has perfect adversarial completeness if for any function predicate $\phi$ expressible in $\mathcal {R}_{\textsf{NP}}$, and any, possibly adversarially created, $(m, z_0,z_m, , z_{m-1},\textbf{w}_{\textsf{loc}}, \pi _{m-1})$ such that

$$ \phi (z_0,z_m, z_{m-1},\textbf{w}_{\textsf{loc}} ) \wedge (\textsf{V}_\textsf{IVC}(m-1, z_0, z_{m-1}, \pi _{m-1}) = 0)$$

it holds that $\textsf{V}_\textsf{IVC}(m, z_0, z_m, \pi _m)$ accepts for proof $\pi _m\leftarrow \textsf{P}_\textsf{IVC}(m,z_0, z_{m-1}, z_m, \textbf{w}_{\textsf{loc}}, \pi _{m-1})$.

The scheme $\textsf{IVC}$ has knowledge soundness if for every expected polynomial-time adversary $\textsf{P}^*$, there exists an expected polynomial-time extractor $\textsf{Ext}_{\textsf{P}^*}$ such that

$$ \Pr \left[ \begin{array}{c} \textsf{V}_\textsf{IVC}(m,z_0, z, \pi _m) = 0 \wedge \\ ([\exists i \in [m]\,, \lnot \phi (z_0,z_i ,z_{i-1}, \textbf{w}_i)]\\ \vee z \ne z_m) \end{array} \left| \begin{array}{c} [\phi , (m, z_0, z, \pi _m)] \leftarrow \textsf{P}^*\\ \left[ z_i, {\textbf{w}}_{i}\right] _{i=1}^{m} \leftarrow \textsf{Ext}_{\textsf{P}^*} \end{array}\right. \right] \le \textsf{negl}\!\!\left( \lambda \right) \,. $$

Here m is a constant.

Efficiency. The runtime of $\textsf{P}_\textsf{IVC}$ and $\textsf{V}_\textsf{IVC}$ as well as the size of $\pi _\textsf{IVC}$ only depend on $|\phi |$ and are independent on the number of iterations.

Recently, [21] introduced the notion of non-uniform IVC, where the predicate $\phi$ is selected from a fixed set of predicates at every step of the computation. The selection depends on the current state of the computation. Non-uniform IVC fits into our model by simply setting the predicate to be the union of all predicates, including the selection circuit. The one key difference is an additional efficiency requirement that the IVC prover in step i only depends on the size of the predicate that is being executed in step i. Our $\textsc {Protostar}$ construction achieves this requirement.

2.2 Simple Accumulation

We take definitions and proofs from [8].

Definition 2 (Accumulation Scheme)

An accumulation scheme for a NARK $(\textsf{P}_{\textsf {NARK}},\textsf{V}_\textsf {NARK})$ is a triple of algorithms $\textsf{acc}=(\textsf{P}_\textsf{acc},\textsf{V}_\textsf{acc},D)$, all of which have access to the same random oracle $\rho _\textsf{acc}$ as well as $\rho _\textsf {NARK}$, the oracle for the NARK. The algorithms have the following syntax and properties:

• $\textsf{P}_\textsf{acc}(\textsf{pi}, \pi =(\pi .x,\pi .\textbf{w}),\textsf{acc}=(\textsf{acc}.x,\textsf{acc}.\textbf{w}))\rightarrow \{\textsf{acc}'=(\textsf{acc}'.x,\textsf{acc}'.\textbf{w}), \textsf{pf}\}$. The accumulation prover $\textsf{P}_\textsf{acc}$ takes as input a statement $\textsf{pi}$, NARK proof $\pi$, and an accumulator $\textsf{acc}$ and outputs a new accumulator $\textsf{acc}'$ and correction terms $\textsf{pf}$.

• $\textsf{V}_\textsf{acc}(\textsf{pi},\pi .x,\textsf{acc}.x,\textsf{acc}'.x,\textsf{pf})\rightarrow v$. The accumulation verifier takes as input the statement $\textsf{pi}$, the instances of the NARK proof, the old and new accumulator, the correction terms, and ‘accepts’ by outputting 0 and ‘rejects’ otherwise.

• $D(\textsf{acc})\rightarrow v$. The decider on input $\textsf{acc}$ ‘accepts’ by outputting 0 and ‘rejects’ otherwise.

An accumulation scheme has knowledge-soundness with knowledge error $\kappa$ if the RO-NARK $(\textsf{P}',\textsf{V}')$ has knowledge error $\kappa$ for the relation

$$ \mathcal {R}_\textsf{acc}((\textsf{pi}, \pi .x, \textsf{acc}.x);(\pi .\textbf{w},\textsf{acc}.\textbf{w})) : \left( \textsf{V}_\textsf {NARK}(\textsf{pi}, \pi )=0 \wedge D(\textsf{acc})=0 \right) \,,$$

where $\textsf{P}'$ outputs $\textsf{acc}',\textsf{pf}$ and $\textsf{V}'$ on input $((\textsf{pi}, \pi .x,\textsf{acc}.x), (\textsf{acc}',\textsf{pf}))$ accepts if $D(\textsf{acc}')$ and $\textsf{V}_\textsf{acc}(\textsf{pi}, \pi .x,\textsf{acc}.x,\textsf{acc}'.x,\textsf{pf})=0$.

The scheme has perfect completeness if the RO-NARK $(\textsf{P}',\textsf{V}')$ has perfect completeness for $\mathcal {R}_\textsf{acc}$.

Theorem 1

(IVC from accumulation [8]). Given a standard-model NARK for circuit-satisfiability and a standard-model accumulation scheme (Definition 2) for that NARK, both with negligible knowledge error, there exists an efficient transformation that outputs an IVC scheme (see Sect. 3.2 of [8]) for constant-depth compliance predicates, assuming that the circuit complexity of the accumulation verifier $\textsf{V}_\textsf{acc}$ is sub-linear in its input.

Random Oracle. Note that both the NARK and accumulation scheme we construct are in the random oracle model. However, Theorem 1 requires a NARK and an accumulation scheme in the standard model. It remains an open problem to construct such schemes. However, we can heuristically instantiate the random oracle with a cryptographic hash function and assume that the resulting schemes still have knowledge soundness.

Definition 3 (Fiat-Shamir Heuristic)

The Fiat-Shamir Heuristic, relative to a secure cryptographic hash function $\textsf{H}$, states that a random oracle NARK with negligible knowledge error yields a NARK that has negligible knowledge error in the standard (CRS) model if the random oracle is replaced with $\textsf{H}$.

Complexity. The IVC transformation from [8] recursively proves that the accumulation was performed correctly. To do that, it implements $\textsf{V}_\textsf{acc}$ as a circuit and proves that the previous accumulation step was done correctly. Note that this recursive circuit is independent of the size of $\pi .\textbf{w}, \textsf{acc}.\textbf{w}$ and the runtime of $D$. The IVC prover is linear in the size of the recursive circuit plus the size of the IVC computation step expressed as a circuit. The final IVC verifier and the IVC proof size are linear in these components. This can be reduced using an additional SNARK as in [22].

PCD. IVC can be generalized to arbitrary DAGs instead of just path graphs in a primitive called proof-carrying data [3]. Accumulation schemes can be compiled into full PCD if they support accumulating an arbitrary number of accumulators and proofs [8, 9]. For simplicity, we only build accumulation for one proof and one accumulator, as well as for two accumulators. This enables PCD for DAGs of degree two. By transforming higher degree graphs into degree two graphs (by converting each degree d node into a $\log _2(d)$ depth tree), we can achieve PCD for these graphs.

Outsourcing the Decider. In the accumulation to IVC transformation, the IVC proof is linear in the accumulator, and the IVC verifier runs the decider. The accumulation schemes we construct are linear in the witness of a single computation step. However, we can outsource the decider by providing a SNARK that, given $\textsf{acc}.x$, proves knowledge of $\textsf{acc}.\textbf{w}$, such that $D(\textsf{acc})=0$. Nova [22] constructs a custom, concretely efficient SNARK for their accumulation/folding scheme.

3 Protocols

3.1 Special-Sound Protocols and Their Basic Transformations

In this section, we describe a class of special-sound protocols whose verifier is algebraic. The protocol $\varPi _\textsf{sps}$ has 3 essential parameters $k, d, \ell \in \mathbb {N}$, meaning that $\varPi _\textsf{sps}$ is a $(2k-1)$-move protocol with verifier degree d and output length $\ell$ (i.e. the verifier checks $\ell$ degree d algebraic equations). In each round i $(1\le i \le k)$, the prover $\textsf{P}_\textsf{sps}(\textsf{pi},\textbf{w},[\textbf{m}_j,r_j]_{j=1}^{i-1})$ generates the next message $\textbf{m}_i$ on input the public input $\textsf{pi}$, the witness $\textbf{w}$, and the current transcript $[\textbf{m}_j,r_j]_{j=1}^{i-1}$, and sends $\textbf{m}_i$ to the verifier; the verifier replies with a random challenge $r_i \in \mathbb {F}$. After the final message $\textbf{m}_k$, the verifier computes the algebraic map $\textsf{V}_\textsf{sps}$ and checks that the output is a zero vector of length $\ell$. More precisely, $\deg (\textsf{V}_\textsf{sps})=d$, s.t.

$$\textsf{V}_\textsf{sps}(\textsf{pi}, [\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1}) \mathrel {\mathop :}=\sum _{j=0}^d f^{\textsf{V}_\textsf{sps}}_j(\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1})\,,$$

where $f^{\textsf{V}_\textsf{sps}}_j$ is a homogeneous degree-j algebraic map that outputs a vector of $\ell$ field elements.

Commit and Open. For a commitment scheme $\textsf{cm}=(\textsf{Setup},\textsf{Commit})$, consider the following relation $\mathcal {R}_\textsf{cm}^\mathcal {R}=(x;\textbf{w}, \textbf{m}\in \mathcal {M}, \textbf{m}'\in \mathcal {M}): \{(x,\textbf{w})\in \mathcal {R}\vee (\textsf{Commit}( \textbf{m})=\textsf{Commit}(\textbf{m}')\wedge \textbf{m}\ne \textbf{m}')\}$. The relation’s witness is either a valid witness for $\mathcal {R}$ or a break of the commitment scheme $\textsf{cm}$. We now design a special-sound protocol $\varPi _\textsf{cm}=(\textsf{P}_\textsf{cm},\textsf{V}_\textsf{cm})$ for $\mathcal {R}_\textsf{cm}^\mathcal {R}$ given $\varPi _\textsf{sps}=(\textsf{P}_\textsf{sps},\textsf{V}_\textsf{sps})$, a special-sound protocol for $\mathcal {R}$. $\textsf{P}_\textsf{cm}$ runs $\textsf{P}_\textsf{sps}$ to generate the ith message and then commits to the message. Along with the final message, $\textsf{P}_\textsf{cm}$ sends the opening to the commitment. The verifier $\textsf{V}_\textsf{cm}$ checks the correctness of the commitments and runs $\textsf{V}_\textsf{sps}$ on the commitment openings.

Lemma 2

($\varPi _\textsf{cm}$ is $(a_1, \dots , a_\mu )$-special-sound). Let $\varPi _\textsf{sps}$ be an $(a_1, \dots , a_\mu )$-out-of-N special-sound protocol for relation $\mathcal {R}$, where the prover messages are all in a set $\mathcal {M}$. Let $(\textsf{Setup},\textsf{Commit})$ be a binding commitment scheme for messages in $\mathcal {M}$. For $\textsf{ck}\leftarrow \textsf{Setup}_\textsf{cm}(1^\lambda )$ let $\mathcal {R}_\textsf{cm}=(\textsf{pi};\textbf{w},m\in \mathcal {M},m' \in \mathcal {M}): (\textsf{pi};\textbf{w})\in \mathcal {R}\vee (\textsf{Commit}(\textsf{ck},m)=\textsf{Commit}(\textsf{ck},m')\wedge m\ne m')$. Then $\varPi _\textsf{cm}=\textsf{cm}[\varPi _{\textsf{sps}}]$ is an $(a_1, \dots , a_\mu )$-out-of-N special-sound protocol for $\mathcal {R}_\textsf{cm}^\mathcal {R}$.

We defer the proof to the full version [7].

Fiat-Shamir Transform. Let $\rho _\textsf {NARK}$ be a random oracle. Let $\varPi _\textsf{cm}$ be the commit-and-open protocol for the special-sound protocol $\varPi _\textsf{sps}= (\textsf{P}_{\textsf{sps}}, \textsf{V}_{\textsf{sps}})$. The Fiat-Shamir Transform $\textsf{FS}[\varPi _\textsf{cm}]$ of the protocol $\varPi _\textsf{cm}$ is the following. The prover generates the round challenges by computing $\rho _\textsf {NARK}$ on input the challenge and the prover message commitment in the previous round. The prover then sends the proof as the list of prover messages and the corresponding commitments. The verifier checks the proof by recomputing the challenges and runs the verifier for $\varPi _\textsf{cm}$. By Lemma 1, $\textsf{FS}[\varPi _\textsf{cm}]$ is knowledge sound if $\varPi _\textsf{sps}$ is special-sound.

3.2 Accumulation Scheme for $\textsf{V}_\textsf {NARK}$

Let $\rho _\textsf{acc}$ and $\rho _\textsf {NARK}$ be two random oracles, and let $\textsf{V}_\textsf {NARK}$ be the verifier of $\textsf{FS}[\varPi _\textsf{cm}]$ in Sect. 3.1, whose underlying special-sound protocol is $\varPi _\textsf{sps}= (\textsf{P}_\textsf{sps}, \textsf{V}_\textsf{sps})$ for a relation $\mathcal {R}$. We describe the accumulation scheme for $\textsf{V}_\textsf {NARK}$.

The accumulated predicate. The predicate to be accumulated is the “relaxed” verifier check of the NARK scheme $\textsf{FS}[\varPi _\textsf{cm}]$ for relation $\mathcal {R}$. Namely, given public input $\textsf{pi}\in \mathcal {M}^{{\ell _{\textsf{in}}}}$, random challenges $[r_i]_{i=1}^{k-1} \in \mathbb {F}^{k-1}$, a NARK proof

$$\pi .x=[C_i]_{i=1}^k,\, \pi .\textbf{w}=[\textbf{m}_i]_{i=1}^k$$

where $[C_i]_{i=1}^k \in \mathcal {C}^k$ are commitments and $[\textbf{m}_i]_{i=1}^k$ are prover messages in the special-sound protocol $\varPi _{\textsf{sps}}$, and a slack variable $\mu$, the predicate checks that (i) $r_i =\rho _\textsf {NARK}(r_{i-1},C_i)$ for all $i \in [k-1]$ (where $r_0 \mathrel {\mathop :}=\rho _\textsf {NARK}(\textsf{pi})$), (ii) $\textsf{Commit}(\textsf{ck},\textbf{m}_i)=C_i$ for all $i \in [k]$, and (iii)

$$ \textsf{V}_\textsf{sps}(\textsf{pi}, \pi .x,\pi .\textbf{w},[r_i]_{i=1}^{k-1}, \mu ) \mathrel {\mathop :}=\sum _{j=0}^d \mu ^{d-j}\cdot f^{\textsf{V}_\textsf{sps}}_j(\textsf{pi}, \pi .\textbf{w},[r_i]_{i=1}^{k-1}) = \textbf{e} $$

where $\textbf{e} = \textbf{0}^\ell$ and $\mu = 1$ for the NARK verifier $\textsf{V}_\textsf {NARK}$. Here $f^{\textsf{V}_\textsf{sps}}_j$ is a degree-j homogeneous algebraic map that outputs $\ell$ field elements. Degree-j homogeneity says that each monomial term of $f^{\textsf{V}_\textsf{sps}}_j$ has degree exactly j.

Remark 1

Without loss of generality, we assume that the public input $\textsf{pi}$ is of constant size, as otherwise, we can set it as the hash of the original public input.

Accumulator. The accumulator has the following format:

• Accumulator instance $\textsf{acc}.x\mathrel {\mathop :}=\{\textsf{pi}, [C_i]_{i=1}^k, [r_i]_{i=1}^{k-1}, E,\mu \}$, where $\textsf{pi}\in \mathcal {M}^{{\ell _{\textsf{in}}}}$ is the accumulated public input, $[C_i]_{i=1}^k \in \mathcal {C}^k$ are the accumulated commitments, $[r_i]_{i=1}^{k-1} \in \mathbb {F}^{k-1}$ are the accumulated challenges, $E \in \mathcal {C}$ is the accumulated commitment to the error terms, and $\mu \in \mathbb {F}$ is a slack variable.

• Accumulator witness $\textsf{acc}.\textbf{w}\mathrel {\mathop :}=\{[\textbf{m}_i]_{i=1}^k\}$, where $[\textbf{m}_i]_{i=1}^k$ are the accumulated prover messages.

Accumulation Prover. On input commitment key $\textsf{ck}$ (which can be hardwired in the prover’s algorithm), accumulator $\textsf{acc}$, an instance-proof pair $(\textsf{pi}, \pi )$ where

$$\begin{aligned} \textsf{acc}&\mathrel {\mathop :}=(\textsf{acc}.x=\{\textsf{pi}',[C'_i]_{i=1}^k,[r'_i]_{i=1}^{k-1}, E, \mu \},\textsf{acc}.\textbf{w}=\{[\textbf{m}'_i]_{i=1}^k\})\,,\\ \pi &\mathrel {\mathop :}=(\pi .x=[C_i]_{i=1}^{k},\pi .\textbf{w}=[\textbf{m}_i]_{i=1}^k), \end{aligned}$$

the accumulation prover $\textsf{P}_\textsf{acc}$ works as in Fig. 3.

Fig. 3.

Accumulation Prover/Verifier for low-degree Fiat-Shamired NARKs

Accumulation Verifier. On input public input $\textsf{pi}$, NARK proof instance $\pi .x$, accumulator instance $\textsf{acc}.x$, accumulation proof $\textsf{pf}$, and the updated accumulator instance $\textsf{acc}'.x:=\{\textsf{pi}'',[C''_i]_{i=1}^k,[r''_i]_{i=1}^k,E', \mu ' \}$, the accumulation verifier $\textsf{V}_\textsf{acc}$ works as in Fig. 3.

Decider. On input the commitment key $\textsf{ck}$ (which can be hardwired) and an accumulator

$$ \textsf{acc}= (\textsf{acc}.x=\{\textsf{pi}, [C_i]_{i=1}^k, [r_i]_{i=1}^{k-1}, E,\mu \}, \textsf{acc}.\textbf{w}=\{[\textbf{m}_i]_{i=1}^k\}), $$

the decider does the checks described in Fig. 4.

Fig. 4.

Accumulation Decider for low-degree Fiat-Shamired NARKs

Theorem 2

Let $(\textsf{P}_\textsf {NARK}, \textsf{V}_\textsf {NARK})$ be the RO-NARK defined in Sect. 3.1. Let $\textsf{cm}=(\textsf{Setup},\textsf{Commit})$ be a binding, homomorphic commitment scheme. Let $\rho _\textsf{acc}$ be another random oracle. The accumulation scheme $(\textsf{P}_\textsf{acc},\textsf{V}_\textsf{acc},D_\textsf{acc})$ for $\textsf{V}_\textsf {NARK}$ satisfies perfect completeness and has knowledge error $(Q+1)\frac{d+1}{|\mathbb {F}|}+ \textsf{negl}\!\!\left( \lambda \right)$ as defined in Definition 2, against any randomized polynomial-time Q-query adversary.

Proof

Completeness: Consider any tuple $((\textsf{pi}, \pi ), \textsf{acc}) \in \mathcal {R}_{\textsf{acc}}$, that is, $\textsf{V}_\textsf {NARK}(\textsf{pi}, \pi )$ and $D(\textsf{acc})$ both accept. Let $(\textsf{acc}', \textsf{pf})$ denote the output of the accumulation prover $\textsf{P}_\textsf{acc}(\textsf{ck},\textsf{acc}, (\textsf{pi}, \pi ))$. We argue that both the decider $D(\textsf{acc}')$ and the accumulation verifier $\textsf{V}_\textsf{acc}(\textsf{pi}, \pi .x, \textsf{acc}.x, \textsf{pf}, \textsf{acc}'.x)$ will accept, which finishes the proof of perfect completeness by Definition 2.

$\textsf{V}_\textsf{acc}$ accepts as $\textsf{P}_\textsf{acc}$ and $\textsf{V}_\textsf{acc}$ go through the same process of computing challenges $[r_i]_{i=1}^{k-1}$ and $\alpha$, thus the linear combinations of $\textsf{acc}.x$ and $(\textsf{pi}, \pi .x; \textsf{pf}, [r_i]_{i=1}^{k-1})$ via $\alpha$ will be consistent.

We prove that $D(\textsf{acc}')$ accepts by scrutinizing the following decider checks.

The check $\textsf{acc}'.C_i \overset{?}{=}\ \textsf{Commit}(\textsf{ck}, \textsf{acc}'.\textbf{m}_i)$ succeeds for all $i \in [k]$. This is because

$$\textsf{acc}'.\{C_i, \textbf{m}_i\} = \textsf{acc}.\{C_i, \textbf{m}_i\} + \alpha \cdot \pi .\{C_i, \textbf{m}_i\}$$

for all $i \in [k]$, where $\pi .C_i = \textsf{Commit}(\textsf{ck}, \pi .\textbf{m}_i)$ because $\textsf{V}_\textsf {NARK}(\textsf{pi}, \pi )$ accepts, and $\textsf{acc}.C_i = \textsf{Commit}(\textsf{ck}, \textsf{acc}.\textbf{m}_i)$ because $D(\textsf{acc})$ accepts. Thus the check succeeds by the homomorphism of the commitment scheme.

The decider computes $\textbf{e}'\leftarrow \sum _{j=0}^d (\textsf{acc}'.\mu )^{d-j} f^{\textsf{V}_\textsf{sps}}_j(\textsf{acc}'.\{\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1}\})$ such that for $\textbf{e}=\sum _{j=0}^d \textsf{acc}.\mu ^{(d-j)} \cdot f^{\textsf{V}_\textsf{sps}}_j(\textsf{acc}.\{\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1}\})$, it holds that

$$\begin{aligned} \textbf{e}' &= \textbf{e} + \sum _{j=1}^{d-1} \alpha ^{j} \cdot \textsf{pf}.\textbf{e}_j \\ &= \sum _{j=0}^{d} (\alpha + \textsf{acc}.\mu )^{d-j} \cdot f^{\textsf{V}_\textsf{sps}}_j(\alpha \cdot \{\textsf{pi}, \pi .[\textbf{m}_i]_{i=1}^{k}, [r_i]_{i=1}^{k-1}\} + \textsf{acc}.\{\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1}\}) \,. \end{aligned}$$

By the definition of $\textsf{pf}.\textbf{e}_j$ and the homomorphism of the commitment scheme, and because $D(\textsf{acc})$ accepts and checks $E = \textsf{Commit}(\textsf{ck}, \textbf{e})$, we have that $E'=\textsf{Commit}(\textsf{ck},\textbf{e}')$.

Knowledge-Soundness: We show that the scheme has knowledge-soundness by showing that there exists an underlying $(d+1)$-special-sound protocol and then applying the Fiat-Shamir transform to show that the accumulation scheme is knowledge sound. Consider the public-coin interactive protocol $\varPi _{I}=(\textsf{P}_I(\textsf{pi},\pi ,\textsf{acc}),\textsf{V}_I(\textsf{pi},\pi .x,\textsf{acc}.x))$ where $\textsf{P}_I$ sends $\textsf{pf}=[E_j]_{j=1}^{d-1} \in \mathbb {G}^{d-1}$ as computed by $\textsf{P}_\textsf{acc}$ to $\textsf{V}_I$. The verifier sends a random challenge $\alpha \in \mathbb {F}$, and the prover $\textsf{P}_{I}$ responds with $\textsf{acc}'$ as computed by $\textsf{P}_\textsf{acc}$. $\textsf{V}_I$ accepts if $D_\textsf{acc}(\textsf{acc}')=0$ and $\textsf{V}_\textsf{acc}(\textsf{pi},\pi .x, \textsf{acc}.x,\textsf{pf},\textsf{acc}'.x)=0$ using the random challenge $\alpha$, instead of a Fiat-shamir challenge.

Claim 1: $\varPi _I$ is $(d+1)$-special-sound Consider the relation $\mathcal {R}_\textsf{acc}$ where $\mathcal {R}_\textsf{acc}$ is defined in Definition 2. Consider $d+1$ accepting transcripts for $\varPi _I:$

$$ \{\mathcal {T}_i \mathrel {\mathop :}=(\textsf{pi}, \pi .x,\textsf{acc}.x; \textsf{acc}'_i, \textsf{pf}_i) \}_{i=1}^{d+1}\,. $$

We construct an extractor $\textsf{Ext}_\textsf{acc}$ that extracts a witness for $\mathcal {R}_\textsf{acc}(\textsf{pi}.\pi .x,\textsf{acc}.x)$ given $\mathcal {T}$.

For all $i \in [d+1]$,

$$ (\textsf{acc}'_i) = (\mu '_i, \textsf{pi}'_i,[C'_{i,j}]_{j=1}^k, [r_{i,j}]_{j=1}^{k-1}, E'_i, [\textbf{m}'_{i,j}]_{j=1}^k) $$

and $\textsf{pf}_i = \textsf{pf}=[E_j]_{j=1}^{d-1}$.

Given that the transcripts are accepting, i.e. both $\textsf{V}_\textsf{acc}$ and $D_\textsf{acc}$ accept, we have that $\textsf{Commit}(\textsf{ck},\textbf{e}'_i)=E'_i=\textsf{acc}.E+\sum _{j=1}^{d-1} \alpha _i^{j} E_j$ for all $i\in [d+1]$, whereas

$$\textbf{e}_i'\mathrel {\mathop :}=\sum _{j=0}^d {\mu '_i}^{d-j} f_j^{\mathcal {R}}(\pi _i',[\textbf{m}_{i,j}']_{j=1}^k,[r_{i,j}]_{j=1}^{k-1})\,.$$

Using a Vandermonde matrix of the challenges $\alpha _1,\dots ,\alpha _{d}$ we can compute $\textbf{e},[\textbf{e}_j]_{j=1}^{d-1}$ such that $E_j=\textsf{Commit}(\textsf{ck},\textbf{e}_j)$ and $\textsf{acc}.E=\textsf{Commit}(\textsf{ck},\textbf{e})$ from the equations above. Therefore we have that $\textbf{e}'_i=\textbf{e}+\sum _{j=1}^{d-1} \alpha _i^j \textbf{e}_j$ for all $i\in [d+1]$.

Additionally using two challenges $(\alpha _1,\alpha _2)$, $\textsf{Ext}_\textsf{acc}$ can compute $\pi .\textbf{w}=[\textbf{m}_{j}]_{j=1}^k=[\frac{\textsf{acc}'.\textbf{m}_{1,j}-\textsf{acc}'.\textbf{m}_{2,j}}{\alpha _1-\alpha _2}]_{j=1}^k$. It holds that $\textsf{acc}.\textbf{m}_j=\textsf{acc}'.\textbf{m}_{1,j}-\alpha _1\cdot \pi .\textbf{m}_j \forall j \in [k]$, such that $\pi .C_j=\textsf{Commit}(\textsf{ck},\pi .\textbf{m}_j)$ and $\textsf{acc}.C_j=\textsf{Commit}(\textsf{ck},\textsf{acc}.\textbf{m}_j)$. If for any other challenge and any j, $\textsf{acc}'.\textbf{m}_j\ne \alpha \pi .\textbf{m}_j +\textsf{acc}.\textbf{m}_j$, then this can be used to compute a break of the commitment scheme $\textsf{cm}$. This happens with negligible probability by assumption.

Otherwise, we have that $\sum _{j=0} \mu _i^{d-j} f_j^{\mathcal {R}}(\pi _j,[\textbf{m}_{i,j}]_{i=1}^k,[r_{i,j}]_{i=1}^{k-1})-\textbf{e}_i=0$ for all $i\in [d+1]$. Together this implies that the degree d polynomial

$$\begin{aligned} p(X)&=\sum _{j=0}^d (X+\textsf{acc}.\mu )^{d-j}\cdot f^{\textsf{V}_\textsf{sps}}_j(X\cdot \textsf{pi}+\textsf{acc}.\textsf{pi}, [X\cdot \textbf{m}_i+\textsf{acc}.\textbf{m}_i]_{i=1}^k,[X\cdot r_i +\textsf{acc}.r_i]_{i=1}^{k-1}) \nonumber \\ &-\textbf{e} - \sum _{j=1}^{d-1} \textbf{e}_j X^j \,, \end{aligned}$$

(1)

is zero on $d+1$ points $(\alpha _1,\dots ,\alpha _{d+1})$, i.e. is zero everywhere. The constant term of this polynomial is

$$\sum _{j=0}^d \textsf{acc}.\mu ^{d-j}\cdot f^{\textsf{V}_\textsf{sps}}_j(\textsf{acc}.\textsf{pi},[\textsf{acc}.\textbf{m}_i]_{i=1}^k ,[\textsf{acc}.r_i]_{i=1}^{k-1})-\textbf{e}\,.$$

It being 0 implies that $D(\textsf{acc})=0$. Additionally, the degree d term of the polynomial is

$$\sum _{j=0}^d f^{\textsf{V}_\textsf{sps}}_j(\textsf{pi},[\pi .\textbf{m}_i]_{i=1}^k ,[\pi .r_i]_{i=1}^{k-1})\,.$$

Together with $\textsf{V}_\textsf{acc}$ checking that the challenges $r_i$ are computed correctly this implies that $\textsf{V}_\textsf {NARK}(\textsf{pi},\pi )=0$. $\textsf{Ext}$ thus outputs a valid witness $( \pi .\textbf{w},\textsf{acc}.\textbf{w})\in \mathcal {R}_\textsf{acc}(\textsf{pi},\pi .x,\textsf{acc}.x)$ and thus $\varPi _I$ is $(d+1)$-special-sound. Using Lemma 1, we have that $\varPi _{AS}=\textsf{FS}[\varPi _I]$ is a NARK for $\mathcal {R}_\textsf{acc}$ with knowledge soundness $(Q+1)\cdot \frac{d+1}{|\mathbb {F}|}+\textsf{negl}\!\!\left( \lambda \right)$. This implies that $\textsf{acc}$ is an accumulation scheme with $((Q+1)\cdot \frac{d+1}{|\mathbb {F}|}+\textsf{negl}\!\!\left( \lambda \right) )$-knowledge soundness.    $\square$

3.3 Compressing Verification Checks for High-Degree Verifiers

Observe that the accumulation prover needs to perform $\varOmega (d\ell )$ group operations to commit to the $d-1$ error vectors $\textbf{e}_j \in \mathbb {F}^{\ell }$ $(1 \le j < d)$; and the accumulation verifier needs to check the combination of d error vector commitments. This can be a bottleneck when the verifier degree d is high. In this circumstance, we can optimize the accumulation complexity by transforming the underlying special-sound protocol $\varPi _\textsf{sps}$ into a new special-sound protocol $\textsf{CV}[\varPi _\textsf{sps}]$ for the same relation $\mathcal {R}$. This optimization compresses the $\ell$ degree-d equations checked by the verifier into a single degree-$(d+2)$ equation using a random linear combination, with the tradeoff of additionally checking $2\sqrt{\ell }$ degree-2 equations. We describe the generic transformation below.

Compressing Verification Checks. W.l.o.g. assume $\ell$ is a perfect square, then we can transform $\varPi _{\textsf{sps}}$ into a special-sound protocol $\textsf{CV}[\varPi _\textsf{sps}]$ where the $\textsf{V}_{\textsf{sps}}$ reduces from $\ell$ degree-d checks to 1 degree-$(d+2)$ check and additionally $2\sqrt{\ell }$ degree-2 checks. Instead of checking the output of $\textsf{V}_{\textsf{sps}}$ to be $\ell$ zeroes, we take a random linear combination of the $\ell$ verification equations using powers of a challenge $\beta$. For example, if the map is $\textsf{V}_{\textsf{sps}}(x_1, x_2) \mathrel {\mathop :}=(\textsf{V}_{\textsf{sps},1}(x_1, x_2), \textsf{V}_{\textsf{sps},2}(x_1, x_2)) = (x_1+x_2, x_1 x_2)$ we can set the new algebraic map as $\textsf{V}'_{\textsf{sps}}(x_1, x_2, \beta ) \mathrel {\mathop :}=\textsf{V}_{\textsf{sps},1}(x_1, x_2) + \beta \cdot \textsf{V}_{\textsf{sps},2}(x_1, x_2) = (x_1+x_2) + \beta x_1 x_2$ for a random $\beta$. Doing this naively reduces the output length to 1 but also requires the verifier to compute the appropriate powers of $\beta$. This would increase the degree by $\ell$, an undesirable tradeoff. To mitigate this, we can have the prover precompute powers of $\beta$, i.e. $\beta ,\beta ^2,\dots ,\beta ^{\ell }$ and send them to the verifier. The verifier then only needs to check consistency between the powers of $\beta$, which can be done using a degree 2 check, e.g. $\beta ^{i+1}=\beta ^i\cdot \beta$ and the degree d verification equation increases in degree by 1. This mitigates the degree increase but requires the prover to send another message of length $\ell$. To achieve a more optimal tradeoff, we write each $i=j+k\cdot \sqrt{\ell }$ for $j,k \in [1,\sqrt{\ell }]$. The prover then sends $\sqrt{\ell }$ powers of $\beta$ and $\sqrt{\ell }-1$ powers of $\beta ^{\sqrt{\ell }}$. From these, each power of $\beta$ from 1 to $\ell$ can be recomputed using just one multiplication. This results in the prover sending an additional message of length $2\sqrt{\ell }$, the original $\ell$ verification checks being transformed into a single degree $d+2$ check and additionally $2\sqrt{\ell }$ degree 2 checks for the consistency of the powers of $\beta$.

Fig. 5.

Compressed verification of $\varPi _\textsf{sps}$.

We describe the transformed protocol in Fig. 5, where

$$\begin{aligned} \textsf{V}'_\textsf{sps}(\textsf{pi},[\textbf{m}_i]_{i=1}^{k+1},([r_i]_{i=1}^{k-1},\beta )) &\mathrel {\mathop :}=\sum _{i=0}^{\sqrt{\ell }-1}\sum _{j=0}^{\sqrt{\ell }-1} \beta _i \cdot \beta '_j \cdot \textsf{V}_{\textsf{sps},i+j\sqrt{\ell }}(\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1})\\ &=\sum _{j=0}^{\ell -1} \beta ^j \cdot \textsf{V}_{\textsf{sps},j}(\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1}) \end{aligned}$$

and $\textsf{V}_{\textsf{sps},j}(\textsf{pi},[\textbf{m}_i]_{i=1}^k,[r_i]_{i=1}^{k-1})$ is the $(j+1)$-th $(0 \le j < \ell )$ equation checked by $\textsf{V}_{\textsf{sps}}$. The transformed protocol is a $(2k+1)$-move special-sound protocol for the same relation $\mathcal {R}$. The transformed verifier now checks 1 degree-$(d+2)$ equation and additionally $2\sqrt{\ell }$ degree-2 equations.

Lemma 3

Let $\varPi _\textsf{sps}$ be a $(2k-1)$-move protocol for relation $\mathcal {R}$ with $(a_1, \dots , a_{k-1})$-special-soundness, in which the verifier outputs $\ell$ elements. The transformed protocol $\textsf{CV}[\varPi _\textsf{sps}]$ of $\varPi _\textsf{sps}$ is $(a_1, \dots , ,a_{k-1}, \ell )$-special-sound.

We defer the proof to the full version [7].

High-Low Degree Accumulation. After the transformation, the error vectors $\textbf{e}_j$ $(1\le j\le d+1)$ become single field elements, and we can use the trivial commitment $E_j \mathrel {\mathop :}=\textsf{Commit}(\textsf{ck}, e_j) \mathrel {\mathop :}=e_j$ without group operations. Additionally, we can use a separate error vector $\textbf{e}' \in \mathbb {F}^{2\sqrt{\ell }}$ to keep track of the error terms for the $2\sqrt{\ell }$ degree-2 checks, and set $E' \mathrel {\mathop :}=\textsf{Commit}(\textsf{ck}, \textbf{e}') \in \mathbb {G}$ to be the corresponding error commitment. The accumulation prover only needs to perform $O(\sqrt{\ell })$ additional group operations to commit $\textbf{m}_{k+1}$ and $\textbf{e}'$, and compute the coefficients of a degree-$(d+2)$ univariate polynomial, which is described as the sum of $O(\ell )$ polynomials. The accumulator instance needs to include one more challenge $\beta$ and two commitments (for $\textbf{m}_{k+1}$ and $\textbf{e}'$). The accumulator verifier needs to do only $k\,+\,2$ (rather than $k\,+\,d\,-\,1$) group scalar multiplications, with the tradeoff of 1 more hash and O(d) more field operations. This high-low degree accumulation is described in detail in the full version [7].

Theorem 3 (IVC for high-degree special-sound protocols)

Let $\mathbb {F}$ be a finite field, such that $|\mathbb {F}|\ge 2^\lambda$ and $\textsf{cm}=(\textsf{Setup},\textsf{Commit})$ be a binding homomorphic commitment scheme for vectors in $\mathbb {F}$. Let $\varPi _\textsf{sps}=(\textsf{P}_\textsf{sps},\textsf{V}_\textsf{sps})$ be a special-sound protocol for an NP-complete relation $\mathcal {R}_{\textsf{NP}}$ with the following properties:

• It’s $(2k-1)$ move.

• It’s $(a_1,\dots ,a_{k-1})$-out-of-$|\mathbb {F}|$ special-sound. Such that the knowledge error $\kappa =1-\prod _{i=1}^{k-1}(1-\frac{a_i}{|\mathbb {F}|})=\textsf{negl}\!\!\left( \lambda \right)$

• The inputs are in $\mathbb {F}^{{\ell _{\textsf{in}}}}$

• The verifier is degree $d=\textsf{poly}\!\!\left( \lambda \right)$ with output in $\mathbb {F}^{\ell }$

Then, under the Fiat-Shamir heuristic for a cryptographic hash function $\textsf{H}$ (Definition 3), there exist two IVC schemes $\textsf{IVC}=(\textsf{P}_\textsf{IVC},\textsf{V}_\textsf{IVC})$ and $\textsf{IVC}_{\textsf{CV}}=(\textsf{P}_{\textsf{CV},\textsf{IVC}},\textsf{V}_{\textsf{CV},\textsf{IVC}})$ with predicates expressed in $\mathcal {R}_{\textsf{NP}}$ with the following efficiencies:

	No $\textsf{CV}$	$\textsf{CV}$
$\textsf{P}_\textsf{IVC}$ native	$\begin{array}{c} \sum _{i=1}^k |\textbf{m}^{*}_i|+(d-1)\ell \mathbb {G}\\ \textsf{P}_\textsf{sps}+ L(\textsf{V}_\textsf{sps},d) \end{array}$	$\begin{array}{c} \sum _{i=1}^k |\textbf{m}^{*}_i| + O(\sqrt{\ell }) \mathbb {G}\\ \textsf{P}_{\textsf{sps}} + L'(\textsf{V}_\textsf{sps},d+2) \end{array}$
$\textsf{P}_\textsf{IVC}$ recursive	$\begin{array}{c} k + d-1 \mathbb {G}\\ k +{\ell _{\textsf{in}}}\mathbb {F}\\ (k+d+O(1)) \textsf{H}+ 1{\textsf{H}_{\textsf{in}}}\end{array}$	$\begin{array}{c} k + 2\mathbb {G}\\ k+{\ell _{\textsf{in}}}+d+1 \mathbb {F}\\ (k+d+O(1)) \textsf{H}+ 1{\textsf{H}_{\textsf{in}}}\end{array}$
$\textsf{V}_\textsf{IVC}$:	$\begin{array}{c} \ell + \sum _{i=1}^k |\textbf{m}_i| \mathbb {G}\\ \textsf{V}_\textsf{sps}\end{array}$	$\begin{array}{c} O(\sqrt{\ell })+ \sum _{i=1}^k |\textbf{m}_i| \mathbb {G}\\ O(\ell )+\textsf{V}_\textsf{sps}\end{array}$
$|\pi _\textsf{IVC}|$ :	$\begin{array}{c} k+{\ell _{\textsf{in}}}\mathbb {F}\\ k+1\mathbb {G}\\ \sum _{i=1}^k |\textbf{m}_i| \end{array}$	$\begin{array}{c} k+{\ell _{\textsf{in}}}+1 \mathbb {F}\\ k+2\mathbb {G}\\ \sum _{i=1}^k |\textbf{m}_i| + O(\sqrt{\ell }) \end{array}$

The first row displays the native operations of the $\textsf{IVC}$ prover (i.e., the complexity of running the accumulation prover). The second row describes the size of the recursive statement representing the accumulation verifier for which $\textsf{P}_\textsf{IVC}$ creates a proof. The third row is the computation of $\textsf{V}_\textsf{IVC}$, and the last row is the size of the proof. In the table, $|\textbf{m}_i|$ denotes the prover message length; $|\textbf{m}^{*}_i|$ is the number of non-zero elements in $\textbf{m}_i$; $\mathbb {G}$ for rows 1–3 is the total length of the messages committed using $\textsf{Commit}$. $\mathbb {F}$ are field operations. $\textsf{H}$ denotes the total input length to a cryptographic hash, and ${\textsf{H}_{\textsf{in}}}$ is the hash to the public input and accumulator instance. $\textsf{P}_\textsf{sps}$ (and $\textsf{V}_\textsf{sps}$) is the cost of running the prover (and the algebraic verifier) of the special-sound protocol, respectively. $L(\textsf{V}_\textsf{sps},d)$ is the cost of computing the coefficients of the degree d polynomial

$$\begin{aligned} \textbf{e}(X)\mathrel {\mathop :}=\sum _{j=0}^d (\mu +X)^{d-j} \cdot f_{j}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+X\cdot \pi )\,, \end{aligned}$$

(2)

and $L'(\textsf{V}_\textsf{sps}, d+2)$ is the cost of computing the coefficients of the degree $d+2$ polynomial

$$\begin{aligned} e(X)\mathrel {\mathop :}=\sum _{a=0}^{\sqrt{\ell }-1}\sum _{b=0}^{\sqrt{\ell }-1} (X\cdot \pi .\beta _a + \textsf{acc}.\beta _a)(X\cdot \pi .\beta '_b + \textsf{acc}.\beta '_b) \sum _{j=0}^d (\mu +X)^{d-j} \cdot f_{j,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+X\cdot \pi )\,, \end{aligned}$$

(3)

where all inputs are linear functions in a formal variable X⁴, and $f^{\textsf{V}_\textsf{sps}}_{j,i}$ is the ith $(0\le i \le \ell -1)$ component of $f^{\textsf{V}_\textsf{sps}}_j$’s output. For the proof size, $\mathbb {G}$ and $\mathbb {F}$ are the number of commitments and field elements, respectively.

Proof

The construction first defines the two NARKs

$$\varPi _\textsf {NARK}=(\textsf{P}_{\textsf {NARK}},\textsf{V}_{\textsf {NARK}})=\textsf{FS}[\textsf{cm}[\varPi _{\textsf{sps}}]],$$

and

$$\varPi _{\textsf {NARK},\textsf{CV}} =(\textsf{P}_{\textsf {NARK}},\textsf{V}_{\textsf {NARK}})=\textsf{FS}[\textsf{cm}[\textsf{CV}[\varPi _{\textsf{sps}}]]].$$

Then we construct the accumulation scheme $(\textsf{P}_\textsf{acc},\textsf{V}_\textsf{acc})=\textsf{acc}[\varPi _\textsf {NARK}]$ using the accumulation scheme from Sect. 3.2 and $(\textsf{P}_{\textsf{acc},\textsf{HL}}\textsf{V}_{\textsf{acc},\textsf{HL}})=\textsf{acc}_\textsf{HL}[\varPi _{\textsf {NARK},\textsf{CV}} ]$ using the accumulation scheme described in Sect. 3.3. Then we apply the transformation from Theorem 1 to construct the IVC schemes $\textsf{IVC}$ and $\textsf{IVC}_{\textsf{CV}}$.

Security: By Lemmas 1, 2, we have that $\varPi _\textsf {NARK}$ has $(Q+1)\cdot \bigl [1-\prod _{i=1}^{k-1} (1-\frac{a_i}{|\mathbb {F}|})\bigr ]$ knowledge error for relation $\mathcal {R}_{\textsf{cm}}^{\mathcal {R}_\textsf{NP}}$ for a polynomial-time Q-query RO-adversary. Witnesses for $\mathcal {R}_{\textsf{cm}}^{\mathcal {R}_\textsf{NP}}$ are either a witness for $\mathcal {R}_\textsf{NP}$ or a break of the binding property of $\textsf{cm}$. Assuming that $\textsf{cm}$ is a binding commitment scheme, the probability that a polynomial time adversary and a polynomial time extractor can compute such a break is $\textsf{negl}\!\!\left( \lambda \right)$. Thus $\varPi _\textsf {NARK}$ has knowledge error $\kappa =(Q+1)\cdot \bigl [1-\prod _{i=1}^{k-1} (1-\frac{a_i}{|\mathbb {F}|})\bigr ]+\textsf{negl}\!\!\left( \lambda \right)$ for $\mathcal {R}_{\textsf{NP}}$. Analogously and using Lemma 3, $\varPi _{\textsf {NARK},\textsf{CV}}$ has knowledge soundness with knowledge error $\kappa '=(Q+1)\cdot \bigl [1-(1-\frac{\ell }{|\mathbb {F}|}) \prod _{i=1}^{k-1} (1-\frac{a_i}{|\mathbb {F}|})\bigr ]+\textsf{negl}\!\!\left( \lambda \right)$ for $\mathcal {R}_{\textsf{NP}}$. By assumption, $\kappa$ and $\kappa '$ are negligible in $\lambda$. Using Theorem 2 and the high-low degree accumulation scheme described previously, we can construct accumulation schemes $\textsf{acc}$ and $\textsf{acc}_\textsf{CV}$ for $\varPi _\textsf {NARK}$ and $\varPi _{\textsf {NARK},\textsf{CV}}$, respectively. The accumulation schemes have negligible knowledge error as $d=\textsf{poly}\!\!\left( \lambda \right)$. Under the Fiat-Shamir heuristic for $\textsf{H}$ we can turn the NARKs and the accumulation schemes into secure schemes in the standard model.

By Theorem 1, this yields $\textsf{IVC}$ and $\textsf{IVC}_{\textsf{CV}}$, secure IVC schemes with predicates expressed in $\mathcal {R}_{\textsf{NP}}$.

Efficiency: We first analyze the efficiency for $\textsf{IVC}$. The IVC-prover runs $\textsf{P}_\textsf{sps}$ to compute all prover messages. It also commits to all the $\textsf{P}_\textsf{sps}$ messages using $\textsf{cm}$. Finally, it needs to compute all error terms $\textbf{e}_1,\dots ,\textbf{e}_{d-1}$ and commit to them. The error terms are computed by symbolically evaluating the polynomial e(X) in Eq. 3 with linear functions as inputs. The recursive circuit combines a new proof $\pi .x$ with an accumulator $\textsf{acc}.x$. The size of the accumulator instance is ${\ell _{\textsf{in}}}$ field elements for the input, $k-1$ field elements for the interactive-proof challenges, 1 field element for the accumulator challenge, and k commitments for the $\textsf{P}_\textsf{sps}$ messages and $d-1$ commitments for the error terms. The IVC verifier checks the correctness of the commitments and runs $\textsf{V}_\textsf{sps}$.

For $\textsf{IVC}_{\textsf{CV}}$, the prover needs to additionally commit to a message $\textbf{m}_{k+1}$ with length $O(\sqrt{\ell })$; the number of error terms also increases from $d-1$ to $d+1$. Fortunately, the error terms are only one element in $\mathbb {F}$, so we can use the identity function as the trivial commitment scheme. Thus, there is no cost for committing to the $d+1$ error terms when using $\textsf{CV}$. However, there is another separate error term $\textbf{e}' \in \mathbb {F}^{2\sqrt{\ell }}$ for the additional $O(\sqrt{\ell })$ degree-2 checks, thus the prover needs to commit to $E' = \textsf{Commit}(\textbf{e}')$. The size of the accumulator instance is ${\ell _{\textsf{in}}}$ field elements for the input, k field elements for the interactive-proof challenges, 1 field element for the accumulator challenge, $k+1$ commitments for the prover messages, $d+1$ field elements for the error terms of the high-degree checks, and 1 commitment for the additional error term $\textbf{e}'$.    $\square$

3.4 Computation of Error Terms

We now give an explicit algorithm for efficiently computing the error terms, that is, computing the polynomial e(X) as defined in (3) (the degree of e(X) is $d'=d+2$). The algorithm has similarities with computing the round polynomials in a single round of the sumcheck protocol [23].

• 1. For each $i=0$ to d define

  $$\begin{aligned} e^{(i)}(X):=\sum _{a=0}^{\sqrt{\ell }-1}\sum _{b=0}^{\sqrt{\ell }-1} (X\cdot \pi .\beta _a + \textsf{acc}.\beta _a)(X\cdot \pi .\beta '_b + \textsf{acc}.\beta '_b) \cdot f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+X\cdot \pi ) \end{aligned}$$

  (4)

• 2. Compute $e^{(i)}(j)$ for all $j\in [0,i+2]$. Use these evaluations to interpolate $e^{(i)}(X)$ using fast interpolation methods, e.g. an iFFT

• 3. Compute the coefficient form of $e(X)=\sum _{i=0}^d e^{(i)}(X)\cdot (\mu +X)^{d-i}$. This is done by computing the coefficients of $e^{(i)}(X)\cdot (\mu +X)^{d-i}$ for every $i \in [0,d]$ using FFTs, and recover e(X) using coefficient-wise addition. The complexity is $O(d^2\log d)$.

In the worst case, this algorithm is equivalent to evaluating the circuit at $d+2$ different inputs. However, it can perform much better in practice. The reason is that many of the n gates may only be low degree. E.g. $90\%$ of the gates are degree 1 or 2 addition and multiplication gates, and $10\%$ are more high degree gates. Then the prover only has to evaluate the $10\%$ of the circuit at $d\,+\,2$ points and $90\%$ of the circuit only at 4 points. Note that the selector polynomials are static in the classification of NP $\text {plonkup}$. This means that each gate has precisely the degree of the active component. This stands in contrast to relations such as high-degree Plonk, where the selectors are pre-processed, and the selectors are preprocessed witnesses. In Plonk and related systems, each gate essentially has the same degree.

Dealing with Branched Gates. In some scenarios, the NARK proof $\pi$ has the property that each gate $f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+X\cdot \pi )$ in Formula 4 can be represented as the sum of I parts where at most one part is related to $\pi$, that is, for some gates $g_1, \dots , g_I$ and some index $pc \in [I]$,

$$ f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+X\cdot \pi ) = g_{pc}(\textsf{acc}+X\cdot \pi ) + \sum _{j \in [I] \setminus \{pc\}} g_{j}(\textsf{acc}) \,. $$

In this case, for any gate $f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}$, we present a caching algorithm for evaluating $f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+k\cdot \pi )$ at all evaluation points $k \in [0, i+2]$. The complexity is only proportional to the evaluation complexity of $g_{pc}$ rather than $f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}$.

• 1. For every $j \in [I]$, initialize $U_j \mathrel {\mathop :}=g_j(\textsf{acc})$, and store $V \mathrel {\mathop :}=\sum _{j=1}^{I} U_j$.

• 2. Upon receiving a new NARK proof $\pi$ during accumulation, for every $k \in [0, i+2]$, compute $f_{i,a+b\sqrt{\ell }}^{\textsf{V}_\textsf{sps}}(\textsf{acc}+k\cdot \pi )= V + g_{pc}(\textsf{acc}+k\cdot \pi ) - U_{pc}$.

• 3. After the accumulation, let $\alpha \in \mathbb {F}$ be the folding challenge and let $U'_{pc} = g_{pc}(\textsf{acc}+\alpha \cdot \pi )$, update $V \leftarrow V + U'_{pc} - U_{pc}$ and update $U_{pc} \leftarrow U'_{pc}$.

The algorithm is correct because V is always $\sum _{j \in [I]} g_j(\textsf{acc})$ where $\textsf{acc}$ is the current accumulator.

4 Special-Sound Subprotocols for ProtoStar

In this section, we present special-sound protocols for permutation, high-degree gate, circuit selection and lookup relations, which are the building blocks for the (non-uniform) Plonkish circuit-satisfiability relations. We can build accumulation schemes for (and thus IVCs from) these special-sound protocols via the framework presented in Sect. 3.

4.1 Permutation Relation

Definition 4

Let $\sigma : [n] \rightarrow [n]$ be a permutation, the relation $\mathcal {R}_{\sigma }$ is the set of tuples $\textbf{w}\in \mathbb {F}^n$ such that $\textbf{w}_i = \textbf{w}_{\sigma (i)}$ for all $i \in [n]$.

Complexity. $\varPi _\sigma$ is a 1-move protocol (i.e. $k=1$); the degree of the verifier is 1.

4.2 High-Degree Custom Gate Relation

Definition 5

Given configuration $\mathcal {C}_{\text {GATE}} \mathrel {\mathop :}=(n, c, d, [\textbf{s}_i\in \mathbb {F}^{n}, G_i]_{i=1}^{m})$ where n is the number of gates, $c$ is the arity per gate, d is the gate degree, $[\textbf{s}_i]_{i=1}^{m}$ are the selector vectors, and $[G_i]_{i=1}^{m}$ are the gate formulas, the relation $\mathcal {R}_{\text {GATE}}$ is the set of tuples $\textbf{w}\in \mathbb {F}^{cn}$ such that $\sum _{j=1}^{m} \textbf{s}_{j,i} \cdot G_j(\textbf{w}_i, \textbf{w}_{i+n}, \dots , \textbf{w}_{i+(c-1)\cdot n}) = 0$ for all $i \in [n]$.

Complexity. $\varPi _\text {GATE}$ is a 1-move protocol (i.e. $k=1$) with verifier degree d.

4.3 Lookup Relation

Definition 6

Given configuration $\mathcal {C}_{\text {LK}} \mathrel {\mathop :}=(T, \ell , \textbf{t})$ where $\ell$ is the number of lookups and $\textbf{t} \in \mathbb {F}^T$ is the lookup table, the relation $\mathcal {R}_{\text {LK}}$ is the set of tuples $\textbf{w}\in \mathbb {F}^{\ell }$ such that $\textbf{w}_i \in \textbf{t}$ for all $i \in [\ell ]$.

We recall a useful lemma for lookup relation from [17], and present a special-sound protocol for the lookup relation.

Lemma 4

(Lemma 5 of [17]). Let $\mathbb {F}$ be a field of characteristic $p > \max (\ell , T)$. Given two sequences of field elements $[\textbf{w}_i]_{i=1}^{\ell }$ and $[\textbf{t}_i]_{i=1}^{T}$, we have $\{\textbf{w}_i\} \subseteq \{\textbf{t}_i\}$ as sets (with multiples of values removed) if and only if there exists a sequence $[\textbf{m}_i]_{i=1}^{T}$ of field elements such that

$$\begin{aligned} \sum _{i=1}^{\ell } \frac{1}{X+\textbf{w}_i} = \sum _{i=1}^{T}\frac{\textbf{m}_i}{X+\textbf{t}_i}\,. \end{aligned}$$

(5)

Achieving Perfect Completeness. Note that the protocol does not have perfect completeness. If there exists an $\textbf{w}_i$ or $\textbf{t}_i$ such that $\textbf{w}_i+r=0$ $\textbf{t}_i+r=0$ then the prover message is undefined. We can achieve perfect completeness by having the verifier set $\textbf{h}_i=0$ or $\textbf{g}_i=0$ in this case and changing the verification equations to

$$(\textbf{w}_i+r)\cdot (\textbf{h}_i \cdot (\textbf{w}_i+r)-1)=0$$

and

$$(\textbf{t}_i+r)\cdot (\textbf{g}_i \cdot (\textbf{t}_i+r)-\textbf{m}_i)=0\,.$$

These checks ensure that either $\textbf{h}_i=\frac{1}{\textbf{w}_i+r}$ or $\textbf{w}_i+r=0$. The checks increase the verifier degree to 3. Without these checks, the protocol has a negligible completeness error of $\frac{\ell +T}{|\mathbb {F}|}$. This completeness error can likely be ignored in practice, and these checks do not need to be implemented. However, to achieve the full definition of PCD (which has perfect completeness) and use Theorem 1 by [8], we require that all protocols have perfect completeness.

Complexity. $\varPi _\text {LK}$ is a 3-move protocol (i.e. $k=2$); the degree of the verifier is 2; the number of non-zero elements in the prover message is at most $4\ell$.

Accumulation with $O(\ell )$ Prover Complexity. The prover complexity of $\varPi _\text {LK}$ is due to the sparseness of $\textbf{g}\in \mathbb {F}^T$ and $\textbf{m}\in \mathbb {F}^T$. However, there is no guarantee that when building an accumulation scheme for $\varPi _\text {LK}$, the accumulated $\textsf{acc}.\textbf{g}$ and $\textsf{acc}.\textbf{m}$ are sparse. This is an issue, as the prover needs to compute the error term $\textbf{e}_1$. If we expand the accumulation procedures, we see that the three verification checks lead to three components of the error term $\textbf{e}_1$:

$$\textbf{e}_1^{(1)}=\left( \sum _{i=1}^{\ell } \textsf{acc}.\textbf{h}_i -\sum _{i=1}^{T}\textsf{acc}.\textbf{g}_i\right) +\mu \left( \sum _{i=1}^{\ell } \pi .\textbf{h}_i -\sum _{i=1}^{T}\pi .\textbf{g}_i\right) \in \mathbb {F}$$

$$\textbf{e}_1^{(2)}=\textsf{acc}.\textbf{h} \circ (\pi .\textbf{w}+\pi .r\cdot {\textbf{1}^{\ell }}) +\pi .\textbf{h}\circ (\textsf{acc}.\textbf{w}+\textsf{acc}.r\cdot {\textbf{1}^{\ell }})-2\mu \cdot {\textbf{1}^{\ell }} \in \mathbb {F}^\ell $$

$$\textbf{e}_1^{(3)} =\textsf{acc}.\textbf{g} \circ (\textbf{t}+\pi .r\cdot {\textbf{1}^{T}})+\pi .\textbf{g}\circ (\mu \cdot \textbf{t}+\textsf{acc}.r\cdot {\textbf{1}^{T}})-\mu \cdot \pi .\textbf{m} - \textsf{acc}.\textbf{m}\in \mathbb {F}^T.$$

We examine all three components below.

For $\textbf{e}_1^{(1)}$, we see that $(\sum _{i=1}^{\ell } \pi .\textbf{h}_i -\sum _{i=1}^{T}\pi .\textbf{g}_i)=0$ by the assumption that $\pi$ is valid, and $(\sum _{i=1}^{\ell } \textsf{acc}.\textbf{h}_i -\sum _{i=1}^{T}\textsf{acc}.\textbf{g}_i)=\textsf{acc}.\textbf{e}^{(1)}/\textsf{acc}.\mu$ (where $\textsf{acc}.\textbf{e}^{(1)}$ is the first component of the error vector for $\textsf{acc}$). Thus $\textbf{e}_1^{(1)}=\textsf{acc}.\textbf{e}^{(1)}/ \textsf{acc}.\mu$. We observe that since in IVC the accumulator $\textsf{acc}.\textbf{e}^{(1)}$ is initiated with 0, this implies that for all iterations $\textbf{e}_1^{(1)}=0$.

For $\textbf{e}_1^{(2)}$, it is computed from terms of size $\ell$, so can be computed in time $O(\ell )$.

For $\textbf{e}_1^{(3)}$, note that $\textsf{acc}.\mu$, $\textsf{acc}.r$ and $\pi .r$ are all scalars. Also note that the accumulation prover only needs to compute the commitment $E_1=\textsf{Commit}(\textsf{ck},\textbf{e}_1)=\textsf{Commit}(\textsf{ck},\textbf{e}_1^{(1)})+\textsf{Commit}(\textsf{ck},0||\textbf{e}_1^{(2)})+\textsf{Commit}(\textsf{ck},\textbf{0}^{\ell +1}||\textbf{e}_1^{(3)})$, not the actual vector $\textbf{e}_1$. We will compute $E_1^{(3)}=\textsf{Commit}(\textsf{ck},\textbf{e}_1^{(3)})$ homomorphically from the commitments below (dropping the zero padding for readability):

• 1. $G=\textsf{Commit}(\textsf{ck},\pi .\textbf{g})$, $G'=\textsf{Commit}(\textsf{ck}, \textsf{acc}.\textbf{g})$,

• 2. $M=\textsf{Commit}(\textsf{ck},\pi .\textbf{m})$, $M'=\textsf{Commit}(\textsf{ck},\textsf{acc}.\textbf{m})$,

• 3. $GT=\textsf{Commit}(\textsf{ck},\pi .\textbf{g}\circ \textbf{t})$, $GT'=\textsf{Commit}(\textsf{ck},\textsf{acc}.\textbf{g}\circ \textbf{t})$.

Given these commitments, we can compute

$$E_1^{(3)}= GT' + \pi .r \cdot G' + \textsf{acc}.\mu \cdot GT + \textsf{acc}.r\cdot G - \textsf{acc}.\mu \cdot M - M'.$$

This reduces the problem to the problem of efficiently computing and updating the commitments. G, M and GT are all commitments to $\ell$-sparse vectors, thus can be efficiently computed. The prover can cache the commitments $G', M'$, and $GT'$ and efficiently update them during accumulation. That is $G''\leftarrow G'+\alpha G$, $M''\leftarrow M'+\alpha M$ and $GT''\leftarrow GT'+\alpha GT$. Additionally, we need to update the accumulation witnesses: $\textsf{acc}'.\textbf{m}\leftarrow \textsf{acc}.\textbf{m}+\alpha \pi .\textbf{m}$ and $\textsf{acc}'.\textbf{g}\leftarrow \textsf{acc}.\textbf{g}+\alpha \pi .\textbf{g}$. Again because $\pi .\textbf{g},\pi .\textbf{m}$ are sparse this can be done in time $O(\ell )$ independent of $T=|\textbf{t}|$.

When $\varPi _\text {LK}$ is used in composition with another special-sound protocol with a higher degree d, the accumulation is made homogeneous using a $(X+\mu )^{d-2}$ factor when computing the error terms. The contribution to the error terms $\textbf{e}_i$ $(1\le i \le d-1)$ is still a linear function in $\textsf{acc}.\textbf{g}$, $\textsf{acc}.\textbf{m}$ and $\textsf{acc}.\textbf{g}\circ \textbf{t}$, and thus can be computed homomorphically from commitments to these values.

Finally, we note that the algorithm above can be generalized to support polynomial $\textbf{e}(X)$ with more general formats and with higher degrees. We refer to the full version [7] for more details.

Special-Soundness. We prove special-soundness for the perfect complete version of $\varPi _\text {LK}$, the proof for $\varPi _\text {LK}$ is almost identical (but even simpler).

Lemma 5

The perfect complete version of $\varPi _\text {LK}$ is $2(\ell +T)$-special-sound.

We defer the proof to the full version [7].

The Special-Sound Protocol for Plonkup. The special-sound protocol for the Plonkup relation is the parallel composition of $\varPi _\sigma$, $\varPi _\text {GATE}$ and $\varPi _\text {LK}$. We refer to the full version [7] for more detailed descriptions.

Vector-Valued Lookup. In some applications (e.g.,  simulating bit operations in circuits), we need to support lookup for a vector, i.e., each table value is a vector of field elements. In this section, we adapt the scheme in Sect. 4.3 to support vector lookups.

Definition 7

Consider configuration $\mathcal {C}_{\text {VLK}} \mathrel {\mathop :}=(T, \ell , v \in \mathbb {N}, \textbf{t})$ where $\ell$ is the number of lookups, and $\textbf{t} \in (\mathbb {F}^v)^T$ is a lookup table in which the ith $(1\le i \le T)$ entry is

$$ \textbf{t}_i \mathrel {\mathop :}=(\textbf{t}_{i, 1}, \dots , \textbf{t}_{i, v}) \in \mathbb {F}^{v}. $$

A sequence of vectors $\textbf{w}\in (\mathbb {F}^v)^{\ell }$ is in relation $\mathcal {R}_{\text {VLK}}$ if and only if for all $i \in [\ell ]$,

$$ \textbf{w}_i \mathrel {\mathop :}=(\textbf{w}_{i,1}, \dots , \textbf{w}_{i,v}) \in \textbf{t} \,. $$

As noted in Sect. 3.4 of [17], we can extend Lemma 4 and replace Eq. 5 with

$$\begin{aligned} \sum _{i=1}^{\ell } \frac{1}{X+w_i(Y)} = \sum _{i=1}^{T}\frac{\textbf{m}_i}{X+t_i(Y)} \end{aligned}$$

(6)

where the polynomials are defined as

$$\begin{aligned} w_i(Y) \mathrel {\mathop :}=\sum _{j=1}^{v} \textbf{w}_{i, j} \cdot Y^{j-1},\quad t_i(Y) \mathrel {\mathop :}=\sum _{j=1}^{v} \textbf{t}_{i,j} \cdot Y^{j-1}, \end{aligned}$$

which represent the witness vector $\textbf{w}_i \in \mathbb {F}^{v}$ and the table vector $\textbf{t}_i \in \mathbb {F}^{v}$. We, therefore, can describe a special-sound protocol for the vector lookup relation as follows.

Achieving Perfect Completeness. We can use the same trick in Sect. 4.3 to achieve perfect completeness for $\varPi ^{v}_\text {VLK}$. Namely, the verifier sets $\textbf{h}_i=0$ or $\textbf{g}_i=0$ when $w_i(\beta )+r = 0$ or $t_i(\beta )+r = 0$ respectively. The verification equations become

$$(w_i(\beta _1, \dots , \beta _v)+r)\cdot (\textbf{h}_i \cdot (w_i(\beta _1, \dots , \beta _v)+r)-1)=0$$

and

$$(t_i(\beta _1,\dots , \beta _v)+r)\cdot (\textbf{g}_i \cdot (t_i(\beta _1,\dots ,\beta _v)+r)-\textbf{m}_i)=0\,,$$

where $w_i(\beta _1, \dots , \beta _v) \mathrel {\mathop :}=\bigl (\sum _{j=1}^{v} \textbf{w}_{i, j} \cdot \beta _j\bigr )$ and $t_i(\beta _1,\dots , \beta _v) \mathrel {\mathop :}=\bigl (\sum _{j=1}^{v} \textbf{t}_{i,j} \cdot \beta _j\bigr )$. The degree of the verifier is 5. In practice, the negligible completeness error can likely be ignored without implementing these checks.

Accumulation Complexity. $\varPi _\text {VLK}$ is a 5-move protocol (i.e. $k=3$) with the 2nd prover message being empty; the degree of the verifier is 3; the number of non-zero elements in the prover message is at most $(v+3)\ell +v$. To ensure that the accumulation procedure only requires $O(v\ell )$ operations independent of $T$, we can apply the same trick as in Sect. 4.3.

Special-Soundness. The perfect complete version of $\varPi ^v_\text {VLK}$ is special-sound.

Lemma 6

For any $v\in \mathbb {N}$, the perfect complete version of $\varPi ^{v}_\text {VLK}$ is $[1+(v-1)\cdot (\ell +T-1), 2(\ell +T)]$-special-sound.

We defer the proof to the full version [7].

4.4 Circuit Selection

We provide a sub-protocol for showing that a vector has a single one-bit (and zeros otherwise) at the location of a program counter pc. This is later used to select the appropriate circuit.

Definition 8

For an integer n the relation $\mathcal {R}_{\text {select}}$ is the set of tuples $(\textbf{b},pc) \in \mathbb {F}^n \times \mathbb {F}$ such that $b_i=0 \forall i \in [n]\setminus \{pc\}$ and if $pc \in [n]$ then $b_{pc}=1$.

Complexity and security. $\varPi _\text {select}$ is a 1-move protocol (i.e. $k=1$); the degree of the verifier is 2.

The protocol trivially satisfies completeness. Note that the protocol is also sound: the checks $b_i \cdot (b_i-1)=0$ ensure that the vector $\textbf{b}$ is Boolean; the checks $b_i \cdot (pc-i) = 0$ ensures that $b_i = 0$ if $i\ne pc$; finally, the last check guarantees that $b_{pc} = 1 - \sum _{i\in [n]\setminus \{pc\}} b_i = 1$ as $b_i = 0$ for all $i\in [n]\setminus \{pc\}$.

5 Protostar

In this section, we describe Protostar, which is built using a special-sound protocol for capturing non-uniform Plonkup circuit computations. In particular, the relation is checking that one of the $I$ circuits is satisfied, where the index of the target circuit is determined by a part of the public input called program counter pc. The non-uniform Plonkup circuit can add arbitrary constraints on input pc.

For ease of exposition, we assume that the $I$ circuits have the same number of (i) gates n, (i) gate arity $c$, (ii) gate degree d, (iii) gate types $m$, (iv) public inputs ${\ell _{\textsf{in}}}$ and (v) lookup gates $\ell _{\textsf{lk}}$.

The scheme naturally extends when different branch circuits have different parameters.

Definition 9

Consider configuration $\mathcal {C}_{{ mplkup}} \mathrel {\mathop :}=\bigl (\textsf{pp}=[n, T, c,d, m, {\ell _{\textsf{in}}}, \ell _{\textsf{lk}}]; [\mathcal {C}_i]_{i=1}^I; \textbf{t}\bigr )$ where the ith $(1 \le i \le I)$ branch circuit has configuration $\mathcal {C}_i \mathrel {\mathop :}=(\textsf{pp},\sigma _i, [\textbf{s}_{i,j}, G_{i,j}]_{j=1}^{m}, L_i)$, and $\textbf{t} \in \mathbb {F}^T$ is the global lookup table. For a public input $\textsf{pi}\mathrel {\mathop :}=(pc, \textsf{pi}') \in \mathbb {F}^{{\ell _{\textsf{in}}}}$ where $pc \in [I]$ is a program counter, we say that $(\textsf{pi},\textbf{w}\in \mathbb {F}^{cn})$ is in the relation $\mathcal {R}_{\text {mplkup}}$ if and only if $(\textsf{pi}, \textbf{w}) \in \mathcal {R}_{\text {plonkup}}$ w.r.t. circuit configuration $(\mathcal {C}_{pc}, \textbf{t})$.

We present the special-sound protocol $\varPi _{\textrm{mplkup}}$ for the multi-circuit Plonkup relation.

Remark 2

The public input check $\sum _{j=1}^{I} b_j \cdot \textbf{w}^{(j)}[1..{\ell _{\textsf{in}}}] \overset{?}{=}\ \textsf{pi}$ is equivalent to $\textbf{w}[1..{\ell _{\textsf{in}}}] = \textbf{w}_{pc}[1..{\ell _{\textsf{in}}}]\overset{?}{=}\ \textsf{pi}$ if the vector $\textbf{b}$ passes the check at Step 2. Thus we guarantee that $\textbf{w}[1] = pc$, and the circuit relation can add constraints on pc depending on the applications.

Special-Soundness. We prove the special-soundness property of $\varPi _\textrm{mplkup}$ below.

Lemma 7

$\varPi _\textrm{mplkup}$ is $2(T+\ell _{\textsf{lk}})$-special-sound.

We defer the proof to the full version [7].

We will now use $\varPi _\textrm{mplkup}$ and our compiler described in Theorem 3 to design $\textsc {Protostar}$. Before that, we address two efficiency issues regarding supporting multiple branch circuits and combining high-degree gates with sparse lookups.

Efficient Accumulation for Supporting Many Branch Circuits. Let $I$ be the number of branch circuits. At first glance, the message $\textbf{w}^*$ has length $O(In)$ and seems the accumulation prover needs to take $O(In)$ time to fold the witness. Fortunately, the prover message $\textbf{w}^* \mathrel {\mathop :}=(\textbf{w}^{(1)}, \dots , \textbf{w}^{(I)}) \in \mathbb {F}^{Icn}$ is sparse: only the witness $\textbf{w}^{(pc)}$ for the single activated branch circuit $\mathcal {C}_{pc}$ is non-zero (where $\textbf{w}^{(pc)}$ can be determined at runtime). Thus, using the commitment to $\textsf{acc}.\textbf{w}^*$ and the commitments homomorphism, the complexity for the prover to fold $\textbf{w}^*$ onto $\textsf{acc}.\textbf{w}^*$ is only O(n).

On the other hand, the accumulation prover also needs to compute the error terms $[\textbf{e}_j]_{j=1}^{d-1}$ described at Step 2 of Fig. 3. Note that each gate check can be split into I parts where at most one part is active, that is, $\sum _{j=1}^{I} b_j \cdot \textsf{GT}_{j,i}(\textbf{w}^{(j)}_i, \dots , \textbf{w}^{(j)}_{i+cn - n})$ can be split into I branch gates where the j-th $(1 \le j \le I)$ branch gate is $b_j \cdot \textsf{GT}_{j,i}(\textbf{w}^{(j)}_i, \dots , \textbf{w}^{(j)}_{i+cn - n})$. Thus we can use the caching algorithm described in Sect. 3.4 to achieve $O(d|\mathcal {C}_{pc}|)$ computational complexity rather than $O(d (|\mathcal {C}_1| + \dots + |\mathcal {C}_{I}|))$ where $\mathcal {C}_i$ $(1 \le i \le I)$ is the evaluation cost of the i-th branch circuit.

Next, we address the issue of combining the high-degree gate and sparse lookup protocols with the generic transform $\textsf{CV}$ in Sect. 3.3.

Efficient Accumulation of $\textsf{CV}[{\varPi _{mplkup}}]$. $\textsf{CV}[{\varPi _\textrm{GATE}}]$ reduces the number of degree-d verification checks in $\varPi _\text {GATE}$ from n to 1, with the tradeoff of $O(\sqrt{n})$ additional degree-2 checks. In the resulting accumulation scheme, the error terms for high-degree gates are, thus, only of length 1. This enables using the trivial identity commitment for these error terms and thus reduces the number of group operations by the accumulation verifier. Unfortunately, applying CV to $\textrm{mplkup}$ seems to have a major tradeoff. The number of verification checks is $n+\ell _{\textsf{lk}}+T+c\cdot n$. This requires using a) $\textsf{CV}[\textrm{mplkup}]$ and b) is not composable with the sparseness optimizations for lookup described in Sect. 4.3. These optimizations make the prover computation independent of $T$.

Fortunately, a closer look at the verification of $\textrm{mplkup}$ reveals that only n of these verification checks are of high degree d, namely the checks in $\varPi _\text {GATE}$. The other checks are of degree 2 or lower. With a slight abuse of notation, we can define $\textsf{CV}[\varPi _\textrm{mplkup}]$ as applying the generic transform $\textsf{CV}$ only to the $\varPi _\text {GATE}$ part of $\varPi _\textrm{mplkup}$. This means that there are $d+1$ cross error vectors (each of length 1) for the degree $d+2$ check in $\textsf{CV}[\varPi _\text {GATE}]$; and 1 cross error vector of length $T+\ell _{\textsf{lk}}+cn+O(\sqrt{n})$ for the rest checks—namely the low-degree checks in $\varPi _\textrm{mplkup}$ and the $O(\sqrt{n})$ degree-2 checks in $\textsf{CV}[\varPi _\text {GATE}]$. By leveraging the error separation technique described in Sect. 3.3, we can use the identity function to commit to the field elements and a vector commitment to commit to the long error term. Again we leverage homomorphism as described in Sect. 4.3 to make the prover independent of $T$.

Corollary 1

(Protostar protocol). Consider the configuration

$$\mathcal {C}_{{ mplkup}} \mathrel {\mathop :}=(n, T, c,d, m, {\ell _{\textsf{in}}}, \ell _{\textsf{lk}}; [\mathcal {C}_i]_{i=1}^I; \textbf{t}).$$

Given a binding homomorphic commitment scheme $\textsf{cm}=(\textsf{Setup},\textsf{Commit})$, and under the Fiat-Shamir Heuristic (Definition 3) for a hash function $\textsf{H}$, there exists an IVC scheme $\textsc {Protostar}$ for $\mathcal {R}_{\text {mplkup}}$ relations with the following efficiencies for $m=1$ (i.e. each circuit has a single degree-d gate type), public input length ${\ell _{\textsf{in}}}= 1$: (we omit cost terms that are negligible compared to the dominant parts)

$\begin{array}{c} \textsf{P}_\textsc {Protostar}\\ {native} \end{array}$	$\begin{array}{c} \textsf{P}_\textsc {Protostar}\\ {recursive} \end{array}$	$\textsf{V}_\textsc {Protostar}$	$|\pi _\textsc {Protostar}|$
$\begin{array}{c} O( |\textbf{w}|+\ell _{\textsf{lk}}) \mathbb {G}\\ L'(\mathcal {C}_{pc},d+2)+2\ell _{\textsf{lk}}\mathbb {F}\end{array}$	$\begin{array}{c} 3 \mathbb {G}\\ d+4 \mathbb {F}\\ d+O(1) H + 1 {\textsf{H}_{\textsf{in}}}\end{array}$	$\begin{array}{c} O(c \cdot n+ T+\ell _{\textsf{lk}}) \mathbb {G}\\ n+\sum _{i=1}^I\mathcal {C}_i + T +\ell _{\textsf{lk}}\mathbb {F}\end{array}$	$O(c\cdot n +T+\ell _{\textsf{lk}})$

Here $|\textbf{w}|\le c n$ is the number of non-zero entries in the witness, $\sum _{i=1}^I\mathcal {C}_i$ is the cost of evaluating all circuits on some random input, and $L'(\mathcal {C}_{pc},d)$ is the cost of computing the coefficients of the polynomial e(X) defined in Eq. 3 using techniques from Sect. 5.⁵ ${\textsf{H}_{\textsf{in}}}$ is the cost of hashing the public input and the (constant-sized) accumulator instance.

We defer the proof to the full version [7].