An Abstract Domain of Linear Templates with Disjunctive Right-Hand-Side Intervals

Abstract

Abstract interpretation provides a general framework for analyzing the value ranges of program variables while ensuring soundness. Abstract domains are at the core of the abstract interpretation framework, and the numerical abstract domains aiming at analyzing numerical properties have received extensive attention. The template constraint matrix domain (also called the template polyhedra domain) is widely used due to its configurable constraint matrix (describing limited but user-concerned linear relationships among variables) and its high efficiency. However, it cannot express non-convex properties that appear naturally due to the inherent disjunctive behaviors in a program. In this paper, we introduce a new abstract domain, namely the abstract domain of linear templates with disjunctive right-hand-side intervals, in the form of $\sum _{i} a_ix_i \in \bigvee _{j=0}^p [c_j,d_j]$ (where $a_i$’s and p are configurable and fixed before conducting analysis). Experimental results of our prototype are encouraging: In practice, the new abstract domain can find interesting non-convex invariants that are out of the expressiveness of the classic template constraint matrix abstract domain.

1 Introduction

The precision of program analysis based on abstract interpretation is largely dependent on the chosen abstract domain [8]. The polyhedra abstract domain [9] is currently one of the most expressive and widely used numerical abstract domains. However, its applicability is severely limited by its worst-case exponential time and space complexity.

In order to reduce the complexity of the polyhedra abstract domain and at the same time derive practical linear invariants, Sankaranarayanan et al. [14, 17] proposed the template constraint matrix (TCM) abstract domain (also called the template polyhedra domain). The domain representation of TCM polyhedra abstract domain is $A \boldsymbol{x} \le \boldsymbol{b}$, where the coefficient matrix A is predetermined before the analysis, $\boldsymbol{x}$ is a vector of variables appearing in the program environment, and the right-hand-side vector of constraint constants $\boldsymbol{b}$ is inferred automatically by the analysis [17]. The expression capability of TCM polyhedra abstract domain covers interval abstract domain [10] and the weakly relational linear abstract domains (e.g., octagonal abstract domain [15], octahedral abstract domain [7], etc.) commonly used in practical static analysis. Therefore, due to the representativeness of the TCM polyhedra abstract domain expressivity and its polynomial time complexity, the TCM polyhedra abstract domain has been receiving much attention from the academic community since its proposal.

However, like most current numerical abstract domains (e.g., interval abstract domain [10], octagonal abstract domain [15], etc.), the TCM abstract domain is based on a series of linear expressions, the corresponding geometric regions is convex, and therefore it can only express convex properties. In the actual analysis, the behavior of the program in the specific or collection semantics are generally non-convex. For example, “if-then-else” statements are often used in programs for case-by-case discussion. In addition, users are concerned about the non-convex numerical properties of a program, e.g., checking that a program does not have a “division-by-zero error” requires verifying a non-convex property such as “$x \ne 0$”.

In this paper, we propose a novel method to combine the TCM abstract domain with fixed partitioning slots based powerset domain of intervals to design a new abstract domain, namely, an abstract domain of linear templates with disjunctive right-hand-side intervals (rhiTCM abstract domain). This domain aims to retain non-convex information of linear inequality relations among values of program variables, in the form of $A x \in \bigvee _{i=0}^p [\boldsymbol{c_i},\boldsymbol{d_i}]$ (where A is the preset template constraint matrix, x is the vector of variables in the program to be analyzed, $\boldsymbol{c_i}$ and $\boldsymbol{d_i}$ are vectors of constants, $\bigvee _{i=0}^p [\boldsymbol{c_i},\boldsymbol{d_i}]$ are a disjunction of interval vectors based on fixed partitioning slots inferred by the analysis). To be more clear, each constraint in $A x \in \bigvee _{i=0}^p [\boldsymbol{c_i},\boldsymbol{d_i}]$ is formed as: $\sum _i a_i x_i \in [c_{0}, d_{0}] \vee [c_{1}, d_{1}] \vee \ldots \vee [c_{p}, d_{p}]$, where $a_i's$ together with p are fixed before analysis, and for each $i \in [0,p-1]$ it holds that $d_i \le c_{i+1}$.

Fig. 1.

Motivating Example

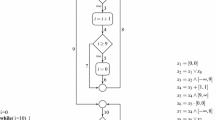
Motivating Example. In Fig. 1, we show a simple typical program that contains division in C language. This example involves non-convex (disjunctive) constraints that arise due to control-flow join. Specifically, at program line 10, the rhiTCM abstract domain is able to deduce that $x + y \in [-1,-1] \vee [1,1]$, and as a result, the program can be deemed safe. In contrast, the classic TCM abstract domain infers that $x + y \in [-1,1]$, leading to false alarms for division-by-zero errors.

The new domain is more expressive than the classic TCM abstract domain and allows expressing certain non-convex (even unconnected) properties thanks to the expressiveness of the disjunctive right-hand-side intervals. We made a prototype implementation of the proposed abstract domain using rational numbers and interface it to the Apron [13] numerical abstract domain library. The preliminary experimental results of the prototype implementation are promising on example programs; the rhiTCM abstract domain can find linear invariants that are non-convex and out of the expressiveness of the conventional TCM polyhedra abstract domain in practice.

The rest of the paper is organized as follows. Section 2 describes some preliminaries. Section 3 presents the new proposed abstract domain of rhiTCM abstract domain. Section 4 presents our prototype implementation together with experimental results. Section 5 discusses some related work before Sect. 6 concludes.

2 Preliminaries

2.1 Fixed Partitioning Slots Based Powerset Domain of Intervals

We describe an abstract domain, namely, fixed partitioning slots based powerset domain of Intervals (fpsItvs). The main idea is to extract fixed partitioning points based on the value characteristics of variables in the program under analysis, and utilize these fixed partitioning points to divide the value space of variables. This approach aims to preserve more stable information regarding the range of variable values during program analysis. We use FP_SET to store the fixed partitioning points ($\text {FP}\_\text {SET} = \{FP_1, FP_2,\ldots , FP_p\}$). Each fixed partitioning point $FP_i\ \in \ \mathbb {R}$ satisfies $FP_i < FP_{i+1}$.

Definition 1

fpsItvs$_p =\{\bigvee _{i=0}^p[c_i,d_i]\,|\,\text {for}\; i \in [0,p-1], c_i \le d_i \le c_{i+1}, c_i,d_i \in \mathbb {R} \}$.

Let II $\in$ fpsItvs$_p$, which means that II is a disjunction of p disjoint intervals. The domain representation of fixed partitioning slots based powerset domain of intervals is $x \in [a_0,b_0] \vee [a_1, b_1] \vee \ldots \vee [a_p, b_p]$, where x is the variable in the program to be analysed, $[a_0, b_0] \subseteq [-\infty , FP_1],\ [a_1, b_1] \subseteq [FP_1, FP_2], \ldots , [a_p, b_p] \subseteq [FP_p, +\infty ],$ $a_i, b_i \in \mathbb {R}$ is inferred by the analysis, $\text {FP}\_\text {SET} = \{ FP_1,FP_2\ldots ,FP_p \}$ is the preset configurable point set. It should be noted that p distinct fixed partitioning points correspond to $p+1$ intervals. Let $\bot _{is}$ denote the bottom value of fpsItvs$_p$ ($\bot _{is} = \bot _{i0} \vee \bot _{i1} \vee \ldots \vee \bot _{ip}$) and let $\top _{is}$ denote the top value of fpsItvs$_p$ ($\top _{is} = [-\infty , FP_1] \vee [FP_1, FP_2] \vee \ldots \vee [FP_p, +\infty ]$).

Domain Operations. Let $\text {II} = [a_0, b_0] \vee [a_1, b_1] \vee \ldots \vee [a_p, b_p]$, II$^\prime =[a_0',b_0'] \vee [a_1',b_1'] \vee \ldots \vee [a_p', b_p']$. For simplicity, abbreviate the above expression as $\text {II} = I_0 \vee I_1 \vee \ldots \vee I_p$ , $\text {II}^\prime = I_0' \vee I_1' \vee \ldots \vee I_p'$. Let $\sqsubseteq _i$, $\sqcap _i$, $\sqcup _i$ respectively denote the abstract inclusion, meet, join operation in the classic interval domain [10].

• Inclusion test $\sqsubseteq _{is}$:

  II $\sqsubseteq _{is}$ II$^\prime$ iff $I_0 \sqsubseteq _i I_0' \wedge I_1 \sqsubseteq _i I_1' \wedge \ldots \wedge I_p \sqsubseteq _i I_p'$

• Meet $\sqcap _{is}$:

  II $\sqcap _{is}$ II$^\prime \triangleq I_0 \sqcap _i I_0' \vee I_1 \sqcap _i I_1' \vee \ldots \vee I_p \sqcap _i I_p'$

• Join $\sqcup _{is}$:

  II $\sqcup _{is}$ II$^\prime \triangleq I_0 \sqcup _i I_0' \vee I_1 \sqcup _i I_1' \vee \ldots \vee I_p \sqcup _i I_p'$

Extrapolations. Since the lattice of fpsItvs has infinite height, we need a widening operation for the fpsItvs abstract domain to guarantee the convergence of the analysis and a narrowing operation to reduce the precision loss caused by the widening operation. The symbol $\underline{I_i}$ represents the lower bound of interval $I_i$ and the symbol $\overline{I_i}$ represents the upper bound of interval $I_i$.

• Widening operation ($\nabla _{is}$):

  II $\nabla _{is}$ II$^\prime \triangleq I_0'' \vee I_1'' \vee \ldots \vee I_p''$

  $$ I_0'' = {\left\{ \begin{array}{ll} I_0 &{} \text {if } I_0' = \bot _i \\ I_0' &{} \text {if } I_0 = \bot _i \\ {}[\underline{I_0} \le \underline{I_0'}\ ?\ \underline{I_0}\ :\ -\infty , \overline{I_0} \ge \overline{I_0'}\ ?\ \overline{I_0}\ :\ FP_1] &{} \text {otherwise} \end{array}\right. } $$

  when $0 < i < p$,

  $$ I_i'' = {\left\{ \begin{array}{ll} I_i &{} \text {if } I_i' = \bot _i \\ I_i' &{} \text {if } I_i = \bot _i \\ {} [\underline{I_i} \le \underline{I_i'}\ ?\ \underline{I_i}\ :\ FP_i, \overline{I_i} \ge \overline{I_i'}\ ?\ \overline{I_i}\ :\ FP_{i+1}] &{} \text {otherwise} \end{array}\right. } $$
  $$ I_p'' = {\left\{ \begin{array}{ll} I_p &{} \text {if } I_p' = \bot _i \\ I_p' &{} \text {if } I_p = \bot _i \\ {}[\underline{I_p} \le \underline{I_p'}\ ?\ \underline{I_p}\ :\ FP_p, \overline{I_p} \ge \overline{I_p'}\ ?\ \overline{I_p}\ :\ +\infty ] &{} \text {otherwise} \end{array}\right. } $$

• Narrowing operation $(\triangle _{is})$:

  II $\triangle _{is}$ II$^\prime$ $\triangleq I_0'' \vee I_1'' \vee \ldots \vee I_p''$

  $$ I_0'' = {\left\{ \begin{array}{ll} I_0 &{} \text {if } I_0' = \bot _i \\ I_0' &{} \text {if } I_0 = \bot _i \\ {}[\underline{I_0} = -\infty \ ?\ \underline{I_0'}\ :\ \underline{I_0}, \overline{I_0} = FP_1\ ?\ \overline{I_0'}\ :\ \overline{I_0}] &{} \text {otherwise} \end{array}\right. } $$

  when $0 < i < p$,

  $$ I_i'' = {\left\{ \begin{array}{ll} I_i &{} \text {if } I_i' = \bot _i \\ I_i' &{} \text {if } I_i = \bot _i \\ {}[\underline{I_i} = FP_i\ ?\ \underline{I_i'}\ :\ \underline{I_i}, \overline{I_i} = FP_{i+1}\ ?\ \overline{I_i'}\ :\ \overline{I_i}] &{} \text {otherwise} \end{array}\right. } $$
  $$ I_p'' = {\left\{ \begin{array}{ll} I_p &{} \text {if } I_p' = \bot _i \\ I_p' &{} \text {if } I_p = \bot _i \\ {}[\underline{I_p} = FP_p\ ?\ \underline{I_p'}\ :\ \underline{I_p}, \overline{I_p} = +\infty \ ?\ \overline{I_p'}\ :\ \overline{I_p}] &{} \text {otherwise} \end{array}\right. } $$

2.2 Mixed-Integer Linear Programming

Mixed-integer Linear Programming (MILP) problem is a type of linear programming problem where both the objective function and constraint conditions are linear equalities or inequalities. The variables in a MILP problem include both continuous and integer variables. Continuous variables can take any value within the real range, while integer variables can only take integer values. Due to the mixed nature of continuous and integer variables in the MILP problem, its optimal solution may exist in multiple local optimal solutions. The general form of a MILP problem can be expressed as:

$$\begin{aligned} \text {minimize (or maximize)} \quad & \boldsymbol{c}^T*\boldsymbol{x} + \boldsymbol{d}^T*\boldsymbol{y} \\ \text {subject to} \quad & A*\boldsymbol{x} + B*\boldsymbol{y} \le \boldsymbol{b} \\ & \boldsymbol{x} \in \mathbb {R}^n \\ & \boldsymbol{y} \in \mathbb {Z}^m \end{aligned}$$

where $\boldsymbol{c}$ and $\boldsymbol{d}$ are given coefficient vectors, $\boldsymbol{x}$ represents the continuous variables, $\boldsymbol{y}$ represents the integer or boolean variables, A and B are known matrices, and $\boldsymbol{b}$ is the right-hand-side vector of constraints.

A MILP problem can have one of three results: (1) the problem has an optimal solution; (2) the problem is unbounded; (3) the problem is unfeasible.

2.3 Template Constraint Matrix Abstract Domain

The template constraint matrix abstract domain [17] is introduced by Sankaranarayanan et al. to characterize the linear constraints of variables under a given template constraint matrix: $A \boldsymbol{x} \le \boldsymbol{b}$, where $A \in \mathbb {Q}^{m \times n}$ is an $m \times n$ matrix of coefficients (determined prior to the analysis), $\boldsymbol{x} \in \mathbb {Q}^{n \times 1}$ is an $n \times 1$ column vector (determined by the environment of the variables in the current analysis), and $\boldsymbol{b} \in \mathbb {Q}^{n \times 1}$ is a right-hand-side vector of constraints inferred by the analysis.

Figure 2 shows an instance of a template constraint matrix polyhedron. Assume that the program has two variables x and y, the template constraint matrix is A. In the TCM polyhedra abstract domain, $\boldsymbol{b}$ is obtained from the derivation of the matrix A during analysis.

Fig. 2.

An Instance of TCM

3 An Abstract Domain of Linear Templates with Disjunctive Right-Hand-Side Intervals

In this section, we present a new abstract domain, namely the abstract domain of linear templates with disjunctive right-hand-side intervals (rhiTCM). The key idea is to use the fixed partitioning slots based powerset of intervals (fpsItvs) to express the right-hand value of linear templates constraints. It can be used to infer relationships of the form $\sum _k a_k x_k \in$ II over program variables $x_k (k=1,\ldots ,n)$, where $a_k\in \mathbb {Q}$, II $\in$ fpsItvs$_p$ is automatically inferred by the analysis.

3.1 Domain Representation

The new abstract domain is used to infer relationships of the form $A \boldsymbol{x} \in$ II, where $A \in \mathbb {Q}^{m \times n}$ is the preset template constraint matrix, $\boldsymbol{x} \in \mathbb {Q}^{n \times 1}$ is the vector of variables in the program to be analysed, II is the vector of II automatically inferred by the analysis (II is composed of II$^{m \times 1}$). For ease of understanding, we also write $A \boldsymbol{x} \in$ II as $\sum _k a_{ik} x_k \in$ II$_i$ ($a_{ik}$ represents the element in the ith row and kth column of the matrix A, II$_i$ represents the element in the ith row of the vector II, $1 \le i \le m, 1 \le k \le n$).

Example 1

Consider a simple rhiTCM abstract domain representation as follows. Assume there are three variables $x_1$, $x_2$ and $x_3$.

$$ A = \begin{bmatrix} 1 &{} 0 &{} 1 \\ 1 &{} -1 &{} 2 \\ 1 &{} 1 &{} 0 \\ 0 &{} 3 &{} -2 \\ 0 &{} 0 &{} -1 \\ \end{bmatrix} \ \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} \text { representing constraints } \begin{bmatrix} x_1+x_3 &{}\in \text {II}_1 \\ x_1-x_2+2x_3 &{}\in \text {II}_2 \\ x_1+x_2 &{}\in \text {II}_3 \\ 3x_2-2x_3 &{}\in \text {II}_4 \\ -x_3 &{}\in \text {II}_5 \\ \end{bmatrix} $$

Since the template matrix A remains unchanged during the analysis process, a vector II in the abstract domain rhiTCM represents the set of states described by the set of constraints $A \boldsymbol{x} \in$ II. The template constraint matrix is nonempty, i.e., $m > 0$, and the abstract domain contains m-dimensional vectors II.

Definition 2

rhiTCM is defined as follows:

$$ rhiTCM \triangleq {\left\{ \begin{array}{ll} \bot _{rhiTCM}, &{}\text {if }\; \exists \text {II}_i = \bot _{is}\\ \top _{rhiTCM}, &{}\text {if }\; \forall \text {II}_i = \top _{is}\\ A \boldsymbol{x} \in {{\textbf {II}}} &{}\text {otherwise} \end{array}\right. }$$

where $\text {II}_i$ is the element in the ith row of ${{\textbf {II}}}$. $\bot _{rhiTCM}$ is the bottom value of the rhiTCM abstract domain, representing this rhiTCM element is infeasible; $\top _{rhiTCM}$ is the top value of rhiTCM domain, representing the entire state space. Figure 3 presents a rhiTCM element.

Fig. 3.

A rhiTCM Element

3.2 Domain Operations

Now, we describe the design of most common domain operations required for static analysis over the rhiTCM abstract domain. Assume that there are n variables in the program to be analyzed ($\boldsymbol{x} = [x_1, x_2, \ldots , x_n]^T$), and the template constraint matrix preset based on the program is A ($A \in \mathbb {Q}^{m \times n}$, representing matrix elements with $a_{ij}$, $i \in {1,2,\ldots ,m}, j\in {1,2,\ldots ,n}$). As mentioned earlier, the template constraint matrix for the domain representation corresponding to the abstract states of different program points in the rhiTCM abstract domain is the same, except for the constraint vector on the right side. Therefore, domain operations mainly act on the vector of II. Assuming there are currently two abstract states, their corresponding domain representations are $rhiTCM \triangleq A \boldsymbol{x} \in$ II and $rhiTCM' \triangleq A \boldsymbol{x} \in$ II$^\prime$, where II $= [\text {II}_1,\text {II}_2,\ldots ,\text {II}_m]^T$ and II$^\prime$ $= [\text {II}_1',\text {II}_2',\ldots ,\text {II}_m']^T$.

Lattice Operations. The lattice operations include abstract inclusion, meet and join operation, represented by symbols $\sqsubseteq , \sqcap , \sqcup$ respectively. Let $\sqsubseteq _{is}$, $\sqcap _{is}$, $\sqcup _{is}$ respectively denote the abstract inclusion, meet, join operation in the fpsItvs abstract domain.

Inclusion Test. The inclusion test for rhiTCM abstract domain is implemented based on the inclusion test for vector II $(\preceq _{is})$.

Definition 3

Inclusion test of vector II $(\preceq _{is})$. Let ${{\textbf {II}}} = [\text {II}_1,\text {II}_2,\ldots ,\text {II}_n]^T$, ${{\textbf {II}}}' = [\text {II}_1',\text {II}_2',\ldots ,\text {II}_n']^T$.

$$\begin{aligned} {{\textbf {II}}} \preceq _{is} {{\textbf {II}}}'\ i\!f\!f\ \bigwedge _{i=1}^n (\text {II}_i \sqsubseteq _{is} \text {II}_i') \end{aligned}$$

For the rhiTCM abstract domain, $rhiTCM \sqsubseteq rhiTCM'$ implies the domain element of rhiTCM is contained in $rhiTCM'$, which is geometrically equivalent to the graph corresponding to rhiTCM is contained within the graph corresponding to $rhiTCM'$. With Definition 3, we define the inclusion test of rhiTCM abstract domain as follows:

$$\begin{aligned} rhiTCM \sqsubseteq rhiTCM'\; i\!f\!f\; {{\textbf {II}}} \preceq _{is} {{\textbf {II}}}'. \end{aligned}$$

Example 2

Assume ${{\textbf {II}}} = \begin{bmatrix} [-2,-2] \vee [2,2] \\ [-3,-2] \vee [2,3] \\ \end{bmatrix}$, ${{\textbf {II}}}' = \begin{bmatrix} [-2,-1] \vee [1,2] \\ [-3,-1] \vee [1,3] \\ \end{bmatrix}$ and $FP\_SET=\{0\}$. Note that:

$([-2,-2] \vee [2,2] \sqsubseteq _{is} [-2,-1] \vee [1,2])\ \wedge \ ([-3,-2] \vee [2,3] \sqsubseteq _{is} [-3,-1] \vee [1,3])$, thus ${{\textbf {II}}} \preceq _{is} {{\textbf {II}}}'$, $rhiTCM \sqsubseteq rhiTCM'.$

Meet. The meet operation of rhiTCM abstract domain is implemented based on the meet operation of vector II.

Definition 4

Meet operation of vector ${{\textbf {II}}}(\curlywedge _{is})$. Let ${{\textbf {II}}} = [\text {II}_1,\text {II}_2,\ldots ,\text {II}_n]^T$, ${{\textbf {II}}}' = [\text {II}_1',\text {II}_2',\ldots ,\text {II}_n']^T$.

$$\begin{aligned} {{\textbf {II}}} \curlywedge _{is} {{\textbf {II}}}'\triangleq [ \text {II}_1 \sqcap _{is} \text {II}_1', \ldots , \text {II}_n \sqcap _{is} \text {II}_n' ]^T \end{aligned}$$

For the rhiTCM abstract domain, $rhiTCM \sqcap rhiTCM'$ is geometrically equivalent to the part that exists simultaneously in both rhiTCM and $rhiTCM'$. With Definition 4, we define the meet operation of rhiTCM domain as follows:

$$\begin{aligned} rhiTCM \sqcap rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \curlywedge _{is} {{\textbf {II}}}') . \end{aligned}$$

Join. The join operation of rhiTCM abstract domain is implemented based on the join operation of vector ${{\textbf {II}}}$.

Definition 5

Join operation of vectors of ${{\textbf {II}}}(\curlyvee _{is})$. Let ${{\textbf {II}}} = [\text {II}_1,\text {II}_2,\ldots ,\text {II}_n]^T$, ${{\textbf {II}}}' = [\text {II}_1',\text {II}_2',\ldots ,\text {II}_n']^T$.

$$\begin{aligned} {{\textbf {II}}} \curlyvee _{is} {{\textbf {II}}}' \triangleq [\text {II}_1 \sqcup _{is} \text {II}_1' ,\ldots , \text {II}_n \sqcup _{is} \text {II}_n']^T \end{aligned}$$

For the rhiTCM abstract domain, $rhiTCM \sqcup rhiTCM'$ is geometrically equivalent to the part that envelope rhiTCM and $rhiTCM'$. With Definition 5, we define the join operation of rhiTCM abstract domain as follows:

$$\begin{aligned} rhiTCM \sqcup rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \curlyvee _{is} {{\textbf {II}}}') . \end{aligned}$$

Example 3

Assume ${{\textbf {II}}} = \begin{bmatrix} [-2,-2] \vee [2,2] \\ [-3,-2] \vee [2,3] \\ \end{bmatrix}$, ${{\textbf {II}}}' = \begin{bmatrix} [-2,-1] \vee [1,2] \\ [-3,-1] \vee [1,3] \\ \end{bmatrix}$ and $FP\_SET=\{0\}$. We note that:

$$\begin{aligned} \begin{aligned} &([-2,-2] \vee [2,2]) \sqcap _{is} ([-2,-1] \vee [1,2]) = [-2,-2] \vee [2,2],\\ & ([-3,-2] \vee [2,3]) \sqcap _{is} ([-3,-1] \vee [1,3]) = [-3,-2] \vee [2,3],\\ & ([-2,-2] \vee [2,2]) \sqcup _{is} ([-2,-1] \vee [1,2]) = [-2,-1] \vee [1,2],\\ & ([-3,-2] \vee [2,3]) \sqcup _{is} ([-3,-1] \vee [1,3]) = [-3,-1] \vee [1,3],\\ \end{aligned} \end{aligned}$$

thus we can get:

$$\begin{aligned} rhiTCM \sqcap rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \curlywedge _{is} {{\textbf {II}}}') = A \boldsymbol{x} \in \begin{bmatrix} [-2,-2] \vee [2,2] \\ [-3,-2] \vee [2,3] \\ \end{bmatrix} , \end{aligned}$$

$$\begin{aligned} rhiTCM \sqcup rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \curlyvee _{is} {{\textbf {II}}}') = A \boldsymbol{x} \in \begin{bmatrix} [-2,-1] \vee [1,2] \\ [-3,-1] \vee [1,3] \\ \end{bmatrix} . \end{aligned}$$

3.3 Extrapolations

The lattice of the rhiTCM abstract domain is of infinite height, and thus we need a widening operation to guarantee the convergence of the analysis. The widening operation of rhiTCM abstract domain is implemented based on the widening operation of vector ${{\textbf {II}}}$.

Definition 6

Widening operation of vector ${{\textbf {II}}} \ (\nabla )$. Let ${{\textbf {II}}} = [\text {II}_1,\text {II}_2,\ldots ,\text {II}_n]^T$, ${{\textbf {II}}}' = [\text {II}_1',\text {II}_2',\ldots ,\text {II}_n']^T$.

$$\begin{aligned} {{\textbf {II}}} \ \nabla {{\textbf {II}}}' \triangleq [\text {II}_1 \nabla _{is} \text {II}_1' ,\ldots , \text {II}_n \nabla _{is} \text {II}_n']^T \end{aligned}$$

The widening operation of rhiTCM abstract domain is as follows:

$$\begin{aligned} rhiTCM\ \nabla \ rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \ \nabla \ {{\textbf {II}}}'). \end{aligned}$$

The widening operation may result in substantial precision loss. To mitigate this, we utilize a narrowing operation to perform decreasing iterations once the widening iteration has converged, effectively reducing precision loss. Notably, this operation is capable of converging within a finite time. The implementation of the narrowing operation for the rhiTCM abstract domain is derived from the narrowing operation of vector ${{\textbf {II}}}$.

Definition 7

Narrowing operation of vector ${{\textbf {II}}}\ (\triangle )$.

$$\begin{aligned} {{\textbf {II}}}\ \triangle \ {{\textbf {II}}}' \triangleq [\text {II}_1 \triangle _{is} \text {II}_1' ,\ldots , \text {II}_n \triangle _{is} \text {II}_n']^T \end{aligned}$$

The narrowing operation of rhiTCM abstract domain is as follows:

$$\begin{aligned} rhiTCM\ \triangle \ rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \ \triangle \ {{\textbf {II}}}'). \end{aligned}$$

Example 4

Assume ${{\textbf {II}}} = \begin{bmatrix} [-2,-2] \vee [2,2] \\ [-3,-2] \vee [2,3] \\ [-2,-2] \vee \,\,\,\bot _i\,\, \\ \end{bmatrix}$, ${{\textbf {II}}}' = \begin{bmatrix} [-3,-2] \vee [2,3] \\ [-3,-1] \vee [1,3] \\ [-2,-2] \vee [2,2] \\ \end{bmatrix}$ and $FP\_SET=\{0\}$. Note that:

$$\begin{aligned} \begin{array}{c} ([-2,-2] \vee [2,2])\ \nabla _{is} \ ([-3,-2] \vee [2,3]) = [-\infty ,-2] \vee [2,+\infty ],\\ ([-3,-2] \vee [2,3]) \ \nabla _{is} \ ([-3,-1] \vee [1,3]) = [-3,0] \vee [0,3], \\ ([-2,-2] \vee \bot _i) \ \nabla _{is} \ ([-2,-2] \vee [2,2]) = [-2,-2] \vee [2,2], \end{array} \end{aligned}$$

thus

$$\begin{aligned} rhiTCM \ \nabla \ rhiTCM' \triangleq A \boldsymbol{x} \in ({{\textbf {II}}} \ \nabla \ {{\textbf {II}}}') = A \boldsymbol{x} \in \begin{bmatrix} [-\infty ,-2] \vee [2,+\infty ] \\ [-3,0] \vee [0,3] \\ [-2,-2] \vee [2,2] \\ \end{bmatrix} , \end{aligned}$$

Let ${{\textbf {II}}}'' = {{\textbf {II}}} \ \nabla \ {{\textbf {II}}}'$, $rhiTCM'' = rhiTCM \ \nabla \ rhiTCM'$, note that:

$$\begin{aligned} \begin{array}{c} ([-\infty ,-2] \vee [2,+\infty ])\ \triangle _{is} \ ([-2,-2] \vee [2,2]) = [-2,-2] \vee [2,2],\\ ([-3,0] \vee [0,3]) \ \triangle _{is} \ ([-3,-2] \vee [2,3]) = [-3,-2] \vee [2,3], \\ ([-2,-2] \vee [2,2]) \ \triangle _{is} \ ([-2,-2] \vee \bot _i) = [-2,-2] \vee [2,2], \end{array} \end{aligned}$$

thus:

$$\begin{aligned} rhiTCM'' \triangle rhiTCM \triangleq A \boldsymbol{x} \in ({{\textbf {II}}}'' \ \triangle \ {{\textbf {II}}}) = A \boldsymbol{x} \in \begin{bmatrix} [-2,-2] \vee [2,2] \\ [-3,-2] \vee [2,3] \\ [-2,-2] \vee [2,2] \\ \end{bmatrix} . \end{aligned}$$

3.4 Transfer Functions

In program analysis based on abstract interpretation, an abstract environment is usually constructed for each program point, mapping the value of each program variable to a domain element on a specified abstract domain. Let $P ^ \#$ represent the abstract environment constructed by the rhiTCM abstract domain. Before introducing the test transfer function and the assignment transfer function of rhiTCM abstract domain, we introduce the MILP encoding of the rhiTCM abstract domain representation.

MILP Encoding. Note that the rhiTCM abstract domain representation $\sum _k a_{ik} x_k \in \text {II}_i$ can be expressed in ordinary linear expressions as $(\sum _k a_{ik} x_k \ge c_{i1} \wedge \sum _k a_{ik} x_k \le d_{i1}) \vee (\sum _k a_{ik} x_k \ge c_{i2} \wedge \sum _k a_{ik} x_k \le d_{i2}) \vee \ldots \vee (\sum _k a_{ik} x_k \ge c_{i(p+1)} \wedge \sum _k a_{ik} x_k \le d_{i(p+1)})$, where p is the number of fixed partitioning points. However, the expression cannot be directly solved using a LP (linear programming) solver because it contains the disjunction symbol “$\vee$”. To tackle such problem, we typically introduce a significantly large number M and auxiliary binary decision variables (0–1 variables). This allows us to convert the linear programming problem, which contains disjunction symbols, into a mixed-integer linear programming problem. Thus, we can employ a mixed-integer linear programming solver to solve it.

We encode $(\sum _k a_{ik} x_k \ge c_{i1} \wedge \sum _k a_{ik} x_k \le d_{i1}) \vee (\sum _k a_{ik} x_k \ge c_{i2} \wedge \sum _k a_{ik} x_k \le d_{i2}) \vee \ldots \vee (\sum _k a_{ik} x_k \ge c_{ip} \wedge \sum _k a_{ik} x_k \le d_{ip})$ as follows:

$$ \begin{aligned}{\left\{ \begin{array}{ll} \sum \nolimits _k a_{ik} x_k \ge c_{i1} - M(1-u_{i1}), &{} \sum \nolimits _k a_{ik} x_k \le d_{i1} + M(1-u_{i1}) \\ \sum \nolimits _k a_{ik} x_k \ge c_{i2} - M(1-u_{i2}), &{} \sum \nolimits _k a_{ik} x_k \le d_{i2} + M(1-u_{i2})\\ \qquad \qquad \qquad \vdots &{}\qquad \qquad \qquad \vdots \\ \sum \nolimits _k a_{ik} x_k \ge c_{ip} - M(1-u_{ip}), &{} \sum \nolimits _k a_{ik} x_k \le d_{ip} + M(1-u_{ip}) \\ \sum \nolimits _j u_{ij} = 1 (u_{ij} \in \{0,1\}, 1 \le j \le p) \end{array}\right. } \end{aligned} $$

To simplify the treatment of the problem, we proceed to convert the constraints in the aforementioned linear system into the following form:

$$ \begin{aligned}{\left\{ \begin{array}{ll} \sum \nolimits _k a_{ik} x_k + M u_{i1} \le -c_{i1} + M, &{} \sum \nolimits _k a_{ik} x_k + M u_{i1} \le b_{i1} + M \\ \sum \nolimits _k a_{ik} x_k + M u_{i2} \le -c_{i2} + M, &{} \sum \nolimits _k a_{ik} x_k + M u_{i2} \le b_{i2} + M \\ \qquad \qquad \qquad \vdots &{}\qquad \qquad \qquad \vdots \\ \sum \nolimits _k a_{ik} x_k + M u_{ip} \le -c_{ip} + M, &{} \sum \nolimits _k a_{ik} x_k + M u_{ip} \le b_{ip} + M \\ \sum \nolimits _j u_{ij} = 1 (u_{ij} \in \{0,1\}, 1 \le j \le p) \end{array}\right. } \end{aligned} $$

The above linear inequality system is a typical mixed-integer linear programming (MILP) problem, so we can directly call the MILP solver to solve the MILP problem. Nevertheless, when solving the MILP problem, it is important to note that the obtained results are limited to providing the maximum and minimum values of the objective function within the feasible domain. However, these extremal values might not reflect the desired outcome of the analysis. In order to tackle this problem, we introduce the fixed partitioning points information as additional sets of constraints into the existing MILP problem linear inequality system. Suppose the objective function is denoted as $\sum _j a_j x_j$. We sequentially introduce the constraints $\sum _j a_j x_j \le FP_1$, $\sum _j a_j x_j \ge FP_1 \wedge \sum _j a_j x_j \le FP_2$, ..., $\sum _j a_j x_j \ge FP_{p-1} \wedge \sum _j a_j x_j \le FP_p$, $\sum _j a_j x_j \ge FP_p$ ($FP_p$ is the last fixed partitioning point).

Therefore, in the process of calculating the extreme values of the objective function, we use an iterative method in which the information of the fixed partitioning points is introduced p times. This enables us to determine the extremum of the objective function across different fixed partitioning slots and consequently obtain the desired representation outcome. The aforementioned encoding and solving process is recorded as “$rhiTCM_{mip}$(objFun) s.t. Cons” in this paper, where objFun represents the objective function, and Cons represents the constraints to determine the extremes of the objective function.

Test Transfer Function. A linear conditional test based on precise arithmetic can be transformed into the form as $\sum _i w_i x_i \le c$. For test transfer function $\llbracket \sum _i w_i x_i \le c \rrbracket ^{\#} (P^\#)$, we simply combine constraint $\sum _i w_i x_i \le c$ with the rhiTCM $P^\# (P^\# \triangleq A \boldsymbol{x} \in {{\textbf {II}}}$) to obtain $P'^\#(P'^\# \triangleq P ^ \# \wedge \sum _i w_i x_i \le c )$, and use $P'^{\#}$ as the constraint system, recalculate the new boundaries of the rhiTCM.

$$\begin{aligned} \begin{array}{c} \llbracket \sum \nolimits _i w_i x_i \le c \rrbracket ^{\#} (P^\#) \triangleq \bigwedge \nolimits _{i=1}^m \{\sum \nolimits _{k=1}^{n} a_{ik} x_k \in \text {II}_{i}^{*} |\text {II}_{i}^{*} \triangleq \\ rhiTCM_{mip}(\sum \nolimits _{k=1}^{n} a_{ik} x_k) s.t. P'^\# \} . \end{array} \end{aligned}$$

Assignment Transfer Function. Assigning expression e to variable $x_j$ is the assignment transfer function $\llbracket x_j := expr \rrbracket ^ \# (P^\#)$. Firstly, we introduce a fresh variable $x_j'$ to rewrite the assignment statement as $x_j' - expr = 0$. Then, add the new assignment statement to the $P^\# \ (P^\# \triangleq A \boldsymbol{x} \in {{\textbf {II}}})$ to get $P''^\# \ (P''^\# \triangleq P^\# \wedge x_j'-expr=0)$. Finally, using $P''^{\#}$ as the constraint system, recalculate the new boundaries of the rhiTCM.

$$\begin{aligned} \begin{array}{c} \llbracket x_j := expr \rrbracket ^{\#} (P^\#) \triangleq \bigwedge \nolimits _{i=1}^m \{ \sum \nolimits _{k=1}^{j-1} a_{ik} x_k + a_{ij} x_j' + \sum \nolimits _{k=j+1}^{n} a_{ik} \in \text {II}_{i}^{*} | \text {II}_{i}^{*} \triangleq \\ rhiTCM_{mip}(\sum \nolimits _{k=1}^{j-1} a_{ik} x_k + a_{ij} x_j' + \sum \nolimits _{k=j+1}^{n} a_{ik}) s.t. P''^\#\} . \end{array} \end{aligned}$$

4 Implementation and Experiments

We have implemented our prototype domain rhiTCM based on Sect. 3 using multi-precision rational numbers. rhiTCM abstract domain is interfaced to the Apron numerical abstract domain library [13]. The linear programming problems that are involved in the rhiTCM abstract domain are solved using an exact arithmetic-based mixed-integer linear programming solver, which is provided by the PPL [3] library.

To demonstrate the expressiveness of the rhiTCM abstract domain, we have firstly analyzed the program itv_pol5 shown in Fig. 4 taken from [5], along with the generated invariants. Program itv_pol5 in Fig. 4 consists two loops, increasing y in the inner loop and increasing x in the outer loop. In Fig. 4, “Polyhedra” is the classic polyhedra abstract domain [9] and “Interval Polyhedra” (itvPol) from [5] is an abstract domain can infer interval linear constraints over program variables (the domain representation is formed as $\sum _k [a_k,b_k]x_k \le c$ and can express non-convex properties). “$\text {rhiTCM}_1$” and “$\text {rhiTCM}_2$” are rhiTCM abstract domain with different configurations. “$\text {rhiTCM}_1$”: $\text {FP}\_\text {SET} = \{0 \}$, $A_1 = \begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \\ \end{bmatrix}^T$; “$\text {rhiTCM}_2$”: $\text {FP}\_\text {SET} = \{0 \}$, $A_2 = \begin{bmatrix} 1 &{}0 &{}1 &{}1\\ 0 &{}1 &{}1 &{}-1\\ \end{bmatrix}^T$.

Fig. 4.

program itv_pol5 and the generated invariants

For program itv_pol5, at program point ➁, polyhedra abstract domain can prove $y \ge -20$ (TCM abstract domain is the same), itvPol can prove that $-20 \le y \le -10\, \vee \, y \ge 10$ (the invariants of itvpol come from [5]) while $\text {rhiTCM}_1$ can prove $y = -20 \vee y \ge 10$ which is more precise than itvPol. And $\text {rhiTCM}_2$ can prove $y \ge 10$. The results have shown that rhiTCM is more powerful on express non-convex properties than these compared abstract domains, and the expressiveness of rhiTCM can be improved with appropriate configurations on FP_SET and the template matrix.

To evaluate the precision and efficiency of rhiTCM further, we have conducted experiments to compare rhiTCM abstract domain with TCM polyhedra abstract domain. Table 1 shows the preliminary experimental results of comparing performance and resulting invariants on a selection of simple while widely used and representative programs. Program MotivEx is the motivating example presented in Sect. 1, programs itv_pol4, itv_pol5 come from [5], other programs are collected from the “loop-zilu”, “loop-simple” and “locks” directory of SV-COMP2022, which are used for analysing programs involving disjunctive program behaviors.

Table 1. Experimental results for benchmark examples

The column “#var” gives the number of variables in the program. As experimental setup, for each program, the value of the widening delay parameter is set to 1. “#iter.” gives the number of increasing iterations during the analysis.

Precision. The column “Precision” in Table 1 compares the invariants obtained. The symbol “$\sqsubset$” indicates the invariants generated by rhiTCM is stronger (i.e., more precise) than TCM, while “$=$” indicates the generated invariants are equivalent. The results in Table 1 show that rhiTCM can output stronger invariants than TCM in certain situations. One such situation is that $\sum _k a_{ik}x_k$ exhibits a discontinuous range of values. As the motivating example shown in Fig. 1, expression $x + y$ has two discontinuous possible values: 1 and -1. The rhiTCM can describe the values of $x + y$ as $x + y \in [-1,-1] \vee [1,1]$ with the fixed partitioning points set $\text {FP}\_\text {SET}=\{0\}$, while TCM describes the values of $x + y$ as $x + y \in [-1,1]$ which is less precise than the former. Another situation arises when the assignment of variables within a loop can be enumerated. As the program itv_pol4, variable “x” is assigned a value of either 1 or -1 within the loop. At the loop header, the widening operation of rhiTCM (with $\text {FP}\_\text {SET}=\{0\}$) is performed as: $([-1,-1] \nabla _i \bot _i) \vee (\bot _i \nabla [1,1])$ and $([-1,-1] \nabla _i [-1,-1]) \vee ([1,1] \nabla _i [1,1])$, which results in $x \in [-1,-1] \vee [1,1]$ while the widening operation of TCM is performed as: $[-1,-1] \nabla _i [1,1]$ and $[-1,+\infty ] \nabla _i [-1,-1]$, which results in $x \in [-1,+\infty ]$.

Performance. All experiments are carried out on a virtual machine (using VirtualBox), with a guest OS of Ubuntu (4GB Memory), host OS of Windows 10, 16GB RAM and Intel Core i5 CPU 2.50 GHz. The column “t(ms)” presents the analysis time in milliseconds. Experimental time for each program is obtained by taking the average time of ten runnings. From Table 1, we can see that rhiTCM is less efficient than TCM. The size of matrix A and the number of the fixed partitioning points will affect the performance of rhiTCM. The smaller the size of matrix A and the fewer fixed partitioning points there are, the closer the performance of rhiTCM will be to the performance of TCM. In program MotivEx, there are two variables $x,\ y$. We set one linear constraint “$x+y$” in the template matrix with one fixed partitioning point “0” in the FP_SET. In this configuration, the analysis time of rhiTCM is almost the same as that of TCM.

5 Related Work

A variety of abstract domains have been designed for the analysis of non-convex properties. Allamigeon et al. [1] introduced max-plus polyhedra to infer min and max invariants over the program variables. Granger introduced congruence analysis [11], which can discover the properties like “the integer valued variable X is congruent to c modulo m”, where c and m are automatically determined integers. Bagnara et al. proposed the abstract domain of grids [2], which is able to represent sets of equally spaced points and hyperplanes over an n-dimensional vector space. The domain is useful when program variables take distribution values. Chen et al. applied interval linear algebra to static analysis and introduced interval polyhedra [5] to infer and propagated interval linear constraints of the form $\sum _k [a_k,b_k] x_k \le c$.

To enhance numerical abstract domain with non-convex expressiveness, some work make use of special decision diagrams. Gurfinkel et al. proposed BOXes, which is implemented based on linear decision diagrams (LDDs) [12]. Gange et al. [16] extended the interval abstract domain based on range decision diagrams (RDDs), which can express more direct information about program variables and supports more precise abstract operations than LDD BOXes. Some work make use of mathematical functions that could express non-convex properties such as the absolute value function [4, 6]. Sankaranarayanan et al. [18] proposed basic power set extensions of abstract domains. The power set extensions will cause exponential explosion problem.

The rhiTCM domain that we introduce in this paper is an extension of template constraint matrix domain, with the right-hand-side intervals to express certain disjunctive behaviors in a program, e.g., the right-hand value of linear expression may be discontinuous. The configurable finite fixed partitioning points restrict the number of the right-hand-side intervals, avoiding the exponential explosion problem.

6 Conclusion

In this paper, we propose a new abstract domain, namely, an abstract domain of linear templates with disjunctive right-hand-side intervals (rhiTCM abstract domain), to infer linear inequality relations among values of program variables in a program. The domain is in the form of $\sum _i a_i x_i \in \bigvee _{j=0}^p [c_j,d_j]$, where $a_i \in \mathbb {Q}$ is the variable coefficient specified in the preset template constraint matrix, x is the variables in the program to be analysed, $\bigvee _{j=0}^p [c_j,d_j]$ is the disjunctions of intervals based on fixed partitioning slots. The key idea is to employ the disjunctive intervals to get and retain discontinuous right-hand-side values of the template constraint thus can deal with non-convex behaviors in the program. We present the domain representation as well as domain operations designed for rhiTCM abstract domain. We have developed a prototype for the rhiTCM abstract domain using rational numbers and interface it to the Apron numerical abstract domain library. Experimental results are encouraging: The rhiTCM abstract domain can discover invariants that are non-convex and out of the expressiveness of the classic TCM abstract domain.

It remains for future work to test rhiTCM abstract domain on large realistic programs, and consider automatic methods to generate the template constraint matrix of the program to be analysed.