Resilient Track Components Modelling Options for Time Domain Train-Track Interaction Simulation

Abstract

Resilient components are widely used in railway tracks. For time domain train-track interaction simulation, the components are usually considered as linear Kelvin-Voigt models. However, the dynamic properties of the resilient components are often dependent on frequency and static preload, and this requires alternative methods to be adopted. The current study aims at comparing four different rheological models for the viscoelastic behaviour of the resilient components: a linear Kelvin-Voigt model, a linear three-element parameter model, a linear five-element parameter model and a non-linear three element model. Except for the linear Kelvin-Voigt, the other three models are able to reproduce the dependence on frequency, and the non-linear three-element model can also reproduce the dependence on static preload. The rheological models are used as the foundation of the rail in vertical direction to study the effect of the different options on train-track dynamic interaction. To that aim, their effects on track dynamics are first studied in frequency domain with unit-length track models comparing the dynamic characteristics of the proposed models. Then the investigation is extended to time domain train-track interaction simulation analysing the force transmitted to the ground. Remarkable differences of the results are observed in the frequency ranges associated with the wheelset-track coupled vibration and the resonance of the track.

1 Introduction

Resilient track components are widely used in different types of tracks in various forms, such as the rail pads, the under sleeper pads, the continuous support of Embedded Rail Systems, with the main objective to tune the track stiffness and therefore to optimise the train-track interaction performance. For the study of train-track dynamic interaction in time domain, in most cases the resilient track components are represented by Kelvin-Voigt models whose parameters are constant. However, it is also well acknowledged that the dynamic properties of the resilient track components, which can be comprehended as the equivalent stiffness and damping (considering the resilient track component as a Kelvin-Voigt model), are usually dependent on different parameters, mainly frequency, static preload and dynamic strain amplitude [1, 2]. Due to the strong influence on the overall track stiffness, for a precise prediction of the track response, the dependence of the dynamic properties of the resilient track components on different parameters should be properly modelled and considered in the numerical modelling of train-track interaction.

The current work aims at comparing four rheological models as the modelling options of the resilient track components, one of which is non-linear, for the frequency- and preload-dependent dynamic properties. In Sect. 2, the equivalent dynamic properties of the modelling options are studied and compared in frequency domain. Then, the effect on the track dynamic characteristics is assessed with unit-length track models in Sect. 3. After that, time domain wheelset-track simulation is performed to investigate the influence on the force transmitted to the ground induced by the moving wheelset and rail roughness excitation in Sect. 4.

2 Rheological Models for Resilient Track Components

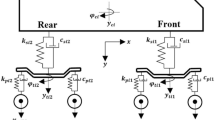
The proposed rheological models are presented in Fig. 1, which includes a linear Kelvin-Voigt model, a linear three-element model, a linear five-element model, and a non-linear three-element model [3]. The element parameters of the last model are dependent on static preload.

Fig. 1

Rheological models for resilient track component modelling: a linear Kelvin-Voigt model; b linear three-element model; c linear five-element model; d non-linear three-element model (the element parameters are dependent on static preload)

The three-element model is composed of a spring with stiffness k₁ in parallel with a Maxwell model with stiffness k₂ and damping c₂. The equivalent stiffness and damping of the linear three-element model can be computed as

$$\begin{aligned} & k_{{{\text{eq}}}} = k_{1} + k_{2} \frac{{\left( {c_{2} \omega /k_{2} } \right)^{2} }}{{1 + \left( {c_{2} \omega /k_{2} } \right)^{2} }}, \\ & c_{{{\text{eq}}}} = c_{2} \frac{1}{{1 + \left( {c_{2} \omega /k_{2} } \right)^{2} }}, \\ \end{aligned}$$

(1)

where ω is the angular frequency of deformation. Equation (1) implies that the equivalent stiffness of the model k_eq is mainly contributed by k₁ for low frequency and approaches (k₁ + k₂) with increasing frequency. The approaching rate is determined by the ratio of c₂ to k₂. For the equivalent damping c_eq, its value decreases from c₂ to zero with increasing frequency. Similar to the composition of the model, the dynamic properties of the model can be seen as the sum of the dynamic property of the single spring and the ones of the Maxwell model in parallel. Indeed, the terms related to k₂ and c₂ in Eq. (1) are respectively the equivalent stiffness and damping of a Maxwell model. For the same reason, the equivalent stiffness and damping of the linear five-element model can be computed as the sum of the single spring and two Maxwell models in parallel. Compared to the three-element model, the equivalent dynamic properties of the five-element model can have two asymptotes if the ratios of c₂ to k₂ and c₃ to k₃ are different, which allows the modelling of more complex dynamic behaviour. For the non-linear three-element model, the equivalent dynamic properties can be computed in the same form presented in Eq. (1), but the element parameters are now dependent on the static preload applied to the model. Taking the single spring as an example, its stiffness is computed as

$$\begin{array}{*{20}c} {k_{1}^{*} \left( {F_{{\text{s}}} } \right) = k_{1,0} \left( {1 + F_{{\text{s}}} /F_{0} } \right)^{\beta } ,} \\ \end{array}$$

(2)

where F_s is the static preload applied on the model; k_1,0 is the reference stiffness of the single spring; F₀ is the reference value of the static preload; and β is a dimensionless parameter. The other two parameters $k_{2}^{*}$ and $c_{2}^{*}$ are computed in the same form of Eq. (2). Compared to other models, the non-linear three-element model can reproduce the dependence of the dynamic properties of the resilient track components on both frequency and static preload. For the present work, the parameters reported in Table 1 are used. They are based on the commonly adopted values for the frequency domain modelling of a rail viscoelastic foundation in vertical direction [4], which is composed of a linear elastic foundation (stiffness per unit length equal to 100 × 10⁶ N/m²) with a constant loss factor (0.1).

Table 1 Parameters of the rheological models

The reference static preload of the non-linear three-element model is set to 40 kN/m because it corresponds to the value of a static distributed load on the track (rail on Winkler foundation) that leads to a uniform rail deflection which is equal to the one of the rail section under a single axle load, considering that the stiffness is equal to 100 × 10⁶ N/m².

The equivalent dynamic properties of the rheological models are computed from 0 to 250 Hz and are presented in Fig. 2. The results of the linear models are reported in part (a) while the ones of the non-linear model with different static preloads are presented in part (b).

Fig. 2

Equivalent stiffness, damping of the rheologic models: a linear models; b linear and non-linear three-element models. – – Linear elastic spring with constant loss factor; blue line indicates linear Kelvin-Voigt model; red line indicates linear three-element model; yellow line indicates linear five-element model; violet line indicates non-linear three-element model with no static preload; green line indicates non-linear three-element model with static preload (40 kN/m)

Regarding the equivalent stiffness shown in part (a), the values of the three- and five-element models increase with frequency as implied by Eqs. (1) and (2). For the five-element model, the trend is almost bilinear with a rapid increase below 20 Hz and a slow one for higher frequency. With the employed data, all the models have similar equivalent stiffness around 200 Hz. Concerning the equivalent damping reported in part (a), the values of all models but the linear Kelvin Voigt model decrease with frequency. For the non-linear three-element model, the results are computed for two cases (static preload equal to 0 and 40 kN/m) and are compared to the ones of the linear three-element model. The results of the equivalent stiffness are strongly dependent on the static preload while the dependence of the equivalent damping is less remarkable. The difference of the equivalent stiffness between the non-linear (40 kN/m static preload) and linear model is negligible around 200 Hz.

3 Unit-Length Track Models

To study the impact of the different rheological models on track dynamics, a unit-length track model configuration is used. The unit-length track model consists of a unit-length rail on a foundation represented by the various rheological models and is essentially a single degree-of-freedom system. Although the unit-length track model does not take into consideration the deformability of the rail, it can still lead to a couple of important comments on the dynamic characteristics of the track. The track Frequency Response Functions (FRFs) are presented in Fig. 3 in terms of rail receptance. The results of the linear models are reported in part (a) while the ones of the non-linear model with different static preloads are presented in part (b).

Fig. 3

Frequency Response Functions of the unit-length track models (rail receptance): a linear models; b linear and non-linear three-element models. – – Linear elastic spring with constant loss factor; blue line indicates linear Kelvin-Voigt model; red line indicates linear three-element model; yellow line indicates linear five-element model; violet line indicates non-linear three-element model with no static preload; green line indicates non-linear three-element model with static preload (40 kN/m)

For all the linear track models, the FRFs suggest that the resonance is located around 205 Hz. The values are similar because the equivalent stiffness represented by the various models are comparable around 200 Hz. The natural frequency of the sectional rail model is named as the “cut-on frequency” of the rail supported by an elastic foundation [4]. The rail vibration is an evanescent wave below such frequency and corresponds to a propagating wave above it. Consequently, the dynamic characteristic of the track is dominated by the foundation stiffness below the cut-on frequency, the foundation damping around the cut-on frequency, and the rail properties above the cut-on frequency. Thus, the frequency range under discussion is limited to 250 Hz since the rail deformability is not taken into account in the sectional model. The difference between the moduli is mainly observed in the resonance zone. The magnitude relationship coincides with the one of the equivalent damping presented in Fig. 2. Regarding the non-linear three-element model, the reasoning is similar for the case where a 40 kN/m static preload is applied. However, when the static preload is low, the resonance of the sectional track model decreases significantly to around 170 Hz. The decrease of the cut-on frequency varies the properties of the waves with the frequency between 170 and 205 Hz, which are evanescent with the linear track models but are propagating with the non-linear three-element model.

4 Time Domain Wheelset-Track Interaction Simulation

To better investigate the effect of the various foundations, time domain wheelset-track interaction simulation is performed. The scheme of the simulation model is presented in Fig. 4.

Fig. 4

Scheme of the time domain wheelset-track interaction simulation model

The simulation model consists of a Finite Element (FE) track model with rail roughness, a moving wheelset, and linear Hertzian contact springs between the rails and wheels. The wheelset moves from the left end towards the right one with constant speed v (200 km/h). A flexible wheelset model is used which describes the wheelset motion adopting the mode superposition technique [5]. Three bending modes (at 69, 132 and 268 Hz) are included. The wheelset mass is approximately 1700 kg. The static load on each wheel F_s equals 55 kN. The wheel-rail contact force is described by a non-linear Hertzian contact relationship,

$$\begin{array}{*{20}c} {F_{{\text{H}}} = G_{{\text{H}}} \left( {y - z_{{{\text{r}},0}} {\text{e}}^{{{\text{j}}2\pi /\lambda_{{\text{r}}} x}} - w} \right)^{3/2} ,} \\ \end{array}$$

(3)

where G_H is the Hertzian coefficient and is equal to 0.69 × 10¹¹ N m^2/3. The track model is composed by the FE rails (60E1) on the foundation made up of a set of rheological models connecting the FE nodes and the ground. The model length L is 160 m, and the mesh size l is 0.08 m so that the finite-element-passing frequency is higher than the frequency range under discussion (0–250 Hz). The structural damping of the rail is taken into account through the Rayleigh damping parameters α and β which are set to 0 and 2e−5. The spectrum of the rail roughness amplitude (z_r,0) is presented in Fig. 5. The amplitude is defined according to ISO 3095 [6] for components whose wavelengths are shorter than 0.7 m and according to ORE B176 [7] for components with longer wavelengths. The defect level is between the small and large levels defined by the ORE B176 to guarantee the continuity of the roughness amplitude at 0.7 m. The excitation frequencies f_d of the roughness components are converted from the wavelength λ_r to the frequency f_d with the wheelset moving speed (f_d = v/λ_r).

Fig. 5

Spectrum of the rail irregularity/roughness components used for time domain wheelset-track interaction simulation. The wavelength is converted to excitation frequency considering a constant wheelset speed of 200 km/h

The simulation is completed by performing numerical integration with Newmark method (the integration step equals 2 × 10^–5 s). No static preload is assigned to the non-linear rheological models and the instantaneous load applied to them is used to compute the parameter values at each integration step. Therefore, the static preload on a single non-linear rheological model varies according to the position of the wheelset and results in a variation of the equivalent dynamic properties of the rheological model itself. To investigate the possible effects of the different foundation models on ground vibration, the one-third octave band spectra of the transmitted force in the middle of the track section are computed (based on a 1 s time window centred at the time instant of the wheelset passage, i.e., 1.44 s) and presented in Fig. 6. It should be noted that the transmitted force at a single FE node depends on the mesh size. Thus, the results are converted to unit length of the track model.

Fig. 6

One-third octave band spectra of the transmitted force in the middle of the 160 m long track section induced by the wheelset passage at 200 km/h (the axle load is 110 kN) and the rail roughness excitation. The transmitted force is converted to force per unit length of the track models. Blue line indicates linear Kelvin-Voigt model; red line indicates linear three-element model; yellow line indicates linear five-element model; violet line indicates non-linear three-element model

The spectra obtained with linear track foundations have similar trends, which are quite different to that with the non-linear foundation. Nonetheless, the differences between the transmitted force levels computed with the linear foundations are not negligible for some bands. For instance, the levels computed with the linear three-/five-element model foundation are about 3.5 dB higher than the one with the linear Kelvin-Voigt foundation at the bands centred at 80 Hz. Similar comments can be raised regarding the bands centred at 62.5, 200 and 250 Hz. The levels of the transmitted force obtained with the non-linear foundation are significantly higher than those of linear foundations for the bands centred at 50, 62.5, 80 and 200 Hz. The higher levels of the bands below the cut-on frequency are associated with the higher amplitudes of the wheelset-track coupled vibration. Concerning the 200 Hz band, the evanescent waves for the linear foundations become propagating for the non-linear foundation and therefore the level becomes much higher (6–10 dB).

5 Conclusion

The current paper investigates the effect of different modelling options for resilient track components on train-track dynamic interaction. Three linear and one non-linear rheological models are used to simulate the rail foundation. The investigated results are the forces transmitted to the ground. The results show that the different modelling options lead to remarkable differences. Specifically, there are two frequency ranges that are affected the most. The first one is the range associated with the wheelset-track coupled vibration and the second one is around the cut-on frequency of the track model (the resonance zone of the unit-length track model). For linear modelling options, the difference is originated by the equivalent stiffness and damping of the rheological models. Concerning the non-linear model, the difference is also related to the non-linear dynamic characteristics of the foundation due to the changing load induced by the wheelset passage and rail roughness excitation. In particular, the frequency domain analysis shows that the equivalent dynamic properties of the non-linear option are comparable to those of linear ones when it is loaded by the wheelset but are significantly different when it is not loaded. Since for most of the time of a wheelset/vehicle passage the track is not loaded, the different modelling options result in considerably different track responses.