Droplet Growth and Drop Size Distribution Model for Dropwise Condensation on Hydrophobic Tubular Surfaces

Abstract

Condensation over a tubular surface has a wide range of applications. A steady-state mathematical model for droplet condensation of saturated water vapor on the outer surface of a hydrophobic tube is proposed. The tube curvature effect on a single drop heat transfer as well as on the drop size distributions has been incorporated. A single droplet growth model utilizing heat conducted through the droplet population to the condensing surface is established. Thermal resistances that include curvature, interfacial, drop and the hydrophobic promoter layer have been considered for model development. The tube curvature effect on a single droplet heat transfer is considered based on condensation over a concave substrate (Zhang and Zhang in ACS Omega 5:22,560–22,567, 2020). The surface wetting phenomena and their characteristics are defined on the basis of an equilibrium contact angle and hysteresis. The developed model is built on the definition of an apparent contact angle. A general transcendental equation for the apparent contact angle via droplet and the tube radius to the intrinsic contact angle is utilized. Population balance theory is used for the droplet number density distribution. The droplet number densities for gravity-driven drop removal and drainage have been iteratively determined. The numerically obtained drop size distribution is integrated with the single droplet heat flux for obtaining the overall heat transfer rate during droplet condensation outside a vertical tube.

1 Introduction

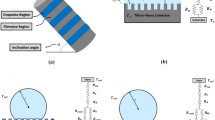
Understanding water vapor condensation is of significant interest due to its considerable influence on process efficiency in many applications [2]. Condensation of water vapor on a substrate can be broadly classified in filmwise and dropwise modes. The transitions between the two on the condensing substrate will depend on its thermophysical properties, the condensate and the condensing environment. The gravity-driven droplet removal phenomena of condensation lead to an order of magnitude higher heat transfer compared to filmwise condensation [3]. Most applications involve flow inside or outside tubes, such as shell-and-tube condensers and air-coupled condensers. Thus, condensation of pure water vapor on a convex-shaped substrate is of particular interest. Most dropwise condensation models are based on a flat surface's equilibrium contact angle and are unsuitable for curved substrates. It is related to the inability to resolve the liquid–solid interface at the curved surfaces correctly. Hence, instead of quantifying the intrinsic contact angle θ’, the apparent contact angle θ is measured in the radial plane, as shown in Fig. 1b. However, it is convenient to measure the intrinsic contact angle θ^o, in the axial plane, as shown in Fig. 1a. Thus, the present droplet condensation model is based on the apparent contact angle θ, estimated from the intrinsic contact angle θ^o by incorporating the tube curvature.

Fig. 1

Schematic of the contact angle measured over orthogonal planes of a tubular surface

2 Literature Review and Objectives

Le Fevre and Rose [3] originally developed the classical steady-state dropwise condensation model for hemispherical drops. The authors integrated single droplet heat flux with the average distribution of drop sizes to estimate the overall heat flux at the condensing surface. Kim and Kim [4] developed the thermal resistance model for flat hydrophobic surfaces by defining the conduction resistance of droplets having non-hemispherical shapes. Here, the equilibrium contact angle was included in the model to predict the overall heat transfer rate. Based on the Kim and Kim model, Miljkovic et al. [5] studied the effect of droplet morphology on single droplet heat transfer for a flat surface. Drop size distributions for different wetting conditions were derived. Bahrami and Saffani [6] studied dropwise condensation heat transfer on structured tubular surfaces. However, the tube curvature effect on a single droplet growth rate and on the droplet number density was largely ignored.

A mathematical model of growth of a liquid droplet on a hydrophobic concave surface has been reported in the literature [1]. The studied model includes the concave substrate curvature in the heat transfer model for a single droplet and subsequently partially in the growth rate. However, the droplet number density was calculated excluding the tube curvature. Xiang and Sun [7], using geometric relations, derived an expression for intrinsic contact angle in terms of the tube and drop radius. Experimentally measured contact angles verified the derived expression. Zheng et al. [8] studied condensation characteristics on groups of non-wetting surfaces by including the dynamically changing nature of thermal resistances with droplet size.

Although several experimental and numerical studies of dropwise condensation of steam on flat surfaces have been carried out, there are only a few on tubular surfaces. Condensation heat transfer rates for tubular surfaces are mostly based on the flat surface formulation. Also, the curvature effect of the convex substrate has not been systematically carried on the heat transfer rate. The current study aims to incorporate the tube curvature on a single droplet heat transfer and develop a mathematical framework for estimating a steady-state droplet number density during dropwise condensation of saturated water vapor. The effect of the tube curvature and the degree of sub-cooling on a single droplet heat flux and total heat transfer are presented. Also, dropwise condensation of water vapor over a vertical flat plate is used for comparison against the vertical tube.

3 Mathematical Model Framework

Droplet condensation begins with drop formation in the nanoscale size at the nucleation site. The nucleated droplet grows on the condensing surface, coalesces with the adjacent drop and departs due to gravitational instability. Droplet growth can be broadly classified into two zones: growth by direct condensation for small size droplets and coalescence-dominated growth for large size droplets. The boundary between the small and large size drops is based on the effective droplet radius at which the coalescence activity initiates. The empirical relation, ${r}_{e}={\left(4{N}_{s}\right)}^{-1/2}$ calculates the effective drop size, where N_s is the nucleation site density [4].

3.1 Estimation of the Apparent Contact Angle

The tube curvature on the apparent contact angle estimation is deduced here. Drop on the convex surface of the tube in radial and axial planes are shown, respectively, in Fig. 2a,b, while the geometrical construction details are shown in Fig. 2c,d. From geometry and the droplet projection, as shown in Fig. 2c,d, the expression for the apparent contact angle incorporating the curvature effect of the tube has been derived and presented as Eqs. (1) and (2). These expressions are non-linear and depend on the droplet size and the tube radius. Hence, estimating the apparent contact angle with varying droplet size and for a given intrinsic contact angle is iteratively solved. These equations are

$$ r\left( {\cos \alpha - \cos \beta } \right) = R\left( {1 - \cos \gamma } \right) $$

(1)

$$ \begin{gathered} \sqrt {r^{2} - b^{2} } - \sqrt {r^{2} - a^{2} } - R + \sqrt {R^{2} - b^{2} } = 0; \hfill \\ \sqrt {\left( \frac{R}{r} \right)^{2} - \sin^{2} \theta } + \sqrt {1 - \sin^{2} \theta } - \sqrt {1 - \sin^{2} \theta^{{\text{o}}} } - \frac{R}{r} = 0 \hfill \\ \end{gathered} $$

(2)

Fig. 2

Geometrical construction of the droplet for estimating apparent contact angle (θ) from the readily available intrinsic contact angle (θ^o)

3.2 Single Droplet Heat Transfer

Heat conducted through droplets contributes to the overall heat flux at the condensing surface during droplet condensation. Thus, understanding the heat flow along a single droplet is essential. Figure 3 shows a geometrical construction of a drop with center O₂ having radius r on the convex surface of the tube with center O₁ having radius R. The apparent contact angle is θ, while T_sat and T_w are the saturated vapor and condensing wall surface temperatures, respectively. Droplet growth over a small time interval during condensation is represented as Δr. The vapor saturation and condensing wall surface temperatures are assumed to be constant and homogeneously distributed. Further, H_l represents the height from the apex of the tube to the line joining the two three-phase contact points in the radial plane. The latent heat released at the liquid–vapor interface during droplet condensation is transferred to the condensing surface through the droplet. The presence of non-condensable gas in the condensing environment is neglected for the present study. The total temperature drop from the vapor saturation temperature to the condensing wall is evaluated based on the heat transfer rate and thermal resistance. Interfacial resistance formed between the vapor phase and the liquid phase at the liquid–vapor interface is given by Eq. (3). The interfacial heat transfer rate is calculated from Eq. (4). Here, h_fg is the latent heat of condensation, R_m is the specific gas constant and υ_fg is the specific volume of vapor phase relative to the liquid phase. The accommodation coefficient α is the fraction of incoming vapor molecules that condenses at the liquid–vapor interface. In the present study, it is taken as unity which is an accepted value for pure steam.

$$ \Delta T_{i} = T_{sat} - T_{i} = \frac{q}{{2\pi r^{2} h_{i} \left( {1 - \cos \theta } \right)}};R_{{\text{int}}} = \frac{{\Delta T_{i} }}{q} $$

(3)

$$ h_{i} = \left[ {\frac{{2\hat{\sigma }}}{{2 - \hat{\sigma }}}} \right]\left( {\frac{{h_{fg}^{2} }}{{T_{sat} v_{fg} }}} \right)\left( {\frac{1}{{2\pi R_{m} T_{sat} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left[ {1 - \frac{{P_{sat} v_{fg} }}{{2h_{fg} }}} \right] $$

(4)

Fig. 3

Schematic of a liquid drop with the thermal resistance network on the surface of a tube

The curvature of the vapor–liquid interface is the source of curvature resistance R_curv, which manifests as a depression in the interfacial saturation temperature and is calculated using Eq. (5). Here, r_min is the minimum drop radius at the time of nucleation.

$$ \Delta T_{c} = \frac{{2T_{sat} \sigma }}{{r\rho h_{fg} }} = \frac{{r_{\min } }}{r}\Delta T;R_{curv} = \frac{{\Delta Tr_{\min } }}{qr} $$

(5)

$$ r_{\min } = \frac{{2T_{sat} \sigma }}{{\rho h_{fg} \Delta T}} $$

(6)

The droplet itself acts as a resistance to heat transfer between the liquid–vapor interface and the condensing wall and the temperature drop due to thermal resistance is modeled as Eq. (7). Here, ΔT_d is the temperature drop due to conduction resistance and k_c is thermal conductivity of the condensate [4]. The effect of tube curvature on the droplet heat transfer is incorporated by subtracting the half portion of cylinder with height H_l in calculating the drop volume and heat conduction through the droplet [1]. The spherical cap approximation is assumed for calculating the droplet volume and interfacial areas of liquid–vapor and liquid–solid. The droplet volume is estimated from Eq. (8), where, R is the radius of the tube.

To make the substrate non-wetting, a coating is applied and adds thermal resistance to heat transfer, Eq. (7), where, δ_hc is the hydrophobic coating layer thickness and k_hc is its thermal conductivity. The total thermal resistance for a single droplet is estimated as the arithmetic sum of the four resistances, Eq. (10).

$$ \Delta T_{d} = \frac{q\theta }{{4\pi rk_{c} \sin \theta }} - \frac{{q\left( {R - \sqrt {R^{2} - \left( {r\sin \theta } \right)^{2} } } \right)}}{{2\pi r^{2} k_{c} \left( {\sin \theta } \right)^{2} }};R_{drop} = \frac{{\Delta T_{d} }}{q} $$

(7)

$$ \begin{gathered} V = \frac{{\pi r^{3} }}{3}\left( {2 - 3\cos \theta + \cos^{3} \theta } \right) - \hfill \\ \, \left( {\pi \left( {r\sin \theta } \right)^{2} \times \left( {\frac{{R - \sqrt {R^{2} - \left( {r\sin \theta } \right)^{2} } }}{2}} \right)} \right) \hfill \\ \end{gathered} $$

(8)

$$ \Delta T_{coat} = \frac{{q\delta_{hc} }}{{\pi r^{2} k_{hc} \sin^{2} \theta }};R_{coat} = \frac{{\Delta T_{coat} }}{q} $$

(9)

$$ R_{total} = \frac{{T_{s} - T_{w} }}{q} = R_{{\text{int}}} + R_{curv} + R_{drop} + R_{coat} $$

(10)

Thus, the heat transfer rate q through a single droplet of radius r is estimated from Eqs. (3, 5, 7 & 9) yielding the final form

$$ q\left( r \right) = \frac{{\Delta T\pi r^{2} \left( {1 - \frac{{r_{\min } }}{r}} \right)}}{{\left[ \begin{gathered} \frac{1}{{2h_{i} \left( {1 - \cos \theta } \right)}} + \frac{r\theta }{{4k_{c} \sin \theta }} - \hfill \\ \frac{{\left( {R - \sqrt {R^{2} - \left( {r\sin \theta } \right)^{2} } } \right)}}{{2k_{c} \left( {\sin \theta } \right)^{2} }} + \frac{{\delta_{hc} }}{{k_{hc} \sin^{2} \theta }} \hfill \\ \end{gathered} \right]}} $$

(11)

3.3 Drop Size Distribution

Dropwise condensation starts with droplet nucleation at preferential nucleation sites. At each initial nucleation site, a drop grows by direct deposition of vapor onto the liquid surface. As the drop grows, the distance between the neighboring droplets diminishes and initiates coalescence. Upon reaching a size, where body force due to gravity exceeds the surface tension, the drop becomes unstable and departs the surface. The falling droplets expose the substrate for renucleation and the cycle continues. The growth process can be divided into two regimes—direct condensation growth and coalescence dominant growth. The boundary between the small and large size drops is defined on the basis of effective droplet radius at which the coalescence is initiated, and is given by the expression, ${r}_{e}={\left(4{N}_{s}\right)}^{-1/2}$ [4]. The population balance theory is used to determine the droplet number densities for small size drop $\left(r<{r}_{e}\right)$. At steady state, the number of drops in a particular size range is conserved. In other words, equal number of droplets will enter and leave a certain drop size interval. Consider drop size in the range ${r}_{1}$ to ${r}_{2}$ having a droplet growth rate represented as, $G=dr/dt$. The number density of the drop, $n(r)$ is defined as the number of droplets of radius r per unit area. The number of droplets entering and leaving the size interval $\left({r}_{1},{r}_{2}\right)$ in an infinitesimally small interval of time dt can be denoted as ${An}_{1}{G}_{1}dt$ and ${An}_{2}{G}_{2}dt$, respectively, where A is the area of any condensing surface. While the number of droplets that are swept away by the departing droplets in the interval $\left({r}_{1},{r}_{2}\right)$ can be written as, $S{n}_{1-2}\Delta rdt$, where, S is the sweeping rate, ${n}_{1-2}$ is the average population density and $\Delta r$ is the drop size interval. Thus, the population balance theory will lead to Eq. (12). As $\Delta r$ approaches zero, the number density ${n}_{2}$ is infinitesimally close to ${n}_{1}$ and becomes a point value $n$, Eq. (12) is reduced to Eq. (13), where τ is the sweeping period defined as $\tau =A/S$.

$$ An_{1} G_{1} dt = An_{2} G_{2} dt + Sn_{1 - 2} \Delta rdt $$

(12)

$$ \frac{{d\left( {Gn} \right)}}{dr} + \frac{n}{\tau } = 0 $$

(13)

The heat transfer rate through a drop of the radius r is the amount of heat released during condensation at the free surface, which is calculated as the product of the rate of mass condensed and the latent heat of phase change. Thus, one can write

$$ q = \rho_{l} \frac{dV}{{dt}}h_{fg} $$

(14)

where, $\rho_{l}$ is density and V is the volume of the liquid drop estimated from the Eq. (8). The derivative of a single droplet volume with respect to time is given by

$$ \frac{dV}{{dt}} = \left\{ \begin{gathered} \pi r^{2} \left( {2 - 3\cos \theta + \cos^{3} \theta } \right) - \hfill \\ \left( \begin{gathered} \pi r\sin^{2} \theta \left( {R - \sqrt {R^{2} - \left( {r\sin \theta } \right)^{2} } } \right) + \hfill \\ \frac{{\pi r^{3} \sin^{4} \theta }}{{2\sqrt {R^{2} - \left( {r\sin \theta } \right)^{2} } }} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right\}\frac{dr}{{dt}} $$

(15)

On substituting Eq. (15) in Eq. (14) and comparing to Eq. (11) yields the single droplet growth rate

$$ \frac{dr}{{dt}} = \frac{{A_{1} \left( {1 - \frac{{r_{\min } }}{r}} \right)}}{\begin{gathered} \left[ {A_{3} + rA_{2} - \frac{{\left( {R - \sqrt {R^{2} - \left( {rA_{5} } \right)^{2} } } \right)}}{{2k_{c} A_{5}^{2} }}} \right] \times \hfill \\ \left\{ {A_{4} - \left( {\frac{{A^{2} }}{r}\left( {R - \sqrt {R^{2} - \left( {rA_{5} } \right)^{2} } } \right) + \frac{{rA_{5}^{4} }}{{2\sqrt {R^{2} - \left( {rA_{5} } \right)^{2} } }}} \right)} \right\} \hfill \\ \end{gathered} } $$

(16)

where $A_{1} = \frac{\Delta T}{{\rho h_{fg} }}$; $A_{2} = \frac{\theta }{{4k_{c} A_{5} }}$; $A_{3} = \frac{1}{{2h_{i} \left( {1 - \cos \theta } \right)}} + \frac{{\delta_{hc} }}{{k_{hc} A_{5}^{2} }}$

$A_{4} = \left( {2 - 3\cos \theta + \cos^{3} \theta } \right)$; $A_{5} = \sin \theta$.

Drop size distribution $N\left(r\right)$ for large droplets $\left(r>{r}_{e}\right)$ has been proposed by Le Fevre and Rose [3] in the form

$$ N\left( r \right) = \frac{1}{{3\pi r^{2} r_{\max } }}\left( {\frac{r}{{r_{\max } }}} \right)^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} $$

(17)

The maximum droplet size at which it departs from the substrate is determined based on forces imbalance at the three phase contact boundary. The forces acting at the three phase contact lines are surface tension and the gravitational, body force. Since the condensing surface is a vertical tube, the gravitational force on the droplet acts along parallel to the condensing surface and is given by Eq. (18). The component of surface tension that holds the droplet to the condensing surface is calculated from the expression provided in [9]. This expression, Eq. 19, uses symbols ${\theta }_{a}^{o}$ and ${\theta }_{r}^{o}$ that are the intrinsic advancing and receding contact angles.

$$ F_{g\parallel } = \rho g\left[ \begin{gathered} \frac{{\pi r^{3} }}{3}\left( {2 - 3\cos \theta + \cos^{3} \theta } \right) - \hfill \\ \frac{{\pi r^{2} \sin^{2} \theta }}{2}\left( {R - \sqrt {R^{2} - r^{2} \sin^{2} \theta } } \right) \hfill \\ \end{gathered} \right] $$

(18)

$$ F_{r\parallel } \simeq cD\sigma \left( {\cos \theta_{r}^{{\text{o}}} - \cos \theta_{a}^{{\text{o}}} } \right) \approx \left( {a + b} \right)\sigma \left( {\cos \theta_{r}^{{\text{o}}} - \cos \theta_{a}^{{\text{o}}} } \right) $$

$$ a = r\sin \theta_{avg}^{{\text{o}}} ;b = r\sin \theta ;\theta_{avg}^{{\text{o}}} = \frac{1}{2}\left( {\theta_{a}^{{\text{o}}} + \theta_{r}^{{\text{o}}} } \right) $$

(19)

Thus, the maximum droplet size at the inception of sliding can be estimated as given by a transcendental equation

$$ F_{g\parallel } - F_{r\parallel } = 0 $$

(20)

It is solved iteratively to get the ${r}_{max}$ value. Equation (13) is the governing equation for the droplet density for small-sized droplets. Here, the droplet growth rate is a function of drop size, tube curvature and apparent contact angle, in turn, a function of the drop size. Thus, Eq. (13) cannot be analytically solved and, instead, it is numerically evaluated from the equation

$$ \frac{dn\left( r \right)}{{dr}} + n\left( r \right)\left[ {\frac{1}{G\left( r \right)}\frac{dG\left( r \right)}{{dr}} + \frac{1}{G\left( r \right)\tau }} \right] = 0 $$

(21)

The above equation has two unknown, n(r) and τ. The required two conditions are the continuity in droplet densities and its slope at the effective droplet size $\left({r}_{e}\right)$ and are expressed as

$$ \left. {n\left( r \right)} \right|_{{r = r_{e} }} = \left. {N\left( r \right)} \right|_{{r = r_{e} }} = \frac{1}{{3\pi r_{e}^{2} r_{\max } }}\left( {\frac{{r_{e} }}{{r_{\max } }}} \right)^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} $$

(22)

$$ \left. {\frac{d\ln n\left( r \right)}{{d\ln r}}} \right|_{{r = r_{e} }} = - \frac{8}{3} $$

(23)

3.4 Overall Condensation Heat Transfer Rate

Once the droplet number densities are estimated, the condensation heat transfer rate per unit area at steady state is calculated by integrating the single droplet heat transfer with the drop size distribution as follows:

$$ q = \int_{{r_{\min } }}^{{r_{e} }} {q\left( r \right)n\left( r \right)dr} + \int_{{r_{e} }}^{{r_{\max } }} {q\left( r \right)N\left( r \right)dr} $$

(24)

4 Results and Discussion

It may be noted that the proposed droplet condensation model is based on the apparent contact angle which depends on the droplet size r, in turn the drop volume V, the tube radius R and hence, the intrinsic contact angle ${\theta }^{o}$, Eq. (2).

4.1 Validation

Figure 4 presents the variation in apparent contact angle with tube diameter and drop volume. Also, the intrinsic contact angle remains nearly constant [7] and an average value is used for the evaluating the expression in Eq. (2). The tube diameter is varied from 5 to 20 mm.

Fig. 4

Comparison of the evaluated apparent contact angle to the measured value [7] for a drop volume of 5 µl, b tube diameter of 10 mm. Red dot represents the measured intrinsic contact angle

In the calculation of the overall condensation heat transfer rate, it is required to evaluate the drop number densities n(r) and N(r). First, ${r}_{max}$ is estimated by solving Eq. (20) iteratively and drop size distribution for large droplets is evaluated from Eq. (17). The small size drop distribution is evaluated by a shooting technique. The continuity of first derivative of the drop size distribution at the effective radius (${r}_{e}$) and the sweeping time $\left(\tau \right)$ are estimated iteratively with Eq. (22). The small size droplet distribution is estimated numerically by a backward Euler method from drop size ${r}_{e}$ to ${r}_{min}$. Thermal properties are evaluated at the wall surface temperature. Newton–Raphson method is used as the iterative algorithm for evaluating $\theta$, ${r}_{max}$ and $\tau$.

Single droplet heat transfer of the present model is compared to that of Zheng et al. [9], Fig. 5. The input parameters used in simulations are shown in Table 1.

Fig. 5

Comparison of the single droplet heat flux and heat transfer rate to [9]. Solid lines show data of the present study while symbols are from [9]

Table 1 Validation parameters

The numerically calculated droplet size distribution is compared to Kim and Kim [4] and is shown in Fig. 6. The present model shows a good match in terms of single droplet heat transfer values and the droplet number densities.

Fig. 6

Numerically obtained droplet number densities compared to Kim and Kim [4]

4.2 Curvature Effect of the Tube

The proposed model incorporates the curvature effect of the tube. Single droplet heat flux is compared for various tube diameters, Fig. 7. When the droplets are small in the micrometer size, tube curvature is insignificant and droplets see the substrate as flat. However, for large droplets in the millimeter range, the curvature effect of the tube is to be seen. Arrow shows that as the tube radius increases, the heat transfer characteristics approach that of a flat surface.

Fig. 7

Effect of tube curvature on the single droplet heat flux and drop-scale heat transfer

4.3 Effect of Degree of Sub-Cooling

Figure 8 shows the heat transfer characteristics of a single droplet with respect to the degree of sub-cooling ranging from 2 to 5 K. The overall qualitative nature of heat flux remains unchanged. However, there is a shift down in droplet size at the initiation of condensation upon an increment in sub-cooling. This is because of the reduction in the energy barrier for the nucleating droplet; that is, the droplets nucleate with a smaller number of vapor molecules at elevated levels of sub-cooling. The total heat flow gradually increases with droplet size. Also, there is a shift up in heat flow rate upon increase in degree of sub-cooling. This is due to higher driving potential for condensation at elevated sub-cooling. Heat flux values rise, attain a peak value at micron size drop and subsequently, diminish for large size drops. For very small droplets, curvature resistance is dominant and reduces with an increase in the drop size. Jointly, conduction resistance increases with the droplet size. Thus, the heat flux distribution qualitatively shows a rise and fall with respect to drop radius.

Fig. 8

The effect of degree of sub-cooling on single droplet heat transfer and drop-scale heat transfer

5 Conclusions

The present study proposes a mathematical model to calculate single droplet heat transfer rate and drop size distribution during dropwise condensation of water vapor on a tubular surface. The model includes the curvature effect of the tube to a point where the droplet condensation model can be applied to the outer surface of a tube down to a wire. The estimated heat flux and heat transfer rate along with the droplet number densities are in good agreement with the published theoretical models. Comparison to experimental data is in progress.