Heat Transfer Enhancement During Dropwise Condensation Over Wettability-Controlled Surfaces

Abstract

Dropwise condensation (DWC) is a complex heat transfer process in which vapor phase changes to liquid phase forming discrete droplets on a surface whose temperature is below the dew temperature of the condensing fluid. DWC mode can strongly enhance the heat transfer compared to filmwise condensation (FWC) mode that usually takes place when a vapor condenses over a metallic surface. The wettability of the surface plays a crucial role on the promotion of DWC instead of FWC. This Chapter is focused on heat transfer measurements and modeling during DWC. The first two Sections are dedicated to a short literature review and to the description of the experimental procedures that can be used for the measurement of the heat transfer coefficient. DWC involves millions of droplets per square meter that form the so-called droplet population. Section 3.3 is dedicated to the description of the droplet size distribution. Section 3.4 presents selected models that can be used for the prediction of heat transfer during DWC. Formed droplets can be removed from the condensing surface by gravity or by other external forces. In the literature, most of the DWC experimental data are taken with quiescent vapor and very few works investigate the effect of the vapor drag force on the droplet departing radius and thus on the heat transfer during DWC. Furthermore, the effect of vapor velocity is not accounted for in available DWC models. Therefore, the last Section of this Chapter is focused on heat transfer modeling in the presence of vapor velocity. A recent approach proposed by the present authors to account for the reduction of droplets departing diameter due to vapor velocity is here presented. The model is then used to show the effect of the main parameters on the DWC heat transfer coefficient.

3.1 Introduction

Condensation is a phase change process encountered in many applications as thermal power plants, desalination of sea water, air conditioning systems, water harvesting, and so on. The surface chemistry and morphology can play a central role to increase the heat transfer coefficient by changing the surface wettability. Wettability can be described by looking at the dynamic contact angles that a liquid (drop) assumes on a surface while moving. Advancing contact angle (θ_a) is defined when the droplet is moving forward to a non-wetted surface and receding contact angle (θ_r) when the contact line is moving backward on a wetted surface [1]. The difference between advancing and receding contact angle is named contact angle hysteresis (Δθ). The changing of wettability can determine a different behavior in the interaction between the liquid and solid phases during the condensation process.

In particular, the vapor can condense on a surface in two modes: filmwise condensation (FWC) mode and dropwise condensation (DWC) mode. The DWC mode is promoted on surfaces with controlled wettability (typically on surfaces with low contact angle hysteresis) and it allows an increase of the heat transfer coefficient (HTC) from 5 to 7 times [2] compared to filmwise mode. Starting from the nanoscale up to the macroscale, DWC involves millions of droplets per square meter. DWC is a cyclic process: condensation begins at a molecular scale with drops formation in preferred nucleation sites. Growing by direct condensation at first and later by coalescence, drops reach the critical size at which external forces (e.g., gravity, vapor drag) overcome adhesion forces and they start to move, sweeping the surface and making new nucleation sites available. The process is, then, renewed [3]. The presence of droplets, instead of a continuous liquid film, allows to reduce the thermal resistance compared to the case of FWC thus increasing the condensation heat transfer coefficient.

The heat transfer characteristics of the DWC mode have attracted several researchers for about 100 years. Since the DWC discovery in 1930 by Schmidt et al. [4], the number of experiments related to DWC has grown over the years and a variety of results are reported in the literature as shown by Rose [5]. In fact, several aspects must be considered while performing DWC measurements to obtain reproducible and comparable results, such as the thermal resistance of the coating, the absence of non-condensable gases, an accurate measurement of surface temperature and heat flux. In the following Sections, the main aspects concerning DWC will be presented.

3.1.1 Surface Coatings

Creation of surfaces that can promote dropwise condensation is one of the main issues. Basically, two approaches can be found in the literature. The first one consists of the modification of the surface chemistry for a given substrate by applying a thin coating over the surface where condensation takes place. The second approach instead involves the modification of both the morphology and the chemistry of the surface and it can allow getting the so-called superhydrophobic behavior. In this Section, we will focus on the first approach considering coatings that can be used for the modification of the surface wettability.

Metals are still the family of materials most used in heat transfer applications, from steel [6,7,8,9] to copper [10, 11] and aluminum [12]. Clean metallic surfaces are generally wetted by the condensate because of their high surface energy (hydrophilic behavior) [13] and the condensation process occurs in filmwise mode. Coatings can be used to reduce the surface free energy of metals and make them hydrophobic. The main issue, in this case, relies on the robustness of such coatings stressed in harsh environments (high saturation temperature conditions, high heat flux, and high vapor velocity). Coating degradation strongly depends on the coating chemistry, thickness, coating-substrate interfacial adhesion [14, 15], and condensation environment.

Satisfactory results in terms of durability have been obtained with different hydrophobic treatments [2] and copper as substrate. Changing the substrate, the affinity between the treatment and the base material can be very different, thus some materials are more challenging than others in order to get prolonged DWC. DWC on copper has been studied for decades [16,17,18,19] and several solutions to promote DWC have been investigated: polymeric coatings [20], self-assembled monolayers (SAMs) [21,22,23], ion implantation [24], and rare-earth oxide ceramics [25]. An alternative solution to sustain DWC on copper substrates can be graphene coating. Uniform graphene coatings are usually fabricated by bottom-up approaches, such as chemical vapor deposition (CVD) on metals. Among the different top-down approaches, the method that has received the most attention is exfoliation and reduction of graphite oxide (GO), the partially oxidized form of graphene that presents low cost. GO coatings are hydrophilic in nature, but their wettability can be converted to hydrophobicity by chemical or thermal reduction. Rafiee et al. [26] demonstrated that a graphene monolayer on copper, gold, and silicon does not change the wettability of the substrate because of its extreme thickness but, with an increase of graphene layers, it is possible to change the contact angles. Colusso et al. [27] fabricated reduced graphene oxide (rGO) coatings using a solution-based process, by dip-coating copper substrates into a suspension containing graphene oxide flakes obtained by chemical exfoliation of graphite oxide in an aqueous solution. They obtained for water an advancing contact angle of ∼84° and a receding contact angle of ∼35°. The coating was found to promote DWC of pure steam with heat transfer coefficients of 170 kW m⁻² K⁻¹ measured during condensation at around 100 °C saturation temperature (with an 8-times increase of the HTC compared to FWC). The durability of the rGO coating is reported to be more than 100 h in the tested conditions.

Regarding aluminum substrates, the available studies about DWC promotion are limited compared to other substrates (copper, titanium, and silicon) [28,29,30]. Steam or liquid at high temperature (>100 °C) etches the aluminum forming boehmite structures [31, 32] enhancing the wettability of the surface and thus efforts must be addressed to protect the surface. Rausch et al. [30] obtained relevant duration results fabricating a hydrophobic aluminum sample by ion implantation: the sample was tested for 8 months but only about 50% of the surface was covered by droplets. At the lowest value of subcooling, the HTC resulted only double as compared to FWC. Paxson et al. [29] obtained interesting results on aluminum processed via initiated chemical vapor deposition (iCVD). The condensation test was performed for 48 h, after which the treatment showed mild signs of degradation; the HTC remained constant around 35 kW m⁻² K⁻¹. Kim and Jeong [24] implanted chromium ions onto an aluminum substrate. Filmwise condensation occurred on the mirror-polished metal surface with no ion implantation. After irradiation with chromium ions, dropwise condensation was induced. The measured FWC heat transfer coefficient showed good agreement with the theoretical values predicted by Nusselt’s film theory whereas, when DWC is promoted, HTCs were two times those expected from Nusselt’s theory.

A different approach to achieve DWC on aluminum surfaces is based on hybrid organic–inorganic sol–gel silica coatings containing hydrophobic moieties (e.g., methyl or phenyl group). The sol–gel method has attracted attention due to: simplicity of the production process which does not involve high temperatures or pressures; versatility since the precursors used are in the liquid state; possibility to deposit the coatings on bare substrates with complex shapes; use of compounds that are not harmful for the environment (e.g., fluorinated molecules). Parin et al. [12] developed a surface that can maintain stable DWC, using SiO₂ hybrid organic–inorganic sol–gel coating functionalized with methyl groups over an aluminum substrate. The sol–gel film was deposited on a mirror-polished substrate. The initial aluminum surface displayed hydrophilic characteristic with θ_a = 65° and θ_r = 10°, whereas, after the coating deposition, the angles were θ_a = 89° and θ_r = 64°. This surface can be classified as hydrophilic according to the classic definition based on the advancing contact angle being lower than 90° [6]. The strong difference between the treated surface and the untreated one is represented by the receding contact angle and the contact angle hysteresis, which results in a key surface parameter to promote DWC of pure steam. Condensation of steam (at 108 °C saturation temperature and 2.7 m s⁻¹ vapor velocity) occurred in dropwise mode with HTCs equal to 150–180 kW m⁻² K⁻¹ (augmentation by 8–10 times compared to FWC) in the heat flux range between 150 and 510 kW m⁻². Durability tests performed at constant heat flux equal to 120 kW m⁻² showed that the coating can sustain DWC for at least 13 h. Recently, Parin et al. [33] investigated three different mixtures of methyl triethoxy silane (MTES) or tetraethyl orthosilicate (TEOS) in combination with phenyl triethoxysilane (PhTES) as reagents for the realization of coatings that are able to promote DWC of saturated steam. The three different coatings displayed similar wettability (θ_a ≈ 90° and θ_r ≈ 60°) and coating thickness (between 200 and 420 nm). In particular, the mixture of PhTES and MTES (7/3 molar ratio) baked at 200 °C resulted in the most robust coating sustaining more than 100 h of continuous DWC (saturated steam at 100 °C with heat flux equal to 400 kW m⁻²) without sign of FWC transition, which is an interesting result obtained on aluminum samples so far. The optimization of the coating’s chemistry is important to increase the coating lifetime while maintaining high HTC. Parin et al. [34] used tetraethyl orthosilicate (TEOS) and methyl triethoxy silane (MTES) as silica precursors in order to study the ability of sol–gel MTES/TEOS hybrid coatings for DWC promotion. Six different MTES/TEOS coatings were considered and all of them promoted pure steam DWC, with a maximum HTC of 300 kW m⁻² K⁻¹ (105 °C saturation temperature, 2.6 m s⁻¹ vapor velocity, 400 kW m⁻² heat flux).

Two important further considerations must be done regarding the contact angle hysteresis and the thermal conductivity of the coating.

Del Col et al. [35] imparted hydrophobic properties over an aluminum substrate by forming onto the metal a low surface energy film (spin coating of a fluorosilane–hexane solution). The substrate was sanded using emery paper. Prior to coating deposition, the advancing contact angle was equal to 32° (hydrophilic) with a contact angle hysteresis of 25°. After coating deposition, the advancing contact angle increased up to 143° (hydrophobic) with 100° of hysteresis. The authors performed saturated steam (at nearly atmospheric pressure) condensation tests at heat flux between 250 and 500 kW m⁻² and vapor velocity between 2.2 and 6.4 m s⁻¹ with both hydrophilic and hydrophobic samples. They found that the condensation mode was purely filmwise, even on the hydrophobic surface, due to the complete flooding of the surface which in turn is caused by the high heat flux and the surface roughness. Although condensation always occurred in filmwise mode, the heat transfer coefficient was higher by 10–45% on the hydrophobic surface as compared to the hydrophilic sample (this increase is however limited compared with the 5–6 times heat transfer coefficient increase expected during DWC). The available literature on liquid flow over hydrophobic surfaces suggests an explanation of the results by assuming some slip of the condensate at the wall. Therefore, it emerges that the DWC is linked to the contact angle hysteresis rather than to the advancing contact angle and thus to the hydrophobic characteristics of the sample.

The use of organic substances as low-surface energy promoters requires strong, long-term adhesion forces between the coating and the metal substrate. Usually, the thicker is the coating, the better its resistance to corrosion/erosion. Each coating has a different thermal resistance depending on its chemistry and thickness, which strongly influences the overall heat transfer coefficient (HTC) as described by Parin et al. [12]. Therefore, from the heat transfer point of view, minimizing the thickness of the layer is essential. In fact, usually, the thermal conductivity of these organic layers (0.2 W m⁻¹ K⁻¹ [36]) is very low compared to the thermal conductivity of the metallic substrate (200 W m⁻¹ K⁻¹ for aluminum, 390 W m⁻¹ K⁻¹ for copper). A wide range of HTCs, up to tens of kW m⁻² K⁻¹ [22, 29, 37, 38], can be found in the literature for DWC of pure steam at atmospheric pressure: the high dispersion of HTC values is also related to the high variety of DWC promoters. Often, the thermal resistance of the hydrophobic layer can be the main resistance in the heat transfer process, greatly influencing the overall HTC during the condensation process. If the thermal conductivity and the thickness of the hydrophobic layer are known, the HTC of the DWC phenomenon itself can be calculated: an evaluation is reported in Rose [2].

On the other hand, in industrial and energy applications, the fundamental parameter is the overall HTC, accounting also for the thermal resistance of the layer. To the best of the authors’ knowledge, when comparing results in terms of overall HTC (thermal resistance between steam and metallic substrate), the highest values measured with pure steam are obtained on a copper substrate plated with gold [39] (about 250 kW m⁻² K⁻¹) or on aluminum samples coated with sol–gel coatings [34] (about 300 kW m⁻² K⁻¹).

3.1.2 Effects of Saturation Pressure, Heat Flux, and Non-condensable Gases

Several studies have been conducted in order to understand how saturation pressure, heat flux, and non-condensable gas concentration affect the DWC mechanism.

Regarding the effect of saturation pressure on the heat transfer coefficient, for a given saturation-to-wall temperature difference, the heat transfer coefficient increases when the saturation pressure is increased [2]. As reported in Rose [5], this is due to the reduction of the interfacial resistance at the liquid–vapor interface. Furthermore, by increasing the saturation pressure, the surface tension of the fluid decreases and this contributes to a reduction of the droplet adhesion force (see Eq. 3.48) and thus to a reduction of the droplet departing radius [6]. It must be considered that a reduction of the surface tension of the condensing fluid makes the DWC more difficult to be sustained from a given surface because the surface tension of the fluid gets closer to the surface energy of the substrate.

Regarding the effect of the heat flux on the DWC heat transfer coefficient, as reported in Le Fevre and Rose [17], several behaviors can be found in the literature: the heat transfer coefficient increases with the heat flux, decreases with the heat flux, or it is independent on the heat flux. The increase of the heat transfer coefficient with the heat flux can be explained with an increase in the number of active nucleation sites.

During DWC experiments, non-condensable gases can be often present inside the vapor chamber. This is because of two reasons: tests are run at saturation pressure below the atmospheric one and thus air enters the test rig; non-condensable gases can be dissolved into the water. A layer of non-condensable gases accumulates near the condensing surface, introducing a mass transfer resistance to the diffusion of molecules of the vapor phase that have to reach the surface to continue condensation. Due to the low heat transfer resistance expected during DWC, a small quantity of non-condensable gas can dramatically reduce the condensation performance. Therefore, particular care must be taken when performing DWC tests to assure that non-condensable gases are get rid of the apparatus. As reported in Citakoglu and Rose [18], the presence of non-condensable gases can be one of the reasons for discrepancy between data from different laboratories.

3.1.3 Vapor Velocity

The heat transfer during DWC depends on both the heat flux through a single drop and the droplet population density function. Since most of the heat exchanged is associated with small droplets [12], strategies for reducing the average drop size can be interesting for the improvement of the condensation HTC. In particular, the droplets' departing radius (r_max) should be decreased. The departing droplet radius r_max is the outcome of a force balance between forces that act for moving the droplet (for instance, gravity and drag forces), and the adhesion force, which sticks the droplet to the surface. In ground applications, the gravity force can be varied by changing the orientation of the condensing surface; adhesion force can be reduced decreasing the wettability of the substrate and the drag force can be increased by acting on the vapor velocity. Experimental data show that an increase of the steam mass flux causes a decrease of the droplet departing radius and, at the same time, an increment of the HTC.

Tanner et al. [16] investigated DWC on copper surfaces coated by wax: experimental tests showed an increase of the HTC from 260 to 400 kW m⁻² K⁻¹ (+50%) when the vapor velocity was increased from 3 to 23 m s⁻¹. Similar results were obtained by Tanasawa and Utaka [40] on hydrophobic copper: increasing the steam velocity from 10 to 100 m s⁻¹, the HTC increased by 2.5 times. Moreover, with the intensification of vapor flow, a decrease of the maximum droplet radius was measured and the HTC, once assessed its independency from the heat flux, was found to depend uniquely upon the departing radius. Investigating DWC on plane copper surfaces, Sharma et al. [41] found that an increase in the vapor velocity from 3 to 9 m s⁻¹ leads to 20% augmentation of the HTC. Torresin et al. [10] performed DWC experiments for investigating the influence of vapor velocity over nanostructured superhydrophobic copper samples. With an increment in the vapor velocity from 6 to 18 m s⁻¹, the departure droplet size was found to decrease and an increase of the HTC from 35 to 60 kW m⁻² K⁻¹ was measured (+90%). Recently, Tancon et al. [42] measured DWC heat transfer coefficients on aluminum sol–gel coated samples at 107 °C saturation temperature, heat flux of 335 kW m⁻² and average vapor velocity between 2.7 and 11 m s⁻¹. The sol–gel coated aluminum sample displays advancing contact angle θ_a = 87.5° and receding contact angle θ_r = 63.5°. In the investigated range of vapor velocity, the authors found that the HTC increases by around 20%, from 104 to 120 kW m⁻² K⁻¹, with a reduction of the droplet departing radius from 1.44 to 0.89 mm. From high-speed visualization, it emerges as the shape of the droplets is clearly affected by the vapor velocity.

3.1.4 Superhydrophobic Surfaces

Superhydrophobic surfaces have recently been identified as a promising solution to several challenges [43], such as drag reduction, anti-icing [44], and enhancement of two-phase heat transfer performance. A drop placed over a surface may assume different states described by the equations of Wenzel [45] and Cassie-Baxter [46]. Excellent droplet mobility is obtained on superhydrophobic surfaces if the Cassie–Baxter state is reached. Superhydrophobic surfaces present high advancing contact angles, greater than 150°, and low contact angle hysteresis, lower than 10°. Superhydrophobic surfaces can be basically produced by combining two factors: micro-/nanoscale surface roughness and low surface free energy. Proper surface roughness can be obtained through different techniques, as micromachining, chemical etching (e.g., using HCl or NaOH), and deep radiative ion etching. Low surface energy can be obtained by coating the substrate with a thin layer of a material with small surface energy, such as organic substances, polymers, and noble metals (Sect. 3.1.1). These two elements allow water drops to sit over the surface with a quasi-spherical shape and to easily roll off from it (lotus effect). Therefore, superhydrophobic surfaces seem to represent a strategy to promote a more efficient DWC.

In presence of non-condensable gases or with pure saturated vapor at low thermal heat flux, the Cassie-Baxter regime can be obtained [47, 48]. At higher heat flux, with pure vapor, the Wenzel state [49] or even the flooding of the surface may occur. In the Wenzel state, the mobility of the droplets is limited since they are retained within the roughness. Thus, the surfaces with the highest droplet mobility in atmospheric conditions may not guarantee the highest performance during the condensation of steam. In fact, several authors measured higher heat transfer coefficients (HTCs) on smooth hydrophobic surfaces than on structured superhydrophobic surfaces.

Zhong et al. [50] reported heat transfer measurements on a superhydrophobic nanostructured copper sample and compared them to those obtained on a mirror-polished hydrophobic specimen. They found that the nanostructured substrate does not improve the condensation heat transfer performance as expected from the higher contact angle, but better results were achieved with the hydrophobic substrate. Flow condensation tests of saturated vapor on superhydrophobic nanotextured copper surfaces presented by Torresin et al. [10] show that condensing drops form and penetrate into the surface texture, with a reduction of their mobility. Parin et al. [28] fabricated four superhydrophobic aluminum surfaces. The metal substrates were etched using three different strategies to impart nanoscale roughness and, as a second step, a fluorosilane film was deposited over them (by spin coating or immersion) to decrease the surface energy. Experimental tests of pure steam condensation showed that DWC was successfully achieved on the superhydrophobic surfaces, measuring heat transfer coefficients as high as 100 kW m⁻² K⁻¹ (at 105 °C saturation temperature and heat flux around 350 kW m⁻²). It is interesting to note that such heat transfer coefficients are lower than the ones measured by Parin et al. [12] on a mirror-polished aluminum surface displaying mildly hydrophobic characteristic (with θ_a = 89° and θ_r = 64°).

In conclusion, as also reported in Miljkovic et al. [51], if the condensation heat flux is relatively low (they referred to a threshold value of 80 kW m⁻²), a proper designed superhydrophobic surface can exceed or match the heat transfer performance of a smooth dropwise condensing surface having low contact angle hysteresis. Instead, at high heat flux values, a smooth surface (e.g., mirror polished) with low contact angle hysteresis will display better performance.

3.1.5 Low Surface Tension Fluids

In most of the DWC studies, steam is used as the working fluid. The reason is due to the fact that water is a common fluid in many industrial processes and it presents a high value of the surface tension. When considering fluids with relatively low surface tension, the promotion of DWC becomes more challenging because, in this case, the surface tension of the fluid can be comparable with the surface energy of the coating. On the other hand, low surface tension fluids can be found in a variety of industrial applications. For example, HFC (hydrofluorocarbons), HFO (hydrofluoroolefins), and HC (hydrocarbons) are low surface tension fluids largely employed in refrigeration and heat pumps. At 40 °C saturation temperature, the surface tension of HFC-134a is equal to 6.1 mN m⁻¹ whereas in the case of water it is equal to 69.6 mN m⁻¹. Furthermore, these low surface tension fluids usually realize in heat exchangers lower heat transfer coefficients compared to water (this is mainly due to their lower thermal conductivity) and thus the possibility to achieve DWC condensation would have important benefits on the efficiency of heat exchangers and systems.

Micro/nanostructured lubricant-infused surfaces (LISs) are studied as a solution to get ultralow contact angle hysteresis and excellent droplet shedding. On a LIS, a lubricant having a low surface energy and vapor pressure is stabilized by capillary forces within a porous or micro/nanostructured surface creating an atomically smooth surface. LIS surfaces present high droplet mobility and thus they are studied as candidates for DWC promotion with low surface tension fluids. However, a LIS surface must satisfy the following two criteria: the lubricant and condensate must be immiscible; the lubricant must be selected to avoid the encapsulation of condensate droplets with the formation of a cloak around them that inhibits droplets growth and shedding. Sett et al. [52] obtained stable DWC of ethanol and hexane on a nanostructured copper oxide (CuO) LIS impregnated with lubricants. For ethanol, the advancing contact angle (θ_a) on the three LISs was 62.4° < θ_a < 71.1° with a maximum contact angle hysteresis, Δθ = θ_a – θ_r ≈ 2.7°. For ethanol on the smooth cooper substrate, the advancing contact angle is equal to 36.5° with contact angle hysteresis of 13.1°. DWC heat transfer coefficient measurements in pure vapor conditions show an increase by 200% when compared to filmwise condensation on smooth copper substrates [52].

Recently, Khalil et al. [53] promoted DWC of low surface tension fluids (ethanol, hexane, and pentane) over titanium and silicon substrates. They used covalently bonded nanometric iCVD films on tubular cylindrical geometries. These iCVD-coated heat exchanger metals are shown to achieve a fourfold to eightfold improvement in vapor-side condenser heat transfer coefficient compared to uncoated surfaces.

Apart from the aforementioned pioneering studies with hydrocarbons, the promotion of DWC with low surface tension fluids is still to be demonstrated.

3.2 Measuring Heat Transfer Coefficients During DWC

Dropwise condensation heat transfer coefficients are usually measured on relatively small heat transfer areas (compared to the heat transfer areas used in industrial heat exchangers) because the objective is often the characterization of the condensation performance of innovative coated samples. The focus is on the heat transfer coefficient measurement and on the visualization of the droplet population. For this reason, almost all the experimental techniques foresee the presence of a glass window that allows the visualization of the condensation process. Analyzing the literature, two main configurations for the condensing surface can be found: in the first case, a vertically oriented surface is maintained below the dew temperature of the fluid, the vapor condenses over it and the liquid is drained by gravity toward the bottom of the vertical surface; in the second case, a horizontal tube is used to promote condensation on its external surface by using a cooling fluid that flows inside the tube. In most of the studies, the condensing surface is placed inside a vapor chamber and the velocity of the vapor is negligible (quiescent vapor). The saturated vapor is supplied to the vapor chamber by an external evaporator [6] or it is produced in the lower part of the chamber [17]. Less frequently the test apparatus can allow the investigation of the effect of vapor velocity on the dropwise condensation. As an example, the experimental technique employed by Bisetto et al. [54] will be explained in detail in Sect. 3.2.2.

3.2.1 Main Measuring Techniques

The quantities that must be measured for the determination of the heat transfer coefficient will be discussed hereafter.

The heat transfer coefficient for a pure fluid is defined as the ratio of heat flux q to saturation-minus-wall temperature difference (T_sat − T_wall):

$$\alpha = \frac{q}{{\left( {T_{sat} - T_{wall} } \right)}} = \frac{Q}{{A\left( {T_{sat} - T_{wall} } \right)}}$$

(3.1)

In Eq. 3.1, the heat flux q is the ratio of condensation heat flow rate Q to the condensing surface area A of the sample. This relationship is valid locally or as an average value if the wall temperature can be assumed to be uniform all over the condensing surface.

For pure vapor, the saturation temperature T_sat can be obtained with two methods: with a direct measurement of the vapor temperature inserting a temperature sensor (e.g., thermocouple, thermistor) inside the vapor chamber or indirectly from the measurement of the saturation pressure. It must be considered that the presence of some liquid in vapor pressure ports should be avoided since it can introduce pressure measurements errors due to hydrostatic head or to capillary effects related to the presence of meniscus in the tubes. One solution consists of heating pressure ports over the saturation temperature to avoid vapor condensation inside the lines. Using both direct and indirect approaches has the advantage to allow a double-check of the saturation temperature.

A direct contact measurement of the surface temperature T_wall of a coated sample (e.g., by soldering thermocouples over it) is not feasible since this would locally modify the surface properties, affecting the condensation process itself. Therefore, the measurement of the wall temperature in Eq. 3.1 is more difficult and it requires the installation of one or more temperature sensors as near as possible to the surface where condensation takes place. Since high values of heat flux are expected during DWC, the measured temperature T_meas must be corrected to account for the temperature variation due to thermal conduction inside the sample. Furthermore, considering that often DWC is promoted by applying a proper coating over the surface (Sect. 3.1.1), the thickness and the thermal conductivity of the layer must also be measured for the determination of the actual surface temperature T_wall. If this contribution is not included, the measured heat transfer coefficient will consider both the DWC thermal resistance and the resistance due to thermal conduction of the coating (overall heat transfer coefficient). The thickness of modern coatings can be in the order of few nanometers making challenging the measurement of the thermal resistance. For this reason, in the literature, the heat transfer coefficient is often defined using as temperature driving difference the difference between the saturation temperature T_sat and the temperature of the substrate material T_sub just below the coating (and thus including the resistance due to thermal conduction inside the coating). Test sections are usually designed to obtain a one-dimensional temperature field with a uniform heat flux inside the specimen. In this way, the temperature T_sub can be obtained from a linear extrapolation of an array of temperature measurements inside the specimen [10] or from a unique value of temperature T_meas (measured at a distance z below the coating) plus the temperature variation due to thermal conduction in the specimen at the distance z:

$$T_{sub} = T_{meas} + \frac{q}{{\lambda_{sub} }}z$$

(3.2)

In Eq. 3.2, λ_sub is the thermal conductivity of the substrate material. It must be pointed out that the size of the temperature sensor must be minimized to avoid disturbance in the temperature field and to get , an as much as possible, punctual value of the temperature. The available space for the installation of temperature probes in many cases is limited. In fact, an augmentation of the thickness of the sample has an adverse effect on the overall heat transfer resistance. In analogy with an electrical circuit, considering as potentials the saturation temperature and the temperature of the cooling medium (usually water), there are three main thermal resistances that hinder the heat transfer: the resistance of the DWC process (this, in turn, is made up of several contributions as it will be illustrated in Sect. 3.4), the thermal resistance due to conduction in the sample and the thermal resistance due to forced convection of the cooling fluid. Considering the maximum available temperature difference between saturation and coolant temperature, thickening the sample will result in decreasing the maximum exchangeable heat flux and thus reducing the range of investigable conditions. This is true in particular when using steel or aluminum samples that present a lower thermal conductivity compared to copper. A low value of the thermal resistance on the coolant side is another desirable characteristic. Usually, the cooling fluid is water in forced convection. To reduce the thermal resistance on the secondary fluid side, enhanced/finned surfaces can be used. For example, Torresin et al. [10] realized a cooling system consisting of a copper plate with 39 fins: the ratio between the enhanced cooling surface and the condensation area of the tested samples was around 25. Water flowed in the space between the fins and a staggered arrangement was used for pins in order to continuously alter the water path and break the boundary layer.

To avoid the need for wall temperature measurement (which is more difficult in the case of condensation on a horizontal tube), the Wilson plot method can be used [6]. With this technique, the condensation heat transfer coefficient is obtained starting from the direct measurement of the overall heat transfer coefficient (between the condensing vapor and the coolant) and from the estimation of the coolant side heat transfer coefficient. More details about the application of the Wilson plot method can be found in Del Col et al. [55]. However, since during DWC the main thermal resistance is usually on the coolant side, the Wilson plot method can lead to high experimental uncertainty.

Considering Eqs. 3.1 and 3.2, it is clear that the third quantity needed for the evaluation of the heat transfer coefficient is the heat flux q that can be obtained from the heat flow rate Q. Three main techniques for the measurement of the heat flow rate during condensation can be found in the literature and they can be used together with redundancy. In the first case [54], the heat flow rate is measured from the mass flow rate of the coolant ṁ_cool and the temperature difference ΔT_cool between coolant inlet and outlet:

$$Q = \dot{m}_{cool} c_{cool} \Delta T_{cool}$$

(3.3)

In Eq. 3.3, c_cool is the specific heat of the cooling medium.

The second method is based on Fourier’s law, with the evaluation of heat flow rate from the temperature profile T(z) inside the sample [10]:

$$Q = \lambda_{sub} A\frac{{{\rm{d}}T}}{{{\rm{d}}z}}$$

(3.4)

where z is the axial coordinate normal to the condensing surface.

When evaluating the heat flow rate Q through Fourier’s law, cylindrical metallic blocks (properly insulated to ensure one-dimensional heat conduction) are typically used and condensation takes place over one of the cylinder bases. These blocks are fitted with thermocouples located at different z positions from the condensing surface. The linear interpolating equation T(z) can be determined by the weighted least squares (WLS) regression method [55]. Uncertainties on fitting parameters can arise from both temperature and position uncertainty. The Monte Carlo method can be used for combining the spatial and temperature uncertainties of multiple measurement points in order to obtain the uncertainty of the temperature gradient and thus the uncertainty on the heat flow rate by applying the law of propagation of uncertainty [56]. With this method, to reduce the uncertainty on the heat flux, several thermocouples can be installed in the sample. The drawback is that, increasing the number of wall thermocouples, the height of the block must be increased to allow thermocouples accommodation and, as a consequence, a larger temperature difference between the condensing surface and the coolant side of the cylindrical sample is needed to exchange the same heat flux. Therefore, this method is easier to be implemented with substrate materials having a high thermal conductivity (e.g., copper) but, for materials displaying low thermal conductivity (e.g., stainless steel), it can request temperature of the cooling fluid below 0 °C, excluding the use of pure water as secondary fluid.

The third method for the measurement of the condensation heat flow rate is based on the measurement, at fixed time steps, of the condensate mass by a precision scale. The heat flow rate can be evaluated as:

$$Q = \dot{m}_{cond} h_{lv}$$

(3.5)

where h_lv is the latent heat of condensation at a given saturation temperature. If the test rig is operating in steady-state conditions, the mass flow of the condensate rate $\dot{m}_{cond}$ can be obtained from a linear interpolation of the measured values of condensate mass plotted versus time. When using this method, particular care must be paid to the fact that all and only the condensate coming from the sample must be collected on the scale. Other liquid that forms at the wall of the vapor chamber must be appropriately separated.

As a last point, it must be remembered that the heat flow rate can affect also the measurement of the surface temperature since the measured temperature must be corrected to account for thermal conduction in the substrate (Eq. 3.2).

3.2.2 Measurements in Presence of Vapor Velocity

In this Section, the experimental technique proposed by Bisetto et al. [54] for the measurement of the DWC heat transfer coefficient during saturated steam condensation over a vertical surface will be illustrated in detail. The reader will find a practical application of some of the concepts previously mentioned.

The technique presents the following main characteristics: possibility to investigate the effect of vapor velocity; reduced thickness of the sample allowing the use of metals with low thermal conductivity (e.g., steel); redundant measurement of the heat flux from Fourier’s law (Eq. 3.4) and from the heat balance at the coolant side (Eq. 3.3); possibility to measure local values of heat flux and the wall temperature along the condensing surface and thus to account for heat transfer coefficient variations along the sample; visualization of the DWC process.

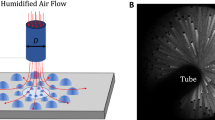
The setup consists of a two-phase flow loop operating as a thermosyphon and made up of four main components: a boiling chamber, a test section, a cooling water loop, and a post-condenser. A sketch of the loop is shown in Fig. 3.1a.

Fig. 3.1

Test apparatus: a schematic of the experimental thermosyphon loop for condensation tests; b side view of the test section; c 3D model of the aluminum sample

Steam is generated in a cylindrical stainless steel boiling chamber by means of four electrical heaters having a maximum power of 4 kW. The electrical power supplied to the heaters is measured using a power analyzer. The pipe connections between the boiler and the test section are insulated and heated by means of an electric resistance installed around the pipe to avoid condensation before the entrance of the test section (the wall temperature is checked through a T-type thermocouple and maintained just above the saturation temperature). The steam enters the test section in saturated conditions. In the test section, the steam is partially condensed over a metallic sample and the latent heat is removed by cold water coming from a thermostatic bath. The coolant inlet temperature is measured by a T-type thermocouple, while the coolant temperature difference between inlet and outlet is measured by means of a three-junction copper-constantan thermopile. The coolant mass flow rate is measured by a Coriolis-effect mass flow meter. The pressure and temperature of the vapor are measured at the inlet of the test section. Downstream the test section, the two-phase mixture passes through a secondary water condenser where the condensation is completed and the liquid subcooled. The subcooled liquid returns to the boiler driven by the density difference between liquid and vapor and it closes the loop. Since the test apparatus does not have a circulating pump, to guarantee the liquid return to the boiler, a liquid head is necessary and the post-condenser is placed at a higher level with respect to the boiling chamber. The water temperature is measured at the inlet and the outlet of the post-condenser by means of T-type thermocouples, while the water mass flow rate is measured using a magnetic flow meter. The system volume is controlled by means of a hydraulic accumulator installed in the liquid line downstream the post-condenser. A precision needle valve, placed before the boiling chamber, is used to regulate the liquid flow. Before entering the boiling chamber, the temperature of the subcooled liquid is measured by means of a T-type thermocouple. Since even a small concentration of non-condensable gases (NCG) in the vapor could lead to a decrease of the condensation heat transfer coefficient, several actions must be undertaken to avoid the presence of NCG. First of all, the test apparatus works at a pressure higher than the atmospheric one. Furthermore, before each test run, the whole system is vacuumed; then the test rig is charged with deionized (DI) water. When boiling is started, some vapor is released from the top of the loop as well as from a vent valve located in the upper part of the post-condenser in order to get rid of the gases dissolved in the water.

The test section (Fig. 3.1b) allows the measurement of the DWC heat transfer coefficient and the visualization of the droplets. Steam condenses on a vertical rectangular surface (50 mm × 20 mm). The test section consists of two rectangular cross-sectional channels inside which the condensing vapor and the water coolant flow. The vapor channel is 160 mm long (cross-section 30 mm × 5 mm) and it was machined from a PEEK block. One side of the channel is covered by a double glass to allow the visualization of the process whereas the other side of the channel, opposite to the glass, is machined for accommodating the metallic substrate over which vapor condenses. The metallic specimen has 10 mm thickness and it is equipped with an array of six T-type thermocouples placed inside holes obtained by electrical discharge machining. Thermocouples are placed inside the substrate at two different depths z₁ and z₂ from the treated surface (Fig. 3.1c). The thermocouples are used to obtain the local surface temperature at three longitudinal locations along the specimen (in the middle and 2 mm from the up and bottom edge on the sample). The sample is located in between the two channels of the test section: the steam channel is in contact with the frontal face of the specimen beside the water channel is in contact with the back face of the specimen. The length of the coolant channel was determined in order to have a hydrodynamically fully developed flow of the water on the back side of the metallic specimen. In this way, there are no entrance effects and the water heat transfer coefficient can be considered uniform along the whole sample length. The cooling water flows in countercurrent with respect to the steam direction inside the test section.

The heat flux q through the sample can be measured by two different techniques. An average value of the heat flux q_mean over the surface can be measured from the coolant side (Eq. 3.3), beside a local value of the heat flux q_loc can be evaluated by applying the Fourier's law to the thermocouples placed in correspondence of the three different longitudinal positions shown in Fig. 3.1b, c (Eq. 3.4).

In Eq. 3.4, dT/dz can be replaced with ΔT/Δz where ΔT is the temperature difference between the two thermocouples at the same axial position along the steam direction and Δz is the distance between the two thermocouples. The Fourier law can be applied assuming one-dimensional heat flux.

The steam saturation temperature T_sat is obtained from the measurement of the saturation pressure in the test section. The specific enthalpy of the subcooled liquid at the inlet of the boiling chamber h_IN,bc is evaluated from the measurements of temperature and pressure. The steam velocity v_v is obtained from

$$v_{v} = \frac{{Q_{bc} }}{{\left( {h_{v} - h_{IN,bc} } \right)}}\frac{1}{{\rho_{v} A_{c} }}$$

(3.6)

where Q_bc is the heat flow rate provided to the boiling chamber (measured using an electrical power meter), h_v is the specific enthalpy of the saturated steam exiting from the boiling chamber, ρ_v is the vapor density, and A_c is the cross-sectional area. By acting on the power supplied to the boiling chamber, it is possible to regulate the mass flow rate of the fluid circulating in the system, thus to perform tests at varying vapor mass velocities.

3.3 Droplet Population

As reported in Sect. 3.1, dropwise condensation is a cyclic process [3]. Condensation begins at the molecular scale with the formation of droplets in favored nucleation sites. The radius of the smallest viable (thermodynamically) drop is called minimum drop radius r_min. Drops grow by direct condensation at first and later by coalescence until they reach the departing radius r_max at which body forces overcome adhesion force and they start to move. Once the moving drops clean their path, nucleation of new droplets ensures that the condensation process is cyclic with characteristic timescale, coverage area, and drop size distribution.

3.3.1 Models for Drop Size Distribution

Drop population models are based on the observation that the drop size distribution on a condensing surface is in steady state from the statistical point of view [3]. Le Fevre and Rose [57] introduced for the first time a relationship for the prediction of the droplet population, while Wu and Maa [58], starting from the work by Tanaka [59], proposed the population balance model. Droplets are categorized into small drops and large drops according to the growth mechanism. Small drops grow primarily due to direct condensation of vapor on the drop surface, whereas large drops grow mainly by coalescence with other drops. The distribution of the big and small droplets will be indicated, respectively, with the symbols N(r) and n(r). The radius which separates the two population is called effective radius r_e and its determination is still an open issue due to technological limitations in the visualization techniques. As it will be discussed later, r_e depends on the nucleation sites density distribution, square array or random Poisson distribution (see Sect. 3.4). By integrating the droplet size density function between two radii r₁ and r₂ it is possible to calculate the number of droplets per unit area having radii in between r₁ and r₂.

The drop size distribution of large drops N(r) is obtained using the empirical expression proposed by Le Fevre and Rose [57] and it is given by

$$N\left( r \right) = \frac{1}{{3\pi r^{2} r_{\max } }}\left( {\frac{r}{{r_{\max } }}} \right)^{{ - \frac{2}{3}}}$$

(3.7)

From Eq. 3.7, it can be observed that the large droplet population only depends on the maximum droplet radius r_max, which is the outcome of the forces acting on a droplet (see Sects. 3.4 and 3.5).

In order to model the drop size distribution of small drops, the population balance method can be employed. This method assumes that the contact angle of a drop remains the same from the nucleation to the departure from the surface. The drop size distribution of small drops n(r) is evaluated assuming the conservation of the number of drops in a certain size range r₁ – r₂. In other words, the number of droplets entering a size range must be equal to the number of drops leaving the same size range. The drop growth rate G is defined as

$$G = \frac{{{\rm{d}}r}}{{{\rm{d}}t}}$$

(3.8)

Considering a surface area A and an infinitesimal time increment dt, in order to conserve the droplet population in the radius range r₁ − r₂, the number of droplets entering this radius range (An₁G₁dt) must be equal to the number of droplets leaving by growth this radius range (An₂G₂dt) plus the number of droplets swept off $(Sn_{1\, - \,2} \Delta r{\text{d}}t)$:

$$An_{1} G_{1} {\text{d}}t = An_{2} G_{2} {\text{d}}t + Sn_{1\, - \,2} \Delta r{\text{d}}t$$

(3.9)

where n is the number of drops per unit area per unit drop radius, S is the sweeping rate at which the surface is renewed by falling drops, n_1 − 2 is the average drop size density in the range r₁ − r₂ and ∆r is equal to r₂ − r₁.

As Δr approaches to zero, n_1 − 2 tends to n and Eq. 3.9 can be written as

$$\frac{{\rm{d}}}{{{\rm{d}}r}}\left( {Gn} \right) + \frac{n}{\tau } = 0$$

(3.10)

where τ = A/S is the sweeping period. Assuming that all the heat transfer occurs through the drops, the heat transfer rate through a single drop (Q_dr) can be equated to the condensation rate of vapor at the drop surface ($\rho_{l} h_{lv} {\text{d}}V/{\text{d}}t$) to obtain the drop growth rate G as

$$Q_{dr} = \rho_{l} h_{lv} \frac{{{\rm{d}}V}}{{{\rm{d}}t}} = \rho_{l} h_{lv} \pi r^{2} \left( {1 - \cos \theta } \right)^{2} \left( {2 + \cos \theta } \right)G$$

(3.11)

$$G = \frac{{Q_{dr} }}{{\rho_{l} h_{lv} \pi r^{2} \left( {1 - \cos \theta } \right)^{2} \left( {2 + \cos \theta } \right)}}$$

(3.12)

where V is the droplet volume, ρ_l the liquid density, h_lv the the vapor–liquid latent heat, and θ the droplet growing contact angle.

Then, the expression of G (Eq. 3.12) can be substituted into Eq. 3.10 and integrated to obtain the drop size density function of small droplets n(r):

$$n\left( r \right) = N\left( {r_{e} } \right)\frac{{r\left( {r_{e} - r_{\min } } \right)\left( {A_{2} r + A_{3} } \right)}}{{r_{e} \left( {r - r_{\min } } \right)\left( {A_{2} r_{e} + A_{3} } \right)}}e^{{B_{1} + B_{2} }}$$

(3.13)

As a first boundary condition, the population of small droplets is imposed to equal the population of large droplets at the effective radius ${{(} {\it \rm {n}} {(}r}_{{\rm{e}}} {{) = } {\it \rm {N}}{(r}}_{{\rm{e}}} {))}$, providing the following expressions for B₁ and B₂:

$$B_{1} = \frac{{A_{2} }}{{A_{1} \tau }}\left[ {\frac{{r_{e}^{2} - r^{2} }}{2} + r_{\min } \left( {r_{e} - r} \right) - r_{\min }^{2} \ln \left( {\frac{{r - r_{\min } }}{{r_{e} - r_{\min } }}} \right)} \right]$$

(3.14)

$$B_{2} = \frac{{A_{3} }}{{A_{1} \tau }}\left[ {\left( {r_{e} - r} \right) - r_{\min } \ln \left( {\frac{{r - r_{\min } }}{{r_{e} - r_{\min } }}} \right)} \right]$$

(3.15)

Imposing ${\rm{d}}\left( {\rm{ln }{\it \text n}{{(}r)}} \right)/{\rm{d}}\left( {{\rm{ln}\it \rm{ r}}} \right) = {\rm{d}}\left( {\rm{ln }{\it \rm N}{{(}r)}} \right)/{\rm{d}}\left( {{\rm{ln}\it \rm{ r}}} \right){ } = - {8}/{3}$ at r = r_e as a second boundary condition, the sweeping period τ is

$$\tau = \frac{{3r_{e}^{2} \left( {A_{2} r + A_{3} } \right)^{2} }}{{A_{1} \left[ {8A_{3} r_{e} - 14A_{2} r_{e} r_{\min } + 11A_{2} r_{e}^{2} - 11A_{3} r_{\min } } \right]}}$$

(3.16)

The three coefficients A₁, A₂, and A₃ in Eqs. 3.13–3.16 are obtained analytically from the heat flow exchanged by a single droplet and, being the formulation of Q_dr different for each heat transfer model, the analytical expressions for A₁, A₂, and A₃ are reported in detail in Sect. 3.4.

3.3.2 Measurement of Drop Size Distribution

In Fig. 3.2a, the theoretical drop size density function for a flat vertical hydrophobic surface is reported at varying droplet radius. The dotted curve on the left side of the graph (r < r_e) represents the small droplet population n(r), which is calculated by Eq. 3.13–3.16 using the formulation for A₁, A_2, and A₃ provided by Miljkovic et al. [60] (see Sect. 3.4.3). Instead, the continuous curve on the right side of the graph represents the formulation proposed by Le Fevre and Rose [57] (Eq. 3.7) for the drop size density of large drops population N(r). Figure 3.2a shows that DWC involves the simultaneous presence of droplets with variable radius by 6 orders of magnitude, ranging from nanometres (r_min) to millimetres (r_max). The drop size density function decreases with an increase in drop radius: for a given surface area, there is a huge number of small droplets and a relatively small number of large droplets.

Fig. 3.2

a Drop size density function compared with experimental data by Parin et al. [33]. The large droplet population N(r) is obtained by the Le Fevre and Rose [57] equation (Eq. 3.7), whereas the small droplet population n(r) is calculated by Eq. 3.13, using the expressions for A₁, A_2, and A₃ provided by Miljkovic et al. [60] (see Sect. 3.4.3). b Enlarge image of DWC taken by a high-speed camera. c Resulting black and white image after processing and reconstruction of the observed droplet population

In addition, Fig. 3.2a presents a comparison between theory and experimental visualizations performed by Parin et al. [33] focusing on the large droplet population N(r). In their work, Parin et al. [33] mapped the droplet population detecting more than 3 million droplets with radii in the range of 15 μm–1 mm. The measured droplet size distribution resulted to be not affected by the heat flux. The experimental technique consists of a high-speed camera coupled with a torus-shaped illumination system for DWC visualizations and a homemade MATLAB^® program for image processing. The torus-shaped light projects its pattern onto each droplet and the external diameter of the torus is proportional to the drop’s diameter itself. To detect droplets and to determine their dimensions, the recorded image is then processed by a MATLAB^® program, considering the relationship between the external radius of the reflected toroidal light path and the effective drop radius. An example of an image taken by the high-speed camera during DWC and the resulting black and white image after processing and reconstruction by the program are shown, respectively, in Fig. 3.2b, c. As it can be seen from Fig. 3.2a, a satisfactory agreement between the equation proposed by Le Fevre and Rose [57] and the experimental data taken by Parin et al. [33] during DWC of steam was obtained down to tens of microns; the mean deviation between measurements and predicted values is below 20%.

3.4 Heat Transfer Models for DWC with Quiescent Vapor

Different models in the literature are aimed at describing the complex phenomena that take place during DWC: the nucleation of a droplet until its departure, the heat exchanged by the drop during its lifetime, and the droplet population on the surface.

Because of the unsteady behavior of DWC, researchers have usually adopted a statistical approach to model the dropwise condensation heat transfer [2, 36, 60]. This method is based on the experimental observation that the overall drop size distribution is constant with time even though the individual drop growth is an unsteady phenomenon. In the literature, several heat transfer models have been proposed for dropwise condensation on flat or structured surfaces and, among them, four different studies have been selected in the present work: Le Fevre and Rose [57], Kim and Kim [36], Miljkovic et al. [60], and Chavan et al. [32]. The models are presented in the Sects. 3.4.1–3.4.4 in chronological order. The models were developed with the same common assumptions:

• the vapor temperature is uniform and equal to the saturation temperature;

• the vapor is in quiescent conditions (negligible vapor velocity);

• the substrate is assumed as a semi-infinite body at uniform temperature;

• the presence of non-condensable gases is neglected.

In the statistical approach, the heat transfer through a single drop of a given radius r is multiplied by the respective drop size density function (n(r) or N(r)) and the product is then integrated between r_min and r_max to obtain the overall condensation heat flux q transferred during steady-state DWC:

$$q = \mathop \smallint \limits_{{r_{\min } }}^{{r_{e} }} Q_{dr} \left( r \right)n\left( r \right)dr + \mathop \smallint \limits_{{r_{e} }}^{{r_{\max } }} Q_{dr} \left( r \right)N\left( r \right)dr$$

(3.17)

As already reported in Sect. 3.3, n(r) and N(r) are, respectively, the small droplet population (r_min ≤ r ≤ r_e) and the population of large droplets (r_e ≤ r ≤ r_max); r_e is the effective radius and it denotes the drop radius at the boundary between small and large drops, whereas Q_dr is the heat transfer through a drop of radius r.

The lower limit of the first integral (r_min) is the minimum radius of a stable droplet, which can be calculated as [61]:

$$r_{\min} = \frac{{2\sigma T_{sat} v_{l} }}{{h_{lv} \Delta T}}$$

(3.18)

where ∆T is the degree of subcooling (that is the temperature difference between the saturated steam and the surface), σ is the liquid-vapor surface tension, ν_l is the specific volume of liquid, T_sat is the saturation temperature, and h_lv is the vapor–liquid latent heat. Equation 3.18 is used in all the selected models. In the second integral, r_max is the departing radius which is the maximum dimension assumed by drops before sliding on the condensation surface. In quiescent vapor, r_max is obtained by applying a balance between adhesion force (which retains the drop) and gravity force (which works for moving the drop) [36, 42, 62]. In the detailed discussion of the models (Sects. 3.4.1–3.4.4), the specific formulations developed for the evaluation of the departing radius and the effective radius will be presented.

The heat transfer coefficient (HTC) is obtained by dividing the condensation heat flux by the saturation-to-wall temperature difference (degree of subcooling):

$${\rm{HTC}} = \frac{q}{\Delta T}$$

(3.19)

To estimate the heat transfer through a single drop Q_dr, a network of thermal resistances is employed. The different assumptions done by the authors of the models can provide different results in terms of overall heat flux q (Eq. 3.17). As already reported in Sect. 3.3.1, the formulation of Q_dr modifies the growth rate G (Eq. 3.12) and thus the expression of the small droplet population (Eq. 3.13).

3.4.1 Le Fevre and Rose (1966) Model

In the model by Le Fevre and Rose [57], the temperature drop due to the droplet curvature is considered and the following thermal resistances are accounted for: the liquid–vapor interfacial resistance, the conduction resistance through the drop, and the resistance of the coating. Their model assumed that within the drop, convection is negligible and conduction is the dominant heat transfer mechanism. However, in the model, all the drops are considered hemispherical with a contact angle of 90°.

The heat flow rate through a single drop is calculated as

$$Q_{dr} \left( r \right) = \frac{{{\Delta }T - \frac{{2\sigma T_{sat} }}{{r\rho_{l} h_{lv} }}}}{{K_{1} \frac{r}{{\lambda_{l} }} + K_{2} \left( {\frac{0.627}{{0.664}}} \right)\frac{{T_{SAT} }}{{h_{lv}^{2} \rho_{v} }}\frac{\gamma + 1}{{\gamma - 1}}\left[ {\frac{{RT_{sat} }}{2\pi }} \right]^{0.5} }}$$

(3.20)

where K₁ and K₂ are constants equal to 2/3 and 1/2, respectively, λ_l is the liquid conductivity, ρ_l is the liquid density, γ is the ratio of the specific heat capacities and R is the specific ideal-gas constant. At the denominator, the first term is the conduction resistance and the second term accounts for the liquid–vapor interfacial resistance plus the conduction resistance through the coating (included in K₂).

In this model, the heat transfer through a single drop Q_dr (Eq. 3.20) is combined with the drop size distribution of large droplets N(r) (Eq. 3.7) to obtain the average heat flux as

$$q = \mathop \smallint \limits_{{r_{\min } }}^{{r_{\max } }} Q_{dr} \left( r \right)N\left( r \right)dr$$

(3.21)

where r_min is the minimum droplet radius (Eq. 3.18) and r_max is the maximum droplet radius evaluated as

$$r_{\max } = K_{3} \left[ {\frac{\sigma }{{\rho_{l} g}}} \right]^{0.5}$$

(3.22)

where K₃ is a constant equal to 0.4 that was determined experimentally.

3.4.2 Kim and Kim (2011) Model

The model by Kim and Kim [36] computes the heat transfer through a single drop incorporating the various thermal resistances from the vapor to the surface and considers both the populations of small and large droplets. Kim and Kim [36] improved the model by Le Fevre and Rose [57] accounting for the effect of the contact angle on the heat transfer performance. In particular, they modeled the conduction resistance through droplets exhibiting larger growing contact angles (θ > 90°). Although superhydrophobic surfaces are considered, the surface morphology is neglected. In this model, the thickness of the coating layer and the number of nucleation sites are also accounted for.

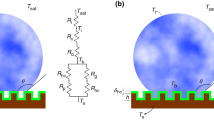
In terms of temperature drop, the total temperature difference between the vapor and the surface is expressed as

$${\Delta }T = {\Delta }T_{i} + {\Delta }T_{c} + {\Delta }T_{d} + {\Delta }T_{HC}$$

(3.23)

where ΔT_i, ΔT_c, ΔT_d, and ΔT_HC are respectively the temperature drops due to the liquid–vapor interface, the droplet curvature, the thermal conduction through the droplet and the coating layer (Fig. 3.3). In particular, the temperature drop due to the interfacial resistance is given by

$${\Delta }T_{i} = \frac{{Q_{dr} }}{{h_{i} 2\pi r^{2} \left( {1 - \cos \theta } \right)}}$$

(3.24)

Fig. 3.3

a Schematic representation of a droplet sitting on the condensing surface coated with a hydrophobic layer. b Resistance network and temperature drop contributions due to the liquid–vapor interface (ΔT_i), the droplet curvature (ΔT_c), the conduction through the droplet (ΔT_d), and the coating layer (ΔT_HC); T_i is the temperature of the liquid–vapor interface and T_b is the temperature at the droplet base

where h_i is the interfacial heat transfer coefficient given by [63]:

$$h_{i} = \frac{2\alpha }{{2 - \alpha }}\frac{1}{{\sqrt {2\pi R_{g} T_{sat} } }}\frac{{h_{lv}^{2} }}{{v_{v} T_{sat} }}$$

(3.25)

In Eq. 3.25, R_g is the specific ideal gas constant, ν_v is the vapor specific volume, and α is the accommodation coefficient. The accommodation coefficient α is the ratio of vapor molecules captured by the liquid phase to the total number of vapor molecules approaching the surface (0 < α < 1). A $\alpha$ close to 0 indicates a high concentration of NCG, while $\alpha$ close to 1 means the absence of NCG [63].

The temperature drop caused by the droplet curvature is evaluated as

$${\Delta }T_{c} = \frac{{2T_{sat} \sigma }}{{h_{lv} r\rho_{l} }}$$

(3.26)

The thermal resistance due to heat conduction through the droplet causes the following temperature drop:

$${\Delta }T_{d} = \frac{{Q_{dr} \theta }}{{4\pi r\lambda_{l} \sin \theta }}$$

(3.27)

Finally, the temperature drop due to the hydrophobic coating is calculated as

$${\Delta }T_{HC} = \frac{{Q_{dr} \delta_{HC} }}{{\lambda_{HC} \pi r^{2} \sin^{2} \theta }}$$

(3.28)

where δ_HC and λ_HC are, respectively, the thickness and the thermal conductivity of the coating layer. Substituting the expressions for temperature drops (Eqs. 3.24, 3.26–3.28) in Eq. 3.23, the heat flow rate through a single drop of radius r is obtained as

$$Q_{dr} \left( r \right) = \frac{{ \pi r^{2} \left( {\Delta T - \frac{{2T_{sat} \sigma }}{{rh_{lv} \rho_{l} }}} \right)}}{{\left( {\frac{{\delta_{HC} }}{{\lambda_{HC} \sin^{2} \theta }} + \frac{r\theta }{{4\lambda_{l} \sin \theta }} + \frac{1}{{2h_{i} \left( {1 - \cos \theta } \right)}}} \right)}}$$

(3.29)

In the model by Kim and Kim [36], the heat transfer through a single drop Q_dr(r) (Eq. 3.29) is combined with the drop size density functions of large droplets N(r) and small droplets n(r) to obtain the overall heat flux during DWC (Eq. 3.17). With regard to the droplet population, N(r) is obtained using the empirical relation given by Le Fevre and Rose [57] (Eq. 3.7), while n(r) is calculated using Eq. 3.13 (see Sect. 3.3).

In Eq. 3.17, the limits of integration are calculated using Eq. 3.18 for r_min and Eqs. 3.30 and 3.31 respectively for r_e and r_max:

$$r_{e} = \frac{1}{{\sqrt {4N_{s} } }}$$

(3.30)

$$r_{\rm{max}} = \sqrt {\frac{{6k_{c} \left( {\cos \theta_{r} - \cos \theta_{a} } \right)\sin \theta }}{{\pi \left( {2 - 3\cos \theta + \cos^{3} \theta } \right)}}\frac{\sigma }{{\rho_{l} g}}}$$

(3.31)

In Eq. 3.30, N_s is the nucleation site density; in Eq. 3.31, θ_a is the advancing contact angle, θ_r is the receding contact angle, and k_c is the retention factor, a constant depending on the droplet geometry. The present formulation for the effective radius r_e assumes that the nucleation sites have a uniform distribution and form a square array over the surface, while the departing radius is deduced by equating the gravity force and the adhesion force.

The coefficients for the population of small droplets (Eqs. 3.13–3.16) were obtained analytically as

$$A_{1} = \frac{{{\Delta }T}}{{2\rho_{l} h_{lv} }}$$

(3.32)

$$A_{2} = \frac{{\theta \left( {1 - \cos \theta } \right)}}{{4\lambda_{l} \sin \theta }}$$

(3.33)

$$A_{3} = \frac{1}{{2h_{i} }} + \frac{{\delta_{HC} \left( {1 - \cos \theta } \right)}}{{\lambda_{HC} \sin^{2} \theta }}$$

(3.34)

3.4.3 Miljkovic et al. (2013) Model

Miljkovic et al. [60] modified the model by Kim and Kim [36] by taking into account the surface morphology with the aim of estimating the condensation heat transfer on micro/nanostructured surfaces. This model extends the previously developed droplet size distribution theory to both constant and non-constant contact angle droplets growing processes. It is worth noting that assuming a constant droplet contact angle during growth is suitable for dropwise condensation on flat hydrophobic surfaces; however, this assumption is not valid for structured superhydrophobic surfaces, since the droplet contact angles have been observed to vary during droplet growth [60]. As for the models described in Sects. 3.4.1 and 3.4.2, Miljkovic et al. [60] combines the single drop heat transfer with the droplet population for the estimation of the average heat flux during DWC (Eq. 3.17). In particular, the model accounts for the temperature drop contributions due to the liquid–vapor interfacial resistance, the droplet curvature, the conduction resistance of the drop, the thermal resistance of the micro/nanostructure (if present), and the thermal resistance of the coating. The heat transfer rate exchanged by a single droplet Q_dr is calculated as follows:

$$Q_{dr} \left( {r,\theta } \right) = \frac{{\pi r^{2} \left( {\Delta T - \frac{{2T_{sat} \sigma }}{{rh_{lv} \rho_{l} }}} \right)}}{{\frac{1}{{2h_{i} \left( {1 - \cos \theta } \right)}} + \frac{r\theta }{{4\lambda_{l} \sin \theta }} + \frac{1}{{\lambda_{HC} \sin^{2} \theta }}\left[ {\frac{{\lambda_{p} \varphi }}{{\delta_{HC} \lambda_{p} + l_{p} \lambda_{HC} }} + \frac{{\lambda_{l} \left( {1 - \varphi } \right)}}{{\delta_{HC} \lambda_{l} + l_{p} \lambda_{HC} }}} \right]^{ - 1} }}$$

(3.35)

where $\varphi$ and $l_{p}$ are geometrical parameters that, in the case of flat surfaces, are equal to 0. For details about the calculation of $\varphi$ and $l_{p}$ in the case of structured surfaces, the reader can refer to the work by Miljkovic et al. [60].

For large drops growing mainly by coalescence, the droplet size distribution N(r) is evaluated by the expression proposed by Le Fevre and Rose [57] (Eq. 3.7), where the departing radius is calculated as follows:

$$r_{\max } = \sqrt {\frac{{6\left( {\cos \theta_{r} - \cos \theta_{a} } \right)\sin \theta_{e} }}{{\pi \left( {2 - 3\cos \theta_{e} + \cos^{3} \theta_{e} } \right)}}\frac{\sigma }{{\rho_{l} g\cos \beta }}}$$

(3.36)

where β is the inclination of the condensing surface (90° corresponds to a horizontal surface and 0° corresponds to a vertical surface) and θ_e is the equilibrium contact angle defined as $\theta_{e} = \cos^{ - 1} \left( {0.5\cos \theta_{a} + 0.5\cos \theta_{r} } \right)$.

To solve the first integral in Eq. 3.17 (which includes the small droplet population), r_min is calculated by Eq. 3.18 and, assuming the nucleation sites randomly distributed on the condensation surface (Poisson distribution), r_e is given by

$$r_{e} = \frac{1}{{4\sqrt {N_{s} } }}$$

(3.37)

In accordance with the expression for the heat transfer through a single droplet developed by Miljkovic et al. [60] (Eq. 3.35), the small droplet population (Eqs. 3.13–3.16) is calculated with the following coefficients:

$$A_{1} = \frac{{{\Delta }T}}{{\rho_{l} h_{lv} \left( {1 - \cos \theta } \right)^{2} \left( {2 + \cos \theta } \right)}}$$

(3.38)

$$A_{2} = \frac{\theta }{{4\lambda_{l} {\text{sin}}\left( \theta \right)}}$$

(3.39)

$$A_{3} = \frac{1}{{2h_{i} \left( {1 - \cos \theta } \right)}} + \frac{1}{{\lambda_{HC} \sin^{2} \theta }}\left[ {\frac{{\lambda_{p} \varphi }}{{\delta_{HC} \lambda_{P} + l_{p} \lambda_{HC} }} + \frac{{\lambda_{l} \left( {1 - \varphi } \right)}}{{\delta_{HC} \lambda_{l} + l_{p} \lambda_{HC} }}} \right]^{ - 1}$$

(3.40)

3.4.4 Chavan et al. (2016) Model

Recently, Chavan et al. [32] proposed a procedure for the calculation of the heat transfer through a droplet that is based on the results of steady-state 2D axisymmetric numerical simulations of the droplet growth. The models reported in Sects. 3.4.1–3.4.3 make the assumption of constant temperature at the liquid–vapor interface (droplet surface) and at the solid–liquid interface (droplet base) for the calculation of the conduction thermal resistance of the single droplet [36, 57, 60]. Instead, Chavan et al. [32] solved the heat equation through a single droplet by means of a numerical model based on the finite element method and replacing the constant temperature boundary condition at the liquid–vapor interface with a convective boundary condition (fixing a constant value of the heat transfer coefficient h_i). The simulations showed that the local heat flux at the three-phase contact line resulted to be four orders of magnitude higher than at the droplet top and this phenomenon was not taken into account by the previous formulations (Eqs. 3.29 and 3.35).

The Chavan et al. [32] model is based on three dimensionless quantities governing the heat transfer through a single drop: the Biot number (Bi), the apparent advancing contact angle (θ_a), and the droplet Nusselt number (Nu). The Nusselt number can be evaluated as a function of the other two dimensionless groups as ${\text{Nu}} = {\it\text{f}} \left( {{\text{Bi}}, \theta_{a} } \right)$. The Biot and Nusselt numbers can be expressed in terms of the droplet base radius (r_b) as

$${\text{Bi}} = \frac{{h_{i} r_{b} }}{{\lambda_{l} }}$$

(3.41)

$${\text{Nu}} = \frac{{Q_{dr} }}{{\lambda_{l} r_{b} \left( {T_{sat} - T_{wall} } \right)}}$$

(3.42)

where the interfacial heat transfer coefficient h_i is calculated from Eq. 3.25. For an easy implementation of their method in DWC heat transfer models, the authors provided the following expressions for the estimation of Nu (θ_a is in radians):

$${\text{Nu}} = 3\theta_{a}^{ 0.65} {\text{Bi}}^{0.83} + 0.007\theta_{a}^{ 5.1} \; {\text{Bi}}^{ - 0.23} {\text{Bi}} \le 0.5$$

(3.43)

$${\text{Nu}} = 0.29\theta_{a}^{ 2.24} {\text{Bi}}^{ - 0.17} + 3.33\theta_{a}^{ - 0.3} {\text{Bi}}^{0.72}\; 0.5 < {\text{Bi}} \le 2$$

(3.44)

$${\text{Nu}} = 5.76e^{{ - 0.28 \theta_{a}^{ 0.68} }} {\text{ln}}\left( {1 + 5{\text{Bi}}^{0.82} - 2.79{\text{Bi}}^{0.83} } \right)\; 2 < {\text{Bi}} \le 10^{5}$$

(3.45)

Replacing the liquid–vapor interfacial thermal resistance and the conduction resistance through the droplet with the thermal resistance obtained by numerical simulations (Eq. 3.42), the heat flow rate through a single droplet can be calculated as

$$Q_{dr} \left( {r,\theta } \right) = \frac{{\Delta T - \frac{{2T_{sat} \sigma }}{{rh_{lv} \rho_{l} }}}}{{\frac{1}{{{\text{Nu}}\lambda_{l} r\sin \theta_{a} }} + \frac{{\delta_{HC} }}{{\lambda_{HC} \pi r^{2} \sin^{2} \theta_{a} }}}}$$

(3.46)

where Nu is the results of Eqs. 3.43–3.45 whereas the thermal resistance of the coating (the second term at denominator) was included in Eq. 3.35 by Birbarah et al. [64] as an additional thermal resistance in series with the one developed by Chavan et al. [32].

In the model by Chavan et al. [32], to obtain the overall condensation heat flux during DWC (Eq. 3.17), the heat transfer through a single droplet (Eq. 3.46) is combined with the drop size distribution. In particular, the authors calculate the drop size density function of large drops N(r) and small drops n(r) accordingly to the model by Miljkovic et al. [60]. For the large droplet population, N(r) is obtained by Eq. 3.7 together with the expression for the departing radius provided by Eq. 3.36. Instead, for the small droplet population, n(r) is evaluated by Eqs. 3.13–3.16 using the coefficients reported in Eqs. 3.38–3.40. With regard to the minimum drop radius and the effective radius, Eqs. 3.18 and 3.37 are, respectively, used.

When the overall condensation heat flux during DWC is calculated using the equation by Chavan et al. [32] for the heat transfer through a single drop, it results that the previous models (Kim and Kim [36] and Miljkovic et al. [60]) underpredict the overall heat transfer.

3.5 Effect of Vapor Velocity on DWC Heat Transfer Coefficient

Vapor velocity is expected to affect the drop size distribution on the condensing surface during DWC. In particular, an increase in vapor velocity causes a decrease of the droplet departing radius and, at the same time, it leads to higher HTC [16, 40, 42]. As reported in Sect. 3.4, droplets grow from the nucleation radius to the departing radius, which is the result of a balance between retentive forces (droplet adhesion) and external forces which promote droplet movement (gravity and drag). The classical formulation of the droplet departing radius (Eqs. 3.31 and 3.36) derives from a force balance between droplet adhesion and gravity. Recently, Tancon et al. [42] proposed a strategy for modeling the effect of vapor velocity during DWC based on accounting for the drag force into the expression for the maximum droplet radius. After the presentation of the Tancon et al. [42] model, the equation accounting for vapor velocity will be included in the Chavan et al. [32] and in the Miljkovic et al. [60] models; the predicted HTC will be compared with datasets from independent laboratories [16, 41, 42].

3.5.1 Description of the Model by Tancon et al. (2021)

When the drop reaches the maximum dimension before sliding, the sum of drag force plus gravity force must equal the adhesion force:

$$F_{ad} \left( {r_{\max } } \right) = F_{d} \left( {r_{\max } } \right) + F_{g} \left( {r_{\max } } \right)$$

(3.47)

Assuming a circular drop, the adhesion force F_ad is evaluated as

$$F_{ad} \left( r \right) = 2k_{c} \sigma \sin \theta_{e} \left( {\cos \theta_{r} - \cos \theta_{a} } \right)r$$

(3.48)

where θ_a and θ_r are the advancing and the receding contact angles, θ_e is the equilibrium contact angle calculated as $\theta_{e} = \cos^{ - 1} \left( {0.5\cos \theta_{a} + 0.5\cos \theta_{r} } \right)$, σ is the surface tension of the condensing fluid and k_c is the retention factor, which can be analytically calculated and, for a circular shaped droplet, it is equal to 2/π [65].

The gravity force F_g acting on a droplet is calculated from the droplet volume as

$$F_{g} \left( r \right) = \frac{{2 - 3\cos \theta_{e} + \cos^{3} \theta_{e} }}{3}\pi \rho_{l} gr^{3}$$

(3.49)

where g is the gravity acceleration and a vertical orientation of the condensing surface is assumed.

The drag force F_d on a droplet due to the action of vapor flow is expressed as [66]:

$$F_{d} \left( r \right) = \frac{1}{2}\rho_{v} v_{v}^{2} C_{d} \left( {\theta_{e} - \sin \theta_{e} \cos \theta_{e} } \right)r^{2}$$

(3.50)

where ρ_v is the density of the vapor, v_v is the vapor mean velocity in the channel where vapor flows and C_d is the drag coefficient. In Eq. 3.50, θ_e is expressed in radians. To estimate the drag coefficient of a droplet, Tancon et al. [42] performed CFD numerical simulations. They found that, for the specific case of a droplet placed on the wall of a rectangular cross-sectional channel (characterized by a large width-to-height ratio, equal to six in their case), the drag coefficient C_d can be expressed as a product of only two dimensionless groups: the ratio of channel height to droplet height L_c/l_dr and the droplet Reynolds number defined as ${\text{Re}}_{dr} = l_{dr} v_{v} \rho_{v} /\mu_{v}$.

$$C_{d} = 5.6053 \left[ {\left( {L_{c} /l_{dr} } \right)^{ - 4/3} {\text{Re}}_{dr}^{ - 1/6} } \right] + 0.1754$$

(3.51)

Substituting the expressions of F_ad, F_g, and F_d (Eqs. 3.48–3.50) into the force balance equation (Eq. 3.47), the droplet departing radius r_max in the case of non-negligible vapor velocity can be calculated as

$$r_{\max } = \frac{{ - C + \sqrt {C^{2} + 4AB} }}{2B}$$

(3.52)

where the coefficients A, B, and C are equal to

$$A = 2k_{c} {\upsigma }\sin \theta_{e} \left( {\cos \theta_{r} - \cos \theta_{a} } \right)$$

(3.53)

$$B = \frac{{2 - 3\cos \theta_{e} + \cos^{3} \theta_{e} }}{3}\pi \rho_{l} g$$

(3.54)

$$C = \frac{1}{2}\rho_{v} v_{v}^{2} C_{d} \left( {\theta_{e} - \sin \theta_{e} \cos \theta_{e} } \right)$$

(3.55)

The present method for the determination of r_max requires an iterative procedure: a guess value of the droplet departing radius r_max (Eq. 3.52) is needed to estimate the drag force (Eq. 3.50). A first attempt value for r_max is calculated from Eq. 3.47 assuming the vapor shear stress component equal to zero. With this initial value of r_max, C_d is obtained by Eq. 3.51 to estimate the drag force on the droplet, thus the force balance equation is solved a second time and a new value of r_max is calculated (Eq. 3.52). The convergence is achieved when the difference between two consecutive r_max is lower than an established value (e.g., 1 μm).

When the formulation for the departing radius proposed by Tancon et al. [42] is included in the models reported in Sect. 3.4, the effect of the vapor velocity on the overall heat transfer can be accounted for.

3.5.2 Comparison Against Experimental Data

The Miljkovic et al. [60] and the Chavan et al. [32] models (described in Sect. 3.4), in their original formulation and modified with the expression for the departing radius proposed by Tancon et al. [42] (Eq. 3.52), have been used to predict the HTC during DWC in presence of vapor velocity. The models are compared against a database composed of the heat transfer data by Tancon et al. [42], Sharma et al. [41] and Tanner et al. [16]. Datasets refer to vapor velocity conditions between 3 and 24 m s⁻¹. The results of the comparison, using the input parameters listed in Table 3.1, are reported in Fig. 3.4, where the ratio of the calculated to experimental HTC is plotted against vapor velocity.

Table 3.1 List of input parameters, for each set of experimental data, used in the models by Miljkovic et al. [60] and Chavan et al. [32] for the evaluation of the DWC heat transfer coefficient

Fig. 3.4

Experimental data by Tancon et al. [42], Tanner et al. [16], and Sharma et al. [41] compared with models predictions at varying vapor velocity: a predictions by the original Chavan et al. [32] and Miljkovic et al. [60] models; b predictions by the present model, coupled with Chavan et al. [32] and Miljkovic et al. [60] models, to account for the effect of vapor velocity. Models input used for the comparison are reported in Table 3.1

As expected, since the original models (Miljkovic et al. [60] and Chavan et al. [32]) predict a constant value of heat transfer coefficient with vapor velocity, the experimental HTC is underpredicted at high vapor velocity (Fig. 3.4a). Instead, the present model, obtained coupling the r_max formulation proposed by Tancon et al. [42] with Miljkovic et al. [60] and Chavan et al. [32] models, is able to predict the heat transfer coefficient increase due to vapor velocity (Fig. 3.4b). For each calculated value, the deviation with respect to measured data is below 10% and the whole experimental dataset is predicted with a mean relative deviation below 4%.

3.6 Effect of Main Parameters on the Heat Transfer Coefficient

After validation, the modified Miljkovic et al. [60] model with the formulation by Tancon et al. [42] for the droplet departing radius is here used to study the effect of the main parameters affecting the heat transfer coefficient during DWC. The following input model parameters have been chosen as reference values: saturation temperature 107 °C, heat flux 335 kW m⁻², coating thermal resistance 1 m² K MW⁻¹, advancing contact angle 90°, contact angle hysteresis 20°, vapor velocity v_v = 3 m s⁻¹. In addition, the condensing surface is assumed to be in a vertical position and it does not present a micro/nanostructure (which implies the input parameters $\varphi$ and $l_{p}$ in the Miljkovic et al. [60] model are equal to 0).

3.6.1 Temperature Drops and Cumulative Normalized Heat Flux Distribution

The temperature drops that arises from the thermal resistances affecting DWC together with the cumulative heat flux distribution function are depicted in Fig. 3.5 for two values of the coating thermal resistance (δ/λ = 1 m² K MW⁻¹ and δ/λ = 0.2 m² K MW⁻¹). Considering a total temperature drop ΔT = 3 K, Fig. 3.5a shows the temperature drops due to the four thermal resistances as a function of the droplet radius. As already reported in Sect. 3.4.3, the Miljkovic et al. [60] model considers the following thermal resistances: liquid–vapor interfacial resistance, droplet curvature resistance, conduction resistance of the drop, and conduction resistance of the coating. The higher the coating resistance, the higher its contribution to the total temperature drop and, consequently, the larger the radius interval at which the conduction through the coating is the dominant thermal resistance (up to 0.5 μm in case of δ/λ = 0.2 m² K MW⁻¹ and up to 2 μm in case of δ/λ = 1 m² K MW⁻¹). The coating thermal resistance is the most important resistance up to 0.5–2 μm of drop radius, whereas the conduction resistance through the droplet is dominant for higher values of droplet radius. It should be noted that, in the early stage of drop growth, when the radius is lower than some tens of nanometers, the thermal resistance due to droplet curvature gives a considerable contribution to the total temperature drop.

Fig. 3.5

a Temperature drops due to the liquid–vapor interface, droplet curvature, conduction through the drop, and through the coating plotted against droplet radius. b Cumulative normalized heat flux distribution versus droplet radius. Input parameters for the modified Miljkovic et al. [60] model using the Tancon et al. [42] formulation for the departing radius: ΔT = 3 K, T_sat = 107 °C, θ_a = 90°, Δθ = 20°, δ/λ = 1 m² K MW⁻¹ and δ/λ = 0.2 m² K MW⁻¹, v_v = 3 m s⁻¹

The percentage of the heat flux exchanged by droplets smaller than a certain value r is shown in Fig. 3.5b where the cumulative normalized heat flux distribution is plotted versus droplet radius. The cumulative normalized heat flux F_{heat flux} is defined as

$$F_{heat flux} \left( r \right) = \frac{{\mathop \smallint \nolimits_{{r_{\min } }}^{r} Q_{dr} \left( r \right)n\left( r \right)dr}}{q}\; r_{\min } \le r \le r_{e}$$

(3.56)

$$F_{heat flux} \left( r \right) = \frac{{\mathop \smallint \nolimits_{{r_{\min } }}^{{r_{e} }} Q_{dr} \left( r \right)n\left( r \right)dr + \mathop \smallint \nolimits_{{r_{e} }}^{r} Q_{dr} \left( r \right)N\left( r \right)dr}}{q} \; r_{e} < r \le r_{\max }$$

(3.57)

where q is the total condensation heat flux, Q_dr(r) is the heat exchanged by a single droplet (Eq. 3.35), n(r) is the drop size density for the small droplet population (Eq. 3.13) and N(r) is the drop size density for the population of large droplets (Eq. 3.7). In both the considered cases (δ/λ = 1 m² K MW⁻¹ and δ/λ = 0.2 m² K MW⁻¹), around 60% of the total heat flux is exchanged in the radius range where conduction through the coating is the dominant thermal resistance (Fig. 3.5a). This result shows the strong effect of the coating thermal resistance on the total heat transfer. Reducing the promoter thermal resistance by lowering the coating thickness can be a strategy to improve the HTC during DWC. However, the coating thickness affects the lifetime of the treatments. The thickness should be increased in order to increase the coating lifetime, as it is reported in the literature [2, 14], but the advantage in terms of HTC would be adversely affected [12].

3.6.2 Predicted Effect of Contact Angle Hysteresis, Coating Thermal Resistance, Heat Flux and Vapor Velocity on the Heat Transfer Coefficient

In Fig. 3.6, the HTC and the departing radius, calculated by the modified Miljkovic et al. [60] model using Eq. 3.52, are plotted against vapor velocity v_v at different values of coating thermal resistance, contact angle hysteresis, and heat flux. As already shown in Sect. 3.6.1, the coating thermal resistance is an important aspect to be considered during DWC since it can affect the overall HTC. In Fig. 3.6a, the HTC is plotted versus vapor velocity v_v considering three different values of the coating thermal resistance, ranging between 0.2 and 5 m² K MW⁻¹. For a given vapor velocity, the HTC is strongly affected by changing the coating thermal resistance, whereas the droplet departing radius remains the same. When the thermal resistance passes from 5 to 1 m² K MW⁻¹, the HTC is doubled. In Fig. 3.6b, the HTC is plotted for different values of the contact angle hysteresis (Δθ); the advancing contact angle θ_a is kept fixed whereas the receding contact angle is varied. For a fixed value of vapor velocity, the droplet departing diameter r_max increases when increasing the contact angle hysteresis Δθ and the HTC decreases. Improving the vapor velocity leads to an HTC increase and this effect is more prominent at low Δθ values. The effect of the heat flux q is reported in Fig. 3.6c. The HTC, according to the literature [2, 67], shows a weak increase with the heat flux for a fixed vapor velocity v_v, while the departing radius r_max is not affected by the heat flux. Increasing the heat flux from 200 to 1000 kW m⁻² leads to an augmentation of the HTC by 10%.

Fig. 3.6

Calculated HTC and droplet departing radius using the modified Miljkovic et al. [60] model with the expression by Tancon et al. [42] for vapor velocity: a effect of coating thermal resistance δ/λ [m² K MW⁻¹] (∆θ = 24° and q = 335 kW m⁻²); b effect of contact angle hysteresis ∆θ [°] (q = 335 kW m⁻² and δ/λ = 1 m² K MW⁻¹); c effect of heat flux q [kW m⁻²] (∆θ = 24° and δ/λ = 1 m² K MW⁻¹)

In particular, it has been calculated from the modified Miljkovic et al. model that, for a given value of contact angle hysteresis (Δθ = 24°), coating thermal resistance (δ/λ = 1 m² K MW⁻¹) and heat flux (q = 335 kW m⁻²), the vapor velocity must be increased from 1 m s⁻¹ to 25 m s⁻¹ to improve the HTC by 50%.

Figure 3.6 shows that, depending on the application, different strategies can be adopted to enhance the heat transfer during DWC. Increasing the vapor velocity positively affects the HTC, but the pressure drop will be higher. Other actions may address the promoter thermal resistance, by using advanced coating methods with very low thermal resistance to achieve HTC increase. Another approach regards the modification of surface wettability, developing coatings with very low contact angle hysteresis [68, 69].

3.7 Conclusions

The present Chapter is focused on measurements and modeling of heat transfer during dropwise condensation (DWC). Despite DWC was initially studied back in 1930, it is still capturing the interest of many researchers. This is mainly related to the recent advances in material sciences and the availability of experimental techniques that allow the investigation of DWC process at micro/nanoscale.

However, lessons learned from the past must be taken into consideration. Accurate heat transfer coefficient measurements that ensure reproducible results among different laboratories are very important. Particular care must be paid to the measurement of heat flux and surface temperature. Furthermore, the presence of non-condensable gases must be avoided when condensing pure vapor since it causes a strong reduction of the heat transfer coefficient.

Considering smooth surfaces, in the literature are available thin coatings that promote DWC with overall heat transfer coefficients (including the thermal resistance of the coating) up to 300 kW m⁻² K⁻¹ (and heat flux of 400 kW m⁻²) with aluminum substrates. The duration of the coatings (especially in harsh environments as it is the case of steam condensation at atmospheric pressure) needs to be improved. In particular, it is important to develop more robust coatings that, at the same time, present a low thermal resistance.

Superhydrophobic surfaces can provide low contact angle hysteresis in air ambient conditions but, when employed during condensation tests with saturated steam, their heat transfer performance can be strongly penalized by flooding.

Different models have been proposed over the years to model the heat transfer during DWC. The small droplet population has been introduced and more complex models have been developed that can be used also with structured surfaces. These models consider DWC in absence of vapor velocity. The shape of the droplets and the droplet departing diameter are clearly affected by the vapor velocity. A modification proposed by the present authors to consider the effect of vapor velocity on droplet departing diameter and thus on the resulting heat transfer coefficient has been illustrated in the present Chapter. The model is then used to study the effect of the main parameters on DWC heat transfer. It results that around 60% of the total heat flux occurs in the droplets radius interval where conduction through the coating represents the dominant thermal resistance. This again confirms the importance of the thermal resistance of the coating. Furthermore, the nucleation site density remains one important parameter that must be set as a boundary condition for the models and its value can strongly affect the predicted values. Strategies devoted to increase the heat transfer coefficient during DWC on flat surfaces should combine low contact angle hysteresis, low thermal resistance of the coating and increased vapor velocity.