Keywords

1 Introduction

Over the last two decades, microfluidic devices such as Lab-on-a-chip (LOC) and Micro-total analysis systems (μTAS) have emerged as efficient tools in the field of medical sciences, biotechnology, and some engineering applications [1]. The dimensions of the mentioned miniaturization systems can vary from ten micrometers to a few hundred micrometers. Distinguished advantages such as low consumption of sample, quick response time, high throughput, portability, simple geometry, and ease to fabricate can be availed. Now-a-days microfluidic systems can be applied to different fields for different purposes such as blood separations [2], drug delivery devices [3], disease diagnostic [4], and micromixing [5, 6]. Among these different applications of the microfluidic device, micromixing requires in the fields like DNA hybridization [7, 8], point-of-care testing [9, 10], chemical synthesis [11], and biological analysis [12]. Electrokinetics refers to the movement of fluid/particles under the action of an externally applied electric field [13, 14]. Recently, researchers attracted by the concept of electrokinetic effects to implement on micromixing, even for a simple geometry one can achieve high mixing quality.

In general, micromixing can be classified into two categories; active micromixing and passive micromixing [6, 12, 15]. In the case of active micromixing, mixing is produced by an externally applied excitation (force). The nature of the excitation may be in the form of electric, magnetic, acoustic, or thermal. The mixing quality achieved from the micromixer is quite high as compared to passive micromixers. On the contrary, passive micromixing refers to the mixing obtained only by considering the shape of the geometry. In a microfluidic device, the hydraulic diameter is in the range of micrometers and the fluid velocity encountered here in terms of mm/s is extremely low. Therefore, the nature of flow exhibits here highly laminar type. In such a situation, it is difficult to achieve high efficient mixing quality as the mixing process primarily depends on molecular diffusion. Consequently, some effective methods should be applied by which mixing can be achieved quickly and also better mixing quality [16, 17]. To encounter this type of problem some researchers considered specific types of geometry to achieve better results in terms of mixing quality [18, 19]. Some researchers applied consequent grooves at the base of their model [20], also some applied their innovative ideas by incorporating a non-conductive plate that may be flexible or nonflexible [21].

Now-a-days, AC microelectrodes have been efficiently used in the application of micromixing. When microelectrodes are excited by an externally applied electric field it can produce electrokinetic forces such as electroosmotic and die-electrophoretic forces and due to these forces micro-vortices generate near the microelectrodes which provide a rapid mixing [22]. Also, this technique can be applied to simple geometry and is easy to fabricate. Inspired by the concept, some researchers investigated the dependency of the mentioned electrokinetic forces on different parameters, viz., AC voltage, frequency of the alternating current, and the electrical properties of fluid medium [23]. One major difficulty they experienced that the fabrication of their huge length model but they reported the mixing quality as 86.5%.

Motivated by the work in enhancing the mixing quality considering the electrokinetic effects, in our present study we have considered a novel geometry that could produce 95.61% mixing quality in 0.8 s with a set of parameters, viz., inlet fluid velocity, frequency of alternating current (AC) and maximum voltage amplitude of AC.

2 Problem Description

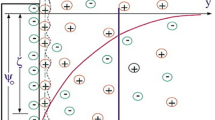
In Fig. 1 the novel geometry consists of two identical pairs of electrodes that are located at the angular positions of 45°, −45°, 135°, −135° and two baffles at the inlet side (keeping clearance from the upper and lower wall). The computational domain is filled with diluted KCL and water as a base fluid. The electrical properties of the fluid are disclosed in Table 1. In our present study, we have simulated our model by considering the inlet velocity of 0.05 mm/s, the voltage amplitude of 0.2 V, and the frequency of the alternating current of 4 Hz. A comparison study has also been performed between the one ring-shaped micromixer with and without the baffles. Results show that better mixing quality can be obtained with baffles.

Fig. 1
A schematic of model geometry. The total length of the structure is 80 micrometers. It has an inlet and outlet of 10 micrometers. The inlet side has 2 baffles at 25 degrees. The central ring has 4 electrodes on the outer surface. It has water and H C L in the domain.

Schematic diagram of model geometry (all dimensions are in \(\upmu \mathrm{m}\))

Full size image
Table 1 Numerical value of different parameters used in the simulation
Full size table

3 Mathematical Modeling

The mathematical model of an electric field, flow field, and concentration field with boundary conditions are presented as follows.

3.1 Electric Field

We apply the Poisson equation [24] to know about the distribution of potential in the computational domain, as follows:

$${\nabla }^{2}{\varphi }=\frac{{\rho }_{{e}}}{\epsilon {\epsilon }_{0}}$$
(1)

where, \({\epsilon }_{0}\) and \(\epsilon\) represent the electrical permittivity of the vacuum and dielectric constant of the medium, respectively. Moreover, \({\varphi }\) and \({\rho }_{{e}}\) demonstrate the distribution of electric potential and free electric charge density in the domain, respectively. As far away from the solid surfaces, the net electric charge density is zero (ρe = 0) therefore, the Poisson equation takes the form Laplace equation [24] as follows:

$${\nabla }^{2}{\varphi }=0$$
(2)

The boundary conditions that are imposed to solve the electric field are as follows:

  • Wall of the microchannel and two baffles:

    $$\mathbf{n}\cdot \nabla {\varphi }=0$$
    (3)

  • Two electrode pairs:

    $${V}={{V}}_{0}\mathrm{sin}(2\pi{ ft})$$
    (4)

  • Outlet of the microchannel:

    $${\varphi }=0$$
    (5)

3.2 Flow Field

We have considered continuity and Navier–Stokes equation to solve the flow field. The fluid is assumed as Newtonian and incompressible. The mentioned two equations can be represented as follows:

  • Continuity equation [25]:

    $$\nabla \cdot \mathbf{u}=0$$
    (6)

  • Navier-Stokes equation:

    $$\rho \left[ {\frac{{\partial {\text{u}}}}{{\partial {{t}}}}+{\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right] = - \nabla {{P}} + \mu \nabla ^{2} {\mathbf{u}} + {\mathbf{E}}\rho _{{{e}}}$$
    (7)

In Eq. (7) \(\mathbf{u}\) and \(\mathbf{E}\) demonstrate the velocity vector and electric field vector, respectively. Furthermore, \(\rho\) and \(\mu\) designate fluid mass density and fluid’s dynamic viscosity, respectively, and \(\nabla {P}\) represents the pressure gradient. The last term is on the right side in Eq. (7) representing the electrostatic body force in the thin electric double layer (EDL). The electric field and potential are related by the expression \(\mathbf{E}=-\nabla {\varphi }\).

From the fact that the most solid surfaces acquire a surface charge when brought into contact with an electrolyte, as a result, counterions are attracted by these charged surfaces, and a thin layer is formed, where the net charge is not zero, at the vicinity of the solid surfaces of the order of nanometers known as an electric double layer (EDL). When an electric field is applied due to electroosmotic flow the charged solution displaces in the electric double layer. This scheme generates a force acting on the positively charged ions and the liquid flows in the direction of the applied electric field. The electric double layer can be expressed as follows:

$${\uplambda }_{{D}}=\sqrt{\frac{\epsilon {\epsilon }_{0}{{k}}_{{B}}{T}}{2{{n}}_{0}{({ze})}^{2}}}$$
(8)

In Eq. (8) kB, T, n0, z, and e demonstrate the Boltzmann constant, absolute temperature, free ionic charge density, valence, and elementary charge, respectively. In our present study, we have neglected the last term Eρe in Eq. (7) outside the electric double layer (EDL) and considered Helmholtz-Smoluchowski slip velocity boundary condition expressed in Eq. (9) for simulating the electroosmotic flow outside EDL.

$$\mathbf{u}=-\frac{{{\epsilon \epsilon }}_{0{\upzeta }_{{w}}}}{\mu }\mathbf{E}$$
(9)

where ζw represents the zeta potential at the channel wall.

The boundary conditions that are imposed to solve the flow field are as follows [27]:

  • Inlet of the microchannel: Fully developed flow.

  • Outlet of the microchannel: P = Pa (local atmospheric pressure) with suppressing backflow.

  • Wall of the microchannel: Electroosmotic slip velocity.

  • Wall of the baffles: No-slip condition.

3.3 Concentration Field

The Convection–Diffusion equation [25] is:

$$\frac{\partial {{C}}_{{i}}}{\partial {t}}+{u}\cdot \nabla {{C}}_{{i}}={{D}}_{{i}}{\nabla }^{2}{{C}}_{{i}}$$
(10)

where, Ci and Di demonstrate the concentration and diffusion coefficient of ith fluid, respectively. To solve the Eq. (10) we have applied the boundary conditions as follows:

  • Inlets of the microchannel: C = 1 mol/m3 (for upper half) and C = 0 (for lower half)

  • Wall of the microchannel and baffles:

$$\frac{\partial {{C}}_{{i}}}{\partial {t}}=0 \;({t}\ge 0)$$
(11)

3.4 Mixing Quality Factor

To verify the performance of our proposed model, we have defined a Mixing Quality (MQ) factor in Eq. (12).

$${MQ}=1-\sqrt{\frac{{\upsigma }_{\mathrm{mean}}^{2}}{{\upsigma }_{\mathrm{max}}^{2}}}$$
(12)
$${\upsigma }_{\mathrm{mean}}^{2}=\int {\left({{C}}_{{i}}-{{C}}_{\mathrm{max}}\right)}^{2}{dy}$$
(13)

In Eq. (13) the integration has been performed at the outlet of the microchannel. Whereas, Cmax (=0.5 mol/m3) is the ideal concentration after mixing at the outlet, and \({\upsigma }_{\mathrm{max}}\) is the maximum variation in the mixture. According to Eq. (12), a value of 1 of MQ signifies 100% mixing quality and a value of 0 indicates 0% mixing quality.

4 Methodology

Comsol Multiphysics® 5.6 software [26] has been considered to perform the simulations of our proposed computational model domain. The mentioned software utilizes its solver, the Backward Euler method to carry out the simulation. In the current simulation, we have considered triangular elements. Discretization of fluid has been performed by considering P2 + P1 efficient elements. PARDISO linear solver has been selected to solve the fluid flow variables. PARDISO linear solver can reuse the factorization of the nonsymmetric type system matrix, which is solved for. As a result, the mentioned solver can solve faster than other available solvers. The constant (Newton) method has been imposed to take care of nonlinearity terms and is considered a method of termination. The tolerance factor has been imposed as the criterion of termination. The absolute tolerance is considered 1 × 10–5 for the convergence. The simulation workflow has been disclosed as follows.

4.1 Model Physics

To test our proposed model, three physics, viz., electric current, laminar flow, and transport of diluted species have been selected. Thereafter, three physics have been coupled by imposing proper boundary conditions. Coupling between the different physics has been performed thoroughly to modify the mixing analysis in our proposed model.

4.2 Model Design

In Fig. 1 one ring-shaped micromixer with two baffles at the inlet side has been depicted. The two corners at the leading edge are separated by a distance of 5 μm and maintain a distance of 13 μm from the inlets. The rotation angle has been considered 25°. Two fluids with different concentrations of 1 mol/m3 and 0 mol/m3 enter the upper half and lower half, respectively. In the present study, we have considered one outlet to achieve the desired concentration of 0.5 mol/m3.

4.3 Model Parameters

To simulate our proposed model we have considered different parameters. The numerical values are presented in Table 1. The different parameters govern the fluid flow variables, fluid compositions, electrical properties, and physiochemical properties of the fluid.

4.4 Model Meshing

Free triangular mesh elements with predefined extremely fine mesh have been considered for the entire computational domain and have been shown in Fig. 2. Mesh refinement for triangular elements has been performed by considering different element size parameters such as maximum element size 0.2, minimum element size 0.006, and maximum element growth rate 1.1. The average mesh quality for the entire 2D geometry environment is 0.8975 which is quite acceptable for getting accurate results. The details of mesh quality are presented in Table 2.

Fig. 2
A diagram of model geometry. The structure has a triangular mesh or grid on the surface. The regions of electrodes and baffles have dark patches.

Triangular meshing system

Full size image
Table 2 Mesh quality in the computational domain
Full size table

4.5 Time-Dependent Approach

In our present simulation, we have simulated our proposed model in two steps. First, we have determined the voltage amplitude of the electric current considering a stationary study. After that, we computed the flow field and concentration field by considering the transient steps. At the start time (t = 0) of the transient step, the initial state is the solution of the stationary study. This technique considerably reduces the simulation time as well as the memory requirement. Besides, we apply a step function for smoothing the concentration differences and also we disregard the discontinuity of the Convection–Diffusion equation. Because most biological molecules are highly fragile and unstable in an inappropriate environment and the threshold value can be considered 0.1 s. Therefore, it is quite reasonable to consider simulation time 0.8 s in our present study.

5 Results and Discussion

Figures 3 and 4 show instantaneous streamline velocity patterns at t = 0.0375 s and surface velocity magnitude at t = 0.43542 s, respectively. From the figures, it has been seen that near the four electrodes two micro-vortices are generated due to electroosmotic flow.

Fig. 3
A diagram of model geometry. The structure has streamlines of the velocity field. The flow is from left to right on the inlet and outlet sides. The region of the ring has micro-vortices of flow near the 4 electrodes.

Streamline velocity field

Full size image
Fig. 4
An illustration of model geometry. The structure has contours of the surface velocity field. The 4 regions of the ring near the 4 electrodes have a 3-petal flower-like pattern of high values of velocity. The other regions have average and low values.

Surface velocity field

Full size image

In the present study, as we have applied an AC electric field, the resulting electroosmotic flow perturbs the highly ordered laminar flow, such that it continuously pushes up and down two different concentration fluids from the two opposite directions at the beginning of the mixing chamber, causing extensive stretching and folding of the fluid elements. Effective mixing mostly relies on vigorously stirring the fluid elements due to electroosmotic flow and a small contribution to diffusion. In addition to this consideration, two baffles at the inlet side act as a diffuser and there will be a pressure drop and can generate vortices, which enhance the mixing.

The mixing phenomenon is further exemplified by considering Figs. 5 and 6. From Fig. 5 it can be seen that the two fluid streams are well separated also at the outlet when no AC field is applied. Figure 6 represents the concentration field when an AC field is applied at a time, t = 0.46875 s. The mixing increases considerably owing to the alternating swirling in the flow.

Fig. 5
An illustration of model geometry. The structure has contours of the surface concentration and streamlines of the velocity field. The upper part of the inlet side has high values. The upper part of the ring and outlet have average values. The lower part has low to average values.

Concentration field at t = 0 s

Full size image
Fig. 6
An illustration of model geometry. The structure has contours of the surface concentration and streamlines of the velocity field. The upper part of the inlet side has high values and the lower part has low values. The ring and outlet have contours of average values and vortices in the ring.

Concentration field at t = 0.46875 s

Full size image

It should be mentioned that the diagram presented in Fig. 7 is the result of integration at the outlet boundary of the criterion, mixing quality as presented in Eq. (12), derived from the concept of square deviation from the desired concentration (0.5 mol/m3). Initially, the mixing quality is not good as can be depicted in Fig. 7. For example, more fluid with a concentration of 1 mol/m3 passes across the outlet boundary as compared to fluid with 0 mol/m3 concentration. Moreover, we have performed a comparative study of mixing quality between one ring-shaped with and without baffles geometries. Figure 7 depicts an increase in mixing quality by considering the baffles.

Fig. 7
A line graph of M Q versus time. It has 2 curves that grow horizontally, descend, and ascend with fluctuations. The curves are labeled With Baffles and Without Baffles. The curve for With Baffles has a higher rise.

Mixing quality for two different geometries

Full size image

6 Conclusions

In this study, an electroosmotic micromixer in one ring-shaped microchamber has been simulated. The mixing quality was further investigated by considering baffles. A set of parameters such as inlet fluid velocity, frequency of AC electric field, and maximum amplitude of AC has been employed to investigate the mixing quality. The results are summarized as follows:

  • By applying AC electric field micro-vortices are generated near the electrodes as a result of efficient mixing.

  • By considering baffles at an angle 25°, the MQ can further be increased.

  • For \({U}_{0}=0.05\,\mathrm{mm}/\mathrm{s}\), \({V}_{0}=0.2\,\mathrm{ V},\) and \(f=4\,\mathrm{ Hz}\) we achieved 95.61% and 94.85% mixing quality with and without baffles, respectively.