Indirect Adaptive Control of Nonlinear System Using Recurrent Neural Network

Abstract

In this article, a locally recurrent neural network with input feed through (LRNNIFT) is presented for control of nonlinear dynamical systems. The rationale of using LRNNIFT is due to its modest structure and mathematical model, which gives it an edge over the existing Elman neural networks (ENN) and feed forward neural networks (FFNN). Results from simulation showed that LRNNIFT-based controller is able to achieve adaptive control in a nonlinear system. It is also tested and observed to counterbalance the effects of disturbances. A comparative analysis is presented with the help of simulation, and it is deduced that overall performance of LRNNIFT controller is better than that of FFNN and ENN controllers.

1 Introduction

The world of science has grown drastically in the past few decades with an increased focus on solving complex real world problems. The growth of such a mindset led the researchers to realise that conventional modelling or control techniques are no longer applicable to complex dynamical systems. This paved way for the rise of the era of soft computing techniques, algorithms based on biological phenomena. One of the earliest significant control techniques in conventional control was the Ziegler Nichols method [1] which was further followed by several modifications [2, 3] and advanced forced oscillation techniques [4, 5] to achieve control on linear plants. Since most processes that require control nowadays are nonlinear, the use of conventional proportional- integral-derivative controller has seen decrease in relevance as majority of the plants are nonlinear in nature or whose dynamics are not fully known. Artificial neural networks (ANNs) are a major breakthrough in this area as these structures help estimate as well as control such systems. Various structures of ANNs have been developed over the time based on the loops, activation function. Simplest ones are feed forward neural networks [6] having low convergence rates which were followed by multi-layered feed forward neural networks [7] which again had issues related to slow learning rates. Recurrent neural networks (RNNs) [8] have gained traction in the recent years for the control [9, 10] of nonlinear systems due to the presence of recurrent loops leading to faster learning. RNNs are further implemented with modifications for adaptive control as well [11].

1.1 Contributions and Novelties of the Paper

• 1. This paper presents a detailed simulation of the LRNNIFT for control of a nonlinear time-delayed plant. Initial and final responses of a system with LRNNIFT controller are shown.

• 2. The proposed controller is also compared with controllers based some of the existing neural network structures such as feed forward neural network (FFNN) and Elman neural network (ENN).

• 3. The popular and robust back-propagation algorithm is used to tune all the controller models.

• 4. Stringent analysis and comparison of robustness of LRNNIFT, ENN and FFNN controllers is performed by considering disturbance signal effects which indicates the adaptive nature of the controller.

2 Overview of LRNNIFT

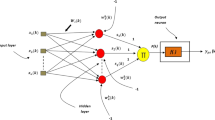
LRNNIFT is essentially a locally recurrent neural network in which each input node is connected directly to the output neuron via weights called as feed through weights. The objective is to compare the performance of the novel controller based on LRNNIFT with FFNN and ENN controllers while considering uniform parameter values for all of them. This helps us gauge the actual behaviour of the controller while having the above two models as a basis for comparison for the control of nonlinear systems. The structure of the proposed controller is shown in Fig. 1. In the figure, the bright red arrows represent the local recurrent weights generated as output of hidden neuron or node and propagated through a lag of a unit instant as connected back to the same neuron. This leads to the formation of a locally recurrent structure. The maroon arrows represent feed through weights connecting the input layer neurons to the output layer node through weights denoted as N = N₁, N₂, …, N_q. The recurrent weights are defined as W_L = w₁, w₂, …, w_p while W_a represents the input weight vector. All weights can be updated. From the figure, it can be seen that if W^L and N are removed or made equal to, the structure is reduced to a FFNN. Furthermore, FFNN and ENN structures are considered to compare the LRNNIFT controller structure. The reason behind these structures to be chosen for comparison was primarily for their proven performance in the fields of both estimation and control. FFNN is a simple structure with no recurrent weights whereas ENN has a rather complex structure with every recurrent weight is fed back to each hidden node. The output weight vector is given as, $W_{b} = w_{b}^{1} ,w_{b}^{2} , \ldots ,w_{b}^{p}$.

Fig. 1

Structure of the proposed controller

The input vector is defined as X = x₁(k), x₂(k), …, x_q(k). Subsequently, the output of any pth recurrent node at any kth instant can be calculated as:

$$ O_{p} \left( k \right) \, = f\left[ {U_{p} \left( k \right)} \right] $$

(1)

The function f is the hyperbolic tangent function. The induced field (IF) of any pth recurrent node can be given as:

$$ U_{p} \left( k \right) \, = W_{p}^{L} \left( k \right)O_{p} \left( {k - { 1}} \right) + \sum\limits_{q} {W_{pq}^{b} \left( k \right)x_{q} \left( k \right)} $$

(2)

The IF of the output node is described below:

$$ S\left( k \right) = \sum\limits_{p} {W_{b}^{p} \left( k \right)O_{p} \left( k \right)} $$

(3)

The output value from the output neuron will be equal to the sum of its own IF and the feed through factor (from input) as a linear function has been considered as the activation function. Hence, we write it as:

$$ S_{{{\text{IFTC}}}} \left( k \right) = S\left( k \right) \, = \sum\limits_{p} {W_{0}^{p} \left( k \right)U_{p} \left( k \right)} + \sum\limits_{q} {N_{pq} \left( k \right)x_{q} \left( k \right)} $$

(4)

2.1 Indirect Adaptive Control of a Time-Delayed Nonlinear System

As discussed previously, designing a controller for a system which is dynamic and nonlinear in nature is a complicated task as linear control techniques fail on such plants. Artificial neural networks have majorly solved this problem due to their flexible nature as there is a vast majority of structures from which an appropriate structure can be chosen whose parameters can be tuned based on system requirements. In this brief, a modified recurrent neural network is used as a controller for a dynamic plant which is to be controlled along a reference model. The general mathematical formulation of a nonlinear time-delayed plant can be given as:

$$ Y_{{{\text{LRN}}}} \left( k \right) = F\left[ \begin{gathered} Y_{{{\text{LRN}}}}^{q} \left( {k - {1}} \right),Y_{{{\text{LRN}}}}^{q} \left( {k - {2}} \right)...Y_{{{\text{LRN}}}}^{q} \hfill \\ \left( {k - O} \right),u_{c} \left( {k - {1}} \right),u_{c} \left( {k - {2}} \right)...u_{c} \left( {k - D} \right) \hfill \\ \end{gathered} \right] $$

(5)

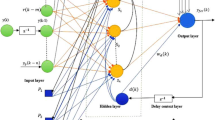
In the above equation, Y_LRN^q (k − 1) represents a previous value of the system delayed by an instant. In a similar fashion, all the outputs of y_LRN are mentioned till qth instant. Similarly, input past values are written u_c(k − 1) to u_c(k − D). Here, u_c is essentially the controller output which will act as an input to the plant. The actual input which will be fed to the controller is r(k).The aim here is to control the above plant, that is, to align its response with the reference model (desired response of the plant). This simply translates to F ≈ Fm, where Fm is the reference model. The potency of any nonlinear control method is established only if it reduces the dependency on plant parameters and structural complexity along with providing faster control response. Therefore, in case of LRNNIFT controller, only three inputs are taken from the vast array of system variables–the present value of input to plant, u_c(k), one previous value of output, $Y_{{{\text{LRN}}}}^{q} (k - 1)$, and a previous value of external input, r(k − 1). The control scheme is estimated relying on these three inputs only and is calculated as Y_LRN(k). Motivation behind selecting few inputs (here, three) is that this minimises plant parameter dependency of the controller along with reducing the computation load by lowering the number of weights to be adjusted. Figure 2 represents the block diagram of proposed LRNNIFT controller.

Fig. 2

Adaptive control scheme using LRNNIFT model (Proposed)

Further, the versatile back-propagation method is applied for adjusting the weights.

3 Simulation Study

In order to evaluate the efficacy of the proposed LRNNIFT-based control strategy, the scheme is implemented on a complex dynamic system. Furthermore, the results obtained from the proposed controller are compared with the FFNN and ENN controllers. Structurally, a single input, hidden and output layer, 4 hidden neurons, uniform learning rate and instantaneous training is applicable to all the three controllers. The reason why we considered uniformity among structure parameters for our analysis is to better judge the performance of LRNNIFT controller. For simulation, the following nonlinear dynamical plant has been considered:

$$ y_{o} (k) = \frac{{y_{o} (k - 1)y_{o} (k - 2)[y_{o} (k - 1) + 2.5]}}{{1 + y_{o}^{2} (k - 1) + y_{o}^{2} (k - 2)}} + u_{c} (k - 1) $$

(6)

where u_c(k) denotes the input to the plant. The reference model is given as,

$$ y_{m} \left( k \right) = 0.{6}y_{m} \left( {k - { 1}} \right) \, + \, 0.{3}y_{m} \left( {k - { 2}} \right) \, + r\left( k \right) $$

(7)

where r(k) is the BIBO stable external input to the system given as,

$$ r(k) = \sin \frac{2\pi k}{{25}} $$

(8)

The control objective here is to bring the difference between reference model and plant’s response e_c(k) = ym(k)y_o(k) approximately equal to zero by introducing an optimal control signal u_c(k) at every instant, to the plant via LRNNIFT as a rectified input to it. u_c(k) can be computed from the knowledge of y′_(k) and its past values as

$$ u_{c} \left( k \right) = F\left[ {y_{o} \left( k \right),y_{o} \left( {k - { 1}} \right)} \right] + 0.{6}y_{o} \left( k \right) + 0.{3}y_{o} \left( {k - { 1}} \right) + r\left( k \right) $$

(9)

Figure 3 represents the plant output response (in dotted pink) along with reference model response (in solid green) without control scheme implementation. From the plot, it can be clearly observed that the two responses do not coincide (as desired). Therefore, we use the adaptive control configuration shown in Fig. 2 and apply it to the plant. The value of learning rate is taken as 0.028. The total number of hidden neurons are 4.

Fig. 3

Plant response without control scheme

Figure 4 shows the response of LRNNIFT controller compared with FFNN and ENN based controllers and plant during the early stages of training. The instantaneous training was done for 60,000 time steps after which it was terminated. Post training, the controllers started tracking the reference plant’s output.

Fig. 4

Response of controllers during initial phases of training

which can be seen in Fig. 5. From Fig. 4, we can clearly observe that LRNNIFT controller has the fastest response among all three. Additionally, it is able to force the plant to track the reference model from the very first instant. Time of response of being a critical aspect in controller design makes the proposed controller better than ENN and FFNN-based control. Table 1. shows the Average Mean Square Error (AMSE) and Total Mean Average Error values for all the three controllers which is also the least for the proposed controller. The proposed controller is also checked for robustness against disturbance signals in the system. This is one of the key aspects of closed loop control. A step signal of amplitude 5 is added as disturbance to the plant at k = 55,000th instant.

Fig. 5

Response of controllers after successful training

Table 1 Output error comparison of ENN, FFNN and LRNNIFT controllers

The disturbance leads to spike in controller response and the instantaneous mean square errors and mean average errors also experience the same. In Fig. 6, we can see the noise signal causing disturbance at k = 55,000 instant but as the training went on it rapidly recovered and went back on the track within few instants. This proves the robust or adaptive nature of the controller. On comparison, we can observe that the FFNN controller has under-performed whereas the ENN controller has performed only slightly better than LRNNIFT controller. This is because the ENN is an extremely complex structure, that is for equal number of inputs and hidden neurons, the number of update parameters (or weights) for ENN is 32 whereas for LRNNIFT it is only 20. FFNN controller has 16 weights only but it is slow and less accurate as it cannot track the plant’s past values.

Fig. 6

Disturbance analysis for robustness

4 Conclusion

In this paper, an adaptive controller for nonlinear plants is proposed based on a locally recurrent network that has input fed through weights to the output (LRNNIFT). Parameter tuning by minimising the error function is done via back-propagation method. The controller is implemented on a nonlinear complex system and its results are compared with FFNN and ENN controllers. The simulation results clearly depict that the proposed controller performs better than the other two controllers both in terms of error mitigation and speed of tracking. The controllers are also tested for robustness by introducing a disturbance signal in the plant equation. It is observed that the proposed controller successfully adapts by moving back to the original track. Although the results of ENN are slightly better than LRNNIFT in b terms of robustness but the drawback here would be the high complexity of ENN network which again leads to the proposed controller to be a better choice. After extensive mathematical analysis and simulation results, we can conclude that the proposed controller provides better control over plants along with having a simpler structure.