Generalizations of the Fibonacci Sequence with Zig-Zag Walks

Abstract

The examination of the recurrence sequences associated with combinatorial constructions has been very extensive in the last decades. One of the most famous recurrence sequences is the Fibonacci sequence. We give two digraph constructions defined on the hyperbolic and on the Euclidean square mosaics, respectively, and we introduce two zig-zag type walks associating to the Fibonacci and its generalized sequences. Then we determine the recurrence relations and we give some examples.

1 Introduction

The investigation of the generalizations of Pascal’s arithmetic triangle has an extensive literature. One generalization is the hyperbolic Pascal triangle defined on a regular squared grid given by Schläfli’s symbol $\{4,q\}$, $q\ge 5$. Belbachir, Németh, and Szalay [1] described some interesting properties. One is that the Fibonacci sequence appears in this structure along a suitable zig-zag walk, considering the directed graph form of the hyperbolic Pascal triangle. Németh and Szalay [2] examined other types of zig-zag walks and presented more recurrence sequences assigned to the hyperbolic Pascal triangle.

The present paper summarizes the studies of diagonal and zig-zag paths on a particular $k+1$ wide, infinite part of the usual Euclidean square lattice as well. Along these paths Németh, and Szalay [3] determined linear recurrence sequences considering a special type of generalized Fibonacci sequences and that are mostly defined in the On-Line Encyclopedia of Integer Sequences (OEIS, [4]). Moreover, we show a new occurrence of the Fibonacci sequence associated with the coefficient of these recurrence sequences.

2 Recurrence Sequences Associated to the Walks on the Hyperbolic Pascal Triangle

In the hyperbolic plane, there are infinite types of square regular mosaics, they are denoted by Schläfli’s symbol $\{4,q\}$, where q satisfy $q>4$. The parameter q means that in one node of the mosaic exactly q regular square meet. Each square regular mosaic induces a hyperbolic Pascal triangle $\mathcal{HPT}$ based on the mosaic $\{4,q\}$, and they can be figured as a digraph, where the vertices and the edges are the vertices and the edges of a well-defined part of the lattice $\{4,q\}$, respectively, further each vertex possesses the value which gives the number of different shortest paths from the base vertex. Fig. 1 illustrates the hyperbolic Pascal triangle $\mathcal{HPT}_{\!\{4,5\}}$. The values of the most left and most right nodes are 1’s and the values inside the triangle are the sums of incoming values (for more details, see Fig. 1 and [1]). In the sequel, we fix the type of $\mathcal{HPT}$ given by mosaic $\{4,5\}$.

Fig. 1

Fibonacci and Pell sequences in the hyperbolic Pascal triangle $\{4,5\}$

Examining the triangle $\mathcal{HPT}_{\!\{4,5\}}$ thoroughly in Fig. 1 and starting a walk from the root vertex, continuing with one-step left and one-step right, then again one-step left, one-step right, and so on—shortly $L,R,L,R,L,\ldots$ (follow the red edges), we find that the values of nodes along this zig-zag walk are the terms of the Fibonacci sequence (defined by $F_0=0$, $F_1=1$ and $F_n=F_{n-1}+F_{n-2}$). Considering a similar zig-zag walk, first we step left and right, second right and left, and so on—shortly $LR,RL,LR,RL,\ldots$ (blue walk), the Pell sequence (defined by $P_0=0$, $P_1=1$ and $P_n=2P_{n-1}+P_{n-2}$ for $n\ge 2$) appears.

It is easy to show (see [2]) that each pair $i<j\in \mathbb {Z}^+$ can be found next to each other in $\mathcal{HPT}_{\!\{4,5\}}$.

Theorem 1

([1, 2]) Assume $\alpha \in \mathbb {Z}^+$, $f_0<f_1\in \mathbb {Z}^+$, and $f_0$ (in the second case $f_1-f_0$) is the left neighbor of $f_1$. Then binary recurrence sequences

$$\begin{aligned} f_{n}=\alpha f_{n-1}\pm f_{n-2}, \quad (n\ge 2) \end{aligned}$$

appear in the triangle $\mathcal{HPT}_{\!\{4,5\}}$ along zig-zag walks.

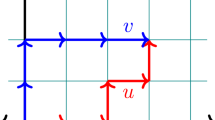
Table 1 shows the information about the location of the terms of the sequences. Here, for example, $LR^{\alpha -1}$ means that going down from a given element having type red circle, via elements type red circle, first turn left, and then ($\alpha -1$)-times right. For illustration, see Fig. 2, when the pattern of steps in the zig-zag walk is LRR (or LLR).

Table 1 Location of the sequences

Fig. 2

Appearance of $f_n=4f_{n-1}-f_{n-2}$, $f_0=1$, $f_1=2$ in $\mathcal{HPT}_{\{4,5\}}$

3 Recurrence Sequences Associated to the Walks on an Euclidean Square Grid

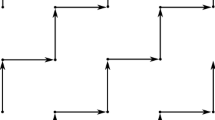
Consider the Euclidean square lattice and take k consecutive pieces of squares. This is the 0th layer of the k–zig-zag shape. The upper corners are the 1st, 2nd, $\ldots$, kth and $(k+1)$st vertices according to Fig. 3. Extend this by an extra 0th vertex, which is the base vertex. We color it yellow in the figures, and we join it to the 1st vertex by an extra edge. We denote the vertices of the 0th line by small boxes in Fig. 3. Now move the 0the layer to reach the right-down position in the square lattice to obtain the 1st layer, and repeat this procedure with the latest layer infinitely many times. Thus, we define the square k–zig-zag shape or graph, where $k\ge 1$ is the size of the array. Finally, we label the vertices such that a label gives the number of different shortest paths from the base vertex. Figure 4 illustrates the first few layers of the square 4–zig-zag digraph, the vertices are denoted by shaded boxes with their label values and the directed edges are the black arrows. Let $a_{i,j}$ denote the label of the vertex located in ith row and jth position ($0\le j\le k+1$, $0\le i$). Clearly, the fundamental rule of the construction is given by

$$\begin{aligned} a_{i,j}={\left\{ \begin{array}{ll} 1, &{} \text { if } i=0; \\ a_{i-1,1}, &{} \text { if } j=0, 1\le i;\\ a_{i,j-1}+a_{i-1,j+1}, &{} \text { if } 1\le j\le k, 1\le i; \\ a_{i,k}, &{} \text { if } j=k+1, 1\le i. \end{array}\right. } \end{aligned}$$

(1)

Fig. 3

Zig-zag shape

For fixed $k\ge 1$ and given $0\le j\le k+1$, let $A_j^{(k)}$ be the sequence defined by $A_j^{(k)}=(a_{i,j})_{i=0}^{\infty }$. The sequence $A_j^{(k)}$ is the jth right-down diagonal sequence of the square k–zig-zag shape. In Fig. 4, the blue arrows represent the sequence $A_1^{(4)}$. We found $A_0^{(k)}= (1,A_{1}^{(k)})$ and $A_k^{(k)}= A_{k+1}^{(k)}$. These sequences are associated with the zig-zag walks with patterns $RL,RL,RL,\ldots$.

Fig. 4

Square 4–zig-zag digraph ($k=4$)

Let $Z_j^{(k)}$, $j\in \{0,1,\ldots ,k\}$ be the jth zig-zag sequence of the square k–zig-zag shape, where $Z_j^{(k)}$ is the merged sequence of $A_j^{(k)}$ and $A_{j+1}^{(k)}$. (In Fig. 4, the red arrows represent the zig-zag sequence $Z_3^{(4)}$). More precisely, $Z_j^{(k)}=(z_{i,j})_{i=0}^{\infty }$, where

$$\begin{aligned} z_{i,j}={\left\{ \begin{array}{ll} a_{\ell ,j}, &{} \text { if } i=2\ell ; \\ a_{\ell ,j+1}, &{} \text { if } i=2\ell +1. \end{array}\right. } \end{aligned}$$

(2)

Since $Z_0^{(k)}$ and $Z_k^{(k)}$ are the ‘double’ of $A_0^{(k)}$ and $A_k^{(k)}$, respectively, usually we examine sequences for $j\in \{1,2,\ldots ,k-1\}$. The $Z_j^{(k)}$ sequences are associated with the zig-zag walks with patterns $R,L,R,L,R,L,\ldots$.

We find that any item $a_{n,j}$, $(n\ge 1)$ is the sum of the certain items of $(n-1)$st row. More precisely, if $0<j<k+1$, then we obtain the system of recurrence relations

$$\begin{aligned} a_{n,j}=a_{n-1,j+1}+a_{n,j-1}=a_{n-1,j+1}+a_{n-1,j}+a_{n,j-2}= \cdots = \sum _{\ell =1}^{j+1}a_{n-1,\ell }. \end{aligned}$$

(3)

Let $p_k(x)$ be the characteristic polynomials of kth recurrence of system (3), then the following theorem holds.

Theorem 2

([3], Theorem 4) The characteristic polynomials $p_k(x)$ can be given by

$$\begin{aligned} p_k(x)=x^{\left\lceil {\frac{{k}}{2}}\right\rceil } \sum _{i=0}^{{\left\lfloor {\frac{{k}}{2}}\right\rfloor +1}} (-1)^i \left( {\begin{array}{c}k+2-i\\ i\end{array}}\right) x^{{\left\lfloor {\frac{{k}}{2}}\right\rfloor +1}-i}, \qquad k\ge 0. \end{aligned}$$

(4)

Now we record the two theorems of zig-zag sequences. The first one is the corollary of Theorem 2 and the second is a simple corollary of the first one.

Theorem 3

Given $k\ge 1$. Then all the right-down diagonal sequences $A_j^{(k)}$ for $j\in \{0,1,\ldots ,k,k+1\}$ have the same $({\left\lfloor {\frac{{k}}{2}}\right\rfloor +1})$-th order homogeneous linear recurrence relation

$$\begin{aligned} a_{n,j}= \sum _{i=0}^{{\left\lfloor {\frac{{k}}{2}}\right\rfloor }{}} (-1)^{i} \left( {\begin{array}{c}k+1-i\\ i+1\end{array}}\right) a_{n-1-i,j}, \qquad n\ge {\left\lfloor {\frac{{k}}{2}}\right\rfloor +1}. \end{aligned}$$

(5)

Theorem 4

Fixing $k\ge 1$, the zig-zag sequences $Z_j^{(k)}$ for $j\in \{0,1,\ldots ,k\}$ satisfy a $(2{\left\lfloor {\frac{{k}}{2}}\right\rfloor }{+2})$-th order homogeneous linear recurrence relation given by

$$\begin{aligned} z_{n,j}= \sum _{i=0}^{{\left\lfloor {\frac{{k}}{2}}\right\rfloor }{}} (-1)^{i} \left( {\begin{array}{c}k+1-i\\ i+1\end{array}}\right) z_{n-1-2i,j}, \qquad n\ge 2{\left\lfloor {\frac{{k}}{2}}\right\rfloor }{+2}. \end{aligned}$$

Fig. 5 illustrates the 3-zig-zag graph and the zig-zag walk when appeared sequence is the Fibonacci sequence.

Fig. 5

Fibonacci sequence associated to zig-zag walk in 3-zig-zag graph

Expressing the item $a_{n,j}$ from Eq. (5) we obtain the result of Theorem 3. For example, the first few recurrence relations are

$$ \begin{aligned} k=0:{} & {} a_{n,j}=a_{n-1,j},\\ k=1:{} & {} a_{n,j}=2a_{n-1,j},\\ k=2:{} & {} a_{n,j}=3a_{n-1,j}-a_{n-2,j},\\ k=3:{} & {} a_{n,j}=4a_{n-1,j}-3a_{n-2,j},\\ k=4:{} & {} a_{n,j}=5a_{n-1,j}-6a_{n-2,j}+a_{n3,j},\\ k=5:{} & {} a_{n,j}=6a_{n-1,j}-10a_{n-2,j}+4a_{n-3,j},\\ k=6:{} & {} a_{n,j}=7a_{n-1,j}-15a_{n-2,j}+10a_{n-3,j}-a_{n-4,j},\\ k=7:{} & {} a_{n,j}=8a_{n-1,j}-21a_{n-2,j}+20a_{n-3,j}-5a_{n-4,j},\\ k=8:{} & {} a_{n,j}=9a_{n-1,j}-28a_{n-2,j}+35a_{n-3,j}-15a_{n-4,j}+a_{n-5,j},\\ k=9:{} & {} a_{n,j}=10a_{n-1,j}-36a_{n-2,j}+56a_{n-3,j}-35a_{n-4,j}+6a_{n-5,j},\\ k=10:{} & {} a_{n,j}=11a_{n-1,j}-45a_{n-2,j}+84a_{n-3,j}-70a_{n-4,j}+21a_{n-5,j}-a_{n-6,j}. \end{aligned} $$

We consider the sum of the absolute values of the coefficients of these recurrence sequences (the left-hand side as well), and we gain the first few items of the Fibonacci sequence. Generally, using the well-known properties of Pascal’s triangle that the rising-up diagonal sum sequence of Pascal’s triangle is the Fibonacci sequence, so

$$\begin{aligned} \sum _{v=0}^{{\left\lfloor {\frac{{u}}{2}}\right\rfloor }{}} \left( {\begin{array}{c}u-v\\ v\end{array}}\right) =F_{u+1}, \end{aligned}$$

and from Eq. (5) when $u=k+2$ and $v=i+1$ we obtain

$$\begin{aligned} \sum _{i=0}^{{\left\lfloor {\frac{{k}}{2}}\right\rfloor }{}} \left( {\begin{array}{c}k+1-i\\ i+1\end{array}}\right) =F_{k+3}-1. \end{aligned}$$

Fig. 6 illustrates this coefficient sequence.

Fig. 6

Fibonacci sequence in Pascal’s triangle

Moreover, considering the polynomials $p_k(x)$ of Eq. (4) we find that for non-negative integer $x=m$ the sequence of polynomials $p_k(x)$ becomes integer recurrence sequence with recurrence

$$\begin{aligned} p_k(m)=m p_{k-1}(m)- p_{k-2}(m),\quad k\ge 1, \end{aligned}$$

where the initial values are $p_{-1}(m)=1$ and $p_{0}(m)=m$. For the first few m the sequences appear yet in OEIS (see Table 2).

Table 2 Sequences in OEIS