Hydrodynamic Analysis and CFD Modeling of PAWEC Interacted with Regular Waves Using CFX

Abstract

The multiplicity of renewable energy sources represents the biggest challenge for environmental scientists and engineers. This research presents a mathematical model and a numerical study using the high-performance ANSYS-CFX software to analyze the dynamic behavior of the point absorber wave energy converter (PAWEC). Two different models were constructed to predict the hydrodynamic response of the wave energy converter in both free and forced oscillations under the action of incident regular waves and external mechanical damping. The differential equations are solved analytically using RKFOM. CFX multiphase model is constructed to solve the 3D Unsteady Reynolds Averaged Navier–Stokes Equation (URANS) using the two-way Fluid–Structure Interaction (FSI) technique. The regular waves were generated in a numerical wave tank, by using a flap-type wavemaker. Mesh densities and solver settings were performed. The numerical results in both models, CFD and RKFOM, are validated against published experimental and numerical data under the same conditions, and the numerical results agreed with both published data. Two additional designs for the body bottom, conical and spherical shapes, were analyzed based on the presented numerical method. The damping coefficient and added mass are obtained for each design in the case of heave motion only.

1 Introduction

The numerical simulation of multiphase applications, coupled with the interaction between the fluids and movable structure, requires a high-performance CFD code. Many CFD platforms are followed for this purpose, especially in ocean engineering. ANSYS-AQWA software is a simple CFD platform accompanied by offshore hydrodynamics in open water which provides an integrated facility for developing primary hydrodynamic parameters required to undertake complex motions and response analysis [1]. OpenFOAM is an open-source CFD software that provides a wide range of features to solve both fluid flows and solid mechanics, it is a C++ toolbox for the development of customized numerical solvers which gave a higher mixing level compared to other software, but it needs a professional programmer [2]. ANSYS-CFX is a high-performance CFD software distinguished for exceptional accuracy and high convergence speed, especially in multiphase applications [3]. CFX can be used to generate a single run to create full operating maps with a simple integration process. Using ANSYS-CFX in the simulation of numerical wave tanks (NWTs) with the corresponding wave energy converters (WECs) provides a broad visualization of both fluid characteristics as well as the hydrodynamic of floating bodies [4].

The numerical simulation of wave energy converters (WECs) is the focus of researchers’ efforts in the last decades. The main challenge facing each researcher is to develop the device's efficiency to produce energy and reduce the cost of power [5]. Most of the previous work uses the numerical simulation by ANSYS-AQWA and OpenFOAM; the experimental setup in this field requires special equipment and a great effort, whether in the preparation of movement receptors or the difficulty of extracting results. Jin, Siya [6] construct a 1/50 scale PAWEC in a wave tank to validate the CFD model generated to study the effect of the floating body geometry and the power take-off (PTO) damping on the wave energy absorption. The mathematical model of PAWEC behaviors was performed using two different models, the first is the non-linear state-space model (NSSM) considering a quadratic viscous term, second is the linear state-space model (LSSM). Three different geometries were investigated in this paper using ANSYS/AQWA software: a flat-bottom cylinder, a hemispherical bottom cylinder, and conical bottom with right streamline angle. The experimental data was compared with the two mathematical models and validated with CFD model using ANSYS-AQWA. Jin, Siya concluded that the flat-bottom cylinder has more damping coefficient, and therefore, more added mass than the other designs by 60%. Moreover, the best design is the conical bottom cylinder, which produced max stroke length 100% more than other designs. The selected design was subjected to PTO damping, and therefore, the optimal power is increased by 70% in both regular and irregular waves. Josh et al. [7] used OpenFOAM to investigate the implementation of NWT containing a rigid body solution. The capabilities of NWT were outlined in the case of fluid–structure interaction between cylindrical floating bodies and incident irregular waves generated using the JONSWAP spectrum. Fifty frequencies were used, which were regularly distributed between 0 and 0.5 Hz with 10 s period and different phases. The body motion was analyzed using two ways, one way is the prescribed way to define the hydrodynamic forces concerning the displacement and time, and another way is the numerical simulation to predict the dynamic response of the body against contribution waves and PTO applied force. Shadman et al. [8] used ANSYS-AQWA software to analyze the hydraulic diffraction of cylindrical PAWEC to optimize the geometry based on the maximization of absorbed power and absorption bandwidth in case of natural conditions nearshore region of the Rio de Janeiro coast. The technique of joint probability distribution and resultant wave spectrum was used to perform the optimization method. The two primary advantages of this optimization method are the reduced computational time and the possibility of performing parametric analyses for the WEC geometry. Sjökvist et al. [9] analyzed the hydrodynamic parameters of cylindrical PAWEC using a CFD model built-in Multiphysics simulation software COMSOL and a numerical linear model computed by WAMIT. The linear model of the interaction between the incident waves and a floating structure is solved for the excitation forces, radiation damping, and added mass using green’s theorem by integrating the diffraction and radiation velocity potentials in closed surfaces extracted from a 3D panel program WAMIT. The numerical results are validated against an experimental work, the hydrodynamic parameters computed with the COMSOL model show good agreement with the ones computed using WAMIT. Ghasemi et al. [10] presented a numerical computational method to solve the 2D Navier–Stokes equations governing the behavior of flow field interacted with two types of WEC, cylindrical and rectangular cross-sectional shape. The fluid–structure interaction parameters were determined using the VOF method; NWT technique was used to generate the waves by using both Flape-type and piston-type wavemakers. The numerical model was obtained by several degrees of freedom in both floating bodies, heave motion for the cylindrical body against incident waves, and a free-fall test, free rotational pitch motion for the rectangular shape. This paper presented the change in floating system efficiency with respect to the coefficient of damping, the maximum efficiency obtained at single degree of freedom wih value 0.5. Büchner et al. [11] constructed a 3D numerical model using ANSYS-fluent to predict the dynamic response of a single degree of freedom floating cylinder against a regular wave. The horizontal and vertical forces on the float due to drag and inertia loads were presented in case of different values of wave amplitudes and frequencies. The effect of irregular wave on the float dynamics was recommended in the future work.

Devolder et al. [12] construct an experimental measurement to validate the CFD results for an array of up to nine semi-circular WECs under the effect of regular waves. The frictional forces and heave motion are presented in both experimental and numerical studies. Rijnsdorp et al. [13] presents a numerical simulation for the interaction between the incident waves and a fully submerged wave energy converter using the non-hydrostatic framework on large scales. This research demonstrates both linear and non-linear waves with a cylinder shape of WEC connected by a mooring line. The results of the linear waves were validated with an analytical solution in both diffraction, radiation, and dynamic response. Jin et al. [14] investigate the non-linear viscosity effect of a wave energy converter prototype with a scall 1/50 by studying the hydrodynamics loads. The point absorber WEC in this paper was designed with only heave motion in the experimental part. The mathematical model of PAWEC behaviors was performed using two different models, the first is the non-linear state-space model (NSSM) considering a quadratic viscous term, the second is the linear state-space model (LSSM). The experimental data were compared with the two mathematical models and validated with the CFD model using ANSYS-AQWA. the main objective of this paper is to achieve the optimal power of the device and to maximize the conversion efficiency by indicating the performance of the device at the resonance case. Zhu and Lim [15] constructed a flume experiment for design optimization of a cylindrical wave energy converter which leads to reducing the undesirable motions due to the surrounding environment. A heave plate is recommended to be mounted with the floating body to reduce these motions. Several experimental tests are performed with different heave plates at various gaps in the body. The response amplitude operator RAO for the cylinder with a heave plate was 40% less than that without plates. Weller et al. [16] set up experimental measurements for the 2D motion of WEC under the action of regular and irregular extreme waves. The translation motion, in both directions, and rotation motion (heave, surge, and pitch) were presented using an optical encoder and the analysis of video footage. The relation between the body and the wave is linear in low frequencies, however, in extreme sea-state conditions, the heave motion and wave breaking are presented to predict the hydrodynamic response of WECs in high frequency.

Our need for validated numerical analysis is increasing in the field of wave energy, especially with the presence of published experimental results and with the difficulty of implementing those experiments. Some of these numerical studies will be mentioned in this section, which will contribute to providing the best in this research. The construction of an NWT capable of creating a variety of waves and being able to study the behavior of the buoy under the influence of those waves is the main objective of this research. Shehab et al. [17] constructed an NWT that can simulate both regular and irregular waves in form of wave spectra. Flap-type wavemaker technique was applied for this purpose using CFX software. The generated regular wave was validated against the wavemaker theory WMT, while the irregular wave was validated against experimental data with real sea conditions in the frequency domain. Very useful parameters were discussed in this research that will greatly contribute to the present work. Finnegan and Goggins [18] used CFX to investigate the effect of using a flap-type wave maker to generate regular waves in both deep and shallow water depths. This method is limited to a low normalized wavenumber. The change of hinge location reduced these limitations.

After the previous work, the modeling of the NWTs using CFX is more effective due to the wide range of parameters provided by CFX which leads to a good understanding of the PAWEC hydrodynamics, CFX is a good choice for executing a CFD-based NWT. The main objective of this research is to understand the hydrodynamics of fluid–structure interaction between a partially submerged free-floating body with an incident regular and irregular generated waves inside NWT through a commercial CFD software CFX, which is rarely used in this field. The followed method used in this research has been presented in a detailed manner in addition to studying the extent of its usability compared to the rest of the methods presented above in the literature. The numerical results are validated against previous experimental data in the same conditions and body geometry.

2 Methodology and Problem Setup

Most of the previous research constructs an NWT using simple computational methods that provide a limited range of parameters as mentioned in the literature. Using CFX to construct an NWT requires more effort and additional techniques than other CFD simulation methods, the formation of NWT using CFX is like creating a miniature model of an integrated lab that gives all the useful results for understanding the factors affecting both the fluid and the moving body. The numerical model in this study consists of two phases for the fluid, air, and water, in addition to a solid phase for the floating body. The differential equations governing the fluid flow inside NWT are presented and solved for both velocity and momentum with a proper boundary condition describing the layers of the tank, an additional equation is applied for the solution of Volume Fraction VF of the fluids to determine the vertical position of the free surface at any time. Newton's second low was applied for the solution of solid phase model under the effect of diffraction, radiation, and excitation forces in heave motion only. Two different approaches are used for the solution of the mathematical model, first by using ANSYS-CFX (release 14.5) approach, the second method is to transform the FSI system to a simple harmonic motion followed by a numerical technique to solve the differential equations called RKFOM. A great effort was made to construct the combination between NWT and movable body using CFX. The two approaches are validated, in the case of free-fall test of the float in the still water, with published experimental work carried out in similar conditions by Guo et al. [19]. The validated model is then used to investigate the damping coefficient and added mass term for several designs of the float operating surface, conical and spherical profiles with the same mass are tested in the free-fall conditions to study the effect of bottom design on motion behavior. The design with the best results was tested against regular and irregular waves generated by a Flap-type wavemaker located at the inlet of the tank, the recommendations mentioned in the research submitted by Shehab et al. [17] regarding the wave generation in NWT were taken into consideration.

3 Mathematical Model

The fluid model in CFX consists of two phases separated by a free surface, the flow of water is considered incompressible in the transient scheme. The 3D form of both continuity and momentum differential equations are solved for velocity and pressure, respectively. The governing equations are defined as [20]. Continuity equation

$$\nabla . \overrightarrow{v}=0, \overrightarrow{v}=\dot{x}\widehat{i}+\dot{y}\widehat{j}+\dot{z}\widehat{k},$$

(1)

where $\overrightarrow{v}$ is the velocity vector, and $\dot{x}, \dot{y}, \dot{z}$ represent the velocity components along the coordinate axes. Momentum equation

$$\frac{\partial (\uprho \overrightarrow{\mathrm{v}})}{\partial \mathrm{t}}+ \nabla .\left(\uprho \overrightarrow{\mathrm{v}}\overrightarrow{\mathrm{v}}\right)=-\nabla \mathrm{P}+\uprho \overrightarrow{\mathrm{g}}+\nabla .\left(\overrightarrow{\uptau }\right),$$

(2)

where P is the static pressure, $\uprho$ is the fluid density, $\overrightarrow{\uptau }$ is the stress tensor, the reference of the coordinate system is located at the centerline of the buoy coincidence with the still water level at the equilibrium position of the buoy. The finite Volume Method FVM is used to solve the previous governing equations in CFX [3]. The simulation of the water-free surface, with respect to time, requires two additional differential equations for the solution of the volume fraction VF for both water ${q}_{w}$ and air ${q}_{a}$. The total summation of volume fractions is equal to 1. The instantaneous position of the free surface is estimated using the minimum value of $\left|{q}_{w}-{q}_{a}\right|$ across the domain. The governing equations for this method, Volume of Fraction VOF, are derived by Liang et al. [21] and defined in the following equations.

$$\frac{\partial ({\mathrm{q}}_{a})}{\partial \mathrm{t}}+\dot{x}\frac{\partial ({\mathrm{q}}_{a})}{\partial \mathrm{x}}+\dot{y}\frac{\partial ({\mathrm{q}}_{a})}{\partial \mathrm{z}}+\dot{z}\frac{\partial ({\mathrm{q}}_{a})}{\partial \mathrm{z}}=0,$$

(3)

$$\frac{\partial ({\mathrm{q}}_{w})}{\partial \mathrm{t}}+\dot{x}\frac{\partial ({\mathrm{q}}_{w})}{\partial \mathrm{x}}+\dot{y}\frac{\partial ({\mathrm{q}}_{w})}{\partial \mathrm{z}}+\dot{z}\frac{\partial ({\mathrm{q}}_{w})}{\partial \mathrm{z}}=0.$$

(4)

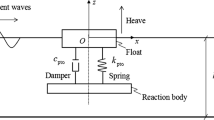
The solid model in CFX is investigated using rigid body dynamics. The float is a cylindrical shape with a curved bottom (S) (see Fig. 1). The mass of the buoy is equal to the displaced fluid in the equilibrium position (at $\Delta z=0$). A single degree of freedom model is used in only heave motion, therefore, the terms of the rotational moment of inertia are eliminated from the differential equations. The differential equations, governing the dynamics of the float, are derived using Newton’s second law (5), and the total forces (gravitational, hydrodynamics, and mechanical) are analyzed in Eq. (6). Sjökvist et al. [9]

Fig. 1

The floating body at displacement Z above the water-free surface

$$\sum \mathop{F}^{\rightharpoonup}=\frac{d}{dt}\left(m*\mathop{v}^{\rightharpoonup}\right),$$

(5)

$${\mathop{F}^{\rightharpoonup}}_{g}+{\mathop{F}^{\rightharpoonup}}_{e}\left(t\right)+{\mathop{F}^{\rightharpoonup}}_{pto}\left(\dot{z}\right)+{\mathop{F}^{\rightharpoonup}}_{h}\left(z,s\right)+{\mathop{F}^{\rightharpoonup}}_{s}\left(\dot{z}\right)+{\mathop{F}^{\rightharpoonup}}_{a}\left(\ddot{z}\right)=m\dot{\mathop{v}^{\rightharpoonup}},$$

(6)

${\mathop{F}^{\rightharpoonup}}_{g}= -mg \widehat{k}$: Gravitational force, constant and directed along negative Z-Direction. ${\mathop{F}^{\rightharpoonup}}_{e}\left(t\right)={C}_{e}*\delta \left(t\right) \widehat{k}$: The excitation force is due to the interaction between the buoy and the externally generated waves. ${C}_{e}$ is the coefficient of the radiation response, $\delta (t)$ is the surface elevation function. ${\mathop{F}^{\rightharpoonup}}_{pto}\left(\dot{z}\right)= -{C}_{pto}*\dot{z}(t) \widehat{k}$: The mechanical loads of the power take-off mechanism due to friction and damping of the mechanical elements. ${C}_{pto}$ is the damping coefficient of the PTO mechanism, $\dot{z}(t)$ is the vertical component of the velocity as a function of time. ${\mathop{F}^{\rightharpoonup}}_{h}\left(z,s\right)=\rho g\left[{A}_{c}\left({H}_{0}-Z(t)\right)+V\left(S\right)\right]\widehat{ k}$: The hydrostatic forces due to buoyancy, variable force depending on the position of the float Z(t), and the bottom surface profile of the buoy (S) which is exposed to the fluid. ${H}_{0}$ is the submerged depth of the float in the equilibrium position, ${A}_{c}$ is the cross-sectional area of the cylinder, $V\left(S\right)$ is the volume of the curved portion below the buoy. ${\mathop{F}^{\rightharpoonup}}_{s}\left(\dot{z}\right)= \mu {A}_{s}\left(\frac{\partial \mathop{v}^{\rightharpoonup}}{\partial r}\right)=-\frac{\mu {A}_{s}}{\Delta r}(\dot{Z)}\widehat{ k}$: the shear stress forces acting on the longitudinal surface of the float due to fluid viscosity and friction. $\frac{\partial \mathop{v}^{\rightharpoonup}}{\partial r}$ is the flow velocity gradient, $\mu$ is the dynamic viscosity of the fluid, ${A}_{s}$ is the longitudinal surface area normal to the vertical axis, $\Delta r$ denotes the radial distance from the body surface to the nearest zero shear stress location. ${\mathop{F}^{\rightharpoonup}}_{a}\left(\ddot{z}\right)= -{m}_{a}\ddot{z} \widehat{k}$: the equivalent added mass term due to the fluid dissipation around the float as a result of fluid linear inertia. ${m}_{a}$ is the added mass. Ghasemi et al. [10].

The numerical model of the float dynamics with a single degree of freedom can be simplified to a spring-damping model with a general Eq. (7) only in heave motion along the vertical axis as

$$\left(M\right)\ddot{Z}\left(t\right)+\left({C}_{d}\right)\dot{Z}\left(t\right)+\left(K\right)Z\left(t\right)={F}_{ext}\left(t\right),$$

(7)

where $M$ denotes the equivalent mass of the system [kg], defined as $M=m+{m}_{a}$, ${C}_{d}$ represents the equivalent damping coefficient [kg/s], defined as ${C}_{d}={C}_{pto}+\frac{\mu {A}_{s}}{\Delta r}$, $K$ denotes the spring constant of the system [kg/s2], defined as $K=\rho g{A}_{c}$, ${F}_{ext}(t)$ denotes the total external forces of the incident-generated wave excitation [N].

3.1 CFD Model and Boundary Conditions

Two different NWTs are constructed for both the free-fall test model and the interaction between the float and excited wave. Davidson et al. [22] recommended using a circular NWT for the free-fall test model when using OpenFOAM. The main idea of the free-fall test is to adjust the float at a certain vertical displacement (∆z) above its equilibrium position, this action gives the device initial potential energy which leads to a restoring motion when leaving it free to move, then the float is dropped from rest to move with the gravitational force in the downward direction, the speed increases in the first stage of the movement as the forces of gravity overcome the rest of the total hydrodynamic forces acting on the float, the device starts to approach its equilibrium position, the potential energy of the device is converted to kinetic energy which causes increase in its velocity, the float begins to slow down till it comes to rest again in the lowest position as the hydrostatic forces overcome the float weight. The energy was dissipated due to the surrounding fluid damping effects. Accordingly, the device continues to oscillate, up by the buoyancy effects and down by the body weight, around its equilibrium position, the amplitude will be reduced by time depending on the amount of dissipating energy in each stroke and the damping coefficient arising from the shear stresses of the surrounding fluid and the PTO resistance. Finally, the device comes to rest in the equilibrium position. The free-fall test was performed experimentally by Guo et al. [19] in a wide-range tank to absorb the wave at tank walls. Jin et al. [6], Zhu and Lim [15], Angense [23], and Devolder et al. [24] used a rectangular NWT generated by other CFD approaches. A rectangular NWT is used in this research for both the cases as shown in Fig. 2; The free-fall test model is subjected to a simple boundary condition. A symmetric plane was used parallel to XZ coordinate plane, tank wall and seabed were treated as fixed walls with no-slip conditions, the free surface was set as interface subjected to a dynamic mesh related to the change in fluid volume of fraction method, the buoy was defined as a rigid body subjected only to hydrostatic forces in this model without other external effects, the buoy diameter is D with submerged height Ho. The numerical beach is not activated in this model because the wave generated by the free movement of the buoy is rather small compared to the generated wave by the Flap in the second model.

Fig. 2

Rectangular NWT for the free test model

A second model with the sane NWT used for FSI, with incident-generated wave using Flap-type wavemaker, and numerical beach NB is used, as shown (see Fig. 2). The boundary conditions for the three phases are set as followed; inlet plane is a flapper subjected to a rotational motion about fixed hinge located below the free surface by distance ho, the position of the movable plane is defined in Eqs. (8), and (9), Eldeen et al. [17]. The top plane is divided into two regions, the first region in the wave generation region is considered as a wall with a dynamic mesh technique to adjust the motion of the inlet plane, and the second region is considered as a fixed wall with zero-gauge pressure. The outlet plane is defined as the opening domain with a pressure gradient from the seabed to the top plane. The seabed is divided into three sections; the first section inside the wave generation region is defined as a movable surface in XY plane subjected to dynamic mesh technique, the second section inside the wave propagation region is considered as a fixed wall with no-slip conditions, the third section is the numerical beach NB designed with a 1:5 sloped surface to reduce the wave reflections from outlet plane [17]. An asymmetric plane is used to reduce the time of calculations. Lal's et al. [25] recommendations for using a Flap-type wavemaker are taken into consideration. The technical information based on wave simulation and wave absorption in NWT using CFX is explained in detail by the author in a related paper [17].

$$X={S}_{max}*\frac{Z+{h}_{o}}{{h}_{a}+{h}_{o}},$$

(8)

$${S}_{max}={A}_{f}\mathrm{sin}\left(\omega t\right),$$

(9)

where ${S}_{max}$ is the flap position at the upper plane of the model, ${A}_{f}$ is the maximum stroke length in the top plane, the air height is ${h}_{a}$, ${h}_{o}$ is the fixed hinge depth. The x position of the inlet plane (Flapper) is varying from one point to another depending on the z position and flow time.

3.2 Grid Independence Test

ANSYS design modeler is used to discretize the model into a finite tetrahedron shape compatible with the dynamic mesh in 3D modeling. To detect the small change in buoy position and free surface of the fluid, 15 inflation layers with a total thickness of 0.2 m were used around the water-free surface and the buoy surface. The minimum element size is tested to check the independence of the mesh, seven cases were generated for this purpose. The float is displaced 5 cm above the equilibrium position before it falls from rest, the time step size in this test is selected with a small value of 0.001 s to produce a high sensitivity for buoy oscillations [22]; the float is of 1 m in diameter, 0.5 m immersed in height, and 392.7 kg in total mass (MO-1). The external force on the buoy was eliminated, and the PTO damping coefficient is set to zero in this test. Figure 3 shows the change of the vertical displacement of the buoy against time, in the first 10 s of motion, in each case. The damping coefficient is plotted in each case to monitor the independence of cell size use; Fig. 4.

Fig. 3

The normalized vertical displacement of the float at ∆z = 0.05 cm and time step size ∆t = 0.001 s (MO-1)

Fig. 4

Damping coefficient variation in each case for grid independence test (MO-1)

The zones near the floating body and the free water surface have meshed with fine cells, and the size of elements increased away from the floating body and near the tank walls, top, and bottom planes, this procedure is followed to reduce the total number of elements and therefore reduce the time of calculation. The accepted minimum element size near the movable surfaces, free water surface, and float, is 0.05 m which is equivalent to 1/20 of the float diameter with a total number of elements is 2 M, average skewness is 0.2, the mesh quality was tested to be larger than 0.75 around the contact surfaces. Figure 5 shows the grid distribution around the float.

Fig. 5

3D Mesh for the model

3.3 Time Step Size Test

Determining the appropriate time step size value for all the different modeling processes contributes greatly to obtaining more accurate results, as it is a very influential factor in the time of calculations. The values for time step size vary from one simulator system to another, Davidson et al. [22] developed a new methodology to study the hydrodynamic models in the simulation of WECs. The results of this new methodology were validated using boundary-element methods (BEMs) in the linear case only (heave motion). The recommended value of time step size by Josh in 2015 is 0.001 s when using OpenFOAM software, this time step is selected to produce a maximum courant number of 0.3 which keeps an acceptable accuracy with a high-speed calculation [22]. A numerical case study in similar conditions was constructed using CFX software to detect the difference in numerical methods to predict the small oscillations of the floating body. A cylindrical buoy with a total height of 1 m (0.5 m immersed height) and a diameter of 1 m was used in a free-fall case (MO-2). The initial displacement in this test is 10 cm above the free surface, the total time is 12 s. The transient scheme used in this model is 2nd order backward Euler, and the solution method is second-order for both continuity and momentum equations. The PTO damping is eliminated in this test, five cases were generated with different time step sizes starting with 0.01 s which produces the minimum damping coefficient, a small deviation in dynamic response between the last two cases 0.002 s and 0.001 s. Figure 6 shows the normalized vertical displacement of the float in free-fall test by CFX compared with the published data by OpenFOAM.

Fig. 6

The dynamic response of the float at different time step sizes by CFX compared with published data (∆z = 10 cm -MO-2)

The damping coefficient in each case and the independence of time step size are presented in Table 1. The recommended time step size in wave modeling using numerical wave tanks is T/60 according to [17]. In this research, the time step size is recommended to be T/925 in the numerical modeling of wave structure interaction compared with T/1840 as recommended in OpenFOAM.

Table 1 Independence of time step size using CFX in free-fall test

4 Validation of the Numerical Results

The previous study shows that there is a noticeable difference in the results of both numerical methods, the numerical results in this research are validated against published experimental data by Guo et al. [19] in the same conditions to check the ability of the mathematical model to predict the hydrodynamics and the applied forces of the float. The cylinder used in this test is 0.3 m in diameter, 0.56 m in total height, and the mass is 19.79 kg typically as used in the experiments (MO-3). The numerical results in both models CFX and RKFOM are compared with the experimental results in the free-fall test with an initial displacement of 3 cm; Fig. 7. The damping effects of the power take-off mechanism were added to the CFD model by applying variable vertical force on the solid body as a function of its velocity and opposite to the direction of motion, the PTO damping coefficient used is 20 kgs^-1 typically as experiments. The governing differential Eq. (7) is solved by MATLAB software using the numerical method RKFOM, the external force term is ignored in this experiment, and the added mass coefficient term could be neglected in case of lower diameter and small displacements compared to the immersed height of the float (∆z*D/ho ≤ 0.05) [15], the term V(s) is zero because the cylinder bottom is flat. Figure 7 shows the agreement of numerical results compared to the published experimental data at time step sizes 0.002 s.

Fig. 7

Normalized vertical displacement for the validation of the numerical results against experimental data (MO-3)

5 Hydrodynamic Analysis

The presented numerical method in this research represents an effective tool that contributes to understanding the factors affecting the dynamic response of the float. A hydrodynamic analysis for both models is performed to understand the effect of each parameter on the dynamic behavior of the floating body. The CFD model, using CFX in the validated case with PTO damping coefficient 20 kgs^-1 and initial displacement 3 cm, and the analytical one using numerical model RKFOM in the same conditions were used to analyze the motion characteristics. Figure 8 shows the time domain comparison of both models to predict the motion kinematics, the extreme lowest position of the float is obtained at the point of maximum positive acceleration and zero velocity at 0.62 s.

Fig. 8

Time-domain comparison for the kinematic variables of CFD and numerical model at (∆z = 3 cm–MO-3)

The hydrodynamic forces are shown in Fig. 9 with other effects in the time domain for each model. The hydrostatic force at the lowest position is maximum, while the viscous and PTO damping is minimum, this leads to maximizing the total forces on the float and increasing its momentum to begin moving up. The highest position is coincidental with the minimum value of the acceleration and zero velocity, this is understood by monitoring the reduction in hydrostatic forces at the same instant at 1.24 s. The vertical acceleration in RKFOM is slightly declining from its value in the CFX model, and this is due to the elimination of the added mass coefficient [26]. The equilibrium position is reached after 5 s. The perturbed waves around the float in the CFD model are presented in Fig. 10, at the lowest position after 0.62 s and the highest position after 1.24 s.

Fig. 9

Time-domain comparison for the hydrodynamic forces in CFD and numerical model at (∆z = 3 cm–MO-3)

Fig. 10

3D view of the perturbed waves around the float a lowest position at t = 0.62 s, b highest position at t = 1.24 s–(MO-3)

The CFX approach provides a wide range of useful variables in this study, the pressure distribution on the floating body is variable based on the float position, Fig. 11 shows the change of this distribution in two cases.

Fig. 11

The pressure distribution on the float surface a lowest position at t = 0.62 s, b highest position at t = 1.24 s–(MO-3)

The presented numerical method is used to investigate the added mass term in another case study with different parameters, in which the effect of the added mass coefficient cannot be neglected. A free-fall case is applied on a buoy with a 1 m diameter and 0.5 m immersed height, the total mass of the buoy is 392.7 kg (MO-4). The float was initially located at 5 cm above SWL, this value is rather large compared to the float diameter and immersed height (∆z*D/ho ≥ 0.05). The CFX model is initially generated with the same boundary conditions as the free-fall test, the numerical model is used to investigate the hydrodynamic forces and the corresponding value of the damping coefficient and added mass, and the PTO damping coefficient is eliminated in this test to visualize the float dynamics for more time and obtain more accurate results. The time domain of the rigid body kinematics through 12 s is presented in Fig. 12. The agreement between the two models is observed in the first 4 s of motion (2 cycles), and the disparity between the two models begins in the oscillation frequency, despite the convergence in the damping coefficient at ${C}_{d}=154 \mathrm{N}.\mathrm{s}/\mathrm{m}$ as a result of viscous damping and the absence of a mechanical PTO system. The float reaches its maximum velocity at the equilibrium position, at this instant, the acceleration is zero.

Fig. 12

Time-domain comparison for the kinematic variables of CFD and numerical model at (∆z = 5 cm–MO-4)

The calculation of added mass can be approximated both experimentally and numerically, Zhu and Lim [15] used a separated heave plate added to a circular cylindrical float to calculate the added mass coefficient experimentally. In the present research, the added mass coefficient ${m}_{a}$ is calculated using the CFD-CFX model and numerically by RKFOM; Fig. 13 shows the hydrodynamic forces for model MO-4. The added mass term is investigated first in the CFX model in two different ways, first method is to integrate the value of shear stresses on the float surface to get the average viscous damping force ${\mathop{F}^{\rightharpoonup}}_{s}\left(\dot{z}\right)$, the calculated pressure variation on the float bottom determined the hydrostatic forces with respect to time ${\mathop{F}^{\rightharpoonup}}_{h}\left(z,s\right)$, then the added mass term can be integrated by Eq. 6, ${\mathop{F}^{\rightharpoonup}}_{pto}\left(\dot{z}\right)$ the PTO damping term and ${\mathop{F}^{\rightharpoonup}}_{e}\left(t\right)$ are zero, $\dot{\mathop{v}^{\rightharpoonup}}$ is the calculated vertical acceleration.

Fig. 13

Time-domain comparison for the hydrodynamic forces in CFD and numerical model at (∆z = 5 cm–MO-4)

The second method is to estimate the value ${m}_{a}$ to match the radiation and diffraction forces on the float as the sum of gravitational force ${\mathop{F}^{\rightharpoonup}}_{g}$ and hydrostatic force ${\mathop{F}^{\rightharpoonup}}_{s}\left(\dot{z}\right)$, the calculated value of the added mass coefficient is ${m}_{a}=244 kg$, the added mass term is investigated using ${\mathop{F}^{\rightharpoonup}}_{a}\left(\ddot{z}\right)={m}_{a}\ddot{z}$. The results of the two methods are presented in Fig. 13. The differential equations were solved numerically (RKFOM) to validate the CFD results, the analytical solution is shown in Fig. 13, and the simplified spring-damper system (Eq. 7) is solved based on the present boundary conditions, the effective mass M = 636.7 kg, damping coefficient ${C}_{d}=154 \mathrm{N}.\mathrm{s}/\mathrm{m}$, the spring constant $K=7697 N/m$, the excitation force is zero. The time step size is 0.002 s, and boundary conditions ${\dot{z}}_{o}=0, {\dot{z}}_{o}=0.05\, \mathrm{m}$.

6 Fluid–Structure Interaction

The numerical method in this research provides an effective tool that can be applied to understand the dynamic characteristics in different conditions under the influence of both regular and irregular waves. A case study including regular wave generation is considered to validate the presented numerical model, and to check its ability in different cases. The CFX model is subjected to the second type of boundary conditions presented in the fourth section of this research, NB with a 1/5 sloped surface is activated to reduce wave reflections, and the inlet plane is a movable surface that rotates about a fixed hinge placed at ${h}_{o}=1.5\, \mathrm{m}$ below SWL, the model height is ${h}_{a}=1.5\, \mathrm{m}$ for air region, and 3 m for water. Equations (8) and (9) define the flap position based on the time and vertical position z. The maximum stroke length is 0.15 m to produce a regular wave with amplitude (H = 0.11 m) as discussed in the author's last paper [17]. The wavelength in this experiment is 3 m, and the fluid model is considered a shallow water condition. A floating body with a mass of 392.7 kg (MO-5) is placed in an equilibrium position ($\dot{{z}_{o}}=0, \Delta z=0)$ so that the center of mass of the float is coincide with SWL (Z = 0). Figure 14 presents a comparison between CFX results and the RKFOM model, the total time is 13.5 s with 0.002 s time step size, the recommendations of grid generation being taken into consideration, the solid body is free to slide only in heave motion, no PTO damping is used, an excitation force is added to detect the change in wave amplitude, this force is equivalent to a water column with height equal to the wave amplitude ${A}_{f}=0.11\, \mathrm{m}$. The generated wave by CFX is compared with the theoretical WMT in Fig. 14, the analytical model RKFOM succeeded to predict the vertical position of the float for the first 6 s. The velocity and acceleration in the z-direction are presented for both models.

Fig. 14

Time-domain comparison for the kinematic variables of CFD and numerical model at (Regular wave–MO-5)

The establishment of the CFX model with a 3D domain and three phases requires great effort and more time, and accordingly, we obtain a comprehensive vision for all phases at any time. Three-dimensional views are presented for the interaction between the generated wave and the float, Fig. 15, at different instants. In the first lower position of the float (t = 3 s), at which the velocity is zero, perturbed waves are observed around the floating body; Fig. 17. The numerical beach reduces the wave reflections from the outlet plane as shown, after 12.5 s the float reaches its highest position, 3D snapshots are presented showing the change in float position depending on the incident wave interaction. Figure 17 shows the pressure distribution inside the NWT at 13.5 s, the pressure is increasing from the top according to the water column height (Fig. 17).

Fig. 15

3D snapshot for the generated regular wave against the float (MO–5) at a t = 3 s, b lowest position at t = 6.4 s, c highest position at t = 12.5 s

Fig. 16

3D snapshot for the perturbed wave around the float (MO–5) at a t = 3 s, b lowest position at t = 6.4 s, c highest position at t = 12.5 s

Fig. 17

Pressure gradient inside NWT at t = 13.5 s (MO–5)

7 Bottom Shape Optimization

Two additional models were generated in this section with different designs, the flat- bottom shape of the cylindrical float is replaced by another conical shape and spherical shape as shown in Fig. 18. The two models have the same total mass m = 392.7 kg as the cylindrical float in the model (MO-4). The conical bottom shape model (CB: MO-6) has a diameter of 1 m, the height of the conical head is 0.5 m (90° taper angle, 45° base angle), and the immersed cylinder part height is 0.333 m to keep the same mass as the model (MO-4). The spherical bottom shape model (SB: MO-7) has a diameter of 1 m, the height of the hemispherical head is 0.5 m, and the immersed cylinder part height is 0.167 m to keep the same mass as the model (MO-4). Determining the optimal design required a full vision of the kinematics of each design. Figure 19 shows the comparison between the modified designs and the original cylindrical design in the time domain kinematics: position, velocity, and acceleration. It is shown that the modified designs started with better performance than the original cylindrical design in the first 6 s, after that time, a dispersion occurred in the SB design due to the increase in the damping coefficient leading to a slowdown of the float. The conical design produces a dynamic response similar to the original design, more results are required to get a clearer vision of the behavior of each design.

Fig. 18

The three models of floating body PAWEC with different bottom shapes: a Flat FB, b Conical CB, and c Spherical SB

Fig. 19

Time-domain comparison for the kinematic variables in the free-fall test for the two modified models compared with model MO-4 (∆z = 5 cm–∆t = 0.002 s)

The first tough positions of the three designs occur simultaneously after 0.9 s, and the peak position after 1.74 s is investigated for each design. The vertical displacement between the two positions is defined as $\Delta S$. Table 2 shows the hydrodynamic specifications for each design. The volume of the curved portion below the float $V\left(S\right)$ is a useful input source in the analytical solution, the second column represents the area of the contact surface with the fluid at the equilibrium position. The damping coefficient and spring constant in each case were investigated in each model from CFX data. The conical design has the highest surface area connected to the fluid; this explains the relative improvement in the conical design. The maximum displacement during the first 2 s is presented in the fourth column in Table 2, a slight relative advantage of the hemispherical design. After the first 6 s, the conical and cylindrical designs have the same response. The damping coefficient in both designs is rather similar to 154 and 156 kg/s, and it is 180 kg/s for the hemispherical design. The spring constant depends on the periodic time of the oscillation and total mass of the system, which tends to increase in the spring constant for the modified designs because of the apparent lack of periodic time.

Table 2 Hydrodynamic specification of each model in the free-fall test (z = 0.05 m)

8 Conclusion

The numerical method in this research provides an effective tool that can be applied to understand the dynamic characteristics of a floating body in different conditions. Two models were investigated for this purpose, the CFD model using the CFX approach, and the numerical model solved analytically. The 3D form of the differential equations governing the dynamic behavior of the rigid body was analyzed and solved by both methods. The differential equations were simplified to a spring-damper system and solved numerically by RKFOM. The incompressible form of (URANS) is presented for the solution of the fluid model (air and water) in addition to two differential equations for the solution of VF by using the VOF method. The minimum cell size was tested for the grid independence; 0.05 m is recommended near the float and water surface, and the time step size independence test was performed for the minimum value equivalent to T/925 for the periodic time before the stability of the solution. Two case studies were generated for the validation of the numerical model. The numerical results agreed with the published experimental data in both models used. A hydrodynamic analysis was performed for each model to explain the effect of different forces on the solid body. The developed method in this research provided an effective tool to define the added mass coefficient in three ways, the dependency of the float dynamics was displayed in only heave motion. The developed model is used to investigate the hydrodynamics of the float under the action of the incident regular wave by using a flap-type wavemaker. Two additional models were generated: conical and hemispherical bottom shapes for the float. Valuable results are presented for design improvement, the conical design has a better performance based on the damping coefficient and hydrodynamic loads. The proposed numerical and analytical methods proved efficient and accurate in the results, and a practical study was presented to improve the performance of PAWEC. This paper introduced a numerical method to predict the hydrodynamic effects in minor wave amplitudes and body displacement, it is recommended in future work to evaluate the model under significant displacement in the same conditions.