Keywords

1 Introduction

In the industrial production process, in order to transport the load to the desired position, various crane systems, including bridge crane, cantilever crane, tower crane, Marine crane and Marine crane, have been widely used. In order to simplify the mechanical structure of the crane system, the load is not often directly controlled, but indirectly drags the load to the target position through the movement of the trolley. As a result of this structure, the control input dimension of the crane system is smaller than the degree of freedom dimension to be controlled. The system with this feature is the so-called underdrive system [1]. Due to the removal of some drivers of the system, increasing the system freedom and improving the system flexibility, the underdrive system is superior to the full drive system in terms of energy saving, price reduction, and enhanced system adaptability. However, external disturbance, crane start and stop, speed change and so on will make the load swing, which will not only reduce the transport efficiency of the crane, but also bring huge safety risks. Therefore, the automatic control method of crane system has practical significance and wide application value, which has received the attention of scholars.

In recent years, domestic and foreign scholars have put forward many control methods for the control problem of bridge crane system. In order to simplify the control algorithm design of bridge crane system, a control method based on partial feedback linearization is proposed [2, 3]. Fang et al. proposed a new two-step design strategy, namely motion planning stage and adaptive tracking control stage to control such an underactuated system as an overhead crane [4]. Peng et al. investigated the impact of uncertainty on the crane movement in the stage of trajectory planning, proposed an uncertain method based on interval model [5]. In literature [6], Singhose et al. used the idea of input shaping to control the crane system, which could effectively suppress the load residual swing. In [7], Fang et al. design a series of energy-based controllers to regulate the trolley to a desired position while reducing the pendulation of the payload at the same time. Chen et al. present a time optimal trajectory planning scheme for double pendulum crane systems, which can yield a global time-optimal swing-free trajectory [8]. Sun et al. proposed an optimal trajectory planning method for double pendulum crane based on differential flatness theory, considering a series of constraints such as system swing angle constraints and trolley speed constraints [9]. In [10], Sun et al. proposes a trajectory planning method based on phase plane analysis, which can better suppress load swing and eliminate residual swing. Vaughan et al. proposed a trajectory planning method based on phase plane analysis, which can better suppress load swing and eliminate residual swing [11]. Guo et al. designed an energy-based control method by analyzing the passivity of the crane system [12]. In [13], a linear sliding mode control method was proposed based on the complex dynamic model of double pendulum overhead crane system, which can effectively weaken the system chattering. Zhang et al. proposed a trajectory planning strategy for double pendulum bridge crane based on swing angle constraint [14]. Wang et al. integrated the smooth shaping technology and active disturbance rejection control as an anti-swing control method for double-pendulum crane, which can solve the problem of long anti-swing time, low positioning accuracy and poor anti-disturbance ability of double-pendulum overhead crane without payload swing angle sensor [15]. Aiming at the problem that the load swing of double pendulum crane is difficult to be measured directly in the actual production process, Xiao et al. proposed a sliding mode control method of double pendulum crane based on load swing state estimation is proposed [16]. Kang et al. proposed a control strategy combining adaptive neural network and packet fuzzy control based on double pendulum bridge crane system to solve the control problem of underdriven nonlinear system [17]. In [5], Peng et al. proposed an uncertainty research method based on interval model to Reduce the influence of uncertainty on crane movement. Although the above control strategies can realize the control of the double-swing crane system, they are difficult to ensure the maximum operation efficiency of the crane system.

In order to improve the transport efficiency of the double pendulum crane system, a global time optimal trajectory planning method is proposed, which can realize the control objectives of accurate positioning of the trolley and rapid load elimination at the same time. Different from the existing methods, the proposed method can obtain the global time optimal trolley trajectory. Specifically, the kinematic model of the crane system is transformed first, and an acceleration-driven system model is obtained. Then, by using this model, considering various physical and safety constraints in the crane system, a function to be optimized with transport time as the optimization objective is constructed. In order to facilitate the solution of the optimization problem, Chebyshev pseudo-spectrum method is used to discretization and approximation the obtained optimization problem and corresponding constraints at Chebyshev-Gauss-Lobatto (CGL) points. Finally, the effectiveness of the proposed method is verified by numerical simulation.

2 Problem Statement

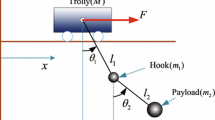
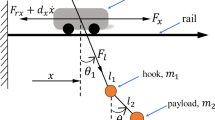
The crane model with double pendulum effect is shown in Fig. 1, whose dynamic characteristics is illustrate as follows:

$$ \begin{array}{*{20}l} {\left( {m_{1} + m_{2} } \right)l_{2} \cos \theta_{1} \ddot{x} + \left( {m_{1} + m_{2} } \right)l_{1}^{2} \ddot{\theta }_{1} + } \hfill \\ {m_{2} l_{1} l_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)\ddot{\theta }_{2} + m_{2} l_{1} l_{2} \sin \left( {\theta_{1} - \theta_{2} } \right)\dot{\theta }_{2}^{2} + } \hfill \\ {\left( {m_{1} + m_{2} } \right)gl_{1} \sin \theta_{1} = 0} \hfill \\ \end{array} $$
(1)
$$ \begin{array}{*{20}l} {m_{2} l_{2} \cos \theta_{2} \ddot{x} + m_{2} l_{1} l_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)\ddot{\theta }_{1} + } \hfill \\ {m_{2} l_{2}^{2} \ddot{\theta }_{2} - m_{2} l_{1} l_{2} \dot{\theta }_{1}^{2} \sin \left( {\theta_{1} - \theta_{2} } \right) + } \hfill \\ {m_{2} gl_{2} \sin \theta_{2} = 0} \hfill \\ \end{array} $$
(2)

where \(m\), \(m_{1}\), \(m_{2}\) denote the masses of the the trolle, the hook and the load, respectively, \(l_{1}\) denote the length of the rope, \(l_{2}\) represent the equivalent rope length, which denote the distance between the load centroid and the centroid of the hook. x(t) represent the trolley movement, \(\theta_{1} \left( t \right)\), \(\theta_{2} \left( t \right)\) describe the angles of the two pendulums, g is the gravity acceleration constant.

Fig. 1.
figure 1

Schematic illustration for the crane model with double-pendulum effects.

Full size image

Divide (1) and (2) by \(\left( {m_{1} + m_{2} } \right) \, l_{1}\) and \(m_{2} l_{2}\), respectively, we can obtain:

$$ \begin{array}{*{20}l} {\cos \theta_{1} \ddot{x} + l_{1} \ddot{\theta }_{1} + \frac{{m_{2} l_{2} }}{{m_{1} + m_{2} }}\cos \left( {\theta_{1} - \theta_{2} } \right)\ddot{\theta }_{2}\, + } \hfill \\ {\frac{{m_{2} l_{2} }}{{m_{1} + m_{2} }}\sin \left( {\theta_{1} - \theta_{2} } \right)\dot{\theta }_{2}^{2} + g\sin \theta_{1} = 0} \hfill \\ \end{array} $$
(3)
$$ \begin{array}{*{20}l} {\cos \theta_{2} \ddot{x} + l_{1} \cos \left( {\theta_{1} - \theta_{2} } \right)\ddot{\theta }_{1} + l_{1} \ddot{\theta }_{2} - } \hfill \\ {l_{1} \dot{\theta }_{1}^{2} \sin \left( {\theta_{1} - \theta_{2} } \right) + g\sin \theta_{2} = 0} \hfill \\ \end{array} $$
(4)

Equations (3) and (4) describe the coupling relationship between vehicle position shift \(x\left( t \right)\) and the two stage swing angles \(\theta_{1} \left( t \right)\) and \(\theta_{2} \left( t \right)\) of the system, that is, the influence of trolley motion on load swing. This method is based on the analysis of the coupling relationship and the planning of a trolley trajectory with the ability to reduce the pendulum.

Considering the safety, efficiency and physical constraints of the actual crane system, this paper will plan a trolley trajectory with analytical expression for the underactuated crane system with double pendulum effect. The specific control objectives to be achieved are as follows [9]:

1) To reach the target position quickly and accurately, the trolley ought to get the destination \(x_{f}\) at time \(t = T\) from its initial position \(x_{0}\) at time \(t = 0\), while velocity and acceleration signals ought to be zero. Then we have

$$ x\left( 0 \right) = \dot{x}\left( 0 \right) = \ddot{x}\left( 0 \right) $$
(5)
$$ x\left( T \right) = x_{f} ,\dot{x}\left( T \right) = \ddot{x}\left( T \right) = 0 $$
(6)

where, \(T\) represents the time required for the transportation process and the initial position \(x_{0}\) = 0.

2) In the entire control task, the trolley velocity and acceleration should be kept in suitable ranges, in sense that

$$ \left| {\dot{x}\left( t \right)} \right| \le v_{\max } ,\left| {\ddot{x}\left( t \right)} \right| \le a_{\max } $$
(7)

where, \(v_{\max }\), \(a_{\max }\) represent the permitted trolley velocity and acceleration, respectively.

3) In order to ensure that the load can be processed directly at the end of the task, when the trolley reaches the target position, there should be no residual swing and the angular velocity is zero, that is

$$ \theta_{1} \left( 0 \right)\,{ = }\,\dot{\theta }_{1} \left( 0 \right)\,{ = }\,0,\,\theta_{1} \left( T \right)\,{ = }\,\dot{\theta }_{1} \left( T \right)\,{ = }\,0 $$
(8)
$$ \theta_{2} \left( 0 \right)\,{ = }\,\dot{\theta }_{2} \left( 0 \right)\,{ = }\,0,\,\theta_{2} \left( T \right)\,{ = }\,\dot{\theta }_{2} \left( T \right)\,{ = }\,0 $$
(9)

4) To avoid the collision caused by the violent swing of the load, the swing angle and angular velocity of the two stage swing should be kept in suitable ranges during the transport process, that is

$$ \left| {\theta_{1} \left( t \right)} \right| \le \theta_{1\max } ,\left| {\theta_{2} \left( t \right)} \right| \le \theta_{2\max } $$
(10)
$$ \left| {\dot{\theta }_{1} \left( t \right)} \right| \le \omega_{1\max } ,\left| {\dot{\theta }_{2} \left( t \right)} \right| \le \omega_{2\max } $$
(11)

where, \(\theta_{1\max }\), \(\theta_{2\max }\), \(\omega_{1\max }\), \(\omega_{2\max }\) represent the permitted payload swing angle and angular velocity amplitudes, respectively.

In summary, the following optimization problems can be constructed:

$$ \begin{array}{*{20}l} {\min } \hfill & T \hfill \\ {s.t. \, } \hfill & {x\left( 0 \right) = \dot{x}\left( 0 \right) = \ddot{x}\left( 0 \right) = 0} \hfill \\ {} \hfill & {x\left( T \right) = x_{f} , \, \,\,\,\, \, \dot{x}\left( T \right) = \ddot{x}\left( T \right) = 0} \hfill \\ {} \hfill & {\left| {\dot{x}\left( t \right)} \right| \le \nu_{\max } , \, \,\,\, \, \left| {\ddot{x}\left( t \right)} \right| \le a_{\max } } \hfill \\ {} \hfill & {\theta_{1} \left( 0 \right) = \dot{\theta }_{1} \left( 0 \right) = 0, \, \,\,\, \, \theta_{1} \left( T \right) = \dot{\theta }_{1} \left( T \right) = 0,} \hfill \\ {} \hfill & {\theta_{2} \left( 0 \right) = \dot{\theta }_{2} \left( 0 \right) = 0,\,\,\, \, \theta_{2} \left( T \right) = \dot{\theta }_{2} \left( T \right) = 0,} \hfill \\ {} \hfill & {\left| {\theta_{1} \left( t \right)} \right| \le \theta_{1\max } ,\,\,\, \, \left| {\theta_{2} \left( t \right)} \right| \le \theta_{2\max } } \hfill \\ {} \hfill & {\left| {\dot{\theta }_{1} \left( t \right)} \right| \le \omega_{1\max } , \, \,\,\, \, \left| {\dot{\theta }_{2} \left( t \right)} \right| \le \omega_{2\max } } \hfill \\ \end{array} $$
(12)

Next, we propose a pseudo-spectral method to solve the optimization problem, and a time optimal trajectory is planned for the trolley.

3 Trajectory Planning

In this section, a time-optimal trajectory planning strategy based on pseudo-spectrum method is proposed, and the trajectory of the trolley is obtained by solving (12). Specifically, the kinematic model of the crane system is transformed into an acceleration driving model, in which the acceleration of the crane can be regarded as the system input. Then, based on the acceleration driving model, the original optimization problem can be rewritten into a new form. Then the constrained optimization problem is transformed into a series of nonlinear programming problems by using Chebyshev pseudo-spectrum method. Finally, by solving the nonlinear optimization problem, we can obtain the time-optimal trolley trajectory.

3.1 Transformation of System Models

In order to facilitate subsequent trajectory planning, the double-pendulum crane system model and optimization problem (12) is transformed here. For this purpose, the system full state vector \(\zeta \left( t \right)\) is defined as follows:

$$ {\varvec{\zeta}}\,{ = }\,\left[ {\begin{array}{*{20}c} x & {\dot{x}} & {\theta_{1} } & {\dot{\theta }_{1} } & {\theta_{2} } & {\dot{\theta }_{2} } \\ \end{array} } \right]^{T} $$
(13)

According to the kinematics model (3) and (4) of the system, the acceleration of the vehicle can be taken as the input of the system. At this point, the kinematic model can be transformed into the following form [8]:

$$ \dot{\user2{\zeta }}\,{ = }\,f\left( \zeta \right)\,{ + }\,h\left( \zeta \right)u $$
(14)

where, \(u\left( t \right)\) is the acceleration of the trolley \(\ddot{x}\left( t \right)\), \(f\left( \zeta \right)\), \(h\left( \zeta \right)\) represents the auxiliary function with respect to \(\zeta \left( t \right)\), in the following form:

$$ f\left( \zeta \right)\,{ = }\,\left[ {\begin{array}{*{20}c} {\dot{x}} & 0 & {\dot{\theta }_{1} } & A & {\dot{\theta }_{2} } & B \\ \end{array} } \right]^{T} $$
(15)
$$ h\left( \zeta \right)\,{ = }\,\left[ {\begin{array}{*{20}c} 0 & 1 & 0 & C & 0 & D \\ \end{array} } \right]^{T} $$
(16)

For the convenience of description, auxiliary variables A, B, C, D are defined as follows:

$$ \left\{ {\begin{array}{*{20}l} {A = - \frac{{m_{2} C_{1 - 2} }}{{l_{1} \left( {m_{1} + m_{2} } \right) - m_{2} l_{1} C_{1 - 2}^{2} }}\left[ {l_{1} S_{1 - 2} \dot{\theta }_{1}^{2} } \right. + \frac{{m_{2} l_{2} }}{{m_{1} + m_{2} }}S_{1 - 2} C_{1 - 2} \dot{\theta }_{2}^{2} } \hfill \\ { \, \,\,\,\,\,\,\,\,\,\,\, - \left. {g\left( {S_{2} - S_{1} C_{1 - 2} } \right)} \right] - \frac{1}{{l_{1} }}gS_{1} - \frac{{m_{2} l_{2} }}{{l_{1} \left( {m_{1} + m_{2} } \right)}}S_{1 - 2} \dot{\theta }_{2}^{2} } \hfill \\ {B = \frac{{m_{1} + m_{2} }}{{l_{2} \left( {m_{1} + m_{2} } \right) - m_{2} l_{2} C_{1 - 2}^{2} }}\left[ {\frac{{m_{2} l_{2} }}{{m_{1} + m_{2} }}} \right.S_{1 - 2} \times C_{1 - 2} \dot{\theta }_{2}^{2} + l_{1} S_{1 - 2} \dot{\theta }_{1}^{2} } \hfill \\ { \, \,\,\,\,\,\,\, - \left. {g\left( {S_{2} - S_{1} C_{1 - 2} } \right)} \right]} \hfill \\ {C \, \,{ = }\,\frac{{m_{2} C_{1 - 2} }}{{l_{1} \left( {m_{1} + m_{2} } \right) - m_{2} l_{1} C_{1 - 2}^{2} }}\left( {C_{2} - C_{1} C_{1 - 2} } \right) - \frac{1}{{l_{1} }}C_{1} } \hfill \\ {D = - \frac{{m_{1} + m_{2} }}{{l_{2} \left( {m_{1} + m_{2} } \right) - m_{2} l_{2} C_{1 - 2}^{2} }}\left( {C_{2} - C_{1} C_{1 - 2} } \right)} \hfill \\ \end{array} } \right. $$
(17)

In formula, the following simplified form is used:

$$ S_{1} = \sin \theta_{1} ,\,S_{2} = \sin \theta_{2} ,\,C_{1} = \cos \theta_{1} ,\,C_{2} = \cos \theta_{2} $$
$$ S_{1 - 2} = \sin \left( {\theta_{1} - \theta_{2} } \right),\,C_{1 - 2} = \cos \left( {\theta_{1} - \theta_{2} } \right) $$

Using the resulting acceleration driven system model (14), the original optimization problem (12) can be transformed into the following form:

$$ \begin{array}{*{20}l} {\min } \hfill & T \hfill \\ \end{array} $$
(18a)
$$ \begin{array}{*{20}l} {{\text{s.t.}}} \hfill & {\dot{\user2{\zeta }}\,{ = }\,f\left( \zeta \right)\,{ + }\,h\left( \zeta \right)u} \hfill \\ \end{array} $$
(18b)
$$ {\varvec{\zeta}}\left( 0 \right)\,{ = }\,\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{T} $$
(18c)
$$ {\varvec{\zeta}}\left( T \right)\,{ = }\,\left[ {\begin{array}{*{20}c} {x_{f} } & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{T} $$
(18d)
$$ \begin{array}{*{20}l} {\left| {\dot{x}\left( t \right)} \right| \le v_{\max } ,} \hfill & {\left| {\dot{u}\left( t \right)} \right| \le a_{\max } } \hfill \\ \end{array} $$
(18e)
$$ \begin{array}{*{20}l} {\left| {\theta_{1} \left( t \right)} \right| \le \theta_{1\max } ,} \hfill & {\left| {\theta_{2} \left( t \right)} \right| \le \theta_{2\max } } \hfill \\ \end{array} $$
(18f)
$$ \left| {\dot{\theta }_{1} \left( t \right)} \right| \le \omega_{1\max } ,\,\left| {\dot{\theta }_{2} \left( t \right)} \right| \le \omega_{2\max } $$
(18g)

By solving this optimization problem, the optimal time \(T^{*}\) required to complete the control objective and the corresponding optimal trolley trajectory can be obtained.

3.2 Trajectory Planning Based on Chebyshev Pseudo-spectrum Method

In order to obtain the time-optimal vehicle trajectory, the key is how to solve the constrained optimization problem. In this paper, the Chebyshev pseudo-spectrum method is used to deal with the optimization problem, and the time optimal solution and the optimal trajectory can be obtained conveniently. Different from most existing methods, this method can analyze and process the original system more directly, and can obtain the global time optimal solution.

In order to adapt to the requirements of the Chebyshev pseudo-spectrum method, it is necessary to use coordinate transformation to transform the time interval corresponding to the trajectory from \(t \in \left[ {0,T} \right]\) to the interval \(\tau \in \left[ {{ - }1,1} \right]\), that is

$$ \tau \,{ = }\,\frac{2t}{T} - 1 $$
(19)

In Chebyshev pseudo-spectrum method, the selection of interpolation points (i.e. CGL points) is

$$ \tau_{i} = \cos \left( {\left( {N - k} \right)\pi /N} \right),i = 0, \cdots ,N $$
(20)

These nodes all fall on the interval \(\left[ { - 1,1} \right]\) and satisfy \(\tau_{0} = - 1\), \(\tau_{N} = 1\). In particular, they are the extreme value of the N degree Chebyshev polynomial \(T_{N} \left( t \right)\), and the jth Chebyshev polynomial is

$$ T_{j} \left( t \right) = \cos \left( {j\cos^{ - 1} t} \right),j = 0, \cdots ,N $$
(21)

Then, the system state quantity and input quantity to be planned can be discretely expressed in the following form:

$$ \zeta \left( {\tau_{0} } \right),\,\zeta \left( {\tau_{1} } \right){,}\, \, \zeta \left( {\tau_{2} } \right),\, \cdots ,\,\zeta \left( {\tau_{N} } \right) $$
$$ u\left( {\tau_{0} } \right),\,u\left( {\tau_{1} } \right),\,u\left( {\tau_{2} } \right),\, \cdots ,\,u\left( {\tau_{N} } \right) $$

Using these nodes, the Lagrange interpolation polynomial is constructed as follows:

$$ \phi_{j} \left( \tau \right) = \frac{{\left( { - 1} \right)^{j + 1} \left( {1 - \tau^{2} } \right)\dot{T}_{N} \left( \tau \right)}}{{N^{2} c_{j} \left( {\tau - \tau_{j} } \right)}} $$
(22)

where

$$ c_{j} = \left\{ {\begin{array}{*{20}l} {2,} \hfill & {j = 0,N} \hfill \\ {1,} \hfill & {1 \le j \le N - 1} \hfill \\ \end{array} } \right. $$

Using Eq. (22) and the values of the system state quantity and input quantity at CGL point, the system state quantity trajectory and input quantity trajectory can be approximated in the following way:

$$ \zeta \left( \tau \right) \approx \sum\limits_{j = 0}^{N} {\zeta \left( {\tau_{j} } \right)} \, \phi_{j} \left( \tau \right), \, \,\,\, \, u\left( \tau \right) \approx \sum\limits_{j = 0}^{N} {u\left( {\tau_{j} } \right)} \, \phi_{j} \left( \tau \right) $$
(23)

where \(\zeta \left( {\tau_{j} } \right)\), \(u\left( {\tau_{j} } \right)\) represent the system state quantity and input quantity at \(\tau = \tau_{j}\), respectively. Take the derivative of Eq. (23), and use the specific form of the interpolation function in Eq. (22) to calculate and simplify, and the derivative of the trajectory of the state quantity can be obtained as follows:

$$ \dot{\user2{\zeta }}\left( {\tau_{i} } \right) = \sum\limits_{j = 0}^{N} {\zeta \left( {\tau_{j} } \right) \, } \dot{\phi }_{j} \left( {\tau_{i} } \right) = \sum\limits_{j = 0}^{N} {\zeta \left( {\tau_{j} } \right)} D_{ji} \left( {\tau_{i} } \right) $$
(24)

where, \(\dot{\zeta }\left( {\tau_{i} } \right)\) represents the derivative of the state locus at \(\tau \,{ = }\,\tau_{i}\). \(D_{ji} \left( {\tau_{i} } \right)\) represents the derivative of \(\phi_{j}\) at \(\tau \,{ = }\,\tau_{i}\), in the following form:

$$ D_{ji} = \left\{ {\begin{array}{*{20}l} {\frac{{c_{i} \left( { - 1} \right)^{i + j} }}{{c_{j} \left( {\tau_{i} - \tau_{j} } \right)}}} \hfill & {,i \ne j} \hfill \\ { - \frac{{\tau_{i} }}{{2\left( {1 - \tau_{i}^{2} } \right)}}} \hfill & {,1 \le i = j \le N - 1} \hfill \\ {\frac{{2N^{2} + 1}}{6}} \hfill & {,i = j = 0} \hfill \\ { - \frac{{2N^{2} + 1}}{6}} \hfill & {,i = j = N} \hfill \\ \end{array} } \right. $$
(25)

By using (24), (25) and the trajectory values at CGL points, the differential equation constraint (18b) in optimization problem (18) can be discretized and approximated. The specific results are as follows:

$$ \sum\limits_{{i{ = }0}}^{N} {\zeta \left( {\tau_{i} } \right)} D_{ji} - \frac{T}{2}\left[ {f\left( {\zeta \left( {\tau_{i} } \right)} \right) + h\left( {\left( {\zeta \left( {\tau_{i} } \right)} \right)} \right)u\left( {\tau_{i} } \right)} \right] = 0 $$
(26)

Next, the boundary condition constraints in the optimization problem also need to be transformed into algebraic constraints, where the formula (18c) can be directly rewritten as follows:

$$ \zeta \left( {\tau_{0} } \right)\,{ = }\,\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{T} $$
(27)

For the end time, using the Clenshaw-Curtis integral, (18d) can be expressed as:

$$ \zeta \left( {\tau_{N} } \right) = \zeta \left( {\tau_{0} } \right) + \frac{T}{2}\sum\limits_{i = 1}^{N} {\omega_{i} } \left[ {f\left( {\zeta \left( {\tau_{i} } \right)} \right) + h\left( {\left( {\zeta \left( {\tau_{i} } \right)} \right)} \right)u\left( {\tau_{i} } \right)} \right] $$
(28)

where, \(\omega_{i}\) is Clenshaw-Curtis weight. When N is even

$$ \left\{ {\begin{array}{*{20}l} {\omega_{0} \,{ = }\,\omega_{N} \,{ = }\,\frac{1}{{N^{2} - 1}}} \hfill \\ {\omega_{s} \, = \,\omega_{N - s} = \frac{4}{N}\sum\limits_{k = 0}^{N/2} {\frac{1}{{1 - 4k^{2} }}\cos \frac{2\pi ks}{N}{ ,}\,{\text{s}}\,{ = }\,{1,}\,{2,}\, \cdots {,}\,\frac{N}{2} \, } } \hfill \\ \end{array} } \right. $$
(29)

When N is odd

$$ \left\{ {\begin{array}{*{20}l} {\omega_{0} \,{ = }\,\omega_{N} \,{ = }\,\frac{1}{{N^{2} }}} \hfill \\ {\omega_{s} \, = \,\omega_{N - s} \, = \,\frac{4}{N}\sum\limits_{k = 0}^{{\frac{{N{ - }1}}{2}}} {\frac{1}{{1 - 4k^{2} }}\cos \frac{2\pi ks}{N}{ ,}\,{\text{s}}\,{ = }\,{1,}\,{2,}\, \cdots {,}\,\frac{{N{ - }1}}{2} \, } } \hfill \\ \end{array} } \right. $$
(30)

To sum up, all constraints in the optimization problem can be expressed in the form of algebraic constraints. Based on this, the original optimization problem can be transformed into a nonlinear programming problem with algebraic constraints, as follows:

$$ \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\min }&T \end{array}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}}\\ {\sum\limits_{i{\rm{ = }}0}^N {\zeta \left( {{\tau _i}} \right)} {D_{ji}} - \frac{T}{2}\left[ {f\left( {\zeta \left( {{\tau _i}} \right)} \right) + h\left( {\left( {\zeta \left( {{\tau _i}} \right)} \right)} \right)u\left( {{\tau _i}} \right)} \right] = 0}\\ {\varsigma ({\tau _0}) = {{\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0 \end{array}} \right]}^T}}\\ {\zeta \left( {{\tau _0}} \right) + \frac{T}{2}\sum\limits_{i = 1}^N {{\omega _i}} \left[ {f\left( {\zeta \left( {{\tau _i}} \right)} \right) + h\left( {\left( {\zeta \left( {{\tau _i}} \right)} \right)} \right)u\left( {{\tau _i}} \right)} \right] = }\\ {{{\left[ {\begin{array}{*{20}{c}} {{x_f}}&0&0&0&0&0 \end{array}} \right]}^{\rm{T}}}}\\ {\zeta \left( \tau \right) - \gamma \le 0,{\rm{ }} - \zeta \left( \tau \right) - \gamma \le 0}\\ {u\left( \tau \right) - {a_{\max }} \le 0,{\rm{ }} - u\left( \tau \right) - {a_{\max }} \le 0} \end{array} $$
(31)

where, the vector \(\gamma\) has the following form:

$$ \gamma \,{ = }\,\left[ {\begin{array}{*{20}c} \infty & {v_{\max } } & {\theta_{1\max } } & {\omega_{1\max } } & {\theta_{2\max } } & {\omega_{2\max } } \\ \end{array} } \right]^{{\text{T}}} $$

For the above constrained nonlinear programming problem, this paper chooses Sequential quadratic programming (SQP) to solve it, and the following time-optimal state vector sequence can be obtained:

$$ \zeta \left( {\tau_{0} } \right),\,\zeta \left( {\tau_{1} } \right),\,\zeta \left( {\tau_{2} } \right),\, \cdots ,\,\zeta \left( {\tau_{N} } \right) $$

The above formula is the optimal sequence of time discrete state vectors. By taking the first two terms of each vector (trolley displacement and trolley velocity) and interpolating them, the corresponding time-optimal trolley displacement and velocity trajectory can be obtained.

4 Simulation Results

In this section, to verify the effectiveness of the designed trajectory planning method, we use MATLAB to conduct some simulations. The used parameters are set as

$$ \begin{gathered} M = 6.5\,{\text{kg,}}\,\,\,\,\,m_{1} = 2.0\,{\text{kg,}}\,\,\,\,\,\,m_{2} = 0.5\,{\text{kg}} \\ {\text{g}} = 9.8\,{\text{kg,}}\,\,\,\,\,\, \, l_{1} = 0.5\,{\text{m,}}\,\,\,\,\,\, l_{2} = 0.4\,{\text{m}} \\ \end{gathered} $$

The target position of the trolley is selected as \(x_{f} = 0.6\,{\text{m}}\), and the trajectory constraints are selected as follows:

$$ \begin{gathered} \theta_{1\max } = \theta_{2\max } \,\,\,\,\,\, = 2\deg , \, v_{\max } = 0.3\,\,\,\,\,\,{\text{m/s}} \hfill \\ \omega_{1\max } = \omega_{2\max } = 5\deg , \,\,\,\,\,\, a_{\max } = 15\,\,\,\,\,\,{\text{m/s}}^{2} \hfill \\ \end{gathered} $$

The simulation results are shown in Fig. 2 and 3. As can be seen from Fig. 2, when the trolley moves according to the planned trajectory, it only takes T* = 5.9895 s to complete the given transport task, and the trolley can accurately reach the target position. In the whole process, the speed of the vehicle does not exceed the given limit \(v_{\max } = 0.3\,{\text{m/s}}\). At the same time, it can be seen from Fig. 3 that the maximum swing angle of both the first and the second order swing angles does not exceed the given value of 2°, and there is no residual swing at the end of transportation. This also ensures the safety of the load during transport. Similarly, the angular velocity corresponding to the two stages of oscillation is also kept within the given range. Then we increased the load weight and rope length, and the simulation results are shown in Fig. 4. As can be seen from Fig. 4, when the load weight and rope length increase, the swing angle is still within the restricted range. In summary, the simulation results verify the efficiency and safety of the proposed optimal trajectory planning method.

Fig. 2.
figure 2

Simulation results of trolley position and velocity

Full size image
Fig. 3.
figure 3

Simulation results of first and second order swing angles and angular velocities

Full size image
Fig. 4.
figure 4

Simulation results after increasing load weight and rope length

Full size image

5 Conclusion

In this paper, a time-optimal trajectory planning strategy based on Chebyshev pseudo-spectrum method is proposed for the overhead crane with double pendulum effect. Specifically, firstly, the kinematic model of the crane system is transformed into an acceleration driving model, and based on this model, a constrained optimization problem is constructed considering various constraints. Then, the optimization problem is processed by Chebyshev pseudo-spectrum method and transformed into nonlinear programming problem which is more convenient to solve. On this basis, the time optimal vehicle trajectory can be obtained. The trajectory planning method proposed in this paper not only considers the object of the pendulum, but also can deal with the actual physical constraints such as the pendulum angle constraint, the angular velocity constraint, the trolley velocity constraint and the acceleration constraint. Different from the existing methods, the proposed method can obtain the global time optimal trolley trajectory. Finally, the effectiveness of the proposed method is verified by numerical simulation. In future work, the angular acceleration constraint will be considered in the trajectory planning process to obtain better control effect.