Keywords

1 Introduction

Estimation of the magnitude and frequency of occurrence of extreme hydrologic events, such as severe storms, floods, and droughts are important in water resources planning and management. Frequency analysis of hydrologic data is one of the widely used methods of estimating the return period associated with a flood of a given magnitude through the use of probability distributions [1–8].

A number of probability distributions are used to fit the probability of occurrence of flood series. Details of these distributions are available in the literature including [9–11] among others. Selection of the most appropriate distribution for annual maximum series has been paid attention worldwide. Log-Pearson Type III distribution is the recommended technique for flood frequency analysis by the U.S. Water Advisory Committee on Water Data, USGS [3]. It is used to estimate the flood discharges for the streams in Iowa, USA [4]. The Generalized Extreme Value distribution is the standard method for UK as reported in [2] and it is adopted in regional flood frequency analysis in Northern Iceland [5] and Nile equatorial basins [6]. Gumbel distribution is used in Nyanyadzi river in Zimbabwe [7]. A World Meteorological Organization survey of 54 agencies in 28 countries reveals that Log-Normal distribution with 3 parameters is not a standard in any country, Generalized Extreme Value is a standard in one country, and Log-Pearson Type III is a standard in seven countries [8].

Numerous goodness-of-fit procedures exist for comparing the fit of alternative probability distributions to streamflow sequences. Since the introduction of L-moments, numerous investigators have recommended them to assess the goodness-of-fit of various probability distributions to regional samples of streamflow [8, 12, 13] and others. Vogel and Wilson [8] constructed L-moments diagrams for annual maximum streamflow at more than 1,455 rivers in the United States and concluded that the Generalized Extreme Value, three-parameter Log-Normal and the Log-Pearson Type III distributions provide good approximations to the distribution of annual maximum flood series. Since Log-Pearson Type III has been selected as the base method in the U.S., they suggested the agencies and countries to reevaluate their standards with respect to the choice of a suitable model for flood frequency analysis. Stedinger and Griffis [14] also recommended that the regional skew map given in [3] be updated to use the additional 30 years of data now available, to appropriately adjust for low outliers identified in the samples used to estimate the regional skew, and to use new and powerful statistical estimation procedures developed to use such data set.

The objectives of the study are hence twofold: (1) to carry out the flood frequency analysis using Log-Normal, Gumbel (Extreme Value Type I), Pearson Type III and Log-Pearson Type III which are commonly used frequency distributions to selected rivers in Myanmar, namely the Chindwin and Yenwe rivers and (2) to identify the most appropriate probability distribution for the basins under study. The estimated flood values can be used in the engineering design of hydraulic structures such as dams, bridges, culverts, levees and other structures located along rivers and streams and for the effective management of flood plains.

2 Data Used in This Study

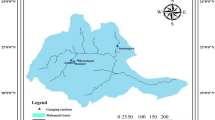
In this study, two rivers namely Chindwin and Yenwe rivers in Myanmar are selected. The Chindwin river has floods several times in a year from the onset of rainy season to the end of the monsoon. Annual maximum discharges are collected at Hkamti, Htamathi and Homalin stations for Chindwin river. Average annual rainfall at Hkamti, Htamathi and Homalin stations are 3,847, 3,262 and 2,314 mm respectively. The mean monthly temperature varies from 28 °C in May to 18 °C in January.

Myochaung station for Yenwe river which is a tributary of Sittoung is also selected in this study. It lies in a tropical monsoon area with an average annual rainfall of about 2,000 mm. The mean monthly temperature varies from 31 °C in April to 25 °C in January. The location and area of these stations are shown in Table 1. Series of annual maximum discharge of each basin is plotted in Fig. 1.

Table 1 Location of gauging stations under study
Full size table
Fig. 1
figure 1

Annual maximum discharge series of Chindwin and Yenwe basins

Full size image

It can be seen from Fig. 1 that the variation of the flood values from the mean in Chindwin is small compared to the variation in Yenwe basin. Statistical characteristic of each series is given in Table 2. Annual maximum series of Chindwin basins have negative skews while Yenwe has a positive skew.

Table 2 Statistical characteristics of each basin
Full size table

3 Methodology

3.1 Testing for Outliers

Reference [9] recommends that adjustments be made for the outliers of the data. If the station skew is greater than +0.4, tests for high outliers are considered first and if the station skew is less than −0.4, tests for low outliers are considered first. Where the skew is between ±0.4, tests for both high and low outliers should be applied before eliminating any outliers from the data set. The following equation is used to detect high outliers:

$$ y_{H} = \bar{y} + K_{N} s $$
(1)

where

yH :

high outlier threshold in log units

\( \bar{y} \) :

mean logarithm of variate

s:

standard deviation of y’s

KN :

10 % significance level K values.

The following equation is used to detect low outliers:

$$ y_{L} = \bar{y} - K_{N} s $$
(2)

where yL = low outlier threshold in log units and other terms are as defined earlier.

3.2 Frequency Analysis Using Frequency Factors

Chow [9] proposed the frequency factor equation shown in (3) which is applicable to many probability distributions used in hydrologic frequency analysis.

$$ x_{T} = \mu + K_{T} \sigma $$
(3)

which may be approximated by

$$ x_{T} = \bar{x} + K_{T} s $$
(4)

where

xT :

value of the variate x of a random hydrologic series with a return period T,

\( \bar{x} \) :

mean of the variate,

s:

standard deviation of the variate,

KT :

frequency factor which depends upon the return period T and assumed frequency distribution

In the event that the variable analyzed is y = log x, then the same method is applied to the statistics for the logarithms of the data using

$$ y_{T} = \bar{y} + K_{T} s $$
(5)

and the required value of xT is found by taking the antilog of yT.

Table 3 summarizes the probability density function, the range of the variable, and equations for estimating the distribution’s parameters from sample moments for each distribution [9]. The theoretical KT relationships for the selected probability distributions: Log-Normal, Pearson Type III, Log-Pearson Type III and Gumbel distributions extracted from [9] are given below.

  1. 1.

    Gumbel distribution

The frequency factor KT for different return period T is given in (6).

$$ K_{T} = - \frac{\sqrt 6 }{\pi }\left\{ {0.5772 + \ln \left[ {\ln \left( {\frac{T}{T - 1}} \right)} \right]} \right\} $$
(6)
  1. 2.

    Log-Pearson Type III distribution

The frequency factor depends on the return period T and the coefficient of skewness CS. When CS = 0, the frequency factor is equal to the standard normal variable z. The value of z corresponding to an exceedence probability of p (p = 1/T) can be calculated by finding the value of an immediate variable w:

$$ w = \left[ {\ln \left( {\frac{1}{{p^{2} }}} \right)} \right]^{1/2} (0 < p\;0.5) $$
(7)

then calculating z using the approximation

$$ z = w - \left[ {\frac{{(2.515517 + 0.802853w + 0.010328w^{2} }}{{(1 + 1.432788w + 0.189269w^{2} + 0.001308w^{3} )}}} \right] $$
(8)
$$ K_{T} = z + \left( {z^{2} - 1} \right)k + \frac{1}{3}\left( {z^{3} - 6z} \right)k^{2} - \left( {z^{2} - 1} \right)k^{3} + zk^{4} + \frac{1}{3}k^{5} $$
(9)

where k = Cs/6, and Cs = coefficient of skewness of logarithms of the series.

Table 3 Probability distributions for fitting hydrologic data
Full size table
  1. 3.

    Pearson Type III distribution

For this distribution, the same equation in Log-Pearson Type III applies except that Cs is skewness of the original series (without taking the logarithmic values).

  1. 4.

    Log-Normal distribution

For this distribution, the same equation in Log-Pearson Type III applies using Cs = 0.

3.3 Statistical Analysis

Goodness of fit between the observed events and the fitted distribution is tested by the two most commonly used tests: Chi square and Kolmogorov–Smirnov (K–S) [15].

  1. 1.

    Chi square test

The statistic is calculated by

$$ \chi^{2} = \sum\limits_{j = 1}^{k} {\frac{{(O_{j} - E_{j} )^{2} }}{{E_{j} }}} $$
(10)

where Oj is the observed number of events in the jth class interval and Ej is the number of events that would be expected from the theoretical distribution.

  1. 2.

    Kolmogorov–Smirnov (K–S) test

The statistic Dn is evaluated by observing the deviation of the sample distribution function P(x) from the completely specified continuous hypothetical distribution function P0(x), such that

$$ D_{n} = Max|P(x) - P_{0} (x)| $$
(11)

The test requires that the computed value Dn from the sample distribution be less than the tabulated value of Dn at the required significance levels of 0.05 and 0.1.

3.4 Reliability of Analysis

The reliability of the results of frequency analysis depends on how well the assumed probability model applies to a given set of hydrologic data. This can be done by calculating confidence limits which are upper and lower boundary values of the confidence interval. For estimating the event magnitude for return period T, the upper limit UT,α and lower limit LT,α may be specified by adjustment of the frequency factor equation given in [9]:

$$ U_{T,\alpha } = \bar{x} + sK_{T,\alpha }^{U} $$
(12)
$$ L_{T,\alpha } = \bar{x} + sK_{T,\alpha }^{L} $$
(13)

where α is a significance level and is obtained by \( \alpha = \frac{1 - \beta }{2} \), β = confidence interval.

\( {{\text{K}}^{\text{U}}}_{{{\text{T,}}\alpha}} \) and \( {\text{K}}^{\text{L}}_{{{\text{T,}}\alpha}} \) are upper and lower confidence factors, which can be determined for normally distributed data using the noncentral t distribution. Approximate values for these factors are given by the following equations:

$$ K_{T,\alpha }^{U} = \frac{{K_{T} + \sqrt {K_{T}^{2} - ab} }}{a} $$
(14)
$$ K_{T,\alpha }^{L} = \frac{{K_{T} - \sqrt {K_{T}^{2} - ab} }}{a} $$
(15)

in which \( a = 1 - \frac{{Z_{\alpha }^{2} }}{2(n - 1)} \) and \( b = K_{T}^{2} - \frac{{Z_{\alpha }^{2} }}{n} \).

The quantity Zα is the standard normal variable with exceedence probability α.

4 Results

4.1 Flood Discharges

Annual maximum discharge series of Chindwin River at Hkamti, Htamathi and Homalin stations and Yenwe at Myochaung station are checked whether outliers exist in the data series before using them. Based on the skewness coefficient of the data series used, outliers are calculated and given in Table 4. KN value based on the number of data in the series is obtained from the table for outlier test in [3].

Table 4 Outliers (cumec) for Chindwin and Yenwe basins
Full size table

It is observed that the annual maximum discharges in the year 1994 are smaller than the low outliers for Chindwin at all stations. However, useful historical information is not available to adjust for low outliers and therefore they are retained in the series. There is no high outlier observed in all series.

Flood discharges with recurrence intervals of 2, 5, 10, 20, 50 and 100 years are calculated using four probability distributions: Log-normal, Gumbel, Pearson Type III and Log Pearson type III distributions. The results are given in Tables 5, 6, 7, 8 that show large differences in results obtained by the different methods, particularly at the larger return periods. It can be seen that Gumbel distribution gives the highest estimated flood discharges for Chindwin and Log-Normal distribution gives the highest for Yenwe. The estimated discharges for high return period (50 and 100 years) using Log-Normal and Gumbel distributions yield about 10–20 % higher than the flood values estimated by Pearson Type III and Log-Pearson Type III distributions for all basins under study.

Table 5 Flood discharges XT (cumec) obtained by different distributions for Chindwin at Hkamti station
Full size table
Table 6 Flood discharges XT (cumec) obtained by different distributions for Chindwin at Htamathi station
Full size table
Table 7 Flood discharges XT (cumec) obtained by different distributions for Chindwin at Homalin station
Full size table
Table 8 Flood discharges XT (cumec) obtained by different distributions for Yenwe at Myochaung station
Full size table

4.2 Statistical Analysis

The two most commonly used tests of goodness of fit namely Chi square and Kolmogorov–Smirnov tests are applied to check the fit of probability distributions used in this study. Tables 9 and 10 list the values of Chi square statistics (χ2) and Kolmogorov–Smirnov (Dn) respectively.

Table 9 Comparison of Chi square statistics for different distributions for the basins under study
Full size table
Table 10 Comparison of Kolmogorov–Smirnov statistics for different distributions for the basins under study
Full size table

It can be observed from the Chi square values of four distributions for all basins given in Table 9 that the values are less than the critical value at 95 % confidence level. From Table 10, it can be seen that all the computed values of Dn are less than the critical value at 95 % confidence level. From both statistical tests, no distinction among all distributions can be made for the basins under study. All distributions are acceptable to fit to the annual maximum series of Chindwin and Yenwe basins at 95 % confidence interval.

Table 11 Confidence limits (cumec) for Chindwin at Hkamti and Htamathi stations
Full size table

If the goodness of fit is the criterion used to select a specified distribution, then the distribution with three parameters will usually provide a much better fit than two parameters [16]. In this study, Log-Pearson Type III is selected as the recommended distribution since it includes the skew coefficient as a variable and therefore is more flexible than the Log-Normal which has a skew of zero of the logarithms. Log-Normal is considered as the special case of Log-Pearson Type III distribution. Another reason is that Pearson Type III is capable of fitting frequency relations that may, for hydrologic reasons, be highly skewed [1].

4.3 Reliability Analysis

Reliability analysis for the basins under study is performed using log-Pearson Type III distribution. The confidence limits with 90 % confidence interval are calculated and shown in Tables 11 and 12.

Table 12 Confidence limits (cumec) for Chindwin Basin at Homalin and Yenwe Basin
Full size table

Graphical presentations of estimated flood discharges using all probability distributions under study together with the confidence limits using Log-Pearson Type III for each basin are shown in Fig. 2.

Fig. 2
figure 2

Flood discharges and confidence interval vs return period for Chindwin and Yenwe basins

Full size image

It can be seen from Fig. 2 that the confidence interval is quite wide especially in Yenwe basin since the sample size of each series is small in this study.

5 Conclusions

Based on the analysis of statistical tests, Gumbel, Pearson Type III and Log-Pearson Type III and Log-Normal distributions are suitable to estimate flood discharges for Chindwin and Yenwe basins.

Log-Pearson Type III distribution can be recommended for Chindwin and Yenwe basins since it includes the skew variable and therefore is more flexible than other distributions.

A study on frequency analysis for other gauging stations of Chindwin basin as well as the other river basins needs to be performed to develop the regional frequency analysis. Future research can be carried out by using other parameter estimator such as L moments in frequency analysis for the river basins in Myanmar.