Keywords

1 Introduction

The world is urbanizing at a greater rate than in history. The urban cities are complex, bringing a host of transportation, infrastructure, health and sustainability issues before and after a major disaster such as an earthquake. During an earthquake, structures interact with the surrounding soil beneath their foundations; this problem is generally known as soil–foundation–structure interaction (SFSI) or Structure–soil interaction, or as it is more commonly known, soil–structure interaction (SSI). Accounting for soil flexibility in the analysis of structure does not generally affect the response significantly. In general, for stiff, heavy buildings (and other structures) soil flexibility can change the response due to SSI. SSI is an important research topic in earthquake engineering that has attracted extensive attention for several decades.

An extension of SSI is an interaction of adjacent structures. The present-day cities’ existence of a high raised and high density of buildings inevitably results in the possibility of seismic interaction of adjacent buildings through the underlying soil. During an earthquake, the presence of one structure may affect the dynamic response of another, resulting in structure–soil–structure interaction (SSSI). The SSSI is important for the performance assessment of buildings in dense urban areas and is receiving some considerable attention in recent years. Although, the limited studies on SSSI are well-documented field and/or experimental data available but still no related provisions are made in any standard code of practice.

A recent review of the SSSI problem can be found in Menglin et al. [1]. Due to the difficulties involved in modelling the multiple interactions, previous studies of the dynamic SSSI phenomena have been explored analytically and also numerically based either on finite element (FE) or boundary element (BE) methods or on coupled FE/BE procedure and provided qualitative evidence of the dynamic interaction effects between adjacent structures [2,3,4,5,6,7,8,9]. Based on these studies on SSSI, the dynamic interaction between adjacent buildings with consideration of the underlying or surrounding soil influences each other through the soil during earthquakes and exhibits dynamic behaviours different from those of isolated building.

In this paper, a numerical investigation is carried out on adjacent buildings idealized as a simplified two-dimensional discrete model and underlying or surrounding soil coupled by a rotational interaction spring and the non-stationary Kanai–Tajimi accelerogram is employed as artificial seismic excitation input to study the dynamic of SSSI phenomena. The dynamic response of two adjacent buildings in the coupled SSSI system due to artificial seismic excitation input is compared and the parameters of the two adjacent buildings that affect the dynamic coupling interaction between adjacent building structures in the coupled SSSI system are also investigated.

2 Equation of Motion of the Coupled SSSI System

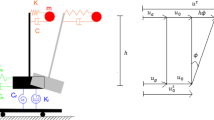
In this paper, the coupled SSSI system consists of two adjacent buildings modelled as a simple 2D-discrete model system with six degrees of freedom (DOF) and underlying or surrounding soil is coupled by a rotational interaction spring. The assumption made to derive the equation of motion of the coupled SSSI system in the present study is as follows, (i) the inter-building spacing, i.e. space between the two adjacent buildings is assumed to be large enough to avoid pounding, (ii) the total height of the two adjacent buildings can vary and be different but is idealized as 2-DOF lumped mass system, (iii) both the buildings have a similar square plan area of \({b}^{2}\), and the average building density, \({\rho }_{b}\) is kept constant, (iv) the soil profile under the two adjacent buildings remains same, and the radius of gyration of the soil-cylinder (directly under the rigid foundation) is calculated according to the Newmark’s empirical expression \({r}_{b}\approx 0.33\). Therefore, \(r_{1} = r_{2} { } = { }0.33b\). [10] (v) the wave passage effects and spatially heterogeneous ground motion are assumed to be negligible; therefore, the foundation of the two adjacent buildings is applied with same ground motion.

The idealized 2D-discrete model of the coupled SSSI system is shown in Fig. 1. The 2D-discrete model system of the two adjacent buildings \(\left( {j{ } \in { }\left[ {1,{ }2} \right]} \right){ }\) consists total of six degrees of freedom (DOF). Each building superstructures consists of two translational DOFs relative to the ground, and the soil/foundation system of each building has one rotational DOF at the foundation level \(\theta_{j}\). \(m_{{b1{ }}} {\text{and }}m_{b2} { }\) are total masses; \(k_{{b1{ }}} {\text{and }}k_{b2} { }\) are lateral stiffnesses; \(m_{b1} .r_{1}^{2} \;{\text{and }}\;m_{b2} .r_{2}^{2} { }\) are foundation/soil mass polar second moments of area; \(k_{{s1{ }}} {\text{and }}k_{s2} { }\) are rotational stiffnesses of foundation–soil beneath each building; \(r_{1} \;{\text{and }}\;r_{2}\) are radii of gyration of soil semi-cylinders; \(h_{1} \;{\text{and}}\;h_{2}\) are the total height; \(b_{1} \;{\text{and}}\;b_{2}\) are the width of the buildings foundation of building 1 and 2, respectively, \(z\) is the non-dimensional inter-building distance, κ is the stiffness of the inter-building soil rotational spring \(\mathrm{and}\,{\ddot{x}}_{g}\) is the horizontal acceleration ground motion.

Fig. 1
figure 1

Idealized 2D-discrete model of the coupled SSSI system

Full size image

The Euler–Lagrange equation of motion in its general form describing the dynamics of the coupled SSSI system can be derived using standard procedure and is formulated in Eq. (1).

$$ {\hat{\mathbf{M}}}{\ddot{\mathbf{x}}} + {\hat{\mathbf{C}}}{\dot{\mathbf{x}}} + {\hat{\mathbf{K}}\mathbf{x}} = {\hat{\mathbf{P}}}\ddot{x}_{g} $$
(1)

where the system matrices are defined as follows

$$ {\hat{\mathbf{M}}} = \left[ {\begin{array}{*{20}c} {\frac{1}{2}m_{b1} } & 0 & { - \frac{1}{4}m_{b1} h_{1} } & 0 & 0 & { - 0} \\ 0 & {\frac{1}{2}m_{b1} } & { - \frac{1}{2}m_{b1} h_{1} } & 0 & 0 & 0 \\ { - \frac{1}{4}m_{b1} h_{1} } & { - \frac{1}{2}m_{b1} h_{1} } & {\frac{5}{8}m_{b1} h_{1}^{2} + m_{s1} r_{1}^{2} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{2}m_{b2} } & 0 & { - \frac{1}{4}m_{b2} h_{2} } \\ 0 & 0 & 0 & 0 & {\frac{1}{2}m_{b2} } & { - \frac{1}{2}m_{b2} h_{2} } \\ 0 & 0 & 0 & { - \frac{1}{4}m_{b2} h_{2} } & { - \frac{1}{2}m_{b2} h_{2} } & {\frac{5}{8}m_{b2} h_{2}^{2} + m_{s2} r_{2}^{2} } \\ \end{array} } \right] $$
$$ {\hat{\mathbf{K}}} = \left[ {\begin{array}{*{20}c} {2k_{b1} } & { - k_{b1} } & 0 & 0 & 0 & 0 \\ { - k_{b1} } & {k_{b1} } & 0 & 0 & 0 & 0 \\ 0 & 0 & {k_{s1} + \kappa } & 0 & 0 & { - \kappa } \\ 0 & 0 & 0 & {2k_{b2} } & { - k_{b2} } & 0 \\ 0 & 0 & 0 & { - k_{b2} } & {k_{b2} } & 0 \\ 0 & 0 & { - \kappa } & 0 & 0 & {k_{s2} + \kappa } \\ \end{array} } \right],\;{\hat{\mathbf{p}}} = \left[ {\begin{array}{*{20}c} { - \frac{1}{2}m_{b1} } \\ { - \frac{1}{2}m_{b1} } \\ {\frac{3}{4}m_{b1} h_{1} } \\ { - \frac{1}{2}m_{b2} } \\ { - \frac{1}{2}m_{b2} } \\ {\frac{3}{4}m_{b2} h_{2} } \\ \end{array} } \right],\;{\mathbf{x}} = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {\theta_{1} } \\ {x_{3} } \\ {x_{4} } \\ {\theta_{2} } \\ \end{array} } \right] $$

The Caughey orthogonal damping matrix \(\widehat{\mathbf{C}}\) of the system defined in Eq. (1) assumes that six eigenvalues of the linear unforced system, each natural mode n ∈ [1, 6] is damped at 2% of critical damping, i.e. \({\xi }_{n}=0.02\). \({\Phi }_{n}\) is the eigenvector for mode \(n,\omega_{n}\) are the natural frequencies of the system. Thus, the damping matrix \(\widehat{\mathbf{C}}\) can be calculated as [11]:

$$ {\hat{\mathbf{C}}} = {\hat{\mathbf{M}}}\left( {\mathop \sum \limits_{{{\text{n}} = 1}}^{6} \frac{{2\xi_{n} \omega_{n} }}{{\Phi_{n}^{T} M\Phi_{n} }}\Phi_{n} \Phi_{n}^{T} } \right){\hat{\mathbf{M}}} $$
(2)

3 Selection of Ground Motion

In this paper, the non-stationary Kanai–Tajimi accelerogram is employed to simulate the artificial seismic excitation [12,13,14]. This artificial seismic accelerogram generated is employed as the horizontal acceleration ground motion input to the simplified idealized 2D-discrete model of the coupled SSSI system to study the dynamic of SSSI phenomena. Guo, and Kareem, [14] developed non-stationary Kanai–Tajimi spectrum as shown in Eq. (3).

$$ F\left( s \right) = {\text{s}}_{o} \frac{{\omega_{g}^{4} + \left( {2\xi_{g} \omega_{g} {\text{s}}} \right)^{2} { }}}{{\left( {\omega_{g}^{2} - s^{2} } \right)^{2} { } + \left( {2\xi_{g} \omega_{g} {\text{s}}} \right)^{2} }}, \quad {\text{s}}_{o} = \sigma_{g}^{2} \frac{{2\xi_{g} { }}}{{{\uppi }\omega_{g} \left( {4\xi_{g}^{2} + 1} \right)}} $$
(3)

where \({\xi }_{g},\) \({\omega }_{g}\) are the ground damping and frequency, respectively. \({\sigma }_{g},\) is the standard deviation of the excitation (assuming a two sided spectrum). The artificial ground acceleration is produced by applying a Gaussian white noise to the filter. In this study, the duration of strong ground motion is assumed to be 40 sec, \({\sigma }_{g}=0.3,\) \({\xi }_{g}=0.3\) and \({\omega }_{g}=10\pi rad/s\) are used in the numerical simulations of non-stationary Kanai–Tajimi accelerogram (Fig. 2).

Fig. 2
figure 2

Artificial seismic accelerogram generated based on non-stationary Kanai–Tajimi filter

Full size image

4 Numerical Simulation

The second-order ODE of the coupled SSSI system in Eq. 1 is solved as a state space model in time domain. The numerical simulations are conducted using MATLAB. The following parameters are adapted for the coupled SSSI system in the present study. The total height \(h_{1} = 6.40\;{\text{m}}\;{\text{and}}\;h_{2} = 6.00\;{\text{m }}\); \(b_{1} = 20\,{\text{m}}\;{\text{and}}\;b_{2} = 20\,{\text{m}},\) is the width of the buildings foundation of building 1 and 2, respectively, \(m_{s} = 0.35b^{3} \rho_{s}\) is the dynamic mass of soil beneath buildings and \(m_{bj} = \rho_{b} h_{j} { }b^{2}\), the mass of the buildings, where \(\rho_{s} = 1600{ }kg/m^{3} \quad {\text{and }}\quad \rho_{b} = 800{ }kg/m^{3} { }\) are the average densities of soil and building, respectively. In the present study, the two buildings are placed in very close proximity to each other, i.e. z, the ratio of the distance between buildings to building width is 0.01\(,i.e.,{ }z = 0.10\). The values of foundation rotational spring \(k_{s1} = k_{s2} = k_{s} q_{2}\), and the interaction spring stiffness \({ }\kappa\) are modelled as an inverse cube function of non-dimensional inter-building separation distance \(z,{ }\)[15]. The rotational stiffness spring coefficient \(k_{s}\) is obtained by using the empirical formula in the absence of building interaction [16].

$$ \kappa = q_{k} q_{2} k_{s} ,q_{k} = - \frac{0.25}{{\left( {1 + z} \right)^{3} }},q_{2} = 1 + \frac{0.5}{{\left( {1 + z} \right)^{3} }},k_{s} = \frac{1}{2}\frac{{G_{s} b^{3} }}{1 - \mu } $$

where \(G_{s} \) is the elastic shear modulus of the soil, the shear wave velocity of the soil \(V_{s} = \sqrt {G_{s} /\omega_{s} }\) in \(250\,{\text{m/s}}\) and the Poisson’s ratio of the soil as \(\mu \) = 0.30.

5 Results and Discussions

The results are obtained by numerical simulations performed in MATLAB. Figure 3 provides the acceleration, velocity and displacement response of the idealized 2D-discrete model of the coupled SSSI system. Figures 4 and 5 provide the acceleration responses of the building model 1 and 2 of the coupled SSSI system both in time and frequency domain, respectively. In general, the maximum displacement and acceleration of buildings increases for the SSSI case and the interaction are found to be amplified when the buildings are very closely spaced.

Fig. 3
figure 3

Acceleration, velocity and displacement response of the Idealized 2D-discrete model of the coupled SSSI system

Full size image
Fig. 4
figure 4

Acceleration response at the mass levels of the building model 1 and 2 of the coupled SSSI system in time domain

Full size image
Fig. 5
figure 5

Acceleration response at the mass levels of the building model 1 and 2 of the coupled SSSI system in frequency domain

Full size image

Table 1 provides the summary of peak acceleration, peak velocity and peak displacement of the building models of the coupled SSSI system. Based on the results, the responses of the building model 2 increased to that of the responses of the building model 1, indicating the amplification of response due to interacting dynamic coupling interaction effects between taller adjacent building structure and the underlying soil when subjected to artificial seismic excitation.

Table 1 Peak acceleration, peak velocity and peak displacement of the building models of the coupled SSSI system
Full size table

6 Conclusions

In this paper, numerical investigations are carried out on a simplified model to study the dynamic of structure–soil–structure interaction (SSSI) phenomena. As expected, the simplified model is effective to study the dynamic coupling interaction effects between adjacent building structures and underlying or surrounding soil.

Based on the initial trails, the eigen frequencies for the coupled and uncoupled system are very similar, i.e. there is a maximum of 11% variation in the natural frequencies between the SSI and SSSI systems, therefore an important feature of the SSSI systems.

The building space has been a major contributing factor to the responses, when the two buildings are placed in very close proximity to each other (i.e. 0.1 d) which is large enough to avoid pounding but is found to be close enough to maximize the SSSI effects. In general, the maximum displacement and acceleration of buildings increase for the SSSI case and the interaction is found to be amplified when the buildings are very closely spaced.

Based on the present study, results indicate that the response of the structure adjacent to the taller building is significantly increased and thereby amplifies the seismic risk; however, the response of the taller building is comparatively reduced indicating reduction of its own seismic risk.

The present study is based on the analyses undertaken for limited parameters and needs further investigation.