Keywords

1 Introduction

Fractional-order systems can be represented as

$$G_{\text{f}} (s) = K_{\text{P}} + \frac{{K_{\text{I}} }}{{s^{\lambda } }} + K_{\text{D}} s^{\mu } ;\quad \lambda ,\mu \in (0,1)$$
(1)

where Kp, KI, KD are the parameters of the conventional PID, and λ and µ are fract-order proportional–integral–derivative (FO-PID) controller parameters, respectively [1]. For analyzing any fract-order system (FOS), it needs to be approximated to an equivalent integer-order system (IOS). Several techniques have been reported in the literature for this conversion [2, 3].

Once this approximation has been made, the design of a FO-PID controller is straightforward using various optimization techniques and random search methods. Conventional PID (CO-PID) controllers have dominated industrial process control applications. Though their use in industry is still prevalent, new avenues have emerged with the advent of soft computing tools.

Several soft computing techniques for implementing conventional PID control have been proposed, e.g., cruise control using genetic algorithm (GA) [4], conical tank regulation using ANT colony optimization (ACO) [5], PID control using multi-objective ACO [6], automatic voltage regulator system (AVR) using particle swarm optimization (PSO) [7], DC motor control using GA, evolutionary programing (EP) and PSO [8, 9]. In [10], authors propose linear quadratic regulator and PID controller for inverted pendulum wherein the parameters of the PID controller are tuned using ACO.

As mentioned earlier, fract-order PID controllers have an advantage over conventional PID controllers in terms of availability of additional tuning parameters. Authors in [11] tune both CO-PID and FO-PID controllers by adjusting GM and PM for temperature control; in [12], authors have applied GA for tuning of seven and eight parameters of the FO-PID controller and test it on integer-order plants (IOP) with delay.

In [13], authors have performed control and stability studies on fractional-order chaotic systems, and in [14, 15], fract-order systems for IOPs and AVRs are tuned using PSO. Zamani et al. [16] presents the design of an H∞ optimal FO-PID controller. Tuning is performed using multiple random search techniques in [17, 18] for control of robotic manipulators and UAV autopilot. A FO-PID heart rate controller is designed in [19] and control of blood glucose levels in diabetes patients is developed in [20] using GA.

Fuzzy logic-based fract-order PID formulation provides better flexibility and control. It is suitable for the control of highly nonlinear systems and facilitates easy computations online. Robust fuzzy PID (FPID) controller for control of permanent magnet synchronous motor (PMSM) has been proposed in [21], and FPID controller for the inverted pendulum is described in [22]. Here, the authors have used ACO to estimate the initial parameters of the FPID.

In [23,24,25], FFPID controllers have been proposed where fract-order parameters are optimized using GA. Other notable approaches include sliding mode control, e.g., steam distillation process and PMSM for electric vehicles using PSO [26]. An FFPID approach using ACO for the control of IOP and FOP is detailed in [27]. Finally, a variable-order FFPID controller is discussed in [28].

In this paper, we propose what may be termed “optimized” tuning method for FFPID controllers using a combination of GA and ant colony techniques on a fuzzy logic platform. The controller is simulated on integer-order and fractional-order systems for validation. Based on minimization of the integral of the square of error, GA outputs a set of fract-order parameters as well as initial input parameter values for the ACO. Thereafter, ACO fine-tunes these initial fract-order parameters. In the final step, PID like fuzzy logic is used with error and derivative of error as inputs for generating a set of fract-order parameters. All the three fract-order parameter sets are algebraically combined to get the resulting nature inspired FFPID controller.

The key benefit is harnessing the generalization capability of fuzzy systems in tandem with optimality provided by nature inspired algorithms for generating a versatile fract-order controller. Section 2 gives brief details on the nature inspired algorithms used in this work, PID like fuzzy knowledge-based controller and our nature inspired fuzzy fractional controller. Section 3 details simulation results and associated discussions, and Sect. 4 concludes the paper.

2 Nature Inspired Algorithms for Fract-Order Systems

2.1 ANT Colony Optimization (ACO)

ACO [29] belongs to the family of algorithms collectively bunched “nature inspired” wherein optimization is carried out on the behavioral pattern of ants. Ants practice an excellent way of optimizing the path they take for food search and other tasks. First, they select an arbitrary path, and then this path is marked for other ants by releasing pheromones.

Next step is to choose the best path based on the probability of pheromone trails. An interesting phenomenon is the disappearance of lower quality pheromones trails. Thus, only the best or most optimal path gets reinforced by repeated pheromone secretion by other ants. The algorithm has the following steps:

  1. (i)

    A pheromone factor matrix τ is chosen for obtaining a good solution.

    $$\tau = \{ \tau_{pq} \} \,{\text{and}}\,\tau_{pq} = \tau_{i} \;\forall \;(p,q)$$
    (2)

    p and q are nodes along the ant path.

  2. (ii)

    Next, the probability that an ant will choose the node q from node p is evaluated as

    $$P_{pq} (t) = \frac{{[\tau_{pq} ]^{\alpha } [\eta_{pq} ]^{\beta } }}{{\sum {[\tau_{pq} ]^{\alpha } [\eta_{pq} ]^{\beta } } }}\;\forall \;p,q \in T^{1}$$
    (3)

In each iteration, a solution is obtained using the probability Ppq(t). In (2), \(\eta_{pq} = \frac{1}{{k_{q} }}\) is a factor which is heuristic in nature; α and β are constants which determine the influence of pheromone and heuristic values on the choice of the trail taken by an ant; and T1 is the path decided by an ant at any given time. When a new trail is chosen, the weaker pheromone trails disappear. The quantity of pheromone on a path is

$$\Delta \tau_{pq}^{1} = \left\{ {\begin{array}{*{20}l} {\frac{{L^{{\min} } }}{{L^{1} }}} \hfill & {if\,p,q \in T^{1} } \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(4)

The structure formula [28] for updating of a pheromone is

$$\tau_{pq} (t) = \rho \tau_{pq} (t - 1) + \sum\limits_{1}^{N} {\Delta \tau_{pq}^{1} (t)}$$
(5)

where N is the number of ants and the evaporation rate is \(\rho \in (0,1]\).

2.2 Genetic Algorithm

Genetic algorithm is a stochastic search technique based on human genome selection procedure and is classified as “evolutionary algorithm.” GA uses the concept of natural selection and genetics and has been widely used for optimization tasks. GA is structured on the processes of natural selection, recombination and mutation of chromosomes. As with the case of any other nature inspired optimization algorithm, this technique follows the principle of survival of the fittest. The algorithm has the following steps:

  1. (i)

    Selection: First a random choice of individuals from a population is done, and the fittest one is selected for crossover. Selection is done by evaluating a fitness function corresponding to each individual.

  2. (ii)

    Modification: Modification is implemented by the process of crossover (recombination) or mutation. Crossover is the process of combining parent solutions and producing an offspring. The process of crossover and mutation attempts at generating a more fit set of individuals. Mutation prevents the algorithm from being trapped in a local minimum. Mutation maintains genetic diversity in the population. It introduces new genetic structures in the population by randomly modifying some of the individuals of the string.

The algorithm terminates when either a maximum number of generations have been produced or a sufficient fitness level has been achieved for the target population.

2.3 PID like Fuzzy Knowledge-Based Control (FKBC)

Fuzzy logic imitates human thinking and modeling of systems and processes. Implementing fuzzy logic-based control typically involves: (a) fuzzifying the inputs or converting crisp inputs to fuzzy membership functions; (b) coding human or process knowledge in terms of a rule base; (c) using fuzzy inputs along with rule base for inferring outputs called fuzzy inference system and (d) converting the aggregated fuzzy output from the fuzzy inference system to a crisp (usable) output by defuzzification.

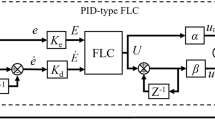
Though any process or state variables can be chosen as input variables for the fuzzy logic-based control, a natural and more efficient method of implementing fuzzy knowledge-based control (FKBC) is to use error (e) and derivative of error (∂e) as inputs to the fuzzy logic controller also termed as “PID like FKBC” in the literature. In this work, fuzzy membership functions (laid over the input variables universe of discourse) have been chosen as Gaussian, and the FIS is “Mamdani” [29]. Table 1 gives the rule base for the PID like FKBC for the variables Kp, Kd, Ki, λ, µ. It is worthwhile to note that we have framed rules for not only the conventional PID parameters Kp, Kd, Ki but also for the additional fractional-order parameters λ, µ.

Table 1 Fract-order PID like FKBC rule base
Full size table

These rules have been framed based on empirical knowledge gained during simulations of fract-order PID control. Three fuzzy subsets are chosen, i.e., “Negative,” “Zero” and “Positive” for the inputs e and ∂e. The output variables Kp, Kd, Ki, λ and µ have been fuzzified using five fuzzy subsets: NL (negative large), NLE (negative less), ZR (zero), PLE (positive less), PL (positive large). Defuzzification has been performed using the centroid method [30]. The plots for the membership functions laid over the inputs and outputs are shown in Fig. 1. This completes the design of the PID like FKBC.

Fig. 1
figure 1

Membership functions for inputs: e and ∂e; outputs: Kp, Ki, Kd

Full size image

2.4 Nature Inspired Fuzzy Fractional PID (NIFFPID)

In this work, we propose to unify all the three approaches outlined above. This is done by obtaining an algebraic sum of all the approaches, i.e., combining the PID like FKBC, ANT colony-based optimizer and the GA-based control. The aim here is to find the best possible values for the fractional PID parameters by using all the three approaches to aid each other in this process. The added advantage is that the inaccuracy of one of the approaches could possibly be covered by the others and the results indeed point to this. Complete structure of the proposed nature inspired fuzzy fractional PID controller is shown in Fig. 2.

Fig. 2
figure 2

Block diagram of NIFFPID controller

Full size image

As can be seen from the figure that each of nature inspired algorithms, i.e., GA and ACO output a set of fract-order parameters which are algebraically added to the parameters provided by the FKBC, and the combined strategy is applied to the plant being controlled.

3 Simulation of Nature Inspired PID like FKBC

The proposed approach is tested on two systems:

3.1 DC Motor

The first plant considered is a DC motor having a transfer function

$$G_{1} = \frac{{ - 0.05963s^{2} + 1.254s + 0.8736}}{{s^{3} + 0.9708s^{2} + 1.796s + 0.8736}}$$
(6)

Unconstrained minimization with GA is used to evaluate the parameters of the fract-order PID controller and the same are fed as inputs to the ANT colony algorithm. Performance index chosen is the integral of square error (ISE). GA-based optimization yields the following parameters:

  1. (i)

    Fract-order PID parameters

$$K_{p1} = 0.1833,K_{i1} = 1.6168,K_{d1} = 1.1348,L_{1} = 0.0001,M_{1} = 0.8712$$
(7)

The GA controller transfer function is

$$F_{{{\text{GA\_FOPID\_}}1}} (s) = 0.1833 + \frac{1.6168}{{s^{0.0001} }} + 1.1348s^{0.8712}$$
(8)
  1. (ii)

    ANT colony initial parameter estimate

$$\alpha = 0.0187,\beta = 0.6283,\rho = 0.0780$$
(9)

Using these values, the ANT colony algorithm (2) is implemented, and the ANT colony-based fract-order PID parameters are obtained:

$$K_{p2} = 0.11,K_{i2} = 0.18,K_{d2} = 0.19,L_{2} = 0.01,M_{2} = 0.05$$
(10)

Transfer function of ACO fract-order PID is

$$F_{{{\text{ANT-FOPID\_}}{1}}} (s) = 0. 1 1+ \frac{0.18}{{s^{0.01} }} + 0.19s^{0.05}$$
(11)

Finally, we merge the outputs of these fractional-order controllers, viz. GA, ANT and FKBC to generate our nature inspired fuzzy fractional PID (NIFFPID) controller with transfer function:

$$F_{{{\text{NIFFPID\_}}{1}}} (s) = 0. 0 8 7 1+ \frac{0.2445}{{s^{0.0204} }} + 2.0204s^{0.9242}$$
(12)

Figure 3 gives the responses obtained on the DC motor with different controllers. The NIFFPID controller proposed in this paper achieves a rise time of 0.27 s which is significantly lower than the best rise time achieved by other controllers (FOPID, FFPID using GA) of 2.143 s. Our NIFFPID control achieves peak time of 1.102 s, settling time of 1.646 s and a peak overshoot of 0.022. These values point to pretty good time response performance.

Fig. 3
figure 3

Step response of various controllers on DC motor

Full size image

3.2 Fract-Order System

The second case study is a fractional-order system with transfer function

$$G_{2} (s) = \frac{5}{{s^{2.3} { + }1.3s^{0.9} + 1.25}}$$
(13)

Once again, GA is used to get the fract-order PID parameters:

$$K_{p2} = 2.3117,K_{i2} = 0.5424,K_{d2} = 0.9052,L_{2} = 0.0172,M_{2} = 0.9997$$
(14)

Resulting GA-FOPID controller transfer function

$$F_{{{\text{GA-FOPID\_}}{2}}} (s) = 2.3117 + \frac{0.5424}{{s^{0.0172} }} + 0.9052s^{0.9997}$$
(15)

ACO initial parameters obtained are

$$\alpha = 0.3,\beta = 0.7,\rho = 0.1$$
(16)

These parameters are used to generate an ACO fract-order PID controller

$$K_{p2} = 0.06,K_{i2} = 0.02,K_{d2} = 0.40,L_{2} = 0.13,M_{2} = 0.2$$
(17)

ACO transfer function of FOPID controller becomes

$$F_{{{\text{ANT-FOPID\_}}{2}}} (s) = 0. 0 6+ \frac{0.02}{{s^{0.13} }} + 0.40s^{0.2}$$
(18)

We combine the three controller realizations to generate NIFFPID controller with transfer function:

$$F_{{{\text{NIFFPID\_}}{2}}} (s) = 2. 4 7 0 4+ \frac{ 0. 6 6 1 8}{{s^{ 0. 1 4 8 4} }} + 1. 4 0 5 2s^{ 0. 9 9 9 8}$$
(19)

Simulation results using different controllers on this plant are given in Fig. 4. Our NIFFPID controller (Fig. 4) is seen to achieve the best response parameters of rise time of 0.89 s and settling time of 3.00 s. Thus, an amalgamation of nature inspired approaches with fuzzy logic control technique, viz. GA, ACO and FKBC does lead to an improved controller response.

Fig. 4
figure 4

Step response of various controllers for fract- order system

Full size image

4 Conclusion and Future Work

An attempt has been made to hybridize two nature inspired algorithms in a PID like fuzzy setting. Our main objective is to use nature-based optimization for tuning of fuzzy logic-based fract-order PID controller. The methodology is implemented on two systems and performance compared with other soft computing-based fract-order controllers. Results indicate that our proposed controller gives better closed loop time response over other controllers.

In future, the authors would like to implement the proposed approach on some fract-order systems. We would also augment our methodology by employing type-2 fuzzy systems and self organizing fuzzy inference system structure.