Advanced Metaheuristics-Based Approach for Fuzzy Control Systems Tuning

Abstract

In this study, a new advanced metaheuristics-based optimization approach is proposed and successfully applied to design and tuning of a PID-type Fuzzy Logic Controller (FLC). The scaling factors tuning problem of the FLC structure is formulated and systematically resolved, using various constrained metaheuristics such as the Differential Search Algorithm (DSA), Gravitational Search Algorithm (GSA), Artificial Bee Colony (ABC) and Particle Swarm Optimization (PSO). In order to specify more time-domain performance control objectives of the proposed metaheuristics-tuned PID-type FLC, different optimization criteria such as Integral of Square Error (ISE) and Maximum Overshoot (MO) are considered and compared The classical Genetic Algorithm Optimization (GAO) method is also used as a reference tool to measure the statistical performances of the proposed methods. All these algorithms are implemented and analyzed in order to show the superiority and the effectiveness of the proposed fuzzy control tuning approach. Simulation and real-time experimental results, for an electrical DC drive benchmark, show the advantages of the proposed metaheuristics-tuned PID-type fuzzy control structure in terms of performance and robustness.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fuzzy logic control approach has been widely used in many successful industrial applications. This control strategy, with the Mamdani fuzzy type inference, demonstrated high robustness and effectiveness properties (Azar 2010a, b, 2012; Lee 1998a, b; Passino and Yurkovich 1998). The known PID-type FLC structure, firstly proposed in Qiao and Mizumoto (1996), is especially established and improved within the practical framework (Eker and Torun 2006; Guzelkaya et al. 2003; Woo et al. 2000). This particular fuzzy controller retains the characteristics similar to the conventional PID controller and can be decomposed into the equivalent proportional, integral and derivative control components (Eker and Torun 2006; Qiao and Mizumoto 1996). In this design case, the dynamic behaviour depends on the adequate choice of the fuzzy controller scaling factors. The tuning procedure depends on the control experience and knowledge of the human operator, and it is generally achieved based on a classical trials-errors procedure. There is not up to now a systematic method to guide such a choice. This tuning problem becomes more delicate and hard as the complexity of the control plant increases.

In order to improve further the performance of the transient and steady state responses of the PID-type fuzzy structure, various strategies and methods are proposed to tune their parameters. In Qiao and Mizumoto (1996) , proposed a peak observer mechanism-based method to adjust the PID-type FLC parameters. This self-tuning mechanism decreases the equivalent integral control component of the fuzzy controller gradually with the system response process time. On the other hand, Woo et al. (2000) developed a method based on two empirical functions evolved with the system’s error information. In Guzelkaya et al. (2003), the authors proposed a technique that adjusts the scaling factors, corresponding to the derivative and integral components, using a fuzzy inference mechanism. However, the major drawback of all these PID-type FLC tuning methods is the difficult choice of their scaling factors and self-tuning mechanisms. The time-domain dynamics of the fuzzy controller depends strongly on this hard choice. The tuning procedure depends on the control experience and knowledge of the human operator, and it is generally achieved based on a classical trials-errors procedure. Hence, having a systematic approach to tune these scaling factors is interesting and the optimization theory may present a promising solution.

In solving this kind of optimization problems, the classical exact optimization algorithms, such as gradient and descent methods, do not provide a suitable solution and are not practical. The relative objective functions are non linear, non analytical and non convex (Bouallègue et al. 2012a, b). Over the last decades, there has been a growing interest in advanced metaheuristic algorithms inspired by the behaviours of natural phenomena (Boussaid et al. 2013; Dréo et al. 2006; Rao and Savsani 2012; Siarry and Michalewicz 2008). It is shown by many researchers that these algorithms are well suited to solve complex computational problems in wide and various ranges of engineering applications summarized around domains of robotics, image and signal processing, electronic circuits design, communication networks, but more especially the domain of process control design (Bouallègue et al. 2011,2012a, b; David et al. 2013; Goswami and Chakraborty 2014; Madiouni et al. 2013; Toumi et al. 2014).

Various metaheuristics have been adopted by researchers. The Differential Search Algorithm (DSA) (Civicioglu 2012), Gravitational Search Algorithm (GSA) (Rashedi et al. 2009), Artificial Bee Colony (ABC) (Karaboga 2005) and Particle Swarm Optimization (PSO) (Eberhart and Kennedy 1995; Kennedy and Eberhart 1995) algorithms are the most recent proposed techniques in the literature. They will be adapted and improved for the considered fuzzy control design problem. Without any regularity on the cost function to be optimized, the recourse to these stochastic and global optimization techniques is justified by the empirical evidence of their superiority in solving a variety of non-linear, non-convex and non-smooth problems. In comparison with the conventional optimization algorithms, these optimization techniques are a simple concept, easy to implement, and computationally efficient algorithms. Their stochastic behaviour allows overcoming the local minima problem.

In this study, a new approach based on the use of advanced metaheuristics, such as DSA, GSA, ABC and PSO is proposed for systematically tuning the scaling factors of the particular PID-type FLC structure. The well known classical GAO algorithm is used in order to compare the obtained optimization results (Goldberg 1989; MathWorks 2009). This work can be considered as a contribution on the results given in Bouallègue et al. (2012a, b), Toumi et al. (2014). The synthesis and tuning of the fuzzy controller are formulated as a constrained optimization problem which is efficiently solved based on the proposed metaheuristics. In order to specify more robustness and performance control objectives of the proposed metaheuristics-tuned PID-type FLC, different optimization criteria such as ISE and MO are considered and compared.

The remainder of this chapter is organized as follows. In Sect. 2, the studied PID-type FLC structure is presented and formulated as a constrained optimization problem. An external static penalty technique is investigated to handle the problem constraints. The advanced DSA, GSA, ABC and PSO metaheuristic algorithms, used in solving the formulated problem, are described in Sect. 3. Section 4 is dedicated to apply the proposed fuzzy control approach on an electrical DC drive benchmark. All obtained simulation results are compared with each other and analysed. Experimental setup and results are presented within a real-time framework.

2 PID-Type FLC Tuning Problem Formulation

In this section, the PID-type fuzzy controller synthesis problem is formulated as a constrained optimization problem which will be resolved through the suggested metaheuristics algorithms.

2.1 A Review of PID-Type Fuzzy Control Structure

The particular PID-type fuzzy controller structure, originally proposed by Qiao and Mizumoto within the continuous-time formalism (Qiao and Mizumoto 1996), retains the characteristics similar to the conventional PID controller. This result remains valid while using a particular structure of FLC with triangular uniformly distributed membership functions for the fuzzy inputs and a crisp output, the product-sum inference and the center of gravity defuzzification methods (Bouallègue et al. 2012a, b; Eker and Torun 2006; Guzelkaya et al. 2003; Haggège et al. 2010; Toumi et al. 2014; Woo et al. 2000).

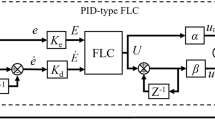
Under these conditions, the equivalent proportional, integral and derivative control components of such a PID-type FLC are given by $\alpha K_{e} {\varPi} + \beta K_{d}\varDelta$, $\beta K_{e} {\varPi}$ and $\alpha K_{d}\varDelta$, respectively, as shown in Qiao and Mizumoto (1996). In these expressions, ${\varPi}$ and $\varDelta$ represent relative coefficients, $K_{e}$, $K_{d}$, $\alpha$ and $\beta$ denote the scaling factors associated to the inputs and output of the fuzzy controller. When approximating the integral and derivative terms within the discrete-time framework (Bouallègue et al. 2012a, b; Haggège et al. 2010; Toumi et al. 2014), we can consider the closed-loop control structure for a digital PID-type FLC, as shown in Fig. 1. The dynamic behaviour of this PID-type FLC structure is strongly depending on the scaling factors, difficult and delicate to tune.

Fig. 1

Proposed discrete-time PID-type FLC structure

As shown in Fig. 1, this particular structure of Mamdani fuzzy controller uses two inputs: the error $e_{k}$ and the variation of error $\varDelta e_{k}$, to provide the output $u_{k}$ that describes the discrete fuzzy control law.

2.2 Optimization-Based Problem Formulation

The choice of the adequate values for the scaling factors of the described PID-type FLC structure is often done by a trials-errors hard procedure. This tuning problem becomes difficult and delicate without a systematic design method. To deal with these difficulties, the optimization of these control parameters is proposed like a promising procedure. This tuning can be formulated as the following constrained optimization problem:

$$\left\{ {\begin{array}{*{20}l} {\mathop {minimize}\limits_{{x = \left( {K_{e} ,K_{d} ,\alpha ,\beta } \right)^{T} \in {\mathcal{S}} \subset {\mathbb{R}}_{ + }^{4} }} f\left( x \right)} \hfill \\ {subject\;\;to:} \hfill \\ {g_{1} \left( x \right) = \delta - \delta^{\hbox{max} } \le \;0} \hfill \\ {g_{2} \left( x \right) = t_{s} - t_{s}^{\hbox{max} } \le \;0} \hfill \\ {g_{3} \left( x \right) = E_{ss} - E_{ss}^{\hbox{max} } \le \;0} \hfill \\ \end{array} } \right.$$

(1)

where $f{:}\;{\mathbb{R}}^{4} \to {\mathbb{R}}$ the cost function, ${\mathcal{S}} = \left\{ {x \in {\mathbb{R}}_{ + }^{4} ,x_{low} \le x \le x_{up} } \right\}$ the initial search space, which is supposed containing the desired design parameters, and $g_{l} :{\mathbb{R}}^{4} \to {\mathbb{R}}$ the nonlinear problem’s constraints.

The optimization-based tuning problem (1) consists in finding the optimal decision variables, representing the scaling factors of a given PID-type FLC structure, which minimizes the defined cost function, chosen as the Maximum Overshoot (MO) and the Integral of Square Error (ISE) performance criteria. These cost functions are minimized, using the proposed particular constrained metaheuristics, under various time-domain control constraints such as overshoot $\delta$, steady state error $E_{ss}$, rise time $t_{r}$ and settling time $t_{s}$ of the system’s step response, as shown in Eq. (1). Their specified maximum values constrain the step response of the tuned PID-type fuzzy controlled system, and can define some time-domain templates.

2.3 Proposed Constraints Handling Method

The considered metaheuristics in this study are originally formulated as an unconstrained optimizer. Several techniques have been proposed to deal with constraints. One useful approach is by augmenting the cost function of problem (1) with penalties proportional to the degree of constraint infeasibility. This approach leads to convert the constrained optimization problem into the unconstrained optimization problem. In this paper, the following external static penalty technique is used:

$$\varphi \left( x \right) = f\left( x \right) + \sum\limits_{l = 1}^{{n_{con} }}\uplambda_{l} \hbox{max} \left[ {0,g_{l} \left( x \right)^{2} } \right]$$

(2)

where $\lambda_{l}$ is a prescribed scaling penalty parameter, and $n_{con}$ is the number of problem constraints $g_{l} \left( x \right)$.

3 Solving Optimization Problem Using Advanced Algorithms

In this section, the basic concepts as well as the algorithm steps of each proposed advanced metaheuristic are described for solving the formulated PID-type FLC tuning problem.

3.1 Differential Search Algorithm

The Differential Search Algorithm (DSA) is a recent population-based metaheuristic optimization algorithm invented in 2012 by Civicioglu (2012). This global and stochastic algorithm simulates the Brownian-like random-walk movement used by an organism to migrate (Civicioglu 2012; Goswami and Chakraborty 2014; Waghole and Tiwari 2014).

Migration behavior allows the living beings to move from a habitat where capacity and diversity of natural sources are limited to a more efficient habitat. In the migration movement, the migrating species of living beings constitute a superorganism containing large number of individuals. Then it starts to change its position by moving toward more fruitful areas using a Bownian-like random-walk model. The population made up of random solutions of the respective problem corresponds to an artificial-superorganism migrating. The artificial superorganism migrates to global minimum value of the problem. During this migration, the artificial-superorganism tests whether some randomly selected positions are suitable temporarily. If such a position tested is suitable to stop over for a temporary time during the migration, the members of the artificial-superorganism that made such discovery immediately settle at the discovered position and continue their migration from this position (Civicioglu 2012).

In DSA metaheuristic, a superorganism $X_{k}^{i}$ of $N$ artificial-organisms making up, at every generation $k = 1,2, \ldots ,k_{\hbox{max} }$, an artificial-organism with members as much as the size of the problem, defined as follows:

$$X_{k}^{i} = \left( {x_{k}^{i,1} ,x_{k}^{i,2} , \ldots ,x_{k}^{i,d} , \ldots ,x_{k}^{i,D} } \right)$$

(3)

A member of an artificial-organism, in initial position, is randomly defined by using Eq. (4):

$$x_{0}^{i,d} = x_{low}^{i,d} + rand\left( {0,1} \right)\left( {x_{up}^{i,d} - x_{low}^{i,d} } \right)$$

(4)

In DSA, the mechanism of finding a so called Stopover Site, which presents the solution of optimization problem, at the areas remaining between the artificial-organisms, is described by a Brownian-like random walk model. The principle is based on the move of randomly selected individuals toward the targets of a Donor artificial-organism, denoted as (Civicioglu 2012):

$$X_{k}^{Donor} = X_{k}^{random\_shuffling\left( i \right)}$$

(5)

where the index $i$ of artificial-organisms is produced by the Shuffling-random function.

The size of the change occurred in the positions of the members of the artificial-organisms is controlled by the Scale factor given as follows:

$$s_{k}^{i} = randG\left\{ {2rand_{1} } \right\}\left( {rand_{2} - rand_{3} } \right)$$

(6)

where $rand_{1}$, $rand_{2}$ and $rand_{3}$ are uniformly distributed random numbers in the interval [0, 1], $randG$ is a Gamma-random number.

The Stopover Site positions, which are very important for a successful migration, are produced by using Eq. (7):

$$Y_{k}^{i} = X_{k}^{i} + s_{k}^{i} \left( {X_{k}^{Donor} - X_{k}^{i} } \right)$$

(7)

So, the individuals of the artificial-organisms of the superorganism to participate in the search process of Stopover Site are determined by a random process based on the manipulation of two control parameters $p_{1}$ and $p_{2}$. The algorithm is not much sensitive to these control parameters and the values in the interval [0, 0.3] usually provide best solutions for a given problem (Civicioglu 2012).

Finally, the steps of the original version of DSA, as described by the pseudo code in Civicioglu (2012), can be summarized as follows:

• 1. Search space characterization: size of superorganism, dimension of problem, random numbers $p_{1}$ and $p_{2}$, …

• 2. Randomized generation of the initial population.

• 3. Fitness evaluation of artificial-organisms.

• 4. Calculation of the Stopover Site positions in different directions.

• 5. Randomly select individuals to participate in the search process of Stopover Site.

• 6. Update the Stopover Site positions and evaluate the new population.

• 7. Update the superorganism by the new Stopover site positions.

• 8. Repeat steps 3–7 until the stop criteria are reached.

3.2 Gravitational Search Algorithm

The Gravitational Search Algorithm (GSA) is population-based metaheuristic optimization algorithm introduced in 2009 by Rashedi et al. (2009). This algorithm is based on the law of gravity and mass interactions as described in Nobahari et al. (2011), Precup et al. (2011), Rashedi et al. (2009). The search agents are a set of masses which interact with each other based on the Newtonian gravity and the law of motion.

Several applications of this algorithm in various areas of engineering are investigated (Nobahari et al. 2011; Precup et al. 2011; Rao and Savsani 2012). In GSA, the particles, called also agents, are considered as bodies and their performance is measured by their masses. All these bodies attract each other by the gravity force that causes a global movement of all objects towards the objects with heavier masses. These agents correspond to the optimum solutions in the search space (Rashedi et al. 2009). Indeed, each agent presents a solution of optimization problem and is characterised by its position, inertial mass, active and passive gravitational masses. The GSA is navigated by properly adjusting the gravitational and inertia masses leading masses to be attracted by the heaviest object.

The position of the mass corresponds to a solution of the problem, and its gravitational and inertial masses are determined using a cost function. The exploitation capability of this algorithm is guaranteed by the movement of the heavy masses, more slowly than the lighter ones.

Let us consider a population with $N$ agents. The position of the $i\text{th}$ agent at iteration time $k$ is defined as:

$$X_{k}^{i} = \left( {x_{k}^{i,1} ,x_{k}^{i,2} , \ldots ,x_{k}^{i,d} , \ldots ,x_{k}^{i,D} } \right)$$

(8)

where $x_{k}^{i,d}$ presents the position of the $i\text{th}$ particle in the $d\text{th}$ dimension of search space of size $D$.

At a specific time “$t$”, denoted by the actual iteration “$k$”, the force acting on mass “$i$” from mass “$j$” is given as follows:

$$F_{k}^{ij,d} = G_{k} \frac{{M_{k}^{pi} \times M_{k}^{aj} }}{{R_{k}^{ij} + \varepsilon }}\left( {x_{k}^{j,d} - x_{k}^{i,d} } \right)$$

(9)

where $M_{k}^{aj}$ is the active gravitational mass related to agent $j$, $M_{k}^{pi}$ is the passive gravitational mass related to agent $i$, $G_{k}$ is the gravitational constant at time $k$, $\varepsilon$ is a small constant, and $R_{k}^{ij}$ is the Euclidian distance between two agents $i$ and $j$, defined as:

$$R_{k}^{ij} = \left\| {X_{k}^{i} ,X_{k}^{j} } \right\|_{2}$$

(10)

To give a stochastic characteristic to this algorithm, authors of GSA suppose that the total force that acts on agent $i$ is a randomly weighted sum of $j\text{th}$ components of the forces exerted from other bodies, given as follows (Rashedi et al. 2009):

$$F_{k}^{i,d} = \sum\limits_{j = 1,j \ne i}^{N} rand^{j} F_{k}^{ij,d}$$

(11)

where $rand^{j}$ is a random number in the interval [0, 1].

By the law of motion, the acceleration of the agent $i$ at time $k$, and in $d\text{th}$ direction, is given as follows:

$$a_{k}^{i,d} = \frac{{F_{k}^{i,d} }}{{M_{k}^{ii} }}$$

(12)

where $M_{k}^{ii}$ is the inertial mass of $i\text{th}$ agent in the search space with dimension $d$.

Hence, the position and the velocity of an agent are updated respectively by the mean of equations of movement given as follows:

$$x_{k + 1}^{i,d} = x_{k}^{i,d} + v_{k + 1}^{i,d}$$

(13)

$$v_{k + 1}^{i,d} = rand^{i} v_{k}^{i,d} + a_{k}^{i,d}$$

(14)

where $rand^{i}$ is a uniform random number in the interval [0, 1], used to give a randomized characteristic to the search.

To control the search accuracy, the gravitational constant $G_{k}$, is initialized at the beginning and will be reduced with time. In this study, we use an exponentially decreasing of this algorithm parameter, as follows:

$$G_{k} = G_{0} e^{{ - \eta \frac{k}{{k_{{\text{max}}} }}}}$$

(15)

where $G_{0}$ is the initial value of $G_{k}$, $\eta$ is a control parameter to set, and $k_{{\text{max}}}$ is the total number of iterations.

In GSA, gravitational and inertia masses are calculated by the fitness evaluation. A heavier mass means a more efficient agent. Better agents have higher attractions and walk more slowly.

As given in Rashedi et al. (2009), the values of masses are calculated using the fitness function and gravitational and inertial masses are updated by the following equations:

$$M_{k}^{ai} = M_{k}^{pi} = M_{k}^{ii} = M_{k}^{i}$$

(16)

$$M_{k}^{i} = \frac{{m_{k}^{i} }}{{\sum\nolimits_{j = 1}^{N} m_{k}^{j} }}$$

(17)

$$m_{k}^{i} = \frac{{fit_{k}^{i} - worst_{k} }}{{best_{k} - worst_{k} }}$$

(18)

where $fit_{k}^{i}$ represents the fitness value of the agent $i$ at iteration $k$, and, $worst_{k}$ and $best_{k}$ are defined, for a minimization problem, as follows:

$$best_{k} = \mathop {\hbox{min} }\limits_{1 \le j \le N} fit_{k}^{j}$$

(19)

$$worst_{k} = \mathop {\hbox{max} }\limits_{1 \le j \le N} fit_{k}^{j}$$

(20)

To perform a good compromise between exploration and exploitation, authors of GSA choose to reduce the number of agents with lapse of iterations in Eq. (11), which will be modified as:

$$F_{k}^{i,d} = \sum\limits_{j \in Kbest,j \ne i} rand^{j} F_{k}^{ij,d}$$

(21)

where $Kbest$ is the set of the first $K$ agents with best fitness and biggest mass that will attract the others.

The algorithm parameter $Kbest$ is a function of iterations with the initial value $K_{0}$, usually set to the total size of population $N$ at the beginning, and linearly decreasing with time. At the end of search, there will be just one agent applying force to the others.

Finally, the steps of the original version of GSA, as described in Rashedi et al. (2009), can be summarized as follows:

• 1. Search space characterization: number of agents, dimension of problem, control parameters $G_{0}$, $K_{0}$, …

• 2. Randomized generation of the initial population.

• 3. Fitness evaluation of agents.

• 4. Update the algorithm parameters $G_{k}$, $best_{k}$, $worst_{k}$ and $M_{k}^{i}$ for each agent and at each iteration.

• 5. Calculation of the total force in different directions.

• 6. Calculation of acceleration and velocity.

• 7. Updating agents’ position.

• 8. Repeat steps 3–7 until the stop criteria are reached.

3.3 Artificial Bee Colony

The Artificial Bee Colony (ABC) is a population-based metaheuristic optimization algorithm introduced in 2005 by Karaboga (2005). The principle of such an algorithm is based on the intelligent foraging behavior of honey bee swarm (Basturk and Karaboga 2006; Karaboga 2005; Karaboga and Akay 2009; Karaboga and Basturk 2007, 2008). The ABC algorithm has been enormously successful in various industrial domains and a wide range of engineering applications as summarized in Karaboga et al. (2012).

In this formalism, the population of the artificial bees’ colony is constituted of three groups: employed bees, onlookers and scouts. Employed bees search the destination where food is available, translated by the amount of their nectar. They collect the food and return back to their origin, where they perform waggle dance depending on the amount of nectar’s food available at the destination. The onlooker bee watches the dance and follows the employed bee depending on the probability of the available food.

In ABC algorithm, the population of bees is divided into two parts consisting of employed bees and onlooker bees. The sizes of each part are usually taken equal to. Employed bee, representing a potential solution in the search space with dimension, updates its new position by using the movement Eq. (22) and follows greedy selection to find the best solution. The objective function associated with the solution is measured by the amount of food.

Let us consider a population with $N/2$ individuals in the search space. The position of the $i\text{th}$ employer at iteration time $k$ is defined as:

$$X_{k}^{i} = \left( {x_{k}^{i,1} ,x_{k}^{i,2} , \ldots ,x_{k}^{i,d} , \ldots ,x_{k}^{i,D} } \right)$$

(22)

where $D$ is the number of decision variables, $i$ is the index on $N/2$ employers.

In the $d\text{th}$ dimension of search space, the new position of the ith employer, as well as of the ith onlooker, is updated by means of the movement equation given as follows:

$$x_{k + 1}^{i,d} = x_{k}^{i,d} + r_{k}^{i} \left( {x_{k}^{i,d} - x_{k}^{m,d} } \right)$$

(23)

where $r_{k}^{i}$ is a uniformly distributed random number in the interval [−1, 1]. It can be also chosen as a normally distributed random number with mean equal to zero and variance equal to one as given in Karaboga (2005). The employer’s index $m \ne i$ is a randomly number in the interval [1, N/2].

Besides, an onlooker bee chooses a food source depending on the probability value of each solution associated with that food source, calculated as follows:

$$p_{k}^{i,d} = \frac{{f_{k}^{i,d} }}{{\sum\nolimits_{n}^{N/2} f_{k}^{n,d} }}$$

(24)

where $f_{k}^{i,d}$ is the fitness value of the $i\text{th}$ solution at iteration $k$.

When the food source of an employed bee cannot be improved for some predetermined number of cycles, called “Limit for abandonment” and denoted by $L$, the source food becomes abandoned and the employer behaves as a scout bee and it searches for the new food source using the following equation:

$$x_{k}^{i,d} = x_{low}^{i,d} + rand\left( {0,1} \right)\left( {x_{up}^{i,d} - x_{low}^{i,d} } \right)$$

(25)

where $x_{low}^{i,d}$ and $x_{up}^{i,d}$ are the lower and upper ranges, respectively, for decision variables in the dimension.

This behaviour of the artificial bee colony reflects a powerful mechanism to escape the problem of trapping in local optima. The value of the “Limit for abandonment” control parameter of ABC algorithm is calculated as follows:

$$L = \frac{N}{2} \times D$$

(26)

Finally, the steps of the original version of ABC algorithm, as described in Basturk and Karaboga (2006), Karaboga (2005), Karaboga and Basturk (2007, 2008), can be summarized as follows:

• 1. Initialize the ABC algorithm parameters: population size $N$, limit of abandonment $L$, dimension of the search space $D$, …

• 2. Generate a random population equal to the specified number of employed bees, where each of them contains the value of all the design variables.

• 3. Obtain the values of the objective function, defined as the amount of nectar for the food source, for all the population members.

• 4. Update the position of employed bees using Eq. (23), obtain the value of objective function and select the best solutions to replace the existing ones.

• 5. Run the onlooker bee phase: onlookers proportionally choose the employed bees depending on the amount of nectar found by the employed bees, Eq. (24).

• 6. Update the value of onlooker bees using Eq. (23) and replace the existing solution with the best new one.

• 7. Identify the abundant solutions using the limit value. If such solutions exist then these are transformed into the scout bees and the solution is updated using Eq. (25).

• 8. Repeat the steps 3–7 until the termination criterion is reached, usually chosen as the specified number of generations.

3.4 Particle Swarm Optimization

The PSO technique is an evolutionary computation method developed in 1995 by Kennedy and Eberhart (1995), Eberhart and Kennedy (1995). This recent meta-heuristic technique is inspired by the swarming or collaborative behaviour of biological populations. The cooperation and the exchange of information between population individuals allow solving various complex optimization problems. The convergence and parameters selection of the PSO algorithm are proved using several advanced theoretical analysis (Bouallègue et al. 2011, 2012a, b; Madiouni et al. 2013). PSO has been enormously successful in several and various industrial domains and engineering fields (Bouallègue et al. 2012a; Dréo et al. 2006; Rao and Savsani 2012; Siarry and Michalewicz 2008).

The basic PSO algorithm uses a swarm consisting of $N$ particles $N_{k}^{i}$, randomly distributed in the considered initial search space, to find an optimal solution $x^{*} = \arg \hbox{min}\,f\left( x \right) \in {\mathbb{R}}^{D}$ of a generic optimization problem. Each particle, that represents a potential solution, is characterised by its position and its velocity $x_{k}^{i,d}$ and $v_{k}^{i,d}$, respectively.

At each iteration of the algorithm, and in the $d\text{th}$ direction, the $i\text{th}$ particle position evolves based on the following update rules:

$$x_{k + 1}^{i,d} = x_{k}^{i,d} + v_{k + 1}^{i,d}$$

(27)

$$v_{k + 1}^{i,d} = w_{k + 1} v_{k}^{i,d} + c_{1} r_{1,k}^{i} \left( {p_{k}^{i,d} - x_{k}^{i,d} } \right) + c_{2} r_{2,k}^{i} \left( {p_{k}^{g,d} - x_{k}^{i,d} } \right)$$

(28)

where $w_{k + 1}$ the inertia factor, $c_{1}$ and $c_{2}$ the cognitive and the social scaling factors respectively, $r_{1,k}^{i}$ and $r_{2,k}^{i}$ the random numbers uniformly distributed in the interval [0,1], $p_{k}^{i,d}$ the best previously obtained position of the $i\text{th}$ particle and $p_{k}^{g,d}$ the best obtained position in the entire swarm at the current iteration $k$.

In order to improve the exploration and exploitation capacities of the proposed PSO algorithm, we choose for the inertia factor a linear evolution with respect to the algorithm iteration (Bouallègue et al. 2011, 2012a, b; Madiouni et al. 2013):

$$w_{k + 1} = w_{\hbox{max} } - \left( {\frac{{w_{\hbox{max} } - w_{\hbox{min} } }}{{k_{{\text{max}}} }}} \right)k$$

(29)

where $w_{\hbox{max} } = 0.9$ and $w_{\hbox{min} } = 0.4$ represent the maximum and minimum inertia factor values, respectively.

Finally, the steps of the original version of PSO algorithm, as described in Eberhart and Kennedy (1995), Kennedy and Eberhart (1995), can be summarized as follows:

• 1. Define all PSO algorithm parameters such as swarm size $N$, maximum and minimum inertia factor values, cognitive and social coefficients, …

• 2. Initialize the particles with random positions and velocities. Evaluate the initial population and determine $p_{0}^{i,d}$ and $p_{0}^{g,d}$.

• 3. For each particle apply the update Eqs. (27)–(29).

• 4. Evaluate the corresponding fitness values and select the best solutions.

• 5. Repeat the steps 3–4 until the termination criterion is reached.

4 Case Study: PID-Type FLC Tuning for a DC Drive

This section is dedicated to apply the proposed metaheuristics-tuned PID-type FLC for the variable speed control of a DC drive. All the obtained simulations results are presented and discussed.

4.1 Plant Model Description

The considered benchmark is a 250 W electrical DC drive shown in Fig. 2. The machine’s speed rotation is 3,000 rpm at 180 V DC armature voltage.

Fig. 2

Electrical DC drive benchmark

The motor is supplied by an AC-DC power converter. The considered electrical DC drive can be described by the following model (Haggège et al. 2009):

$$G\left( s \right) = \frac{\varLambda }{{\left( {1 + \tau_{e} s} \right)\left( {1 + \tau_{m} s} \right)}}$$

(30)

The model’s parameters are obtained by an experimental identification procedure and they are summarized in Table 1 with their associated uncertainty bounds. This model is sampled with 10 ms sampling time for simulation and experimental setups.

Table 1 Identified DC Drive model parameters

4.2 Simulation Results

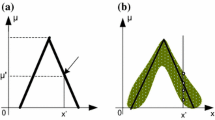
For this study case, product-sum inference and center of gravity defuzzification methods are adopted. Uniformly distributed and symmetrical membership functions, are assigned for the fuzzy input and output variables, as shown in Fig. 3.

Fig. 3

Membership functions for fuzzy inputs and output variables

The linguistic levels assigned to the input variables $e_{k}$ and $\Delta e_{k}$, and the output variable $\Delta u_{k}$ are given as follows: N (Negative), Z (Zero), P (Positive), NB (Negative Big) and PB (Positive Big). The associated fuzzy rule-base is given in Table 2. The view of this rule-base is illustrated in Fig. 4.

Table 2 Fuzzy rule-base for the standard FLC

Fig. 4

View of the fuzzy rule-base for the standard FLC

For our design, the initial search domain of PID-type FLC parameters is chosen in the limit range of $x_{low} = \left( {1,5,2,25} \right)$ and $x_{up} = \left( {5,10,10,50} \right)$. For all proposed metaheuristics, we use a population size equal to $N = 30$ and run all used algorithms under $k_{{\text{max}}} = 100$ iterations. The size of optimization problem is equal to $D = 4$. The decision variables are the scaling factors of the studied particular PID-type FLC structure, i.e., $\alpha$, $\beta$, $K_{e}$ and $K_{d}$.

In this study, the control problem constraints are defined by the maximum values of the performance criteria: overshoot ($\delta^{\hbox{max} } = 20\,\%$), settling time ($t_{s}^{\hbox{max} } = 0.9\,\text{s}$) and steady state error ($E_{ss}^{\hbox{max} } = 0.0001$). The scaling penalty parameter is chosen as constant equal to $\lambda_{l} = 10^{4}$. The algorithm stops when the number of generations reaches the specified value for the maximum number of generations.

For the software implementation of the proposed metaheuristics, the control parameters of each algorithm are set as follows:

• DSA: random numbers Stopover site research $p_{1} = p_{2} = 0.3rand\,\left( {0,1} \right)$;

• GSA: initial value of gravitational constant $G_{0} = 75$, parameter $\eta = 20$, initial value of the $Kbest$ agents $K_{0} = N = 30$ which is decreased linearly to 1;

• ABC: Limit of abandonment $L = 60$;

• PSO: cognitive and social coefficients equal to $c_{1} = c_{2} = 2$, inertia factor decreasing linearly from 0.9 to 0.4;

• GAO: Stochastic Uniform selection and Gaussian mutation methods, Elite Count equal to 2 and Crossover Fraction equal to 0.8.

In order to get statistical data on the quality of results and so to validate the proposed approaches, we run all implemented algorithms 20 times. Feasible solutions are usually found within an acceptable CPU computation time. The obtained optimization results are summarized in Tables 3 and 4.

Table 3 Optimization results from 20 trials of problem (1.1): ISE criterion

Table 4 Optimization results from 20 trials of problem (1.1): MO criterion

4.3 Results Analysis and Discussion

According to the statistical analysis of Tables 3 and 4, as well as the numerical simulations in Figs. 5, 6, 7 and 8, we observe that the proposed approaches produce near results in comparison with each other and with the standard GAO-based method. Globally, the algorithms convergences always take place in the same region of the design space whatever is the initial population. This result indicates that the algorithms succeed in finding a region of the interesting research space to explore.

Fig. 5

Robustness convergence under control parameters variation of the DSA-based approach: ISE criterion case

Fig. 6

Robustness convergence under control parameters variation of the GSA-based approach: ISE criterion case

Fig. 7

Robustness convergence under control parameters variation of the ABC-based approach: ISE criterion case

Fig. 8

Robustness convergence under control parameters variation of the PSO-based approach: ISE criterion case

In this case study, we tested the proposed algorithms with different values of the population size in the range of [20, 50]. Globally, all the results found are close to each other. The best values of this control parameter are usually obtained while using a population size equal to 30.

Both for the MO and ISE criteria, the robustness on convergence of the proposed algorithms is guaranteed under their main control parameters variation. The qualities of the obtained solution, the fast convergence as well as the simple software implementation are comparable with the standard GAO-based approach. According to the convergence plots of the implemented metaheuristics, i.e., results of Figs. 5, 6, 7 and 8, the exploitation and exploration capabilities of these algorithms are ever guaranteed.

In this study, only simulation results from the ISE criterion case are illustrated. The main difference between performances of the implemented metaheuristics is their relative quickness or slowness in terms of CPU computation time. For this particular optimization problem, the quickness of DSA and PSO is specially marked in comparison with other techniques. Indeed, while using a Pentium IV, 1.73 GHz and MATLAB 7.7.0, the CPU computation times for the PSO algorithm are about 328 and 360 s in the MO and ISE criterion, respectively. For the DSA algorithm, these are about 296 and 310 s, respectively. For example and in the case of GSA metaheuristic, we obtain about 540 and 521 s for the above criterion respectively.

For the ISE criterion case, all optimization results are close to each other in terms of solutions quality, except those obtained by the ABC-based method. The relative numerical simulation shows the sensitivity of this algorithm under the “Limit for abandonment” parameter variation. The best optimization result, with fitness value equal to $0.1928$, is obtained with $L = 60$.

On the other hand, the scaling parameters $\lambda_{l}$, given in Eq. 2, will be linearly increased at each iteration step so constraints are gradually enforced. In a generic and typical optimization problem, the quality of the solution will directly depend on the value of this algorithm control parameter. In this chapter and in order to make the proposed approach simple, great and constant scaling penalty parameters, equal to $10^{4}$, are used for numerical simulations. Indeed, simulation results show that with great values of $\lambda_{l}$, the control system performances are weakly degraded and the effects on the tuning parameters are less meaningful. The proposed constrained and improved algorithms convergence is faster than the case with linearly variable scaling parameters.

The time-domain performances of the proposed metaheuristics-tuned PID-type FLC structure are illustrated in Figs. 9 and 10. Only simulations from the DSA and PSO techniques implementation are presented. All results, for various obtained decision variables, are acceptable and show the effectiveness of the proposed fuzzy controllers tuning method. The robustness, in terms of external disturbances rejection, and tracking performances are guaranteed with degradations for some considered methods. The considered time-domain constraints for the PID-type FC tuning problems, such as the maximum values of overshoot $\delta^{\hbox{max} } = 20\;\%$, steady state $E_{ss}^{\hbox{max} } = 0.0001$ and settling time $t_{s}^{\hbox{max} } = 0.9\,\text{s}$, are usually respected.

Fig. 9

Step responses of the DSA-tuned PID-type fuzzy controlled system: ISE criterion case

Fig. 10

Step responses of the PSO-tuned PID-type fuzzy controlled system: ISE criterion case

4.4 Experimental Results

In order to illustrate the efficiency of the proposed metaheuristics-tuned PID-type fuzzy control structure, we try to implement the controller within a real-time framework. The developed real-time application acquires input data, speed of the DC drive, and generates control signal for thyristors of AC-DC power converter as a PWM signal (Haggège et al. 2009). This is achieved using a digital control system based on a PC computer and a PCI-1710 multi-functions data acquisition board which is compatible with MATLAB/Simulink as described in Fig. 11.

Fig. 11

The proposed experimental setup schematic for DC drive control

The power part of the controlled process is constituted of the single-phase bridge rectifier converter. Figure 11 shows the considered half-controlled bridge rectifier, constituted by two thyristors and two diodes. The presence of thyristors makes the average output voltage controllable. A thyristor can be triggered by the application of a positive gate voltage and hence a gate current supplied from a gate drive circuit. The control voltage is generated with the help of a gate drive circuit, which is called a firing or triggering circuit. The used bridge thyristors are switched ON by a train of high-frequency impulses.

In order to obtain an impulse train, beginning with a fixed delay after the AC supply source zero-crossing, it is necessary to generate a sawtooth signal, synchronized with this zero-crossing. This is achieved using a capacitor charged with a constant current during the 10 ms half period of the AC source, and abruptly discharged at every zero-crossing instant. The constant current is obtained using a BC547 bipolar transistor whose base voltage is maintained constant due to a polarization bridge constituted by a resistor and two 1N4148 diodes in series. This transistor acts as a current sink, whose value can be determined by an adjustable emitter resistor, to make the capacitor be fully charged after exactly 10 ms. The obtained synchronous saw-tooth signal is compared with a variable DC voltage, using an LM393 comparator, in order to generate a PWM signal which drives a NE555 timer, used as an astable multi-vibrator, producing the impulse train needed to control the thyristors firing. This impulse train is applied to the base of a 2N1711 bipolar transistor which drives an impulse transformer that ensuring the galvanic isolation between the control circuit and the power circuit.

The nominal model of the studied plant and the controller model obtained in synthesis development phase were used to implement the real-time controller. The model of the plant was removed from the simulation model, and instead of it, input device drivers (sensor) and output device driver (actuator) were introduced as shown in Fig. 12. These device drivers close the feedback loop when moving from simulations to experiments. According to this concept, the Fig. 13 illustrates the principle of the implementation based on the Real-Time Windows Target tool of MATLAB/Simulink.

Fig. 12

Synoptic of the PCI-1710 based real-time controller implementation

Fig. 13

PCI-1710 board based implementation of the proposed FLC structure

The real-time fuzzy controller is developed through the compilation and linking stage, in a form of a Dynamic Link Library (DLL), which is then loaded in memory and started-up. The used environment of real-time controller has some capabilities such as automatic code generation in C language, automatic compilation, start-up of a real-time program and external mode start-up of the simulation phase model allowing for real-time set monitoring and on-line adjustment of its parameters.

The real-time implementation of the proposed metaheuristics-tuned PID-type FLC leads to the experimental results of Figs. 14, 15, 16 and 17.

Fig. 14

Experimental results of the PID-type FLC implementation: controlled speed variation

Fig. 15

Experimental results of the PID-type FLC implementation: speed tracking error

Fig. 16

Robustness of the external disturbance rejection: controlled speed variation

Fig. 17

Robustness of the external disturbance rejection: speed tracking error

In comparison with the results in Haggège et al. (2009) for a such plant, obtained by the use of a full order ${\mathcal{H}}_{\infty }$ controller, as well as those obtained by PID-type FLC with trials-errors tuning method in Haggège et al. (2010), the experimental results of this study are satisfactory for a simple, non conventional and systematic metaheuristics-based control approach. They point out the controller’s viability and performance. As shown in Figs. 14 and 15, the measured speed tracking error is small (less than 10 % of set point) showing the high performances of the proposed control, especially in terms of tracking. The robustness, in terms of external load disturbances of the proposed PID-type FLC approach, is shown in Figs. 16 and 17. The proposed fuzzy controller leads to reject the additive disturbances on the controlled system output with a fast and more damped dynamic.

Globally, the obtained simulation and experimental results for the considered ISE and MO criteria are satisfactory. Others performance criteria, such as gain and margin specifications (Azar and Serrano 2014), can be used in order to improve the robustness and efficiency of the proposed fuzzy control approach.

5 Conclusion

A new method for tuning the scaling factors of Mamdani fuzzy controllers, based on advanced metaheuristics, is proposed and successfully applied to an electrical DC drive speed control. This efficient metaheuristics-based tool leads to a robust and systematic PID-type fuzzy control design approach. The comparative study shows the efficiency of the proposed techniques in terms of convergence speed and quality of the obtained solutions. This hybrid PID-type fuzzy design methodology is systematic, practical and simple without need to exact analytical plant model description. The obtained simulation and experimental results show the efficiency in terms of performance and robustness. All used DSA, GSA, ABC and PSO techniques produce near results in comparison with each others. Small degradations are always marked by going from one technique to another. The application of the proposed control approach, for more complex and non linear systems, constitutes our future works. The tuning of other fuzzy control structures, such as those described by Takagi-Sugeno inference mechanism, will be investigated.