Keywords

1 Introduction

In 1965, Zadeh [1] invented the idea of a fuzzy set. Since then, scholars from other fields have utilized this key set. The fuzzy set has shown to be highly promising and effective in modeling human involvement in human-based intelligence to achieve modernism in various sectors like data analysis, data mining, picture coding and explanation, as well as in intelligence systems [2].

The fuzzy set has also established itself as a legitimate area of study in both pure and practical statistics and mathematics, demonstrating this theory’s broad applicability and usefulness. Despite being a hot topic for many years, fuzzy sets continue to draw academics because they offer solutions to pressing problems with particular qualities that these notions call into question.

Through cooperative problem solving, the fuzzy set may solve a variety of physical world issues that may be beyond the scope of traditional methods. This suggests that the fuzzy set would be able to handle a variety of issues, including decision-making, intelligent data analysis, information processing, pattern identification, and optimization [3, 4].

The main goal of this paper is to dive deeper into present a comparative study of basic two types of fuzzy convergence with midpoint as image segmentation techniques.

2 Image Segmentation

Image processing and pattern recognition depend basically on image segmentation. Image segmentation becomes a very important challenge in various fields such as political, medical, and others [5]. Image segmentation is playing an essential role in the medical sector because it makes it easier or automatically delineates anatomical structures and other regions of interest [6]. Image segmentation techniques play a major and important role in the investigation of political fields and can provide evidence for the trial and litigation of the case [7].

There are three classes into which the segmentation methods can be classified: (1) characteristic feature thresholding or clustering, (2) edge detection, and (3) region extraction [8,9,10]. The first type will be employed in this paper [11, 12].

3 Related Works

Cheng et al. [5] used a mixing of several approaches such as histogram thresholding, region-based approaches, fuzzy approaches, and edge detection methods that were applied together for color image segmentation [13].

Shi [7] discussed the notion of image processing techniques in regard to a criminal investigation, using different processes of fuzzy image technology and taking into his consideration the enhancement of the contrast ratio analyses [14].

Dass et al. [15] investigated and combined some of the image segmentation technologies. Also, a survey of several image segmentation techniques is discussed, and finally, general tendencies in image segmentation are presented [16].

Sharma and Aggarwal [17] explained the details of image segmentation techniques mostly in the situation of CT and MR images. The aim of this study to solve the problem faced by the segmentation method of CT and MR images and explains the available limitations for medical image segmentation [18].

4 Fuzzy Concepts

Definition 4.1

Reference [1] Let \({\mathfrak{U}}\) be a non-empty set, then a function from a non-empty set \({\mathfrak{U}}\) into a closed unit interval \({\mathfrak{I}}\), where \({\mathfrak{I}} = \left[ {0,1} \right]\) is said to be a fuzzy set \({\mathfrak{N}}\) of a set \({\mathfrak{U}}\), , i.e., (\({\mathfrak{N}}:{\mathfrak{U}} \to {\mathfrak{I}}\) be a function). For all \({\mathfrak{u}} \in {\mathfrak{U}}\), \({\mathfrak{N}}\left( {\mathfrak{u}} \right)\) is an interpretation of the degree of membership of element \({\mathfrak{u}}\) in a fuzzy set \({\mathfrak{N}}\).

One manner in which a fuzzy subset \({\mathfrak{N}}\) of \({\mathfrak{U}}\) can be expressed as the pairs \({\mathfrak{N}} = \left\{ {\left( {{\mathfrak{u}},{\mathfrak{N}}\left( {\mathfrak{u}} \right):{\mathfrak{u}} \in {\mathfrak{U}}} \right)} \right\}\). The symbol \({\mathfrak{I}}^{{\mathfrak{U}}}\) symbolizes to the class of all fuzzy subsets of a set \({\mathfrak{U}}\).

Definition 4.2

Reference [1] For any fuzzy subsets \({\mathfrak{N}}\) and \({\mathfrak{M}}\) of a set \({\mathfrak{U}}\), we can say that \({\mathfrak{N}}\) is a fuzzy subset of a fuzzy set \({\mathfrak{M}}\) symbolized by \({\mathfrak{N}} \le {\mathfrak{M}}\) if and only if \({\mathfrak{N}}\left( {\mathfrak{u}} \right) \le {\mathfrak{M}}\left( {\mathfrak{u}} \right)\), for all \({\mathfrak{u}} \in {\mathfrak{U}}\).

Definition 4.3

Reference [19] A function from \({\mathfrak{U}}\) into the unit closed interval \({\mathfrak{I}}\) is said to be a fuzzy (singleton) point in \({\mathfrak{U}}\) which is a fuzzy subset of \({\mathfrak{U}}\) and symbolized by \({\mathfrak{u}}_{{\mathfrak{r}}}\). In other words, a fuzzy point in \({\mathfrak{U}}\) is, \({\mathfrak{u}}_{{\mathfrak{r}}} :{\mathfrak{U}} \to {\mathfrak{I}}\) be a function defined by:

$${\mathfrak{u}}_{{\mathfrak{r}}} \left( {\mathfrak{y}} \right) = \left\{ {\begin{array}{*{20}l} {{\mathfrak{r}},} \hfill & {{\text{if }}{\mathfrak{u}} = {\mathfrak{y}}} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(1)

The single point \({\mathfrak{u}}\) is said to be the support of \({\mathfrak{u}}_{{\mathfrak{r}}}\) whenever \({\mathfrak{u}} \in {\mathfrak{U}}\) and \({\mathfrak{r}} \in \left( {0,1} \right]\) is called value of \({\mathfrak{u}}_{{\mathfrak{r}}}\). \({\mathcal{F}\mathcal{P}}\left( {\mathfrak{U}} \right)\) denoted to the class of all fuzzy points in \({\mathfrak{U}}\). A fuzzy point \({\mathfrak{u}}_{{\mathfrak{r}}}\) is said to be belongs to a fuzzy set \({\mathfrak{N}}\) or contained in a fuzzy set \({\mathfrak{N}}\), i.e., \({\mathfrak{u}}_{{\mathfrak{r}}} \in {\mathfrak{N}}\) if and only if \({\mathfrak{r}} \le {\mathfrak{N}}\left( {\mathfrak{u}} \right)\).

Definition 4.4

Reference [20] A set \({\mathfrak{D}}\) with a relation \({ \succcurlyeq }\) is said to be a directed set and symbolized by \(\left( {{\mathfrak{D}},{ \succcurlyeq }} \right)\), if the following conditions hold:

  1. (1)

    \({\mathfrak{n} \succcurlyeq \mathfrak{n}}\), for each \({\mathfrak{n}} \in {\mathfrak{D}}\).

  2. (2)

    For each \({\mathfrak{n}}_{1}\), \({\mathfrak{n}}_{2}\), and \({\mathfrak{n}}_{3}\) \(\in {\mathfrak{D}}\), if \({\mathfrak{n}}_{1} { \succcurlyeq \mathfrak{n}}_{2}\) and \({\mathfrak{n}}_{2} { \succcurlyeq \mathfrak{n}}_{3}\), then \({\mathfrak{n}}_{1} { \succcurlyeq \mathfrak{n}}_{3}\).

  3. (3)

    If \({\mathfrak{n}}_{1}\) and \({\mathfrak{n}}_{2} \in {\mathfrak{D}}\), then there is some \({\mathfrak{n}}_{3} \in {\mathfrak{D}}\) with \({\mathfrak{n}}_{3} { \succcurlyeq \mathfrak{n}}_{1}\) and \({\mathfrak{n}}_{3} { \succcurlyeq \mathfrak{n}}_{2}\).

Definition 4.5

Reference [21, 22] A pair \(\left( {{\mathfrak{U}},{\mathfrak{T}}} \right)\) is said to be fuzzy topological space on a set \({\mathfrak{U}}\) (in short fts), and defined as a family \({\mathfrak{T}}\) of fuzzy subsets of \({\mathfrak{U}}\), which is satisfies the following conditions:

  1. (1)

    \(0_{{\mathfrak{U}}}\), \(1_{{\mathfrak{U}}} \in {\mathfrak{T}}\).

  2. (2)

    If \({\mathfrak{N}}\), \({\mathfrak{M}} \in {\mathfrak{T}}\), then \({\mathfrak{N}} \wedge {\mathfrak{M}} \in {\mathfrak{T}}\).

  3. (3)

    If \({\mathfrak{N}}_{{\mathfrak{j}}} \in {\mathfrak{T}}\) for each \({\mathfrak{j}} \in {\mathfrak{L}}\), then \(V_{{{\mathfrak{j}} \in {\mathfrak{L}}}} {\mathfrak{N}}_{{\mathfrak{j}}} \in {\mathfrak{T}}.\)

\({\mathfrak{T}}\) is said to be a fuzzy topology for \({\mathfrak{U}}\) and \({\mathfrak{U}}\) is called a fuzzy space.

Definition 4.6

Reference [23] A fuzzy net of a set \({\mathfrak{U}}\) is denoted by \(\left\{ {{\mathfrak{S}}\left( {\mathfrak{n}} \right):{\mathfrak{n}} \in {\mathfrak{Q}}} \right\}\) and defined as the function \({\mathfrak{F}}:{\mathfrak{Q}} \to {\mathcal{F}\mathcal{P}}\left( {\mathfrak{U}} \right)\), where \({\mathfrak{Q}}\) is a directed set. If \({\mathfrak{S}}\left( {\mathfrak{n}} \right) = {\mathfrak{u}}_{{{\mathfrak{r}\mathfrak{n}}}}^{{\mathfrak{n}}}\) for each \({\mathfrak{n}} \in {\mathfrak{Q}}\), whenever \({\mathfrak{u}} \in {\mathfrak{U}}\), \({\mathfrak{n}} \in {\mathfrak{Q}}\) and \({\mathfrak{r}}_{{\mathfrak{n}}} \in \left( {0,1} \right]\), then the fuzzy net \({\mathfrak{F}}\) is symbolized by \(\left\{ {{\mathfrak{u}}_{{{\mathfrak{r}\mathfrak{n}}}}^{{\mathfrak{n}}} :{\mathfrak{n}} \in {\mathfrak{Q}}} \right\}\) or simply \(\left\{ {{\mathfrak{u}}_{{{\mathfrak{r}\mathfrak{n}}}}^{{\mathfrak{n}}} } \right\}\).

Definition 4.7

Reference [23] If \({\mathfrak{F}} = \left\{ {{\mathfrak{u}}_{{{\mathfrak{r}\mathfrak{n}}}}^{{\mathfrak{n}}} :{\mathfrak{n}} \in {\mathfrak{D}}} \right\}\) is a fuzzy net in \({\mathfrak{U}}\), and let \(\left( {{\mathfrak{U}},{\mathfrak{T}}} \right)\) be an fts. Then \({\mathfrak{F}}\) is said to be:

  1. (1)

    Eventually with a fuzzy subset \({\mathfrak{N}}\) of \({\mathfrak{U}}\) if and only if \(\exists { }{\mathfrak{m}} \in {\mathfrak{Q}}\), such that \(\forall { }{\mathfrak{n}} \in {\mathfrak{Q}}\) and \({\mathfrak{n}} \ge {\mathfrak{m}}\), \({\mathfrak{u}}_{{{\mathfrak{r}\mathfrak{n}}}}^{{\mathfrak{n}}} \le {\mathfrak{N}}\).

  2. (2)

    Frequently with a fuzzy subset \({\mathfrak{N}}\) of \({\mathfrak{U}}\) if and only if \(\forall {\mathfrak{m}} \in {\mathfrak{Q}}\), \(\exists { }{\mathfrak{n}} \in {\mathfrak{Q}}\), with \({ }{\mathfrak{n}} \ge {\mathfrak{m}}\), such that \({\mathfrak{u}}_{{{\mathfrak{r}\mathfrak{n}}}}^{{\mathfrak{n}}} \le {\mathfrak{N}}\).

5 Proposed Segmentation Methodology

The steps algorithm for using convergence of fuzzy nets is given as follows:

Algorithm 1

Algorithm for eventually convergence

  • Step 1: Read an image and converting it within the closed unit interval \(\left[ {0,1} \right]\).

  • Step 2: Choose a midpoint in the matrix with the smallest image value.

  • Step 3: Calculate the convergence of the image for each point after midpoint of the image.

  • Step 4: Print image.

  • Step 5: Apply performance criteria to determine the best method such as mean and peak signal-to-noise ratio.

Algorithm 2

Algorithm for frequently convergence

  • Step 1: Read an image and converting it within the closed unit interval \(\left[ {0,1} \right]\).

  • Step 2: Choose a random midpoint in the matrix.

  • Step 3: Calculate the convergence of the image for each point after midpoint of the image, the stop else go to step 2.

  • Step 4: Print image.

  • Step 5: Apply performance criteria to determine the best method such as mean and peak signal-to-noise ratio.

6 Results and Discussion

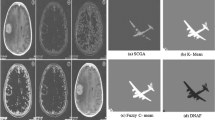
Reading the color images and converting them within the closed period \(\left[ {0,1} \right]\) and then applying the Algorithms 1 and 2, respectively (Figs. 1, 2 and 3; Table 1).

Fig. 1
4 images from a through d. A woman with a hat in image a, coins in image b, grains in image c, and landscape in image d.

Sample of different types of images, a and d: Color images, b and c: Grayscale images

Full size image
Fig. 2
4 grayscale images from a through d. The high-contrast images are as follows. A woman with a hat in image a, bright coins in a dark background in image b, grains in image c, and landscape in image d.

Applying Algorithm 1 on samples images

Full size image
Fig. 3
4 grayscale images from a through d. The high-contrast images are as follows. A woman with a hat in image a, coins in image b, bright grains in a dark background in image c, and landscape in image d.

Applying Algorithm 2 on samples images

Full size image
Table 1 Statistical features (mean and peak signal-to-noise ratio)
Full size table

7 Conclusion

In this paper, we used the basic two types of fuzzy convergence with midpoints to segment images into two regions. The light region represents the convergence points, but the dark regions represent the points that do not achieve convergence. Our two algorithms can be applied to any type of image (color, indexes, grayscale, and others) and any format.

According to the above results and when applying the mean on the resulting images, we conclude that the values of grayscale images are highest than the values of color images as well as the values of grayscale images when used the second algorithm highest than the values of those images when applying the first algorithms.

As well as when applying the peak-to-signal noise ratio on images, the results show that the color images have the highest values of noise.

In general, the results showed that using the frequent convergence algorithm achieved better results in image segmentation than the eventual convergence algorithm.