Keywords

1 introduction

Concrete filled steel tubes (CFSTs) are composite members where the concrete is filled in hollow steel tubes (HSTs). The presence of concrete in steel tubes improves the performance of concrete and steel compared to their individual performances. The steel tube not only acts as the longitudinal reinforcement but also provides lateral confinement to the inner concrete. This confinement effect increases the compressive strength and ductility of the concrete core. Besides providing confinement, the steel tube also functions like a formwork which further provides speedy and economical construction, whereas the concrete in CFSTs delays the occurrence of local buckling in steel tubes.

CFSTs are predominantly used as compression members. Since CFSTs have low cross-sectional area to load carrying capacity ratio, they are used as columns for the lower storeys of high-rise buildings. Due to its inherent properties of high strength and ductility, CFSTs are mainly adopted for construction of buildings situated in seismic zones, bridge piers (with internal reinforcements), transmission towers and retrofitting purposes.

Circular CFSTs in which both the steel tube and concrete core are simultaneously loaded, both the constituent materials contribute to its axial load carrying capacity. During the initial stages of loading, as the Poisson’s ratio of steel and concrete is different, they do not influence the mechanical behaviour of each other and share the load independently. The development of micro-cracks in concrete at approximately 0.4 to 0.7 \( f_{c}^{^{\prime}}\). Chen and Han [1] causes it to dilate more than steel. This increases the Poisson’s ratio of concrete, which causes the concrete to apply a lateral pressure on the steel tube. The lateral pressure in-turn introduces tensile hoop stress in steel, which results in a reduction in the axial stresses in the steel tube. On the other hand, the steel tube confines the lateral expansion of the core concrete thereby improving its strength and ductility. Even though there is a reduction in the axial capacity of the steel tube, the overall capacity of the CFST is enhanced due to the increase in strength of concrete due to confinement.

2 Classification of Circular CFSTs

AISC 360-16 [2] classifies circular CFSTs as compact, non-compact and slender based on section slenderness Îğ, defined as the ratio of overall diameter to the thickness of the steel tube (D/t) of concrete filled steel tubes. Compact sections are those in which yielding of steel happens before buckling, thus providing adequate confinement to the concrete core. Non-compact sections are those in which yielding and local buckling of the steel tube happens simultaneously. Owing to the local buckling of steel tube in non-compact sections, the concrete core does not attain its unconfined compressive strength \( f_{c}^{^{\prime}}\). In slender sections, the steel is assumed to buckle locally before yielding, resulting in ineffective confinement of the concrete core. Depending on the section classification, AISC 360-16 [2] proposes different expressions for calculating the ultimate capacity of circular CFSTs based on slenderness limits and is given as:

$$ {\text{Cpact}}\,{\text{CFSTs}}, \lambda \le \lambda_{p} = 0.15\,E_{s} /F_{y} \quad P = F_{y} A_{s} + 0.95 f_{c}^{^{\prime}} A_{c} , $$
(1)
$$ {\text{Non}} - {\text{compact}}\,{\text{CFSTs}},\lambda_{p} < \lambda \le \lambda_{r} = 0.{19}E_{s} /F_{y} \quad P = P_{p} - \frac{{(P_{p} - P_{y} )(\lambda - \lambda_{p} )}}{{(\lambda_{r} - \lambda_{p} )}}, $$
(2)
$$ {\text{Slender CFSTs}},\lambda > \lambda_{r} \le 0.{31}E_{s} /F_{y} \quad P = F_{cr} A_{s} + 0.7 f_{c}^{^{\prime}} A_{c} , $$
(3)

where Fy = yield strength of steel; \(f_{c}^{^{\prime}}\).  = compressive strength of unconfined concrete; As, Ac = area of steel and concrete, respectively; Es = modulus of elasticity of steel; Pp = P as defined in Eq. (1); and the yield load Py and the critical buckling stress Fcr are given as:

$$ P_{y} = F_{y} A_{s} + 0.7 f_{c}^{^{\prime}} A_{c} . $$
(4)
$$ F_{cr} = \frac{{0.72 F_{y} }}{{\left( {\frac{D}{t} \frac{{F_{y} }}{{E_{s} }}} \right)^{2} }}. $$
(5)

The above expressions are valid for steel strength less than 525 MPa and concrete strength between 21 and 69 MPa.

Figure 1 presents a comparison of the AISC 360-16 [2] expression for the axial load carrying capacity of CFST with the experimental database reported in Lai and Varma [3] and Lai and Ho [4]. It is evident from Fig. 1 that the expressions defined in AISC 360-16 [2] underestimate the axial load carrying capacity of circular CFSTs, particularly for slender sections with a mean and standard deviation of 1.345 and 0.131, respectively. This warrants further investigation on the behaviour of slender CFSTs.

Fig. 1
A scatter plot compares the N subscript experiment over the N subscript A I S C versus D over t, F subscript y over the E subscript s. It plots the data in terms of the increasing trend between compact, non-compact, and slender.

Comparison of axial load capacity of CFSTs with AISC 360-16 [2]

Full size image

3 Finite-Element Modelling Details

In order to understand the behaviour of concrete and steel in axially loaded CFSTs, a numerical model is prepared using the finite-element (FE) software, ABAQUS (SIMULIA 2016), that accounts for both material and geometric nonlinearities. FE models of axially loaded slender HSTs and CFSTs are validated and are further adopted to analyse the stresses acting in the steel tubes. The details of the model are presented in this section.

3.1 Geometric Details

Four-noded shell elements with reduced integration (S4R) and eight-noded linear brick elements with reduced integration are, respectively, used for modelling the steel tube and the concrete core of the CFST. The size of the elements is finalised based on the mesh convergence study of HST sections. Optimal mesh sizes are determined based on the ratio of theoretical buckling load PTh to the buckling load PFE generated from the FE analysis and considering the trade-off between accuracy and computational time. The theoretical value of the buckling load PTh is determined using the following equation [5]:

$$ P_{Th} = \frac{{2E_{s} }}{{\sqrt {3(1 - \mu_{s}^{2} )} }}\frac{t}{D}. $$
(6)

where \(\mu_{s}\)  = Poisson’s ratio of steel.

For the present study, a mesh size of 15 mm is adopted. In order to ensure compatibility at the interface between steel and concrete in CFST, the same mesh size is adopted for the concrete core as well.

3.2 Contact Between Steel and Concrete

To ensure compatible deformation between concrete and steel during compression, a hard contact in the normal direction is specified at the interface between concrete and steel [6]. For the tangential contact, the coefficient of friction between concrete and steel is taken as 0.6 as reported by Schneider (1998) and Tao et al. [6].

3.3 Loading and Boundary Conditions

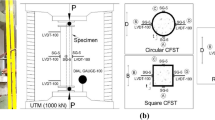
In order to accurately represent the loading condition during experimental tests on CFSTs, loads are applied as uniform displacements at the top nodes of concrete and steel. The boundary conditions at both ends of the CFST are restrained against all translational movements except the axial deformation of the top nodes.

3.4 Geometric Imperfections

Study the effects of geometric nonlinearity on the behaviour of CFSTs, geometric imperfections are incorporated into the FE analysis. In the absence of experimentally measured imperfections, the buckling mode shapes of the steel tube obtained from the buckling analysis of CFSTs may be used. In the present study, the mode shape for the first eigenvalue is used to define the geometric imperfection in the steel tube, with a magnitude of 0.1 times the thickness of the steel tube [3].

3.5 Material Constitutive Relationships

Appropriate material models of steel and concrete are essential to closely simulate the actual behaviour of CFSTs. The concrete in CFSTs gets confined due to the hoop stress applied by the outer steel tube. Therefore, the effects of concrete confinement should also be considered. The constitutive relation of steel and confined concrete is discussed in this section.

3.5.1 Constitutive Relation for Steel

Figure 2a shows the stress–strain relation of steel adopted in this study. The initial modulus of elasticity Es and Poisson’s ratio \(\mu_{s}\) is taken as 200 GPa and 0.3, respectively, for defining the elastic portion of the stress–strain relation of steel. Since the stress–strain behaviour of steel considered for the present study is not reported in the literature, the plastic portion is defined by specifying the yield strength Fy up to a strain of 10 \(\varepsilon_{y}\), \(\varepsilon_{y}\). being the yield strain of steel. Beyond this, the strain hardening part is taken into consideration by specifying the ultimate strength Fu, where the ultimate strain of steel \(\varepsilon_{u}\) is taken as 0.15. The ultimate strength of steel is determined using Eq. (7) [7].

$$ \frac{{F_{u} }}{{F_{y} }} = 1 + 2\left( {\frac{150}{{F_{y} }}} \right)^{2} . $$
(7)
Fig. 2
4 line graphs plot stress versus strain. a. It plots an increasing curve for steel. b and c. It plots a decreasing curve for the behavior of steel. d. It plots 3 decreasing trends for the unconfined model, the confined model, and the modified model for C F S Ts. Each trend has projection lines.

Stress–strain behaviour of a steel; and concrete by b Schneider (1998), c Tao et al. [6] and d proposed

Full size image

3.5.2 Constitutive Relation for Confined Concrete

The concrete in axially loaded CFSTs, as a result of the confinement offered by the steel tube, is subjected to a triaxial state of stress. Concrete under triaxial stress state can be modelled using the concrete damage plasticity (CDP) model (Lubliner et al. 1989). The CDP model requires several input parameters, which includes the plasticity parameters and the compressive and tensile behaviour of concrete. The plasticity parameters predict the confinement in concrete offered by the outer steel tube. The parameters required to define the plasticity of concrete are the dilation angle ψ, flow potential eccentricity ratio e, ratio of the second stress invariant on tensile meridian to compressive meridian Kc, ratio of biaxial compressive strength to uniaxial compressive strength \(f_{bo} / f_{co}\) and viscosity ν. Table 1 presents the plasticity parameters used in the present study that are adopted from literature [6, 8, 9] for modelling concrete in slender CFST specimen.

Table 1 Plasticity parameters for concrete damage plasticity model
Full size table

Figure 2b and c presents the stress–strain models proposed by Schneider (1998) and Tao et al. [6] for modelling confined concrete in CFSTs. Schneider proposed a concrete model based on the experimental results of CFSTs, where the stress and strain values of the confined concrete model were retained to be the same for all CFSTs regardless of the confinement offered by the outer steel tube. Tao et al. proposed a three-stage stress–strain model for confined concrete where the post-peak branch is a function of the confining pressure acting on concrete. Since the confining pressure is an unknown at the beginning of the analysis, Tao et al. proposed an empirical equation for the confining pressure based on their numerical studies. In this study, a rational new modification is proposed to the concrete constitutive model based on the confined model proposed by Karthik and Mander [10].

Figure 2d shows the compressive stress–strain behaviour of unconfined concrete adopted in this study [10]. From the preliminary FE analysis of CFST using the unconfined concrete model, it is found that the plasticity parameters of the CDP model and the interaction between steel and concrete only partially account for the increase in compressive strength of concrete due to confinement. Similar observations were also reported by Tao et al. [6] and Lin and Zhao (2019). Hence, a novel methodology is proposed to simulate the confined concrete behaviour accurately. Figure 2d shows the modified stress–strain relation for confined concrete that is adopted in this study. To obtain this, the confinement ratio \(K = f_{cFE}^{^{\prime}} /f_{c}^{^{\prime}}\) which is the ratio of peak concrete stress from the FE model \(f_{cFE}^{^{\prime}}\) to the unconfined compressive strength of concrete \(f_{c}^{^{\prime}}\) extracted from the preliminary FE analysis using unconfined concrete model. The confined concrete model proposed by Karthik and Mander [10] is then defined using the extracted confinement ratio K as shown in Fig. 2d. The post-peak branch of the confined model is then parallelly shifted to the post-peak branch of unconfined concrete to obtain the modified concrete model. Since the FE analysis with the modified stress–strain model of concrete showed a further increase in the confinement ratio, the procedure is iterated until the confinement ratio K defined in the analysis and that obtained from the FE analysis converge. The tensile behaviour of concrete is defined based on the model proposed by Karthik and Mander [10].

3.6 Validation of FE Analysis Methodology

The FE analysis methodology adopted in this study is validated with experimental observations reported in the literature. Towards this, the validation of the FE analysis of both HST and CFST columns is presented in the following sections.

3.6.1 Hollow Steel Tubes

To ensure that the numerical model appropriately simulates the behaviour of hollow steel tubes without any infill, an experimental slender steel tube S10BS [11] with D/t = 220 is modelled using the FE method.

Table 2 presents the geometric and material properties of the HST specimen. The effects of geometric imperfections and residual stresses are also incorporated into the analysis. Figure 3a shows a comparison of the load-strain behaviour of the hollow steel tube member obtained from the FE analysis with the experimental test result. The initial part of the load-strain behaviour is modelled quite accurately. The reduction in stiffness of the HST at approximately 70 kN is attributed to the effects of geometric imperfections and residual stresses. Even though the ultimate load simulated by the FE analysis is slightly under predicted (by 3%), the simulated post-peak behaviour agrees quite well with the experimental observations.

Table 2 Details of specimens used for validation of FE models
Full size table
Fig. 3
2 line graphs plot the load in kilonewtons versus strain. Each plot has two decreasing curves for the experiment and the F E model of S 10 B S and C u-150, with pinpoints of steel tube and crushing of concrete.

Comparison of experimental load versus strain behaviour with FE results. a Hollow steel tube, b concrete filled steel tube

Full size image

3.6.2 Concrete Filled Steel Tubes

In order to verify the accuracy of the FE analysis in simulating the behaviour of CFSTs, a slender CFST experimental specimen CU-150 [12] with D/t = 150 is considered for validation. Table 2 presents the geometric and material properties of the experimental specimen. Geometric nonlinearities are implemented into the analysis as described earlier. Figure 3b presents a comparison of load versus axial strain behaviour of the slender CFST obtained from the finite-element analysis with the experimental results. The load-strain curve presented in Fig. 3b that is obtained from the FE analysis corresponds to the results from the final iteration, where the confinement ratio K converges to a value of 1.23. The initial slope and the post-peak behaviour simulated by the FE analysis compare well with the experimental results. However, the analysis slightly overpredicts the peak axial load by approximately 6%. Considering the complexities associated with the interaction between the steel tube and the concrete core in CFSTs, the FE analysis simulates the overall behaviour quite well. The load-strain behaviour therefore validates the modelling approach adopted for axially loaded CFSTs.

4 Results and Discussions

Figure 3b shows the key events along the load-strain curve of the axially loaded CFST. In this, point ‘a’ corresponds to the yielding of the steel tube, where the Von Mises stress reaches the yield strength of steel, and point ‘b’ corresponds to the ultimate load of the CFST. Figure 3b also shows the strains corresponding to yield stress of steel (\(\varepsilon_{y}\)) and confined concrete stress (\(\varepsilon_{cc}\)). As evident from the figure, the maximum load capacity of the CFST is attained corresponding to the peak confined concrete strain of \(\varepsilon_{cc}\). This clearly indicates that the post-peak reduction in the load carrying capacity of CFST corresponds to crushing of the concrete core. The observation is contradictory to the AISC 360-16 [2] classifications of CFSTs, where slender CFSTs are assumed to fail due to the elastic local buckling of the steel tube. This observation alludes that the section classification of CFST may have to be reconsidered. However, further studies are necessary.

Figure 4 presents the failure modes of HST and CFST obtained from the FE analysis. It is observed that at failure, the slender HSTs displays elephant foot buckling at the ends (Fig. 4a). However, in CFSTs along with elephant foot buckling at its ends, the column bulges out at the mid-section due to the dilation of concrete (Fig. 4b).

Fig. 4
2 three-dimensional models of cylindrical-shaped structures with the distribution of the elastic local buckling, in a gradient of colors. The predominant color ranges are positive 2.182 e positive 01 and positive 3.423 e positive 02, respectively.

Failure modes of a SB10S (HST) and b CU-150 (CFST) obtained from FE analysis

Full size image

The validated FE analysis is also used to understand and compare the behaviour of slender HST and CFST with similar geometry and material properties. Towards this, a HST column with similar geometry and material property as that of CFST specimen CU-150 (Table 2) is analysed using the FE technique described earlier.

4.1 Comparison of Axial Stress of Steel in Slender HST and CFST

Figure 5 shows a comparison of the axial steel stresses in concentrically loaded slender HST and CFST columns of similar cross-section and material properties. Point ‘a’ corresponds to the yielding of steel tube in CFST, where the Von Mises stress reaches the yield strength of steel, whereas point ‘b’ corresponds to the local buckling of the steel tube in HST. From Fig. 5, it is evident that the maximum steel stress in HST reaches a value of approximately 0.6 Fy, indicating that slender HST column fails under elastic local buckling as specified by AISC 360-16 [2]. The axial stress in the steel tube of the CFST column reaches a maximum of approximately 0.8 Fy. However, the Von Mises stress reaches yield and exhibits strain hardening behaviour owing to the presence of hoop stresses that arise due to the lateral expansion of the concrete core. This clearly shows that the steel tube in CFST yields before local buckling.

Fig. 5
A line graph plots the steel stress, or yield stress, versus strain. It plots 1 increasing and 3 decreasing trends for H S T and C F S T of axial and Von Mises stress. C F S T-Von Mises stress trend has two points of steel tube and local buckling.

Comparison of axial steel stresses in HST and CFST

Full size image

4.2 Comparison of Existing Expressions for Axial Stress of Steel in CFSTs

Many researchers [13,14,15] have proposed different expressions for determining the ultimate capacity of axially loaded slender CFSTs. Each of these expressions considers the contribution of both the steel tube and the concrete core towards the axial load capacity of CFST. However, the contribution of steel towards the axial capacity of CFST varies significantly. Table 3 presents the maximum axial stress in the steel tube corresponding to the ultimate load of axially loaded slender CFST. The table also presents a comparison of the axial stress proposed by the various references \(f_{{\text{sz, predicted}}}\) with the axial stress that is obtained from the FE analysis \(f_{{\text{sz, FE}}}\). It is evident that most of the current expressions overpredict the axial stress of steel in CFSTs. This is despite the fact that most of these expressions predict the ultimate load capacity of CFSTs quite well.

Table 3 Comparison of existing expressions for axial capacity of steel in CFST
Full size table

From Table 3, it is evident that most of the existing expressions (ACI 318–14; [13, 14]) do not consider the reduction in axial stress in steel due to the presence of hoop stress. Even though the expression proposed by Sakino et al. [15] accounts for a reduction in the axial stress in the steel tube, the reduction factor is taken as a constant function of Fy. Among the various expressions predicting the axial stress of steel in CFSTs, the expression proposed in EN 1994-1-1 (2004) is found to fairly predict the axial stress in steel. The reduction factor accounted in EN 1994-1-1 (2004) is taken as a function of relative slenderness of CFST irrespective of whether the column is stub or long. Therefore, from these observations, it is evident that further investigation is necessary to accurately predict the axial stress of steel in CFSTs.

5 Conclusions

To investigate the changes in the behaviour of steel tubes in axially loaded slender CFSTs in comparison to slender HSTs, a numerical FE-based study was conducted using ABAQUS (SIMULIA 2016). The FE models were developed and validated to simulate the behaviour of axially loaded slender HST and CFST and validated with experimental results. The validated FE models were then further adopted to analyse the steel stresses in HST and CFST columns and to understand the failure mechanism of CFSTs. The following are the major conclusions that can be drawn from the analysis:

  • Steel tubes in slender CFSTs are not subjected to elastic local buckling, which is contrary to AISC 360-16 [2] provisions.

  • Reduction in the load carrying capacity beyond peak of slender CFST was due to the crushing of concrete core which was preceded by the yielding of the steel tube. Elastic local buckling was not the cause of failure.

  • Results from the present study show that further studies are necessary to look into the behaviour of axially loaded slender CFSTs.

  • Further studies are also necessary to accurately predict the axial stresses in the steel tubes of CFSTs.