Quasi-oppositional Whale Optimization Algorithm for Solving Multi-objective Optimal DG Emplacement Problem in Radial Distribution Network

Abstract

Optimization of system losses and quality power is still a major concern for many researchers. DG, i.e., Distributed Generation is a newly developed effective technology, when placed optimally in power system helps in raising overall efficiency and quality of power by minimizing distribution losses. This paper presents a methodology based on quasi-oppositional whale optimization algorithm (QOWOA) to locate DG with appropriate size in distribution system for reducing losses along with minimization of voltage deviance and enhancement of voltage stability index. The above-mentioned methodology is tested on three different test systems consisting of 33, 69 and 118 buses. The computer simulation results obtained using projected methodology is compared with the earlier optimization techniques proposed by various author.

1 Introduction

Distribution network connects the power station with the consumer located far away for the transfer of electricity. Consumers called for load demand is obtained through distribution system. With the advancement of human civilization and technology, demand for superior quality electric power has reached the maximum capability of the existing radial distribution network (RDN). This causes distribution system operation to become more complex, having tendency to failure and discontinuity. Therefore, the very objective of power system is haltered. Moreover, bulk power exchange that takes place in the distribution system incorporates huge power loss in the form of $I^{2} R$ resulting in reducing power system efficiency.

Thus, distribution network is drawing much attention of researchers for ascertaining solutions to the existing problem in supplying load demand and making the power system reliable. One solution to above-mentioned difficulty could be modification or enhancing the capacity of the existing distribution system network. But it will not be an easy task and at the same time, it is not economical. Another most effective and efficient solution could be integrating DG with the existing power system. Bhatt et al. [1] gives an overview concerning integration of DG, its impact in steady-state operation, and dynamic behavior. Integration of DG helps in the minimization of distribution system losses, enhancing voltage profile and reliability. Moreover, DG’s acts as a support to grid distribution system by fulfilling both active and reactive power requirements and also assist in future network enhancement. Robert et al. [2] suggested a solution to rural electrification problem by extending central power grid with the help of renewable energy generation and storage.

Many researchers have used analytical methods for finding solution to optimum DG allocation (ODGA) problem. Viral and Khatod [3], Hung et al. [4], and Acharya et al. [5] utilized an analytical methodology to locate DG with appropriate size in the RDN with the purpose to minimize loss in the system. A hybrid method by combining sensitivity and power factor method to find optimum DG size and location was introduced by Mirzaei et al. [6]. Dulau et al. [7] suggested extended version Newton–Raphson methodology for emplacement of DG in RDN taking into account power loss at each bus with which it is connected. Babu et al. [8] put forward power loss sensitivity (PLS) and nonlinear programming (NLP) method to obtain optimality in finding correct position of DG with exact size in the distributed network for considerable reduction in system losses. Zaineb et al. [9] proposed load flow analysis method to solve ODGA problem in RDN to deal with losses and voltage stability.

Analytical techniques for finding solutions to ODGA problem are easy to implement and shows good convergence rate while dealing with small-scale optimization problem but it has some limitations. The complexity of the problem increases with multi-DG in a diverse load-generation condition. Analytical methods often deal with by considering some unrealistic assumption which causes an error in the output when implemented on real system. Moreover, the probabilistic techniques used for finding solution to (ODGA) problem requires large amount of computational data and huge processing ability. On the other hand, meta-heuristic methods are capable of producing near-optimal solution to ODGA problem considering single or multi-DG with satisfactory computational speed and processing capability.

In recent decades, meta-heuristic methods have become very popular for finding solution to optimum location of DG and its sizing. In Refs. [10,11,12,13,14] a partial swarm optimization (PSO) based methodology is utilized to obtain the DG site in RDN for the synchronous power loss optimization with voltage enhancement. Ahmed et al. [15] considered DG in the RDN to convert radial section to loop using PSO algorithm. Legha et al. [16], Ud Din et al. [17] utilized genetic algorithm (GA) for finding solution to ODGA problem in the RDN. In Ref. [18], an optimization technique based on GA and ds evidence theory to find optimal allocation of DG with minimum system losses was discussed by Zhao et al. Kanaan et al. [19] presented a simple method established on the comparison of fast voltage stability index (VSI) and simulated annealing (SA) to find optimum location and appropriate DG size. The suggested methodology was simulated on MATLAB and MATPOWER software and the results obtained resembles that the losses in system and voltage profile depends on appropriate location and DG size. Sultana et al. [20] applied a modified teaching-learning-based optimization methodology to obtain optimum DG siting with side-by-side reduction in power loss, voltage variation- and voltage stability index enhancement in RDN. Cuckoo search algorithm to solve optimization problem related to DG with sizing in a distribution system has been addressed in Nguyen et al. [21]. Muthukumar et al. [22] presented harmony search algorithm (HSA) to search for both allocating DG and compensating device with the significant reduction in power loss. Hashemabadi et al. [23] used bacteria foraging algorithm and binary genetic algorithm to obtain optimum location of DG to cut down system loss and variation in voltage. The search for optimal location and sizing of multi-DG in presence of SVC using adaptive differential search algorithm (DSA) for reducing system losses was developed by Mahdad et al. [24]. An improved differential search algorithm (IDSA) for solving optimization problem related to DG allocation and sizing with the technical, financial benefits of DG was objective was introduced by Injeti et al. [25]. A firefly algorithm (FA) in balanced/unbalanced distribution system for optimal sitting of voltage operated DG was utilized by Othman et al. [26]. Katamble et al. [27] presented a fuzzy logic to find candidate node for DG installation with reduced power loss and voltage deviance. In Ref. [28], a hybrid imperialistic competitive algorithm (ICA) method for getting optimum location of DG for the purpose of loss reduction was introduced by Poornazaryan et al. Home-Ortiz et al. [29] proposed mixed integer conic programming (MICP) that shows better potential and performance in find optimum DG place in RDN. Nguyen and Vo [30] introduced a stochastic fractal search algorithm (SFSA) for minimizing loss, enhancing voltage profile and stability with the satisfaction of various constraints. Reddy et al. [31] proposed whale optimization algorithm (WOA) and power loss index (PLI) to locate DG with appropriate size for loss minimization and improvement in voltage profile in RDN.

Moreover, according to “no-free-lunch” theorem, there is no optimization technique which is well-defined for all types of optimization problems. This motivated the author to come up with a new algorithm to solve the desired objective function, namely, Quasi-Oppositional Whale Optimization Algorithm to solve multi-objective optimal DG emplacement problem in RDN as well as improvement of voltage profile and voltage stability index. QOWAO is relatively new, much simpler, and more robust optimization algorithm on comparison to other optimization problems. This paper used quasi-oppositional whale optimization algorithm (QOWOA) for obtaining optimum DG location and size for the minimization losses and betterment voltage profile and stability index in distribution system. Simulation outcomes obtained with the help of MATLAB software are described in comparison to other techniques proposed by different authors in the later part of paper.

The arrangement of paper is done in following manner. Mathematical formulation is described under Sect. 2. The Whale Optimization algorithm is described under Sect. 3. Oppositional-based learning is described under Sect. 4. QOWOA applied to ODGA problem is discussed under Sect. 5. Results and discussion are described under Sect. 6. Conclusion is described under Sect. 7.

2 Mathematical Formulation

2.1 Multi-objective Function

Multi-objective optimization is also known as Pareto optimization having more than one decision-making criteria that mainly concern with the optimization of more than one objective functions. This paper aims at minimizing system power loss $({\text{Of}}_{{{\text{Ploss}}}} )$ and voltage deviance $({\text{Of}}_{{{\text{vpi}}}} )$, and voltage stability index $({\text{Of}}_{{{\text{vsi}}}} )$ enhancement by optimally sizing and allocating DG. This multi-objective function expressed as:

$${\text{Of}} = \min [{\text{Of}}_{{{\text{ploss}}}} + \alpha_{1} {\text{Of}}_{{{\text{vpi}}}} + \alpha_{2} {\text{Of}}_{{{\text{vsi}}}} ]$$

(1)

where,

$${\text{Of}}_{{{\text{ploss}}}} = \min (P_{{{\text{loss}}}} )$$

(2)

$${\text{Of}}_{{{\text{vpi}}}} = \sum\limits_{i = 1}^{N} {(v_{i} - v_{{{\text{rated}}}} )^{2} }$$

(3)

$${\text{Of}}_{{{\text{vsi}}}} = v_{i}^{4} - 4(p_{i + 1} r_{i} + q_{i + 1} x_{i} )v_{i}^{2} - 4(p_{i + 1} x_{i} - q_{i + 1} r_{i} )^{2}$$

(4)

$$p_{{{\text{loss}}}} = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {c_{ij} (p_{i} p_{j} + q_{i} q_{j} ) + d_{ij} (q_{i} p_{j} - p_{\text{i}} q_{j} )} }$$

(5)

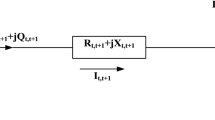
$c_{ij} = \frac{{r_{ij} }}{{|v_{i} ||v_{j} |}}\cos (\phi_{i} - \phi_{j} ),d_{ij} = \frac{{r_{ij} }}{{|v_{i} ||v_{j} |}}\sin (\phi_{i} - \phi_{j} )$, $q_{i} \;{\text{and}}\;q_{j} ,\;p_{i} \;{\text{and}}\;p_{j}$ are the respective reactive, active power of ith and jth bus; v_i and v_rated are the voltage and the rated voltage of ith bus respectively; $p_{i + 1} \;{\text{and}}\;q_{i + 1}$ are $i + 1{\text{th}}$ bus power, i.e., active reactive; $v_{j}$ is the jth bus voltage, resistance, reactance of the line associated in-between the buses ith and jth are r_ij and x_ij severally.

2.2 Constraints

Load Equilibrium Constraints

For the purpose of power equilibrium, the sum of the power generated by DG $(p_{{{\text{DG}},i\,}} \;{\text{and}}\;q_{{{\text{DG}},i}} )$ at a particular bus ith and that supplied by the substation $(p_{{\text{sub - station}}} \;{\text{and}}\;q_{{\text{sub - station}}} )$ must meet the total demand $(p_{{{\text{TD}},i}} \;{\text{and}}\;q_{{{\text{TD}},i}} )$ at ith bus and system losses. The load equilibrium constraints given below:

$$p_{{\text{sub - station}}} + \sum\limits_{i = 1}^{N} {p_{{{\text{DG}},i}} = \sum\limits_{i = 1}^{N} {p_{{{\text{TD}},i}} + p_{{{\text{loss}}}} } }$$

(6)

$$q_{{\text{sub - station}}} + \sum\limits_{i = 1}^{N} {q_{{{\text{DG}},i}} = } \sum\limits_{i = 1}^{N} {q_{{{\text{TD}},i}} + q_{{{\text{loss}}}} }$$

(7)

Bus Voltage Limit

Bus voltage must be in the range of its maximum and minimum voltage limit for guaranteed system stability and quality of power given by;

$$v_{i,\min } \, \le v_{i} \, \le \,v_{i,\max }$$

(8)

Voltage Angle Limit

Voltage angle at the bus must be in-between the maximum $(\partial_{i,\max } )$ and minimum $(\partial_{i,\min } )$ angle limit.

$$\partial_{i,\min } \le \partial_{i} \le \partial_{i,\max }$$

(9)

3 Whale Optimization Algorithm

The WAO [32] is a swarm intelligence-based meta-heuristic method first introduced by Lewis and Mirjalili in the year 2016. The WAO technique is rooted on the hunting or foraging behavior in humpback whales, also referred to as bubble-net foraging. This optimization is designed on the distinctive hunting method of humpback whales to find small fish or prey on the surface by forming bubbles in a 9-shaped path in order to search the prey. WAO has mathematically designed three different behaviors used by humpback whales during hunting, which are prey encircling, bubble-net attacking, and prey searching.

3.1 Encircling Prey

Humpback whales can perceive the prey’s location and encircle them. To emulate the procedure presuming that the present optimal solution is the final optimal solution or near it. After which, other search agents will move towards the best searching agent present there and hence updating their position. This can describe as below:

$$\overrightarrow {R} = \left| {\overrightarrow {H} \cdot \overrightarrow {L}^{*} (T) - \overrightarrow {L} (T)} \right|$$

(10)

$$\overrightarrow {L} (T + 1)\, = \,\overrightarrow {L}^{*} (T) - \overrightarrow {E} \overrightarrow {R}$$

(11)

where T indicates the present iteration, $\overrightarrow {A}$ and $\overrightarrow {B}$ are co-efficient vectors, $L^{*}$ is the position vector of the best solution in every particular iteration, $\overrightarrow {L}$ is the position vector, || is the absolute value and. is an element-by-element multiplication.

The $\overrightarrow {E}$ and $\overrightarrow {H}$ vectors are,

$$\overrightarrow {E} = 2\overrightarrow {\alpha } \cdot \overrightarrow {x} - \overrightarrow {\alpha }$$

(12)

$$\overrightarrow {H} = 2.\overrightarrow {x}$$

(13)

where $\alpha$ is linearly decreased from 2 to 0 amidst the iterations and $\overrightarrow {x}$ is a random vector in $\left[ {0,1} \right]$.

3.2 Bubble Net Attack Method

This method uses two different outlooks where humpback whales swim across the prey in a spiral-shaped path along a shrinking circle where bubble nets are created during the entire process to hunt down their prey. The mathematical formulation is as follows:

$$\overrightarrow {{R^{\prime}}} = \left| {\overrightarrow {{L^{*} }} (T) - \overrightarrow {L} (T)} \right|$$

(14)

$$\overrightarrow {L} (T + 1) = \overrightarrow {R^{\prime}} e^{\,yz} \cdot\cos (2\pi z) + \overrightarrow {{L^{*} }} (T)$$

(15)

where y is a constant for defining the shape of logarithmic spiral and $z$ is random number in $\left[ { - 1,1} \right]$.

While swimming around its prey, the whale swims in a shrinking circle and spiral-shaped path concurrently which can be mathematically given together for optimization as:

$$\overrightarrow {L} (T + 1) = \left\{ {\begin{array}{*{20}l} {\overrightarrow {L}^{*} (T) - \overrightarrow {E} \cdot \overrightarrow {R} } \hfill & {{\text{if}}\;n < 0.5} \hfill \\ {\overrightarrow {R} \cdot e^{yz} \cdot \cos (2\pi z) + \overrightarrow {L}^{*} (T)} \hfill & {{\text{if}}\;n \ge 0.5} \hfill \\ \end{array} } \right\}$$

(16)

3.3 Prey Search

Humpback whales arbitrarily hunt on the perception of the prey. The location in the searching phase is arbitrarily updated and taken as the best solution.

$$\overrightarrow {R} = \left| {\overrightarrow {H} \cdot \overrightarrow {L}_{{{\text{rand}}}} - \overrightarrow {L} } \right|$$

(17)

$$\overrightarrow {L} (T + 1) = \overrightarrow {L}_{{{\text{rand}}}} - \overrightarrow {E} \cdot \overrightarrow {R}$$

(18)

where $\overrightarrow {L}_{{{\text{rand}}}}$ is the number of random whales at the present situation.

4 Quasi-oppositional Based Learning

In general, Oppositional Based Learning is a Novel soft computing or intelligence-based concept to enhance various optimization techniques, first introduced by Tizhoosh [33], apparently one of the most successful concepts in computational intelligence, which enhances the searching abilities of the conventional population-based optimization techniques in solving nonlinear optimization problems. The main objective in OBL is to consider the opposite or reciprocal of a guess or an assumption thereby comparing it with the original assumption and accordingly improve the chances of finding a solution faster. The OBL algorithm starts with the initialization of initial estimate that is based on some prior information about the solution or randomly. Optimal Solution could be in any direction or at least in opposite direction. For convergence opposite set of estimates is considered, which iteratively replaces the initial estimates for better solution in the direction of optimality.

4.1 Opposite Number

Let, $P\, \in [y,z]$ be a real number. Its opposite number $P^\circ$ is defined by:

$$P^\circ = y + z - P$$

(19)

4.2 Opposite Point

Let $R = (X_{1} ,X_{2} ,...,X_{n} )$ be a point in n-dimensional space, where $P_{{r_{{}} }} \in \,[y_{r} ,z_{r} ]$, $r \in \{ 1,2, \ldots ,n\}$. The opposite point $R^\circ = (X_{1}^\circ ,X_{2}^\circ , \ldots ,X_{n}^\circ )$ is defined by its components:

$$P_{r}^\circ \, = y_{r} + z_{r} - P_{r}$$

(20)

4.3 Quasi-opposite Number

Let $P$ be a real number between $[y,z]$. The quasi-opposite number $P^{Qo}$ is defined as:

$$P^{Qo} = {\text{rand}}(C,\mathop{P}\limits^{\smile} )$$

(21)

where $C$ is given by:

$$C = \frac{y + z}{2}$$

4.4 Quasi-opposite Point

Let P be a real number between $[a,b]$. The quasi-opposite point $P_{r}^{Qo}$ is defined as:

$$P_{r}^{Qo} = {\text{rand}}(C_{r} ,\mathop{P}\limits^{\smile}_{r} )$$

(22)

where $C_{r} = \frac{{y_{r} + z_{r} }}{2},\;P_{r} \in [y_{r} ,z_{r} ];\;r = \{ 1,2,3, \ldots ,n\}$.

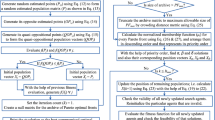
5 QOWOA to Solve ODGA Problem in RDN

This paper developed QOWOA by emerging the conception of QOBL in WOA.

The key points involved in above-mentioned methodology are mentioned below.

Point 1: The read data for the system with constraints, size of population $(P_{n} )$, the maximal iteration count, the maximal DG count that is to be set up in the network, and the parametric quantity of WOA.

Point 2: The randomly generated DG size is normalized between the running limits. The ith DG value is normalized to $P^{i}$ for satisfying the capacity constraint as given below:

$$P^{i} \, = \,P^{i}_{\min } + r^{ * } (P^{i}_{\max } - P^{i}_{\min } )$$

(23)

The KW rating and location of all setup DGs, make a sender $S_{k}$ representing starting status of each factor for ODGA problem.

$$S_{k} = [{\text{loc}}_{k,1} ,{\text{loc}}_{k,2} , \ldots ,{\text{loc}}_{k,N} ,P_{k,1} ,P_{k,2} , \ldots ,P_{k,N} ]$$

(24)

Depending on size of the population, starting solvent $S$ is created as given below:

$$S = [S_{1} ,S_{2} , \ldots ,S_{k} , \ldots ,S_{N,P} )$$

(25)

Point 3: Start the load flow for finding power losses utilizing BIBC matrix and BCBV matrix [34].

Point 4: The motion status for each of the whale is updated using different steps encircling Prey, bubble net attack method, and prey search Eqs. (11), (16), and (18).

Point 5: The starting status for each one of the whales is modified using (19). The ith solution to ODGA problem represents ith whale starting status.

Point 6: The jumping rate is used for the generation of opposite population given by:

$$\mathop{x}\limits^{\smile}_{1} ,\, = \,a + b - x$$

$$\mathop{x}\limits^{\smile}_{i} = p_{i} + q_{i} - y_{i}$$

Point 7: Choose the fittest individual $N_{p}$ from the current and the oppositional population. Check if the experimental value is larger than the above limit then set the obtained value as maximum. If the experimental value is smaller than the lower limit then set the obtained value as minimum.

Point 8: The point from 3 to 8 is repeated until and unless the maximum count for the iteration is attained.

6 Results and Discussions

To examine the utility and superiority in finding solution to ODGA problem, the above-proposed methodology QOWOA is tested with three different test systems consisting 33, 69 and 118 buses, with operating voltage 12.66 kV. The simulations are done on MATLAB software using a computer having Intel i3-7020U @ 2.30 GHz and 8 GB of RAM. For the algorithm population size and iteration count are considered as 50 and 100, respectively.

6.1 33-Bus Test Radial Distribution Network

The QOWOA methodology is tested on 33-bus test RDN that have 33 buses and 32 branches are shown in Fig. 1. The line values and respectively real (3.7 MW) and reactive (2.3 MVAR) power demand for the systems are obtained from Ref. [35]. The voltage stability index, deviance in voltage, and power loss for 33-bus test system with QOWOA are 0.9543, 0.0009 p.u, 0.10235 MW respectively. Results are obtained using QOWOA optimization techniques are indicated in Table 1. The multi-objective of power loss minimization is greatly achieved with the simultaneous enhancement of voltage stability and profile.

Fig. 1

33-Bus test RDN

Table 1 Computational results of different approaches for 33-bus RDN

6.2 69-Bus Test Radial Distribution Network

The above-mentioned methodology i.e., QOWOA is tested on 69-bus large distribution network consisting of 69 buses and 68 branches are shown in Fig. 2. The line values and respective real (3.8 MW) and reactive (2.69 MVAR) power demand for the systems are obtained from Ref. [36]. The simulation outcomes for the methodology are indicated in Table 2. The obtained results then are compared with the results of various author derived using different optimization. The result shows the effectiveness QOWOA algorithm with side by side by optimization of voltage deviance (0.00069), power loss (0.079085), and voltage stability index (0.9872) better than other techniques in comparison.

Fig. 2

69-Bus test RDN

Table 2 Computational results of different approaches for 69-bus RDN

6.3 118-Bus Test Radial Distribution Network

With the intention of showing the superiority of QOWOA methodology, it is applied to 118 bus test system consisting of 118 buses and 116 branches shown in Fig. 3. System base values are 100 $({\text{MVA}})_{b}$ and 11 $({\text{KV}})_{b}$. The respective reactive, real power demands are 17.04 Mega-VAR and 22.70 MW severally. The line and load data are taken form [37]. The simulation result considering 7 DGs at different locations is shown in Table 3. System loss, voltage deviance, and index of voltage stability for the system under consideration come out to be 0.67646 MW, 0.0121 p.u, and 0.8890, respectively. The result shows its potency in comparison to the methodologies proposed by other authors.

Fig. 3

118-Bus test RDN

Table 3 Computational results of different approaches for 118-bus RDN

7 Conclusion

The paper presents WOA and QOWOA for finding ideal site for DG installation with appropriate size in RDN for multi-objective optimization along with the satisfaction of system constraints. The methodology analysis is done with 33, 69 and 118 bus test system with more than one DG at different locations. The results exhibit the potency of the proposed QOWOA to solve multi-objective optimal DG emplacement problem in RDN. The results clearly demonstrate that QOWOA converges to better quality solutions co whereas WOA provides quite inferior solutions on comparison to QOWOA. The results obtained are compared with the results of other methodologies to show the effectiveness of the proposed techniques. The results establishes that the proposed QOWOA gives better results in finding solution to ODGA problem with simultaneous optimization of losses along with the voltage profile enhancement in the RDN.