Abstract
Simulation is a well-established technique for verifying wheth-er the behaviors of one labeled transition system (LTS) can mimic all behaviors of another LTS. Transition systems with regular expressions (RE-TSs) are an extension of LTSs, which are used as semantic models in modal or temporal logics to solve model checking problems. This paper presents approximate simulation, an extension of simulation of an LTS by a RE-TS, by combining general simulation and metrics, and discusses its properties. First, the notion of approximate simulation is introduced. Then, we investigate properties and an equivalent formalism of approximate simulation. On the other hand, we propose two approaches of fixed point characterization for approximate simulation, and study the relationship between them.
This research is supported by National Natural Science Foundation of China under Grant 62162014.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Analysis and verification of concurrent and reactive systems [1] is a well-established research field. Labeled transition systems (LTSs) [1, 2] are typically used as models to describe the behaviors of concurrent and reactive systems. In order to compare the behaviors of LTSs, researchers proposed a variety of verification methods. Among them, simulations [1, 3, 4, 30] have a wide range of applications in the analysis of LTSs.
Classical simulation verification techniques return a boolean answer that indicates whether one system can mimic all behaviors of another system. However, as pointed out in [8, 11,12,13], these techniques are restrictive and not robust: Two systems either are simulated or are not simulated, regardless of how close the behaviors of two systems are. To overcome this limitation, the majority of existing works can be roughly grouped into two directions. One of them is based on the notion of metric, which assigns a non-negative real number to each pair of states of systems (e.g., [7, 8, 13, 18, 25,26,27]). The other direction is to propose numerous approximate simulations (e.g., [10,11,12, 14, 28]), which characterize two almost similar states by a parameter \(\delta \).
In fact, in order to model the systems which are required to satisfy the requirements of different aspects, there are a large number of extensions of LTSs in existing literatures (e.g., [5,6,7,8,9, 16, 21, 24]), such as transition systems with regular expressions (RE-TSs) (e.g., [15, 17, 19, 20, 22, 23]), fuzzy transition systems (e.g., [31, 33, 34]) and probabilistic transition systems (e.g., [11, 12]). RE-TSs have been used in classical modal and temporal logics as semantic models to express the properties of models of systems. For example, Bozzelli [17] investigated the model checking problem for interval temporal logic extended with regular expressions. Beer [20], Brazdil [23] and Mateescu [22] extended computation tree logic (CTL) by applying regular expressions so as to enhance the expression of CTL. From a different point of view, Fan [15] added regular expressions to pattern graphs, and used simulation to solve graph pattern matching which is a classical graph challenge, and considered as one of the most studied problems in the literature. It is regrettable that the simualtion of an LTS by a RE-TS has been ignored in the setting of approximate. To alleviate the aforementioned problem, we will use the notion of metrics to propose an approximate simulation, and study some properties about the approximate simulation.
The paper is organized as follows. Some preliminaries are given in Sect. 2. In Sect. 3, we give the notion of the approximate simualtion. We study some related properties about the approximate simualtion, and provide two fixed point characterizations in Sect. 4 and conclude the paper in Sect. 5.
2 Preliminaries
In this section, we recall some notations and definitions about regular expressions, metric spaces and transition systems with regular expressions.
We denote the sets of real numbers, non-negative reals, natural numbers and positive integers by \(\mathbb {R}\), \(\mathbb {R}^{+}\), \(\mathbb {N}\), \(\mathbb {Z}^{+}\), respectively. We use I to denote the set of indexes. Let \(\varSigma \) be a finite set. We denote the set of finite strings over \(\varSigma \) by \(\varSigma ^{*}\). We write \(\mathcal {P}(\varSigma )\) for the power set of \(\varSigma \). Let \(\rho =a_1\ldots a_n\), \(\sigma =b_1\ldots b_m\in \varSigma ^{*}\) be two strings. Then, the concatenation of \(\rho \) and \(\sigma \) is the string \(\rho \sigma =a_1\ldots a_nb_1\ldots b_m\). We also denote the i-th symbol of \(\rho \) and the length of \(\rho \) by \(\rho _{i}\) and \(|\rho |\), respectively. Let \(\mathcal {P}\), \(\mathcal {Q}\subseteq \varSigma ^{*}\). The concatenation of \(\mathcal {P}\) and \(\mathcal {Q}\) is \(\mathcal{P}\mathcal{Q}=\{\rho \sigma \in \varSigma ^{*}:\rho \in \mathcal {P},\sigma \in \mathcal {Q}\}\).
Regular expressions [29] \(\omega \) over \(\varSigma \) are defined by the following grammar,
where \(a\in \varSigma \). The set of all regular expressions over \(\varSigma \) is written as \(\varpi (\varSigma )\). The language \(L(\omega )\subseteq \varSigma ^{*}\) of a regular expression \(\omega \in \varpi (\varSigma )\) is defined indutively by
-
(1)
\(L(a)=\{a\}\);
-
(2)
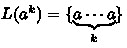 ;
; -
(3)
\(L(a^{+})=L(a)\cup L(a^{2})\cup \cdots \);
-
(4)
\(L((\omega _{1}))=L(\omega _{1})\);
-
(5)
\(L(\omega _{1}\omega _{2})=L(\omega _{1})L(\omega _{2})\);
-
(6)
\(L(\omega _{1}+\omega _{2})=L(\omega _{1})\cup L(\omega _{2})\).
We recall the definition of metrics taken from [32]. A function \(d:\varSigma \times \varSigma \rightarrow \mathbb {R}\) is a metric over \(\varSigma \) if for all \(x,y,z\in \varSigma \)
-
(1)
\(d(x,y)\ge 0\), \(d(x,y)=0\) iff \(x=y\);
-
(2)
\(d(x,y)=d(y,x)\);
-
(3)
\(d(x,z)\le d(x,y)+d(y,z)\).
And, the pair \((\varSigma ,d)\) is called a metric space. When d is clear from context, we write \(\varSigma \) instead of \((\varSigma ,d)\).
Next, we review the definition of transition system with regular expressions [15, 17, 20, 22, 23]. A transition system with regular expressions (for short, RE-TS) is a tuple \(\mathcal{R}\mathcal{T}=(S,s_{0},\varpi (\varSigma ),\rightarrow )\) where S is a finite set of states, \(s_{0}\in S\) is a initial state, \(\varpi (\varSigma )\) is the set of all regular expressions over \(\varSigma \), and \(\rightarrow \subseteq S\times \varpi (\varSigma )\times S\) is a set of transitions.
A labeled transition system (LTS) can be viewed as a special case of RE-TS, where \(\varpi (\varSigma )\) is replaced with \(\varSigma \). Let \(\mathcal{R}\mathcal{T}=(S,s_{0},\varpi (\varSigma ),\rightarrow )\) be a RE-TS. We write \(s\xrightarrow {\omega }s'\) for \((s,\omega ,s')\in \rightarrow \), where \(s,s'\in S\). A trace \(\sigma \) is an infinite sequence of elements in \(\varpi (\varSigma )\). For \(j\ge 1\), let \(\sigma _{j}\) denote the jth element. A path from s in \(\mathcal{R}\mathcal{T}\) is an infinite sequence \(\pi =s\xrightarrow {\omega _1}s'\xrightarrow {\omega _2}s''\cdots \), and we denote by \(\textrm{tr}(\pi )=\omega _1\omega _2\cdots \) the trace induced by it. For \(s\in S\), we denote by \(\textrm{Path}(s)\) the set of paths from s and by \(\textrm{Trace}(s)=\{tr(\pi ):\pi \in \textrm{Path}(s)\}\) the set of traces from s. We use \(\mathcal {L}(\mathcal{R}\mathcal{T})\) to denote the languages of \(\mathcal{R}\mathcal{T}\), where \(\mathcal {L}(\mathcal{R}\mathcal{T})=\textrm{Trace}(s_0)\). If \(\mathcal{R}\mathcal{T}\) is an LTS, \(\rightarrow \subseteq S\times \varSigma \times S\) can be extended to \(\rightarrow ^{*}\subseteq S\times \varSigma ^{*}\times S\). We write \(s\xrightarrow {\rho }\!{^*}s'\) for \((s,\rho ,s')\in \rightarrow ^{*}\).
3 Approximate Simulation
In this section, we define an approximate simulation. Before formally defining approximate simulation, we will introduce the notion of exact simulation of an LTS by a RE-TS [15].
Definition 1
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS and \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS. A relation \(R\subseteq S_1\times S_2\) is called a simulation if for any \((s_1,s_2)\in R\) and for each \(s_{1}\xrightarrow {\rho }\!{^*}s'_{1}\), there exists \(s_{2}\xrightarrow {\omega }s'_{2}\) such that \(\rho \in L(\omega )\) and \((s_{1}',s_{2}')\in R\). We say that \(\mathcal{R}\mathcal{T}_{2}\) simulates \(\mathcal{R}\mathcal{T}_{1}\), denoted by \(\mathcal{R}\mathcal{T}_{1}\preceq \mathcal{R}\mathcal{T}_{2}\), if there exists a simulation R such that \((s_{1,0},s_{2,0})\in R\).
Example 1
Consider an LTS \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) and a RE-TS \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\rightarrow _{2})\). The transition diagrams of \(\mathcal{R}\mathcal{T}_{1}\) and \(\mathcal{R}\mathcal{T}_{2}\) are depicted in Fig. 1. By Definition 2, we can find a relation \(R=\{(s_{1,0},s_{2,0}),(s_{1,1},s_{2,1}),(s_{1,2},s_{2,1}),\) \((s_{1,3},s_{2,2}),(s_{1,4},s_{2,2})\}\) which is a simulation, and \((s_{1,0},s_{2,0})\in R\). Therefore, we can obtain \(\mathcal{R}\mathcal{T}_{1}\preceq \mathcal{R}\mathcal{T}_{2}\).
The following definitions and propositions will help us to define the approximate simulation.
The definition of string distance sd will be developed in a discounted version [7, 8], in which distance of each step is decreased exponentially over time by a discounting factor \(\alpha \in (0,1]\).
Let \((\varSigma ,d)\) be a metric space, and \(\alpha \in (0,1]\). The string distance \(sd:\varSigma ^{*}\times \varSigma ^{*}\rightarrow \mathbb {R}\cup \{+\infty \}\) is defined as
for all strings \(\rho ,\sigma \in \varSigma ^{*}\).
Proposition 1
Let d be a metric over \(\varSigma \). Then, sd is a metric on the set \(\varSigma ^{*}\).
Proof
By the definition of metric, we need to prove the follow properties:
-
(1)
\(sd(\rho ,\sigma )\ge 0\) and \(sd(\rho ,\sigma )=0\) iff \(\rho =\sigma \),
-
(2)
\(sd(\rho ,\sigma )=sd(\sigma ,\rho )\),
-
(3)
\(sd(\rho ,\varsigma )+sd(\varsigma ,\sigma )\ge sd(\rho ,\sigma )\)
where \(\rho ,\sigma ,\varsigma \in \varSigma ^{*}\).
The properties (1) and (2) are obvious.
For property (3): We have to discuss the following four cases.
The cases of \(|\rho |\ne |\sigma |\ne |\varsigma |\), \(|\rho |=|\sigma |\ne |\varsigma |\), and \(|\rho |\ne |\sigma |=|\varsigma |\) follow immediately from the definition of sd. We only consider the case of \(|\rho |=|\sigma |=|\varsigma |=n\).
From the definition of sd, we know that
and \(sd(\rho ,\sigma )=\max \limits _{1\le k\le n}\alpha ^{k-1}d(\rho _{k},\sigma _{k})\). It is sufficient to show that there exists a \(1\le p\le n\) such that \(\alpha ^{p-1}d(\rho _{p},\sigma _{p})=sd(\rho ,\sigma )\). Then, \(d(\rho _{p},\sigma _{p})\le d(\rho _{p},\varsigma _{p})+d(\varsigma _{p},\sigma _{p})\). Therefore,
Let \((\varSigma ,d)\) be a metric space. The distance between a string \(\rho \in \varSigma ^{*}\) and the language \(L(\omega )\subseteq \varSigma ^{*}\) of a regular expression \(\omega \in \varpi (\varSigma )\) is defined as
Proposition 2
Let \((\varSigma ,d)\) be a metric space. Then, the following properties hold:
-
(1)
\(d^{*}(\rho ,L(\omega ))\ge 0\), for all \(\rho \in \varSigma ^{*}\) and \(\omega \in \varpi (\varSigma )\).
-
(2)
\(\rho \in L(\omega )\) iff \(d^{*}(\rho ,L(\omega ))=0\), where \(\rho \in \varSigma ^{*}\), \(\omega \in \varpi (\varSigma )\).
Proof
For property (1): It follows immediately from Proposition 1.
For property (2): First, for the ‘if’ part, let \(d^{*}(\rho ,L(\omega ))=0\). Without loss of generality, suppose |\(\rho \)|=n. Since \(\varSigma \) is a finite set, assume that there are m elements in \(\varSigma \). According to the definition of sd, there are at most \(nm+1\) values. Then, there exists \(\sigma \in L(\omega )\) such that \(sd(\rho ,\sigma )=0\). So by Proposition 1 and the definition of sd, \(\rho =\sigma \) holds. Hence \(\rho \in L(\omega )\).
Second, for the ‘only if’ part, suppose that \(\rho \in L(\omega )\). Then, there exists \(\sigma \in L(\omega )\) such that \(\rho =\sigma \). By Proposition 1 and the definition of sd, \(sd(\rho ,\sigma )=0\) holds. Therefore, \(\inf \limits _{\sigma \in L(\omega )}sd(\rho ,\sigma )=0\), and \(d^{*}(\rho ,L(\omega ))=0\).
By the above definitions and propositions, we will introduce the definition of approximate simulation.
Definition 2
Let \(\mathcal{R}\mathcal{T}_1=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, \((\varSigma ,d)\) be a metric space, and \(\delta \in \mathbb {R}^{+}\). A relation \(R_{\delta }\subseteq S_1\times S_2\) is called a \(\delta \)-simulation if for any \((s_1,s_2)\in R\) and for each \(s_{1}\xrightarrow {\rho }\!{^*}s'_{1}\), there exists \(s_{2}\xrightarrow {\omega }s_{2}'\) such that \(d^{*}(\rho ,L(\omega ))\le \delta \) and \((s_{1}',s_{2}')\in R\). We say that \(\mathcal{R}\mathcal{T}_{2}\) \(\delta \)-simulates \(\mathcal{R}\mathcal{T}_{1}\), denoted by \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{2}\), if there exists a \(\delta \)-simulation \(R_{\delta }\) such that \((s_{1,0},s_{2,0})\in R_{\delta }\).
We replace \(s_{1,0}\xrightarrow {a}s_{1,1}\) by \(s_{1,0}\xrightarrow {c}s_{1,1}\) in Fig. 1, where \(d(a,c)=0.5\). Then, according to Definition 2, we can obtain that there exists a 0.5-simulation \(R_{0.5}\) such that \((s_{1,0},s_{2,0})\in R_{0.5}\). Thus, \(\mathcal{R}\mathcal{T}_{1}\preceq _{0.5}\mathcal{R}\mathcal{T}_{2}\).
In above definition, when \(\delta =0\), we recover the established definition of exact simualtion.
4 Related Properties
In this section, we will introduce some properties related with the approximate simulation.
Given a precision parameter \(\delta \), which used to measure the degree of simulation, the following lemma ensures that the set of \(\delta \)-simulation has a maximal element, denoted by \(R_{\delta }^{\max }\). Moreover, by using \(R_{\delta }^{\max }\), we give an equivalent expression for \(\delta \)-simulation.
Lemma 1
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, \((\varSigma ,d)\) be a metric space, and \(\delta \in \mathbb {R}^{+}\). Suppose that \(\{R_{\delta }^{i}\}_{i\in I}\) is a family of \(\delta \)-simulation of \(\mathcal{R}\mathcal{T}_{1}\) by \(\mathcal{R}\mathcal{T}_{2}\), and \(R_{\delta }^{\max }=\bigcup \limits _{i\in I}R_{\delta }^{i}\). Then, the following properties hold:
-
(1)
\(R_{\delta }^{\max }\) is a \(\delta \)-simulation of \(\mathcal{R}\mathcal{T}_{1}\) by \(\mathcal{R}\mathcal{T}_{2}\).
-
(2)
\(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{2}\) iff \((s_{1,0},s_{2,0})\in R_{\delta }^{\max }\).
Proof
For property (1): Consider any \((s_1,s_2)\in R_{\delta }^{\max }=\bigcup \limits _{i\in I}R_{\delta }^{i}\). It is enough to show that there exists a \(i\in I\) such that \((s_1,s_2)\in R_{\delta }^{i}\). By Definition 2, we can know that for each \(s_1\xrightarrow {\rho }\!{^*}s'_1\) in \(\mathcal{R}\mathcal{T}_{1}\), there exists \(s_2\xrightarrow {\omega }s'_2\) in \(\mathcal{R}\mathcal{T}_{2}\) such that \(d^{*}(\rho ,L(\omega ))\le \delta \) and
Hence, \(R_{\delta }^{\max }\) is a \(\delta \)-simulation of \(\mathcal{R}\mathcal{T}_{1}\) by \(\mathcal{R}\mathcal{T}_{2}\).
For property (2): It follows immediately from Definition 2 and property (1).
Proposition 3
Let \(\mathcal{R}\mathcal{T}_{i}=(S_{i},s_{i,0},\varSigma ,\rightarrow _{i})\), \(i=1,2\), be two LTSs, \(\mathcal{R}\mathcal{T}_{3}=(S_{3},s_{3,0},\varpi (\varSigma ),\) \(\rightarrow _{3})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. Then, the following properties hold:
-
(1)
For all \(\delta \ge 0\), \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{1}\).
-
(2)
For all \(\delta \ge 0\), if \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{3}\), then for all \(\delta '>\delta \), \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta '}\mathcal{R}\mathcal{T}_{3}\).
-
(3)
For all \(\delta ,\delta '\ge 0\), if \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{2}\) and \(\mathcal{R}\mathcal{T}_{2}\preceq _{\delta '}\mathcal{R}\mathcal{T}_{3}\), then \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta +\delta '}\mathcal{R}\mathcal{T}_{3}\).
Proof
For property (1): Let \(R=\{(s,s)\in S_1\times S_1:s\in S_1\}\). Then, for each \((s,s)\in R\) and \(s\xrightarrow {a}\!{^*}s'\), it is obvious that \(s\xrightarrow {a}s'\), \(d^{*}(a,L(a))=0\le \delta \) and \((s',s')\in R\). Therefore, R is a \(\delta \)-simulation by Definition 2. Thus \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{1}\) because \((s_{1,0},s_{1,0})\in R\).
For property (2): Suppose that \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{3}\) and \(\delta '>\delta \ge 0\). From Lemma 1, we can know that \((s_{1,0},s_{3,0})\in R_{\delta }^{\max }=\bigcup \limits _{i\in I}R_{\delta }^{i}\). Therefore, there exists \(i\in I\) such that \((s_{1,0},s_{3,0})\in R_{\delta }^{i}\). By Definition 2, we have that for each \((s_1,s_3)\in R_{\delta }^{i}\) and \(s_1\xrightarrow {\rho }\!{^*}s'_1\), there exists \(s_3\xrightarrow {\omega }s'_3\) such that \(d^{*}(\rho ,L(\omega ))\le \delta <\delta '\) and \((s'_1,s'_3)\in R_{\delta }^{i}\). Hence, \(R_{\delta }^{i}\) is a \(\delta '\)-simulation. Thus, \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta '}\mathcal{R}\mathcal{T}_{3}\).
For property (3): Let \(R=\{(s_1,s_3)\in S_1\times S_3:\exists s_2\in S_2,(s_1,s_2)\in R_{\delta }^{\max }\,\mathrm {and\,}\) \( (s_2,s_3)\in R_{\delta '}^{\max }\}\). For each \((s_1,s_3)\in R\), suppose that
We know from Lemma 1 that there exists
such that \(d^{*}(a_{i},L(a'_{i}))\le \delta \) and \((s''_1,s''_2)\in R_{\delta }^{\max }\), where \(a_{i},a'_{i}\in \varSigma \) for every \(i\in \mathbb {N}\). Let \(\rho =a_{1}a_{2}\cdots a_{n}\) and \(\rho '=a'_{1}a'_{2}\cdots a'_{n}\). By the definition of sd, we have \(sd(\rho ,\rho ')\le \delta \). From Lemma 1, we know that there exists \(s_3\xrightarrow {\omega }s'_3\) such that \(d^{*}(\rho ',L(\omega ))\le \delta '\) and \((s''_2,s'_3)\in R_{\delta '}^{\max }\) for each \(s_2\xrightarrow {\rho '}\!{^*}s''_2\) and \((s_2,s_3)\in R_{\delta '}^{\max }\). Therefore, there exists \(\sigma \in L(\omega )\) such that \(sd(\rho ',\sigma )\le \delta '\). By Proposition 1,
Thus, \(d^{*}(\rho ,L(\omega ))\le \delta +\delta '\) and \((s''_1,s'_3)\in R\). Therefore, R is a \(\delta +\delta '\)-simulation, and \((s_{1,0},s_{3,0})\in R\) because \((s_{1,0},s_{2,0})\in R_{\delta }^{\max }\) and \((s_{2,0},s_{3,0})\in R_{\delta '}^{\max }\). Hence, \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta +\delta '}\mathcal{R}\mathcal{T}_{3}\).
Given an LTS \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) and a RE-TS \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\), we say that \(\textrm{Trace}(s_1)\subseteq \textrm{Trace}(s_2)\) if for each \(\sigma _1=\rho _1\rho _2\cdots \in \textrm{Trace}(s_1)\), there exists \(\sigma _2=\omega _{1}\omega _{2}\cdots \in \textrm{Trace}(s_2)\) such that \(\rho _{i}\in L(\omega _{i})\) for all \(i\in \mathbb {Z}^{+}\), where \((s_1,s_2)\in S_1\times S_2\).
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, \((\varSigma ,d)\) be a metric space, and \((s_1,s_2)\in S_1\times S_2\). Given two traces \(\sigma _1=\rho _1\rho _2\cdots \in \textrm{Trace}(s_1)\) and \(\sigma _2=\omega _{1}\omega _{2}\cdots \in \textrm{Trace}(s_2)\), the trace distance between \(\sigma _1\) and \(\sigma _2\) is defined as
The trace distance between \(s_1\) and \(s_2\) is defined as
The language distance between \(\mathcal{R}\mathcal{T}_{1}\) and \(\mathcal{R}\mathcal{T}_{2}\) is defined as
Proposition 4
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. Then, the following properties hold:
-
(1)
\(\textrm{Trace}(s_1)\subseteq \textrm{Trace}(s_2)\) iff \(\mathcal {T}d(s_1,s_2)=0\), where \(s_1\in S_1\) and \(s_2\in S_2\).
-
(2)
\(\mathcal {L}(\mathcal{R}\mathcal{T}_{1})\subseteq \mathcal {L}(\mathcal{R}\mathcal{T}_{2})\) iff \(\mathcal {L}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})=0\).
Proof
For property (1): First, for the ‘if’ part, suppose that \(\mathcal {T}d(s_1,s_2)=0\). It is sufficient to know from the definition of \(\mathcal {T}d\) that \(\inf \limits _{\sigma _2\in \textrm{Trace}(s_2)}td(\sigma _1,\sigma _2)=0\) for each \(\sigma _1=\rho _{1}\rho _{2}\cdots \in \textrm{Trace}(s_1)\). Therefore, there exists \(\sigma _2=\omega _{1}\omega _{2}\cdots \in \textrm{Trace}(s_2)\) such that \(td(\sigma _1,\sigma _2)=0\). From the definition of td, we have \(d^{*}(\rho _{i},L(\omega _{i}))=0\) for all \(i\in \mathbb {Z}^{+}\). From Proposition 2, there is \(\rho _{i}\in L(\omega _{i})\) for all \(i\in \mathbb {Z}^{+}\). Hence, \(\textrm{Trace}(s_1)\subseteq \textrm{Trace}(s_2)\).
Second, for the ‘only if’ part, let \(\textrm{Trace}(s_1)\subseteq \textrm{Trace}(s_2)\). In other words, for each \(\sigma _1=\rho _{1}\rho _{2}\cdots \in \textrm{Trace}(s_1)\), there exists \(\sigma _2=\omega _{1}\omega _{2}\cdots \in \textrm{Trace}(s_2)\) such that \(\rho _{i}\in L(\omega _{i})\) for all \(i\in \mathbb {Z}^{+}\). And, there is \(d^{*}(\rho _{i},L(\omega _{i}))=0\) from Proposition 2 for all \(i\in \mathbb {Z}^{+}\). Moreover, we have \(td(\sigma _1,\sigma _2)=0\) from the definition of td. Hence, \(\inf \limits _{\sigma _2\in \textrm{Trace}(s_2)}td(\sigma _1,\sigma _2)=0\) for each \(\sigma _1\in \textrm{Trace}(s_1)\). Therefore, \(\mathcal {T}d(s_1,s_2)=0\).
For property (2): For the ‘if’ part, suppose that \(\mathcal {L}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})=0\). It is sufficient to show that \(\inf \limits _{\sigma _2\in \mathcal {L}(\mathcal{R}\mathcal{T}_{2})}td(\sigma _1,\sigma _2)=0\) for each \(\sigma _1=\rho _{1}\rho _{2}\cdots \in \mathcal {L}(\mathcal{R}\mathcal{T}_{1})\). Therefore, there exists \(\sigma _2=\omega _{1}\omega _{2}\cdots \in \mathcal {L}(\mathcal{R}\mathcal{T}_{2})\) such that \(td(\sigma _1,\sigma _2)=0\). From the definition of td, there is \(d^{*}(\rho _{i},L(\omega _{i}))=0\) for all \(i\in \mathbb {Z}^{+}\). Then, we have \(\rho _{i}\in L(\omega _{i})\) by Proposition 2. Hence, \(\mathcal {L}(\mathcal{R}\mathcal{T}_{1})\subseteq \mathcal {L}(\mathcal{R}\mathcal{T}_{2})\).
For the ‘only if’ part, consider that \(\mathcal {L}(\mathcal{R}\mathcal{T}_{1})\subseteq \mathcal {L}(\mathcal{R}\mathcal{T}_{2})\). In other words, for each trace \(\sigma _1=\rho _{1}\rho _{2}\cdots \) in \(\mathcal{R}\mathcal{T}_{1}\), there exists a trace \(\sigma _2=\omega _{1}\omega _{2}\cdots \) in \(\mathcal{R}\mathcal{T}_{2}\) such that \(\rho _{i}\in L(\omega _{i})\) for all \(i\in \mathbb {Z}^{+}\). We know from Proposition 2 that \(d^{*}(\rho _{i},L(\omega _{i}))=0\). By the definition of td, we have \(td(\sigma _1,\sigma _2)=0\). Hence, \(\inf \limits _{\sigma _2\in \mathcal {L}(\mathcal{R}\mathcal{T}_{2})}td(\sigma _1,\sigma _2)=0\) for each \(\sigma _1=\rho _{1}\rho _{2}\ldots \in \mathcal {L}(\mathcal{R}\mathcal{T}_{1})\). Thus, we have \(\mathcal {L}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})=0\) from the definition of \(\mathcal {L}d\).
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\rightarrow _{2})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. The simulation distance between \(\mathcal{R}\mathcal{T}_{1}\) and \(\mathcal{R}\mathcal{T}_{2}\) is defined as
Lemma 2
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS and \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. Then, the following properties hold:
-
(1)
\(\mathcal {S}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})\ge 0\).
-
(2)
\(\mathcal {S}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})=0\) if \(\mathcal{R}\mathcal{T}_{1}\preceq \mathcal{R}\mathcal{T}_{2}\).
Proof
For property (1): It follows immediately from Proposition 2.
For property (2): Consider that \(\mathcal{R}\mathcal{T}_{1}\preceq \mathcal{R}\mathcal{T}_{2}\). By Definition 1, there exists a simulation \(R\subset S_1\times S_2\) such that: For each \((s_1,s_2)\in R\) and \(s_1\xrightarrow {\rho }\!{^*}s'_1\), there exists \(s_2\xrightarrow {\omega }s'_2\) such that \(\rho \in L(\omega )\) and \((s'_1,s'_2)\in R\). And, we have \(d^{*}(\rho ,L(\omega ))=0\) by Proposition 2. Then, there exists a \(\delta =0\) and R is a \(\delta \)-simulation. By the definition of \(\mathcal {S}d\) and property (1), \(\mathcal {S}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})=0\).
The relationship between the simulation distance and the language distance is captured by the following theorem.
Theorem 1
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. Then,
Proof
Consider a \(\delta \ge \mathcal {S}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})\). By Proposition 3, \(\mathcal{R}\mathcal{T}_{1}\preceq _{\delta }\mathcal{R}\mathcal{T}_{2}\) holds. Let \(\sigma _1=\rho _{1}\rho _{2}\cdots \in \mathcal {L}(\mathcal{R}\mathcal{T}_{1})\). Then, there exists a path
in \(\mathcal{R}\mathcal{T}_{1}\) where \(s_1=s_{0,1}\). By Lemma 1, we know \((s_{0,1},s_{0,2})\in R_{\delta }^{\max }\). Therefore, there exists a path
such that \((s_i,s'_i)\in R_{\delta }^{\max }\) for all \(i\in \mathbb {Z}^{+}\), where \(s'_1=s_{0,2}\). Let \(\sigma _2=\omega _{1}\omega _{2}\cdots \). By Proposition 2 and the definition of td, it is obvious that \(td(\sigma _1,\sigma _2)\le \delta \). Hence, \(\inf \limits _{\sigma _2\in \mathcal {L}(\mathcal{R}\mathcal{T}_{2})}td(\sigma _1,\sigma _2)\le \delta \) for each \(\sigma _1\in \mathcal {L}(\mathcal{R}\mathcal{T}_{1})\). Thus \(\mathcal {L}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})\le \mathcal {S}d(\mathcal{R}\mathcal{T}_{1},\mathcal{R}\mathcal{T}_{2})\).
We next propose two approaches of fixed point characterization of approximate simulation.
We first give a fixed point characterization of maximal \(\delta \)-simulation for a given \(\delta \).
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. For a given \(\delta \ge 0\), we define the following sequence \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\) of subsets of \(S_1\times S_2\):
Since \(S_1\) and \(S_2\) are finite, it is clear that \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\) reaches a fixed point in a finite number steps by the definition of \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\).
Lemma 3
Let \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\) be the sequence of sets defined by definition of \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\). Then, the following properties hold:
-
(1)
\(R_{\delta }^{i+1}\subseteq R_{\delta }^{i}\) for every \(i\in \mathbb {N}\).
-
(2)
For each \(i\in \mathbb {N}\), \(R_{\delta }^{\max }\subseteq R_{\delta }^{i}\).
-
(3)
There exists some \(n\in \mathbb {N}\) such that \(R_{\delta }^{\max }=R_{\delta }^{n}\).
Proof
For property (1): It follows immediately from the definition of \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\).
For property (2): This will be proved by induction with regard to i.
The initial step is for \(i=1\). It follows from the definition of \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\).
The induction hypothesis is that (2) holds for \(i=k\). We now show that (2) holds for \(i=k+1\), i.e., \(R_{\delta }^{\max }\subseteq R_{\delta }^{k+1}\).
We have to discuss the following two cases.
The first case is that \(R_{\delta }^{\max }=\emptyset \). Then, \(R_{\delta }^{\max }=\emptyset \subseteq R_{\delta }^{k+1}\) obviously.
The second case is that \(R_{\delta }^{\max }\ne \emptyset \). Then there exists some \((s_1,s_2)\in R_{\delta }^{\max }\). For each \((s_1,s_2)\in R_{\delta }^{\max }\subseteq R_{\delta }^{k}\), we know rom Lemma 1 that for each \(s_1\xrightarrow {\rho }\!{^*}s'_1\), there exists \(s_2\xrightarrow {\omega }s'_2\) such that \(d^{*}(\rho ,L(\omega ))\le \delta \), and \((s'_1,s'_2)\in R_{\delta }^{\max }\). Then, by the induction hypothesis, \((s'_1,s'_2)\in R_{\delta }^{\max }\subseteq R_{\delta }^{k}\). Hence, It follows from the definition of \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\) that \((s_1,s_2)\in R_{\delta }^{k+1}\).
Thus (2) holds for \(i=k+1\), which proves the property.
For property (3): By using propery (1) and the definition of \(\{R_{\delta }^{i}\}_{i\in \textrm{N}}\), we can obtain that there exists some \(k\in \mathbb {N}\) such that \(R_{\delta }^{j}=R_{\delta }^{k}\) for every \(j\ge k\).
We have to discuss the following two cases.
The first case is that there exists a k such that \(R_{\delta }^{k}=\emptyset \). By property (1) and (2), \(R_{\delta }^{j}\subseteq R_{\delta }^{k}\) for every \(j\ge k\), and \(R_{\delta }^{\max }\subseteq R_{\delta }^{k}\). Hence, \(R_{\delta }^{\max }\subseteq R_{\delta }^{k}=\emptyset \).
The second case is that \(R_{\delta }^{j}\ne \emptyset \) for all \(j\in \mathbb {N}\). Let \((s_1,s_2)\in R_{\delta }^{k+1}\). Then, for each \(s_1\xrightarrow {\rho }\!{^*}s'_1\), there exists \(s_2\xrightarrow {\omega }s'_2\) such that \(d^{*}(\rho ,L(\omega ))\le \delta \) and \((s'_1,s'_2)\in R_{\delta }^{k}\). Since \(R_{\delta }^{k+1}=R_{\delta }^{k}\), it is sufficient to show that \(R_{\delta }^{k+1}\) is a \(\delta \)-simulation and \(R_{\delta }^{k}=R_{\delta }^{k+1}\subseteq R_{\delta }^{\max }\). By property (2), \(R_{\delta }^{\max }\subseteq R_{\delta }^{k}\). Hence, \(R_{\delta }^{\max }=R_{\delta }^{k}\).
We will introduce another approach, which characterizes the maximal \(\delta \)-simualtion as the level sets of a function for a given \(\delta \).
Let \(\mathcal{R}\mathcal{T}_{1}=(S_{1},s_{1,0},\varSigma ,\rightarrow _{1})\) be an LTS, \(\mathcal{R}\mathcal{T}_{2}=(S_{2},s_{2,0},\varpi (\varSigma ),\) \(\rightarrow _{2})\) be a RE-TS, and \((\varSigma ,d)\) be a metric space. Define the following sequence \(\{f^{i}\}_{i\in \textrm{N}}\) of functions from \(S_1\times S_2\) to \(\mathbb {R}^{+}\cup \{+\infty \}\):
Lemma 4
Let \(\{f^{i}\}_{i\in \mathbb {N}}\) be the sequence of functions defined by definition of \(\{f^{i}\}_{i\in \mathbb {N}}\). Then, the sequence \(\{f^{i}(s_1,s_2)\}_{i\in \mathbb {N}}\) is non-decreasing for all \((s_1,s_2)\in S_1\times S_2\).
Proof
To prove the lemma, it suffices to verify that
for every \(i\ge 0\).
This will be proved by induction on i.
The initial step is for \(i=0\). It follows from the definition of \(\{f^{i}\}_{i\in \mathbb {N}}\) and Proposition 2.
The induction hypothesis is that the lemma holds for \(i=k\). We now show that the lemma holds for \(i=k+1\), i.e., \(f^{k+1}(s_1,s_2)\le f^{k+2}(s_1,s_2)\) for each \((s_1,s_2)\in S_1\times S_2\). Then,
This completes the proof of the lemma.
\(\{f^{i}\}_{i\in \mathbb {N}}\) reaches a fixed point in a finite number of steps, which is shown in [8]. Then, for each \((s_1,s_2)\in S_1\times S_2\), there exists a \(k\in \mathbb {N}\) such that; for each \(i\le k\), \(f^{k}(s_1,s_2)\ge f^{i}(s_1,s_2)\), and for each \(j\ge k\), \(f^{k}(s_1,s_2)= f^{j}(s_1,s_2)\). Let \(f^{\min }\) be the branching distance between \(\mathcal{R}\mathcal{T}_{1}\) and \(\mathcal{R}\mathcal{T}_{2}\). Then, \(f^{\min }(s_1,s_2)=f^{k}(s_1,s_2)\) for all \((s_1,s_2)\in S_1\times S_2\) [9].
The following theorem will give the relationship between the two approaches.
Theorem 2
Let \(\delta \ge 0\), \(\{R_{\delta }^{i}\}_{i\in \mathbb {N}}\) be the sequence defined by the definition of \(\{R_{\delta }^{i}\}_{i\in \mathbb {N}}\), \(\{f^{i}\}_{i\in \mathbb {N}}\) be the sequence defined by the definition of \(\{f^{i}\}_{i\in \mathbb {N}}\), \(R_\delta ^{\max }\) be the maximal \(\delta \)-simulation of \(\mathcal{R}\mathcal{T}_{1}\) by \(\mathcal{R}\mathcal{T}_{2}\), and \(f^{\min }\) be the branching distance between \(\mathcal{R}\mathcal{T}_{1}\) and \(\mathcal{R}\mathcal{T}_{2}\). Then, the following assertions hold:
-
(1)
\(R_\delta ^i=\{(s_1,s_2)\in S_1\times S_2:f^{i}(s_1,s_2)\le \delta \}\) for every \(i\in \mathbb {N}\) and \(\delta \ge 0\).
-
(2)
\(R_\delta ^{\max }=\{(s_1,s_2)\in S_1\times S_2:f^{\min }(s_1,s_2)\le \delta \}\) for every \(\delta \ge 0\).
Proof
Assertions (1): This will be proved by induction with regard to i.
The initial step is for \(i=0\). Let \(\delta \ge 0\), if \(i=0\), then the theorem states that \(R_\delta ^0=\{(s_1,s_2)\in S_1\times S_2:f^0(s_1,s_2)\le \delta \}\). By definitions of \(\{R_{\delta }^{i}\}_{i\in \mathbb {N}}\) and \(\{f^{i}\}_{i\in \mathbb {N}}\), \(R_\delta ^0=\{(s_1,s_2)\in S_1\times S_2:f^0(s_1,s_2)\le \delta \}=S_1\times S_2\).
The induction hypothesis is that property (1) holds for \(i=k\). We now show that property (1) holds for \(i=k+1\), i.e.,
First, assume \((s_1,s_2)\in R_\delta ^{k+1}\). Then, it is sufficient to show that there exists \(s_2\xrightarrow {\omega }s'_2\) and \((s'_1,s'_2)\in R\) for each \(s_1\xrightarrow {\rho }\!{^*}s'_1\). In fact, by induction hypothesis we obtain
Since \((s_1,s_2)\in R_\delta ^{k+1}\subseteq R_\delta ^{k}\),
Therefore, \(f^{k+1}(s_1,s_2)\le \delta \).
Second, let \(f^{k+1}(s_1,s_2)\le \delta \). Then, for each \(s_1\xrightarrow {\rho }\!{^*}s'_1\), there exists \(s_2\xrightarrow {\omega }s'_2\) such that \(f^{i}(s'_1,s'_2)\le \delta \). It follows from the definition of \(\{R_{\delta }^{i}\}_{i\in \mathbb {N}}\), Lemma 4 and induction hypothesis that
Hence, \((s_1,s_2)\in R_\delta ^{k+1}\). This completes the proof of the property (1).
Assertion (2): Consider \((s_1,s_2)\in S_1\times S_2\). Suppose \(f^{\min }(s_1,s_2)\le \delta \).Then, there exists \(f^{i}(s_1,s_2)\le \delta \) for each \(i\in \mathbb {N}\). We obtain by Lemma 3 and property (1) that \((s_1,s_2)\in R_\delta ^{\max }\). On the contrary, let \((s_1,s_2)\in R_\delta ^{\max }\). Then, \((s_1,s_2)\in R_\delta ^{i}\) for each \(i\in \mathbb {N}\). We obtain by property (1) that \(f^{i}(s_1,s_2)\le \delta \) for each \(i\in \mathbb {N}\). By using Lemma 4, we have \(f^{\min }(s_1,s_2)\le \delta \).
5 Conclusion
In this paper, we have proposed an approximate simulation by using the notion of metrics to measure the behavioral closeness between a RE-TS and an LTS. The approximate simuation has some properties: First, it satisfies reflexivity, and satisfies transitivity with some limitations. Second, like exact simualtion, it has a maximal element. Then we study the relationship between trance disdance and trance inclusion, and the relationship between language distance and language inclusion. Moreover, we give the relationship between language distance and simualtion distance. Finally, we present two approaches to characterize approximate simualtion by using fixed point, and give the relationship between the two approaches.
As a future work, we will use the results of this paper to graph partten matching query, and consider logical characterizations of \(\delta \)-simulation.
References
Aceto, L., Ingólfsdóttir, A., Larsen, K.G., Srba, J.: Reactive Systems: Modelling, Specification and Verification. Cambridge University Press, Cambridge (2007)
Baier, C., Katoen, J.P.: Principles of Model Checking. MIT Press, Cambridge (2008)
Milner, R.: Communication and Concurrency. Prentice Hall, New Jersey (1989)
Milner, R.: Communicating and Mobile Systems: The \(\pi \)-Calculus. Cambridge University Press, Cambridge (1999)
Pan, H.Y., Cao, Y.Z., Zhang, M., Chen, Y.X.: Simulation for lattice-valued doubly labeled transition systems. Int. J. Approx. Reason. 55(3), 797–811 (2014). https://doi.org/10.1016/j.ijar.2013.11.009
Pan, H., Li, Y., Cao, Y.: Lattice-valued simulations for quantitative transition systems. Int. J. Approx. Reason. 56, 28–42 (2015). https://doi.org/10.1016/j.ijar.2014.10.001
Thrane, C.R., Fahrenberg, U., Larsen, K.G.: Quantitative analysis of weighted transition system. J. Log. Algebraic Program. 79(7), 689–703 (2010). https://doi.org/10.1016/j.jlap.2010.07.010
de Alfaro, L., Faella, M., Stoelinga, M.: Linear and branching system metrics. IEEE Trans. Softw. Eng. 35(2), 258–273 (2009). https://doi.org/10.1109/TSE.2008.106
Girard, A., Pappas, G.J.: Approximation metrics for discrete and continuous systems. IEEE Trans. Autom. Control 52(5), 782–798 (2007). https://doi.org/10.1109/TAC.2007.895849
Ying, M.S.: Bisimulation indexes and their applications. Theor. Comput. Sci. 275(12), 1–68 (2002). https://doi.org/10.1016/S0304-3975(01)00124-4
Desharnais, J., Gupta, V., Jagadeesan, R., Panangaden, P.: Metrics for labelled Markov processes. Theoret. Comput. Sci. 318(3), 323–354 (2004). https://doi.org/10.1016/j.tcs.2003.09.013
Desharnais, J., Laviolette, F., Tracol, M.: Approximate analysis of probabilistic processes: logic, simulation and games. In: 5th International Conference on Quantitative Evaluation of Systems, pp. 264–273. IEEE Computer Society, Saint-Malo (2008). https://doi.org/10.1109/QEST.2008.42
Cerný, P., Henzinger, T.A., Radhakrishna, A.: Simulation distances. Theoret. Comput. Sci. 413(1), 21–35 (2012). https://doi.org/10.1016/j.tcs.2011.08.002
Julius, A.A., D’Innocenzo, A., Benedetto, M.D.D., Pappas, G.J.: Approximate equivalence and synchronization of metric transition systems. Syst. Control Lett. 58(2), 94–101 (2009). https://doi.org/10.1016/j.sysconle.2008.09.001
Fan, W.F., Li, J.Z., Ma, S., Tang, N., Wu, Y.H.: Adding regular expressions to graph reachability and pattern queries. Front. Comp. Sci. 6(3), 313–338 (2012). https://doi.org/10.1007/s11704-012-1312-y
Salaün, G.: Quantifying the similarity of non-bisimilar labelled transition systems. Sci. Comput. Program. 202, 102580 (2021). https://doi.org/10.1016/j.scico.2020.102580
Bozzelli, L., Molinari, A., Montanari, A., Peron, A.: Model checking interval temporal logics with regular expressions. Inf. Comput. 272, 104498 (2020). https://doi.org/10.1016/j.ic.2019.104498
Fahrenberg, U., Legay, A., Quaas, K.: Computing branching distances with quantitative games. Theor. Comput. Sci. 847, 134–146 (2020). https://doi.org/10.1016/j.tcs.2020.10.001
Wolper, P.: Temporal logic can be more expressive. Inf. Control 56(1/2), 72–99 (1983). https://doi.org/10.1016/S0019-9958(83)80051-5
Hu, A.J., Vardi, M.Y. (eds.): CAV 1998. LNCS, vol. 1427. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0028725
Juhl, L., Larsen, K.G., Srba, J.: Modal transition systems with weight intervals. J. Log. Algebr. Program. 81(4), 408–421 (2012). https://doi.org/10.1016/j.jlap.2012.03.008
Mateescu, R., Monteriro, P.T., Dumas, E., de Jong, H.: CTRL: extension of CTL with regular expressions and fairness operators to verify genetic regulatory networks. Theoret. Comput. Sci. 412(26), 2854–2883 (2011). https://doi.org/10.1016/j.tcs.2010.05.009
Brázdil, T., Cerná, I.: Model checking of RegCTL. Comput. Artif. Intell. 25(1), 81–97 (2006)
Larsen, K.G.: Modal specifications. In: Automatic Verification Methods for Finite State Systems, pp. 232–246 (1989). https://doi.org/10.1007/3-540-52148-8_19
van Breugel, F.: On behavioural pseudometrics and closure ordinals. Inf. Process. Lett. 112(19), 715–718 (2012). https://doi.org/10.1016/j.ipl.2012.06.019
Fahrenberg, U., Legay, A.: The quantitative linear-time-branching-time spectrum. Theor. Comput. Sci. 538, 54–69 (2014). https://doi.org/10.1016/j.tcs.2013.07.030
Zhang, J.J., Zhu, Z.H.: Characterize branching distance in terms of (\(\eta \),\(\alpha \))-bisimilarity. Inf. Comput. 206(8), 953–965 (2008). https://doi.org/10.1016/j.ic.2008.06.001
Qia, S., Zhu, P.: Limited approximate bisimulations and the corresponding rough approximations. Int. J. Approx. Reason. 130, 50–82 (2021). https://doi.org/10.1016/j.ijar.2020.12.005
Hopcroft, J.E., Motwani, R., Ullman, J.D.: Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing, MA (1979)
Sangiorgi, D.: Introduction to Bisimulation and Coinduction. Cambridge University Press, Cambridge (2012)
Pan, H.Y., Cao, Y.Z., Chang, L., Qian, J.Y., Lin, Y.M.: Fuzzy alternating refinement relations under the Gödel semantics. IEEE Trans. Fuzzy Syst. 29(5), 953–964 (2021). https://doi.org/10.1109/TFUZZ.2020.2965860
Munkres, J.R.: Typology. Prentice Hall, Englewood Cliffs (1975)
Pan, H.Y., Song, F., Cao, Y.Z., Qian, J.Y.: Fuzzy pushdown termination games. IEEE Trans. Fuzzy Syst. 27(4), 760–774 (2019). https://doi.org/10.1109/TFUZZ.2018.2869127
Pan, H., Li, Y., Cao, Y., Li, P.: Nondeterministic fuzzy automata with membership values in complete residuated lattices. Int. J. Approx. Reason. 82, 22–38 (2017). https://doi.org/10.1016/j.ijar.2016.11.020
Acknowledgements
The authors would like to thank the anonymous referees for their very helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Cui, X., Li, Z., Chang, Y., Pan, H. (2022). Approximate Simulation for Transition Systems with Regular Expressions. In: Chen, Y., Zhang, S. (eds) Artificial Intelligence Logic and Applications. AILA 2022. Communications in Computer and Information Science, vol 1657. Springer, Singapore. https://doi.org/10.1007/978-981-19-7510-3_4
Download citation
DOI: https://doi.org/10.1007/978-981-19-7510-3_4
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-19-7509-7
Online ISBN: 978-981-19-7510-3
eBook Packages: Computer ScienceComputer Science (R0)





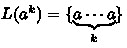 ;
;