Seismic Stability of Reinforced Soil Wall Using Horizontal Slice Method: Effect of Surcharge on Cohesive-Frictional Soils

Abstract

The reinforced soil structures were popular owing to their ability and performance under seismic situations. Despite the effective use of cohesionless soil in reinforced earth walls, cohesive soil is adopted in various locations worldwide for economic reasons. Very few studies are available for the c-ϕ soil in a pseudo-static approach. The current process evaluated vertical reinforced soil walls considering oblique pull-out force/displacement with c-ϕ backfill, under the kinematics of failure, adopting the limit equilibrium approach for sliding soil of the inextensible sheet reinforcement subjected to oblique pull-out force in the pseudo-static framework. The present study evaluates the impact of various parameters such as the geometry of the wall, surcharge, c-ϕ soil backfill, and the safety factor of the pull-out resistance of inextensible reinforcement sheets under seismic loading.

Introduction

The fundamental theories for the design of RE walls depended on rankine’s/coulomb. Further, the coulomb’s hypothesis was extended and elaborated the seismic acceleration for cohessionless soil using the pseudo-static methodology [1, 2]. The Mononobe-Okabe theory was incorporates soil having a combined effect of cohesion and friction [3]. The conventional method of slope stability was to verify slope failure is a vertical slice procedure. Shahgholi et al. [4] introduced the horizontal slice approach, and the seismic stability was elaborated [5]. Nouri et al. [6] estimated the tensile force required to maintain the stability of the reinforced wall. The geosynthetic vertical wall is analyzed, followed by pseudo-static and pseudo-dynamic solution subjected to transverse pull [7].

The cohesive-frictional soils are adopted in various locations over the universe for monetary motive, and few kinds of literatures are available in static solution. The value of cohesion and surcharge under seismic loading for the reinforced soil was analyzed using HSM [8]. Ghose and Debnath [9] examine the horizontal (H_i) and vertical (V_i) magnitude of the forces, and the reliable relation is assumed as under [10]:

$$H_i = \lambda . \, f_i . \, V_i$$

(31.1)

As indicated by [11] is an improvement over the above study, and the yield strength is a constant value of shear (H_i) is a constant fraction of the shear strength, and this coefficient for each slice is average shear stress along with each slice. This coefficient (λ_i) is always less than unity, written as

$$H_i = \left[ {V_i \tan \phi + C} \right]\lambda_i$$

(31.2)

The utilization of poor backfill (ϕ < 30°) and higher ranges of seismic coefficients (k_h > 0.20) require the higher resistive forces and reinforcement length for the stability [12]. Soil friction angle is an important parameter on the strength of inextensible sheet; with the increase of friction angle, the normalized reinforcement strength decreases with the different horizontal seismic coefficients for inclined a vertical earth structures. The influence of ϕ is bigger for greater values of K_h [13]. The use of cohesive soils with ϕ < 30° and the values of K_h > 0.2 necessitate the increase of reinforcement length and higher factor of safety to maintain the stability of soil structure [5].

The current investigation focused on vertical reinforced soil with c-ϕ backfill, the horizontal slice concept proposed by [6] adopted, and the limit equilibrium strategy utilized to the pseudo-static approach with sheet reinforcement undergoes transverse pull under kinematics of failure. In any case, no investigation is available on the impact of cohesion and surcharge. The proposed technique depends on the extension of the strategy [7] and linear backfill response due to transverse pull. On this observation, the solution is analyzed in MATLAB Program to evaluate the variation in wall geometry, angle of internal friction, cohesion, seismic coefficients, and q on backfill.

Methodology

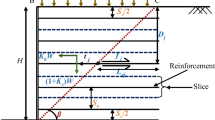
Figure 31.1 shows the wall supporting horizontal cohesive backfill of height, H, embedded with of length (L) reinforcement with unit weight (γ). The angle of internal friction (ϕ) and the interface friction between the sheet–soil (ϕ_r). The backfill is reinforced with ‘n’ no. of reinforcements and the vertical spacing in top and bottom most layers of S_v/2 and have equal spacing of S_v.

Fig. 31.1

Geometrical characteristics of RE Wall

Figure 31.2 portrays the slice of horizontal reinforcement undergoing pull-out and the moving soil oblique to the aligned reinforcement. This oblique component gives extra normal stress, which gives additional stresses and relatively more pull-out.

Fig. 31.2

Single slice with central reinforcement subjected to transverse pull

Assumption

• Vertical stress acting on a horizontal slice is assumed to be overburden pressure, V_i = q. L_a + γ. h_i (for the vertical wall). Where L_a is the active length of reinforcement.

• The method is applies to homogeneous cohesive-frictional soils.

• The F.O.S (FS_r) is assumed to be equal to individual slices.

• The Shear force between each horizontal slice is considered to be $H_i = \left( {V_i \tan \phi + C} \right)\lambda_i$

• The surcharge load acting above the wall must be q. L_a

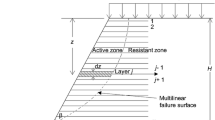
• The length of failure ith slice is b_i = $\frac{H.i}{{n.{\text{sin}} \propto }}$

Proposed Formulation

Tensile Force Due to Oblique Pull

The precise solution shows satisfying ∑F_x, ∑F_y, ∑M equilibrium equations. The vertical equilibrium of the forces are;

$$\sum F_y = 0$$

$$V_{i + 1} - V_i - \left[ {1 + K_v } \right]W_i + S_i {\text{sin}} \propto + N_i {\text{cos}} \propto = 0$$

(31.3)

where the interslice forces (V_i and V_i+1), weight (W_i), K_v is a vertical seismic coefficient, the failure angle (α). The shear force (S_i) is

$$S_i = \frac{Cb_i + N_i tan\phi }{{FS_{sr} }}$$

(31.4)

where FS_sr is unity, b_i = $\frac{H.i}{{n.{\text{sin}} \propto { }}}$ is the length of the base of the slice. Sub. For S_i from Eq. (31.4) into Eq. (31.3) and solving for normal force (N_i)

$$\overline{N}_i = \frac{{V_i - V_{i + 1} + \left( {1 + k_v } \right)W_i - \frac{C.b_i sin\alpha }{{FS_{sr} }}}}{{\frac{tan\emptyset }{{FS_{sr} }}.sin \propto + cos \propto }}$$

(31.5)

$$\sum F_x = 0$$

$$\mathop \sum \limits_{j = 1}^m \overline{t}_j = \mathop \sum \limits_{i = 1}^n \overline{N}_i \sin \propto - \mathop \sum \limits_{i = 1}^n \overline{S}_i \cos \propto + \mathop \sum \limits_{i = 1}^n \overline{W}_i K_h + \overline{H}_i - \overline{H}_{i + 1}$$

(31.6)

Sum of the tensile forces generated in the reinforcement considering mobilized transverse force determined by the Eq. (31.6), we get

$$\begin{aligned} \overline{N}_i \sin {\upalpha } & = \left[ {\frac{{\sin \propto .FS_{sr} }}{{\tan \phi .\sin \propto + FS_{sr} .\cos \propto }}} \right]\left[ {1 + K_v } \right]{\upgamma }h_i {\text{l}}_{\text{i}} - \left[ {1 + K_v } \right]{\upgamma }h_{i + 1} l_{i + 1} \\ & \quad + \left[ {1 + K_v } \right]\frac{{{\upgamma }H}}{2n}\left[ {l_i + { }l_{i + 1} } \right] - \frac{CH}{n} \\ \end{aligned}$$

$$\begin{aligned} \overline{S}_i \cos \propto & = \left[ {\frac{{\tan \emptyset .{ }\cos \propto }}{{\tan \phi .\sin \propto + FS_{sr} .\cos \propto }}} \right]\left[ {1 + K_v } \right]{\upgamma }h_i l_i - \left[ {1 + K_v } \right]{\upgamma }h_{i + 1} l_{i + 1} \\ & \quad + \left[ {1 + K_v } \right]\frac{{{\upgamma }H}}{2n}\left[ {l_i + l_{i + 1} } \right] - \frac{CH}{{n\sin \propto }}.\cot \phi .\cos \propto \\ \end{aligned}$$

$$\overline{W}_i K_h = { }\frac{{{\upgamma }H}}{n}\left[ {\frac{{l_i + l_{i + 1} }}{2}} \right]K_h$$

$$\begin{aligned} \mathop \sum \limits_{j = 1}^m \overline{T}_{Tj} & = \left[ {\frac{\tan \emptyset_r }{n}\left[ \frac{L}{H} \right] - \frac{\tan \emptyset_r }{n}\tan \left[ {90 - \propto } \right]} \right]\mathop \sum \limits_{j = 1}^m \left[ {2 + P_j^* } \right]\left[ {j - \frac{1}{2}} \right] \\ & \quad + \left[ {\frac{2 \tan \emptyset_r }{{n^2 }}\tan \left[ {90 - \propto } \right]} \right]\mathop \sum \limits_{j = 1}^m \left[ {2 + P_j^* } \right]\left[ {j - \frac{1}{2}} \right]^2 \\ \end{aligned}$$

(31.7)

$$\begin{aligned} \mathop \sum \limits_{j = 1}^m \overline{P}_j & = \left[ {\frac{1}{n}\left[ \frac{L}{H} \right] - \frac{1}{n}\tan \left[ {90 - \propto } \right]} \right]\mathop \sum \limits_{j = 1}^m P_j^* \left[ {j - \frac{1}{2}} \right] \\ & \quad + \left[ {\frac{1}{n^2 }\tan \left[ {90 - \propto } \right]} \right]\mathop \sum \limits_{j = 1}^m P_j^* \left[ {j - \frac{1}{2}} \right]^2 \\ \end{aligned}$$

(31.8)

$$P^* = \mu_j \frac{W_L }{{L_{ej} }}\frac{1}{n_e }\left[ {\frac{{W_{i + 1} }}{2} + \mathop \sum \limits_{k = 2}^n W_k } \right]$$

(31.9)

$$W_k = \frac{{T_i^* n_e^2 \left[ {W_{k - 1} + W_{k + 1} } \right]}}{{\left[ {2n_e^2 T_k^* + \frac{\mu_j }{{2\tan \emptyset_r }}} \right]}}$$

(31.10)

$$T_{k + 1}^* = \frac{1}{2n_e }\left[ {\mu_j W_k \frac{W_L }{{L_{ej} }} + 2} \right] + T_k^*$$

(31.11)

The inextensible reinforcements are divided into sub elements (n_e), the normalized displacement, and tension at node k (W_k and T_k*). Based on Eq. (31.9), the normalized transverse force (P*) for a single reinforcement assuming linear backfill response utilizing local factors µ_j and W_L/L_ej expressed as follows. The inextensible reinforcement normalized to a parameter K [dimensionless], which is equivalent to the earth pressure coefficient [8]

$$K = \frac{{\sum_{i = 1}^n \overline{{\overline{t}}}_{pj} }}{0.5\gamma H^2 }$$

(31.12)

Incorporating the local normalized displacements & relative stiffness factors and from Eqs. (31.12) and (31.13), the normalized transverse force is determined from Eq. (31.7) considering linear backfill response. The factor of safety due to transverse pull [component of oblique] from Eq. (31.15) is as follows (Table 31.1);

$$\mu_j = \mu \frac{{\left[ {{\raise0.7ex\hbox{${L_{ej} }$} \!\mathord{\left/ {\vphantom {{L_{ej} } L}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$L$}}} \right]}}{{\left[ {{\raise0.7ex\hbox{${h_j }$} \!\mathord{\left/ {\vphantom {{h_j } H}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$H$}}} \right]}}$$

(31.13)

$$\frac{w_L }{{L_{ej} }} = \frac{w_l }{L}\frac{1}{{\left[ {{\raise0.7ex\hbox{${L_{ej} }$} \!\mathord{\left/ {\vphantom {{L_{ej} } L}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$L$}}} \right]}}$$

(31.14)

$$FS_T = \frac{{\sum_{j = 1}^m \overline{T}_{Tj} }}{{\sum_{j = 1}^m \overline{t}_j }}$$

(31.15)

Table 31.1 Backfill properties of the wall

Results and Discussion

Variation in FOS (FS_T) with an Angle of Friction of Soil (Φ)

The F.O.S (FS_T) on angle of internal friction ϕ = 30°, 35°, 40°, 45° with K_h = 0, 0.2, 0.4, 0.6, 0.8, 1.0 shown in Fig. 31.3. In the present analysis, as ϕ increase from 30° to 45°, the angle of the failure plane with horizontal increases due to the reduction in soil pressure on the wall. The reinforcement strength to maintain the stability of the wall is the same as earth pressure. The factor of safety due to oblique pull-out (FS_T from 2 to 3.51) increases with an increase of ϕ for K_h = 0.

Fig. 31.3

Variation of FS_T w.r.t ϕ

Effect of Stiffness of Backfill

The transverse displacement to the soil stiffness for various seismic coefficients (K_h), shown in Fig. 31.4. For n = 5, L/H = 0.5, ϕ = 30⁰, ϕ_r/ϕ = 2/3, K_v/k_h = 0.5, W_L = 0.005, and q = 50 kN/m². Due to the backfill surcharge and cohesion, the factor of safety due to transverse displacement and increases with an increase in soil stiffness for low values of seismic coefficients. According to Motlagh et al. [12], for K_h > 0.2, provide the higher length of reinforcement and shear resistance to increase the factor of safety due to normalized displacement. FS_T increases by 116% for K_h = 0, q = 50 kN/m², c = 0 with an increase in subgrade stiffness from 50 to 10,000. The increases in FS_T is 60% for K_h = 0, q = 50 kN/m², c = 5 kN/m² for corresponding values of µ. The Cohesion of backfill increases from c = 0 to 5 kN/m² with an increase in FS_T from 1.2 to 5.0 due to surcharge conditions. Hence, the scope for increased in tension of the reinforcement with the stiffness of C-ϕ soil is more.

Fig. 31.4

Variation of backfill stiffness (µ) with F.O.S (FS_T)

Variation in FS_T with K_h

The effect of L/H ratio on safety considering transverse pull on K_h is shown in Fig. 31.5. Due to transverse pull, the F.O.S decreases with K_h increases (L/H = 0.3, 0.4, 0.5, 0.6). The rise in FS_T with an increase in length due to additional shear with transverse pull. Hence, the influence of additional transverse pull is very effective for a larger range of K_h.

Fig. 31.5

Variation in K_h w.r.t F.O.S (FS_T)

Effect of No. Of Reinforcements (N) on FS_T

Figure 31.6 elaborates on F.O.S with the transverse force (FS_T) increase in no. of layers for K_h = 0–1.0. FS_T decreases nonlinearly with the increase in k_h (= 0–1.0) and no. of reinforcement layers in the c-ϕ soil. The difference between cohesion C = 0 and 15 kN/m² increases inversely proportionately w.r.t number of reinforcement layers from 3 to 9 because of additional shear resistance increase with the transverse pull; hence reinforcement opposes the failure within FS_T. Therefore, the mobilized transverse pull is more significant for static case (K_h = 0) as compared to dynamic seismic coefficient (K_h > 0) with no. of reinforcement layers.

Fig. 31.6

Variation in K_h with F.O.S (FS_T)

Effect of K_h with Cohesion on Various Horizontal Seismic Coefficients

The effect of friction on the transverse pull, the cohesion of soil under seismic coefficient is shown in Fig. 31.7. The influence of FS_T with cohesion C on various horizontal seismic coefficients. As the value of cohesion increases (0–15 kN/m²), the required value of K (equivalent earth pressure coefficient) increases to maintain the wall’s stability. For a vertical wall with K_h > 0.2, the value of FS_T reduces when C improves from 0 to 15 kN/m². The effect of surcharge loading on the backfill is a negligible effect of the factor of safety. Hence the impact of the increase of cohesion is critical, with a decrease of ϕ.

Fig. 31.7

Variation of the angle of internal friction with the factor of safety

Conclusion

The present evaluation shows the vertical reinforced wall with cohesive-frictional soil carrying uniform surcharge made the following conclusions:

• 1. The tensile force required to maintain the stability of the reinforcement is a function of seismic coefficients. Also, the increase in cohesion (0–15 kN/m²) and internal friction decrease in FS_T due to a reduction in force in reinforcement.

• 2. The failure wedge angle in cohesive-frictional soils is linear. Due to the backfill surcharge and cohesion, the safety factor due to transverse displacement increases with an increase in soil stiffness for low values of seismic coefficients.

• 3. The no. of reinforcement layers increase with the increase in factor of safety is due to shear resistance opposing the failure.

• 4. The FOS (FS_T) increases with the L/H ratio for the normalized displacement of 0.005 for about 1.2 (L/H = 0.3) to about 2.4 (For L/H = 0.6).