Analysis on Fractal Spaces and Heat Kernels

Abstract

We give overview of heat kernel estimates on fractal spaces in connection with the notion of walk dimension.

Dedicated to Masatoshi Fukushima on the occasion of his .

1 Introduction

Since the time of Newton and Leibniz, differentiation and integration have been major concepts of mathematics. The theory of integration has come a long way from Riemann’s integration of continuous functions to measure theory, including construction of Hausdorff measures on metric spaces.

In this survey we discuss the notion of differentiation in metric spaces, especially in fractals with self-similar structures. The existing theory of the upper gradient of Heinonen and Koskela [24] and Cheeger [12] provides an analogue of Rademacher’s theorem about differentiability of Lipschitz functions. However, it imposes quite strong assumptions on the metric space in question, including the Poincaré inequality with the quadratic scaling factor. Such assumptions are typically satisfied on the limits of sequences of non-negatively curved manifolds, but never on commonly known fractal spaces.

More specifically, our goal is the notion of a Laplace-type operator on general metric measure spaces, in particular, on fractal spaces. The Laplace operator in $\mathbb {R}^{n}$ is a second order differential operator. Hence, unlike the upper gradient that is a generalization of the first order differential operator, we aim at a generalization of a second order differential operator. Our present understanding is that such operators should be carried by a larger family of metric spaces.

By a Laplace-type operator we mean the generator of a strongly local regular Dirichlet form. The theory of Dirichlet forms was developed by M. Fukushima et al., and its detailed account can be found in [15] (see also [31]). Although the original motivation of this theory was to create a universal framework for construction of Markov processes in $\mathbb {R}^{n}$, it suits perfectly for development of analysis on metric measure spaces.

Strongly local regular Dirichlet forms and associated diffusion processes have been successfully constructed on large families of fractals, in particular, on the Sierpinski gasket by Barlow and Perkins [8], Goldstein [16] and Kusuoka [28], on p.c.f. fractals by Kigami [26, 27], and on the Sierpinski carpet by Barlow and Bass [3] and Kusuoka and Zhou [29].

It has been observed that the quantitative behavior of the diffusion processes on fractals is drastically different from that in $\mathbb {R}^{n}$. In particular, the expected time needed for the diffusive particle to cover distance r is of the order $r^{\beta }$ with some $\beta >2$, whereas in $\mathbb {R}^{n}$ it is $r^{2}.$ In physics such a process is called an anomalous diffusion. The parameter $\beta$ is called the walk dimension of the diffusion. It also determines sub-Gaussian estimates of the heat kernel.

It was shown in [20] that the walk dimension $\beta$ is, in fact, an invariant of the metric space alone, and it can be characterized in terms of the family of Besov seminorms.

In this note we give an overview of some results related to the notion of the walk dimension.

2 Classical Heat Kernel

The heat kernel in $\mathbb {R}^{n}$ is the fundamental solution of the heat equation $\frac{\partial u}{\partial t}=\Delta u$:

$$\begin{aligned} p_{t}(x)=\frac{1}{\left( 4\pi t\right) ^{n/2}}\exp \left( -\frac{\left| x\right| ^{2}}{4t}\right) . \end{aligned}$$

This function is also called the Gauss-Weierstrass function. Let us briefly mention some applications of this notion.

• 1. The Cauchy problem for the heat equation with the initial condition $u|_{t=0}=f$ is solved by $u\left( t,\cdot \right) =p_{t}*f$, under certain restriction on f, for example, for $f\in C_{b}\left( \mathbb {R}^{n}\right)$ (where $C_{b}\left( X\right)$ stands for the space of bounded continuous functions on X). Since then $p_{t}*f\rightarrow f\ \$as $t\rightarrow 0+$, the smooth function $p_{t}*f$ can be regarded as a mollification of f. This idea was used by Weierstrass in his proof of the celebrated Weierstrass approximation theorem.

• 2. It is less known but the heat kernel can be used to prove some Sobolev embedding theorems (see [17, pp. 156–157]).

• 3. The function $p_{t/2}(x)$ coincides with the transition density of Brownian motion $\left\{ X_{t}\right\}$ in $\mathbb {R}^{n}$ (Fig. 1).

• 4. Approximation of the Dirichlet integral: for any $f\in W^{1,2}\left( \mathbb {R}^{n}\right)$ we have

  $$\begin{aligned} \int \limits _{\mathbb {R}^{n}}\left| \nabla f\right| ^{2}dx=\lim _{t\rightarrow 0}\frac{1}{2t}\int \limits _{\mathbb {R}^{n}}\int \limits _{\mathbb {R}^{n}}p_{t}\left( x-y\right) \left| f(x)-f(y)\right| ^{2}dxdy. \end{aligned}$$

Fig. 1

The probability that $X_{t}\in A$ is given by integration of the heat kernel $p_{t/2}\left( X_{0}-\cdot \right)$ over A

3 Examples of Fractals

Let $\left( M,d\right)$ be a locally compact separable metric space and $\mu$ be a Radon measure on M with full support. A triple $\left( M,d,\mu \right)$ will be referred to as a metric measure space. A metric measure space $\left( M,d,\mu \right)$ is called $\alpha$-regular for some $\alpha >0$ if all metric balls

$$\begin{aligned} B\left( x,r\right) :=\left\{ y\in M:d\left( x,y\right) <r\right\} \end{aligned}$$

are relatively compact and if for all $x\in M$ and $r<\mathop {\textrm{diam}}\nolimits M$ we have

$$\begin{aligned} \mu \left( B\left( x,r\right) \right) \simeq r^{\alpha }. \end{aligned}$$

(1)

The sign $\simeq$ means that the ratio of the two sides is bounded from above and below by positive constants, and $\mathop {\textrm{diam}}\nolimits M=\sup _{x,y\in M}d\left( x,y\right) .$

It follows from (1) that

$$\begin{aligned} \dim _{H}M=\alpha \ \ \ \text {and}\ \ \ \mathcal {H}_{\alpha }\simeq \mu \end{aligned}$$

where $\dim _{H}M$ denotes the Hausdorff dimension of M (with respect to the metric d) and $\mathcal {H}_{\alpha }$ denotes the Hausdorff measure of dimension $\alpha$. The number $\alpha$ is also referred to as the fractal dimension of M. In some sense, $\alpha$ is a numerical characteristic of the integral calculus on M.

The original meaning of the popular term “fractal” refers to $\alpha$-regular spaces with fractional values of $\alpha$. Such spaces first appeared in mathematics as curious examples and initially served as counterexamples to various theorems. The most famous example of a fractal set is the Cantor set that was introduced by Georg Cantor in 1883. However, Mandelbrot [32] in 1982 put forward a novel point of view according to which fractals are typical of nature rather than exceptional. This point of view is also confirmed from within pure mathematics by the spectacular development of the analysis on fractals and metric measure spaces over the past three decades, which sheds new light on some aspects of classical analysis in $\mathbb {R}^{n}$. See [1] for a very good introduction to analysis on fractals.

Fig. 2

Sierpinski gasket$,\ \ \alpha =\frac{\log 3}{\log 2}\approx 1.58$

Fig. 3

Three interations of construction of SG

Fig. 4

Sierpinski carpet, $\alpha =\frac{\log 8}{\log 3}\approx 1.89$

Fig. 5

Two iterations of construction of SC

Another example of a fractal is the Vicsek snowflake (VS) shown on Figs. 6 and 7.

Fig. 6

Vicsek snowflake

Fig. 7

Three iterations of construction of VS

There is nowadays no commonly accepted rigorous definition of the term “fractal”. Typical fractal sets are obtained by some self-similar constructions as limits of sequences of iterations. Important examples of fractal sets are the Sierpinski gasket (SG) and Sierpinski carpet (SC) that were introduced by Wacław Sierpi$\acute{\text {n}}$ski in 1915. They are shown on Figs. 2, 3 and 4, 5, respectively.

4 Dirichlet Forms

On certain metric spaces, including fractal spaces, it is possible to construct a Laplace-type operator, by means of the theory of Dirichlet forms by Fukushima [15].

A (symmetric) Dirichlet form in $L^{2}\left( M,\mu \right)$ is a pair $\left( \mathcal {E},\mathcal {F}\right)$ where $\mathcal {F}$ is a dense subspace of $L^{2}\left( M,\mu \right)$ and $\mathcal {E}$ is a symmetric bilinear form on $\mathcal {F}$ with the following properties:

• 1. It is positive definite, that is, $\mathcal {E}\left( f,f\right) \ge 0$ for all $f\in \mathcal {F}$.

• 2. It is closed, that is, $\mathcal {F}$ is complete with respect to the norm

  $$\begin{aligned} \left( \int \limits _{M}f^{2}d\mu +\mathcal {E}\left( f,f\right) \right) ^{1/2}. \end{aligned}$$

• 3. It is Markovian, that is, if $f\in \mathcal {F}$ then $\widetilde{f}:=\min (f_{+},1)\in \mathcal {F}$ and $\mathcal {E}(\widetilde{f},\widetilde{f})\le \mathcal {E}\left( f,f\right)$.

Any Dirichlet form has the generator: a positive definite self-adjoint operator $\mathcal {L}$ in $L^{2}\left( M,\mu \right)$ with domain $\mathop {\textrm{dom}}\nolimits \left( \mathcal {L}\right) \subset \mathcal {F}$ such that

$$\begin{aligned} \left( \mathcal {L}f,g\right) =\mathcal {E}\left( f,g\right) \ \ \text {for all }f\in \mathop {\textrm{dom}}\nolimits \left( \mathcal {L}\right) \text { and }g\in \mathcal {F}. \end{aligned}$$

For example, the bilinear form

$$\begin{aligned} \mathcal {E}\left( f,g\right) =\int \limits _{\mathbb {R}^{n}}\nabla f\cdot \nabla g\,dx \end{aligned}$$

(2)

in $\mathcal {F}=W^{1,2}\left( \mathbb {R}^{n}\right)$ is a Dirichlet form in $L^{2}\left( \mathbb {R}^{n},dx\right)$, whose quadratic part is the Dirichlet integral. Its generator is $\mathcal {L}=-\Delta$ with $\mathop {\textrm{dom}}\nolimits \left( \mathcal {L}\right) =W^{2,2}\left( \mathbb {R}^{n}\right) .$

Another example of a Dirichlet form in $L^{2}\left( \mathbb {R}^{n},dx\right)$:

$$\begin{aligned} \mathcal {E}(f,f)=\int \limits _{\mathbb {R}^{n}}\int \limits _{\mathbb {R}^{n}}\frac{\left( f(x)-f(y)\right) ^{2}}{\left| x-y\right| ^{n+s}}dx\,dy, \end{aligned}$$

(3)

where $s\in \left( 0,2\right)$ and $\mathcal {F}=B_{2,2}^{s/2}\left( \mathbb {R}^{n}\right) .$ It has the generator $\mathcal {L}=c_{n,s}\left( -\Delta \right) ^{s/2}$ with a positive constant $c_{n,s}.$

A Dirichlet form $\left( \mathcal {E},\mathcal {F}\right)$ is called local if $\mathcal {E}\left( f,g\right) =0$ for any two functions $f,g\in \mathcal {F}$ with disjoint compact supports, and $\left( \mathcal {E},\mathcal {F}\right)$ is called strongly local if $\mathcal {E}\left( f,g\right) =0$ whenever $f=\mathop {\textrm{const}}\nolimits$ in a neighborhood of $\mathop {\textrm{supp}}g$. The Dirichlet form $\left( \mathcal {E},\mathcal {F}\right)$ is called regular if $C_{0}\left( M\right) \cap \mathcal {F}$ is dense both in $\mathcal {F}$ and $C_{0}\left( M\right)$, where $C_{0}\left( M\right)$ is the space of continuous functions on M with compact supports endowed with the $\sup$-norm.

For example, both Dirichlet forms (2) and (3) are regular, the form (2) is strongly local, while the form (3) is nonlocal.

The generator of any regular Dirichlet form determines the heat semigroup $\left\{ e^{-t\mathcal {L}}\right\} _{t\ge 0}$, as well as a Markov process $\left\{ X_{t}\right\} _{t\ge 0}$ on M with the transition semigroup $e^{-t\mathcal {L}}$, that is,

$$\begin{aligned} \mathbb {E}_{x}f\left( X_{t}\right) =e^{-t\mathcal {L}}f(x)\ \ \ \ \text {for all }f\in C_{0}\left( M\right) . \end{aligned}$$

If $\left( \mathcal {E},\mathcal {F}\right)$ is local then $\left\{ X_{t}\right\}$ is a diffusion while otherwise the process $\left\{ X_{t}\right\}$ contains jumps.

For example, the Dirichlet form (2) determines Brownian motion in $\mathbb {R}^{n},$ whose transition density is exactly the Gauss-Weierstrass function

$$\begin{aligned} p_{t}(x)=\frac{1}{\left( 4\pi t\right) ^{n/2}}\exp \left( -\frac{\left| x\right| ^{2}}{4t}\right) . \end{aligned}$$

The Dirichlet form (3) determines a jump process: a symmetric stable Levy process of the index s. In the case $s=1$ its transition density is the Cauchy distribution

$$\begin{aligned} p_{t}(x)=\frac{c_{n}t}{\left( t^{2}+\left| x\right| ^{2}\right) ^{\frac{n+1}{2}}}=\frac{c_{n}}{t^{n}}\left( 1+\frac{\left| x\right| ^{2}}{t^{2}}\right) ^{-\frac{n+1}{2}}, \end{aligned}$$

where $c_{n}=\Gamma \left( \frac{n+1}{2}\right) /\pi ^{(n+1)/2}.$ For an arbitrary $s\in \left( 0,2\right)$ we have

$$\begin{aligned} p_{t}(x)\simeq \frac{1}{t^{n/s}}\left( 1+\frac{\left| x\right| }{t^{1/s}}\right) ^{-\left( n+s\right) }. \end{aligned}$$

If a metric measure space M possesses a strongly local regular Dirichlet form $\left( \mathcal {E},\mathcal {F}\right)$ then we consider its generator $\mathcal {L}$ as an analogue of the Laplace operator. In this case the differential calculus is defined on M.

Nontrivial strongly local regular Dirichlet forms have been successfully constructed on large families of fractals, in particular, on SG by Barlow and Perkins [8], Goldstein [16] and Kusuoka [28], on SC by Barlow and Bass [3] and Kusuoka and Zhou [29], on nested fractals (including VS) by Lindstrøm [30], and on p.c.f. fractals by Kigami [26, 27].

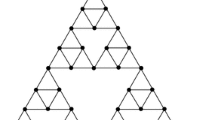
In fact, each of these fractals can be regarded as a limit of a sequence of approximating graphs $\Gamma _{n}$ (Fig. 8).

Fig. 8

Approximating graphs $\Gamma _{1},\Gamma _{2},\Gamma _{3}\$for SG

Define on each $\Gamma _{n}$ a Dirichlet form $\mathcal {E}_{n}$ by

$$\begin{aligned} \mathcal {E}_{n}\left( f,f\right) =\sum _{x\sim y}\left( f(x)-f(y)\right) ^{2} \end{aligned}$$

where $x\sim y$ means that the vertices x and y are neighbors, and then consider a scaled limit

$$\begin{aligned} \mathcal {E}\left( f,f\right) =\lim _{n\rightarrow \infty }R_{n}\mathcal {E}_{n}\left( f,f\right) \end{aligned}$$

(4)

with an appropriately chosen renormalizing sequence $\left\{ R_{n}\right\} .$ The main difficulty is to ensure the existence of $\left\{ R_{n}\right\}$ such that this limit exists and is nontrivial for a dense family of f. For p.c.f. fractals one chooses $R_{n}=\rho ^{n}$ where, for example, $\rho =\frac{5}{3}$ for SG and $\rho =3$ for VS, and the limit exists due to monotonicity [27].

For SC the situation is much harder. Initially a strongly local Dirichlet form on SC was constructed by Barlow and Bass [3] in a different way by using a probabilistic approach. After a groundbreaking work of Barlow et al. [6] proving the uniqueness of a canonical Dirichlet form on SC, it became possible to claim that the limit (4) exists for a certain sequence $\left\{ R_{n}\right\}$ such that $R_{n}\simeq \rho ^{n}$, where the exact value of $\rho$ is still unknown. Numerical computation in [7] indicates that $\rho \approx 1.25.$ It is also an open question whether the limit $\lim _{n\rightarrow \infty }\rho ^{-n}R_{n}\$exists (see [4, Sect. 5, Problem 1]). Other ways of constructing a strongly local Dirichlet form on SC can be found in [29] and [23].

5 Walk Dimension

In all the above examples, the heat semigroup $e^{-t\mathcal {L}}$ of the Dirichlet form $\left( \mathcal {E},\mathcal {F}\right)$ is an integral operator:

$$\begin{aligned} e^{-t\mathcal {L}}f(x)=\int \limits _{M}p_{t}\left( x,y\right) f(y)d\mu (y), \end{aligned}$$

whose integral kernel $p_{t}\left( x,y\right)$ is called the heat kernel of $\left( \mathcal {E},\mathcal {F}\right)$ or of $\mathcal {L}$. Moreover, in all the above examples of strongly local Dirichlet forms the heat kernel satisfies the following estimates

$$\begin{aligned} p_{t}\left( x,y\right) \asymp \frac{C}{t^{\alpha /\beta }}\exp \left( -c\left( \frac{d^{\beta }(x,y)}{t}\right) ^{\frac{1}{\beta -1}}\right) , \end{aligned}$$

(5)

for all $x,y\in M$ and $t\in \left( 0,t_{0}\right)$ for some $t_{0}>0$ [5, 8]. The sign $\asymp$ means that the both inequalities $\le$ and $\ge$ take place but possibly with different values of the positive constants c, C.

Here $\alpha$ is necessarily the Hausdorff dimension, while $\beta$ is a new parameter that is called the walk dimension of the heat kernel (or that of the Dirichlet form). It can be regarded as a numerical characteristic of the differential calculus on M.

We say that a metric space $\left( M,d\right)$ satisfies the chain condition $\left( CC\right)$ if there exists a constant C such that for all $x,y\in M$ and for all $n\in \mathbb {N}$ there exists a sequence $\left\{ x_{k}\right\} _{k=0}^{n}$ of points in M such that $x_{0}=x$, $x_{n}=y$, and

$$\begin{aligned} d(x_{k-1},x_{k})\le C\frac{d(x,y)}{n},\quad \text {for all }k=1,\ldots ,n. \end{aligned}$$

For example, if the metric d is geodesic then this condition is satisfied with $C=1.$

Assume that (5) holds with $t_{0}=\infty .$ By Ref. [33], (5) implies $\left( CC\right)$, while by Ref. [20], $\left( CC\right)$ together with (5) yields

$$\begin{aligned} \alpha \ge 1\ \ \text {and}\ 2\le \beta \le \alpha +1. \end{aligned}$$

(6)

Conversely, it was shown by Barlow [2], that any pair $\left( \alpha ,\beta \right)$ satisfying (6) can be realized in the estimate (5) on a geodesic metric space.

Hence, we obtain a large family of metric measure spaces, each of them being characterized by a pair $\left( \alpha ,\beta \right)$ where $\alpha$ is responsible for integration while $\beta$ is responsible for differentiation. The Euclidean space $\mathbb {R}^{n}$ belongs to this family with $\alpha =n$ and $\beta =2$. In the case $\beta =2$ the estimate (5) is called Gaussian, while in the case $\beta >2$—sub-Gaussian.

On fractals the value of $\beta$ is determined by the scaling parameter $\rho$. It is known that:

• on SG: $\beta =\frac{\log 5}{\log 2}\approx 2.32$

• on VS: $\beta =\frac{\log 15}{\log 3}\approx 2.46\ \ \$

• on SC: $\beta =\frac{\log \left( 8\rho \right) }{\log 3}$ where the exact value of $\rho$ is unknown; the approximation $\rho \approx 1.25$ indicates that $\beta \approx 2.10.$

The walk dimension $\beta$ has the following probabilistic meaning. Denote by $\tau _{\Omega }$ the first exit time of $X_{t}$ from an open set $\Omega \subset M$, that is,

$$\begin{aligned} \tau _{\Omega }=\inf \left\{ t>0:X_{t}\notin \Omega \right\} \end{aligned}$$

(Fig. 9). Then in the above setting, for any ball $B\left( x,r\right)$ with $r<\mathop {\textrm{const}}\nolimits t_{0}^{1/\beta }$ we have

$$\begin{aligned} \mathbb {E}_{x}\tau _{B\left( x,r\right) }\simeq r^{\beta }. \end{aligned}$$

Fig. 9

Exit from a ball $B\left( x,r\right)$

6 Besov Spaces and Characterization of $\beta$

Given an $\alpha$-regular metric measure space $\left( M,d,\mu \right) ,$ it is possible to define a family $B_{p,q}^{\sigma }$ of Besov spaces (see [18]). However, here we need only the following special cases: for any $\sigma >0$ the space $B_{2,2}^{\sigma }$ consists of functions such that

$$\begin{aligned} \left\| f\right\| _{B_{2,2}^{\sigma }}^{2}:=\left\| f\right\| _{2}^{2}+\underset{M\times M}{\mathop {\int \int }}\frac{\left| f(x)-f(y)\right| ^{2}}{d\left( x,y\right) ^{\alpha +2\sigma }}d\mu (x)d\mu (y)<\infty \end{aligned}$$

and $B_{2,\infty }^{\sigma }$ consists of functions such that

$$\begin{aligned} \left\| f\right\| _{B_{2,\infty }^{\sigma }}^{2}:=\left\| f\right\| _{2}^{2}+\sup _{0<r<1}\frac{1}{r^{\alpha +2\sigma }}\underset{\left\{ d(x,y)<r\right\} }{\mathop {\int \int }}\left| f(x)-f(y)\right| ^{2}d\mu (x)d\mu (y)<\infty . \end{aligned}$$

It is easy to see that $B_{2,2}^{\sigma }$ shrinks as $\sigma$ increases and that in the case $\sigma <1$ the space $B_{2,2}^{\sigma }$ contains the space $Lip_{0}$ of compactly supported Lipschitz functions. In $\mathbb {R}^{n}$ the space $B_{2,2}^{\sigma }$ becomes $\left\{ 0\right\}$ if $\sigma >1$, so that for $\sigma >1$ the definition of the Besov spaces in $\mathbb {R}^{n}$ changes. However, in our setting we are interested in the borderline value of $\sigma$ at which the space $B_{2,2}^{\sigma }$ degenerates. Hence, define the critical value of the parameter $\sigma$ by

$$\begin{aligned} \sigma _{crit}:=\sup \left\{ \sigma >0:B_{2,2}^{\sigma }\text { is dense in }L^{2}\right\} . \end{aligned}$$

(7)

In the next theorem, $\left( M,d,\mu \right)$ is a metric measure space with relatively compact balls.

Theorem 1

[20] Let $\left( \mathcal {E},\mathcal {F}\right)$ be a Dirichlet form on $L^{2}\left( M,\mu \right)$ such that its heat kernel exists and satisfies for some $\alpha >0$, $\beta >1$ the sub-Gaussian estimate

$$\begin{aligned} p_{t}\left( x,y\right) \asymp \frac{C}{t^{\alpha /\beta }}\exp \left( -c\left( \frac{d^{\beta }(x,y)}{t}\right) ^{\frac{1}{\beta -1}}\right) \end{aligned}$$

(8)

for all $t>0$ and $\mu$-almost all $x,y\in M$. Then the following is true:

• 1. the space $\left( M,d,\mu \right)$ is $\alpha$-regular, $\alpha =\dim _{H}M$ and $\mu \simeq \mathcal {H}_{\alpha }$;

• 2. $\sigma _{crit}=\beta /2$ (consequently, $\beta \ge 2$);

• 3. $\mathcal {F}=B_{2,\infty }^{\beta /2}\ \$and $\mathcal {E}\left( f,f\right) \simeq \left\| f\right\| _{\overset{.}{B}_{2,\infty }^{\beta /2}}^{2}.$

Partial results in this direction were previously obtained by Jonsson [25] and Pietruska-Paluba [34].

Corollary 2

Both $\alpha$ and $\beta$ in (8) are invariants of the metric structure $\left( M,d\right)$ alone.

Note that the value $\sigma _{crit}$ is defined by (7) for any $\alpha$-regular metric space. In the view of Theorem 1 it makes sense to redefine the notion of the walk dimension simply as $2\sigma _{crit}.$ In this way, the walk dimension becomes a second important invariant of any regular metric space, after the Hausdorff dimension.

An open question Let $\left( M,d,\mu \right)$ be an $\alpha$-regular metric measure space (even self-similar). Assume that $\sigma _{crit}<\infty$ and set $\beta =2\sigma _{crit}.$ When and how can one construct a strongly local Dirichlet form on $L^{2}\left( M,\mu \right)$ with the heat kernel satisfying (8)?

The result of [11] hints that such a Dirichlet form is not always possible.

7 Dichotomy of Self-similar Heat Kernels

Let $\left( M,d\right)$ be a metric space where all metric balls are relatively compact, and let $\mu$ be a Radon measure on M with full support. A Dirichlet form $\left( \mathcal {E},\mathcal {F}\right)$ on $L^{2}\left( M,\mu \right)$ is called conservative if its heat semigroup satisfies $e^{-t\mathcal {L}}1\equiv 1.$

Theorem 3

[22] Assume that $\left( M,d\right)$ satisfies in addition the chain condition $\left( CC\right)$ (see Sect. 5). Let $\left( \mathcal {E},\mathcal {F}\right)$ be a regular conservative Dirichlet form on $L^{2}\left( M,\mu \right)$ and assume that the heat kernel of $\left( \mathcal {E},\mathcal {F}\right)$ satisfies for all $t>0$ and $x,y\in M$ the estimate

$$\begin{aligned} p_{t}\left( x,y\right) \asymp \frac{C}{t^{\alpha /\beta }}\Phi \left( c\frac{d\left( x,y\right) }{t^{1/\beta }}\right) , \end{aligned}$$

where $\alpha ,\beta >0$ and $\Phi$ is a positive monotone decreasing function on $[0,\infty ).$ Then $\left( M,d,\mu \right)$ is $\alpha$-regular, $\beta \le \alpha +1,$ and the following dichotomy holds:

$\bullet$ either the Dirichlet form $\mathcal {E}$ is strongly local, $\beta \ge 2$, and

$$\begin{aligned} \Phi \left( s\right) \asymp C\exp \left( -cs^{\frac{\beta }{\beta -1}}\right) , \end{aligned}$$

$\bullet$ or the Dirichlet form $\mathcal {E}$ is non-local and

$$\begin{aligned} \Phi \left( s\right) \simeq \left( 1+s\right) ^{-\left( \alpha +\beta \right) }. \end{aligned}$$

That is, in the first case $p_{t}\left( x,y\right)$ satisfies the sub-Gaussian estimate

$$\begin{aligned} p_{t}\left( x,y\right) \asymp \frac{C}{t^{\alpha /\beta }}\exp \left( -c\left( \frac{d^{\beta }(x,y)}{t}\right) ^{\frac{1}{\beta -1}}\right) \end{aligned}$$

(9)

while in the second case we obtain a stable-like estimate

$$\begin{aligned} p_{t}\left( x,y\right) \simeq \frac{1}{t^{\alpha /\beta }}\left( 1+\frac{d\left( x,y\right) }{t^{1/\beta }}\right) ^{-\left( \alpha +\beta \right) }\simeq \min \left( \frac{1}{t^{\alpha /\beta }},\frac{t}{d\left( x,y\right) ^{\alpha +\beta }}\right) . \end{aligned}$$

(10)

8 Estimating Heat Kernels: Strongly Local Case

Let $\left( M,d,\mu \right)$ be an $\alpha$-regular metric measure space. Let $\left( \mathcal {E},\mathcal {F}\right)$ be a strongly local regular Dirichlet form on $L^{2}\left( M,\mu \right)$. For any Borel set $E\subset M$ and any $f\in \mathcal {F}$ denote

$$\begin{aligned} \mathcal {E}_{E}\left( f,f\right) =\int \limits _{E}d\nu _{\left\langle f\right\rangle }, \end{aligned}$$

where $\nu _{\left\langle f\right\rangle }$ is the energy measure of f (see [15, p. 123]). For example, in $\mathbb {R}^{n}$ with the classical Dirichlet form (2) we have $d\nu _{\left\langle f\right\rangle }=\left| \nabla f\right| ^{2}dx.$

Definition

We say that $\left( \mathcal {E},\mathcal {F}\right)$ satisfies the Poincaré inequality with exponent $\beta$ if, for any ball $B=B\left( x,r\right)$ on M and for any function $f\in \mathcal {F},$

$$\begin{aligned} \mathcal {E}_{B}\left( f,f\right) \ge \frac{c}{r^{\beta }}\int \limits _{\varepsilon B}\left( f-\overline{f}\right) ^{2}d\mu , \qquad \qquad \qquad \qquad \quad \quad \quad \quad \quad \quad \quad \quad \quad (PI) \end{aligned}$$

where $\varepsilon B=B\left( x,\varepsilon r\right)$, $\overline{f}=\frac{1}{\mu \left( \varepsilon B\right) }\int \nolimits _{\varepsilon B}fd\mu$, and $c,\varepsilon$ are small positive constants independent of B and f. For example, in $\mathbb {R}^{n}$ (PI) holds with $\beta =2$ and $\varepsilon =1$.

Let $A\Subset B$ be two open subsets of M. Define the capacity of the capacitor $\left( A,B\right)$ as follows:

$$\begin{aligned} \mathop {\textrm{cap}}\nolimits (A,B):=\inf \left\{ \mathcal {E}\left( \varphi ,\varphi \right) :\varphi \in \mathcal {F},\ \varphi |_{\overline{A}}=1,\ \mathop {\textrm{supp}}\varphi \Subset B\ \right\} . \end{aligned}$$

Here $E\Subset B$ means that the closure $\overline{E}$ of E is a compact set and $\overline{E}\subset B.$

Definition

We say that $\left( \mathcal {E},\mathcal {F}\right)$ satisfies the capacity condition if, for any two concentric balls $B_{0}:=B(x,R)$ and $B:=B(x,R+r),$

$$\begin{aligned} \mathop {\textrm{cap}}\nolimits (B_{0},B)\le C\frac{\mu \left( B\right) }{r^{\beta }}. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \quad \quad \text {(cap)} \end{aligned}$$

For any function $u\in L^{\infty }\cap \mathcal {F}$ and a real number $\kappa \ge 1$ define the generalized capacity $\mathop {\textrm{cap}}\nolimits _{u}^{\left( \kappa \right) }(A,B)$ by

$$\begin{aligned} \mathop {\textrm{cap}}\nolimits _{u}^{\left( \kappa \right) }(A,B)=\inf \left\{ \mathcal {E}\left( u^{2}\varphi ,\varphi \right) :\varphi \in \mathcal {F},\ 0\le \varphi \le \kappa ,\ \ \varphi |_{\overline{A}}\ge 1,\ \varphi =0\text { in }B^{c}\right\} . \end{aligned}$$

If $u\equiv 1$ then $\mathop {\textrm{cap}}\nolimits _{u}^{\left( \kappa \right) }(A,B)=\mathop {\textrm{cap}}\nolimits (A,B)$.

Definition

We say that the generalized capacity condition $\left( \textrm{Gcap}\right)$ holds if there exist $\kappa \ge 1$ and $C>0$ such that, for any $u\in \mathcal {F}$ $\mathbf {\cap }L^{\infty }$ and for any two concentric balls $B_{0}:=B(x,R)$ and $B:=B(x,R+r),$

$$\begin{aligned} \mathop {\textrm{cap}}\nolimits _{u}^{\left( \kappa \right) }(B_{0},B)\le \frac{C}{r^{\beta }}\int \limits _{B}u^{2}d\mu . \qquad \qquad \qquad \qquad \qquad \quad \quad \quad \quad \quad \quad \quad \quad {(\text {Gcap})} \end{aligned}$$

Theorem 4

[21] The following equivalence takes place

$$\begin{aligned} \left( CC\right) +\left( PI\right) +(\textrm{Gcap})\Leftrightarrow (9). \end{aligned}$$

(11)

In fact, this result was proved in [21] in a slightly weaker form: assuming the chain condition $\left( CC\right)$, we have the equivalence

$$\begin{aligned} \left( PI\right) +(\textrm{Gcap})\Leftrightarrow (9). \end{aligned}$$

It was later proved by Murugan [33] that

$$\begin{aligned} (9) \Rightarrow \left( CC\right) , \end{aligned}$$

whence (11) follows. Besides, the condition $(\textrm{Gcap})$ was formulated in [21] in a different, more complicated form. The present form of $(\textrm{Gcap})$ was introduced in [19].

The main open question in this field is whether the following conjecture is true.

Conjecture $\left( CC\right) +\left( PI\right) +(\mathop {\textrm{cap}}\nolimits )\Leftrightarrow (9).$

The implication $\Leftarrow \$clearly is true by Theorem 4, so the main difficulty is in the implication $\Rightarrow .$

9 Estimating Heat Kernels: Jump Case

Let $\left( M,d,\mu \right)$ be an $\alpha$-regular metric measure space. Let now $\left( \mathcal {E},\mathcal {F}\right)$ be a regular Dirichlet form of jump type on $L^{2}\left( M,\mu \right)$, that is,

$$\begin{aligned} \mathcal {E}\left( f,f\right) =\iint \limits _{M\times M}\left( f(x)-f(y)\right) ^{2}J(x,y)d\mu (x)d\mu (y) \end{aligned}$$

for all $f\in \mathcal {F}\cap C_{0}\left( M\right) .$ Here $J\left( x,y\right)$ is a symmetric non-negative function in $M\times M$ that is called the jump kernel of $\left( \mathcal {E},\mathcal {F}\right)$.

We use the following condition instead of the Poincaré inequality:

$$\begin{aligned} J(x,y)\simeq d\left( x,y\right) ^{-\left( \alpha +\beta \right) }. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \quad \quad \quad (J) \end{aligned}$$

Theorem 5

[14] and [19]

$$\begin{aligned} \left( J\right) +(\textrm{Gcap})\Leftrightarrow (10). \end{aligned}$$

In the case $\beta <2$ it is easy to show that (J)$\Rightarrow \left( \textrm{Gcap}\right)$ so that in this case we obtain the equivalence

$$\begin{aligned} \left( J\right) \Leftrightarrow (10). \end{aligned}$$

The latter was also shown by Chen and Kumagai [13], although under some additional assumptions about the metric structure of $\left( M,d\right)$.

Conjecture $\left( J\right) +\left( \mathop {\textrm{cap}}\nolimits \right) \Leftrightarrow (10).$

10 Ultra-metric Spaces

Let $\left( M,d\right)$ be a metric space. The metric d is called an ultra-metric and $\left( M,d\right)$ is called an ultra-metric space if, for all $x,y,z\in M,$

$$\begin{aligned} d(x,y)\le \max \{d(x,z),d(z,y)\}. \end{aligned}$$

(12)

A famous example of an ultra-metric space is the field $\mathbb {Q}_{p}$ of p-adic numbers endowed with the p-adic distance (here p is a prime). Also $\mathbb {Q}_{p}^{n}$ is an ultra-metric space with an appropriate choice of a metric. Denoting by $\mu$ the Haar measure on $\mathbb {Q}_{p}^{n}$, we have $\mu \left( B\left( x,r\right) \right) \simeq r^{n}$ so that $\mathbb {Q}_{p}^{n}$ is n-regular.

Ultra-metric spaces are totally disconnected and, hence, cannot carry non-trivial strongly local regular Dirichlet forms. However, it is easy to build jump type forms. Let $\left( M,d\right)$ be an ultra-metric space where all balls are relatively compact, and let $\mu$ be a Radon measure on M with full support. Let us fix a cumulative probability distribution function $\phi \left( r\right)$ on $(0,\infty )$ that is strictly monotone increasing and continuous, and consider on $M\times M$ the function

$$\begin{aligned} J(x,y)=\int \limits _{d(x,y)}^{\infty }\frac{d\log \phi (r)}{\mu \left( B_{r}(x)\right) }, \end{aligned}$$

(13)

where the integration is done over the interval $[d\left( x,y\right) ,\infty )$ against the Lebesgue-Stieltjes measure associated with the function $r\mapsto \log \phi \left( r\right)$.

Theorem 6

[10] The jump kernel (13) determines a regular Dirichlet form $\left( \mathcal {E},\mathcal {F}\right)$ in $L^{2}\left( M,\mu \right)$, and its heat kernel is

$$\begin{aligned} p_{t}(x,y)=\int \limits _{d(x,y)}^{\infty }\frac{d\phi ^{t}(r)}{\mu \left( B_{r}(x)\right) }. \end{aligned}$$

(14)

See also [9] for further heat kernel bounds on ultra-metric spaces.

For example, take $M=\mathbb {Q}_{p}^{n}$ and

$$\begin{aligned} \phi (r)=\exp \left( -\left( \frac{p}{r}\right) ^{\beta }\right) , \end{aligned}$$

(15)

where $\beta >0$ is arbitrary. Then one obtains from (13) by an explicit computation that

$$\begin{aligned} J(x,y)=c_{p,n,\beta }\,d(x,y)^{-\left( n+\beta \right) } \end{aligned}$$

(16)

and

$$\begin{aligned} p_{t}(x,y)\simeq \frac{1}{t^{n/\beta }}\left( 1+\frac{d(x,y)}{t^{1/\beta }}\right) ^{-\left( n+\beta \right) }. \end{aligned}$$

It follows that, for any $\beta >0$, the space $B_{2,2}^{\beta /2}$ coincides with the domain of the Dirichlet form with the jump kernel (16) and, hence, is dense in $L^{2}.$ Consequently, we obtain by (7) $\sigma _{crit}=\infty$ so that $\mathbb {Q}_{p}^{n}$ has the walk dimension $\infty$.

On Fig. 10 we represent graphically a classification of regular metric spaces according to the walk dimension $\beta =2\sigma _{crit}$. Clearly, the Euclidean spaces $\mathbb {R}^{n}$ and p-adic spaces $\mathbb {Q}_{p}^{n}$ form the boundaries of this scale, and the entire interior is filled with fractal spaces.

Fig. 10

Classification of regular metric spaces by the walk dimension $\beta =2\sigma _{crit}$