Two-Sided Heat Kernel Estimates for Symmetric Diffusion Processes with Jumps: Recent Results

Abstract

This article gives an overview of some recent progress in the study of sharp two-sided estimates for the transition density of a large class of Markov processes having both diffusive and jumping components in metric measure spaces. We summarize some of the main results obtained recently in [11, 18] and provide several examples. We also discuss new ideas of the proof for the off-diagonal upper bounds of transition densities which are based on a generalized Davies’ method developed in [10].

1 Introduction

Transition density function p(t, x, y) of a Markov process X, if exists, satisfies the Kolmogorov backward equation, which is a parabolic equation involving the infinitesimal generator $\mathcal {L}$ of X. Thus p(t, x, y) is also called a heat kernel of $\mathcal {L}$ or a fundamental solution of $\partial _t u=\mathcal {L}u$. Analysis of heat kernels is an important research topic both in analysis and in probability theory. Most of the studies on sharp two-sided estimates of the heat kernel concentrate on cases when X is a diffusion or a pure jump Markov process; that is, when the infinitesimal generator $\mathcal {L}$ is local or purely non-local. However, there are classes of Markov processes that can have both diffusive and jumping components. Discontinuous Lévy processes having Gaussian parts are such typical examples.

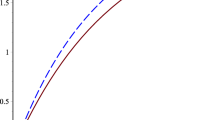
Markov processes having both diffusive (continuous) and jumping components have interesting features. Such processes run on two different scales: on the small scale one expects the continuous component to be dominant, while on the large scale the jumping component of the process should be the dominant one. In fact, there are even ranges of times and sizes of distances where both components appear together (in a short-time and short-distance region). See Figs. 1 and 2. Therefore, both components play essential roles. These are also the source of challenges in the study of such processes.

The literature on the potential theory of Markov processes having both continuous and jumping components is scarce. Elliptic Harnack inequalities for some of these processes are studied in [20, 25, 26]. Two-sided heat kernel estimates for a family of Lévy processes having Gaussian components with variable drifts are derived in [8]. The first work that establishes sharp two-sided bounds for a large class of symmetric diffusions with jumps is [15]. More precisely, consider the following regular Dirichlet form $(\mathcal {E}, \mathcal {F})$ on $L^2(\mathbb {R}^d; dx)$ given by

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \mathcal {E}(u,v)=\frac{1}{2} \int \limits _{\mathbb {R}^d} \nabla u(x)\cdot A(x) \nabla v(x)\,dx\\ \quad \quad \qquad \qquad +\displaystyle \int \limits _{\mathbb {R}^d\times \mathbb {R}^d \setminus \textrm{diag}}\!\!\!\,\,\, (u(x)-u(y))(v(x)-v(y))J(x,y)\,dx\,dy , \\ \qquad \mathcal {F}\, = \, \overline{C^1_c (\mathbb {R}^d)}^{\mathcal {E}_1}, \end{array}\right. } \end{aligned}$$

(1)

where $C^1_c (\mathbb {R}^d)$ is the space of $C^1$-functions on ${\mathbb {R}}^d$ with compact support and $\mathcal {E}_1(u,u):=\mathcal {E}(u,u)+\int \nolimits _{{\mathbb {R}}^d}|u(x)|^2dx$. Here $A(x)=(a_{ij}(x))_{1\le i, j\le d}$ is a measurable symmetric $d\times d$ matrix-valued function on $\mathbb {R}^d$ that is uniform elliptic and bounded in the sense that there exists a constant $c\ge 1$ such that

$$\begin{aligned} c^{-1}\sum \limits _{i=1}^d\xi _i^2 \le \sum \limits _{i,j=1}^d a_{ij}(x)\xi _i\xi _j\le c\sum \limits _{i=1}^d\xi _i^2 \quad \text {for every}\, x \,\text {and}\, \xi = (\xi _1,\ldots ,\xi _d)\in \mathbb {R}^d, \end{aligned}$$

and J(x, y) is a symmetric non-negative measurable kernel on $\mathbb {R}^d\times \mathbb {R}^d \setminus \text {diag}$ that satisfies condition

$$ \frac{1}{c_1|x- y|^d \phi _j (|x-y|)}\le J(x, y) \le \frac{c_1}{|x- y|^d \phi _j (|x-y|)} $$

for all $x,y\in \mathbb {R}^d\times \mathbb {R}^d \setminus \textrm{diag}$, where $\phi _j$ is a strictly increasing function on $(0, \infty )$ satisfying

$$\begin{aligned} c_2^{-1}\Big (\frac{R}{r}\Big )^{\alpha _*} \le \frac{\phi _j (R)}{\phi _j (r)} \ \le c_2\Big (\frac{R}{r}\Big )^{\alpha ^*} \quad \text {for all}\, 0<r \le R \end{aligned}$$

(2)

with $0<\alpha _*\le \alpha ^*<2$ and $c_1, c_2 \ge 1$. Here and in what follows, $\textrm{diag}$ is the diagonal of a given state space $\mathcal {X}$; that is, $\textrm{diag}:=\{(x, x): x\in \mathcal {X}\}$. It is shown in [15] that the symmetric strong Markov process X associated with the regular Dirichlet form $(\mathcal {E}, \mathcal {F})$ on $L^2({\mathbb {R}}^d; dx)$ is conservative and has a jointly Hölder continuous transition density function p(t, x, y) that enjoys

$$\begin{aligned} \begin{aligned}&c_1\, \left( t^{-d/2}\wedge \phi _j^{-1}(t)^{-d} \right) \wedge \left( p^{(c)}(t, c_2|x- y|)+p^{(j)}(t, |x- y|) \right) \le p(t, x, y)\\&\quad \le c_3\, \left( t^{-d/2}\wedge \phi _j^{-1}(t)^{-d} \right) \wedge \left( p^{(c)}(t, c_4 |x- y|)+p^{(j)}(t, |x- y|) \right) , \end{aligned} \end{aligned}$$

(3)

for every $t>0$ and $x, y\in \mathbb {R}^d$. Here

$$\begin{aligned} p^{(c)}(t, r):= t^{-d/2} \exp (-r^2/t) \quad \text {and} \quad p^{(j)}(t, r):= (\phi _j^{-1}(t))^{-d} \wedge \frac{t}{r^d \phi _j (r)}. \end{aligned}$$

Note that there are two scaling functions involved in the transition density function p(t, x, y) of diffusions with jumps on ${\mathbb {R}}^d$; namely the diffusive scaling function $\phi _c(r):=r^2$ and the scaling function $\phi _j$ for the pure jump part of the process. In the special case when X is the independent sum of a Brownian motion B and an isotropic stable process $\alpha$-stable process Z, the transition density function $p(t, x, y)=p(t, x-y)$ for the Lévy process X is the convolution of those of B and Z from which the estimates on p(t, x, y) can be derived. Indeed, in this case estimates on p(t, x) have been derived in [27] by computing the convolution; however the upper and lower bounds obtained there do not match for the case of $|x|^2<t<|x|^\alpha \le 1$.

The study of heat kernel for symmetric diffusion with jumps has been conducted further in two directions. One is to establish analytic characterizations of heat kernels of the form (3) for symmetric diffusions with jumps on general metric measure doubling spaces that are stable under bounded perturbation; see the last paragraph of Sect. 2.1 for its precise meaning. This has been carried out in [18]. In addition, stability results for upper bound heat kernel estimates and parabolic Harnack inequalities are also established in [18]. The other direction is to obtain sufficient conditions on the jumping kernels J(x, y) under which sharp two-sided heat kernel estimates for symmetric diffusions with jumps can be obtained, and to investigate how the shape of the jumps influence the behavior of the heat kernels. Our recent work [11] is in this direction, in which the ideas and techniques from [16,17,18] have played an essential role.

The purpose of this paper is to survey recent results on sharp two-sided heat kernel estimates for symmetric diffusions with jumps obtained in [11, 18]. In this paper, we focus on symmetric diffusions with jumps on inner uniform domains of complete measure metric spaces. We mention that recently in [9], heat kernel estimates are established for quite general non-symmetric time-dependent diffusions with jumps in ${\mathbb {R}}^d$. Estimates for Dirichlet heat kernels of the Lévy processes that are the independent sum of a Brownian motion and an isotropic stable process have been obtained in [12, 13]. Dirichlet heat kernel estimates for more general subordinate Brownian motions with Gaussian components can be found in [2, 14].

The rest of the article is organized as follows. In Sect. 2, we present the stability result for heat kernel estimates (3) from [18]. In Sect. 3, we present the main results from [11], where the jumping kernel can have exponential decays at infinity. In both papers [11, 18], the state spaces satisfy the volume doubling condition but the volumes of balls with same radius may not be comparable. Two different arguments are used in [11, 18] for upper bound estimates of the heat kernels. In Sect. 3.4, we give a brief explanation of the argument used in [11] for off-diagonal heat kernel upper bound estimates.

Notations. We write $f(s, x)\simeq g(s, x)$, if there exist constants $c_{1},c_{2}>0$ such that $c_{1}g(s, x)\le f(s, x)\le c_{2}g(s, x)$ for the specified range of the argument (s, x). Similarly, we write $f(s, x)\asymp g(s, x)$, if there exist constants $c_k>0$, $k=1, \ldots , 4$, such that $c_1g(c_2 s, x)\le f(s, x)\le c_3 f(c_4 s, x)$ for the specified range of (s, x). We write $a\wedge b:=\min \{a, b\}$ and $a\vee b:=\max \{a, b\}$ for $a,b\in {\mathbb {R}}$.

Denote $\log ^+(x):=\log (x\vee 1)$. For a given metric measure space $(\mathcal {X}, \rho ,\mu )$ and for any $p\in [1,\infty ]$, we will use $\Vert f\Vert _p$ to denote the $L^p$-norm in $L^p(\mathcal {X};\mu )$. For any $x\in \mathcal {X}$ and $r>0$, we use B(x, r) to denote the open ball of radius r under the metric $\rho$ centered at x. For a function space $H=H(U)$ on an open set U in $\mathcal {X}$, we let $H_c(U):=\{f\in H(U): f\, \text {has compact support in U}\}$ and $H_b:=\{f\in H: f\, \text {is bounded}\}$.

2 Stability of Heat Kernel Estimates for Symmetric Diffusions with Jumps

In this section, we discuss stability of heat kernel estimates for symmetric processes that contain both diffusive and jumping components on general metric measure spaces, obtained recently in [18]. See also [19].

Let $(\mathcal {X}, \rho )$ be a locally compact separable metric space equipped with a positive Radon measure $\mu$ with full support. We assume that all balls are relatively compact, and that $\mu (\mathcal {X})=\infty$. (Note that we do not assume $(\mathcal {X}, \rho )$ to be neither connected nor geodesic.) Denote the ball centered at x with radius r by B(x, r), and set $V(x,r)=\mu (B(x,r))$.

Definition 1

• (i) We say that $(\mathcal {X}, \rho ,\mu )$ satisfies the volume doubling property ($\textrm{VD}$), if there exists ${C_\mu }\ge 1$ such that

  $$ V(x,2r) \le {C_\mu } V(x,r)\quad \text {for all}\, x \in \mathcal {X},\, r>0. $$

• (ii) We say that $(\mathcal {X}, \rho ,\mu )$ satisfies the reverse volume doubling property ($\textrm{RVD}$), if there exist ${l_\mu }, {c_\mu }>1$ such that,

  $$ V(x,{l_\mu } r) \ge {c_\mu } V(x,r)\quad \text {for all}\, x \in \mathcal {X}, r > 0, $$

Note that under RVD, $\mu (\mathcal {X})=\infty$ if and only if $\mathcal {X}$ has infinite diameter; and if $\mathcal {X}$ is connected and unbounded, then $\textrm{VD}$ implies $\textrm{RVD}$.

Suppose that we have a regular Dirichlet form $(\mathcal {E}, \mathcal {F})$ on $L^2(\mathcal {X}; \mu )$. By the Beurling-Deny formula, such a form can be decomposed into the strongly local term, the pure-jump term and the killing term; see [7, 21]. In this section, we consider the Dirichlet form $(\mathcal {E}, \mathcal {F})$ having no killing term, namely

$$\begin{aligned} \begin{aligned} \mathcal {E}(f,g)&= \, \mathcal {E}^{(c)}(f,g)+\int \limits _{\mathcal {X}\times \mathcal {X}\setminus \text {diag}}(f(x)-f(y)(g(x)-g(y))\,J(dx,dy)\\&=:\mathcal {E}^{(c)}(f,g)+\mathcal {E}^{(j)}(f,g),\qquad f,g\in \mathcal {F}, \end{aligned} \end{aligned}$$

where $(\mathcal {E}^{(c)},\mathcal {F})$ is the strongly local part of $(\mathcal {E}, \mathcal {F})$ and $J(\cdot ,\cdot )$ is a symmetric Radon measure on $\mathcal {X}\times \mathcal {X}\setminus \text {diag}$. Here and in what follows, we always take a quasi-continuous version of a function in $\mathcal {F}$. We assume that neither $\mathcal {E}^{(c)}(\cdot ,\cdot )$ nor $J(\cdot ,\cdot )$ is identically zero.

Given the regular Dirichlet form $(\mathcal {E}, \mathcal {F})$ on $L^2(\mathcal {X}; \mu )$, there is an associated $\mu$-symmetric Hunt process $X:=\{X_t, t \ge 0; \, \mathbb {P}^x, x \in \mathcal {X}\setminus \mathcal {N}\}$ that is unique up to a properly exceptional set, where $\mathcal {N}\subset \mathcal {X}$ is a properly exceptional set for $(\mathcal {E}, \mathcal {F})$; see [7, 21]. In this case, X is a symmetric diffusion with jumps. We fix X and $\mathcal {N}$, and write $\mathcal {X}_0 = \mathcal {X}\setminus \mathcal {N}$. Define

$$ P_t f(x) = \mathbb {E}_x f(X_t), \quad x \in \mathcal {X}_0 $$

for bounded Borel measurable function f on $\mathcal {X}$. The heat kernel associated with the semigroup $\{P_t\}_{t\ge 0}$ (if it exists) is a jointly measurable function $p(t, x,y): (0,\infty )\times \mathcal {X}_0 \times \mathcal {X}_0 \rightarrow (0,\infty )$ so that

$$ \mathbb {E}_x f(X_t) = P_tf(x) = \int p(t, x,y) f(y) \, \mu (dy) \quad \hbox {for all } x \in \mathcal {X}_0, f \in L^\infty (\mathcal {X};\mu ). $$

Let $\phi _c: \mathbb {R}_+\rightarrow \mathbb {R}_+$ (resp. $\phi _j: \mathbb {R}_+\rightarrow \mathbb {R}_+$) be a strictly increasing continuous function with $\phi _c (0)=0, \phi _c(1)=1$ (resp. $\phi _j(0)=0, \phi _j(1)=1$) such that there exist constants $C_1\ge 1$ and $1<\gamma _* \le \gamma ^*$ (resp. $C_2\ge 1$ and $0<\alpha _* \le \alpha ^*$) so that

$$\begin{aligned} C_1^{-1} \Big (\frac{R}{r}\Big )^{\gamma _*} \le \frac{\phi _c (R)}{\phi _c (r)} \ \le C_1 \Big (\frac{R}{r}\Big )^{\gamma ^*} \quad \text {for all}\, 0<r \le R, \end{aligned}$$

(4)

(resp. (2)). The function $\phi$ will serve as the diffusive scaling, while $\phi _j$ corresponds to the scaling function for the pure jump part. We assume that

$$\begin{aligned} \phi _c(r)\le \phi _j(r) \quad \text {for}\, r\in (0,1] \quad \text {and}\quad \phi _c(r)\ge \phi _j(r) \quad \text {for}\, r\in [1,\infty ). \end{aligned}$$

(5)

This assumption is natural in view of (3) where $\phi _c(r):=r^2$ and $\phi _j (r)$ satisfies (2). Set

$$ \phi (r):=\phi _c(r)\wedge \phi _j(r) ={\left\{ \begin{array}{ll} \phi _c(r), &{} r\in (0, 1], \\ \phi _j(r), &{} r\in [1, \infty ). \end{array}\right. } $$

It is well known that for any $f\in \mathcal {F}_b$, there exist unique positive Radon measures $\mu _{\langle f \rangle }$ and $\mu ^c_{\langle f \rangle }$ (called the energy measures of f for the Dirichlet forms $(\mathcal {E},\mathcal {F})$ and $(\mathcal {E}^{(c)}, \mathcal {F})$) on $\mathcal {X}$ so that for every $g\in \mathcal {F}$,

$$\begin{aligned}&\int \limits _{\mathcal {X}} g \, d\mu _{\langle f \rangle }=\mathcal {E}(f, fg)-\frac{1}{2}\mathcal {E}(f^2,g) \quad \text {and} \quad \nonumber \\&\int \limits _{\mathcal {X}} g \, d \mu ^c_{\langle f \rangle } = \mathcal {E}^{(c)}(f, fg)-\frac{1}{2}\mathcal {E}^{(c)}(f^2,g). \end{aligned}$$

Let $U \subset V$ be open sets of $\mathcal {X}$ with $U \subset \overline{U} \subset V$. We say a non-negative bounded measurable function ${\varphi }$ is a cut-off function for $U \subset V$, if ${\varphi }\ge 1$ on U, ${\varphi }=0$ on $V^c$ and $0\le {\varphi }\le 1$ on $\mathcal {X}$.

Definition 2

• (i) We say that $\textrm{J}_{\phi _j}$ holds if there exists a non-negative symmetric function J(x, y) such that for $\mu \times \mu$-almost all $x, y \in \mathcal {X}$,

  $$ J(dx,dy)=J(x, y)\,\mu (dx)\, \mu (dy), $$

  and

  $$ J(x, y) \asymp \frac{1}{V(x,\rho (x, y)) \phi _j (\rho (x, y))}. $$

• (ii) We say that the (weak) Poincaré inequality $\textrm{PI}(\phi )$ holds (for $\mathcal {E}$) if there exist $C>0$ and $\kappa \ge 1$ such that for any ball $B_r=B(x,r)$ with $x\in \mathcal {X}$, $r>0$ and for any $f \in \mathcal {F}_b$,

  $$ \int \limits _{B_r} (f-\overline{f}_{B_r})^2\, d\mu \le C \phi (r)\left( \mu ^c_{\langle f \rangle } (B_{\kappa r}) + \int \limits _{{B_{\kappa r}}\times {B_{\kappa r}} \setminus \textrm{diag}} (f(y)-f(x))^2\,J(dx,dy)\right) , $$

  where $\overline{f}_{B_r}= \frac{1}{\mu ({B_r})}\int \nolimits _{B_r} f\,d\mu$.

  When $\phi (r)$ is a power function $r^{d_w}$ with $d_w>1$, we write $\textrm{PI}(d_w)$ for $\textrm{PI}(\phi )$.

• (iii) We say that the cut-off Sobolev inequality $\textrm{CS}(\phi )$ holds if there exist $\delta _0\in [1/2,1)$ and $C_1, C_2>0$ such that the following holds: for any $0<r\le R$, $x_0\in \mathcal {X}$ and any $f\in \mathcal {F}$, there exists a cut-off function ${\varphi }\in \mathcal {F}_b$ for $B(x_0,R) \subset B(x_0,R+\delta _0 r)$ so that

  $$\begin{aligned}&\int \limits _{B(x_0,R+r)} f^2 \, d \mu _{\langle {\varphi }\rangle } \le C_1 \bigg (\int \limits _{B(x_0,R+r)} {\varphi }^2\,d\mu _{\langle f \rangle }^c \\&\qquad \qquad +\int \limits _{B(x_0,R+r)\times B(x_0,R+r) \setminus \textrm{diag}} {\varphi }^2(x) (f(x)-f(y))^2\, J(dx,dy)\bigg ) \\&\qquad \qquad + \frac{C_2}{\phi (r)} \int \limits _{B(x_0,R+r)} f^2 \,d\mu . \end{aligned}$$

2.1 Two-Sided Heat Kernel Estimates

In the following, we write $\phi _c^{-1}(t)$ (resp. $\phi _j^{-1}(t)$) to denote the inverse function of the strictly increasing function $t\mapsto \phi _c (t)$ (resp. $t\mapsto \phi _j(t)$). Define

$$\begin{aligned} p^{(c)}(t,x,y):=\frac{1}{V(x,\phi _c^{-1}(t))} \exp \left( - \sup _{s>0}\left\{ \frac{\rho (x, y)}{s}-\frac{t}{\phi _c(s)}\right\} \right) ,\quad t>0,x,y\in \mathcal {X}, \end{aligned}$$

(6)

which arises in the two-sided estimates of heat kernels for strongly local Dirichlet forms; see, e.g., [1]. There is another expression of heat kernels for strongly local Dirichlet forms, which is given by

$$\begin{aligned} p^{(c)}(t,x,y)= \frac{1}{V(x, \phi _c^{-1}(t))} \exp \left( -\frac{\rho (x, y)}{\bar{\phi }_c^{-1}(t/\rho (x, y))} \right) , \quad t>0, x, y\in \mathcal {X}, \end{aligned}$$

(7)

where $\bar{\phi }_c (r): \mathbb {R}_+\rightarrow \mathbb {R}_+$ is a strictly increasing continuous function such that

$$ c_1 \frac{ \phi _c(r)}{r} \le \bar{\phi }_c (r)\le c_2 \frac{\phi _c(r)}{r} \quad \text {for all}\, r>0 $$

with some $c_2\ge c_1>0$. When $\phi _c(r)=r^{d_w}$ with $d_w\ge 2$, $p^{(c)}(t,x,y)$ is reduced into Gaussian ($d_w=2$) and sub-Gaussian $(d_w>2)$ estimates. Set

$$ p^{(j)}(t, x, y):= \frac{1}{V(x, \phi _j^{-1}(t))}\wedge \frac{t}{V(x, \rho (x, y)) \phi _j (\rho (x, y))}. $$

It can be verified that under mild conditions the expressions (6) and (7) are equivalent; see [18, Corollary 2.3].

Definition 3

Let $\phi :=\phi _c\wedge \phi _j$.

• (i) We say that $\textrm{HK}(\phi _c, \phi _j)$ holds if there exists a heat kernel p(t, x, y) for the semigroup $\{P_t\}_{t\ge 0}$ associated with $(\mathcal {E},\mathcal {F})$ such that the following holds for all $t>0$ and all $x,y\in \mathcal {X}_0$,

  $$\begin{aligned} \begin{aligned}&c_1\Big (\frac{1}{V(x,\phi _c^{-1}(t))}\wedge \frac{1}{V(x,\phi _j^{-1}(t))} \wedge \big (p^{(c)}(c_2 t,x,y)+p^{(j)}(t,x,y)\big )\Big ) \\&\quad \le \ p(t, x,y) \\&\quad \le c_3\Big (\frac{1}{V(x,\phi _c^{-1}(t))}\wedge \frac{1}{V(x,\phi _j^{-1}(t))} \wedge \big (p^{(c)}(c_4 t,x,y)+p^{(j)}(t,x,y)\big )\Big ), \end{aligned} \end{aligned}$$

  (8)

  where $c_k>0$, $k=1, \ldots , 4$, are constants independent of $x,y\in \mathcal {X}_0$ and $t>0$. Below, we abbreviate the two-sided estimate (8) as

  $$ p(t, x, y) \asymp \frac{1}{V(x,\phi _c^{-1}(t))}\wedge \frac{1}{V(x,\phi _j^{-1}(t))} \wedge \left( p^{(c)}(t,x,y)+p^{(j)}(t,x,y) \right) . $$

• (ii) We say $\textrm{HK}_- (\phi _c, \phi _j)$ holds if the upper bound in (8) holds but the lower bound is replaced by the following: there are $c_0, c_1>0$ so that

  $$\begin{aligned} \begin{aligned} p(t, x, y) \ge&c_0 \bigg ( \frac{t}{V(x,\rho (x, y))\phi _j(\rho (x, y))}{} \textbf{1}_{\{\rho (x, y)>c_1 \phi ^{-1}(t)\}} \\&\quad +\frac{1}{V(x,\phi ^{-1}(t))}{} \textbf{1}_{\{\rho (x, y) \le c_1 \phi ^{-1}(t)\}} \bigg ), \quad \forall t>0,\, \forall x,y\in \mathcal {X}_0. \end{aligned} \end{aligned}$$

With the notations above, we now state the following stable characterizations of two-sided heat kernel estimates for symmetric diffusions with jump from [18].

Theorem 1

Suppose that the metric measure space $(\mathcal {X}, \rho , \mu )$ satisfies $\textrm{VD}$ and $\textrm{RVD}$, and that the scale functions $\phi _c$ and $\phi _j$ satisfy (2), (4) and (5). Let $\phi :=\phi _c\wedge \phi _j$. Then the following are equivalent:

• (i) $\textrm{HK}_- (\phi _c, \phi _j)$.

• (ii) $\textrm{J}_{\phi _j}$, $\textrm{PI}(\phi )$ and $\textrm{CS}(\phi )$.

  If in addition, $(\mathcal {X}, \rho ,\mu )$ is connected and $\rho$ is geodesic, then all the conditions above are equivalent to:

• (iii) $\textrm{HK}(\phi _c, \phi _j)$.

Note that statement (ii) in Theorem 1 is stable under bounded perturbation in the sense that if it holds for the Dirichlet form $(\mathcal {E}, \mathcal {F})$ on $L^2(\mathcal {X}; \mu )$, then it holds for any other Dirichlet form $(\mathcal {E}^{\prime }, \mathcal {F})$ on $L^2(\mathcal {X}; \mu )$ with jumping kernel $J^{\prime }$ as long as there is a constant $c>1$ so that $c^{-1} \mathcal {E}^{(c)} (f, f) \le \mathcal {E}^{\prime ,(c)} (f, f)\le c\mathcal {E}^{(c)}(f, f)$ for all $f\in \mathcal {F}$ and $c^{-1}J(x, y) \le J^{\prime }(x, y) \le cJ(x, y)$ for all $x\ne y\in \mathcal {X}$. We refer [18, Theorem 1.13] for more equivalent characterizations of $\textrm{HK}_- (\phi _c, \phi _j)$. We note that the connectedness and the geodesic condition (in fact, so-called chain condition suffices) of the underlying metric measure space $(\mathcal {X}, \rho ,\mu )$ are only used to derive optimal lower bounds off-diagonal estimates for the heat kernel when the time is small (i.e., from $\textrm{HK}_- (\phi _c, \phi _j)$ to $\textrm{HK}(\phi _c, \phi _j)$).

2.2 Example

In this section, we give an example to illustrate a typical application of Theorem 1.

Example 1

(Transferring Method on d-Set) Let $(\mathcal {X}, \rho , \mu )$ be an Alfhors d-regular set and suppose that there is a strongly local Dirichlet form $(\bar{\mathcal {E}},\bar{\mathcal {F}})$ on $L^2(\mathcal {X}; \mu )$ such that there is a transition density function q(t, x, y) with respect to the measure $\mu$ that has the following two-sided estimates:

$$ q(t, x, y) \asymp t^{-d/d_w} \exp \left( - \left( \frac{ \rho (x, y)^{d_w}}{ t} \right) ^{1/({d_w} -1)} \right) , \quad t>0, x, y\in \mathcal {X}$$

for some ${d_w} \ge 2$. Let $\{Z_t, t\ge 0; \mathbb {P}_x, x\in \mathcal {X}\}$ be the corresponding $\mu$-symmetric diffusion on $\mathcal {X}$. A typical example is a Brownian motion on the n-dimensional unbounded Sierpiński gasket; see for instance [4]. In this case, $d=\log (n+1)/\log 2$ and ${d_w}=\log (n+3)/\log 2$.

For any $\alpha \in (0, {d_w})$, let $s=\alpha /{d_w}$ and $\xi _t= t + \eta _t$, where $\eta _t$ is the s-subordinator independent of Z. Then one can verify by direct computations that the subordinated process $X_t:=Z_{\xi _t}$ has a transition density function that enjoys $\textrm{HK}(\phi _c, \phi _j)$ with $\phi _c(r)=r^{d_w}$ and $\phi _j (r) = r^\alpha$.

Now consider the following symmetric regular Dirichlet form $(\mathcal {E},\bar{\mathcal {F}})$ in $L^2(\mathcal {X}; \mu )$:

$$\begin{aligned} \mathcal {E}(u,v)= & {} \mathcal {E}^{(c)} (u,v) + \int \limits _{\mathcal {X}\times \mathcal {X}\setminus \textrm{diag}} (u(x)-u(y))(v(x)-v(y))\nonumber \\ {}&\quad \times \frac{c(x,y)}{\rho (x, y)^{d+\alpha }}\,\mu (dx)\,\mu (dy), \end{aligned}$$

where $(\mathcal {E}^{(c)}, \bar{\mathcal {F}})$ is a strongly local regular Dirichlet form on $L^2(\mathcal {X}; \mu )$ such that $\mathcal {E}^{(c)} (f,f)\asymp \bar{\mathcal {E}} (f,f)$ for all $f\in \bar{\mathcal {F}}$, and c(x, y) is a symmetric measurable function on $\mathcal {X}\times \mathcal {X}\setminus \text {diag}$ that is bounded between two positive constants. Clearly, $\textrm{J}_{\phi _j}$ and $\textrm{PI}(\phi )$ hold for $(\mathcal {E}, \bar{\mathcal {F}})$. $\textrm{CS}(\phi )$ also holds for $(\mathcal {E}, \bar{\mathcal {F}})$ because it holds for the subordinated process $\{X_t\}_{t\ge 0}$. Hence, by Theorem 1 we obtain $\textrm{HK}(\phi _c, \phi _j)$.

This type of argument (i.e. first establishing heat kernel estimates for a particular process and then use the stability results to obtain heat kernel estimates for more general processes) is sometimes called “transferring method”.

In [18], relations between heat kernel estimates and parabolic Harnack inequalities are also established. Unlike the cases of local operators/diffusions, for pure-jump processes, parabolic Harnack inequalities are no longer equivalent to (in fact weaker than) the two-sided heat kernel estimates—see [3, 17]. For the cases of diffusions with jumps, it is even more complex. We refer the readers to [18, Theorem 1.18], for more details and for further characterizations of parabolic Harnack inequalities.

3 Symmetric Reflected Diffusions with Jumps in Inner Uniform Domains

In this section, we consider the case that $\mathcal {X}$ is an inner uniform domain D on a Harnack-type space E. In this framework, there exists a reflected diffusion on D whose heat kernel enjoys two-sided Gaussian estimates (see Theorem 2). We will consider this reflected diffusion perturbed by jumps which may decay exponentially (even super-exponentially). Thus, this setting does not belong to that studied in [18], where the jumps will decay at most polynomially; see (4). This section is a survey of the recent paper [11]. In contrast with the previous section, this section as well as [11] is concerned with sufficient conditions under which we have two-sided sharp heat kernel estimates rather than stable characterization of the heat kernel estimates. However, as mentioned earlier, the ideas and techniques developed from the study of the stability results for heat kernel estimates and parabolic Harnack inequalities in [16,17,18] play an essential role in the work [11].

3.1 Reflected Diffusions on Inner Uniform Domains

Let E be a locally compact separable metric space, and m a $\sigma$-finite Radon measure with full support on E. Suppose that there is a strongly local regular Dirichlet form $(\mathcal {E}^0, \mathcal {F}^0)$ on $L^2(E; m)$, and let $\mu ^0_{\langle u \rangle }$ be the ($\mathcal {E}^0$-) energy measure of $u\in \mathcal {F}^0$ so that $\mathcal {E}^0 (u,u)= \frac{1}{2} \mu ^0_{\langle u \rangle }(E)$. Then the intrinsic metric $\rho$ of $(\mathcal {E}^0, \mathcal {F}^0)$ is defined by

$$\rho (x, y)=\sup \big \{f(x)-f(y): \ f\in \mathcal {F}^0 \cap C_c(E) \quad \text {with}\, \mu _{\langle f \rangle }^0(dz) \le m(dz)\big \}. $$

We assume that $\rho (x, y)<\infty$ for any $x,y\in E$ and induces the original topology on E, and that $(E, \rho )$ is a complete metric space. It is known (see for example [23, Theorem 2.11]) that $(E, \rho )$ is a geodesic length space; that is, for each $x, y\in E$, there exists a continuous curve $\gamma : \ [0, 1]\rightarrow E$ with $\gamma (0) = x$, $\gamma (1)=y$ such that for every $s, t \in [0, 1]$, $\rho (\gamma (s), \gamma (t)) =|t-s|\, \rho (x, y)$. In the following, we will always use the intrinsic metric $\rho$ for E.

We assume that $(E,\rho , m)$ enjoys (VD) and $(\mathcal {E}^0, \mathcal {F}^0)$ enjoys $\textrm{PI}(2)$; see Definitions 1 and 2(ii) for these definitions. According to [23], such a space is called a Harnack-type Dirichlet space. It is known that the state space E for Harnack-type Dirichlet space $(\mathcal {E}^0, \mathcal {F}^0)$ is connected and the diffusion process $Z^0$ associated with $(\mathcal {E}^0, \mathcal {F}^0)$ is conservative—see [23, Lemma 2.33].

For a domain D of the length metric space $(E, \rho )$, define for $x, y\in D$,

$$ \rho _D (x, y)=\inf \{\textrm{length}(\gamma ): \,\textrm{a curve}\, \gamma \,\textrm{in}\, D \,\textrm{with}\, \gamma (0)=x \,\textrm{and}\, \gamma (1)=y\}. $$

The completion of D under the metric $\rho _D$ is denoted by $\bar{D}$. We extend the definition of $m|_D$ to $\bar{D}$ by setting $m|_D (\bar{D}\setminus D)=0$. For notational simplicity, we will use m to denote this measure $m|_D$.

Definition 4

([23, Definition 3.6]) We say that D is inner uniform if there are constants $C_1, C_2 \in (0,\infty )$ such that, for any $x, y \in D$, there exists a continuous map $\gamma _{x, y}: [0, 1] \rightarrow D$ with $\gamma _{x, y}(0) = x$, $\gamma _{x, y}(1)=y$ that satisfies the following:

• (i) The length of $\gamma _{x,y}$ is at most $C_1 \rho _D (x, y)$.

• (ii) For any $z \in \gamma _{x,y}([0, 1])$, it holds that

  $$ \rho (z, \partial D):=\inf _{w \in \partial D} \rho (z, w) \ge C_2 \frac{\rho _D (z, x) \rho _D (z, y)}{\rho _D(x, y)}. $$

When D is inner uniform, $(\bar{D},\rho _D)$ is locally compact—see [23, Lemma 3.9]. It is well known that $(\mathcal {E}^0, \mathcal {F}^0_D)$ is the part Dirichlet form of $(\mathcal {E}^0, \mathcal {F}^0)$ on D, where $\mathcal {F}^0_D=\{f\in \mathcal {F}^0: \ f=0 \, \mathcal {E}^0\, \mathrm {-q.e. on}\, D^c\}$. In other words, $(\mathcal {E}^0, \mathcal {F}^0_D)$ is the Dirichlet form on $L^2(D; m)$ of the subprocess of the diffusion process $Z^0$ associated with $(\mathcal {E}^0, \mathcal {F}^0)$ killed upon leaving D. We write $f\in \mathcal {F}^0_{D, \textrm{loc}}$ if for every relatively compact subset U of D, there is $g\in \mathcal {F}^0_D$ such that $f=g$ m-a.e. on U. By [23, Proposition 2.13], it holds that for $x,y \in D$,

$$ \rho _D (x, y)=\sup \left\{ f(x)-f(y): \ f\in \mathcal {F}^0_{D,\textrm{loc}} \cap C_c(D)\, \text {with}\, \mu _{\langle f \rangle }^0 (dz) \le m(dz) \right\} . $$

Let $\mathcal {F}_D^{0, \textrm{ref}} :=\{f\in \mathcal {F}^0_{D,\textrm{loc}}: \mu _{\langle f \rangle }^0(D)<\infty \}$ and define $\mathcal {E}^{0, \textrm{ref}} (f, f):=\frac{1}{2} \mu _{\langle f \rangle }^0(D)$ for $f\in \mathcal {F}_D^{0, \textrm{ref}}$. $(\mathcal {E}^{0, \textrm{ref}}, \mathcal {F}_D^{0, \textrm{ref}} \cap L^2(D; m) )$ is the active reflected Dirichlet form of $(\mathcal {E}^0, \mathcal {F}^0_D)$, which is known to be a Dirichlet form on $L^2(\bar{D}; m)=L^2(D; m)$—see [7, Chap. 6]. Let $B_{\bar{D}}(x, r):=\{y\in \bar{D}: \rho _D (x, y)<r\},$ and denote $V_D(x, r):= m(B_{\bar{D}}(x, r))$. Let $\textrm{Lip}_c( \bar{D})$ be the space of compactly supported Lipschitz functions in $\bar{D}$. Then the following holds.

Theorem 2

([23, Sect. 3]) Suppose that $(\mathcal {E}^0, \mathcal {F}^0)$ is a strongly local regular Dirichlet form on $L^2(E; m)$ which admits a carré du champ operator $\varGamma _0$ (that is, $\mu _{\langle u \rangle }^0(dx)=\varGamma _0 (u, u)\,m(dx)$ and $\varGamma _0 (u, u) \in L^1(E; m)$ for every $u\in \mathcal {F}$). Assume that (VD) and (PI(2)) hold for $(\mathcal {E}^0, \mathcal {F}^0)$ on $(E, \rho , m)$, and suppose that D is an inner uniform subdomain of E. Then $(\mathcal {E}^{0, \textrm{ref}}, \mathcal {F}_D^{0, \textrm{ref}} \cap L^2(D; m))$ is a strongly local regular Dirichlet form on $L^2(D; m)$ with core $\textrm{Lip}_c( \bar{D})$, and the following hold for $\big (\mathcal {E}^{0, \textrm{ref}}, \mathcal {F}_D^{0, \textrm{ref}} \cap L^2(D; m) \big )$ on $(\bar{D}, \rho _D, m)$:

• (VD) (Volume doubling property on  $\bar{D})$ There exists $C_3>0$ such that for every $x\in \bar{D}$ and $r>0$, $V_D(x, 2r)\le C_3\, V_D(x, r)$.

• (PI(2)) (Poincaré inequality on $\bar{D})$ There exists $C_4>0$ such that for every $x\in \bar{D}$, $r>0$ and $f\in \mathcal {F}_D^{0, \textrm{ref}} \cap L^2(D; m)$,

  $$ \min \limits _{a\in \mathbb {R}}\int \limits _{B_{\bar{D}}(x, r)}(f(y)-a)^2 \,m(dy) \le C_4 r^2 \, \mu _{\langle f \rangle }^0(B_{\bar{D}}(x, r)). $$

Consequently, $(\mathcal {E}^{0, \textrm{ref}}, \mathcal {F}_D^{0, \textrm{ref}})$ admits a jointly continuous transition density function $p_D^N(t, x, y)$ on $(0, \infty )\times \bar{D}\times \bar{D}$, and there exist $c_1, c_2 \ge 1$ depending on $C_3,C_4$ such that

$$ \frac{c_1^{-1}}{V_D(x, \sqrt{t})} \exp \left( -\frac{c_2\rho _D (x, y)^2}{t}\right) \le p_D^N(t, x, y)\le \frac{c_1}{V_D(x, \sqrt{t})} \exp \left( -\frac{\rho _D (x, y)^2}{c_2 t}\right) $$

for every $x, y\in \bar{D}$ and $t>0$.

In the rest of this section we assume that the strongly local Dirichlet form $(\mathcal {E}^0, \mathcal {F}^0)$ on $L^2(E; m)$ and $D\subset E$ satisfy the assumptions of Theorem 2.

Characteristic Constants. Recall that $(C_1, C_2)$ are constants appearing in the definition of the inner uniform domain D, and $(C_3,C_4)$ are constants in (VD) and ($\textrm{PI}(2)$) of Theorem 2. We will call $(C_1, C_2, C_3, C_4)$ the characteristic constants of the domain D.

3.2 Reflected Diffusions with Jumps

Let $(\mathcal {E}, \mathcal {F})$ be a symmetric Dirichlet form $(\mathcal {E}, \mathcal {F})$ on $L^2(D; m)$, where $\mathcal {F}:=\mathcal {F}_D^{0, \textrm{ref}} \cap L^2(D; m)$, such that for $u\in \mathcal {F}$,

$$\begin{aligned} \mathcal {E}(u, u) = \mathcal {E}^{0,\textrm{ref}}(u, u)+ \frac{1}{2} \int \limits _{D\times D} (u(x)-u(y))^2\,J(x, y)\, m(dx)\,m(dy). \end{aligned}$$

(9)

Here J(x, y) is a non-negative symmetric measurable function on $D\times D \setminus \textrm{diag}$ satisfying certain conditions to be specified below.

Let $\phi _j$ be a strictly increasing function on $[0, \infty )$ such that $\phi _j (0)=0$, $\phi _j (1)=1$ and (2) holds for $0<\alpha _* \le \alpha ^*<2$. Since $\alpha ^*<2$, there exists $c_1>0$ such that

$$\int \limits _0^r\frac{s}{\phi _j (s)}\, ds \le \frac{ c_1 r^2}{\phi _j (r)} \qquad \hbox {for every } r>0. $$

Definition 5

Let $\beta \in [0, \infty ]$ and $\phi _j$ be a strictly increasing function on $[0, \infty )$ with $\phi _j (0)=0$ and $\phi _j (1)=1$ that satisfies the condition (2) (with $0<\alpha _* \le \alpha ^*<2$). Let J(x, y) be a non-negative symmetric measurable function on $D\times D \setminus \textrm{diag}$.

• (i) We say condition $(\textbf{J}_{\phi _j, \beta , \le })$ holds if there are $\kappa _1,\kappa _2>0$ so that

  $$\begin{aligned} J(x, y) \le \frac{\kappa _1 }{V_D(x, \rho _D(x, y))\phi _j (\rho _D(x, y) )\exp (\kappa _2 \rho _D(x, y)^\beta )}, {(\textbf{J}_{\phi _j, \beta , \le })} \end{aligned}$$

  for $(x, y) \in D\times D \setminus \textrm{diag}$. Similarly, we say condition $(\textbf{J}_{\phi _j, \beta , \ge })$ holds if the opposite inequality holds, and we say condition $(\textbf{J}_{\phi _j, \beta })$ holds if both $(\textbf{J}_{\phi _j, \beta , \le })$ and $(\textbf{J}_{\phi _j, \beta , \ge })$ hold with possibly different constants $\kappa _i$ in the upper and lower bounds.

• (ii) We say condition $(\textbf{J}_{\phi _j, 0_+, \le })$ holds if there are $\kappa _3,\kappa _4>0$ so that

  $$\begin{aligned} \left\{ \begin{array}{l} \sup _{x\in D}\int \limits _{\{y\in D: \rho _D(x,y)>1\}} \rho _D(x,y)^2 J(x, y)\,m(dy) \le \kappa _3<\infty ,\\ J(x, y) \le \frac{\kappa _4 }{V_D(x, \rho _D(x, y)) \phi _* (\rho _D(x, y) ) } \\ \end{array} \right. {(\textbf{J}_{\phi _j, 0_+, \le })} \end{aligned}$$

  for $(x, y) \in D\times D \setminus \textrm{diag}$, where

  $$\begin{aligned} \phi _*(r):= \phi _j(r) {\mathbbm {1}}_{\{r \le 1\}} + r^2{\mathbbm {1}}_{\{r>1\}} \quad \hbox {for } r\ge 0. \end{aligned}$$

  (10)

Clearly, $(\textbf{J}_{\phi _j, \beta , \le }) \Longrightarrow (\textbf{J}_{\phi _j, 0_+, \le })\Longrightarrow (\textbf{J}_{\phi _j, 0, \le })$ for any $\beta \in (0, \infty ]$. When $\beta =0$, $(\textbf{J}_{\phi _j, 0 })$ coincides with $\textrm{J}_{\phi _j}$ in Definition 2(i). When $\beta =\infty$, condition $(\textbf{J}_{\phi _j, \infty , \le })$ is equivalent to

$$ J(x, y) \le \frac{\widetilde{\kappa }_1 }{V_D(x, \rho _D(x, y))\phi _j (\rho _D(x, y) ) } {\mathbbm {1}}_{\{\rho (x, y) \le 1\}} \quad \text {for}\, (x, y) \in D\times D \setminus \textrm{diag}. $$

It can be easily proved (see [11, Proposition 2.1]) that, under condition $(\textbf{J}_{\phi _j, 0, \le })$, $(\mathcal {E}, \mathcal {F})$ is a regular Dirichlet form on $L^2(D; m)$. Moreover, the corresponding process Y is conservative; namely, Y has infinite lifetime almost surely.

For notational convenience, we regard $0_+$ as an “added" or “extended" number and declare that it is larger than 0 but smaller than any positive real number. With this notation, we can write, for instance, $(\textbf{J}_{\phi _j, \beta , \le })$ for $\beta \in [0, \infty ] \cup \{0_+\}$.

In the following, we present results concerning global two-sided sharp estimates on the heat kernel of Dirichlet form $(\mathcal {E}, \mathcal {F})$ under the assumption that J(x, y) satisfies $(\textbf{J}_{\phi _{j,1}, \beta _*, \le })$ and $(\textbf{J}_{\phi _{j,2}, \beta ^*, \ge })$ for some strictly increasing functions $\phi _{j,1}$ and $\phi _{j,2}$ satisfying $\phi _{j,i}(0)=0$, $\phi _{j,i}(1)=1$ and (2) (with $\phi _{j,i}$ in place of $\phi _j)$ for $1\le i\le 2$, and for $\beta _*$ and $\beta ^*$ in $[0, \infty ] \cup \{0_+\}$ (but excluding $\beta _*=\beta ^*=0_+$).

First let us consider the case $\beta _*=\beta ^*=0$ and $\phi _{j,1}=\phi _{j,2}=:\phi _j$. Note that, in the present setting, $\textrm{diam}(D)=\infty$ is equivalent to $m(D)=\infty$; see [22, Corollary 5.3]. In this case, it is easy to check that, with $\phi _c (r):=r^2$, $\phi _j(r):=r^\alpha$ and $\phi (r):=\phi _c (r) \wedge \phi _j(r)$, $\textrm{J}_{\phi _j}$, $\textrm{PI}(\phi )$ and $\textrm{CS}(\phi )$ hold; see [18, Example 1.1 and Remark 1.7] for the details. Thus we can apply the stable characterization of Theorem 1 to conclude that $\textrm{HK}(\phi _c, \phi _j)$ holds. When $\textrm{diam}(D)<\infty$, according to [18, Theorem 1.13] (noting that the results of the paper [18] continue to hold for bounded state space with obvious localized versions), one can obtain estimates of p(t, x, y) for $t\in (0, 1]$. Now, when D is bounded, it holds that $V_D(x, \sqrt{t}) \simeq 1$ for all $x\in D$ and $t\ge 1$, and the large time estimates of $\textrm{HK}(\phi _c, \phi _j)$ are simply

$$ p(t,x,y)\simeq 1 \quad \text {for}\, x,y\in \bar{D} \,\text {and}\, t\ge 1, $$

which is a consequence of the strong ergodicity of the Markov process Y. Hence $\textrm{HK}(\phi _c, \phi _j)$ is the desired estimates for $\textrm{diam}(D)<\infty$ as well.

The main contribution of [11] is to obtain two-sided heat kernel estimates for $0_+\le \beta _*\le \beta ^*\le \infty$ excluding $\beta _*=\beta ^*=0_+$ when D is unbounded. Note that when D is bounded, $( \textbf{J}_{\phi _j, \beta , \le })$ and $(\textbf{J}_{\phi _j, \beta , \ge })$ with $\beta \in \{0_+ \} \cup (0, \infty ]$ are reduced to $(\textbf{J}_{\phi _j, 0, \le })$ and $( \textbf{J}_{\phi _j, 0, \ge })$, respectively. We present the precise statement in the next subsection.

3.3 Heat Kernel Estimates for the $\beta _*\le \beta ^* \le \infty$ in $\{0_+\}\cup (0, \infty ]$ Case

We need some notations. Let

$$ p^{(c)}(t,x, r) := \frac{\exp ( - r^2/t)}{V_D(x,\sqrt{t})}, \quad p_{\phi }^{(j)}(t,x, r) := \frac{1}{V_D(x,\phi ^{-1}(t))} \wedge \frac{t}{V_D(x, r) \phi (r)}. $$

For $\beta \in [0, \infty ]$ and a strictly increasing function $\phi _j$ on $[ 0, \infty )$ with $\phi _j (0)=0$ and $\phi _j (1)=1$, set for $x\in \bar{D}$, $t>0$ and $r\ge 0$,

$$ p^{(j)}_{\phi _j, \beta } (t,x, r) := \frac{1}{V_D(x,\phi _j^{-1}(t))} \wedge \frac{t}{V(x, r) \phi _j (r) \exp (r^\beta ) }. $$

In particular, $p^{(j)}_{\phi _j, 0} (t,x, r) \simeq p^{(j)}_{\phi _j} (t,x, r)$. Define for $\beta \in (0, 1]$,

$$ H_{\phi _j,\beta } (t, x, r) := {\left\{ \begin{array}{ll} \displaystyle \frac{1}{V_D(x,\sqrt{t})} \wedge \left( p^{(c)}(t, x, r)+p^{(j)}_{\phi _j, \beta } (t, x, r)\right) \quad &{} \hbox {if } t \in (0,1] , \\ \displaystyle \frac{1}{V_D(x, \sqrt{t} ) } \exp \left( - \left( r^\beta \wedge ({r^2}/{t})\right) \right) &{}\hbox {if } t \in (1,\infty ); \end{array}\right. } $$

for $\beta \in (1,\infty )$,

$$ H_{\phi _j,\beta } (t,x,r) := {\left\{ \begin{array}{ll} \displaystyle \frac{1}{V_D(x,\sqrt{t})} \wedge \left( p^{(c)}(t,x, r)+p_{\phi _j, \beta }^{(j)}(t, x, r) \right) \\ \qquad \qquad \qquad \qquad \hbox {if } t \in (0,1], r \le 1, \\ \displaystyle \frac{t}{V_D(x, r )\phi _j(r)} \exp \left( - \left( r(1+\log ^+ (r/t))^{(\beta -1)/\beta }\right) \wedge r^\beta \right) \\ \qquad \qquad \qquad \qquad \hbox {if } t \in (0,1], r> 1 , \\ \displaystyle \frac{1}{V_D(x,\sqrt{t})}\exp \left( - \left( r\, ( 1+\log ^+ (r/t) )^{(\beta -1)/\beta } \right) \wedge (r^2/t)\right) \\ \qquad \qquad \qquad \qquad \hbox {if } t \in (1,\infty ); \end{array}\right. } $$

where $H_{\phi _j,\infty } (t,x,r) := \lim _{\beta \rightarrow \infty } H_{\phi _j,\beta } (t, x, r)$ for $\beta =\infty$, that is,

$$\begin{aligned}&H_{\phi _j,\infty } (t,x,r)\\&\quad := {\left\{ \begin{array}{ll} \displaystyle \frac{1}{V_D(x,\sqrt{t})} \wedge \left( p^{(c)}(t,x, r)+p_{\phi _j, \beta }^{(j)}(t, x, r)\right) &{} \text {if } t \in (0,1], r \le 1, \\ \displaystyle \frac{t}{V_D(x, r )\phi _j(r)} \exp \left( - r(1+\log ^+ (r/t) ) \right) &{} \text {if } t \in (0,1], r >1 , \\ \displaystyle \frac{1}{V_D(x,\sqrt{t})}\exp \left( - \left( r\, \big ( 1+\log ^+ (r/t) \big )\right) \wedge (r^2/t)\right) &{} \text {if}\, t \in (1,\infty ) . \end{array}\right. } \end{aligned}$$

Fig. 1

$\beta \in (0,1]$: dominant terms in the heat kernel estimates $H_{\phi _j,\beta } (t, x, r)$ for p(t, x, y)

Fig. 2

$\beta \in (1,\infty ]$: dominant terms in the heat kernel estimates $H_{\phi _j,\beta } (t, x, r)$ for p(t, x, y)

See Figs. 1 and 2 for a more explicit expression on the dominate terms in $H_{\phi _j,\beta } (t, x, r)$.

The following is the main result on the two-sided heat kernel estimates of Y.

Theorem 3

([11, Theorem 1.6]) Suppose that D is unbounded. Assume that J(x, y) satisfies $(\textbf{J}_{\phi _{j,1}, \beta _*, \le })$ and $(\textbf{J}_{\phi _{j,2}, \beta ^*, \ge })$ for some strictly increasing functions $\phi _{j,1},\phi _{j,2}$ satisfying $\phi _{j,i}(0)=0$, $\phi _{j,i}(1)=1$ and (2) (with $\phi _{j,i}$ in place of $\phi _j$ $)$ for $i=1,2$, and for $\beta _*\le \beta ^*$ in $\{0_+\} \cup (0, \infty ]$ excluding $\beta _*=\beta ^*=0_+$. Then the transition density function p(t, x, y) of the conservative Feller process Y associated with $(\mathcal {E}, \mathcal {F})$ has the following estimates: for every $t>0$ and $x, y \in \bar{D}$,

$$ c_1 H_{\phi _{j,2}, \beta ^*} ( t, x, c_2 \rho _D(x, y) ) \le p(t, x, y) \le c_3 H_{\phi _{j,1}, \beta _*} (t, x, c_4 \rho _D(x, y)), $$

where $c_i>0$, $1\le i \le 4$, depend only on the characteristic constants $(C_1, C_2, C_3, C_4)$ of D and the constant parameters in $(\textbf{J}_{\phi _{j,1}, \beta _*, \le })$ and $(\textbf{J}_{\phi _{j,2}, \beta ^*, \ge })$ as well as in (2) for $\phi _{j,1}$ and $\phi _{j,2}$, respectively.

3.4 Discussion on Off-Diagonal Heat Kernel Upper Bound

In this subsection, we present results on the heat kernel upper bound under milder condition and give a brief explanation of the argument for the off-diagonal upper bound of heat kernels.

Assume that diam$(D)=\infty$. Then, from the volume doubling and the reverse volume doubling property of D, we have that there exist positive constants $c_1, c_2, d_1, d_2$ such that

$$\begin{aligned} c_1 \Big (\frac{R}{r}\Big )^{d_1} \le \frac{V_D(x,R)}{V_D(x,r)}\le c_2 \Big (\frac{R}{r}\Big )^{d_2}\quad \text {for}\, R\ge r>0. \end{aligned}$$

(11)

Since one can verify the localized version of Faber-Krahn inequality and the cut-off Sobolev inequality with order 2 for the Dirichlet form $(\mathcal {E},\mathcal {F})$, under the condition $(\textbf{J}_{\phi _j, 0_+, \le })$, the heat kernel upper bound in the next result essentially follows from (the local version of) [18, Theorem 1.14] and a modification of Doeblin’s result (see [5, p. 365, Theorem 3.1]).

Proposition 1

([11, Theorem 1.5]) Suppose that condition $(\textbf{J}_{\phi _j, 0_+, \le })$ holds for some strictly increasing function $\phi _j$ on $[0, \infty )$ satisfying (2). Then $(\mathcal {E},\mathcal {F})$ in (9) is regular on $L^2(D; m)$ and the corresponding process Y on $\bar{D}$ is a conservative Feller process that starts from every point in $\bar{D}$. Moreover, Y has a jointly Hölder continuous transition density function p(t, x, y) on $(0, \infty ) \times \bar{D} \times \bar{D}$ with respect to the measure m, and there exist constants $c_1,c_2>0$ such that

$$ p(t,x,y)\le \frac{c_1}{V_D(x, \sqrt{t} ) } \wedge \left( p^{(c)}(t,x, c_2 \rho _D(x, y))+ p_{\phi _*}^{(j)}(t, x, c_2 \rho _D(x, y)) \right) $$

for all $x,y\in \bar{D}$ and $t>0$, where $\phi _*$ is given by (10). The positive constants $c_1, c_2$ depend only on the characteristic constants $(C_1,$ $C_2, C_3, C_4)$ of D and on the constant parameters in $(\textbf{J}_{\phi _j, 0_+, \le })$ and (2) for the function $\phi _j$.

The Meyer’s construction [24] is very useful to obtain off-diagonal upper bounds for p(t, x, y). Based on this, the main part of proving the off-diagonal upper bounds is to obtain the correct off-diagonal upper bounds of $q^{\langle \lambda \rangle }(t,x,y)$, the transition density of truncated process $Y^{(\lambda )}$ obtained from Y by removing jumps of size larger than $\lambda$. In order to deal with the general VD setting (11), we first consider off-diagonal upper bounds for Dirichlet heat kernel of the truncated process $Y^{(\lambda )}$. For an open set $U\subset \bar{D}$, let $q^{\langle \lambda \rangle , U}(t,x,y)$ be the (Dirichlet) heat kernel of the subprocess $Y^{(\lambda ), U}$ of $Y^{(\lambda )}$ killed up exiting U.

Very recently, in [10] we have established the equivalences between on-diagonal heat kernel upper bounds and off-diagonal heat kernel upper bounds for a large class of symmetric Markov processes, which are generalizations of the results in [6]. The results in [10] are applicable for $q^{\langle \lambda \rangle , U}(t,x,y)$ in the present setting. For the remainder of this subsection, we provide the outline of the proof of the upper bound of $q^{\langle \lambda \rangle }(t,x,y)$.

In the following, suppose that $(\textbf{J}_{\phi _{j}, \beta _*, \le })$ holds with $\beta _*\in (0,\infty ]$. Using [10, Theorem 5.1], we can check that for any $\beta _* \in (0, \infty ]$ and $l\ge 2$, there exists a constant $c_0 >0$ such that for any $x_0\in \bar{D}$, $\lambda > 0$, any $f \in \textrm{Lip}_c( \bar{D})$, any $t>0$ and any $x,y\in B_{\bar{D}}(x_0,l\lambda )$,

$$\begin{aligned}&q^{\langle \lambda \rangle , B_{\bar{D}}(x_0,l\lambda )}(t,x,y)\nonumber \\&\quad \le \frac{c_0}{V_D(x_0,\lambda )}\,\left( \left( \frac{\lambda }{\sqrt{t}}\right) ^{d_1}\vee \left( \frac{\lambda }{\sqrt{t}}\right) ^{d_2}\right) \,\exp \left( -|f(y)-f(x)|+2 \varLambda ^{\langle \lambda \rangle }(f)^2\, t\right) , \end{aligned}$$

(12)

where $d_1, d_2>0$ are the constants in (11) and

$$ \varLambda ^{\langle \lambda \rangle } (f)^2 =\Vert e^{-2f} \varGamma _{\langle \lambda \rangle }(e^{f}) \Vert _\infty \vee \Vert e^{2f} \varGamma _{\langle \lambda \rangle }(e^{-f})\Vert _\infty $$

with

$$ \varGamma _{\langle \lambda \rangle }(f ) (\xi ) = \varGamma _0 (f, f) (\xi ) + \int \limits _{ B_{\bar{D}}(\xi , \lambda )} \left( {f(\xi )-f(\eta )}\right) ^2 J(\xi , \eta )\, m(d\eta ). $$

For fixed $x, y\in B_{\bar{D}}(x_0,l\lambda )$, by taking $f(\xi )=s \left( \rho _D(\xi ,x) \wedge \rho _D(x,y) \right)$ with $s>0$, we see that $|f(y)-f(x)|=s\rho _D(x,y)$ and, thanks to $(\textbf{J}_{\phi _{j}, \beta _*, \le })$,

$$\begin{aligned} \begin{aligned}&e^{-2f (\xi )} \varGamma _{\langle \lambda \rangle }(e^f ) (\xi ) \\&= e^{-2f(\xi )} \varGamma _0 (e^f , e^f ) (\xi )+ \int \limits _{ B_{\bar{D}}(\xi , \lambda )}(e^{f (\xi )-f (\eta )}-1)^{2} J(\xi , \eta )\,m(d\eta ) \\&\le \varGamma _0 (f , f ) (\xi )+ s ^{2} \int \limits _{ B_{\bar{D}}(\xi , \lambda )} \rho _D(\xi ,\eta )^{2}e^{2\,s \rho _D(\xi ,\eta ) } J(\xi , \eta )\,m(d\eta ) \\&\le s^2+ c_1 s ^{2} \int \limits _{{D}} \rho _D(\xi ,\eta )^{2}\frac{e^{2s\rho _D(\xi ,\eta )- \kappa _2 \rho _D(\xi ,\eta )^{\beta _*}} }{V_D(\xi ,\rho _D(\xi ,\eta )) \phi _j(\rho _D(\xi ,\eta ))}\,m(d\eta ). \end{aligned} \end{aligned}$$

(13)

In [11], we consider the cases $\beta _* \in (0, 1]$, $\beta _*\in (1, \infty )$ and $\beta _*=\infty$ separately and find a proper s for each case to bound (12) optimally.

Let $\tau _B^{(\lambda )}$ by the first exit time from the ball B by $Y^{(\lambda )}$ and $\tau _B^{(\lambda ),U}$ be the first exit time from the ball B of the process $Y^{(\lambda ),U}$. Since the size of jumps of $Y^{(\lambda )}$ is less than $\lambda$, we see that

$$ \mathbb {P}_x \big ( \tau _{B(x,r)}^{(\lambda )}\le t \big ) =\mathbb {P}_x\big (\tau _{B(x,r)}^{(\lambda ),B(x,\lambda +r)}\le t\big ), \quad x\in \bar{D},\, \lambda , t, r>0. $$

Using this and the strong Markov property, we have that for any $x\in \bar{D}$ and $\lambda , t, r{>}0$,

$$\begin{aligned}&\int \limits _{B_{\bar{D}}(x,r)^{c}} q^{\langle \lambda \rangle }(t,x,y)\,m(dy) \nonumber \\&\quad \le \mathbb {P}_x \big ( \tau _{B(x,r)}^{(\lambda )}\le t \big ) = \mathbb {P}_x \big ( \tau _{B(x,r)}^{(\lambda ),B(x,r+\lambda )}\le t \big ) \nonumber \\&\quad \le \mathbb {P}_x\big (\rho _D( Y_{2t}^{(\lambda ),B(x,r+\lambda )},x)\ge r/2\big ) \nonumber \\&\qquad + \mathbb {P}_x\big (\sup _{0<s\le t}\rho _D( Y_s^{(\lambda ),B(x,r+\lambda )},x)\ge r, \, \rho _D( Y_{2t}^{(\lambda ),B(x,r+\lambda )},x)\le r/2\big ) \nonumber \\&\quad \le \mathbb {P}_x\big (\rho _D( Y_{2t}^{(\lambda ),B(x,r+\lambda )},x)\ge r/2\big ) \nonumber \\&\qquad + \mathbb {P}_x\Big ( \tau _{B(x,r)}^{(\lambda )}\le t , \, \rho _D( Y_{2t}^{(\lambda ),B(x,r+\lambda )},Y^{(\lambda )}_{\tau _{B(x,r)}^{(\lambda )}})\ge r/2\Big ) \nonumber \\&\quad \le \mathbb {P}_x\big (\rho _D( Y_{2t}^{(\lambda ),B(x,r+\lambda )},x)\ge r/2\big ) \nonumber \\&\qquad + \sup _{z\in B(x,r+\lambda )}\sup _{t\le s\le 2t}\mathbb {P}_z\big (\rho _D( Y_s^{(\lambda ),B(x,r+\lambda )},z)\ge r/2\big ) \nonumber \\&\quad \le 2\sup _{z\in B(x,r+\lambda )}\sup _{t\le s\le 2t} \int \limits _{B_{\bar{D}}(z,r/2)^{c}} q^{\langle \lambda \rangle , B(x,r+\lambda )}(s,z,y)\,m(dy). \end{aligned}$$

(14)

We now assume that $\rho _D(x,y)\ge C(\sqrt{t} \vee 1)$ where $C \ge 1$. Let $R=\rho _D(x,y)$ and $\lambda =R/k$ where k will be determined later. By [16, Lemma 7.2(2)] and Proposition 1,

$$ q^{\langle \lambda \rangle }(t,x,y)\le \frac{c_2}{V_D(x,\sqrt{t})}. $$

Using this, (11) and (14), we obtain that

$$\begin{aligned}&q^{\langle \lambda \rangle }(t,x,y)\nonumber \\&\quad =\int \limits _{\bar{D}} q^{\langle \lambda \rangle }(t/2,x,z) q^{\langle \lambda \rangle }(t/2,z,y) \,m(dz)\nonumber \\&\quad \le \left( \int \limits _{B_{\bar{D}}(x,R/2)^{c}}+\int \limits _{B_{\bar{D}}(y,R/2)^{c}}\right) q^{\langle \lambda \rangle }(t/2,x,z) q^{\langle \lambda \rangle }(t/2,z,y) \,m(dz)\nonumber \\&\quad \le \frac{c_2}{V_D(y,\sqrt{t})}\int \limits _{B_{\bar{D}}(x,R/2)^{c}} q^{\langle \lambda \rangle }(t/2,x,z)\,m(dz)\nonumber \\&\qquad +\frac{c_2}{V_D(x,\sqrt{t})}\int \limits _{B_{\bar{D}}(y,R/2) ^c} q^{\langle \lambda \rangle }(t/2,y,z)\,m(dz)\nonumber \\&\quad \le \frac{c_3}{V_D(x,R)}\left( \frac{R}{\sqrt{t}}\right) ^{d_2} \times \nonumber \\&\qquad \sup _{w\in \bar{D}} \sup _{z\in B(w,R/2+\lambda )}\sup _{t/2\le s\le t} \int \limits _{B_{\bar{D}}(z,R/4)^c} q^{\langle \lambda \rangle , B(w,R/2+\lambda )}(s,z,u)\,m(du). \end{aligned}$$

(15)

Therefore, to obtain upper bounds of $q^{\langle \lambda \rangle }(t,x,y)$, it suffices to bound (15). Recall that, in (12), (13) and the sentence below, we have discussed how to get the upper bounds of $q^{\langle \lambda \rangle , B(w,R/2+\lambda )}(s,z,u)$. Using such upper bounds, with proper C and k, in [11, Proposition 4.3] we have obtained upper bounds of (15) for the cases $\beta _* \in (0, 1]$, $\beta _*\in (1, \infty )$ and $\beta _*=\infty$ separately. Finally, we have the following

Proposition 2

([11, Theorem 4.4]) Suppose that $(\textbf{J}_{ \phi _j, \beta _*, \le })$ holds for some $\beta _*\in (0, \infty ]$. Then there exist $c_1,c_2>0$ that depend only on characteristic constants $(C_1, C_2, C_3, C_4)$ of D and the constant parameters in $(\textbf{J}_{ \phi _j, \beta _*, \le })$ and (2) for $\phi _j$ so that

$$ q(t, x, y) \le c_1 H_{ \phi _j, \beta _*} (t, x, c_2 \rho _D(x, y)) \quad \text {for every}\, t>0 \,\text {and}\, x, y \in \bar{D}. $$

3.5 Example

Example 2

A typical example for Theorem 3 is the following. In (1) with D instead of $\mathbb {R}^d$ where D is a Lipschitz domain in $\mathbb {R}^d$, suppose that J(x, y) is a symmetric function on $D\times D \setminus \textrm{diag}$ defined by

$$ J(x,y)= \int \limits _{[\alpha _1, \alpha _2]} \frac{c(\alpha , x,y)}{|x-y|^{d+\alpha } \, \varPhi (|x-y|)}\, \nu (d\alpha ), $$

where $\nu$ is a probability measure on $[\alpha _1, \alpha _2] \subset (0, 2)$, $\varPhi$ is an increasing function on $[ 0, \infty )$ with

$$ c_1e^{c_2r^{\beta }} \le \varPhi (r) \le c_3 e^{c_4r^{\beta }} \quad \text {for some}\, \beta \in [0,\infty ], $$

and $c(\alpha , x, y)$ is a jointly measurable function that is symmetric in (x, y) and is bounded between two positive constants. When $\beta =0$ and $D=\mathbb {R}^d$, the two sided heat kernel estimates are obtained in [15] as mentioned in the introduction.

Finally, we would like to mention that unde the setting in this section, parabolic Harnack inequalities do not hold for the whole range. In fact under conditions $(\textbf{J}_{\phi _1, \beta _*, \le })$ and $(\textbf{J}_{\phi _2, \beta ^*, \ge })$ with $\beta _{*} <\beta ^{*}$ in $\{0_+\} \cup (0, \infty ]$, the jumping kernel J(x, y) may not satisfy the $\textbf{UJS}$ condition, see [3] and [11, Sect. 6.2] for more details. Thus, it follows from (the proof of) [17, Proposition 3.3], that parabolic Harnack inequalities of full ranges do not hold. Thus, the results of [18] in particular give a family of Feller processes that satisfy global two-sided heat kernel estimates, but the associated parabolic Harnack inequalities for full ranges fail. We further mention that, under condition $(\textbf{J}_{\phi , 0_+, \le })$, we always have the joint Hölder continuity for the heat kernel q(t, x, y) so that we can establish two-sided estimates for q(t, x, y) for every $t>0$ and $x, y\in \bar{D}$ without introducing any exceptional set.