Polyurethane Foam-Filled Energy Absorption Connectors Under Impact

Abstract

Two types of polyurethane (PU) foam-filled energy absorption connectors were proposed, aiming to improve the energy absorption performances of aluminum foam-filled connectors. The multiple pleated (MP) plates and asymmetric pleated (AP) plates were employed for the PU foam-filled energy absorption connectors, which could trigger more plastic hinges and achieve higher energy absorption. Drop-weight impact tests and Finite Element simulations on the PU foam-filled energy absorption connectors were carried out to obtain their deformation modes and energy absorption performances. In addition, an analytical model including strain rate effects of both steel and PU foam was proposed, and it could be employed as a simple alternative to quickly obtain the force–displacement relation of the connector. The accuracy of the developed analytical model was also validated against the experimental and numerical results.

2.1 Introduction

In this chapter, two types of polyurethane (PU) foam-filled energy absorption connectors were proposed, aiming to enhance the energy absorption performances of the aluminum foam-filled energy absorption connectors presented in Chap. 1. The PU foam, which generally exhibits higher specific energy absorption as compared to aluminum foam, was employed as the filler material. In addition, the multiple pleated (MP) plates and asymmetric pleated (AP) plates were employed for the PU foam-filled energy absorption connectors (with their names of type III and type IV connectors, as shown in Figs. 2.1 and 2.2, respectively), and the MP and AP plates could trigger more plastic hinges and achieve higher energy absorption as compared to type II connectors.

Fig. 2.1

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Type III energy absorption connectors with varying a angle θ₀ and b MP plate thickness,

Fig. 2.2

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Type IV energy absorption connectors: a Without foam; b Variant parameter k; c Variant plate thickness,

Recently, PU foam was increasingly employed for energy absorbers owing to its high energy absorption capacity and lightweight (Gilchrist and Mills 2001; Koohbor et al. 2016; Deb and Shivakumar 2009). Up to date, most of the studies on the PU foam-filled energy absorbers were focused on their behaviors under quasi-static crushing load. Lateral crushing on PU foam-filled tubes usually yielded smoother force–displacement responses (i.e., higher crushing force efficiency) as compared to axial crushing. It was also demonstrated that PU foam filler could enhance the energy absorption capacity as compared to the empty tubes (Niknejad et al. 2013, 2012; Yan et al. 2014; Elahi et al. 2017). Moreover, the PU foam filler could also bring more regular deformation mode as compared to empty ones, which could be attributed to the interaction effect between the foam filler and tube (Niknejad et al. 2013; Hanssen et al. 2000; Song et al. 2005). The absorbed energy of foam-filled circular tube under axial loading was generally higher as compared to that under lateral loading, thus attracting a lot of interest (Rezaei et al. 2015; Niknejad et al. 2015; Haorongbam et al. 2017). It was observed that PU foam filler could lead to deformation mode change of aluminum square tubes under axial crushing (Hussein et al. 2017). In terms of PU foam-filled circular composite tubes, the specific energy absorption was shown to increase with smaller diameter to thickness ratio (Zhang et al. 2018). The metallic tubes with grooves were generally employed to stabilize the deformation mode (Darvizeh et al. 2013; Daneshi and Hosseinipour 2002), and the varying grooves distance could lead to the deformation mode change when studying grooved circular tubes with PU foam filler under axial crushing (Abedi et al. 2018). The foam-filled bi-tubular tubes were also developed to enhance the energy absorption capability of the foam-filled single tubes (Azarakhsh et al. 2015; Jafarian and Rezvani 2017). With regard to PU foam-filled energy absorbers under dynamic loading, fewer works were conducted. It was found by Onsalung et al. (2014) that the PU foam-filled circular aluminum tube exhibited the change of collapse modes as compared to the empty counterpart when subjected to impact loading. In addition, the foam filler could also reduce the force fluctuations owing to the smooth stress–strain curve of PU foam (Onsalung et al. 2014; Reid and Reddy 1986), and this effect was more pronounced under dynamic loading conditions (Reid and Reddy 1986). For the foam-filled connector under low-velocity impact loading that did not trigger the deformation mode change, the strain rate effect mainly contributed to the improvement of energy absorption capability. Hence, the energy absorption capability of PU foam-filled absorbers was closely related to the strain rate effect (Zhou et al. 2016; Reid and Reddy 1986).

In this chapter, two types of PU foam-filled energy absorption connectors were developed, and their energy absorption performances were experimentally, numerically and analytical studied. Drop-weight impact tests on the PU foam-filled connectors were first conducted to obtain their deformation modes, force–displacement responses and energy absorption behaviors. Moreover, the main parameters that affect the energy absorption performances of the PU foam-filled connectors were also experimentally investigated. The analytical models incorporating strain rate effects of PU foam and steel were developed to predict the force–displacement responses of the proposed connectors.

2.2 Methodologies

2.2.1 Experimental Approach

The deformation modes and force–displacement responses of the proposed PU foam-filled connectors were obtained by conducting drop-weight impact tests. The details of specimens, test setup and instrumentation are described in this section.

2.2.1.1 Test Specimens

Figures 2.1 and 2.2 present the type III and type IV energy absorption connectors designed for drop-weight impact tests. The connector consists of mild steel and PU foam as face plates and core material, respectively. Two MP plates (for type III connector) or AP plates (for type IV connector) were attached to the top and bottom flat plates, respectively, through bolt connection to form a four-sides enclosed space for the filling of PU foam. As shown in Table 2.1, Eight type III connectors were prepared for the impact loading tests, and the investigated parameters include angle θ₀ (the angle between MP plate and flat plate in Fig. 2.3), MP plate thickness and PU foam filler. The detailed geometry of the fabricated type III connector is illustrated in Fig. 2.3. It should be mentioned that the MP plate is designed with different lever arms (i.e., the lever arm of 1–2 is twice of that of 2–3) to ensure the successive development of plastic hinges at the corners and stabilize the deformation mode of the MP plate. This will be further discussed in Sect. 2.3, together with the deformation modes and force–displacement responses of type III connectors. With regard to type IV connectors, there are eight specimens being fabricated, and the investigated parameters include geometric parameter of AP plate k, AP plate thickness and PU foam filler, as shown in Table 2.1. The geometric parameter k, which is employed to describe the shape of the pleated plate, is illustrated in Figs. 2.2 and 2.4. The material properties of PU foam and mild steel used to fabricate the connectors are given in Table 2.2, and they were determined via conducting uniaxial compression loading test and tensile coupon test, respectively.

Table 2.1 Geometries of PU foam-filled energy absorption connectors

Fig. 2.3

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Dimensions of type III connectors (unit: mm),

Fig. 2.4

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Dimensions of type IV connectors (unit: mm),

Table 2.2 Material parameters of mild steel and PU foam

2.2.1.2 Test Setup and Instrumentation

Figure 2.5 presents the test setup and instrumentations. The impact tests were conducted via employing a drop-weight impact test system. As illustrated in Fig. 2.5, the specimen was firstly bolted to a 30-mm-thick steel plate on the top and bottom in order to prevent bending of the top plate of the connector during impact. Then, the specimen was placed on a force transducer which was seated on the rigid support. The 400 kg hammer was lifted up to the pre-determined height and dropped freely along the vertical guide rails to hit the connector. The piezoelectric force transducer with measuring range of 600 kN was placed below the connector to record the pure force. To ensure that all the tested connectors could reach densification and the maximum impact force was smaller than the allowable value of piezoelectric force transducer, the trial numerical analyses were carried out to obtain the drop height for each connector (as given in Table 2.1) via assuring the FE-calculated impact force within the range of 550–600 kN. The magnetic scale displacement transducer was utilized to measure displacement of the hammer. In addition, the high-speed camera was utilized to capture the deformation process during impact with a speed of 2000 frames per second.

Fig. 2.5

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Drop-weight impact test setup and instrumentation,

2.2.2 Finite Element Models

The explicit code in LS-DYNA was used to reproduce the responses of the tested PU foam-filled connectors under impact loading, and the FE model of the typical PU foam-filled connector is given in Fig. 2.6. The PU foam, hammer and support were modeled with eight-node hexahedral element with reduced integration, and the MP plates and flat plates were modeled with shell element with five integration points in the thickness direction. The contacts between two parts were treated via “master–slave” contact options, which could be defined in LS-DYNA with surface to surface contact option. The dynamic and static friction coefficients between all the contact surfaces were selected to be 0.2. The bolt connection in the specimens was simulated by utilizing the keyword *CONTACT_TIED_SHELL_EDGE_TO_SURFACE. To apply an impact loading, the hammer was defined with an initial velocity via the keyword *INITIAL_VELOCITY_GENERATION.

Fig. 2.6

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

FE model of PU foam-filled connector under drop-weigh impact loading,

The Piecewise Linear Plastic material model (MAT_24) was chosen to model the mechanical behavior of mild steel, and the input true stress–effective plastic strain curves are given in Fig. 2.7a. The Cowper-Symonds model was chosen to enhance the yield stress (as defined in Eq. (1.8)), and the strain rate parameters C and P were defined as 802 s⁻¹ and 3.585 for mild steel (Abramowicz and Jones 1986). PU foam also exhibits strain rate dependency. Hence, the Modified Crushable Foam model (MAT_163), which is allowed to define the yield stress to be a formula of volumetric strain as well as volumetric strain rate, was employed to model PU foam. To account for strain rate effect, the yield stress–volumetric strain curves corresponding to variant strain rates need to be defined. As given in Fig. 2.7b, the yield stress–volumetric strain curve of PU foam with strain rate of 8e−4 s⁻¹ was determined by conducting uniaxial compression loading tests, and the yield stress–volumetric strain curves for other strain rates could be determined by scaling reference yield stress–volumetric strain curve with a factor as (Jeong et al. 2012)

$$ 1 + \left( {a_{0} + b_{0} \varepsilon } \right)\ln \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right) $$

(2.1)

Fig. 2.7

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Input stress–strain curves of: a mild steels and b PU foam,

where the strain rate parameters a₀ and b₀ are 0.0430 and 0.0165, respectively, and the reference strain rate $\dot{\varepsilon }_{0}$ is 8e−4 s⁻¹.

2.3 Results and Discussions

2.3.1 FE Model Validation

Figures 2.8 and 2.9 present the force–displacement responses of the tested connectors obtained from FE analyses and impact tests, and generally well matches between them can be observed. However, there are still slight differences between the numerical and experimental results. This may be caused by the geometric imperfections of the fabricated connectors. Generally, the PU foam-filled connectors show better agreement as compared to empty connectors, as shown in Figs. 2.8 and 2.9. This is because the PU foam-filled connectors are less sensitive to the geometric imperfections of MP/AP plates owing to the presence of PU foam. In addition, the material parameters defined in the FE model (e.g., strain rate parameters of mild steel and PU foam) may slightly differ from those in the experiments, which can also result in the differences between the numerical and experimental results. The deformation processes of the two type III connectors (one with PU foam and the other without PU foam) obtained from FE predictions are also validated against the test observations in Fig. 2.10, and the FE model is able to accurately capture the deformation shapes of type III connectors. The FE-predicted deformation processes of type IV connectors are presented in Fig. 2.11, which are close to the test results in Fig. 2.15. In addition, Fig. 2.12 exhibits the plastic strain contours of the AP plate of type IV connector. The formation and rotation process of plastic hinges are consistent with the experimental observations. From above comparisons, the established FE models of the tested connectors are deemed to be reasonable and can be used for the further calculation and in-depth analysis.

Fig. 2.8

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Comparison of force–displacement curves of type III connectors obtained from test, FE and analytical models,

Fig. 2.9

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Comparison of force–displacement curves of type IV connectors obtained from test and FE model: a Variant pleated plate parameter k without foam; b Variant pleated plate parameter k with foam; c Variant pleated plate thickness with foam,

Fig. 2.10

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Comparison of deformation processes of type III connectors between test and FE: a without PU foam; b with PU foam,

Fig. 2.11

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Deformation processes of type IV connectors from FE analyses: a without PU foam; b with PU foam,

Fig. 2.12

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Plastic strain contours of the AP plate of type IV connector: a Deformation stage I; b Deformation stage II; c Deformation stage III,

2.3.2 Deformation Mode

Figure 2.10a illustrates the typical deformation modes of the type III connector without PU foam, and continuous plastic deformation of the MP plate in way of plastic hinge rotation at the corners can be observed. Generally, two evidently different deformation patterns can be identified during impact, which are more clearly illustrated in Fig. 2.13. Since the lever arm of 1–2 is longer than that of 2–3, the plastic hinges are firstly formed at point 1, 2, 4 and 5, and the plastic hinges keep rotating with continuous compression. This is called deformation pattern I (from stage A to B in Fig. 2.13). When the MP plate touches the top and bottom plate, the plastic hinge at point 3 is developed and rotates together with plastic hinges at point 2 and 4. However, the plastic hinges at point 1 and 5 stop rotating. This is called deformation pattern II (from stage B to C in Fig. 2.13). Figure 2.10a shows that the deformation patterns of the type III connector without PU foam are consistent to the designed deformation patterns, showing two deformation patterns with boundary displacement of 75 mm. The typical deformation mode of the type III energy connector with PU foam is illustrated in Fig. 2.10b. Besides the plastic deformation of MP plates, the PU foam compression also helps to absorb impact energy. Comparing the deformation patterns of MP plates of type III connectors with and without PU foam reveals that the presence of PU foam does not change the plastic hinge locations (at the corners); whereas it slightly changes the plastic hinge rotation angle for each point. Generally, the total plastic hinge rotation angles of MP plates for type III connectors with and without PU foam are almost identical, which can be observed from their permanent deformations, as shown in Fig. 2.10.

Fig. 2.13

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Deformation patterns of MP plate under impact loading,

All the tested type III connectors show designed deformation mode except for the connector A60T5N which experiences unsymmetrical deformation with shifting between top plate and bottom plate, as illustrated in Fig. 2.14. In fact, A60T5N nearly follows the designed deformation mode with plastic hinges developed at point 1, 2, 4 and 5 (refer to Fig. 2.13 for the locations of plastic hinges) within deformation pattern I when the displacement is less 78 mm. However, the plastic hinge at point 3 is not developed with further compression due to the evident shifting between the top and bottom plate. This also leads to the sudden drop of impact force, as shown in Fig. 2.8. The unsymmetrical deformation of A60T5N can be induced by geometric imperfection of the fabricated specimen. In fact, the connector A60T5N with highest angle θ₀ (or shortest level arm) among the tested type III connectors is more sensitive to the geometric imperfection and prone to behave unstable deformation mode during impact. However, the presence of PU foam seems to stabilize the deformation mode, as the connector A60T5 with same angle θ₀ does not experience unsymmetrical deformation shape.

Fig. 2.14

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Deformation mode of connector A60T5N,

Fig. 2.15

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Deformation processes of type IV connectors: a without PU foam; b with PU foam,

The typical deformation modes and distributions of plastic hinges of the type IV connectors with and without PU foam observed from drop-weight impact tests are shown in Fig. 2.15. Because of the asymmetry of pleated plates, the deformation mode of the type IV connector without PU foam can be divided into three stages, as illustrated in Fig. 2.15a. At the first stage, three pairs of plastic hinges occur at point 1, 2 and 3. When the plastic hinge at point 2 and flat plate come into contact, the deformation mode enters the second stage, and the critical displacement between stage I and II is defined as D₁. At this stage, the long arms of AP plates start to buckle, and subsequently the forth pair of plastic hinges occur at point 4. Meanwhile, plastic hinges at point 3 continue rotating, plastic hinges at 2 rotate reversely, and plastic hinges at point 1 stop rotating. When plastic hinges at point 4 and flat plate come into contact, the deformation mode enters the third stage, and the critical displacement between stage II and III is defined as D₂. At this stage, the AP plates buckle again, and subsequently the fifth pair of plastic hinges occurs at point 5. Meanwhile, plastic hinges at point 2 continue rotating, plastic hinges at point 4 rotate reversely, and plastic hinges at point 3 stop rotating.

As for the deformation mode of the type IV connector with PU foam shown in Fig. 2.15b, it is similar to the deformation mode of the type IV connector without PU foam in Fig. 2.15a, which may be owing to the significant difference of the Young’s modulus between PU foam and steel. Hence, the deformation mode of the type IV connectors with PU foam can also be divided into three stages on the basis of the sequence of plastic hinge development. However, the PU foam filler can reduce the critical displacements of D₁ and D₂, i.e., the plastic hinges at point 4 and 5 of type IV connectors with PU foam form earlier as compared to the counterparts without PU foam, since the AP plates cannot completely contact with flat plates.

2.3.3 Force–Displacement Responses

Figure 2.16 presents the typical force–displacement curves of type III connectors with and without PU foam. The PU foam filler is found to significantly increase the crushing force, but leads to slight decrease of densification displacement. Both the two curves show initial peak force and followed by sudden drops with increase of displacement. The observed fluctuations of the force–displacement curves are mainly induced by the inertial force. Without considering the inertial force, the analytical model can provide smooth curves, as given in Fig. 2.8. For the type III connector without PU foam, the force shows sudden rise with displacement of 65 mm when the MP plate start to touch the top/bottom plate and the deformation pattern shift from I to II. This is because the lever arm of 2–3 is smaller than that of 1–2 (shown in Fig. 2.13) and the force is mainly governed by the lever arm of 2–3 at this moment. Relatively smoother curve can be observed for the PU foam-filled connector owing to the smooth stress–strain curve of PU foam, as given in Fig. 2.7b. Figure 2.8 shows that all the tested type III connectors have three deformation processes, including initial elastic deformation, following plastic deformation and final inner surface contact (without PU foam) or PU foam densification (with PU foam) (Wang et al. 2018). The displacement range at plastic deformation stage is significantly higher than the other two deformation stages. In addition, the varying magnitude of crushing force is not significant at this stage, especially for the type III connectors with PU foam. Both of them are of benefit to an energy absorber. Figure 2.8 also shows that the force and energy absorption capability can be generally increased by increasing angle θ₀ and MP plate thickness as well as filling the connector with PU foam.

Fig. 2.16

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Typical force–displacement curves of type III connectors with and without PU foam,

The typical force–displacement curves of type IV connectors with and without PU foam are presented in Fig. 2.17. For the connector B3T5N without PU foam, when the displacement of connector, δ, reaches 26.9 and 94.2 mm, the force–displacement curve shows sudden changes because the AP plates are in contact with flat plates. Meanwhile, AP plates start buckling, and the connector enters the next deformation stage. The curve also exhibits that the force tends to decrease during the deformation stage II and III, which may be induced by the continuous increase of arm length. For the connector B3T5 with PU foam, there is no significant sudden change in the force versus displacement curve because of the presence of PU foam which shows smooth stress–strain response. When displacement, δ, reaches 25.2 mm, a peak value of the force appears, and the critical point corresponding to the boundary of stage I and II (D₁) is near the peak point. However, the critical displacement corresponding to the boundary of stage II and III (D₂) is not evident, owing to the presence of PU foam. For the deformation stage I, the PU foam is in the elastic region at first, and the force increases rapidly. When the PU foam enters the plateau region, the increasing rate of the force slows down. For the deformation stage II, the force shows decrease with increasing displacement. This is because the force contributed by the plastic deformation of AP plates decreases, and the force contributed by PU foam, which is still within the plateau region, increases slowly. For the deformation stage III, the force shows continuously rising because of the densification of PU foam.

Fig. 2.17

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Typical force–displacement curves of type IV connectors with and without PU foam,

2.3.4 Energy Absorption Performance of Type III Connector

Several energy absorption parameters, including energy absorption (EA), specific energy absorption (SEA) and crushing force efficiency (CFE) were employed to quantitatively evaluate the energy absorption performances of type III connectors and reveal the corresponding influential parameters. EA, SEA and CFE can be obtained from Eqs. (1.1)–(1.3). To fairly assess the effect of PU foam filler on EA, SEA and CFE, the identical densification displacement should be determined for all the eight type III connectors. It can be observed from CFE–displacement curves in Fig. 2.18 that the CFE value decreases when the peak crushing force (PCF) shows monotonic increase with increasing displacement. Hence, the CFE value will show sudden drop after densification of the connector when the force increase suddenly and monotonically. By carefully examine all the tested type III connectors, the densification displacement is chosen to be 96 mm, which can ensure all the densification displacements of the tested connectors appearing after this value, as illustrated in Fig. 2.18.

Fig. 2.18

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

CFE versus displacement curves of type III connectors,

2.3.4.1 Effect of PU Foam Filler

Table 2.3 summarizes the values of EA, SEA and CFE corresponding to densification displacement of 96 mm for all the tested type III connectors. The foam filler is found to evidently improve the energy absorption performance via increasing EA, SEA and CFE. The average increasing percentages of EA, SEA and CFE for the three type III connectors without PU foam (i.e., A30T5N, A45T5 and A60T5N) are 122.5%, 93.1% and 69.4%, respectively, by filling PU foam. The 122.5% increase of EA indicates that PU foam filler contributes more than half of the absorbed energy. The increase of SEA by filling PU foam is mainly owing to the higher SEA of PU foam than that of MP plate. The FE-calculated SEA values of PU foam and MP plate are 12.62 kJ/kg and 1.12 kJ/kg, 12.44 kJ/kg and 2.15 kJ/kg, and 15.40 kJ/kg and 3.09 kJ/kg for A30T5, A45T5 and A60T5, respectively. The averaged SEA of PU foam is 6.36 times of SEA of MP plate. The CFE is also improved with the presence of PU foam, as the PU foam filler can smooth the force–displacement curves, as shown in Fig. 2.8.

Table 2.3 Energy absorption parameters of PU foam-filled energy absorption connectors

2.3.4.2 Effect of MP Plate Thickness

Table 2.3 shows that both EA and SEA of type III connectors can be improved by increasing MP plate thickness, whereas the variation of CFE by changing MP plate thickness is insignificant. The EA and SEA are improved by 243.1% and 53.9%, respectively, by increasing the thickness of MP plate from 2.67 to 7.62 mm. thicker MP plate means higher plastic bending moment (or accumulated plastic strain energy), which leads to the improvement of EA. In addition, the increasing rate of plastic bending moment is higher than that of mass via increasing MP plate thickness, which results in the improved SEA of the connector.

2.3.4.3 Effect of Angle θ₀

As for the influence of angle θ₀ on energy absorption performances of type III connectors, increasing angle θ₀ is found to result in higher EA and SEA, as shown in Table 2.3. The values of EA and SEA of the type III connector without PU foam are increased by 97.5% and 161.3%, respectively, by increasing angle θ₀ from 30° to 60°. This is because increasing angle θ₀ leads to higher total plastic hinge rotation angles, and thus resulting in improved EA. In addition, the total length (or mass) of the MP plate is reduced with increasing angle θ₀, which results in more significant increase of SEA as compared to EA. In terms of the type III connector with PU foam, less significant improvement of EA and SEA is observed, i.e., 60.9 and 99.6% increase of EA and SEA via increasing angle θ₀ from 30° to 60°. This is because the improved EA of the MP plate via increasing total plastic hinge rotation angle is more significant as compare to the improved EA of PU foam through increased volume of PU foam. Although the improved energy absorption performance of the type III connector without PU foam is more significant than that of the connector with PU foam, the angle θ₀ should be limited to an acceptable value to prevent the unsymmetrical deformation mode. Moreover, the PU foam filler can also help to stabilize the deformation mode.

2.3.5 Energy Absorption Performance of Type IV Connector

The energy absorption parameters, EA, SEA and CFE, were employed to evaluate the energy absorption performances of type IV connectors, and CFE–displacement curves were also referred to determine densification displacement of the connectors. As shown in Fig. 2.19, the densification displacement of all the type IV connectors can be determined as 88 mm.

Fig. 2.19

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

CFE versus displacement curves of type IV connectors,

2.3.5.1 Effect of PU Foam Filler

Table 2.3 gives the values of energy absorption parameters with x_D of 88 mm for all the type IV connectors. Because of the good energy absorption capability of PU foam, the increasing percentages of EA for the three connectors (B1T5N, B2T5N and B3T5N) are 376.8%, 269.4% and 165.0%, respectively, by filling them with PU foam, as shown in Table 2.3. In addition, the corresponding increasing percentages of SEA are 314%, 222% and 132%, respectively, owing to the low density of PU foam. Moreover, the CFE is also improved because the force fluctuation of the connectors with PU foam is less significant as compared to the connectors without PU foam, i.e., the force–displacement curve of the connector becomes smoother with the presence of PU foam.

2.3.5.2 Effect of Geometric Parameter k

For the type IV connectors without PU foam, Table 2.3 shows that EA and SEA increase by 57.3% and 53.5%, respectively, by changing symmetric pleated plates (B1T5N) into AP plates (B2T5N) owing to the increase in the number of plastic hinges as well as the total plastic hinge rotation angle. In addition, higher parameter k can also lead to 65% and 61% increase of EA and SEA, respectively, by comparing the specimen B3T5N and B2T5N, as higher parameter k leads to higher total plastic hinge rotation angle with the same crushing displacement. However, the CFE shows decrease when the parameter k is increased, since the force–displacement curve of the connector with higher parameter k shows higher peak crushing force. For the type IV connectors with PU foam, the energy absorption parameters (EA and SEA) of specimen B2T5 are 21.9% and 19.6% higher than those of B1T5, and these energy absorption parameters of specimen B3T5 are 18.3% and 15.8% higher than those of B2T5. The improvement of energy absorption parameters for the connectors with PU foam is less significant as compared to the connectors without PU foam. This indicates that the improvement of energy absorption performance by increasing geometric parameter k is mainly contributed by pleated plates.

2.3.5.3 Effect of AP Plate Thickness

Table 2.3 shows that EA of the type IV connector is significantly improved by increasing AP plate thickness, owing to the increased energy absorption from plastic hinge rotation of the AP plate with higher plastic moment capacity. For the same reason, the SEA of specimen B2T8 is 26.5% higher than that of specimen B2T5. However, the SEA of specimen B2T5 is lower than specimen B2T3 because of the lower mass of specimen B2T3. Moreover, increasing AP plate thickness also leads to higher CFE, since the fluctuation of force is not significant as compared to its increased mean crushing force.

2.4 Analytical Model

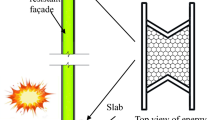
The force–displacement curves of PU foam-filled connectors are necessary to evaluate their energy absorption performances and conduct the blast resistant design when employing the proposed connectors as blast energy absorber in Fig. 1.1b. The following assumptions are employed to facilitate the calculations: (a) nominal stress–strain relation of steel employed for the connectors pertains to rigid-linear strain-hardening behavior, (b) stress state of the MP/AP plate is plane stress and (c) PU foam is uniformly compressed and its influence on the deformation pattern of the MP/AP plate is negligible.

2.4.1 Analytical Model for Type III Connector

2.4.1.1 Energy Absorption from MP Plate

As observed from the experimental and numerical results, the energy absorption from MP plates is through plastic hinge rotation, and two different deformation patterns during impact is determined, as shown in Fig. 2.20. Based on the observed deformation patterns, EA of the type III connector without PU foam is first formulated with respect to displacement. Then, the force–displacement relation can be obtained by differentiating EA with respect to displacement. In addition, the varying Dynamic Increase Factor (DIF) with respect to transient strain rate is included into the analytical model to accurately consider the strain rate effect of MP plates.

Fig. 2.20

reprinted from Wang et al. (2019), copyright 2022, with permission from Elsevier

Deformation patterns of the type III connector: a Deformation pattern I; b Deformation pattern II,

The variation of internal energy for one plastic hinge of the MP plate considering strain rate effect is presented in Eq. (1.13). It is noted that the energy absorption rate of each plastic hinge may vary with different deformation patterns, and therefore the formulae for describing the force–displacement relationships of the type III connector without PU foam in different deformation patterns are calculated separately and given as below.

In the stage of deformation pattern I (refer to Fig. 2.20a), namely, $0 \le \delta \le 2H$, the two MP plates totally have eight plastic hinges (point 1, 2, 4 and 5) rotating during crushing, and the rotation rates of all the plastic hinges are identical. Hence, the total force contributed by two MP plates within deformation pattern I (F_p1) can be obtained as

$$ \begin{aligned} F_{{p1}} & = 8\frac{{{\text{d}}U}}{{{\text{d}}\delta }} \\ & = 8bt_{{ph}} \left[ {\frac{{\sigma _{y} t_{p} ^{2} }}{4} + \frac{{E^{\prime } \kappa _{1} t_{p} ^{3} }}{{12}} + \frac{{\sigma _{y} t_{p} ^{{1/P + 2}} }}{{2^{{1/P + 1}} \left( {1/P + 2} \right)}}\left( {\frac{{\dot{\kappa }_{{\text{1}}} }}{C}} \right)^{{1/P}} } \right. \\ & \quad \quad \quad \; \left. { + \;\frac{{E^{\prime } \kappa _{1} t_{p} ^{{1/P + 3}} }}{{2^{{1/P + 2}} \left( {1/P + 3} \right)}}\left( {\frac{{\dot{\kappa }_{{\text{1}}} }}{C}} \right)^{{1/P}} } \right]\frac{{{\text{d}}\kappa _{1} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.2)

where $\kappa_{1}$ and $\dot{\kappa }_{{1}}$ are curvature change and its rate at the plastic hinge point 1 within deformation pattern I, and they can be formulated with respect to displacement $\left( \delta \right)$ and velocity $\left( {\dot{\delta }} \right)$ by referring to the geometric relation in Fig. 2.20a as follows:

$$ \kappa_{1} = (\varphi_{0} - \theta_{1} )/t_{ph} $$

(2.3)

$$ \theta_{1} = \arcsin \frac{{\left( {H - \delta /2} \right)\sin \varphi_{0} }}{H} $$

(2.4)

$$ \frac{{{\text{d}}\kappa_{1} }}{{{\text{d}}\delta }} = \left[ {2t_{ph} \sqrt {\left( {\frac{H}{{\sin \varphi_{0} }}} \right)^{2} - \left( {H - \frac{\delta }{2}} \right)^{2} } } \right]^{ - 1} $$

(2.5)

$$ \dot{\kappa }_{1} = - \frac{{\dot{\theta }_{1} }}{{t_{ph} }} = \dot{\delta }\left[ {2t_{ph} \sqrt {\left( {\frac{H}{{\sin \varphi_{0} }}} \right)^{2} - \left( {H - \frac{\delta }{2}} \right)^{2} } } \right]^{ - 1} $$

(2.6)

When the end of deformation pattern I is reached, i.e., $\delta_{Ie} = 2H$, let $\overline{\kappa }_{1} = \kappa_{1} \left( {\delta_{Ie} } \right)$.

In the stage of deformation pattern II (refer to Fig. 2.20b), namely, $2H < \delta < 4H$, the plastic hinges at point 2, 3 and 4 rotate during crushing. It is noted that the rotation rates of plastic hinges at point 2 and 4 are identical, and the rotation rate at point 3 is double of point 2 and 4. Therefore, the force contributed by MP plates within deformation pattern II can be divided into two groups according to the plastic hinge rotation rates. They are given as

$$ \begin{aligned} F_{p21} & = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4}} \right. + \frac{{E^{\prime } \left( {\kappa_{2} + \overline{\kappa }_{1} } \right)t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{1/P + 2} }}{{2^{1/P + 1} \left( {1/P + 2} \right)}}\left( {\frac{{\dot{\kappa }_{{2}} }}{C}} \right)^{1/P} \\ & \quad + \frac{{E^{\prime } \left( {\kappa_{2} + \overline{\kappa }_{1} } \right)t_{p}^{1/P + 3} }}{{2^{1/P + 2} \left( {1/P + 3} \right)}}\left. {\left( {\frac{{\dot{\kappa }_{{2}} }}{C}} \right)^{1/P} } \right]\frac{{{\text{d}}\kappa_{2} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.7)

$$ F_{p22} = 2bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \kappa_{2} t_{p}^{3} }}{{6}} + \frac{{\sigma_{y} t_{p}^{1/P + 2} }}{{2\left( {1/P + 2} \right)}}\left( {\frac{{\dot{\kappa }_{{2}} }}{C}} \right)^{1/P} } \right.\left. { + \frac{{E^{\prime } \kappa_{2} t_{p}^{1/P + 3} }}{{2\left( {1/P + 3} \right)}}\left( {\frac{{\dot{\kappa }_{{2}} }}{C}} \right)^{1/P} } \right]\frac{{{\text{d}}\kappa_{2} }}{{{\text{d}}\delta }} $$

(2.8)

where F_p21 and F_p22 are forces contributed by the rotation of plastic hinge at point 2 (or 4) and point 3, respectively. The unknown parameters in Eqs. (2.7) and (2.8) are given in Eqs. (2.9)–(2.11) according to the geometric relation in Fig. 2.20b.

$$ \kappa_{2} = {{\left[ {\arcsin \left( \frac{H}{L} \right) - \arcsin \frac{2H - \delta /2}{L}} \right]} \mathord{\left/ {\vphantom {{\left[ {\arcsin \left( \frac{H}{L} \right) - \arcsin \frac{2H - \delta /2}{L}} \right]} {t_{ph} }}} \right. \kern-\nulldelimiterspace} {t_{ph} }} $$

(2.9)

$$ \frac{{{\text{d}}\kappa_{2} }}{{{\text{d}}\delta }} = \left[ {2t_{ph} \sqrt {L^{2} - \left( {2H - \frac{\delta }{2}} \right)^{2} } } \right]^{ - 1} $$

(2.10)

$$ \dot{\kappa }_{2} = \dot{\delta }\left[ {2t_{ph} \sqrt {L^{2} - \left( {2H - \frac{\delta }{2}} \right)^{2} } } \right]^{ - 1} $$

(2.11)

where $L = H\sqrt {1 + \frac{1}{{4\tan^{2} \varphi_{0} }}}$. Then, the total force contributed by two MP plates within deformation pattern II can be obtained as

$$ F_{p2} = 4F_{p21} + 2F_{p22} $$

(2.12)

Hence, the force–displacement relation of the type III connector without PU foam (F_p) can be summarized as

$$ F_{p} = \left\{ {\begin{array}{*{20}l} {F_{p1} } \hfill & {\delta \le 2H} \hfill \\ {F_{p2} } \hfill & {2H < \delta \le 4H} \hfill \\ \end{array} } \right. $$

(2.13)

2.4.1.2 Energy Absorption from PU Foam

The experimental results showed that both PU foam compression and plastic deformation of MP plates contributed to the absorbed energy of the type III connector with PU foam. Hence, its total crushing force can be obtained by summing the forces contributed by MP plates and PU foam. Assuming the uniform compression of PU foam leads to the force contributed by PU foam (F_f) as

$$ F_{f} = - \sigma_{f} \frac{{{\text{d}}V_{c} }}{{{\text{d}}\delta }} $$

(2.14)

where V_c and $\sigma_{f}$ are current volume and compressive stress of PU foam, and $\sigma_{f}$ can be formulated in Eq. (2.15) with the strain rate effect being considered (Jeong et al. 2012).

$$ \sigma_{f} = \left[ {1 + \left( {a_{0} + b_{0} \varepsilon } \right)\ln \left( {\frac{{\dot{\varepsilon }_{V} }}{{\dot{\varepsilon }_{0} }}} \right)} \right]\left[ {A\left( {1 - e^{{ - (E/A)\varepsilon_{V} (1 - \varepsilon_{V} )^{m} }} } \right) + B\left( {\frac{{\varepsilon_{V} }}{{1 - \varepsilon_{V} }}} \right)^{n} } \right] $$

(2.15)

where A, B, E, m and n are material parameters of PU foam and given in Table 2.4 via fitting the material test data. The reference strain rate $\dot{\varepsilon }_{0}$ as well as strain rate parameters a₀ and b₀ are given in Sect. 2.2.2. The volumetric strain and strain rate can be given as follows:

$$ \varepsilon = 1 - V_{c} /V_{0} $$

(2.16)

$$ \dot{\varepsilon } = - \frac{{\dot{\delta }}}{{V_{0} }}\frac{{{\text{d}}V_{c} }}{{{\text{d}}\delta }} $$

(2.17)

Table 2.4 Material parameters of PU foam

where $\dot{\delta }$ is velocity, and V₀ is initial volume of PU foam and can be obtained as

$$ V_{0} = \left( {8HL_{1} - \frac{{5H^{2} }}{{\tan \varphi_{0} }}} \right)b $$

(2.18)

The geometric properties in Eq. (2.12) can be found in Fig. 2.20, and the formulae of V_c and dV_c/dδ in deformation pattern I and II are summarized as below.

In the stage of deformation pattern I, namely, $0 \le \delta \le 2H$, the current volume of PU foam and its differential with respect to displacement can be obtained as

$$ V_{c} = \left[ {8HL_{1} - 2\delta L_{1} + \frac{{H^{2} }}{{\tan \varphi_{0} }} - \left( {6H - \delta } \right)\sqrt {\left( {\frac{H}{{\sin \varphi_{0} }}} \right)^{2} - \left( {H - \frac{\delta }{2}} \right)^{2} } } \right]b $$

(2.19)

$$ \frac{{{\text{d}}V_{c} }}{{{\text{d}}\delta }} = \left[ { - 2L_{1} + \sqrt {\left( {\frac{H}{{\sin \varphi_{0} }}} \right)^{2} - \left( {H - \frac{\delta }{2}} \right)^{2} } + \frac{{\left( {\delta - 6H} \right)\left( {2H - \delta } \right)}}{{4\sqrt {\left( {\frac{H}{{\sin \varphi_{0} }}} \right)^{2} - \left( {H - \frac{\delta }{2}} \right)^{2} } }}} \right]b $$

(2.20)

In the stage of deformation pattern II, i.e., $2H < \delta < 4H$, the current volume of PU foam and its differential with respect to displacement can be obtained as

$$ V_{c} = \left[ {2L_{1} - \frac{2H}{{\sin \varphi_{0} }} + \sqrt {\left( {1 + \frac{1}{{4\tan^{2} \varphi_{0} }}} \right)H^{2} - \left( {2H - \frac{\delta }{2}} \right)^{2} } } \right]\left( {4H - \delta } \right)b $$

(2.21)

$$ \begin{aligned} \frac{{{\text{d}}V_{c} }}{{{\text{d}}\delta }} & = \frac{2Hb}{{\sin \varphi_{0} }} - 2L_{1} b - b\sqrt {\left( {1 + \frac{1}{{4\tan^{2} \varphi_{0} }}} \right)H^{2} - \left( {2H - \frac{\delta }{2}} \right)^{2} } \\ & \quad + \frac{{\left( {\delta - 4H} \right)^{2} b}}{{4\sqrt {\left( {1 + \frac{1}{{4\tan^{2} \varphi_{0} }}} \right)H^{2} - \left( {2H - \frac{\delta }{2}} \right)^{2} } }} \\ \end{aligned} $$

(2.22)

Then, substituting Eqs. (2.15)–(2.22) into Eq. (2.14) leads to the force contributed by PU foam. Finally, the total force of the type III connector with PU foam (F_u) can be obtained as

$$ F_{u} = F_{p} + F_{f} $$

(2.23)

2.4.1.3 Validation with Experimental and Numerical Results

The force–displacement curves obtained from the analytical model are compared with those obtained from experiments and FE analyses in Fig. 2.8. Consistent results among them can be seen. The sudden change of force induced by deformation mode change can be reasonably captured by the analytical model. However, the fluctuations of the force–displacement curves induced by inertial effect are not captured by the analytical model. However, these differences are not significant and will not affect the energy absorption evaluation of the connectors. From above discussions, the developed analytical model is proven to be accurate in predicting the force–displacement responses and energy absorptions of the type III connectors.

2.4.2 Analytical Model for Type IV Connector

2.4.2.1 Energy Absorption from AP Plate

As analyzed in Sect. 2.3.2, EA of the type IV connector without PU foam is generally concentrated at the plastic hinge zones, and its deformation mode is divided into three stages. Hence, an analytical model to calculate EA of the connector contributed by plastic hinge rotation is proposed, and its geometric parameters are presented in Fig. 2.21. According to geometric relation, the critical displacement D₁ and D₂ can be calculated as:

$$ D_{1} = \left( {k + 1} \right)H - H_{0} \quad {\text{and}}\quad D_{2} = \left( {k + 1} \right)H - \sqrt {H_{0}^{2} + L^{2} } + L $$

(2.24)

Fig. 2.21

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Deformation patterns of the type IV connector: a Deformation stage I; b Deformation stage II; c Deformation stage III,

where $H_{0} = \sqrt {k^{2} - 1} H$. Similar to the type III connector, the energy absorption rate of each plastic hinge for the type IV connector also varies with different deformation stages. Hence, the force–displacement relationship of the type IV connector at different deformation stages should be calculated separately, and EA can be subsequently calculated by numerically integrating the force to displacement.

In deformation stage I (Fig. 2.21a), i.e., $0 \le \delta \le D_{1}$, the total force contributed by AP plates, $F_{p1}$, is determined by summing the forces contributed by the six plastic hinges at point 1, 2 and 3, i.e.,

$$ F_{p1} = 2\left( {F_{11} + F_{12} + F_{13} } \right) $$

(2.25)

and the forces contributed by the plastic hinges at point 1, 2 and 3 in deformation stage I (i.e., $F_{11}$, $F_{12}$ and $F_{13}$) can be obtained as

$$ \begin{aligned} F_{11} & = \frac{{{\text{d}}U_{11} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \kappa_{11} t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{11} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \quad \left. { + \frac{{E^{\prime } \kappa_{11} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{11} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{11} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.26)

$$ \begin{aligned} F_{12} & = \frac{{{\text{d}}U_{12} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \left( {\kappa_{11} + \kappa_{13} } \right)t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{11} + {\text{d}}\kappa_{13} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \quad \left. { + \frac{{E^{\prime } \left( {\kappa_{11} + \kappa_{13} } \right)t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{11} + {\text{d}}\kappa_{13} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\left( {\kappa_{11} + \kappa_{13} } \right)}}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.27)

$$ \begin{aligned} F_{13} & = \frac{{{\text{d}}U_{13} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \kappa_{13} t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{13} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \quad \left. { + \frac{{E^{\prime } \kappa_{13} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{13} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{13} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.28)

where

$$ \kappa_{11} = \frac{1}{{t_{ph} }}\left( {\arcsin \frac{H}{L} - \arcsin \frac{{H - \delta_{{{\text{IA}}}} }}{L}} \right) $$

(2.29)

$$ \kappa_{13} = \frac{1}{{t_{ph} }}\left( {\arcsin \frac{kH}{{\sqrt {H_{0}^{2} + L^{2} } }} - \arcsin \frac{{kH - \delta_{{{\text{IB}}}} }}{{\sqrt {H_{0}^{2} + L^{2} } }}} \right) $$

(2.30)

$$ \frac{{{\text{d}}\kappa_{11} }}{{{\text{d}}\delta }} = \frac{{4\left( {kH - \delta } \right)\left( {kH + H - \delta } \right) + 2\delta \left( {2kH - \delta } \right)}}{{t_{ph} \left[ {2H\left( {k + 1} \right) - 2\delta } \right]^{2} \sqrt {L^{2} - \left( {H - \delta_{{{\text{IA}}}} } \right)^{2} } }} $$

(2.31)

$$ \frac{{{\text{d}}\kappa_{13} }}{{{\text{d}}\delta }} = \frac{{4\left( {H - \delta } \right)\left( {kH + H - \delta } \right) + 2\delta \left( {2H - \delta } \right)}}{{t_{ph} \left[ {2H\left( {k + 1} \right) - 2\delta } \right]^{2} \sqrt {\left( {H_{0}^{2} + L^{2} } \right) - \left( {kH - \delta_{{{\text{IB}}}} } \right)^{2} } }} $$

(2.32)

$$ \delta_{{{\text{IA}}}} = \frac{{\left( {2kH - \delta } \right)\delta }}{{2H\left( {k + 1} \right) - 2\delta }} $$

(2.33)

$$ \delta_{{{\text{IB}}}} = \frac{{\left( {2H - \delta } \right)\delta }}{{2H\left( {k + 1} \right) - 2\delta }} $$

(2.34)

In Eqs. (2.29)–(2.34), $\kappa_{11}$ and $\kappa_{13}$ are the changes of curvature at point 1 and 3, $\delta_{{{\text{IA}}}}$ and $\delta_{{{\text{IB}}}}$ are the displacements of bottom plate and top plate relative to point 2 (refer to Fig. 2.21a), and $\delta = \delta_{IA} + \delta_{IB}$ is the total displacement. When $\delta = D_{1}$, let $\overline{\kappa }_{13} = \kappa_{13} \left( {D_{1} } \right)$.

In deformation stage II (Fig. 2.21b), i.e.,$D_{1} \le \delta \le D_{2}$, as analyzed in Sect. 2.3.2, the forth pair of plastic hinges occur at point 4, and plastic hinge 1 stops rotating. Meanwhile, plastic hinge 3 continues rotating, and plastic hinge 2 starts to rotate reversely. Hence, the total force in deformation stage II, $F_{p2}$, is obtained by summing the forces contributed by the six plastic hinges at point 2, 3 and 4, i.e.,

$$ F_{p2} = 2\left( {F_{22} + F_{23} + F_{24} } \right) $$

(2.35)

and the forces contributed by the plastic hinges at point 2, 3 and 4 in deformation stage II (i.e., $F_{22}$, $F_{23}$ and $F_{24}$) can be obtained as

$$ \begin{aligned} F_{22} & = \frac{{{\text{d}}U_{22} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \kappa_{22} t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{22} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \quad \left. { + \frac{{E^{\prime } \kappa_{22} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{22} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{22} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.36)

$$ \begin{aligned} F_{23} & = \frac{{{\text{d}}U_{23} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \left( {\kappa_{23} + \overline{\kappa }_{13} } \right)t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{23} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \quad \left. { + \frac{{E^{\prime } \left( {\kappa_{23} + \overline{\kappa }_{13} } \right)t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{23} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{23} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.37)

$$ \begin{aligned} F_{24} & = \frac{{{\text{d}}U_{24} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \left( {\kappa_{22} + \kappa_{23} } \right)t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{22} + {\text{d}}\kappa_{23} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \quad \left. { + \frac{{E^{\prime } \left( {\kappa_{22} + \kappa_{23} } \right)t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{22} + {\text{d}}\kappa_{23} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{22} + {\text{d}}\kappa_{23} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.38)

where

$$ \kappa_{22} = \frac{{\theta_{22} - \theta_{20} }}{{t_{ph} }} $$

(2.39)

$$ \kappa_{23} = \frac{{\theta_{20} - \theta_{23} }}{{t_{ph} }} $$

(2.40)

$$ \begin{aligned} \frac{{{\text{d}}\kappa_{22} }}{{{\text{d}}\delta }} & = \frac{{\left( {H_{0} - \delta_{{{\text{II}}}} } \right)\left( {2L\sqrt {H_{0}^{2} + L^{2} } - 2H_{0} \delta_{{{\text{II}}}} + \delta_{{{\text{II}}}}^{2} } \right)}}{{t_{ph} \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right]\sqrt {4L^{2} \left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right)^{2} - \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} - \left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right)^{2} } \right]^{2} } }} \\ & \quad - \frac{L}{{t_{ph} \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right]}} \\ \end{aligned} $$

(2.41)

$$ \begin{aligned} \frac{{{\text{d}}\kappa_{23} }}{{{\text{d}}\delta }} & = \frac{{\left( {H_{0} - \delta_{{{\text{II}}}} } \right)\left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + 2L^{2} + H_{0}^{2} - 2L\sqrt {H_{0}^{2} + L^{2} } } \right]}}{{t_{ph} \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right]\sqrt {4L^{2} \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right] - \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + 2L\sqrt {H_{0}^{2} + L^{2} } - H_{0}^{2} } \right]^{2} } }} \\ & \quad + \frac{L}{{t_{ph} \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right]}} \\ \end{aligned} $$

(2.42)

$$ \theta_{20} = \arctan \frac{{H_{0} }}{L} $$

(2.43)

$$ \theta_{22} = \pi - \arcsin \frac{{\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + \left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right)^{2} }}{{2\left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right)\sqrt {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } }} - \arctan \frac{L}{{H_{0} - \delta_{{{\text{II}}}} }} $$

(2.44)

$$ \theta_{23} = \arcsin \frac{{\delta_{{{\text{II}}}}^{2} - 2H_{0} \delta_{{{\text{II}}}} + 2L\sqrt {H_{0}^{2} + L^{2} } }}{{2L\sqrt {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } }} - \arctan \frac{L}{{H_{0} - \delta_{{{\text{II}}}} }} $$

(2.45)

$$ \delta_{{{\text{II}}}} = \delta - \left( {k + 1 - \sqrt {k^{2} - 1} } \right)H $$

(2.46)

In Eqs. (2.39)–(2.46), $\kappa_{22}$ and $\kappa_{23}$ are the changes of curvature at point 2 and 3, $\theta_{20}$ is the initial angle at point 2, and $\theta_{22}$ and $\theta_{23}$ are the angle changes at point 2 and 3 (refer to Fig. 2.21b), and $\delta_{{{\text{II}}}}$ is the displacement increment during deformation stage II. When $\delta = D_{2}$, let $\overline{\kappa }_{22} = \kappa_{22} \left( {D_{2} } \right)$.

In deformation stage III (Fig. 2.21c), i.e., $D_{2} \le \delta \le \left( {k + 1} \right)H$, the fifth pair of plastic hinges occur at point 5, and plastic hinge 3 stops rotating. Meanwhile, plastic hinge 2 continues rotating, and plastic hinge 4 starts to rotate reversely. Hence, the total force in deformation stage III, $F_{p3}$, is obtained by summing the forces contributed by the six plastic hinges at point 2, 4 and 5, i.e.,

$$ F_{p3} = 2\left( {F_{32} + F_{34} + F_{35} } \right) $$

(2.47)

and the forces contributed by the plastic hinges at point 2, 4 and 5 in deformation stage III (i.e., $F_{32}$, $F_{34}$ and $F_{35}$) can be obtained as

$$ \begin{aligned} F_{32} & = \frac{{{\text{d}}U_{32} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \left( {\kappa_{32} { + }\overline{\kappa }_{22} } \right)t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \qquad \left. { + \frac{{E^{\prime } \left( {\kappa_{32} { + }\overline{\kappa }_{22} } \right)t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.48)

$$ \begin{aligned} F_{34} & = \frac{{{\text{d}}U_{34} }}{{{\text{d}}\delta }} = bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \kappa_{32} t_{p}^{3} }}{12} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 1}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \qquad \left. { +\, \frac{{E^{\prime } \kappa_{32} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} \left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.49)

$$ \begin{aligned} F_{35} & = \frac{{{\text{d}}U_{35} }}{{{\text{d}}\delta }} = 2bt_{ph} \left[ {\frac{{\sigma_{y} t_{p}^{2} }}{4} + \frac{{E^{\prime } \kappa_{32} t_{p}^{3} }}{6} + \frac{{\sigma_{y} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2}} }}{{2\left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 2} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right. \\ & \qquad \left. { +\, \frac{{E^{\prime } \kappa_{32} t_{p}^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3}} }}{{2\left( {{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P} + 3} \right)}}\left( {\frac{{\dot{\delta }}}{C} \cdot \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 P}} \right. \kern-\nulldelimiterspace} P}}} } \right]\frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.50)

where

$$ \kappa_{32} = \frac{1}{{t_{ph} }}\theta_{{{32}}} $$

(2.51)

$$ \frac{{{\text{d}}\kappa_{32} }}{{{\text{d}}\delta }} = \frac{1}{{t_{ph} \sqrt {2\delta_{{{\text{III}}}} \left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right) - \delta_{{{\text{III}}}}^{2} } }} $$

(2.52)

$$ \theta_{{{32}}} = \arccos \frac{{\sqrt {H_{0}^{2} + L^{2} } - L - \delta_{{{\text{III}}}} }}{{\sqrt {H_{0}^{2} + L^{2} } - L}} $$

(2.53)

$$ \delta_{{{\text{III}}}} = \delta - \left( {k + 1} \right)H + \sqrt {H_{0}^{2} + L^{{2}} } - L $$

(2.54)

In Eqs. (2.51)–(2.53), $\kappa_{32}$ and $\theta_{{{32}}}$ are curvature change and angle change at point 2, and $\delta_{{{\text{III}}}}$ is the displacement increment during deformation stage III, as illustrated in Fig. 2.21c.

In summary, the EA of the type IV connector without PU foam can be formulated as

$$ EA_{p} \left( \delta \right) = \left\{ {\begin{array}{*{20}l} {\int_{0}^{\delta } {F_{p1} } \left( \delta \right){\text{d}}\delta \quad 0 \le \delta \le D_{1} } \hfill \\ {\int_{0}^{{D_{1} }} {F_{p1} } \left( \delta \right){\text{d}}\delta + \int_{{D_{1} }}^{\delta } {F_{p2} } \left( \delta \right){\text{d}}\delta \quad D_{1} \le \delta \le D_{2} } \hfill \\ {\int_{0}^{{D_{1} }} {F_{p1} \left( \delta \right)} {\text{d}}\delta + \int_{{D_{1} }}^{{D_{2} }} {F_{p2} } \left( \delta \right){\text{d}}\delta + \int_{{D_{2} }}^{\delta } {F_{p3} } \left( \delta \right){\text{d}}\delta \quad D_{2} \le \delta \le D_{3} } \hfill \\ \end{array} } \right. $$

(2.55)

2.4.2.2 Energy Absorption from PU Foam

The some method presented in Sect. 2.4.1.2 (i.e., Eqs. (2.14)–(2.17)) can be employed herein to calculate the force–displacement response of the type IV connector contributed by PU foam. According to the geometric relationship shown in Fig. 2.21a, the initial volume of PU foam filled in the type IV connector, $V_{0}$, can be formulated as

$$ V_{0} = \left( {k + 1} \right)\left( {2L_{1} - \sqrt {L^{2} - H^{2} } } \right)bH $$

(2.56)

To obtained the volumetric strain ε and strain rate $\dot{\varepsilon }$, the current volume, $V_{c}$, and its derivative of current volume of PU foam with respective to displacement $\left( {{{{\text{d}}V} \mathord{\left/ {\vphantom {{{\text{d}}V} {{\text{d}}\delta }}} \right. \kern-\nulldelimiterspace} {{\text{d}}\delta }}} \right)$ in three deformation stages should be calculated and presented as follows.

In deformation stage I, i.e.,$0 \le \delta \le D_{1}$, the current volume of PU foam, $V_{c1}$, is calculated as

$$ V_{c1} = \left[ {(k + 1)H - \delta_{{{\text{IA}}}} - \delta_{{{\text{IB}}}} } \right]\left[ {2L_{1} - \sqrt {L^{2} - (H - \delta_{{{\text{IA}}}} )^{2} } } \right]b $$

(2.57)

and ${{{\text{d}}V_{c1} } \mathord{\left/ {\vphantom {{{\text{d}}V_{c1} } {{\text{d}}\delta }}} \right. \kern-\nulldelimiterspace} {{\text{d}}\delta }}$ is calculated as

$$ \begin{aligned} \frac{{{\text{d}}V_{c1} }}{{{\text{d}}\delta }} & = b\left( { - \frac{{{\text{d}}\delta_{{{\text{IA}}}} }}{{{\text{d}}\delta }} - \frac{{{\text{d}}\delta_{{{\text{IB}}}} }}{{{\text{d}}\delta }}} \right)\left( {2L_{1} - \sqrt {L^{2} - (H - \delta_{{{\text{IA}}}} )^{2} } } \right) \\ & \quad + b\left[ {(k + 1)H - \delta_{{{\text{IA}}}} - \delta_{{{\text{IB}}}} } \right]\frac{{\delta_{{{\text{IA}}}} - H}}{{\sqrt {L^{2} - (H - \delta_{{{\text{IA}}}} )^{2} } }} \cdot \frac{{{\text{d}}\delta_{{{\text{IA}}}} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.58)

where

$$ \frac{{{\text{d}}\delta_{{{\text{IA}}}} }}{{{\text{d}}\delta }} = \frac{{2H\left( {k + 1} \right)\left( {kH - \delta } \right) + \delta^{2} }}{{2\left[ {H\left( {k + 1} \right) - \delta } \right]^{2} }} $$

(2.59)

$$ \frac{{{\text{d}}\delta_{{{\text{IB}}}} }}{{{\text{d}}\delta }} = \frac{{2H\left( {k + 1} \right)\left( {H - \delta } \right) + \delta^{2} }}{{2\left[ {H\left( {k + 1} \right) - \delta } \right]^{2} }} $$

(2.60)

In deformation stage II, i.e., $D_{1} < \delta < D_{2}$, the current volume of PU foam, $V_{c2}$, is calculated as

$$ V_{c2} = \left[ {\left( {2L_{1} - L - L\cos \theta_{23} } \right)\left( {H_{0} - \delta_{{{\text{II}}}} } \right) + L^{2} \sin \theta_{23} } \right]b $$

(2.61)

and ${{{\text{d}}V_{c2} } \mathord{\left/ {\vphantom {{{\text{d}}V_{c2} } {{\text{d}}\delta }}} \right. \kern-\nulldelimiterspace} {{\text{d}}\delta }}$ is calculated as

$$ \frac{{{\text{d}}V_{c2} }}{{{\text{d}}\delta }} = bL\left( {H_{0} - \delta_{{{\text{II}}}} } \right)\sin \theta_{23} \frac{{{\text{d}}\theta_{23} }}{{{\text{d}}\delta }} - b\left( {2L_{1} - L - L\cos \theta_{23} } \right) + bL^{2} \cos \theta_{23} \frac{{{\text{d}}\theta_{23} }}{{{\text{d}}\delta }} $$

(2.62)

where

$$ \begin{aligned} \frac{{{\text{d}}\theta_{23} }}{{{\text{d}}\delta }} & = \frac{{\left( {\delta_{{{\text{II}}}} - H_{0} } \right)\left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + 2L^{2} + H_{0}^{2} - 2L\sqrt {H_{0}^{2} + L^{2} } } \right]}}{{\left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right]\sqrt {4L^{2} \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} } \right] - \left[ {\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + 2L\sqrt {H_{0}^{2} + L^{2} } - H_{0}^{2} } \right]^{2} } }} \\ & \quad - \frac{L}{{\left( {H_{0} - \delta_{{{\text{II}}}} } \right)^{2} + L^{2} }} \\ \end{aligned} $$

(2.63)

In deformation stage III, i.e., $D_{2} \le \delta \le \left( {k + 1} \right)H$, the current volume of PU foam,$V_{c3}$, is calculated as

$$ V_{c3} = b\left( {2L_{1} - {2}L - \frac{{\sqrt {H_{0}^{2} + L^{2} } - L}}{2}\sin \theta_{{{32}}} } \right)\left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right)\cos \theta_{{{32}}} $$

(2.64)

and ${{{\text{d}}V_{c3} } \mathord{\left/ {\vphantom {{{\text{d}}V_{c3} } {{\text{d}}\delta }}} \right. \kern-\nulldelimiterspace} {{\text{d}}\delta }}$ is calculated as

$$ \begin{aligned} \frac{{{\text{d}}V_{c3} }}{{{\text{d}}\delta }} & = - b\left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right)^{2} \cdot \frac{{\cos^{2} \theta_{{{32}}} }}{2} \cdot \frac{{{\text{d}}\theta_{{{32}}} }}{{{\text{d}}\delta }} \\ & \quad - b\left( {2L_{1} - {2}L - \frac{{\sqrt {H_{0}^{2} + L^{2} } - L}}{2}\sin \theta_{{{32}}} } \right) \cdot \sin \theta_{{{32}}} \cdot \frac{{{\text{d}}\theta_{{{32}}} }}{{{\text{d}}\delta }} \\ \end{aligned} $$

(2.65)

where

$$ \frac{{{\text{d}}\theta_{32} }}{{{\text{d}}\delta }} = \frac{1}{{\sqrt {2\delta_{{{\text{III}}}} \left( {\sqrt {H_{0}^{2} + L^{2} } - L} \right) - \delta_{{{\text{III}}}}^{2} } }} $$

(2.66)

In summary, the EA of the type IV connector contributed by PU foam can be obtained as

$$ EA_{f} \left( \delta \right) = \int\limits_{0}^{\delta } {F_{f} } \left( \delta \right){\text{d}}\delta $$

(2.67)

and the total EA of the type IV connector with PU foam, $EA_{u}$, is obtained as

$$ EA_{u} \left( \delta \right) = EA_{p} \left( \delta \right) + EA_{f} \left( \delta \right) $$

(2.68)

2.4.2.3 Validation with Experimental Results

Figure 2.22 shows the EA–displacement curves of type IV connectors obtained from experiments and analytical predictions, and the analytical-predicted results are found to be generally consistent with test results. However, the analytical predictions are still slightly different from experimental results. This is mainly because the analytical model does not consider the initial bending of AP plates corresponding to the critical displacements D₁ and D₂, which leads to the sudden changes of EA–displacement curves from the analytical model. Another reason is that the influence of PU foam on the deformation shape of AP plates becomes increasingly significant after densification, especially in the deformation stage III (as shown in Fig. 2.22b, c). Moreover, geometric imperfection as well as cracking and peeling of PU foam can also cause the difference between the analytical and experimental results. However, the differences are not significant and will not affect the rationality of the analytical results, especially for the deformation stage I and II. Hence, the proposed analytical model can be employed to predict the EA (or force) of the type IV connector under impact loading.

Fig. 2.22

reprinted from Wang et al. (2020), copyright 2022, with permission from Elsevier

Comparison of EA–displacement curves of type IV connectors between tests and analytical predictions: a Variant pleated plate parameter k without foam; b Variant pleated plate parameter k with foam; c Variant pleated plate thickness with foam,

2.5 Summary

Two types of PU foam-filled energy absorption connectors were proposed in this chapter, and their energy absorption performances were experimentally, numerically and analytically studied. The deformation modes, force–displacement responses of the PU foam-filled connectors with varying geometries were investigated via conducting drop-weight impact tests. Finally, the analytical models were developed for predicting force–displacement responses of the proposed connectors. The main findings from this chapter could be summarized as follows:

• (1) The deformation process of type III connectors could be divided into two patterns according to the different distributions of plastic hinge zones, and three patterns could be observed for the type IV connectors.

• (2) PU foam filler could evidently improve the energy absorption performances of both type III and IV connectors in terms of the improvement of EA, SEA and CFE, which could be attributed to the higher energy absorption, lightweight and smooth stress–strain curve of PU foam.

• (3) Increasing MP plate thickness and angle θ₀ resulted in significant increase of EA and SEA for type III connectors. In addition, the type III connector without PU foam was found to be more sensitive to the variation of angle θ₀. With regard to type IV connectors, increasing the geometric parameter k could increase EA and SEA. In addition, increasing AP thickness could increase EA, whereas the SEA was not necessarily increased owing to the increase in mass.

• (4) The developed analytical models could provide acceptable predictions on the force–displacement relations of the PU foam-filled connectors via comparing with the experimental and numerical results. Hence, they could be utilized to evaluate the energy absorption performances of proposed connectors.