Keywords

1 Introduction

In recent years, there has been a growing interest in satellite formation flying and there are many space applications of formation flying, such as stereo observation, SAR interferometry etc. [1]. The earliest and most prevalent model governing relative motion is given by the Clohessy-Wiltshire (C-W) equation [2] which assumes a circular reference orbit for target satellite, providing an analytic description of relative motion. The Tschauner-Hempel (T-H) equation [3] extend the C-W model to accommodate non-circular reference orbit, by expressing the equations of motion in terms of target orbit eccentricity and initial true anomaly [4]. Currently, there have been many scientific papers written on the subjects of high precision models and configuration designing for relative motion. Katsuhiko [5] developed expansion of T-H equation which considering J2 perturbation to improve the calculating precision. Mai [6] developed a graphical analysis for T-H equation based on the period orbit. Schaub [7] proposed a new presentation which is based on the orbital elements difference. For configuration controlling of relative motion, Vadali [8] designed a digital filter to eliminate the period vibration which can reduce the fuel consumption. Balaji [9] has parameterized C-W equation in terms of mean value for configuration controlling.

There is a wealth of literature on relative motion models. Nevertheless, the averaged equation over orbit period is useful for relative motion analysis, especially for long term prediction and formation configuration designing. Based on the average calculation in an orbit period, two different averaged relative motion equations are presented in this paper. Then, the characteristic of averaged models are also been developed. The analysis thought and calculation of this method is simple, and the effectiveness of the model was proved by digital simulations.

2 Relative Motions in Two-Body Orbit

We take the orbit coordinate systems oxyz of the target satellite as the relative motion coordinate system. The origin is the center of the mass of the target satellite, and move in orbit with it. The x-axis coincides with geocentric vector r of the target satellite, and points from geocenter to target satellite. The y-axis is normal to x-axis in the orbit plane, and points to the direction of motion. The z-axis determined by right-hand rule, coincides with the angular momentum vector of the target satellite. The relative motion coordinate system oxyz and geocentric inertial coordinate system OXYZ is shown in Fig. 1.

Fig. 1.
figure 1

The oxyz and OXYZ coordinate.

Full size image

2.1 Relative Motion Model and Analytical Equation

Consider two satellites in elliptical orbits about a common gravitational source, as shown in Fig. 1. Employing the common designations associated with relative motions, tracking satellite denotes the second satellite, moving close to the target and with position \({\varvec{r}}_{t}\).

By form the relative position vector \({\varvec{\rho}} = [x \, y \, z]^{{\text{T}}}\). Based on the condition of \(\rho < < r\), the relative motion equation in two-body orbit can be described by [4].

$$ \left[ {\begin{array}{*{20}c} {x^{\prime\prime}} \\ {x^{\prime}} \\ {y^{\prime\prime}} \\ {y^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{2e\sin f}{{\lambda_{f}^{{}} }}} & {1 + \frac{2}{{\lambda_{f}^{{}} }}} & 2 & { - \frac{2e\sin f}{{\lambda_{f}^{{}} }}} \\ 1 & 0 & 0 & 0 \\ { - 2} & {\frac{2e\sin f}{{\lambda_{f}^{{}} }}} & {\frac{2e\sin f}{{\lambda_{f}^{{}} }}} & {\frac{e\cos f}{{\lambda_{f}^{{}} }}} \\ 0 & 0 & 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x^{\prime}} \\ x \\ {y^{\prime}} \\ y \\ \end{array} } \right] $$
(1)
$$ \left[ {\begin{array}{*{20}c} {z^{\prime\prime}} \\ {z^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{2e\sin f}{{\lambda_{f}^{{}} }}} & { - \frac{1}{{\lambda_{f}^{{}} }}} \\ 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {z^{\prime}} \\ z \\ \end{array} } \right] $$
(2)

where \(\lambda_{f} = 1 + e\cos f\), \(e\) is the eccentricity of target satellite, \(f\) is true anomaly of target satellite, \(( \cdot )^{\prime} = d( \cdot )/df\). In two body orbit, the analytical model of Eq. 1 can be written as follows [4]:

$$ \left. {\begin{array}{*{20}l} {x(f)} \hfill & = \hfill & {\left[ {d_{1} e + 2d_{2} e^{2} H(f)} \right]\sin f - (d_{2} e\lambda_{f}^{ - 2} + d_{3} )\cos f} \hfill \\ {y(f)} \hfill & = \hfill & {d_{3} (1 + \lambda_{f}^{ - 1} )\sin f + \left[ {d_{1} e + 2d_{2} e^{2} H(f)} \right]\cos f + \left[ {d_{1} + d_{4} \lambda_{f}^{ - 1} + 2d_{2} eH(f)} \right]} \hfill \\ {z(f)} \hfill & = \hfill & {d_{5} \lambda_{f}^{ - 1} \sin f + d_{6} \lambda_{f}^{ - 1} \cos f} \hfill \\ \end{array} } \right\} $$
(3)
$$ \left. {\begin{array}{*{20}l} {x^{\prime}(f)} \hfill & = \hfill & {[d_{2} e\lambda_{f}^{ - 2} + d_{3} ]\sin f + \left[ {d_{1} e + 2d_{2} e^{2} H(f)} \right]\cos f} \hfill \\ {y^{\prime}(f)} \hfill & = \hfill & {\left[ {d_{3} e\lambda_{f}^{ - 2} \sin f + d_{4} e\lambda_{f}^{ - 2} - d_{1} e - 2d_{2} e^{2} H(f)} \right]\sin f + \left[ {d_{3} (1 + \lambda_{f}^{ - 1} ) + 2d_{2} e\lambda_{f}^{ - 2} } \right]\cos f} \hfill \\ {z^{\prime}(f)} \hfill & = \hfill & {(d_{5} e\lambda_{f}^{ - 2} \sin f - d_{6} \lambda_{f}^{ - 1} )\sin f + (d_{5} \lambda_{f}^{ - 1} + d_{6} e\lambda_{f}^{ - 2} \sin f)\cos f} \hfill \\ \end{array} } \right\} $$
(4)

where \(d_{i} (i = 1,...,6)\) is the integral constant, \(H(f)\) is integral expansion item.

2.2 The Averaged Equation of Relative Motion

It is well known that typical character of the T-H equations is periodicity of orbit because each equation contains trigonometric function. For applications to surveillance, the first goal is to survey the averaged equation in an orbit period.

Because the integral expansion item \(H(f)\) is very complex, and it is difficult to directly calculate the average equation. Nevertheless, the series of \(H(f)\) can be used to express the equations. Based on the power series

$$ \lambda_{f}^{m} = \left( {1 + e\cos f} \right)^{m} = 1 + me\cos f + \cdots + \frac{m(m - 1) \cdots (m - n + 1)}{{n!}}e^{n} \cos^{n} f + \cdots $$
(5)

The integral expansion item \(H(f)\) can be rewritten as

$$ H(f) = \sin f - 3e{[}\frac{f}{2} + \frac{{{\text{sin2}}f}}{{4}}{]} + 6e^{{2}} {[}\sin f + \frac{{{\text{sin}}^{{3}} f}}{{3}}{] - }10e^{{3}} {[}\frac{3f}{8} + \frac{3}{16}{\text{sin2}}f + \frac{{\sin f{\text{cos}}^{{3}} f}}{{4}}{]} + \cdots - H_{{f_{0} }} $$
(6)

where

$$ H_{{f_{0} }} = \sin f_{0} - 3e{[}\frac{{f_{0} }}{2} + \frac{{{\text{sin2}}f_{0} }}{{4}}{]} + 6e^{{2}} {[}\sin f_{0} + \frac{{{\text{sin}}^{{3}} f_{0} }}{{3}}{] - }10e^{{3}} {[}\frac{{3f_{0} }}{8} + \frac{3}{16}{\text{sin2}}f_{0} + \frac{{\sin f_{0} {\text{cos}}^{{3}} f_{0} }}{{4}}{] + } \cdots $$
(7)

\(f_{0}\) is the true anomaly at initial time. For satellites in low earth orbit, \(e^{4}\) and higher items are very small which can be omitted in calculation. The Eq. 7 can be approximated as

$$ H(f) \approx \sin f - 3e{[}\frac{f}{2} + \frac{{{\text{sin2}}f}}{{4}}{]} + 6e^{{2}} {[}\sin f - \frac{{{\text{sin}}^{{3}} f}}{{3}}{] - }10e^{{3}} {[}\frac{3f}{8} + \frac{3}{16}{\text{sin2}}f + \frac{{\sin f{\text{cos}}^{{3}} f}}{{4}}{]} - H_{{f_{0} }} $$
(8)

Then, the x-axis averaged motion in an orbit period can be calculated as

$$ \overline{x} = \frac{1}{2\pi }\int_{0}^{2\pi } {\left\{ {\left[ {d_{1} e + 2d_{2} e^{2} H(f)} \right]\sin f - (d_{2} e\lambda_{f}^{ - 2} + d_{3} )\cos f} \right\}df} $$
(9)

Substituting Eq. 8 into Eq. 9, omitting \(e^{4}\) and higher order items, we obtain

$$ \begin{array}{*{20}l} {\overline{x}} \hfill & { \approx \frac{{d_{2} e}}{2\pi }\int_{0}^{2\pi } {\left\{ {{2}e\left[ {{\text{sin}}^{{2}} f - 3e{(}\frac{f\sin f}{2} + \frac{{\sin f{\text{sin2}}f}}{{4}}{)}} \right]{ - 2}e\sin fH_{{f_{0} }} - \cos f\left[ {1 - 2e\cos f + 3e^{{2}} {\text{cos}}^{{2}} f} \right]} \right\}df} } \hfill \\ {} \hfill & { = (2e^{2} + 3e^{3} )d_{2} } \hfill \\ \end{array} $$
(10)

In the same way the averaged relative position and averaged relative velocity in y-axis and z-axis can be obtained

$$ \left. {\begin{array}{*{20}l} {\overline{x}} \hfill & = \hfill & {(2e^{2} + 3e^{3} )d_{2} } \hfill \\ {\overline{y}} \hfill & = \hfill & {d_{1} - (3e^{2} \pi + 2eH_{{f_{0} }} )d_{2} + (1 + \frac{{e^{{2}} }}{2})d_{4} } \hfill \\ {\overline{z}} \hfill & = \hfill & { - (\frac{e}{{2}} + \frac{{{3}e^{{3}} }}{{8}}{)}d_{6} } \hfill \\ \end{array} } \right\} $$
(11)
$$ \left. {\begin{array}{*{20}l} {\overline{x}^{\prime}} \hfill & { = 0} \hfill \\ {\overline{y}^{\prime}} \hfill & { = [ - 3e^{2} - 6e^{3} ]d_{2} } \hfill \\ {\overline{z}^{\prime}} \hfill & { = 0} \hfill \\ \end{array} } \right\} $$
(12)

The averaged equations, Eq. 11 and Eq. 12, are simple and convenient for analysis and designing. In two-body elliptical orbit, if \(d_{2} \ne 0\), the relative motion in along-track direction is not closed. The averaged drift velocity in y-axis is \(\overline{y}^{\prime}\), which can be decided by eccentricity and initial constant \(d_{2}\). The mean velocity in x-axis and z-axis is zero, which is correspond to the relative motion.

3 Averaged Equation of Relative Motion with Orbital Perturbation

For LEO satellite, the earth’s non-spherical shape and atmosphere perturbation greatly affects the relative motion of satellite. The perturbations make the satellite rotate or drift, and the relative motion will not be closed. Equation 11 and Eq. 12 are not convenient to analyze the orbital perturbation, so the orbital elements will be considered in this section.

We denote

$$ \left. \begin{gathered} {\varvec{\sigma}} = (a,e,i,\omega ,\Omega ,M)^{{\text{T}}} \hfill \\ {\varvec{\sigma}}_{t} = (a_{t} ,e_{t} ,i_{t} ,\omega_{t} ,\Omega_{t} ,M_{t} )^{{\text{T}}} \hfill \\ \end{gathered} \right\} $$
(13)

where \(a\) is semi-major axis, \(e\) is eccentricity, \(i\) is inclination, \(\omega\) is perigee anomaly, \(\Omega\) is right ascension of ascending node, \(M\) is mean anomaly. The orbital element differences between the target satellite and tracking satellite defined as \({\updelta }{\varvec{\sigma}} = {\varvec{\sigma}}_{t} - {\varvec{\sigma}}\). Based on the relations between the integral constant \(d_{i}\) and the orbital element difference \({\updelta }{\varvec{\sigma}}_{0}\) [10]

$$ \left. \begin{gathered}\updelta a_{0} = \frac{{2e^{2} }}{{\eta^{4} }}d_{2}, \updelta e_{0} = \frac{e}{{a\eta^{2} }}d_{2} + \frac{1}{a}d_{3}, \updelta \omega_{0} = \frac{1}{{a\eta^{2} }}d_{4} - \frac{\sin \omega \cot i}{{a\eta^{2} }}d_{5} + \frac{\cos \omega \cot i}{{a\eta^{2} }}d_{6} \hfill \\\updelta M_{0} = \frac{\eta }{a}(d_{1} - 2eH_{{f_{0} }} d_{2} ), \updelta i_{0} = \frac{\cos \omega }{{a\eta^{2} }}d_{5} + \frac{\sin \omega }{{a\eta^{2} }}d_{6}, \updelta \Omega_{0} = \frac{{\sin \omega \sin^{ - 1} i}}{{a\eta^{2} }}d_{5} - \frac{{\cos \omega \sin^{ - 1} i}}{{a\eta^{2} }}d_{6} \hfill \\ \end{gathered} \right\} $$
(14)

where \(\eta = \sqrt {1 - e^{2} }\), Eq. 11 can be rewritten as

$$ \left. {\begin{array}{*{20}l} {\overline{x}} \hfill & { = (1 + \frac{3}{2}e)\eta^{4} {\updelta }a_{0} } \hfill \\ {\overline{y}} \hfill & { = \frac{a}{\eta }{\updelta }M_{0} - \frac{{3\pi \eta^{4} }}{2}{\updelta }a_{0} + a\eta^{2} (1 + \frac{{e^{{2}} }}{2})({\updelta }\omega_{0} + \cos i{\updelta }\Omega_{0} )} \hfill \\ {\overline{z}} \hfill & { = - (\frac{e}{{2}} + \frac{{{3}e^{{3}} }}{{8}}{)}a\eta^{2} (\sin \omega {\updelta }i_{0} - \cos \omega \sin i{\updelta }\Omega_{0} )} \hfill \\ \end{array} } \right\} $$
(15)

Considering the orbital perturbation, the orbital element difference would not be a constant, that means \({\updelta }\dot{\user2{\sigma }} \ne {\mathbf{0}}\). In each calculation step, the instantaneous orbital element of satellite can be calculated in high precision. So the orbital element difference can be obtained in real time, the averaged relative motion can also be calculated by following equations.

$$ \left. {\begin{array}{*{20}l} {\overline{x}(t)} \hfill & { = (1 + \frac{3}{2}e)\eta^{4} {\updelta }a} \hfill \\ {\overline{y}(t)} \hfill & { = \frac{a}{\eta }{\updelta }M - \frac{{3\pi \eta^{4} }}{2}{\updelta }a + a\eta^{2} (1 + \frac{{e^{{2}} }}{2})({\updelta }\omega + \cos i{\updelta }\Omega )} \hfill \\ {\overline{z}(t)} \hfill & { = - (\frac{e}{{2}} + \frac{{{3}e^{{3}} }}{{8}}{)}a\eta^{2} (\sin \omega {\updelta }i - \cos \omega \sin i{\updelta }\Omega )} \hfill \\ \end{array} } \right\} $$
(16)

The time derivative of Eq. 16 can be approximated as

$$ \left. {\begin{array}{*{20}l} {\dot{\overline{x}}(t)} \hfill & { \approx (1 + \frac{3}{2}e)\eta^{4} {\updelta }\dot{a}} \hfill \\ {\dot{\overline{y}}(t)} \hfill & { \approx \frac{a}{\eta }{\updelta }\dot{M} - \frac{{3\pi \eta^{4} }}{2}{\updelta }\dot{a} + a\eta^{2} (1 + \frac{{e^{{2}} }}{2})({\updelta }\dot{\omega } + \cos i{\updelta }\dot{\Omega })} \hfill \\ {\dot{\overline{z}}(t)} \hfill & { \approx - (\frac{e}{{2}} + \frac{{{3}e^{{3}} }}{{8}}{)}a\eta^{2} (\sin \omega {\updelta }\dot{i} - \cos \omega \sin i{\updelta }\dot{\Omega })} \hfill \\ \end{array} } \right\} $$
(17)

Moreover, with the theory of the secular orbit perturbation, we can obtain the following conclusion:

  1. (1)

    Out of orbit plane: The averaged relative motion of the z-axis is decided by \({\updelta }\overline{i}\) and \({\updelta }\overline{\Omega }\), which is affected by the J2 perturbation. In short-term, for example, in several orbit periods, z-axis drift is small that can be omitted.

  2. (2)

    In-orbit plane: The averaged relative motion in x-axis is only decided by \({\updelta }\overline{a}\), which is mainly affected by the atmospheric perturbation. The averaged relative motion in y-axis is complex, which is decided by \({\updelta }\overline{M}\), \({\updelta }\overline{a}\), \({\updelta }\overline{\omega }\) and \({\updelta }\overline{\Omega }\). If the cross-section mass ratio is different between the target satellite and tracking satellite, there will be a long-term drift in x-axis and y-axis.

4 Simulation

4.1 Simulation in Two-Body Orbit

In order to evaluate the accuracy of averaged equations which described above, the following test case are considered. The orbit elements of satellites listed in Table 1.

Table 1. Initial orbit elements of satellites
Full size table

The initial relative conditions (integral constants of T-H equation) of chaser satellite in two test cases are.

Case 1: \(d_{1} = 225.9\), \(d_{2} = 0.0\), \(d_{3} = 1001.0\), \(d_{4} = 499.1\), \(d_{5} = 19.8\), \(d_{6} = - 9.4\)

Case 2: \(d_{1} = 12.2\), \(d_{2} = 110911.2\), \(d_{3} = - 2630.3\), \(d_{4} = 10.4\), \(d_{5} = 14.1\), \(d_{6} = - 10.2\)

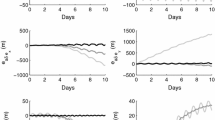
Simulation duration corresponds to 25 orbit periods of target satellite. Both the true relative position and averaged relative position are shown in Fig. 2 and Fig. 3, coloured in blue and red respectively. Figure 2 shows the results of test case 1, the relative motion is closed or periodic, which means no drift in along-track (y-axis). Figure 3 shows the results of test case 2, if \(d_{2} \ne 0\) the averaged along track distance is significantly changed. It can be seen that simulation results are consistent with the analysis reported above.

Fig. 2.
figure 2

Relative track with no perturbation (Case-1:\(d_{2} = 0\))

Full size image
Fig. 3.
figure 3

Relative track with no perturbation (Case-2:\(d_{2} \ne 0\))

Full size image

4.2 Simulation Considering the Effect of J2 Perturbation and Atmosphere Perturbation

With the same initial orbit parameters of satellite which are listed in Table 1. Two different test cases are considered for comparing the effect of atmosphere perturbation.

Case 3: The cross-section mass ratio of target satellite and chaser satellite are same, \(0.01{\text{ m}}^{2} /{\text{kg}}\).

Case 4: The cross-section mass ratio of target satellite and chaser satellite are different, \(0.01{\text{ m}}^{2} /{\text{kg}}\) and \(0.02{\text{ m}}^{2} /{\text{kg}}\) respectively.

Simulation duration corresponds to 25 orbit periods. Both the true relative position and mean relative position are shown in Fig. 4 and Fig. 5, coloured in blue and red respectively. Figure 4 shows the results of test case 3, with the same cross-section mass ratio, the averaged relative motion shown a linear drift in along-track (y-axis), which is mainly caused by J2 perturbation. Figure 5 shows the results of test case 4, the averaged relative motion shown a long-term drift in radial direction (x-axis) which is mainly caused by atmosphere perturbation. In other words, with different cross-section mass ratio, the orbit altitude of two satellites decreased in different velocity. There is an approximate parabola drift in along-track, which is an integrated affection of J2 perturbation and atmosphere perturbation.

Fig. 4.
figure 4

Relative track with J2 and atmosphere perturbation (Case-3:\(d_{2} = 0\))

Full size image
Fig. 5.
figure 5

Relative track with J2 and atmosphere perturbation (Case-4:\(d_{2} \ne 0\))

Full size image

Simulation results indicated that curves based on the averaged equation of relative motion are well consistent with the numerical calculation. Using the result of averaged equation, it is more intuitionistic and convenient to analysis the long-term movement trend, and that is also helpful for the formation designing and configuration maintaining.

5 Conclusions

The averaged equations of satellite relative motion in elliptic orbit have been presented. Based on the homogeneous solutions of T-H equations, a simple averaged relative motion equation is derived over an orbit period. Then, the improved averaged relative motion equation which is described by the orbit elements difference is developed for considering the orbital perturbation. This representation of averaged relative motion is convenient to understand Earth oblateness and atmospheric perturbation effects on formation dynamics. Simulation results have verified the effectiveness of the proposed models. The averaged model can eliminate the periodicity movement of relative motion, and it is useful for formation designing and configuration maintaining.