An Improved Chattering-Suppressed Sliding-Mode Observer for Sensorless Controlled PMSM

Abstract

The chattering of sliding mode control is indirectly transmitted by traditional sliding mode observer when estimating the back EMF, which eventually leads to larger estimation error and affects the system performance. In this paper, in order to weaken the chattering of the system, an improved fuzzy hyperbolic tangent function is designed to replace the traditional symbolic function with the idea of quasi-sliding mode. After the improved sliding mode observer (SMO) enters the sliding mode, the boundary layer thickness can be adjusted adaptively. The simulation results show that the PMSM sensorless sliding mode control system based on the proposed method has good anti-interference ability and accurate tracking performance. Compared with the traditional SMO, the improved SMO can track the rotor position quickly and effectively, accurately estimate the rotor velocity, and has better dynamic characteristics.

1 Introduction

With the improvement of servo system’s control accuracy and anti-interference ability, the control algorithm for the nonlinear characteristics of motor drive system has become the focus of research. Permanent magnet synchronous motor (PMSM) is widely used because of its high-power factor and adjustable parameters. The motor with the mechanical sensors will not only increase the production cost, increase the weight of the motor, but also vulnerable to the interference of the external environment, which leads to the instability of the motor. While motor without sensor control can overcome the above shortcomings, and scholars on the sensorless control research more and more.

The SMO based on the idea of quasi-sliding mode not only retains the advantages of sliding mode control, but also reduces chattering further. Compared with the standard sliding mode, the merit of the quasi-sliding mode are as follows: it has a boundary layer which can regulate the sliding mode switching process, and when the system enters the boundary layer, it is considered to enter the sliding mode [1, 2]. In [3], a soft switching SMO for sensorless control of PMSM is proposed. The traditional switching function is replaced by a sinusoidal saturation function with a variable boundary layer. The equivalent convergence time is derived from the sliding mode state expression in the boundary layer of the sinusoidal saturation function, and a comparison is made with the existing functions. In [4], the sigmoid function is changed into a sign function and a linear function, and a reasonable linear function is adopted to change the gain according to the speed. In [5], an improved SMO for PMSM sensorless VC method to solve the LPF and calculation delay problems is proposed. A brand-new hyperbolic function is selected as the switching function following the boundary layer theory. In this case, the LPF can be eliminated because it is found that the chattering phenomenon can be repressed by adjusting the width of the boundary layer. In [6], a new dynamic sliding mode control system is proposed. By using the saturated function method, a new nonlinear switching function was designed to eliminate chattering in the sliding mode arrival stage, and the global robust sliding mode control was realized, which effectively solved the control jitter problem of a class of nonlinear mechanical systems. Most of these literatures indagate the relationship between speed and gain, change the size of sliding mode gain and the switching function to reform the system performance, and prove the feasibility of improving the system performance by varying the sliding mode gain and improving the boundary layer width. The large width of the boundary layer can effectively reduce chattering but sacrifice the control strength. As the boundary layer breadth is small, the control effect is good but the chattering is aggravated [7,8,9]. Therefore, the boundary layer breadth should be adjusted adaptatively.

In this paper, a new SMO is proposed to solve the problem that the error of estimating back EMF becomes larger due to the improper selection of internal switching function of traditional SMO. Firstly, the characteristics of the new function under different coefficients are studied, and then a fuzzy algorithm is introduced according to the observed current error and the relationship between the derivative of the current error and the coefficient, and a hyperbolic tangent function fuzzy SMO (FSMO) with adjustable boundary layer width is designed. Through the adaptive adjustment of boundary layer width parameters, the noise is reduced and the accuracy of rotor position observation is refined.

2 The Model of PMSM

Assuming that the PMSM is an ideal motor, and meets the following conditions: (1) to ignore the saturation of the motor core; (2) the eddy current and hysteresis loss in the motor are excluded. (3) The three-phase current in the motor is sine wave current, then the voltage equation of PMSM in the two-phase stationary reference frame is shown in (1):

$$\left\{ {\begin{array}{*{20}c} {u_\alpha = L_s \frac{di_\alpha }{{dt}} + R_s i_\alpha + E_\alpha } \\ {u_\beta = L_s \frac{di_\beta }{{dt}} + R_s i_\beta + E_\beta } \\ \end{array} } \right.$$

(1)

where $R_s$ is the stator resistance; u_α, u_β, i_α, and i_β are stator α-and β-axis voltages and currents, respectively; L_s is the stator inductance; E_α and E_β are the EMF of $\alpha$- and $\beta$-axis, they can be expressed by (2):

$$\left\{ {\begin{array}{*{20}l} {E_\alpha = - \psi_f w_e \sin \theta_e } \hfill \\ {E_\beta = \psi_f w_e \cos \theta_e } \hfill \\ \end{array} } \right.$$

(2)

where w_e is the rotor electrical angular velocity;$\theta_e$ is rotor position electric angel;$\psi_f$ is the rotor permanent magnet flux-linkage.

It can be seen from (2) that the extended back EMF of the voltage equation contains information about the rotor position and speed. As long as the extended back EMF can be obtained, the rotor position and speed can be calculated.

3 The Analysis of Conventional SMO

The state equation of current in the two-phase stationary reference frame can be obtained from (1):

$$\left\{ {\begin{array}{*{20}c} {\frac{{d\hat{i}_\alpha }}{dt} = - \frac{R_s }{{L_s }}i_\alpha + \frac{u_\alpha }{{L_s }} - \frac{E_\alpha }{{L_s }}} \\ {\frac{{d\hat{i}_\beta }}{dt} = - \frac{R_s }{{L_s }}i_\beta + \frac{u_\beta }{{L_s }} - \frac{E_\beta }{{L_s }}} \\ \end{array} } \right.$$

(3)

The sliding surface is defined as $s\left( x \right) = - i_s$, $\hat{i}_s$ is the observed value of stator current; $i_s$ is the actual value of stator current, and the SMO is constructed, as shown in (4):

$$\left\{ {\begin{array}{*{20}c} {\frac{{d\hat{i}_\alpha }}{dt} = - \frac{R_s }{{L_s }}i_\alpha + \frac{u_\alpha }{{L_s }} - \frac{k}{L_s }sign(\hat{i}_\alpha - i_\alpha )} \\ {\frac{{d\hat{i}_\beta }}{dt} = - \frac{R_s }{{L_s }}i_\beta + \frac{u_\beta }{{L_s }} - \frac{k}{L_s }sign(\hat{i}_\beta - i_\beta )} \\ \end{array} } \right.$$

(4)

where sign(s) is the sign function, k is the switching gain, and its value should meet the existence, accessibility and stability of sliding mode. The dynamic error equation can be obtained by subtracting (3) from (4):

$$\left\{ {\begin{array}{*{20}c} {\frac{{d(\hat{i}_\alpha - i_\alpha )}}{dt} = - \frac{R_s }{{L_s }}(\hat{i}_\alpha - i_\alpha ) - \frac{k}{L_s }sign(\hat{i}_\alpha - i_\alpha ) + \frac{E_\alpha }{{L_s }}} \\ {\frac{{d(\hat{i}_\beta - i_\beta )}}{dt} = - \frac{R_s }{{L_s }}(\hat{i}_\beta - i_\beta ) - \frac{k}{L_s }sign(\hat{i}_\beta - i_\beta ) + \frac{E_\beta }{{L_s }}} \\ \end{array} } \right.$$

(5)

When the moving point reaches and moves on the sliding surface, $s\left( x \right) = \dot{s}\left( x \right) = 0$,that is:

$$\left\{ {\begin{array}{*{20}c} {E_\alpha = ksign(\hat{i}_\alpha - i_\alpha )} \\ {E_\beta = ksign(\hat{i}_\beta - i_\beta )} \\ \end{array} } \right.$$

(6)

It can be seen from (6) that the current error switch signal contains the estimation information of the back EMF. The switching signal is passed through a low-pass filter to filter out the high frequency components, and the smooth back EMF estimation signal is obtained:

$$\left\{ {\begin{array}{*{20}c} {\hat{E}_\alpha = \frac{w_c }{{s + w_c }}E_\alpha } \\ {\hat{E}_\beta = \frac{w_c }{{s + w_c }}E_\beta } \\ \end{array} } \right.$$

(7)

where $w_c$ is the cut-off frequency of the low-pass filter, The angular position of the rotor can be calculated from the mathematical expression of the back EMF, and the estimated value of the rotational speed can be obtained directly by differentiating the angle:

$$\theta = - \arctan \left( {\frac{E_\alpha }{{E_\beta }}} \right)$$

(8)

$$\hat{w} = \frac{d\theta }{{dt}}$$

(9)

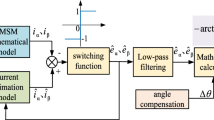
The control diagram of the conventional SMO is show in Fig. 1.

Fig. 1

Block diagram of a conventional SMO

4 Improved SMO Design

The traditional SMO uses the fixed gain sign(s) function to estimate the back EMF, which cannot achieve good control effect and is easy to cause chattering. In this part, a new hyperbolic tangent function is designed, as shown in Fig. 2. First, the function characteristics under different coefficients are studied. Then, the fuzzy algorithm is introduced according to the relationship between the current error and the derivative of the current error and the coefficient, and fuzzy rules of the three are designed. A new FSMO which can adjust the thickness of boundary layer is proposed to reform the accuracy of rotational speed observation.

Fig. 2

Block diagram of the improved SMO

4.1 Design a Hyperbolic Tangent Function SMO

To reduce the chattering caused by the discontinuities of switching functions such as traditional sign() functions, we researched the continuous smooth hyperbolic tangent functions. In order to conveniently control the width of the boundary layer, the improved hyperbolic tangent function is designed as:

$$f\tanh \left( {\frac{x}{\varepsilon }} \right) = \frac{{e^{\frac{x}{\varepsilon }} - e^{\frac{x}{\varepsilon }} }}{{e^{\frac{x}{\varepsilon }} + e^{\frac{x}{\varepsilon }} }}$$

(10)

Parameter $\varepsilon$ is used to adjust the breadth of the boundary layer, when $\varepsilon$ is of different values, the function images are shown in Fig. 3. The smaller $\varepsilon$ is, the better control effect of the system is achieved, but it will also lead to the aggravation of chattering. Thus, it can also be testified that chattering is more obvious when the switch function adopts the symbol function. When $\varepsilon$ is larger, the effect of chattering suppression will be significantly better, so it is necessary to balance chattering suppression and control effect.

Fig. 3

Graph of different ${\varvec{\varepsilon}}$-valued functions

Therefore, $\varepsilon$ should be adjusted adaptatively according to the system state, the sliding mode observer based on the new hyperbolic tangent function is:

$$\left\{ \begin{gathered} \frac{{d\hat{i}_d }}{dt} = \frac{1}{L_s }\left( { - R\hat{i}_d + u_d + p_n \omega_n L_s \hat{i}_q - kf\tanh (\hat{i}_d - i_d )} \right) \hfill \\ \frac{{d\hat{i}_q }}{dt} = \frac{1}{L_s }\left( { - R\hat{i}_q + u_q - p_n \omega_n L_s \hat{i}_d - kf\tanh (\hat{i}_q - i_q )} \right) \hfill \\ \end{gathered} \right.$$

(11)

where $\hat{i}_d$ and $\hat{i}_q$ are the observed current values of the d- and q-axis of the stator, respectively; $\tilde{i}_d = \hat{i}_d - i_d$, $\tilde{i}_q = \hat{i}_q - i_q$ are the current observation error; k is the sliding mode surface switching gain value. Then the state equation of the current error system is:

$$\left\{ {\begin{array}{*{20}c} {\frac{{d\widetilde{i_d }}}{dt} = \frac{1}{L_s }( - R\widetilde{i_d } + u_d + p_n w_n L_s \widetilde{i_q } - kf\tanh \left( {\widetilde{i_d }} \right) + E_d } \\ {\frac{{d\widetilde{i_q }}}{dt} = \frac{1}{L_s }( - R\widetilde{i_q } + u_q + p_n w_n L_s \widetilde{i_d } - kf\tanh \left( {\widetilde{i_q }} \right) + E_q } \\ \end{array} } \right.$$

(12)

The sliding surface is defined as $i = [\begin{array}{*{20}c} {\hat{i}_d } & {\hat{i}_q } \\ \end{array} ]^T$ = 0, When the system enters the sliding surface:

$$E = [E_d \, E_q ] = \left[ {kf\tanh \left( {\frac{{\hat{i}_d - i_d }}{\varepsilon }} \right)kf\tanh \left( {\frac{{\hat{i}_q - i_q }}{\varepsilon }} \right)} \right]^T$$

(13)

The new hyperbolic tangent function belongs to the switching function, so the collected signal E will contain high-frequency signals, and the equivalent control quantity can be obtained after filtering them out, as follows:

$$E = \left[ {\begin{array}{*{20}c} {kf\tanh \left( {\frac{{\hat{i}_d - i_d }}{\varepsilon }} \right)} \\ {kf\tanh \left( {\frac{{\hat{i}_q - i_q }}{\varepsilon }} \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {w_n \psi_f } \\ \end{array} } \right]$$

(14)

It can be seen that (14) contains rotor velocity information. In order to improve the accuracy of rotor position in sensorless control, it is necessary to improve the observation accuracy of E.

4.2 Parameter Fuzzy Design

In order to accurately observe the value of E, a fuzzy algorithm is introduced. The current error ${\tilde{\text{i}}}$ and its derivative $\dot{\tilde{i}}$ are taken as input and $\varepsilon$ as output. The thickness of the boundary layer is reasonably adjusted according to the changes of the system, so as to obtain the accurate observed value of E. Where, the system inputs ${\tilde{\text{i}}}$ and $\dot{\tilde{i}}$, and the fuzzy set of output $\varepsilon$ is defined as follows:

PB: positive, ZO :zero, NB :negative

$$\begin{gathered} \tilde{i} = \left\{ {NB,ZO,PB} \right\}; \hfill \\ \dot{\tilde{i}} = \left\{ {NB,ZO,PB} \right\}; \hfill \\ \varepsilon = \left\{ {NB,ZO,PB} \right\}. \hfill \\ \end{gathered}$$

The ranges are:

$$\begin{gathered} \tilde{i} = \left\{ { - 1,0, + 1} \right\}; \hfill \\ \dot{\tilde{i}} = \left\{ { - 1,0, + 1} \right\}; \hfill \\ \varepsilon = \left\{ {0, + 1, + 2, + 3, + 4, + 5, + 6} \right\} \hfill \\ \end{gathered}$$

Figure 4a–c are membership functions of input and output, respectively.

Fig. 4

a Membership function graph of ${\tilde{\text{i}}}$; b membership function graph of $\dot{\tilde{i}}$; c membership function graph of $\varepsilon$

The setting principle of fuzzy rule is as follows: when the current error is large, the control effect should be enhanced to make the system closer to the sliding mode surface, that is, the boundary layer thickness should be smaller, and $\varepsilon$ should be reduced; If the current error is small, system chattering should be reduced, that is, the thickness of the boundary layer should be larger, $\varepsilon$ should be increased. Therefore, the fuzzy rules are set in Table 1.

Table 1 Fuzzy rule

Substituting the improved hyperbolic tangent function after fuzziness into (16), the equivalent control quantity is:

$$E = \left[ {\begin{array}{*{20}c} {\left[ {kf\tanh \left( {\frac{{\hat{i}_d - i_d }}{\varepsilon }} \right)} \right]_{eq} } \\ {\left[ {kf\tanh \left( {\frac{{\hat{i}_q - i_q }}{\varepsilon }} \right)} \right]_{eq} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {kf\tanh \left( {\frac{{\hat{i}_d - i_d }}{{fuzzy(\hat{i}_d ,\hat{\dot{i}}_q )}}} \right)} \right]_{eq} } \\ {\left[ {kf\tanh \left( {\frac{{\hat{i}_q - i_q }}{{fuzzy(\hat{i}_q ,\hat{\dot{i}}_q )}}} \right)} \right]_{eq} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {\omega_n \psi_f } \\ \end{array} } \right]$$

(15)

Compared with the control effect before fuzzification, the equivalent control quantity E can enter the sliding mode surface more quickly, improve the accuracy of current observation, and obtain accurate rotor position information.

4.3 Rotor Position Estimation

It can be seen from (15) that E contains rotor information, and the rotor velocity is:

$$\hat{w}_n = \frac{E_q }{{\psi_f }}$$

(16)

Since the motor’s flux is not constant in actual operation, the rotor position angle cannot be obtained simply by integrating (16), it should be obtained by comparing the frequency of the phase of the reference signal and the feedback signal. Therefore, the position of rotor is estimated by phase-locked loop (PLL).

Set the terminal voltage of three-phase winding of the motor as:

$$\left\{ \begin{gathered} u_a = u\cos \theta_e \hfill \\ u_b = u\cos (\theta_e - 2\pi /3) \hfill \\ u_c = u\cos (\theta_e + 2\pi /3) \hfill \\ \end{gathered} \right.$$

(17)

where u is the terminal voltage;$\theta_e$ is the rotor angle. $\hat{\theta }_e$ is defined as an estimate of rotor position angle, variate the three-phase voltage to the d-q reference frame:

$$T(\hat{\theta }_e ) = \frac{1}{3}\left[ {\begin{array}{*{20}c} \begin{gathered} \cos \hat{\theta }_e \hfill \\ - \sin \hat{\theta }_e \hfill \\ \end{gathered} & \begin{gathered} \cos (\hat{\theta }_e - 2\pi /3) \hfill \\ - \sin (\hat{\theta }_e - 2\pi /3) \hfill \\ \end{gathered} & \begin{gathered} \cos (\hat{\theta }_e + 2\pi /3) \hfill \\ - \sin (\hat{\theta }_e + 2\pi /3) \hfill \\ \end{gathered} \\ \end{array} } \right]$$

(18)

$\tilde{\theta }_e = \hat{\theta }_e - \theta_e$ is defined as the estimation error, and the closed-loop control system is established. When the estimation error is set to zero, $\tilde{\theta }_e = \theta_e$ is obtained, thus the actual position of the rotor is estimated:

$$\left[ \begin{gathered} V_d \hfill \\ V_q \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} u\sin (\hat{\theta }_e - \theta_e ) \hfill \\ ucon(\hat{\theta }_e - \theta_e ) \hfill \\ \end{gathered} \right]$$

(19)

When $|\hat{\theta }_e - \theta_e | < \pi /6$, $\sin (\hat{\theta }_e - \theta_e ) = \hat{\theta }_e - \theta_e$ is considered to be true. A closed-loop PI regulator is built and the estimation error is set to zero to obtain the rotor information position. The rotor position estimation process is shown in Fig. 5.

Fig. 5

The process of rotor position estimation

5 The Simulation Results

In order to verify the effectiveness of the sensorless SMO based on the new fuzzy hyperbolic tangent function, the designed SMO is added into the vector control position loop as shown in Fig. 6. The reference speed is set as 1000 r/min, other parameters used in the simulation are shown in Table 2.

Fig. 6

Simulation principle block diagram

Table 2 Parameter settings used in the simulation

To simplify the expression, the symbol FSMO is used to represent the proposed observer, and the SMO represents the conventional SMO based on the sign() function. The results are as follows:

Figure 7 shows the comparison between the motor rotor positions of the two methods and the estimated positions. Figure 8 show the comparison of the motor position estimation errors of the two methods. It is obvious from the simulation diagram that compared with the traditional method, the FSMO with improved hyperbolic tangent function is used to estimate the motor position more accurately.

Fig. 7

Actual and estimated motor rotor position under sign() and ftanh()

Fig. 8

Rotor position estimation error under sign() and ftanh()

Figure 9 is the comparison diagram of the estimated motor speed of the two methods, and Fig. 10 is the comparison diagram of the estimated error of motor speed. As can be seen from the simulation results, the switching of sign() amplifies the error of the back EMF, which makes certain error exist in the estimation of speed. The speed error is large between 0 and 0.2 s, and the system is unstable. Waveform chattering is shown in Figs. 9 and 10. While the FSMO based on the improved hyperbolic tangent function reaches the target velocity after 0.1 s, the wave is relatively stable, almost no chattering phenomenon, and the velocity error is relatively small. The effectiveness of the new sliding mode observer is verified.

Fig. 9

Motor speed estimation under sign() and ftanh()

Fig. 10

Motor speed estimation error under sign() and ftanh()

Figure 11 shows the curve of d-axis induced EMF using the two methods, and Fig. 12 shows the curve of q-axis induced EMF using the two methods. The simulation results show that the d.q-axis induced EMF of the motor with the improved hyperbolic tangent function can be stabilized around a fixed value more quickly, and the system tends to be stable. However, the system using the traditional methods fluctuates up and down the induced EMF chattering, which is not conducive to the stability of the system, and the control effect is not good. The effectiveness of the new method is testified again.

Fig. 11

d-axis induced EMF under sign() and ftanh()

Fig. 12

q-axis induced EMF under sign() and ftanh()

6 Conclusion

A novel SMO based on the idea of quasi-sliding mode was designed to solve the large observation error and chattering caused by the traditional SMO using the sign() function. Firstly, the modified hyperbolic tangent function is proposed by studying the characteristics of the hyperbolic tangent function. Then, the fuzzy algorithm is used to optimize the new hyperbolic tangent function. The errors and derivatives between the observed current and the actual current are taken as the input, and the boundary layer width control parameters of the new hyperbolic tangent function are taken as the output. The improved fuzzy SMO can adjust the breadth of the boundary layer, and the system can enter the sliding mode more quickly, which can effectively suppress chattering and improve the accuracy of current observation. In the simulation, a SMO with symbolic function is compared to study the variation curves of speed, position and induced EMF in the sensorless control. The simulation results verify the effectiveness of the new method.