Keywords

1 Introduction

The elastic property of concrete, i.e. the modulus of elasticity measures its rigidity. This property of concrete is defined as the ratio between the stress applied and the strain obtained within the defined limit of proportionality. The limit of proportionality is “the maximum stress the material tolerates without deviating from the stress–strain proportionality (Hooke’s law).” The applied stress may be static or dynamic; however, this study is limited to static stress. It is generally related to the compressive strength of concrete; it increases with an increase in compressive strength. Hence, the modulus of elasticity of concrete may be articulated as a function of the compressive strength of concrete [1]. But the increase in the rate of modulus of elasticity is comparatively less than that of the compressive strength of concrete [2]. Modulus of elasticity generally depends upon many parameters like aggregate type, the mix proportions, curing conditions, rate of loading, etc. The larger the amount of coarse aggregate with a high elastic modulus, the higher would be the modulus of elasticity of concrete. Researchers have also studied that the addition of mineral admixtures enhances the strength, modulus of elasticity and durability of concrete [2,3,4,5,6,7,8,9]. The concrete specimens tested in wet conditions show about 15% higher elastic modulus than those tested in dry conditions [10]. This property is evaluated by drawing the slope for the stress–strain curve. As most of the part of the stress–strain curve is non-linear, different methods for computing the modulus of elasticity are shown in Fig. 1. The secant modulus is the commonly used method for evaluating this property by different codes and researchers [11,12,13,14]. Now the modulus of elasticity of reinforced concrete members is very indifferent to the modulus of elasticity of concrete alone [15, 16]; hence, the use of the modulus of elasticity of concrete overestimates the design values in the design of structural members. Also, in the design of structural members, the total cross-sectional area of the section is considered neglecting the effect of confining steel reinforcements. The high-strength concrete and the high-performance concrete differ largely from the conventional cement concrete because of use of the cementitious material like silica fume, fly ash, etc. and hence because of which the mechanical properties of HSC/ HPC also differs [17,18,19] and the proposed equation for modulus of elasticity of concrete or reinforced concrete may not be applied either for HPC or reinforced HPC.

Fig. 1
A graph depicts the Stress-strain curve for concrete. A slanting curve has dashed lines, marked as secant modulus, tangent modulus, and chord modulus.

Stress–strain curve for concrete

Full size image

The database for modulus of elasticity of concrete, reinforced concrete and high-strength concrete/high-performance concrete as proposed by different codes and researchers is presented in Tables 1, 2 and 3.

Table 1 Modulus of elasticity of concrete
Full size table
Table 2 Modulus of elasticity of reinforced concrete
Full size table
Table 3 Modulus of elasticity of HSC/ HPC
Full size table

2 Research Objectives

The main objective of this research study is to predict the equation for modulus of elasticity for reinforced HPC beam and is stated as follows:

  1. i.

    To analyse and evaluate Stress–Strain parameters for varying percentages of longitudinal reinforcement experimentally.

  2. ii.

    To evaluate the secant modulus of elasticity of reinforced HPC beam for 60, 80 and 100 MPa strength from experimental results through bending equation and Stress–Strain curve.

  3. iii.

    Prediction of the equation for secant modulus of elasticity of reinforced HPC beam by regression investigation.

3 Methodology

In this study, four beam models of each 60, 80 and 100 MPa reinforced HPC are studied for different longitudinal reinforcement ratios (0.132–0.407) experimentally, and the secant modulus of elasticity is evaluated. The secant modulus of elasticity is evaluated using the experimental stress–strain curves and using bending equation (1). The beam is subjected to two-point loads.

$$E = \frac{23WL^3 }{{648\delta I}}$$
(1)

where E = Modulus of Elasticity,

W = Load,

L = Effective Span of the beam,

δ = deflection and

I = Moment of Inertia of the section.

3.1 Experimental Setup

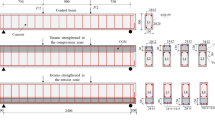
The reinforced HPC beam is tested as a simply supported beam with 2.0 m effective span, 150 mm in width and 300 mm in depth as shown in Figs. 2 and 3 for beam 60SB2. Steel plates of size 90 mm × 150 mm × 12.5 mm were used as cushions at loading and support points [20, 21]. The details of longitudinal reinforcement, area of steel and reinforcement ratio for HPC beams studied are shown in Table 4.

Fig. 2
A diagram depicts the experimental setup, which shows the reinforced H P C beam is tested as a supported beam with 2.0 meter effective 77 spans, 150 millimeters in width and 300 millimeters in depth. Two steel plates are placed on the top.

Experimental setup

Full size image
Fig. 3
A photograph of the experimental setup for the reinforced H P C beam 60SB2. The beam is tested as a supported beam with 2.0 meter effective 77 spans, 150 millimeters in width and 300 millimeters in depth.

Experimental setup for HPC beam 60SB2

Full size image
Table 4 Details of beam models
Full size table

4 Evaluation of Stress–Strain Parameters

4.1 Using Experimental Data

Under pure flexure test for single-span HPC beams subjected to monotonic two-point loading, the load and the corresponding deformations were recorded by using LVDTs at extreme tensile and compression fibre at the centre of the span. The LVDT at the tensile fibre was kept closed so that it was allowed to open during expansion, while the LVDT at the extreme compression fibre was opened and allowed to close during compression. Later, the tensile and the compressive strains were calculated from the deformations. The stresses are calculated using the bending equation (2). The applied Moment ‘M’ under two-point loading is determined using Eq. (3).

$$f_c = \frac{M\,y_t }{I}$$
(2)
$$M = \frac{wl}{6}$$
(3)

The stresses-strain curves obtained for varying longitudinal reinforcement ratios and HPC grades for single-span HPC beams are shown in Figs. 4, 5 and 6.

Fig. 4
A line graph illustrates stress in Newton versus strain in millimeters for 60 M P a single-span H P C beam specimen. The curve is a hyperbola.

Experimental stress–strain curves for 60 MPa single-span HPC beam specimens

Full size image
Fig. 5
A line graph illustrates stress in Newton versus strain in millimeters for 80 M P a single-span H P C beam specimen. The curve is a hyperbola.

Experimental stress–strain curves for 80 MPa Single-span HPC beam specimens

Full size image
Fig. 6
A line graph illustrates stress in Newton versus strain in millimeters for 100 M P a single-span H P C beam specimen. The curve is a hyperbola.

Experimental stress–strain curves for 100 MPa single-span HPC beam specimens

Full size image

5 Evaluation of Modulus of Elasticity of HPC Beam

  1. (a)

    Using experimental stress–strain curves

    The commonly used method of secant modulus is employed for evaluating the modulus of elasticity of the HPC beam from the stress–strain curves. The modulus of elasticity is determined from the slope of the line joining origin and a point on the curve representing 40% stress at failure. Thus, the modulus of elasticity obtained using experimental stress–strain curves is shown in Table 5.

    Table 5 Modulus of elasticity from experimental stress–strain parameters
    Full size table
  2. (b)

    Using bending equation from the experimental data

    Experimental evaluation of the secant modulus of elasticity is also done for the same beam specimens by using the bending equation. The single-span HPC beam being subjected to two-point loads, and the maximum deflection due to the applied load ‘W’ is given by Eq. 4.

    $$\,\delta_l = \frac{23\,Wl^3 }{{648\,E_c \,I}}$$
    (4)

    The deflection due to the self-weight of the HPC beam is given by Eq. 5 and the total deflection considering the self-weight of the HPC beam is given by Eq. 6.

    $$\,\delta_s = \frac{5wl^4 }{{384E_c I}}$$
    (5)
    $$\,\delta = \delta_s + \delta_l$$
    (6)

The applied load ‘W’ is taken as half the load at the first visible crack and the corresponding deflection as ‘δ’. The values of load at the first visible crack and its corresponding deflection for different beam specimens tested with varying strength of the HPC and longitudinal reinforcement ratio are shown in Table 6. By substituting these values, the static modulus of elasticity is determined using Eq. 7 for HPC beam specimens.

$$\,E_c = \frac{1}{\delta \,I}\left[ {\frac{5wl^4 }{{384}} + \frac{23\,Wl^3 }{{648}}} \right]$$
(7)
Table 6 Modulus of elasticity from experimental data using bending equation
Full size table

6 Results and Discussion

The static modulus of elasticity of HPC beam specimens determined using experimental stress–strain curves and bending equation from experimental data are compared in Table 7. The average static modulus of elasticity is also presented in Table 7 for different longitudinal reinforcement ratios.

Table 7 Comparison of modulus of elasticity from different methods
Full size table

The stiffness of the HPC beam increases with an increase in longitudinal reinforcement ratio as such, and the trend line of the average variation of modulus of elasticity from different methods shows that it increases with an increase in the grade of HPC and longitudinal reinforcement ratio (Fig. 7). The values obtained from different methods are almost the same for the same longitudinal reinforcement ratio with a variation of 9.61%. However, from Fig. 7, the variation for M80 grade HPC beams was found to be lesser compared to M60 and M100 grade because the variation of percentage of tension reinforcement within the beams was kept smaller in the range of 0.778–1.091, while the range for M60 and M100 grade was higher and of same ratios (0.789–1.972). It is also observed that the variation of modulus of elasticity within the same grade does not have higher variation as compared to variation within the different grades of HPC.

Fig. 7
A line graph illustrates the modulus of elasticity in the megapascal, for the percentage of tension reinforcement. The plotted lines depict 60, 80, and 100 megapascals single-span HPC beam specimens.

Average variation of modulus of elasticity with longitudinal tension reinforcement

Full size image

Taking the data of Modulus of Elasticity from bending equation, a regression test is performed, and following generalized Eq. 8 is derived, for reinforced single-span HPC beams.

$$E_{{\text{Ref}},{\text{HPC}}} = 5000\sqrt {1.075f_{ck} } + \left( {300\sqrt {1.36f_{ck} } } \right)\,\rho$$
(8)

Equation 8 predicts the value of Modulus of Elasticity for varying grades of HPC and percentage of tension reinforcement. The first part of the equation represents stiffness due to the HPC element, while the second part represents stiffness due to reinforcement. The second part of the equation is itself the additional stiffness because of the reinforcement (Fig. 7).

7 Conclusions

The present work evaluates the modulus of elasticity of HPC beam under flexure for 60–80 MPa strength of concrete. The following are the conclusions drawn based on the present experimental and analytical study.

  1. 1.

    The modulus of elasticity of reinforced HPC beam under flexure increases with the increase in longitudinal reinforcement ratio of the concrete section.

  2. 2.

    The modulus of elasticity of reinforced HPC beam for 60–80 MPa can be determined for different longitudinal reinforcement ratios by the proposed Eq. (2).

  3. 3.

    The maximum variation obtained was 11% from the different methods of evaluation of modulus of elasticity of HPC beam (Table 7).