Keywords

1 Introduction

Deterioration of engineering structures, such as bridges, roads, dams, tunnels, and buildings, due to aging and corrosion, accidents, or overuses is one of the main concerning issues. To avoid any catastrophic failure, these engineering structures are kept under constant vigilance. Such monitoring provides valuable information that helps in estimating the structural integrity, durability, and ensures that the structures are in proper condition. This monitoring mechanism can also be used as a preventive system where before any catastrophic failure, signals can be identified by focusing on areas that are most likely to fail and identifying early signs of failures, like the initiation of cracks. The most likely regions in these structural materials are the points of the highest strain or stress triaxiality, initiating the formation of cracks [1]. Therefore, to have an anticipatory accurate prediction of the life of a structural component, many times, it becomes necessary to have prior knowledge of regions of stress concentrations or distribution of the stress in the structural components.

In this regard, digital image correlation (DIC) techniques have tremendous scope as these techniques could be used to identify the regions of stress concentrations in a material undergoing deformation. For example, the deformation of a specimen can be monitored by estimating displacements of pixels of digitally acquired images of the surface. DIC technique was developed to measure the full-field displacement (FFD) and displacement gradient of a specimen under load [2, 3]. Since then, the DIC method has been optimized and improved in terms of accuracy and computational complexity by various researchers. DIC has been used to understand the behavior of systems in biological materials [4, 5], metallic alloys [6], and polymers [7], to name a few. DIC has also been used to understand the nonlinear behavior of materials during the formation of slip bands [8] and crack tips [9].

Typically, by analyzing microscopic images prior to and subsequent to deformation DIC can provide semi-quantitative to quantitative information in terms of displacement and strain fields [10]. DIC technique, without any presumption, provides accurate estimation of strain locally as well as globally and that too of a real system. In addition, DIC being a non-contact technique is superior to other contact-based techniques in providing more accurate estimate of full-field displacement (FFD) and strain.

In current scanning electron microscope (SEM) with the capability of nanometer resolution, it is possible to estimate deformation at submicron level. Application of 2D-DIC techniques on high spatial resolution images obtained under such SEM finds applications in broader areas [11]. In this paper, a 2-D DIC system that makes use of an open-source MATLAB-based 2D DIC software, Ncorr, has been used to compute the distribution of FFD as well as strain [12] in the samples which were subjected to in situ deformation under an SEM. For this purpose, intermittently images were recorded during deformation. In this study, microstructural features within samples were utilized to study the deformation, and later on, the study was extended to featureless samples to prove the wider application of the technique. In addition, a brief description of the algorithm used to process the images has also been presented.

2 Methodology

2.1 Fundamentals of DIC

2D-DIC involves tracking of the image points on the digital images obtained prior and subsequent to deformation. The DIC approach has two successive stages:

  1. (1)

    First stage involves recording of the images of the same region of the specimen. In order to have high accuracy, intermittently images of the same region of the sample during deformation were recorded.

  2. (2)

    In second stage, DIC software is applied to attain the required results as per the desired analysis. The image taken prior to deformation is taken as reference and images obtained after deformation are compared with respect to this reference image to identify the displacements of pixels within a given region.

To implement DIC analysis, the undeformed image is divided into smaller portions called subsets. It is assumed that within each subset, deformation is homogenous, and the relationship between the reference and the deformed images is linear (Eq. 1). It is also assumed that the transformation of the coordinate of the points of the undeformed image to the points of deformation uses a first-order shaping function that involves translation and rotation only.

$$\begin{aligned} & x_{i}^{\rm{\prime }} = x_{i} + u + Du + u_{x} Dx_{i} + u_{y} Dy_{i} \quad {\text{and}} \\ & y_{i}^{\rm{\prime }} = y_{i} + v + Dv + v_{x} Dx_{i} + v_{y} Dy_{i} \\ \end{aligned}$$
(1)

where xi, yi are the coordinates of a pixel in the reference image which after deformation become x'i and y'i in deformed images, u and v are the integer pixel displacements, and ∆u and ∆v are subpixel displacements in the x and y directions, respectively.

To find out deformation within a subset, the extrema of a correlation function are established using DIC algorithm. To initiate the computation, a seed point is located at an integer position. Similarity, between the reference and deformed subset is compared through a pre-defined correlation criterion. This is achieved by DIC algorithms by finding the extremum of a correlation cost function. The normalized cross-correlation (NCC) [4, 10] could be expressed as:

$$C_{{{\text{NCC}}}} = \mathop \sum \limits_{i = - M}^{M} \mathop \sum \limits_{j = - M}^{M} \left[ {\frac{{f\left( {x_{i} , y_{j} } \right)g\left( {x_{i}^{\rm{\prime }} ,y_{i}^{\rm{\prime }} } \right)}}{{\overline{f}\overline{g}}}\} } \right]$$
(2)

In this equation, f(xi, yi) and g(x'i, y'i) are the grayscale intensity functions of the reference image and deformed image at a specified location (xi, yi), respectively, and \(\overline{f}\), \(\overline{g}\) are determined by using functions given in Eqs. 3 and 4:

$$\overline{f} = \sqrt {\mathop \sum \limits_{i = - M}^{M} \mathop \sum \limits_{j = - M}^{M} \left[ {f\left( {x_{i} , y_{j} } \right)} \right]^{2} }$$
(3)
$$\overline{g} = \sqrt {\mathop \sum \limits_{i = - M}^{M} \mathop \sum \limits_{j = - M}^{M} \left[ {g\left( {x_{i}^{\rm{\prime }} , y_{j}^{\rm{\prime }} } \right)} \right]^{2} }$$
(4)

Lagrangian strains can be obtained using the following equations [4, 12]:

$$E_{XX} = \frac{1}{2}\left( {2 \frac{\partial u}{{\partial x}} + \left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right)$$
(5)
$$E_{XY} = \frac{1}{2}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial x}}\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}\frac{\partial v}{{\partial y}}} \right)$$
(6)
$$E_{YY} = \frac{1}{2}\left( {2 \frac{\partial v}{{\partial y}} + \left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{\partial v}{{\partial y}}} \right)^{2} } \right)$$
(7)

Strain contour maps computed by the DIC method were used to calculate local true strain using the following equation:

$$\varepsilon_{{{\text{eng}}}} = - 1 + \sqrt {2 \times \varepsilon_{{{\text{Lag}}}} + 1}$$
(8)
$$\varepsilon_{{{\text{true}}}} = {\text{ln}}\left( {1 + \varepsilon_{{{\text{eng}}}} } \right)$$
(9)

where subscripts “eng” stands for engineering, “Lag” stands for Lagrangian, respectively.

To investigate relationships between displacements and between strains Pearson correlation coefficient “r” was calculated using following relationship [13]:

$$r = \frac{1}{n - 1}\sum \frac{{\left( {x_{i} - \overline{X}} \right)\left( {y_{i} - \overline{Y}} \right)}}{{s_{x} s_{y} }}$$
(10)

where n represents number of samples, x and y represent variables, \(\overline{X}\) and \(\overline{Y}\) represent their mean values, sx and sy represent their standard deviations, respectively. The value of “r” attains values between + 1 and −1. In the case, variables do not bear any relationship, there will be no systematic pattern in \(\left( {x_{i} - \overline{X}} \right)\) and \(\left( {y_{i} - \overline{Y}} \right)\) and summation of \(\left( {x_{i} - \overline{X}} \right)\left( {y_{i} - \overline{Y}} \right)\) would cancel each other, reducing r to a negligible value. However, if the variables are positively associated, i.e., increment in one brings increment in other, the positive values of \(\left( {x_{i} - \overline{X}} \right)\) will coincide with the positive values of \(\left( {y_{i} - \overline{Y}} \right)\) and negative values of \(\left( {x_{i} - \overline{X}} \right)\) with negative values of \(\left( {y_{i} - \overline{Y}} \right)\) and summation of \(\left( {x_{i} - \overline{X}} \right)\left( {y_{i} - \overline{Y}} \right)\) will yield a positive value of r. In the case variables are negatively associated, the summation of \(\left( {x_{i} - \overline{X}} \right)\left( {y_{i} - \overline{Y}} \right)\) will give negative value of r.

When the distribution is not completely known, Pearson’s coefficient, r, does not provide the proper relationship between the variables, in such cases, the Spearman rank correlation coefficient test can be performed to cross-check the validity of correlation between the two variables. The Spearman rank correlation can be expressed as [13]:

$$r_{s} = 1 - 6\sum \frac{{d^{2} }}{{N\left( {N^{2} - 1} \right)}}$$
(11)

where N is the number of samples, and d is the difference in statistical rank of corresponding variables (u and v). Because of the use of formulation ranks, computation of the Spearman rank correlation coefficient is easier in comparison to the Pearson coefficient [13].

2.2 Materials

In the present study, deformation in the Fe–Ni–W-based alloy was studied using the DIC technique. The Fe–Ni–W alloy is generally used as a single-phase structural material for high-temperature applications. Specimens of the alloys were ground using successive grades of emery papers up to grade 2000. Finally, these samples were mirror-polished using colloidal silica to reveal their microstructures. Samples of the Fe–Ni–W alloys were subjected to in situ deformation, and images were recorded using the secondary electron detector. Images of the sample were intermittently recorded to observe the progression of deformation in the sample. These images were later subjected to DIC analysis to find out the displacements and distribution of the stress in the material.

3 Results and Discussion

3.1 Computation of Strain and Statistical Analysis in Fe–Ni–W Alloys

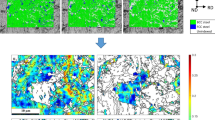
Images at successive deformations of the Fe–Ni–W alloy are shown in Fig. 1. From these images, a bimodal distribution of grains with small grains (~1μm) and large grains (~10μm) could be noticed. In this study, the region of the large grain was selected, as coarse grains require lower stress for plastic yielding [14], and therefore, the major portion of deformation is expected to confine mainly to this region. In addition, the large grain regions surrounded by difficult to deform small grain regions, deform under constrained rigid boundaries; because of which the displacement of grains will not remain uniform. Due to this bimodal distribution of grain, as may be noticed from Fig. 2, u and v displacements along x and y directions show band structures. The relevant computed parameters and their ranges are tabulated in Table 1. By comparing images of samples (Fig. 2) deformed 10, 20, and 40%, a gradual change in the microstructure due to deformation could be noticed. The clear-cut bands of displacements noticed in Fig 2a and b became relatively diffused in successive deformation (compare Fig 2 a and b with Fig 2 a and f). It may be noticed from the color chart representing the band of displacement that the band is effectively increasing with deformation. It is worth mentioning here that these bands should not be considered in the absolute sense. For example, in the case of a 10% deformed sample, minimum value of u-displacement is -1.542 μm, and the maximum value is 55.06 μm. In the case of v displacement, minimum and maximum displacements were 23.43 μm and 76.48 μm. The mean values of u and v displacements are 21.65 μm and 52.34 μm, respectively and their standard deviations were computed as 11.12 and 7.75, respectively. In the case of the 40% deformation frame, the minimum and maximum displacements of u-displacement became −4.63 μm and 158.46 μm, and for v displacement, these values are −9.6 and 105.48, respectively. These values are summarized in Table 1. It can, therefore, can be inferred that with increasing deformation, the range of displacements, means, and deviations are increasing, which is consistent with the process of deformation. This analysis, therefore, shows that DIC is providing consistent results.

Fig. 1
figure 1

showing images of the same region under (a) undeformed, (b) 10% deformed, (c) 20% deformed, and (d) 40% deformed

Full size image
Fig. 2
figure 2

showing images of the u-displacements (a) 10%, (c) 20%, (e) 40% deformed and v displacements (b) 10%, (d) 20%, and (f) 40% deformed samples

Full size image
Table 1 Values of displacements under successive deformation
Full size table

This analysis has also shown that the v displacement is more pronounced as compared to u-displacement which could be attributed to the orientation of boundary of regions comprising smaller grains. In the images Fig 2 a and f representing u and v displacements, it may be noticed that localization of large displacements visible in both images indicating initiation of strain concentration regions. However, before making comments, it is necessary to have a detailed statistical analysis to find out the correlation between u and v displacements.

The scattered plots for 10 and 40% of the Pearson’s function are shown in Fig. 3. By comparing Figs. 3 a and b, it can be seen that the relationship between the displacements is nonlinear in nature and with increasing deformation, the correlation between the two displacements becomes weaker. Equation 10 has used to compute Pearson’s correlation coefficients which came out to be −0.44 and 0.182 for the case of 10% deformation and 40% deformation, respectively. The value of −0.44 suggests that if the value of one of the displacements increases, the value of the other reduces. The magnitude of 0.44 suggests that the strength of the relationship is medium in nature. Such correlation indicated that the displacements are not independent and due to the constraints imposed by the boundary, an increase in one displacement is partially compensated by the reduction of the other. With increasing deformation, the correlation becomes relatively weak which indicates that the restrictions imposed by the boundaries have reduced considerably. However, detailed information could only be extracted by converting these displacements into strains.

Fig. 3
figure 3

Pearson’s function between u and v displacements (a) 10% and (b) 40% deformed samples

Full size image

Using Eqs. 5–7, all the three components of the strains (Exx, Eyy, Exy) were estimated. Figure 4 shows the computed Exx, Exy, and Eyy strains of samples deformed by 10, 20 and 40%, respectively. In addition, detailed statistical analysis of values of strains has also been carried out. The values of relevant parameters and their ranges are tabulated in Table 2. It may be noted that all the components of strains increase with increasing deformation. In all deformed samples, Exx is mainly positive in nature (Fig. 4a, d and g; Table 2) means Exx strain is mainly tensile in nature. Exy remains nearly insignificant as in most of the region its value is close to zero (Fig. 4 b, e, and h). In contrast, Eyy is mainly negative in all the deformed samples (Fig. 4c, f, and i). Such behavior arises due to the uniaxial deformation generating elongation on the x-direction and as reactionary compressive stress is generated in the y-direction. It may also be noted that with increasing deformation, localization of strain started and regions with large positive strains are always having regions of large negative strains in their vicinity. Up to 10% deformation, the stain was mainly confined to the region of large grains, and the region of small grain remained more or less undeformed. With deformation reaching 40%, the presence of strain in the region of small grains could be noticed (Fig. 4g). Because of the transfer of strain into the regions of small grains, fluctuations in the strain observed in 20% deformation get reduced (compare Fig. 4 d and g). Detailed statistical analysis to find out the correlation between the components of strains has been carried out and presented in Fig. 5, and the value of the coefficient of Pearson correlation is given in Table 3.

Fig. 4
figure 4

Strain distribution in the deformed samples. (a) Exx, (b) Exy, (c) Eyy in 10% deformed sample, (d) Exx, (e) Exy, (f) Eyy in 20% deformed sample, and (g) Exx, (h) Exy, (i) Eyy in 40% deformed sample

Full size image
Table 2 Values of strain under successive deformation
Full size table
Fig. 5
figure 5figure 5

Pearson correlation scattered graphs (a–c) Eyy for 10% deformed sample, (d–f) for 20% deformed sample, and (g–i) for 40% deformed sample

Full size image
Table 3 Pearson correlation coefficient of strains
Full size table

As the bimodal distribution of the grain’s constraints the distribution of the strains in the matrix, the elongation strains (Exx, Eyy) show a weak but positive correlation with the shear strain (Exy) during early deformation (10%), which means that increase in one helps in increasing the magnitude of the other. Due to restrictions imposed by the small grain regions, the elongation in the region of large grain is associated with the shear deformation (Exy). This conjecture is supported by the fact that the correlation between the elongation strains (Exx, Eyy) is weakly negative, which means an increase in the magnitude of one reduces the others. In another word, any tensile strain generated in one direction promotes compressive strain in another which is the manifestation of the rigid body constrained condition.

With increasing strain (20% deformation), correlation between the elongation strains (Exx, Eyy) becomes more negative suggesting relatively more severe constraints imposed by the system. In addition, the correlation between the Exx and Exy also becomes negative. However, for elongation along with perpendicular directions Eyy, Exy shows a medium correlation. It can be inferred that the rigid body restriction imposed by small grains confined most of the deformation in the y-direction. Between 20 and 40% deformation, the accumulated strain in the regions of large grains induces deformation in the regions of small grains. This helps in increasing the deformation. As a consequence of this induced deformation in the region of small grains, the correlation between the shear strain (Exy) and elongation strains (Exx, Eyy) becomes weak, but a moderate correlation between the elongation strains is established.

4 Conclusion

In the present work, a single-phase Fe–Ni–W alloy was studied for microstructural changes imparted by deformation. Images under SEM were recorded when the sample was deformed from 5–50%. Bimodal distribution of grains introduced heterogeneity in the displacement and strains as shown by the DIC of images obtained before and after deformation. Detailed Pearson correlation analysis showed that the displacements, u and v, determined using first-order shape functions, depending upon the amount of deformation showed medium to the weak correlation between them. Similar correlations among various components of strains were changing with the deformation. These changes were attributed to the heterogeneous distribution of grains which led to forming two separate regions, one containing large grains and the other with smaller grains. It has been shown that till the deformation is confined to the region of large grains, the correlation between shear deformation and elongation strains were existing, but as the deformation initiated in the regions of small grains also, the correlation between the two became weak.