Keywords

1 Introduction

The T-S fuzzy systems [1] as a very important tool are used to depict the complex nonlinear systems. For this type of system, by means of a compact set, a weight sum of linear system describes them. Then the traditional linear systems and the fuzzy logical control theory can be employed into this class of nonlinear model. Therefore T-S fuzzy systems attracted many researchers’ attention [2,3,4,5,6,7]. [2, 3] discussed T–S fuzzy systems’ robust stabilization and membership-function-dependent stability. For complex robot model, [4] designed a fuzzy neural network–backstepping control scheme. [5] proposed a integral sliding mode control based on event-trigger method. A based-event method was proposed to solve T-S fuzzy networked systems’ control problem [6]. For T-S fuzzy Markov jump model, [7] was provided a \(H_\infty \) switched fuzzy filter approach.

As an important means to improve the safety and reliability of the system, the fault diagnosis and fault-tolerant control (FTC) technology [8] has been paid more and more attentions, and become another main content of control theory, which is an involved in automatic control theory, computer science, signal processing, optimization theory, artificial intelligence and other multi-disciplinary new edge discipline. Fault diagnosis is a prerequisite for FTC, which has fault detection (FD), fault isolation (FI) and fault identify, where fault estimation (FE) is one of main contents. Recently, there are many literature reports about this content. [9, 10] considered the FD programs for discrete systems by applying a descriptor system method. [11, 12] provided two different design schemes to solve FE and FTC problem for discrete systems. Meanwhile, the results on FD and FTC of T-S Fuzzy models have been reported in [13,14,15,16,17,18,19]. [13, 14] respectively designed robust FD observer of continuous and discrete T-S fuzzy models. In finite frequency domain, [15, 16] provided FD design method for T-S fuzzy systems. [17] discussed the adaptive fuzzy FTC problem with sensor faults and dead zone input. [18] was concerned with FTC problem by resetting an observer. For fuzzy switched singular model containing actuator fault, [19] gave a FTC plan.

In particular, there are many achievements on FE of T-S fuzzy model. [20] solved actuator and sensor FE for switched T-S fuzzy model. With digital communication constraints, [21] proposed a FE method by designing a sliding mode observer. A modified FE technique was introduced for nonlinear model [22]. The observer-based FE and FTC technique provided for stochastic fuzzy model with Brownian parameter perturbations [23]. [24] applied a finite-frequency method to provide a sensor FE scheme for fuzzy system. For switched fuzzy stochastic systems [25,26,27], the different FE and FTC strategies were shown.

There are a lot of good works out but still many problems will be solved. However, to our knowledge, the problem of sensor FE for discrete T-S fuzzy model has not been fully investigated yet, which motivates us to make the effort in this paper.

2 Problem Formulation

Consider discrete T-S fuzzy system:

$$\begin{aligned} x_{k+1}= & {} \sum _{i=1}^{\mathbb {N}}\phi _i(k)[A_ix_{k}+B_iu_{k} +C_id_k+d_kw_k],\nonumber \\ y_k= & {} \sum _{i=1}^{\mathbb {N}}\phi _i(k)[Dx_k+f_{sk}], \end{aligned}$$
(1)

where \(x_k\in \mathbb {R}^n\) is state, \(y_k\in \mathbb {R}^r\) is measured output, \(f_{sk} \in \mathbb {R}^r\) denotes sensor fault. \(u_k\in \mathbb {R}^s\) denotes control input. \(d_k\in \mathbb {R}^p\) denotes unknown bounded disturbance. \(u_k\), \(d_k\) belong to \(\mathbb {L}_2[0,\infty )\). \(A_i\in \mathbb {R}^{n\times n}\), \(B_i\in \mathbb {R}^{n\times s}\), \(C_i\in \mathbb {R}^{n\times p}\), \(D\in \mathbb {R}^{r\times n}\) are real constant matrices. \(w_k\) is a stochastic process on a probability space \((\Upsilon ,\mathbb {F},\mathbb {P})\) refer to \((\mathbb {F}_k)_{k\in S}\) of \(\upsilon \)-algebras \(\mathbb {F}_k\subset \mathbb {F} \) generated by \((w_k)_{k\in S}\) and \(w_k\) is independent with \(E\{w_k\}=0\), \(E\{w^2_k\} =d>0\). Assume that \((A_i, D)\) is observable. The weight of the ith fuzzy rule is \(\phi _i(k)>0\) and \(\sum _{i=1}^{\mathbb {N}}\phi _i(k)=1\).

Define

$$\begin{aligned}&\bar{E_0}=\left[ \begin{array}{ccc} I&{}0\\ 0&{}0\end{array}\right] , \bar{A}_i=\left[ \begin{array}{ccc}A_i&{}0\\ 0&{}-I\end{array}\right] , \bar{B}_i=\left[ \begin{array}{ccc} B_i\\ 0\end{array}\right] , \bar{C}_i=\left[ \begin{array}{ccc} C_i\\ 0\end{array}\right] , \bar{I}_1=\left[ \begin{array}{ccc} 0\\ I\end{array}\right] ,\nonumber \\&\bar{D}=\left[ \begin{array}{ccc} D&I\end{array}\right] , \bar{\bar{D}}=\left[ \begin{array}{ccc} D&0\end{array}\right] , \bar{x}_k=\left[ \begin{array}{ccc}x_k\\ f_{sk}\end{array}\right] , \bar{I}_{2}=\left[ \begin{array}{ccc}I\\ 0\end{array}\right] , \end{aligned}$$

then the augmented system is that

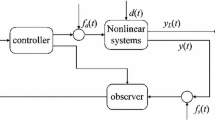
$$\begin{aligned} \bar{E}_0\bar{x}_{k+1}= & {} \sum _{i=1}^{\mathbb {N}}\phi _i(k)[\bar{A}_i\bar{x}_k+\bar{B}_iu_{k}+\bar{C}_id_{k} +\bar{I}_1f_{sk}+\bar{I}_{2}d_kw_k],\nonumber \\ y_k= & {} \sum _{i=1}^{\mathbb {N}}\phi _i(k)[\bar{D}\bar{x}_k] =\sum _{i=1}^{\mathbb {N}}\phi _i(k)[\bar{\bar{D}}\bar{x}_k+f_{sk}], \end{aligned}$$
(2)

where the components of \(\bar{x}_k\in \mathbb {R}^{n+r}\) are states \(x_k\) and faults \(f_{sk}\). To obtain the estimation of \(x_k\), \(y_k\), \(f_{sk}\), simultaneously, we design a FE observer.

For system (2), design the following FE observer:

$$\begin{aligned} \hat{\bar{x}}_k= & {} z_{k}+Qy_k,\nonumber \\ \sum _{i=1}^{\mathbb {N}}\phi _i(k)H_iz_{k+1}= & {} \sum _{i=1}^{\mathbb {N}}\phi _i(k)[R_iz_{k}+\bar{B}_iu_k],\nonumber \\ \hat{y}_k= & {} \bar{D}\hat{\bar{x}}_k, \end{aligned}$$
(3)

where \(z_k\in \mathbb {R}^{n+r}\) is the auxiliary state and \(\hat{\bar{x}}_k=\left[ \begin{array}{ccc}\hat{x}_k^T&\hat{f}_{sk}^T\end{array}\right] ^T\) is the estimation of \(\bar{x}_k\). Matrices Q, \(R_i\) and \(H_i\) are the observer’s parameters to be determined.

Set \(\bar{E}_0+H_iQ\bar{D}-H_i=0\), \(\bar{A}_i+R_iQ\bar{\bar{D}}-R_i=0\), \(I+R_iQ=0\), then

$$\begin{aligned} R_i=\left[ \begin{array}{cc}A_i&{}0\\ {-}D&{}{-}I\end{array}\right] , Q=\left[ \begin{array}{c}0\\ I\end{array}\right] , \end{aligned}$$
(4)

and design

$$\begin{aligned} H_{i}=\left[ \begin{array}{cc}I+S_iD&{}S_i\\ T_iD&{}T_i\end{array}\right] , \end{aligned}$$
(5)

define \(s_k=\bar{x}_k-\hat{\bar{x}}_k\), \(r_k=\bar{y}_k-\hat{\bar{y}}_k\), then global dynamic error system is that

$$\begin{aligned} s_{k+1}= & {} \sum _{i=1}^{\mathbb {N}}\phi _i(k)[H_{i}^{-1}R_is_k+H_{i}^{-1}\bar{C}_id_k +H_{i}^{-1}\bar{I}_2d_kw_k],\nonumber \\ r_k= & {} \bar{y}_k-\hat{\bar{y}}_k=\bar{D}(\bar{x}_k-\hat{\bar{x}}_k)=\bar{D}s_k. \end{aligned}$$
(6)

Remark 1

\(S_i\) and \(T_i\) are free matrices to be determined in order to guarantee the non-singularity of matrix \(\bar{E}_0\). Similar to [9, 10, 13], the design method of \(S_i\) and \(T_i\) are shown. Therefore, the proposed FE observer design can be obtained based on matrices \(T_i\) and \(S_i\) to guarantee that system (6) be asymptotically stable with \(H_\infty \) performance.

For \(\gamma >0\), consider system (1), observer (3) is a \(H_\infty \) fault estimator such that system (6) is asymptotically stable with \(d_k=0\), and for \(d_k\ne 0\), then (7) holds.

$$\begin{aligned} E\{\sum _{k=0}^{\infty }r_k^Tr_k\}<\gamma ^2E\{\sum _{k=0}^{\infty }d_k^Td_k\}. \end{aligned}$$
(7)

3 Main Results

Theorem 1

For given scalar \(\gamma >0\), there exists matrix \(P_i=P_i^T>0\) such that

$$\begin{aligned} \left[ \begin{array}{ccccc} -P_i&{}0&{}\bar{D}^T&{}(H_{i}^{-1}R_i)^T&{}0\\ \star &{}-\gamma ^2&{}0&{}(H_{i}^{-1}\bar{C}_i)^T&{}(H_{i}^{-1}\bar{I}_2)^T\\ \star &{}\star &{}-I&{}0&{}0\\ \star &{}\star &{}\star &{}-P_j^{-1}&{}0\\ \star &{}\star &{}\star &{}\star &{}-\frac{1}{d}P_j^{-1}\\ \end{array}\right] <0 \end{aligned}$$
(8)

holds so that system (6) is asymptotically stable with \(d_k=0\) and (7) holds.

Proof: When \(d_k=0\), construct Lyapunov functional: \(V(e_{k})=s_k^TP_is_k\), calculate the difference of V(k) along (6), then

$$\begin{aligned} \varDelta V_k= & {} E\{V(e_{k+1})-V(e_{k})\}\nonumber \\= & {} E\{s_{k}^T\{ \sum _{i=1}^\mathbb {N}\phi _i^2(k) \sum _{j=1}^\mathbb {N}\phi _j(k+1)) [(H_i^{-1}R_i)^TP_j(H_i^{-1}R_i)-P_i]\}s_{k}\}. \end{aligned}$$
(9)

By using Schur complement to (8), then \(s_{k}^T[(H_i^{-1}R_i)^TP_j(H_i^{-1}R_i)-P_i]s_{k}<0\) holds. Therefore, system (6) with \(d_k=0\) is asymptotically stable.

Considering zero initial condition, set \(J=E\{\sum _{k=0}^{N-1}[r_{k}^Tr_{k}-\gamma ^2d_k^Td_k]\}\), then

$$\begin{aligned} J= & {} E\{\sum _{k=0}^{N-1}\{r_{k}^Tr_{k}-\gamma ^2d_k^Td_k+\varDelta V_k\}-V_{N}\}\nonumber \\\le & {} E\{\sum _{k=0}^{N-1}\{[r_{k}^Tr_{k}-\gamma ^2d_k^Td_k]+s_{k+1}^TP_js_{k+1} -s_k^TP_id_k\}\}\nonumber \\= & {} E\{\sum _{k=0}^{N-1}\{\sum _{i=1}^\mathbb {N}\phi _i^2(k) \sum _{j=1}^\mathbb {N}\phi _j({k+1}) \{(\bar{D}s_k)^T\bar{D}s_k-\gamma ^2d_k^Td_k-s_k^TP_is_k\nonumber \\&+[H_{i}^{-1}R_is_k+H_{i}^{-1}\bar{C}_id_k+H_{i}^{-1}\bar{I}_2d_kw_k]^T\nonumber \\& \times P_j[H_{ij}^{-1}R_is_k+H_{ij}^{-1}\bar{C}_id_k+H_{i}^{-1}\bar{I}_2d_kw_k]\}\nonumber \\= & {} \sum _{k=0}^{N-1}\{\sum _{i=1}^\mathbb {N}\phi _i^2(k) \sum _{j=1}^\mathbb {N}\phi _j(k+1)\varTheta ^T\varOmega \varTheta \}, \end{aligned}$$
(10)

where \(\varOmega =\left[ \begin{array}{cc}\varOmega _{11}&{}(H_{i}^{-1}R_i)^TP_j(H_{i}^{-1}\bar{C}_i)\\ *&{}\varOmega _{22}\end{array}\right] \), \(\varTheta =\left[ \begin{array}{ccc}s_k\\ d_k\end{array}\right] \), \(\varOmega _{11}=(H_{i}^{-1}R_i)^TP_j(H_{i}^{-1}R_i)-P_i+\bar{D}^T\bar{D}\), \(\varOmega _{22}=-\gamma ^2I+(H_{i}^{-1}\bar{C}_i)^TP_i(H_{i}^{-1}\bar{C}_i) +d(H_{i}^{-1}\bar{I}_2)^TP_j(H_{i}^{-1}\bar{I}_2)\).

From (8), it is obtained that \(\varOmega <0\) as \(N\rightarrow \infty \), which shows that \(J<0\). Therefore (7) holds for \(d_k\ne 0\). That completes the proof.

Considering the nonlinear of (8), we can give the follow content to solve this problem. Then the fault estimator’s gains are shown.

Multiplying matrix \(diag\{I,I,I,\varPhi _i,\varPhi _i\}\) to the left and right side of (8), and considering \(P_j>0\) are non-singular, it has that \((P_j-\varPhi _i)^TP_j^{-1}(P_j-\varPhi _i)\ge 0\), that is, \(-\varPhi _i^TP_j^{-1}\varPhi _i\le P_j-(\varPhi _i^T+\varPhi _i)\), then

$$\begin{aligned} \left[ \begin{array}{cccccc} -P_i&{}0&{}\bar{D}&{}\varpi _1&{}0\\ \star &{}-\gamma ^2&{}0&{}\varpi _2&{}\varpi _3\\ \star &{}\star &{}-I&{}0&{}0\\ \star &{}\star &{}\star &{}\varpi _4&{}0\\ \star &{}\star &{}\star &{}\star &{}\frac{1}{d}\varpi _4 \end{array}\right] <0. \end{aligned}$$
(11)

where \(\varpi _1=(H_{i}^{-1}R_i)^T\varPhi _i\), \(\varpi _2=(H_{i}^{-1}\bar{C}_i)^T\varPhi _i\), \(\varpi _3=(H_{i}^{-1}\bar{I}_2)^T\varPhi _i\), \(\varpi _4=P_j-(\varPhi _i^T+\varPhi _i)\).

Define \(P_i=diag\{P_{i1}, P_{i2}\}\), \(\varPhi _i=diag\{\varPhi _{i1},\varPhi _{i2}\}\), and then they are substituted into (11), combined with (5), one has

$$\begin{aligned}&\left[ \begin{array}{cccccc} -P_{i1}&{}0&{}0&{}D^T\\ \star &{}-P_{i2}&{}0&{}I\\ \star &{}\star &{}-\gamma ^2I&{}0\\ \star &{}\star &{}\star &{}-I\\ \star &{}\star &{}\star &{}\star \\ \star &{}\star &{}\star &{}\star \\ \star &{}\star &{}\star &{}\star \\ \star &{}\star &{}\star &{}\star \\ \end{array}\right. \left. \begin{array}{cccccc} &{}\varPsi _{15}&{}\varPsi _{16}&{}0&{}0\\ &{}\varPsi _{25}&{}\varPsi _{26}&{}0&{}0\\ &{}C_i^T\varPhi _{i1}&{}\varPsi _{36}&{}\varPhi _{i1}&{}\varPsi _{38}\\ &{}0&{}0&{}0&{}0\\ &{}\varPsi _{55}&{}0&{}0&{}0\\ &{}\star &{}\varPsi _{66}&{}0&{}0\\ &{}\star &{}\star &{}\frac{1}{d}\varPsi _{55}\\ &{}\star &{}\star &{}\star &{}\frac{1}{d}\varPsi _{66} \end{array}\right] <0, \end{aligned}$$
(12)

where

$$\begin{aligned}&\varPsi _{15}=(A_i+S_iT_i^{-1}D)^T\varPhi _{i1}, \varPsi _{25}=(S_iT_{i}^{-1})^T\varPhi _{i1}, \varPsi _{36}=-C_i^TD^T\varPhi _{i2},\\&\varPsi _{16}=(-DA_i-(T_i^{-1}+DS_iT_i^{-1})D)^T\varPhi _{i2}, \varPsi _{55}=P_{j1}-(\varPhi _{i1}^T+\varPhi _{i1}),\\&\varPsi _{26}=-(T_i^{-1}+DS_iT_i^{-1})^T\varPhi _{i2}, \varPsi _{38}=-D^T\varPhi _{i2}, \varPsi _{66}=P_{j2}-(\varPhi _{i2}^T+\varPhi _{i2}). \end{aligned}$$

Set \(\varGamma _i^T=T_i^{-1}S_i^T\varPhi _{i1}\), \(\Upsilon _i^T=T_i^{-T}\varPhi _{i2}+T_i^{-T}S_i^TD^T\varPhi _{i2}\), then (12) becomes

$$\begin{aligned}&\left[ \begin{array}{cccccc} -P_{i1}&{}0&{}0&{}D^T\\ \star &{}-P_{i2}&{}0&{}I\\ \star &{}\star &{}-\gamma ^2I&{}0\\ \star &{}\star &{}\star &{}-I\\ \star &{}\star &{}\star &{}\star \\ \star &{}\star &{}\star &{}\star \\ \star &{}\star &{}\star &{}\star \\ \star &{}\star &{}\star &{}\star \\ \end{array}\right. \left. \begin{array}{cccccc} &{}\varLambda _{15}&{}\varLambda _{16}&{}0&{}0\\ &{}\varGamma _i^T&{}-\Upsilon _i^T&{}0&{}0\\ &{}C_i^T\varPhi _{i1}&{}\varPsi _{36}&{}\varPhi _{i1}&{}\varPsi _{38}\\ &{}0&{}0&{}0&{}0\\ &{}\varPsi _{55}&{}0&{}0&{}0\\ &{}\star &{}\varPhi _{66}&{}0&{}0\\ &{}\star &{}\star &{}\frac{1}{d}\varPsi _{55}\\ &{}\star &{}\star &{}\star &{}\frac{1}{d}\varPsi _{66} \end{array}\right] <0, \end{aligned}$$
(13)

where \(\varLambda _{15}=A_i^T\varPhi _{i1}+D^T\varGamma _i^T\), \(\varLambda _{16}=-A_i^TD^T\varPhi _{i2}-D^T\Upsilon _i^T\).

Based on what has been discussed above, we show the following theorem.

Theorem 2

For a given scalar \(\gamma >0\), system (6) is asymptotically stable with \(d_k=0\) and satisfies (7), if there exist symmetric matrices \(P_{i1}\), \(P_{i2}\), matrices \(\varPhi _{i1}\), \(\varPhi _{i2}\), \(\varGamma _i\) and \(\Upsilon _i\) such that (13) holds. Then \(S_i\) and \(T_i\) satisfy

$$\begin{aligned} T_i=(\Upsilon _i-\varPhi _{i2}^TD\varPhi _{i1}^{-T}\varGamma _i^{-1})^{-1}\varPhi _{i2}^T, S_i=\varPhi _{i1}^{-T}\varGamma _iT_i. \end{aligned}$$
(14)

Based on the aforementioned analysis, the FE problem for system (1) can be viewed as the appropriate fault estimator design so that system (9) is asymptotically stable and the effect of disturbances meets (7).

4 An Example

To prove the feasibility of the proposed \(H_\infty \) FE scheme, consider that system contains two rules, where membership function is that \(\phi _1(k)=\frac{1}{5}e^{\sin (k-0.5)}\) and \(\phi _2(k)=1-\phi _1(k)\) with the parameters:

\(A_1=\left[ \begin{array}{ccc}0.9&{}0.5\\ 0&{}0.4\end{array}\right] \),  \(B_1=\left[ \begin{array}{ccc}0.2&{}0\\ 0.2&{}-0.1\end{array}\right] \),  \(C_1=\left[ \begin{array}{ccc}0.9&{}0.2\\ 0.3&{}0.8\end{array}\right] \),  \(D=\left[ \begin{array}{ccc}-0.5&{}0\\ 0&{}0.8\end{array}\right] \),

\(A_2=\left[ \begin{array}{ccc}0.2&{}0.4\\ 0.1&{}0.5\end{array}\right] \),  \(B_2=\left[ \begin{array}{ccc}0.3&{}0\\ 0&{}-0.4\end{array}\right] \),  \(C_2=\left[ \begin{array}{ccc}0.2&{}0.5\\ 0&{}0.7\end{array}\right] \),  \(Q=\left[ \begin{array}{cccc}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1\end{array}\right] ^T\).

For \(\gamma =2.4\) and \(d=0.9\), according to Theorem 2, the gains in observer (3) are shown:

\(R_1=\left[ \begin{array}{cccc}0.9&{}0.5&{}0&{}0\\ 0&{}0.4&{}0&{}0\\ 0.5&{}0&{}1&{}0\\ 0&{}-0.8&{}0&{}1\end{array}\right] \),  \(H_1 =\left[ \begin{array}{cccc} 0.6906&{}0.2438&{}0.6187&{}0.3048\\ -0.0839&{}1.0492&{}0.1677&{}0.0615\\ -0.5868&{}0.5665&{}1.1736&{}0.7082\\ -0.0916&{}0.1985&{}0.1832&{}0.2481 \end{array}\right] \),

\(R_2=\left[ \begin{array}{cccc}0.2&{}0.4&{}0&{}0\\ 0.1&{}0.5&{}0&{}0\\ 0.5&{}0&{}1&{}0\\ 0&{}-0.8&{}0&{}1\end{array}\right] \),  \(H_2=\left[ \begin{array}{cccc} 0.8263&{}-0.0043&{} 0.3474&{}-0.0054\\ -0.0776&{} 0.8501&{} 0.1551&{}-0.1873\\ -0.9170&{} 0.2073&{} 1.8339&{} 0.2592\\ 0.7863&{} 0.4996&{}-1.5725&{} 0.6244 \end{array}\right] \).

To show the effectiveness of the designed FE observer, consider

$$\begin{aligned} u_k=\left[ \begin{array}{ccc}0&0\end{array}\right] ^T, d_k=\left[ \begin{array}{ccc}0.2rand-0.1&0.4rand-0.2\end{array}\right] ^T, f_{sk}=\left[ \begin{array}{ccc}f_{sk1}&f_{sk2}\end{array}\right] ^T, \end{aligned}$$

where

\(f_{sk1}=\left\{ \begin{array}{ccc} 0.5~~100<k\le 200\\ 0,~~other\end{array}\right. \),   \(f_{sk2}=\left\{ \begin{array}{ccc} \sin (0.2k-0.2)~~100<k\le 200\\ 0,~~other\end{array}\right. .\)

Set \(x_k =\left[ \begin{array}{ccc}0.8&-0.6\end{array}\right] ^T\), fault estimation \(\hat{f}_k\) is shown in Fig. 1, in which fso1 and fso2 denote estimations of \(f_{sk1}\) and \(f_{sk2}\), respectively.

Fig. 1.
figure 1

Fault estimation \(\hat{f}_{sk}\)

Full size image

5 Conclusions

The FE problem for discrete T-S system is considered. An observer-based fault estimator is designed by applying the extended state method and the error dynamic system is asymptotically stable and meets \(H_\infty \) performance. Sufficient conditions and observer gains of the FE problem are shown. An example proves that the proposed method’s effectiveness.