Keywords

1 Introduction

Fuzzy logic has been used to describe complicated nonlinear system, which is effective. By applying the existing fuzzy approaches, the fuzzy IF-THEN rule has been firstly used to describe this kind of model [1], namely T-S fuzzy model. This method can simplify analysis of nonlinear model. By applying T-S fuzzy methodology, different linear models are described by local dynamics in different state-space regions. Therefore, membership functions smoothly blend these local models together so that overall fuzzy model is obtained. The issues [2,3,4,5,6] on fuzzy systems attracted attention.

Recently, [7] has introduced generalized Kalman–Yakubovich–Popov (GKYP) lemma which is a very significant development. Frequency domain property is converted into a LMI for a finite-frequency range. GKYP lemma has many practical applications. T-S fuzzy models’ \(H_\infty \) control [8] was solved. Fault detection problem [9] was proposed in T-S fuzzy networked models. Fuzzy filter problem for nonlinear systems [10] was solved. T-S fuzzy fault detection method was designed in [11].

In past decades, when demands for industrial manufacture are growing, more and more people pay attention to fault-tolerant control (FTC). For obtaining the same control objective, different design methodologies are used in two approaches: passive FTC (PFTC) and active FTC (AFTC) in accordance with how redundancy is used. The system performance lies on the availability of redundancy and FTC design method. Each method can produce some unique properties based on the distinctive design approaches used. Passive and active FTC were considered simultaneously in [12, 13]. PFTCs were provided for affine nonlinear models [14] and stochastic systems [15, 16], respectively. At the same time, there were also many results on AFTC. Fault estimation and AFTC of discrete systems [17] are considered by finite-frequency method. Nonlinear stochastic AFTC system [18] was analyzed by applying fuzzy interpolation approach. For stochastic systems [19], the descriptor observer was given to solve fault estimation and FTC problem by the sliding mode method. FTC [20] for fuzzy delta operator models was proposed.

However, there are few papers on fault estimation and compensation for T-S fuzzy models with sensor faults in low-frequency domain. Therefore, this paper solves the problem above, whose contributions are that: For this models considered, in terms of the descriptor system approach, a fuzzy observer is designed so as to make the stability of dynamic error in low-frequency domain be ensured. State and fault’s estimations are showed by the observer above, then a \(H_\infty \) output feedback controller is proposed so as to make controlled systems with sensor faults have certain fault-tolerant function. A numerical simulation shows the effectiveness of this designed scheme.

2 Problem Formulation

T-S fuzzy model is shown: Plant Rule i: If \(\theta _{1k}\) is \(\phi ^i_1\), \(\theta _{2k}\) is \(\phi ^i_2\), \(\ldots \), \(\theta _{mk}\) is \(\phi ^i_m\), then

$$\begin{aligned}&x_{k+1}=A_{1i}x_k+B_{1i} u_k+D_{1i}d_k,\nonumber \\&y_k=A_2x_k+F_2 f_k, \end{aligned}$$
(1)

where \(i=1,\ldots ,\mathcal {M}\), \(\mathcal {M}\) is IF-THEN rules’s number; \(\theta _{1k}\), \(\theta _{2k}\), \(\ldots \), \(\theta _{mk}\) are premise variables; \(\phi _1^i\), \(\phi _2^i\), \(\ldots \), \(\phi _s^i\) are fuzzy set; \(x_k\in \mathcal {R}^g\) is state, \(y_k\in \mathcal {R}^{gy}\) is output. \(d_k\in \mathcal {R}^{gd}\), \(u_k\in \mathcal {R}^{gu}\) and \(f_k\in \mathcal {R}^{gf}\) are disturbance, input and sensor fault, respectively, which belong to \(\mathcal {L}_2[0,\infty )\). \(A_{1i}\), \(B_{1i}\), \(D_{1i}\), \(A_2\), and \(F_2\) are matrixes. Hypothesis that \((A_{1i}, A_2)\) is observable and \(F_2\) has full rank.

A fuzzy inference and weighted center average defuzzifier is given by considering a singleton fuzzifier, the form of (1) is

$$\begin{aligned}&x_{k+1}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}[A_{1i}x_k+B_{1i} u_k+D_{1i}d_k],\nonumber \\&y_k=A_2x_+F_2 f_k, \end{aligned}$$
(2)

where \(\eta _{i\theta _k}=\frac{\prod ^m_{l=1}\phi ^i_{l\theta _{lk}}}{\sum _{i=1}^{\mathcal {M}}\prod ^n_{l=1}\phi ^i_{l\theta _{lk}}}\), \(\sum _{i=1}^\mathcal {M}\eta _i=1\).

Define \( \left[ \begin{array}{cc} x_k^T&f_k^T\ \end{array} \right] ^T=\bar{x}_k\), then the dynamic global model is that

$$\begin{aligned}&\bar{E}\bar{x}_{k+1}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}[\bar{A}_{1i}\bar{x}_k+\bar{B}_{1i} u_k+\bar{D}_{1i}d_k],\nonumber \\&\bar{y}_k=\bar{A}_2\bar{x}_k, \end{aligned}$$
(3)

where \(\bar{E}=\left[ \begin{array}{ccc}I&{}0\\ 0&{}0\end{array} \right] \), \(\bar{A}_{1i}=\left[ \begin{array}{ccc} A_{1i}&{}0\\ 0&{}0\end{array}\right] \), \(\bar{B}_{1i}=\left[ \begin{array}{ccc} B_{1i}\\ 0\end{array}\right] \), \(\bar{D}_{1i}=\left[ \begin{array}{ccc} D_{1i}\\ 0\end{array}\right] \), \(\bar{A}_{2}=\left[ \begin{array}{ccc} A_2&F_2\end{array} \right] \).

For the same IF-Then rule, design the fuzzy observer

$$\begin{aligned}&\hbar _{k+1}=(\bar{A}_{1i}-L_{1i}\bar{A}_2)\hat{\bar{x}}_k+\bar{B}_{1i}u_k+L_{1i}\bar{y}_k,\nonumber \\&\hat{\bar{x}}_k=(\bar{E}+L_{2}\bar{A}_2)^{-1}(\hbar _k+L_{2}\bar{y}_k),\nonumber \\&\hat{\bar{y}}_k=\bar{A}_2\hat{\bar{x}}_k, \end{aligned}$$
(4)

and the output feedback controller

$$\begin{aligned} u_k=K_v y_k=K_v\bar{y}_k, \end{aligned}$$
(5)

with \(\bar{x}_k\)’s estimate is that \(\hat{\bar{x}}_k\), \(x_k\)’s estimate is that \(\hat{x}_k= \left[ \begin{array}{ccc}I&0\end{array}\right] \hat{\bar{x}}_k\), \(f_k\)’s estimate is \(\hat{f}_k=\left[ \begin{array}{ccc}0&I\end{array}\right] \hat{\bar{x}}_k\) , and \(y_k\)’s estimate is \(\hat{\bar{y}}\). \(L_{1i}\), \(L_2\), \(K_v\) are gains to be determined.

Hence, dynamic global model is obtained as follows:

$$\begin{aligned}&\hbar _{k+1}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}[(\bar{A}_{1i}-L_{1i}\bar{A}_2)\hat{\bar{x}}_k+\bar{B}_{1i}u_k+L_{1i}y_k],\nonumber \\&\hat{\bar{x}}_k=(\bar{E}+L_{2}\bar{A}_2)^{-1}(\hbar _k+L_{2}\bar{y}_k),\nonumber \\&\hat{\bar{y}}_k=\bar{A}_2\hat{\bar{x}}_k, \end{aligned}$$
(6)

and

$$\begin{aligned} u_k=\sum _{v=1}^\mathcal {M}\eta _{v\theta _k}K_v y_k =\sum _{v=1}^\mathcal {M}\eta _{v\theta _k}K_v\bar{y}_k. \end{aligned}$$
(7)

Equation (6) becomes

$$\begin{aligned} (\bar{E}+L_{2}\bar{A}_2)\hat{\bar{x}}_{k+1}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}[(A_{1i}-L_{1i}\bar{A}_2)\hat{\bar{x}}_k +\bar{B}_{1i}u_k+L_{1i}\bar{y}_k+L_2\bar{y}_{k+1}]. \end{aligned}$$
(8)

Meanwhile, adding \(L_2y_{k+1}\) on the two sides of (3), then

$$\begin{aligned}&(\bar{E}+L_{2}\bar{A}_2)\bar{x}_{k+1}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}[(A_{1i}-L_{1i}\bar{A}_2)\hat{\bar{x}}_k +\bar{B}_{1i}u_k+L_{1i}\bar{y}_k +\bar{D}_{1i}d_k]. \end{aligned}$$
(9)

Define \(\tilde{\bar{x}}_k=\bar{x}_k-\hat{\bar{x}}_k\), \(r_k=\bar{y}_k-\hat{\bar{y}}_k\), then

$$\begin{aligned}&\tilde{\bar{x}}_{k+1}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}[(\bar{E}+L_{2}\bar{A}_2)^{-1}(A_{1i}-L_{1i}\bar{A}_2)\tilde{\bar{x}}_k+\bar{D}_{1i}d_k],\nonumber \\&r_k=\bar{A}_2\tilde{\bar{x}}_k. \end{aligned}$$
(10)

3 Main Results

Theorem 1

Considering constant \(\gamma >0\), the gain of (4) is addressed so as to make (10) with \(H_\infty \) level \(\gamma \) asymptotic stability in \(|\vartheta |\le \vartheta _1\) if there is symmetric matrixes \(P_i>0\), \(P_l>0\), \(Q>0\) and matrixes \(X_i\) for all \(i,l\in \{1,\ldots ,\mathcal {M}\}\) so that (11) and (12) hold:

$$\begin{aligned}&\left[ \begin{array}{ccc} P_l-g_2X_i-g_2X_i^T&{}g_1X_i+g_2\xi _1\\ *&{}-P_i-g_1\xi _1-g_1\xi _1^T \end{array}\right] <0,\end{aligned}$$
(11)
$$\begin{aligned}&\left[ \begin{array}{cccc} -P_l&{}Q+X_i&{}0&{}0\\ *&{}\varphi _1&{}-X_i^T\bar{D}_{1i}&{}\bar{A}_2^T\\ *&{}*&{}-\gamma ^2I&{}0\\ *&{}*&{}*&{}-I \end{array}\right] <0, \end{aligned}$$
(12)

where \(\xi _1=X_i^T(\bar{E}+L_{2}\bar{A}_2)^{-1} \bar{A}_{1i}-Y_i\bar{A}_2\), \(\varphi _1=P_i-2\cos \vartheta _1Q-\xi _1^T-\xi _1\), \(L_2=\left[ \begin{array}{cccc}0&I\end{array}\right] ^T\), and \(g_1\), \(g_2\) are arbitrary fixed scalars satisfying \(g_1^2\sigma _{\max }(P_i)<g_2^2\sigma _{\min }(P_i)\). Then gains of (4) are that \(L_{1i}=(\bar{E}+L_2\bar{A}_2)X_i^{-T}Y_i\).

Proof

Define \(V_k=\tilde{\bar{x}}_k^T[\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}P_i]\tilde{\bar{x}}_k\), differences of \(V_k\) along (10) is that \(\Delta V_k=(\sum _{i=1}^\mathcal {M}\eta _{i\theta _k})^2\sum _{l=1}^\mathcal {M}\eta _{l\theta _{k+1}}\tilde{\bar{x}}_k^T [\varrho ^T P_l\varrho -P_i]\tilde{\bar{x}}_k\), where \(\varrho =(\bar{E}+L_{2}\bar{A}_2)^{-1}(A_{1i}-L_{1i}\bar{A}_2)\). Notice that \(\varrho ^TP_l\varrho -P_i<0\) so \(\Delta V_k<0\). Easily, it is obtained that

$$\begin{aligned} \left[ \begin{array}{cc}\varrho \\ I\end{array}\right] ^T \left[ \begin{array}{cc}P_l&{}0\\ 0&{}-P_i\end{array}\right] \left[ \begin{array}{cc}\varrho \\ I\end{array}\right] <0. \end{aligned}$$
(13)

There exist \(g_1\) and \(g_2\) such that \(g_1^2\sigma _{\max }(P_i)<g_2^2\sigma _{\min }(P_i)\), then

$$\begin{aligned} \left[ \begin{array}{cc} g_1I\\ g_2I\end{array}\right] ^T \left[ \begin{array}{cc} P_l&{}0\\ 0&{}-P_i \end{array}\right] \left[ \begin{array}{cc}g_1I\\ g_2I\end{array}\right] =g_1^2P_l-g_2^2P_i<0. \end{aligned}$$
(14)

Since that \(\left[ \begin{array}{cc}g_2I&-g_1I\end{array}\right] ^{T\perp }=\left[ \begin{array}{cc}g_1I&g_2I\end{array}\right] \) and \(\left[ \begin{array}{cc}\varrho ^T&I\end{array}\right] \) belongs to the null subspace of \(\left[ \begin{array}{cc}-I&\varrho \end{array}\right] ^{T}\), it has

$$\begin{aligned} \left[ \begin{array}{cc}-I\\ \varrho ^T\end{array}\right] X_i\left[ \begin{array}{cc}g_2I\\ -g_1I\end{array}\right] ^T +\left[ \begin{array}{cc} g_2I\\ -g_1I\end{array}\right] X_i^T\left[ \begin{array}{cc}-I\\ \varrho ^T\end{array}\right] ^T +\left[ \begin{array}{cc}P_l&{}0\\ 0&{}-P_i\end{array}\right] <0. \end{aligned}$$
(15)

Set \(Y_i=X_i^T(\bar{E}+L_2\bar{A}_2)^{-1}L_{1i}\), (15) holds after some matrix manipulations.

According to GKYP Lemma [7], then

$$\begin{aligned} \left[ \begin{array}{cc}\bar{A}_{1\eta }&{}\bar{D}_{\eta }\\ I&{}0\end{array}\right] ^T \left[ \begin{array}{cc}-P_{\eta +}&{}Q\\ Q&{}P_{\eta }-2\cos \vartheta _1Q\end{array}\right] \left[ \begin{array}{cc}\bar{A}_{1\eta }&{}\bar{D}_{\eta }\\ I&{}0\end{array}\right] \nonumber \\ +\left[ \begin{array}{cc}\bar{A}_2&{}0\\ 0&{}I\end{array}\right] ^T \left[ \begin{array}{cc}I&{}0\\ 0&{}-\gamma ^2I\end{array}\right] \left[ \begin{array}{cc}\bar{A}_2&{}0\\ 0&{}I\end{array}\right] <0. \end{aligned}$$

Define \(P_{\eta +}=\sum _{l=1}^\mathcal {M}\eta _{l\theta _(k)}P_l\), \(P_{\eta }=\sum _{i=1}^\mathcal {M}\eta _{i\theta _(k)}P_i\), then

$$\begin{aligned}&\left[ \begin{array}{cc}\bar{A}_{1i}&{}\bar{D}_i\\ I&{}0\end{array}\right] ^T \Theta _1 \left[ \begin{array}{cc}\bar{A}_{1i}&{}\bar{D}_i\\ I&{}0\end{array}\right] +\left[ \begin{array}{cc}\bar{A}_2&{}0\\ 0&{}I\end{array}\right] ^T \Theta _2 \left[ \begin{array}{cc}\bar{A}_2&{}0\\ 0&{}I\end{array}\right] <0, \end{aligned}$$
(16)

where \(\Theta _1=\left[ \begin{array}{cc}-P_l&{}Q\\ Q&{}P_i-2\cos \vartheta _1Q\end{array}\right] \), \(\Theta _2=\left[ \begin{array}{cc}I&{}0\\ 0&{}-\gamma ^2I\end{array}\right] \), then (16)’s form is that

$$\begin{aligned}& \Upsilon ^{\perp T} \left( \begin{array}{ccc} \varrho _1^T \Theta _1 \varrho _1 +\varrho _2^T \Theta _2 \varrho _2 \end{array}\right) \Upsilon ^\perp <0, \end{aligned}$$
(17)

where \(\Upsilon ^\perp =\left[ \begin{array}{ccc} \bar{A}_{1i}^T&{}I&{}0\\ \bar{D}_i^T&{}0&{}I\end{array}\right] \), \(\varrho _1=\left[ \begin{array}{ccc} I&{}0&{}0\\ 0&{}I&{}0\\ \end{array}\right] ^T\), \(\varrho _2=\left[ \begin{array}{ccc} 0&{}\bar{A}_2&{}0\\ 0&{}0&{}I\\ \end{array}\right] \).

For \(\Upsilon ^\perp \), then \(\Upsilon =\left[ \begin{array}{ccc} -I&\bar{A}_{1i}&\bar{D}_i \end{array}\right] \). According to Projection Lemma, then \(\varrho _1^T\Theta _1\varrho _1+\varrho _2^T\Theta _2\varrho _2<\Upsilon X_iR^T+(\Upsilon X_iR^T)^T\). Let \(R^T=\left[ \begin{array}{ccc}0&I&0\end{array}\right] \), then (18) holds:

$$\begin{aligned}&\left[ \begin{array}{ccc} -P_l&{}Q&{}0\\ *&{}P_i-2\cos \vartheta _1Q&{}0\\ *&{}*&{}-\gamma ^2I \end{array}\right] +\left[ \begin{array}{ccc} 0\\ \bar{A}_2^T\\ 0 \end{array}\right] \left[ \begin{array}{ccc} 0\\ \bar{A}_2^T\\ 0 \end{array}\right] ^T -\left[ \begin{array}{ccc} 0&{}-X_i&{}0\\ *&{}\nu &{}X_i^T\bar{D}_i\\ *&{}*&{}0 \end{array}\right] <0. \end{aligned}$$
(18)

with \(\nu =\bar{A}_{1i}^TX_i+X_i^T\bar{A}_{1i}\). By matrix manipulations, (18) and (12) are equivalent. Therefore, (12) satisfies \(H_\infty \) index \(\gamma \) in \(|\vartheta |\le \vartheta _1\) if (16) holds. The proof is finished.

Secondly, we give the controller in low-frequency domain. This system may not work normally with sensor faults. This motivates us to consider the fault-tolerant method, which is shown in the following.

Based on observer technique, \(f_k\) is designed as \(\hat{f}_k=\left[ \begin{array}{cc}0&I\end{array}\right] \hat{\bar{x}}_k\). By subtracting \(\hat{f}_k\) from \(y_k\), then \(y_{ck}=y_k-F_2\hat{f}_k =A_2x_{k}+F_2f_{k}-F_2\hat{f}_k =A_2x_{k}+\bar{F}_2\tilde{\bar{x}}_k\) with \(\bar{F}_2=F_2\left[ \begin{array}{ccc}0&I\end{array}\right] \).

Consider controller (5), and use \(y_{ck}\) to replace \(y_k\), then \(u_{ck}=\sum _{v=1}^\mathcal {M}\eta _v(\theta _k)K_v y_{ck}\) so closed-loop models are that

$$\begin{aligned}&x(k+1)=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}\sum _{v=1}^\mathcal {M}\eta _{v\theta _k}[(A_{1i}+B_{1i}K_v A_2) x_k+B_{1i}K_v\bar{F}_2\tilde{\bar{x}}_k+D_{1i}d_k],\nonumber \\&y_{ck}=A_2x_k+F_2\left[ \begin{array}{ccc}0&I\end{array}\right] \tilde{\bar{x}}_k. \end{aligned}$$

Considering system (10), a new system is obtained

$$\begin{aligned}&X_{ek}=\sum _{i=1}^\mathcal {M}\eta _{i\theta _k}\sum _{v=1}^\mathcal {M}\eta _{v\theta _k}[\bar{\bar{A}}_{iv}X_k+\bar{\bar{D}}_{1i}d_k],\nonumber \\&y_{ck}=\bar{\bar{A}}_2X_k, \end{aligned}$$
(19)

where \(X_k=\left[ \begin{array}{ccc}x(k)\\ \tilde{\bar{x}}_k\end{array}\right] \), \(\bar{\bar{D}}_{1i}=\left[ \begin{array}{ccc}D_{1i}\\ \bar{D}_{1i}\end{array}\right] \), \(\bar{\bar{A}}_{iv}=\left[ \begin{array}{ccc}\Upsilon _{11}&{}\Upsilon _{12}\\ 0&{}\Upsilon _{22}\end{array}\right] \), \(\bar{\bar{A}}_2=\left[ \begin{array}{ccc}A_2&\bar{F}_2\end{array}\right] \), \(\Upsilon _{11}=A_{1i}+B_{1i}K_vA_2,\Upsilon _{12}=B_{1i}K_v\bar{F}_2\), \(\Upsilon _{22}=(\bar{E}+L_{2}\bar{A}_2)^{-1}(\bar{A}_{1i}-L_{1i}\bar{A}_2)\).

It is not difficult to show that equation (19) for this controlled system adopting the static output feedback control strategy, by applying this proposed technology, it can reduce sensor fault’s influence on controlled models, so whole closed-loop ones have a certain fault-tolerant function.

4 Numerical Simulations

A example can prove effectiveness of this proposed method. These systems have Rule 1 and 2, their membership functions are \(\phi _{1x_{1k}}=\frac{1}{1+exp(-3x_{1k})}\), \(\phi _{2x_{1k}}=1-\phi _{1x_{1k}}\), and consider \(x_{1k}\) is \(\phi _1\) and \(\phi _2\), respectively, and

$$\begin{aligned}&A_{11}=\left[ \begin{array}{cc} 0.3&{}0\\ 0&{}0.6\end{array}\right] , B_{11}=\left[ \begin{array}{cc}0.1&{}0\\ 0&{}-0.1\end{array}\right] , D_{11}=\left[ \begin{array}{cc} -0.2\\ 0.5\end{array}\right] , A_{12}=\left[ \begin{array}{cc}0.6&{}0\\ 0&{}0.5\end{array}\right] ,\\&B_{12}=\left[ \begin{array}{cc}0.4&{}0\\ 0&{}-0.4\end{array} \right] , D_{12}=\left[ \begin{array}{cc} 0.8\\ 0.4\end{array}\right] , A_{2}=\left[ \begin{array}{cc}0.1&{}0\\ 0&{}0.1\end{array}\right] , F_{2}=\left[ \begin{array}{cc}1.0&{}0\\ 0&{}1.0\end{array}\right] , \end{aligned}$$

let \(g_1=1\), \(g_2=3\), in \(|\vartheta _1|\le 1.7\), for \(\gamma =0.15\), by (11) and (12), gains of (4) are

$$\begin{aligned} L_{11}=\left[ \begin{array}{cc} -2.2563&{}0.8171\\ 1.1779&{}-1.0420\\ -0.0744&{}-0.0817\\ -0.1178&{}-0.4958\\ \end{array}\right] , L_{12}=\left[ \begin{array}{cc} -1.6636&{}-1.0563\\ -1.4917&{}-0.3082\\ -0.4336&{}0.1056\\ 0.1492&{}-0.4692\\ \end{array}\right] , L_{2}=\left[ \begin{array}{cc} 0&{}0\\ 0&{}0\\ 1&{}0\\ 0&{}1\\ \end{array}\right] . \end{aligned}$$

Assumed that \(d_k=0.1\sin _k\) and \(f_k=\left[ \begin{array}{cc}f_{1k}\\ f_{2k}\end{array}\right] \) with

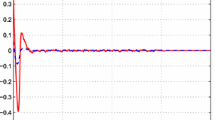
$$\begin{aligned} f_{1k}=\left\{ \begin{array}{ll} 0, ~~0<k\le 30\\ 0.3\sin _k,70\ge k\ge 30 0, ~~k>70\\ \end{array}\right. , f_{2k}=\left\{ \begin{array}{ll} 0, ~~0<k\le 30\\ 0.4\sin _k,70\ge k\ge 30 0, ~~k>70\\ \end{array}\right. . \end{aligned}$$

Considering \(x_0=\left[ \begin{array}{cc}x_{1k}^T&x_{2k}^T\end{array}\right] ^T=\left[ \begin{array}{cc}-1&2\end{array}\right] ^T\), Fig. 1 depicts the estimation of fault \(f_k\) , where \(fo_i\) is the estimation of \(f_{ik}\) with \(i=1,2\). \(\hat{y}_k\)’s estimations are shown in Fig. 2, where \(yo_1\) means \(\hat{y}_{1k}\) and \(yo_2\) means \(\hat{y}_{2k}\).

Fig. 1
figure 1

\(f_{k}\)’s estimation

Full size image
Fig. 2
figure 2

Estimate output \(\hat{y}_k\)

Full size image

5 Conclusion

The fault estimation and compensation scheme of fuzzy T-S discrete models is addressed for low-frequency range. A fuzzy observer is given so as to ensure error model’s stability with \(H_\infty \) performance for low-frequency range. The fault estimations are obtained via the observer above, then a fuzzy \(H_\infty \) output feedback controller is shown so as to ensure certain fault-tolerant function of controlled model with sensor fault considered. A numerical simulation proves the effectiveness of this method. The conclusion of this paper can also be expended into finite middle- and high-frequency domain.