Keywords

1 Introduction

In order to find the most appropriate solutions, multi-criteria decision-making methods (MCDM) are the translation systems, which translate decision-making problems, from less complex such as the daily decision-making problems to advanced decision-making problems, to the mathematical algorithms. MCDM methods are developed to analyze alternatives against the criteria with the various algorithms to lead the decision-maker (DM) to the optimal solutions for the decision-making problems.

In general, MCDM methods are employed to handle MCDM problem with the selection of a suitable solution among alternatives concerning a variety of factors [1]. Eyvindson et al. [2] described MCDM techniques as the mathematical methods employed to find a best compromise solution based on judgments provided by stakeholders [3]. According to [4], MCDM methods consist of ranking alternatives, or selecting an appropriate alternative, with respect to several multiple, conflicting, and interactive criteria. To solve different decision-making problems, MCDM methods are designed into integrated method, which two or three MCDM methods constitute an integrated approach, or group decision-making methods [5–7]. MCDM methods have been applied to a wide range of problems such as Supply chain management [8], Energy [9], Transportation [10], Logistic [11], Agriculture and water resource management [12], Civil engineering and construction management [13], Strategic decision-making [9], and Strategic management [13, 14].

MCDM methods are designed to analyze a set of alternatives given by the problem against a set of criteria in order to offer the solutions; yet, in the real-world processes, the decisions are affected by multiple variables originating from the external forces from outside of the decision matrices that are constructed by the MCDM methods. These variables possibly seem irrelevant to the decision-making problem; however, their impact is hidden in the final result. This brings a serious shortage when the problem is observed through a holistic view. To illustrate how the aforementioned process functions, in this chapter, a mathematical framework is proposed to calculate the impact and interaction between two irrelevant decision matrices. In fact, as discussed in advance, there are many issues that affect the decision-making where they need to be identified while they are not considered in the conventional decision-making methods. For instance, in the supplier selection problem, the lack of consideration of the firm’s strategies may cause the wrong selection when the supplier selection, as the part of operational strategies execution, needs to be in line with the firm’s strategies.

Supplier selection is a typical MCDM activity [15]. According to [16], selection of the proper suppliers will reduce costs and provide high quality products. El Hiri et al. [17] defined selection of the most proper suppliers as a vital activity for elevating the result of a company's efforts to conserve its market position. Indeed, as stated by [18], one of the key issues in supply chain management is supplier selection and also finding the best supplier among several alternatives against various criteria, such as services, cost, and risks. As mentioned heretofore, in real world the selections which they upon DM’s decision occur under uncertainty environment.

As mentioned heretofore, the supplier selection process highly depends on experts’ assessments. Yet, the issue emerges when the firms’ strategies are not considered by DMs or in general in the decision-making process to select the suppliers. Ignoring the strategies in the supplier selection process mainly causes the lack of a comprehensive approach to select a supplier, provisional supplier selection, and inappropriate selection of the supplier as an integral part of the operational strategies implementation. On the other hand, all environmental planning and management decisions are subject to a number of uncertainties ranging from complexities of natural systems, variable degrees of unpredictable randomness, frequent lack of sufficient data, and at times, the politicized and therefore variable interpretation of information [19]. The certain decision approaches have been applied on various studies in the field of supplier selection such as Abdel-Baset et al. [20, 21], while certain decisions addressing are based upon classical assumptions and always tend to be so in deterministic conditions [22].

In the real-world application, with emerge of vagueness, uncertainty, or imprecision in the solutions evaluation, the final output is not a crisp value, but rather a distribution, a fuzzy value or a numerical interval which is called the grey number. In this chapter, the grey system is exercised for the computation of the interactions. The Grey System was first introduced by Deng [23]. The grey system theory is found as a channel in order to materialize incomplete information of individuals, professionals, etc., into discrete data [24]. It is widely applied in various fields of research and projects such as systems analysis, data processing, modeling, and prediction, as well as in control and decision-making [25]. Deng [23, 26] developed the grey decision-making systems. The grey decision is made in the situation that the decision model has grey elements or the normal decision model and grey model are combined, and the key research is the scheme selection problem [27]. Nowadays, the grey systems theory is broadly applied to different decision-making problems to handle the uncertainty [28, 29]. To calculate the interaction between the firm’s strategies, which have been derived from grey strategies interaction model, and the supplier selection, grey TOPSIS (G-TOPSIS) and Grey-Entropy are utilized in this chapter. Indeed, the objective of this chapter is to propose a solution for the problem of connection between two irrelevant decision matrices which have impact on each other in real-world problems.

The rest of this chapter is organized as follows: in the Sect. 2, the grey numbers and their operation are demonstrated; the methods which are used in this chapter are represented in the Sect. 3. In Sect. 4, the proposed methodology is illustrated; in the Sect. 5, the application and results are discussed. The comparisons and discussion are stated in Sect. 6; and finally, Sect. 7 is devoted to the conclusion and future research.

2 Grey Numbers and Operations

The grey information refers to the partial knowledge and incomplete information in a three-section information box including the complete and known information, the incomplete information and the unknown information, where they are cited as the white, grey, and black information categories, respectively [30]. The grey systems theory presents three categories of uncertainty comprising the white, grey, and black numbers in accordance with the level of information. The meaning of information in the category of grey is given in the following table (Table 1).

Table 1 The information meaning of the grey
Full size table

According to [31], the four possibilities of emergence of grey information is given in the following list:

  1. (1)

    The information about elements is grey;

  2. (2)

    The structural information is grey;

  3. (3)

    The boundary information is grey;

  4. (4)

    The behavior information of motion is grey.

Grey systems theory and its operations are founded on the grey numbers which play a vital role in the application of grey methods [32]. Limited between two lower and upper bounds, the exact value of grey number is unknown, yet, the range where the value is located is known [31]. In fact, grey numbers stand for such numbers that are not crisp values, but some incomplete information [33]. Furthermore, Darvishi et al. [34] defined a grey number as a number with clear upper and lower boundaries, but which has an unclear position within the boundaries. The following equations (Eqs. 1–10) address the grey number operations:

$$If \otimes {G}_{1}=\left[\underline{{G}_{1}}, \overline{{G}_{1}}\right], \otimes {G}_{2}=\left[\underline{{G}_{2}}, \overline{{G}_{2}}\right] \,\,then\,\, \overline{{G}_{1}}>\underline{{G}_{1}}\,\,and \,\,\overline{{G}_{2}}> \underline{{G}_{2}}$$
(1)
$$-\otimes {G}_{1}=\left[\overline{{-G}_{1}}, -\underline{{G}_{1}}\right]$$
(2)
$$\otimes {G}_{1}+\otimes {G}_{2}=\left[\underline{{G}_{1}}+\underline{{G}_{2}}, \overline{{G}_{1}}+\overline{{G}_{2}}\right]$$
(3)
$$\otimes {G}_{1}-\otimes {G}_{2}=\otimes {G}_{1}+\left(-\otimes {G}_{2}\right)=\left[\underline{{G}_{1}}-\overline{{G}_{2}}, \overline{{G}_{1}}-\underline{{G}_{2}}\right]$$
(4)
$$\otimes {G}_{1}\times {\otimes G}_{2}= \left[min\left\{\underline{{G}_{1}} \underline{{G}_{2}} , \underline{{G}_{1}}\overline{{G}_{2}} , \overline{{G}_{1}}\underline{{G}_{2}} , \overline{{G}_{1}} \overline{{G}_{2}}\right\}, \mathrm{max}\left\{\underline{{G}_{1}} \underline{{G}_{2}} , \underline{{G}_{1}}\overline{{G}_{2}} , \overline{{G}_{1}}\underline{{G}_{2}} , \overline{{G}_{1}} \overline{{G}_{2}}\right\} \right]$$
(5)
$$r\times {\otimes G}_{1}= \left[ r\underline{{G}_{1}} , r\overline{{G}_{1}} \right]$$
(6)
$$\begin{array}{ccccc}{\raise0.7ex\hbox{${ \otimes {G_1}}$} \!\mathord{\left/ {\vphantom {{ \otimes {G_1}} { \otimes {G_2}}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${ \otimes {G_2}}$}} = & \left[ {\underline{{{G_1}}},\overline{{{G_1}}}} \right] \times \left[ {\frac{1}{{\underline{{{G_2}}}}},\frac{1}{{\overline{{{G_2}}}}}} \right] = \left[ {\underline{{{G_1}}},\overline{{{G_1}}}} \right] \times \left[ {\underline{{G_2^{ - 1}}},\overline{{G_2^{ - 1}}}} \right]\\ = & \left[ {\min \left\{ {\underline{{{G_1}}}\underline{{G_2^{ - 1}}},\underline{{{G_1}}}\overline{{G_2^{ - 1}}},\overline{{{G_1}}}\overline{{G_{}^{ - 1}}}} \right\},\,\,\max \left\{ {\underline{{{G_1}}}\underline{{G_2^{ - 1}}},\underline{{{G_1}}}\overline{{G_2^{ - 1}}},\overline{{{G_1}}}\overline{{G_{}^{ - 1}}}} \right\}} \right]\end{array}$$
(7)
$$\frac{{\otimes G}_{1}}{a}= \left[\frac{\underline{{G}_{1}}}{a}, \frac{\overline{{G}_{1}}}{a}\right]$$
(8)
$$\frac{a}{\overline{\otimes {G}_{1}}}=\left[\frac{a}{\underline{{G}_{1}}}, \frac{a}{\overline{{G}_{1}}}\right]$$
(9)

The possibility degree of \({\otimes G}_{1}\le {\otimes G}_{2}\):

$$p\left\{{\otimes G}_{1}\le {\otimes G}_{2}\right\}= \frac{\mathrm{max}(0, {L}^{*}-\mathrm{max}(0, \underline{{G}_{1}}-\overline{{G}_{2}}))}{{L}^{*}}$$
(10)

where \({L}^{*}=L\left({\otimes G}_{1}\right)+L\left( {\otimes G}_{2}\right)\).

3 Methods and Tools

The proposed approach has been applied on a strategic supplier selection problem where the suppliers are selected in accordance with the firm’s strategies. To run the approach, the grey Shannon’s Entropy and grey TOPSIS are employed. In this section, these two methods of algorithms are discussed.

3.1 Strategies Interaction Model (SIM)

Strengths, weaknesses, opportunities, and threats (SWOT) analysis is a management tool to formulate strategic action plans [35]. As a strategic management tool, SWOT analysis has been extensively utilized for the decision-making process [36]. According to Gao and Peng [37], SWOT analysis is an important decision-making support tool, and is commonly used to systematically analyze the strategic situations and identify the level of organizations from their internal and external environments. SWOT matrix analyzes the internal strengths and weaknesses as well as external opportunities and threats to derive promising future strategies [38]. It also prioritizes the strategies by the Quantitative Strategic Planning Matrix (QSPM) in the classic form. However, due to the flexible structure of its approach and the fact that SWOT provides only a qualitative analysis that merely prioritizes the factors’ importance by measuring them quantitatively, thus, fails to address the rank of the strategies, hence, mostly, it integrates other decision-making methods such as MCDM techniques [39]. Application and integration of MCDM methods with SWOT analysis process could be addressed in different studies such as Anser et al. [40, 41]. The strategies derived from SWOT matrix are categorized into four groups of SO strategies where they use strengths to take advantage of opportunities, WO strategies where they overcome weaknesses by taking advantage of opportunities, ST strategies in which they use strengths to avoid threats, and WT strategies which minimize weaknesses to avoid threats [42], likewise, these strategies are addressed as the aggressive strategies, competitive strategies, conservative strategies, and the defensive strategies.

The classic form of SWOT itself and its integration with MCDM methods is suffering from a number of shortages including [43]:

  1. 1.

    Ignoring the strategic position ignorance in MCDM and SWOT integrated methodologies.

  2. 2.

    Lack of an integrated model for the selection of an organization strategies and also alternative strategies in order to the organization strategic position.

  3. 3.

    In spite of the shared resources for the execution of strategies, there is no framework to assess the interaction of strategies due to their budget requirement.

  4. 4.

    Lack of a formulated paradigm to support the assessment of the interaction of the possible unselected strategies on the main selected strategies ranking.

To cover the aforementioned lacks through the classic SWOT analysis process, Zakeri et al. [43] proposed an approach to analyze SWOT, called strategies interaction model which is divided into two main areas: the evaluations area where the evaluation and all computation activities are executed, and the selection area in which the results are processed (see Fig. 1).

Fig. 1
figure 1

The proposed methodology procedure of SIM

Full size image

SIM are designed in the grey environment. According to [43], the SIM phases are as follows:

  • Phase I. Analysis of internal and external factors.

  • Phase II. Construction of SWOT matrix.

    • Phase II.I. Selection of the strategies (All strategic positions).

    • Phase II.II. Determination of strategic position and selection of the strategies in accordance with the strategic position.

  • Phase III. Computation of the value of interaction.

  • Phase IV. Ranking of the selected strategies.

  • Phase V. Evaluation and selection of the alternative strategies.

3.2 Shannon’s Entropy

One of the major results of information theory is the Shannon entropy [28], Shannon [44]. This method has been utilized to compute the weights of the criteria in a decision-making problem. With respect to [45], the grey entropy is in accordance with (Eqs. 11 and 12).

$${e}_{{\underline{G}}_{j}}=-\frac{1}{\mathrm{ln}m} \sum_{i=1}^{m}{\underline{G}}_{ij}\mathrm{ln}{\underline{G}}_{ij}$$
(11)
$${e}_{{\overline{G}}_{j}}=-\frac{1}{\mathrm{ln}m} \sum_{i=1}^{m}{\overline{G}}_{ij}\mathrm{ln}{\overline{G}}_{ij}$$
(12)

The weight of Jth criterion is computed by following Eqs. (13 and 14):

$${w}_{{\underline{G}}_{j}}= \left( 1-{e}_{{\underline{G}}_{j}} \right). {\left( \sum_{j=1}^{n}(1-{e}_{{\underline{G}}_{j}}) \right)}^{-1}$$
(13)
$${w}_{{\overline{G}}_{j}}=(1-{e}_{{\overline{G}}_{j}}).{\left( \sum_{j=1}^{n}(1-{e}_{{\overline{G}}_{j}}) \right)}^{-1}$$
(14)

3.3 Grey TOPSIS

One of the most popular MCDM technique which is widely applied to solve MCDM problems is TOPSIS. Hwang and Yoon [46] first proposed a technique for establishing order performance by referencing its similarity to the ideal solution (TOPSIS). The TOPSIS philosophy is that the selected alternative’s value should have the shortest distance from the ideal solution and the farthest distance from the negative ideal solution [47]. The grey TOPSIS has the following steps [22, 48]:

Step.3.2.1. Constructing the decision matrix.

Step.3.2.2. Establishing the normalized decision matrices with respect to the cost or benefit (Eqs. 15 and 16).

For benefit attribute of \(\otimes {G}_{ij}^{*}\), the normalization is defined as in the following equation:

$$\otimes {G}_{ij}^{+}=\left[\frac{\underline{{G}_{ij}}}{{G}_{j}^{max}}, \frac{\overline{{G}_{ij}}}{{G}_{j}^{max}}\right]$$
(15)

where \(\otimes {G}_{ij}=\left[\underline{{G}_{ij}}, \overline{{G}_{ij}}\right]\) and \(\otimes {G}_{j}^{max}=\underset{1\le i\le m}{\mathrm{max}}\left\{\overline{{G }_{ij}}\right\}\).

And for a cost attribute of \(\otimes {G}_{ij}^{*}\), there is the following equation:

$$\otimes {G}_{ij}^{-}=\left[\frac{{G}_{j}^{min}}{\overline{{G}_{ij}}}, \frac{{G}_{j}^{min}}{\underline{{G}_{ij}}}\right]$$
(16)

where \(\otimes {G}_{j}^{max}=\underset{1\le i\le m}{\mathrm{min}}\left\{\overline{{G }_{ij}}\right\}\).

Step 3.2.3. Construction of the weighted normalized matrix.

Step 3.2.4. Calculation of ( \({S}^{max}\)) as the ideal alternative where (\({S}^{max}\)) is a referential alternative (Eq. 17).

$$\left\{\begin{array}{c}{S}^{max}=\left\{{G}_{1}^{max}, {G}_{2}^{max}, {G}_{3}^{max}, \dots , {G}_{n}^{max}\right\}; \\ { S}^{max}=\left\{\left[\underset{1\le i\le m}{\mathrm{max}}\underline{{V}_{i1}}, \underset{1\le i\le m}{\mathrm{max}}\overline{{V}_{i1}}\right], \dots , \left[\underset{1\le i\le m}{\mathrm{max}}\underline{{V}_{in}}, \underset{1\le i\le m}{\mathrm{max}}\overline{{V}_{in}}\right]\right\};\end{array}\right.$$
(17)

Step 3.2.5. Computation of the distance between each of the alternatives’ sequences (Eq. 18).

$$d={\Delta}_{\otimes {G}_{1}-\otimes {G}_{2}}=\left(\underline{{G}_{1}}-\underline{{G}_{2}}\right)+\left(\overline{{G}_{1}}-\overline{{G}_{2}}\right)$$
(18)

where \(\Delta\) is the distance \(d\) between two grey numbers of \(\otimes {G}_{1}\) and \(\otimes {G}_{2}\).

Step 3.2.6. Determination of the grey relation coefficient between each of the alternatives (Eq. 19)

$${\gamma }_{oi}=\gamma \left({x}_{o}\left(j\right), {x}_{i}\left(j\right)\right)=\frac{\underset{i}{\mathrm{min}}\underset{j}{\mathrm{min}}{d}_{ij}+\xi \underset{i}{\mathrm{max}}\underset{j}{\mathrm{max}}{d}_{ij}}{{d}_{ij}+\xi \underset{i}{\mathrm{max}}\underset{j}{\mathrm{max}}{d}_{ij}}$$
(19)

Step 3.2.7. Computing the grade of grey relation of each alternative to the ideal solution in accordance with the following equation (Eq. 20):

$${C}_{i}=\left(1-\frac{1}{n}\cdot sum_{j=1}^{n}{\gamma }_{ij}\right) i=0, 1, \dots , m$$
(20)

Step 3.2.8. The final step is the prioritization of the alternatives according to the higher score of \({C}_{i}\).

4 Proposed Methodology

In this chapter, to address the proposed approach, a computation of interaction between a firm’s strategies and its supplier selection problem is presented in order to have a supplier selection in line with the firm’s strategies. Various studies have employed SWOT analysis for the supplier selection [5, 49], while none of them did not exercise SWOT analysis for the specific reason of alignment of the supplier selection with the firm’s strategies. The implementation of the proposed approach is designed in four steps including:

Step 1. Selecting the firm’s strategies through the grey strategies’ interaction model (G-SIM).

Step 2. Evaluation of the criteria. The main purpose of this section is calculating of \((\lambda )\). Indeed, \((\lambda )\) is the proposed method’s key element. In this step, the strategies derived from the first section are playing the role of the criteria and the main criteria of supplier selection are the alternatives in a decision matrix.

Step 3. Prioritization of criteria is based on relation matrix. In this step, the \((\lambda )\) is determined by the normalized performance of each criteria ranking. The strategies directly impact on supplier selection by \((\lambda )\).

Step 4. The final section is selection of the best supplier.

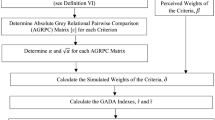
The proposed method’s steps are illustrated in (Fig. 2).

Fig. 2
figure 2

The proposed method’s chart

Full size image

5 Method Application and Results

In this section, the proposed model is represented as a numerical example. This section is separated into three main parts including: 1. Selection of the strategies; 2. Evaluation of Criteria: Prioritization of Criteria based on the Selected Strategies; 3. Supplier selection.

5.1 Selection of Strategies SIM

SWOT analysis of a firm is illustrated (Fig. 3). Selected strategies have been carried out by implementation of SIM. In the following figure, SO, ST, WO, WT stand for the aggressive, competitive, conservative, and defensive strategies.

Fig. 3
figure 3

SIM structure of SWOT analysis for ranking and selection of the strategies

Full size image

According to the scores, S1O1, S2O1, S1T1, 2, W1O2, W2T3 are selected as the best strategies. These strategies are shown as the ST1, ST2, ST3, ST4, and ST5 in next steps of the proposed method application.

5.2 Evaluation of Criteria: Prioritization of Criteria Due to the Selected Strategies

In this section, the criteria for the supplier selection are prioritized in accordance with the selected strategies derived from the previous section. To rank the criteria, the relation matrix has been utilized. In the relation matrix, the interaction of the variables is investigated through computation of their relationship. With respect to the relation matrix, the degree of the relationship between alternatives and criteria are evaluated by the linguistic variables. In this step, the prioritization process is performed by the G-TOPSIS algorithm. The grey linguistic variables are presented in Table 2.

Table 2 The grey attributes scale of rating of \(\otimes G\)
Full size table

The following tables (Tables 3 and 4) demonstrate the relation matrix, where the supplier evaluation criteria are the alternatives, and the selected strategies are the criteria.

Table 3 The relation matrix between selected strategies and supplier selection criteria with linguistic variables
Full size table
Table 4 The relation matrix between selected strategies and supplier selection criteria
Full size table

With respect to the Eqs. (11–13), in most grey-based MCDM problems, for objective calculation of the weights of criteria, the grey entropy is employed. In this chapter, a novel form of grey entropy algorithm is designed to transform the grey numbers to white numbers (Eqs. 30–33); indeed, the new algorithm is in line with the grey entropy which is proposed by [45] with respect to the Eqs. (11–13).

If

$$\Gamma \ge \left({\underline{G}}_{ij}+{\overline{G}}_{ij}\right)$$
(21)

And

$$\Phi \ge \left({\underline{G}}_{ij}-{\overline{G}}_{ij}\right)$$
(22)

Then:

$${e}_{{\otimes G}_{j}}\ge \left[\sum_{i=1}^{m}\left({\left(\sum_{i=1}^{m}{(\left({\Phi }^{2}\right)\mathrm{ln}\left({\Phi }^{2}\right))}^{2}\right)}^\frac{1}{4}. {\left({\left(\sum_{i=1}^{m}{(\left({\Gamma }^{2}\right)\mathrm{ln}\left({\Gamma }^{2}\right))}^{2}\right)}^\frac{1}{4}\right)}^{-1}\right)\right]{\left(\mathrm{ln}m\right)}^{-1}$$
(23)
$${w}_{{\otimes G}_{j}}\ge {\left(\sum_{j=1}^{n}\left(1-{e}_{{\otimes G}_{j}}\right)\right)}^{-1}.\left(1-{e}_{{\otimes G}_{j}}\right)$$
(24)

The first step of Entropy is the normalization of the decision matrix. The normalization process is as given in (Eqs. 25 and 26):

If \(\otimes P=\left[\underline{{P}_{ij}}, \overline{{P}_{ij}}\right]\) stands for a normalized grey number of \(\otimes G=\left[\underline{{G}_{ij}}{, \overline{G}}_{ij}\right]\) in a decision matrix, therefore

$$\underline{{P}_{ij}}={\left({(\sum_{i=1}^{m}{({\underline{G}}_{ij})}^{2})}^\frac{1}{2}\right)}^{-1}.{\underline{G}}_{ij}$$
(25)
$$\overline{{P}_{ij}}={\left({(\sum_{i=1}^{m}{({\overline{G}}_{ij})}^{2})}^\frac{1}{2}\right)}^{-1}.{\overline{G}}_{ij}$$
(26)

With the following transportation of grey numbers to white numbers, introduced in (Eqs. 21 and 22), another transportation of the normalization process is proposed in this chapter which can be found in (Eq. 27), where \((P)\) is a crisp number and white number of \(\otimes G=\left[\underline{{G}_{ij}}{, \overline{G}}_{ij}\right]\). Yet, the proposed framework of this chapter deals with the original normalization processes in accordance with Eqs. (25 and 26).

$$P\ge {\left(\prod_{i=1}^{m}(\sum_{i=1}^{m}\underline{{G}_{ij}}+{\overline{G}}_{ij})\right)}^{-1}.\left(\underline{{G}_{ij}}+\underline{{G}_{ij}}\right)$$
(27)

ccording to Eqs. (25 and 26), the normalized decision matrix is displayed in Table 5.

Table 5 The normalized relation matrix
Full size table

Weights of each selected strategies in the relation matrix can be found in Table 6.

Table 6 Entropy and weight of each strategies
Full size table

For calculation of the (\({e}_{j}^{^{\prime}}\)), the process followed is given in Eq. (28). As pictured in Table 6, there are some anomalies for the normalized interval of each strategies; in other words, in some intervals, lower bound is larger than upper bound. To overcome this problem, for the calculation of the weight of each strategy, we have proposed the following equation (Eq. 28).

If \({e}_{j}=\left[\underline{G}, \overline{G}\right],\)then:

$${e}_{j}^{^{\prime}}={\left({(\underline{G}+\overline{G})}^{2}\right)}^{-1}.\left({\underline{G}}^{2}+{\overline{G}}^{2}\right)$$
(28)

In this chapter, to rank the criteria of supplier selection, we have used the transformation methodology proposed by [43]. The method is developed from the weighted product model (WPM)’s procedure. The proposed methodology could be found in Eqs. (29–31), where \(\otimes G=\left[{\underline{G}}_{ij}, {\overline{G}}_{ij}\right]\) and \(\otimes {G}^{^{\prime}}=\left[{\underline{G}}_{ij}^{^{\prime}}, {\overline{G}}_{ij}^{^{\prime}}\right]\):

$${\underline{G}}_{ij}^{^{\prime}}={\left(\sum_{i=1}^{m}{\underline{G}}_{ij}\right)}^{-1}.{\underline{G}}_{ij}$$
(29)
$${\overline{G}}_{ij}^{^{\prime}}={\left(\sum_{i=1}^{m}{\overline{G}}_{ij}\right)}^{-1}.{\overline{G}}_{ij}$$
(30)
$$P\left({{G}^{^{\prime}}}_{m}\right)=\prod_{j=1}^{n}{\left({\underline{G}}_{ij}+{\overline{G}}_{ij}\right)}^{{w}_{j}}$$
(31)

The prioritization is based on the larger value of \(P\left({{G}^{^{\prime}}}_{m}\right)\), thus, with respect to the Eqs. (29–31), the normalized relation matrix is shown in Table 7, and (λ) values are displayed in Table 8.

Table 7 The normalized relation matrix
Full size table
Table 8 Value of \((\lambda )\) for each criteria
Full size table

Therefore, according to Eq. (31), the larger value of \(P\left({{G}^{^{\prime}}}_{m}\right)\) possesses the best rank:

$$P\left({{G}^{^{\prime}}}_{1}\right)=4.0304803878022140410191260588243$$
$$P\left({{G}^{^{\prime}}}_{2}\right)=4.2006219001599303350681892865139$$
$$P\left({{G}^{^{\prime}}}_{3}\right)=4.1836985480191150780837110210309$$
$$P\left({{G}^{^{\prime}}}_{4}\right)=4.2833361779410137110629886275380$$
$$P\left({{G}^{^{\prime}}}_{5}\right)=4.1665975424376581947939114823975$$

Hence, the ranking is as follows:

$${C}_{4}>{C}_{2}>{C}_{3}>{C}_{5}>{C}_{1}$$

As mentioned heretofore, the next step of the proposed methodology is calculation of \((\lambda )\). To calculate \((\lambda )\), the number of each criteria ranking will be normalized by the normalized performance method. In this chapter, Eqs. (31 and 32) are employed to compute \((\lambda )\).

$${{\lambda }^{^{\prime}}}_{m}=1-\left({R}_{m}.{\left(\sum_{m}^{1}{R}_{m}\right)}^{-1}\right)$$
(32)
$${\lambda }_{m}={{\lambda }^{^{\prime}}}_{m}.{\left(\sum_{m}^{1}{{\lambda }^{^{\prime}}}_{m}\right)}^{-1}$$
(33)

where \({(R}_{m})\) is the ranking of \(mth\) alternative, therefore, \((\lambda )\) of each criteria is.

5.3 Supplier Selection

The final step of the proposed approach is the selection of the best supplier. In this chapter, Grey-TOPSIS is utilized for the supplier selection procedure. The classic Grey-TOPSIS algorithm is as followed in Eqs. (14–20), while in this chapter, we have proposed a novel algorithm for Grey-TOPSIS.

The following steps and equations express the new process of Grey-TOPSIS algorithm.

Step 5.3.1. Construction of Normalized Decision Matrix

$${N}_{D}=\left[{N}_{{\underline{G}}_{ij}}, {N}_{{\overline{G}}_{ij}}\right]$$
(34)
$${N}_{D}=\left\{\begin{array}{c}{N}_{{\underline{G}}_{ij}}={\left(\sum_{i=1}^{m}{\underline{G}}_{ij}\right)}^{-1}.{\underline{G}}_{ij} \\ {N}_{{\overline{G}}_{ij}}={\left(\sum_{i=1}^{m}{\overline{G}}_{ij}\right)}^{-1}.{\overline{G}}_{ij} \end{array}\right.$$
(35)

where \(D\) denotes the decision matrix and \({N}_{D}\) stands for the normalized decision matrix of \(D\).

Step 5.3.2. Establishing Weighted Normalized Decision Matrix

$$V=W\times {N}_{D }$$
(36)

where \(V\) states weighted normalized matrix.

Step 5.3.3. Calculation of Positive and Negative Ideal Solution

$${S}^{max}=\left\{{G}_{1}^{max}, {G}_{2}^{max}, {G}_{3}^{max}, \dots , {G}_{n}^{max}\right\};$$
(37)
$$\begin{array}{c}\\ {S}^{max}=\left\{\left[\underset{1\le i\le m}{\mathrm{max}}\underline{{V}_{i1}}, \underset{1\le i\le m}{\mathrm{max}}\overline{{V}_{i1}}\right], \dots , \left[\underset{1\le i\le m}{\mathrm{max}}\underline{{V}_{in}}, \underset{1\le i\le m}{\mathrm{max}}\overline{{V}_{in}}\right]\right\};\end{array}$$
(38)
$${S}^{min}=\left\{{G}_{1}^{min}, {G}_{2}^{min}, {G}_{3}^{min}, \dots , {G}_{n}^{min}\right\};$$
(39)
$${S}^{min}=\left\{\left[\underset{1\le i\le m}{\mathrm{min}}\underline{{V}_{i1}}, \underset{1\le i\le m}{\mathrm{min}}\overline{{V}_{i1}}\right], \dots , \left[\underset{1\le i\le m}{\mathrm{min}}\underline{{V}_{in}}, \underset{1\le i\le m}{\mathrm{min}}\overline{{V}_{in}}\right]\right\};$$
(40)

To calculate \({S}^{max}\) and \({S}^{min}\), we have proposed the following equation:

$${\omega }_{ij}={\left({\underline{G}}_{ij}+{\overline{G}}_{ij} \right)}^{{W}_{j}}$$
(41)

Larger value of (\({\omega }_{ij}\)) is \({S}^{max}\) and the smaller value is \({S}^{min}\).

Step 5.3.4. Prioritization of Alternatives

$$\begin{array}{ccccc}{\gamma _i} = & \left( {\xi .{{\left( {\mathop \sum \limits_{j = 1}^n {{({V_{ij}} - V_{ij}^ - )}^2}} \right)}^{0.5}}} \right).\left( {\left( {\xi .{{\left( {\mathop \sum \limits_{j = 1}^n {{({V_{ij}} - V_{ij}^ - )}^2}} \right)}^{0.5}}} \right)} \right.\\ & + {\left. {{{\left( {\mathop \sum \limits_{j = 1}^n {{({V_{ij}} - V_{ij}^ - )}^2}} \right)}^{0.5}}} \right)^{ - 1}}\end{array}$$
(42)

where \({\upgamma }_{\mathrm{i}}\) is larger, the ranking order of alternative is better. Otherwise, the ranking order is worse. To implement the proposed developed Grey-TOPSIS algorithm, first, the decision matrix needs to be normalized. The decision matrix has been expressed in Tables 9 and 10 in which \({\mathrm{C}}_{\mathrm{j}}=\left\{{\mathrm{C}}_{1}, ..., {\mathrm{C}}_{5}\right\}\) is the set of criteria.

Table 9 Supplier selection decision-making matrix with the attributes scale of rating
Full size table
Table 10 Supplier selection decision-making matrix
Full size table

Next step is the normalization of the decision matrix with respect to the Eqs. (34 and 35). The normalized decision matrix is demonstrated in Table 11.

Table 11 The normalized supplier selection decision matrix
Full size table

To calculate the weighted normalized decision matrix, weight of each criterion needs to be computed. Indeed, the key of the proposed approach appears in this step. For the computation of the weights of criteria, we utilized Entropy in accordance with Eqs. (11–13), while to calculate the impact of (\(\uplambda\)), the chapter deals with the following equations:

$${w}_{{\underline{G}}_{j}}={\lambda }_{n}\left(1-\left(-\frac{1}{\mathrm{ln}m} \sum_{i=1}^{m}{\underline{G}}_{ij}\mathrm{ln}{\underline{G}}_{ij}\right)\right)\left(\sum_{j=1}^{n}{\lambda }_{n}\left(-\frac{1}{\mathrm{ln}m} \sum_{i=1}^{m}{\underline{G}}_{ij}\mathrm{ln}{\underline{G}}_{ij}\right)\right)$$
(43)
$${w}_{{\overline{G}}_{j}}={\lambda }_{n}\left(1-\left(-\frac{1}{\mathrm{ln}m} \sum_{i=1}^{m}{\overline{G}}_{ij}\mathrm{ln}{\overline{G}}_{ij}\right)\right)\left(\sum_{j=1}^{n}{\lambda }_{n}\left(-\frac{1}{\mathrm{ln}m} \sum_{i=1}^{m}{\overline{G}}_{ij}\mathrm{ln}{\overline{G}}_{ij}\right)\right)$$
(44)

As the interaction between supplier selection criteria and the selected strategies, (\(\lambda\)) impact on the suppliers’ prioritization. In real-world problems, there are other elements which impact on supplier prioritization and increase complexity of selection. In this chapter, we also have added DM’s decision as the weight of criteria other than weights which are derived from Entropy’s equations and (\(\lambda\)). To apply DM’s decision, the chapter deals with other proposed equations as follows:

$${W^{\prime}}_{{{\underline{G}}_j}} = \left( {{w_{{{\underline{G}}_j}}}.{w_{{{\underline{G}}_j}_{DM}}}} \right).{\left( {\mathop \sum \limits_{J = 1}^n {w_{{{\underline{G}}_j}}}.{w_{{{\underline{G}}_j}_{DM}}}} \right)^{ - 1}}$$
(45)
$${{W}^{\prime}}_{{\overline{G}}_{j}}=({w}_{{\overline{G}}_{j}}.{w}_{{{\overline{G}}_{j}}_{DM}}).{\left( \sum_{J=1}^{n}{w}_{{\overline{G}}_{j}}.{w}_{{{\overline{G}}_{j}}_{DM}} \right)}^{-1}$$
(46)

where, as DM’s decision, \({\otimes w}_{{{G}_{j}}_{DM}}=[{w}_{{{\underline{G}}_{j}}_{DM}}, {w}_{{{\overline{G}}_{j}}_{DM}}\)] is a grey numerical interval number. However, if DM's decision is a crisp number, the process needs to follow the application of Eqs. (47 and 48). In this equation, (Eq. 6) procedure is also exercised.

$${{W}^{\prime}}_{{\underline{G}}_{j}}=({w}_{{\underline{G}}_{j}}.{w}_{DM}).{ \left( \sum_{J=1}^{n}{w}_{{\underline{G}}_{j}}.{w}_{DM} \right)}^{-1}$$
(47)
$${{W}^{\prime}}_{{\overline{G}}_{j}}=({w}_{{\overline{G}}_{j}}.{w}_{DM}).{ \left( \sum_{J=1}^{n}{w}_{{\overline{G}}_{j}}.{w}_{DM} \right)}^{-1}$$
(48)

The weights (by DM’s decision), (\(\uplambda\)), derived weights from Entropy algorithm, and the final weights have been exposed in Table 12 where DM’s decisions are in the form of the grey numbers and calculation of \({\mathrm{e}}_{\mathrm{j}}\) is in accordance with Eq. (29).

Table 12 Normalized supplier selection decision matrix and weights of criteria
Full size table

The weighted normalized matrix with respect to Eq. (38) is displayed in Table 13.

Table 13 The weighted normalized matrix
Full size table

In this paper, to find positive and negative ideal solutions (Eqs. 37–41), we proposed a methodology to calculate the (GUV) of each interval where (\(\updelta\)) stands for GUV. The larger value of (\(\updelta\)) in each column of decision matrix is the (\({S}^{max}\)), otherwise it is (\({S}^{min}\)). The following algorithm shows the steps of the computation of (\(\updelta\)).

Step 5.4.1. First step of the algorithm is making a cloud of number for each number in decision matrix. The cloud includes the set of (\({\propto }_{n}\)) where \({\propto }_{n}=\left\{1, 2, ..., 9\right\}\). The elements are the set of numbers which are closest to the zero in the weighted decision matrix.

Step 5.4.2. Making another cloud of another set of (\({\propto }_{n}\)), which includes (\({\propto }_{1}^{\prime}, {\propto }_{2}^{\prime}\), …, \({\propto }_{n}^{\prime}\)). In this proposed methodology, it is assumed that two clouds by default (at least), but, if it is more than two zero in the first numbers, creating the clouds will continue to the first number. For instance, in (0.0027) there are three clouds, while in (0.00027) there are four clouds, yet, for (0.0273) and (0.2734) there are two clouds.

Step 5.4.3. Calculating distance between the elements of each cloud with lower and upper bound with respect to Eqs. (51–52).

$$\underline{\mathcal{l}}={ \left( \sum_{\mathrm{j}=1}^{\mathrm{n}}{\left(\underline{{G}_{ij}}-{\propto }_{n} \right)}^{2} \right)}^{0.5}, n=1, 2, ..., 9;$$
(49)
$$\overline{\mathcal{l}}={ \left( \sum_{\mathrm{j}=1}^{\mathrm{n}}{ \left(\overline{{G}_{ij}}-{\propto }_{n} \right)}^{2} \right)}^{0.5}, n=1, 2, ..., 9;$$
(50)
$$\underline{{\mathcal{l}}^{\prime}}={ \left( \sum_{\mathrm{j}=1}^{\mathrm{n}}{ \left(\underline{{G}_{ij}}-{\propto }_{n}^{\prime} \right)}^{2} \right)}^{0.25}, n=1, 2, ..., 9;$$
(51)
$$\overline{{\mathcal{l}}^{\prime}}={ \left( \sum_{\mathrm{j}=1}^{\mathrm{n}}{\left(\overline{{G}_{ij}}-{\propto }_{n}^{\prime} \right)}^{2} \right)}^{0.25}, n=1, 2, ..., 9;$$
(52)

Distance between cloud’s elements and two bounds of \(\otimes G\) is exhibited in Fig. 4.

Fig. 4
figure 4

The number clouds around the upper and lower bound of \(\otimes G\)

Full size image

Step 5.4.3. The final step is the computation of GUV in accordance with Eq. (53):

$$\begin{array}{cccc} \mathrm{\varrho }= & { \left( \left(\left(\left(\underline{\mathcal{l}}+\overline{\mathcal{l}}\right)+\left(\underline{{\mathcal{l}}^{\prime}}+\overline{{\mathcal{l}}^{\prime}}\right)\right){\left({\left(\otimes \underline{{G}_{ij}}- \otimes \overline{{G}_{ij}}\right)}^{2}\right)}^{0.5}\right).{\left(\otimes \underline{{G}_{ij}}-\otimes \overline{{G}_{ij}} \right)}^{2} \right)}^{-1} \\ & \left({\otimes \underline{{G}_{ij}}}^{2}+{\otimes \overline{{G}_{ij}}}^{2}\right) \end{array}$$
(53)

Hence, the \({S}^{max}\) and \({S}^{min}\) have been defined in Table 14.

Table 14 The positive and negative ideal solutions
Full size table

The final section is to prioritize suppliers by Eq. (51). To compute the (\({V}_{ij}\)), we have proposed in simple equation:

$${\mathrm{V}}_{\mathrm{ij}}=\upxi .(\otimes \underline{{\mathrm{G}}_{\mathrm{ij}}}+\otimes \overline{{\mathrm{G}}_{\mathrm{ij}}})$$
(54)

where (\(\upxi\)) is the coefficient of uncertainty/probability in which in this chapter, (\(\upxi\)=0.05); the results of Eq. (54) is exposed in Table 15.

Table 15 \({V}_{ij}\) in accordance with Eq. (54)
Full size table

With respect to Eq. (42) and Tables 14 and 15, the prioritization is:

$${\gamma }_{i}=\left\{\begin{array}{c}{\gamma }_{1}=0.2078\\ {\gamma }_{2}=0.7785\\ {\gamma }_{3}=0.4135\\ {\gamma }_{4}=0.3642\end{array}\right.$$

then

$${A}_{2}>{A}_{3}>{A}_{4}>{A}_{1}$$

Hence (\({A}_{2}\)) is selected as the best supplier. In the next section of this chapter, the difference between the original G-TOPSIS and the proposed algorithm is investigated. Furthermore, the impact of strategies on the supplier selection is showed.

6 Comparison

In this section, two parts of the paper are investigated. First, we implemented the original G-TOPSIS algorithm on the data and compared it with the proposed novel algorithm. According to the Grey original TOPSIS procedure (Eqs. 14–19), the following tables carry the information of each steps (Tables 16, 17 and 18).

Table 16 Supplier selection decision-making matrix
Full size table
Table 17 The normalized decision-making matrix
Full size table
Table 18 The weighted normalized decision-making matrix
Full size table

Next step is the calculation of (\({S}^{max}\)) as the ideal alternative:

$$\begin{array}{ccccc}{S^{max}} = & \left\{ {\left[ {0.124,{\rm{~}}0.124} \right],\left[ {0.262,{\rm{~}}0.262} \right],} \right.\left[ {0.297,{\rm{~}}0.297} \right],\left[ {0.202,{\rm{~}}0.202} \right]\\ & \left. {\left[ {0.114,{\rm{~}}0.114} \right]} \right\}\end{array}$$

According to Eq. (18), the distance between each alternative sequence needs to be computed (Table 19).

Table 19 The distance between alternative sequences
Full size table

With respect to Eq. (19), if (\(\upxi\)=0.05), then, the grey relation coefficient between each of the alternatives is computed as:

$${\gamma }_{i}=\left\{\begin{array}{c}{\gamma }_{1}=0.02015\\ {\gamma }_{2}=0.0340\\ {\gamma }_{3}=0.04320\\ {\gamma }_{4}=0.02640\end{array}\right.$$

then

$${A}_{3}>{A}_{2}>{A}_{4}>{A}_{1}$$

By comparison of two obtained results, the difference between rank of each alternatives has been illustrated in Fig. 5.

Fig. 5
figure 5

The comparison between rankings of each alternatives from the proposed and original method

Full size image

As it has been illustrated in Fig. 5, the ranks of the supplier number 1 and the supplier number 2 are equal in the two methodologies; however, the supplier number 2 possesses the first ranking in the proposed novel grey-TOPSIS method and stood in the second place in the original methodology of Grey-TOPSIS. There is a same story for supplier number 3; it possesses first rank in the proposed methodology and second place in the original method, while both methodologies take the impact of (\({\lambda }_{j}\)) into account.

The most important part of this section is the comparison between supplier selection with the impact of the selected strategies, which are derived from SWOT matrix by SIM method, and the selection of the alternatives without the impact of the firm’s strategies. As mentioned before, in order to select the best supplier in accordance with the organization’s strategies, first (\({\lambda }_{j}\)) ought to be computed. In this section, we have investigated the difference between selected suppliers with the impact of (\({\lambda }_{j}\)) as the value of interaction which shows the effects of the selected strategies and the evaluation of the suppliers from supplier selection procedure without the impact of the selected strategies. The supplier evaluation/selection process without taking the (\({\lambda }_{j}\)) impact into account through the novel Grey-TOPSIS algorithm is given in the following tables.

With respect to Tables 20, 21, 22 and 23, the normalized decision matrix is demonstrated in Table 20.

Table 20 The normalized supplier selection decision matrix
Full size table
Table 21 The weighted normalized decision matrix
Full size table
Table 22 The positive and negative solutions
Full size table
Table 23 (\({\mathrm{V}}_{\mathrm{ij}}\)) where (\(\upxi =0.05\))
Full size table

Therefore, according to Eq. (43), the prioritization of the suppliers is as follows:

$${\gamma }_{i}=\left\{\begin{array}{c}{\gamma }_{1}=0.3051\\ {\gamma }_{2}=0.0570\\ {\gamma }_{3}=0.6847\\ {\gamma }_{4}=0.4553\end{array}\right.$$

then

$${A}_{3}>{A}_{4}>{A}_{1}>{A}_{2}$$

To investigate the impact of strategies on the supplier selection, the comparative analysis of the suppliers evaluation considering the impact of the selected strategies is illustrated in Fig. 6.

Fig. 6
figure 6

Suppliers evaluation with the impact of the selected strategies (the orange lines) and without their impact (the blue lines)

Full size image

As illustrated in the above, there is a deep difference between rankings due to the impact of the firm’s strategies. According to the results, in the process without the consideration of the strategies, supplier number 3 stood in the first place, while it possessed the second rank in the proposed method. The most alteration happened to the supplier number 2, which possesses first rank in the proposed approach affected by the firm’s strategies, while stood in the last place in the process without taking the firm’s strategies into account. It indicates to what extent the strategies could impact the firm’s internal decisions, in this case, supplier evaluation.

7 Conclusion

In this chapter, a new mathematical approach is proposed to compute the relation and interaction between two groups of irrelevant variables of decision matrices in decision-making problems using MCDM methods. To show the process of the novel approach, it is implemented on an MCDM problem, strategic supplier evaluation problem. In real-world problems, with the emergence of intensive undulations in environmental variables, decision-makers constantly encounter uncertainty. In the approach, we have benefited from the grey systems theory to deal with the uncertainty generated through the decision-making process.

In the paper, to architect the structures of irrelevant variables in decision matrices, the effects of a firm’s strategies have been investigated on the evaluation and selection of the best supplier. The novel approach deals with grey form of TOPSIS and grey Entropy. To convey the effect of strategies on the suppliers evaluation, a relation matrix is used to compose the interaction between firm’s strategies and the suppliers evaluation criteria. The output of the matrix used in the weighting process of those criteria in another MCDM matrix to evaluate the suppliers and select the best one. Indeed, the approach is constituted on a relation matrix between output of one matrix, in our case, the selected strategies through SWOT analysis by SIM, and criteria of another decision-making matrix which is suppliers evaluation in our case. To carry the approach, Shannon’s Entropy played the main role which could potentially change for other problems. Furthermore, in this paper, we have proposed new form of Grey-TOPSIS and some transformation methods for the transforming of the grey numbers to white numbers.

In this chapter, new algorithms have been proposed, therefore, we suggest these topics for further research:

  1. 1.

    Application of the proposed grey entropy for objective weighting in other grey-based MCDM problems.

  2. 2.

    In this paper, we used many new transformation equations in each step of the proposed methodology. Researchers can develop those equations with new ideas.

  3. 3.

    One of the most important concepts that have been proposed in this research is the grey uncertainty value (GUV). It is a numerical platform for the comparison of grey numbers. Another exciting suggestion for future work could be the expansion of the GUV.

  4. 4.

    In this paper, to analyze the SWOT matrix, the grey SIM is utilized in the grey environment. To handle the uncertainty of the SWOT analysis, developing the method in fuzzy form is another interesting suggestion.