Synchronization and Fluctuation of Cardiac Muscle Cells

Abstract

Exploiting the combination of latest microfabrication technologies and measurement technologies, which we call on-chip cellomics technologies, we can select, control, and reconstruct the environment, interaction of single cells, and cell networks from “ algebraic” and “geometric” perspectives. However, to overcome the limitations regarding the quality of single cells and their condition control in experimental constructive single-cell-based cell network studies, mathematical modeling is one of the most powerful complementary approaches. In this chapter, starting from the modeling of the firing of cardiomyocytes as an oscillating stochastic phase model, in which the concepts of refractory period and induced beating are involved, and progressing to spatially arranged cardiomyocyte networks, we explain our experimental results of the “community effect” of beating cardiomyocyte networks as part of a series of cell network-based “algebraic” and “geometric” studies of cellular systems. The mathematical interpretation of this synchronous behavior of cardiomyocyte networks also fitted well with the experimental results after incorporating the fluctuation–dissipation theorem into the oscillating stochastic phase model. We summarize our results of the developed mathematical modeling and constructive experiments to understand the “community effect” of synchronization behavior of beating cardiomyocyte networks. The results suggest that the fluctuation can predict the synchronous behavior of cell networks, and that the synchronization of spontaneous beating of cardiomyocytes is a kind of stability-oriented synchronization phenomenon.

3.1 Introduction

Following on from the dramatic progress in the life sciences in the twentieth century, starting with determination of the way in which genetic information is stored, encoded, and transmitted, another challenge has arisen regarding epigenetic information. Epigenetic information is complementary to genetic information and essential to understand the entire landscape of living systems, such as how living cells can choose, reserve, share, and inherit acquired epigenetic information among neighboring cells and between generations. As we move into the post-genomic/proteomic era, such complementarity to genetic information should become more apparent. The cells in a group are individual entities, and differences arise even among cells with identical genetic information that have developed under the same conditions. These cells respond differently to perturbations [42]. Why and how do these differences arise? How are these differences of individual cells ironed out when they become groups, clusters, or tissues? We call this behavior the “community effect” of cells as induced uniformity. To understand the community effect, we need to understand the potential underlying differences of cells, and why and how their characteristics change when they form networks as epigenetic information.

If we are to obtain a comprehensive understanding of a living system, we need to analyze its epigenetic information, such as adaptation processes and community effect in a group of cells. As cells are minimal units in terms of both genetic and epigenetic information, we must analyze their epigenetic information starting from the twin complementary perspectives of cell regulation being an “algebraic” system (with emphasis on temporal aspects; nongenetic adaptation) and a “geometric” system (with emphasis on spatial aspects; spatial pattern-dependent community effect) using identified single cells and their patterned groups. We thus commenced a series of studies to analyze the epigenetic information of single cells and the spatial structures of cell networks to expand our understanding of how the fates of living systems are determined and how they can be changed.

The importance of understanding epigenetic information is expected to become apparent in cell-based biological and medical fields such as cell-based drug screening and the regeneration of organs from stem cells, fields in which phenomena cannot be interpreted without taking epigenetic factors into account. We thus started a series of studies focusing on developing a system that could be used to evaluate the epigenetic information in cells by continuously observing specific examples of cells and their interactions under fully controlled conditions as a constructive experimental method. However, the issues of limitations regarding the quality of cells and control of their conditions remained. Mathematical modeling is one of the most powerful approaches to overcome these problems.

In this chapter, a mathematical approach for analyzing the synchronization behavior of spontaneously beating cardiomyocytes was examined, starting from modeling of the firing of cardiomyocytes and progressing to spatially arranged cardiomyocyte networks, based on the twin complementary perspectives of cell regulation, namely, as an “algebraic” system (emphasis on temporal aspects) and as a “ geometric” system (emphasis on spatial aspects). Our experimental and mathematical results on the community effect in the synchronization behavior of beating in cardiomyocyte networks are introduced and discussed.

3.2 The Stochastic Phase Models for the Cardiomyocyte Beating

Massive mathematical models have been proposed to investigate the mechanism of cardiomyocyte beating. For example, the work [10] studies an elaborated mathematical model composed of a large number of equations, which looks into the complex electrophysiological processes causing cardiomyocyte synchronization. On the other hand, using just a few ordinary equations, one can reproduce the key phenomenon of the membrane currents and action potentials (see, for example, [22, 37]), such as the famous Hodgkin–Huxley model, the FitzHugh–Nagumo model, and the Van der Pol model. In this section, we focus on investigating the statistical behavior of beating/synchronization period of cardiomyocyte. To explain the essence of synchronization period, we can regard the cardiac muscle cells as oscillators, to which the phase model is well applicable [29, 32, 56]. It is also regarded as the well-known integrate-and-fire model which has been widely used as a spiking neuron model [2, 23, 40]. However, to capture the features of cardiomyocyte beating, we have to incorporate the conventional stochastic phase models with three important conceptions: irreversible at firing, a refractory period after firing, and induced pulsation associated with firing of neighboring cells. In this section, we introduce the stochastic phase models for the beating of the isolated and coupled cardiac muscle cells. The theoretical analysis concerned with the synchronization period is provided, which involves the stochastic equation, the Itô formula, and the calculation of expected value, variance, and coefficient of variance (CV) of the beating/synchronization period.

3.2.1 Some Preliminaries for the Stochastic Phase Model

Before describing the stochastic phase models for the cardiomyocyte beating, we briefly introduce some mathematical preliminaries on the phase model and stochastic differential equation.

3.2.1.1 The Phase Model

We start from a simple phase model. Let ϕ be the phase of an oscillator with intrinsic frequency (or drift) μ > 0 and initial state ϕ(0) = 0. The phase model is given by

$$\displaystyle \begin{aligned} \phi(t) = \mu t. \end{aligned} $$

(3.1)

Assuming that the phase returns to 0 when approaching 2π, we see that $T = \frac {2\pi }{\mu }$ is the period of the oscillator. We can also write (3.1) into an equivalent differential form:

$$\displaystyle \begin{aligned} & d\phi(t) = \mu dt, \end{aligned} $$

(3.2a)

$$\displaystyle \begin{aligned} & \phi(0) = 0. \end{aligned} $$

(3.2b)

Think of the oscillator as a cardiomyocyte, which beats when the phase reaches 2π and then returns to 0 immediately to begin a new beating process (see Fig. 3.1a). The phase equation (3.1) describes the rhythmic beating with period T.

Fig. 3.1

(a) The phase model with constant drift μ = 1, where the beating interval is 2π. (b) The phase model with drift μ = 1 and “white noise” ζ, where the beating interval varies each time

In general, one can consider the phase model with time-dependent and state-dependent drift, that is, μ(t, ϕ(t)) is a function depending on t and ϕ. Then, the phase model with initial value ϕ ₀ becomes

$$\displaystyle \begin{aligned} d\phi = \mu(t,\phi) dt, \quad \phi(0) = \phi_0. \end{aligned}$$

The above equation is equivalent to the following integration form:

$$\displaystyle \begin{aligned} \phi(t) = \int_0^t \mu(s,\phi(s))~ds + \phi_0, \end{aligned} $$

(3.3)

which is also called the “integrate-and-fire” model.

However, for a cardiomyocyte, the beating process is often affected by the internal/external noise. As a result, the beating interval varies each time (see Fig. 3.1b for an example of beating process with noise).

3.2.1.2 The Brownian Motion and White Noise

Incorporating the phase model (3.2) with noise effect, we write the phase model in a formal way:

$$\displaystyle \begin{aligned} & d\phi(t) = \mu dt + \sigma \zeta(t), {} \end{aligned} $$

(3.4a)

$$\displaystyle \begin{aligned} & \phi(0) = 0, {} \end{aligned} $$

(3.4b)

where ζ(t) denotes the “white noise” (which has been widely applied in many mathematical models), and σ is a constant representing the strength of the noise. In general, one can take σ as a function of ϕ, i.e., σ(ϕ). Since the white noise can be regarded as the time derivative of Brownian motion (or called the Winner process) denoted by W(t), (3.4a) becomes

$$\displaystyle \begin{aligned} d\phi(t) = \mu dt + \sigma dW(t), \end{aligned} $$

(3.5)

which is a stochastic differential equation. Figure 3.1b shows a sample path of ϕ with μ = σ = 1.

Before we discuss the stochastic differential equation (3.5), let us explain the conceptions of the Brownian motion and white noise, where we need the Gaussian (or normal) distribution.

For μ ≥ 0 and σ > 0, N(μ, σ ²) represents the Gaussian (or normal) distribution with mean μ and variance σ ². The probability density function of N(μ, σ ²) is given by

$$\displaystyle \begin{aligned} f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{|x-\mu|{}^2}{2\sigma^2}}, \quad -\infty < x < \infty. \end{aligned} $$

(3.6)

For an N(μ, σ ²) random variable X (i.e., X ∼ N(μ, σ ²)), one can compute the probability of the event a < X < b using the density function f:

$$\displaystyle \begin{aligned} P(a < X < b) = \int_a^b f(x)~dx. \end{aligned}$$

The expected value (or mean) of X is calculated as

$$\displaystyle \begin{aligned} \mathbf{E}(X) & = \int_{-\infty}^\infty x dP(X\le x) = \int_{-\infty}^\infty xf(x) dx \\ & = \int_{-\infty}^\infty x \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{|x-\mu|{}^2}{2\sigma^2}} dx = \mu. \end{aligned} $$

(3.7)

And we derive the variance of X:

$$\displaystyle \begin{aligned} \mathbf{Var}(X) & = \mathbf{E}([X - \mathbf{E}(X)]^2) \\ & = \mathbf{E}(X^2) - [\mathbf{E}(X)]^2 \\ & = \int_{-\infty}^\infty x^2 \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{|x-\mu|{}^2}{2\sigma^2}} dx - \mu^2 = \sigma^2. \end{aligned} $$

(3.8)

The two (Gaussian) random variables X ₁ and X ₂ are independent means the probability of the events a ₁ < X ₁ < b ₁ and a ₂ < X ₂ < b ₂ equals the product of P(a ₁ < X ₁ < b ₁) and P(a ₂ < X ₂ < b ₂), i.e.,

$$\displaystyle \begin{aligned} P(a_1<X_1<b_1, \ a_2<X_2<b_2) = P(a_1<X_1<b_1) P(a_2<X_2<b_2), \end{aligned}$$

where $\{a_i\}_{i=1}^2$ and $\{b_i\}_{i=1}^2$ are any real numbers with a _i < b _i.

For two independent random variables X ₁ and X ₂, we have

$$\displaystyle \begin{aligned} \mathbf{E}(X_1 X_2) = \mathbf{E}(X_1) \mathbf{E}(X_2). \end{aligned} $$

(3.9)

With the help of Gaussian random variable, we introduce the one-dimensional Brownian motion.

A collection of random variables {X _t∣t ≥ 0} is called a stochastic process. The Brownian motion {W(t)∣t ≥ 0} is a stochastic process satisfying:

• W(0) = 0.

• For all 0 ≤ s < t, W(t) − W(s) ∼ N(0, t − s).

• For any 0 < t ₁ < t ₂ < ⋯ < t _n, the random variables W(t ₁), W(t ₂) − W(t ₁), ⋯ , W(t _n) − W(t _n−1) are independent.

We plot four sample paths (or trajectories) of Brownian motion W(t) (see Fig. 3.2). Noting that W(t) ∼ N(0, t), we have the mean and variance of W(t):

$$\displaystyle \begin{aligned} \mathbf{E}[W(t)] = 0, \quad \mathbf{Var}[W(t)] = \mathbf{E}[W^2(t)] - 0^2 = t. \end{aligned} $$

(3.10)

Moreover, for t > s ≥ 0,

$$\displaystyle \begin{aligned} \mathbf{E} [W(t) W(s)] & = \mathbf{E} [(W(t) - W(s) + W(s)) W(s)] \\ & = \mathbf{E} [(W(t) - W(s))W(s)] + \mathbf{E} [W^2(s)] \\ & = \mathbf{E} [W(t) - W(s)] \mathbf{E} [W(s)] + s \quad \quad (\text{by (3.9)}) \\ & = 0 + s, \end{aligned} $$

(3.11)

where we have used the fact that W(t) − W(s) ∼ N(0, t − s), W(s) ∼ N(0, s), and the random variables W(t) − W(s) and W(s) are independent.

Fig. 3.2

Four sample paths of Brownian motion W(t)

We have described Brownian motion. As mentioned above, the “white noise” ζ(t) is the formal time derivative of W(t), i.e., $\zeta (t) = \frac {dW(t)}{dt}$. However, in fact, the sample path of W(t) is not differentiable for t ≥ 0; that is, $\frac {dW(t)}{dt}$ does not really exist (in the classical sense).

To get a better understanding of the “white noise” (or dW(t)), we introduce Itô’s integral to interpret dW(t) in the integral form.

3.2.1.3 Itô’s Integral

Analogously to the integral form (3.3) of the phase model, we write the model (3.5) into the integral equation

$$\displaystyle \begin{aligned} \phi(t) = \int_0^t \mu dt + \int_0^t \sigma dW(s) + \phi_0. \end{aligned} $$

(3.12)

The task is to provide a proper definition of the integral that involves dW(s), i.e., $\int _0^t \sigma ~dW(s)$, such that (3.12) makes sense. For the simple case that μ and σ are constants, we immediately have (by $\int _0^t dW(s) = W(t)$)

$$\displaystyle \begin{aligned} \phi(t) = \mu t + \sigma W(t) + \phi_0. \end{aligned}$$

See Fig. 3.1b for a sample path of ϕ(t) with μ = σ = 1 and ϕ ₀ = 0 and under the setting that ϕ jumps to 0 when ϕ(t) reaching 2π. However, for a stochastic process X(t), the definition of $\int _0^T X(t)~dW(t)$ is not straightforward. The famous Itô’s integral addresses this issue.

The rigorous mathematical definition of Itô’s integral involves the filtration and measurability theories of stochastic process, which is omitted in the following argument and replaced by some intuitive description. One can refer to [6, 35] for a detailed mathematical definition.

First, we consider a simple case that X(t) is a step process: for 0 = t ₀ < t ₁ < ⋯ < t _n = T,

$$\displaystyle \begin{aligned} X(t) = X_k \quad \text{ for } t_k \le t < t_{k+1}, \quad k = 0, 1, \ldots, n-1, \end{aligned}$$

where $\{X_k\}_{k=0}^n$ are the random variables independent of t, satisfying:

(c1):

X _k is independent of the information of W(t) for all t ≥ t _k.

(c2):

$\mathbf {E}(\int _0^T |X(t)|{ }^2~dt)<\infty$.

Then, the Itô stochastic integral of X(t) on (0, T) is defined by

$$\displaystyle \begin{aligned} \int_0^T X(t)~dW(t) = \sum_{k=0}^{n-1} X_k (W(t_{k+1}) - W(t_k)). \end{aligned} $$

(3.13)

It is apparent that, for any constants a and b and the step processes X ₁ and X ₂ satisfying (c1) and (c2), the following equality holds:

$$\displaystyle \begin{aligned} \int_0^T a X_1(t) + b X_2(t)~dW(t) = a \int_0^T X_1~dW(t) + b \int_0^T X_2~dW(t). \end{aligned} $$

(3.14)

In statistical analysis, the expected value (mean) and variance (fluctuation) are important features of a random variable. Let us investigate the expected value involving Itô’s integral.

The assumption that X(t) only depends on the past history of the Brownian motion {W(s)∣s < t} but is independent of the future behavior {W(s)∣s ≥ t} plays crucial role in the obtention of the following properties of Itô’s integral.

According to the definition (3.13),

$$\displaystyle \begin{aligned} \mathbf{E}\left( \int_0^T X(t)~dW(t) \right) = \sum_{k=0}^{n-1} \mathbf{E}\left[ X_k (W(t_{k+1}) - W(t_k))\right]. \end{aligned}$$

The assumption (c1) implies that X _k is independent of W(t _k+1) and W(t _k)). As a result,

$$\displaystyle \begin{aligned} \mathbf{E}\left[ X_k (W(t_{k+1}) - W(t_k))\right] & = \mathbf{E} (X_k) \mathbf{E} (W(t_{k+1}) - W(t_k)) \\ & = 0 \quad (\text{by } W(t_{k+1}) - W(t_k) \sim N(0,t_{k+1}-t_k)). \end{aligned}$$

Hence, we conclude

$$\displaystyle \begin{aligned} \mathbf{E}\left( \int_0^T X(t)~dW(t) \right) = 0. \end{aligned} $$

(3.15)

Next, we consider the expected value of $\left ( \int _0^T X(t)~dW(t) \right )^2$. By the definition (3.13),

$$\displaystyle \begin{aligned} \mathbf{E}\left[ \left( \int_0^T X(t)~dW(t) \right)^2 \right] &= \sum_{k=0}^{n-1} \sum_{j=0}^{n-1} \mathbf{E} \big[ X_k (W(t_{k+1}) \\&\quad - W(t_k)) X_j (W(t_{j+1}) - W(t_j)) \big]. \end{aligned} $$

For k ≠ j, without loss of generality, we assume k > j. Since (W(t _k+1) − W(t _k)) and (W(t _j+1) − W(t _j)) are independent, and X _j is only dependent upon the past information {W(t)∣t < t _j} and independent of the future behavior {W(t)∣t ≥ t _j}, we find that (W(t _k+1) − W(t _k)) is independent of X _k X _j(W(t _j+1) − W(t _j)), which implies

$$\displaystyle \begin{aligned} & \mathbf{E} \left[ X_k (W(t_{k+1}) - W(t_k)) X_j (W(t_{j+1}) - W(t_j)) \right] \\ &\quad = \mathbf{E}(W(t_{k+1}) - W(t_k)) \mathbf{E}[X_j X_k (W(t_{j+1}) - W(t_j))] \\ &\quad = 0 \quad (\text{because } W(t_{k+1}) - W(t_k) \sim N(0, t_{k+1}-t_k)). \end{aligned}$$

Therefore,

$$\displaystyle \begin{aligned} \mathbf{E}\left[ \left( \int_0^T X(t)~dW(t) \right)^2 \right] = \sum_{k=0}^{n-1} \mathbf{E} \left[ X_k^2 (W(t_{k+1}) - W(t_k))^2 \right]. \end{aligned}$$

Again, the assumption (c1) yields the independence between $X_k^2$ and (W(t _k+1) − W(t _k))², which gives

$$\displaystyle \begin{aligned} & \mathbf{E} \left[ X_k^2 (W(t_{k+1}) - W(t_k))^2 \right] = \mathbf{E} (X_k^2) \mathbf{E} \left[(W(t_{k+1}) - W(t_k))^2 \right] \\ &\quad = \mathbf{E} (X_k^2) \mathbf{E} \left[ W^2(t_{k+1}) - 2W(t_{k+1})W(t_k) + W^2(t_k) \right] \\ &\quad = \mathbf{E} (X_k^2) (t_{k+1} - 2t_k + t_k) \quad (\text{by (3.10) and (3.11)}) \\ &\quad = \mathbf{E} (X_k^2) (t_{k+1} - t_k ) = \mathbf{E} \left[ \int_{t_k}^{t_{k+1}} X^2(t)~dt \right], \end{aligned} $$

where we have used the fact that X(t) = X _k for $t_k \le t < t_{t_{k+1}}$. Summing up the above equation from k = 0 to k = n − 1 yields

$$\displaystyle \begin{aligned} \mathbf{E}\left[ \left( \int_0^T X(t)~dW(t) \right)^2 \right] = \mathbf{E} \left( \int_0^T X^2(t)~dt \right). \end{aligned} $$

(3.16)

We have introduced Itô’s integral for the step process X(t) and derived the properties (3.14), (3.15), and (3.16). For arbitrary progressive measurable process X(t) (generally speaking, X is a progressive measurable process means that X(t) is independent of the future behavior of the Brownian motion {W(s)∣s ≥ t} and is well defined and measurable providing the past information of the Brownian motion {W(s)∣s < t}) satisfying the boundedness $\int _0^T |X(t)|{ }^2~dt < \infty$, we can approximate X(t) by a sequence of step processes $\{X^{(m)}(t)\}_{m=1}^\infty$ and define Itô’s integral as the limitation of $\int _0^T X^{(m)}(t)~dW(t)$, i.e.,

$$\displaystyle \begin{aligned} \int_0^T X(t)~dW(t) = \lim_{m\rightarrow \infty}\int_0^T X^{(m)}(t)~dW(t). \end{aligned}$$

The readers can refer to [6, 35] for the detailed approximation technique and convergence analysis. In fact, one can verify that the properties (3.14), (3.15), and (3.16) are also satisfied. Therefore, we have extended Itô’s integral to arbitrary progressive measurable process X(t) with bounded L ²-norm (i.e., $\int _0^T |X(t)|{ }^2~dt <~\infty$).

Itô’s integral ensures the meaning of the integral equation (3.12). Usually, it is more convenient to write (3.12) into the differential form (3.5), where the white noise ζ = dW(t) should be understood in the sense of Itô’s integral.

3.2.1.4 Itô’s Formula

Given a smooth function g(x) and a stochastic process X(t) satisfying the following stochastic differential equation:

$$\displaystyle \begin{aligned} & dX(t) = \mu(X(t)) dt + \sigma(X(t)) dW(t), \end{aligned} $$

(3.17a)

$$\displaystyle \begin{aligned} & X(0) = X_0, \end{aligned} $$

(3.17b)

where μ(X(t)) and σ(X(t)) are two functions depending on X(t), we aim to investigate the random variable g(X(t)).

We give an explicit statement of Itô’s formula. Assume that g(x) is a twice continuously differentiable function and X satisfies (3.17). Then, we have

$$\displaystyle \begin{aligned} g(X(t)) - g(X(0)) = \int_0^t g' \mu + \frac{1}{2} g'' \sigma^2~ds + \int_0^t g' \sigma ~dW(s), \end{aligned} $$

(3.18)

where g′, g″, σ, and μ are all functions of X(s). One can write the above formula in a more compact form:

$$\displaystyle \begin{aligned} dg(X) & = g'(X) dX + \frac{1}{2}g''(X)\sigma^2 dt \\ & = \left( g'(X) \mu + \frac{1}{2}g''(X)\sigma^2 \right) dt + g'(X) \sigma dW. \end{aligned} $$

(3.19)

The readers can refer to [6, 35] for the proof of (3.18).

We introduce another expression of (3.19) by the following expansion of dg(X):

$$\displaystyle \begin{aligned} dg(X) & = g'(X) dX + \frac{1}{2}g''(X) (dX)^2, \end{aligned} $$

(3.20)

where (dX)² is decomposed by

$$\displaystyle \begin{aligned} (dX)^2 = \mu^2 (dt)^2 + \mu \sigma (dt dW + dWdt) + \sigma^2 (dW)^2. \end{aligned}$$

Roughly speaking, we have

$$\displaystyle \begin{aligned} (dW)^2 = dt \quad \big(\text{or equivalently, } dW = (dt)^{\frac{1}{2}}\big), \end{aligned}$$

according to which $dWdt=dtdW=(dt)^{\frac {3}{2}}$. And we omit the terms of (dt)², dWdt, and dtdW since they are of a higher order than dt. Then, the expansion (3.20) reduces to (3.19). But rigorously speaking, dX and dW have no meaning alone.

If we apply the ordinary differential chain rule, then we get

$$\displaystyle \begin{aligned} dg(X) = g'(X) dX = g'(X) \mu dt + g'(X) \sigma dW, \end{aligned}$$

which is not correct.

For g(x, t) with continuous differential $\frac {\partial g}{\partial t}, \frac {\partial g}{\partial x}$, and $\frac {\partial ^2 g}{\partial x^2}$, Itô’s formula becomes

$$\displaystyle \begin{aligned} g(X(t),t) - g(X(0),0) = & \int_0^t \frac{\partial g}{\partial s} + \frac{\partial g}{\partial x} \mu + \frac{1}{2} \frac{\partial^2 g}{\partial x^2} \sigma^2~ds + \int_0^t \frac{\partial g}{\partial x} \sigma ~dW(s), \end{aligned} $$

(3.21)

or equivalently,

$$\displaystyle \begin{aligned} dg(X,t) & = \frac{\partial g}{\partial t} dt + \frac{\partial g}{\partial x}dX + \frac{1}{2}\frac{\partial^2 g}{\partial x^2} \sigma^2 dt \\ & = \left( \frac{\partial g}{\partial t} dt + \frac{\partial g}{\partial x} \mu + \frac{1}{2}\frac{\partial^2 g}{\partial x^2}\sigma^2 \right) dt + \frac{\partial g}{\partial x} \sigma dW. \end{aligned} $$

(3.22)

We end up this section with an application of Itô’s formula. Consider a particle moves with a constant drift μ in one-dimensional space starting from the position x = 0. Moreover, the particle is affected by a white noise with strength σ. There are two barriers at x = ±1, and we assume that the particle is absorbed when touching the barriers. We denote by ϕ(t) the position of the particle at time t. Suppose that the particle touches the barriers at time τ, i.e., ϕ(τ) = ±1. τ is a random variable. What is the expected value (mean) of τ?

To compute the expected value of τ, we first notice that ϕ satisfies the stochastic differential equation

$$\displaystyle \begin{aligned} d\phi(t) = \mu dt + \sigma dW(t), \quad \phi(0) = 0. \end{aligned}$$

See Fig. 3.3 for two examples. Noting that

$$\displaystyle \begin{aligned} \phi(t) = \mu t + \sigma W(t), \end{aligned}$$

Fig. 3.3

(a) A sample path of ϕ(t) with μ = 0 and σ = 1. (b) A sample path of ϕ(t) with μ = 1 and σ = 1. The movement is stopped when reaching the boundary ± 1

ϕ is the stochastic process with mean

$$\displaystyle \begin{aligned} \mathbf{E}(\phi(t)) = \mu t \end{aligned}$$

and variance

$$\displaystyle \begin{aligned} \mathbf{Var}(\phi(t)) = \mathbf{E}(\phi^2(t)) - [\mathbf{E}(\phi(t))]^2 = \sigma^2 t. \end{aligned}$$

In fact, ϕ(t) is called the (μ, σ) Brownian motion, and W(t) is the standard Brownian motion. And we see that ϕ(t) ∼ N(μt, σ ² t) and W(t) ∼ N(0, t).

By Itô’s formula (3.18), for a function g with continuous g′ and g″,

$$\displaystyle \begin{aligned} g(\phi(\tau)) - g(0) = \int_0^\tau g' \mu + \frac{1}{2} g'' \sigma^2~dt + \int_0^\tau g' \sigma ~dW(t). \end{aligned}$$

Since τ is regarded as the first time that the particle reaches x = ±1, we see that g(ϕ(τ)) = g(±1). Assume that g is the solution of the following boundary value problem:

$$\displaystyle \begin{aligned} & g' \mu + \frac{1}{2} g'' \sigma^2 = -1 &\quad \text{ for } -1<x<1, \end{aligned} $$

(3.23a)

$$\displaystyle \begin{aligned} & g(\pm 1) = 0. & \end{aligned} $$

(3.23b)

Then, we find that

$$\displaystyle \begin{aligned} 0 - g(0) = -\int_0^\tau 1~dt + \int_0^\tau g' \sigma ~dW(t) = -\tau + \int_0^\tau g' \sigma ~dW(t). \end{aligned}$$

Applying (3.15),

$$\displaystyle \begin{aligned} 0 - g(0) & = -\mathbf{E}(\tau) + \mathbf{E}\left( \int_0^\tau g' \sigma ~dW(t) \right) \\ & = -\mathbf{E}(\tau) + 0. \end{aligned}$$

Therefore, the expected value of the absorbed time is given by

$$\displaystyle \begin{aligned} \mathbf{E}(\tau) = g(0). \end{aligned}$$

The problem reduces to solving the boundary value problem (3.23). For the case that μ = 0, it is obvious that

$$\displaystyle \begin{aligned} g(x) = \sigma^{-2}(1-x^2), \end{aligned}$$

which yields E(τ) = σ ⁻².

We have introduced some preliminaries of stochastic differential equation. Next, we turn attention to our stochastic phase models for the beating process of cardiomyocyte, where we apply the properties of Itô’s integral and Itô’s formula for analysis.

3.2.2 The Phase Model for an Isolated Cardiomyocyte

The beating process for an isolated cardiomyocyte is regarded as the increase of a stochastic phase function from 0 to 2π, where the phase starts from 0, increases with an intrinsic frequency μ, and is effected by a white noise with strength σ. When the phase approaches 2π, we say the cell beats and the phase then returns to 0. Hence, from 0 to 2π, the cell completes an oscillation cycle (see Fig. 3.4). To incorporate the irreversibility of beating, we impose a reflective boundary at 0 state (see Figs. 3.4b and 3.5a).

Fig. 3.4

(a) The cardiac action potential. (b) The beating process is modeled by the increase of the phase function ϕ(t) from 0 to 2π. The cell beats when the phase ϕ approaches 2π and then returns to 0 to start a new oscillation circle. The reflective boundary is imposed at ϕ(t) = 0, which ensures that ϕ ≥ 0 always holds even when ϕ(t) = 0 and the noise σdW(t) is negative

Fig. 3.5

(a) A trajectory of ϕ(t) with (μ, σ) = (1, 2), 0 ≤ t ≤ 6. When ϕ approaches 2π, it returns to 0 immediately. (b) The CV of beating interval

Let ϕ(t) denote the phase of an isolated cardiomyocyte at time t. The model is stated as follows:

$$\displaystyle \begin{aligned} d\phi(t) = \mu dt + \sigma dW(t) + dL(t), \end{aligned} $$

(3.24)

where μ denotes the intrinsic frequency, σ represents the noise strength, and W(t) stands for the standard Brownian motion. dW(t) is the generalized derivative of W(t), which is known as the Gaussian white noise. We impose the conception of irreversibility after beating. When the cell beats, we have ϕ(t−) = 2π and ϕ(t) = 0. Since the phase is affected by noise σdW, when ϕ(t−) = 0 and σdW(t−) < 0, the phase may become negative, i.e., ϕ(t) goes back to 2π (see Fig. 3.4b). The irreversibility says that when ϕ(t−) = 0, ϕ cannot be driven back to 2π by negative noise. To prevent the reversibility of beating, we add the process L(t) to cancel the negative part of noise such that ϕ(t) ≥ 0 always holds (see Fig. 3.5a). Hence, the reflective boundary is described by L(t), which satisfies [9, 41]:

• 1. L(t) increases only when ϕ(t) = 0 such that ϕ(t) ≥ 0.

• 2. L(t) = 0 when the cell beats.

Every time ϕ approaches 2π, ϕ returns to 0, which means that ϕ is a renewal process. The beating interval T is a random variable owing to the noise dW(t). Next, we investigate the expected value and variance of T, i.e., the mean and fluctuation of beating interval of cardiomyocyte.

For any function g with continuous differential $\frac {d g}{dx}$ and $\frac {d^2 g}{dx^2}$, Itô formula gives

$$\displaystyle \begin{aligned} g(\phi(T)) - g(\phi(0)) = & \int_0^T \left[ \mu \frac{dg}{dx}(\phi(t)) + \frac{\sigma^2}{2} \frac{d^2 g}{d x^2}(\phi(t)) \right]~dt \\ & + \int_0^T \frac{dg}{dx}(\phi(t))[\sigma dW(t) + dL(t)]. \end{aligned} $$

(3.25)

By the properties of Itô’s integral [6, 35], we have, for any G(t) and H(t) satisfying $\int _0^T |G|{ }^2~dt < \infty$ and $\int _0^T |H|{ }^2~dt < \infty$,

$$\displaystyle \begin{aligned} & \mathbf{E}\left(\int_0^T G(t)~dW(t)\right) = 0, {} \end{aligned} $$

(3.26a)

$$\displaystyle \begin{aligned} & \mathbf{E}\left(\int_0^T G(t)~dW(t) \int_0^T H(t)~dW(t)\right) = \mathbf{E}\left(\int_0^T GH~dt \right). {} \end{aligned} $$

(3.26b)

Equation (3.26a) means that the expected value of Itô’s integral with respect to dW equals 0.

Now, in view of ϕ(0) = 0 and ϕ(T) = 2π, if g satisfies

$$\displaystyle \begin{aligned} g(2\pi) = 0, \quad \mu \frac{dg}{dx} + \frac{\sigma^2}{2} \frac{d^2 g}{d x^2} = -1, \end{aligned} $$

(3.27)

then it follows from (3.25) that

$$\displaystyle \begin{aligned} 0-g(0) = -T + \int_0^T \frac{dg}{dx}(\phi(t))\sigma~dW(t) + \int_0^T \frac{dg}{dx}(\phi(t))~dL(t). \end{aligned}$$

Since L(t) is a process that increases only when ϕ(t) = 0, dL(t) is nonzero only when ϕ(t) = 0. Thus, we have

$$\displaystyle \begin{aligned} \int_0^T \frac{dg}{dx}(\phi(t))~dL(t) = \int_{\{t \mid 0<t<T, \ \phi(t)=0\}} \frac{dg}{dx}(0)~dL(t). \end{aligned}$$

Therefore, if g satisfies additionally

$$\displaystyle \begin{aligned} \frac{dg}{dx}(0) = 0, \end{aligned} $$

(3.28)

then we get

$$\displaystyle \begin{aligned} 0-g(0) = -T + \int_0^T \frac{dg}{dx}(\phi(t))\sigma~dW(t) + 0. \end{aligned} $$

(3.29)

Taking the expected value of the above equation and according to (3.26a),

$$\displaystyle \begin{aligned} \mathbf{E}[T] = g(0). \end{aligned}$$

Now, what is left is to find the function g satisfying (3.27) and (3.28). In fact, one can validate that

$$\displaystyle \begin{aligned} g(x) = \left\{ \begin{aligned} & \frac{4\pi^2-x^2}{\sigma^2} & \text{ for } \mu = 0, \\ & \frac{2\pi-x}{\mu} - \frac{\sigma^2\Big(e^{-\frac{2\mu x}{\sigma^2}} - e^{-\frac{4\pi\mu}{\sigma^2}}\Big)}{2\mu^2} & \text{ for } \mu > 0. \end{aligned} \right. \end{aligned}$$

As a result, we obtain the mean value of the beating interval T:

$$\displaystyle \begin{aligned} \mathbf{E}(T) = g(0) = \left\{ \begin{aligned} & \frac{4\pi^2}{\sigma^2} & \text{ for } \mu = 0, \\ & \frac{2\pi}{\mu} - \frac{\sigma^2\Big(1- e^{-4\pi\mu/\sigma^2}\Big)}{2\mu^2} & \text{ for } \mu > 0. \end{aligned} \right. \end{aligned} $$

(3.30)

Next, we consider the fluctuation of beating interval T, i.e., the variance Var(T) = E(T ²) − [E(T)]². By virtue of (3.29),

$$\displaystyle \begin{aligned} T^2 = g^2(0) + 2g(0) \int_0^T \frac{dg}{dx}(\phi(t))~dt + \left[ \int_0^T \frac{dg}{dx}(\phi(t))~dt \right]^2. \end{aligned}$$

Taking the expectation of the above equation and with the help of (3.26), we derive

$$\displaystyle \begin{aligned} \mathbf{E}[T^2] = g^2(0) + \sigma^2 \mathbf{E} \left[ \int_0^{T} \left| \frac{d g}{d x}(\phi(t)) \right|{}^2~dt \right]. \end{aligned}$$

Recalling that g(0) = E(T),

$$\displaystyle \begin{aligned} \mathbf{Var}(T) = & \mathbf{E} \left[ \int_0^{T} \sigma^2 \left| \frac{d g}{dx}(\phi(t)) \right|{}^2~dt \right] = \int_0^{2\pi} \sigma^2 \left| \frac{d g}{d x}(x) \right|{}^2 \mathbf{E} \left[ \int_0^T 1_{dx}(\phi(t))~dt \right] \\ = & \mathbf{E}(T) \int_0^{2\pi} \sigma^2 \left| \frac{d g}{dx}\right|{}^2 p(x)~dx, \end{aligned}$$

where p(x)dx represents that the probability of ϕ(t) exists in [x, x + dx) for t →∞ (see [4, Chapter 9 (1.22) (2.25)]). Via a similar calculation to [9], one can obtain the probability density p:

$$\displaystyle \begin{aligned} p(x) = \left\{ \begin{aligned} & \frac{2\pi-x}{2\pi^2} & \text{ for } \mu = 0, \\ & \frac{\theta(e^{2\pi \theta} - e^{\theta x})}{1+2\pi\theta e^{2\pi \theta} - e^{2\pi \theta}} & \text{ for } \mu > 0, \end{aligned} \right. \end{aligned}$$

where θ = 2μ∕σ ². With the help of g and p, we calculate the variance of beating interval:

$$\displaystyle \begin{aligned} \mathbf{Var}(T) = \left\{ \begin{aligned} & \frac{32 \pi^4}{3 \sigma^4} & \text{ for } \mu =0, \\ & \frac{-5+e^{-4\pi\theta}+4e^{-2\pi\theta}+8\pi\theta e^{-2\pi\theta} + 4\pi\theta }{\mu^2 \theta^2} & \text{ for } \mu >0. \end{aligned} \right. \end{aligned} $$

(3.31)

The coefficient of variance (CV) of beating interval T is given by

$$\displaystyle \begin{aligned} \mathbf{CV}(T) = \frac{\sqrt{\mathbf{Var}(T)}}{\mathbf{E}(T)} = \left\{ \begin{aligned} & \sqrt{2/3} & \text{ for } \mu =0, \\ & K(\theta) & \text{ for } \mu >0, \end{aligned} \right. \end{aligned} $$

(3.32)

where $K(\theta ) = \frac {e^{2\pi \theta }\sqrt {-5+e^{-4\pi \theta }+4e^{-2\pi \theta }+8\pi \theta e^{-2\pi \theta } + 4\pi \theta } }{1+2\pi \theta e^{2\pi \theta }-e^{2\pi \theta }}$. We find that CV only depends on θ = 2μ∕σ ². Moreover, one can validate that the CV decreases as θ increases, and it has an upper bound $\sqrt {2/3} \approx 0.8165$ (see Fig. 3.5b), i.e.,

$$\displaystyle \begin{aligned} \mathbf{CV}(T) \uparrow \sqrt{3/2} \quad \quad \theta \downarrow 0. \end{aligned}$$

Hence, the phase model (3.24) is only suitable for the cardiomyocyte with CV less than $\sqrt {2/3}$.

In experiment, the distribution of the beating interval T of each isolated cardiomyocyte has been recorded [28, Figure 3. a, Table 1 and Table 2]). Using the above formulas (3.30) and (3.32), we can determine the parameters (μ, σ) of the phase model (3.24) for each cardiomyocyte from the mean and CV of beating interval obtained from experiments. To validate the efficiency of our model, we compare the numerical simulation results with the experimental data (see Sect. 3.3).

3.2.3 The Phase Model for Two Coupled Cardiomyocytes

For two coupled cardiomyocytes, denoting by ϕ _i the phase function of cell i (i = 1, 2), we introduce the reaction term A _i,j f(ϕ _j − ϕ _i) between cell i and cell j, where {A _i,j}_i,j are constants and f is a 2π-periodic function with f(x) = −f(−x) (for example, $f(x) = \sin {}(x)$). We denote by (μ _i, σ _i) the intrinsic frequency and noise strength of cell i. Then, (ϕ ₁, ϕ ₂) satisfies, for i, j = 1, 2, i ≠ j,

$$\displaystyle \begin{aligned} & d\phi_i(t) = \mu_i dt + A_{i,j} f (\phi_j-\phi_i) dt+ \sigma_i dW_i(t) + dL_i(t), \end{aligned} $$

(3.33a)

$$\displaystyle \begin{aligned} & \phi_i(0) = 0, \end{aligned} $$

(3.33b)

where dW _i represents the white noise of cell i (W ₁ and W ₂ are independent Brownian motion), and L _i(t) is the process to cancel the negative noise when ϕ _i(t) = 0 such that ϕ _i(t) ≥ 0, which ensures the irreversibility of beating (see (i) and (ii) of Sect. 3.2.2).

For two coupled cardiomyocytes, we also incorporate the conception of induced beating and refractory:

(R1):

When cardiac muscle cell i beats, if cell j is out of refractory, then both the cells beat.

(R2):

When cardiac muscle cell i beats, if cell j is in refractory, then only cell i beats.

In phase model, the beating of cell i is described by the phase ϕ _i approaching 2π. For cell j, we set a refractory threshold 0 ≤ B _j < 2π. Then, the above (R1) and (R2) are equivalent to the following statements:

(R1):

If ϕ _i(t−) = 2π and ϕ _j(t−) > B _j, then both the cells beat and return to 0 phase, that is, ϕ _i(t) = ϕ _j(t) = 0 (see Fig. 3.6a).

Fig. 3.6

(a) (R1) Cell 1 beats and cell 2 is out of refractory, and then cell 2 is induced to beat. ϕ(t−) = 2π and ϕ ₂(t−) > B ₂, then ϕ ₁(t) = ϕ ₂(t) = 0. (b) (R2) Cell 1 beats, but cell 2 is in refractory, and then only cell 1 returns to 0 phase. ϕ(t−) = 2π and ϕ ₂(t−) <= B ₂, then ϕ ₁(t) = 0 and ϕ ₂(t) = ϕ ₂(t−)

(R2):

If ϕ _i(t−) = 2π and ϕ _j(t−) ≤ B _j, then only cell i beats and returns to 0 phase, that is, ϕ _i(t) = 0, ϕ _j(t) = ϕ _j(t−) (see Fig. 3.6b).

In fact, (R1) represents the synchronization of beating, and (R2) is the independent beating of cell i. In Fig. 3.7, we show two examples of (ϕ ₁, ϕ ₂) with different noise strengths.

Fig. 3.7

The trajectories of (ϕ ₁(t), ϕ ₂(t)) with parameters (μ ₁, μ ₂) = (2, 1), A _1,2 = A _2,1 = 2, and B ₁ = B ₂ = 0.6π. (a) The strong noise strength (σ ₁, σ ₂) = (1, 1). (b) The weak noise strength (σ ₁, σ ₂) = (0.3, 0.3)

In the numerical simulation of Sect. 3.3, we also impose a tiny delay τ for the induced beating, which means that the induced beating of cell j happens at time t + τ when its neighborhood cell i beats at time t (i.e., if ϕ _i(t−) = 2π and ϕ _j(t) > B _j, then ϕ(t) = 0 and ϕ _j(t + τ) = 0).

3.2.4 The CV of Synchronization

For sufficiently small noise, we introduce the synchronization phase function $\phi _i^s$ for two coupled cardiomyocytes, i = 1, 2,

$$\displaystyle \begin{aligned} \phi_i^s = \mu^s t + \psi_i^s, \end{aligned} $$

(3.34)

where μ ^s is the synchronization frequency for the two cardiomyocytes, and $\{\psi _i^s\}_{i=1,2}$ are two constants. When the noise strengths {σ _i}_i=1,2 are small, one can take the synchronization phase function $\{\phi _i^s\}_{i=1,2}$ as the linear approximation of the expected value of {ϕ _i}_i=1,2 (see Fig. 3.8).

Fig. 3.8

(a) A trajectory of (ϕ ₁(t), ϕ ₂(t)) with parameters (μ ₁, μ ₂, σ ₁, σ ₂) = (1, 2, 0.3, 0.5), A _1,2 = A _2,1 = 2, and B ₁ = B ₂ = 0.6π. The synchronization solution $(\phi _1^s, \phi _2^s)$ is a linear approximation of (E(ϕ ₁(t)), E(ϕ ₂(t))). (b) (E(ϕ ₁(t)), E(ϕ ₂(t)))

Without loss of generality, we assume $\psi _1^s \ge \psi _2^s$. Then, the expected value of synchronization period is given by $T^s = (2\pi - \psi _1^s)/\mu ^s$.

For simplicity of analysis, the effect of reflective boundary at ϕ _i(t) = 0 is approximated by adding a small positive constant $\psi _i^{\text{app}}$ to the initial state:

$$\displaystyle \begin{aligned} & d \phi_i^{\text{app}} = \big[\mu_i + A_{i,j} f\big(\phi_j^{\text{app}} - \phi_i^{\text{app}}\big)\big] dt + \sigma_i dW_i(t), \end{aligned} $$

(3.35a)

$$\displaystyle \begin{aligned} & \phi_i^{\text{app}}(0) = \psi_i^{\text{app}}. \end{aligned} $$

(3.35b)

The phase function $\phi _i^{\text{app}}$ is regarded as the approximation of ϕ _i.

Instead of considering the CV of the synchronization period, we investigate the variance of the difference between the phase $\phi _i^{\text{app}}(T^s)$ and the synchronization phase $\phi ^s_i(T^s)$ (cf. [29]):

$$\displaystyle \begin{aligned} \mathbf{CV}_i \approx \sqrt{\mathbf{Var}[\phi_i^{\text{app}}(T^s) -\phi^s_i(T^s)]}. \end{aligned}$$

Putting $\xi _i = \phi _i^{\text{app}} - \phi _i^s$,

$$\displaystyle \begin{aligned} & f(\phi_j^{\text{app}} - \phi_i^{\text{app}}) = f(\xi_j - \xi_i + \phi_j^s - \phi_i^s) \\ &\quad = f(\phi_j^s - \phi_i^s) + f'(\phi_j^s - \phi_i^s)(\xi_j - \xi_i ) + O(|\xi_j - \xi_i |{}^2). \end{aligned}$$

Since ξ _i is a small variable when the noise strength is small (see Fig. 3.8a), ignoring the tiny quadratic term O(|ξ _j − ξ _i|²), and noting that $\phi _j^{\text{app}} - \phi _i^{\text{app}} = \psi _j^s - \psi _i^s$, the above equation becomes

$$\displaystyle \begin{aligned} f(\phi_j^{\text{app}} - \phi_i^{\text{app}}) = f(\psi_j^s - \psi_i^s) + f'(\psi_j^s - \psi_i^s)(\xi_j - \xi_i ). \end{aligned}$$

The equations of ξ _i are stated as follows: for 0 < t < T ^s and i, j = 1, 2, i ≠ j,

$$\displaystyle \begin{aligned} & d\xi_i = \nu_i dt + A_{i,j} f'(\psi_j^s - \psi_i^s) (\xi_j - \xi_i)dt + \sigma_i dW_i, \end{aligned} $$

(3.36a)

$$\displaystyle \begin{aligned} & \xi_i(0) = \xi_i^0, \end{aligned} $$

(3.36b)

where $\nu _i = \mu _i - \mu ^s + A_{i,j}f(\psi _j^s - \psi _i^s)$ and $\xi _i^0 = \psi _i^{\text{app}} - \psi _i^s$.

In view of

$$\displaystyle \begin{aligned} \xi_i(T^s) - \xi_i(0) = \phi_i^{\text{app}}(T^s) - \phi_i^{\text{app}}(0) - ( \phi_i^s(T^s) - \phi_i^s(0) ), \end{aligned}$$

$\mathbf {CV}_i \approx \sqrt {\mathbf {Var}[\phi _i^{\text{app}}(T^s) -\phi ^s_i(T^s)]}$ is equivalent to

$$\displaystyle \begin{aligned} \mathbf{CV}_i \approx \sqrt{\mathbf{Var}[\xi_i(T^s) - \xi_i^0]} = \sqrt{\mathbf{Var}[\xi_i(T^s)]}. \end{aligned}$$

Setting the notations

$$\displaystyle \begin{aligned} \boldsymbol{\xi} = \left[ \begin{array}{c} \xi_1 \\ \xi_2 \end{array}\right], \quad \boldsymbol{\nu} = \left[ \begin{array}{c} \nu_1 \\ \nu_2\end{array}\right], \quad \boldsymbol{\xi}^0 = \left[ \begin{array}{c} \xi_1^0 \\ \xi_2^0 \end{array}\right], \quad \boldsymbol{W} = \left[ \begin{array}{c} W_1 \\ W_2 \end{array}\right], \end{aligned}$$

$$\displaystyle \begin{aligned} \boldsymbol{B} = \left[ \begin{array}{cc} b_{12} & -b_{12} \\ -b_{21} & b_{21} \end{array} \right], \quad \boldsymbol{\sigma} = \left[ \begin{array}{cc} \sigma_1 & 0 \\ 0 & \sigma_2 \end{array} \right], \end{aligned}$$

where $b_{ij} = A_{i,j} f'(\psi _j^s - \psi _i^s)$, we rewrite (3.36) into

$$\displaystyle \begin{aligned} d \boldsymbol{\xi} = \boldsymbol{\nu} dt - \boldsymbol{B} \boldsymbol{\xi} dt + \boldsymbol{\sigma} d \boldsymbol{W}(t). \end{aligned}$$

Next, we compute the solution ξ. Multiplying the above equation by e ^−Bt, we get

$$\displaystyle \begin{aligned} d\Big(e^{\boldsymbol{B}t} \boldsymbol{\xi}\Big) = e^{\boldsymbol{B}t} [\boldsymbol{\nu} dt + \boldsymbol{\sigma} d \boldsymbol{W}], \end{aligned}$$

which yields

$$\displaystyle \begin{aligned} \boldsymbol{\xi}(t) = e^{-\boldsymbol{B} t} \boldsymbol{\xi}^0 + \int_0^t e^{-\boldsymbol{B}(t-s)}\boldsymbol{\nu} ~ds + \int_0^t e^{-\boldsymbol{B}(t-s)} \boldsymbol{\sigma}~d\boldsymbol{W}(s). \end{aligned} $$

(3.37)

By Itô’s integral (3.26a), we calculate

$$\displaystyle \begin{aligned} \mathbf{E}(\boldsymbol{\xi}(t)) &= [ \mathbf{E}(\xi_1(t)), \mathbf{E}(\xi_2(t)) ]^\top = e^{-\boldsymbol{B} t} \boldsymbol{\xi}^0 + \int_0^t e^{-\boldsymbol{B}(t-s)}\boldsymbol{\nu} ~ds, \\ \mathbf{E}((\xi_i(t))^2) &= [\mathbf{E}(\xi_i(t))]^2 + \mathbf{E}\left[ \int_0^t \big[e^{-(t-s)\boldsymbol{B}} \boldsymbol{\sigma} d\boldsymbol{W}(s)\big]_i \right]^2, \end{aligned} $$

where [u]_i denotes the ith component of vector u. Together with Var[ξ _i(t)] = E[(ξ _i(t))²] − (E[ξ _i(t)])², we have

$$\displaystyle \begin{aligned} \mathbf{Var}[\xi_i(t)] = \mathbf{E}\left[ \int_0^t \big[e^{-(t-s)\boldsymbol{B}} \boldsymbol{\sigma} d\boldsymbol{W}\big]_i \right]^2. \end{aligned}$$

Noting that B has two eigenvalues

$$\displaystyle \begin{aligned} \lambda_1=0, \quad \lambda_2 = b := b_{12}+b_{21}, \end{aligned}$$

with the corresponding eigenvectors

$$\displaystyle \begin{aligned} \boldsymbol{u}_1=[1,1]^\top, \quad \boldsymbol{u}_2=[b_{12},-b_{21}]^\top, \end{aligned}$$

we introduce the decomposition

$$\displaystyle \begin{aligned} \boldsymbol{\sigma} d \boldsymbol{W} = b^{-1} (b_{21}\sigma_1 dW_1 + b_{12}\sigma_2 dW_2) \boldsymbol{u}_1 + b^{-1} (\sigma_1 dW_1 - \sigma_2 dW_2) \boldsymbol{u}_2. \end{aligned}$$

Putting together with

$$\displaystyle \begin{aligned} e^{-t\boldsymbol{B}}\boldsymbol{u}_1 = e^{-t0}\boldsymbol{u}_1 = \boldsymbol{u}_1, \quad e^{-t\boldsymbol{B}}\boldsymbol{u}_2 = e^{-tb} \boldsymbol{u}_2, \end{aligned}$$

one can compute [e ^−(t−s)B σ d W]_i. Then, applying Itô’s integral (3.26b), it is not difficult to validate that

$$\displaystyle \begin{aligned} \mathbf{CV}_i^2 & \approx \mathbf{Var}[\xi_i(T^s)]\\ & = \frac{1}{b^2}\left[ \big(b_{12}^2\sigma_2^2 + b_{21}^2\sigma_1^2\big)T^s + \frac{1-e^{-2bT^s}}{2b}b_{ij}^2\big(\sigma_1^2 + \sigma_2^2\big) \right. \\ & \quad + \left. \frac{1-e^{-bT^s}}{b}2b_{ij} \big(b_{ji} \sigma_i^2 - b_{ij} \sigma_j^2 \big) \right]. \end{aligned} $$

(3.38)

As stated above (cf. [29]), one can approximate the CV of synchronization period by Var[ξ _i(T ^s)].

To reduce the difference between CV ₁ and CV ₂, we take $b_{21} \sigma _1^2 = b_{12} \sigma _2^2 = D$ such that

$$\displaystyle \begin{aligned} \mathbf{CV}_i^2 \approx & \frac{1}{b^2}\left[ 2DT^s + \frac{1-e^{-2bT^s}}{2b}\frac{D^2}{\sigma_j^4}\big(\sigma_1^2 + \sigma_2^2\big) \right]. \end{aligned}$$

Furthermore, for σ ₁ = σ ₂ = σ and b ₂₁ = b ₁₂ = b∕2, we have

$$\displaystyle \begin{aligned} \mathbf{CV}_1^2 = \mathbf{CV}_2^2 \approx & \frac{\sigma^2}{2}\left[ T^s + \frac{1-e^{-2bT^s}}{2b} \right], \end{aligned}$$

which is regarded as the CV of the synchronization period.

In numerical simulation, we set $f(x) = \sin {}(x)$. Noting that $\psi _i^s \approx 0$ for small noise, we have $f'(\psi ^s_j-\psi ^s_i) \approx \cos {}(0)=1$ such that b _ij ≈−A _i,j. Therefore, choosing $A_{i,j} \sigma _j^2 = A_{j,i}\sigma _i^2$, one can reduce the difference between CV ₁ and CV ₂, which yields a more stable synchronization solution in simulation. This has been applied to our numerical simulation in Sect. 3.3.

3.2.5 The Phase Model for N-cardiomyocytes Network

For N-cardiomyocytes network, we need to consider the neighborhood cells of each cell. For simplicity, we consider the full connected network, where the cells are connected with each other. The equations of $\{\phi _i\}_{i=1}^N$ are stated as follows:

$$\displaystyle \begin{aligned} & d \phi_i(t) = \mu_i dt + \sum_{j=1, \ j \neq i}^N A_{i,j} f(\phi_j - \phi_i) dt + \sigma_i d W_i(t) + dL_i(t), {} \end{aligned} $$

(3.39a)

$$\displaystyle \begin{aligned} & \phi_i(0) = 0. {} \end{aligned} $$

(3.39b)

In (3.39a), the reaction term A _i,j f(ϕ _j − ϕ _i) between cells i and j is imposed for j = 1, 2, …, N, j ≠ i, which corresponds to the full connection of the cell network. The process L _i(t) is added to (3.39a) to guarantee that ϕ _i(t) ≥ 0 always holds even when the noise dW _i is negative and ϕ _i(t) = 0, which represents the irreversibility of beating (see (i) and (ii) of Sect. 3.2.2).

Moreover, we also incorporate the conception of the induced beating and refractory to the mathematical model: for i, j = 1, …, N and i ≠ j,

(R1):

when the cardiac muscle cell i beats (i.e., ϕ _i(t−) = 2π) and the cell j is out of refractory (i.e., ϕ _j(t−) > B _j), then both the cells beat and the phase of cells i and j returns to 0 (i.e., ϕ _i(t) = 0 and ϕ _j(t) = 0).

(R2):

when the cardiac muscle cell i beats (i.e., ϕ _i(t−) = 2π) and the cell j is in refractory (i.e., ϕ _j(t−) ≤ B _j), then only the cell i is beating and the phase of cell i returns to 0 (i.e., ϕ _i(t) = 0 and ϕ _j(t) = ϕ _j(t−)).

In Fig. 3.9, we show two examples of (ϕ ₁, ϕ ₂, ϕ ₃, ϕ ₄) with different noise strengths.

Fig. 3.9

The trajectories of (ϕ ₁(t), ϕ ₂(t), ϕ ₃(t), ϕ ₄(t)) with parameters (μ ₁, μ ₂, μ ₃, μ ₄) = (2, 2, 1, 1) and A _i,j = 2, B _i = 0.6π for i, j = 1, …, 4, i ≠ j. (a) The strong noise strength σ _i = 1. (b) The weak noise strength σ _i = 0.3

As with the case of two coupled cells, we investigate the CV of the synchronization period using the approximated calculation. For sufficiently small noise, let $\phi _i^{\text{app}}$ denote the approximation of the phase function ϕ _i, satisfying: 1 ≤ i ≤ N,

$$\displaystyle \begin{aligned} & d \phi_i^{\text{app}} = \left[ \mu_i + \sum_{j=1, j\neq i}^N A_{i,j} f\big(\phi_j^{\text{app}} - \phi_i^{\text{app}}\big) \right] dt + \sigma_i dW_i(t), \end{aligned} $$

(3.40a)

$$\displaystyle \begin{aligned} & \phi_i^{\text{app}}(0) = \psi_i^{\text{app}}. \end{aligned} $$

(3.40b)

If the noise is sufficiently small, then we can approximate the synchronization by linear equations:

$$\displaystyle \begin{aligned} \phi_i^s = \mu^s t + \psi_i^s, \quad 1 \le i \le N. \end{aligned} $$

(3.41)

Without loss of generality, we assume $\psi _1^s = \max _{1 \le i \le N} \psi _i^s$. Then, the synchronization period is given by $T^s= (2\pi -\psi _1^s)/\mu ^s$. Introducing the difference $\xi _i = \phi _i^{\text{app}} - \phi _i^s$, we introduce the approximated CV of the synchronization (cf. [29]): $\mathbf {CV}_i \approx \sqrt {\mathbf {Var}[\xi _i(T^s) - \xi _i(0)]} = \sqrt {\mathbf {Var}[\xi _i(T^s) ]}$. In the following, we calculate Var[ξ _i(T ^s)].

First, we see that $\{\xi _i\}_{i=1}^N$ satisfy the following equations: i = 1, …, N,

$$\displaystyle \begin{aligned} & d \xi_i= \left[ \nu_i + \sum_{j=1, j \neq i}^N A_{i,j}f'(\psi_j^s - \psi_i^s) (\xi_j - \xi_i) \right]dt + \sigma_i dW_i, \end{aligned} $$

(3.42a)

$$\displaystyle \begin{aligned} & \xi_i(0) = \xi_0 \end{aligned} $$

(3.42b)

where $\nu _i = \mu _i - \mu ^s + \sum _{j=1, j \neq i}^N A_{i,j}f(\psi _j^s - \psi _i^s)$ and $\xi _i^0 = \psi _i^{\text{app}} - \psi _i^s$. Setting the notations

$$\displaystyle \begin{aligned} & \boldsymbol{\xi} = [\xi_1,\ldots,\xi_N]^\top, \quad \boldsymbol{W}=[W_1,\ldots,W_N]^\top, \end{aligned} $$

(3.43a)

$$\displaystyle \begin{aligned} & \boldsymbol{\nu} = [\nu_1,\ldots,\nu_N]^\top, \quad \boldsymbol{\xi}^0 = [\xi_1^0,\ldots,\xi_N^0]^\top, \end{aligned} $$

(3.43b)

$$\displaystyle \begin{aligned} & \boldsymbol{\sigma} = \text{diag}(\sigma_1, \ldots, \sigma_N), \quad \boldsymbol{B} = [b_{ij}]_{1\le i,j \le N}, \end{aligned} $$

(3.43c)

where $b_{ii} = \sum _{j=1, j \neq i}^N A_{i,j} f'(\psi _j^s - \psi _i^s)$ and $b_{ij} = -A_{i,j} f'(\psi _j^s - \psi _i^s)$, we rewrite (3.42) into

$$\displaystyle \begin{aligned} d \boldsymbol{\xi} &= \boldsymbol{\nu}dt - \boldsymbol{B} \boldsymbol{\xi} dt + \boldsymbol{\sigma} d\boldsymbol{W}, \\ \boldsymbol{\xi}(0) &= \boldsymbol{\xi}_0. \end{aligned}$$

The solution ξ is given by

$$\displaystyle \begin{aligned} \boldsymbol{\xi}(t) = e^{-\boldsymbol{B} t} \boldsymbol{\xi}^0 + \int_0^t e^{-\boldsymbol{B}(t-s)}\boldsymbol{\nu} ~ds + \int_0^t e^{-\boldsymbol{B}(t-s)} \boldsymbol{\sigma}~d\boldsymbol{W}(s). \end{aligned}$$

Putting $|\boldsymbol {\xi }|{ }^2 = \sum _{i=1}^N |\xi _i|{ }^2$, we see that

$$\displaystyle \begin{aligned} |\boldsymbol{\xi}(t)|{}^2 & = |\boldsymbol{\xi}^0|{}^2 + 2 \boldsymbol{\xi}^0 \cdot \int_0^t e^{-(t-s)\boldsymbol{B}} \boldsymbol{\sigma} d\boldsymbol{W} + \left| \int_0^t e^{-(t-s)\boldsymbol{B}} \boldsymbol{\sigma} d\boldsymbol{W} \right|{}^2. \end{aligned}$$

To obtain Var(ξ(T ^s)), we introduce the properties of Itô’s formula for the N-dimensional version [6, 35]: for any G = [G _ij]_i,j satisfying $\int _0^t |\boldsymbol {G}|{ }^2~ds < \infty$ ($|\boldsymbol {G}|{ }^2 = \sum _{i,j=1}^N |G_{ij}|{ }^2$ ), the following equalities hold:

$$\displaystyle \begin{aligned} & \mathbf{E}\left(\int_0^t \boldsymbol{G}(s)~d\boldsymbol{W}(s)\right) = 0, {} \end{aligned} $$

(3.44a)

$$\displaystyle \begin{aligned} & \mathbf{E}\left[ \left| \int_0^t \boldsymbol{G}(s)~d\boldsymbol{W}(s)\right|{}^2 \right] = \mathbf{E}\left(\int_0^t |\boldsymbol{G}|{}^2~ds \right). {} \end{aligned} $$

(3.44b)

Applying (3.44),

$$\displaystyle \begin{aligned} & \mathbf{E}[\boldsymbol{\xi}(t)] = e^{-\boldsymbol{B} t} \boldsymbol{\xi}^0 + \int_0^t e^{-\boldsymbol{B}(t-s)}\boldsymbol{\nu} ~ds, {} \end{aligned} $$

(3.45a)

$$\displaystyle \begin{aligned} & \mathbf{E}[|\boldsymbol{\xi}(t)|{}^2] = (\mathbf{E}[\boldsymbol{\xi}(t)])^2 + \mathbf{E} \left[\int_0^t \left| e^{-(t-s)\boldsymbol{B}} \boldsymbol{\sigma} \right|{}^2 ds \right]. {} \end{aligned} $$

(3.45b)

For the case σ _i = σ, A _i,j = A _j,i, and $\psi _i^s = \psi ^s$, we have

$$\displaystyle \begin{aligned} \left| e^{-(t-s)\boldsymbol{B}} \boldsymbol{\sigma} \right|{}^2 &= \sigma^2 \sum_{i,j=1}^N \left| \big(e^{-(t-s)\boldsymbol{B}} \big)_{ij} \right|{}^2 \\ &= \text{tr}\big(\big(e^{-(t-s)\boldsymbol{B}}\big)^\top e^{-(t-s)\boldsymbol{B}}\big) = \text{tr}\big(e^{-2(t-s)\boldsymbol{B}}\big) \quad (\text{by } \boldsymbol{B}^\top = \boldsymbol{B}) \\ &= \sum_{i=1}^N e^{-2(t-s)\lambda_i}, \end{aligned} $$

(3.46)

where tr(B) and $\{ \lambda _i\}_{i=1}^N$ denote the trace and the eigenvalues of B, respectively.

Following from A _i,j = A _j,i and f′(x) = f′(−x) (by f(x) = −f(−x)), the symmetry B ^⊤ = B holds. Without loss of generality, let λ _N ≥ λ _N−1 ≥⋯ ≥ λ ₂ > λ ₁ = 0 (0 is an eigenvalue of B because of $\sum _{j=1}^N b_{ij}=0$). We obtain from (3.45), (3.46), and $\sum _{i=1}^N\mathbf {Var}[\xi _i(t)] = \mathbf {E}[|\boldsymbol {\xi }(t)|{ }^2] - |\mathbf {E}[\boldsymbol {\xi }(t)]|{ }^2$ that

$$\displaystyle \begin{aligned} \sum_{i=1}^N\mathbf{Var} [\xi_i(T^s)] & = \sigma^2 \int_0^{T^s} \sum_{i=1}^N e^{-2(T^s-s)\lambda_i}~ds. \\ & = \sigma^2T^s + \sigma^2 \sum_{i=2}^N \frac{1-e^{-2T^s \lambda_i}}{2\lambda_i}. \end{aligned} $$

(3.47)

For the case of the identical parameter (μ _i, σ _i, A _i,j) = (μ, σ, A), ξ _i has identical distribution for each i, as well as $\sqrt {\mathbf {Var} [\xi _i(T^s)]}$. As a result, we have, for all i = 1, 2, …, N,

$$\displaystyle \begin{aligned} \mathbf{CV}_i \approx \sqrt{\mathbf{Var} [\xi_i(T^s)]} & =\sqrt{ \sum_{i=1}^N\mathbf{Var}[\xi_i(T^s)/N]} \\ & = \frac{\sigma}{\sqrt{N}} \sqrt{ T^s + \sum_{i=2}^N \frac{1-e^{-2 T^s \lambda_i}}{2 \lambda_i}}. \end{aligned}$$

Noting that there exists a constant c _∞ such that

$$\displaystyle \begin{aligned} \frac{1}{N}\sum_{i=2}^N \left( \frac{1-e^{-2 T^s \lambda_i}}{2 \lambda_i} \right) \rightarrow c_\infty \quad \text{ as } N \rightarrow \infty, \end{aligned} $$

(3.48)

we have $\mathbf {CV}_i \rightarrow \sigma c_\infty ^{1/2}$ as N →∞.

In Sect. 3.4, the numerical simulations are carried out for several N-cell models with various network, where we observe that the CV decreases by $O(1/\sqrt {N})$ when N is small and converges to some constant when N →∞. The simulations correspond to the theoretical result (3.48). Moreover, the comparison between the numerical simulation and biological experimental result (cf. [18, Figure 3]) indicates the well consistency between the model and biological experiment.

3.3 Experimental Approach

3.3.1 On-Chip Cellomics Technology: Reconstructive Understanding of the Community Effect in Cardiomyocytes

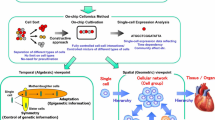
We have developed a constructive experimental approach for understanding epigenetic information. As shown in Fig. 3.10, the strategy behind our on-chip microfabrication methods, which we call “on-chip cellomics technologies” [58], is constructed through three steps. First, we purify target cells from tissue individually in a nondestructive manner using several technologies, such as digestible DNA-aptamer labeling and cell collection, ultrahigh-speed camera-based real-time imaging cell sorting, or noninvasive handling of cells using an acoustic radiation force [1, 12, 57, 59,60,61]. We then cultivate and observe the cells under fully controlled conditions (e.g., cell population, network patterns, or nutrient conditions) using an on-chip single-cell cultivation chip [14, 15, 21, 34, 50,51,52,53,54] or an on-chip agarose microchamber system exploiting photothermal etching technology, which can control the microstructure of microchambers even during cell cultivation [11, 24, 24,25,26,27,28, 36, 43,44,45,46,47,48,49]. Finally, we undertake single-cell-based genome/proteome analysis through a set of nanoprobes and adaptive electron microscopy, single-cell-based DNA/RNA release technology, or a 3-min ultrahigh-speed polymerase chain reaction (PCR) measurement technology [62].

Fig. 3.10

On-chip cellomics analysis. The aim of single-cell-based analysis of multicellular systems: temporal (algebraic) aspect and spatial (geometric) aspect

The advantage of the experimental on-chip cellomics approach is that, as it is a reconstructive approach of the simplified artificial minimum cell network model on a chip, it removes the complexity of the underlying physicochemical reactions that are not always completely understood and for which most of the necessary variables cannot be measured. Moreover, this approach shifts the view of cell regulatory processes from basic chemical grounds to a paradigm of the cell as an information processing unit working as an intelligent machine capable of adapting to changing environmental and internal conditions. This is an alternative representation of the cell and can provide new insights into cellular processes. Thus, models derived from such a viewpoint can directly help in more conventional biochemical and molecular biological analyses that assist in our understanding of control in cells.

From the geometric perspective, two more detailed viewpoints of analysis should also be taken: one is on the population/community size dependence and the other is on the spatial (network) pattern dependence of groups of cells. In conventional cell-based studies, cell lines are usually used for acquiring the same type of cells and are then cultivated in a cultivation dish without any control of their population or any formation of a community with other cell types. Finally, they are analyzed as a group regardless of any differences in their cell cycle regardless of their possible differences. In contrast, on-chip cellomics technology involves a new strategy with three steps: First, the cells are taken from a community using a nondestructive cell sorting procedure. Then, the cells are cultivated in a microchamber, in which cell network formation and medium environment are controlled. Finally, the genome/proteome measurement in each cell is measured (Fig. 3.10).

3.3.2 Photothermal Etching on Agarose Layer for Cell Network Formation Control

Flexible change of microstructures of cell-to-cell interactions or cell network shapes on a chip during cultivation is necessary for the “temporal” and “geometric” reconstructive approach of cell network studies. To accomplish this requirement, we have developed a photothermal etching method [11, 24, 26, 36, 46] with an agarose microchamber cell cultivation system (Fig. 3.11). This involves the area-specific melting of a portion of agarose of a whole light pathway by spot heating using a focused infrared laser beam of 1480 nm, which absorbs water, and of a portion of agarose close to a thin layer made of a light-absorbing material, such as chromium, with a laser beam of 1064 nm, which is permeable to water. When we combine infrared lasers with these two different wavelengths, we can fabricate microchambers and microtunnels flexibly for the noncontact three-dimensional photothermal etching of agarose. In other words, as the 1480-nm infrared beam is associated with the absorption of water and agarose gel, the agarose gel in the 1480-nm infrared light pathway was heated and completely melted. Moreover, as the 1064-nm infrared beam was not associated with this absorbance, the agarose melted just near the thin chromium layer, which absorbed the beam.

Fig. 3.11

Photothermal etching method. Using focused infrared (IR) lasers of two different wavelengths, the thin layer of low-melting point agarose on the chip was selectively melted in different manners. (a) As the 1064-nm IR laser is not associated with the absorption of water, only a portion of the agarose near the thin absorption layer is heated and melted, changing its state from a gel to a sol. In contrast, (b) as the 1480-nm IR laser is associated with the absorption of water, all of the agarose in the light pathway is heated and melted. (c) The agarose changed to a sol state is dispersed into the agarose gel, holes or tunnels are formed in the agarose layer, and (d) cells are inserted in agarose microchambers with a micropipette

For phase-contrast microscopy and this μm-scale photothermal etching, light of three different wavelengths (visible light for observation and 1480-nm/1064-nm infrared lasers for spot heating to construct microchambers/microtunnels, respectively) was used simultaneously to observe the positions of the agarose chip surface and to melt a portion of the agarose in the area being heated. As described above, the advantage of this method is that we can apply this stepwise network formation (addition) approach even during cultivation, so we can change the network size and pattern of cardiomyocyte cells during cultivation by adding microchannels between two adjacent microchambers in a step-by-step fashion; moreover, this approach is also applicable for neuronal networks [27, 28, 43, 45,46,47,48,49].

3.3.3 Community Effect of Cells for Their Synchronization (1): Two-Cell Model

As described in the previous subsection, the ability of photothermal etching of agarose microstructures to control the cell arrangement is beneficial for cardiomyocyte network studies. In this subsection, we introduce the application of this technology to reveal the involvement of the community effect in cardiomyocyte beating synchronization[17, 17,18,19,20, 24,25,26,27,28].

First, we investigated the roles of the beat rates (interbeat intervals) and beat rate fluctuation of isolated single cardiomyocytes in the reestablishment of synchronous beating by analyzing the changes of beating rates and their fluctuations before and after the synchronization of two cardiomyocytes through narrow channels with initially different rhythms (e.g., Fig. 3.12A and B)[27, 28]. The results showed three types of synchronization of two cardiomyocyte networks: (1) the beating of the two cardiomyocytes synchronized at the faster of the two initial rates, but there was beating fluctuation at the lower of the two initial rates (Fig. 3.12C), (2) the beating of the two cells synchronized at the lower of the two initial rates but fluctuated at the lower of the two initial rates (Fig. 3.12D), and (3) the synchronization occurred at neither of the initial rates of single cardiomyocytes, with fluctuation of smaller of the initial fluctuations (Fig. 3.12E).

Fig. 3.12

Synchronization of two cardiomyocytes. (A) Micrographs of two cardiomyocytes under isolated conditions (a), just after they were connected together (b), and just after synchronization started (c). (B) Beating waveforms at (a) and (c) in (A). (C)–(E) (left graph and center graph) Beating frequency spectrum before and after synchronization, respectively; distribution of interbeat intervals of two cardiomyocytes, and the change of the mean value of beating rhythm fluctuation at intervals of 1 min measured for 5 min before and after synchronization. Blue and red triangles show the mean values before synchronization, and black triangles show the mean value for the two cells after synchronization. (right graph) The change of the mean value of beating rhythm fluctuation [CV%: coefficient of variation (100 × standard deviation/mean beat rate)] at intervals of 1 min measured for 5 min before and after synchronization. Blue circles and red squares show the corresponding mean values of beating rhythm fluctuation for 1 min. Three types of synchronization tendencies were described: (C) synchronization to a faster beating cell, (D) synchronization to a slower beating cell, and (E) synchronization with a new beating frequency

The interbeat intervals of 14 two-cell pairs before and after synchronization are listed in Table a of Fig 3.13. Five of the two-cell pairs synchronized at the initial rate of the faster cell, two of the pairs synchronized at the initial rate of the slower cell, and the other seven pairs synchronized at a rate other than one of the initial rates. In Table b of Fig. 3.13, the fluctuation data for the 14 cell pairs whose rate data are listed in Table A are grouped according to the change of the fluctuation before and after synchronization. Thirteen pairs synchronized with a fluctuation equal to or less than the initial fluctuation of the slower member of the pair, and one pair synchronized with a fluctuation larger than that of either of the two initial fluctuations.

Fig. 3.13

Tendency of synchronization of two cardiomyocytes. (a) Three types of synchronization of two cardiomyocytes from the perspective of beating intervals. (b) Two types of synchronization from the perspective of beating stability (fluctuation of beating)

These results suggest that the fluctuation of reestablished synchronous beating by isolated cardiomyocytes is influenced more strongly by the fluctuation of the initial fluctuation of the beat rates of the isolated cardiomyocytes than the rate of the reestablished synchronous beating is influenced by the initial beat rates of the isolated cardiomyocytes. It is therefore possible that a cardiomyocyte whose beat rate fluctuates less than that of another cardiomyocyte entrains the beating rhythm of that cardiomyocyte, but we observed one pair of cells in which this did not happen. This indicates that the influence of a single cell is still not sufficiently strong to account for the process of entrainment in heart tissue.

3.3.4 Community Effect of Cells for Their Synchronization (2): Cell Number Dependence

Figure 3.14 also describes the community size effect of a cardiomyocyte network on its beating stability. In this work, we explore the relationship between entrainment and community size by examining the synchronization process of a cardiomyocyte network formed by the interaction of single cardiomyocytes cultured in a 3 × 3 grid of agarose microchambers with connecting microchannels[28]. After nine isolated cells had been cultured in the nine-chamber agarose microcultivation chip for 24 h, we started to measure the synchronization process continuously and found that, when an isolated single cell came into contact with another cell and formed a two-cell network (Fig. 3.14 top and middle), these two cells synchronized at the initial rate of the first cell and the fluctuation decreased from the initial fluctuation of the first cell. When all nine cells came into contact and formed a nine-cell network (Fig. 3.14 bottom), it synchronized at a rate equal to the initial rate of the first cell, with a decrease of fluctuation.

Fig. 3.14

Effect of increase in connected cell number on increase in beating stability. (a) Isolated single cell, (b) two-cell network, and (c) nine-cell network. (d) Dependence of beating interval fluctuation on cell number

These results suggest that the beating rhythm of a single cardiomyocyte tends to entrain the rhythm of the cell network, and the strength of this tendency increases with the size of the network. Therefore, it is thought that the fluctuation of the rate at which a network of cardiomyocytes beats decreases as the size of the network increases. The tendency of the synchronization above was simply explained by asserting that the synchronization of two cardiomyocytes was caused by the more unstable cell (the one with the more variable beating intervals) following the more stable cell. Such tendency for reduced fluctuation was more pronounced when the number of cardiomyocytes in the network increased; we call this phenomenon the “community effect” of synchronization.

Using the agarose microchambers, we can examine the dependence on the spatial arrangement of the synchronization stability of cardiomyocyte networks [18]. As shown in Fig. 3.15, we can arrange the cardiomyocytes in three different shapes, a linear shape, a radial shape, and a lattice shape and compare their tendencies for beating stabilization relative to cell numbers. The results indicated that there was no apparent relationship between the number of cells and their shape and that the most important index for the stabilization of cell beating is not the geometry of cells but their number.

Fig. 3.15

Dependence of spatial arrangement of cardiomyocyte networks on cell number for beating stability. Three types of spatial arrangements: (a) linear shape, (b) radial shape, and lattice shape (see Fig. 3.14). (c) Fluctuation of beating interval versus network size in linear (green triangles), radial (red squares), and lattice (blue circles) cardiomyocyte networks. These plots show mean ± standard deviation

3.3.5 Community Effect of Cells on Their Synchronization (3): Mixture of Different Types of Cells

We also examined the contribution of fibroblasts to the synchronization of cardiomyocytes[19]. We connected two cardiomyocytes through a single fibroblast and synchronized them, as shown in Fig. 3.16A and B, and then used this heterogeneous cardiomyocyte–fibroblast coupling to examine the tendency of the stability of interbeat intervals and beating rhythm fluctuation of two cardiomyocytes through a fibroblast before and after their synchronization.

Fig. 3.16

Synchronization of two cardiomyocytes through a fibroblast. (A) Micrographs of two cardiomyocytes under isolated conditions (a), when a fibroblast was added between two cardiomyocytes (b), and when two cardiomyocytes were connected through a fibroblast and synchronization started (c). (B) Beating waveforms at (a) and (c) in (A). (C)–(E) Three types of synchronization tendencies. Beating frequency spectrum before (left graphs) and after (center graphs) synchronization and their beating fluctuation (right graphs). (C) Synchronization to a cell beating faster and more stably. (D) Synchronization and creation of new beating intervals contributing to beating stability. (E) Synchronization with new beating frequency, but beating fluctuation increased

The first type of synchronization involved the tendency for the fluctuation to decrease due to synchronization, which is the same tendency as seen in a network formed by the direct connection of two cardiomyocytes. As shown in Fig. 3.16C and D, in this type, the two cells having different interbeat intervals before synchronization synchronized to achieve an interbeat interval of less than a second after synchronization (e.g., Fig. 3.16B). The fluctuation of the synchronized network became almost equal to or smaller than either of the two initial fluctuations.

In contrast, the second type involved the tendency for the fluctuation to increase due to synchronization, which did not occur in the cardiomyocyte network (Fig. 3.16E). In this case, two cardiomyocytes having two different interbeat intervals before synchronization exhibit a higher mean interbeat interval after synchronization, and the fluctuation of the synchronized network is greater than that of the cell that had the lower fluctuation before the synchronization.

Our photothermal etching method with agarose microchambers allows us to regulate the cell type and community size of cultured cells at the single-cell level. This could not be done when using the conventional cell cultivation method, so the prolific growth of cardiac fibroblasts made it difficult to culture only cardiomyocytes and investigate the properties of a single cell within a group of cells. By using single-cell-based cultivation, we were able to investigate how the fluctuation of the rates at which cardiomyocytes beat affects the reestablishment of synchronized beating.

3.3.6 Summary of Experimental Results

The results of the on-chip constructive experiments are summarized as follows:

• 1. When two isolated independently beating cardiomyocytes come into contact, they tend to beat synchronously at a rate that fluctuates no more than that of the cell whose beat rate fluctuated less than did that of the other cell.

• 2. When initially isolated cardiomyocytes form a network, its rhythm tends to entrain the beating rhythm of single cells whose beating rhythm fluctuated more than that of the network.

• 3. The entrainment activity of cell networks increases with their size, i.e., the fluctuation decreases.

• 4. Spatial arrangement does not affect the manner of synchronization of cardiomyocytes, and only the cell number of the network determines their tendency for synchronization.

• 5. The interbeat interval after the synchronization of two cardiomyocytes connected by a fibroblast is not the same as that after the synchronization of two cardiomyocytes directly connected to each other, and the tendency for the community effect to occur appears to be suppressed when the cardiomyocytes are heterogeneously coupled through a fibroblast.

They might indicate that unstable isolated cardiomyocytes reestablish a cell network that beats stably and synchronously. A novel finding of this study is that a cardiomyocyte network containing only a few cells acquires a stable rhythm. Moreover, once the cell or cell network achieves stable beating, an additionally attached unstable cell can synchronize to the stable cell or cell network and follow its stable beating intervals. This phenomenon also suggests that the factor of stability is very important in determining the fate of the beating frequency of the network after the connection of unstable cells.

3.3.7 Ability and Limitation of Constructed Experimental Approach

As described above, the constructed experimental approach is one of the potential solutions to solve the issue of quality control of cells. However, cells inherently display a variety of dynamic characteristics, even when cultivating cells in completely the same conditions and also when using those from the same single stem cells[33]. Figure 3.17 shows an example of this diversity of their expression. Although isolated single human iPS (hiPS) cardiomyocytes and human ES (hES) cardiomyocytes were derived from the same stem cells, their interbeat intervals (IBIs) and fluctuations [in this graph, we use the coefficient of variation (CV) as the index of fluctuation] were larger than those of the primary mouse cardiomyocytes. In contrast, two clusters made of the same dispersed cardiomyocytes showed similar characteristics and appeared to represent their species (two red triangles in each graph of Fig. 3.17C). These results clearly indicate the ability and limitation of the experimental approach of single-cell-based assays. Each isolated single cell does not inherently show the same dynamics; however, once they formed a network, their diversity disappeared and stable shared characteristics appeared. We call this phenomenon the “community effect.” To understand the meaning of the community effect, we need to have a set of completely controlled single cells. However, this is beyond the scope of the experimental approach. Even using the on-chip cellomics technologies, this experimental approach has a limitation of not allowing full control of the condition of all of the cells, especially in a dynamic context such as beating of the heart.

Fig. 3.17

Distribution of the interbeat intervals (IBIs) and fluctuations of isolated single cardiomyocytes and their clusters of primary, human iPS (hiPS), and human ES (hES) cells. (A) Method of cardiomyocyte cluster formation. (a) In the regular untreated culture dish, cardiomyocytes were dispersed and isolated. (b) In the agarose concave-coated culture dish, cardiomyocytes were gathered and clustered during incubation. (B) Micrographs of single cardiomyocytes and their clusters. (a) Isolated mouse primary cardiomyocyte, (b) clustered mouse primary cardiomyocytes, (c) single isolated hiPS cardiomyocyte, (d) clustered hiPS cardiomyocytes, (e) isolated hES cardiomyocyte, and (f) clustered hES cardiomyocytes. (C) Fluctuation–IBI relationship of mouse primary cardiomyocytes (a), hiPS cardiomyocytes (b), and hES cardiomyocytes (c). Green open circles are the 60-s mean IBIs and CVs of isolated single cardiomyocytes, and red filled triangles are those of clusters. The error bar indicates standard deviation. The coefficient of variation (CV) value of IBI was used as the fluctuation of beating

3.4 Numerical Approach to Synchronization of Cardiomyocytes

3.4.1 Comparison of the Mathematical Modeling with Experimental Results and Numerical Simulations

The mathematical model by modifying the integrate-and-fire model was shown in Sect. 3.2.1.1. This model is constructed on the basis of the simple Peskin’s model [39], including refractory periods, stochastic process, and weak cell-to-cell interactions, which modulate phase variables [32, 56].

When cardiomyocytes are isolated, they only beat independently. However, if cardiomyocytes come into contact and interact with each other, their beating rhythms become synchronized. The experiments shown in Sect. 3.3 revealed that other cardiomyocytes are synchronized not to the fastest cardiomyocyte, but to the cardiomyocyte with the least fluctuation in beating rhythm [28].

In this section, we discuss the comparison of the numerical simulations to the experimental results and aim to theoretically understand the phenomenon that the synchronized beating of cardiomyocytes is tuned to the cardiomyocyte with a stable rhythm [13]. Using our model, we also aim to investigate the community effect of cardiomyocytes in different configurations of networks constituted by cardiomyocytes with specified characteristics of beating rhythms and to clarify how an assembly of cardiomyocytes acquires stability, one of the most important universal features in biological systems.

3.4.1.1 Mathematical Modeling for Synchronization of Cardiomyocytes

We consider a network of N cardiomyocytes and call ith cardiomyocyte cell i. The model was described by the phase variables ϕ _i(t) (0 ≤ ϕ _i(t) ≤ 2π, i = 1, 2, …, N), which denote the state of cell i at a time t. We assumed that the cell i fires (beats) when ϕ _i(t) = 0(≡ 2π). This firing occurs either at ϕ _i(t), reaches 2π, or the following conditions are satisfied: ϕ _i(t − 0) ≥ θ _i (ϕ _i(t − 0) :=lim_𝜖→+0 ϕ _i(t − 𝜖)). Additionally, one of the cardiomyocytes connected to cell i (e.g., cell j) fired at a retardation time τ ago (i.e., ϕ _j(t − τ) = 0). Otherwise, we assumed that ϕ _i(t) is governed by the following interacting stochastic differential equation. Our mathematical modeling for cell i is as follows:

(3.49)

where ω _i is the average phase velocity of cell i, dW(σ) is a stochastic process with standard deviation σ, and θ _i is a phase corresponding to the refractory period of cell i(0 < θ _i < 2π). V (ϕ _i, ϕ _j) shows the weak interaction between cardiomyocytes through the membrane potential, which we assumed as the following form:

$$\displaystyle \begin{aligned} V(\phi_i, \phi_j):= \mu \sin (\phi_j - \phi_i), \end{aligned} $$

(3.50)

where μ is a positive constant. An important point is that the stochastic process and the cell-to-cell interaction are correlated through the fluctuation–dissipation theorem that gives the relation between fluctuations and linear response to external force [31]. This will be discussed again in Sect. 3.4.3. The positive constant μ is the only free parameter in our model that cannot be directly determined by experiments, while ω _i, θ _i, and σ _i can be determined by single-cell experiments for each cardiomyocyte. In addition, we assumed that the boundary at ϕ _i(t) = 0 is the reflective boundary condition, which ensures that the phase fluctuation is irreversible after firing. The schematic diagram of the dynamics of the phase variable ϕ _i(t) is shown in Fig. 3.18.

Fig. 3.18

Schematic diagram of the trajectory of the state variables ϕ _i(t)(i = 1, 2). The circle represents the trajectory of a state variable in the phase space of cardiomyocytes from one firing to the next firing. If cell 2 fires at a time t (ϕ ₂(t)=0) and cell 1 is not in the refractory period, then cell 1 fires at the retardation time τ after cell 2 fires

3.4.1.2 Numerical Simulation Method

The stochastic process in our simulation is described by an extended random walk. We used the following difference equations as a numerical approximation of Eq. (3.49). For almost all cardiomyocytes with a standard beating rhythm, we considered an ordinary random walk as follows:

(3.51)

$$\displaystyle \begin{aligned} \varDelta \phi_i = \, \begin{cases} +\varDelta x_i \qquad (\text{with probability}\ 0.5), \\ -\varDelta x_i \qquad (\text{with probability}\ 0.5), \end{cases} \end{aligned} $$

(3.52)

where the standard deviation is defined by $\sigma :=\varDelta x/\sqrt {2 \varDelta t}$, Δt is the time difference interval, $\varDelta x_i = \sqrt {2 \varDelta t \, \sigma _i^2}$ is the spatial difference determined by σ _i, and the delay time τ is set as Δt × k (k is a nonnegative integer). However, we could not reproduce the same beating fluctuation by using an ordinary random walk for cardiomyocytes with a large fluctuation. This is because the coefficient variation (CV%), which is defined by 100 × standard deviation/mean beating rate, could be proved less than $100 \sqrt {2/3}\simeq 81.65$ in Sect. 3.2.2. As shown in Fig. 3.13, some cardiomyocytes with the CV% which exceed this value are observed. Therefore, we adopted the following extended random walk, which is a history-dependent stochastic process, when beating fluctuation was larger than 81.65 (CV%):

(3.53)

The noise term $\varDelta \tilde {\phi _i}(t)$ is defined as

(3.54)

However,

(3.55)

The model could reproduce the large fluctuation observed in the experiments by setting appropriate values of q and r.

3.4.1.3 Comparison of the Model with Experimental Results of Two Cardiomyocytes

In the experiments shown in Sect. 3.3.3, the mean beating rate and its fluctuation before and after synchronization were observed for 14 pairs of cardiomyocytes (Fig. 3.13). We investigated whether our model could reproduce the results of these pairs of cardiomyocytes. We numbered these 14 pairs from Nos. 1 to 14 and distinguished the two cardiomyocytes in a pair by denoting “cell 1” and “cell 2.” For each pair, we defined ω _i, σ _i, and θ _i in Eq. (3.49) for cell i (i = 1, 2), so that the model reproduced the same mean beating rate and fluctuation in beating rhythm. Since refractory periods of cardiomyocytes are almost the same as those for normal cardiomyocytes, we assumed that each cell had the common refractory period t _ref = 0.3 s. Therefore, θ _i is given by θ _i = t _ref ω _i. Figure 3.19 shows the mean beating rates and the beating fluctuation after synchronization for the 14 pairs obtained by the experiments and numerical results by our model. We could regard the retardation time τ as almost 0 because it was estimated as 10⁻³ ∼ 10⁻⁴ of the mean beating rate. Therefore, we put τ = 0. We used μ = 6.5 in numerical simulations. The dependence of theoretical calculation on μ is shown later. We found that the simulated values accurately agree with the experimental values except for pair No. 14. The experimental result of pair No. 14 is exceptional because it is the only pair in which fluctuation increased after synchronization. Beating fluctuation of a pair of synchronized cardiomyocytes was equal to or less than that of less fluctuating cardiomyocytes, while the mean beating rate was widely distributed. Some pairs synchronized at faster rates of the two initial rates, some at slower rates of the two initial rates, and others at intermediate rates of the initial rates of the pair. We demonstrate how to determine the free parameter μ. Let us define an index ε, to evaluate the deviation of the theoretical values from the experimental values.

$$\displaystyle \begin{aligned} \varepsilon := \sum^{13}_{k=1} \sum^{2}_{i=1} \Bigl\{ (T^i_k-T^{\mathrm{ex}}_k)^2+ (F^i_k-F^{\mathrm{ex}}_k)^2 \Bigr\}, \end{aligned} $$

(3.56)

where $T^{\mathrm {ex}}_k$ denotes the experimental value of the mean beating rate of the cell i in the pair k after synchronization, and $T^i_k (i=1,2)$ denotes the corresponding theoretical value obtained by our model. Similarly, $F^{\mathrm {ex}}_k$ denotes the experimental value of fluctuation (CV) of the cell i in the pair k after synchronization, and $F^i_k (i=1,2)$ denotes its theoretical value. Figure 3.20 shows the dependence of ε on μ. For $6 \lesssim \mu \lesssim 12$, ε keeps to take the lowest value. The results of the numerical simulations were almost constants for a relatively wide range of μ. This finding indicated that our model was robust against the free parameter μ.

Fig. 3.19

The mean beating rate and beating fluctuation after synchronization. Numerical simulations for the 14 pairs of cardiomyocytes (28 cardiomyocytes) before synchronization in the experiments shown in Sect. 3.3.3 were performed using our integrate-and-fire model. Experimental values (circles) and theoretical values (filled circles) are plotted for (a) the mean beating rate and (b) beating fluctuation (CV%). For all numerical simulations, we used the same parameter values τ = 0 and μ = 6.5. The fluctuation in beating rhythm is expressed by the CV

Fig. 3.20

Parameter μ dependence of deviation of numerical values from experimental data. The deviation between numerical simulation and experimental data is measured with the quantity ε by changing parameter μ

3.4.1.4 Comparison with the Kuramoto Model

The two-oscillator phase model (the Kuramoto model [32]) with noise is as follows: for i, j = 1, 2, i ≠ j,

$$\displaystyle \begin{aligned} d \psi_i(t) = \bar{\omega_i} dt + A_{i,j} \sin (\psi_j - \psi_i ) dt + \bar{\sigma_i} d W_i(t) ,\hspace{0.5cm} \psi_i(0) = 0, \end{aligned} $$

(3.57)

where $\bar {\omega _i}$ and $\bar {\sigma _i}$ denote the drift and noise strength constants, respectively, A _i,j are nonnegative constants, and {W _i}_i=1,2 is independent standard Brownian motion (see Sect. 3.2.3). For two cases (Case (i) and Case (ii)), we applied the Kuramoto model (3.57) and our model (3.49) to synchronization of two coupled cardiomyocytes. The numerical simulation results were compared with biological experiment data (Fig. 3.12).

Case (i) A Case of Synchronization to a Cardiomyocyte with a Fast and Stable Beating Rhythm

Two cardiomyocytes that we used in the Case (i) were cell 1 and cell 2 of pair No. 1, which have a mean beating rhythm of 0.64 s and fluctuation of 12.3 [CV%] and cell 2 with 1.23 s and 25.1 [CV%], respectively. When the two cardiomyocytes were coupled, we found that the bating rhythm after synchronization was tuned to cell 1 with a fast and stable beating rhythm (Fig. 3.21a). We investigated whether our model and the Kuramoto model could reproduce the experimental results. Figure 3.21b and c shows the theoretical predictions from our model and the Kuramoto model, respectively. The mean beating rate and beating fluctuation for the experimental result, our model, and the Kuramoto model are shown in Table 3.1.

Fig. 3.21

Comparison of experimental data and the two models. The change in beating fluctuation before and after synchronization is shown. The blue circles and brown squares represent the corresponding mean values for 1 min of beating fluctuation of cell 1 and cell 2, respectively. Panels a–c show the results for Case (i), which was a case of synchronization to a cardiomyocyte with a fast and stable beating rhythm. (a) The experimental result, (b) the numerical result of our model, and (c) the numerical result of the Kuramoto model with ($\bar {\omega _1}, \bar {\sigma _1}$) =  (9.80, 0.94)and($\bar {\omega _2}, \bar {\sigma _2}$) =  (5.09, 1.45)

Table 3.1 Comparison between the experimental result and the numerical results. The symbols T _i and F _i denote the mean beating rate and the beating fluctuation of the cell i(i = 1, 2), respectively. The symbol T denotes the mean beating rate and F the beating fluctuation after synchronization

Case (ii) A Case of Synchronization to a Cardiomyocyte with a Slow and Stable Beating Rhythm

Two cardiomyocytes that we used in the Case (ii) were cell 1 and cell 2 of pair No. 6, which have a mean beating rhythm of 1.10 s and fluctuation of 149 [CV%] and cell 2 with 1.40 s and 41.2 [CV%], respectively. When the two cardiomyocytes were coupled, we found that the bating rhythm after synchronization was tuned to cell 2 with a slow and stable beating rhythm (Fig. 3.22a). When we compared the numerical result of our model with that of the Kuramoto model, we found that our model was closer to the experimental data than the Kuramoto model. Our model showed that the beating rhythm after synchronization was tuned to the rhythm of the slow and stable cardiomyocyte (Fig. 3.22b). However, the Kuramoto model showed that beating fluctuation of the slow and stable cardiomyocyte was increased after synchronization, which differed from the experimental results (Fig. 3.22c). The mean beating rate and beating fluctuation of the experimental result, those of our model, and those of the Kuramoto model are shown in Table 3.2.

Fig. 3.22

Comparison of experimental data and the two models. The change in beating fluctuation before and after synchronization is shown. The blue circles and brown squares represent the corresponding mean values for 1 min of beating fluctuation of cell 1 and cell 2, respectively. Panels (a)–(c) show the results for Case (ii), which was a case of synchronization to a cardiomyocyte with a slow and stable beating rhythm. (a) The experimental result, (b) the numerical result of our model, and (c) the numerical result of the Kuramoto model with ($\bar {\omega _1}, \bar {\sigma _1}$) =  (5.03, 6.28)and($\bar {\omega _2}, \bar {\sigma _2}$) =  (4.46, 1.57)

Table 3.2 Comparison between the experimental result and the numerical results. The symbols T _i and F _i denote the mean beating rate and the beating fluctuation of the cell i(i = 1, 2), respectively. The symbol T denotes the mean beating rate and F the beating fluctuation after synchronization

Therefore, our model showed that even though the mean beating rate of a cardiomyocyte was slow, a cardiomyocyte with more stable beating fluctuation dominated the beating rhythm after synchronization. In previous numerical simulations, we did not consider the effect of retardation time (τ = 0). When we incorporated this effect, the behavior of our model barely changed because of the existence of a refractory period much longer than τ. However, if the refractory period is not taken into account, then a couple of cardiomyocytes continuously fire with the period of the retardation time, which is biologically unacceptable. In a system of two cardiomyocytes, we can use a retardation time τ = 0, but we should consider the effect of retardation time as the size of the system increases. In this case, the existence of the refractory period will have significant effects on the system.

3.4.2 Numerical Experiments

As an application of our mathematical modeling, we then performed two numerical experiments on networks of cardiomyocytes and investigated the community effect of cardiomyocytes.

3.4.2.1 Size and Configuration Dependence on Fluctuation of the System

First, we investigated the dependence of fluctuation in beating rhythm of cardiomyocytes on the size and configuration of the system. Network patterns in cardiomyocyte groups that we considered were star, 2D lattice, and 1D lattice networks (Fig. 3.23).

Fig. 3.23

Configurations and the order of placing cells. Three types of networks of configuration are shown. (a) Star network, (b) 2D lattice network, and (c) 1D lattice network. A cardiomyocyte is represented as a circle and it interacts with another cardiomyocyte if they are connected by a line. Cardiomyocytes are connected in ascending order according to the numbers in the circles from 1 to 20

We assumed that all the elements in cell networks have the same beating properties. Figure 3.24a–c shows the size dependence of fluctuation of networks with three types of configurations. The model cardiomyocyte that was used in Fig. 3.24a was cell 1 of pair No. 1, which had a mean beating rhythm of 0.64 s and fluctuation of 12.4 [CV%], that in Fig. 3.24b was cell 2 of pair No. 1 with 1.23 s and 25.1 [CV%], and that in Fig. 3.24c was cell 2 of pair No. 8 with 2.71 s and 43.0 [CV%]. We found that the beating fluctuation decreased as the size of the system increased irrespective of network pattern. Among the three configurations, a reduction in fluctuation tended to be most rapid in the 2D lattice network, and fluctuation in the 1D lattice network tended to be always larger than that in the other two configurations. In addition, we considered the larger size (about 1000 cells) of the network in the 2D lattice network. Figure 3.25a–c shows the size dependence of fluctuation of the 2D lattice network where all the elements had the same beating properties. The numerical results suggested that the beating fluctuation decreased as the community size increased, but the CV value of the system approached a constant value for large system size N. For an ordinary stochastic ensemble, such as an independently identical distributed ensemble, the dependence of standard deviation of fluctuation on system size N was proportional to N ^−1∕2. However, we found that the data of fluctuation plotted on the graph (Fig. 3.25) considerably diverged from the line of N ^−1∕2 and the features of beating fluctuation behave differently from that of ordinary stochastic ensembles.

Fig. 3.24

Size dependence of fluctuation for three types of configuration. Size dependence of fluctuation is shown in double logarithmic graphs. The components of the network are model cardiomyocytes with the same characteristics. Panels( a)–(c) show the size dependence of fluctuation for three types of configurations: (a) ω = 9.80, σ = 0.69, θ = 2.94, (b) ω = 5.00, σ = 1.01, θ = 1.50, and (c) ω = 2.10, σ = 1.18, θ = 0.63. Circles indicate beating fluctuation (CV%) of cardiomyocytes in the star network, triangles indicate beating fluctuation in the 2D lattice network, and crosses indicate beating fluctuation in the 1D lattice network. The black straight line denotes ∝ N ^−1∕2, where N is the number of cardiomyocytes in the network

Fig. 3.25

Size dependence of fluctuation for a large network. Size dependence of fluctuation is shown in double logarithmic graphs. The components of the network are model cardiomyocytes with the same characteristics. Panels a–c show the size dependence of fluctuation for a larger 2D lattice network. (a) ω = 9.80, σ = 0.69, θ = 2.94, (b) ω = 5.00, σ = 1.01, θ = 1.50, and (c) ω = 2.10, σ = 1.18, θ = 0.63. The black straight line denotes ∝ N ^−1∕2, where N is the number of cardiomyocytes in the network

3.4.2.2 Dependence of Cell Properties and Numbers on Fluctuation of the System

We then investigated the change in beating rhythms after connecting two subsystems of cardiomyocytes. First, we prepared referential subsystems of four model cells and nine model cells. We assumed that these subsystems had the property of a standard beating rhythm (mean beating rate 1.20–1.30 s and fluctuation 15.0–20.0 [CV%]). As for the subsystems that are connected to referential subsystems, we considered subsystems comprising four types of cardiomyocytes: (1) first and stable cell, (2) first and unstable cell, (3) slow and stable cell, and (4) slow and unstable cell. We considered the three types of cell network patterns shown in Fig. 3.23. A single cardiomyocyte was connected to a center cardiomyocyte of the referential star network, to a cardiomyocyte on a link of the referential 2D lattice network, and to a cardiomyocyte on an edge of the 1D lattice network (Fig. 3.26a and b). When subsystems were the same size, we connected them by a single link between two cardiomyocytes at the same positions in the cell network. We used the two center cardiomyocytes for the star networks, cardiomyocytes on the links for the 2D lattice network, and the two cardiomyocytes at the edges for the 1D lattice network (Fig. 3.26c and d).

Fig. 3.26

Configurations of a combination between a referential network and a single cell or an assembly of cells. In panels (a) and (b), the filled circles denote a single cell, which adds to the referential network, of which cells are denoted by open circles. (a) Referential network of four cells + a single cell and (b) that of nine cells + a single cell. Panels (c) and (d) show the configurations of combined subsystems of four cells and those of nine cells. The cells in referential networks are denoted by open circles and those in counterparts are denoted by filled circles. (c) Referential network of four cells + four cells and (d) that of nine cells + nine cells

We showed three typical results of the numerical simulation. First, we considered the referential 2D lattice network with nine cardiomyocytes and a single cardiomyocyte with a fast and unstable beating rhythm (Fig. 3.27a). When the nine-cell network came into contact with the single cardiomyocyte, the single cardiomyocyte synchronized at the beating rhythm of the nine-cell network and with a beating fluctuation equal to that of the nine-cell network (Fig. 3.27b). Second, the rhythm of a single cardiomyocyte was fast and stable (Fig. 3.27c). We then found that even a single cardiomyocyte could lower fluctuation of the referential network and the beating rhythm of the referential network synchronized to a stable single cardiomyocyte (Fig. 3.27d). Finally, we considered a referential 2D lattice network with four cardiomyocytes and four cardiomyocytes grouped with a fast and stable beating rhythm (Fig. 3.27e). When the two subsystems were coupled, the synchronized beating rhythm was also tuned to the rhythm of the more stable group (Fig. 3.27f). In the above three cases (Fig. 3.27a–f), every cardiomyocyte started synchronizing when two subsystems were connected and formed a cell network. However, synchronization did not occur when the referential network was connected to a fast and stable 1D lattice network with nine cardiomyocytes. The cardiomyocytes near the edge of 1D lattice network with nine cardiomyocytes showed an exceptionally large fluctuation compared with the other cardiomyocytes. Furthermore, fluctuations of combined systems reduced their intensity, except for when there was a single cardiomyocyte or cardiomyocyte group with a slow and stable beating rhythm. However, the increment in fluctuation was small, even in these cases (e.g., Fig. 3.27g and h). When a referential subsystem came into contact with a counterpart consisting of one of the other three types of cardiomyocytes, the constituent cardiomyocytes acquired a common intensity of fluctuation. The intensity was intermediate between that of the prior two subsystems but was similar to that of the less fluctuating subsystem.

Fig. 3.27

Change in the beating fluctuation before and after synchronization. (a) The referential subsystem is the 2D lattice network and the counterpart is the single cell with a fast andunstable beating rhythm. (b) The change in mean value of beating fluctuation. The data for the referential networks and the counterparts are shown by circles and squares, respectively. The circles and squares show the corresponding mean values for 1 min of beating fluctuation. The results for the other combined systems (c), (e), and (g) are shown similarly in (d), (f), and (h), respectively

3.4.3 Discussion

To investigate the community effect of networks of cardiomyocytes, we used an interacting integrate-and-fire model with a refractory period. The reliability of the present mathematical model was verified by accurately reproducing recent experiments on pairs of cultured cardiomyocytes by Kojima et al.[28], despite the fact that the mathematical model has only one free parameter. One of the interesting points is that the fluctuation observed in their experiments cannot be accounted for simple Brownian motion or equivalently random walks. This is because some of the beating rhythm fluctuations (CV%) exceeded the theoretical limit evaluated for Brownian motion. An important observation in their experiments is the finding that when two isolated independently beating cardiomyocytes came into contact, they tended to beat synchronously at a rate of the cardiomyocyte with a stable beating rhythm, but not the cardiomyocyte with a faster beating rhythm. This community effect of cardiomyocytes toward stability was confirmed with the present mathematical model by investigating cell networks of various configurations and constituent cardiomyocytes with various beating rhythms. Even a single stable cardiomyocyte could lower beating fluctuation of a cell network comprising some cardiomyocytes. The reason why a cardiomyocyte with an unstable beating rhythm tends to follow a cardiomyocyte with a stable beating rhythm may be explained as follows. A cardiomyocyte with a stable beating rhythm has the property where its dynamics are only slightly affected by external or internal disturbance. Therefore, there is little effect of interactions from neighboring cardiomyocytes. While, a cardiomyocyte with an unstable beating rhythm has the opposite property and is strongly affected by its neighbors. A cardiomyocyte with a stable beating rhythm corresponds to a pendulum with a heavy mass in contrast to a cardiomyocyte with an unstable beating rhythm that corresponds to that with a light mass (Fig. 3.28). When these pendulums are connected, the pendulum with a light mass tends to follow that with a heavy mass. This feature is a consequence of the fluctuation–dissipation theorem, which provides a universal relation between fluctuation and a linear response[3, 31]. In our model, the coefficient $\sigma _i^2$ of the interaction term ∑_j V (ϕ _j, ϕ _i) in Eq. (3.49) was because of this theorem. This factor plays an essential role in stabilizing the beating rhythm after synchronization. Stability is one of the most significant and universal features of biological systems. It is an interesting finding that one of the origins of biological stability is a universal principle in statistical physics, that is, the fluctuation–dissipation theorem.

Fig. 3.28

Schematic explanation of why the beating rhythm tend to be synchronized to that of more stable cardiomyocytes after connection of two cardiomyocytes. A stable cardiomyocyte can be compared with a heavy pendulum and an unstable cardiomyocyte with a light pendulum. (a) External fluctuation has little effect on a pendulum’s period of swing if its weight is heavy, but has strong effects if its weight is light. (b) When two pendulums are coupled and synchronized, their period of swing is close to that of the heavier pendulum, and fluctuation will be reduced because the total mass of weight increases

3.5 Summary

As described in this chapter, we examined the community effect with a mathematical model of cardiomyocyte synchronization behavior using the following three steps: first, to initiate the mathematical approach, we modeled the firing of cardiomyocytes as an oscillating stochastic phase model, involving the concepts of refractory period and induced beating, and also discussed its characteristics of single cardiomyocyte beating, two coupled cardiomyocytes, and the network of plurality of cardiomyocytes (Sect. 3.2). Next, we introduced the experimental results of the synchronous behavior of cardiomyocyte networks after a brief explanation of the experimental setup of microfabrication techniques regarding how the constructed approach of stepwise synchronization of cardiomyocytes was accomplished (Sect. 3.3). Finally, we proposed the oscillating stochastic phase model with the fluctuation–dissipation theorem and revealed that the model of cardiomyocyte networks with various cell numbers and spatial arrangements showed the same tendencies as the experimental results of synchronization behavior. Specifically, it revealed that the stability-oriented synchronization phenomenon and the fluctuation of beating intervals determine the cell network synchronous behavior (Sect. 3.4).

We here speculate about the macroscopic behavior behind the synchronization of beating cardiomyocytes. Such a synchronized network of living organisms appears to be a macroscopic system in which part of its behavior is not just purely mechanical, but it also exhibits statistical features that all systems tend to present. Hence, the community effect of cells should also be based on the statistical tendency of matter to become disordered as a part of the ordinary laws of physics.

At present, however, it is not clear whether and how this synchronization rule or community effect is regulated at the molecular ion channel level. In other words, no detailed information about the functioning of the community effect can emerge from a description of the genetic mechanism and its expression as general as that given above. In this regard, the next step for a mathematical approach to studying the community effect is to connect the macroscopic interpretation with the microscopic interpretation. For this, the in silico membrane potential model should become more precise [5, 7, 8, 16, 30, 38, 55], and it can also be applied in practical applications for drug discovery or predictive toxicity screening.

Finally, with regard to the community effect, living systems appear to maintain and perhaps encourage orderly and regulated behaviors, acting against the tendency for natural systems to progress from order to disorder, but based partly on some hidden existing order that is retained.