Keywords

1 Introduction

Overhead cranes play a very important role in cargo transfer in industrial sites because of their small footprint, convenience, and fast transportation. As a large-scale mechanical equipment, with the popularization and use of overhead cranes in various industrial environments, higher and higher requirements are put forward for its stable, efficient and safe operation. Therefore, research on crane automation control technology is gradually becoming more important [1].

The crane has a process of acceleration or deceleration during operation, which is bound to cause the swing of load. This kind of swing phenomenon is particularly obvious during the starting and braking of the crane. In addition, overhead crane use hook to connect load during lifting operation, so it exhibits double pendulum characteristics. When the crane trolley moves to a predetermined position, the swing of the load will cause difficulty in hoisting and positioning, increase the duration of hoisting operations, and lower the work efficiency of the crane. Aiming at the problem of trolley positioning and swing angle suppression, many scholars have provided solutions and optimization strategies, which can be divided into open loop control, and closed loop control. Open loop control includes motion planning optimal control [2,3,4] and input shaping control [5,6,7]. Closed-loop control includes sliding mode control [8,9,10], adaptive control [11,12,13], passivity-based control [14,15,16] and intelligent control [17,18,19].

Then, some typical control strategies are enumerated and analyzed. Fu et al. proposed a minimum time motion online planning method under constrained conditions in [20]. Considering the coupling relationship between trolley positioning and load swing, an optimization problem is proposed and the solution of the motion planning problem is calculated in real time. Taking into account the problem of load assignment of multiple cranes in real work scenarios, Ji et al. created a mixed integer programming in which a mathematical equation can solve the optimization problem. Through case analysis, this method can improve crane transportation efficiency [21]. In order to achieve the control objectives of trolley positioning and anti swing, Zhang et al. designed an online motion planning method in [22]. The proposed method includes the correlation functions of trolley positioning and swing angles, and the effectiveness of the method is verified by theoretical proof and simulation. A disturbance observer control strategy that can eliminate unknown disturbances in finite time is designed by Wu in [23]. During the design process, some conversions were made to the original dynamic model of the crane system. Mathematical analysis and experiments verify the superiority of this method. Combining adaptive control and sliding mode control, an adaptive integral sliding mode controller is derived by Zhang et al. in [24]. At the same time, the purpose of swing angle suppression is achieved by increasing the state vector coupling. In [25], Le et al. designed a hierarchical sliding mode controller based on the crane system, and then used an intelligent algorithm to determine the control gains.

After careful investigation, it is certain that the existing literature provides ideas for the control method of the three-dimensional double pendulum crane system to a large extent. However, some problems still need to be resolved for the crane system studied in this article: (1) Due to the complexity of the three-dimensional double pendulum overhead crane model, it is challenging to design the controller to achieve the control goal. It can be found that in most literatures, when faced with a complex model with many degrees of freedom, the author ignores some nonlinear terms to simplify the model, and then performs controller design or theoretical analysis on the basis of the simplified model. (2) There are often some unknown disturbances in actual working scenarios, and this issue should also be considered when designing the controller. (3) Many existing controllers contain velocity signals, but in reality, the velocity signals are unmeasurable when the crane is hoisting.

Thus, in order to solve the above problems, an improved adaptive tracking controller without velocity feedback is proposed. In summary, the main contributions of this method are as follows: (1) Unlike the traditional controllers, it does not need to linearize the dynamic model of crane system when designing the controller. (2) In practice, there are always unknown external disturbances in the crane system, which is considered in this paper. (3) The problem of unmeasurable velocity and angular velocity is overcome by introducing velocity function.

2 Three-Dimensional Overhead Cranes with Double-Pendulum Modeling and Control Objective

2.1 System Modeling

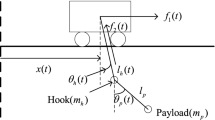
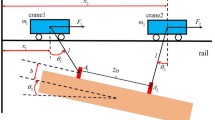
According to Fig. 1, the dynamic model of the crane can be obtained as follows [26, 27].

$$\begin{aligned}&M\left( q \right) \ddot{q} + C\left( {q,\dot{q}} \right) \dot{q} + G\left( q \right) = \varGamma - \varXi \end{aligned}$$
(1)

The specific expressions of M(q), \(C({q,\dot{q}})\), G(q) and \(\varGamma \) can be calculated mathematically as follows:

$$\begin{aligned}&M(q)=\left[ \begin{array}{cccccc} m_{11} &{} m_{12} &{} m_{13} &{} m_{14} &{} m_{15} &{} m_{16} \\ m_{21} &{} m_{22} &{} m_{23} &{} m_{24} &{} m_{25} &{} m_{26} \\ m_{31} &{} m_{32} &{} m_{33} &{} m_{34} &{} m_{35} &{} m_{36} \\ m_{41} &{} m_{42} &{} m_{43} &{} m_{44} &{} m_{45} &{} m_{46} \\ m_{51} &{} m_{52} &{} m_{53} &{} m_{54} &{} m_{55} &{} m_{56} \\ m_{61} &{} m_{62} &{} m_{63} &{} m_{64} &{} m_{65} &{} m_{66} \\ \end{array} \right] , C ({q,\dot{q}})=\left[ \begin{array}{cccccc} c_{11} &{} c_{12} &{} c_{13} &{} c_{14} &{} c_{15} &{} c_{16} \\ c_{21} &{} c_{22} &{} c_{23} &{} c_{24} &{} c_{25} &{} c_{26} \\ c_{31} &{} c_{32} &{} c_{33} &{} c_{34} &{} c_{35} &{} c_{36} \\ c_{41} &{} c_{42} &{} c_{43} &{} c_{44} &{} c_{45} &{} c_{46} \\ c_{51} &{} c_{52} &{} c_{53} &{} c_{54} &{} c_{55} &{} c_{56} \\ c_{61} &{} c_{62} &{} c_{63} &{} c_{64} &{} c_{65} &{} c_{66} \\ \end{array} \right] , \nonumber \\&G(q)=\left[ \begin{array}{cccccc} 0&0&g_3&g_4&g_5&g_6 \end{array} \right] ^T, \varGamma =\left[ \begin{array}{cccccc} {F_x} - {F_{rx}}&{F_y} - {F_{ry}}&0&0&0&0 \end{array} \right] ^T, \nonumber \\&\varXi =\left[ \begin{array}{cccccc} \varXi _1&\varXi _2&\varXi _3&\varXi _4&\varXi _5&\varXi _6 \end{array} \right] ^T, q=\left[ \begin{array}{cccccc} x&y&\theta _{1}&\theta _{2}&\theta _{3}&\theta _{4} \end{array} \right] ^T, \nonumber \\&{m_{11}} = {M_1} + {m_1} + {m_2},{m_{12}} = 0,{m_{13}} = ({m_1} + {m_2}){l_1}{C_1}{C_2},\nonumber \\&{m_{14}} = - ({m_1} + {m_2}){l_1}{S_1}{S_2},{m_{15}} = {m_2}{l_2}{C_3}{C_4},{m_{16}} = - {m_2}{l_2}{S_3}{S_4},\nonumber \\&{m_{21}} = 0,{m_{22}} = {M_2} + {m_1} + {m_2},{m_{23}} = 0,{m_{24}} = ({m_1} + {m_2}){l_1}{C_2},\nonumber \\&{m_{25}} = 0,{m_{26}} = {m_2}{l_2}{C_4},{m_{31}} = ({m_1} + {m_2}){l_1}{C_1}{C_2},{m_{32}} = 0,\nonumber \\&{m_{33}} = ({m_1} + {m_2})l_1^2C_2^2,{m_{34}} = 0,{m_{35}} = {m_2}{l_1}{l_2}{C_{\mathrm{{1 - 3}}}}{C_2}{C_4},\nonumber \\&{m_{3\mathrm{{6}}}} = {m_2}{l_1}{l_2}{S_{\mathrm{{1 - 3}}}}{C_2}{S_4},{m_{41}} = - ({m_1} + {m_2}){l_1}{S_1}{S_2},\nonumber \\&{m_{42}} = ({m_1} + {m_2}){l_1}{C_2},{m_{43}} = 0,{m_{44}} = {m_1}l_1^2 + {m_2}l_2^2,\nonumber \\&{m_{45}} = - {m_2}{l_1}{l_2}{S_{\mathrm{{1 - 3}}}}{S_2}{C_4},\nonumber \\&{m_{46}} = {m_2}{l_1}{l_2}({C_2}{C_4} + {C_1}{C_3}{S_2}{S_4} + {S_1}{S_2}{S_3}{S_4}),\nonumber \\&{m_{51}} = {m_2}{l_2}{C_3}{C_4},{m_{52}} = 0,{m_{53}} = {m_2}{l_1}{l_2}{C_{\mathrm{{1 - 3}}}}{C_2}{C_4},\nonumber \\&{m_{54}} = - {m_2}{l_1}{l_2}{S_{\mathrm{{1 - 3}}}}{S_2}{C_4},{m_{55}} = {m_2}l_2^2C_4^2,{m_{56}} = 0,\nonumber \\&{m_{61}} = - {m_2}{l_2}{S_3}{S_4},{m_{62}} = {m_2}{l_2}{C_4},{m_{63}} = {m_2}{l_1}{l_2}{S_{\mathrm{{1 - 3}}}}{C_2}{S_4},\nonumber \\&{m_{64}} = {m_2}{l_1}{l_2}({C_2}{C_4} + {C_1}{C_3}{S_2}{S_4} + {S_1}{S_2}{S_3}{S_4}),{m_{65}} = 0,{m_{66}} = {m_2}l_2^2 \nonumber \\&{c_{11}} = 0,{c_{12}} = 0,{c_{13}} = - ({m_1} + {m_2}){l_1}({C_2}{S_1}{{\dot{\theta }}_1} + {C_1}{S_2}{{\dot{\theta }}_2}), \nonumber \\&{c_{14}} = - ({m_1} + {m_2}){l_1}({C_1}{S_2}{{\dot{\theta }}_1} + {C_2}{S_1}{{\dot{\theta }}_2}),{c_{15}} = - {m_2}{l_2}({C_4}{S_3}{{\dot{\theta }}_3} + {C_3}{S_4}{{\dot{\theta }}_4}),\nonumber \\&{c_{16}} = - {m_2}{l_2}({C_3}{S_4}{{\dot{\theta }}_3} + {C_4}{S_3}{{\dot{\theta }}_4}),{c_{21}} = 0,{c_{22}} = 0,{c_{23}} = 0,\nonumber \\&{c_{24}} = - ({m_1} + {m_2}){l_1}\sin {\theta _2}{{\dot{\theta }}_2},{c_{25}} = 0,{c_{26}} = - {m_2}{l_2}\sin {\theta _4}{{\dot{\theta }}_4},\nonumber \\&{c_{31}} = 0,{c_{32}} = 0,{c_{33}} = - ({m_1} + {m_2})l_1^2{S_2}{C_2}{{\dot{\theta }}_2},\nonumber \\&{c_{34}} = - ({m_1} + {m_2})l_1^2{S_2}{C_2}{{\dot{\theta }}_1},{c_{35}} = {m_2}{l_1}{l_2}{S_{1 - 3}}({C_2}{C_4}{{\dot{\theta }}_3} + {S_2}{S_4}{{\dot{\theta }}_4}),\nonumber \\&{c_{36}} = - {m_2}{l_1}{l_2}{C_2}({C_1}{C_3}{S_4}{{\dot{\theta }}_3} + {S_1}{S_3}{S_4}{{\dot{\theta }}_3} + {C_1}{C_4}{S_3}{{\dot{\theta }}_4} - {C_3}{C_4}{S_1}{{\dot{\theta }}_4}),\nonumber \\&{c_{41}} = 0,{c_{42}} = 0,{c_{43}} = ({m_1} + {m_2})l_1^2{S_2}{C_2}{{\dot{\theta }}_1},{c_{44}} = 0,\nonumber \\&{c_{45}} = {m_2}{l_1}{l_2}{S_2}({C_1}{C_3}{C_4}{{\dot{\theta }}_3} + {C_4}{S_1}{S_3}{{\dot{\theta }}_3} - {C_1}{S_3}{S_4}{{\dot{\theta }}_4} + {C_3}{S_1}{S_4}{{\dot{\theta }}_4}),\nonumber \\&{c_{46}} = {m_2}{l_1}{l_2}({C_1}{C_3}{C_4}{S_2}{{\dot{\theta }}_4} + {C_4}{S_1}{S_2}{S_3}{{\dot{\theta }}_4} - {C_2}{S_4}{{\dot{\theta }}_4} - {C_1}{S_2}{S_3}{S_4}{{\dot{\theta }}_3}\nonumber \\&+ {C_3}{S_1}{S_2}{S_4}{{\dot{\theta }}_3}),{c_{51}} = 0,{c_{52}} = 0,\nonumber \\&{c_{53}} = - {m_2}{l_1}{l_2}{C_4}({C_2}{C_3}{S_1}{{\dot{\theta }}_1} - {C_1}{C_2}{S_3}{{\dot{\theta }}_1} + {C_1}{C_2}{S_2}{{\dot{\theta }}_2} + {S_1}{S_2}{S_3}{{\dot{\theta }}_2}),\nonumber \\&{c_{54}} = - {m_2}{l_1}{l_2}{C_4}({C_1}{C_3}{S_2}{{\dot{\theta }}_1} + {S_1}{S_2}{S_3}{{\dot{\theta }}_1} - {C_1}{C_2}{S_3}{{\dot{\theta }}_2} + {C_2}{C_3}{S_1}{{\dot{\theta }}_2}),\nonumber \\&{c_{55}} = - {m_2}l_2^2{S_4}{C_4}{{\dot{\theta }}_4},{c_{56}} = - {m_2}l_2^2{S_4}{C_4}{{\dot{\theta }}_3},{c_{61}} = 0,{c_{62}} = 0,\nonumber \\&{c_{63}} = {m_2}{l_1}{l_2}{S_4}({C_1}{C_2}{C_3}{{\dot{\theta }}_1} + {C_2}{S_1}{S_3}{{\dot{\theta }}_1} + {C_1}{C_2}{S_3}{{\dot{\theta }}_2} - {C_3}{S_1}{S_2}{{\dot{\theta }}_2}),\nonumber \\&{c_{64}} = {m_2}{l_1}{l_2}({C_1}{C_2}{C_3}{S_4}{{\dot{\theta }}_2} + {S_1}{S_3}{S_4}{C_2}{{\dot{\theta }}_2} - {C_4}{S_2}{{\dot{\theta }}_2} + {C_1}{S_2}{S_3}{S_4}{{\dot{\theta }}_1}\nonumber \\&- {S_1}{S_2}{S_4}{C_3}{{\dot{\theta }}_1}),{c_{65}} = {m_2}l_2^2{S_4}{C_4}{{\dot{\theta }}_3},{c_{66}} = 0, \nonumber \\&{g_\mathrm{{3}}} = ({m_1} + {m_2})g{l_1}{S_1}{C_2},{g_4} = ({m_1} + {m_2})g{l_1}{C_1}{S_2}, \nonumber \\&{g_5} ={m_2}g{l_2}{S_3}{C_4},{g_6} = {m_2}g{l_2}{C_3}{S_4} \end{aligned}$$
(2)

where \(M_{1}\) represent the mass of the trolley, the result of trolley’s mass plus bridge’ mass is set to \(M_{2}\), \(m_{1}\) represent the mass of hook, the mass of load is set to \(m_{2}\). \(l_{1}\) is the length of cable, \(l_{2}\) is the distance from the hook to the load. \(\theta _{1}\), \(\theta _{2}\) are used to depict the swing of hook, \(\theta _{3}\) and \(\theta _{4}\) are used to depict the swing of load. Besides, for ease of reading, \({S_j}\) is the abbreviation of \(\sin {\theta _j}\) and \({C_j}\) is the abbreviation of \(\cos {\theta _j}\) \((j = 1,2,3,4)\). x and y denote the displacement variables of the trolley along the X-axis and the Y-axis. The force applied to the trolley along the X-axis, is set to \({F_x}\). Then, the force applied to the trolley along the Y-axis, is set to \({F_y}\). \({F_{rx}}\), \({F_{ry}}\) describes the force of friction along the X-axis and the Y-axis, which are defined as follows:

$$\begin{aligned}&{F_{rx}} = {f_{rox}}\tanh \left( {\dot{x}/{\delta _x}} \right) + {\kappa _{rx}}\left| {\dot{x}} \right| \dot{x} \end{aligned}$$
(3)
$$\begin{aligned}&{F_{ry}} = {f_{roy}}\tanh \left( {\dot{y}/{\delta _y}} \right) + {\kappa _{ry}}\left| {\dot{y}} \right| \dot{y} \end{aligned}$$
(4)

where \({f_{rox}}\) , \({f_{roy}}\) , \({{\delta _x}}\) , \({{\delta _y}}\) represent the static friction coefficients, and \({\kappa _{rx}}\) and \({\kappa _{ry}}\) denote the viscous friction coefficients.

From (1), (2), it can be known that \(M\left( q \right) \) is positive definite, and the antisymmetric relation between the \(M\left( q \right) \) and \(C\left( {q,\dot{q}} \right) \) is as follows:

$$\begin{aligned}&{\alpha ^T}\left[ {\frac{1}{2}\dot{M}\left( q \right) - C\left( {q,\dot{q}} \right) } \right] \alpha = 0,\forall \alpha \in {R^6} \end{aligned}$$
(5)

In general, the following assumption is reasonable:

  • In practical application, the swing angle components studied in this paper have the following restrictions:

    $$\begin{aligned}&-\frac{\pi }{2}< \theta _1, \theta _2, \theta _3, \theta _4 < \frac{\pi }{2} \end{aligned}$$
    (6)

2.2 Control Objective

The control objective is that, on the one hand, the trolley can accurately reach the target position along the set trajectory, and on the other hand, it can effectively eliminate the swing angle of the hook and load. It can be elaborated as the following expressions:

$$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } x = {x_r},\mathop {\lim }\limits _{t \rightarrow \infty } y = {y_r},\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _1} = 0,\nonumber \\&\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _2} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _3} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } {\theta _4} = 0 \end{aligned}$$
(7)

where \(x_{r}\), \(y_{r}\) denotes the reference trajectories of trolley. Regarding the reference trajectories \(x_{r}\), \(y_{r}\) corresponding to x and y, the following conditions are generally guaranteed:

$$\begin{aligned}&{x_r},{y_r},{{\dot{x}}_r},{{\dot{y}}_r} \in {L_\infty }\nonumber \\&{x_r}\left( 0 \right) = {x_0},{y_r}\left( 0 \right) = {y_0}\nonumber \\&{{\dot{x}}_r}\left( 0 \right) = 0,{{\dot{y}}_r}\left( 0 \right) = 0\nonumber \\&{{\ddot{x}}_r}\left( 0 \right) = 0,{{\ddot{y}}_r}\left( 0 \right) = 0 \end{aligned}$$
(8)

When \(t \ge {t_s}\), it can be obtained that,

$$\begin{aligned}&{x_r}\left( t \right) = {x_d},{y_r}\left( t \right) = {y_d},\nonumber \\&{{\dot{x}}_r}\left( t \right) = 0,{{\dot{y}}_r}\left( t \right) = 0\nonumber \\&{{\ddot{x}}_r}\left( t \right) = 0,{{\ddot{y}}_r}\left( t \right) = 0 \end{aligned}$$
(9)

where \({x_0}\), \({y_0}\) denote the initial displacement values, \({x_d}\), \({y_d}\) represent the desired positions, \(t_s\) is used to describe the settling time.

3 Controller Design

The energy equation of the crane system studied in this paper is described as follows

$$\begin{aligned}&E = \frac{1}{2}\dot{q}_{}^TM(q)\dot{q} + \left( {{m_1} + {m_2}} \right) g{l_1}(1 - {C_1}{C_2}) + {m_2}g{l_2}(1 - {C_3}{C_4}) \end{aligned}$$
(10)

Combining with Eq. (5), the expression of \(\dot{E}\) can be obtained:

$$\begin{aligned} \dot{E}= & {} {{\dot{q}}^T}M(q)\ddot{q} + \frac{1}{2}{{\dot{q}}^T}\dot{M}(q)\dot{q} + \left( {{m_1} + {m_2}} \right) g{l_1}({S_1}{C_2}{{\dot{\theta }}_1} + {C_1}{S_2}{{\dot{\theta }}_2})\nonumber \\+ & {} {m_2}g{l_2}({S_3}{C_4}{{\dot{\theta }}_3} + {C_3}{S_4}{{\dot{\theta }}_4})\nonumber \\= & {} \left( {{F_x} - {F_{rx}} - {\varXi _1}} \right) \dot{x} + \left( {{F_y} - {F_{ry}} - {\varXi _2}} \right) \dot{y} \nonumber \\- & {} {\varXi _3}{{\dot{\theta }}_1} - {\varXi _4}{{\dot{\theta }}_2} - {\varXi _5}{{\dot{\theta }}_3} - {\varXi _6}{{\dot{\theta }}_4} \end{aligned}$$
(11)

where \({\varXi _1}\), \({\varXi _2}\), \({\varXi _3}\), \({\varXi _4}\) represent air frictions and \({\xi _1}\), \({\xi _2}\), \({\xi _3}\), \({\xi _4}\) denote friction-related parameters.

$$\begin{aligned}&{\varXi _1} = - {\xi _1}\dot{x},{\varXi _2} = - {\xi _2}\dot{y},{\varXi _3} = - {\xi _3}{{\dot{\theta }}_1},\nonumber \\&{\varXi _4} = - {\xi _4}{{\dot{\theta }}_2},{\varXi _5} = - {\xi _5}{{\dot{\theta }}_3},{\varXi _6} = - {\xi _6}{{\dot{\theta }}_4} \end{aligned}$$
(12)

In order to improve the control performance, we built the following new signals by enhancing the coupling between the system state variables, and used them in the subsequent controller analysis and design.

$$\begin{aligned}&{\psi _x} = x + {\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}\end{aligned}$$
(13)
$$\begin{aligned}&{\psi _y} = y + {\kappa _3}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _4}{S_\mathrm{{4}}}\end{aligned}$$
(14)
$$\begin{aligned}&{e_{\psi x}} = {\psi _x} - {x_r} = {e_x} + {\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}\end{aligned}$$
(15)
$$\begin{aligned}&{e_{\psi y}} = {\psi _y} - {y_r} = {e_y} + {\kappa _3}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _4}{S_\mathrm{{4}}} \end{aligned}$$
(16)

where \({\kappa _1}\), \({\kappa _2}\), \({\kappa _3}\) and \({\kappa _4}\) \( \in R\).

Hence, the tracking error vector can be expressed as follows:

$$\begin{aligned} {{\dot{q}}_{e\psi }} = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\dot{e}}_{\psi x}}}&{{{\dot{e}}_{\psi y}}}&{{{\dot{\theta }}_1}} \end{array}}&{{{\dot{\theta }}_2}}&{{{\dot{\theta }}_3}}&{{{\dot{\theta }}_4}} \end{array}} \right] ^T} \end{aligned}$$
(17)

where \({{\dot{e}}_{\psi x}} = \dot{x} + {\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime }} - {{\dot{x}}_r}, {{\dot{e}}_{\psi y}} = \dot{y} + {\left( {{\kappa _3}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _4}{S_\mathrm{{4}}}} \right) ^{\prime }} - {{\dot{y}}_r}\).

Based on the new error vector, the system energy equation can be rewritten as follows:

$$\begin{aligned} {V_{\mathrm{E}\varPsi }} = \frac{1}{2}\dot{q}_{e\psi }^TM{{\dot{q}}_{e\psi }} + \left( {{m_1} + {m_2}} \right) g{l_1}(1 - {C_1}{C_2}) + {m_2}g{l_2}(1 - {C_3}{C_4}) \end{aligned}$$
(18)

Substituting Eq. (2) and Eq. (17) into the derivative of \({V_{\mathrm{E}\varPsi }}\) with respect to time, the following expressions are obtained through mathematical calculation and sorting

$$\begin{aligned} \begin{array}{l} {{\dot{V}}_{\mathrm{E}\varPsi }} = \left[ {{F_x}} \right. - {F_{rx}} - {\varXi _1}\mathrm{{ + }}({M_1} + {m_1} + {m_2}){\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime }} \\ - \left( {{M_1} + {m_1} + {m_2}} \right) \left. {{{\ddot{x}}_r}} \right] {{\dot{e}}_{\psi x}} + \left[ {{F_y}} \right. - {F_{ry}} - {\varXi _2}\mathrm{{ + }}({M_\mathrm{{2}}} + {m_1} + {m_2}) \\ \times {\left( {{\kappa _\mathrm{{3}}}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{4}}}{S_\mathrm{{4}}}} \right) ^{\prime \prime }} - \left. {\left( {{M_2} + {m_1} + {m_2}} \right) {{\ddot{y}}_r}} \right] {{\dot{e}}_{\psi y}} \\ + \left[ { - {\varXi _3}} \right. \mathrm{{ + }}({m_1} + {m_2}){l_1}{C_1}{C_2}{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime }} \\ - \,({m_1} + {m_2}){l_1}{C_1}{C_2}\left. {{{\ddot{x}}_r}} \right] {{\dot{\theta }}_1} \\ + \left[ { - {\varXi _4} - } \right. ({m_1} + {m_2}){l_1}{S_1}{S_2}{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime }}\\ - \,({m_1} + {m_2}){l_1}{C_2}{\left( {{\kappa _\mathrm{{3}}}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{4}}}{S_\mathrm{{4}}}} \right) ^{\prime \prime }} + ({m_1} + {m_2}){l_1}{S_1}{S_2}{{\ddot{x}}_r} \\ \left. { -\, ({m_1} + {m_2}){l_1}{C_2}{{\ddot{y}}_r}} \right] {{\dot{\theta }}_2} + \left[ { - {\varXi _5}} \right. \mathrm{{ + }}{m_2}{l_2}{C_3}{C_4}{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime }}\\ -\, {m_2}{l_2}{C_3}{C_4}\left. {{{\ddot{x}}_r}} \right] {{\dot{\theta }}_3} + \left[ { - {\varXi _6}} \right. - {m_2}{l_2}{S_3}{S_4}{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime }} \\ -\, {m_2}{l_2}{C_4}{\left( {{\kappa _\mathrm{{3}}}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{4}}}{S_\mathrm{{4}}}} \right) ^{\prime \prime }} + {m_2}{l_2}{S_3}{S_4}\left. {{{\ddot{x}}_r} - {m_2}{l_2}{C_4}{{\ddot{y}}_r}} \right] {{\dot{\theta }}_4} \end{array} \end{aligned}$$
(19)

where

$$\begin{aligned} {\varUpsilon _x}= & {} {\left[ {\begin{array}{*{20}{c}} {\tanh \left( {\frac{{\dot{x}}}{{{\delta _x}}}} \right) }&{\left| {\dot{x}} \right| x}&{\begin{array}{*{20}{c}} {\dot{x}}&{\begin{array}{*{20}{c}} {{{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) }^{\prime \prime }}}-{{{\ddot{x}}_r}} \end{array}} \end{array}} \end{array}} \right] ^\mathrm{{T}}}\end{aligned}$$
(20)
$$\begin{aligned} {\varUpsilon _y}= & {} {\left[ {\begin{array}{*{20}{c}} {\tanh \left( {\frac{{\dot{y}}}{{{\delta _y}}}} \right) }&{\left| {\dot{y}} \right| y}&{\begin{array}{*{20}{c}} {\dot{y}}&{\begin{array}{*{20}{c}} {{{\left( {{\kappa _\mathrm{{3}}}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{4}}}{S_\mathrm{{4}}}} \right) }^{\prime \prime }}}-{{{\ddot{y}}_r}} \end{array}} \end{array}} \end{array}} \right] ^\mathrm{{T}}}\end{aligned}$$
(21)
$$\begin{aligned} {\sigma _x}= & {} {\left[ {\begin{array}{*{20}{c}} {{f_{rox}}}&{{\kappa _{rx}}}&{\begin{array}{*{20}{c}} {{\xi _1}}&{\begin{array}{*{20}{c}} {{M_1} + {m_1} + {m_2}} \end{array}} \end{array}} \end{array}} \right] ^\mathrm{{T}}}\end{aligned}$$
(22)
$$\begin{aligned} {\sigma _y}= & {} {\left[ {\begin{array}{*{20}{c}} {{f_{roy}}}&{{\kappa _{ry}}}&{\begin{array}{*{20}{c}} {{\xi _2}}&{\begin{array}{*{20}{c}} {{M_2} + {m_1} + {m_2}} \end{array}} \end{array}} \end{array}} \right] ^\mathrm{{T}}}\end{aligned}$$
(23)
$$\begin{aligned} {\mathrm{H}_1}= & {} -{\xi _3}\dot{\theta }_1^2\mathrm{{ + }}\left[ {({m_1}} \right. + {m_2}){l_1}{C_1}{C_2}{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime } }\nonumber \\- & {} ({m_1} + \left. {{m_2}){l_1}{C_1}{C_2}{{\ddot{x}}_r}} \right] {{\dot{\theta }}_1}\end{aligned}$$
(24)
$$\begin{aligned} {\mathrm{H}_2}= & {} -{\xi _4}\dot{\theta }_2^2 + \left[ { - ({m_1} + {m_2})} \right. {l_1}{S_1}{S_2}{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime } }\nonumber \\- & {} ({m_1} + {m_2}){l_1}{C_2}{\left( {{\kappa _\mathrm{{3}}}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{4}}}{S_\mathrm{{4}}}} \right) ^{\prime \prime } }\nonumber \\+ & {} ({m_1} + {m_2}){l_1}{S_1}{S_2}{{\ddot{x}}_r} - ({m_1} + {m_2})\left. {{l_1}{C_2}{{\ddot{y}}_r}} \right] {{\dot{\theta }}_2}\end{aligned}$$
(25)
$$\begin{aligned} {\mathrm{H}_3}= & {} -{\xi _5}\dot{\theta }_3^2 + \left[ {{m_2}{l_2}{C_3}{C_4}\left. {{{\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) }^{\prime \prime } } - {m_2}{l_2}{C_3}{C_4}{{\ddot{x}}_r}} \right] {{\dot{\theta }}_3}} \right. \end{aligned}$$
(26)
$$\begin{aligned} {\mathrm{H}_4}= & {} -{\xi _6}\dot{\theta }_4^2 + \left[ { - {m_2}{l_2}{S_3}{S_4}} \right. {\left( {{\kappa _\mathrm{{1}}}{S_\mathrm{{1}}}{C_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{2}}}{S_\mathrm{{3}}}{C_\mathrm{{4}}}} \right) ^{\prime \prime } } - {m_2}{l_2}{C_4}{\left( {{\kappa _\mathrm{{3}}}{S_\mathrm{{2}}}\mathrm{{ + }}{\kappa _\mathrm{{4}}}{S_\mathrm{{4}}}} \right) ^{\prime \prime } } \nonumber \\+ & {} {m_2}{l_2}{S_3}{S_4}\left. {{{\ddot{x}}_r} - {m_2}{l_2}{C_4}{{\ddot{y}}_r}} \right] {{\dot{\theta }}_4} \end{aligned}$$
(27)

Inspired by Eq. (19), the following control laws can be constructed:

$$\begin{aligned}&{F_x} = - {k_{px}}{e_{\psi x}} - {k_{dx}}{{\dot{e}}_{\psi x}} + \varUpsilon _x^\mathrm{{T}}{{\hat{\sigma }}_x} \end{aligned}$$
(28)
$$\begin{aligned}&{F_y} = - {k_{py}}{e_{\psi y}} - {k_{dy}}{{\dot{e}}_{\psi y}} + \varUpsilon _y^\mathrm{{T}}{{\hat{\sigma }}_y} \end{aligned}$$
(29)

where \({k_{px}}\), \({k_{py}}\), \({k_{dx}}\), \({k_{dy}}\) are undetermined control parameters, \({{\hat{\sigma }}_x}\), \({{\hat{\sigma }}_y}\) denotes the estimators of \({{\sigma _x}}\), \({{\sigma _y}}\) and the specific expressions are as follows:

$$\begin{aligned}&\hat{\sigma }_x = {\left[ {\begin{array}{*{20}{c}} {{{\hat{f}}_{rox}}}&{{{\hat{\kappa }}_{rx}}}&{\begin{array}{*{20}{c}} {{{\hat{\xi }}_1}}&{\begin{array}{*{20}{c}} {\widehat{{M_1} + {m_1} + {m_2}}} \end{array}} \end{array}} \end{array}} \right] ^\mathrm{{T}}}\end{aligned}$$
(30)
$$\begin{aligned}&\sigma _y = {\left[ {\begin{array}{*{20}{c}} {{{\hat{f}}_{roy}}}&{{{\hat{\kappa }}_{ry}}}&{\begin{array}{*{20}{c}} {{{\hat{\xi }}_2}}&{\begin{array}{*{20}{c}} {\widehat{{M_2} + {m_1} + {m_2}}} \end{array}} \end{array}} \end{array}} \right] ^\mathrm{{T}}} \end{aligned}$$
(31)

Then, the adaptive laws are designed as follows:

$$\begin{aligned}&{{\dot{\hat{\sigma }} }_x} = - {\mathrm{A}^{ - 1}}{\varUpsilon _x}{{\dot{e}}_{\psi x}}, {{\dot{\hat{\sigma }} }_y} = - {\mathrm{B}^{ - 1}}{\varUpsilon _y}{{\dot{e}}_{\psi y}}\end{aligned}$$
(32)
$$\begin{aligned}&\mathrm{A} = diag\left\{ {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}&{\begin{array}{*{20}{c}} {{a_4}} \end{array}} \end{array}} \right\} \in {R^{4 \times 4}}\end{aligned}$$
(33)
$$\begin{aligned}&\mathrm{{B}}= diag\left\{ {\begin{array}{*{20}{c}} {{b_1}}&{{b_2}}&{{b_3}}&{\begin{array}{*{20}{c}} {{b_4}} \end{array}} \end{array}} \right\} \in {R^{4 \times 4}} \end{aligned}$$
(34)

However, in actual application, the velocity signals are not measurable during the crane operation, which is also the weakness of the controller in Eqs. (28), (29). Therefore, we construct auxiliary functions \({\varpi _x}\) and \({\varpi _y}\) containing the velocity signals and introduce it into the controller in Eqs. (28), (29). Whereupon a novel adaptive output feedback control method, which can handle the aforementioned issue, is presented.

$$\begin{aligned}&{F_x} = - {k_{px}}{e_{\psi x}} - {k_{dx}}{\varpi _x} + \varUpsilon _x^\mathrm{{T}}{{\hat{\sigma }}_x} \end{aligned}$$
(35)
$$\begin{aligned}&{F_y} = - {k_{py}}{e_{\psi y}} - {k_{dy}}{\varpi _y} + \varUpsilon _y^\mathrm{{T}}{{\hat{\sigma }}_y} \end{aligned}$$
(36)

where

$$\begin{aligned} {\varpi _x}= & {} {\lambda _x} + {k_{dx}}{e_{\psi x}},{{\dot{\lambda }}_x} = - {k_{dx}}\left( {{\lambda _x} + {k_{dx}}{e_{\psi x}}} \right) \end{aligned}$$
(37)
$$\begin{aligned} {\varpi _y}= & {} {\lambda _y} + {k_{dy}}{e_{\psi y}},{{\dot{\lambda }}_x} = - {k_{dy}}\left( {{\lambda _y} + {k_{dy}}{e_{\psi y}}} \right) \end{aligned}$$
(38)
$$\begin{aligned} {{\dot{\varpi }}_x}= & {} - {k_{dx}}{\varpi _x} + {k_{dx}}{{\dot{e}}_{\psi x}}\end{aligned}$$
(39)
$$\begin{aligned} {{\dot{\varpi }}_y}= & {} - {k_{dy}}{\varpi _y} + {k_{dy}}{{\dot{e}}_{\psi y}} \end{aligned}$$
(40)

4 Results and Discussion

To further conform the superiority of the control strategy, as mentioned in Eqs. (35), (36), in terms of trolley positioning and swing angles reduction, the MATLAB is used for simulation verification and analysis.

4.1 Simulation Conditions

Firstly, the dynamic model given in Eq. (1) is operated by the proposed controller. When selecting these control gains, the first step is to adjust the control gains \({k_{px}},{k_{dx}},{k_{py}},{k_{dy}}\) on the basis of PD controller, and then fine tune the control gains \(\kappa _{1},\kappa _{2}, \mathrm{A}, \mathrm{B}\). After repeated trial and error, the controller gains used in the simulation are selected as follows:

$$\begin{aligned}&k_{px}=8, k_{dx}=6,k_{py}=8, k_{dy}=10\nonumber \\&\kappa _{1}=-0.27, \kappa _{2}=-0.25\nonumber \\ \mathrm{A}= & {} diag\left\{ {\begin{array}{*{20}{c}} {{0.01}}&{{0.01}}&{{0.01}}&{\begin{array}{*{20}{c}} {{0.01}} \end{array}} \end{array}} \right\} \nonumber \\ \mathrm{{B}}= & {} diag\left\{ {\begin{array}{*{20}{c}} {{0.01}}&{{0.01}}&{{0.01}}&{\begin{array}{*{20}{c}} {{0.01}} \end{array}} \end{array}} \right\} \end{aligned}$$
(41)

The target positions of the trolley are set as \({x_{d}} = 0.3\left[ m \right] \), \({y_{d}} = 0.3\left[ m \right] \) \(t_s=3[s]\), and the initial positions \(x_0\), \(y_0\) are set to zero. The physical parameters of the crane model are set as follows: \(M_1=0.5\)[kg], \(M_2=2.5\)[kg], \(m_1=0.5\)[kg], \(m_2=0.5\) [kg], \(l_1=0.4\)[m], \(l_2=0.3\)[m].

4.2 Comparative Simulations

In this subsection, in order to verify the effectiveness of the proposed control strategy, the comparative simulations are carried out.

(1) Sliding mode controller

$$\begin{aligned}&F = {\left( {{P^T}P} \right) ^{ - 1}}{P^T}\left( {R + \ddot{q} - \varLambda \dot{e} - ks - \mu \tanh \left( s \right) } \right) \end{aligned}$$
(42)

with \(s = \dot{e} + \beta \dot{e}\) and \(e = q - {q_d}\) representing the chosen sliding surface and error matrix respectively, where \(q = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} x&y \end{array}}&{{\theta _1}}&{{\theta _2}} \end{array}}&{{\theta _3}}&{{\theta _4}} \end{array}} \right] ^T},{q_d} = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{x_d}}&{{y_d}}&0&0 \end{array}}&0&0 \end{array}} \right] ^T}\). Meanwhile, \(\varLambda \) is a positive gain matrix and k, \(\mu \) are undetermined parameters. After carefully selecting parameters by trial and error, the following values can be obtained: \(\varLambda = diag\left\{ {0.085,0.1,1,1,1,1} \right\} , k = \mu = 5\). P and R are the auxiliary matrix functions in Eq. (43), which are defined as:

$$\begin{aligned} \begin{array}{l} P = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{p_{11}}}&{}{{p_{21}}} \end{array}}&{}{{p_{31}}}&{}{{p_{41}}}&{}{{p_{51}}} \end{array}}&{}{{p_{61}}} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{p_{12}}}&{}{{p_{22}}} \end{array}}&{}{{p_{32}}}&{}{{p_{42}}}&{}{{p_{52}}} \end{array}}&{}{{p_{62}}} \end{array}} \right] ^T}\\ R = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{r_{11}}}&{}{{r_{21}}} \end{array}}&{}{{r_{31}}} \end{array}}&{}{{r_{41}}}&{}{{r_{51}}}&{}{{r_{61}}} \end{array}} \right] ^T} \\ \end{array} \end{aligned}$$
(43)

with

$$\begin{aligned}&{p_{11}} = \frac{1}{{{M_1}}},{p_{21}} = 0,{p_{31}} = - \frac{1}{{{M_2}{l_1}}},{p_{41}} = 0,{p_{51}} = 0,{p_{61}} = 0, \nonumber \\&{p_{12}} = 0,{p_{22}} = \frac{1}{{{M_2}}},{p_{32}} = 0,{p_{42}} = - \frac{1}{{{M_2}{l_1}}},{p_{52}} = 0,{p_{62}} = 0, \nonumber \\&{r_{11}} = \frac{{\left( {{m_1}g{\theta _1} + {m_2}g{\theta _1}} \right) }}{{{M_1}}},{r_{21}} = \frac{{\left( {{m_1}g{\theta _2} + {m_2}g{\theta _2}} \right) }}{{{M_2}}}, \nonumber \\&{r_{31}} = \frac{(M_1+m_1+m_2)m_1g\theta _1+m_1m_2g(\theta _1-\theta _3)}{M_1m_1l_1}, \nonumber \\&{r_{41}} = \frac{(M_2+m_1+m_2)m_1g\theta _2+M_2m_2g(\theta _2-\theta _4)}{M_2m_1l_1}, \nonumber \\&{r_{51}} = \frac{{\left( {{m_1} + {m_2}} \right) g\left( {{\theta _1} - {\theta _3}} \right) }}{{{m_1}{l_2}}}, \nonumber \\&{r_{61}} = \frac{{\left( {{m_1} + {m_2}} \right) g\left( {{\theta _2} - {\theta _4}} \right) }}{{{m_1}{l_2}}} \end{aligned}$$
(44)

(2) LQR controller

$$\begin{aligned}&{F_x} = - {k_{px}}{e_x} - {k_{dx}}\dot{x} - {k_1}{\theta _1} - {k_2}{\theta _3} - {k_3}{{\dot{\theta }}_1} - {k_4}{{\dot{\theta }}_3} + {F_{rx}},\nonumber \\&{F_y} = - {k_{py}}{e_y} - {k_{dy}}\dot{y} - {k_5}{\theta _2} - {k_6}{\theta _4} - {k_7}{{\dot{\theta }}_2} - {k_8}{{\dot{\theta }}_4} + {F_{ry}}, \end{aligned}$$
(45)

with \(k_{px}\), \(k_{py}\), \(k_{dx}\), \(k_{dy}\), \(k_a\), \(k_b\), \(k_c\), \(k_d\), \(k_e\), \(k_f\), \(k_g\), \(k_h\) \( \in R\) denote control gains, which are calculated \(k_{px}= 11.3137 \), \(k_{py}=11.3137 \), \(k_{dx}=18.5403\), \(k_{dy}=22.9924\), \(k_{a}=-76.0345 \), \(k_{b}= -15.2300 \), \(k_{c}=40.6143 \), \(k_{d}-0.1772\), \(k_{e}=-44.4926\), \(k_{f}=-17.7791 \), \(k_{g}= 21.5435\) and \(k_{h}=1.2262\).

In order to intuitively demonstrate the superiority of the proposed controller in trolley tracking and positioning and restraining the load swing angles, the simulation results of actuated state components x, y, underactuated state components \(\theta _1\), \(\theta _2\), \(\theta _3\), \(\theta _4\), and input force \(F_{x}\), \(F_{y}\), when the three controllers act on the crane are all reflected in Fig. 2. The sub-figure in the first row of Fig. 2 describes the tracking and positioning performance of the trolley. Through comparative analysis, the conclusion can be drawn that the proposed controller can drive the trolley to reach the set position significantly faster than the other two control methods. The second and third rows of Fig. 2 display the simulation results of the swing angles of the crane during operation. Under the control of the proposed control strategy, when the trolley reaches the target position, the swing angles are also suppressed to 0. Although the swing angles can also be eliminated by the other two controllers, they takes longer time because of their longer positioning time. In addition, when adopting the proposed controller, the amplitude of the load swing angles are smaller than that of the other two controllers. In conclusion, the proposed control strategy achieves better performance than the other two control methods in terms of trolley positioning, swing angles elimination.

4.3 Robust Performance

In order to verify the robustness of the proposed controller, we carried out the following three sets of simulation to reflect the control performance under the perturbation of the system model parameters and the non-zero initial swing angle. Meanwhile, The control parameters in the following sets of simulations are all the same values in Eq. (42). For easy analysis, the parameter changes are placed together with the original image In order to facilitate the analysis, the figure with the changed parameters and the original picture are plotted together.

In the first set of simulation, we obtained the simulation results presented in Fig. 3 by changing the load mass from 0.5 [kg] to 1 [kg], 1.5 [kg]. It can be the control performance of the proposed controller is basically the same. Next, we changed the rope length \(l_2\) to 0.2[m], 0.4[m] and got the conclusion that different \(l_2\) can not impose the influence on control performance. The results reveal that the control method has strong robustness to the changes of crane model parameters.

Finally, non-zero initial value of double-pendulum load sway angles, which were set as \(\theta _1(0)=-4.6[\deg ]\), \(\theta _2(0)=-4.6[\deg ]\), \(\theta _3(0)=-4.6[\deg ]\), and \(\theta _4(0)=-4.6[\deg ]\), were also considered in this study. It can be seen intuitively from Fig. 5 that the controller can still maintain an excellent control effect which is shown in the positioning time of the trolley and the elimination effect of the swing angles are basically unchanged when existing non-zero initial swing angle.

Fig. 1.
figure 1

Three-dimensional overhead cranes with double-pendulum effect model

Full size image
Fig. 2.
figure 2

Comparative simulation results

Full size image
Fig. 3.
figure 3

Simulation results with different load mass

Full size image
Fig. 4.
figure 4

Simulation results with different rope length

Full size image
Fig. 5.
figure 5

Simulation results with non-zero initial hook and load sway angles

Full size image

5 Conclusion

Aiming at the complex dynamics model of the three-dimensional double pendulum overhead crane, an improved adaptive tracking controller is derived. By constructing new signals to increase the coupling relationship of the state vector, all the controlled state vectors are included in the controller. In addition, auxiliary functions are designed to handle the issue that the velocity signals cannot be measured. A series of simulation results intuitively confirmed the feasibility and robustness of the proposed controller.