Rate-Induced Tipping Phenomena in Compartment Models of Epidemics

Abstract

The aim of this chapter is to explore non-autonomous compartment models of epidemics, like, e.g., SIR models with time-dependent transmission and recovery rates as parameters, and particularly the occurrence of rate-induced tipping phenomena. Specifically, we are interested in the question, whether there can exist parameter paths that do not cross any bifurcation points, but yet give rise to tipping if the parameters vary over time. From literature, it is known that such rate-induced tipping occurs, e.g., in two-dimensional models of ecosystems or predator–prey systems. We show in this chapter that rate-induced tipping can also occur in compartment models of epidemics. Thus, regarding the Covid-19 crisis, not only the measures established in a lockdown and the moment of the lockdown, but also the rate by which lockdown measures are implemented may have a drastic influence on the number of infectious.

1 Introduction

Why do we see during the Covid-19 crisis in some states a very high relative number of infectious, while in other states the relative number of infectious is significantly lower, although the measures established by states in a lockdown are comparable? Maybe, this does not only depend on the moment in time at which a lockdown is decided, but also on the rate by which lockdown measures are implemented. In this chapter, we show that corresponding rate-induced tipping phenomena can occur in compartment models of epidemics with time-dependent parameters.

The foundations of compartment models of epidemics, which divide the population into compartments and assume a certain form of the time rates for transfer from one compartment to another, were laid by Ross (Nobel Prize in Medicine 1902) [13,14,15], McKendrick and Kermack [10,11,12] prior to 1935. Usually, spatial dependence is neglected in compartment models, and instead a homogeneous mixing of the population is assumed. Thus, mathematically a compartment model of an epidemic is usually given by a system of ordinary differential equations (ODEs) for continuous time, or by a system of finite difference equations for discrete time, or by a system of delay differential equations (DDEs) if, e.g., the period of temporary immunity is modeled, but not by a system of partial differential equations (PDEs) involving spatial derivatives. Therefore, autonomous compartment models for epidemics are not suitable for describing the beginning of a disease outbreak, because at the beginning the assumption of a homogeneous mixing of the population is invalid. Instead, models viewing the social network as a graph may be used. However, this graph is usually not known, and if it is considered as random, then compartment models and network models are related; see, e.g., [3, Sect. 9.4], [5, Sect. IV.B]. Particularly, this problem can be circumvented by using a time-dependent transmission rate, which at the beginning is significantly reduced in comparison with the transmission rate of the disease in a homogeneously mixed population.

The aim of using compartment models in epidemiology [2, 3] is to better understand the underlying mechanisms of the spread of a disease and to obtain during the mathematical analysis of the model threshold values [1]. A threshold for a parameter in a model is a value, where the system shows a different behavior below the threshold than above the threshold. Most mathematical epidemic models exhibit threshold behavior, e.g., for $R_0 < 1$ the disease will die out, while for $R_0 > 1$ there will be an epidemic. This behavior is consistent with observations and has been used, e.g., to estimate the effectiveness of vaccination policies and the likelihood that a disease may be eliminated or eradicated.

However, when calculating threshold values, one has to be very precise. One source of confusion is the interpretation of parameters. For example in a stochastic model, the basic reproduction number is defined as the expected number of infections caused by one infectious in a population where all individuals are susceptible to infection. However, if in a compartment model “the basic reproduction number is calculated by the Jacobian method,” i.e., by linearizing the system about the state where all individuals are susceptible, and by writing the condition that this state is linearly unstable in the form $R_0 > 1$, then the so defined parameter $R_0$ may not be identical with the basic reproduction number, i.e., with the expected number of infections caused by one infectious, but just allows to test linear stability of the state where all individuals are susceptible. Thus, in general, it would be wrong to say that this parameter denoted by $R_0$ “is” the basic reproduction number. Yet, it resembles the basic reproduction number, as it allows to answer the question, whether the disease will become endemic or die out. Further, in reality, parts of the population may be immune to a disease. The basic reproduction number does not say anything about such a state of the population, but instead the effective reproduction number should be used, which is defined as expected number of new infections caused by one infectious in the actual state of the population.

Another source of confusion may be the interpretation what is meant by “different behavior” of a system below and above a threshold. The dynamics of an autonomous system below and above a threshold value are usually considered to be different, if they are not topologically equivalent, i.e., if crossing the threshold results in a (local or global) bifurcation of the system. Yet, for non-autonomous systems [4], particularly SIR models with time-dependent parameters studied, e.g., in [5], it is not so clear how to define different behavior, because if we start from the same initial value but at different times, then of course we usually obtain different solution curves. Remarkably, the dynamics in systems with time-dependent parameters may not only change drastically due to a bifurcation, but also due to other tipping phenomena. Particularly, transient resp. irreversible rate-induced tipping may occur, where the system fails to track a continuously changing quasi-static attractor uniformly resp. up to the end point due to a fast rate of change of parameters.

The focus of this chapter lies on such rate-dependent tipping phenomena in compartment models of epidemics with continuous time. From literature, it is known that rate-induced tipping occurs generically, e.g., in climate models [16], in two-dimensional models of ecosystems [7], in predator–prey systems [8] or in chaotic systems [6]. We show that irreducible rate-induced tipping can also occur in idealized compartment models of epidemics with $R_0>1$, where due to the slow dynamics near the stable endemic equilibrium (EE), the state may fail to track the EE for a fast parameter change and may leave its basin of attraction bounded by a homoclinic orbit resp. by the stable manifold connecting the boundary to the disease-free equilibrium (DFE), resulting in an eradication of the disease, while else the disease becomes endemic. Further, we show that artifacts of this tipping phenomenon can also be observed in non-idealized models.

1.1 Outline

In Sect. 2, we introduce basic facts about compartment models with continuous time and time-dependent parameters. Further, we derive basic properties of the classical SIR and SIRS models. In Sect. 3, we discuss linear compartment models of epidemics and particularly in the time-dependent case phenomena related to tipping. In Sect. 4, we turn to nonlinear compartment models of epidemics and discuss a typical bifurcation of compartment models at the DFE. By center manifold reduction, we obtain an idealized planar system, which governs the dynamics and shows irreducible rate-induced tipping. Finally, in Sect. 5, we study tipping phenomena in nonlinear compartment models of epidemics.

2 Preliminaries

Throughout this chapter, we consider compartment models with continuous time, and we normalize systems so that each state variable models the percentage of the whole population in the corresponding compartment.

2.1 Compartment Models with Time-Dependent Parameters

Definition 1

A compartment model with $n+1$ compartments is a semi-process on the n-dimensional probability simplex $\Sigma ^n := \{x \in \mathbb {R}^{n+1} \,|\, x \ge 0\,,\, 1^Tx = 1 \} \subset \mathbb {R}^{n+1}$, i.e., a family of continuous maps $\Phi ^{t,s}:\Sigma ^n \rightarrow \Sigma ^n$, $s \le t$, such that $\Phi ^{t,t} = {\text {Id}}_{\Sigma ^n}$ for all $t \in \mathbb {R}$ and the cocycle condition $\Phi ^{t,r} = \Phi ^{t,s} \circ \Phi ^{s,r}$ holds for all $r \le s \le t$, and which is generated by an ODE $\dot{x}(t) = f(t,x(t))$ in the sense that $\Phi ^{t,s}(x)$ is identical with the value x(t) of the unique ODE solution to the initial value $x \in \Sigma ^n$ at time s.

An ODE $\dot{x}(t) = f(t,x(t))$ with a time-dependent vector field $f:\mathbb {R} \times \mathbb {R}^{n+1} \rightarrow \mathbb {R}^{n+1}$ generates such a semi-process $\Phi$ on $\Sigma ^n$, if the probability simplex $\Sigma ^n$ is positively invariant, and this is the case iff

• (A1) $f_i(t,x) \ge 0$ holds for every $x \ge 0$ with $1^Tx = 1$ and $x_i = 0$, and every $t \in \mathbb {R}$,

• (A2) $1^Tf(t,x) = 0$ holds for every $x \in \Sigma ^n$ and every $t \in \mathbb {R}$.

Under these conditions, global existence of solutions forward in time to initial values in $\Sigma ^n$ holds for a continuous f due to compactness of $\Sigma ^n$. Additionally, in compartment models of epidemics, we require that $(1,0,\dots ,0)$ is for all times an equilibrium, i.e.,

• (A3) $f_i(t,(1,0,\dots ,0)) = 0$ holds for every $t \in \mathbb {R}$,

We call this equilibrium disease-free equilibrium (DFE) and correspondingly consider the first component of $x \in \Sigma ^n$ as percentage of susceptibles in the population. Due to $1^Tx=1$, every compartment model can be reduced by one dimension to an n-dimensional ODE $\dot{\hat{x}} = \hat{f}(t,\hat{x})$ on the image $\hat{\Sigma }^n := \{\hat{x} \in \mathbb {R}^{n} \,|\, \hat{x} \ge 0\,,\, 1^T\hat{x} \le 1\}$ of the diffeomorphism from $\Sigma ^n$ onto $\hat{\Sigma }^n$ given by $x=(x_1,\dots ,x_n,x_{n+1}) \mapsto (x_1,\dots ,x_n)=\hat{x}$ with inverse $\hat{x} \mapsto (\hat{x},1-1^T\hat{x}) = x$, i.e., by eliminating $x_{n+1} = 1 - \sum _{i=1}^n x_i$ from the ODE. The assumptions (A1)-(A3) then translate into

• (A1)’ $\hat{f}_i(t,\hat{x}) \ge 0$ holds for every $\hat{x} \ge 0$ with $1^T\hat{x} < 1$ and $\hat{x}_i = 0$ and every $t \in \mathbb {R}$,

• (A2)’ $\sum _{i=1}^n \hat{f}_i(t,\hat{x}) \le 0$ holds for every $\hat{x} \ge 0$ with $1^T\hat{x} = 1$, and every $t \in \mathbb {R}$,

• (A3)’ $\hat{f}_i(t,(1,0,\dots ,0)) = 0$ holds for every $t \in \mathbb {R}$.

The longtime behavior of a semi-process $\Phi$ on $\Sigma ^n$ is governed by its global pullback attractor, i.e., by the time-dependent family of non-empty compact sets

$$\begin{aligned} A(t) := \bigcap _{s \le t} \overline{\bigcup _{r \le s} \Phi ^{t,r}(D)} \,, \end{aligned}$$

(1)

with $D:=\Sigma ^n$ chosen to be the whole state space. Note that A(t) consists of all values of solutions at time t originating from D for times $s \rightarrow -\infty$, i.e., A(t) is a kind of non-autonomous $\omega$-limit set of orbits originating from D. The global pullback attractor is the minimal closed set which attracts all subsets $B \subset \Sigma ^n$ at time $-\infty$, i.e., ${\lim_{_{_{\!\!\!\!\!\!\!\!\!\! s \rightarrow -\infty }}}} {\text {dist}}(\Phi ^{t,s}(B),A(t)) = 0$ holds for every subset $B \subset \Sigma ^n$, and it is invariant, i.e., $\Phi ^{t,s}A(s) = A(t)$ holds for all $s \le t$. In the autonomous case, where $\Phi ^{t,s} = \Phi ^{t-s}$ is a continuous dynamical system on $\Sigma ^n$ and the vector field f in the generating ODE $\dot{x}(t) = f(x(t))$ does not depend on time, the global pullback attractor does not depend on time, i.e., $A(t) = A$ is a constant set, and A is identical with the global attractor of the autonomous dynamical system on $\Sigma ^n$.

If D in (1) is not chosen as the whole space $\Sigma ^n$ but replaced by a locally pullback absorbing family of time-dependent sets D(r), i.e., there exists a sufficiently small distance $\varepsilon >0$ and a sufficiently large time $T>0$ such that $\Phi ^{t,r}(B_{\varepsilon }(D(r))) \subset D(t)$ holds for all (t, r) with $t \ge r+T$, where $B_{\varepsilon }(D) := \{x \in \Sigma ^n\,|\, {\text {dist}}(x,D)<\varepsilon \}$ denotes the $\varepsilon$-neighborhood of $D \subset \Sigma ^n$, then A(t) is called the local pullback attractor of the absorbing family D(t). Given a local pullback attractor A(t), the largest locally pullback absorbing family D(t) of time-dependent sets is such that $A(t) \subset D(t)$ is called its time-dependent basin of attraction.

In this chapter, we are particularly interested in compartment models

$$\begin{aligned} \dot{x}(t) = f(x(t),\lambda (t)) \end{aligned}$$

(2)

which are non-autonomous due to time dependence of parameters. Hereby, we assume that the system is driven, i.e., that we can write the system in skew-product form

$$\begin{aligned} \begin{aligned} \dot{x}(t) =&f(x(t),\lambda (t)) \\ \dot{\lambda }(t) =&r g(\lambda (t)) \end{aligned} \end{aligned}$$

(3)

with parameter path induced by a vector field $g(\lambda )$ in parameter space for a fixed rate $r \ge 0$. Often, we assume that $\lambda (t)$ approaches constant values $\lambda _{\pm }$ for times $t \rightarrow \pm \infty$ with a flat derivative, i.e., $\lambda (t)$ is a heteroclinic orbit in parameter space connecting $\lambda _{\pm }$ and satisfies $\dot{\lambda }(t) \rightarrow 0$ as $t \rightarrow \pm \infty$ due to $g(\lambda _{\pm })=0$. We are mainly interested in the dependence of x on the rate r. Note that the derivative of x(t) w.r.t. r is given by the solution y of

$$\begin{aligned} \begin{aligned} \dot{y}(t) =&\frac{\partial f}{\partial x} (x(t),\lambda (t)) y(t) + \frac{\partial f}{\partial \lambda }(x(t),\lambda (t)) \kappa (t) \\ \dot{\kappa }(t) =&rg'(\lambda (t)) \kappa (t) + g(\lambda (t)) \end{aligned} \end{aligned}$$

(4)

to the initial values $y(s)=0$ and $\kappa (s)=0$, where $\kappa = \frac{\partial \lambda }{\partial r}$. This equation can be used to obtain information about the dependence of x on the rate, e.g., if $y(t) = \frac{\partial x}{\partial r}(t) \rightarrow 0$ for $t \rightarrow \infty$, then a change of the rate does not lead to a different longtime behavior of the solution.

Fig. 1

On the left, the solution (8) of Eq. (7) with rate $r=1$ to the initial value $x(-10)=0.1$ is shown. In the middle, the derivative of this solution w.r.t. the rate is plotted, obtained by solving (4) for y. Observe that the rate mainly has an influence on the behavior of the solution shortly after the bifurcation at $t=0$. Particularly, the rate does not have any influence on the long time behavior. This can also be seen by comparing the left picture to the right picture, which shows the solution of Eq. (7) with rate $r=0.1$ to the same initial value $x(-10)=0.1$

Example 1

For $g(\lambda ) := -(\lambda -\lambda _-)(\lambda -\lambda _+)$ with $\lambda _{\pm } = \pm 1$, i.e., $g(\lambda ) = 1 - \lambda ^2$, the parameter path is given by

$$\begin{aligned} \lambda (t) = \tanh (rt) \end{aligned}$$

(5)

due to $\tanh ' = 1 - \tanh ^2$. In this case, the second equation $\dot{\kappa }(t) = -2 \lambda (t) r \kappa + 1 - \lambda (t)^2$ in (4) has for the rate $r=1$ and the initial value $\kappa (-10)=0$ the exact solution

$$\begin{aligned} \kappa (t) = (t+10){\text {sech}}^2(t) \,. \end{aligned}$$

(6)

Let us consider as one-dimensional example the parameter-dependent autonomous vector field $f(x,\lambda ):=-x(x^2+\lambda )$, i.e., a pitchfork. Depending on $\lambda$ being positive resp. negative, $x=0$ is the only equilibrium resp. there are additionally the two equilibria $x_{\pm } := \pm \sqrt{-\lambda }$. If $\lambda <0$, then $x=0$ is unstable and $x_{\pm }$ are asymptotically stable, while if $\lambda >0$, then $x=0$ is asymptotically stable. Now our parameter path $\lambda (t) = \tanh (rt)$ runs at $t=0$ through the bifurcation point $\lambda =0$, thus eventually the solution of

$$\begin{aligned} x'(t) = -x(t)(x(t)^2 + \tanh (rt)) \end{aligned}$$

(7)

to the initial value $x(-10)=0.1$ first tends to $x_+ \approx 1$, but at time $t=0$ the bifurcation happens and merely the asymptotically stable equilibrium $x=0$ survives. As (7) is a Bernoulli ODE, we can calculate the exact solution, which is given for the rate $r=1$ by

$$\begin{aligned} x(t) = \left( \cosh (t)(2\sinh (t)+C\cosh (t))\right) ^{-1/2} \end{aligned}$$

(8)

with $C = \frac{100}{\cosh ^2(-10)} - 2\tanh (-10) \approx 2 + 8.162 \cdot 10^{-7}$ put this solution x(t), the parameter path $\lambda (t)$ from (5) and the function $\kappa (t)$ from (6) into the first equation of (4) and solve this linear inhomogeneous ODE to the initial value $y(-10)=0$ to obtain as solution $y(t) = \frac{\partial x}{\partial r}(t)$ the derivative of the solution x(t) w.r.t. r, without explicitly solving (7) for other rates than $r=1$, see Fig. 1.

The sudden qualitative change of the state in Example 1 is mainly due to the bifurcation point $\lambda =0$ of the autonomous system. To fix notation, if in (2) the parameter $\lambda (t)=\lambda$ is constant (or $r=0$ in (3)), then we call

$$\begin{aligned} \dot{x}(t) = f(x(t),\lambda ) \end{aligned}$$

(9)

the autonomous frozen ODE. In such a parameter-dependent autonomous ODE, a sudden qualitative change of the behavior of the system at a threshold $\lambda _0$ can only occur due to a bifurcation. In fact, by definition, a bifurcation is said to occur at the parameter $\lambda _0$, if there are arbitrarily close parameters for which the generated dynamics are not topologically equivalent. The solution x(t) of (9) to a fixed initial value $x(s)=x_0$ depends differentiably on the parameter $\lambda$, and moreover the derivative $\frac{\partial x}{\partial \lambda }$ of x w.r.t. $\lambda$ solves

$$\begin{aligned} y' = \frac{\partial f}{\partial x}(x(t),\lambda _0)y + \frac{\partial f}{\partial \lambda }(x(t),\lambda _0) \end{aligned}$$

(10)

to the initial value $y(s)=0$. Compare Eq. (10) in the autonomous case with the corresponding first equation of (4) in the non-autonomous case to note that time dependence of parameters has a strong influence, if $\frac{\partial f}{\partial \lambda }$ is large. While for autonomous systems, a sudden qualitative change is related to a bifurcation, and for non-autonomous systems there are other sources of a sudden qualitative change. Particularly, rate-induced tipping may happen, where the system fails to track a continuously changing quasi-static attractor due to a fast rate of change of parameters.

Definition 2

For a non-autonomous ODE (2), a local attractor $A(\lambda )$ of the corresponding autonomous ODE (9) at parameter $\lambda$ is called a local quasi-static attractor.

Let us assume that along $\lambda (t)$ there is no bifurcation, so that $A(\lambda _-)$ has a unique continuation $A(\lambda (t))$ for all times t. If the rate $r>0$ is sufficiently small, then the local pullback attractor A(t) originating form $A(\lambda _-)$ uniformly tracks $A(\lambda (t))$, i.e., $\sup _{t \in \mathbb {R}} {\text {dist}}(A(t),A(\lambda (t)))$ is continuous w.r.t. to the rate r on which $\lambda (t)$ depends for small $r>0$, and ${\text {dist}}(A(t),A(\lambda (t)))$ tends to 0 as $t \rightarrow \pm \infty$. This property was obtained in [9] and allows to define rate-induced tipping. We use the following definition.

Definition 3

Under the assumption that along the path $\lambda (t)$ there is no bifurcation of the local quasi-static attractor $A(\lambda (t))$, we say that at points of discontinuity of $r \mapsto \sup _{t \in \mathbb {R}} {\text {dist}}(A(t),A(\lambda (rt)))$ the system (2) has

• 1. transient rate-induced tipping, if ${\lim_{_{_{\!\!\!\!\!\!\!\! t \rightarrow \infty }}}} {\text {dist}}(A(t),A(\lambda (rt))) = 0$,

• 2. irreducible rate-induced tipping, if ${\lim_{_{_{\!\!\!\!\!\!\!\! t \rightarrow \infty }}}} {\text {dist}}(A(t),A(\lambda (rt))) > 0$.

In case of irreducible rate-induced tipping, the local pullback attractor A(t) may tend for $t \rightarrow \infty$ to a local attractor at $\lambda _+$ different from $A(\lambda _+)$, while in case of transient rate-induced tipping A(t) tends for $t \rightarrow \infty$ to $A(\lambda _+)$, but in between A(t) approached another local attractor of the autonomous system. Rate-induced tipping is intimately related to basin instability; see [7, Definition 5.1]. Particularly, for equilibria the following definition makes sense.

Definition 4

Suppose $A(\lambda )$ is a stable equilibrium of the autonomous frozen ODE (9) for every $\lambda$ on the chosen parameter path $\lambda (t)$, and let $B(A(\lambda ))$ denote the basin of attraction of $A(\lambda )$. Then $A(\lambda )$ is said to be basin unstable on the parameter path, if there are two $\lambda _1,\lambda _2$ on the parameter path such that $A(\lambda _1)$ is outside the closure of the basin of attraction of $A(\lambda _2)$, i.e., $A(\lambda _1) \not \in \overline{B(A(\lambda ))}$.

The main result about basin instability is that it implies the existence of a parameter path along which rate-induced tipping happens.

Theorem 1

([7]) If a stable equilibrium $A(\lambda )$ of the autonomous frozen ODE (9) is basin unstable for all $\lambda$ on the parameter path, then there is a time-varying external input $\lambda (t)$ of sufficiently fast rate that traces out the path and gives irreversible rate-induced tipping from $A(\lambda (t))$ in the non-autonomous system.

Thus briefly, if the system is in a state where the dynamics is slow, but the actual parameter change is fast, then it may happen that the state may leave the basin of attraction of the continuation $A(\lambda (t))$ of the attractor $A(\lambda _-)$ and the local pullback attractor A(t) tends to a different local attractor of the system.

Our main goal is to describe a mechanism how this kind of basin instability and the corresponding rate-induced tipping can happen in compartment models of epidemics. The difficulty hereby is that usually the endemic equilibrium (EE) is globally asymptotic stable, and then there is no way how basin instability can happen. Therefore, we consider idealized systems which has at least two different basins of attraction and argue that even in systems which do not have this idealized property, artifacts of rate-induced tipping can be seen. But first let us introduce basic compartment models of epidemics.

2.2 Autonomous SIR Model

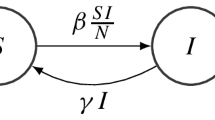
The classical autonomous SIR model of McKendrick and Kermack [10,11,12] reads in full form as

$$\begin{aligned} \begin{aligned} S'&= -\beta SI \\ I'&= \beta SI - \alpha I \\ R'&= \alpha I \end{aligned} \end{aligned}$$

(11)

with constant transmission rate $\beta >0$ and recovery rate $\alpha >0$, or in reduced form as

$$\begin{aligned} \begin{aligned} S'&= -\beta SI \\ I'&= (\beta S - \alpha ) I \end{aligned} \end{aligned}$$

(12)

with $R:= 1 - S - I$. This system has a whole line segment $\{(S,0) \,|\, 0 \le S \le 1\}$ of equilibrium points bounded to the right by the disease-free equilibrium (DFE) $(S,I) = (1,0)$, and the parameter $R_0 := \frac{\beta }{\alpha }$ resembles the basic reproduction number: The Jacobian of the reduced model is

$$\begin{aligned} D\hat{f}(S,I) = \begin{pmatrix} -\beta I &{} -\beta S \\ \beta I &{} \beta S - \alpha \end{pmatrix} \,, \end{aligned}$$

(13)

and therefore the linearization at the DFE

$$\begin{aligned} D\hat{f}(1,0) = \begin{pmatrix} 0 &{} -\beta \\ 0 &{} \beta - \alpha \end{pmatrix} \end{aligned}$$

(14)

has eigenvalues $\lambda = 0$ and $\lambda = \beta - \alpha$. Thus, linear instability holds if $R_0 := \frac{\beta }{\alpha } > 1$, but due to the degenerated eigenvalue $\lambda =0$, which corresponds to the whole line segment of equilibria, even in the case $R_0<1$ we do not have local attractivity but just stability of the disease-free equilibrium $(S,I)=(1,0)$. Nonetheless, in the case $R_0<1$, the system tends for every initial state $(S_0,I_0)$ with $I_0>0$ to the disease-free equilibrium $(S,I)=(1,0)$, i.e., the DFE attracts all states (S, I) with $I>0$ and the disease dies out.

In the case $R_0 > 1$, solutions have a maximum number of infectious where $I'=0$, i.e., at $S = \frac{\alpha }{\beta } = \frac{1}{R_0}$. Afterward the number of infectious decreases and tends for $t \rightarrow +\infty$ to an equilibrium with $S_\infty < 1$ and $I_\infty =0$, i.e., the disease becomes epidemic. Let us calculate the value $S_\infty$: By integration over $t \in [0,\infty )$ on the one hand $(S+I)' = - \alpha I$ implies $S_{\infty } - (S_0 + I_0) = - \alpha \int _0^\infty I(t) \,dt$, and on the other hand $S'/S = -\beta I$ implies $\ln (S_\infty /S_0) = - \beta \int _0^\infty I(t) \,dt$. Thus, $S_{\infty } - (S_0 + I_0) = \frac{\alpha }{\beta } \ln (S_\infty /S_0)$ holds and allows to calculate $S_\infty$. Under the assumption that at the beginning, there are no recovered, we have to solve $S_{\infty } - 1 = \frac{\alpha }{\beta } \ln (S_\infty /S_0)$, and with the product log function W(x), which solves $x = w\mathrm {e}^w$ for w, the solution can be written as $S_{\infty } = - \frac{\alpha }{\beta } W(- S_0 \frac{\beta }{\alpha }\mathrm {e}^{-\frac{\beta }{\alpha }})$.

2.3 Autonomous SIRS Model

Instead of a more appropriate DDE taking into account the period of temporary immunity, we consider in this subsection as model with temporary immunity the SIRS model given by

$$\begin{aligned} \begin{aligned} S'&= -\beta SI + \gamma R \\ I'&= \beta SI - \alpha I \\ R'&= \alpha I - \gamma R \end{aligned} \end{aligned}$$

(15)

with an additional rate $\gamma >0$ of loss of immunity. The reduced model

$$\begin{aligned} \begin{aligned} S'&= -\beta SI + \gamma (1-S-I)\\ I'&= (\beta S - \alpha ) I \end{aligned} \end{aligned}$$

(16)

has the disease-free equilibrium (DFE) $(S,I) = (1,0)$, and for $\alpha < \beta$ additionally the endemic equilibrium (EE) $(S,I) = (\frac{\alpha }{\beta },\frac{\gamma }{\alpha +\gamma }(1 - \frac{\alpha }{\beta }))$.

Particularly, for $\gamma \searrow 0$, we obtain $(S,I) = (\frac{\alpha }{\beta },0)$ as limit of the endemic equilibrium, i.e., a distinguished point on the line segment of equilibria of the autonomous SIR model. Thus, if the SIR model is considered as limit of the SIRS model with vanishing $\gamma$, then for $R_0>1$ the unique equilibrium with $S_\infty := \frac{\alpha }{\beta }$ on the whole line segment of equilibria should be considered as epidemic equilibrium in the SIR model. Again the parameter $R_0 := \frac{\beta }{\alpha }$ resembles the basic reproduction number: The Jacobian of the reduced model is

$$\begin{aligned} D\hat{f}(S,I) = \begin{pmatrix} -(\beta I +\gamma ) &{} -(\beta S + \gamma ) \\ \beta I &{} \beta S - \alpha \end{pmatrix} \,, \end{aligned}$$

(17)

and we obtain that the linearization at the DFE

$$\begin{aligned} D\hat{f}(1,0) = \begin{pmatrix} -\gamma &{} -\beta -\gamma \\ 0 &{} \beta - \alpha \end{pmatrix} \end{aligned}$$

(18)

has the eigenvalues $\lambda = -\gamma$ and $\lambda = \beta - \alpha$. Thus, the DFE is asymptotically stable if $R_0 := \frac{\beta }{\alpha } < 1$ and unstable if $R_0 > 1$. In the case $R_0 > 1$, the eigenvector $(-(\beta +\gamma ),\beta +\gamma -\alpha )^T$ to $\lambda = \beta -\alpha > 0$ of sign structure $(-,+)^T$ has a second component which is smaller than the negative of the first component, thus the unstable manifold of the DFE points into the probability simplex $\hat{\Sigma }^n$. Further, the Jacobian at the EE

$$\begin{aligned} D\hat{f}\left( \frac{\alpha }{\beta },\frac{\gamma }{\alpha +\gamma }\left( 1 - \frac{\alpha }{\beta }\right) \right) = \begin{pmatrix} - \gamma \frac{\beta +\gamma }{\alpha +\gamma } &{} - (\alpha +\gamma ) \\ \gamma \frac{\beta -\alpha }{\alpha +\gamma } &{} 0 \end{pmatrix} \end{aligned}$$

(19)

has for $R_0 > 1$ a negative trace as well as a positive determinant, i.e., the eigenvalues have negative real parts and thus the EE is asymptotically stable. The EE is a stable focus if $\gamma < 4(\beta -\alpha )(\frac{\alpha +\gamma }{\beta +\gamma })^2$, else it is a stable node. Observe that the linearization (18) at the DFE has for $\gamma =0$ and $\beta =\alpha > 0$ a zero eigenvalue of algebraic multiplicity two and geometric multiplicity one. Therefore, when considered as a two-parameter system on whole $\mathbb {R}^2$, there is a bifurcation not very different from (but also not identical with) a Bogdanov–Takens bifurcation.

3 Linear Compartment Models

Linear compartment models of epidemics model the behavior near an endemic equilibrium. First, let us discuss the case of constant parameters and let us introduce some special names for matrices, which are unfortunately not used completely uniformly in the literature.

Definition 5

A matrix $A = (a_{ij}) \in \mathbb {R}^{n \times n}$ is called

• 1. Z-matrix, if $a_{ij} \le 0$ holds for $i \not = j$,

• 2. Metzler matrix, if $a_{ij} \ge 0$ holds for $i \not = j$, or equivalently $-A$ is a Z-matrix,

• 3. M-matrix, if A is a Z-matrix and additionally $\mathfrak {R}(\lambda ) \ge 0$ holds for every eigenvalue $\lambda$ of A, or equivalently there is a non-negative matrix $B \ge 0$ and a scalar $\alpha \ge \rho (B)$ such that $A = \alpha E - B$.

These terms have to do a lot with non-negative linear flows. In fact, exactly the linear flows generated by Metzler matrices preserve the cone condition $x \ge 0$:

Theorem 2

The non-negative cone $\{x \in \mathbb {R}^n\,|\,x \ge 0\}$ is positively invariant w.r.t. the linear flow generated by $x' = Ax$, iff A is a Metzler matrix.

Proof

On the one hand, if the non-negative cone $\{x \in \mathbb {R}^n\,|\,x \ge 0\}$ is positively invariant w.r.t. the linear flow $\exp (tA)$, then $0 \le e_i^T\exp (tA)e_j = e_i^Te_j + t e_i^TAe_j + O(t^2)$ holds for i, j as $t \searrow 0$. Thus, $0 \le e_i^TAe_j + O(t)$ is valid for $i \not = j$ as $t \searrow 0$, and this implies $a_{ij} = e_i^TAe_j \ge 0$ for $i \not = j$. On the other hand, if A is a Metzler matrix, then there is a scalar $\alpha \in \mathbb {R}$ and a matrix $B \ge 0$ such that $A + \alpha E = B$. Thus, $\exp (tA) = \mathrm {e}^{-\alpha t}\exp (tB)$, where $\exp (tB) \ge 0$, and hence $\exp (tA)x \ge 0$ for all $x \ge 0$. $\square$

The invariance of the affine linear subspace consisting of all vectors whose entries sum up to 1 can be tested via the following criterion.

Theorem 3

The affine linear subspace $\{x \in \mathbb {R}^n\,|\, 1^Tx=1\}$ is invariant w.r.t. the linear flow generated by $x' = Ax$, iff $1^TA = 0$ or equivalently $A^T1=0$, i.e., the vector 1 containing just ones is an eigenvector of $A^T$ to the eigenvalue 0.

Proof

If the flow generated by $x'=Ax$ preserves the condition $1^Tx = 1$, then $0 = \frac{d}{dt} 1 = \frac{d}{dt} 1^Tx = 1^TAx$ for every solution x(t) and thus $1^TA=0$. On the other hand, if $1^TA=0$ holds, then $\frac{d}{dt} 1^Tx = 1^TAx = 0$ so that $1^Tx$ is constant. $\square$

Of particular interest are matrices A, for which the linear flow generated by $x'= Ax$ is non-negative and leaves the subspace $\{x \in \mathbb {R}^n\,|\,1^Tx = 1\}$ invariant, as then the linear flow is a compartment model.

Corollary 1

The probability simplex $\Sigma ^{n-1}:=\{x \in \mathbb {R}^n\,|\,x \ge 0\,,\, 1^Tx = 1\}$ is positively invariant w.r.t. the linear flow generated by $x' = Ax$, iff A is a Metzler matrix with $A^T1 = 0$. In this case, $-A$ is a M-matrix with semi-simple eigenvalue 0. If additionally $A = B - \rho (B) E$ for an irreducible matrix $B \ge 0$, then there is a unique equilibrium in the interior of the simplex, and this equilibrium is globally asymptotically stable.

Proof

The first claim follows from a combination of Theorems 2 and 3. A Metzler matrix A with $A^T1=0$ is automatically an M-matrix, as $x \mapsto 1^Tx$ is due to $1^TA=0$ a Lyapunov function on the non-negative cone $\{x \in \mathbb {R}^n\,|\,x \ge 0\}$, i.e., 0 is a stable equilibrium of $x'=Ax$ on the non-negative cone as underlying space. Thus, all eigenvalues $\lambda$ of A satisfy $\mathfrak {R}(\lambda ) \le 0$, and every eigenvalue with $\mathfrak {R}(\lambda )=0$ is semi-simple. Additionally, the condition $A^T1=0$ implies that A has the eigenvalue 0, too. Other eigenvalues $\lambda \not = 0$ of A with $\mathfrak {R}(\lambda ) = 0$ cannot exist, because due to $A = B - \alpha E$ with $\alpha \ge \rho (B)$ for every eigenvalue $\lambda$ of A with $\mathfrak {R}(\lambda )=0$, there is an eigenvalue $\beta$ of B with $\lambda = \beta - \alpha$, $\mathfrak {R}(\beta ) = \alpha$, and $0 = \mathfrak {R}(\lambda ) = \mathfrak {R}(\beta ) - \alpha \le \rho (B) - \alpha \le 0$ implies $\alpha = \rho (B) = \beta$, i.e., $\lambda =0$. Moreover, if $A = B - \rho (B) E$ holds with an irreducible non-negative matrix $B \ge 0$, then the last statement follows from Frobenius–Perron’s famous theorem, which states that for an irreducible non-negative matrix B the spectral radius $\rho (B) > 0$ is an algebraically (as well as geometrically) simple eigenvalue of B and the only eigenvalue of B with positive eigenvector $x> 0$. Since for $A = B - \alpha E$ the equation $Ax = 0$ is equivalent to $\alpha$ being an eigenvalue of B with eigenvector x, there is exactly one point $x_0>0$ with $Ax_0 = 0$ and $1^Tx_0 = 1$, namely the eigenvector normalized by $1^Tx_0 = 1$ to the eigenvalue $\rho (B)$ of B. Since $-A$ is an M-matrix with a simple eigenvalue 0 and A otherwise has only eigenvalues with negative real part, the asymptotic stability of the equilibrium $x_0$ in the simplex follows. $\square$

Example 2

The matrix $B:=\begin{pmatrix} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \end{pmatrix}$ is non-negative, but not irreducible. It has eigenvalues $-1,0,1$, thus $A := B - E$ is a Metzler matrix with simple eigenvalue 0, and $A^T1=0$ holds. Nonetheless, $x'=Ax$ has no equilibrium in the interior of the simplex $\{x \in \mathbb {R}^n\,|\,x \ge 0\,,\, 1^Tx = 1\}$, because every eigenvector of A to the eigenvalue 0 is a multiple of the boundary point $x_0 = (0,1/2,1/2)^T$ of the simplex. This shows that in the final statement in Corollary 1, the irreducibility of B cannot be waived or replaced by the assumption that 0 is a simple eigenvalue of A.

Example 3

Two-dimensional linear compartment models have the full form

$$\begin{aligned} \begin{pmatrix} S' \\ I' \\ R' \end{pmatrix} = \begin{pmatrix} - \beta &{} \delta &{} \gamma - \zeta \\ \beta - \varepsilon &{} - \alpha &{} \zeta \\ \varepsilon &{} \alpha - \delta &{} - \gamma \end{pmatrix} \begin{pmatrix} S \\ I \\ R \end{pmatrix} \end{aligned}$$

(20)

with constants $\alpha \ge \delta \ge 0$, $\beta \ge \varepsilon \ge 0$, $\gamma \ge \zeta \ge 0$. Here, we do not require (A3), because we consider the system (20) as linearization of a nonlinear system at the endemic equilibrium (EE). Let the transmission rate $\beta$ of S be the maximum of the three constants $\alpha ,\beta ,\gamma$, then the system matrix can be written as $A = B - \beta E$ with the non-negative matrix

$$\begin{aligned} B = \begin{pmatrix} 0 &{} \delta &{} (\gamma - \zeta ) \\ (\beta - \varepsilon ) &{} (\beta - \alpha ) &{} \zeta \\ \varepsilon &{} (\alpha - \delta ) &{} (\beta - \gamma ) \end{pmatrix} \end{aligned}$$

This matrix is irreducible iff $\beta$ is strictly larger than $\alpha ,\gamma > 0$ (even if $\delta =\varepsilon =\zeta =0$).

3.1 Artifacts of Rate-Induced Tipping

Although linear compartment models cannot exhibit true rate-dependent tipping, because by Corollary 1 the unique equilibrium is globally asymptotically stable, some artifacts of rate-induced tipping in nearby nonlinear systems can be observed, as will be explained in more detail in Sect. 5. For example, consider the most simple one-dimensional non-autonomous SIS model

$$\begin{aligned} \begin{aligned} S' =&- \beta (rt)S + \delta I\\ I' =&\beta (rt)S - \delta I \end{aligned} \end{aligned}$$

(21)

with a time-dependent transmission rate $\beta (rt) \ge 0$ of rate r and constant rate $\delta > 0$. The ODE (21) can be viewed as model of a disease, where susceptibles get ill without any contacts to infectious, and where there is no immunity. The reduced ODE reads as $\dot{S}(t) = -(\beta (rt)+\alpha )S(t) + \alpha$. If $\beta (t)$ connects $\beta _-$ and $\beta _+$ with $\beta _- > \beta _+$ monotonely decreasing, then it depends on the rate r, whether the solution $S(t) = \left( S_0 + \int _{0}^t \exp (B(rs)/r+\alpha s) \alpha \,ds\right) \exp (-B(rt)/r-\alpha t)$, $B(t):=\int _{0}^t \beta (s)\,ds$, to the initial value $S(0) = S_0 \in [0,1]$ has a local minimizer or not. For $r \rightarrow 0$, the solution tends to $\frac{\alpha }{\beta _- + \alpha } + (S_0 - \frac{\alpha }{\beta _- + \alpha }) \exp (-(\beta _- + \alpha ) t))$ and thus is monotone decreasing for $S_0 > \frac{\alpha }{\beta _- + \alpha }$, while for $r \rightarrow \infty$ it tends to the same function with $\beta _-$ replaced by $\beta _+$. Therefore, there is a threshold $r_c$, i.e., a critical rate, such that for rates $r<r_c$ there is a kind of overshooting when approaching the longtime equilibrium $\frac{\alpha }{\beta _- + \alpha }$, while for rates $r>r_c$ the solution does not show overshooting; see Fig. 2.

Fig. 2

Solution S in blue, I in red, of (21) to the initial value $(S_0,I_0)=(0.95,0.05)^T$ for $\beta (rt) = (2-\tanh (rt))$ decreasing from the value 2 at $t=0$ to a value near $\alpha :=1$ approaches the equilibrium $(S,I) = (\frac{1}{2},\frac{1}{2})$ for the fast rate $r=2$ on the left directly, while for the slow rate $r=1$ on the right there is a kind of overshooting. The critical rate lies between $r=1.9$ and $r=2$

4 Nonlinear Compartment Models

In this section, we consider autonomous nonlinear compartment models $\dot{x} = f(x)$ of epidemics on the probability simplex $\Sigma ^n$ and discuss the situation, where the asymptotically stable disease-free equilibrium (DFE) becomes unstable due to a local bifurcation. Note that the DFE does not lie in the interior but at a boundary vertex of the simplex $\Sigma ^n$. As our knowledge about boundary equilibrium bifurcations is still a little patchy, the bifurcation theory of the DFE is not completely standard. Here we are mainly interested in a bifurcation of codimension two. In this case, by center manifold reduction we can consider the equation induced by $\dot{x} = f(x)$ on the two-dimensional center manifold, and this equation determines the dynamics of the full n-dimensional compartment model near the bifurcation point. However, center manifold reduction requires that f is sufficiently smooth, but as the DFE lies at a boundary vertex, the vector field f can be smooth in the interior but merely continuous up to the boundary. Then terms occur, which due to missing differentiability cannot be obtained by linearization, and we use such terms to obtain idealized models where after a transcritical bifurcation of the DFE the arising endemic equilibrium (EE) is surrounded by a homoclinic orbit (HO), see Fig. 3, or there is at least a trajectory from the boundary to the DFE such that the EE does not attract the whole interior of the simplex.

Fig. 3

On the left, the DFE is a stable node on a boundary vertex of the simplex, while the EE is an unstable saddle outside the simplex. On the right, the EE has entered the simplex through the boundary vertex and has become a stable focus, while the DFE lost its stability and has become an unstable saddle. Additionally, the unstable manifold of the DFE runs into the stable manifold and forms a homoclinic orbit HO surrounding the EE

4.1 Local Normal Form for a Bifurcation of Codimension Two

Under the assumption that f is sufficiently smooth near the DFE, let us derive a normal form for the planar system on the two-dimensional center manifold of a compartment model $\dot{x}=f(x)$ of epidemics. If a two-parameter family of autonomous vector fields $\hat{f}(S,I)$ on $\hat{\Sigma }^2$ satisfying (A1)’,(A2)’,(A3)’ has a local bifurcation at the DFE $(S,I)=(1,0)$, then generically the linearization $A:=D\hat{f}(1,0)$ has a zero eigenvalue of algebraic multiplicity two, but geometric multiplicity one. Let $q_0$ be an eigenvector to the zero eigenvalue, i.e., $Aq_0 = 0$, and let $q_1$ be a corresponding generalized eigenvector, i.e., $Aq_1 = q_0$. Via a change of coordinates to

$$\begin{aligned} \begin{pmatrix} S-1 \\ I \end{pmatrix} = x q_0 + y q_1 \,, \end{aligned}$$

the Taylor expansion $T_2\hat{f}$ of second order of $\hat{f}$ around $(S,I)=(1,0)$ reads as

$$\begin{aligned} \begin{aligned} T_2\hat{f}(S,I)&= \hat{f}(1,0) + A\begin{pmatrix} S-1 \\ I \end{pmatrix} + \frac{1}{2} B\left( \begin{pmatrix} S-1 \\ I \end{pmatrix},\begin{pmatrix} S-1 \\ I \end{pmatrix}\right) \\&= y q_0 + \frac{1}{2}x^2 B(q_0,q_0) + xy B(q_0,q_1) + \frac{1}{2}y^2 B(q_1,q_1) \end{aligned} \end{aligned}$$

with the second derivative $B:=D^2\hat{f}(1,0)$. Using an eigenvector $p_1$ of $A^T$ to the zero eigenvalue and a corresponding generalized eigenvector $p_0$ with $A^Tp_0=p_1$ as dual basis vectors satisfying $\langle p_0,q_1 \rangle = 0 = \langle p_1,q_0 \rangle$ and $\langle p_0,q_0 \rangle = 1 = \langle p_1,q_1 \rangle$, we obtain due to (A3)’, which excludes constant terms, under the genericity conditions

$$\begin{aligned} \begin{aligned} \langle p_1,B(q_0,q_1) \rangle \not = 0 \,,\qquad \frac{1}{2}\langle p_1,B(q_1,q_1) \rangle \not = 0 \,, \end{aligned} \end{aligned}$$

(22)

similar as in Bogdanov–Takens bifurcation the normal form

$$\begin{aligned} \begin{aligned} x'&= \langle p_0,x'q_0+y'q_1 \rangle = - \beta _1 x + y \\ y'&= \langle p_1,x'q_0+y'q_1 \rangle = \beta _2 y - xy - y^2 \end{aligned} \end{aligned}$$

(23)

with parameters $\beta _1$, $\beta _2$ vanishing at the bifurcation. Beneath (0, 0), there is a second equilibrium $(\frac{\beta _2}{1+\beta _1}, \frac{\beta _1\beta _2}{1+\beta _1})$ in $\hat{\Sigma }^2$ for $\beta _1 \ge 0$, $\beta _2 > 0$. This normal form differs from Bogdanov–Takens normal form

$$\begin{aligned} \begin{aligned} x'&= y \\ y'&= - \beta _1 + \beta _2 x - x^2 - xy \end{aligned} \end{aligned}$$

(24)

mainly in that A is perturbed in the Bogdanov–Takens case to $\begin{pmatrix} 0 &{} 1 \\ \beta _2 &{} 0 \end{pmatrix}$, and the equilibrium (0, 0) is split up into the two equilibria $(\frac{\beta _2}{2} \pm \frac{1}{2}\sqrt{\beta _2^2 - 4\beta _1},0)$ for $\beta _2^2 \ge 4\beta _1$, while our normal form (23) perturbs A to $\begin{pmatrix} -\beta _1 &{} 1 \\ 0 &{} \beta _2 \end{pmatrix}$ and leaves—as required by (A3)’—the DFE fixed. A coordinate transform of x, y, t and a substitution of the parameters in (23) leads to

$$\begin{aligned} \begin{aligned} x'&= - \gamma x + \alpha y \\ y'&= (\beta - \alpha - \delta - \beta x - \beta y)y \,, \end{aligned} \end{aligned}$$

(25)

where the bifurcation happens at parameters $\gamma = 0$ resp. $\delta = \beta -\alpha$. Particularly, if $A = \begin{pmatrix} 0 &{} -1 \\ 0 &{} 0 \end{pmatrix}$ and correspondingly $q_0 = (-1,0)^T$, $q_1 = (-1,1)$, then $x = 1-S-I = R$ and $y=I$ so that in the coordinates (S, I) the reduced normal form is given by

$$\begin{aligned} \begin{aligned} S'&= - \beta SI + \delta I + \gamma (1-S-I) \\ I'&= (\beta S - \alpha - \delta )I \,, \end{aligned} \end{aligned}$$

(26)

where additionally after an infection there may be partially no immunity due to $\delta >0$. This normal form is a combination of SIRS and SIS models, wherein the SIS model $\alpha =0$, $\gamma =0$ so that all infectious become after the infect directly again susceptible. The Jacobian of the right-hand side of (26) is

$$\begin{aligned} D\hat{f}(S,I) = \begin{pmatrix} -\beta I -\gamma &{} \delta - \beta S - \gamma \\ \beta I &{} \beta S - \alpha - \delta \end{pmatrix} \,, \end{aligned}$$

(27)

and for $\gamma > 0$ the DFE is asymptotically stable if $R_0 := \frac{\beta }{\alpha +\delta } < 1$ resp. unstable if $R_0 > 1$. In the case $R_0 > 1$, the EE has the coordinates $(\frac{\alpha +\delta }{\beta },\frac{\gamma }{\alpha +\gamma }(1 - \frac{\alpha +\delta }{\beta }))$, and it is a stable focus for small $\gamma >0$ resp. a stable node for large $\gamma >0$.

Fig. 4

On the left, the homoclinic orbit arising in (24) for $\beta _2=1$, $\beta _1 \approx -\frac{6}{25}\beta _2^2$, after a Bogdanov–Takens bifurcation. On the right, the homoclinic orbit occurring in (28). Note that trajectories outside but near to the homoclinic orbit miss the equilibrium and tend to infinity, while in our idealized model due to invariance of the axes they tend to the DFE

Yet, while in Bogdanov–Takens bifurcation a homoclinic orbit arises around the stable equilibrium for a rather specifically chosen combination of the two bifurcation parameters, see Fig. 4, this does not seem to be the case for (26) and parameters $\beta > \alpha + \delta$, $\alpha ,\gamma ,\delta \ge 0$. In the following subsection, we indicate how to construct compartment models of epidemics with this idealized behavior.

4.2 Idealized Models

In this subsection, we aim to construct an idealized system, where after a transcritical bifurcation of the DFE, the arising EE is surrounded by a homoclinic orbit HO; see Fig. 3. Although the HO may be deformed or may vanish for a slight perturbation of the two parameters, see Fig. 5, such idealized models will help us to explain tipping phenomena in compartment models of epidemics in Sect. 5. To obtain an idealized model with this behavior, we add non-smooth terms to the normal forms (25) resp. (26). Note that already the standard example of a system with a homoclinic orbit

$$\begin{aligned} \begin{aligned} x'&= - x + xy + (y-x)\sqrt{x^2 + y^2} \\ y'&= - y - x^2 + (x+y)\sqrt{x^2 + y^2} \end{aligned} \end{aligned}$$

(28)

contains the non-smooth term $\sqrt{x^2 + y^2}$. In polar coordinates, this system (28) reads as

$$\begin{aligned} \begin{aligned} r' = -r(1-r) \\ \varphi ' = r(\cos (\varphi )-1) \end{aligned} \end{aligned}$$

(29)

and obviously has the circle $r=1$ as invariant set, which consists of a homoclinic orbit and the equilibrium at $r=1$, $\varphi =0$, see Fig. 4.

Fig. 5

On the left, compared to the right picture in Fig. 3 the EE has moved and the HO is a little deformed. On the right, it is shown that the HO vanishes for slight perturbations. Yet, due to the trajectory connecting the boundary with the DFE, the EE still is merely locally and not globally asymptotically stable

Fig. 6

On the left, for $\alpha :=1$, $\beta :=1.5$, $\gamma :=0.1$ and $\delta :=0$, the EE and the surrounding HO in (30) are shown. On the right, for $\alpha :=0.5$, $\beta :=1$ and $\gamma :=0.1$ and $\delta :=0$, the EE and the surrounding HO in (31) are shown

Similarly, if we add the term $\varepsilon -\frac{x-y}{(x^2+y^2)^{1/2}}y$ to the right-hand side of the second equation in (25) for $\varepsilon :=\frac{\alpha -\gamma }{(\alpha ^2+\gamma ^2)^{1/2}}$ chosen such that the term vanishes at the line where the first equation vanishes, i.e., for a rather specific combination of parameters, then the system

$$\begin{aligned} \begin{aligned} x'&= - \gamma x + \alpha y \\ y'&= \left( \beta - \alpha - \delta - \beta x - \beta y + \varepsilon - \frac{x-y}{(x^2+y^2)^{1/2}}\right) y \,, \end{aligned} \end{aligned}$$

(30)

seems to have a HO at the DFE; see Fig. 6 on the left. Note that $\frac{x-y}{(x^2+y^2)^{1/2}}y$ is continuous due to $|\frac{x-y}{(x^2+y^2)^{1/2}}y| \le |x-y|$. Yet, a disadvantage of this system is that trajectories starting far away from the HO may leave the simplex $\hat{\Sigma }^2$, but of course the vector field can be modified so that the simplex is positively invariant while the dynamics near the HO is not changed. Another example is the modification

$$\begin{aligned} \begin{aligned} S'&= - \beta SI + \gamma (1-S-I) \\ I'&= \left( \beta S - \alpha \left( 2 + \tanh \left( \frac{1-x}{2y}-5\right) \right) \right) I \,, \end{aligned} \end{aligned}$$

(31)

of (26) with $\delta :=0$, i.e., a modified SIRS system. Again, the term $\tanh (\frac{1-x}{2y}-5)$ is smooth in the interior and continuous up to the boundary, as it tends to 1 for $(x,y) \rightarrow (x_0,0)$ approaching the boundary. The HO and EE are given in Fig. 6 on the right. Yet, there seems to be an additional small instable periodic orbit around the EE, and again the system needs to be modified far away from the DFE.

5 Irreducible Rate-Induced Tipping in Non-autonomous Models

Regardless, whether there is a homoclinic orbit (HO) surrounding the endemic equilibrium (EE) after a transcritical bifurcation at the disease-free equilibrium (DFE) like in the idealized system on the left of Fig. 5, or whether there is an orbit connecting the boundary $R=1-S-I=1$ with the DFE like in Fig. 5 on the right, if there are two different basins of attraction, one of the EE and one of the DFE, then irreducible rate-induced tipping may occur for time-dependent parameters. Hereby, starting with the pullback attractor $A(t_0)$ near the EE, if the parameters evolve so that the homoclinic orbit shrinks fast while the dynamics near A(t) are slow, it may happen that A(t) leaves the basin of attraction of the EE and enters the basin of attraction of the DFE; see Fig. 7. Then the disease will die out, while for a slower rate A(t) would have tracked the EE and the disease would have stayed endemic. The critical rate for which A(t) leaves the basin of attraction of the EE is a threshold for the occurrence of rate-induced tipping.

Fig. 7

On the left, the pullback attractor A lies near to the EE, but then the parameters are changed fast while the dynamics near A is slow. Therefore, the pullback attractor leaves the basin of attraction of the EE, which in the middle is the interior of the HO and on the right is separated by a trajectory from the boundary to the DFE. As A has entered the basin of attraction of the DFE marked in green, the disease will die out, while for a slow rate of parameter change the pullback attractor would have tracked the EE and the disease would have become endemic

Of course, in application, it is necessary to estimate the time-dependent parameters from data. But this is not so difficult, e.g., in the SIR model (11) with time dependent $\beta =\beta (t)$ and $\alpha =\alpha (t)$, for S near 1 and small h as in [5] the parameters can be estimated by

$$\begin{aligned} \begin{aligned} \alpha (t)&\approx \frac{R(t+h) - R(t)}{hI(t)} \\ \beta (t)&\approx \frac{(I(t+h) - I(t)) + (R(t+h) - R(t))}{hI(t)} \end{aligned} \end{aligned}$$

(32)

from time series for I(t), R(t), due to $\alpha = R'/I$ and $\beta = (I+R)'/SI$.

5.1 Artifacts of Rate-Induced Tipping

Many compartment models in epidemics are not idealized, i.e., the DFE with its unstable manifold does not have a basin of attraction intersecting the interior of the simplex $\Sigma$. But even in the case, where the whole interior of the simplex belongs to the basin of attraction of the EE, artifacts of rate-induced tipping in nearby idealized systems can be seen. For example, instead of the SIRS model (15), consider

$$\begin{aligned} \begin{aligned} S'&= -\beta (t)SI + \gamma R\\ I'&= \beta (t)S - \alpha I \\ R'&= \alpha I \end{aligned} \end{aligned}$$

(33)

with a time-dependent transmission rate $\beta =\beta (t) := 1 - \frac{1}{3}\tanh (rt)$ and constant $\alpha =1/2$, $\gamma =1/10$, i.e., $\beta (t)$ decreases from 1 at $t=0$ to 2/3 at time $t \rightarrow \infty$. Then Fig. 8 shows an artifact of rate-induced tipping in a nearby idealized systems where the red curve tends to the DFE.

Fig. 8

For the slow rate $r=0.05$, the blue solution curve (33) tracks the EE of the frozen system rather well, while for the higher rate $r=0.1$ along the red curve, there is a reduced percentage of infectious in the middle part, and this can be considered as artifact of rate-induced tipping in a system where the red curve tends to the DFE. However, in (33), the EE attracts the whole interior of the simplex, and this enforces an additional turn at the end, i.e., a second wave with a little higher percentage of infectious than for the blue curve

6 Conclusion

We identified a mechanism which allows to have rate-induced tipping in idealized compartment models of epidemics with $R_0>1$, where not only the endemic equilibrium (EE) but also the disease-free equilibrium (DFE) has a basin of attraction intersecting the interior of the probability simplex. Moreover, even in the case that the compartment model is not idealized and the EE attracts every point in the interior of the simplex, we showed that artifacts of nearby idealized compartment models can be observed. Thus, in models it can happen that in two countries the same kind of lockdown measures is decided at the same time, corresponding to the same initial and final values of a parameter path at the same times, but that the measures are established by different rates so that the disease becomes endemic in a country where the measures are slowly established (or there is at least a high number of infectious), while in a country where the measures are established fast the disease is eradicated (or there is at least a lower number of infectious).

Yet, there are various open research questions: Is there an idealized compartment model of epidemics with polynomial right-hand side? How to determine the critical rate, i.e., the threshold for the rate below which a rate-induced tipping happens in idealized compartment models? Can (4) help to determine this threshold? Can we obtain quantitative and not only qualitative results for non-idealized systems? Maybe an answer to these questions can help us to better handle a pandemic disease like Covid-19 in future.